Context-Aware Local Optimization of Sensor Network Deployment
Abstract
:1. Introduction
2. Optimization Algorithms for Sensor Network Deployment
3. Context and Context-Awareness for Sensor Networks Deployment
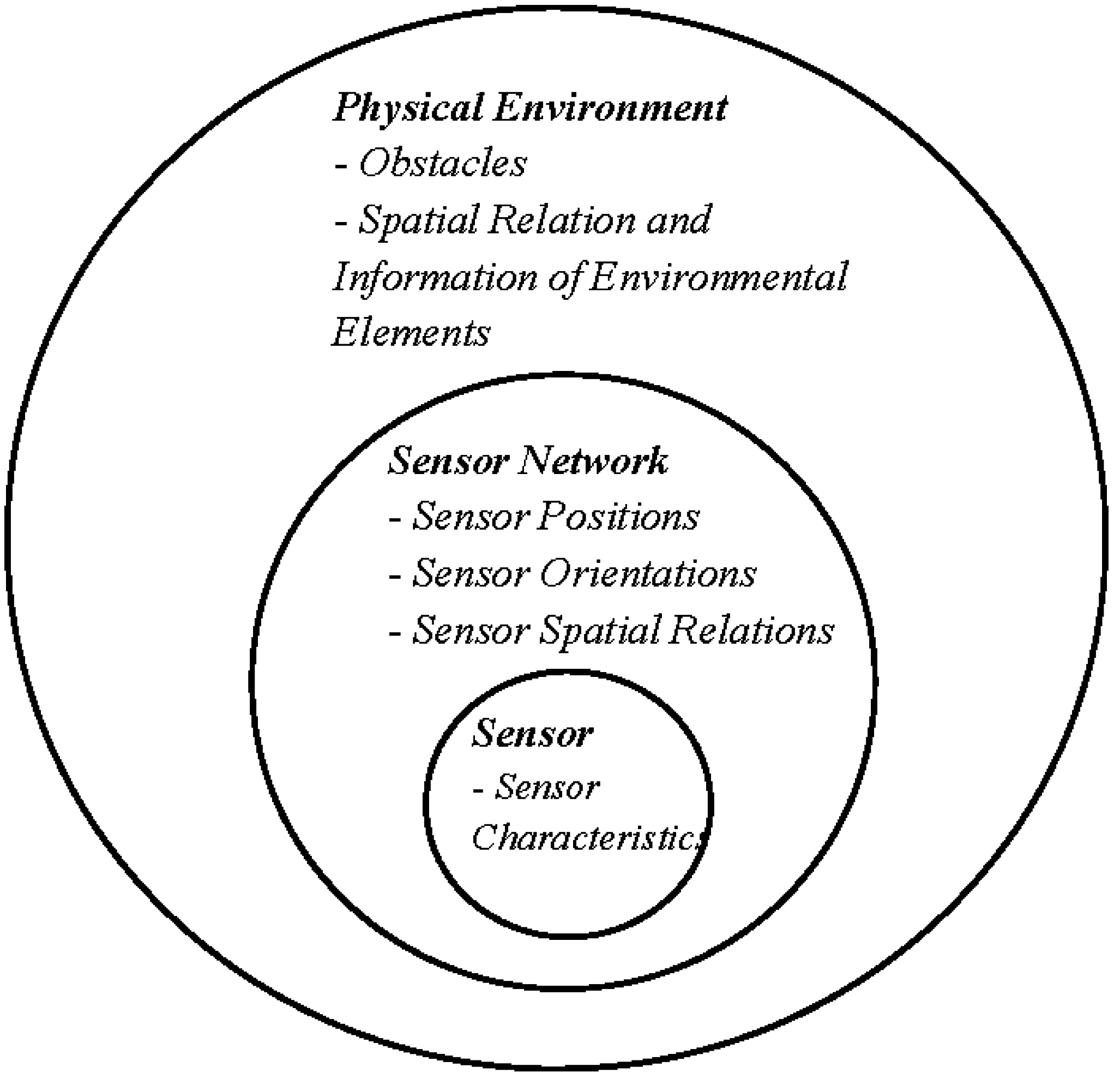
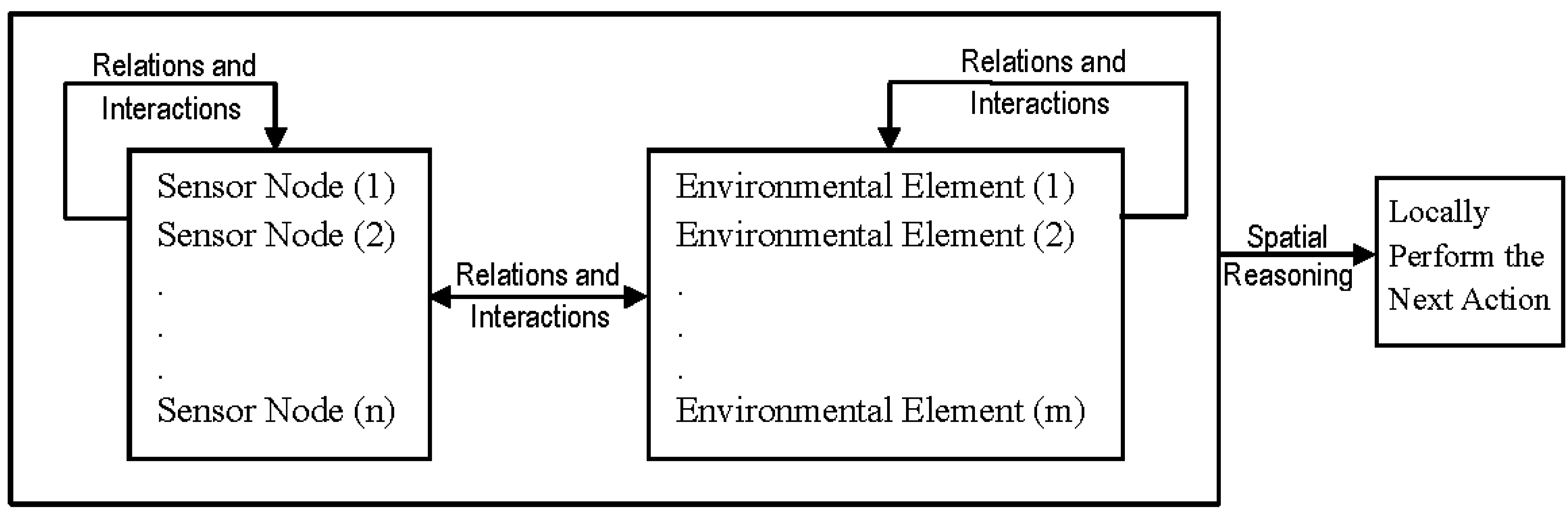
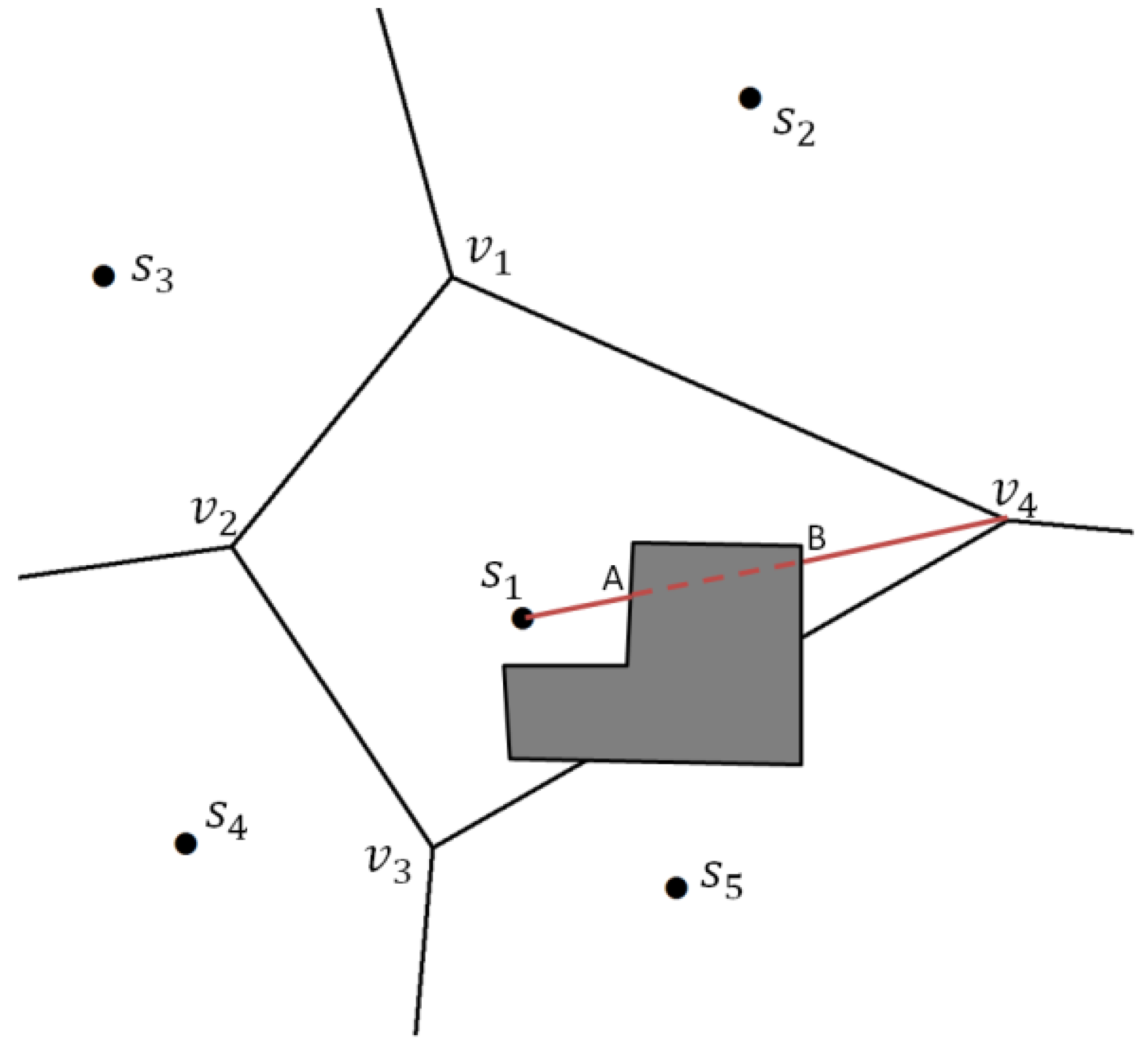
4. A Conceptual Framework for Sensor Network Deployment Using Voronoi Diagram and Contextual Information
- -
- Spatial contextual information refers to the ability of defining objects positions, and geometric relations. Spatial CI is not only about 2D or 3D position of sensors. A comprehensive framework of spatial contextual information may include sensors orientation, movement, routing, targeting, topology, and spatial dependencies and interactions. Hence, all information of spatial relations, interactions, proximity, and adjacency lie in this category.
- -
- Temporal contextual information concerns the temporal information, and the temporal dependencies in data. Temporal information characterizes the dependency of a situation in the sensor network framework with the time, and also indicates an instant or period during which some other CI is known or relevant. The objects and activities in the physical environment may change. For instance, position or attributes of an obstacle (e.g., its height) may change during a given period of time. A specific example of temporal CI is the information of a sensor movement and its trajectory in the network. Previous actions and movements of a sensor node may provide useful information for the next actions of current sensor or its neighbors.
- -
- Thematic contextual information in sensor networks constitutes the sensor specifications, network objectives, environment specifics, legal rules, etc. The information regarding the nodes names and roles, and their activity in the network is included in this category. Sensors activities may include measurements of the temperature, humidity, sound, or light. In terms of deployment, the type of sensor movement and its trajectory could be the sensor activity inside the network. Node name should be unique in the network in order to make it possible to be recognized and devolve its roles in multi task networks. Sensor characteristics are sensor specifications, which have been designed during their manufacturing, e.g., their power supply, battery life, sensing range, temperature resistance, dimensions, input and output terminals, processing power, data storage capacity, send and receive information protocols. Network objective expresses the mission of sensor networks to be fulfilled. This objective could be various in multi task networks. It may be varied from covering a whole, or a part of study area to monitor a phenomenon, or sensing different characteristics of the environment. Legal rules define specified terms and conditions for constructing and deploying the sensor networks, e.g., in which locations sensor deployment is allowed, or which parameters are permissible to be measured.
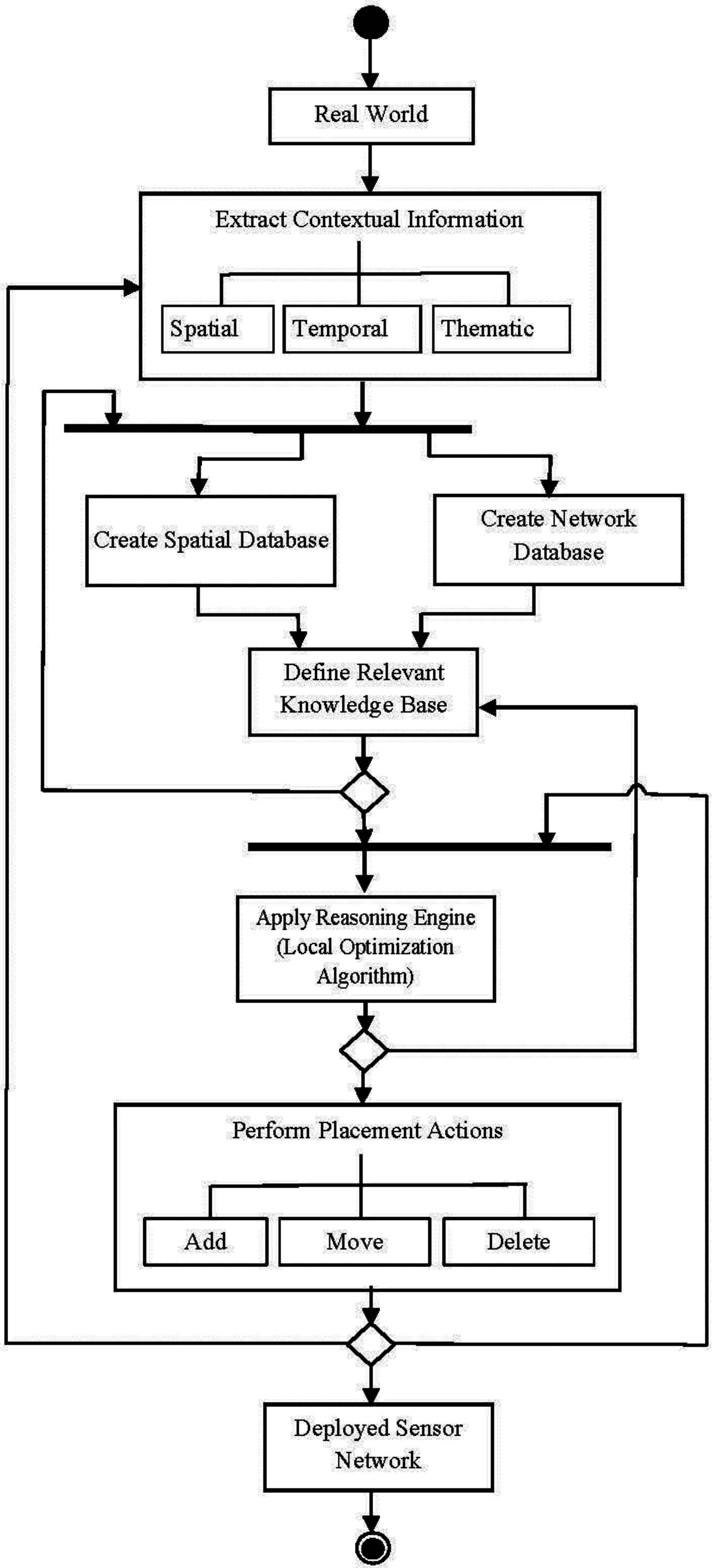
5. Implemented Local Context-Aware Optimization Method for Sensor Placement
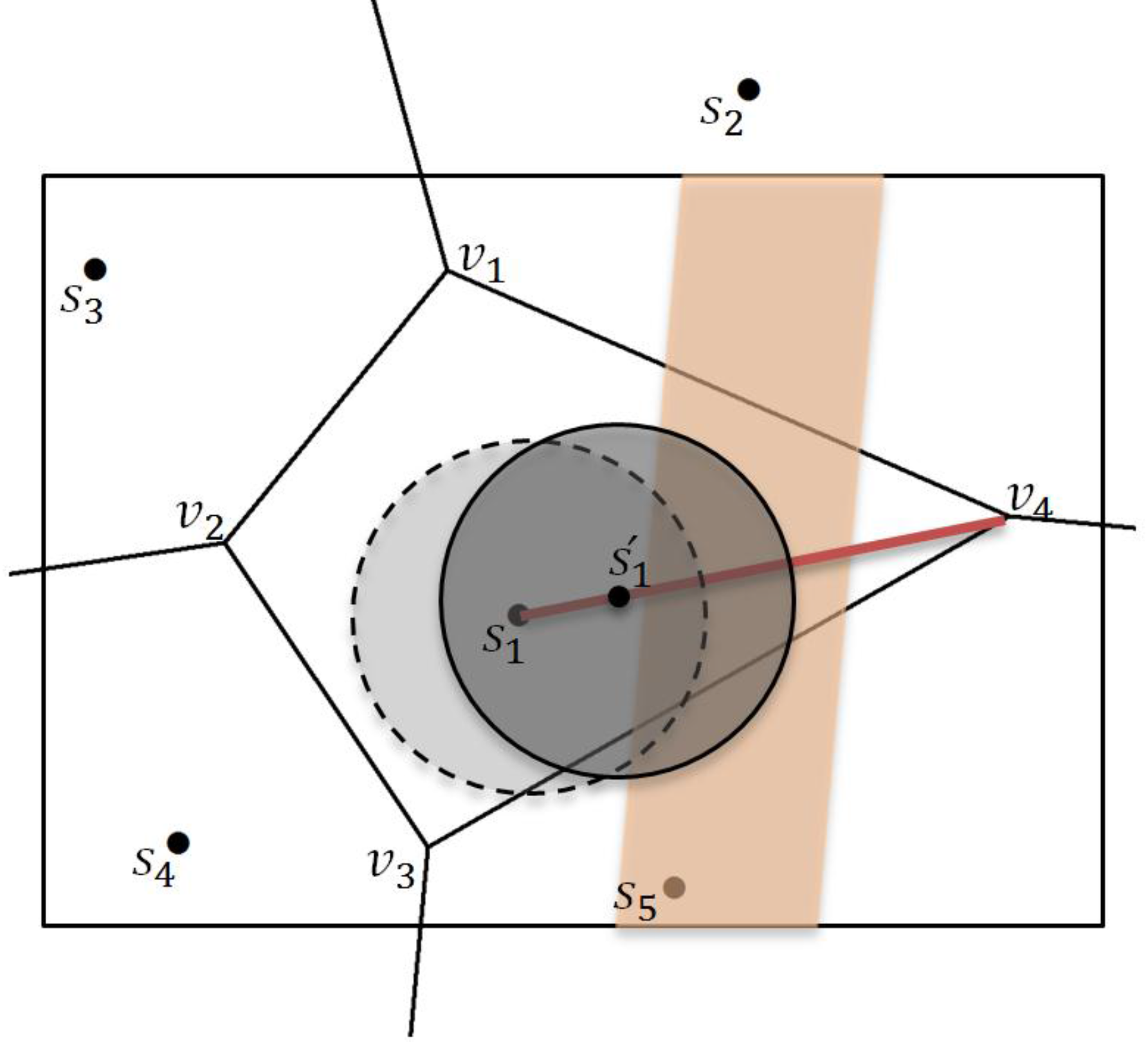
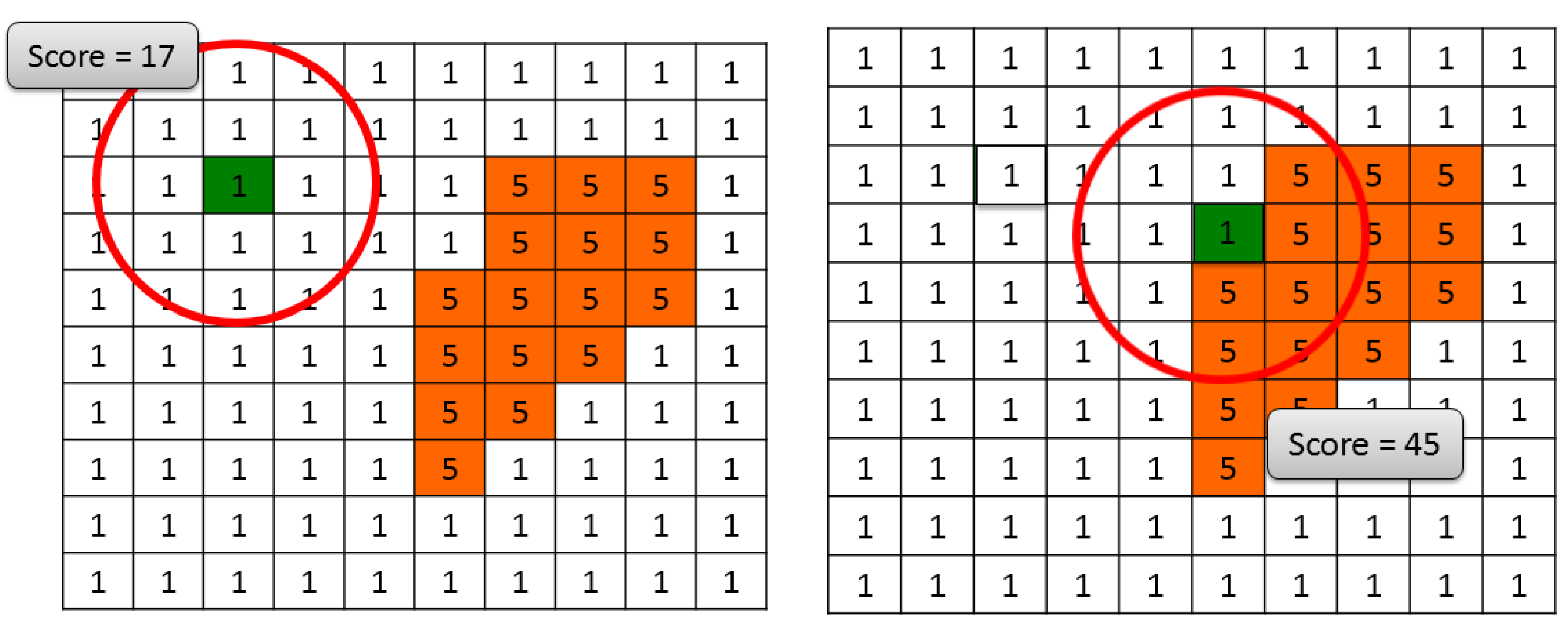
5.1. Formal Presentation of the Local Context-Aware Algorithm

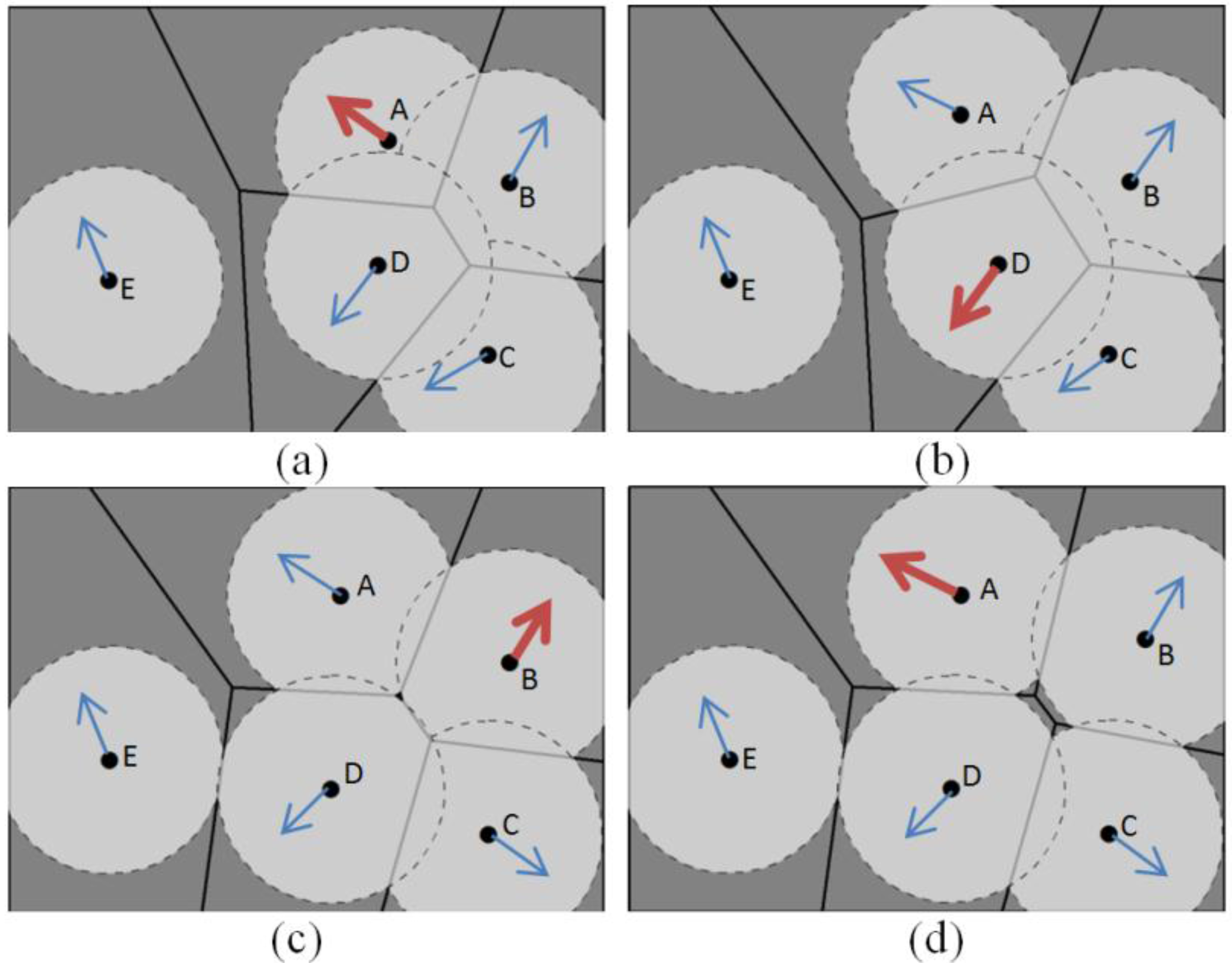
5.2. Strategies for Sensor Movement in the Proposed Local Optimization Algorithm
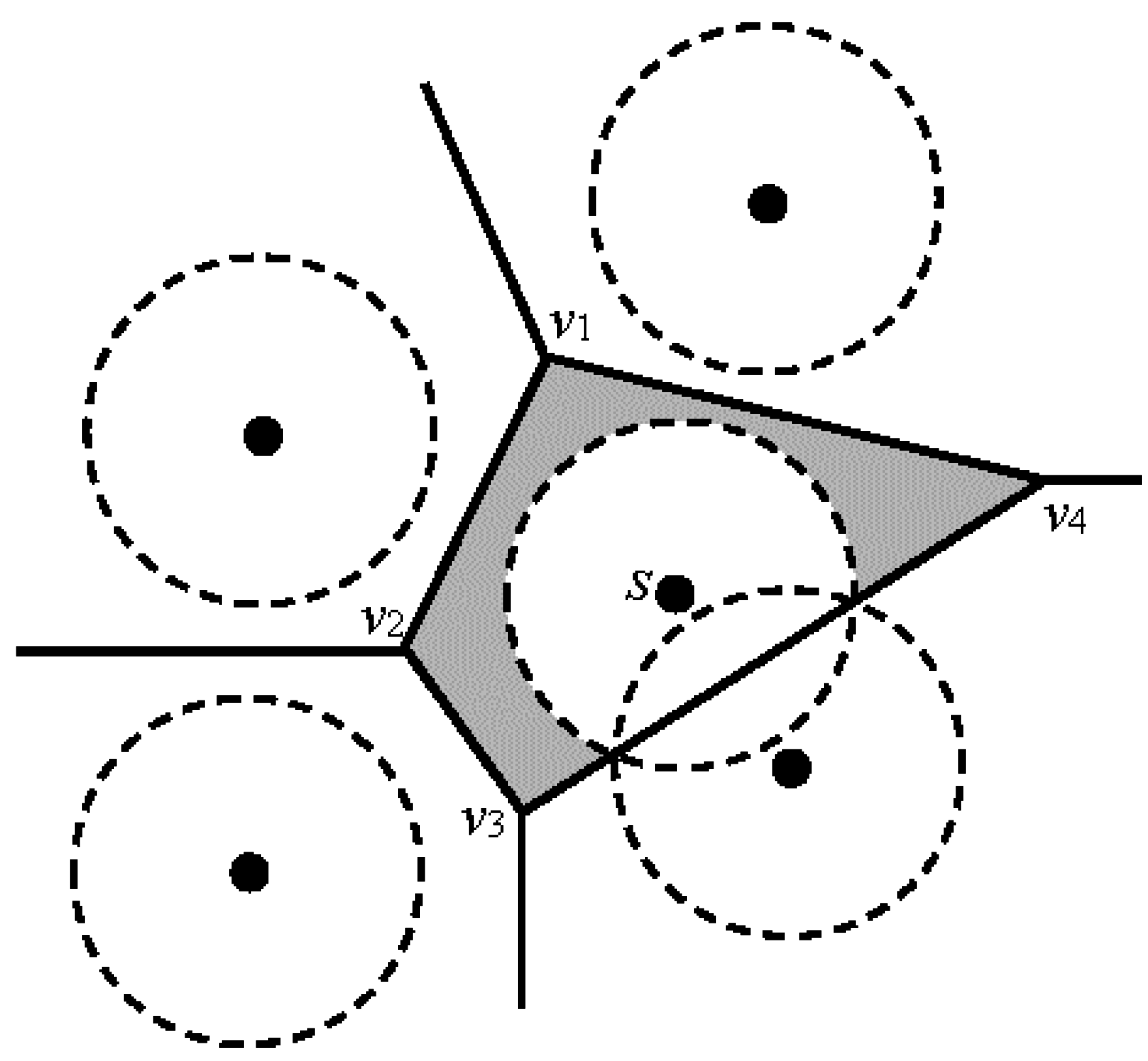
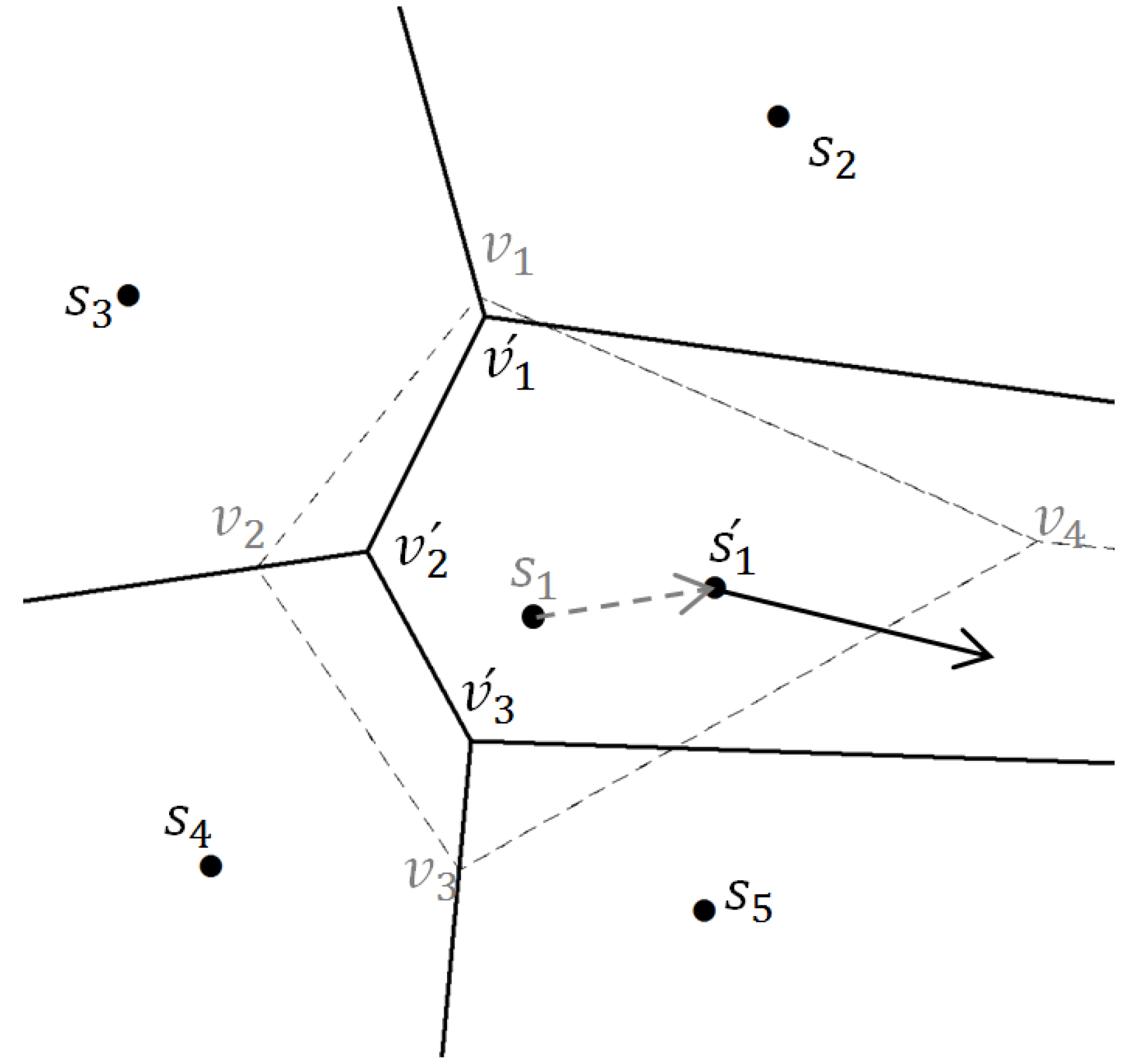
5.3. Strategies for CI Integration in the Proposed Local Optimization Algorithm
6. Different Case Studies for Evaluation of the Proposed Local Context-Aware Sensor Network Deployment Optimization Algorithm

- -
- Spatial positions of environmental elements and obstacles are known,
- -
- Digital Surface Model (DSM) of the environment is provided,
- -
- For each sensor, visible and invisible areas are recognized by calculation of line-of-sight and viewshed,
- -
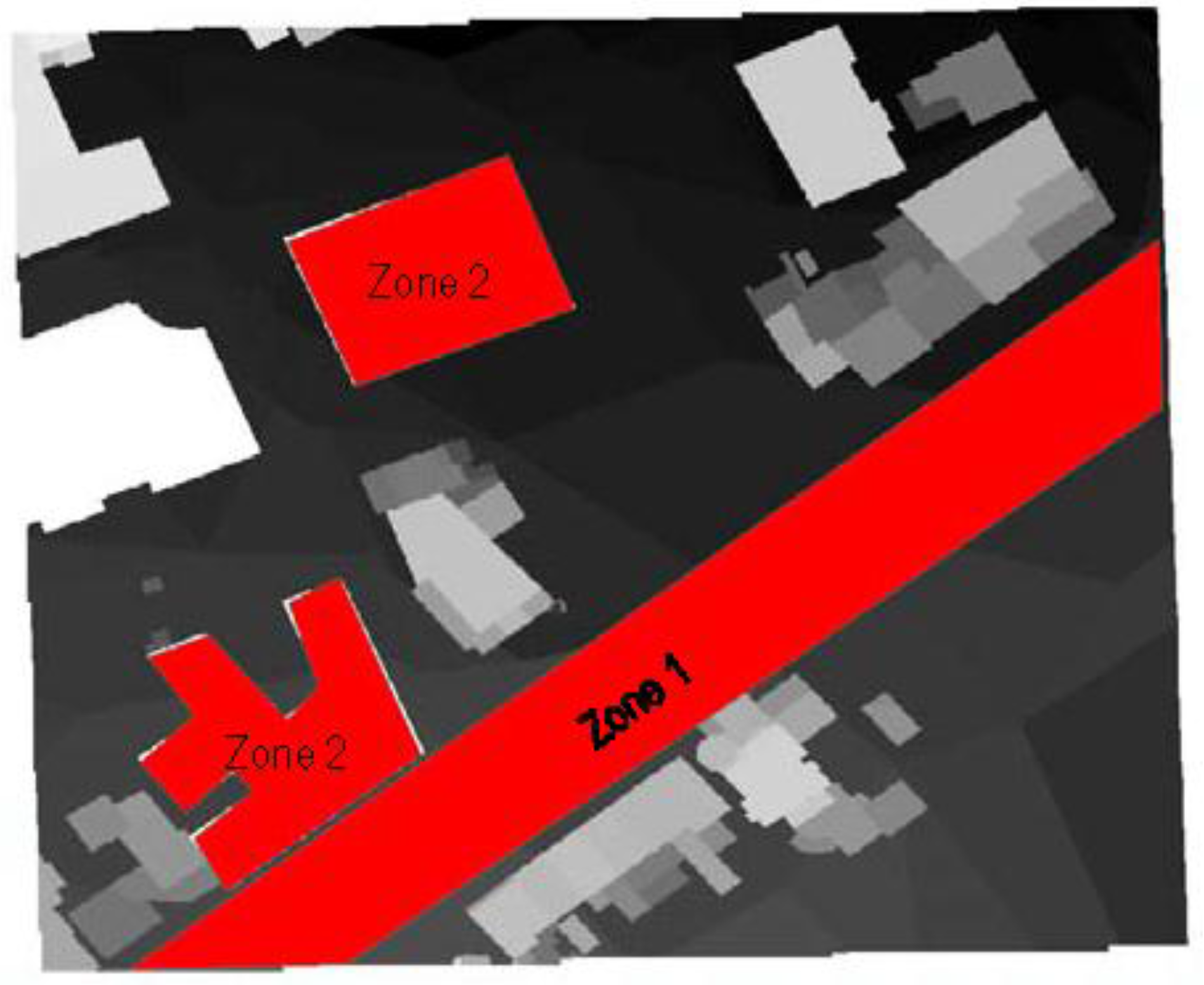
- Some restricted zones for sensor installation exist in the study area,
- -
- There is a zone with high desirability of coverage, with prohibition for sensor installation,
- -
- There is a zone with low level of activity, and high desirability of coverage. This zone is located close to a zone with high level of activity but low desirability of coverage. In both zones sensor installation is forbidden.

6.1. Optimization Considering the Obstacles and Surface Model as CI
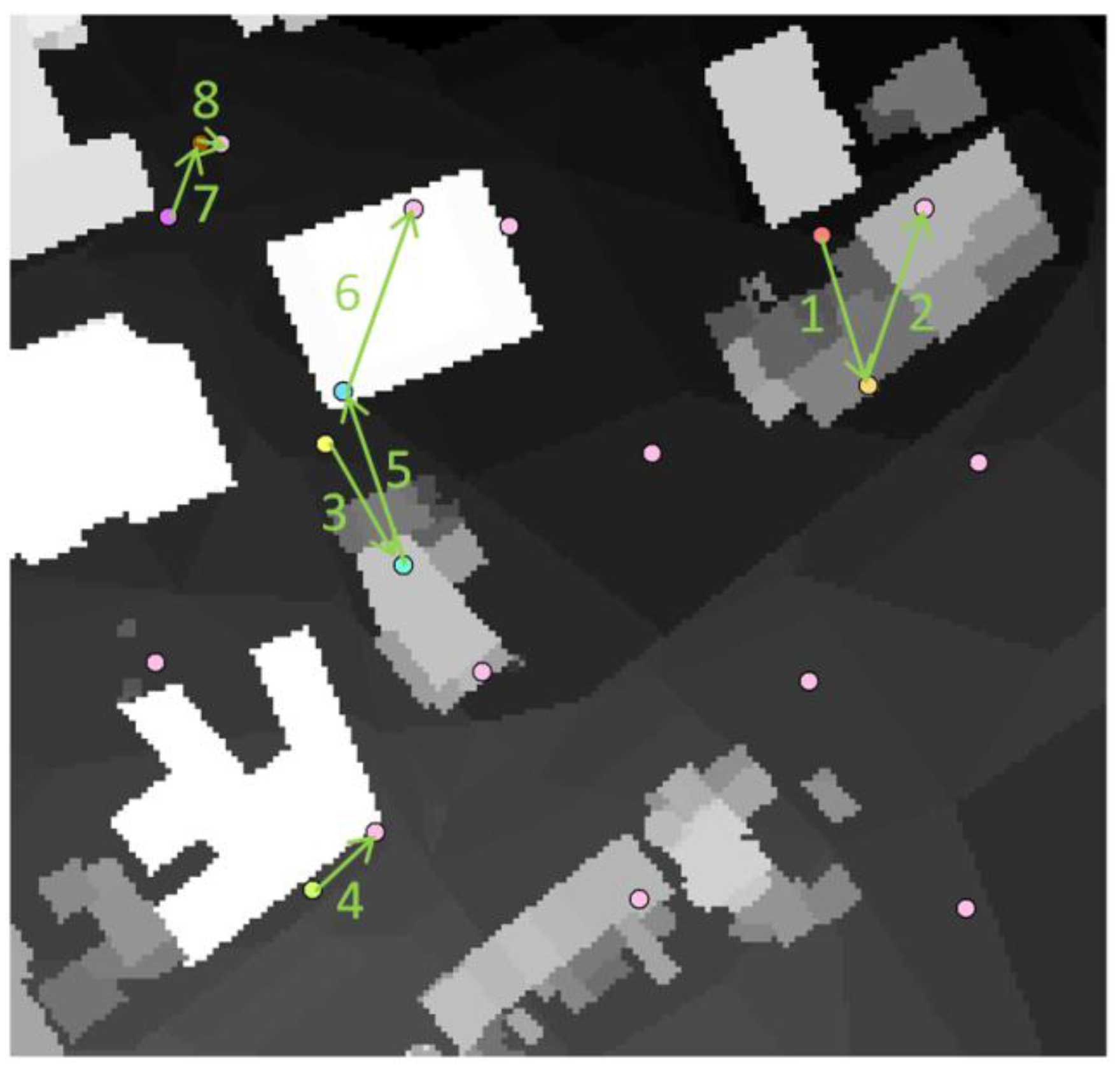
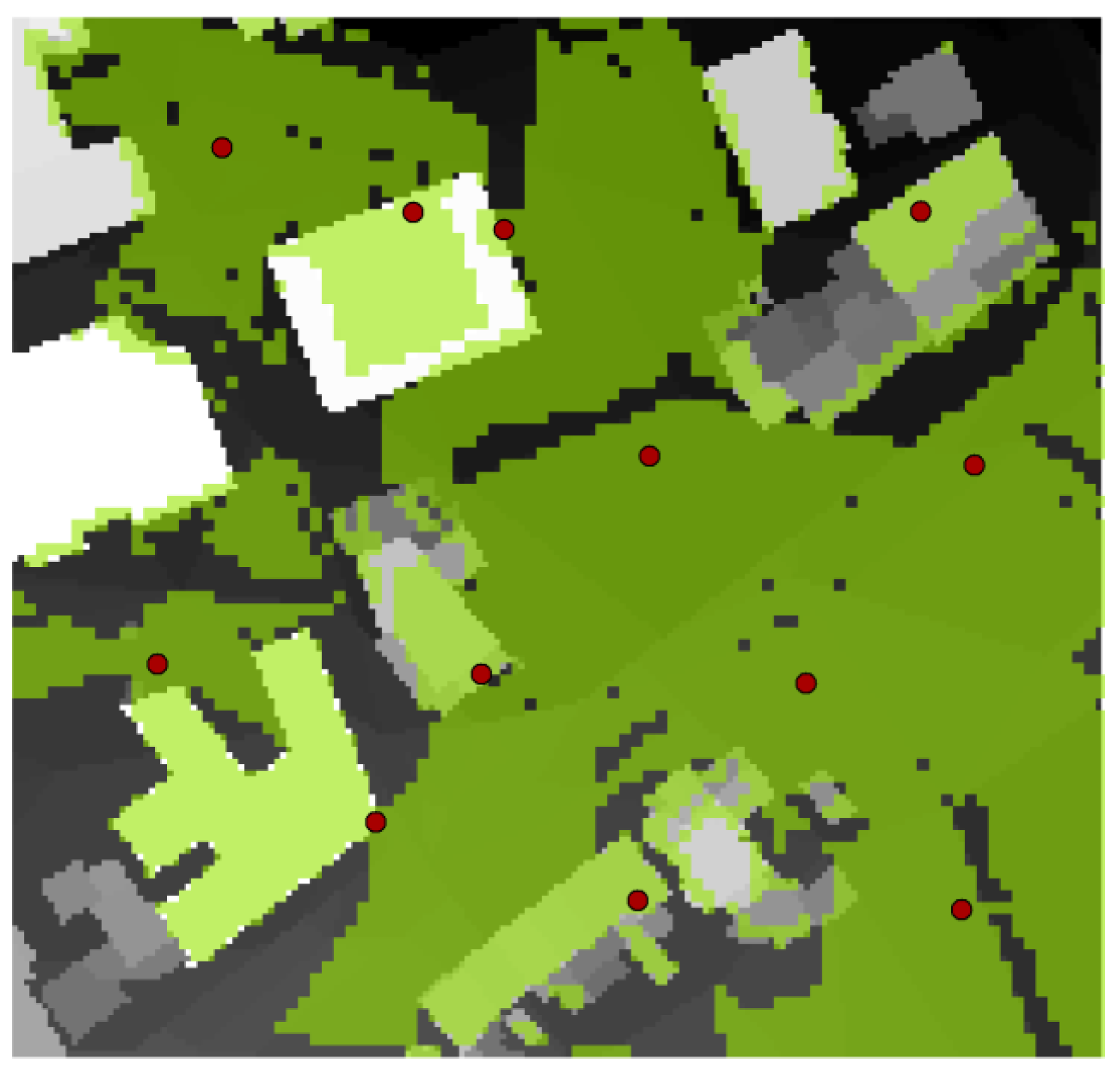
| Method | Avg. Coverage (%) | Best Coverage (%) |
|---|---|---|
| Context-Aware | 51.17 | 52.83 |
| CMA-ES | 49.09 | 51.33 |
6.2. Optimization Considering the Restricted Area as CI

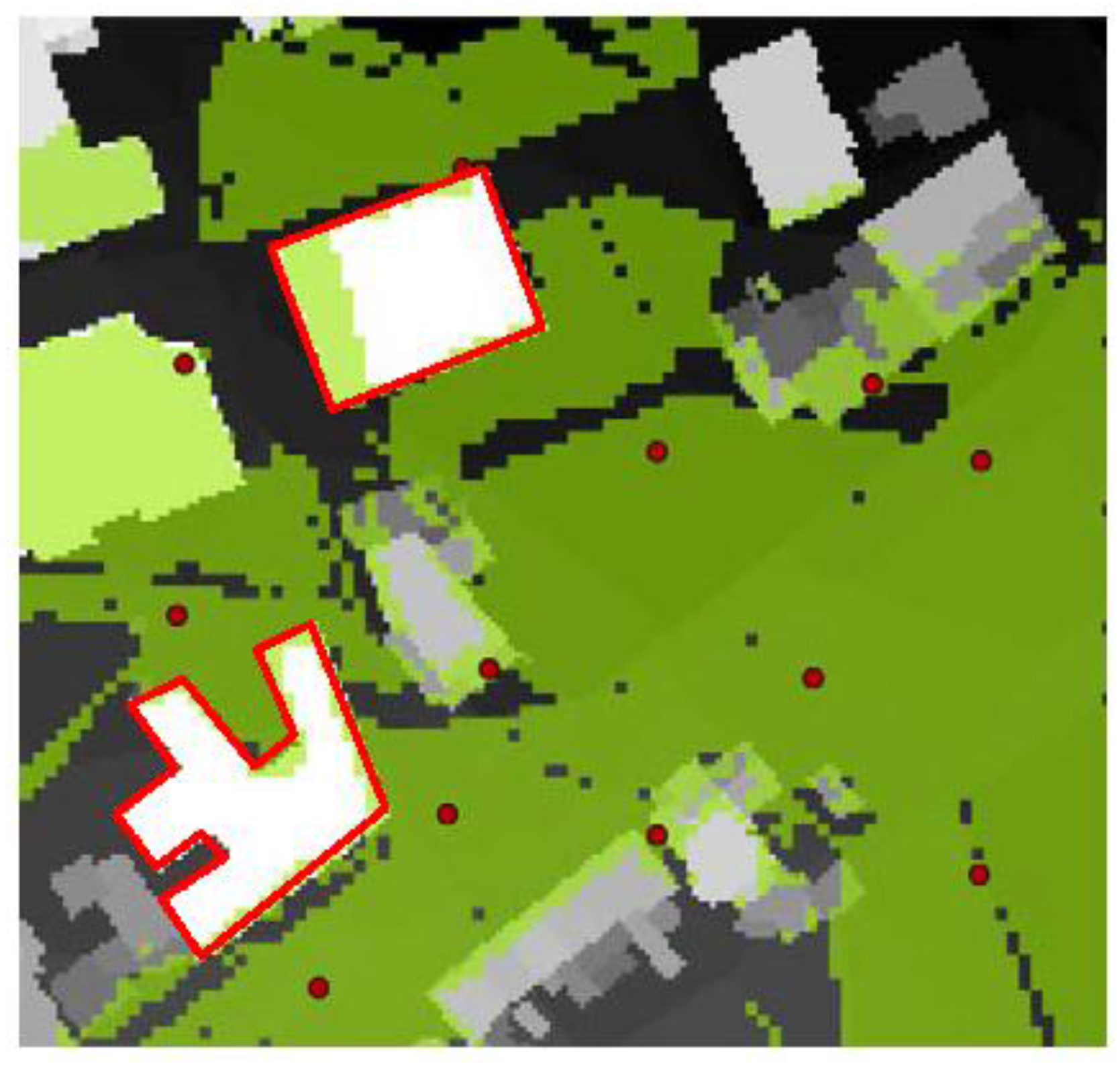
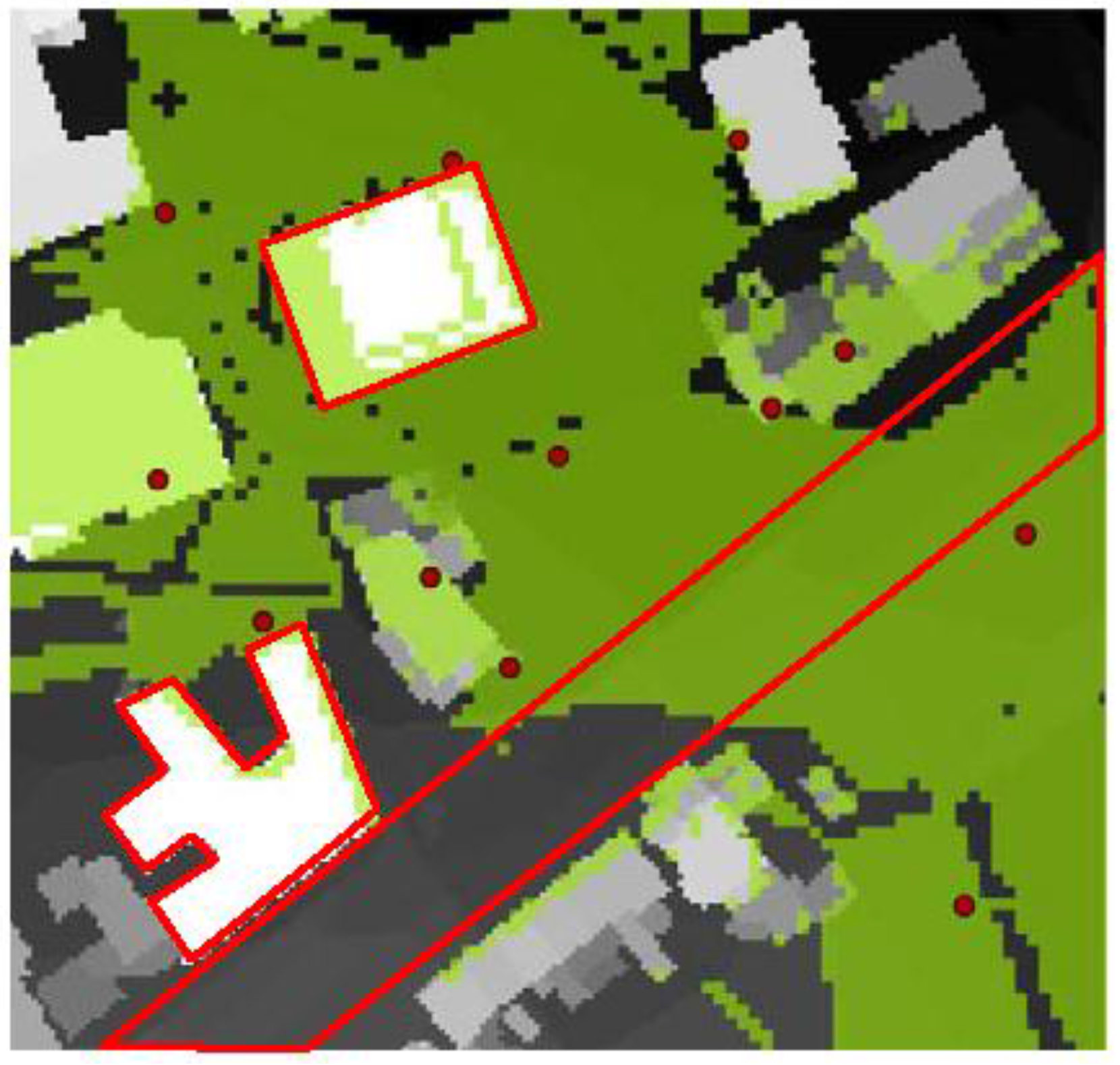
| Num. of Sensors | 12 | 16 | 20 | 24 | 28 | 35 |
| Coverage (%) | 55.52 | 58.15 | 59.51 | 66.14 | 73.08 | 87.56 |
| Num. of Iteration | 11 | 8 | 9 | 19 | 15 | 34 |

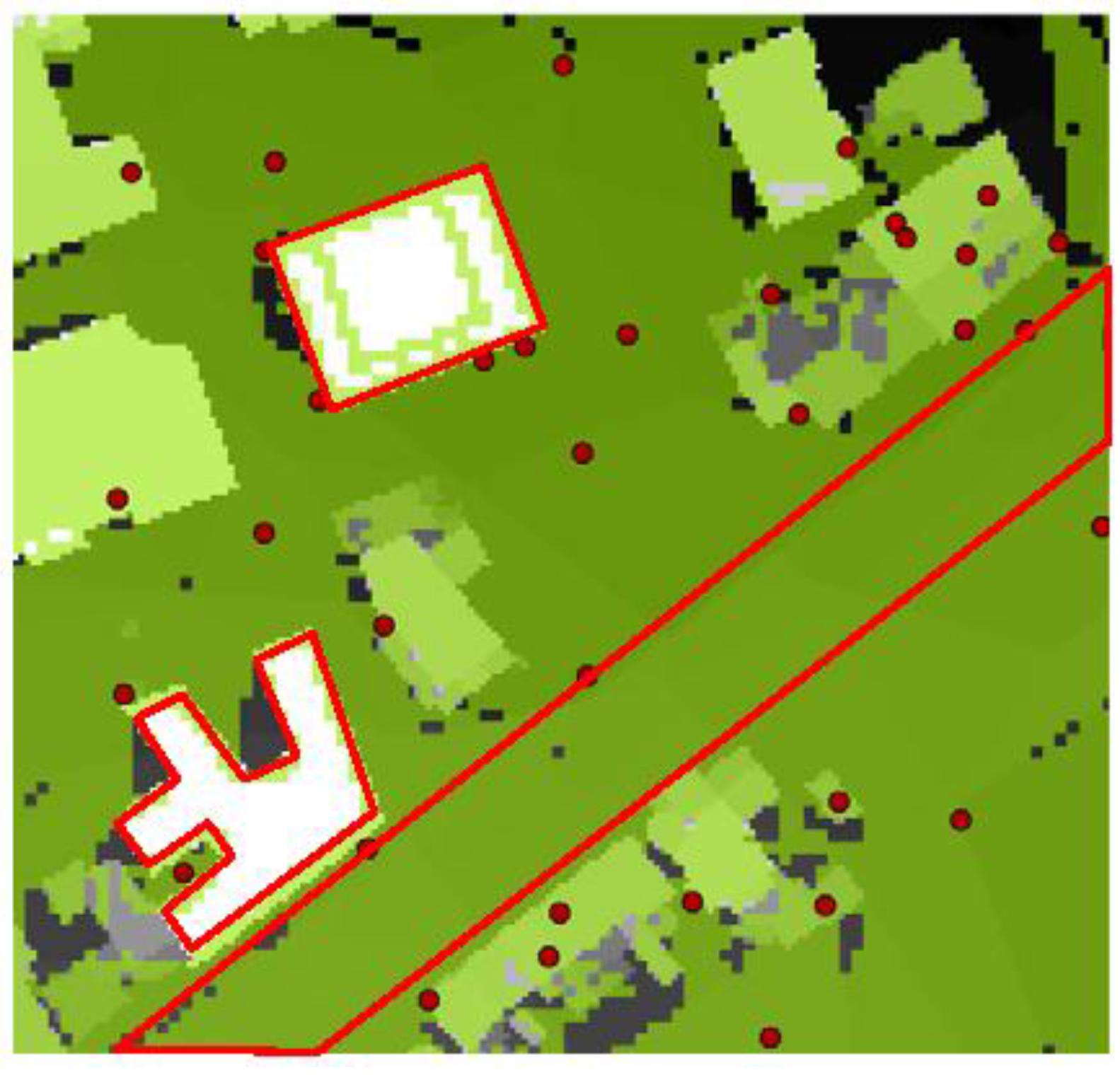
6.3. Optimization Considering Desirability of Coverage in a Given Area as CI
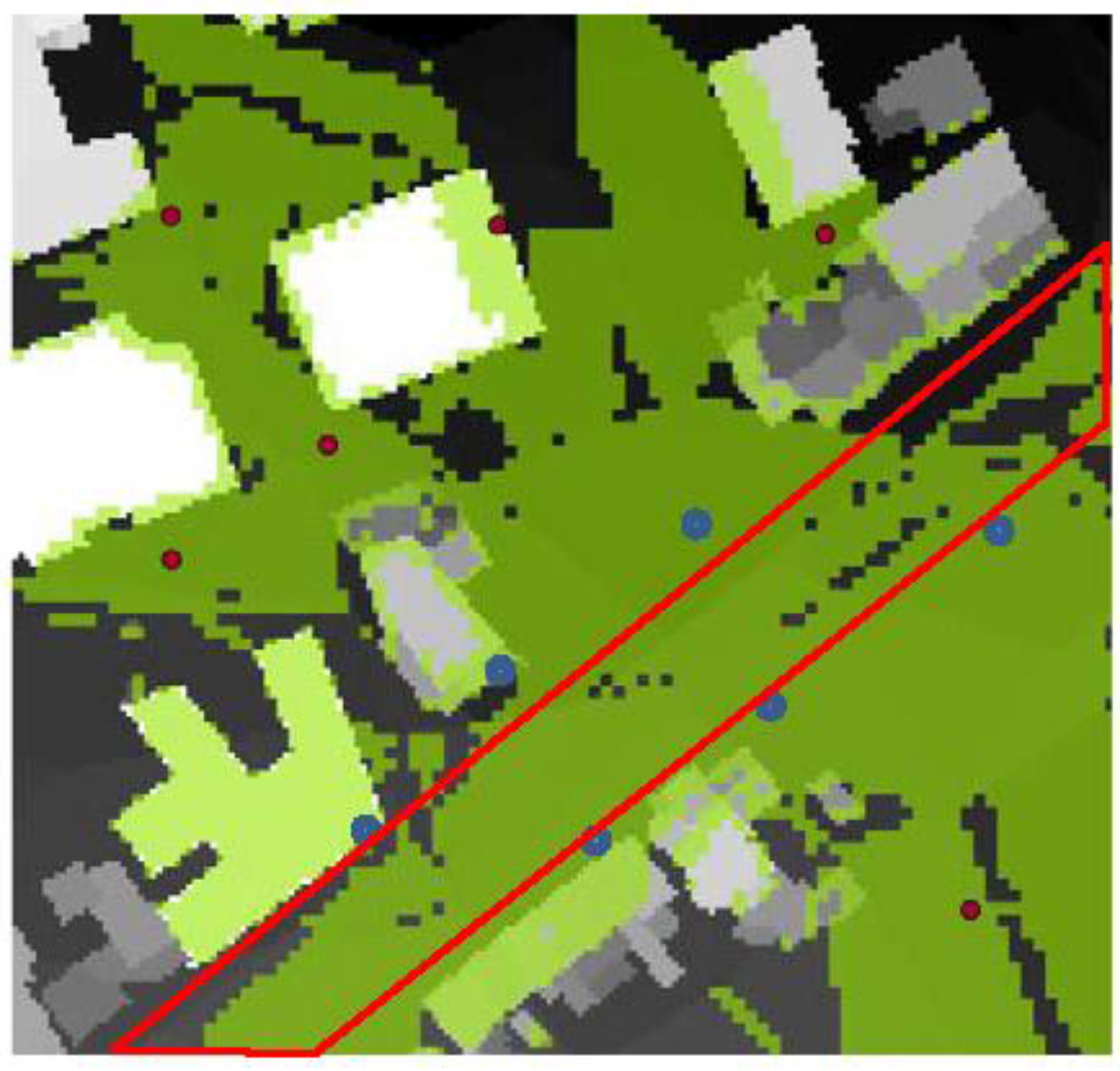
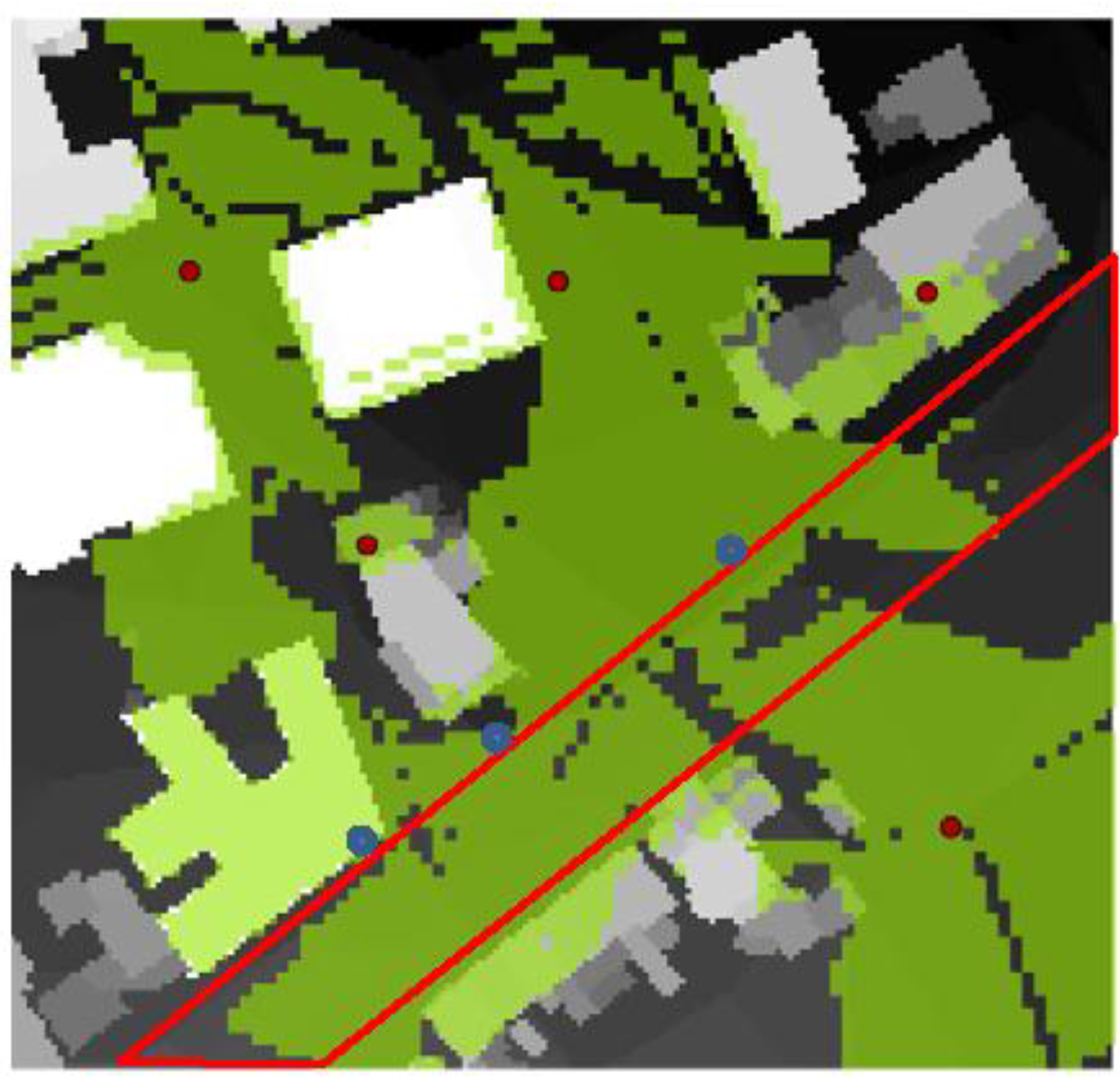
6.4. Optimization Considering the Environment Activities as CI
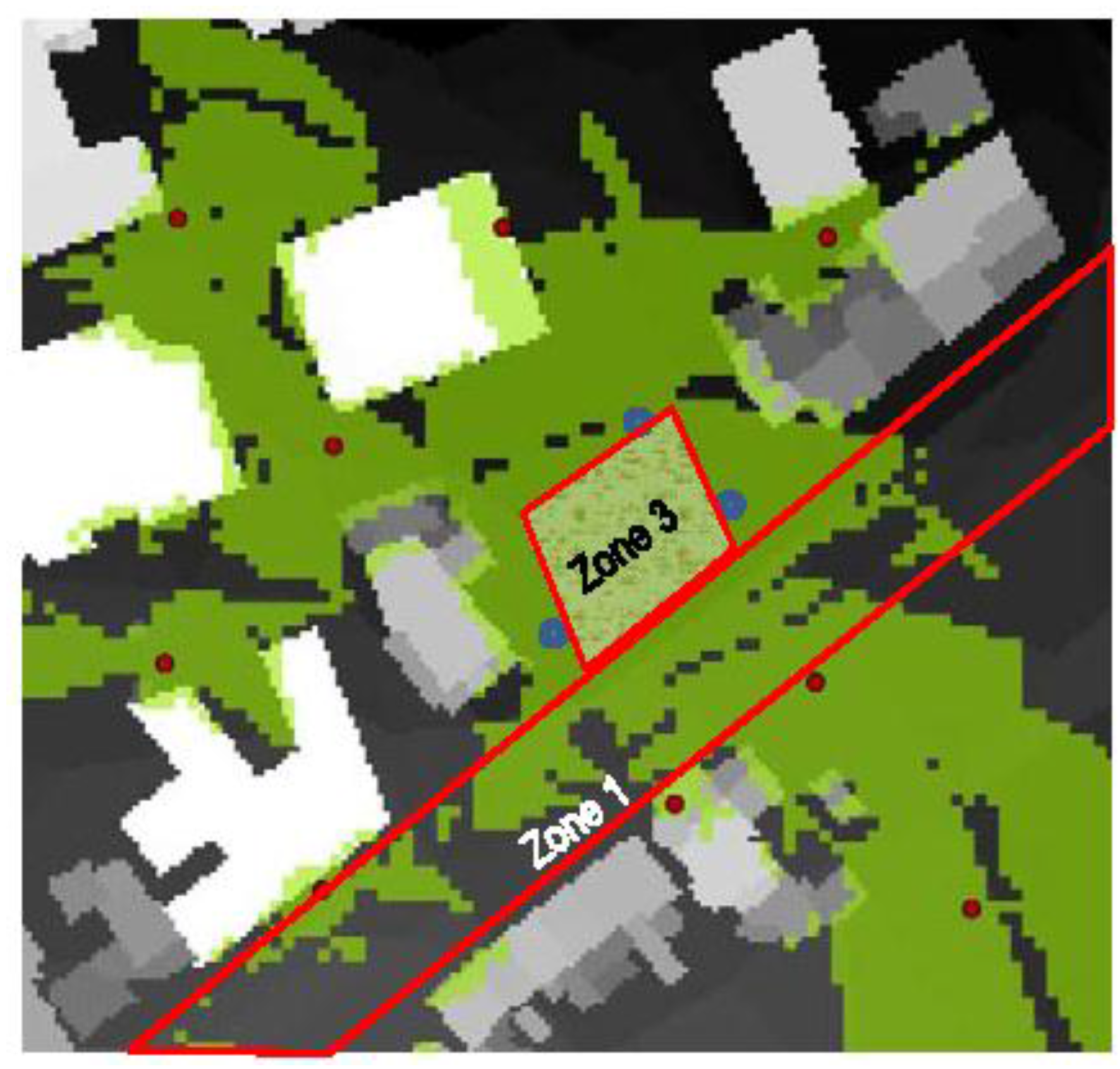
7. Discussions and Conclusions
Author Contributions
Conflicts of Interest
References
- Aziz, N.; Aziz, K.; Ismail, W. Coverage strategies for wireless sensor networks. World Acad. Sci. Eng. Technol. 2009, 50, 145–150. [Google Scholar]
- Ahmed, N.; Kanhere, S.; Jha, S. The holes problem in wireless sensor networks: A survey. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2005, 1, 1–14. [Google Scholar] [CrossRef]
- Ghosh, A.; Das, S.K. Coverage and connectivity issues in wireless sensor networks: A survey. Pervasive Mob. Comput. 2008, 4, 303–334. [Google Scholar] [CrossRef]
- Huang, C.; Tseng, Y. A survey of solutions to the coverage problems in wireless sensor networks. J. Internet Technol. 2005, 1, 1–9. [Google Scholar]
- Megerian, S.; Koushanfar, F.; Potkonjak, M.; Srivastava, M.B. Worst and best-case coverage in sensor networks. IEEE Trans. Mob. Comput. 2005, 4, 84–92. [Google Scholar] [CrossRef]
- Meguerdichian, S.; Koushanfar, F.; Potkonjak, M.; Srivastava, M.B. Coverage problems in wireless ad-hoc sensor networks. In Proceedings of the Twentieth Annual Joint Conference of the IEEE Computer and Communications Society (IEEE INFOCOM 2001), Anchorage, AK, USA, 22–26 April 2001; Volume 3, pp. 1380–1387.
- Loscrí, V.; Natalizio, E.; Guerriero, F.; Mitton, N. Efficient coverage for grid-based mobile wireless sensor networks. In Proceedings of the 11th ACM Symposium on Performance Evaluation of Wireless Ad Hoc, Sensor, and Ubiquitous Networks (PE-WASUN’14), Montreal, QC, Canada, 21–26 September 2014.
- Urrutia, J. Art Galleries and Illumination Problems. In Handbook on Computational Geometry; Elsevier Sciences Publisher: New York, NY, USA, 2000; Chapter 22; pp. 973–1026. [Google Scholar]
- Gonzales-Banos, H.; Latombe, J.-C. A Randomized Art-Gallery Algorithm for Sensor Placement. In Proceedings of the Symposium on Computational Geometry (SCG 2001), Medford, MA, USA, 3–5 June 2001; pp. 232–240.
- Wang, G.; Cao, G.; la Porta, T. Movement-assisted sensor deployment. IEEE Trans. Mob. Comput. 2006, 5, 640–652. [Google Scholar] [CrossRef]
- Thai, M.T.; Wang, F.; Du, D.H.; Jia, X. Coverage problems in wireless sensor networks: Designs and analysis. Int. J. Sens. Netw. 2008, 3, 191–203. [Google Scholar] [CrossRef]
- Cardei, M.; Wu, J. Coverage in Wireless Sensor Networks. PhD Thesis, Department of Computer Science and Engineering, Florida Atlantic University, Boca Raton, FL, USA, 2004. [Google Scholar]
- Zou, Y.; Chakrabarty, K. Sensor deployment and target localization based on virtual forces. In Proceedings of the Twenty-Second Annual Joint Conference of the IEEE Computer and Communications, IEEE Societies, INFOCOM 2003, San Francisco, CA, USA, 30 March–3 April 2003; Volume 2.
- Niewiadomska-Szynkiewicz, E.; Marks, M. Optimization Schemes For Wireless Sensor Network Localization. Int. J. Appl.Math. Comput. Sci. 2009, 19, 291–302. [Google Scholar] [CrossRef]
- Romoozi, M.; Ebrahimpour-komleh, H. A Positioning Method in Wireless Sensor Networks Using Genetic Algorithms. In Proceedings of 2012 International Conference on Medical Physics and Biomedical Engineering (ICMPBE2012), Singapore, 12–14 September 2012; pp. 174–179.
- Argany, M.; Mostafavi, M.A.; Karimipour, F.; Gagné, C. A GIS based wireless sensor network coverage estimation and optimization: A voronoi approach. Trans. Comput. Sci. XIV 2011, 6970, 151–172. [Google Scholar]
- Argany, M.; Mostafavi, M.A.; Akbarzadeh, V.; Gagné, C.; Yaagoubi, R. Impact of the Quality of Spatial 3D City Models on Sensor Networks. Geomatica 2012, 66, 291–305. [Google Scholar] [CrossRef]
- Akbarzadeh, V.; Gagne, C.; Parizeau, M.; Argany, M.; Mostafavi, M.A. Probabilistic Sensing Model for Sensor Placement Optimization Based on Line-of-Sight Coverage. IEEE Trans. Instrum. Meas. 2013, 62, 293–303. [Google Scholar] [CrossRef]
- Erdelj, M.; Loscrí, V.; Natalizio, E.; Razafindralambo, T. Multiple point of interest discovery and coverage with mobile wireless sensors. Ad Hoc Netw. 2013, 1, 2288–2300. [Google Scholar] [CrossRef]
- Dey, A.; Abowd, G.; Salber, D. A Conceptual Framework and a Toolkit for Supporting the Rapid Prototyping of Context-Aware Applications. Hum.-Comput. Interact. 2001, 16, 97–166. [Google Scholar] [CrossRef]
- Brown, P.; Bovey, J.; Chen, X. Context-Aware Applications: From the Laboratory to the Marketplace. Pers. Commun. 1997, 4, 58–64. [Google Scholar] [CrossRef]
- Ryan, N.; Pascoe, J.; Morse, D. Enhanced Reality Fieldwork: The Context-Aware Archaeological Assistant. Bar Int. Ser. 1999, 750, 269–274. [Google Scholar]
- Dey, A. Context-aware computing: The CyberDesk project. In Proceedings of the AAAI 1998 Spring Symposium on Intelligent Environments, Palo Alto, CA, USA, 23–25 March 1998; pp. 51–54.
- Schilits, B.N.; Theimer, M.M. Disseminating Active Map Information to Mobile Hosts. IEEE Netw. 1994, 8, 22–32. [Google Scholar] [CrossRef]
- Franklin, D.; Flaschbart, J. All gadget and no representation makes jack a dull environment. In Proceedings of the AAAI 1998 Spring Symposium on Intelligent Environment, Palo Alto, CA, USA, 23–25 March 1998; pp. 155–160.
- Hull, R. Towards situated computing. In Proceeding of the 1st International Symposium on Wearable Computers, Boston, MA, USA, 13–14 October 1997; pp. 146–153.
- Shermer, T. Recent results in art galleries. Proc. IEEE 1992, 80, 1384–1399. [Google Scholar] [CrossRef]
- Argany, M.; Mostafavi, M.A.; Karimipour, F. Voronoi-Based Approaches for Geosensor Networks Coverage Determination and Optimisation: A Survey. In Proceedings of the 2010 International Symposium on Voronoi Diagrams in Science and Engineering, Quebec, QC, Canada, 28–30 June 2010; pp. 115–123.
- Fan, G.; Jin, S. Coverage Problem in Wireless Sensor Network: A Survey. J. Netw. 2010, 5, 1033–1040. [Google Scholar] [CrossRef]
- Wang, L.; Shen, H.; Chen, Z.; Lin, Y. Voronoi tessellation based rapid coverage decision algorithm for wireless sensor networks. In Proceedings of 4th International Conference on Ubiquitous Intelligence and Computing, Hong Kong, China, 11–13 July 2007; pp. 495–502.
- Bai, X.; Lai, T.H. Deploying Wireless Sensors to Achieve Both Coverage. In Proceedings of the MobiHoc’06, Florence, Italy, 22–25 May 2006; pp. 131–142.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Argany, M.; Mostafavi, M.A.; Gagné, C. Context-Aware Local Optimization of Sensor Network Deployment. J. Sens. Actuator Netw. 2015, 4, 160-188. https://doi.org/10.3390/jsan4030160
Argany M, Mostafavi MA, Gagné C. Context-Aware Local Optimization of Sensor Network Deployment. Journal of Sensor and Actuator Networks. 2015; 4(3):160-188. https://doi.org/10.3390/jsan4030160
Chicago/Turabian StyleArgany, Meysam, Mir Abolfazl Mostafavi, and Christian Gagné. 2015. "Context-Aware Local Optimization of Sensor Network Deployment" Journal of Sensor and Actuator Networks 4, no. 3: 160-188. https://doi.org/10.3390/jsan4030160
APA StyleArgany, M., Mostafavi, M. A., & Gagné, C. (2015). Context-Aware Local Optimization of Sensor Network Deployment. Journal of Sensor and Actuator Networks, 4(3), 160-188. https://doi.org/10.3390/jsan4030160







