Abstract
In this paper we present a unified comparison of the performance of four detection techniques for centralized data-fusion cooperative spectrum sensing in cognitive radio networks under impulsive noise, namely, the eigenvalue-based generalized likelihood ratio test (GLRT), the maximum-minimum eigenvalue detection (MMED), the maximum eigenvalue detection (MED), and the energy detection (ED). We consider two system models: an implementation-oriented model that includes the most relevant signal processing tasks realized by a real cognitive radio receiver, and the theoretical model conventionally adopted in the literature. We show that under the implementation-oriented model, GLRT and MMED are quite robust under impulsive noise, whereas the performance of MED and ED is drastically degraded. We also show that performance under the conventional model can be too pessimistic if impulsive noise is present, whereas it can be too optimistic in the absence of this impairment. We also discuss the fact that impulsive noise is not such a severe problem when we take into account the more realistic implementation-oriented model.
1. Introduction
Spectrum scarcity in the fixed allocation policy is one of the main obstacles to the deployment of existing wireless communication systems and services, and to the development of new ones. With the advent of the cognitive radio (CR) paradigm [1], cognition-inspired dynamic spectrum access [2] techniques come into action by exploring the underutilized portions of the spectrum in time and space, while causing no or minimum harm in the system that pays for using that portion of the spectrum. Among the many cognitive tasks that a CR can perform, spectrum sensing is the task of detecting holes in frequency bands licensed to primary wireless networks for opportunistic use by secondary cognitive radios. Although sensing can be performed by each secondary receiver in a non-cooperative fashion, cooperative spectrum sensing has been considered a possible solution for problems experienced by CR networks in a non-cooperative sensing situation, like receiver uncertainty, multipath fading, hidden terminals, and correlated shadowing. Among the existing spectrum sensing techniques [3], eigenvalue-based schemes are receiving a lot of attention [4,5,6], mainly because they do not require prior information on the transmitted signal, and, unlike in energy-detection, in some eigenvalue-based schemes the knowledge of noise variance is not needed either [6].
Cooperative spectrum sensing can be classified as centralized and distributed, with the possibility of being relay-assisted [3] in both situations. In centralized cooperative sensing, data collected by each cooperating CR (e.g., received samples) are sent via a reporting control channel to a fusion center (FC), in a process called data-fusion. After the FC processes the data from the CRs, it decides upon the occupancy of the sensed channel. Centralized cooperative sensing can also be performed based on the hard decisions made by all cooperating CRs, in a process called decision-fusion. In this case, these decisions are combined at the FC using binary arithmetic before the final decision is arrived at. In both centralized schemes, the final decision is reported back to the CRs via a control channel, and an access algorithm takes place in the sequel. In distributed cooperative sensing, no FC exists and the final decision is iteratively reached by the cooperating CRs that communicate among themselves. In the case of relay-assisted cooperative sensing, a given CR may serve as a relay to forward the sensing information from one CR to another, for centralized or distributed operation.
It is worth mentioning that the role of an FC in a centralized cooperative spectrum sensing can be assigned to a cluster-head in the context of clustered network topologies [7], which is the case of most wireless sensor networks (WSN). This clustering approach can be of particular value in large area networks, where the adoption of a single FC could increase prohibitively the control channel traffic and lead to inefficient spectrum utilization. This inefficiency can be caused by the distinctive spectrum occupancy in different regions of the network, which could be misled by large-area-based centralized decisions.
1.1. The Realistic Implementation-Oriented Model
Conventionally, the well-known memoryless linear discrete-time multiple-input multiple-output (MIMO) fading channel model has been indistinctively adopted for modeling the received samples for single-receiver, multi-sensor and for multiple-receiver, single-sensor cognitive devices in data-fusion cooperative spectrum sensing. However, this model, henceforth called conventional model (C-model), is not well suited to the case of multiple CR receivers cooperating, at least not without appropriate modifications in the receiver model. These modifications are needed because, in the conventional model, the samples collected by each CR are considered forwarded to the FC exactly as they are, as if no signal processing task is performed in advance. Here, supported by the results in [8], we consider a more realistic implementation-oriented MIMO (R-model) approach in which typical signal processing operations realized within a direct-conversion CR receiver architecture are taken into account, such as filtering, automatic gain control (AGC) and quantization.
1.2. Eigenvalue-based Sensing Schemes
Moreover, we investigate the performance of four eigenvalue-based sensing schemes under impulsive noise (IN) circumstances using the conventional MIMO channel model and the implementation-oriented model. Specifically, we assess the performance of the eigenvalue-based generalized likelihood ratio test (GLRT); the maximum-minimum eigenvalue detection (MMED), also known as the eigenvalue ratio detection (ERD); the maximum eigenvalue detection (MED), also known as Roy’s largest root test (RLRT); and the energy detection (ED) [6] under several IN conditions and system parameters. Although ED is not an exclusively eigenvalue-based detection technique, it can be implemented using eigenvalue information. It has been included in the analysis in this paper for the sake of completeness, also giving support to a broader pool of comparisons.
1.3. Impulsive Noise
Impulsive noise in wireless systems may arise from several different sources, such as lightning, electrical switches, motors, vehicle ignition circuits, and reflections from sea waves, and it is known that it can severely degrade the performance of communications systems [9,10].
In [11], for instance, the performance of energy detection with selection combining and equal gain combining is investigated, and it is shown that the sensing performance can be affected by impulsive noise. Also in [11] a non-linear method based on GLRT was proposed. However, apart from this work, little effort has been put in the investigations on the influence of impulsive noise in cognitive radio receivers in the context of spectrum sensing. In particular no analysis has been previously made considering the different eigenvalue based methods, and the non-realistic conventional model has been applied in the literature.
1.4. Our Contribution
Motivated by the above issues, this paper aims at contributing with investigations on the performance of eigenvalue-based spectrum sensing algorithms in view of two important issues, namely, the effect of impulsive noise and the behavior in a realistic implementation oriented model.
Although it is known that IN can severely degrade the performance of communication receivers, little effort has been put into investigations about the influence of IN in cognitive radio receivers in the context of spectrum sensing. This paper also aims to contribute with such investigations.
This paper presents a unified analysis about the influence of IN in four important detection techniques for data-fusion cooperative spectrum sensing, namely, GLRT, MMED, MED, and ED, not only regarding the conventional model that is often adopted in the literature, but also considering a more realistic approach in which an implementation-oriented CR receiver model is taken into account.
We show that GLRT and MMED are quite robust in the IN environment, while MED and ED performance is drastically affected. We also show that the sensing performance under the conventional model can be rather pessimistic if IN is present, while it can be optimistic in the absence of such impairment. We further show that the implementation-oriented model is intrinsically able to combat IN.
Given the large differences in performance attained by these models in some situations, our main conclusion is that the implementation-oriented model should be preferred for spectrum sensing design and assessment, as it more closely reflects the reality. Furthermore, this model shows that sensing can be more robust than expected with the conventional model under impulsive noise circumstances. To the best of our knowledge, no publication so far has considered such a unified approach.
Many papers in the literature, such as [12,13,14], deal with the detection of samples affected by impulsive noise. Supposing that these samples can be perfectly identified, we also investigate some simple techniques to mitigate the impact of IN in spectrum sensing. These techniques consist in simply ignoring the affected samples or the affected receivers when performing detection algorithms. We show that these simple procedures can help improving the sensing performance.
The rest of the paper is organized as follows. Section 2 presents the system model for the eigenvalue-based sensing techniques and for IN generation. Section 3 describes the simulation setup, and Section 4 presents simulation results and discussions concerning the influence of the system parameters on spectrum sensing performance. Section 5 does the same as section 4, but now considering the influence of IN. The effect of some countermeasures added specifically to combat IN is also analyzed in section 5. Finally, Section 6 concludes the paper.
2. Model
2.1. Centralized Eigenvalue-based Spectrum Sensing
In what concerns the baseband memoryless linear discrete-time MIMO fading channel model, assume that there are m sensors (e.g., antennas) in a CR, or m single-sensor CRs, each one collecting n samples of the received signal from p primary transmitters during the sensing period. Consider that these samples are arranged in a matrix Y ∈ ℂm×n. Similarly, consider that the transmitted signal samples from the p primary transmitters are arranged in a matrix X ∈ ℂp×n. Let H ∈ ℂm×p be the channel matrix with elements {hij}, i = 1,2,...,m and j = 1,2,...,p, representing the channel gain between the j-th primary transmitter and the i-th sensor (antenna or receiver). Finally, let V and VIN ∈ ℂm×n be the matrices containing thermal noise and IN samples that corrupt the received signal, respectively. The matrix of collected samples is then
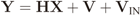
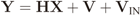
In eigenvalue-based sensing, spectral holes are detected using test statistics based on the eigenvalues of the sample covariance matrix of the received signal matrix Y. If a multi-sensor device is used to decide upon the occupation of a given channel in a non-cooperative fashion, or even in a centralized cooperative scheme with data-fusion (see Section 1), matrix Y is formed, and the sample covariance matrix
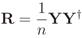 is estimated, where (·)† means complex conjugate and transpose. The eigenvalues {λ1 ≥ λ2 ≥ … λm} of R are then computed, and assuming a single primary transmitter (p = 1), the test statistics for GLRT, MMED, MED, and ED are respectively calculated according to [6]:
is estimated, where (·)† means complex conjugate and transpose. The eigenvalues {λ1 ≥ λ2 ≥ … λm} of R are then computed, and assuming a single primary transmitter (p = 1), the test statistics for GLRT, MMED, MED, and ED are respectively calculated according to [6]:
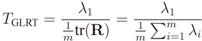
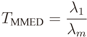
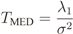
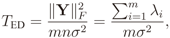 where σ2 is the thermal noise power that is assumed to be known and the same in each sensor input, and tr(·) and ǁ · ǁF are the trace and the Frobenius norm of the underlying matrix, respectively.
where σ2 is the thermal noise power that is assumed to be known and the same in each sensor input, and tr(·) and ǁ · ǁF are the trace and the Frobenius norm of the underlying matrix, respectively.
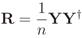
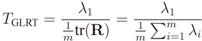
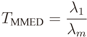
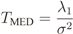
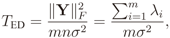
All the eigenvalue based methods rely on the fact that the covariance matrix in the presence of noise only is a diagonal matrix with all its elements equal to σ2, and, hence, has a single eigenvalue also equal to σ2 . In the presence of a primary user, this is no longer true, and these methods try to identify this situation. As we can see in Equation (3), with GLRT we calculate the ratio between the largest eigenvalue and the average of all the remaining eigenvalues. In MMED we consider the ratio between the largest and the smallest eigenvalues. In MED we assume that the noise variance σ2 is known, and compare the largest eigenvalue with σ2. In all these methods, the test statistic should be equal to one, in case only Gaussian noise is present.
In the conventional model, when a centralized cooperative sensing with single-sensor (e.g., single antenna) CRs is considered, matrix Y is presumed to be available at the fusion center as if no signal processing is needed before each row of Y is forwarded to the FC by each CR. A more realistic model was originally proposed in [8] and called the implementation-oriented model. It considers the main signal processing tasks performed by each CR before the collected sample values are sent to the FC. The diagram shown in Figure 1, which adopts a direct-conversion receiver (DCR) architecture [15], was the main reference for constructing such a model. The choice of this architecture was made based on the consensus that DCR is the one that is promised to be adopted for cognitive radio applications in the majority of situations [15].
The analog radiofrequency front-end is made up of a wideband antenna, a wideband band-pass filter (BPF), a low-noise amplifier (LNA), and quadrature local oscillators (LO) and mixers responsible for non-coherent direct conversion of the target channel to in-phase and quadrature (I&Q) baseband signals. These signals are amplified using an AGC, which is responsible for maintaining its output signal within the dynamic range of the analog-to-digital converters (ADC) in the I&Q signal paths. I&Q channel low-pass filters (LPF) select the desired bandwidth to be sampled and avoid aliasing. A noise-whitening process takes place to guarantee that noise components are kept uncorrelated when the received signal matrix is built at the fusion center. This is done because the detection techniques considered here assume, for optimum operation, that the noise samples are uncorrelated.
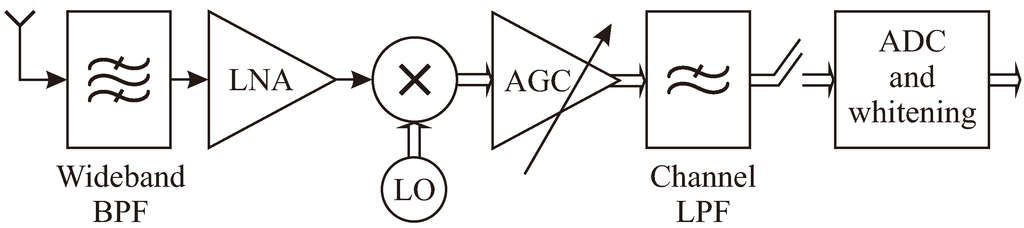
Figure 1.
CR receiver diagram (adapted from [8]).
Remembering that the samples are quantized at the ADC with Nq quantization levels, the log2 Nq bits per sample at both I and Q after whitening can then be forwarded to the fusion center by a given digital modulation scheme. At this stage, bit errors in the transmission may cause further impairments at the available samples. This is however not the subject of this study.
It is well known that the DC offset is one of the most relevant problems in a direct-conversion receiver [16,17,18]. It corresponds to a DC value at the mixer output produced by the self-mixing of the LO signal, which is originated from the non-ideal isolation between the mixer ports and substrate leakage in integrated receivers. DC offset can also be generated by a strong in-band interferer, second-order distortion in the signal path, and LO reradiation. This DC level, which can be constant or time-varying, can saturate subsequent amplifiers or reduce the ADC dynamic range, causing severe performance degradation. DC-blocking via capacitive coupling is the simplest way of cancelling the DC offset, but can produce performance degradation due to the time-slotted nature of the spectrum sensing process: higher capacitances produces low signal distortion, but increases the sensing settling time and hinder receiver integration; lower capacitances reduces the settling time, but causes more signal distortion. Additionally, DC blocking works only if the DC offset is constant. For these reasons, capacitive DC blocking is not well suited for DC offset cancellation in CR receivers with spectrum sensing capabilities. Fortunately, a number of DC offset compensation techniques have been proposed, some of them capable of almost eliminating the DC offset, maintaining low settling time, see [19,20] and references therein. In this paper we do not consider the DC offset problem, assuming that it was completely removed by some appropriate technique at the receiver. In [8], where the model considered here was proposed, the influence of imperfect DC offset removal on the spectrum sensing performance is addressed.
2.2. IN Model
Impulsive noise can be (i) generated from the electrical mains or by direct induction on the receiver; or (ii) captured by the receiver antenna. In the first category, the main noise sources are the ignition system of ovens, the control system of dishwasher machines, thermostats of heaters, and switches of fluorescent and incandescent lamps. In the second category, typical sources are lightning and the ignition system of cars.
Several models are available in the literature for characterizing IN [21,22,23]. Here we adopt the one discussed in [22], in which the IN waveform is generated by properly gating a white noise signal, as illustrated in Figure 2. The main parameters that govern the IN waveform are also shown in this figure. They are configured according to the noise source type, as described in detail in [22].
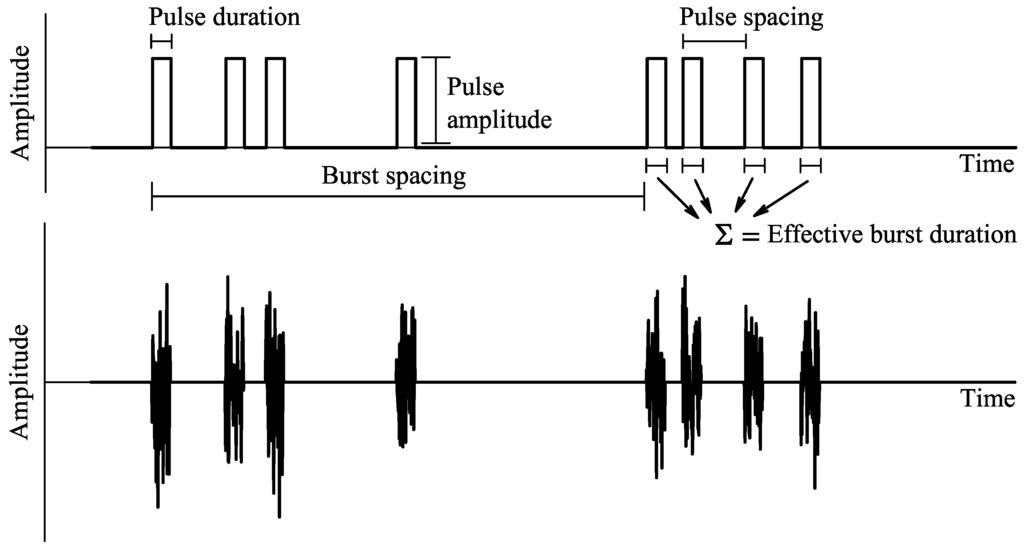
Figure 2.
Gating waveform (top) and impulsive noise waveform (bottom).
To adhere the above parameters to the context of spectrum sensing, we translated them into five other parameters: K is the ratio between the time-series average IN power and the average thermal noise power; pIN denotes the probability of occurrence of IN during a given sensing period, and pCR represents the fraction of CRs hit by IN, when it occurs. As a result, the probability of the occurrence of IN is a Bernoulli random variable with probability of success pIN, and the number of CRs independently hit by IN, when it occurs, is a binomial random variable with parameters m and pCR. A configurable number Nb of IN bursts occurs during a sensing period, each burst having configurable length Ns, i.e., each IN burst corrupts Ns consecutive samples collected by a given CR. The separation between consecutive bursts is uniformly distributed in the discrete-time interval [0, n − Nb × Ns].
3. Simulation Setup
3.1. Conventional Model (C-Model)
The simulation setup under the conventional discrete-time memoryless MIMO model (C-model) just considers that Y, the matrix with received signal samples in Equation (1), is available to the FC as if no signal processing is performed by each CR before the sample values are forwarded to the FC. Matrices X, H, V, and VIN under the C-model are generated as follows: To simulate a Gaussian distributed noise-like transmitted signal, X is formed by unitary variance (unitary power), independent and identically distributed (i.i.d.) zero mean complex Gaussian samples. The Gaussian distribution for the entries of X is adopted because it accurately models several modulated signals, for instance the amplitude of a multicarrier signal, such as orthogonal frequency-division multiplexing (OFDM), with a large number of subcarriers, which is the preferred modulation technique in most modern wireless technologies, including several digital television standards. The elements in the channel matrix H are zero mean i.i.d. complex Gaussian variables that simulate a flat Rayleigh fading channel between each primary transmitter and sensor (CR), assumed to be constant during a sensing period and independent from one period to another. The entries in V and VIN are complex Gaussian variables that represent, respectively, the additive thermal and the impulse noise corrupting the received samples. The desired received signal-to-noise ratio (SNR), in dB, and the desired average IN power are guaranteed by making the variance of the noise samples equal to 10−SNR/10 and the variance of the IN samples equal to K10−SNR/10, for an average IN power K times the thermal noise power. Moreover, matrix H is normalized so that 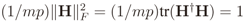 .
.
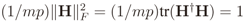 .
. The received matrix Y = HX + V + VIN in the conventional model is then assumed to be available at the FC, from which the covariance matrix R is computed, and then the eigenvalues {λi}, i = 1,2,...,m. The test statistics for GLRT, MMED, MED, and ED are respectively computed from Equations (3)–(6). In each detection technique, the corresponding test statistic is compared with a threshold computed from the desired false alarm probability, and a final decision upon the occupancy of the sensed channel is reached.
3.2. Implementation-Oriented Model (R-Model)
The simulation setup under the realistic implementation-oriented model (R-model) has been built to mimic the system diagram shown in Figure 1, in which the direct conversion to baseband is assumed ideal, as also implicitly assumed in the conventional model.
Matrices X, H, V, and VIN under the R-model are generated as follows: To simulate a Gaussian distributed noise-like transmitted signal with controllable time correlation at the receiver side, X is formed by filtering i.i.d. zero mean complex Gaussian samples with a length-L moving average (MA) filter with no quantization (using floating-point computations). This type of filter was chosen for reasons of simplicity; any other low-pass filter could be adopted as well. The memory elements in the structure of this and subsequent MA filtering processes are assumed to have zero initial value before the first valid sample is applied to their inputs. As a result, the first (L − 1) samples resulting from the MA filtering, out of (n + L − 1), are discarded before subsequent operations. As in the case of the C-model, the Gaussian distribution for the entries of X is adopted because it accurately models several modulated signals. The time correlation introduced by the filter models the limited bandwidth of the transmitted signal, which is proportional to the symbol rate.
The elements in the channel matrix H are zero mean i.i.d. complex Gaussian variables that simulate a flat Rayleigh fading channel between each primary transmitter and sensor (CR), assumed to be constant during a sensing period and independent from one period to another.
To take into account the effect of the CR receive filters on the thermal and impulsive noises the entries in V and VIN are MA-filtered complex Gaussian variables that represent, respectively, the colored additive thermal and the impulse noise at the output of the receive filters.
A normalization of filtered samples was done to guarantee the desired received signal-to-noise ratio (SNR), in dB, and the desired average IN power. Specifically, 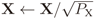 for unitary average received signal power,
for unitary average received signal power, 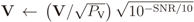 for an SNR-dependent average thermal noise power, and
for an SNR-dependent average thermal noise power, and 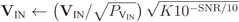 for an average IN power K times the thermal noise power, where the symbol “←” represents the normalization process, PX, PV, and PVIN are the average time-series powers in X, V, and VIN before normalization, respectively. Moreover, to guarantee the desired received SNR, matrix H is normalized so that
for an average IN power K times the thermal noise power, where the symbol “←” represents the normalization process, PX, PV, and PVIN are the average time-series powers in X, V, and VIN before normalization, respectively. Moreover, to guarantee the desired received SNR, matrix H is normalized so that 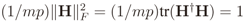 .
.
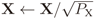 for unitary average received signal power,
for unitary average received signal power, 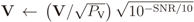 for an SNR-dependent average thermal noise power, and
for an SNR-dependent average thermal noise power, and 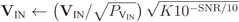 for an average IN power K times the thermal noise power, where the symbol “←” represents the normalization process, PX, PV, and PVIN are the average time-series powers in X, V, and VIN before normalization, respectively. Moreover, to guarantee the desired received SNR, matrix H is normalized so that
for an average IN power K times the thermal noise power, where the symbol “←” represents the normalization process, PX, PV, and PVIN are the average time-series powers in X, V, and VIN before normalization, respectively. Moreover, to guarantee the desired received SNR, matrix H is normalized so that 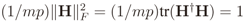 .
. The effect of the LNA and the AGC on the samples processed by the i-th CR, i = 1,2,...,m, is given by the gain
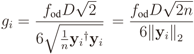 where yi is the i-th row of Y, i.e., the set of n samples collected by the i-th CR, and ǁyiǁ2 is the Euclidean norm of yi. The reasoning behind proposing these gains is explained as follows: The combined gains of the LNA and the AGC are those that maintain the signal amplitude at the inputs of the in-phase and quadrature ADCs within their dynamic ranges D. By dividing the sample values by the square root of yi†yi/n, which is the average power of yi, one obtains a sequence with unitary average power. Since X is Gaussian, {yi} have Gaussian distributed sample values, conditioned on the corresponding channel gain. If σ2 is the variance of these (complex) samples after the effect of the LNA and the AGC, to guarantee that six standard deviations (practically the whole signal excursion or 99.73% of the sample values) of the I&Q signals will be within [−D/2, D/2], we shall have
where yi is the i-th row of Y, i.e., the set of n samples collected by the i-th CR, and ǁyiǁ2 is the Euclidean norm of yi. The reasoning behind proposing these gains is explained as follows: The combined gains of the LNA and the AGC are those that maintain the signal amplitude at the inputs of the in-phase and quadrature ADCs within their dynamic ranges D. By dividing the sample values by the square root of yi†yi/n, which is the average power of yi, one obtains a sequence with unitary average power. Since X is Gaussian, {yi} have Gaussian distributed sample values, conditioned on the corresponding channel gain. If σ2 is the variance of these (complex) samples after the effect of the LNA and the AGC, to guarantee that six standard deviations (practically the whole signal excursion or 99.73% of the sample values) of the I&Q signals will be within [−D/2, D/2], we shall have 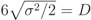 , which means that the signal power at the output of the AGC will be σ2 = 2D2/36. This justifies the factor
, which means that the signal power at the output of the AGC will be σ2 = 2D2/36. This justifies the factor 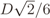 in Equation (7). Finally, as the name indicates, the overdrive factor fod ≥ is included as a multiplier in Equation (7) to simulate different levels of signal clipping caused by real ADCs, i.e., it produces signal amplitudes greater than or equal to 6 . For example, an fod = 1.2 means that the dynamic ranges of the signals at the input of the I&Q ADCs will be 20% larger than the dynamic ranges of the ADC’s inputs. The I&Q clippings act on each sample value s applied to their inputs according to s ← sign(s)min(|s|, D/2).
in Equation (7). Finally, as the name indicates, the overdrive factor fod ≥ is included as a multiplier in Equation (7) to simulate different levels of signal clipping caused by real ADCs, i.e., it produces signal amplitudes greater than or equal to 6 . For example, an fod = 1.2 means that the dynamic ranges of the signals at the input of the I&Q ADCs will be 20% larger than the dynamic ranges of the ADC’s inputs. The I&Q clippings act on each sample value s applied to their inputs according to s ← sign(s)min(|s|, D/2).
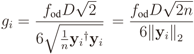
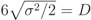 , which means that the signal power at the output of the AGC will be σ2 = 2D2/36. This justifies the factor
, which means that the signal power at the output of the AGC will be σ2 = 2D2/36. This justifies the factor 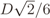 in Equation (7). Finally, as the name indicates, the overdrive factor fod ≥ is included as a multiplier in Equation (7) to simulate different levels of signal clipping caused by real ADCs, i.e., it produces signal amplitudes greater than or equal to 6 . For example, an fod = 1.2 means that the dynamic ranges of the signals at the input of the I&Q ADCs will be 20% larger than the dynamic ranges of the ADC’s inputs. The I&Q clippings act on each sample value s applied to their inputs according to s ← sign(s)min(|s|, D/2).
in Equation (7). Finally, as the name indicates, the overdrive factor fod ≥ is included as a multiplier in Equation (7) to simulate different levels of signal clipping caused by real ADCs, i.e., it produces signal amplitudes greater than or equal to 6 . For example, an fod = 1.2 means that the dynamic ranges of the signals at the input of the I&Q ADCs will be 20% larger than the dynamic ranges of the ADC’s inputs. The I&Q clippings act on each sample value s applied to their inputs according to s ← sign(s)min(|s|, D/2). From above one can see that the AGC will affect not only the noise level that corrupts the received samples in the i-th CR, but will also change the statistical behavior of the amplified samples of yi. Based on this we conjecture that ED as well as other detection techniques that demand knowledge of the noise variance information, such as MED (or RLRT), must take the gains in Equation (7) into account in both the noise variance estimate and in the derivation of new test statistics different from Equations (5) and (6). Further investigations on this issue are beyond the scope of this paper, representing an opportunity for future contributions.
Back to the description of the implementation-oriented model based on Figure 1, the whitening filter matrix W [24] that multiplies the MA-filtered, amplified and perhaps clipped versions of {yi} is computed with floating point according to W = UC−1, where U is the orthogonal matrix from Q = UΣKT, the singular-value decomposition of the covariance matrix Q. The elements of Q are Qij = a|i −j|, with {ak} representing the discrete autocorrelation function of the MA filter impulse response, i.e., ak = (1 − k/L), for k ≤ L, and ak = 0 otherwise, for i, j, k = 0,1,..., (n − 1). Matrix C is the lower triangular matrix from the Cholesky decomposition of Q. The effect of the analog to digital conversion of the processed sample values that will be sent to the FC is modeled by a quantizer with configurable number Nq of quantization levels.
Assuming no bit errors in the reporting channels, the modified received matrix Y = HX + V + VIN in the implementation-oriented model is then formed at the FC, from which the covariance matrix R is computed, and then the eigenvalues {λi}, i = 1,2,...,m. The test statistics for GLRT, MMED, MED, and ED are respectively computed from Equations (3)–(6). In each detection technique, the corresponding test statistic is compared with a threshold computed from the desired false alarm probability, and a final decision upon the occupancy of the sensed channel is reached.
4. Influence of the System Parameters
In this section we present simulation results and discussions concerning the influence of the system parameters under the R-model on the spectrum sensing performance for GLRT, MMED, MED, and ED (the simulation file used in our simulations is available for download as a supplementary material). Curves for the C-model are also included for purposes of comparison. It is worth mentioning that the receiver operating characteristic (ROC) curves for all the detection techniques under the C-model, for m = 6, n = 50, and SNR = −10 dB, are in perfect agreement with those reported in [6]. The results in this section were reported in [8] and were included here so that this paper becomes self-contained.
The ROC curves shown hereafter were obtained with a minimum of 5,000 runs in Monte Carlo simulations implemented according to the setup described in Section 3. System parameters are those in Table 1, unless otherwise indicated. Shaded areas in the graphs represent positions of ROC curves for Nq = 8, and for fod and L ranging from 1 to 2, and 1 to 20, respectively. They are meant to reflect parameter variations within empirical limits of practical significance.

Table 1.
Reference System Parameters.
| C-Model and R-Model | |
| Signal-to-noise ratio | SNR = −10 dB |
| Number of primary transmitters | p = 1 |
| Number of CRs | m = 6 |
| Number of samples collected by each CR | n = 50, 100 |
| Impulsive to thermal noise power ratio | K = 0 |
| Signal-to-noise ratio | SNR = −10 |
| MA-filter length | L = 1-20 |
| ADC dynamic range | D = 2 |
| ADC overdrive factor | fod = 1-2 |
| Number of quantization levels | Nq = 4, 8, 256 |
4.1. GLRT
Figure 3 shows the ROC curves relating the probability of false alarm (Pfa) and the probability of detection (Pd) for GLRT. It can be seen that the performance of the sensing scheme under the R-model is poor for Nq = 4, changing slightly from Nq = 8 to Nq = 256. Following [8], this suggests that 3 bits per sample are enough for the transmission of the sample values collected by each CR to the FC, a result that can be useful to the analysis of the necessary bandwidth and traffic over the reporting control channel. Still referring to Figure 3, one can observe that, for a given false alarm probability, the GLRT detection probability under the C-model is slightly overestimated if compared with the results produced under the R-model. In other words, ignoring the signal processing tasks typically performed in digital receivers may lead us to optimistic results. Figure 3 also shows that the ROC curves under the R-model suffer little or no influence of variations of L and fod. These results support the choice of the following system parameters to mimic a real CR using the GLRT strategy: (i) number of quantization levels Nq = 8, which corresponds to a 3-bit quantization of the sample values; (ii) low-pass MA receive filter length was chosen by assumption as L = 0.2n; and (iii) AGC overdrive factor fod = 1.2, which corresponds to a value that will produce a signal clipping in approximately 1.2% of the time for un-quantized Gaussian-distributed sample values, and around 3% for Nq = 8. This value of 3% was obtained experimentally.
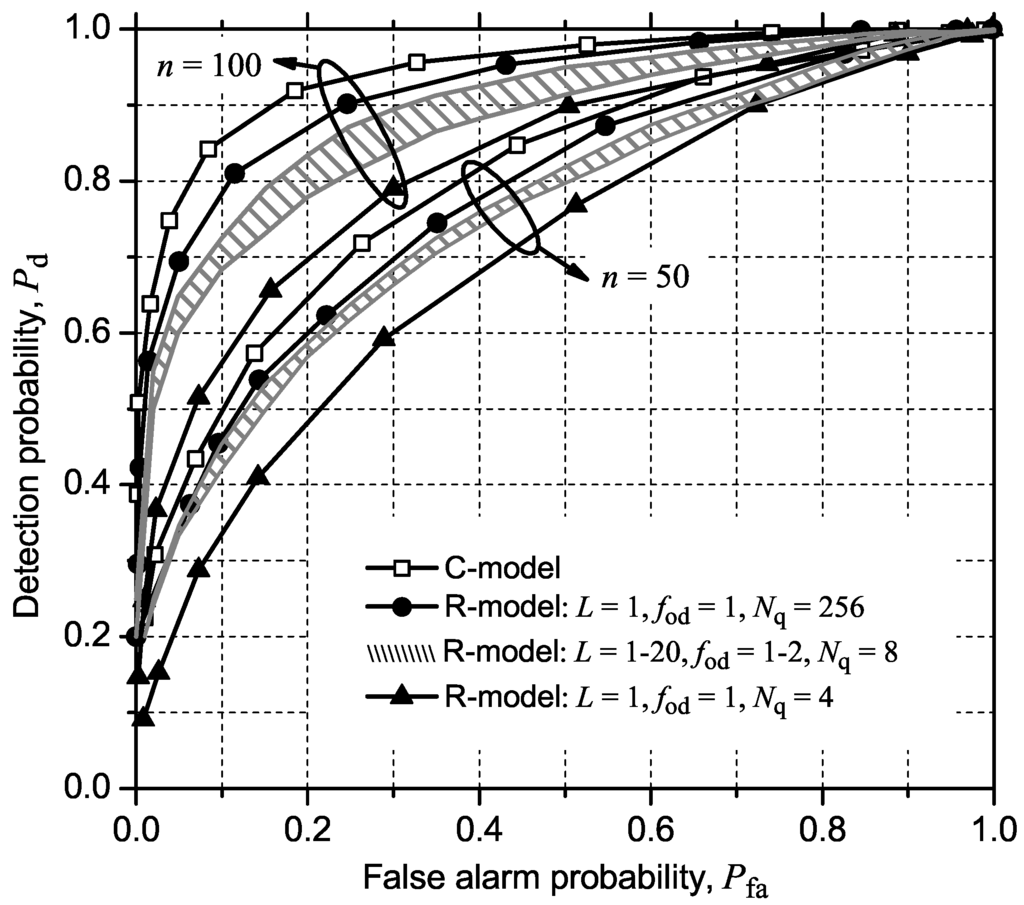
Figure 3.
ROC curves for GLRT under parameter variations.
Since the influence of increasing the number n of collected samples per CR is a performance improvement, considering as fixed the remaining system parameters, from this point on we present simulation results only for n = 50. This is to avoid polluting unnecessarily the graphs (clusters of curves for n = 50 and n = 100 are not necessarily separated from each other in the cases of other detection techniques, as they are in the case of GLRT in Figure 3).
In what concerns the effect of increasing the SNR, we also know that it has no influence on Pfa, although it produces an increase in Pd, pushing up the positions of the ROC curves. This motivates the presentation of results with a fixed value of SNR, which was chosen to be small (−10 dB) to represent a more degrading, but yet realistic, situation from the perspective of spectrum sensing performance. For instance, IEEE 802.22 requires that the presence of digital TV transmissions should be sensed with 0.9 detection probability with a sensitivity of −114dBm, which may be translated into very low SNR levels [25].
4.2. MMED (or ERD)
Figure 4 shows the ROC curves for MMED (or ERD), also considering the system parameters in Table 1, but only for n = 50. Most observations drawn from Figure 3 apply to Figure 4, but, as expected, MMED performs worse than GLRT, because the former has lower statistical power [6]. Furthermore, the differences between the results obtained with the C- and with the R-model are less pronounced for MMED than for GLRT.
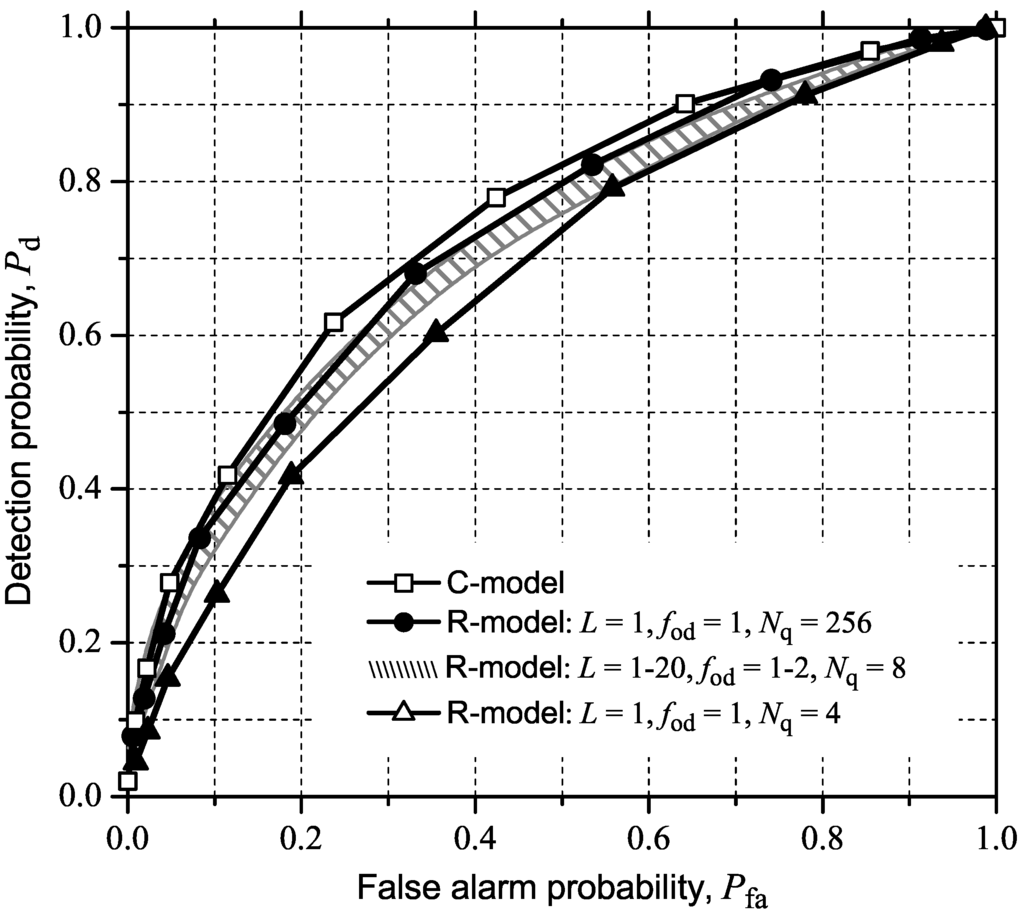
Figure 4.
ROC curves for MMED (or ERD) under parameter variations.
From the results in Figure 3 and Figure 4 one can notice the small variation in performance due to the variation in L, the length of the impulse response of the MA filter adopted in the R-model. This is credited to the inherent ability of eigenvalue detection strategies in dealing with correlated samples, whose correlation information is somewhat transferred to the covariance matrix from where the eigenvalues are computed.
4.3. MED (or RLRT) and ED
We now turn our attention to MED (or RLRT) and ED. In both cases the noise variance is assumed to be known. Figure 5 shows the ROC curves for both detection strategies, again adopting the parameters in Table 1, but only for n = 50. Although severely degraded in performance, MED still works, unveiling a behavior similar to GLRT and MMED (see Figure 3 and Figure 4) concerning the way it is influenced by the variations of the system parameters. Again one can notice the small susceptibility of an eigenvalue-based detection to the variations on the temporal signal correlation, which are produced in the R-model by varying L, the impulse response length of the MA filters. The situation for ED in Figure 5, however, is quite dramatic: it produces useless values of Pfa = Pd for the whole range of variations of the decision threshold and system parameters. This poor performance of ED remains unchanged for n as large as 500. An explanation for this can be found on the presence of the AGC at the receiver, which makes the received sampled noise and signal power vary dynamically. This should be taken into account when the detection thresholds are set or, equivalently, when the decision statistic is computed. This was not considered in this paper.
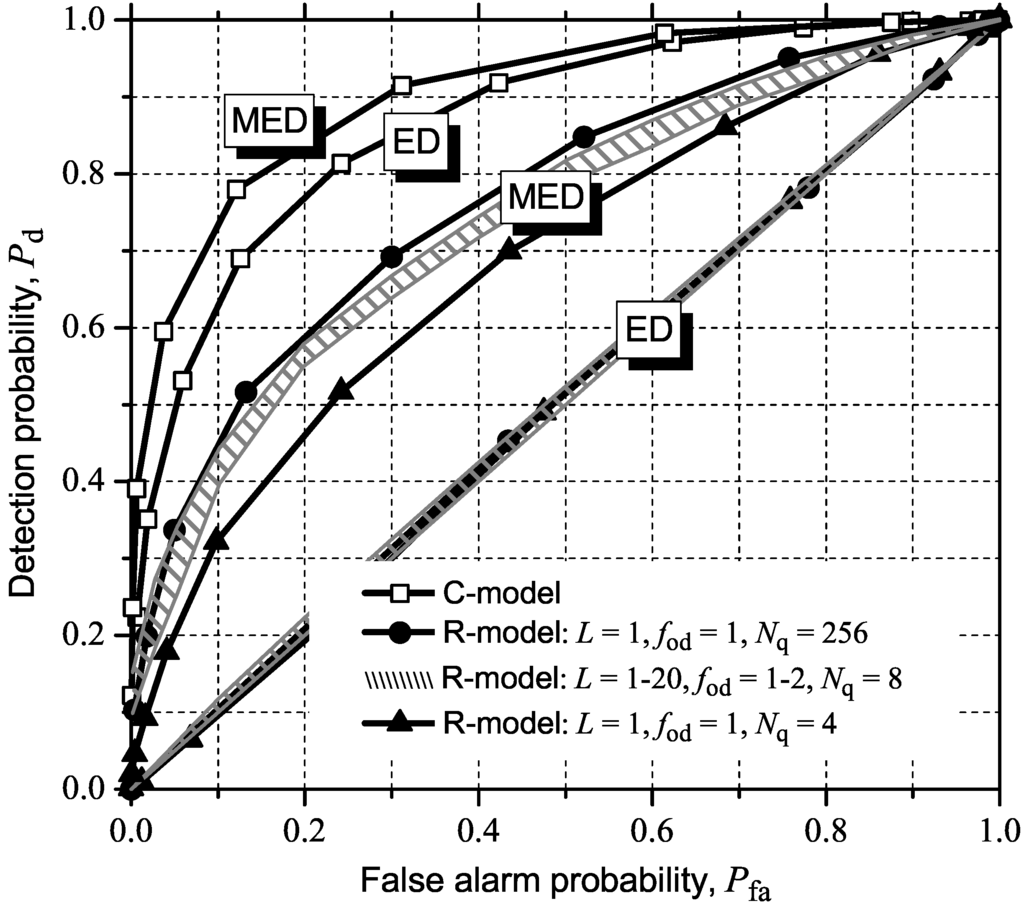
Figure 5.
ROC curves for MED (or RLRT) and ED under parameter variations.
5. Influence of IN
5.1. Influence on the Entries of the Covariance Matrix
The first big difference between the C-model and the R-model under IN appears when observing the three-dimensional (3D) representation of the matrices Y and R. Since no signal processing is assumed in the C-model, IN samples appear added to the thermal-noise-only version of Y (Figure 6, left) and are clearly noticed as pronounced peaks in the sample covariance matrix R, plotted in the right-hand side of Figure 6. On the other hand, one can notice from Figure 7 that IN peaks were practically eliminated when the R-model is considered. This shows the intrinsic ability of the implementation-oriented model (R-model) to combat IN, i.e., IN has been reduced by the inherent signal-processing tasks performed by each CR in the R-model, particularly by the low-pass receiver filtering, the hard limitation at the ADC and the whitening filtering. It is worth mentioning that no countermeasure specifically designed to combat IN was added to the R-model at this point. Figure 6 and Figure 7 were obtained considering the system parameters listed in Table 2.
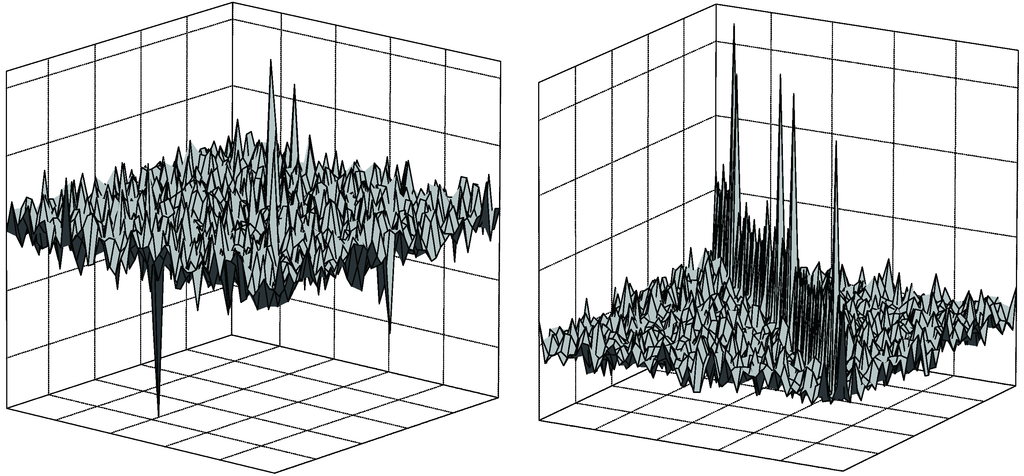
Figure 6.
3D plots of matrices Y (left) and R (right) under the C-model.
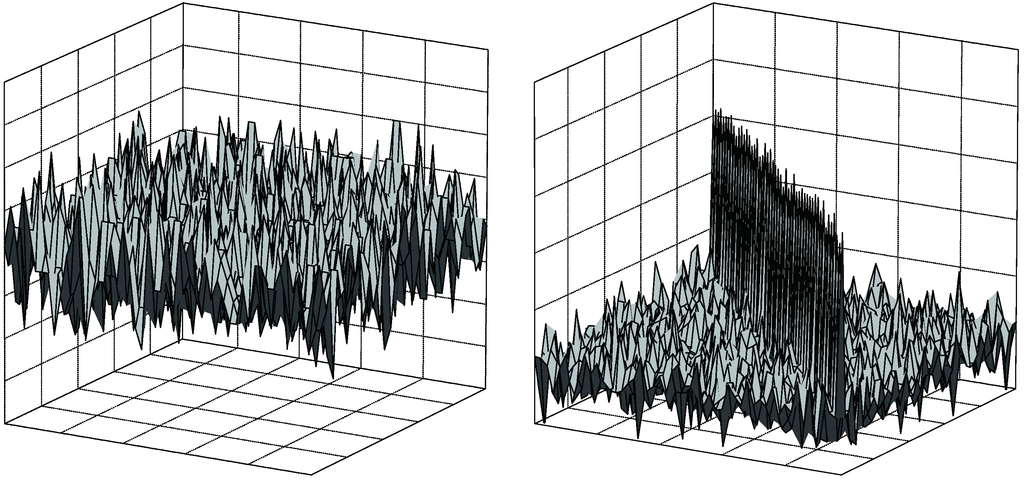
Figure 7.
3D plots of matrices Y (left) and R (right) under the R-model.

Table 2.
System Parameters for IN Analysis.
| C-model and R-model | |||
|---|---|---|---|
| Matrices plots | ROC curves | ||
| Moderate IN | Strong IN | ||
| Signal-to-noise ratio (SNR) in dB | −10 | −10 | −10 |
| Number of primary transmitters (p) | 1 | 1 | 1 |
| Number of CRs (m) | 50 | 6 | 6 |
| Samples collected by each CR (n) | 50 | 50 | 50 |
| Impulsive to thermal noise power ratio (K) | 2 | 1 | 10 |
| Probability of impulsive noise (pIN) | 1 | 1 | 0.2 |
| Fraction of CRs hit by impulsive noise (pCR) | 0.1 | 0.5 | 0.5 |
| Samples affected by impulsive noise (Ns) | 3 | 10 | 10 |
| Number of impulsive noise bursts (Nb) | 1 | 1 | 1 |
| R-model | |||
| MA-filter length | L = 10 | ||
| AGC dynamic range | D = 2 | ||
| AGC overdrive fac | fod = 8 | ||
| Number of quantization levels | Nq = 8 | ||
5.2. Influence of IN on ROC Curves
We now analyze the spectrum sensing performance under IN. We show that the low influence of this noise on Y and R in the case of the R-model, as graphically illustrated in the previous subsection, is translated into a robustness of Pfa and Pd, when compared with the C-model. We consider three IN conditions for all results presented in this subsection: absence, moderate IN, and strong concentrated IN. The system parameters are also in Table 2. When moderate IN is considered, we are simulating a situation in which IN is generated during all sensing intervals (pIN = 1), but it is not very strong (not concentrated, K = 1), affecting on average 50% of the cooperating CRs. Under strong IN we are simulating a situation in which IN is not very frequent (pIN = 0.2), but is very strong (concentrated, K = 10), also affecting 50% of the CRs, on average.
The ROC curves referred to in this subsection were inserted in Section 5.3, closer to other results related to IN countermeasures.
5.2.1. GLRT
Figure 8 shows the ROC curves for GLRT. It can be noticed, again, that the detection performance can be too optimistic if the conventional model (C-model) is adopted in the absence of IN. On the other hand, the performance can be pessimistic if the C-model is adopted with IN present. Moreover, one can notice from Figure 8 that the detection performance under the more realistic R-model suffers less influence of IN, as previously inferred visually in the shape of the received and covariance matrices (see Figure 7). It is also worth mentioning that the ranges of decision thresholds used for plotting the ROC curves under the R-model were the same for the scenarios with and without IN. This is an important result, because new decision thresholds need not be computed under IN circumstances, i.e., IN need not be detected. New decision thresholds must be determined for the C-model under IN, since the corresponding ROC curves in Figure 8, with and without IN, were plotted using very different decision threshold ranges.
As we can see in Figure 8, with the C-model, moderate impulsive noise seriously degrades the performance for all false alarm probability values. However, in the case of strong concentrated IN, an inflection is evident in the ROC curves. As the threshold is increased in the case of concentrated IN, the decision statistic starts to become strongly influenced by the IN. This is because the strong concentrated IN will govern the instantaneous SNR. As a consequence of the low instantaneous SNR regime beyond a given value of the threshold, Pfa becomes equal to Pd all the way up to zero. The performance under the R-model reveals that the signal processing tasks performed at each CR can increase the robustness of the spectrum sensing technique in the IN environment, as inferred from the analysis in Section 5.1. Moreover, it can be found that the detection performance values with strong concentrated IN and without IN are very close to one another in the case of the R-model. The better performance with strong concentrated IN, when compared with moderate IN, may be explained by the hard limiter at the AGC, which clips the high amplitudes that happen with strong IN. Similar to what had happened in the moderate IN condition, the ranges of decision thresholds for plotting the ROC curves under the R-model were the same for the scenarios with and without strong concentrated IN, and very different under the C-model.
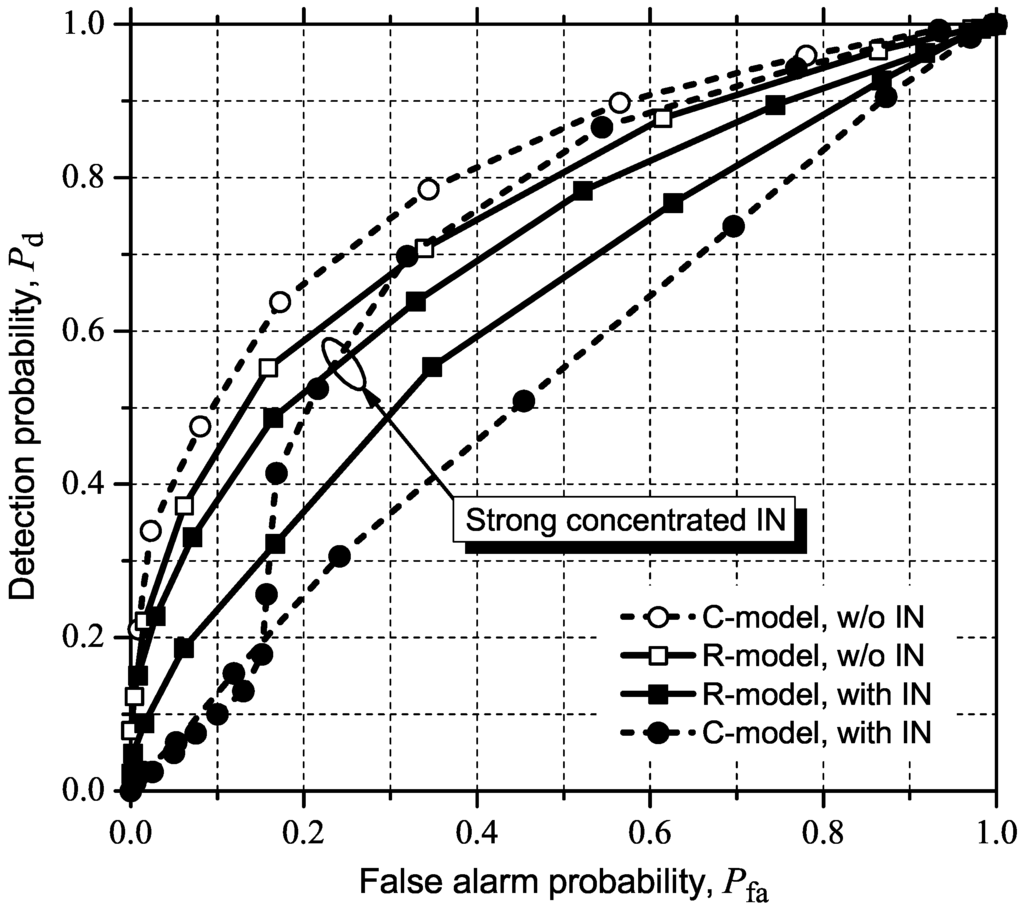
Figure 8.
ROC curves for the eigenvalue-based GLRT with and without (w/o) moderate or strong, concentrated IN.
5.2.2. MMED (or ERD)
Figure 9 shows the simulation results forMMED (or ERD). The system parameters and IN conditions are those mentioned at the beginning of the subsection. The same comments concerning Figure 8 apply, with the difference thatMMED seems to be less sensitive than GLRT to IN, although it is in fact because MMED’s performance is worse. In other words, we can infer that the susceptibility to IN is roughly the same for the eigenvalue-based GLRT and for MMED.
5.2.3. MED (or RLRT) and ED
Figure 10 shows the ROC curves for MED (or RLRT). Again, the system parameters and IN conditions are those mentioned at the beginning of the subsection. We can see that MED is heavily affected by IN under the C-model, more than GLRT and MMED are. The inflection is present again in the case of strong concentrated IN. The performance under the R-model is now more severely degraded than in GLRT and MMED, but the difference considering the presence and the absence of IN is by far smaller than in the case of the C-model. The poor performance of MED under the R-model, even in the case of no IN, is mainly due to the influence of the AGC, as previously stated. A similar behavior can be observed in Figure 11, which shows the performance results for ED. The performance degradation under the C-model is around the same order of magnitude of that observed in the case of MED. However, ED simply does not work under the R-model, with or without IN, this behavior being also credited to the influence of the AGC.
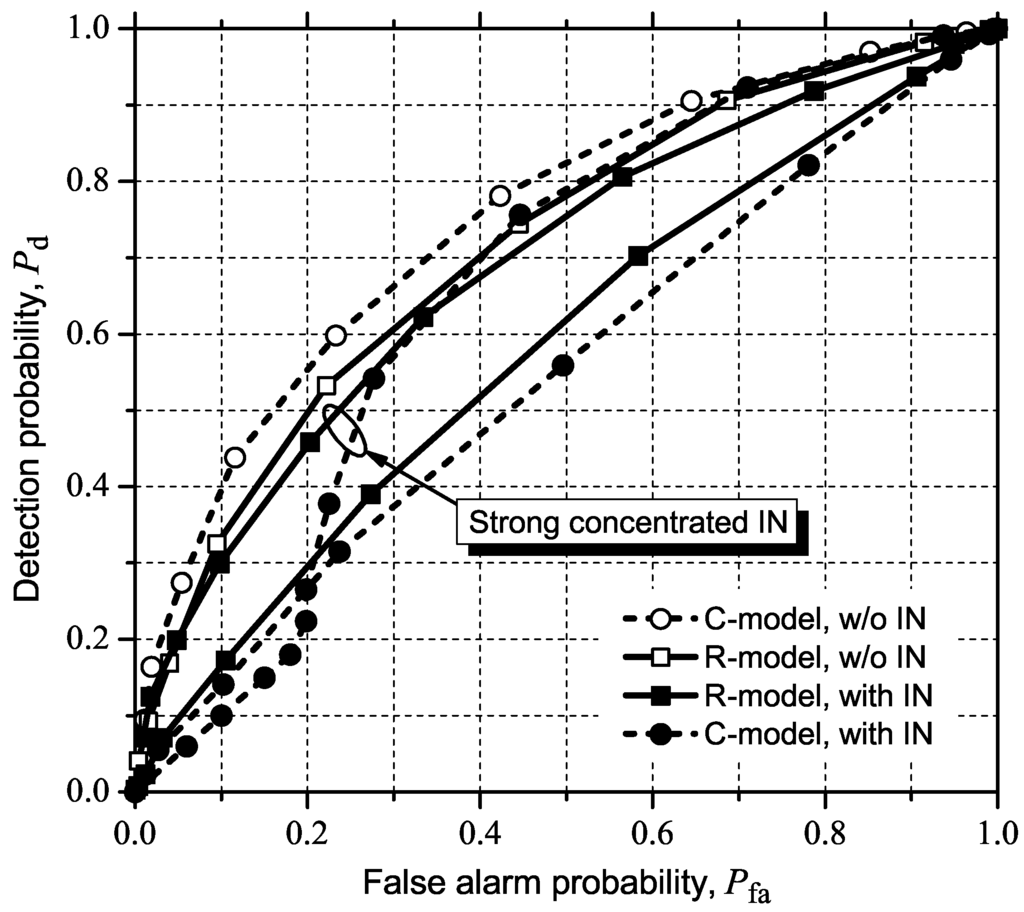
Figure 9.
ROC curves for MMED (or ERD) with and without (w/o) moderate or strong, concentrated IN.
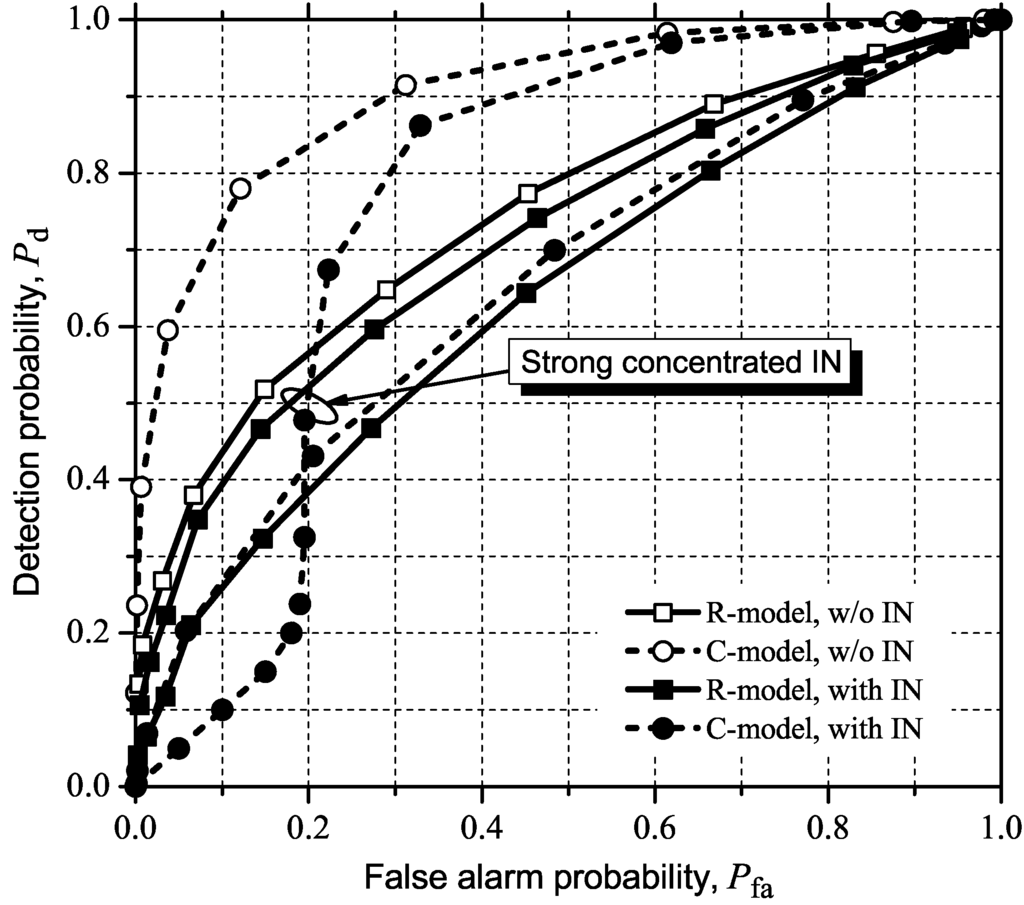
Figure 10.
ROC curves for MED (or RLRT) with and without (w/o) moderate or strong, concentrated IN.
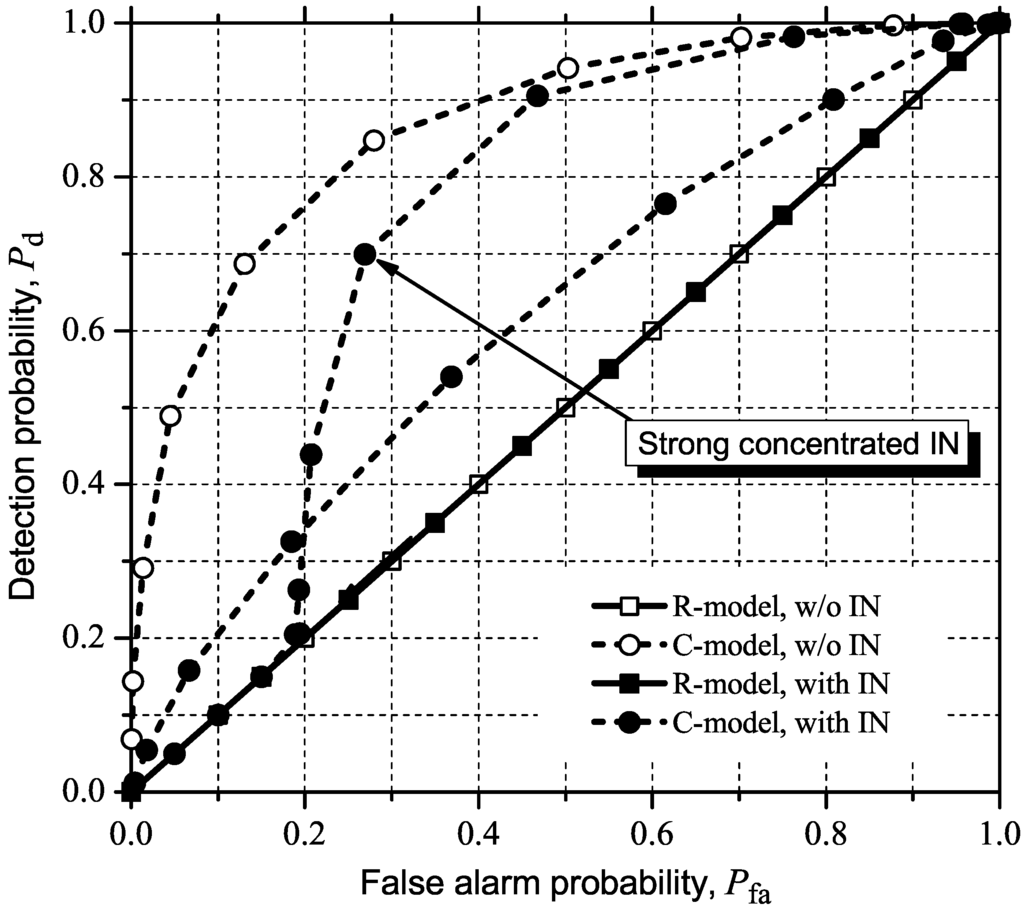
Figure 11.
ROC curves for ED with and without (w/o) moderate or strong, concentrated IN.
The bad performance of MED and ED under the R-model, with or without IN, confirms the need to consider the AGC gains in determining the noise variance used in the test statistics, and in deriving appropriate test statistics.
5.3. Detecting and Combating IN
Although some eigenvalue-based sensing schemes are robust against IN, particularly with the R-model, as shown in this paper, one might consider additional countermeasures to further reduce IN influence.
Detecting and removing IN influence is an active research topic in audio, image processing, and radio communications [12,13,14], and is beyond the scope of this contribution. In what follows we investigate the efficacy of two simple strategies for combating IN in eigenvalue-based spectrum sensing techniques, assuming that IN presence is perfectly known. This assumption aims at decoupling IN-detection performance from spectrum sensing performance, directing the attention towards the latter. Furthermore, it is particularly useful for determining the spectrum sensing performance gain under the R-model and measure its intrinsic ability for combating IN. In other words, small performance improvements brought by the IN countermeasures are an indication of the inherent IN immunity of the R-model. Particularly, we investigate the following heuristic strategies for combating IN when it is present: muting the samples under IN and eliminating from cooperation those CRs under IN.
In the second countermeasure, the effective number of cooperating CRs is found as
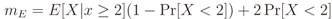 where X is the random variable that models the number of CRs not hit by IN (see details in the Appendix).
where X is the random variable that models the number of CRs not hit by IN (see details in the Appendix).
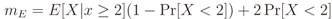
Figure 12, Figure 13, Figure 14, Figure 15 show the simulation results considering the above-mentioned IN countermeasure strategies for GLRT, MMED (or ERD), MED (or RLRT), and ED. As previously emphasized, these figures were inserted close to the corresponding results from subsection 5.2 to facilitate comparisons. The system parameters for moderate IN are those in Table 2. In CR elimination, the number of CRs, m, was modified so that the effective number of cooperating CRs, mE , was made as close as possible to 6. We have not chosen to keep m = 6, since mE would be smaller than six, pushing the ROC curves towards Pfa = Pd and approximating them from each other. This would prevent a clear view of the effect of the CR elimination countermeasure.
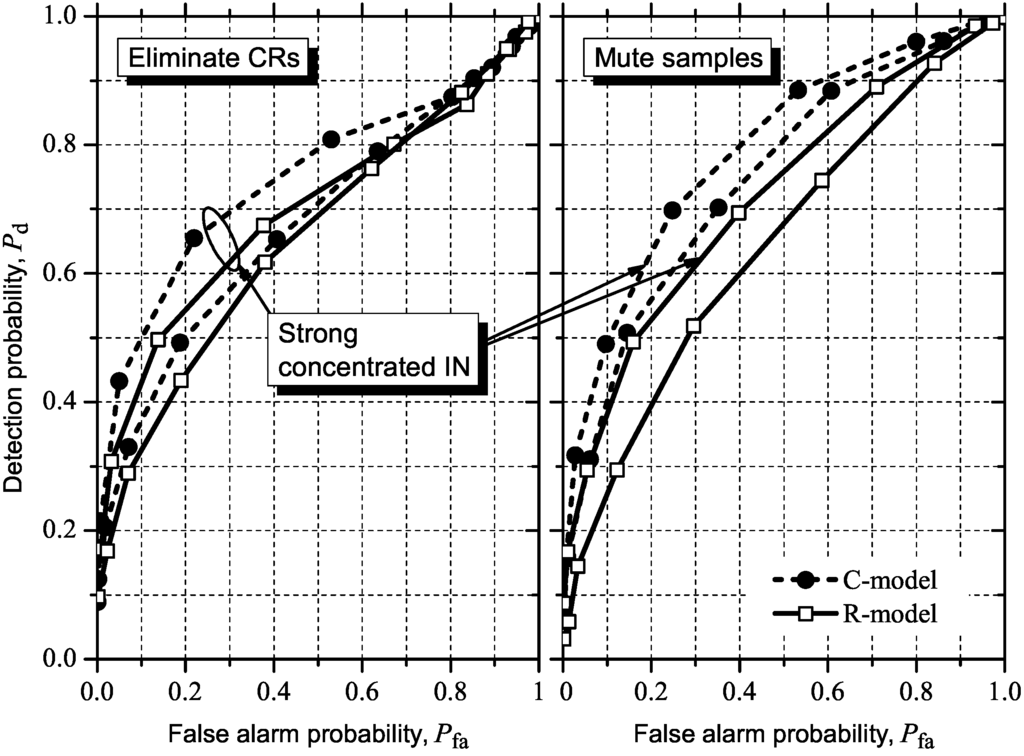
Figure 12.
Effect of muting samples and CR elimination under moderate or strong concentrated IN on GLRT.
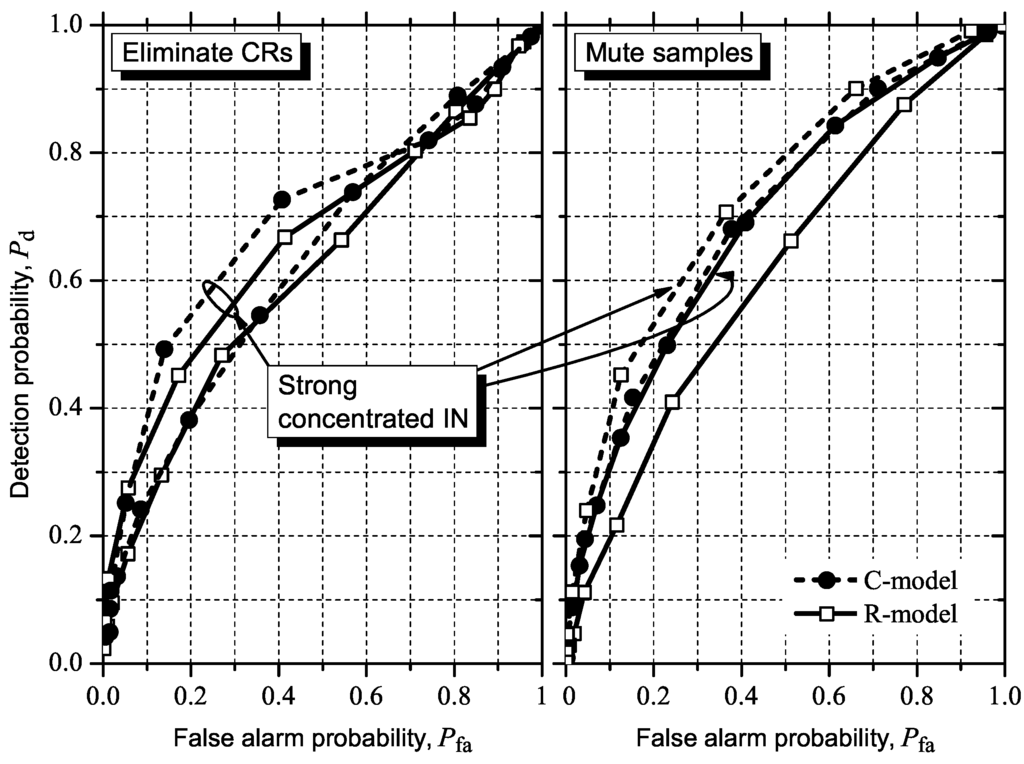
Figure 13.
Effect of muting samples and CR elimination under moderate or strong concentrated IN on MMED (or ERD).
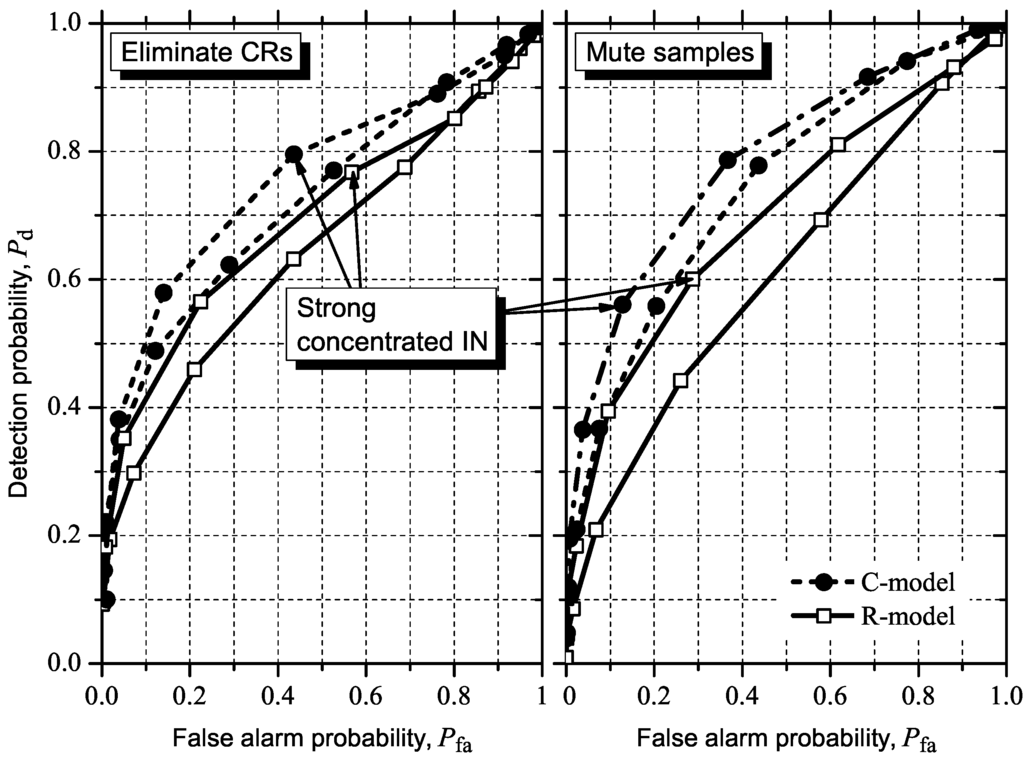
Figure 14.
Effect of muting samples and CR elimination under moderate or strong concentrated IN on MED (or RLRT).
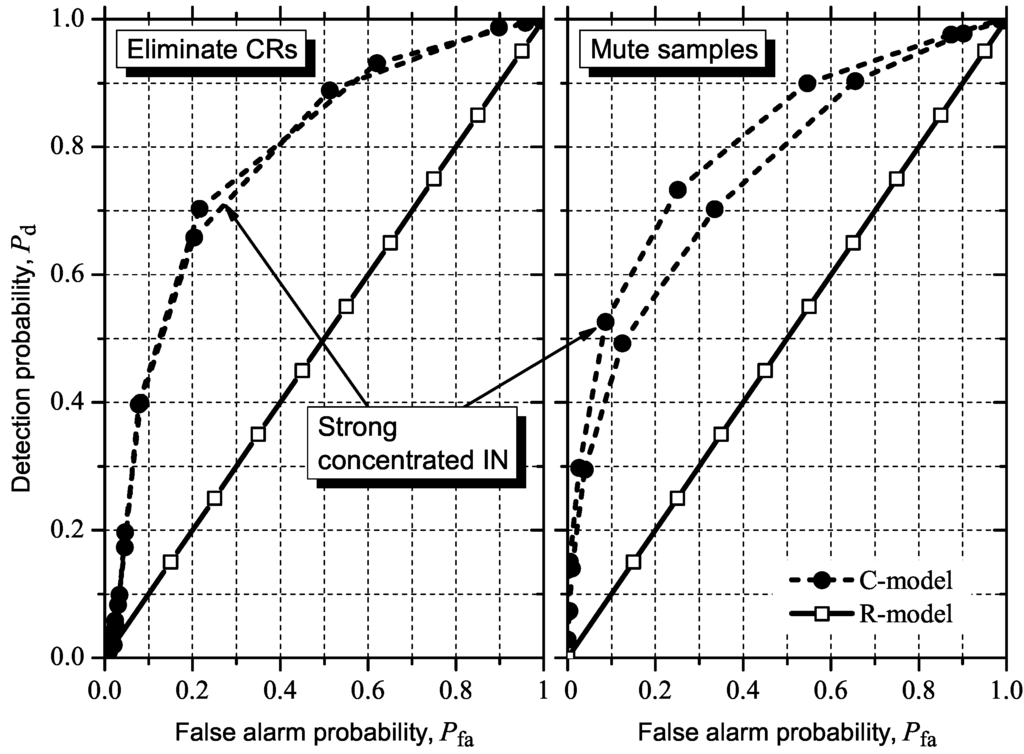
Figure 15.
Effect of muting samples and CR elimination under moderate or strong concentrated IN on ED.
In what concerns GLRT, we compare all ROC curves in Figure 12 with the corresponding curves in Figure 8. Under the C-model, we can see that both CR elimination and sample muting significantly improve performance, with an advantage of muting, which pushes the ROC curve with IN towards the neighborhood of the curve without IN. In other words, the IN countermeasures are effective under the C-model. Under the R-model, however, the IN countermeasures produce only marginal improvements for both moderate and strong concentrated IN. This indeed is evidence that the implementation-oriented model has inherent IN robustness.
The above comparisons and conclusions closely hold for MMED (or ERD), as can be seen by comparing all ROC curves in Figure 13 with the corresponding curves in Figure 9. A small improvement can be observed for both IN countermeasures under the R-model, in the case of moderate IN. A small performance reduction is observed under the R-model in the case of strong concentrated IN and CR elimination; a marginal gain is observed for the sample muting. The improvement under the C-model, however, is noticeable larger in all situations. Once more, this is evidence that the implementation-oriented model has inherent IN robustness.
For MED (or RLRT), we compare all ROC curves in Figure 14 with the corresponding curves in Figure 10. Now we can see that the performance improvements caused by the IN countermeasures under the C-model, though evident, are not as large as in the cases of GLRT and MMED (or ERD). Under the R-model we observe no improvement in the case of strong concentrated IN for both IN countermeasures, and a performance reduction for moderate IN and sample muting. No improvement is observed under the R-model also for moderate IN and CR elimination. The marginal variations in performance under the R-model are, once more, evidence of the ability of the implementation-oriented model in combating IN.
6. Conclusions
From the results presented in this paper we can conclude that typical signal-processing tasks performed at each cognitive radio before the collected samples are sent to the fusion center must be taken into account when investigating soft-values fusion algorithms, as the performance results may vary significantly between an idealized and a realistic model. Furthermore, the realistic model shows that the impact of impulsive noise is not as negative in real life as it could be implied from an idealized model.
We also conclude that GLRT performs better under IN circumstances, closely followed by MMED. The performance of MED and ED is drastically degraded by the effect of IN, with a clear advantage of MED over ED, since the latter did not work at all in any of the simulated scenarios. The superior performance of GLRT and MMED is attributed to the inherent ability of the eigenvalues of the covariance matrix Y in reflecting the presence of IN. MED and ED, on the contrary, are very sensitive to IN and suffer from the need to use the thermal noise variance that, in practice, is very difficult to estimate if IN is present. Noise variance uncertainty can itself bring forth severe performance degradation in MED and ED [6,26]. Additionally, the decision thresholds for all detection techniques investigated under the conventional model had to be drastically modified from the situation of absence to the presence of IN for the techniques to work. This would be a strong limitation in practice, since it would demand detecting the presence of IN for posterior adaptation of the threshold.
Last but not least, we conjecture that the performance of MED and ED under the implementation-oriented model can be improved if the known normalization gains before the ADC are taken into account for the design of new test statistics and for producing the estimate of the thermal noise power in each cognitive radio. ED has a stronger demand for such improvement, since it simply does not work based on the test statistic (6). As already stated, this remains an open problem for future investigation
Appendix
From the impulsive noise model described in Section 2.2, let Y be a binomial random variable with parameters m and pCR, and let U be a Bernoulli random variable with probability of success pIN. The random variable that models the number of CRs not affected by impulsive noise can be defined by
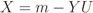
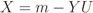
The number of CRs under cooperation resulting from the CR elimination IN countermeasure will be the random variable
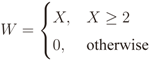
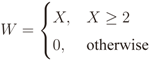
The average number of CRs under cooperation, mE , is the expected value of W, which is given by Equation (8). The reasoning behind the definition of W is the following: If the number of CRs not hit by IN is greater than or equal to 2, this will be the number of CR signals used for cooperation. If the number of CRs not hit by IN is smaller than 2, a minimum of 2 CR signals must be used, since we are dealing with covariance matrix-based spectrum sensing, whose matrix order must be greater than or equal to two. In the simulations, if all CRs are under IN, two of them are randomly chosen for cooperation. If only one CR is free of IN, it is chosen for cooperation, plus any other CR hit by IN.
The values of E[X|x ≥ 2] and Pr[X < 2] in Equation (8) can be computed from the probability mass function (pmf) of the random variable Z = YU, which is
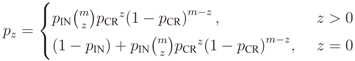 and from the pmf of X = m − Z, which is given by
and from the pmf of X = m − Z, which is given by
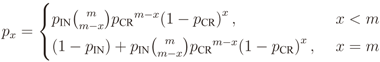 where
where 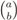 is the binomial coefficient and where we have used the shorthand notations pz and px for Pr[Z = z] and Pr[X = x], respectively. Then we finally have
is the binomial coefficient and where we have used the shorthand notations pz and px for Pr[Z = z] and Pr[X = x], respectively. Then we finally have
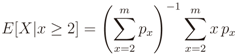
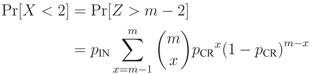
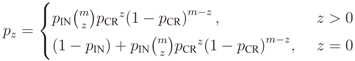
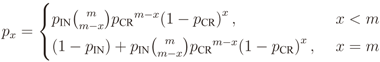
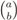 is the binomial coefficient and where we have used the shorthand notations pz and px for Pr[Z = z] and Pr[X = x], respectively. Then we finally have
is the binomial coefficient and where we have used the shorthand notations pz and px for Pr[Z = z] and Pr[X = x], respectively. Then we finally have
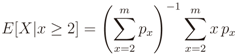
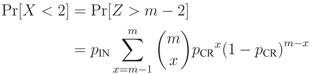
Supplementary Files
References
- Mitola, J., III.; Maguire, G., Jr. Cognitive radio: Making software radios more personal. IEEE Pers. Commun. 1999, 6, 13–18. [Google Scholar] [CrossRef]
- Qiu, R.; Guo, N.; Li, H.; Wu, Z.; Chakravarthy, V.; Song, Y.; Hu, Z.; Zhang, P.; Chen, Z. A unified multi-functional dynamic spectrum access framework: Tutorial, theory and multi-ghzwideband testbed. Sensors 2009, 9, 6835–6835. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Lo, B.; Balakrishnan, R. Cooperative spectrum sensing in cognitive radio networks: A survey. Phys. Commun. 2011, 4, 40–62. [Google Scholar] [CrossRef]
- Zeng, Y.; Liang, Y.-C. Eigenvalue-based spectrum sensing algorithms for cognitive radio. IEEE Trans. Commun. 2009, 57, 1784–1793. [Google Scholar] [CrossRef]
- Kortun, A.; Ratnarajah, T.; Sellathurai, M.; Zhong, C.; Papadias, C. On the performance of eigenvalue-based cooperative spectrum sensing for cognitive radio. IEEE J. Sel. Top. Signal Process. 2011, 5, 49–55. [Google Scholar] [CrossRef]
- Nadler, B.; Penna, F.; Garello, R. Performance of Eigenvalue-Based Signal Detectors with Known and Unknown Noise Level. In Proceedings of the 2011 IEEE International Conference on Communications, ICC, Kyoto, Japan, 5–9 June 2011; pp. 1–5.
- Liu, X. A survey on clustering routing protocols in wireless sensor networks. Sensors 2012, 12, 11113–11153. [Google Scholar] [CrossRef]
- Guimarães, D.A.; Souza, R.A.A. Implementation-oriented model for centralized data-fusion cooperative spectrum sensing. IEEE Commun. Lett. 2012, 16, 1804–1807. [Google Scholar] [CrossRef]
- Martinez-Rodriguez-Osorio, R.; de Haro-Ariet, L.; Calvo-Ramon, L.M.; Sanchez, M.G. Performance evaluation of W-CDMA in actual impulsive noise scenarios using adaptive antennas. IEEE Proc. Commun. 2004, 151, 589–594. [Google Scholar] [CrossRef]
- Budsabathon, M.; Hara, S. Robustness of OFDM Signal Against Temporally Localized Impulsive Noise. In Proceedings of the IEEE VTS 54th Vehicular Technology Conference, VTC 2001 Fall, Atlantic City, NJ, USA, 7–11 October 2001; Volume 3, pp. 1672–1676.
- Kang, H.G.; Song, I.; Yoon, S.; Kim, Y.H. A class of spectrum-sensing schemes for cognitive radio under impulsive noise circumstances: Structure and performance in nonfading and fading environments. IEEE Trans. Veh. Tech. 2010, 59, 4322–4339. [Google Scholar] [CrossRef]
- Pander, T. Application of weighted myriad filters to suppress impulsive noise in biomedical signals. TASK Quarterly 2004, 8, 199–216. [Google Scholar]
- Saarnisaari, H.; Henttu, P. Impulse Detection and Rejection Methods for Radio Systems. In Proceedings of the 2003 IEEE Military Communications Conference, MILCOM’03, Boston, MA, USA, 13–16 October 2003; Volume 2, pp. 1126–1131.
- Carrillo, R.; Aysal, T.; Barner, K. A Theoretical Framework for Problems Requiring Robust Behavior. In Proceedings of the 3rd IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, CAMSAP, Aruba, Dutch Antilles, 13–16 December 2009; pp. 25–28.
- Sendora Project Public deliverable D4.1. Interference Model Based on Scenarios and System Requirements. Available online: http://www.sendora.eu/node/86 (accessed on 1 March 2012).
- Mashhour, A.; Domino, W.; Beamish, N. On the direct conversion receiver-a tutorial. Microw. J. 2001, 44, 114–128. [Google Scholar]
- Svitek, R.; Raman, S. DC offsets in direct-conversion receivers: Characterization and implications. IEEE Microw. Mag. 2005, 6, 76–86. [Google Scholar] [CrossRef]
- Razavi, B. Design considerations for direct-conversion receivers. IEEE Trans. Circuits Syst. II: Analog Digital Signal Process. 1997, 44, 428–435. [Google Scholar]
- Mailand, M.; Jentsche, H.J. Compensation of DC-Offsets and RF-Self-Mixing Products in Six-Port-Based Analog Direct Receivers. In Proceedings of the 14th IST Mobile & Wireless Comm. Summit, Dresden, Germany, 19–22 June 2005.
- Zheng, Y.; Tear, C.B.; Wong, S.J. DC Offset-Free RF Front-End Circuits and Systems for Direct Conversion Receivers. US Patent No. 7,164,901 B2, 2007. [Google Scholar]
- Mann, I.; McLaughlin, S.; Henkel, W.; Kirkby, R.; Kessler, T. Impulse generation with appropriate amplitude, length, inter-arrival, and spectral characteristics. IEEE J. Sel. Areas Commun. 2002, 20, 901–912. [Google Scholar] [CrossRef]
- Lago-Fernández, J.; Salter, J. Modeling Impulsive Interference in DVB-T: Statistical Analysis, Test Waveforms and Receiver Performance 2004. BBC R&D White Paper WHP 080.
- Middleton, D. Non-Gaussian noise models in signal processing for telecommunications: New methods an results for class A and class B noise models. IEEE Trans. Inf. Theory 1999, 45, 1129–1149. [Google Scholar] [CrossRef]
- Cichocki, A.; Amari, S. Adaptive Blind Signal and Image Processing; John Wiley and Sons, Inc.: Chichester, UK, 2002. [Google Scholar]
- IEEE Standard for Information Technology–Telecommunications and information exchange between systems Wireless Regional Area Networks (WRAN)–Specific requirements Part 22: Cognitive Wireless RAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications: Policies and Procedures for Operation in the TV Bands. IEEE Std 802.22-2011, 2011, pp. 1–680
- Lim, T.J.; Zhang, R.; Liang, Y.C.; Zeng, Y. GLRT-Based Spectrum Sensing for Cognitive Radio. In Proceedings of the Global Telecommunications Conference, IEEE GLOBECOM 2008, New Orleans, LA, USA, 30 November–4 December 2008; pp. 1–5.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).