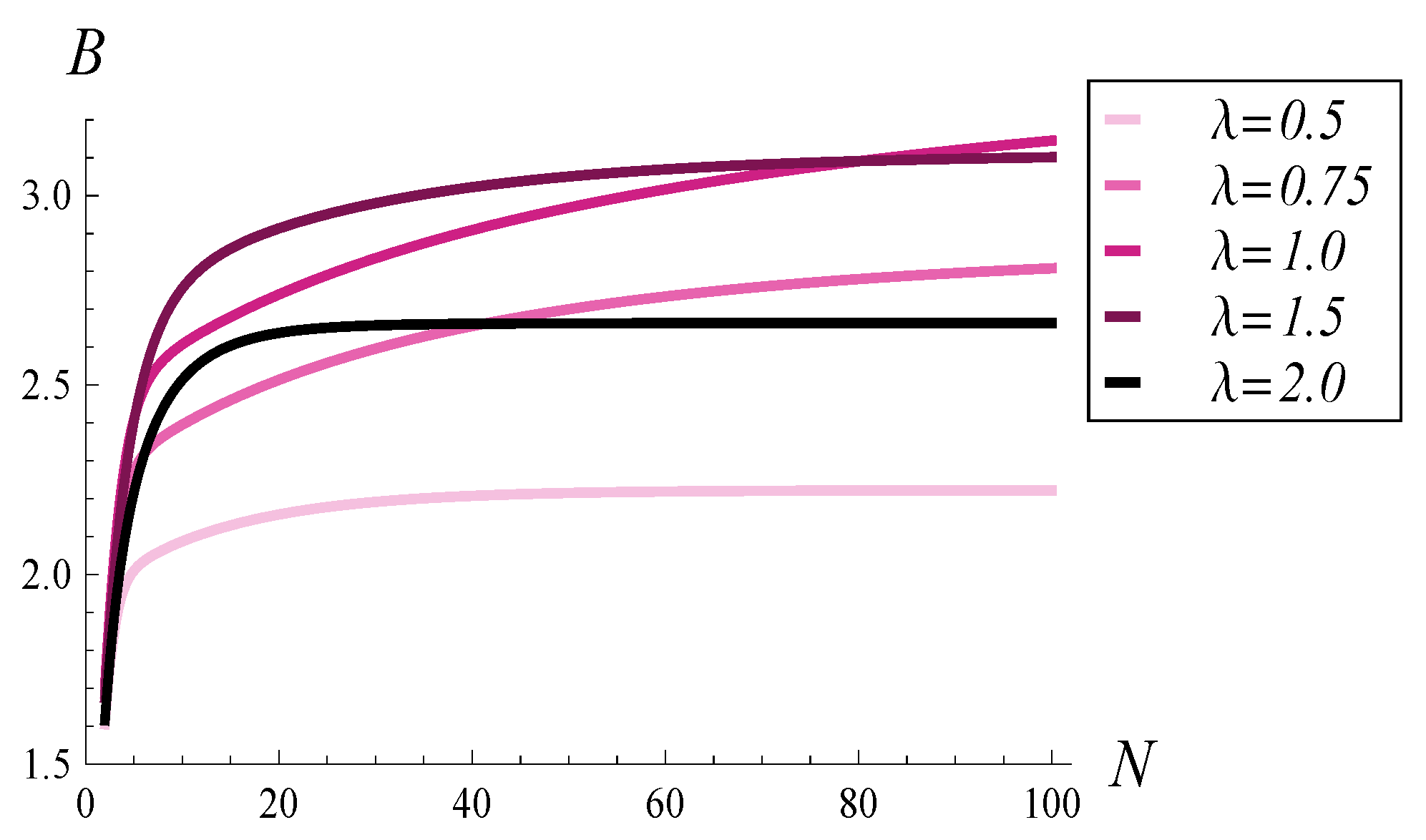Loss Clustering at MSP Buffer

Abstract

Packet losses cause a decline in the performance of packet networks, and this decline is related not only to the percentage of losses but also to the clustering of them together in series. We study how the correlation of packet sizes influences this clustering when the losses are caused by buffer overflows. Specifically, for a model of a buffer with correlated packet sizes, we derive the burst ratio parameter, an intuitive metric for the inclination of losses to cluster. In addition to the burst ratio, we obtain the sequential losses distribution in the first, k-th, and stationary overflow periods. The Markovian Service Process (MSP) used by the model empowers it to mimic arbitrary packet size distributions and arbitrary correlation strengths. Using numeric examples, the impact of packet size correlation, buffer size, and traffic intensity on the burst ratio is showcased and discussed.

1. Introduction

Packet buffers are omnipresent in computer networking, in virtually all types of networks and networking devices, including sensor and actuator networks [1,2,3,4,5,6,7]. These buffers have several roles to play: they decrease packet loss by capturing traffic bursts, increase the throughput by preventing the output link from experiencing starvation, smooth the packet transmission process, and more. However, what makes the buffers less effective than wanted and expected is the autocorrelation of traffic. In particular, the consecutive packet sizes are often correlated, which arises out of the design of networking protocols.

Packets of correlated sizes, processed by a buffer, have several negative effects on queueing performance. Firstly, the packet transmission times are correlated in the same manner as the packet sizes (see the egress link in Figure 1), which causes a decline in the throughput of the link. Secondly, the mean buffer occupancy is higher, leading to longer queueing delays. Thirdly, the buffer overflows for more time on average, resulting in greater packet loss (again, see Figure 1).

All three of these negative effects are well understood and documented in the literature, which will be covered in the next section. There is, however, one more negative consequence of correlated packet sizes that will be studied herein: the aggregation of packet losses in groups, one after another.

Why is this important? When transmitting information of different types, it is often the case that short, isolated gaps are much less damaging than long, continuous gaps, even if the latter occur less frequently. This can be credited to the natural redundancy of information in the transmitted stream, the time-critical nature of the information, redundant coding built into the transmission, or a combination of these factors.

Consider, for illustration, a simple example of a text that is supposed to be transmitted:

SHE_HAS_BLUE_EYES

Then, consider two unsuccessful transmissions of this text, such that in each of them, four letters are lost (black squares):

SH◼_H◼S_◼LUE_EYE◼

SHE_HAS_BL◼◼◼◼YES

We can successfully guess the full message in the first transmission, while, in the second one, it is very difficult or impossible. In both cases, the loss probability is the same, 4/17, but, in the second case, the losses are grouped together. Obviously, the recovery of missing information in the first case occurs due to the natural redundancy of information in the English language. Unfortunately, this redundancy cannot help when the gap is too long.

In sensor and actuator networks, longer gaps can cause problems because of the nature of the transmitted information. For example, if a network is used to monitor temperature, pressure, or chemical solution content, it can be much more damaging when information is missing for a relatively long time–even if rarely—than when it is missing for only short moments—even if more frequently.

The International Telecommunication Union has studied in detail the decline in the quality of packetized voices due to the occurrence of packet losses in series (see the references in the next section). When a video stream is transmitted, it is perhaps less annoying for the viewer if one frame is lost after every nine frames, rather than losing ten frames in a row after ninety frames.

In general, there are many networking scenarios where a structure of losses like this:

$$◻◻◼◻◻◼◻◻◼◻◻◻◻◻◻◻◼$$

is better than a structure of losses like this:

◻◻◻◻◻◻◻◻◻◻◼◼◼◼◻◻◻

while it is hard to think of an example where the reverse is true.

The best parameter to express the clustering of loss is the burst ratio, B. It is defined as the mean number of sequential losses, $\overline{H}$, to the theoretical mean number of sequential losses, $\overline{K}$, that occur in a Bernoulli process, i.e., when all losses happen independently of each other. By definition, we have

$$B={\displaystyle \frac{\overline{H}}{\overline{K}}}.$$

(1)

If the packet loss probability is L, then it is easy to establish that $\overline{K}=1/(1-L)$. Thus, we get

$$B=\overline{H}(1-L).$$

(2)

Parameter B has a very nice, intuitive explanation. When $B>1$, the losses must have a statistical inclination to cluster together. The larger B, the more pronounced this inclination. Naturally, $B>1$ may occur only when the losses are strongly dependent on each other and when the chance that a packet is lost given that the previous one was also lost is higher than L. When $B<1$, the losses must have a statistical inclination to be isolated. Again, the smaller B, the more pronounced this inclination. When $B=1$, the occurrence of losses is random and independent, with clustering characteristics typical of a Bernoulli process. It is simple to confirm that for the two examples above of 17 transmitted packets with four losses, the burst ratios are 0.76 and 3.06, respectively. The very high $B=3.06$ in the latter case indicates a very strong clustering inclination.

In this study, we will calculate the burst ratio, assuming the model of a buffer with correlated packet sizes. To the best of the authors’ knowledge, such a formula has not been derived before. Then, we will examine the effect of packet size correlation, buffer size, and traffic intensity on the value of B. To derive B, we will also establish the sequential loss distribution in both transient and stationary cases. These not only constitute intermediate steps for computing the burst ratio but are also interesting as standalone characteristics.

In networking, correlated packet sizes are synonymous with correlated service (transmission) times. Therefore, in the rest of this paper, the term “correlated packet sizes” will be used interchangeably with the term “correlated service times.” To model this phenomenon, the Markovian Service Process (MSP) will be employed herein. MSP combines analytical tractability with great modeling flexibility. Specifically, it enables the modeling of arbitrary distributions of service times (packet sizes) as well as arbitrary correlations between service times.

In detail, the contributions made by this study are

• a formula for the sequential loss distribution in the first and k-th buffer overflow periods (Theorems 1 and 2, respectively);
• a formula for the sequential loss distribution in the stationary overflow period (Theorem 3);
• a formula for the burst ratio (Theorem 4);
• numerical results illustrating the impact of packet size correlation, buffer size, and traffic intensity on the burst ratio.

This study proceeds as follows. In Section 2, previous work related to the burst ratio and buffers with MSP service is reviewed. In the next section, the model of the buffer and the packet transmission process is presented in detail. Then, in Section 4 and Section 5, three intermediate formulas needed for the burst ratio are given. In particular, Section 4 presents a formula for the sequential loss distribution in the first overflow period. Section 5 provides formulas for the sequential loss distribution in the k-th overflow period and the stationary case.

The central result of this paper, the formula for B, is given in Section 6. Section 7 discusses computational aspects of all the previously derived formulas. Section 8 is devoted to numerical examples. First, the impact of buffer size and traffic intensity on B is demonstrated for both positive and negative correlations of service times. Second, the effect of correlation strength is examined for the two types of correlation and compared with the uncorrelated case. Third, two examples of concrete engineering problems related to loss clustering and the burst ratio are presented and solved. Fourth, theoretical results are compared with simulation results at the end of Section 8. Finally, Section 9 presents concluding remarks, discusses the limitations of this study, and proposes directions for future research.

2. Related Work

To the best of the authors’ knowledge, the results of this paper are new. No previously published study has addressed the burst ratio or loss clustering at a buffer with correlated packet sizes.

Early approaches to modeling packet loss were based on abstract stochastic processes, decoupled from the actual causes of loss. These included two-state Markov chains [8], k-state Markov chains [9], and the Gilbert–Elliott model [10]. Later, the loss process was modeled using the actual, common cause of packet loss, namely, buffer overflows [11].

The burst ratio was originally introduced in [12]. It was initially studied for a two-state Markov loss model in [12,13,14]. Specifically, the formula for B in one loss channel was derived in [12]. In [13,14], the burst ratio was established for multiple concatenated channels, where the model of each channel was founded upon a two-state Markov chain. The International Telecommunication Union studied the decline of packetized voice quality related to B in [15,16]. In [15], provisional planning values were provided for codec performance under extreme burst ratio values above 4 (see Tables I.4–5 of [15]). In [16], a formula expressing voice transmission impairment based on B was proposed (see Formulas (7–29) of [16]). More recently, the burst ratio was calculated using a buffer overflow model of losses [17]. The study demonstrated that the buffering mechanism itself can be a source of high burst ratio values. This is relatively easy to understand: when the buffer is overflowed, it may remain so for some period of time. During this overflow period, all arriving packets are dropped consecutively, thus increasing the burst ratio. The buffer overflow period itself has also been studied as a distinct characteristic, independent of the burst ratio (see, e.g., [18]).

It must be emphasized that up to now, studies related to the burst ratio have not incorporated correlations of packet sizes (service times). As we will see in Section 8, this correlation has a significant impact on B.

The correlation of service times, as incorporated in this work, is modeled using the Markovian Service Process (MSP) [19]. This stochastic process has been used to derive various performance characteristics of buffering mechanisms [20,21,22,23,24,25,26,27,28,29,30,31]. These studies differed in several respects: the assumed buffer size (finite in [20,21,22,28,29,31] versus infinite in [23,24,25,26,27,30]); the performance characteristics analyzed (e.g., buffer occupancy, waiting time, loss probability, sojourn time, busy period, idle period, buffer throughput); the analytical approach (e.g., the root method in [24]); and the treatment of batch arrivals or services.

However, none of these studies on buffers with MSP service addressed the burst ratio parameter.

Finally, note that this study deals with the FIFO policy with tail dropping, which is the simplest and most commonly used policy. Since the burst ratio strongly depends on the packet discarding policy, the results of this paper are not applicable to any of the active management policies, e.g., [32,33,34,35,36].

3. Buffer Model

We assume a FIFO buffer with a capacity of N packets, including the one currently being transmitted, if applicable. If, on a packet arrival, the buffer is full—i.e., it already stores N packets—the new packet is discarded. Packets are served (transmitted) from the buffer’s head. Since the packet sizes are correlated, the transmission times are correlated in the same manner, which is modeled by the Markovian Service Process (MSP).

An MSP is parameterized by two square $M\times M$ matrices, ${\mathbf{L}}_0$ and ${\mathbf{L}}_1$, such that ${\mathbf{L}}_0$ has negative elements only on the diagonal, while ${\mathbf{L}}_1$ has all entries non-negative. Furthermore, $\mathbf{L}={\mathbf{L}}_0+{\mathbf{L}}_1$ must have each row summing to zero so that it can serve as the infinitesimal generator of a Markov chain with service states set as $1,\dots ,M$.

Once an MSP is parameterized, its evolution can be described as follows. If, at time t, the buffer is non-empty, the service state $S\left(t\right)$ evolves as a Markov chain with infinitesimal generator L. Moreover, if $S\left(t\right)=j$, then at $t+\mathrm{d}t$, the service state may change to k with probability ${\mathbf{L}}_0(j,k)\mathrm{d}t+o\left(\mathrm{d}t\right)$, in which case, the ongoing packet service continues. Alternatively, it may change to k with probability ${\mathbf{L}}_1(j,k)\mathrm{d}t+o\left(\mathrm{d}t\right)$, in which case, the ongoing packet service is completed.

During any idle period, $S\left(t\right)$ remains unchanged and equal to the last service state prior to the buffer becoming empty.

The mean packet service rate, $\mu$, can be calculated by means of the relation

$$\mu =\mathsf{\pi }{\mathbf{L}}_1\mathbf{e},$$

(3)

where $\mathsf{\pi }$ stands for the stationary vector for infinitesimal generator L and

$$\mathbf{e}={[1,\dots ,1]}^T.$$

(4)

Packet arrivals follow the Poisson process of rate $\lambda$. The traffic intensity $\rho$ is, therefore,

$$\rho ={\displaystyle \frac{\lambda }{\mu }},$$

(5)

where $\mu$ is given in (3).

We denote the buffer occupancy at time t by $X\left(t\right)$, including the packet being transmitted, if applicable.

Finally, the correlation coefficient of two consecutive service times, $corr$, is

$$corr={\displaystyle \frac{\mu \mathsf{\pi }{(-{\mathbf{L}}_0)}^{-1}{\mathbf{L}}_1{(-{\mathbf{L}}_0)}^{-1}\mathbf{e}-1}{2\mu \mathsf{\pi }{(-{\mathbf{L}}_0)}^{-1}\mathbf{e}-1}},$$

(see, e.g., [37]).

4. First Series of Losses

Naturally, a few packets are lost sequentially only within a single buffer overflow period. The overflow period ends when at least one free position becomes available in the buffer. Thus, the next arriving packet will be accepted, terminating the loss sequence.

In order to derive B using (2), we first need to compute $\overline{H}$, which is the mean number of sequential losses in the stationary regime. Before this can be accomplished, however, we must establish the distribution of the count of losses in the first and, more generally, the k-th overflow period.

Therefore, the overall plan of the work requires the derivation of the following:

• Sequential loss distribution in the first overflow period.
• Sequential loss distribution in the k-th overflow period, $k\ge 2$.
• Sequential loss distribution in the stationary overflow period.
• Burst ratio, B.

Each of these tasks depends on the preceding one and must be carried out in the specified order. Task 1 is described in this section, Tasks 2 and 3 in Section 5, and the final task in Section 6. The characteristics obtained in Tasks 1–3 not only serve as intermediate steps toward Task 4 but are also valuable as standalone performance metrics.

Lastly, note that to compute B from (2), we need not only $\overline{H}$ but also the loss probability L. This has already been computed at this stage and will be recalled in Section 7.

We now begin with the first task. Naturally, the sequential loss distribution during the first overflow period depends on the initial conditions, specifically, the initial service state and buffer occupancy. Let $a_i(n,l)$ be the probability that there are l packet losses during the first overflow period, given that $S\left(0\right)=i$ and $X\left(0\right)=n$.

Assume first that the buffer is initially almost full, with one free position, i.e., $X\left(0\right)=N-1$. We can assemble the following equation expressing $a_i(N-1,l)$:

$$\begin{array}{cc}\hfill a_i(N-1,l)=& \sum _{j=1}^M{\int }_0^{\infty }{f}_{i,j}(t,0)\lambda e^{-\lambda t}\mathrm{d}t\sum _{k=1}^M{\int }_0^{\infty }{\displaystyle \frac{e^{-\lambda y}{\left(\lambda y\right)}^l}{l!}}{h}_{j,k}\left(y\right)\mathrm{d}y\hfill \\ \hfill & +\sum _{m=1}^{N-2}\sum _{j=1}^M{\int }_0^{\infty }{f}_{i,j}(t,m)a_j(N-m,l)\lambda e^{-\lambda t}\mathrm{d}t\hfill \\ \hfill & +\sum _{j=1}^M{\int }_0^{\infty }{g}_{i,j}(t,N-1)a_j(1,l)\lambda e^{-\lambda t}\mathrm{d}t.\hfill \end{array}$$

(6)

Before we can explain (6), we need to present definitions of functions $f_{i,j}(t,m)$, $g_{i,j}(t,m)$, and $h_{i,j}\left(t\right)$ which are present there. First, $f_{i,j}(t,m)$ denotes the probability of m packet services finished in $(0,t)$ and the service state being j at t, given that $X\left(0\right)>m$ and $S\left(0\right)=i$. Second, $g_{i,j}(t,m)$ denotes the probability of m packet services finished in $(0,t)$ and having the service state j at the end of the m-th service, given that $X\left(0\right)>m$ and $S\left(0\right)=i$. Third, $h_{i,j}\left(t\right)\mathrm{d}t$ stands for the probability of the first service ending at $(t,t+\mathrm{d}t)$ and the service state being j just after that, given that $S\left(0\right)=i$.

Equation (6) can be detailed as follows. We have conditions for the time of the first arrival, t, which yields an integral involving the exponential density $\lambda e^{-\lambda t}$. This integral is then split into three parts, corresponding to three distinct scenarios:

• No service completions by time t, which occurs with probability $f_{i,j}(t,0)$: In this case, the arrival at time t triggers the start of the first overflow period. The packets lost after time t form the first series of losses. Clearly, the probability that this series has length l is ${\int }_0^{\infty }{\displaystyle \frac{e^{-\lambda y}{\left(\lambda y\right)}^l}{l!}}{h}_{j,k}\left(y\right)\mathrm{d}y$.
• m services completed by time t, where $m=1,\dots ,N-2$: In this case, no overflow occurs by time t and, just after t, the buffer occupancy is $N-m$. Thus, counting from t, the new probability that there will be l losses during the first overflow period is then $a_j(N-m,l)$.
• $N-1$ services completed by time t: In this scenario, the service state stops at state j when the last service is completed. The buffer occupancy is zero just before t and becomes 1 at time t due to the arriving packet. Thus, counting from t, the new probability that there will be l losses during the first overflow period is $a_j(1,l)$.

Assume now the initial buffer occupancy n of $1,\dots ,N-2$. In this case, the equation for $a_i(n,l)$ is constructed as follows:

$$\begin{array}{cc}\hfill a_i(n,l)=& \sum _{m=0}^{n-1}\sum _{j=1}^M{\int }_0^{\infty }{f}_{i,j}(t,m)a_j(n-m+1,l)\lambda e^{-\lambda t}\mathrm{d}t\hfill \\ \hfill & +\sum _{j=1}^M{\int }_0^{\infty }{g}_{i,j}(t,n)a_j(1,l)\lambda e^{-\lambda t}\mathrm{d}t.\hfill \end{array}$$

(7)

Equation (7) can be justified just like Equation (6), except for the first term of (6), which is absent in (7). The first term of (6) accounts for an overflow event occurring at time t. However, when starting with the buffer occupancy of no more than $N-2$ packets, an overflow upon the first arrival is not possible. Therefore, no corresponding term appears in (7).

Finally, if the buffer is vacant at the beginning, it must first reach a state where it contains exactly one packet before any overflow can occur. Moreover, the service state remains unchanged until the first arrival takes place. These considerations yield

$$\begin{array}{c}\hfill a_i(0,l)=a_i(1,l).\end{array}$$

(8)

Denoting

$$F_{i,j}\left(m\right)=\lambda {\int }_0^{\infty }{e}^{-\lambda t}{f}_{i,j}(t,m)\mathrm{d}t,$$

(9)

$$G_{i,j}\left(m\right)=\lambda {\int }_0^{\infty }{e}^{-\lambda t}{g}_{i,j}(t,m)\mathrm{d}t,$$

(10)

$$H_{i,j}\left(m\right)={\displaystyle \frac{1}{m!}}{\int }_0^{\infty }{e}^{-\lambda t}{\left(\lambda t\right)}^m{h}_{i,j}\left(t\right)\mathrm{d}t$$

(11)

we obtain the following from (6):

$$\begin{array}{cc}\hfill a_i(N-1,l)=& \sum _{j=1}^M\sum _{k=1}^M{F}_{i,j}(t,0)H_{j,k}\left(l\right)+\sum _{m=1}^{N-2}\sum _{j=1}^M{F}_{i,j}(t,m)a_j(N-m,l)\hfill \\ \hfill & +\sum _{j=1}^M{G}_{i,j}(t,N-1)a_j(1,l),\hfill \end{array}$$

(12)

while obtaining the following from (7):

$$\begin{array}{cc}\hfill a_i(n,l)=& \sum _{m=0}^{n-1}\sum _{j=1}^M{F}_{i,j}(t,m)a_j(n-m+1,l)\hfill \\ \hfill & +\sum _{j=1}^M{G}_{i,j}(t,n)a_j(1,l),0<n<N-1.\hfill \end{array}$$

(13)

Vectors and matrices are applied as follows:

$$\mathbf{a}(n,l)={[a_1(n,l),\dots ,a_M(n,l)]}^T,$$

(14)

$$\mathbf{F}\left(m\right)={\left[F_{i,j}\left(m\right)\right]}_{i,j=1,\dots ,M},$$

(15)

$$\mathbf{G}\left(m\right)={\left[G_{i,j}\left(m\right)\right]}_{i,j=1,\dots ,M},$$

(16)

$$\mathbf{H}\left(m\right)={\left[H_{i,j}\left(m\right)\right]}_{i,j=1,\dots ,M}.$$

(17)

Equation (12) yields

$$\begin{array}{c}\hfill \mathbf{a}(N-1,l)=\mathbf{F}\left(0\right)\mathbf{H}\left(l\right)\mathbf{e}+\sum _{m=1}^{N-2}\mathbf{F}\left(m\right)\mathbf{a}(N-m,l)+\mathbf{G}(N-1)\mathbf{a}(1,l),\end{array}$$

(18)

while (13) gives

$$\begin{array}{c}\hfill \mathbf{a}(n,l)=\sum _{m=0}^{n-1}\mathbf{F}\left(m\right)\mathbf{a}(n-m+1,l)+\mathbf{G}\left(n\right)\mathbf{a}(1,l),0<n<N-1.\end{array}$$

(19)

Similarly, (8) in this notation has the form

$$\begin{array}{c}\hfill \mathbf{a}(0,l)=\mathbf{a}(1,l).\end{array}$$

(20)

Exploiting Formula (7) of [38], from (19), we have

$$\mathbf{a}(n,l)=\mathrm{R}\left(n\right)\mathbf{c}\left(l\right)+\sum _{m=1}^n\mathbf{R}(n-m)\mathbf{z}(m,l),n>1,$$

(21)

where

$$\mathbf{R}\left(0\right)=\mathbf{0},\mathbf{R}\left(1\right)={\mathbf{F}}^{-1}\left(0\right),$$

(22)

$$\begin{array}{c}\hfill \mathbf{R}\left(m\right)=\mathbf{R}\left(1\right)(\mathbf{R}(m-1)-\sum _{k=0}^{m-1}\mathbf{F}(k+1)\mathbf{R}(m-1-k)),m>1,\end{array}$$

(23)

$$\mathbf{z}(m,l)=\left(\mathbf{F}\left(m\right)-\mathbf{G}\left(m\right))\right)\mathbf{a}(1,l),$$

(24)

$\mathbf{0}$ stands for the $M\times M$ matrix of 0 s and $c\left(l\right)$ is a vector of length M. The substitution $n=1$ in (21) produces the following relation between $c\left(l\right)$ and $a(1,l)$:

$$\mathbf{c}\left(l\right)=\mathbf{F}\left(0\right)\mathbf{a}(1,l).$$

(25)

Hence, (21) can be rewritten with the help of (24) and (25) as follows:

$$\mathbf{a}(n,l)=\mathbf{X}\left(n\right)\mathbf{a}(1,l),n>1,$$

(26)

where

$$\mathbf{X}\left(n\right)=R\left(n\right)\mathbf{F}\left(0\right)+\sum _{m=1}^{n}R(n-m)\mathbf{F}\left(m\right)-\sum _{m=1}^{n}R(n-m)\mathbf{G}\left(m\right).$$

(27)

Then, combining (18) with (26), we get

$$\mathbf{X}(N-1)\mathbf{a}(1,l)=\mathbf{F}\left(0\right)\mathbf{H}\left(l\right)\mathbf{e}+\sum _{m=1}^{N-2}\mathbf{F}\left(m\right)\mathbf{X}(N-m)\mathbf{a}(1,l)+\mathbf{G}(N-1)\mathbf{a}(1,l),$$

(28)

leading to

$$\mathbf{a}(1,l)={\left(\mathbf{X}(N-1)-\sum _{m=1}^{N-2}\mathbf{F}\left(m\right)\mathbf{X}(N-m)-\mathbf{G}(N-1)\right)}^{-1}\mathbf{F}\left(0\right)\mathbf{H}\left(l\right)\mathbf{e},$$

(29)

which we know to be also equal to $\mathbf{a}(0,l)$, according to (20).

This completes the derivations of $\mathbf{a}(n,l)$ for every n, which can be compiled as follows.

Theorem 1.

Sequential loss distribution in the first overflow period is

$$\begin{array}{cc}\hfill \mathbf{a}(n,l)=\mathbf{X}\left(n\right)(\mathbf{X}(N-1)-\sum _{m=1}^{N-2}\mathbf{F}\left(m\right)\mathbf{X}(N-m)-& \mathbf{G}(N-1){)}^{-1}\mathbf{F}\left(0\right)\mathbf{H}\left(l\right)\mathbf{e},\hfill \\ \hfill & 1<n<N,l\ge 0,\hfill \end{array}$$

(30)

where n is the initial buffer occupancy, while $\mathbf{X}\left(n\right)$, $\mathbf{F}\left(n\right)$, $\mathbf{G}\left(n\right)$, and $\mathbf{H}\left(n\right)$ are defined in (27), (9), (10), and (11), respectively. Moreover, $\mathbf{a}(0,l)=\mathbf{a}(1,l)$ is given in (29).

In Section 8, it will be shown how numerical values of $\mathbf{F}\left(n\right)$, $\mathbf{G}\left(n\right)$, and $\mathbf{H}\left(n\right)$ can be obtained while $\mathbf{X}\left(n\right)$ is a function of these three. Hence, Theorem 1 allows the distribution to be obtained effectively.

5. Subsequent and Stationary Series of Losses

We now derive the sequential loss distribution in the k-th overflow period, where $k\ge 2$. To do this, we must first establish the distribution of the service state at the end of the first overflow period.

Let $P_{i,j}\left(n\right)$ denote the probability of the service state being j at the end of the first overflow period, given that $S\left(0\right)=i$ and $X\left(0\right)=n$.

Assume first that the buffer initially contains $N-1$ packets. We can assemble the following equation for $P_{i,k}(N-1)$:

$$\begin{array}{cc}\hfill P_{i,k}(N-1)=& \sum _{j=1}^M{\int }_0^{\infty }{f}_{i,j}(t,0)\lambda e^{-\lambda t}\mathrm{d}t{\int }_0^{\infty }{h}_{j,k}\left(y\right)\mathrm{d}y\hfill \\ \hfill & +\sum _{m=1}^{N-2}\sum _{j=1}^M{\int }_0^{\infty }{f}_{i,j}(t,m)P_{j,k}(N-m)\lambda e^{-\lambda t}\mathrm{d}t\hfill \\ \hfill & +\sum _{j=1}^M{\int }_0^{\infty }{g}_{i,j}(t,N-1)P_{j,k}\left(1\right)\lambda e^{-\lambda t}\mathrm{d}t.\hfill \end{array}$$

(31)

This equation is established in the same way as (6) (see the explanation below (6)). If the buffer initially has $n=1,\dots ,N-2$ packets, then we have

$$\begin{array}{cc}\hfill P_{i,k}\left(n\right)=& \sum _{m=0}^{n-1}\sum _{j=1}^M{\int }_0^{\infty }{f}_{i,j}(t,m)P_{j,k}(n-m+1)\lambda e^{-\lambda t}\mathrm{d}t\hfill \\ \hfill & +\sum _{j=1}^M{\int }_0^{\infty }{g}_{i,j}(t,n)P_{j,k}\left(1\right)\lambda e^{-\lambda t}\mathrm{d}t,\hfill \end{array}$$

(32)

which is justified like (7). Then, we have

$$\begin{array}{c}\hfill P_{i,k}\left(0\right)=P_{i,k}\left(1\right),\end{array}$$

(33)

(see the explanation below (Section 8)). Denoting

$$\mathbf{P}\left(n\right)={\left[P_{i,j}\left(n\right)\right]}_{i,j=1,\dots ,M},$$

(34)

$$E_{i,j}={\int }_0^{\infty }{h}_{i,j}\left(t\right)\mathrm{d}t,$$

(35)

$$\mathbf{E}={\left[E_{i,j}\right]}_{i,j=1,\dots ,M},$$

(36)

System (31)–(33) is equivalent to

$$\begin{array}{c}\hfill \mathbf{P}(N-1)=\mathbf{F}\left(0\right)\mathbf{E}+\sum _{m=1}^{N-2}\mathbf{F}\left(m\right)\mathbf{P}(N-m)+\mathbf{G}(N-1)\mathbf{P}\left(1\right).\end{array}$$

(37)

$$\begin{array}{c}\hfill \mathbf{P}\left(n\right)=\sum _{m=0}^{n-1}\mathbf{F}\left(m\right)\mathbf{P}(n-m+1)+\mathbf{G}\left(n\right)\mathbf{P}\left(1\right),0<n<N-1,\end{array}$$

(38)

$$\begin{array}{c}\hfill \mathbf{P}\left(0\right)=\mathbf{P}\left(1\right).\end{array}$$

(39)

It is noticeable that system (37)–(39) has exactly the same composition as system (18)–(20). Hence, it can be solved likewise. Consequently, we obtain

$$\mathbf{P}\left(n\right)=\mathbf{X}\left(n\right){\left(\mathbf{X}(N-1)-\sum _{m=1}^{N-2}\mathbf{F}\left(m\right)\mathbf{X}(N-m)-\mathbf{G}(N-1)\right)}^{-1}\mathbf{F}\left(0\right)\mathbf{E},1<n<N,$$

(40)

which is an analog of (30), and

$$\mathbf{P}\left(0\right)=\mathbf{P}\left(1\right)={\left(\mathbf{X}(N-1)-\sum _{m=1}^{N-2}\mathbf{F}\left(m\right)\mathbf{X}(N-m)-G(N-1)\right)}^{-1}\mathbf{F}\left(0\right)\mathbf{E},$$

(41)

which is an analog of (29).

Now, consider a sequence ${\alpha }_0$, ${\alpha }_1$, …, where ${\alpha }_0$ is the initial service state, i.e., ${\alpha }_0=S\left(0\right)$, and ${\alpha }_k$ for $k\ge 1$ is the service state just after the k-th overflow period. The sequence ${\alpha }_k$ forms a Markov chain, since the distribution of ${\alpha }_k$ depends only on ${\alpha }_{k-1}$ and not on ${\alpha }_{k-2}$, ${\alpha }_{k-3}$, etc.

Clearly, the transition ${\alpha }_0\to {\alpha }_1$ is governed by the transition matrix $\mathbf{P}\left(n\right)$, as given in either (40) or (41), depending on whether $n=X\left(0\right)>1$ or $n\le 1$, respectively. The transition ${\alpha }_{k-1}\to {\alpha }_k$ for $k\ge 2$ is always governed by the transition matrix $\mathbf{P}(N-1)$ given in (40) since, immediately after an overflow period, the buffer always contains $N-1$ packets.

Consequently, the transition of the service state from the time origin to the end of the k-th overflow period for $k\ge 1$ is covered by the matrix

$$\mathbf{P}\left(n\right){\mathbf{P}}^{k-1}(N-1).$$

(42)

Let $a_i^k(n,l)$ be the probability that there are l packet losses during the k-th overflow period, given that $S\left(0\right)=i$, $X\left(0\right)=n$, and denote

$${\mathbf{a}}^k(n,l)={[a_1^k(n,l),\dots ,a_M^k(n,l)]}^T.$$

(43)

To obtain $a_i^k(n,l)$, $k\ge 2$, we consider the fact that at end of the $(k-1)$th overflow period, the buffer occupancy is $N-1$, while the service state can be obtained using transition matrix $\mathbf{P}\left(n\right){\mathbf{P}}^{k-2}(N-1).$

These considerations can be recapped as follows.

Theorem 2.

Sequential loss distribution in the k-th overflow period, $k\ge 2$, is:

$$\begin{array}{c}\hfill {\mathbf{a}}^k(n,l)=\mathbf{P}\left(n\right){\mathbf{P}}^{k-2}(N-1)a(N-1,l),0\le n<N,l\ge 0,\end{array}$$

(44)

where n is the initial buffer occupancy, $\mathbf{P}\left(n\right)$ is given in (40) and (41), while $\mathbf{a}(N-1,l)$ in (30).

Denote now:

$$a\left(l\right)=\underset{k\to \infty }{lim}{\mathbf{a}}^k(0,l).$$

(45)

Namely, $a\left(l\right)$ denotes the stationary probability that there are l packet losses during an overflow period. Clearly, the initial buffer occupancy of 0 used in (45) is irrelevant—any value can be used without affecting $a\left(l\right)$.

As $k\to \infty$, the Markov chain ${\alpha }_k$ reaches its stationary distribution. In other words, the distribution of the service state at the end of an overflow period will be given by the vector p, which is a stationary distribution vector of the matrix $\mathbf{P}(N-1)$. It can be found by solving the well-known system

$$\left\{\begin{array}{c}\mathbf{p}\mathbf{P}(N-1)=\mathbf{p},\hfill \\ \mathbf{p}\mathbf{e}=1.\hfill \end{array}\right.$$

From this, we get the final result of this section.

Theorem 3.

Sequential loss distribution in the stationary overflow period is

$$\begin{array}{c}\hfill a\left(l\right)=\mathbf{p}\mathbf{a}(N-1,l),l\ge 0,\end{array}$$

(46)

where p stands for the stationary vector for matrix $\mathbf{P}(N-1)$, given in (40), while $\mathbf{a}(N-1,l)$ is obtained in (30).

6. Burst Ratio

We are now prepared to obtain the burst ratio by means of Formula (2).

Note first that $\overline{H}$, defined as the mean number of sequential losses, cannot be computed directly as the mean of the distribution $a\left(l\right)$ given in Theorem 3. This is because in some overflow periods, no loss may happen at all. Certainly, every series of losses occurs within a particular overflow period, but not every overflow period results in a series of losses.

To account for this, we may calculate the probability of no packet losses in a stationary overflow period. According to Theorem 3, this probability is $\mathbf{p}\mathbf{a}(N-1,0)$. Therefore, the probability of forming a proper sequence—i.e., with non-zero losses—within a stationary overflow period is $1-\mathbf{p}\mathbf{a}(N-1,0)$. Thus, we have

$$\overline{H}={\displaystyle \frac{{\sum }_{l=1}^{\infty }l\mathbf{p}\mathbf{a}(N-1,l)}{1-\mathbf{p}\mathbf{a}(N-1,0)}}.$$

(47)

By gathering the above formula together with all previous results, we obtain the final theorem.

Theorem 4.

The burst ratio of losses at a buffer with correlated MSP service is

$$B={\displaystyle \frac{{\sum }_{l=1}^{\infty }l\mathbf{p}\mathbf{a}(N-1,l)}{1-\mathbf{p}\mathbf{a}(N-1,0)}}(1-L),$$

(48)

where

$$\mathbf{a}(N-1,l)=\mathbf{X}(N-1)\mathbf{F}\left(0\right)\mathbf{H}\left(l\right)\mathbf{e}{\left(\mathbf{X}(N-1)-\sum _{m=1}^{N-2}\mathbf{F}\left(m\right)\mathbf{X}(N-m)-\mathbf{G}(N-1)\right)}^{-1},$$

(49)

L is the packet loss probability; p stands for the stationary vector for matrix $\mathbf{P}(N-1)$:

$$\mathbf{P}(N-1)=\mathbf{X}(N-1)\mathbf{F}\left(0\right)\mathbf{E}{\left(\mathbf{X}(N-1)-\sum _{m=1}^{N-2}\mathbf{F}\left(m\right)\mathbf{X}(N-m)-\mathbf{G}(N-1)\right)}^{-1},$$

(50)

while $\mathbf{X}\left(n\right)$, $\mathbf{F}\left(n\right)$, $\mathbf{G}\left(n\right)$, $\mathbf{H}\left(n\right)$, and E are given in (27), (9), (10), (11), and (35), respectively.

Effective numerical calculation of B therefore requires computing $\mathbf{F}\left(n\right)$, $\mathbf{G}\left(n\right)$, $\mathbf{H}\left(n\right)$, E, and L (note that $\mathbf{X}\left(n\right)$ is a function of $\mathbf{F}\left(n\right)$ and $\mathbf{G}\left(n\right)$). In the next section, we will show how all these characteristics can be computed efficiently.

7. Computational Aspects

A formula for the loss probability in the model of interest, needed in (48), is found in [31], page 11. Namely, it holds

$$\begin{array}{c}\hfill L=\underset{s\to 0+}{lim}{\lambda }^{-1}s\mathbf{U}\left(s\right)\mathbf{A}(0,s)\mathbf{e},\end{array}$$

(51)

where

$$\mathbf{A}(m,s)={\left[\lambda {\int }_0^{\infty }{e}^{-(s+\lambda )t}{f}_{i,j}(m,t)\mathrm{d}t\right]}_{i,j=1,\dots ,M},$$

(52)

$$\begin{array}{c}\hfill \mathbf{U}\left(s\right)={\left(\mathbf{W}(N,s)-\mathbf{D}(N,s)-\mathbf{A}(0,s)\mathbf{W}(N,s)-\sum _{m=1}^{N-1}\mathbf{A}(m,s)\mathbf{W}(N-m+1,s)\right)}^{-1},\end{array}$$

(53)

$$\mathbf{W}(m,s)=\mathbf{Q}(m,s)\mathbf{A}(0,s)+\sum _{k=1}^m\mathbf{Q}(m-k,s)\left(\mathbf{A}(k,s)-\mathbf{D}(k,s)\right),$$

(54)

$$\mathbf{D}(m,s)={\left[\lambda {\int }_0^{\infty }{e}^{-(s+\lambda )t}{g}_{i,j}(m,t)\mathrm{d}u\right]}_{i,j=1,\dots ,M},$$

(55)

$$\mathbf{Q}(0,s)=\mathbf{0},\mathbf{Q}(1,s)={\mathbf{A}}^{-1}(0,s),$$

(56)

$$\mathbf{Q}(m+1,s)=\mathbf{Q}(1,s)(\mathbf{Q}(m,s)-\sum _{i=0}^m\mathbf{A}(i+1,s\left)\mathbf{Q}\right(m-i,s\left)\right),m>0.$$

(57)

Therefore, L can be calculated numerically using a very small s in (51), e.g., $s={10}^{-8}$, but calculations of $\mathbf{A}(m,s)$ and $\mathbf{D}(m,s)$ are required first.

$\mathbf{A}(m,s)$ can be determined using the uniformization technique (see, e.g., [37], p. 66, for details), while $\mathbf{D}(m,s)$ can be determined using Formulas (40)–(42) of [31]. Applying all of these, we obtain

$$\mathbf{A}(m,s)=\lambda \sum _{k=0}^{\infty }{\displaystyle \frac{{\theta }^k}{{(\lambda +s+\theta )}^{k+1}}}\mathbf{K}(m,k),$$

(58)

where

$$\theta =\underset{i=1,\dots ,M}{max}\{-{\mathbf{L}}_0(i,i)\},$$

(59)

$$\mathbf{K}(0,0)=I,\mathbf{K}(m,0)=\mathbf{0},m\ge 1,$$

(60)

$$\mathbf{K}(0,k+1)=\mathbf{K}(0,k)(\mathbf{I}+{\mathbf{L}}_0/\theta ),$$

(61)

$$\mathbf{K}(m,k+1)=\mathbf{K}(m-1,k){\mathbf{L}}_1/\theta +\mathbf{K}(m,k)(\mathbf{I}+{\mathbf{L}}_0/\theta ),$$

(62)

I is the identity matrix, and

$$\begin{array}{c}\hfill \mathbf{D}(m,s)={\displaystyle \frac{1}{\lambda }}\mathbf{A}(m-1,s){\mathbf{L}}_1-s\mathbf{H}(m,s),\end{array}$$

(63)

$$\begin{array}{c}\hfill \mathbf{H}(1,s)={\displaystyle \frac{1}{\lambda }}\mathbf{A}(0,s){\mathbf{L}}_0^{-1}{\mathbf{L}}_1-{\displaystyle \frac{1}{\lambda +s}}{\mathbf{L}}_0^{-1}{\mathbf{L}}_1,\end{array}$$

(64)

$$\begin{array}{c}\hfill \mathbf{H}(m+1,s)={\displaystyle \frac{1}{\lambda }}\mathbf{A}(m,s){\mathbf{L}}_0^{-1}{\mathbf{L}}_1-\mathbf{H}(m,s){\mathbf{L}}_0^{-1}{\mathbf{L}}_1,m>0.\end{array}$$

(65)

Having $\mathbf{A}(m,s)$ and $\mathbf{D}(m,s)$, we can compute not only L, using (51), but also $\mathbf{F}\left(m\right)$ and $\mathbf{G}\left(m\right)$, following the obvious relations:

$$\mathbf{F}\left(m\right)=\mathbf{A}(m,0),\mathbf{G}\left(m\right)=\mathbf{D}(m,0).$$

(66)

Therefore, what remains is to calculate $\mathbf{H}\left(m\right)$ and E. A formula for E is well known:

$$\mathbf{E}={(-{\mathbf{L}}_0)}^{-1}{\mathbf{L}}_1,$$

(67)

(see [37], p. 68), whereas $\mathbf{H}\left(m\right)$ can be determined using the uniformization technique once more. Specifically, we have

$$\mathbf{H}\left(m\right)={\displaystyle \frac{{\lambda }^m}{m!}}\sum _{k=0}^{\infty }{\displaystyle \frac{{\theta }^k(k+m)!}{k!{(\lambda +\theta )}^{m+k+1}}}\mathbf{K}(0,k){\mathbf{L}}_1.$$

(68)

8. Examples

8.1. Impact of Traffic Intensity and Buffer Size

We will first use a moderately strong positive correlation of packet sizes (service times), with a correlation coefficient of 0.4. The following MSP matrices produce such a correlation:

$${\mathbf{L}}_0^{+}=\left[\begin{array}{ccc}\hfill -0.964135& \hfill 0.921707& \hfill 0.007896\\ \hfill 0.118844& \hfill -0.635838& \hfill 0.014067\\ \hfill 0.004706& \hfill 0.001578& \hfill -1.961343\end{array}\right],$$

(69)

$${\mathbf{L}}_1^{+}=\left[\begin{array}{ccc}\hfill 0.005524& \hfill 0.017211& \hfill 0.011797\\ \hfill 0.492461& \hfill 0.005493& \hfill 0.004973\\ \hfill 0.019695& \hfill 0.000944& \hfill 1.934420\end{array}\right].$$

(70)

The service rate for matrices (69) and (70) is normalized to 1 packet per time unit. The arrival rate is varied from $\lambda =0.5$ to $\lambda =2$ packets per time unit, representing a range from very light to very heavy traffic. A summary of all system settings described in this subsection is shown in

Table 1. System settings described in Section 8.1.

Parameter	Value
service times matrices	(69) and (70)
correlation of service times, $corr$	0.4
service rate, $\mu$	1
buffer size, N	variable, from 2 to 100
arrival rate, $\lambda$	variable, from 0.5 to 2

.

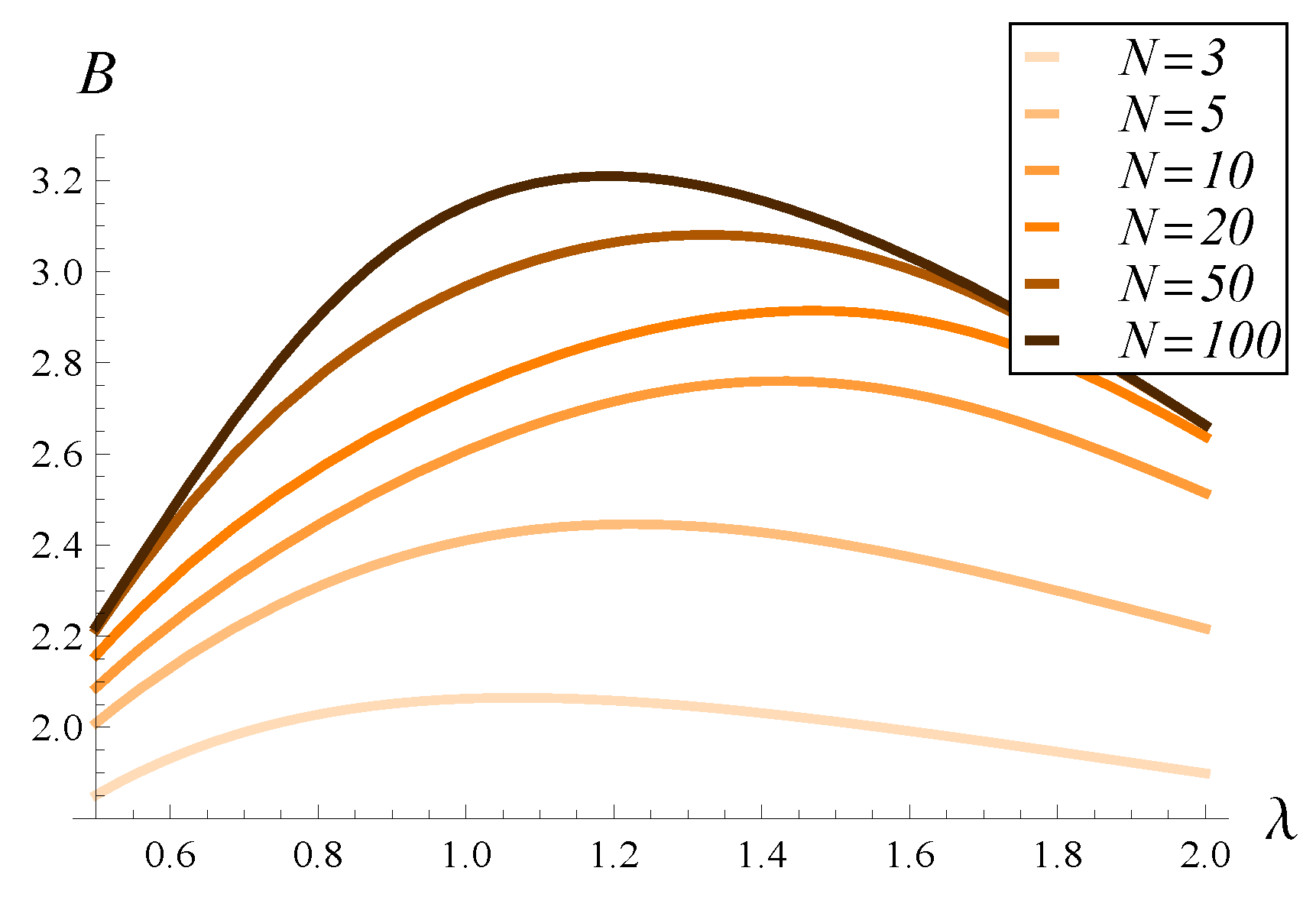
In Figure 2, the effect of traffic intensity on the burst ratio is presented for six buffer sizes: $N=3$, 5, 10, 20, 50, and 100 packets.

We observe that all values of B are very high, ranging from about 1.8 up to 3.2. This indicates that the mean series of packet losses is 2–3 times longer than it would be in the case of independent losses. Such loss clustering may have a significant impact on many applications, as was explained in Section 1 and will be further illustrated in Section 8.4.

Intuitively, loss clustering can be explained as follows. The buffering mechanism causes loss clustering because losses can occur only in continuous time intervals, i.e., during buffer overflow periods. During an overflow period, all arriving packets are lost consecutively, forming a sequence of losses. In other words, when a particular packet is lost at time $t_l$, this means that the buffer is full at $t_l$ and will remain full after $t_l$ for at least some time. Therefore, it is likely that the next packet arriving after $t_l$ will also be lost.

This effect is further strengthened by the correlation of packet sizes. Specifically, the correlation makes it more likely that a sequence of longer-than-average service times occurs. A sequence like this has two possible consequences. First, it quickly increases the buffer occupancy, raising the risk of buffer overflow. Second, if an overflow does occur, the overflow period is exceptionally long because its duration equals an exceptionally long service time.

In summary, the high burst ratio is due to two factors: the buffering mechanism itself (which would increase B even without correlation) and the correlation of packet sizes. The separate influence of these two factors will be demonstrated later.

In Figure 2, we see the burst ratio changing in a non-monotonic manner with traffic intensity. Specifically, it reaches a maximum at a certain intensity, and the position of this maximum is conditioned by the buffer size. For a very small buffer, the maximum occurs near an intensity of 1 (slightly more than 1). Then, as the buffer grows, it gets closer to 1.5. Then, when the buffer grows even more, the maximum returns to a position near 1 again.

The existence of such a maximum can be understood by considering two extreme cases: $\lambda \to \infty$ and $\lambda \to 0+$. In the former case, both $\overline{H}$ and $\overline{K}$ are large, but similar, due to the fact that the loss probability is very high (most packets are lost). In the latter case, losses are extremely rare, and both $\overline{H}$ and $\overline{K}$ are small. Somewhere between these two extremes, a maximum can be expected. However, it is difficult to explain intuitively why this maximum occurs at a specific position, e.g., at $\lambda =1.3$, for a specific system parameterization. Such a specific position is a consequence of the interplay between various system parameters, each having possibly a different influence on B.

In Figure 3, the dependence of B on buffer size is depicted for five traffic intensities: 0.5, 0.75, 1, 1.5, and 2. We observe the burst ratio increasing with buffer size in every case. Furthermore, for both low and high traffic intensities, the burst ratio approaches its maximum relatively quickly. For example, when $\lambda =0.5$, it does not change significantly beyond a buffer size of 40 packets. Similarly, when $\lambda =2.0$, it stabilizes at a buffer size as small as 30 packets. However, when $\lambda$ is close to 1, the burst ratio continues to grow even beyond $N=100$.

As is evident in Figure 2 and Figure 3, a very small buffer results in a low burst ratio. This can be explained as follows. The burst ratio, as defined in (1), accounts for the extra clustering tendency, additional to the pure random formation of loss sequences. For this reason, there is a denominator in (1). When the buffer is very small, the loss probability is high, and there are many losses. Apparently, in this case, the purely random formation of loss sequences prevails, i.e., the value of B is low because of the high denominator in (1).

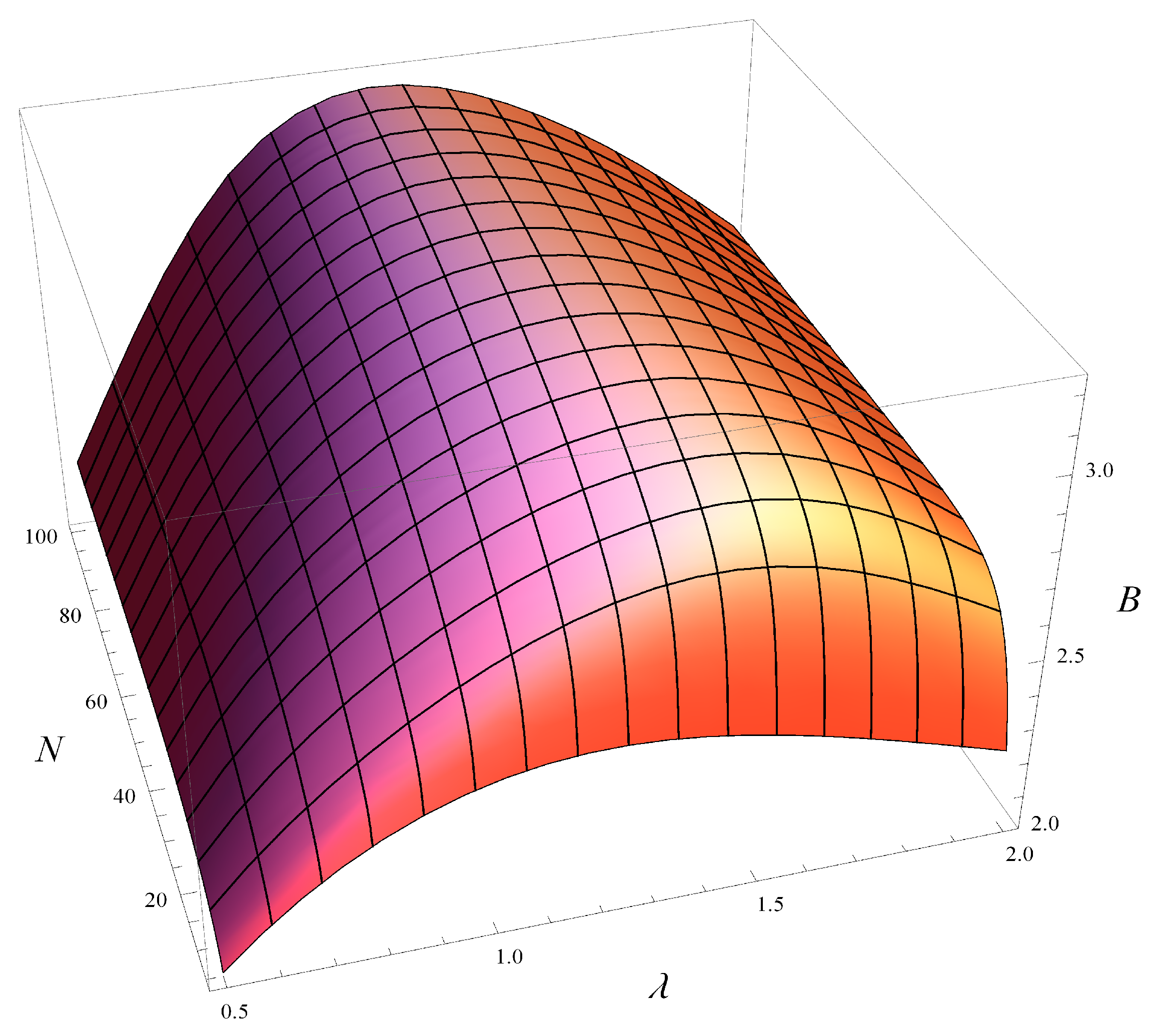
The combined impact of buffer size and traffic intensity on B is shown in Figure 4 for $N=5,\dots ,100$ and $\lambda \in [0.5,2]$. We can observe how the maximum shifts as the buffer size increases.

8.2. Impact of Negative Correlation

In the next batch of examples, we apply a correlation of the same magnitude but with the opposite sign. The following MSP matrices yield a negative correlation of −0.4, while preserving the service rate of 1:

$${\mathbf{L}}_0^{-}=\left[\begin{array}{ccc}\hfill -1.468954& \hfill 1.400560& \hfill 0.013478\\ \hfill 0.040341& \hfill -0.858689& \hfill 0.023735\\ \hfill 0.638451& \hfill 0.012277& \hfill -22.86338\end{array}\right],$$

(71)

$${\mathbf{L}}_1^{-}=\left[\begin{array}{ccc}\hfill 0.010037& \hfill 0.028383& \hfill 0.016496\\ \hfill 0.008620& \hfill 0.009706& \hfill 0.776287\\ \hfill 21.97520& \hfill 0.013028& \hfill 0.224424\end{array}\right].$$

(72)

A summary of all system settings described in this subsection is shown in

Table 2. System settings described in Section 8.2.

Parameter	Value
service times matrices	(71) and (72)
correlation of service times, $corr$	−0.4
service rate, $\mu$	1
buffer size, N	variable, from 2 to 100
arrival rate, $\lambda$	variable, from 0.5 to 2

.

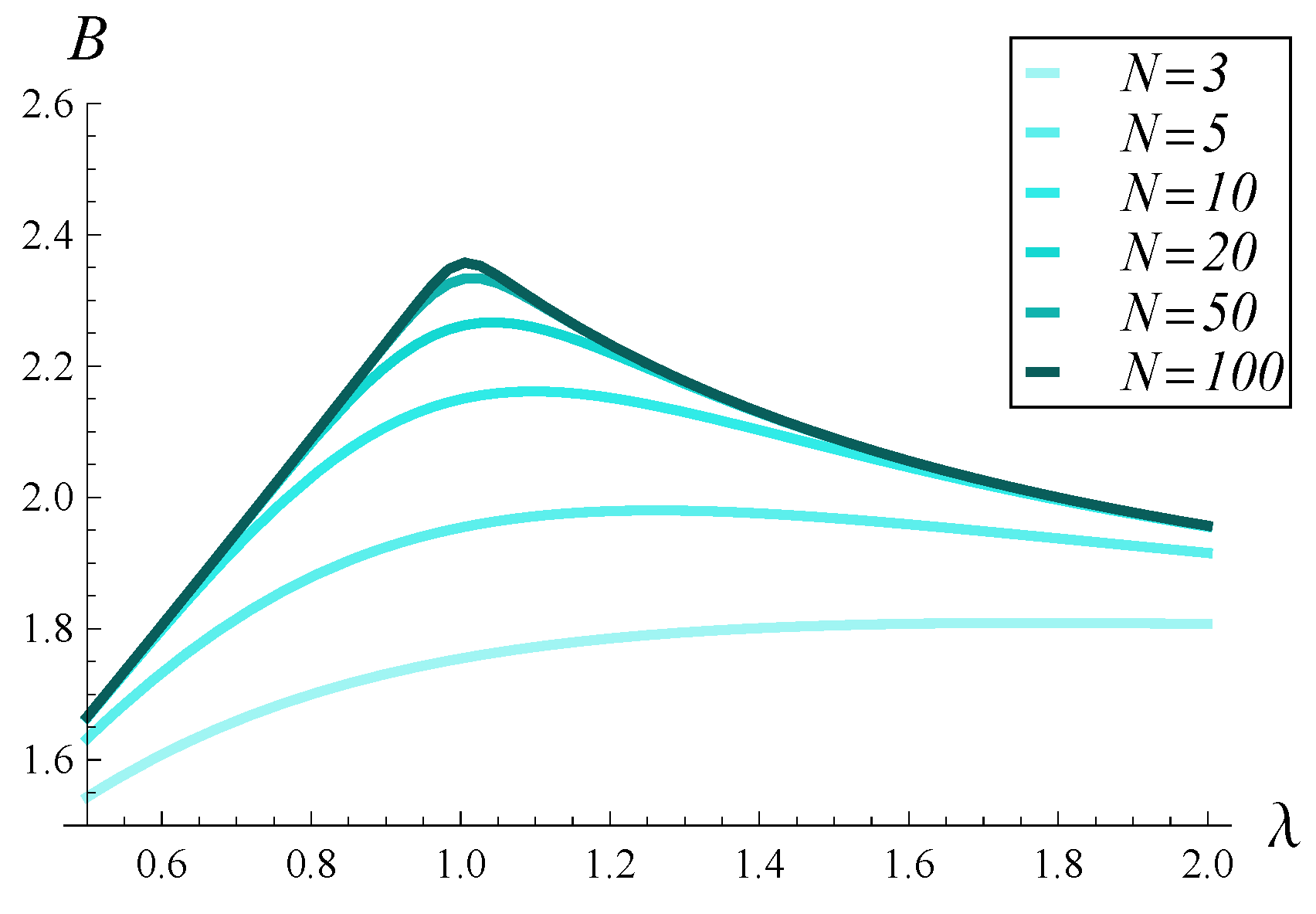
In Figure 5, the impact of traffic intensity on B is shown for six buffer sizes: $N=3$, 5, 10, 20, 50, and 100 packets.

We observe that in the case of a negative correlation, the burst ratio values remain high—ranging from 1.5 to 2.4—but are noticeably lower than those in Figure 2. Once again, the burst ratio is a non-monotonic function of traffic intensity; however, in this case, the maximum is consistently located near $\lambda =1$ for all buffer sizes considered.

In Figure 6, the impact of buffer size on B is shown for five traffic intensities: 0.5, 0.75, 1, 1.5, and 2. In every setting, the burst ratio increases with buffer size, but it now stabilizes much more quickly than in the positive correlation setting. Specifically, for all the considered cases, except $\lambda =1$, a buffer size as small as 15 packets is sufficient for the burst ratio to reach full saturation. In the case of $\lambda =1$, convergence is slower, but still significantly faster than what is observed in Figure 3.

In Figure 7, the combined influence of buffer size and traffic intensity on the burst ratio is represented for $N=5,\dots ,100$ and $\lambda \in [0.5,2]$. Figure 7 ought to be contrasted with Figure 4, obtained for a positive correlation of packet sizes.

8.3. Impact of Correlation Strength

So far, we have considered a fixed correlation of service times. In this subsection, we will examine how correlations of varying strength influence the burst ratio. To accomplish this, we will use nine parameterizations of service times, with correlations of −0.4, −0.3, −0.2, −0.1, 0, 0.1, 0.2, 0.3, and 0.4.

The correlation of −0.4 is obtained using matrices (71) and (72). The correlation of −0.3 is obtained using matrices

$${\mathbf{L}}_0=1.125({\mathbf{L}}_0^{-}+{\mathbf{L}}_1^{-})-{\mathbf{L}}_1^{-},{\mathbf{L}}_1={\mathbf{L}}_1^{-},$$

(73)

where ${\mathbf{L}}_0^{-}$ and ${\mathbf{L}}_1^{-}$ are given in (71) and (72), respectively. The correlation of −0.2 is procured using matrices

$${\mathbf{L}}_0=1.33({\mathbf{L}}_0^{-}+{\mathbf{L}}_1^{-})-{\mathbf{L}}_1^{-},{\mathbf{L}}_1={\mathbf{L}}_1^{-}.$$

(74)

The correlation of −0.1 is obtained using matrices

$${\mathbf{L}}_0=1.78({\mathbf{L}}_0^{-}+{\mathbf{L}}_1^{-})-{\mathbf{L}}_1^{-},{\mathbf{L}}_1={\mathbf{L}}_1^{-},$$

(75)

The correlation of 0 is achieved using i.i.d. service times, exponentially distributed with $\mu =1$. The correlation of 0.1 is obtained using matrices

$${\mathbf{L}}_0=18.35({\mathbf{L}}_0^{+}+{\mathbf{L}}_1^{+})-{\mathbf{L}}_1^{+},{\mathbf{L}}_1={\mathbf{L}}_1^{+},$$

(76)

where ${\mathbf{L}}_0^{+}$ and ${\mathbf{L}}_1^{+}$ are given in (69) and (70), respectively. The correlation of 0.2 is accomplished using matrices

$${\mathbf{L}}_0=6.88({\mathbf{L}}_0^{+}+{\mathbf{L}}_1^{+})-{\mathbf{L}}_1^{+},{\mathbf{L}}_1={\mathbf{L}}_1^{+}.$$

(77)

The correlation of 0.3 is obtained using matrices

$${\mathbf{L}}_0=2.49({\mathbf{L}}_0^{+}+{\mathbf{L}}_1^{+})-{\mathbf{L}}_1^{+},{\mathbf{L}}_1={\mathbf{L}}_1^{+}.$$

(78)

Finally, the correlation of 0.4 is obtained using unaltered matrices (69) and (70).

A summary of all system settings described in this subsection is shown in

Table 3. System settings described in Section 8.3.

Parameter	Value
service times matrices	(71) and (72), (73), (74), (75), (76), (77), (78), (69) and (70)
correlation of service times, $corr$	variable, from −0.4 to 0.4
service rate, $\mu$	1
buffer size, N	variable, from 2 to 100
arrival rate, $\lambda$	variable, from 0.5 to 2

.

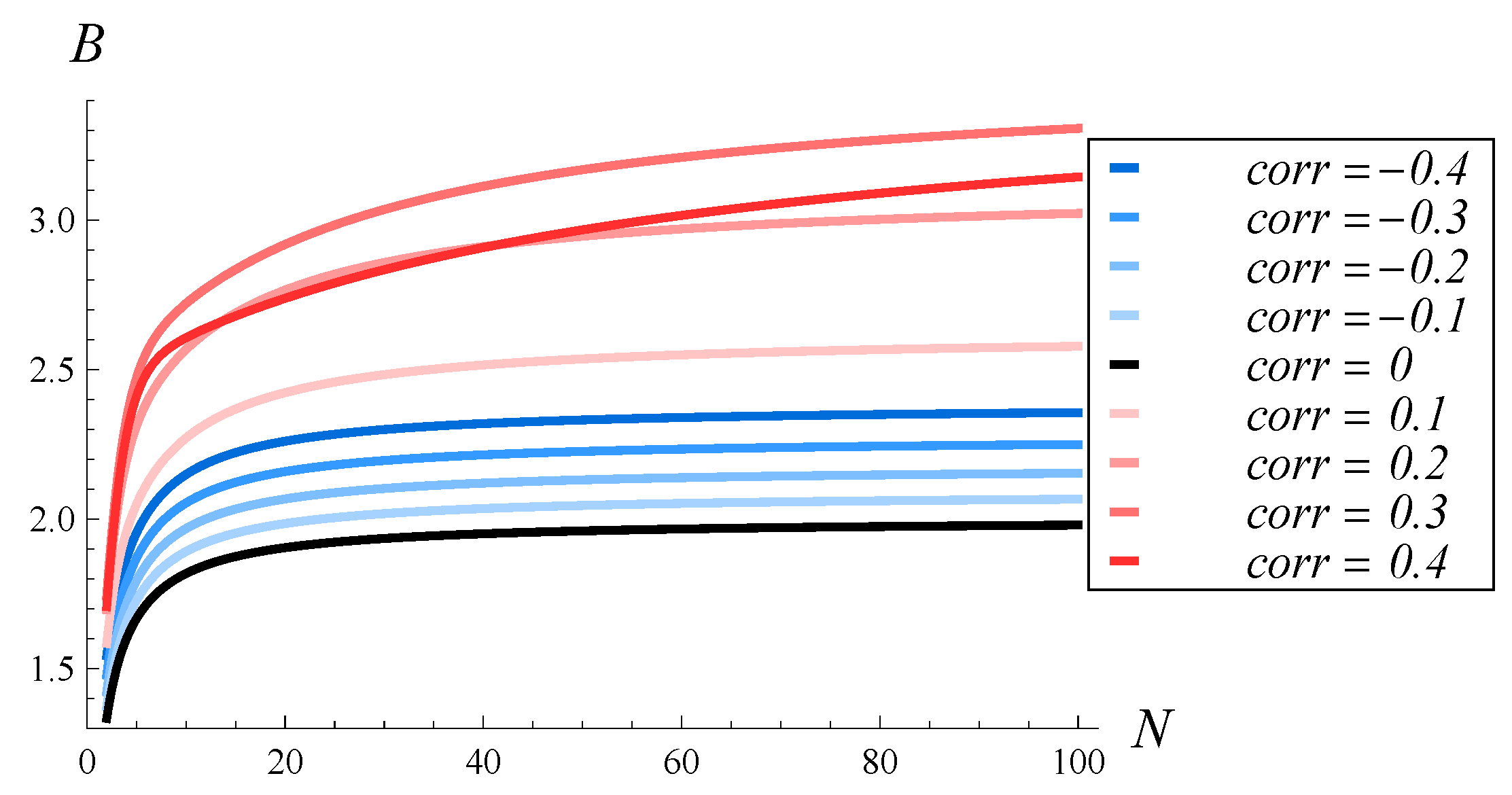
In Figure 8, the dependence of B on traffic intensity is depicted for the nine considered correlations and a fixed buffer size of 100. Similarly, in Figure 9, the burst ratio versus buffer size is presented for the same nine correlation values, with a fixed traffic intensity of 1.

As we observe in Figure 8 and Figure 9, the dependence of B on the strength and sign of the correlation is complex. First of all, the smallest B is always achieved for zero correlation. A negative correlation induces a higher B than no correlation at all—compare the blue lines with the black line in Figure 8 and Figure 9. Second, positive correlations result in higher burst ratios than their negative counterparts—compare the red lines with the blue lines in Figure 8 and Figure 9. Third, the burst ratio generally increases with the strength of the correlation, whether positive or negative. Namely, B is higher for $corr=0.2$ than for $corr=0.1$ and, similarly, higher for $corr=-0.2$ than for $corr=-0.1$. However, when the correlation is strong, the burst ratio also depends heavily on $\lambda$ and N. Therefore, for low $\lambda$ or low N, a correlation of 0.3 can produce a higher burst ratio than a correlation of 0.4.

Finally, by comparing the red and blue lines with the black one in Figure 8 and Figure 9, we can assess the impact of correlation on B, separated from the impact of the buffering mechanism itself. Specifically, the buffering mechanism alone can cause the burst ratio to rise up to 1.9, even in the absence of a correlation (see the black line in Figure 8). A negative correlation can increase it further, up to 2.3 (top blue line), while a positive correlation pushes it even higher, up to 3.3 (top red line).

8.4. Concrete Problem Solutions

Now, we can demonstrate how the obtained theoretical results can be used to solve concrete engineering problems.

Assume, for instance, that a sensor node is monitoring a system or device. The monitoring data is transmitted in packets. A critical system error occurs when 10 packets of monitoring data are missing in a row.

Problem 1. Compute the probability that a critical error occurs within a week of system operation. Assume buffer size $N=50$, $\lambda =0.5$, and the correlation structure as in (69), (70).

Problem 2. What buffer size is needed to make the probability of a critical error occurring less than 0.001?

Problem 1 solution. From (51), we can obtain the overall packet loss probability for $N=50$. We have

$$L=0.003283.$$

(79)

Given such a loss probability, one might naively deduce that it is very unlikely to lose 10 packets in a row because $0.{003283}^{10}$ is an extremely small number (on the order of ${10}^{-25}$). As we will see, this conclusion is completely wrong. To find the correct solution, we first compute the burst ratio from Theorem 4. We have

$$B=2.215300.$$

(80)

Then, we obtain the average length of the series of losses:

$$\overline{H}=B/(1-L)=2.222596.$$

(81)

Using Theorem 3, we calculate the probability that an arbitrary series of losses has a length less than 10:

$${\tilde{p}}_{10}={\displaystyle \frac{{\sum }_{l=1}^{9}a\left(l\right)}{1-a\left(0\right)}}={\displaystyle \frac{{\sum }_{l=1}^9\mathbf{p}\mathbf{a}(49,l)}{1-\mathbf{p}\mathbf{a}(49,l)}}=0.995948.$$

(82)

Within a week, the node sends, on average, 302,400 packets with monitoring data, out of which 993 packets are lost. Therefore, we can expect the following number of separate series of losses within a week:

$$993/\overline{H}\approx 447.$$

(83)

The probability that at least one of these series of losses consists of 10 or more packets is then

$$P\left(\mathrm{critical} \mathrm{error}\right)\approx 1-{\tilde{p}}_{10}^{447}=0.837.$$

(84)

As we can see, it is very likely to have a critical system error within a week, with a probability exceeding 0.8.

Problem 2 solution. To solve this problem, we can simply increase N and repeat all the calculations as long as is necessary, i.e., until the probability of the critical error occurring goes below 0.001. In Figure 10, we can see the full dependence of the critical error probability on the buffer size, up to $N=160$. Specifically, for $N>154$, we have $\mathrm{P}\left(\mathrm{critical} \mathrm{error}\right)<0.001$, which completes the solution of the second problem.

Naturally, the solutions to the problems presented above depend on matrices (69) and (70), which here constitute only one selected example. What is crucial is that there are well-known methods to fit these matrices precisely to any packet size correlation structure and packet size distribution. These methods are described in detail in Section 5 of the excellent monograph in [39]. In Section 7 of the same monograph, the reader can find recommended software tools to automate the fitting process. Therefore, the problems in this section can be solved for streams of packets with arbitrary size distributions and correlations.

8.5. Verification via Simulations

Theoretical results were also verified through simulations performed in the OMNeT++ network simulator [40], version 5.6. The simulation granularity was set to ${10}^{-9}$, i.e., the setting simtime-scale = −9 was used in the OMNeT++ configuration file. The buffer model presented in Section 3 was implemented manually, without the use of any specialized libraries, except for the general OMNeT++ libraries.

Twelve simulation scenarios were conducted, featuring various combinations of traffic intensity, buffer size, and correlation type. In each scenario, $50\times {10}^6$ packets were processed by the buffer, and the resulting burst ratio was measured and compared with its theoretical counterpart.

The results are summarized in

Table 4. Theoretical and simulated B for various combinations of $\lambda$, N, and service correlation.

Scenario	Theoretical	Simulated
Parameters	Burst Ratio	Burst Ratio
$\lambda =0.75$, $N=20$, positive correlation (69), (70)	2.514	2.514
$\lambda =1.0$, $N=20$, positive correlation (69), (70)	2.740	2.740
$\lambda =1.5$, $N=20$, positive correlation (69), (70)	2.914	2.912
$\lambda =0.75$, $N=100$, positive correlation (69), (70)	2.808	2.809
$\lambda =1.0$, $N=100$, positive correlation (69), (70)	3.145	3.140
$\lambda =1.5$, $N=100$, positive correlation (69), (70)	3.101	3.099
$\lambda =1.0$, $N=10$, negative correlation (71), (72)	2.150	2.149
$\lambda =1.5$, $N=10$, negative correlation (71), (72)	2.074	2.074
$\lambda =2.0$, $N=10$, negative correlation (71), (72)	1.955	1.956
$\lambda =1.0$, $N=50$, negative correlation (71), (72)	2.332	2.333
$\lambda =1.5$, $N=50$, negative correlation (71), (72)	2.090	2.089
$\lambda =2.0$, $N=50$, negative correlation (71), (72)	1.957	1.957

. As we see, there is excellent agreement between the simulated values and their theoretical counterparts in every scenario.

9. Conclusions

We studied the effect of the correlation of packet sizes (service times) on the packet loss clustering, when the losses are caused by overflows of a FIFO buffer. Specifically, we established formulae for the sequential losses distribution in the first, k-th, and stationary overflow periods, using a model that allows for arbitrarily strong correlation (MSP). Based on these results, we derived the final formula for the burst ratio. All computational aspects were addressed, making the formulae fully applicable.

The mathematical results were then exploited in numeric examples, showing the effects of packet size correlation, buffer size, and traffic intensity on the burst ratio. Several noteworthy observations were made. Most importantly, we found that a positive correlation of service times significantly increased the burst ratio compared to the uncorrelated case across all scenarios, regardless of buffer size or traffic intensity. A negative correlation also increased the burst ratio, but to a lesser extent than a positive correlation.

We also observed that the burst ratio varies non-monotonically with traffic intensity, exhibiting a clear maximum. In the case of a positive correlation, the location of this maximum depends on the buffer size. Specifically, for very small buffers, the maximum occurs near a traffic intensity of 1. As the buffer grows, it gets closer to 1.5. Then, when the buffer grows even more, the maximum returns to a position near 1. This effect does not appear in negative or uncorrelated cases, where the maximum consistently occurs near a traffic intensity of 1, regardless of buffer size.

The burst ratio increases monotonically with buffer size, regardless of traffic intensity and correlation type. In most scenarios, it saturates quickly, reaching a maximum value at relatively small buffer sizes, after which, further increases in buffer size have no effect. This convergence is significantly slower, however, in scenarios with a positive service time correlation and a traffic intensity of 1.

In addition to these numeric calculations, we presented two examples of concrete engineering problems related to loss clustering and the burst ratio. The problems were then solved using two main theoretical results of this paper, i.e., Theorems 3 and 4.

The limitations of this study are twofold. Firstly, we considered only one particular buffer policy, namely, the FIFO policy with tail dropping. This policy is commonly used in networking devices of all types, but it is not the only existing approach. For instance, many active buffer management policies have been proposed for various devices and networks. Since the burst ratio strongly depends on the packet discarding policy, the results of this paper are not applicable to any of the active management policies.

The second limitation of this study is related to the fact that, in addition to packet service times, packet interarrival times can also be correlated in real networks. This effect is not taken into account in the model considered here, although it can certainly affect the burst ratio. Therefore, the results of this paper are applicable to traffic with uncorrelated or only weakly correlated interarrival times. For moderate or strong correlations of interarrival times, the model would likely produce significant errors.

These limitations clearly suggest two directions for future research. First, the burst ratio under buffer policies other than FIFO with tail dropping can be investigated. A promising starting point could be a RED-type active buffer management policy. Second, the burst ratio could be studied in a model incorporating both interarrival time correlations and service time correlations. A natural candidate for modeling correlated interarrival times would be the Markovian Arrival Process (MAP), in the addition to the Markovian Service Process (MSP) used here.