Abstract
High power density and better efficiency make the multiterminal high-voltage direct current (MT-HVDC) system the best candidate for long-distance bulk power transfer in the cases of onshore and offshore power systems. Many machine learning-based algorithms have been developed for the protection of MT-HVDC systems. However, the exploration of the effects of change in the fault and ground resistances of MT-HVDC systems has not been studied comprehensively. In this study, a four-terminal HVDC test system is employed for the analysis of the effects on fault diagnosis under change in the fault and ground resistances. A simplified medium tree-based machine learning algorithm that works on Gini’s index of diversity is developed for fault diagnosis in the MT-HVDC system. It is found from the simulation analysis that the preprocessing based on mean and differences in featured data extracted for fault current is required to reduce the impacts of the accuracy of machine learning algorithms. The preprocessing not only retains the accuracy of the machine learning algorithm in different cases of faults, but also minimizes the reduction in accuracy in some fault cases. In the test cases, the accuracy is 88.7%, 60%, and 57.1% without preprocessing of featured data for the machine learning algorithm under different values of fault and ground resistances, but the accuracy is improved to 99.5%, 84.1%, and 77.8%, respectively. Hence, the machine learning algorithm can be made applicable under different values of fault and ground resistances for the protection of the MT-HVDC system. This helps to develop a protected MT-HVDC system for long distances without the fear of different soil conditions.
1. Introduction
In high-voltage direct current (HVDC) transmission systems, the localization of faults is significantly influenced by fault and ground resistance. To pinpoint issues in HVDC systems with accuracy, several techniques have been developed, taking into account fault resistance, fault kind, and system configuration.
To examine the fault, one technique compares the initial current change, current rise time interval, or current oscillation pattern at various switch locations [1]. This method takes advantage of the fault current characteristics to determine the fault location and isolation. Another method for finding problems in voltage source converter-based high-voltage direct current (VSC-HVDC) systems is the concept of the two-terminal traveling wave range. Using fault signals, this method uses the Teager energy operator (TEO) and variational mode decomposition (VMD) to locate traveling wave faults [2]. This technique offers high fault location accuracy, but with extensive computational burden and limited adaptability.
The similarity measure of voltage signals has also been proposed as a unique fault location technique for HVDC transmission lines [3]. By comparing the recorded voltage signal to known patterns, this approach uses the voltage signal obtained at one of the line terminals to identify the failure site. It is quite accurate and devoid of the technical challenges that traveling wave-based approaches have [4,5], but it is ineffective in discriminating internal and external faults, and less accurate in far-end faults with high fault and ground resistance.
In the case of bipolar HVDC grids, when multiple earthing may not be acceptable, a design with a metallic return and a single earthing point is taken into account. This arrangement minimizes steady-state stray currents and ground potential in adjacent alternating current (AC) cables and pipelines [6].
A fault localization model based on wavelet decomposition and the deep belief network (DBN) has been developed for difficult-to-find high-resistance ground faults [7]. The challenge of locating high-resistance ground faults in modular multilevel converter-based high-voltage direct current (MMC-HVDC) transmission lines is what this model attempts to solve. However, overfitting and sensitivity of wavelets against variable fault and ground resistances are some of the challenges associated with this technique.
In terms of measurement requirements, a method based on single-terminal direct current (DC) signals has been devised for fault location in thyristor-based line commutated converter-based high-voltage direct current (LCC-HVDC) transmission lines [8]. This method uses boosting ensembles to predict the fault site and uses the root mean square of DC signals as its input features. It has been proven to work more effectively than competing strategies.
Modal transient analysis has also been used to locate faults online in HVDC cable bundles [9]. Using modal analysis and the variation in the modal velocities, the fault location is calculated. For some HVDC cable bundles, its correctness has been verified.
Another technique for identifying problems in VSC HVDC systems makes use of deep belief networks and efficient feature extraction [10]. This approach extracts relevant attributes from fault current signals using the Hilbert–Huang and Karenbauer phase mode transformations and then feeds those features into a deep belief network for learning. Evidence supports its exceptional fault location accuracy. A data-driven method based on long short-term memory (LSTM) is applicable for the detection of different types of DC faults in MT-HVDC systems because of its capability to capture temporal patterns of non-linear faults built up, but the regularization setting offers some computational complexity [11,12].
These methods demonstrate a variety of methods for identifying faults in HVDC transmission networks. They consider factors such as fault current characteristics, voltage signal similarity, system setup, and measurement requirements to find faults properly. However, the simultaneous effects of fault resistance and ground resistance have still not been studied explicitly for machine learning (ML)-based fault diagnosis in HVDC systems.
In this study, a multiterminal (four-terminal) high-voltage direct current (MT-HVDC) transmission test system is analyzed to observe the effects of fault resistance and ground resistance on ML-based diagnosis. Variations in fault resistance and ground resistance are applied to study the performance of ML-based fault diagnosis.
2. Machine Learning-Based Fault Diagnosis
In artificial intelligence (AI), the area of study and practice known as “machine learning” is devoted to creating models and algorithms that allow computers or machines to learn and make judgments based on data without being explicitly programmed. Making a model for machine learning is necessary so that it can understand more data and make predictions after being trained on a set of training data. Without relying on a previous equation as a model, machine learning algorithms employ computer techniques to learn information directly from data. Supervised learning and unsupervised learning are the two primary categories of machine learning techniques. Both of these categories are employed by researchers for fault estimation in different real-life applications [13,14,15]. Figure 1 presents the generalized flow chart of ML-based fault diagnosis in MT-HVDC systems.
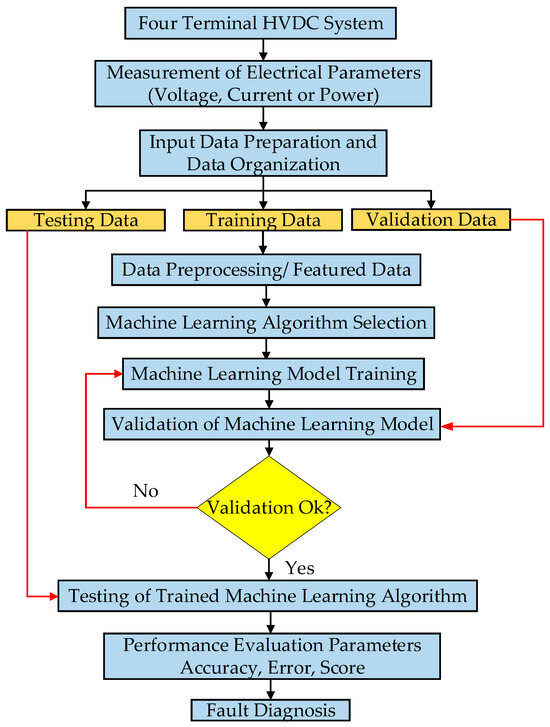
Figure 1.
Generalized flow chart of ML-based fault diagnosis in MT-HVDC system.
Fault diagnosis is the most sensitive issue in the MT-HVDC system. Because of the sudden build-up of DC fault current, there is a need to have a rapid protection system; otherwise, abrupt rises in DC fault current would burn the power electronic circuitries in the converter stations.
In the literature, several methods have been formulated based on machine learning [16]. A long short-term memory-based support vector machine (LSTM-SVM) fusion model has been developed to explore the advantages of feature extraction by long short-term memory (LSTM) and classification by support vector machine (SVM) [14]. A wavelet entropy-based support vector machine has been made to analyze the accuracy and rapidness against transient faults in HVDC transmission lines [17]. A K-nearest neighbor and support vector machine-based machine learning technique has been developed for different fault locations and types. This protection strategy works on one terminal measurement [18]. A Hilbert–Huang transform-based convolutional neural network has been employed for a double-ended unsynchronized HVDC transmission system. This method is reliable in identifying fault locations at high resistances [19]. A discrete wavelet has been embedded with a fuzzy neural pattern recognizer for the identification of traveling waves generated from the fault locations on DC transmission lines. This method is demonstrably useful for far-distant-located renewable energy sources (RES)-integrated MT-HVDC systems [20]. Shannon’s entropy and signal’s energy, evaluated through the coefficient of wavelet transform, has been employed in extreme machine learning for the estimation of single-line-to-ground fault [21]. For offshore windfarms-based MT-HVDC systems, a fuzzy logic voter system has been designed for the identification of traveling waves. A discrete wavelet analyzer has been employed for the decomposition of traveling waves for fault estimation [22]. The rapid interruption of DC faults is the main objective of protection in MT-HVDC systems [23]. The traveling wave’s velocity and reflection coefficient are used to estimate the natural frequency, which in turn is used to evaluate the fault location with the help of machine learning techniques [24,25]. Reduced overlapping in traveling waves, robustness against attenuation, and variable ground resistances in VSC-HVDC systems are resolved by the protection technique, based on a stacked auto-encoder [26]. Limited window data are required for the estimation of faults in MT-HVDC systems by the application of the electromagnetic time reversal technique [27]. Wavefronts are detected by a simplified machine learning algorithm working on morphological filters and structuring elements. The detected wavefronts are then used for the estimation of fault location [28]. The speed of traveling waves varies with the fault distance. The accuracy is then analyzed for the estimation of fault location. These methods not only ensure the rapidity of the protection system, but also the effective estimation of fault location. One of the major challenges observed in research is that fault resistance and ground resistance effects are not analyzed comprehensively [29].
It is demonstrated in the literature that fault resistance and ground resistance have a significant impact on fault estimation in HVDC systems. Support vector machines and wavelet-based machine learning approaches [17], traveling waves-based protection strategies [4], distance relays-based protection techniques [30], and pilot and non-pilot-based protection methods [31,32] in MT-HVDC systems are adversely affected by change in fault and ground resistances.
3. Proposed Methodology for Fault Diagnosis
The proposed methodological flow chart of the ML-based fault diagnosis technique is presented in Figure 2.
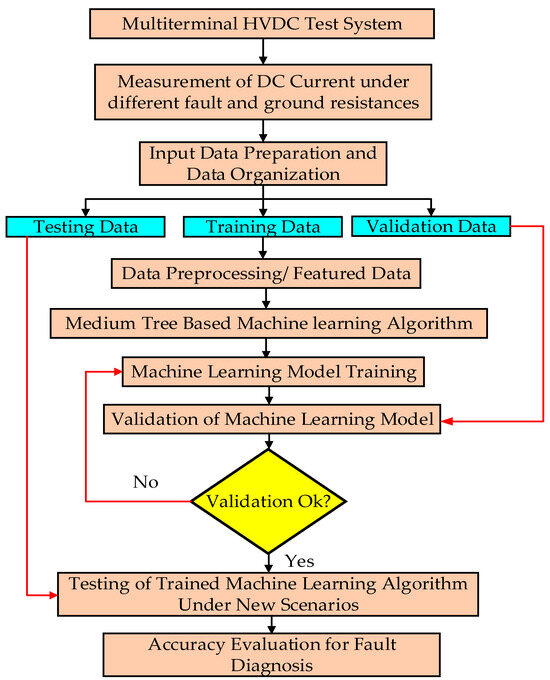
Figure 2.
Proposed flow chart of ML-based fault diagnosis in MT-HVDC system.
Because of the complications raised during the classification of faults with the help of fault current data, a machine learning-based algorithm was applied to develop an insight into the fault diagnosis. In this study, medium tree-based classification was applied for faults because of its ability to maintain a balance between interpretation and performance without compromising on computational time [33]. Preprocessing of the data was performed because of the very large data set, of size 47,265 × 21. The repetition of the values and empty values of the data set was examined and removed, resulting in the reduction in rows of the data set. Further, based on the time scale, the resolution was reduced for the data set up to about 929 × 5.
Preprocessed data were then applied to a medium tree-based classification algorithm to train it. The medium tree-based classification algorithm classifies with the Gini’s index of diversity. Gini’s index of diversity shows relatively better classification in comparison to entropy [34]. Further, it performs well for large data sets with less computational overhead as compared to information gain [33,34]. The likelihood that two things drawn at random from the relevant data set (with replacement) reflect the same type is the original Simpson index λ. Therefore, its transformation 1 − λ is equal to the likelihood that the two things represent various kinds. Mathematically,
where is Gini’s index of diversity, is the probability of occurrence, is Simpson’s index and is the total number of types in the data set.
The motivation behind the application of this diversity index is its less computational time over large datasets without compromising accuracy.
3.1. Evaluation of Trained Algorithm
A machine learning algorithm’s performance can be shown using a confusion matrix, a particular table arrangement that is usually used in supervised learning. It is a table with identical sets of “classes” in each of its dimensions—“actual” and “predicted”—and two different dimensions. The matrix shows how many true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN) the model generated using the test data. When evaluating the effectiveness of classification models, which seek to assign a category label to each input occurrence, confusion matrices are frequently utilized.
The matrix has the shape of a table for binary classification and for multi-class classification, where n is the number of classes. The confusion matrix, which displays the number of correct and erroneous guesses for each class, aids in interpreting the prediction summary in matrix form.
Understanding the effectiveness of a machine learning model requires interpreting the numbers in a confusion matrix. The stages of interpreting a confusion matrix are as follows:
The actual and anticipated classes are represented, accordingly, by rows and columns in the confusion matrix. Determining the classes facilitates the determination of which class is genuine and which class is being forecasted. The correctly categorized samples are represented by the diagonal cells of the matrix. The number of successfully identified samples may be determined by looking at the values in the diagonal cells. The model flaws are shown by the off-diagonal cells. To find out the number of incorrectly identified samples, look at the values in these cells. Accuracy, precision, recall, and F1-score may all be determined using the data from the confusion matrix. These measures provide a more thorough analysis of the model’s effectiveness.
To comprehend the advantages and disadvantages of the model, the metrics and values in the confusion matrix are analyzed. The analytical knowledge is utilized to raise the performance of the model. Interpreting a confusion matrix helps to understand how well a machine learning model performs and offers suggestions on how to make the model better.
3.2. Proposed Modification for Accuracy Improvement
Accuracy is compromised for training the scenarios under the increase in fault and ground resistance. The poorly trained algorithm also shows decreased accuracy under testing with new scenarios. Therefore, some modifications in the preprocessing of the data will be required to improve the accuracy. Figure 3 shows the steps involved in the preprocessing of featured data.
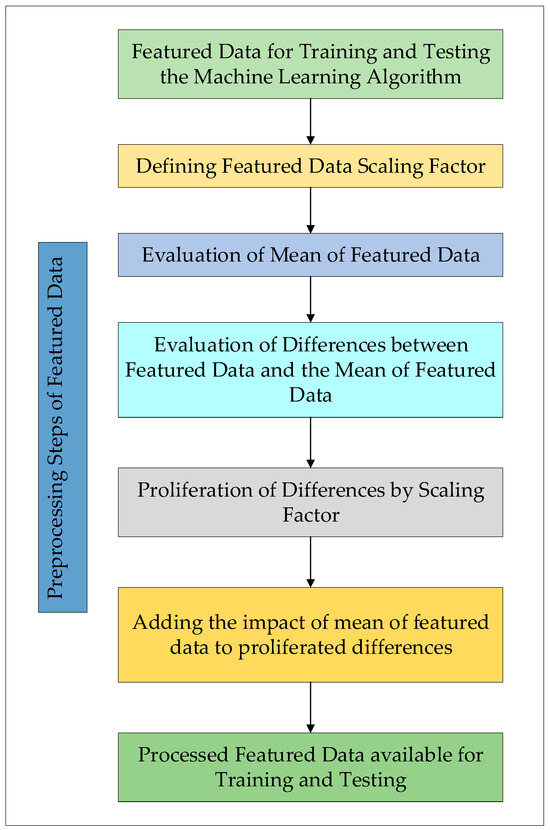
Figure 3.
Steps for preprocessing featured data employed in the machine learning algorithm.
The featured data available for preprocessing are expressed in mathematical form as:
The mean of the featured data is evaluated by the following expression:
Since the featured data have five columns, hence, there will be five mean values. The next step involves the creation of five columns of data. is based on the difference between the featured data and the mean value of featured data.
Now, the scaling factor is defined to be between . The scaling factor is applied for the proliferation of new data created by the difference between featured data and the mean of featured data.
In the last step of preprocessing, the scaled data is added to the mean value calculated in (3) as:
The preprocessed featured data for training and testing highlights the distinct and discriminative features of data, aiding in the fault diagnosis in the locations having the same characteristics. The preprocessing widens the gap between the characteristics of fault current observed at different locations and different fault and ground resistances, resulting in more observable decision boundaries for fault diagnosis.
4. Simulation Results and Analysis
The four-terminal HVDC test system was developed and simulated in Matlab/Simulink 2017b. The effect of fault resistance and ground resistance were studied in this system. The four-terminal test system consists of two onshore and two offshore power generation setups, as shown in Figure 4. The offshore power generation setups were made up of wind farms. Offshore wind farms are treated as weak AC grids. The voltage source inverter regulates the voltages and reactive power of the weak wind farms. The details of the four-terminal test systems are presented in Table 1.
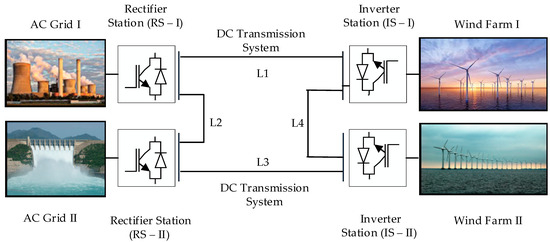
Figure 4.
Four-terminal HVDC test system.

Table 1.
Details of four-terminal HVDC test system.
Four-terminal HVDC test system is composed of different parameters and components as presented in Table 2.

Table 2.
Different parameters of four-terminal HVDC test system.
4.1. Fault Current Based Scenarios
Different simulation scenarios were created in Matlab/Simulink to explain the impact of fault resistance and ground resistance on machine learning-based fault diagnosis. A pole-to-pole ground fault was analyzed at three different locations of the test system, as mentioned in Table 3.

Table 3.
Different scenarios of the test system.
4.1.1. Scenario 1
A pole-to-pole ground fault was applied at 0 km from the rectifier station at line L1 of the test system. DCs were observed for the fault under different values of fault resistance and ground resistance to gain an insight into the behavior of machine learning-based fault diagnosis, as shown in Figure 5.
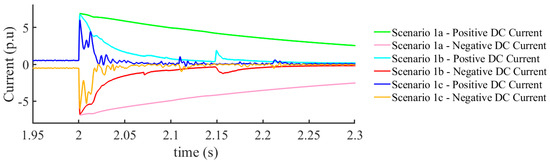
Figure 5.
Pole-to-pole ground fault at different values of fault and ground resistances 0 km from RS-I.
4.1.2. Scenario 2
A pole-to-pole ground fault was applied 100 km from the rectifier station at line L1 of the test system. To understand the behavior of machine learning-based fault diagnostics, DCs were monitored for the fault under various fault resistance and ground resistance levels, as shown in Figure 6.
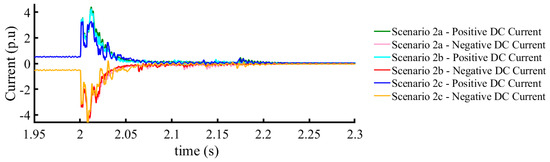
Figure 6.
Pole-to-pole ground fault at different values of fault and ground resistances 100 km from RS-I.
4.1.3. Scenario 3
A pole-to-pole ground fault was applied at a test system line L1, 200 km from the converter station. DCs were measured for the fault at different levels of fault resistance and ground resistance, as shown in Figure 7, to understand how machine learning-based fault diagnostics behave.
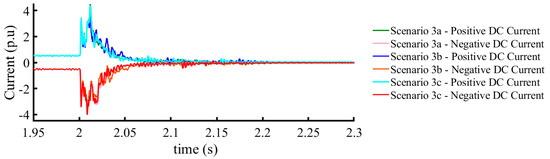
Figure 7.
Pole-to-pole ground fault at different values of fault and ground resistances 200 km from RS-I.
Based on the graphical results for the pole-to-pole ground fault, it is observed that as the fault and ground resistances increase, it is difficult to differentiate between pole-to-pole ground faults at different locations. Therefore, these complications were studied under machine learning-based classifications to determine the effects of fault and ground resistance on fault diagnosis processes.
4.2. Featured Data-Based Simulation Cases
In this study, data classification was performed based on information presented in Table 4.

Table 4.
Data classification based on data features.
4.2.1. Case I
In case I, scenario 1, as mentioned in Table 3, is used for the training of the proposed algorithm. The graphical representation of featured data for case I is given in Figure 8. Based on the training of data on a medium tree-based classification algorithm, it is found that accuracy up to about 88.7% is attained with 40 splits in medium tree. The graph of correct and incorrect predicted data obtained after medium tree-based classification is given in Figure 9. The dot represents that the prediction is successful and the cross represents the unsuccessful prediction, resulting in the reduction in accuracy. Blue line dots/crosses indicate the scenario 1a (FR = 0.001 Ω and GR = 0.1 Ω), orange line dots/crosses indicate the scenario 1b (FR = 0.1 Ω and GR = 1 Ω), pale yellow line dots/crosses indicate scenario 1c (FR = 1 Ω and GR = 100 Ω) and purple line dots/crosses indicate normal scenario for Figure 8 and Figure 9, as mentioned in Table 4.
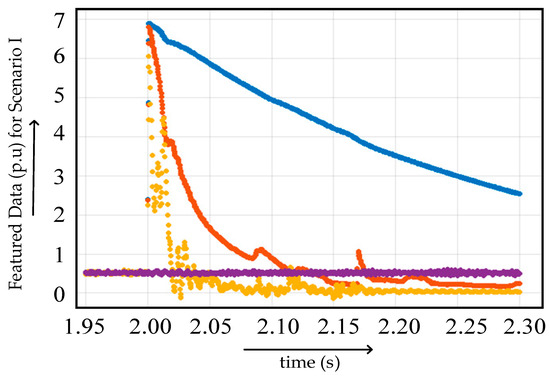
Figure 8.
Featured data derived from the current data measured at different fault locations in fault scenario 1.
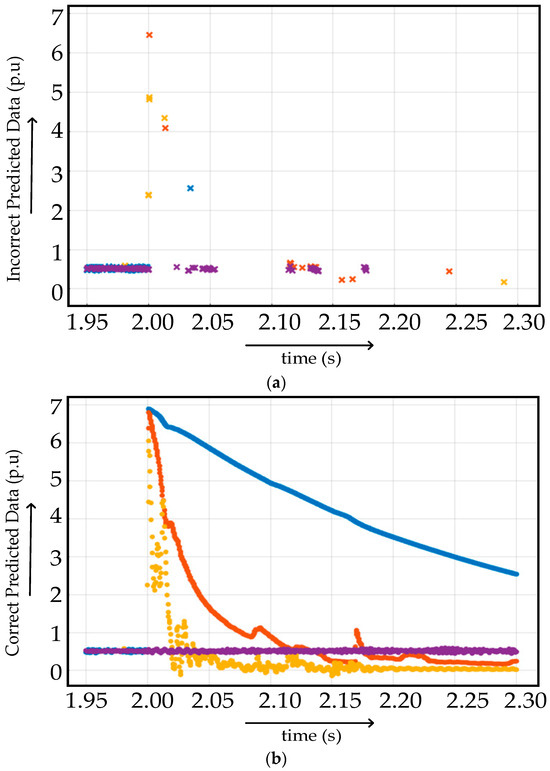
Figure 9.
(a) Incorrect and (b) correct predicted data at different fault locations in fault scenario 1.
To compute the number of successful predictions from the trained algorithm, it is necessary to analyze the confusion matrices.
Confusion Matrices for Training Under Case I
In this study, the accuracy of the trained algorithm was the metric used to predict the performance of the algorithm. The confusion matrices obtained under scenario I are given in Figure 10.
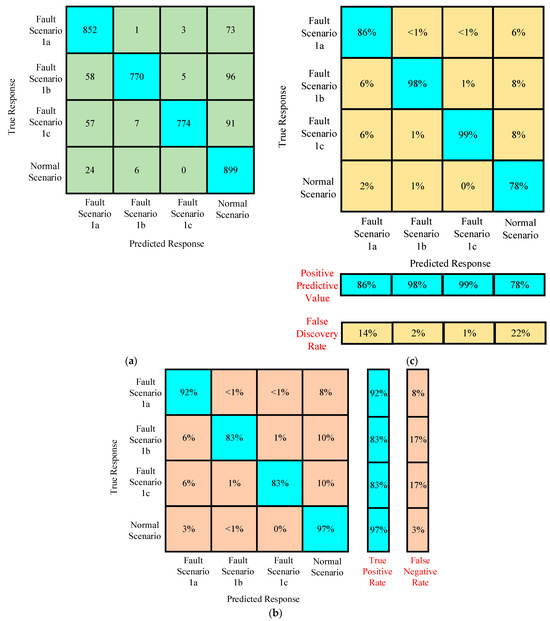
Figure 10.
(a–c) Confusion matrices of the trained algorithm for assessing the performance before testing.
Confusion Matrices for Testing Under Case I
The trained algorithm was then tested for the new data obtained under scenario 2 and scenario 3 to evaluate the performance of medium tree-based classification. It was found from the confusion matrices that the accuracy of the trained algorithm decreased to 45.53%. The confusion matrices are presented in Figure 11.
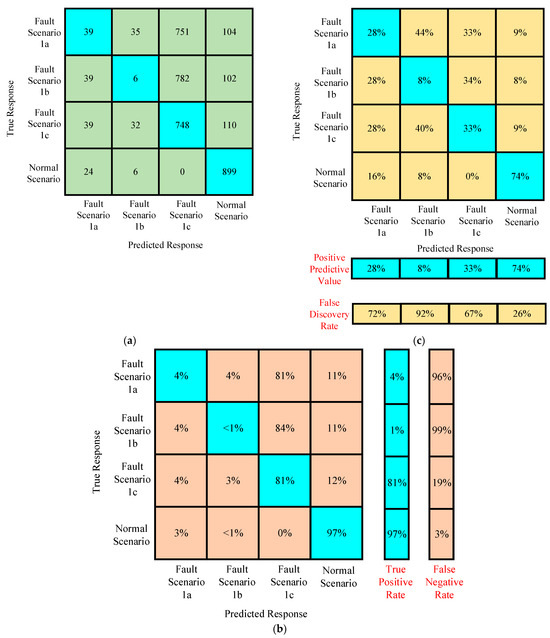
Figure 11.
(a–c) Confusion matrices of the trained algorithm for assessing the performance under testing with the new data of scenario 2 and scenario 3.
The decrease in the accuracy of the trained algorithm depicts the shortcomings in two ways. Firstly, the proposed machine learning technique is not suitable for this fault classification. Secondly, preprocessing is required to attain distinct features of the different faults in HVDC systems.
The proposed algorithm was further trained with the new data sets to analyze the performance comprehensively. The scenario 2 data collected 100 km from the converter station were applied to the algorithm for training. The accuracy of training decreased to 60% under the scenario 2.
4.2.2. Case II
In case II, the featured data extracted from scenario 2, as mentioned in Table 3, were used to assess the performance of the proposed algorithm. The graphical representation of the featured data of scenario 2 is given in Figure 12. The training of data was conducted on a medium tree-based classification algorithm. The accuracy of prediction was 60%. The reduced accuracy exposes the fact that a simplified classification algorithm alone is not enough in the case of highly sensitive multiterminal HVDC system fault diagnosis and classification. There is a need for immense hard work on preprocessing to make the medium tree-based classification algorithm viable. The graph of correct and incorrect predicted data obtained after medium tree-based classification is presented in Figure 13. Blue dots/crosses indicate the scenario 2a (FR = 0.001 Ω and GR = 0.1 Ω), orange dots/crosses indicate the scenario 2b (FR = 0.1 Ω and GR = 1 Ω), pale yellow dots/crosses indicate scenario 2c (FR = 1 Ω and GR = 100 Ω) and purple dots/crosses indicate normal scenario for Figure 12 and Figure 13, as mentioned in Table 4.
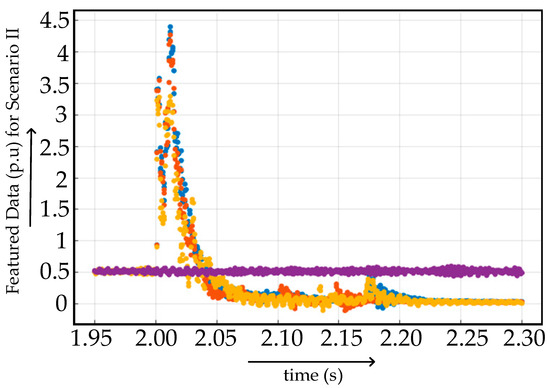
Figure 12.
Featured data derived from the current data measured at different fault locations in fault scenario 2.
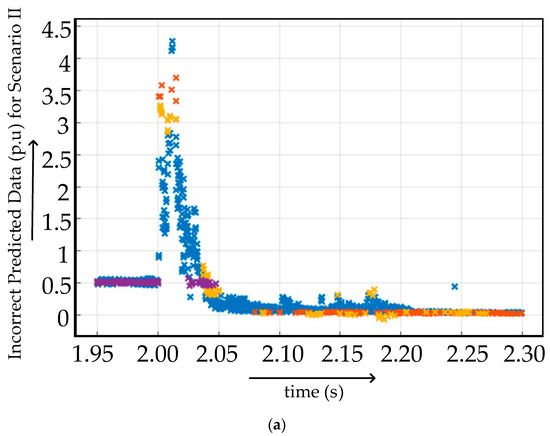
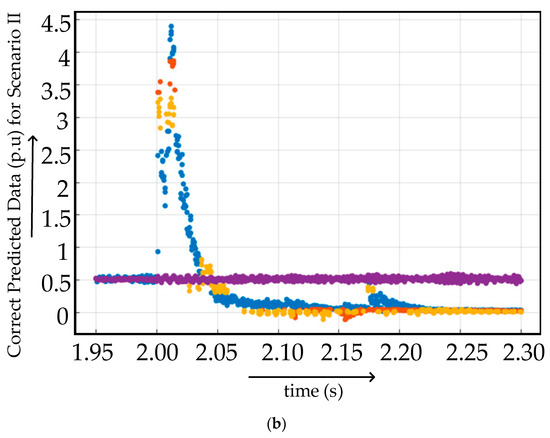
Figure 13.
(a) Incorrect and (b) correct predicted data at different fault locations in fault scenario 2.
Confusion Matrices for Training Under Case II
Confusion matrices were generated for the training data of scenario 2. In Figure 14a, the confusion matrix helps to understand the relationship between true response and predicted response. In the training data set, it is found that the normal scenario has a true positive rate of 97% as shown in Figure 14b. This is entirely because of very different characteristics of fault current as compared to the normal scenarios. Moreover, it is also observed that the true positive rate decreases with the increase in the fault resistance and ground resistance. This information helps not only in the designing of the protection of multiterminal systems, but also raises the importance of in-depth preprocessing in the case of simplified machine learning algorithms. Figure 14c depicts the interesting details about the positive predictive values and negative discovery rate. The positive predictive value is higher and the negative discovery rate is lower in the case of normal scenario as compared to the fault scenarios. In the fault scenarios, the positive predictive value increases and the negative discovery rate decreases with the increase in the value of fault resistance and ground resistance of the test system. This information helps to design the relay pickup and time settings for the multiterminal HVDC systems.
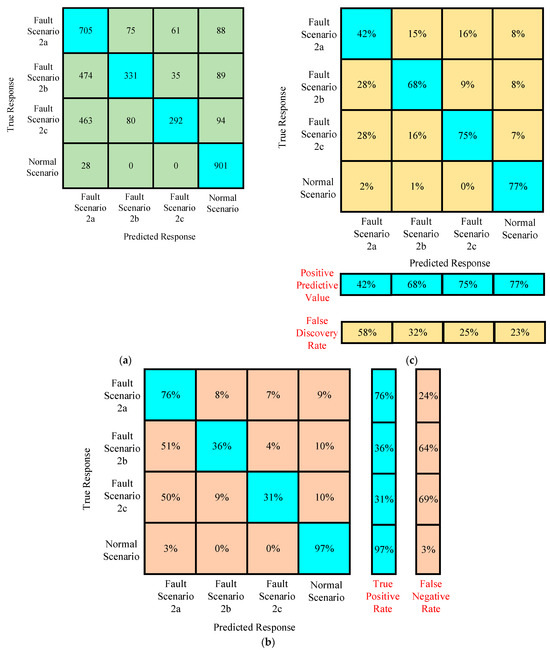
Figure 14.
(a–c) Confusion matrices of the trained algorithm for assessing the performance before testing in scenario 2.
Confusion Matrices for Testing Under Case II
As the accuracy of training in scenario 2 reduced to 60%, the accuracy of the trained algorithm had non-linear and variable behavior. It was found that accuracy did not affect the predicted response against the true response in the normal scenario, as shown in Figure 15a under testing with the new data of scenario 1. The true positive rate is 97% under the normal scenario, as given in Figure 15b. Hence, the proposed algorithm performed well with compromised accuracy under training in the case of distinct and different characteristics, as in normal scenarios in comparison to fault scenarios. The higher false negative rate depicts the poor classification among faults, resulting in raising the requirement of preprocessing of fault features. The positive predictive value reduced to 43% for the normal scenario under testing data because of the reduced accuracy of the proposed algorithm under training, as shown in Figure 15c.
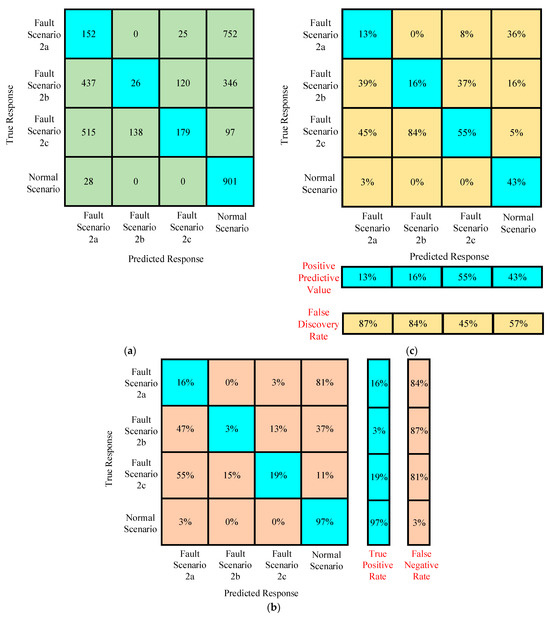
Figure 15.
(a–c) Confusion matrices of the trained algorithm for assessing the performance under testing with the new data of scenario 1.
Among all the fault scenarios, the higher positive predictive value obtained under testing the proposed algorithm was only 55%, which was for higher values of fault resistance and ground resistance, as shown in Figure 15c. There is a need for in-depth preprocessing in the case of the simplified machine learning algorithm.
Another testing scenario, i.e., scenario 3, is used to assess the performance of the proposed algorithm trained under scenario 2, as shown in Figure 16. The results are similar to the previous testing data in Figure 15. The performance of the proposed algorithm was better only for the highly different characteristics than for the normal scenario, as shown in Figure 16a. The true positive rate was only 97% in the case of the normal scenario under the compromised training accuracy of the proposed algorithm of 60%. This is presented in Figure 16b. The false negative rate was higher for all the fault scenarios of the testing data, which depicts its poor performance. Moreover, the false discovery rate was higher for all the fault scenarios, as shown in Figure 16c, which highlights the importance of exploring more features of data, resulting in better distinction and classification for different fault and ground resistances.
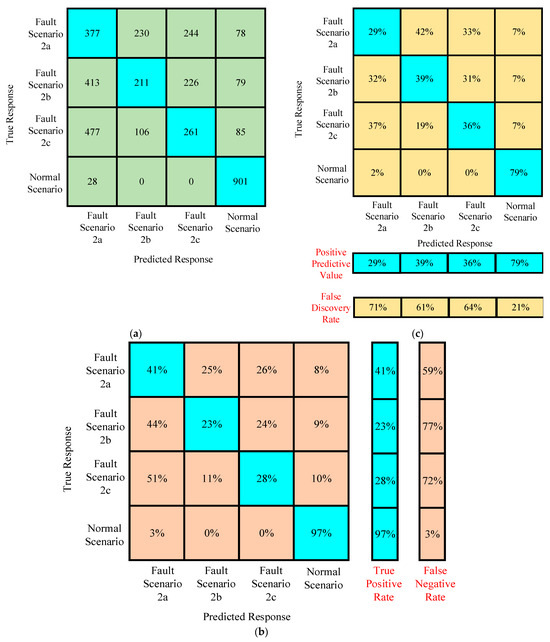
Figure 16.
(a–c) Confusion matrices of the trained algorithm for assessing the performance under testing with the new data of scenario 3.
The proposed algorithm was trained with the new data sets to comprehensively analyze the performance. The scenario 3 data collected 200 km from the converter station were applied to the algorithm for training. The accuracy of training decreased to 57.1% under scenario 3.
4.2.3. Case III
The graphical representation of featured data extracted from scenario 3, as mentioned in Table 3, is given in Figure 17. The training of scenario III data was conducted on a medium tree-based classification algorithm. The accuracy of prediction was 57.1%. The reduced accuracy concludes that only a simplified classification algorithm is not enough in the case of highly sensitive multiterminal HVDC system fault diagnosis and classification. There is a need for useful preprocessing to make the medium tree-based classification algorithm viable. The graph of correct and incorrect predicted data obtained after medium tree-based classification is presented in Figure 18. Blue dots and crosses indicate the scenario 3a (FR = 0.001 Ω and GR = 0.1 Ω), orange dots and crosses indicate the scenario 3b (FR = 0.1 Ω and GR = 1 Ω), pale yellow dots and crosses indicate scenario 3c (FR = 1 Ω and GR = 100 Ω) and purple dots and crosses indicate normal scenario for Figure 17 and Figure 18, as mentioned in Table 4.
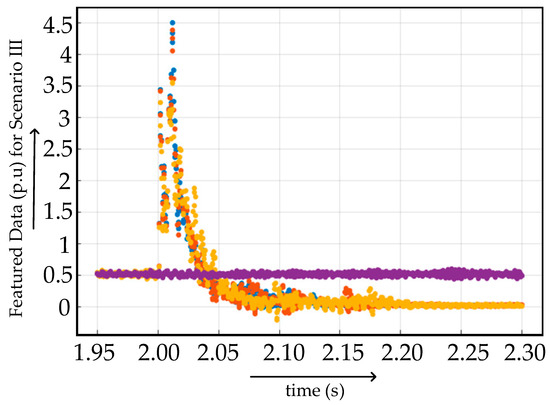
Figure 17.
Featured data derived from the current data measured at different fault locations in fault scenario III.
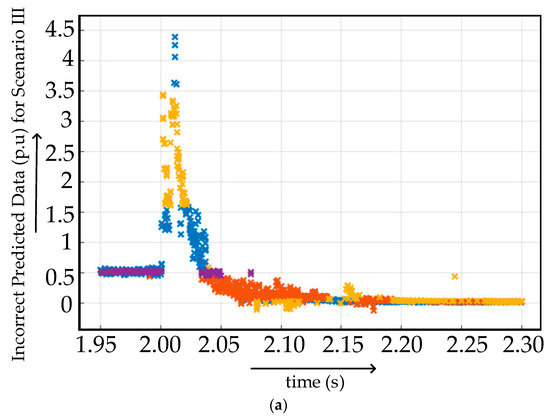
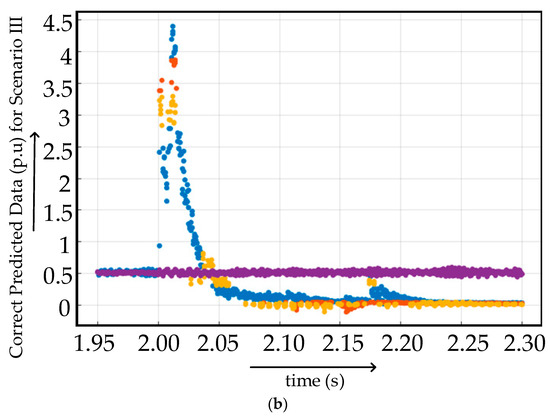
Figure 18.
(a) Incorrect and (b) correct predicted data at different fault locations in fault scenario II.
Confusion Matrices for Training Under Case III
Confusion matrices were generated for the training data of scenario II. In Figure 19a, the confusion matrix helps to understand the relationship between true response and predicted response. In the training data set, it was found that the normal scenario has a true positive rate of 98%, as shown in Figure 19b. Faults at different fault resistances and different ground resistances generated identical characteristics, resulting in exposing the limitations of the proposed algorithm. The accuracy of the true positive rate reduced to 50%, as shown in Figure 19b. This information helps not only in the designing of the protection of multiterminal systems, but also raises the importance of in-depth preprocessing in the case of simplified machine learning algorithms. Figure 19c depicts the interesting details about the positive predictive values and negative discovery rate. The positive predictive value is higher and the negative discovery rate is lower in the case of normal scenario as compared to the fault scenarios. In the fault scenarios, the positive predictive value increased and the negative discovery rate decreased with the increase in the value of fault resistance and ground resistance of the test system. This information helps to design the relay pickup and time settings for the multiterminal HVDC systems.
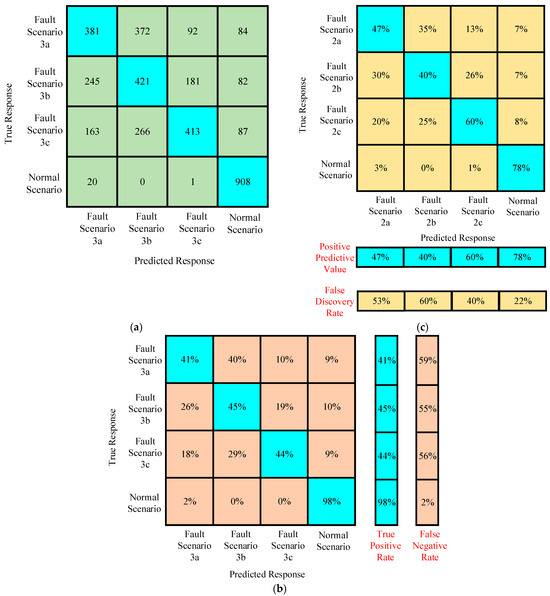
Figure 19.
(a–c) Confusion matrices of the trained algorithm for assessing the performance before testing in scenario III.
Confusion Matrices for Testing Under Case III
As the accuracy of training in scenario III reduced to 57.1%, the accuracy of the trained algorithm was compromised in the identification and classification of faults based on fault and ground resistance. To assess the performance, the trained algorithm was tested on scenario I. It was found that accuracy does not affect the predicted response against the true response in the normal scenario, as shown in Figure 20a. The true positive rate was 98% under the normal scenario, as shown in Figure 20b. Hence, the proposed algorithm performs well with compromised accuracy under training in the case of distinct and different characteristics, as in normal scenarios in comparison to fault scenarios. The higher false negative rate depicts the poor classification among faults, resulting in raising the requirement of preprocessing of fault features. The positive predictive value reduced to 43% for the normal scenario under testing data because of the reduced accuracy of the proposed algorithm under training, as shown in Figure 20c.
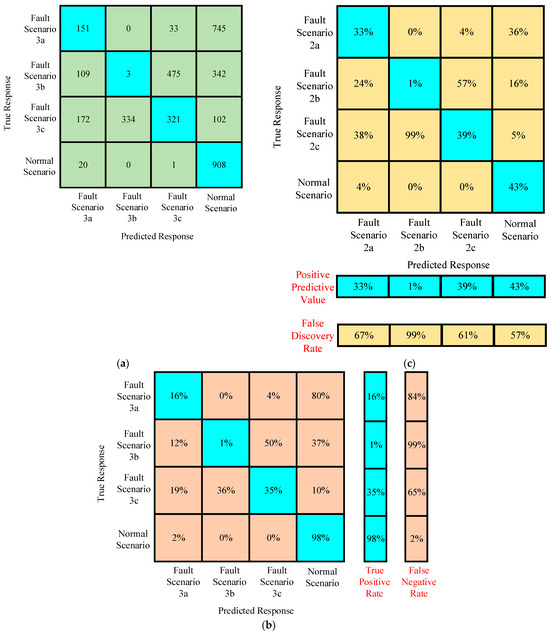
Figure 20.
(a–c) Confusion matrices of the trained algorithm for assessing the performance under testing with the new data of scenario I.
Among all the fault scenarios, the higher positive predictive value obtained under testing the proposed algorithm was only 39%, as shown in Figure 20c. The algorithm performance is compromised under fault scenarios. There is a need for in-depth preprocessing in the case of the simplified machine learning algorithm.
Another testing scenario, i.e., scenario 2, is used to assess the performance of the proposed algorithm trained under scenario 3, as shown in Figure 21. The results are similar to the previous testing data in Figure 20. The performance of the proposed algorithm was better only for the highly different characteristics rather than for the normal scenario, as shown in Figure 21a. The true positive rate was only 98% in the case of the normal scenario under the compromised training accuracy of the proposed algorithm of 60%. This is presented in Figure 21b. The false negative rate was higher for all the fault scenarios of the testing data, which depicts its poor performance. A maximum of 43% true positive rate was acquired in one of the fault cases under testing with scenario 2. Moreover, the false discovery rate was higher for all the fault scenarios, as shown in Figure 21c. The exploration of more features of data results in better distinction and classification for different fault and ground resistances.
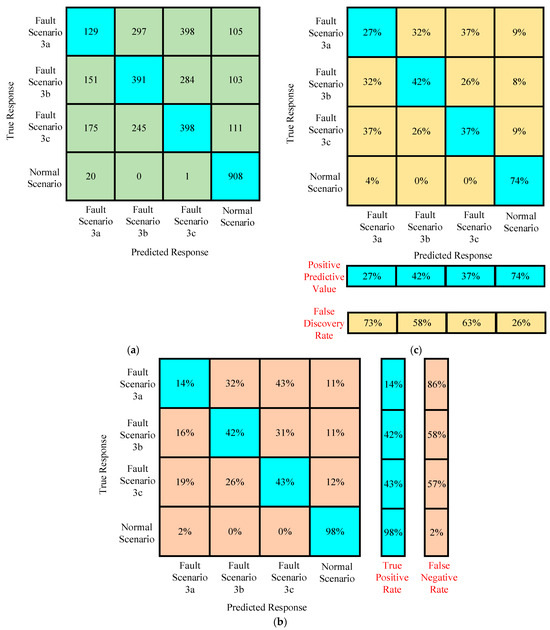
Figure 21.
(a–c) Confusion matrices of the trained algorithm for assessing the performance under testing with the new data of scenario 2.
An overview of the performance of the proposed algorithm is presented in terms of accuracy in Table 5. Table 5 depicts the limitations of the proposed algorithm. The limitations cannot be overcome without the exploration of more features of the data for training and testing.

Table 5.
Performance analysis based on accuracy under different simulation scenarios.
4.3. Accuracy Improvement-Based Simulation Cases
It is observed from the evaluation of the trained algorithm in Section 4.2 that accuracy is compromised when training the scenarios under an increase in fault and ground resistance. The poorly trained algorithm also shows decreased accuracy under testing with new testing scenarios. Therefore, based on the evaluation, the treatment of preprocessing was formulated in the methodological section. After preprocessing, the proposed algorithm is re-evaluated and accuracy was determined in the preceding subsections.
4.3.1. Case I
In case I, the featured data extracted from scenario 1 was further processed via the proposed modification. The graphical representation of featured data under different events of normal and faults is shown in Figure 22. The featured data were used for the training of the medium tree-based machine learning algorithm. The accuracy of training improved to 99.5%. This remarkable improvement in accuracy is depicted via incorrect and correct prediction, as shown in Figure 23. Blue line dots/crosses indicate the scenario 1a (FR = 0.001 Ω and GR = 0.1 Ω), orange line dots/crosses indicate the scenario 1b (FR = 0.1 Ω and GR = 1 Ω), pale yellow line dots/crosses indicate scenario 1c (FR = 1 Ω and GR = 100 Ω) and purple line dots/ crosses indicate normal scenario for Figure 22 and Figure 23, as mentioned in Table 4.
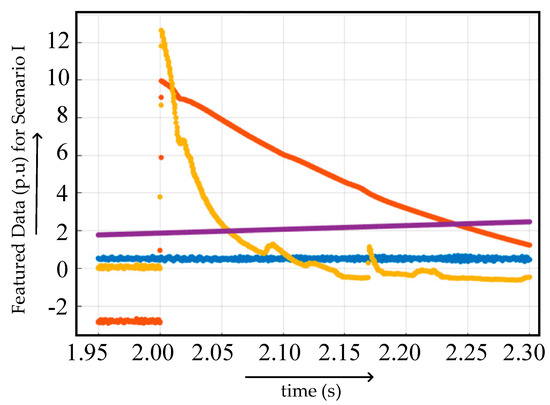
Figure 22.
Featured data processed under proposed modification at different fault locations in fault scenario.
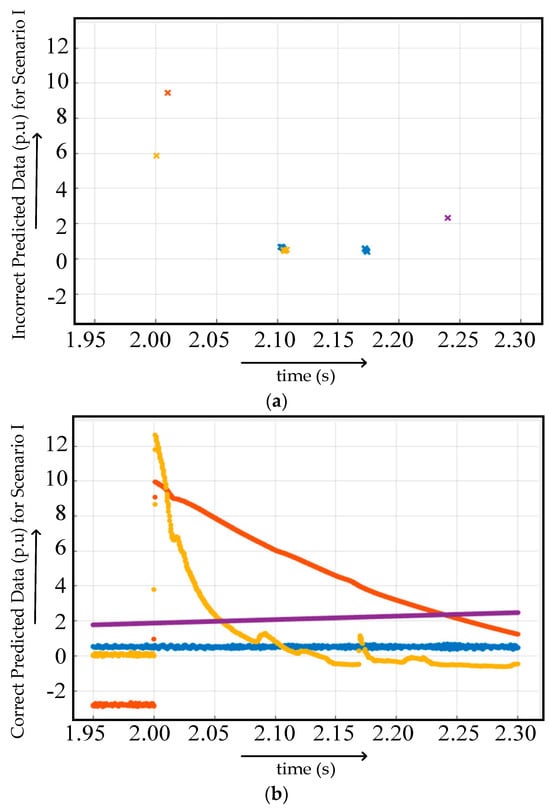
Figure 23.
(a) Incorrect and (b) correct predicted data at different fault locations in fault scenario 1 after preprocessing.
Confusion Matrices for Training of Algorithm Under Preprocessed Featured Data of Case I
In this study, the performance of the trained algorithm was assessed with the results of confusion matrices under different events of normal and fault states of the MT-HVDC test system. The confusion matrices obtained under case I with the proposed preprocessing of featured data are given in Figure 24.
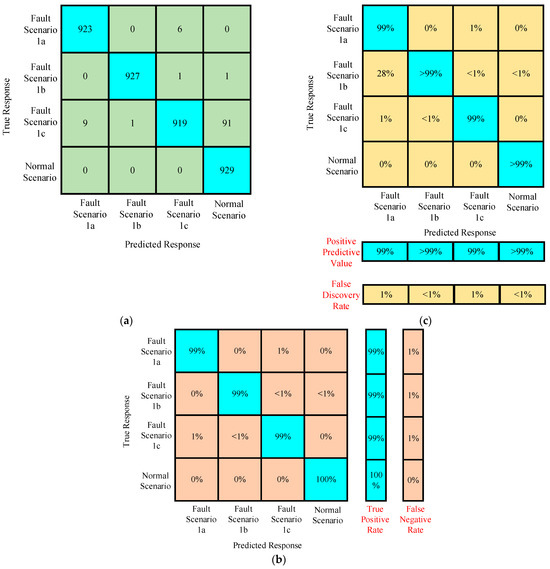
Figure 24.
(a–c) Confusion matrices of the trained algorithm for assessing the performance under preprocessed featured data in case I.
Confusion Matrices for Testing of Algorithm Under Preprocessed Featured Data of Case I
The trained algorithm was then tested for the new featured data preprocessed under scenario 2 and scenario 3 to evaluate the performance of medium tree-based classification. It is found from the confusion matrices that the accuracy of the trained algorithm was found to be 71.56%. The confusion matrices are presented in Figure 25.
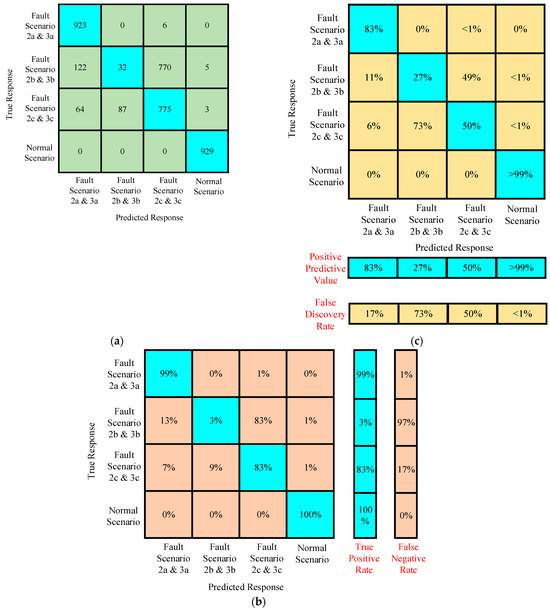
Figure 25.
(a–c) Confusion matrices of the trained algorithm for assessing the performance under testing with the newly featured preprocessed data of scenario 2 and scenario 3.
Some of the interesting observations made are:
- The accuracy of testing the trained algorithm with the data having the same features used for training was around 99.5%.
- The accuracy of testing the trained algorithm with the new data improved to 26.03%.
4.3.2. Case II
In case II, the featured data extracted from Scenario 2, as mentioned in Table 3, were further preprocessed. The graphical representation of preprocessed featured data of scenario 2 is given in Figure 26. The medium tree-based classification algorithm is trained on the preprocessed featured data. The accuracy of prediction is 84.1%. The increased accuracy as compared to the without preprocessed featured data enables the better classification of faults at the same location, and also at other locations. The graph of correct and incorrect predicted data obtained after medium tree-based classification is presented in Figure 27. Blue line dots/crosses indicate the scenario 2a (FR = 0.001 Ω and GR = 0.1 Ω), orange line dots/crosses indicate the scenario 2b (FR = 0.1 Ω and GR = 1 Ω), pale yellow line dots/crosses indicate scenario 2c (FR = 1 Ω and GR = 100 Ω) and purple line dots/crosses indicate normal scenario for Figure 26 and Figure 27, as mentioned in Table 4.
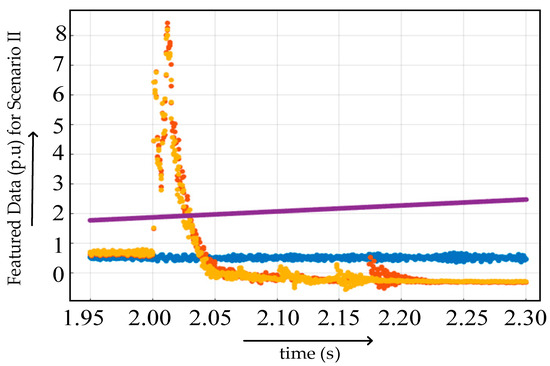
Figure 26.
Featured data processed under proposed modification at different fault locations in fault scenario 2.
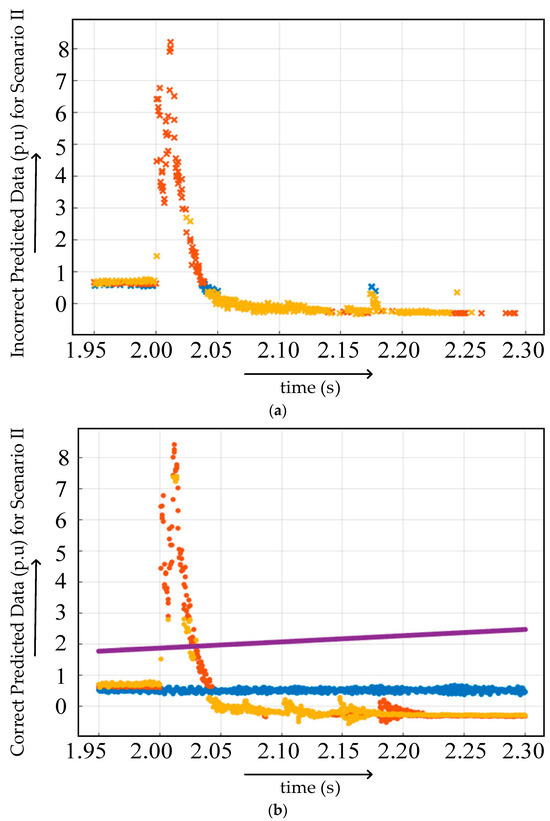
Figure 27.
(a) Incorrect and (b) correct predicted data at different fault locations in fault scenario 2.
Confusion Matrices for Training of Algorithm Under Preprocessed Featured Data of Case II
The performance of the proposed algorithm over preprocessed featured data was assessed via confusion matrices. Confusion matrices were generated for the training of the proposed algorithm on the featured data of scenario 2. In Figure 28a, the confusion matrix helps to understand the relationship between the true response and the predicted response. In the training data set, it was found that the normal scenario had a true positive rate of 100%, as shown in Figure 28b. This is entirely because of the very different characteristics of fault current as compared to the normal scenarios. Moreover, it is also observed that the true positive rate for fault scenario 2a, i.e., fault at 100 km with FR = 0.001 Ω, GR = 0.1 Ω, is also greater than 99%. This information not only helps in the designing of the protection of multiterminal systems, but also raises the importance of in-depth preprocessing in the case of simplified machine learning algorithms. Figure 28c depicts the interesting details about the positive predictive values and negative discovery rate. The positive predictive value was higher and the negative discovery rate was lower in the case of normal scenario as compared to the fault scenarios. In the fault scenarios, the positive predictive value increased and the negative discovery rate decreased with the increase in the value of fault resistance and ground resistance of the test system. This information helps to design the relay pickup and time settings for the multiterminal HVDC systems.
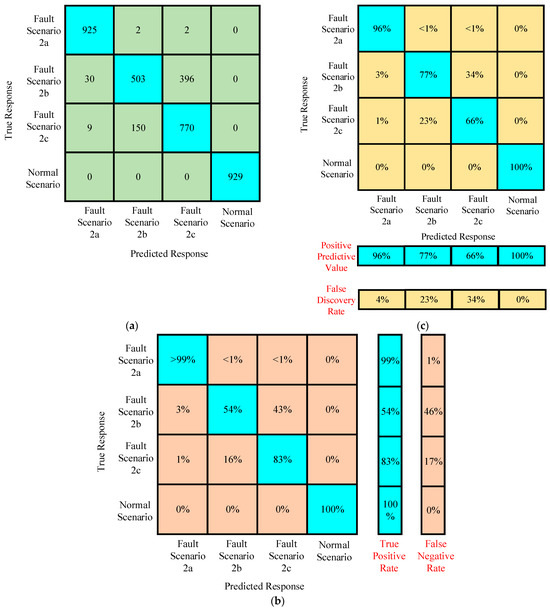
Figure 28.
(a–c) Confusion matrices of the trained algorithm for assessing the performance under preprocessed featured data in case II.
Confusion Matrices for Testing Algorithm Under Preprocessed Featured Data of Case II
As the accuracy of training in scenario 2 was 84.1%, the trained algorithm comparatively performed better over the identification and classification of faults based on fault and ground resistances. To assess the performance, the trained algorithm was tested on the preprocessed featured data with characteristics similar to the training data of case II. The accuracy was maintained at 84.1%. To widen the scope of the trained algorithm, the testing was performed on new preprocessed featured data. The accuracy under testing was 77.99%.
Based on the observations, the following results were obtained:
- 3.
- The accuracy of testing the trained algorithm with the data having the same features used for training is around 84.1%. Hence, preprocessing of featured data increases the accuracy by up to 24.1%.
- 4.
- The accuracy of testing the trained algorithm with the new data is improved up to an average of 37.52%.
It was found that accuracy does not affect the predicted response against the true response in the normal scenario, as shown in Figure 29a. The true positive rate was 100% under normal scenarios, even for the new preprocessed featured data, as given in Figure 29b. Hence, the proposed algorithm performed well under testing with the new data, particularly in the case of distinct and different characteristics, as in normal scenarios in comparison to fault scenarios. The higher false negative rate is observed in only one fault scenario among all the normal and fault scenarios, as shown in Figure 29c. The positive predictive value is higher in three scenarios under testing, with the new preprocessed featured data resulting in adaptability and certainty in more than 75% of scenarios of fault identification and classification with this simplest proposed algorithm, as shown in Figure 29c.
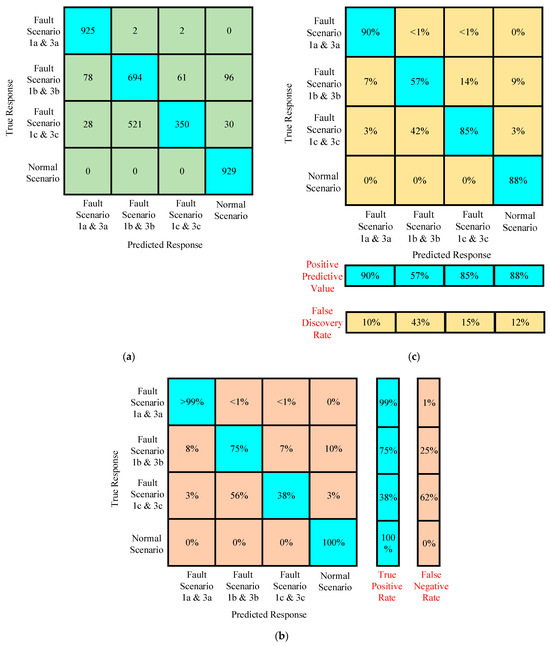
Figure 29.
(a–c) Confusion matrices of the trained algorithm for assessing the performance under testing with the newly featured preprocessed data of scenario 1 and scenario 3.
4.3.3. Case III
The graphical representation of preprocessed featured data extracted from scenario 3, as mentioned in Table 3, is given in Figure 30. The medium tree-based classification algorithm’s training is performed with the preprocessed featured data of scenario 3. The accuracy of prediction is 77.8%. The accuracy is 20.7% more than the training performed on the non-preprocessed data of Scenario 3.
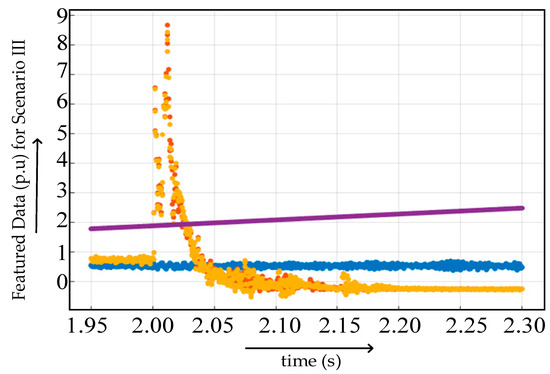
Figure 30.
Featured data processed under proposed modification at different fault locations in fault scenario 3.
The improved accuracy demonstrates that a simplified classification algorithm can perform better in the case of highly sensitive multiterminal HVDC system fault diagnosis and classification if preprocessed featured data are used. The graph of correct and incorrect predicted data obtained after medium tree-based classification is presented in Figure 31. Blue line dots/crosses indicate the scenario 3a (FR = 0.001 Ω and GR = 0.1 Ω), orange line dots/crosses indicate the scenario 3b (FR = 0.1 Ω and GR = 1 Ω), pale yellow line dots/crosses indicate scenario 3c (FR = 1 Ω and GR = 100 Ω) and purple line dots/crosses indicate normal scenario for Figure 30 and Figure 31, as mentioned in Table 4.
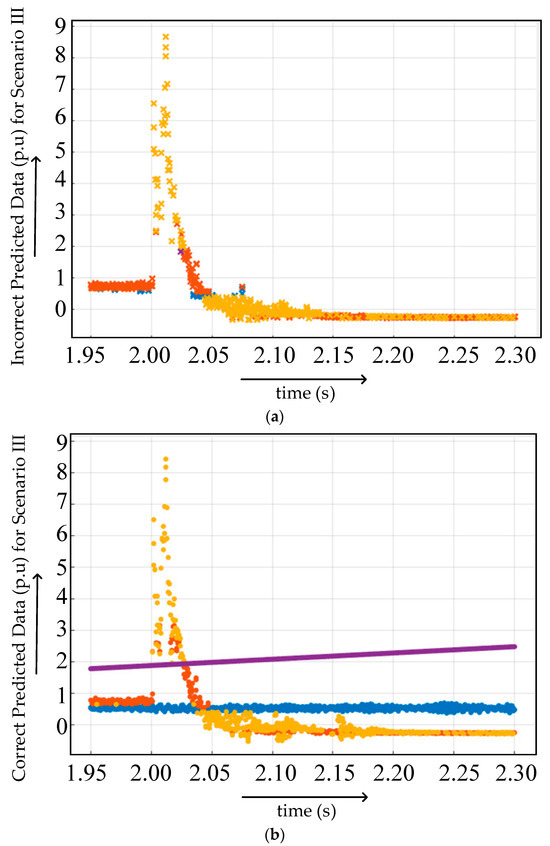
Figure 31.
(a) Incorrect and (b) correct predicted data at different fault locations in fault scenario 3.
Confusion Matrices for Training Algorithm Under Preprocessed Featured Data of Case III
The confusion matrices are generated for the preprocessed training data of scenario 3. In Figure 32a, the confusion matrix generates the understanding between true response and predicted response. In the training data set, it was found that the normal scenario had a true positive rate of 100%, as shown in Figure 32b. Faults at 100 km with greater fault resistances and greater ground resistances generate identical characteristics, resulting in exposing the limitations of the proposed algorithm. The accuracy of the true positive rate reduced to an average of 58%, as shown in Figure 32b. This information not only helps in designing the protection of multiterminal systems, but also raises the limitations in the case of simplified machine learning algorithms after the preprocessing of featured data. Figure 32c depicts the interesting details about the positive predictive values and negative discovery rate. The positive predictive value is higher and the negative discovery rate is lower in the case of the normal scenario and fault scenario (with lower fault and ground resistance values) as compared to the other fault scenarios. In the fault scenarios, the positive predictive value increases and the negative discovery rate decreases with the increase in the value of fault resistance and ground resistance of the test system, as shown in Figure 32c. This information helps to design the relay pickup and time settings for the multiterminal HVDC systems.
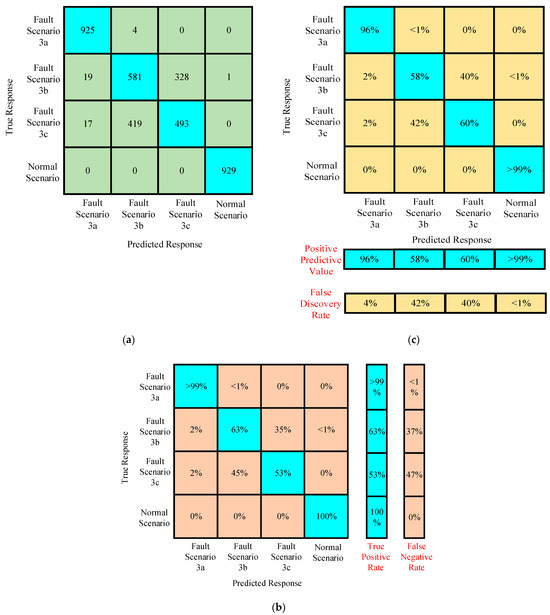
Figure 32.
(a–c) Confusion matrices of the trained algorithm for assessing the performance with preprocessed featured data in case III.
Confusion Matrices for Testing Algorithm Under Preprocessed Featured Data of Case III
If the accuracy of training of the proposed algorithm in scenario 3 is limited to 77.8%, the testing accuracy of the trained algorithm for new preprocessed featured data will compromise the identification and classification of faults based on fault and ground resistances. To assess the performance, the trained algorithm was tested on preprocessed featured data with the same characteristics as the training data. It was found that accuracy remains the same as training the data. However, the accuracy of the trained algorithm reduced to 69.54%. This is entirely because of the cases of fault with higher ground and fault resistances at any location.
The accuracy of the predicted response against the true response was higher than 99% in the case of normal and fault scenarios (1a and 2a), as shown in Figure 33a. The true positive rate was greater than 99% under the normal scenario and fault scenario (1a and 2a), as shown in Figure 33b. Hence, the proposed algorithm performed well in the case of distinct and different characteristics, such as in normal scenarios and fault scenarios (1a and 2a). The higher false negative rate depicts the poor classification among faults with relatively high fault and ground resistances, resulting in raising the limitation of the proposed algorithm, even with the preprocessed featured data. The positive predictive value reduced to 88% for normal scenarios and 90% for fault scenarios (1a and 2a) with preprocessed featured data. The improved accuracy, as compared to testing without preprocessed featured data, highlights the benefits of using the proposed simplified machine learning algorithm, as shown in Figure 33c.
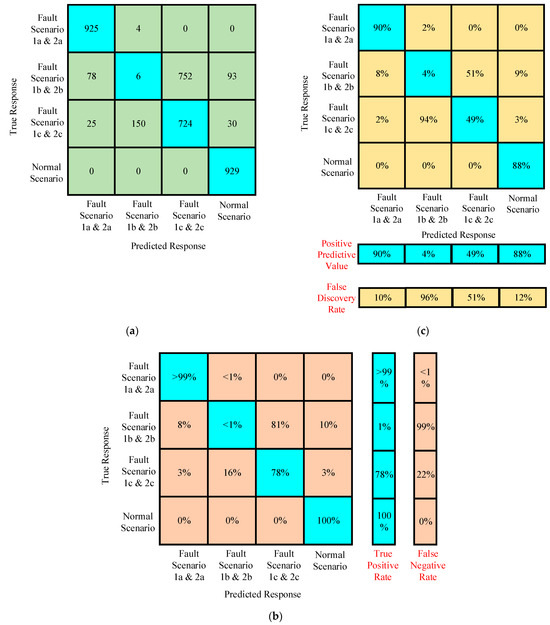
Figure 33.
(a–c) Confusion matrices of the trained algorithm for assessing the performance with preprocessed featured data in case III.
An overview of the performance of the proposed algorithm presented in terms of accuracy is in Table 6. Table 6 depicts the accuracy of the proposed algorithm with preprocessed featured data used for training and testing.

Table 6.
Performance analysis of machine learning algorithm based on accuracy under different simulation scenarios, trained and tested with preprocessed featured data.
It is observed that the preprocessed featured data not only increased the accuracy of training, but also testing with new featured data, resulting in increasing the application of the proposed machine learning algorithm. Figure 34 elaborates the performance comparison of machine learning algorithms trained and tested with and without preprocessed featured data.
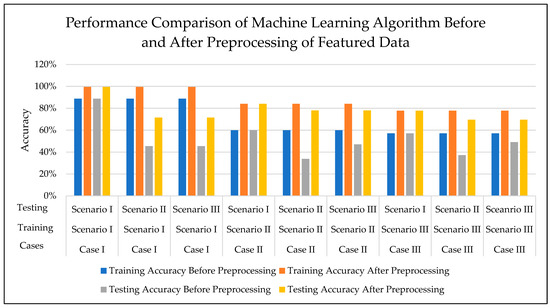
Figure 34.
Performance comparison of machine learning algorithm trained and tested with and without preprocessed featured data for fault diagnosis in MT-HVDC system.
4.4. Research Limitations
One of the significant challenges associated with fault diagnosis in multiterminal HVDC transmission systems is the need for the rapid interruption of DC fault current because of its sudden build-up to failure levels in converter stations. In the literature, many advanced machine learning approaches of protection have been developed that can interrupt the DC fault current with a computational overhead. The proposed medium tree-based algorithm offers relatively better interruption based on location-based classification with easy interpretation. Easy interpretation offers a reduction in computational time, which is the heart of the protection technique. However, the proposed research is only carried out for the pole-to-pole faults. Moreover, it is observed from the simulations that the classification accuracy of proposed preprocessing and machine learning-based protection is slightly compromised in the scenarios with high ground and fault resistances, particularly for the new data. Therefore, there is a need to establish a mechanism for high ground and fault resistance faults that could be classified with better accuracy. In addition to this, the research also indicates the limitations of the simplified medium tree-based machine learning algorithm. Without preprocessing the data for training and testing, the accuracy is not acknowledgeable. Therefore, preprocessing not only improves the accuracy of results, but also enables the location-based classification of DC faults in MT-HVDC systems with relatively higher discriminative features.
4.5. Annotations of Research for Protection
Preprocessing of featured data before the application of the proposed machine learning algorithm offers significant improvement in accuracy. The improvement in accuracy is presented in Table 7.

Table 7.
Improvement in accuracy of ML based fault diagnosis by preprocessing.
The following are the benefits obtained through this proposed technique for fault diagnosis:
- The accuracy of fault classification is improved significantly without adding challenging computational overheads.
- Preprocessing based on the simple computation of mean and differences has aided Gini’s index of diversity-based classification remarkably.
- Table 7 indicates that scenarios with high values of fault and ground resistances in the test system are associated with a significant improvement in accuracy.
- Less complexity offers a relatively better classification of faults based on location with easy interpretation.
4.6. Comparison with Existing Machine Learning Techniques
Significant work has been performed in the field of the protection of multiterminal HVDC systems based on machine learning. However, the proposed work offers easier interpretation with relatively better classification, resulting in much lower computational overhead. Table 8 presents the comparative study between medium tree-based machine learning techniques and advanced machine learning techniques for protection against faults in MT-HVDC systems.

Table 8.
Performance comparison of the proposed technique with the existing machine learning techniques for fault diagnosis in MT-HVDC systems.
4.7. Computational Complexity Analysis of Proposed Technique
The proposed technique involves the evaluation of the diversity index and tree splitting. All the abovementioned evaluations are not complex and are easier to handle. Further, the preprocessing also reduces the data required for training from to . Based on reduced complexity, the proposed technique can be used for online fault diagnosis. In this study, the scenarios are created based on different locations and with different fault and ground resistances. The very short training time of 0.876 s makes this technique an excellent relaying candidate for the system, which changes its configuration because of distributed energy source because of retraining in a minimal time.
4.8. Real-Time Implementation Consideration of Proposed Technique
In the real-time implementation, data on fault characteristics based on fault current values were gathered. The fault current data was, then, preprocessed and features were extracted. Extracted features were used as an input to decision-making based on Gini’s index of diversity. The trip signal was generated. In short, the real implementation scenario was composed of steps of data acquisition, data preprocessing, feature extraction, decision-making process, and initiation of the trip signal. Every step offers low latency, resulting in rapid responses against fault scenarios. The proposed real-time structure is presented in Figure 35.
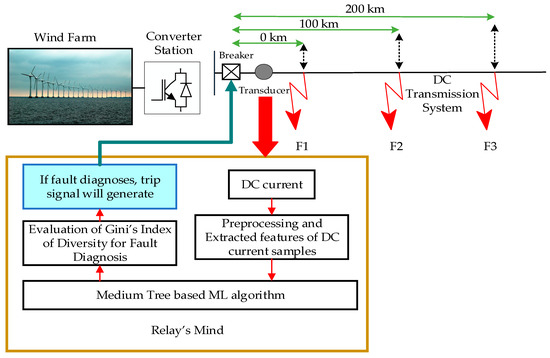
Figure 35.
Proposed structure of real-time implementation of medium tree-based machine learning algorithm for fault diagnosis in MT-HVDC systems.
5. Conclusions
A comprehensive study and analysis was performed on the fault diagnosis in the MT-HVDC system under varying fault and ground resistances. It was found from the simulation that significant effects are produced by the fault and ground resistances on the fault characteristics. Relaying methods undergo maloperations, resulting in limitations of the protection techniques. MT-HVDC systems are the preferred way of bulk power transfer to remote areas. The installations related to HVDC systems are performed on different soil conditions, resulting in an impact generated to the ground resistances. Also, atmospheric conditions not only have a huge impact on the fault resistances of HVDC systems, but also on ground resistances.
Therefore, to avoid maloperation resulting in a significant outage, the effects of ground and fault resistances on protection strategies are required to be analyzed. In this study, a simplified machine learning technique was developed. Its performance was analyzed under the variable nature of fault and ground resistances. A significant reduction in the accuracy of fault diagnosis was observed under increased fault resistance and ground resistance. Therefore, preprocessing of featured data was carried out in this study based on mean, differences, and scaling factors to highlight the hidden characteristics of faults under high fault and ground resistances. It is observed that more than 99% accuracy is obtained for fault diagnosis with the machine learning algorithm. However, a significant improvement is also observed with the new data, making it a viable option for the protection of long-distance HVDC systems. The proposed research of fault diagnosis is not limited to four-terminal HVDC systems, but also to more than four or less than four multiterminal HVDC systems. The only significant modification required will be the deployment of transducers according to terminals for pilot communication-based protection strategy or the adjustment of settings of the relay according to terminals for a non-pilot communication-based protection strategy.
Possible Future Directions
The following are the future directions that can be explored regarding fault diagnosis based on machine learning techniques:
- Pole-to-pole faults can be made part of the research under different fault and ground resistances and with a medium tree-based machine learning algorithm.
- The hybrid approach of machine learning techniques for fault diagnosis can be developed in which online fault diagnosis can be performed with the simplified machine learning algorithm, and offline in-depth fault studies can be performed with the advanced and computationally extensive machine learning algorithms.
- More methods of preprocessing can be explored so that the accuracy can be retained at higher values with the higher values of fault and ground resistances.
- Internal and external faults based on zones and protection can be analyzed for the multiterminal system. Fault diagnosis can be carried out with the medium tree-based machine algorithm which has the wonderful feature of avoiding overfitting and outliers.
- Relay coordination setup can be simulated with the medium tree-based machine learning algorithm because of its rapid response with less data and computational time.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The author is thankful to the Department of Electrical Engineering, the University of Lahore, Lahore, Pakistan for providing facilities to conduct this research.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Sneath, J.; Rajapakse, A.D. Fault Detection and Interruption in an Earthed HVDC Grid Using ROCOV and Hybrid DC Breakers. IEEE Trans. Power Deliv. 2016, 31, 973–981. [Google Scholar] [CrossRef]
- Wang, L.; Liu, H.; Dai, L.; Liu, Y. Novel Method for Identifying Fault Location of Mixed Lines. Energies 2018, 11, 1529. [Google Scholar] [CrossRef]
- Farshad, M.; Sadeh, J. A Novel Fault-Location Method for HVDC Transmission Lines Based on Similarity Measure of Voltage Signals. IEEE Trans. Power Deliv. 2013, 28, 2483–2490. [Google Scholar] [CrossRef]
- Muzzammel, R. Traveling Waves-Based Method for Fault Estimation in HVDC Transmission System. Energies 2019, 12, 3614. [Google Scholar] [CrossRef]
- Muzzammel, R.; Raza, A.; Hussain, M.R.; Abbas, G.; Ahmed, I.; Qayyum, M.; Rasool, M.A.; Khaleel, M.A. MT–HVdc Systems Fault Classification and Location Methods Based on Traveling and Non-Traveling Waves—A Comprehensive Review. Appl. Sci. 2019, 9, 4760. [Google Scholar] [CrossRef]
- Yang, J.; Fletcher, J.E.; O’Reilly, J. Short-Circuit and Ground Fault Analyses and Location in VSC-Based DC Network Cables. IEEE Trans. Ind. Electron. 2012, 59, 3827–3837. [Google Scholar] [CrossRef]
- Ye, X.; Lan, S.; Xiao, S.; Yuan, Y. Single Pole-to-Ground Fault Location Method for MMC-HVDC System Using Wavelet Decomposition and DBN. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 238–247. [Google Scholar] [CrossRef]
- Swetapadma, A.; Agarwal, S.; Chakrabarti, S.; Chakrabarti, S.; El-Shahat, A.; Abdelaziz, A.Y. Locating Faults in Thyristor-Based LCC-HVDC Transmission Lines Using Single End Measurements and Boosting Ensemble. Electronics 2022, 11, 186. [Google Scholar] [CrossRef]
- Ashouri, M.; da Silva, F.F.; Bak, C.L. On the Application of Modal Transient Analysis for Online Fault Localization in HVDC Cable Bundles. IEEE Trans. Power Deliv. 2020, 35, 1365–1378. [Google Scholar] [CrossRef]
- Zhai, S.; Cui, Y.; Li, F.; Wang, R.; Su, W.; Tang, H. VSC-HVDC Fault Location Method Based on Effective Feature and Depth Belief Network. J. Phys. Conf. Ser. 2022, 2409, 012027. [Google Scholar] [CrossRef]
- Chen, Q.; Wu, J.; Li, Q.; Gao, X.; Yu, R.; Guo, J.; Peng, G.; Yang, B. Long Short-Term Memory Network-Based HVDC Systems Fault Diagnosis under Knowledge Graph. Electronics 2023, 12, 2242. [Google Scholar] [CrossRef]
- Li, K.-Q.; Yin, Z.-Y.; Zhang, N.; Liu, Y. A Data-Driven Method to Model Stress-Strain Behaviour of Frozen Soil Considering Uncertainty. Cold Reg. Sci. Technol. 2023, 213, 103906. [Google Scholar] [CrossRef]
- Angra, S.; Ahuja, S. Machine Learning and Its Applications: A Review. In Proceedings of the 2017 International Conference on Big Data Analytics and Computational Intelligence (ICBDAC), Chirala, Andhra Pradesh, India, 23–25 March 2017; IEEE: Piscataway, NJ, USA; pp. 57–60. [Google Scholar]
- Li, L.; Wu, Y.; Ou, Y.; Li, Q.; Zhou, Y.; Chen, D. Research on Machine Learning Algorithms and Feature Extraction for Time Series. In Proceedings of the 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017; IEEE: Piscataway, NJ, USA; pp. 1–5. [Google Scholar]
- Kumar, Y.; Kaur, K.; Singh, G. Machine Learning Aspects and Its Applications Towards Different Research Areas. In Proceedings of the 2020 International Conference on Computation, Automation and Knowledge Management (ICCAKM): Dubai, United Arab Emirates, 9–10 January 2020; IEEE: Piscataway, NJ, USA; pp. 150–156. [Google Scholar]
- Li, K.; Horton, R.; He, H. Application of Machine Learning Algorithms to Model Soil Thermal Diffusivity. Int. Commun. Heat Mass Transf. 2023, 149, 107092. [Google Scholar] [CrossRef]
- Luo, G.; Yao, C.; Tan, Y.; Liu, Y. Transient Signal Identification of HVDC Transmission Lines Based on Wavelet Entropy and SVM. J. Eng. 2019, 2019, 2414–2419. [Google Scholar] [CrossRef]
- Chen, M.-J.; Lan, S.; Chen, D.-Y. Machine Learning Based One-Terminal Fault Areas Detection in HVDC Transmission System. In Proceedings of the 2018 8th International Conference on Power and Energy Systems (ICPES), Colombo, Sri Lanka, 21–22 December 2018; IEEE: Piscataway, NJ, USA; pp. 278–282. [Google Scholar]
- Lan, S.; Chen, M.-J.; Chen, D.-Y. A Novel HVDC Double-Terminal Non-Synchronous Fault Location Method Based on Convolutional Neural Network. IEEE Trans. Power Deliv. 2019, 34, 848–857. [Google Scholar] [CrossRef]
- Hossam-Eldin, A.; Lotfy, A.; Elgamal, M.; Ebeed, M. Artificial Intelligence-based Short-circuit Fault Identifier for MT-HVDC Systems. IET Gener. Transm. Amp; Distrib. 2018, 12, 2436–2443. [Google Scholar] [CrossRef]
- Unal, F.; Ekici, S. A Fault Location Technique for HVDC Transmission Lines Using Extreme Learning Machines. In Proceedings of the 2017 5th International Istanbul Smart Grid and Cities Congress and Fair (ICSG), Istanbul, Turkey, 19–21 April 2017; IEEE: Piscataway, NJ, USA; pp. 125–129. [Google Scholar]
- Hossam-Eldin, A.; Lotfy, A.; Elgamal, M.; Ebeed, M. Combined Traveling Wave and Fuzzy Logic Based Fault Location in Multi-Terminal HVDC Systems. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016; IEEE: Piscataway, NJ, USA; pp. 1–6. [Google Scholar]
- Dudve, R.; Goad, S. A Review on Automated Techniques for Fault Location in HVDC Systems. IJSREM 2022, 6, 1–5. [Google Scholar] [CrossRef]
- He, Z.; Liao, K.; Li, X.; Lin, S.; Yang, J.; Mai, R. Natural Frequency-Based Line Fault Location in HVDC Lines. IEEE Trans. Power Deliv. 2014, 29, 851–859. [Google Scholar] [CrossRef]
- Muzzammel, R. Machine Learning Based Fault Diagnosis in HVDC Transmission Lines. In Intelligent Technologies and Applications; Bajwa, I.S., Kamareddine, F., Costa, A., Eds.; Communications in Computer and Information Science; Springer: Singapore, 2019; Volume 932, pp. 496–510. ISBN 978-981-13-6051-0. [Google Scholar]
- Luo, G.; Yao, C.; Liu, Y.; Tan, Y.; He, J.; Wang, K. Stacked Auto-Encoder Based Fault Location in VSC-HVDC. IEEE Access 2018, 6, 33216–33224. [Google Scholar] [CrossRef]
- Razzaghi, R.; Paolone, M.; Rachidi, F.; Descloux, J.; Raison, B.; Retiere, N. Fault Location in Multi-Terminal HVDC Networks Based on Electromagnetic Time Reversal with Limited Time Reversal Window. In Proceedings of the 2014 Power Systems Computation Conference, Wroclaw, Poland, 18–22 August 2014; IEEE: Piscataway, NJ, USA; pp. 1–7. [Google Scholar]
- Triveno, J.P.; Dardengo, V.P.; De Almeida, M.C. An Approach to Fault Location in HVDC Lines Using Mathematical Morphology. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; IEEE: Piscataway, NJ, USA; pp. 1–5. [Google Scholar]
- Yi-ning, Z.; Yong-hao, L.; Min, X.; Ze-xiang, C. A Novel Algorithm for HVDC Line Fault Location Based on Variant Travelling Wave Speed. In Proceedings of the 2011 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Weihai, China, 6–9 July 2011; IEEE: Piscataway, NJ, USA; pp. 1459–1463. [Google Scholar]
- Abdollahzadeh, H. A New Approach to Eliminate Impacts of High-Resistance Faults by Compensation of Traditional Distance Relays’ Input Signals. Electr. Power Syst. Res. 2021, 194, 107098. [Google Scholar] [CrossRef]
- Ma, J.; Xiao, Z.; Cheng, P. A Pilot Protection Scheme for Flexible HVDC Transmission Lines Based on Modulus Power. Int. J. Electr. Power Energy Syst. 2022, 137, 107849. [Google Scholar] [CrossRef]
- Sorrentino, E.; Ayala, C. Measurement of Fault Resistances in Transmission Lines by Using Recorded Signals at Both Line Ends. Electr. Power Syst. Res. 2016, 140, 116–120. [Google Scholar] [CrossRef]
- Gurucharan, M.K. Gini Index Formula: A Complete Guide for Decision Trees and Machine Learning. Artif. Intell. 2025. [Google Scholar]
- Liu, Y.; Yang, S. Application of Decision Tree-Based Classification Algorithm on Content Marketing. J. Math. 2022, 2022, 6469054. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).