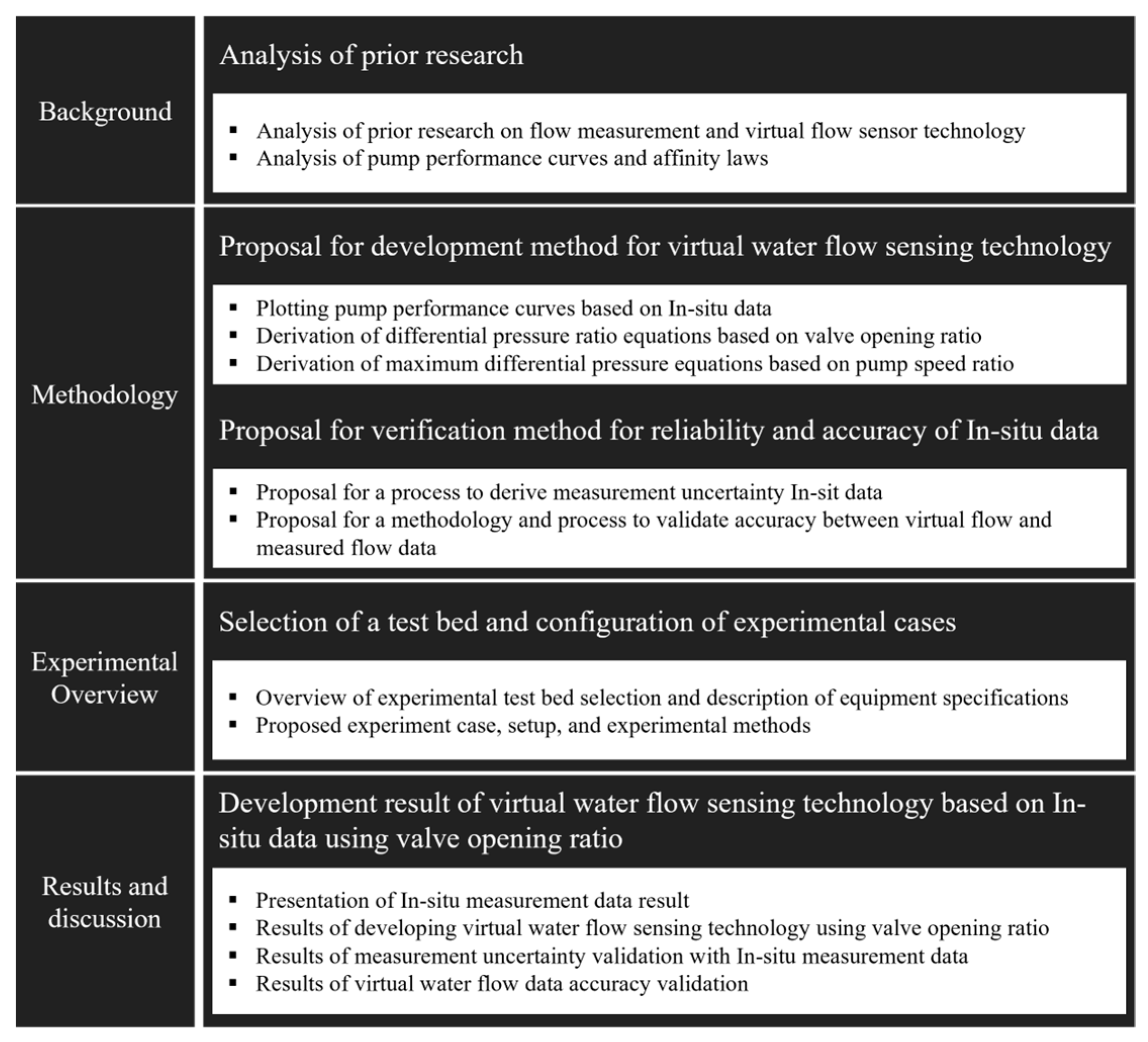
Development of Virtual Water Flow Sensor Using Valve Performance Curve
Abstract
:1. Introduction
1.1. Research Background
1.2. Relative Research
2. Methodology
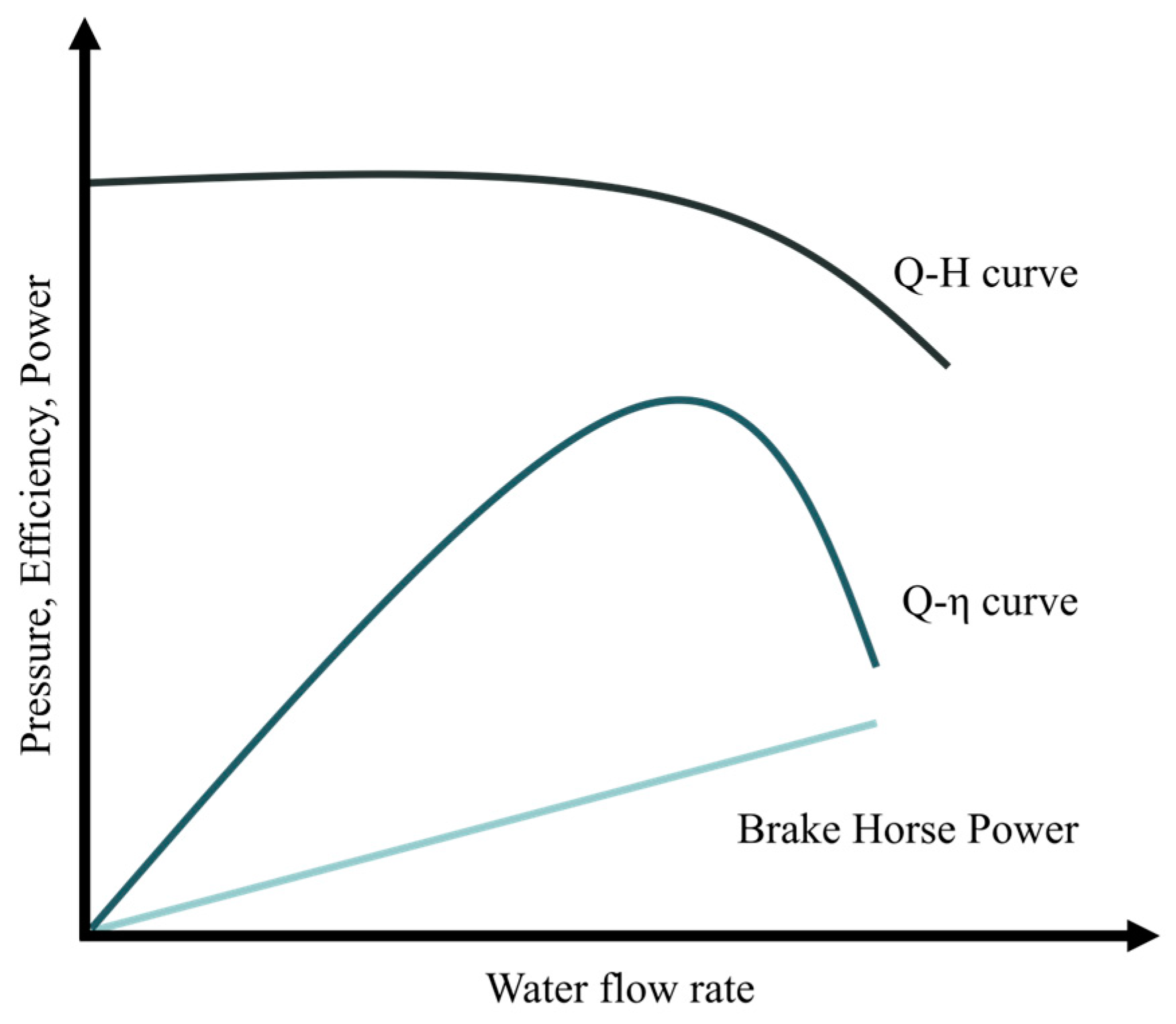
2.1. Pump Performance Curve
2.2. Development Method for Virtual Water Flow-Sensing Technology
2.3. Verification Method for Reliability of In Situ Data
2.4. Verification Method for Accuracy of Virtual Water Flow-Sensing Technology
3. Experimental Overview
3.1. Selection of Test Bed
3.2. Experimental Case Setup and Methodology
4. Results and Discussion
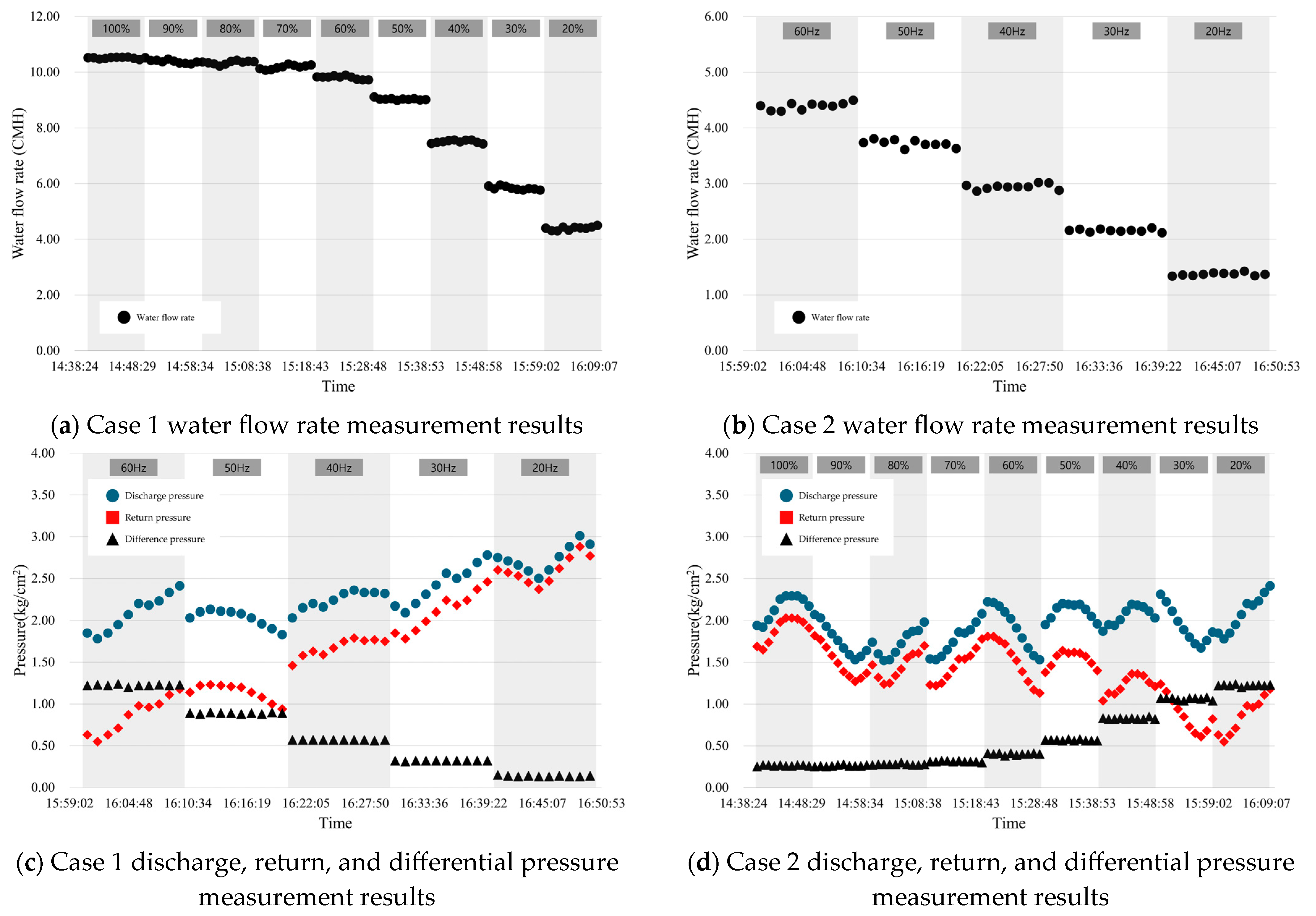
4.1. Results of In Situ Data by Case
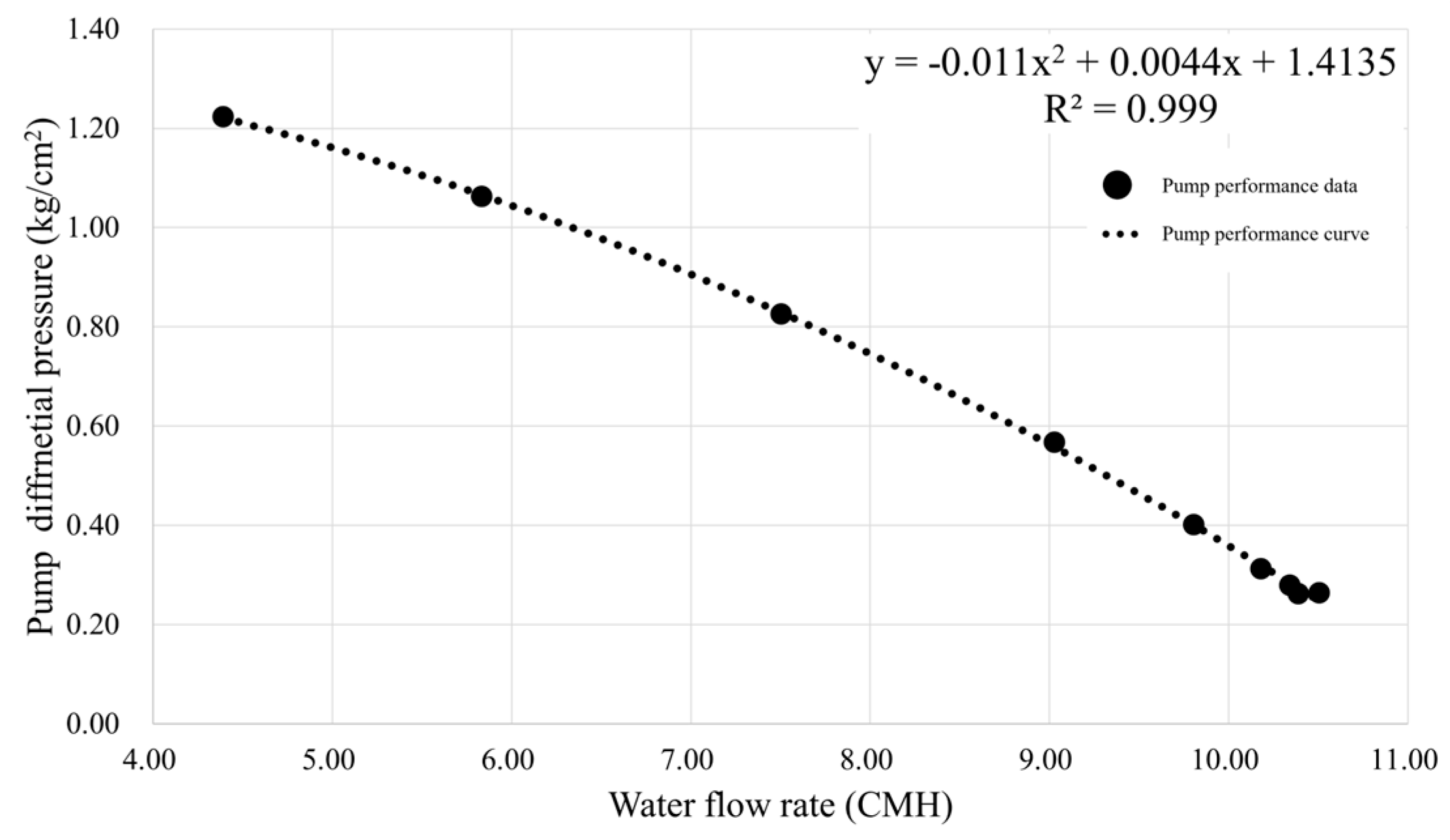
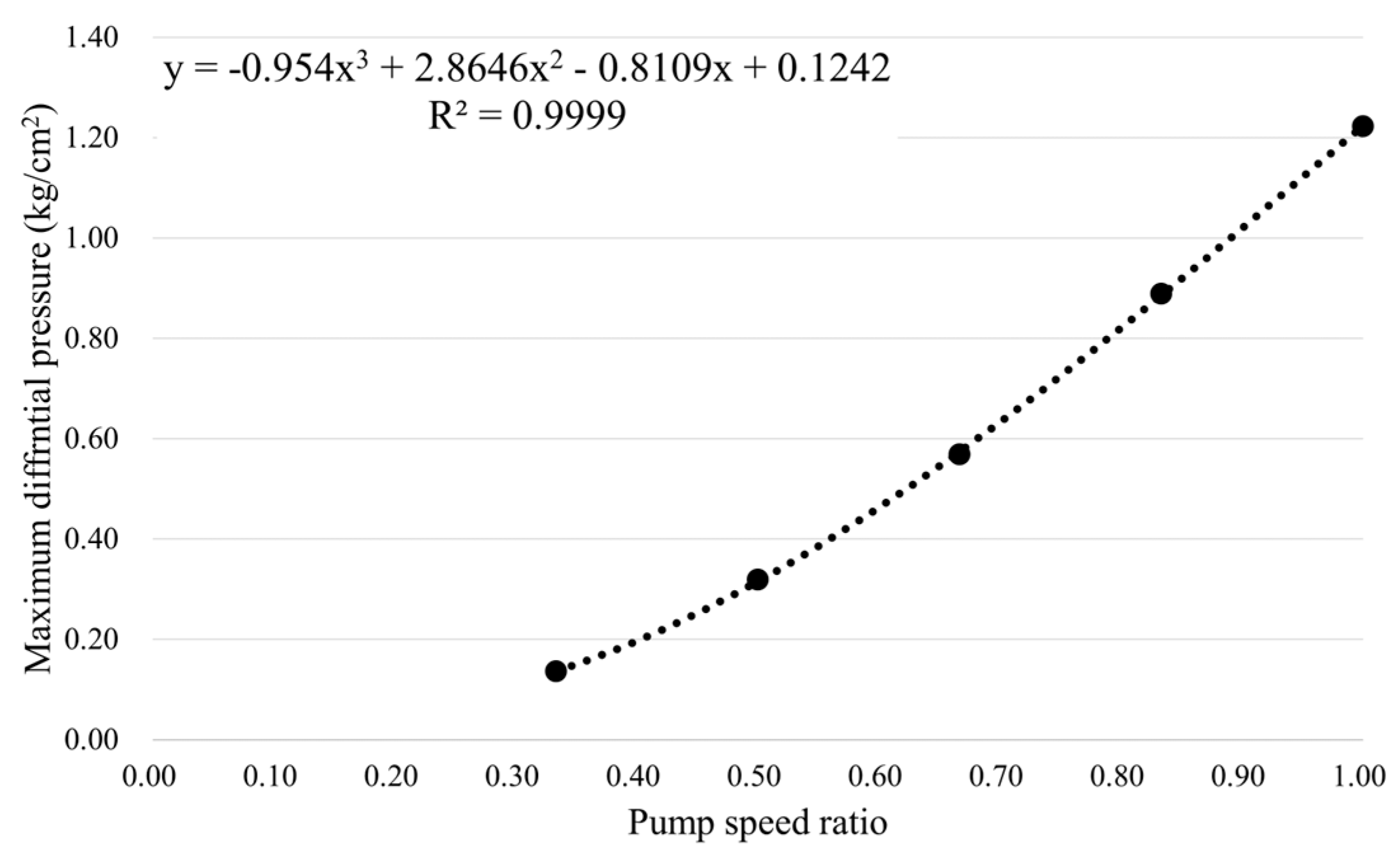
4.2. Development of Water Virtual Flow-Sensing Technology Using Valve Opening Rate
4.3. Validation Results of the Water Virtual Flow Meter
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jung, R.B. A Study on the EU’s Response to the United Nations Framework Convention on Climate Change. Master’s Thesis, Hankuk University of Foreign Studies, Seoul, Republic of Korea, 2022. [Google Scholar]
- Jeong, Y.S. Decomposition Analysis and Reduction Implementation Indicator of Greenhouse Gas Emission in Building Sector. J. Archit. Inst. Korea 2024, 40, 225–234. [Google Scholar]
- Chae, Y.G. Legislative Challenges to Realize the 2050 Carbon Neutral Goal in Korea. Inha Law Rev. Inst. Leg. Stud. Inha Univ. 2022, 25, 63–99. [Google Scholar] [CrossRef]
- UNFCCC. 2050 Carbon Neutral Strategy of the Republic of Korea; UNFCCC: Rio de Janeiro, Brazil, 2020. [Google Scholar]
- Jin, J.T.; Seok, Y.J.; Cho, H.J.; Choi, S.G.; Hwang, D.K. Design of Chilled Water Temperature Condition of Large Temperature Differential Chiller for Saving Building Energy. Korean J. Air-Cond. Refrig. Eng. 2023, 35, 90–98. [Google Scholar]
- Asim, N.; Badiei, M.; Mohammad, M.; Razali, H.; Rajabi, A.; Chin Haw, L.; Jameelah Ghazali, M. Sustainability of Heating, Ventilation and Air-Conditioning (HVAC) Systems in Buildings—An Overview. Int. J. Environ. Res. Public Health 2022, 19, 1016. [Google Scholar] [CrossRef]
- Ministry of Trade, Industry and Energy. Statistics on Energy Use and Greenhouse Gas Emissions; Ministry of Trade, Industry and Energy: Sejong, Republic of Korea, 2019.
- Lee, J.N.; Kim, Y.I.; Chung, K.S. Flow Control of a Centralized Cooling Plant for Energy Saving. J. Energy Eng. 2015, 24, 48–54. [Google Scholar] [CrossRef]
- Kim, W.U. Experimental Study on the Water Flow Control of Partial Cooling/Heating Load in Water to Water Heat Pump. In Proceedings of the SAREK Annual Conference, Pyeongchang, Republic of Korea, 22–24 June 2022; pp. 303–306. [Google Scholar]
- Lee, C.U.; Jin, S.; Do, S.L. Development of Virtual Sensor for Measurement of Heating Mass Flow Rate in Apartment Buildings using District Heating System. Proc. Korean Inst. Archit. Sci. Conf. 2021, 41, 632. [Google Scholar]
- Wotzka, D.; Zmarzły, D. Low-Cost Device for Measuring Wastewater Flow Rate in Open Channels. Sensors 2024, 24, 6607. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.W.; Yoon, S.M. Time Series Data Downscaling Method for Backup Virtual Sensor Performance Improvement in a Building Energy Sensor Network. Korean J. Air-Cond. Refrig. Eng. 2022, 34, 111–122. [Google Scholar]
- Guzmán, C.H.; Carrera, J.L.; Durán, H.A.; Berumen, J.; Ortiz, A.A.; Guirette, O.A.; Arroyo, A.; Brizuela, J.A.; Gómez, F.; Blanco, A.; et al. Implementation of Virtual Sensors for Monitoring Temperature in Greenhouses Using CFD and Control. Sensors 2019, 19, 60. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Yu, D.; Braun, J. A review of virtual sensing technology and application in building systems. HVAC&R Res. 2011, 17, 619–648. [Google Scholar]
- Jung, Y.J.; Jo, J.H.; Kim, Y.S.; Cho, Y.H. A Study on the Geothermal Heat Pump System Performance Analysis according to Water Flow Rate Control of the Geothermal Water Circulation Pump. J. Korean Sol. Energy Soc. 2014, 34, 103–109. [Google Scholar] [CrossRef]
- Sarbu, I.; Valea, E.S. Energy Savings Potential for Pumping Water in District Heating Stations. Sustainability 2015, 7, 5705–5719. [Google Scholar] [CrossRef]
- Shin, J.H.; Cho, Y.H. Development of an Operating Method for Variable Water Flow Rate Control Method in Geothermal Heat Pump System. J. Korean Inst. Archit. Sustain. Environ. Build. Syst. 2018, 12, 510–518. [Google Scholar]
- Wang, Y.; Zhang, H.; Han, Z.; Ni, X. Optimization design of centrifugal pump flow control system based on adaptive control. Processes 2021, 9, 1538. [Google Scholar] [CrossRef]
- Swamy, S.; Song, L.; Wang, G. A Virtual Chilled-Water Flow Meter Development at Air Handling Unit Level. ASHRAE Trans. 2012, 118, 1013–1020. [Google Scholar]
- Song, L.; Joo, I.; Wang, G. Uncertainty analysis of a virtual water flow measurement in building energy consumption monitoring. HVAC&R Res. 2012, 18, 997–1010. [Google Scholar]
- Kim, Y.J.; Kim, P.H.; Lee, K.S.; Kim, B.H.; Chung, H.S.; Jeong, H.M. A Study on the Application of Pump Similarity Re-quirements according to Performance Variation of the Centrifugal Pump. In Proceedings of the KSME Spring Annual Meeting 2008, Jeongseon, Republic of Korea, 24–25 April 2008; p. 2614. [Google Scholar]
- Liu, G. Development and Applications of Fan Airflow Station and Pump Water Flow Station in Heating, Ventilating, and Air-Conditioning (HVAC) Systems; University of Nebraska Lincoln ProQuest Dissertations Publishing: Lincoln, NE, USA, 2006; p. 3237050. [Google Scholar]
- Kim, H.J.; Jae, H.J.; Cho, H.J. Development of Virtual Air Flow Sensor Using In-Situ Damper Performance Curve in VAV Terminal Unit. Energies 2019, 12, 4307. [Google Scholar] [CrossRef]
- Wiora, J.; Wiora, A. Measurement Uncertainty Calculations for pH Value Obtained by an Ion-Selective Electrode. Sensors 2018, 18, 1915. [Google Scholar] [CrossRef]
- Pham, H. A New Criterion for Model Selection. Mathematics 2019, 7, 1215. [Google Scholar] [CrossRef]
- Pawłowski, E.; Szlachta, A.; Otomański, P. The Influence of Noise Level on the Value of Uncertainty in a Measurement System Containing an Analog-to-Digital Converter. Energies 2023, 16, 1060. [Google Scholar] [CrossRef]
- ISO. Guide to the Expression of Uncertainty in Measurement; Aenor: Madrid, Spain, 1993. [Google Scholar]
- Taylor, J.R. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements, 2nd ed.; University Science Books: Sausalito, CA, USA, 1997. [Google Scholar]
- Dobra, P.; Jósvai, J. Cumulative and Rolling Horizon Prediction of Overall Equipment Effectiveness (OEE) with Machine Learn-ing. Big Data Cogn. Comput. 2023, 7, 138. [Google Scholar] [CrossRef]
- Abe, C.F.; Dias, J.B.; Notton, G.; Faggianelli, G.A. Experimental Application of Methods to Compute Solar Irradiance and Cell Temperature of Photovoltaic Modules. Sensors 2020, 20, 2490. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Ye, Y.; Liu, J.; Zhang, L.; Li, W.; Mohtaram, S. Machine Learning Approach to Predict Building Thermal Load Consider-ing Feature Variable Dimensions: An Office Building Case Study. Buildings 2023, 13, 312. [Google Scholar] [CrossRef]
- EVO. International Performance Measurement and Verification Protocol (IPMVP); EVO: Washington, DC, USA, 2018. [Google Scholar]
- Bhakare, S.; Dal Gesso, S.; Venturini, M.; Zardi, D.; Trentini, L.; Matiu, M.; Petitta, M. Intercomparison of Machine Learning Models for Spatial Downscaling of Daily Mean Temperature in Complex Terrain. Atmosphere 2024, 15, 1085. [Google Scholar] [CrossRef]





| Reference | Main Research Focus | Results/Impact |
|---|---|---|
| Jung et al., 2014 [15] | Optimization of pump flow rate in geothermal heat pump systems. | Reduced pump energy consumption and operational cost savings. |
| Sarbu et al., 2015 [16] | Energy efficiency in district heating systems using variable-speed pumps. | Energy savings of 20% to 50% through dynamic flow control. |
| Shin et al., 2018 [17] | Flow rate control in primary geothermal heat pump systems. | Improved system efficiency and stability. |
| Wang et al., 2021 [18] | Optimization of secondary centrifugal pump flow control. | Enhanced energy efficiency and system stability. |
| Swamy et al., 2012 [19] | Virtual chilled-water flow meter for HVAC systems. | Cost-effective solution for accurate flow estimation. |
| Song et al., 2012 [20] | Impact of uncertainty on virtual flow measurement accuracy. | Improved reliability and accuracy in virtual flow sensing. |
| Category | Content |
|---|---|
| Use | Laboratory |
| Floor area | 35.5 m2 |
| Height | 3.4 m |
| Volume | 120 m3 |
| Equipment | Category | Specification |
|---|---|---|
| Pump | Handling liquid | 0~120 °C (pH 6~8) |
| Water flow rate | 0~480 m3/h | |
| Head | 0~55 m | |
| Motor power | 1~100 HP | |
| Full pump speed | 60 Hz | |
| Ultrasonic flow meter | Measuring category | Water flow rate |
| Measuring range | 0~±15 m/s | |
| Accuracy | ±1% |
| Parameter | Initial Condition | Parameter | Boundary Condition |
|---|---|---|---|
| Pump speed | 60 Hz (Maximum) | Heat pump outlet temperature | 9.4~16.9 °C |
| Water density | 999.0~999.1 kg/m3 | ||
| Valve opening rate | 100% (Maximum) ~20% (Minimum) | Pipe outer diameter | 41.28 mm |
| Pipe wall thickness | 1.24 mm |
| Case | Pump Speed (Hz) | Valve Opening Rate (%) | |
|---|---|---|---|
| 1 | 1 | 60 | 100 |
| 2 | 90 | ||
| 3 | 80 | ||
| 4 | 70 | ||
| 5 | 60 | ||
| 6 | 50 | ||
| 7 | 40 | ||
| 8 | 30 | ||
| 9 | 20 | ||
| 2 | 1 | 50 | 20% |
| 2 | 40 | ||
| 3 | 30 | ||
| 4 | 20 | ||
| Case | Pump Speed (Hz) | Valve Opening Rate (%) | Water Flow Rate (CMH) | DP (kg/cm2) | |
|---|---|---|---|---|---|
| 1 | 1 | 60 | 100 | 10.51 | 0.26 |
| 2 | 90 | 10.39 | 0.26 | ||
| 3 | 80 | 10.34 | 0.28 | ||
| 4 | 70 | 10.18 | 0.31 | ||
| 5 | 60 | 9.81 | 0.40 | ||
| 6 | 50 | 9.03 | 0.57 | ||
| 7 | 40 | 7.50 | 0.83 | ||
| 8 | 30 | 5.83 | 1.06 | ||
| 9 | 20 | 4.39 | 1.22 | ||
| Case | Pump Speed (Hz) | Valve Opening Rate (%) | Water Flow Rate (CMH) | DP (kg/cm2) | |
|---|---|---|---|---|---|
| 2 | 1 | 50 | 20 | 3.72 | 0.89 |
| 2 | 40 | 2.94 | 0.57 | ||
| 3 | 30 | 2.16 | 0.32 | ||
| 4 | 20 | 1.37 | 0.14 | ||
| Case | Type A Uncertainty (CMH) | Type B Water Flow Rate Uncertainty (CMH) | Type B DP Uncertainty (kg/cm2) | Combined Standard Uncertainty (CMH) | Expanded Uncertainty (CMH) | |
|---|---|---|---|---|---|---|
| 1 | 1 | 0.010 | 0.026 | 0.058 | 0.059 | 0.117 |
| 2 | 0.022 | 0.026 | 0.062 | 0.124 | ||
| 3 | 0.023 | 0.026 | 0.061 | 0.122 | ||
| 4 | 0.023 | 0.025 | 0.062 | 0.124 | ||
| 5 | 0.018 | 0.025 | 0.061 | 0.121 | ||
| 6 | 0.011 | 0.023 | 0.059 | 0.118 | ||
| 7 | 0.016 | 0.019 | 0.060 | 0.120 | ||
| 8 | 0.020 | 0.015 | 0.061 | 0.122 | ||
| 9 | 0.020 | 0.011 | 0.061 | 0.122 | ||
| 2 | 1 | 0.020 | 0.009 | 0.058 | 0.060 | 0.120 |
| 2 | 0.016 | 0.007 | 0.058 | 0.117 | ||
| 3 | 0.008 | 0.005 | 0.058 | 0.117 | ||
| 4 | 0.009 | 0.001 | 0.058 | 0.117 | ||
| Test Number | Type A Uncertainty (CMH) | Type B Water Flow Rate Uncertainty (CMH) | Type B DP Uncertainty (kg/cm2) | Combined Standard Uncertainty (CMH) | Expanded Uncertainty (CMH) |
|---|---|---|---|---|---|
| 1 | 0.020 | 0.023 | 0.058 | 0.061 | 0.122 |
| 2 | 0.015 | 0.023 | 0.060 | 0.119 | |
| 3 | 0.023 | 0.022 | 0.062 | 0.124 | |
| 4 | 0.019 | 0.022 | 0.061 | 0.122 | |
| 5 | 0.014 | 0.021 | 0.059 | 0.119 | |
| 6 | 0.022 | 0.019 | 0.062 | 0.124 | |
| 7 | 0.011 | 0.016 | 0.059 | 0.118 | |
| 8 | 0.019 | 0.012 | 0.061 | 0.121 | |
| 9 | 0.017 | 0.018 | 0.058 | 0.060 | 0.120 |
| 10 | 0.018 | 0.018 | 0.061 | 0.121 | |
| 11 | 0.017 | 0.018 | 0.060 | 0.120 | |
| 12 | 0.016 | 0.018 | 0.060 | 0.120 | |
| 13 | 0.015 | 0.017 | 0.060 | 0.120 | |
| 14 | 0.013 | 0.015 | 0.059 | 0.119 | |
| 15 | 0.018 | 0.013 | 0.060 | 0.121 | |
| 16 | 0.010 | 0.010 | 0.059 | 0.117 | |
| 17 | 0.013 | 0.013 | 0.058 | 0.059 | 0.118 |
| 18 | 0.008 | 0.013 | 0.058 | 0.117 | |
| 19 | 0.011 | 0.013 | 0.059 | 0.118 | |
| 20 | 0.012 | 0.013 | 0.059 | 0.118 | |
| 21 | 0.013 | 0.012 | 0.059 | 0.118 | |
| 22 | 0.013 | 0.011 | 0.059 | 0.118 | |
| 23 | 0.011 | 0.009 | 0.059 | 0.118 | |
| 24 | 0.010 | 0.007 | 0.059 | 0.117 |
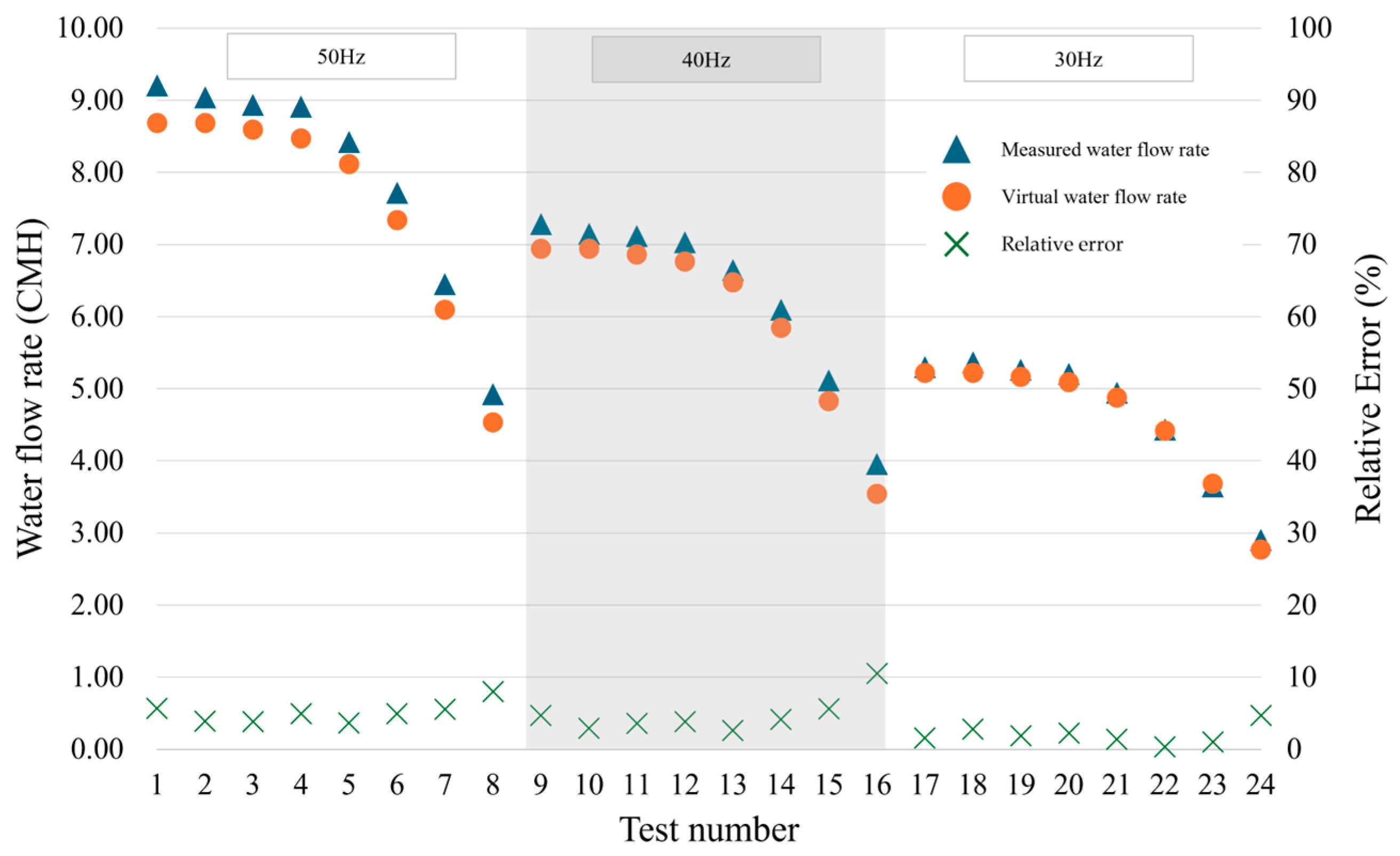
| Test Number | Pump Speed (Hz) | Valve Opening Rate (%) | Measured Water Flow Rate (CMH) | Virtual Water Flow Rate (CMH) | Absolute Error (CMH) | Relative Error (%) |
|---|---|---|---|---|---|---|
| 1 | 50 | 100 | 9.21 | 8.69 | 0.52 | 5.66 |
| 2 | 90 | 9.04 | 8.69 | 0.35 | 3.92 | |
| 3 | 80 | 8.93 | 8.59 | 0.34 | 3.82 | |
| 4 | 70 | 8.91 | 8.47 | 0.44 | 4.94 | |
| 5 | 60 | 8.42 | 8.11 | 0.31 | 3.64 | |
| 6 | 50 | 7.72 | 7.34 | 0.38 | 4.91 | |
| 7 | 40 | 6.45 | 6.09 | 0.36 | 5.52 | |
| 8 | 30 | 4.92 | 4.53 | 0.39 | 7.99 | |
| 9 | 40 | 100 | 7.28 | 6.94 | 0.34 | 4.67 |
| 10 | 90 | 7.14 | 6.94 | 0.21 | 2.89 | |
| 11 | 80 | 7.12 | 6.86 | 0.26 | 3.59 | |
| 12 | 70 | 7.03 | 6.76 | 0.27 | 3.85 | |
| 13 | 60 | 6.65 | 6.47 | 0.17 | 2.61 | |
| 14 | 50 | 6.09 | 5.84 | 0.25 | 4.11 | |
| 15 | 40 | 5.11 | 4.83 | 0.29 | 5.59 | |
| 16 | 30 | 3.96 | 3.54 | 0.42 | 10.54 | |
| 17 | 30 | 100 | 5.30 | 5.22 | 0.08 | 1.55 |
| 18 | 90 | 5.37 | 5.22 | 0.15 | 2.78 | |
| 19 | 80 | 5.26 | 5.16 | 0.10 | 1.85 | |
| 20 | 70 | 5.21 | 5.09 | 0.12 | 2.25 | |
| 21 | 60 | 4.95 | 4.88 | 0.07 | 1.38 | |
| 22 | 50 | 4.43 | 4.42 | 0.01 | 0.32 | |
| 23 | 40 | 3.65 | 3.68 | −0.04 | −1.01 | |
| 24 | 30 | 2.90 | 2.77 | 0.14 | 4.67 |
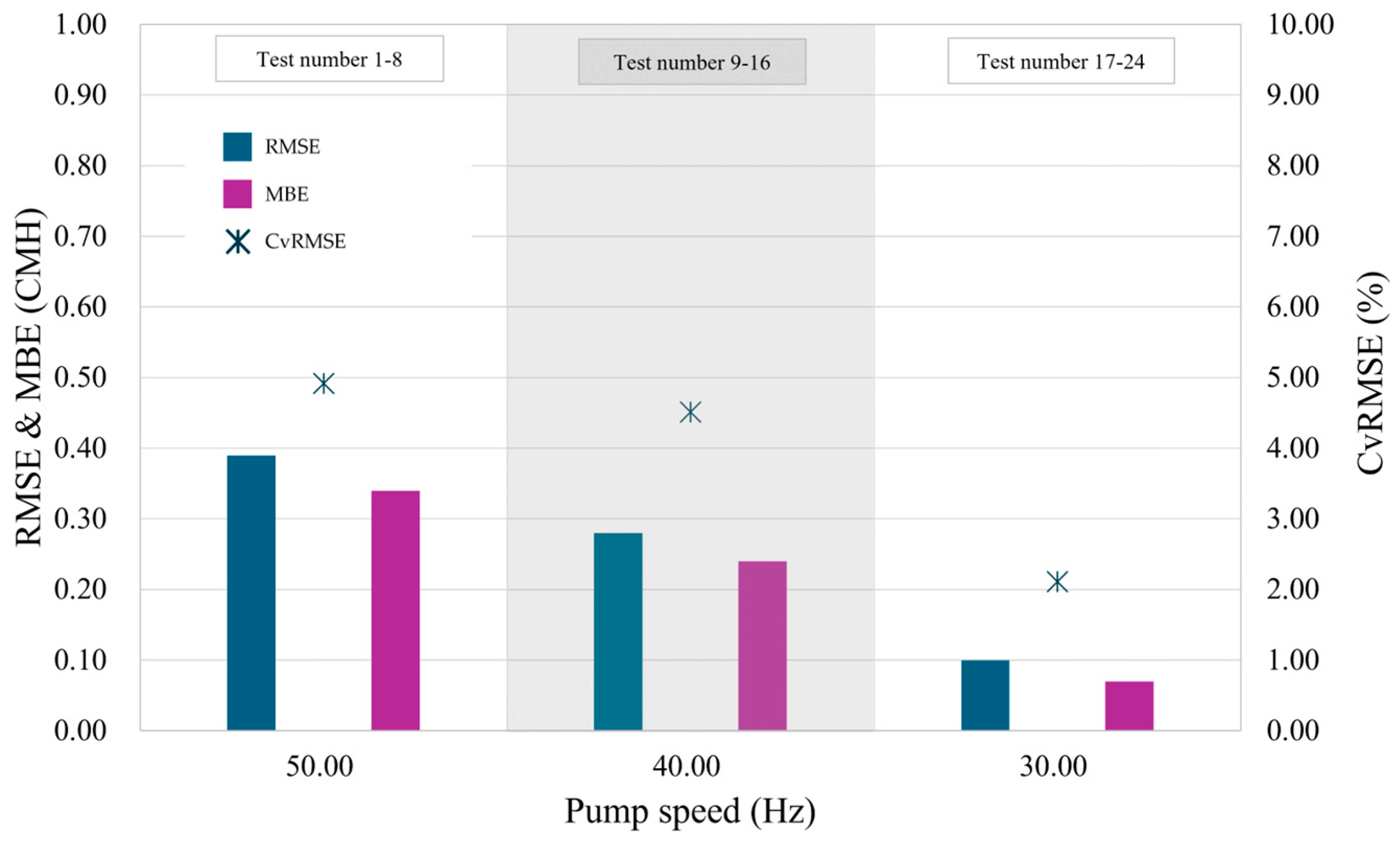
| Test Number | Pump Speed | RMSE (CMH) | MBE (CMH) | nRMSE (-) | CvRMSE (%) | R2 (-) |
|---|---|---|---|---|---|---|
| 1–8 | 50 | 0.39 | 0.34 | 0.09 | 4.92 | 0.998 |
| 9–16 | 40 | 0.28 | 0.24 | 0.09 | 4.51 | 0.998 |
| 17–24 | 30 | 0.10 | 0.07 | 0.04 | 2.11 | 0.996 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, T.; Kim, H.; Lee, J.; Cho, Y. Development of Virtual Water Flow Sensor Using Valve Performance Curve. J. Sens. Actuator Netw. 2025, 14, 1. https://doi.org/10.3390/jsan14010001
Kim T, Kim H, Lee J, Cho Y. Development of Virtual Water Flow Sensor Using Valve Performance Curve. Journal of Sensor and Actuator Networks. 2025; 14(1):1. https://doi.org/10.3390/jsan14010001
Chicago/Turabian StyleKim, Taeyang, Hyojun Kim, Jinhyun Lee, and Younghum Cho. 2025. "Development of Virtual Water Flow Sensor Using Valve Performance Curve" Journal of Sensor and Actuator Networks 14, no. 1: 1. https://doi.org/10.3390/jsan14010001
APA StyleKim, T., Kim, H., Lee, J., & Cho, Y. (2025). Development of Virtual Water Flow Sensor Using Valve Performance Curve. Journal of Sensor and Actuator Networks, 14(1), 1. https://doi.org/10.3390/jsan14010001






