A Proof-of-Concept Study of Stability Monitoring of Implant Structure by Deep Learning of Local Vibrational Characteristics
Abstract
1. Introduction
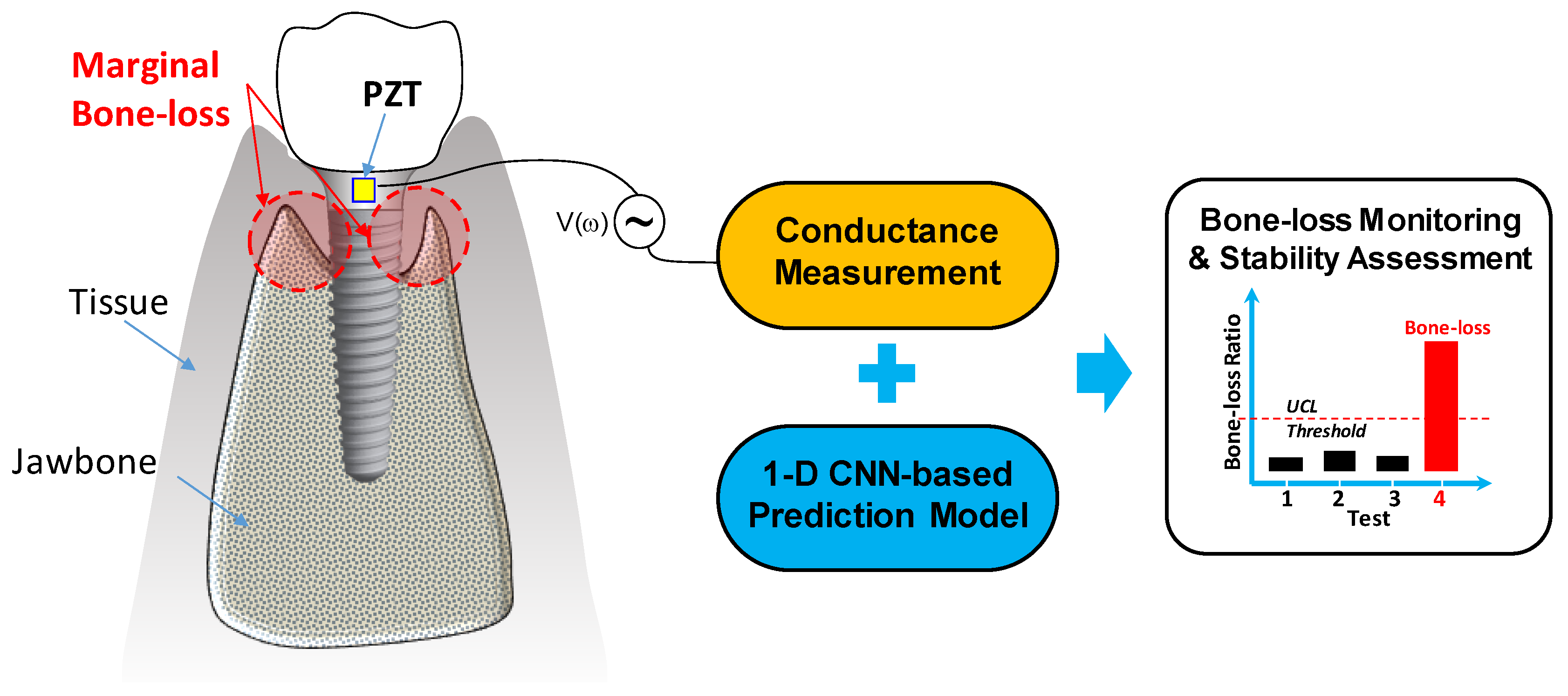
2. Stability Monitoring Method for Implant Structure
2.1. Overview of the Methodology
2.2. PZT-Based Conductance Measurement Approach
2.3. 1D CNN-Based Prediction Models
2.4. Classification Criteria
3. Local Vibrational Characteristics of PZT–Implant–Bone
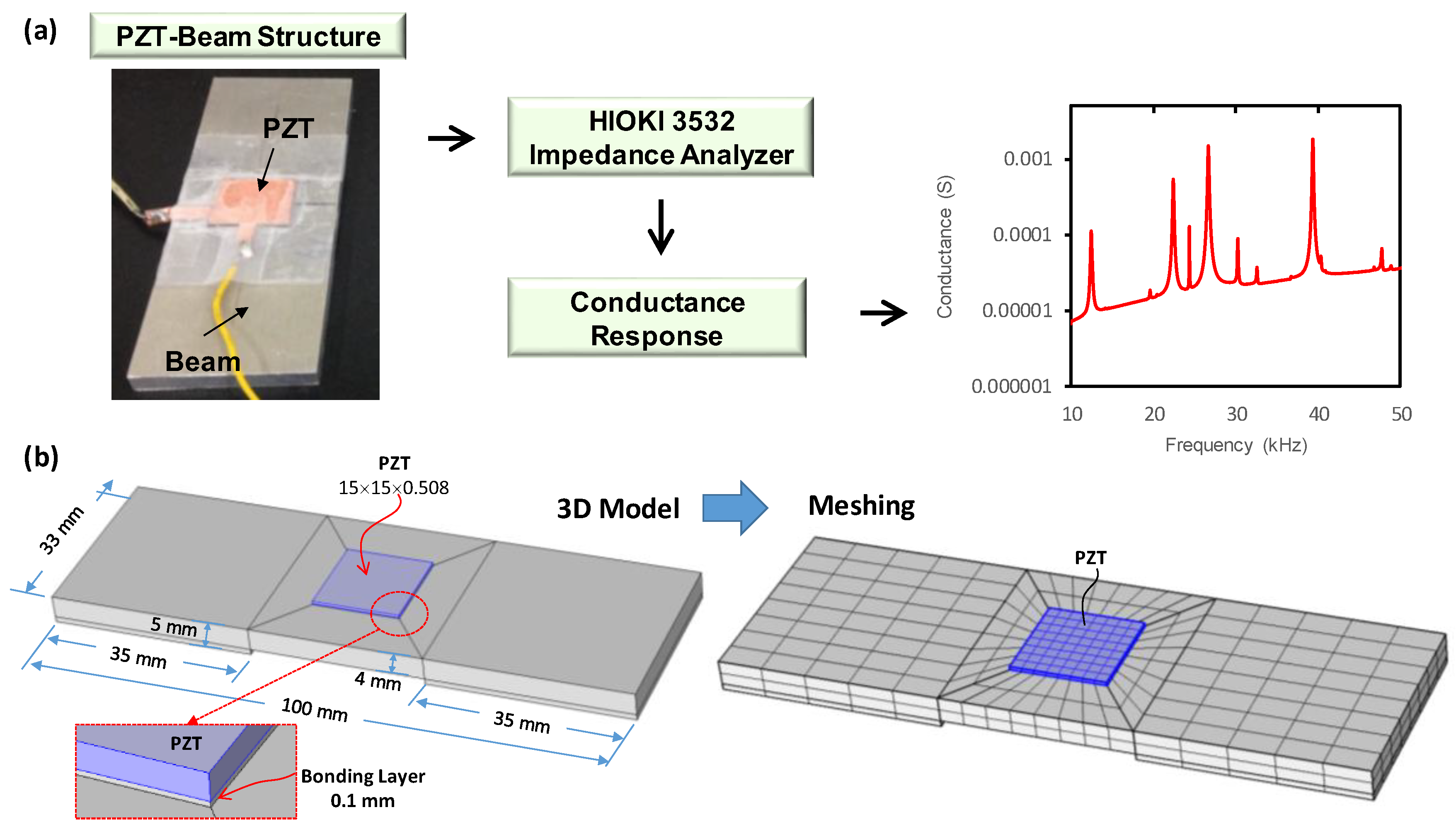
3.1. Finite Element Modelling Strategy
3.1.1. Experiment on a PZT-Beam Model
3.1.2. FE Modeling of Conductance Response of Experimental PZT–Beam Model
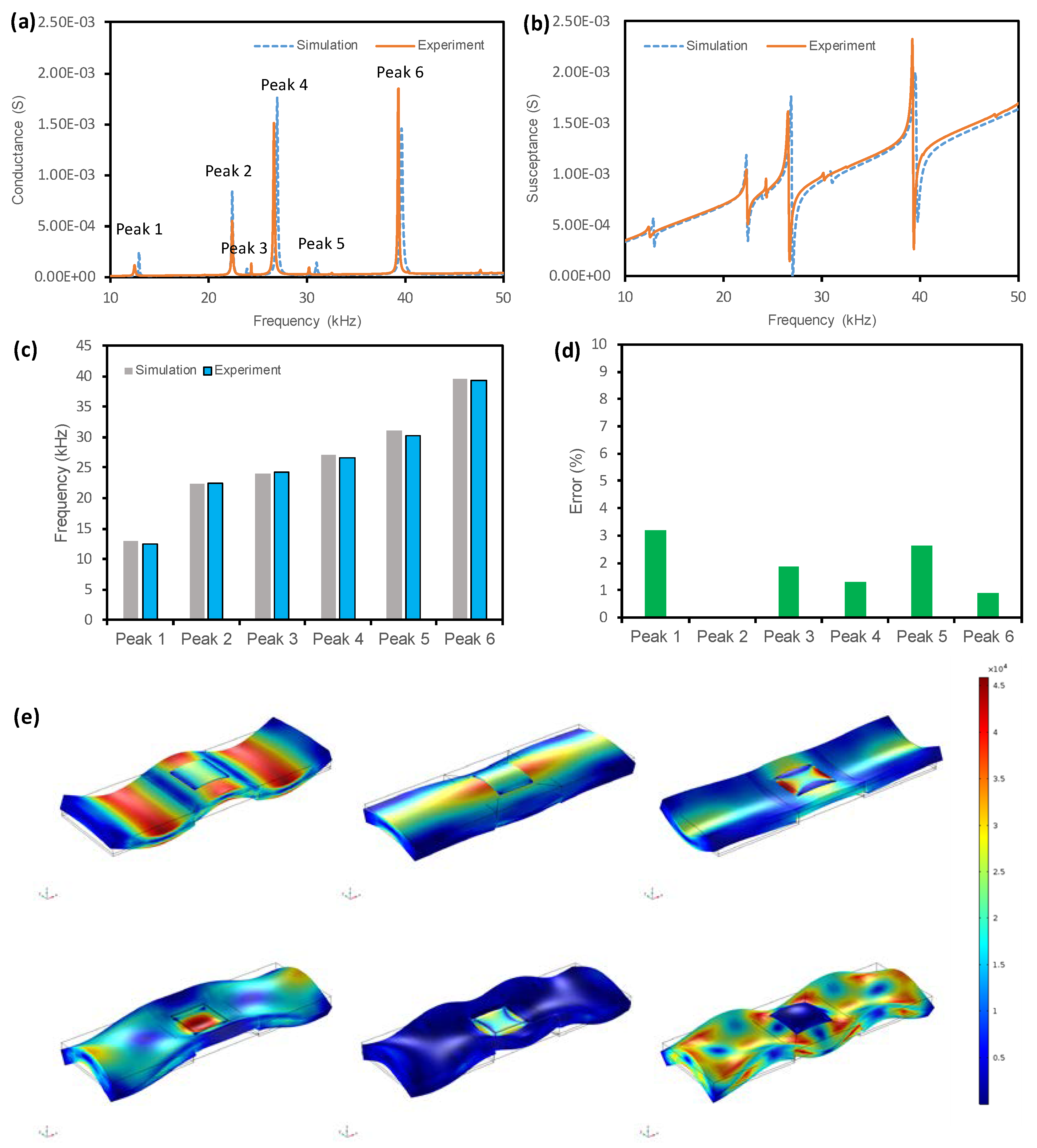
3.1.3. Accuracy of the FE Modelling Strategy
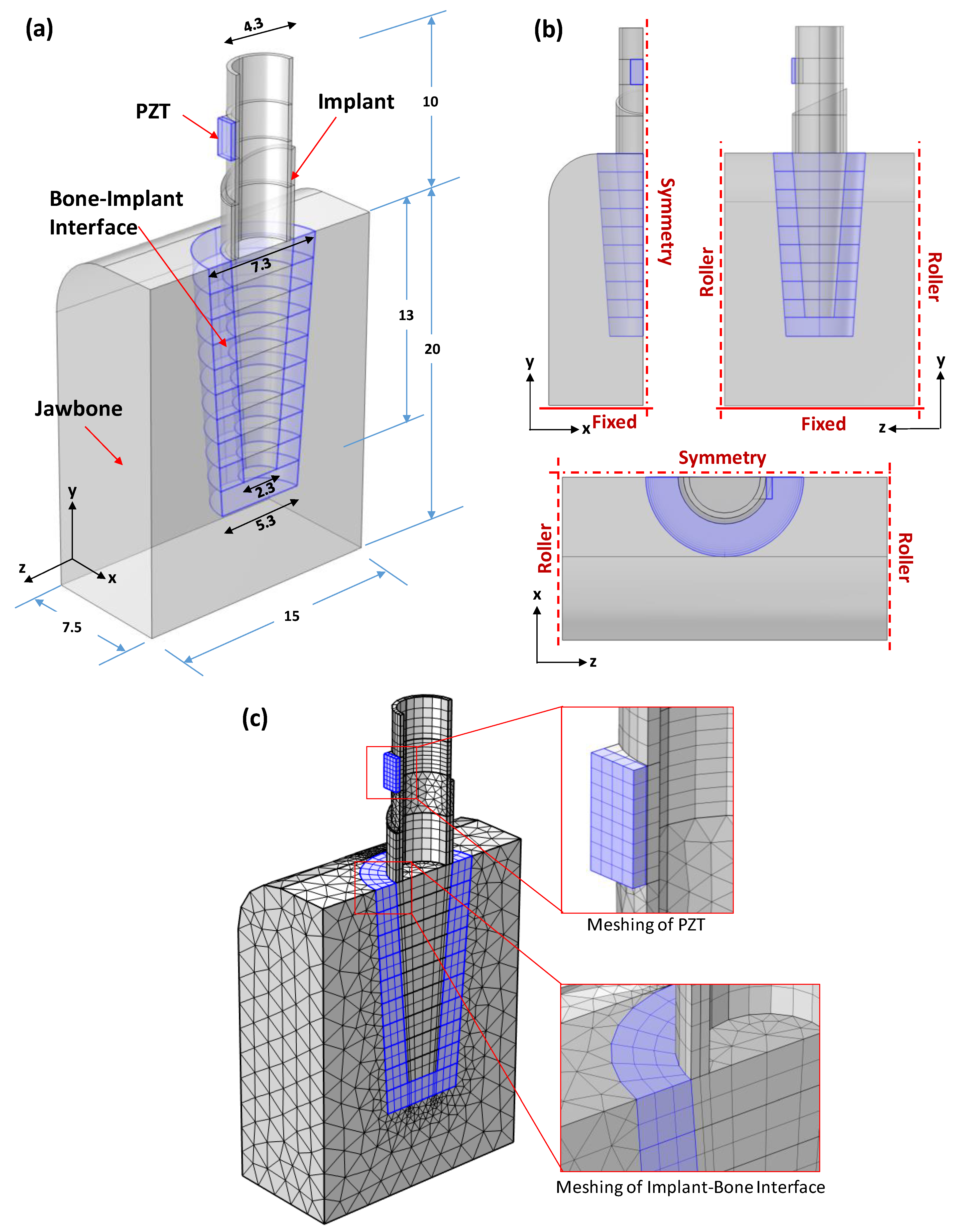
3.2. PZT–Commerical Implant–Bone Model
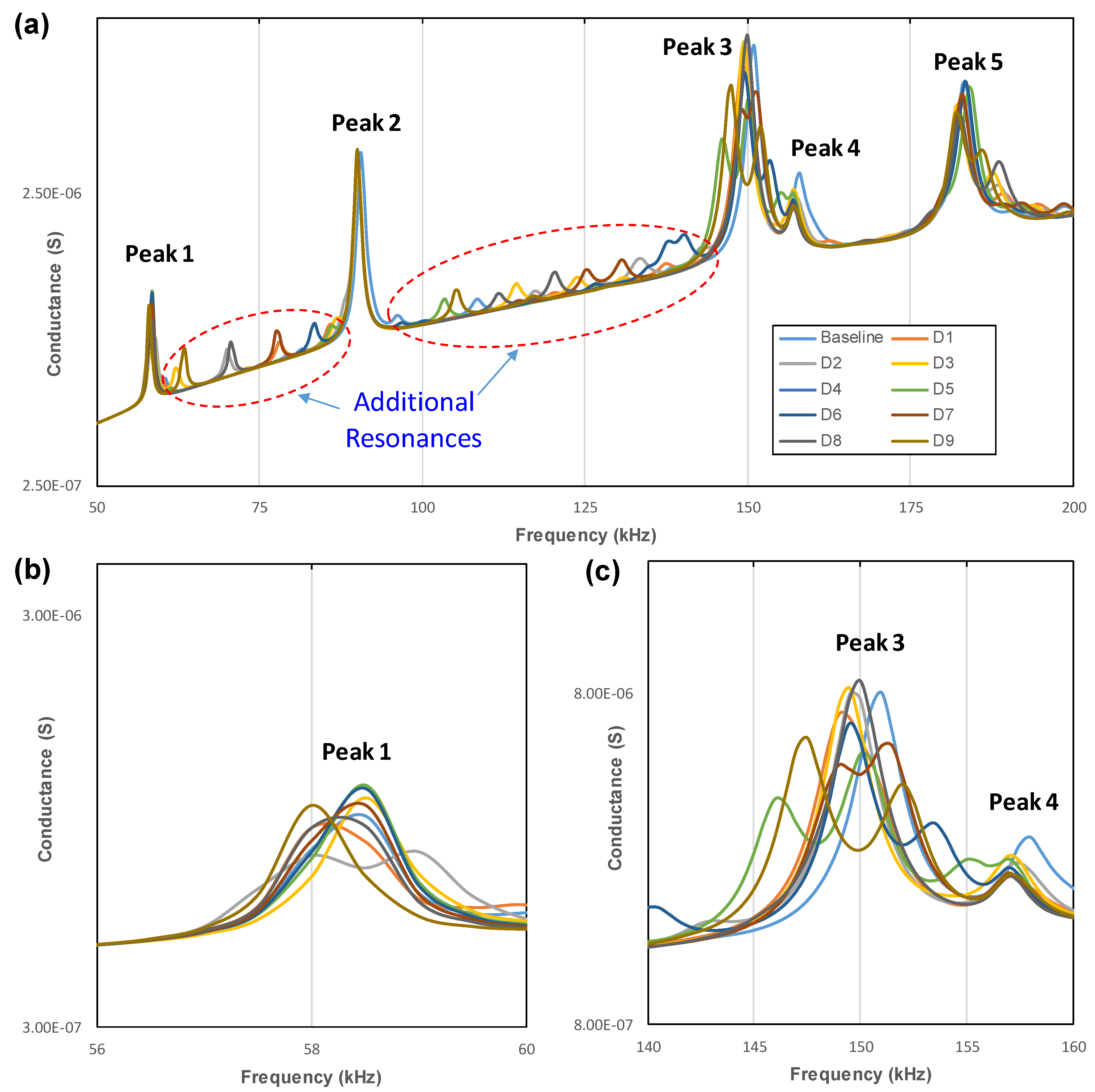
3.3. Identification of Local Vibrational Modes
4. Feasibility Verification
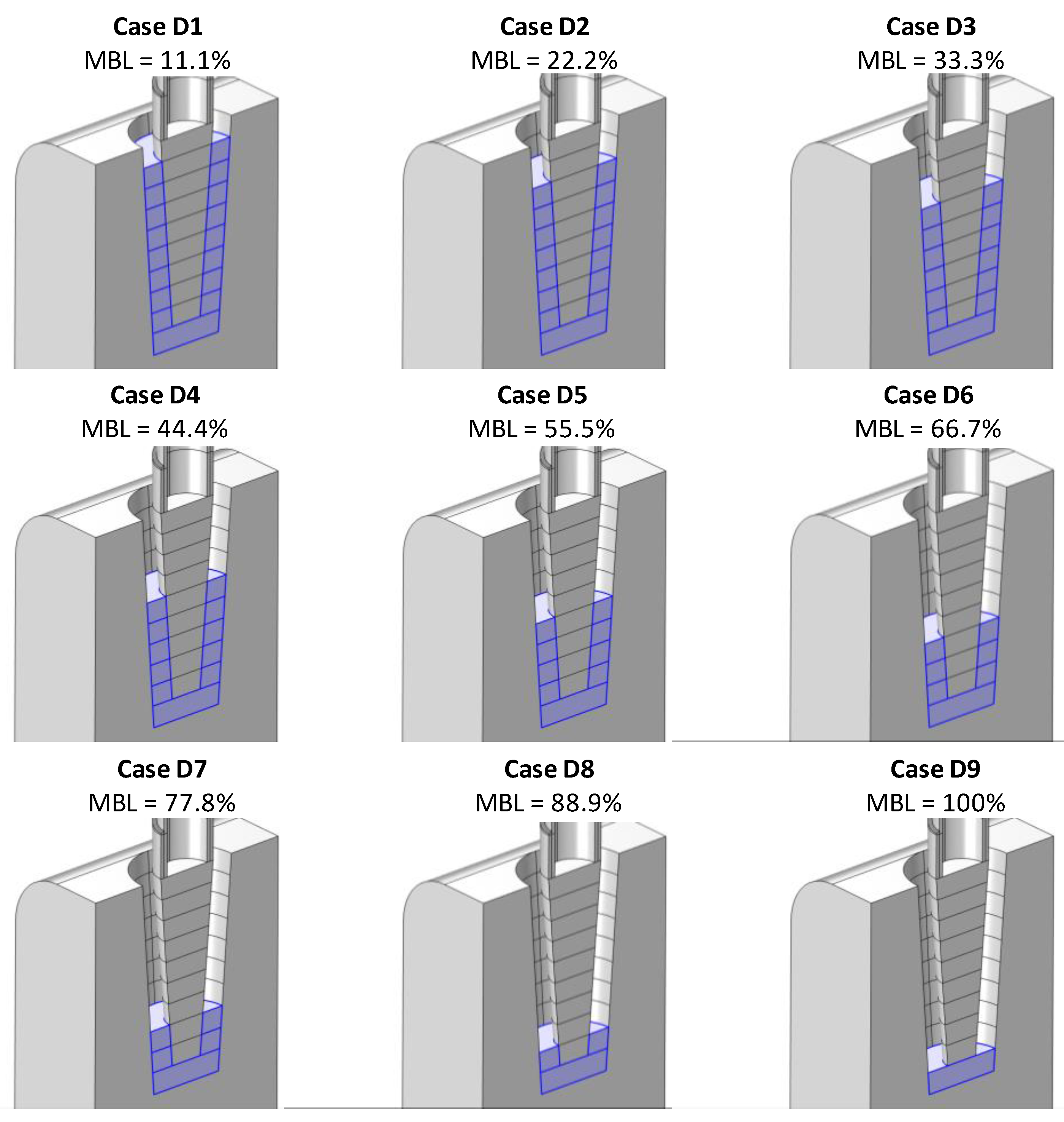
4.1. Simulation of Conductance Response under Different Bone-Loss Levels
4.2. Stability Monitoring Using Statistical Metrics
4.2.1. Conventional Statistical Metrics
4.2.2. Stability Monitoring Result
4.3. Stability Assessment Using 1D CNN Models
4.3.1. Datasets and Setup for 1D CNN Models
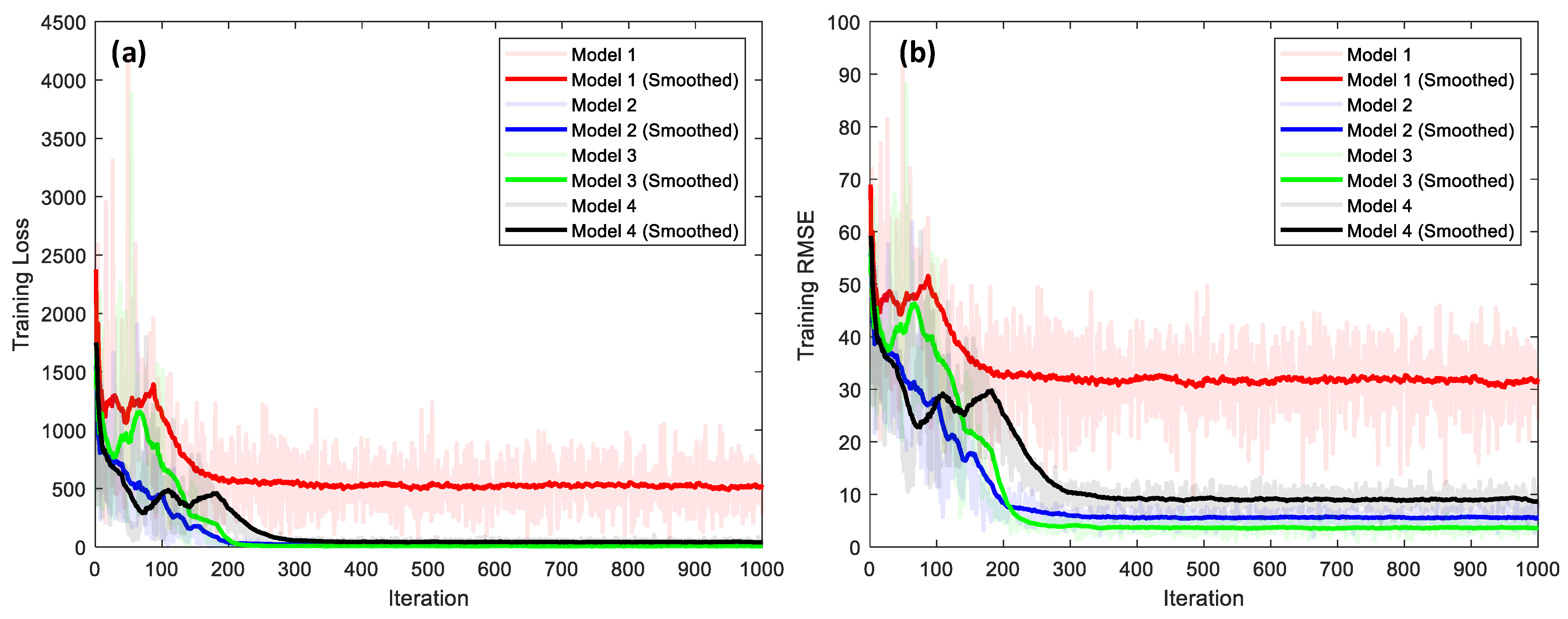
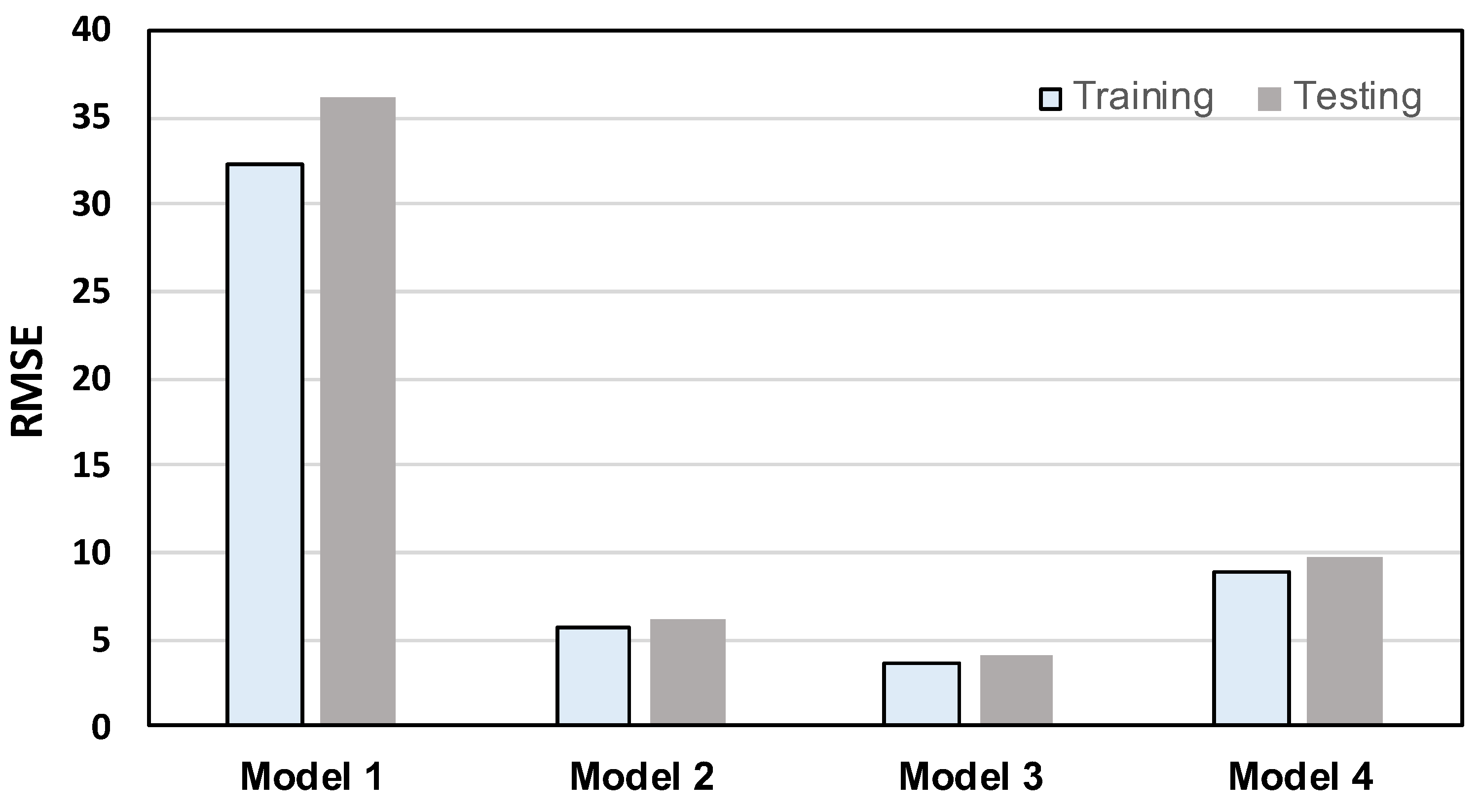
4.3.2. Performance Comparison of 1D CNN-Based Bone-Loss Prediction Models
4.3.3. 1D CNN-Based Monitoring Results
5. Discussion
6. Concluding Remarks and Future Work
- (1)
- The FE modeling approach for PZT-enabled conductance sensing was successfully validated by comparing the FE modeling results with experimental data.
- (2)
- The PZT transducer activated the local circumferential modes of the implant. Some of these vibration modes were ignorable in the conductance spectrum of the implant due to the constraint of the jawbone in FE modeling.
- (3)
- Traditional statistical approaches showed their unsuitability for estimating the MBL severity at the bone–implant interface due to the nonlinearities in the conductance characteristics.
- (4)
- Among the four models, Model 3 yielded the best MBL monitoring results. The prediction and the groundtruth were consistent when evaluated on training and testing datasets, with RMSE values of only 3.704 and 4.021, respectively.
- (5)
- The proposed method offers the unique advantage of directly extracting optimal features from the raw conductance signals without the need for extensive preprocessing, rendering it highly suitable for autonomous MBL monitoring in dentistry.
- (6)
- The application of deep learning can reduce the need for high-performance impedance analyzers, allowing the use of low-cost devices for impedance-based stability monitoring of implant structures.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nandal, S.; Ghalaut, P.; Shekhawat, H. A radiological evaluation of marginal bone around dental implants: An in-vivo study. Natl. J. Maxillofac. Surg. 2014, 5, 126–137. [Google Scholar] [CrossRef] [PubMed]
- Albrektsson, T.; Zarb, G.; Worthington, P.; Eriksson, A. The long-term efficacy of currently used dental implants: A review and proposed criteria of success. Int. J. Oral Maxillofac. Implant. 1986, 1, 11–25. [Google Scholar]
- Smith, D.E.; Zarb, G.A. Criteria for success of osseointegrated endosseous implants. J. Prosthet. Dent. 1989, 62, 567–572. [Google Scholar] [CrossRef] [PubMed]
- Bergman, B. Evaluation of the results of treatment with osseointegrated implants by the Swedish National Board of Health and Welfare. J. Prosthet. Dent. 1983, 50, 114–115. [Google Scholar] [CrossRef] [PubMed]
- Yoo, S.Y.; Kim, S.K.; Heo, S.J.; Koak, J.Y.; Jeon, H.R. New Rehabilitation Concept for Maxillary Edentulism: A Clinical Retrospective Study of Implant Crown Retained Removable Partial Dentures. J. Clin. Med. 2021, 10, 1773. [Google Scholar] [CrossRef] [PubMed]
- Kittur, N.; Oak, R.; Dekate, D.; Jadhav, S.; Dhatrak, P. Dental implant stability and its measurements to improve osseointegration at the bone-implant interface: A review. Mater. Today Proc. 2021, 43, 1064–1070. [Google Scholar] [CrossRef]
- Ribolla, E.L.M.; Rizzo, P.; Gulizzi, V. On the use of the electromechanical impedance technique for the assessment of dental implant stability: Modeling and experimentation. J. Intell. Mater. Syst. Struct. 2015, 26, 2266–2280. [Google Scholar] [CrossRef]
- Blanes, R.J.; Bernard, J.P.; Blanes, Z.M.; Belser, U.C. A 10-year prospective study of ITI dental implants placed in the posterior region. I: Clinical and radiographic results. Clin. Oral Implant. Res. 2007, 18, 699–706. [Google Scholar] [CrossRef] [PubMed]
- Atsumi, M.; Park, S.-H.; Wang, H.-L. Methods used to assess implant stability: Current status. Int. J. Oral Maxillofac. Implant. 2007, 22, 743–754. [Google Scholar]
- Swain, R.; Faulkner, G.; Raboud, D.; Wolfaardt, J. A Dynamic Analytical Model for Impact Evaluation of Percutaneous Implants. J. Biomech. Eng. 2008, 130, 051013. [Google Scholar] [CrossRef]
- Swain, R.; Faulkner, G.; Raboud, D.; Wolfaardt, J. An improved impact technique for monitoring percutaneous implant integrity. Int. J. Oral Maxillofac. Implant. 2008, 23, 263–269. [Google Scholar]
- Reuben, R.L. 13—Acoustic emission and ultrasound for monitoring the bone-implant interface. In Bone Response to Dental Implant Materials; Piattelli, A., Ed.; Woodhead Publishing: Sawston, UK, 2017; pp. 247–259. [Google Scholar] [CrossRef]
- Aoki, H. The mobility of healthy teeth as measured with the impact hammer method. Kanagawa Shigaku 1987, 22, 13–31. [Google Scholar] [PubMed]
- Meredith, N. Assessment of implant stability as a prognostic determinant. Int. J. Prosthodont. 1998, 11, 491–501. [Google Scholar]
- Salvi, G.E.; Lang, N.P. Diagnostic parameters for monitoring peri-implant conditions. Int. J. Oral Maxillofac. Implant. 2004, 19, 116–127. [Google Scholar]
- Geckili, O.; Bilhan, H.; Cilingir, A.; Bilmenoglu, C.; Ates, G.; Urgun, A.C.; Bural, C. Comparative Ex Vivo Evaluation of Two Electronic Percussive Testing Devices Measuring the Stability of Dental Implants. J. Periodontol. 2014, 85, 1786–1791. [Google Scholar] [CrossRef] [PubMed]
- Hériveaux, Y.; Vayron, R.; Fraulob, M.; Albini Lomami, H.; Lenormand, C.; Haiat, G. Assessment of dental implant stability using resonance frequency analysis and quantitative ultrasound methods. J. Prosthodont. Res. 2020, 65, 421–427. [Google Scholar] [CrossRef]
- Pattijn, V.; Van Lierde, C.; Van der Perre, G.; Naert, I.; Vander Sloten, J. The resonance frequencies and mode shapes of dental implants: Rigid body behaviour versus bending behaviour. A numerical approach. J. Biomech. 2006, 39, 939–947. [Google Scholar] [CrossRef] [PubMed]
- Watzek, G. Implants in qualitatively compromised bone. Br. Dent. J. 2004, 197, 163. [Google Scholar] [CrossRef][Green Version]
- Boemio, G.; Rizzo, P.; Nardo, L.D. Assessment of dental implant stability by means of the electromechanical impedance method. Smart Mater. Struct. 2011, 20, 045008. [Google Scholar] [CrossRef]
- Ribolla, E.L.; Rizzo, P. Modeling the electromechanical impedance technique for the assessment of dental implant stability. J. Biomech. 2015, 48, 1713–1720. [Google Scholar] [CrossRef]
- Bahl, S.; Nagar, H.; Singh, I.; Sehgal, S. Smart materials types, properties and applications: A review. Mater. Today: Proc. 2020, 28, 1302–1306. [Google Scholar] [CrossRef]
- Sony, S.; Laventure, S.; Sadhu, A. A literature review of next-generation smart sensing technology in structural health monitoring. Struct. Control Health Monit. 2019, 26, e2321. [Google Scholar] [CrossRef]
- Park, G.; Inman, D.J. Structural health monitoring using piezoelectric impedance measurements. Philos. Trans. A Math. Phys. Eng. Sci. 2007, 365, 373–392. [Google Scholar] [CrossRef] [PubMed]
- Jiao, P.; Egbe, K.-J.I.; Xie, Y.; Matin Nazar, A.; Alavi, A.H. Piezoelectric sensing techniques in structural health monitoring: A state-of-the-art review. Sensors 2020, 20, 3730. [Google Scholar] [CrossRef] [PubMed]
- Le, T.-C.; Luu, T.-H.-T.; Nguyen, H.-P.; Nguyen, T.-H.; Ho, D.-D.; Huynh, T.-C. Piezoelectric Impedance-Based Structural Health Monitoring of Wind Turbine Structures: Current Status and Future Perspectives. Energies 2022, 15, 5459. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Y.; Qing, X. A real-time electromechanical impedance-based active monitoring for composite patch bonded repair structure. Compos. Struct. 2019, 212, 513–523. [Google Scholar] [CrossRef]
- Li, H.; Ai, D.; Zhu, H.; Luo, H. Integrated electromechanical impedance technique with convolutional neural network for concrete structural damage quantification under varied temperatures. Mech. Syst. Signal Process. 2021, 152, 107467. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Hoang, N.-D.; Nguyen, T.-H.; Huynh, T.-C. Analytical impedance model for piezoelectric-based smart Strand and its feasibility for prestress force prediction. Struct. Control Health Monit. 2022, 29, e3061. [Google Scholar] [CrossRef]
- Truong, T.-D.-N.; Pradhan, A.M.S.; Nguyen, T.-T.; Tran, M.-H.; Nguyen, C.-K.; Ho, D.-D.; Huynh, T.-C. Bone-Implant Osseointegration Monitoring Using Electro-mechanical Impedance Technique and Convolutional Neural Network: A Numerical Study. J. Nondestruct. Eval. 2024, 43, 10. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Kiranyaz, M.S.; Boashash, B.; Sodano, H.; Inman, D.J. 1-D CNNs for structural damage detection: Verification on a structural health monitoring benchmark data. Neurocomputing 2018, 275, 1308–1317. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Kiranyaz, S.; Gabbouj, M.; Inman, D.J. Real-time vibration-based structural damage detection using one-dimensional convolutional neural networks. J. Sound Vib. 2017, 388, 154–170. [Google Scholar] [CrossRef]
- Cha, Y.-J.; Choi, W.; Büyüköztürk, O. Deep Learning-Based Crack Damage Detection Using Convolutional Neural Networks. Comput.-Aided Civ. Infrastruct. Eng. 2017, 32, 361–378. [Google Scholar] [CrossRef]
- Azimi, M.; Pekcan, G. Structural health monitoring using extremely compressed data through deep learning. Comput.-Aided Civ. Infrastruct. Eng. 2020, 35, 597–614. [Google Scholar] [CrossRef]
- Huynh, T.-C. Vision-based autonomous bolt-looseness detection method for splice connections: Design, lab-scale evaluation, and field application. Autom. Constr. 2021, 124, 103591. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Tuong Vy Phan, T.; Ho, D.-D.; Man Singh Pradhan, A.; Huynh, T.-C. Deep learning-based autonomous damage-sensitive feature extraction for impedance-based prestress monitoring. Eng. Struct. 2022, 259, 114172. [Google Scholar] [CrossRef]
- Yan, Q.; Liao, X.; Zhang, C.; Zhang, Y.; Luo, S.; Zhang, D. Intelligent monitoring and assessment on early-age hydration and setting of cement mortar through an EMI-integrated neural network. Measurement 2022, 203, 111984. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Ta, Q.-B.; Ho, D.-D.; Kim, J.-T.; Huynh, T.-C. A method for automated bolt-loosening monitoring and assessment using impedance technique and deep learning. Dev. Built Environ. 2023, 14, 100122. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Kim, J.-T.; Ta, Q.-B.; Ho, D.-D.; Phan, T.T.V.; Huynh, T.-C. Deep learning-based functional assessment of piezoelectric-based smart interface under various degradations. Smart Struct. Syst. Int. J. 2021, 28, 69–87. [Google Scholar]
- Ince, T.; Kiranyaz, S.; Eren, L.; Askar, M.; Gabbouj, M. Real-Time Motor Fault Detection by 1-D Convolutional Neural Networks. IEEE Trans. Ind. Electron. 2016, 63, 7067–7075. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Gabbouj, M. Real-Time Patient-Specific ECG Classification by 1-D Convolutional Neural Networks. IEEE Trans. Biomed. Eng. 2016, 63, 664–675. [Google Scholar] [CrossRef] [PubMed]
- Acharya, U.R.; Fujita, H.; Oh, S.L.; Hagiwara, Y.; Tan, J.H.; Adam, M. Application of deep convolutional neural network for automated detection of myocardial infarction using ECG signals. Inf. Sci. 2017, 415–416, 190–198. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Le, B.-T.; Le, T.-C.; Luu, T.-H.-T.; Ho, D.-D.; Huynh, T.-C. Fault Assessment in Piezoelectric-Based Smart Strand Using 1D Convolutional Neural Network. Buildings 2022, 12, 1916. [Google Scholar] [CrossRef]
- Perera, R.; Pérez, A.; García-Diéguez, M.; Zapico-Valle, J. Active Wireless System for Structural Health Monitoring Applications. Sensors 2017, 17, 2880. [Google Scholar] [CrossRef]
- Pham, Q.-Q.; Ta, Q.-B.; Park, J.-H.; Kim, J.-T. Raspberry Pi Platform Wireless Sensor Node for Low-Frequency Impedance Responses of PZT Interface. Sensors 2022, 22, 9592. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Shin, H.-H.; Yun, C.-B. Wireless impedance sensor nodes for functions of structural damage identification and sensor self-diagnosis. Smart Mater. Struct. 2009, 18, 055001. [Google Scholar] [CrossRef]
- Min, J.; Park, S.; Yun, C.-B.; Song, B. Development of a low-cost multifunctional wireless impedance sensor node. Smart Struct. Syst. 2010, 6, 689–709. [Google Scholar] [CrossRef]
- Liang, C.; Sun, F.P.; Rogers, C.A. Coupled Electro-Mechanical Analysis of Adaptive Material Systems—Determination of the Actuator Power Consumption and System Energy Transfer. J. Intell. Mater. Syst. Struct. 1994, 5, 12–20. [Google Scholar] [CrossRef]
- Caliendo, C. Acoustic Wave Conductometric Sensors. In Encyclopedia of Sensors and Biosensors, 1st ed.; Narayan, R., Ed.; Elsevier: Oxford, UK, 2023; pp. 591–616. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, G. A modified electro-mechanical impedance model of piezoelectric actuator-sensors for debonding detection of composite patches. J. Intell. Mater. Syst. Struct. 2002, 13, 389–396. [Google Scholar] [CrossRef]
- Wang, L.; Yuan, B.; Xu, Z.; Sun, Q. Synchronous detection of bolts looseness position and degree based on fusing electro-mechanical impedance. Mech. Syst. Signal Process. 2022, 174, 109068. [Google Scholar] [CrossRef]
- Park, G.; Sohn, H.; Farrar, C.R.; Inman, D.J. Overview of piezoelectric impedance-based health monitoring and path forward. Shock Vib. Dig. 2003, 35, 451–464. [Google Scholar] [CrossRef]
- Zhang, Y.; Wallace, B. A Sensitivity Analysis of (and Practitioners’ Guide to) Convolutional Neural Networks for Sentence Classification. arXiv 2015, arXiv:1510.03820. [Google Scholar]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, L.; Wang, G. Recent advances in convolutional neural networks. arXiv 2015, arXiv:1512.07108. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Geng, J.-P.; Tan, K.B.C.; Liu, G.-R. Application of finite element analysis in implant dentistry: A review of the literature. J. Prosthet. Dent. 2001, 85, 585–598. [Google Scholar] [CrossRef] [PubMed]
- Qiu, P.; Cao, R.; Li, Z.; Fan, Z. A comprehensive biomechanical evaluation of length and diameter of dental implants using finite element analyses: A systematic review. Heliyon 2024, 10, e26876. [Google Scholar] [CrossRef] [PubMed]
- Ceddia, M.; Lamberti, L.; Trentadue, B. FEA Comparison of the Mechanical Behavior of Three Dental Crown Materials: Enamel, Ceramic, and Zirconia. Materials 2024, 17, 673. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.-H.; Phan, T.T.V.; Le, T.-C.; Ho, D.-D.; Huynh, T.-C. Numerical Simulation of Single-Point Mount PZT-Interface for Admittance-Based Anchor Force Monitoring. Buildings 2021, 11, 550. [Google Scholar] [CrossRef]
- Huynh, T.-C.; Dang, N.-L.; Kim, J.-T. Preload monitoring in bolted connection using piezoelectric-based smart interface. Sensors 2018, 18, 2766. [Google Scholar] [CrossRef]
- Kitts, D.J.; Zagrai, A.N. Finite Element Modeling and Effect of Electrical/Mechanical Parameters on Electromechanical Impedance Damage Detection. In Proceedings of the ASME 2009 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Oxnard, CA, USA, 21–23 September 2009. [Google Scholar]
- Tashakori, S.; Farhangdoust, S.; Baghalian, A.; Tansel, I.N.; Mehrabi, A. Evaluating the performance of the SuRE method for inspection of bonding using the COMSOL finite element analysis package. In Proceedings of the Health Monitoring of Structural and Biological Systems XIII, Denver, CO, USA, 4–7 March 2019; SPIE: Bellingham, WA, USA, 2019. [Google Scholar]
- Rugina, C.; Enciu, D.; Tudose, M. Numerical and experimental study of circular disc electromechanical impedance spectroscopy signature changes due to structural damage and sensor degradation. Struct. Health Monit. 2015, 14, 663–681. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Ho, D.-D.; Huynh, T.-C. Electromechanical impedance-based prestress force prediction method using resonant frequency shifts and finite element modelling. Dev. Built Environ. 2022, 12, 100089. [Google Scholar] [CrossRef]
- Lobur, M.; Vivchar, D.; Jaworski, N. MEMS pressure sensors design by the COMSOL system. In Proceedings of the 2016 13th International Conference on Modern Problems of Radio Engineering, Telecommunications and Computer Science (TCSET), Lviv, Ukraine, 23–26 February 2016. [Google Scholar]
- Massimino, G.; Colombo, A.; Ardito, R.; Quaglia, F.; Foncellino, F.; Corigliano, A. Air-Coupled Array of Pmuts at 100 kHz with PZT Active Layer: Multiphysics Model and Experiments. In Proceedings of the 2019 20th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Hannover, Germany, 24–27 March 2019. [Google Scholar]
- Demkowicz, L. A note on symmetry boundary conditions in finite element methods. Appl. Math. Lett. 1991, 4, 27–30. [Google Scholar] [CrossRef]
- Beaupré, G.; Orr, T.; Carter, D. An approach for time-dependent bone modeling and remodeling—Theoretical development. J. Orthop. Res. 1990, 8, 651–661. [Google Scholar] [CrossRef] [PubMed]
- Hambli, R. Numerical procedure for multiscale bone adaptation prediction based on neural networks and finite element simulation. Finite Elem. Anal. Des. 2011, 47, 835–842. [Google Scholar] [CrossRef]
- Giurgiutiu, V.; Zagrai, A.; Jing Bao, J. Piezoelectric wafer embedded active sensors for aging aircraft structural health monitoring. Struct. Health Monit. 2002, 1, 41–61. [Google Scholar] [CrossRef]
- Min, J.; Park, S.; Yun, C.-B. Impedance-based structural health monitoring using neural networks for autonomous frequency range selection. Smart Mater. Struct. 2010, 19, 125011. [Google Scholar] [CrossRef]
- Huynh, T.-C.; Kim, J.-T. Compensation of temperature effect on impedance responses of PZT interface for prestress-loss monitoring in PSC girders. Smart Struct. Syst. 2016, 17, 881–901. [Google Scholar] [CrossRef]
- Wandowski, T.; Malinowski, P.; Radzienski, M.; Opoka, S.; Ostachowicz, W. Methods for Assessment of Composite Aerospace Structures. In Smart Structures and Materials: Selected Papers from the 7th ECCOMAS Thematic Conference on Smart Structures and Materials; Araujo, A.L., Mota Soares, C.A., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 227–244. [Google Scholar] [CrossRef]
- Baptista, F.G.; Budoya, D.E.; Almeida, V.A.D.d.; Ulson, J.A.C. An Experimental Study on the Effect of Temperature on Piezoelectric Sensors for Impedance-Based Structural Health Monitoring. Sensors 2014, 14, 1208–1227. [Google Scholar] [CrossRef]
- Wang, R.; Sui, J.; Wang, X. Natural Piezoelectric Biomaterials: A Biocompatible and Sustainable Building Block for Biomedical Devices. ACS Nano 2022, 16, 17708–17728. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, M.-H.; Hoang, N.-D.; Kim, J.-T.; Le, H.-K.; Dang, N.-L.; Phan, N.-T.-V.; Ho, D.-D.; Huynh, T.-C. A Proof-of-Concept Study of Stability Monitoring of Implant Structure by Deep Learning of Local Vibrational Characteristics. J. Sens. Actuator Netw. 2024, 13, 52. https://doi.org/10.3390/jsan13050052
Tran M-H, Hoang N-D, Kim J-T, Le H-K, Dang N-L, Phan N-T-V, Ho D-D, Huynh T-C. A Proof-of-Concept Study of Stability Monitoring of Implant Structure by Deep Learning of Local Vibrational Characteristics. Journal of Sensor and Actuator Networks. 2024; 13(5):52. https://doi.org/10.3390/jsan13050052
Chicago/Turabian StyleTran, Manh-Hung, Nhat-Duc Hoang, Jeong-Tae Kim, Hoang-Khanh Le, Ngoc-Loi Dang, Ngoc-Tuong-Vy Phan, Duc-Duy Ho, and Thanh-Canh Huynh. 2024. "A Proof-of-Concept Study of Stability Monitoring of Implant Structure by Deep Learning of Local Vibrational Characteristics" Journal of Sensor and Actuator Networks 13, no. 5: 52. https://doi.org/10.3390/jsan13050052
APA StyleTran, M.-H., Hoang, N.-D., Kim, J.-T., Le, H.-K., Dang, N.-L., Phan, N.-T.-V., Ho, D.-D., & Huynh, T.-C. (2024). A Proof-of-Concept Study of Stability Monitoring of Implant Structure by Deep Learning of Local Vibrational Characteristics. Journal of Sensor and Actuator Networks, 13(5), 52. https://doi.org/10.3390/jsan13050052






