Closed-Loop Optical Tracking of a Micro-Conveyor over a Smart Surface

Abstract

In this work, a closed loop control system is developed to optically localize and track micro-robots with high precision. These micro-robots (i.e., micro-conveyors) are in motion simultaneously across a smart surface.The developed method’s primary objectives are to optimize their trajectories, avoid collisions between them, and control their position with micrometric resolution. This article presents and characterizes the tracking of a single micro-conveyor, and the method works similarly when multiple micro-robots move over the surface. Our tracking method starts with a scanning phase, where a 2D steering mirror, placed above the smart surface, reflects a laser beam toward the conveying surface seeking for the target. Localization occurs when this light beam reaches the micro-conveyor. By adding a retro-reflective element, that reflects the light in the same direction of the the incident light, onto the surface of the micro-conveyor, the light will be reflected towards a photodetector. Depending on the feedback from the photodetector, the steering mirror rotates to track the trajectory of the micro-conveyor. The tip-tilt angular values of the steering mirror allows the micro-conveyor position to be obtained via calibrated localization system. The aim of this work is to regulate the micro-conveyor, within a closed-loop control system, to reduce the positional error between the actual and desired position. The actual position value is measured in real-time application using our developed optical sensor. Results for tracking in the x-and y-axis have validated the proposed method, with an average tracking error less than 30 µm within a range 150 mm × 150 mm.

1. Introduction

Over the years, the need of micro-robotics has been on the rise for micro-factory application [1]. Micro-conveying is one of the micro-factory’s most essential tasks. In this case, the micro-conveying is performed throughout the act of transporting mechanical parts from one place to another. This serves in achieving tasks such as pick and place operations, wrapping, micro-assembly, etc., …, [2].

A monitoring system is necessary, first, to ensure that micro-conveyors do not lose their trajectory because of certain factors such as malfunctioning of the actuation mechanism, friction, or collisions with other objects, etc., and second to ensure the arrival of each micro-conveyor with high precision to its final position. The aim of this work is to track micro-conveyors via closed-loop control, in order to control their trajectories at high resolution over a large working area.

Numerous solutions have been developed and presented in literature to detect the robot’s position in real-time applications [3]. Radio frequency based systems is widely used for positioning and tracking purposes [4], using technologies such as WIFI [5] and Bluetooth [6]. Radio frequency identification (RFID) is one of the popular solutions used for localization and tracking applications. The target holds an RFID reader and receives radio signals from multiple tags that are distributed in the robot environment at known positions. The target’s position can be calculated by applying triangulation method [7]. In [8], the target is localized using RFID technologies with a positioning accuracy equal to 15 cm for a range of tenth of meter order.

Another wireless communication technique used for tracking and localization is ultra wide band (UWB) radio technology, which has a high bandwidth exceeding 500 MHz [9]. A communication between the UWB tag and several anchors is required to estimate the position of the target. The duration of the signal’s travel from the UWB tag towards the anchors is measured, in order to obtain the separated distance between them. The mobile tag position is determined by measuring time of arrival (ToA) or time difference of arrival (TDoA), based on at least three stationary anchors with known positions. The average positioning error, obtained in [10,11], is on order tens of centimeter for a range of hundreds of centimeters. Thus, the relatively low accuracy is the main drawback of using radio technologies with a high accuracy is acquired.

Positioning mobile targets is one of the applications of Visible Light Communication (VLC), including illumination and data transfer communications [12]. The target mounted with a VLC receiver is localized when receiving signals from the optical source (i.e., Light Emitting Diodes (LEDs). The VLC receiver may be a photodiode or a camera, and the LEDs must be distributed with known positions in the environment [13]. In [14], using the VLC technology, a mobile robot is localized with a positioning accuracy equal to of 2.1 cm for a path of $800\mathrm{cm}$.

The aforementioned solutions cannot be adopted for micro-conveyors, because they do not deliver micrometer level resolution. In addition, heavy embedded electronic cannot be embedded on the micro-conveyor. In general, the vision based supervision solution is mainly adopted for micro-systems [15,16]. However, the resolution is inversely proportional to the size of the surface under observation. In [15], the positioning static error is over 200 µm, given that the conveyor surface is rectangular and measures 228 mm by 204 mm. In [16], for a 5 mm square working space, the positioning error is about 400 µmfor open loop control and 200 µmfor closed loop control. For micro-scale vision positioning systems, a better resolution can be obtained but with a limited range [17,18]. In [19], for a range of 221 µm, the target position is obtained with a resolution below 0.5 nm. This is achieved by analyzing a pseudo-periodic pattern detected by a standard visual configuration. In [20], the target object has a footprint of 270 × 270 micrometers and using two set of cameras the obtained XY position error is 4.882 µm and 8.206 µm for x and y axis respectively. In a vision-based surveillance scenario, in order to achieve high-resolution localization with large range, more than one camera will be required, making the system more complex [21,22].

This paper presents the development of an optical remote system for tracking and guiding micro-conveyors to reach their desired final destination with micrometer level precision. The method is based on scanning the conveying surface with a laser beam (emitted from a laser source) and analyzing the feedback (i.e., reflected light beam) from the micro-conveyor. A retro-reflective element is placed onto the micro-conveyor surface to ensure that the reflected beam is parallel to the incident beam. This optical remote method can be applied for any kind of micro-conveyor system such as: i—Aerodynamic based system, where the micro-conveyor movement is subjected to air jets or an injection of a fluid [23,24], ii—Electrostatic based system utilizes electrostatic induction motors to transport dielectric items [25,26], iii—Piezoelectric based system, where the micro-conveyor’s motion is ensured according to the principle of micro-sliding [27,28], iv—Electromagnetic based system, the motion of the micro-conveyor is ensured via the Lorentz force, which is generated by the interaction of the magnetic field from permanent magnet and current carrying conductors [29,30], etc.

The aim of this work is to supervise the trajectory of micro-conveyors moving over a large electromagnetic conveying surface with high positioning accuracy, regardless of the actuation principle. The movement of each micro-conveyor is regulated by a closed-loop control system to correct micro-metric positioning errors. In this article, the developed method is validated by tracking a single micro-conveyor, but it can be applied to numerous micro-conveyors navigating simultaneously over a single smart surface.

In this work, a closed-loop system is developed to regulate the micro-conveyor’s trajectory moving over an electromagnetic surface. The feedback of the closed-loop is provided by our developed optical sensor, previously presented and evaluated in [31]. There are several benefits of controlling the micro-conveyor path in a closed-loop control system, such as none-cumulative error, low inertia, and similar dynamic features along both working axes (x and y-axis), etc., …, [32,33]. In addition, higher positioning accuracy can be reached using a closed-loop control system [16,34,35].

This paper is organized as follow: in Section 2, the electromagnetic smart surface is described, along with the localization and tracking principle. Then, the experimental setup and calibration of the smart surface are described in Section 3. In Section 4, the closed loop is detailed. The experimental results are provided in Section 4.2. In last, conclusion and perspectives are provided.

2. System Description

2.1. Micro-Conveyor’s Design

The micro-conveyor developed at our Roberval laboratory [36], has a dimension of 68 mm × 68 mm and it can move in a 2D plane based on electromagnetic actuation principle. The conveyance surface, measuring 150 mm by 150 mm, consists of 5 × 5 cell matrix [37]. Each cell include two sets of serpentine coils oriented at 90 degrees. These sets are spread across two layers (i.e., Top layer and Second layer) as shown in Figure 1. Each cell is composed of two sets of serpentine coils arranged at right angles and spread across two layers.

The top and the bottom layer coils generate motion through electromagnetic forces along x-axis and y-axis, respectively. The coils located in the top (bottom) layer are supplied with the currents denoted as $I_{x1}$, $I_{x2}$ ($I_{y1}$, $I_{y2}$), respectively. A phase shift of $\pi /2$ is applied to the injected currents $I_{x1}$ ($I_{y1}$), relative to $I_{x2}$ ($I_{y2}$). The micro-conveyor consists of a cross structure shape [see Figure 1]. Four linear motors (LM) composed of north-south magnet array configuration are implemented into each corner. In practice, a pair of LM such as LM₁ and LM₂ (LM₃ and LM₄) aids in generating motion along x-axis (y-axis). By controlling the injected current in both top and second layer coils, complex motion trajectories in $xy$-plane can be achieved. The details regarding the actuation principle and modeling can be found in [38]. In addition, by changing the polarity of the injected current among the LMs situated along an axis leads to a rotation of the conveyor around its center in $xy$-plane. The micro-conveyor’s trajectory is determined by controlling the supplied currents in the top and second layer coils of the smart surface. This is done using a closed-loop control system that relies on sensors feedback.

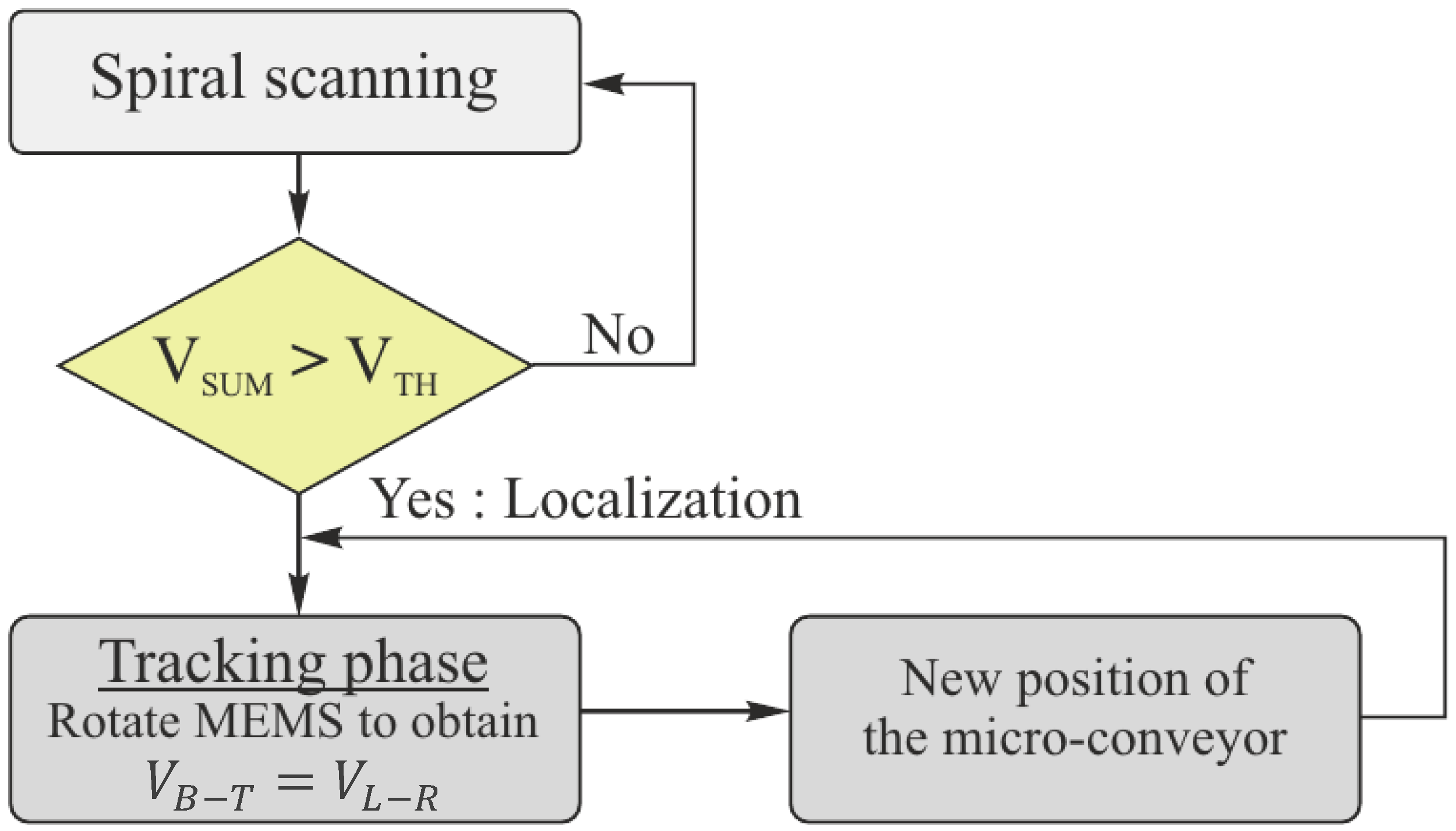
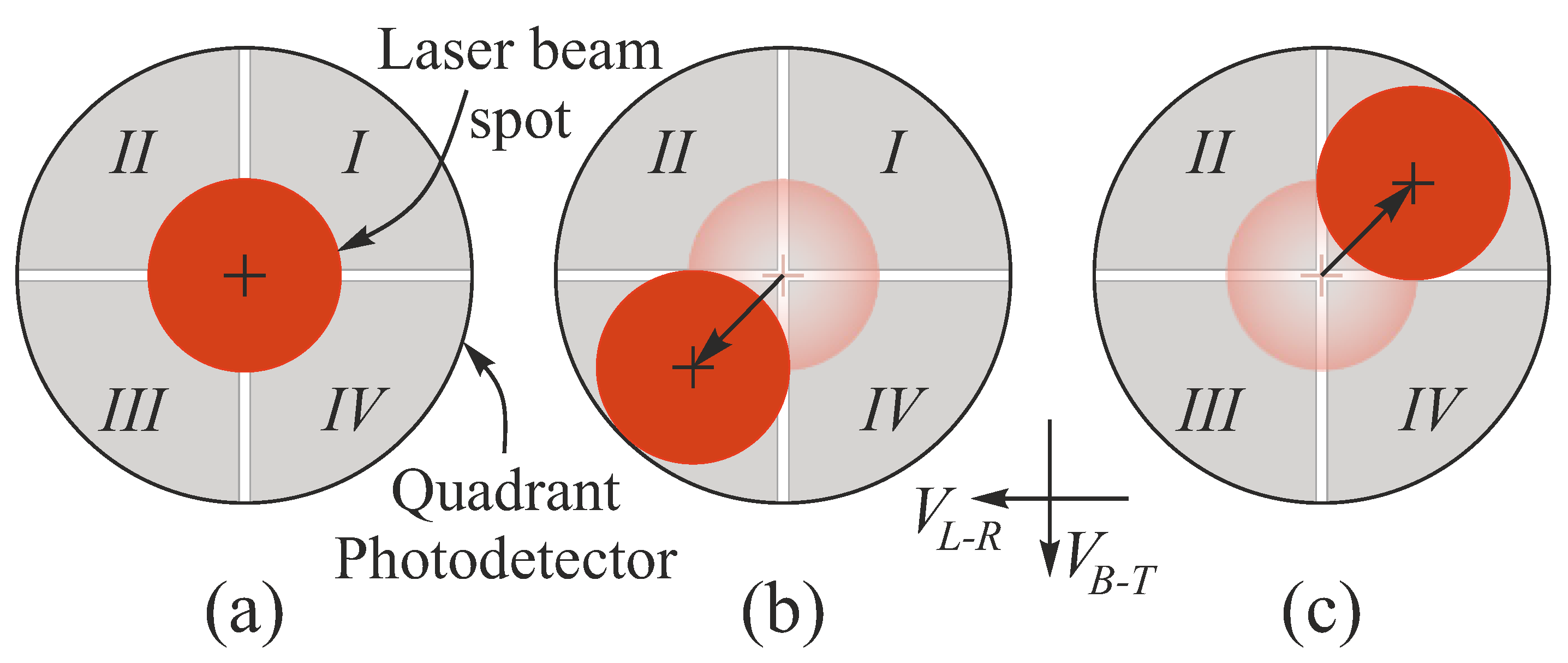
2.2. Localization and Tracking Architecture

For a meso-scale robotic system, it is crucial to monitor the micro-conveyor’s movement via a wireless positioning system, particularly when several micro-conveyors move simultaneously over the same conveying surface, or if there exist defective regions in this conveying surface. By employing a remote positioning system, the accurate real-time location of the micro-conveyors can be acquired. Next, the path for each micro-conveyor can be refined and collisions between micro-conveyors can be avoided by adjusting their motion velocity, either by speeding up or slowing down, based on their locations and the priority order of their tasks. Our proposed localization and tracking method of the micro-conveyor is based on a remote optical system. The incident optical beam generated by a fixed laser diode is oriented by a steering mirror which reflects the incident light beam towards the conveying surface. In this work, a high resolution Micro Electro Mechanical System (MEMS) mirror, developed by Mirrorcle Inc., is used as steering mirror [39]. It can rotate over two orthogonal axes. Two differential high voltages ($v_x$, $v_y$) are sent to its electrostatic actuators to control the MEMS’s mirror orientation using a dedicated driver module [40]. There exists one to one correspondence between the tip-tilt angles of the MEMS mirror (${\theta }_x$, ${\theta }_y$) and the voltage values ($v_x$, $v_y$), i.e., $v_{x\left(y\right)}=K\times {\theta }_{x\left(y\right)}$, where K represents a linear coefficient. In first phase, the MEMS mirror scans the surface in attempt to find the micro-conveyor’s position. The selected scan pattern is of spiral type to prevent the use of high frequencies to protect the MEMS’s mirror actuators. The drive voltages $v_x$ and $v_y$ for the MEMS mirror are sent having a Cartesian equation of a spiral in order to obtain the desired scanning pattern shape. The micro-conveyor is localized, when its surface is illuminated by the laser beam reflected from MEMS mirror. An optical reflective element, such as reflective tape or a corner cube reflector (CCR), should be placed onto the target’s surface (i.e., micro-conveyor). The role of this reflective element is to reflect the light (beam number 1) towards the optical detector with the same incident direction (beam number 2), as shown in Figure 2. Reflective tape has low efficiency due to the imperfect parallelism it provides between the incident and reflected light beams. In this work, We adopted the CCR for its reflective precision, which is a necessity for our high-resolution and precise application. Knowing that the CCR has a small dimension, with a diameter of less than 10 mm and a weight around 1 g, while the micro-conveyor has a load carrying capacity of 11.07 g when driven with 0.8 A current, as provided in the reference [38].

The fixed optical detector is positioned in such a way to receive the optical intensity reflected by the micro-conveyor. The optical detector’s output voltage is directly proportional to the light intensity received by its detecting surface. The target is considered localized when the detector’s output voltage exceeds a defined threshold. Thus, the tracking procedure is triggered. In the tracking phase, the MEMS mirror interrupts the spiral scan and begins to track the position of the micro-conveyor.

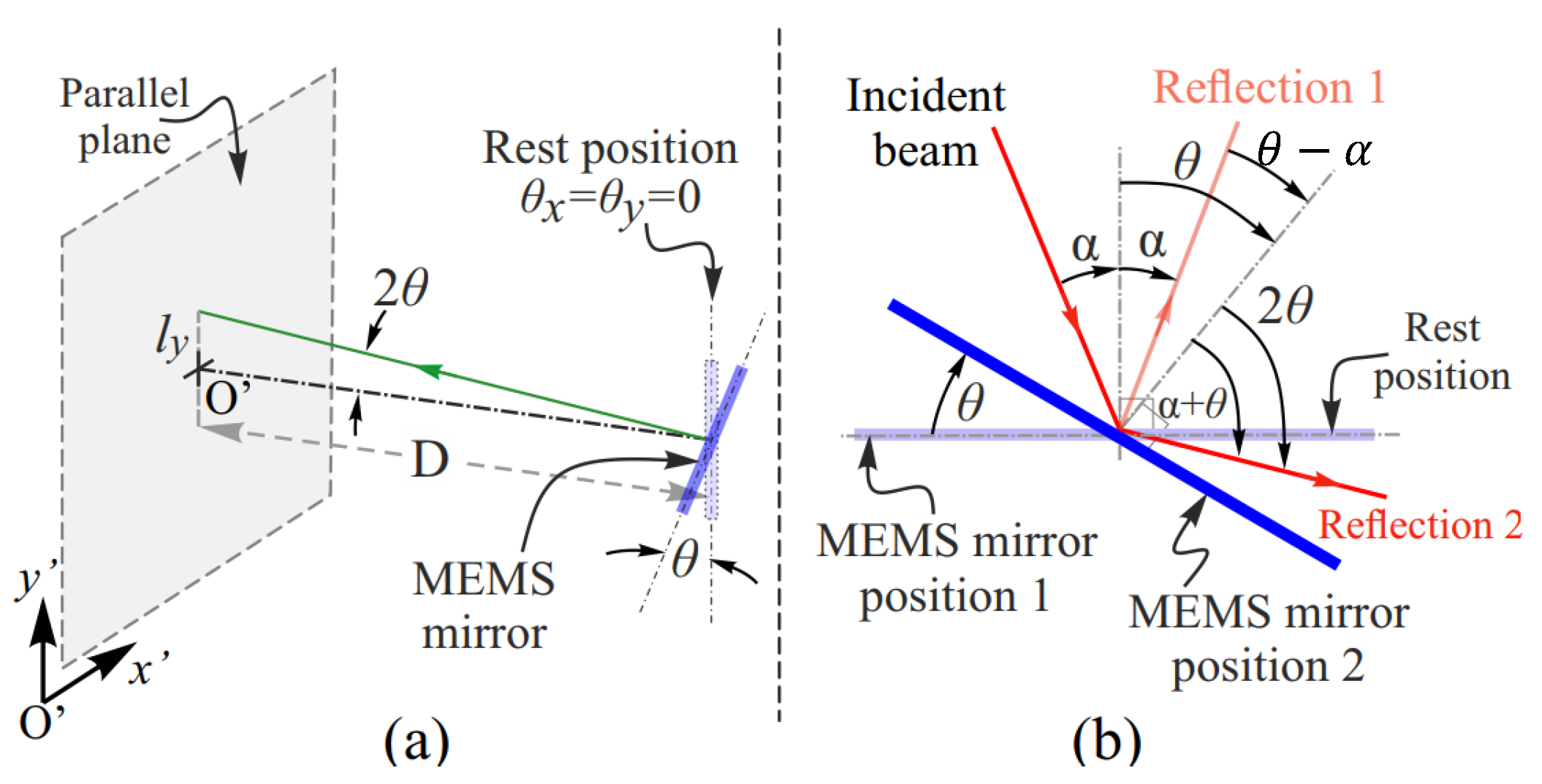
2.3. Localization and Tracking Control

To localize and track the target (i.e., micro-conveyor) position, a quadrant photodetector (QPD), composed of four separate detecting surfaces, is used. Each of the four detecting surfaces generates a photo-voltage proportional to the received light intensity. In this work, the quadrant photodetector ‘QP50-6-TO8, First Sensor Inc. (Berlin, Germany)’ is used to analyze the following generated voltages [41]:

$$V_{SUM}=[V_I+V_{II}+V_{III}+V_{IV}]$$

(1)

$$V_{L-R}=[(V_{II}+V_{III})-(V_I+V_{IV})]$$

(2)

$$V_{B-T}=[(V_{III}+V_{IV})-(V_I+V_{II})]$$

(3)

where the voltage produced by the ith quadrant ($i=I,II,III$ or $IV$) is denoted by $V_i$. $V_{SUM}$ corresponds to the summation of the four output voltages. $V_{L-R}$ represents the left minus right quadrants voltages. Likewise, $V_{B-T}$ represents the bottom minus top quadrants voltages. $V_{SUM}$ gives information, if the micro-conveyor is localized or not, with the help of reception of laser beam (2) [see Figure 2], on the QPD’s active surface.

The algorithm of localization and tracking is presented in Figure 3. As mentioned above, the system starts with a spiral scanning. Then, a $V_{SUM}$ value higher than a certain threshold implies that the micro-conveyor is localized. Tracking is then launched by analyzing the $V_{L-R}$ and $V_{B-T}$ values. The primary objective of the tracking phase is to maintain $V_{B-T}$ and $V_{L-R}$ values close to zero. In this scenario, the received laser beam is precisely positioned in the middle of the active surface of the QPD and the four quadrants are evenly illuminated [see Figure 4a]. The displacement of the micro-conveyor can be detected when the reflected beam 2 [see Figure 2] deviates from the central position causing significant variation in the values of $V_{B-T}$ and/or $V_{L-R}$. For example, in Figure 4b, the beam light is at the bottom left of the detector, giving positive values for $V_{B-T}$ and $V_{L-R}$. In Figure 4c, the reflected beam light is at the top right position giving negative values for $V_{B-T}$ and $V_{L-R}$. In this situation, the system generates the adapted differential voltages $v_x$ and $v_y$ values rotating the MEMS mirror in such a way those previous values return near to zero [see Figure 3 and Figure 4a]. More details concerning our developed optical sensor, which is used for localization and tracking, can be found in [31].

3. Experimental Setup and Surface Calibration

3.1. Experimental Setup

The experimental setup used to realize our localization and tracking method is illustrated in Figure 5. A laser diode source emits the light towards a (50/50) beam splitter and towards the MEMS mirror’s surface.

The beam splitter is used to direct the reflected beam, coming from the target (CCR), towards the QPD’s active surface. The MEMS mirror is placed at the focal plane of a convergent lens (Lens 1) in order to concentrate the incident laser beam onto the surface of the MEMS mirror and to ensure there is a reflection of all the incident light towards the conveying surface. Another diverging lens (Lens 2) is placed in front of the area of the QPD to increase the diameter of the light beam received over its surface, making it more suitable for tracking algorithm. To achieve the best resolution, the diameter of this laser beam spot should be the same as the QPD active surface’s radius. Implementing the MEMS mirror above the conveying surface is not a simple task, thus, an inclined stationary mirror is used to redirect the light beam towards the conveying surface. The MEMS mirror adopted in this work has a diameter of 1700 µm. It has a maximum value of ${\theta }_x$ and ${\theta }_y$ of 5.21 degrees and 5.33 degrees, respectively. In this configuration, the MEMS mirror detects the micro-conveyor over a scan range of up to 168 mm in diameter. A broader range can be obtained by adjusting the distance between the MEMS mirror, the conveying surface and the lenses. However, The current range of 168 mm in diameter is sufficient here because the conveying surface used in this work measures 150 mm by 150 mm.

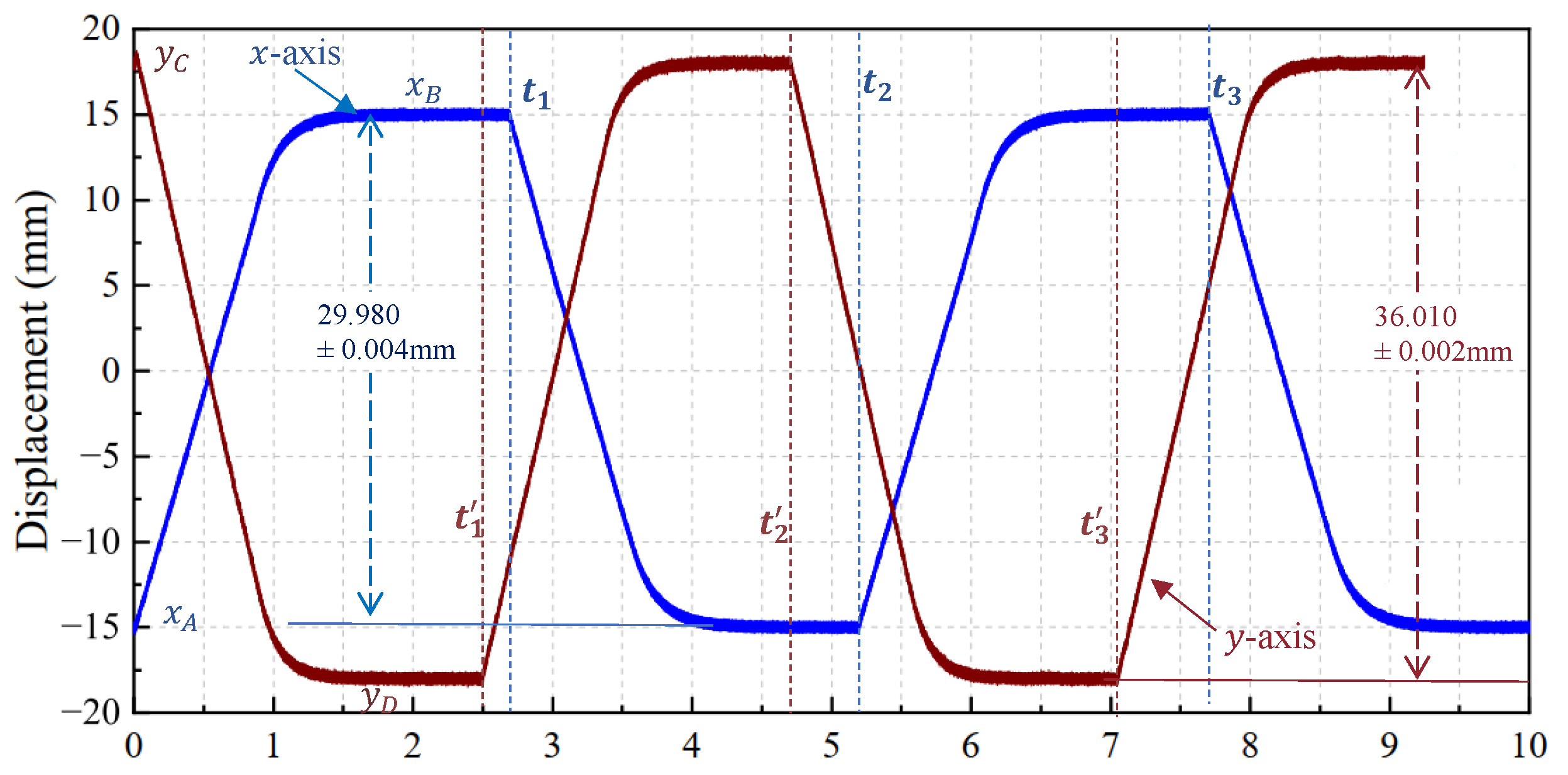
3.2. Conveying Surface Calibration

Conveying surface calibration is a mandatory step to establish the relationship between the tip-tilt angles ${\theta }_x$ and ${\theta }_y$ of the MEMS mirror (which corresponds to their associated voltages $v_x$ and $v_y$, respectively) and the coordinate system x and y of the conveying surface. In this work, the plane projection method, called homography is used to find the relation between the conveying surface coordinates (x, y) and the coordinates of a plane parallel to the MEMS mirror ($x^{\prime }$ and $y^{\prime }$). The parallel plane’s origin ($O^{\prime }$) is defined by the spot’s position at which the MEMS mirror is in its rest state, i.e., $v_x=v_y=0$. The $x^{\prime }$ and $y^{\prime }$ values are calculated using the following trigonometric formula [see Figure 6a]:

$$x^{\prime }=D\times tan\left(2{\theta }_x\right)$$

(4)

$$y^{\prime }=D\times tan\left(2{\theta }_y\right)$$

(5)

where D represents the separating distance between the fixed mirror and the MEMS mirror.

As illustrated in Figure 6a, whenever the MEMS mirror pivots by an angle $\theta$, the reflected beam undergoes an angular displacement of $2\theta$. In the example of Figure 6b, the incident beam undergoes reflection at an angle $\alpha$, which corresponds to MEMS mirror rest position (i.e., position 1). Next, the MEMS mirror undergoes a rotation by an angle denoted as $\theta$, the incident laser beam is then reflected at a new angle equal to $\alpha +\theta$. As a result, the angle difference between the first and second reflection is $2\theta$.

Using the homography principal describe in [42], the relation between $(x^{\prime }$, $y^{\prime })$ and $(x,y)$ values is obtained as following:

$$\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)=\left(\begin{array}{ccc}{h}_{11}& h_{12}& h_{13}\\ h_{21}& h_{22}& h_{23}\\ h_{31}& h_{32}& h_{33}\end{array}\right)\times \left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right)$$

(6)

where $h_{ij}$$(i,j=1,$ 2 or $3)$ are the elements of the matrix H, which is the projection matrix obtained by applying the direct linear transformation algorithm (DLT). For each pair of applied voltages $v_x$, $v_y$ (i.e, ${\theta }_x$, ${\theta }_y$), the corresponding x, y values can be calculated by applying the Equations (4)–(6). On the other hand, $x^{\prime }$ and $y^{\prime }$ values are determined by multiplying the desired x, y values by the inverse of matrix H. The next step is to regulate the micro-conveyor’s trajectory by applying the closed-loop tracking system.

4. Closed-Loop Control of Micro-Conveyor’s Trajectory and Experimental Results

4.1. Closed Loop Control System

Figure 7 illustrates the block diagram of the closed-loop control system managing the displacement of the micro-conveyor. The objective is to navigate the micro-conveyor from its current position to a targeted position with high accuracy, leveraging the feedback obtained from our developed optical sensor. Initially, the intended coordinates ($X_{des}$, $Y_{des}$) are compared to the actual measured coordinates ($X_{mes}$, $Y_{mes}$). The subtraction between these two coordinates ($\mathsf{\Delta }x$, $\mathsf{\Delta }y$) are adjusted using a proportional controller, integrated in a LabVIEW interface, to generate the corresponding supplied currents values ($I_{x1}$, $I_{x2}$, $I_{y1}$ and $I_{y2}$) sent to coils integrated in the conveying surface. As a consequence, due to the influence of Lorentz force, the micro-conveyor is moved to a new location. The QPD will detect any variation in $V_{B-T}$ and $V_{L-R}$ values. So, the MEMS mirror then corrects its angle accordingly to realign the laser beam with the CCR surface, consequently, over the active surface of the QPD (as explained in Section 3).

Using homography method, the micro-conveyor’s position is determined by acquiring the updated voltage values of $v_x$ and $v_y$. The variables $\mathsf{\Delta }x$ and $\mathsf{\Delta }y$ represent the positioning errors along the x-axis and y-axis, respectively. The closed-loop control system stops if the preceding values fall below a predetermined experimentally measured threshold value.

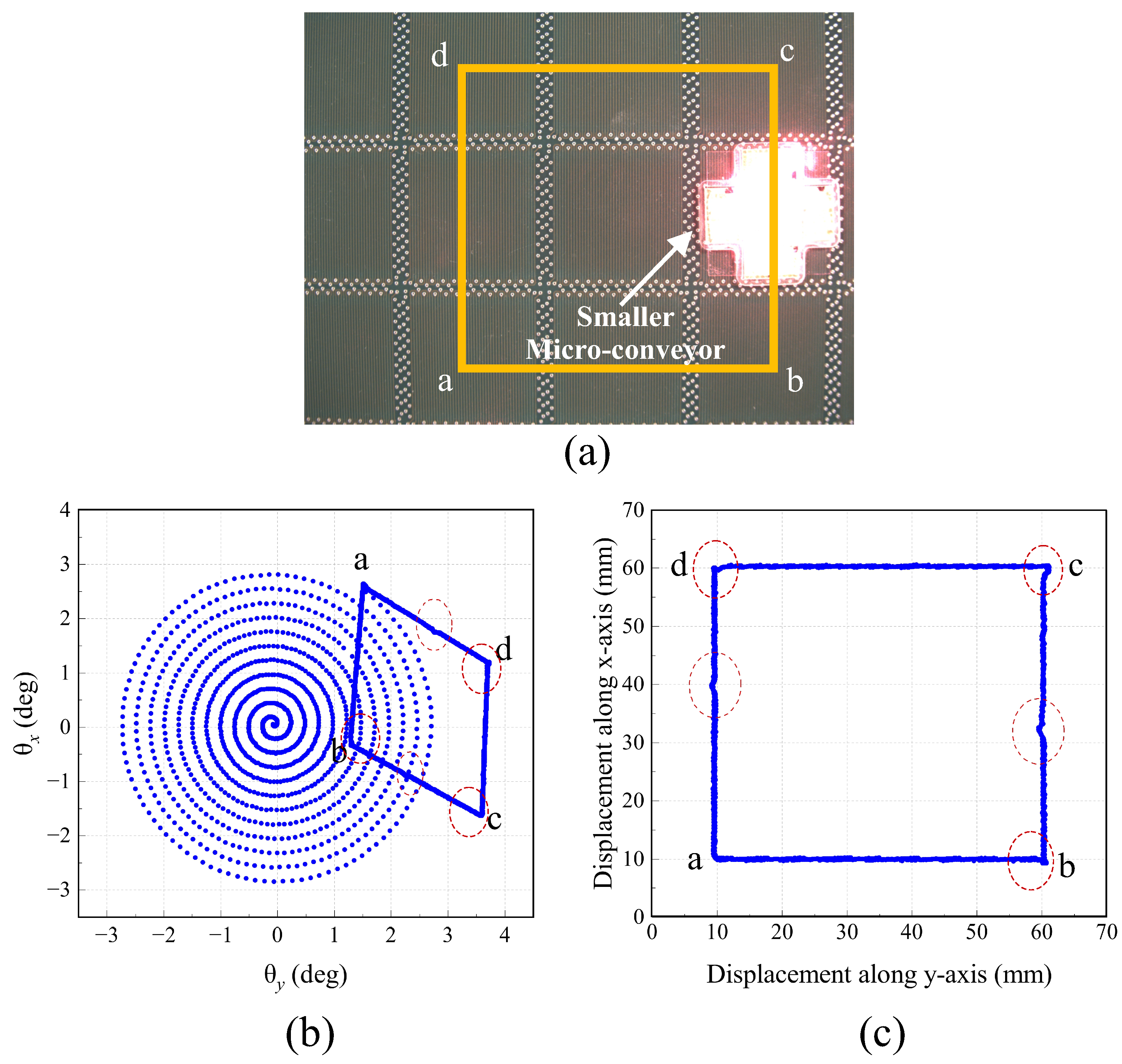
4.2. Experimental Results

This section presents a validation test of the suggested method along the x-axis and y-axis. Figure 8 presents a photograph of the conveying surface, showing the micro-conveyor located at position A and being targeted by the laser beam spot reflected via the MEMS mirror. Given this scenario, the magnitude of $V_{SUM}$ exceeds the threshold value, indicating that the QPD received the light beam reflected by the CCR onto the micro-conveyor. Then, the system exits the scanning phase to start the tracking of the micro-conveyor, for more details see [31].

The center of the conveying surface serves as the origin of the coordinate system, denoted by O($x,y$) [see Figure 8]. Each point on the surface has known coordinates by applying the homography method. A static noise point observed on the conveying surface is due to the reflection coming from a glass protection placed in front of the MEMS mirror. This static noise point is low in intensity and does not affect the sensor output. In addition, it exists some anti-reflection treatment for MEMS mirrors that eliminates this undesired spot.

In the first experiment, the closed-loop control system guided the micro-conveyor to follow a horizontal round trip path (along x-axis). The motion speed during this experiment was 16 mm/s. This trajectory is from point A to point B, separated by a distance of 30 mm [see Figure 8], and vice versa. The displacement along x-axis over time is presented in Figure 9 (in blue color). The micro-conveyor was at position A at time $t=0s$. In this example, the value of $X_{des}$, presented in Figure 7, is equal to $x_B=+15$ mm. The values of $X_{mes}$ are measured from the developed optical sensor in a real-time application. Depending on the difference between the measured and desired values (i.e., positioning error $\mathsf{\Delta }x$), the system will send controlled currents $I_{x1}$, $I_{x2}$, so that the micro-conveyor moves to the desired position B. Once the micro-conveyor becomes near the point B, it will oscillate and stabilize around it, in order to obtain an acceptable low positioning error $\mathsf{\Delta }x$. After a certain time from reaching the desired position, $t=t_1$, a new command value $X_{des}$ equal to $x_A=-15$ mm, is sent to the system. This command instructs the micro-conveyor to move back to point A. This approach is executed again at time $t=t_2$, and time $t=t_3$. The closed-loop control system successfully adjusted the position of the micro-conveyor, resulting in average and root mean square (RMS) error values of 20 µm and 4 µm, respectively.The errors in this work arise from the resolution limitation of the MEMS mirror’s driver and the QPD, as well as electronic noise, and optical noise. Better accuracy can be achieved by replacing the proportional controller with a proportional integral controller to further reduce the static error.

The same experiment is repeated for the y-axis. The trajectory of the micro-conveyor shown in Figure 9 (in red color) represents the vertical round trip displacement. The micro-conveyor moves from position C to D, and vice versa, [see Figure 8]. The micro-conveyor is directed along the y-axis to achieve a vertical movement of 36 µm. The initial position of the micro-conveyor is at point C and $Y_{des}$ is equal to $Y_D=+18$ mm. After reaching this desired position and at time $t=t_1^{\prime }$, a new command is sent to the control system so that the micro-conveyor goes back to position at point C having $Y_C=-18$ mm. This process is repeated for $t=t_2^{\prime }$ and $t=t_3^{\prime }$. The corresponding average positioning error is equal to 10 µm and RMS value is equal to 2 µm.

Figure 10, is a staircase step trajectory of the micro-conveyor moving over the x and y axis. For the horizontal displacement, the micro-conveyor is guided to move from point A to point B [see Figure 8], then it returns back to its initial position A. Its total path of 30 mm is divided into three identical paths, each of 10 mm [see Figure 10 (in blue color)].

The first command was at the time $t_1$. After completing the trajectory of 10 mm, the micro-conveyor stays at its position for a certain time before receiving a new command, at time $t_2$, to do another 10 mm path. The third command sent to the micro-conveyor to reach the point B occurs at time t = $t_3$. For the return trip, the command instances occur at time $t_4$, $t_5$, and $t_6$ for each command. The closed-loop control system establishes new values of $X_{des}$ to achieve the desired staircase step trajectory as seen in Figure 10 (in blue color). For the first 10 mm step, the extracted average and RMS error values are found to 20 µm and 2 µm, respectively. The second step gave average and RMS error values of 30 µm and 4 µm, respectively. The average and RMS values obtained for the last step are equal to 30 µm and 7 µm, respectively. The same experiment is replicated for the y-axis. The path of the micro-conveyor shown in Figure 10 (in red color) corresponds to the vertical staircase step trajectory. The micro-conveyor moves from position C to D [see Figure 8], and vise versa. For this experiment, the distance of 36 mm between these two points is divided into three identical paths equal to 12 mm. Time instances $t=t_1,t_2,$ and $t_3$ correspond respectively to the commands given to the micro-conveyor in order to move from point C to D. For the return path, time instances $t=t_4,t_5,$ and $t_6$ correspond respectively to the commands given to the micro-conveyor to move back to point C. The extracted average and RMS error values for the first 12 mm step are equal to 12 µm and 3 µm, respectively. The second step gave average and RMS error values of 17 µm and 4 µm, respectively. The average and RMS values obtained for the last step are equal to 13 µm and 9 µm, respectively. Due to the fact that each step requires the micro-conveyor to relocate 10 mm from its initial position, the error accumulates. If the instruction was to directly reach the final destination point relative to the surface’s origin point, in this case, the resulting error would not cumulative. To note that, our system applies error correction continuously based on our data acquisition refresh rate of 50 kHz. In this scenario, our developed optical sensor achieves closed-loop tracking with the conveying surface along both axes.

In another experiment, we used a smaller version of the micro-conveyor, measuring 30 mm × 30 mm, so that we could test each cell separately [see Figure 8], and multiple micro-conveyors can be carried in the same workspace. In the example of Figure 11a, the smaller version of the micro-conveyor is guided to move along a square trajectory measuring 50 mm by 50 mm. The corners of the square, labeled as points a, b, c, and d, serve as the desired coordinates input for the closed-loop control system illustrated in Figure 7. A larger actuation zone is achieved compared to the previous experiment, due to the use of a downsized model of the micro-conveyor. In this work, it is not possible to achieve a square path greater than 50 mm × 50 mm, because the cells at the edge of the conveying surface are not supplied with current. In this experiment, after localizing the micro-conveyor at position a, the next steps is to go to point b, followed by points c, and d, before returning to its initial position a, following a square trajectory. Figure 11b represents the variation of ${\theta }_x$ with respect to ${\theta }_y$ throughout the scanning and tracking phase. Initially, the MEMS mirror undergoes rotation in a spiral pattern, until the laser beam reaches the micro-conveyor being at position a. Subsequently, the MEMS mirror executes rotations in a deformed square pattern, mirroring the intended square trajectory of the micro-conveyor as it moves across the conveying surface. Figure 11c, illustrates the trajectory followed by the micro-conveyor as it departs from point a and returns back to this starting point, tracing a square path.

The imperfections observed in the square trajectory highlighted by red circles (see Figure 11b,c) are caused by the change in direction at each square corner and the micro-conveyor’s transition between adjacent cells. Indeed, the absence of integrated coils in the transition zone results in a reduction in the control effectiveness of the micro-conveyor. Upon entering the next cell, the closed-loop control system promptly adjusts its trajectory. Trajectory deformations are not observed along x-axis because the coils responsible for horizontal movements are situated in the top layer, while the coils responsible for regulating movements along y-axis are situated in the second layer, which results in a higher energy loss. This clearly demonstrates one of the primary objectives of the closed-loop control system, which is rectifying paths when the surface is dysfunctioning, as observed in the above scenario. In conclusion, these outcomes validate the system’s ability to monitor and preserve the desired path of the micro-conveyor as it moves across a two-dimensional plane.

5. Conclusions

In this work, an optical localization and tracking method is adopted to control the movement of a micro-conveyor over a conveying surface along two axes. This method is carried out using a MEMS mirror, a quadrant photodetector and a reflective corner cube placed onto the micro-conveyor’s surface. The conveying surface is calibrated by applying a plane projection method called homography. The principle of actuation of the micro-conveyor is based on electromagnetic principle. The micro-conveyor’s trajectory is determined according to the regulated currents feeding the surface. A tracking closed-loop control system is designed to guide the micro-conveyor to follow a desired path along the x- and y-axis, by injecting the corresponding currents into the coils of the surface. Results for tracking in the x and y axis have validated the proposed method, with an average tracking error around 20 µm for a horizontal displacement of 30 mm, and an accuracy of 10 µm for a vertical displacement of 36 mm. This displacement range is limited by the geometry of the conveying surface used in this work. In addition, the tracking system successfully tracked and adjusted the trajectory of a smaller micro-conveyor prototype when it moved in a square trajectory of 50 mm × 50 mm. The importance and novelty of this work derives from achieving micrometer-level resolution over a large conveying surface covering the centimeter range. In future work, different approaches could be adopted to improve accuracy: (1) implementation and design of a proportional integral control, (2) improving the homography matrix by using a high resolution camera as a measurement system during the calibration procedure. In perspective, it is planned also to do a tracking of multiple micro-conveyors simultaneously. In fact, we plan to employ time multiplexing in order to accurately identify the location and track several micro-conveyors. By scanning the entire conveying surface in a spiral pattern, a new record of the micro-conveyor’s position is stored each time when it is illuminated by the laser beam. As a result the target’s trajectory can be reconstructed. Furthermore, this work will be extended, to implement multiple sensors in a given sensor network. One of the challenges that needs innovative solution is to optimize the placement of these multiple sensors in a novel configuration. We intend to exploit the solutions provided in [43,44], to achieve high accuracy and precision.