1. Introduction
The Internet of Things (IoT) is an emerging paradigm concerned with bringing the connectivity of real-world objects and things [
1]. Such a situation opens up opportunities for a large number of various devices or things, such as wearable devices, laptops, portable devices, and vehicles, to impart, communicate, and interact with one another. Some applications include, yet are not restricted to, smart healthcare [
2], smart cities [
3], smart environmental monitoring systems [
4], and Smart Business [
5]. In such sophisticated scenarios, there is the possibility of finding heterogeneous static and mobile devices (e.g., smartphones carried by individuals) equipped with different radios enabling data transmission that might interact. The communication might occur only during specific contact opportunities (i.e., depending on the communication protocol and range of coverage) between heterogeneous and possibly disconnected static networks [
1]. In a smart city scenario, due to the high mobility and flexibility, the mobile sinks (e.g., cars, taxis, and buses) might be utilized to collect the data from the static nodes (e.g., traffic sensors, environmental monitoring stations) or disseminate control information.
Hence, such data might be relayed by any node and forwarded through other nodes (e.g., via smartphones) even in the absence of a predefined end-to-end path between data sources and sinks, exploiting opportunities through alternative nodes and routes for communication as soon as they become available.
Therefore, such an Opportunistic Networking might stand at the heart of IoT as a communication enabler, where the scope of the wireless sensor network (WSN) of static devices might be augmented through new communication possibilities with opportunistically present mobile devices. Therefore, opportunistic routing paths contribute to connecting the disconnected networks of devices to the Internet world. This might be of great importance in situations where a communication infrastructure is unavailable due to, for example, public disaster in healthcare, which is of priority [
6,
7,
8,
9]. For such communications, some fundamental-less networks emerged that could opportunistically transmit data via each other using short-range communication protocols such as Bluetooth, Bluetooth low energy (BLE), and Zigbee [
10,
11]. One of these communication channels is Opportunistic Networks (OppNets) [
12]. In OppNets, the network topology is unknown, and the connections are random and unstable [
13], mobile nodes use the save-carry-forward method. When nodes are in the communication range, they exchange messages, save them in their buffers, and carry them until they visit another suitable node for carrying the message. Then, the messages are forwarded to the next relay node to bring them closer to the destination [
14].
OppNets are delay-tolerant so improving the message delivery probability and reducing the network overhead [
15] is of great importance and a great challenge. Parameters such as buffer size [
16], number of messages, number of nodes [
17], and nodes movement [
14] are effective in terms of the network performance. A basic and straightforward method for forwarding messages is to flood the network. Each node forwards a message copy to each available node and keeps one copy. This method increases the network overhead and discards many messages due to the buffer overflow [
18].
Despite significant attention to the various aspects of OppNets [
14,
19,
20] so far, maximizing the network performance using the optimized and effective parameters using real-world application has remained unknown. This work identifies and explores the impact of message copies, buffer size, message interval, and node mobility as significant parameters on network performance by finding the optimized setting and configuration.
Additionally, we study two use cases exploring the network’s performance using real-world application data, considering the realistic restricting conditions. We consider taxis and buses the nodes of the network, equipped with devices with limited buffers for sending and receiving data. The device can be either the driver’s smartphone or another smart embedded system (built-in or added to the car/bus) that has the ability to send and receive messages. In addition, the impact of buffer size as a vital parameter on network performance has been studied in [
21,
22,
23]. Despite the usual configuration in only simulation-based studies that arbitrarily extend the buffer size, we restrict the buffer size of these devices to mimic the actual network performance. Such an assumption in extending the buffer size arbitrarily during a simulation study does not sound like an actual case in daily living since smartphones and other devices have a limited buffer size. Hence, we have calculated the optimal parameters in both cases to provide an overview of the actual scenarios.
Furthermore, in the second use case, we study the presence of selfish nodes in the network. Several works in the literature have addressed the selfish node as a parameter severely impacting the network performance [
24,
25]. Selfish nodes can be devices that are not cooperating in the network and refuse to carry messages or delete them in their buffer without reason. The motivation of these malicious nodes is not to use their resources, such as battery and buffer, but to use other nodes to send their messages. This can compromise the network performance. Therefore, we evaluated the network’s performance with the presence of selfish nodes (10, 20, and 50 percent of nodes were selfish) as well as when they were not present in the network (all nodes were trusted).
We collected data from three real-world scenarios in three cities using GPS coordinates of taxis and buses. We extended the results by applying machine learning (ML) regression models. As the output, we found the optimized parameters to estimate the network performance using networks with limited resources and the simulation output.
The results showed that the network structure influenced by the node density and node mobility impacts the optimized parameters and the network performance. We also predicted the impact of malicious nodes in the network and considered the necessary security measures. The contribution of this paper is as follows:
Performing a comprehensive evaluation of the network’s performance and the impact of the most influential parameters, such as the number of message copies, the node’s buffer size, messages interval, number of nodes, and node movement, on the network performance allocated in terms of messages delivery probability, dropped messages probability, and network overhead;
Applying ML in OppNet in large networks extends the simulation results for predicting the effective, optimized parameters;
Specifying and customizing the appropriate optimized parameters in real-world applications with limited resources;
Constructing a database based on the movement of buses in Münster, Germany;
Comparing the network performance under three different routing algorithms in the presence and absence of selfish nodes in three real-world nodes’ movements.
The rest of the paper is organized as follows: In
Section 2, related works are reviewed. Materials and methods are discussed in
Section 3.
Section 3.4 describes the optimized parameters. Then,
Section 4.3 presents the simulation results, and
Section 5 discusses the results. Lastly,
Section 6 presents the paper’s conclusion.
2. Related Work
Exploring the impact of influential factors such as message copies, buffer size, message interval, and node mobility on network performance is challenging. Considering each of these factors as a dimension, simultaneous multidimensional evaluation of the impact of all factors is complex and less known. Thus, the majority of the related work is focused on one or two-dimensional evaluation. This section presents some existing studies on these challenges. We have outlined their main characteristics and specified the results obtained from each. These papers evaluated the boundary of the number of nodes, messages, buffer size, and node mobility on network performance utilizing the most prevalent routing algorithms. Additionally, regarding the number of available copies of messages, solutions to improve network performance have been proposed in addition to examining its impact.
The effect of number of message copies in the network are studied in [
26,
27,
28]. The authors in [
26] evaluated the effect of the number of message copies in two different areas in terms of delivery probability, average latency, overhead ratio, hop count, average buffer time, and the number of contacts. According to their results, the lower-size region showed better performance. The number of nodes in this paper (25 pedestrian and 25 cars) are not enough for the wide-area selected for simulation. Additionally, a concrete node movement was not chosen for the simulation.
In [
27], message distribution on the network is examined, and the number of message copies is controlled comparatively. The authors aimed to increase the message delivery rate and reduce network overhead and delay. The structure estimated the probability of a successful message leaving the intermediate node and the extent of the network to determine the replication and forwarding strategy. For simulations, the authors did not consider any specific circumstances.
In order to control the number of message copies in the network, the authors in [
28] suggested a feedback mechanism. When the destination node receives a message, it sends a feedback message to all other network nodes such that they can delete the message from their buffer. It could improve the message transmission success rate, overhead, and delay. Nodes in this research move randomly within the simulation environment, which is considered small (
).
The authors of [
6] considered the number of nodes, messages, and message size to check their impact on the network performance in OppNets. Epidemic, Prophet, MaxProp, and Time to Return routing algorithms are used for this evaluation. The results of the network performance of each of these routing algorithms are compared. The simulation environment in this paper is also considered small (zone1 =
, zone2 =
).
The effect of buffer size on the OppNets’ performance is evaluated in [
22,
23,
29]. Likewise, the effect of increasing the buffer size in different routing algorithms is studied in [
29]. The authors considered the number of vehicular and terminal nodes to change the buffer size in this paper. As the buffer increased, the performance of nodes in the Epidemic and MaxProp algorithms also increased, and only vehicle nodes improved in the Spray and Wait algorithm. The number of nodes in this paper was limited to 25 stationary nodes and 6 mobile nodes.
In [
22], the effect of buffer size on the Epidemic algorithm is evaluated, and an optimal buffer scheme is presented to improve the efficiency of this algorithm. In this paper, nodes move randomly in a square of 1000 m × 1000 m. The proposed algorithm improved the message delivery and end-to-end delay in the Epidemic algorithm.
The authors of [
23] examined the effect of buffer size on packet delivery and showed how buffer size could affect the network performance. They also evaluated the inverse effect of buffer size on network overhead and packet delivery rate. As the buffer size decreases, the delivery rate and network overhead increase, and with a large buffer size, the proposed algorithms have better message delivery and less network overhead. In this paper, the authors did not take a specific movement situation into account.
The effect of message generation interval and buffer size on the message delivery probability, delay, and network overhead were studied in [
30]. This paper compared the results for OBSBM (their proposed algorithm), Epidemic, Binary Spray, and Wait routing algorithms. The results show that by increasing messages interval, the message delivery increased, messages delay decreased slightly, and network overhead increased a little. Additionally, increasing the buffer size from 20 to 40 messages does not affect the network performance.
Node density is evaluated in [
31,
32,
33]. The authors of [
31] evaluated the effect of node density and messages TTL on network performance in vehicular delay-tolerant networks in terms of messages delivery probability, network overhead, average latency, and the average number of hops. The results showed that raising the density of the nodes enhanced network performance; on the other hand, it may increase the delay. They also showed that increasing TTL did not affect improving network performance. The authors of this paper concluded that a single-copy protocol has more hops and latency than multiple-copy protocols.
The effect of node density on different routing algorithms was evaluated in [
32]. The environments they evaluated included extremely sparse environment (3–5 nodes per km
2), sparse environment (6–15 nodes per km
2), average environment (16–25 nodes per km
2), populated environment (26–400 nodes per km
2), and dense environment (more than 400 nodes per km
2). The results showed that the Spray-and-Wait algorithm works better in a dense environment. TheRandom Waypoint movement is also used in this article for node movements.
The effect of node density on message delivery probability, latency, and network overhead is examined in [
33]. Based on the paper results, by increasing the number of nodes, messages delivery probability and network overhead are increased, and message latency decreases. The authors employed the random movement model in this paper without taking into account the actual database. Additionally, they made the supposition that every node in the network was trustworthy and free of malicious nodes.
In [
34], an OppNet with fixed and moving nodes was examined. This paper showed that the mobility of the nodes does not have much effect. Moreover, increasing the number of moving nodes can increase efficiency, which was not seen in fixed nodes.
The impact of malicious nodes on the network was evaluated in [
24,
25,
35]. The authors of [
24] analyzed the impact of selfish nodes on the network performance and proposed a routing mechanism to manage such nodes in the network. They discussed that increasing the number of selfish nodes can effectively decrease the network performance.
In [
25] the effect of selfish nodes on network performance based on data memory size is estimated. The authors took advantage of social knowledge to detect the selfish nodes to mitigate this destructive effect of selfish nodes.
The authors of [
35] analyzed the impact of the malicious nodes on messages delivery probability, dropped messages, and average latency in the network. The outcomes of this paper indicate that by increasing the number of malicious nodes in the network, the message delivery decreases, the number of messages dropped increases, and the message latency increases. The simulation environment was limited to 1000 mt × 1000 mt in this research, the authors did not use actual movement data set, and they considered a large buffer size (100 M) for nodes.
The nodes’ mobility, buffer size, message interval, number of nodes, and number of messages copied in OppNets influence the network’s performance. The main disadvantages of the previous works are as follows:
The majority of the previous works suffer from the lack comprehensive evaluation method in which they often consider a limited number of the influential factors on the network performance (ca. two);
These works usually do not use the actual dataset collected from the real-world scenarios. Therefore, the works are restricted to a limited number of nodes which do not reflect the actual output in the simulation;
Lacking the actual data from the actual scenario forces the authors to use the random node’s movement in the environment. In some cases, such as pedestrians (carrying the wearable devices such as smartphones and wearable devices), this could be a valid assumption, but in many other cases, such as, for example, an individual riding a bus or taxi, the requirements cannot be met.
In this work, we conducted a comprehensive evaluation study by considering all influential factors in network performance. Additionally, we have used concrete datasets to make the results less error-prone.
3. Materials and Methods
To show the network resources’ limitations in real-world applications, we used three datasets collected the GPS coordinates of taxis and buses in public transportation in three different cities. The datasets differ in network structure, mobility, and density coping with the requirements of our study.
The rest of this section describes the databases and routing algorithms used in this paper, the simulator environment, and finally, how optimized parameters are determined.
3.1. Scenarios
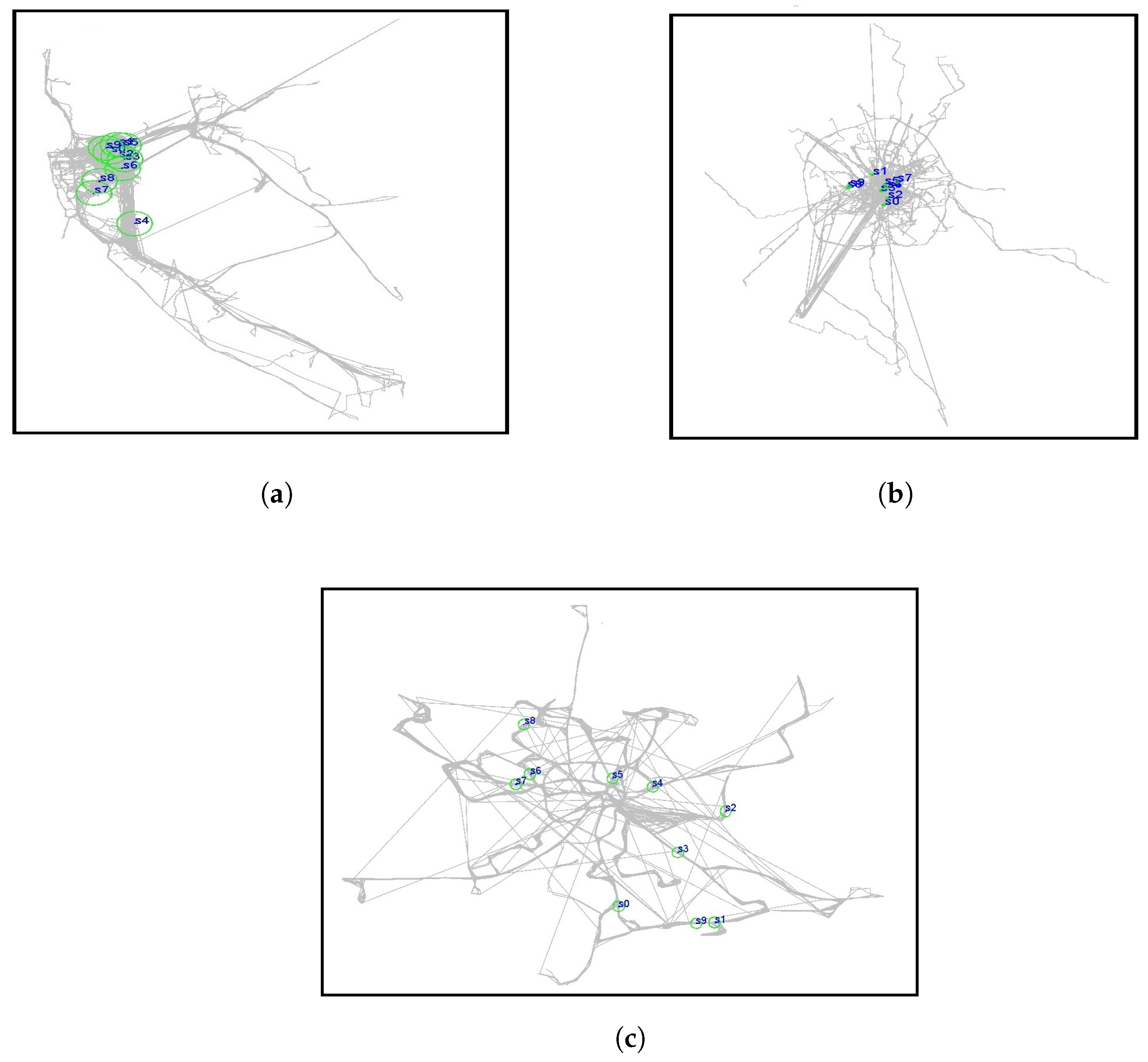
Providing a model requires data based on individual daily activity and movement, but such data are often unavailable in large sizes. During daily mobility, people make different decisions in various situations and may choose routes based on rush hour and traffic. This point is often missed in simulators. Therefore, for a solid overview, we used datasets with GPS coordinates of public transportation (bus) and taxis during routine daily work rather than the preset defaults in the simulator. We used three datasets, of which two are the mobility of taxis over some time based on passenger requests in the cities of San Francisco and Rome, and one is the mobility of buses in the city of Münster in Germany on a daily schedule. We chose these cities as they differ in urban structures (
Figure 1). San Francisco is categorized as a modern urban structure with stylish and structured streets. Rome is a city with an old texture that has expanded irregularly. Münster is a town with an irregular street structure. We aimed to obtain the mobility of taxis and buses in San Francisco, Rome, and Münster, respectively. While taxis’ restrictions are less than those for buses, and some taxis drive on the streets without following all traffic regulations, buses in Münster have to follow specific routes, instructions, and driving regulations in the city. This reflects departing at a particular time from predetermined routes and stopping at specific points at a predefined time. With such structural differences in datasets, we expect changes in the mobility and density of the network nodes caused by the structure (city) and nature of the nodes (bus/taxi). We will describe the features and characteristics of each data set in the following subsections.
3.1.1. San Francisco Taxis
The first scenario is taxi mobility in San Francisco, USA [
36]. This dataset contains GPS coordinates of 500 taxis during 30 days in the San Francisco Bay Area. The data were collected from Exploratorium—the science, art, and human perception museum, through the cab spotting project. Each taxi was equipped with a GPS receiver that sent the location of each taxi to a server. The time interval for sending data was less than 10 s (i.e., the status update of the taxi location). During the simulation studies, we used the GPS coordinates of 100 to 500 taxis and their timestamps for two days.
3.1.2. Rome Taxis
The second scenario is taxi mobility in Rome, Italy [
37]. This dataset contains the GPS coordinates of 320 taxis during 30 days in Rome. This dataset was collected in February 2014. In the simulation studies, we used the GPS coordinate of 50 to 198 taxis and their timestamps for two days (1 February 2014 and 2 February 2014). We used the data of only 198 taxis because only 198 taxis were active within these two days.
3.1.3. Muenster Buses
To consider a scenario for public transportation, we created a novel dataset containing the route of buses following the schedule of public transportation in the city of Münster. We collected and converted data from Münster public utilities, live data website
http://api.busradar.conterra.de/demo/. We collected the data on 4 July 2021 and 5 July 2021. There were 149 buses operating, but not all were active simultaneously. For example, only a limited number of buses were active at night.
3.2. Routing Algorithms
The most prevalent routing algorithms in OppNets are flooding-based, prediction-based, and history-based algorithms. Therefore, to measure and compare the performance of the networks under various conditions, we have used three routing algorithms of Epidemic, Prophet, and PPHB++ which are flooding, prediction, and history-based, respectively. In addition, PPHB++ is flexible in changing the number of message copies in the network. The performance is addressed in terms of Message Delivery Probability (MDP), Dropped Message Probability (DMP), and Network Overhead (NetO). In the following, we explain these algorithms briefly.
Epidemic algorithm: is the most straightforward algorithm in which messages are broadcast to all available neighbors [
18]. This process is repeated until the message reaches the destination or expires (end of its Time To Live (TTL)). The network suffers a high overhead in this algorithm, and there is no optimal routing algorithm.
Prophet algorithm: is the most well known prediction-based algorithm [
38]. The contact history of nodes is used to calculate MDP. Then, nodes with higher MDP carry the messages. When nodes are within the communication range of each other, they update their predictability list. Furthermore, nodes that are often in the communication range of each other will receive higher MDP.
PPHB++ algorithm: is based on Privacy-Preserving History-Based routing in the opportunistic networks (PPHB+) [
39]. We have upgraded this algorithm to PPHB++ by restricting the Number of Message Copies (NumMC). In Prophet and Epidemic algorithms, when a node wants to send a message to a neighbor, it will send a message copy to the neighbor, and a copy remains in its buffer. While this is not the case in the PPHB++ algorithm, the nodes do not keep a copy for themselves.
Each node produces a polynomial in this algorithm, and the root of the polynomial is considered the node’s nickname. When a node constantly detects a neighbor in its communication range, it multiplies its polynomial to the neighbor’s polynomial and updates and delivers its new polynomial. When a node decides on carrying a message, it checks whether the message’s receiver nickname is the root of its polynomial. Suppose the message’s receiver nickname is the root of a node polynomial. In that case, it means that this node will most likely meet the receiver of the message, so it is a suitable candidate for carrying a message, and it can bring the message nearer to the destination.
3.3. Simulation Environment
We used the Opportunistic Network Environment (ONE) [
40] to simulate and evaluate scenarios. Additionally, we used Matlab to calculate the outputs and depict the graphs and charts.
We imported the datasets into ONE. Each scenario continuance was 48 h, and the updating interval was 100 ms. Node mobility is according to the recorded GPS coordinate data in the datasets. The First-In, First-Out (FIFO) method is used for queuing models in buffers. The following parameters were configured and remained the same in all scenarios and simulations:
Message size: 500 k to 1 M;
Message Time To Live (TTL): 5 h;
Transmission interface: Bluetooth is the transmission interface in all simulations;
Transmission range: The maximum distance of forwarding a message from a node to a neighbor is 23 m. This range is based on experiments performed in [
41].
We evaluated the performance of networks in the different scenarios, using the algorithms in terms of MDP, DMP, and NetO. We explicitly define these parameters in the ONE simulator as follows:
MDP: specifies the probability of delivering messages to the destination; Where:
DMP: specifies the probability of deleting messages in the nodes’ buffer due to the buffer saturation or TTL messages; Where:
Started messages are the number of message copies produced in the network. Nodes for forwarding a message to a neighbor in usual routing algorithms in ONE produce a copy of the message, forward it to the neighbor and retain a copy for themselves. Therefore, a considerable number of messages are started in the network.
NetO: is the ratio of passed relayed nodes subtracted by delivered messages to delivered messages; Where:
3.4. Optimized Parameters
In order to investigate the network performance, we performed a two-phase study: (i) We considered the San Francisco dataset due to the nodes’ mobility and PPHB++ algorithm due to higher flexibility. We conducted the simulations to investigate the effect of different configurations of parameters on the network’s performance by calculating the optimized parameters for this particular dataset and algorithm. (ii) During the second phase, we used the optimized parameters obtained from the first phase to calculate the network performance under the other datasets and algorithms discussed earlier. We have identified the five most influential parameters on network performance: The Number of Message Copies (NumMC), Number of Nodes (NumN), Buffer Size (BuffS), Messages Interval (MI), and Node Mobility (NM). The first four parameters are configurable, while the fifth one is correlated with the structure of the dataset, collected data, and network topology. We configured these five parameters to observe their impact on the network performance (
Table 1). Due to simulation restrictions, we considered four NumMC (1, 5, 10, and 50), three NumN (100, 250, and 500), three BuffS (5, 10, and 15), and three MI intervals with appropriate configurations (see
Table 1). The rest of the states of these parameters were restricted to 50, 500, 15, and 25 to 35 for NumMC, NumN, BuffS, and MI, respectively. We used Machine Learning (ML) techniques, including decision tree, multiple linear, polynomial, random forest, and support vector regression (Reg), to predict the optimal outputs (
Table 2). The Radial Basis Function (RBF) was used for the kernel of Support vector regression. We predict the optimized parameters for the extended versions of the configurations and network using ML. Furthermore, to mimic the real-world application and consider the restrictions, we have assumed that nodes in the network have limited resources, and the buffer size is 5 Mb.
While changing a parameter according to
Table 1, the rest of the parameters remain constant and set as NumMC: 1, NumN: 100, BuffS: 5, MI: 25 to 30, Map: San Francisco, routing algorithm: PPHB++.
We evaluated the network’s performance using the regression score based on the coefficient of determination (). We only considered those with a score of above for no less than three influencing terms of the performance. We used two different algorithms to predict the optimized parameters for each regression algorithm.
Algorithm 1: In each regression model, (i) the first row is the result (
), (ii) in
ith row of regression the following condition is checked: (iii) if the MDP
i is greater than MDP in
and DMP
i is less than the DMP in
, and the NetO
i is less than the NetO in
, (iv) the
changes to
i (
).
| Algorithm 1 Regression model |
- Require:
- Ensure:
Alg1 result - 1:
Initialization: - 2:
Mechanism Initialization - 3:
Read the value R from row i - 4:
- 5:
for i = 2 to the end of the array do - 6:
if and and then - 7:
- 8:
end if - 9:
end for - 10:
Alg1=NumMC(),NumN(),BuffS(),MI() - 11:
return
|
In Algorithm 2, with the inverse MDP, as well as with DMP and NetO as the influencing terms of network performance, the minimum X should be delivered in order to obtain the maximum performance. In this equation, we considered
, and
. Depending on the application and the aim of the study, the user can change the coefficients.
| Algorithm 2 Regression model |
- Input:
- Output:
Alg2 result - 1:
Initialization: - 2:
Mechanism Initialization - 3:
Read X from row i of the performance terms - 4:
▹ a and b are the coefficient - 5:
- 6:
=IndexMin (X) - 7:
Alg2=NumMC(),N(),B(),MI() - 8:
return
|
Additionally, we considered the network with and without malicious nodes (
Section 4.3.2). In order to compare the networks, we varied the NumN as: San Francisco: 100 to 500 nodes, Rome: 50 to 200 nodes, Münster: 50 to 150 nodes.
We set all networks based on the obtained optimized simulation results.
5. Discussion
5.1. Restrictions of the Study
We investigated the effect of NumMC, BuffS, MI, NumN, and NM as the influencing parameters on OppNets performance. We also evaluated the effect of the presence of malicious nodes on the network performance. Despite performing an extensive simulation study using three datasets, our work is limited in the number of datasets (restricted by node density and mobility), the number of nodes (maximum 500 nodes), and the amount of collected data (two days).
5.2. Influencing Parameters on the Network Performance
Our study shows that reducing NumMC has little effect on receiving or deleting messages, but it significantly reduces NetO. Compared to other algorithms, this reduction in the number of copies of messages has a notable impact on reducing DMP, NetO and increasing the MDP. Increasing node’s BuffS has little effect on MDP, DMP, and NetO.
Increasing the message generation interval, which produces fewer messages, can significantly reduce DMP, and increase MDP, but it has little effect on NetO.
Increasing the mobility of the nodes causes a notable increase in MDP and a significant reduction in DMP.
Increasing the network’s NumN causes more nodes’ interactions and enhances the MDP and DMP. It can also raise the NetO.
Therefore, as an output and application of our study in real world cases, we would suggest, for example, that in a VANET approach on a highway which is considered as a network with a low number of nodes and mobility where network overhead is not the case, and forwarding emergency and traffic messages has the priority, we should increase the message generation interval only to produce prioritized massages and increase the number of messages copy and buffer size in order to achieve the best network performance.
As the other scenario in real-world application, in which the network has a large number of nodes, low mobility, and a significant message generation, we can decrease the number of messages copied and prioritize the messages to increase message generation interval. Consequently, we can decrease the network overhead and improve message delivery in the network. An example of such a network might be an event such as a carnival in a city.
5.3. Machine Learning Techniques and Real Work Applications
By examining these parameters in various simulations and regression in ML (decision tree, multiple linear, polynomial, random forest, and support vector regressions), we found the optimized parameters for different networks. Utilizing three networks with different features represented by three datasets in the real world shows that the optimal results are obtained when NumMC is one, the NumN is 100, the BuffS is 10, and MI is 15 to 25 s. Since the buffer is one of the limited resources in each node and is considered a severe restriction in real-world applications, we also calculated the best result when the BuffS is 5. The optimized parameters under this conditions are obtained as BuffS = 5, the NumMC = 1, the number of nodes in the network = 100, and the MI = 55 to 65 s. We used these parameters to set the network. However, to improve the accuracy and efficiency of using the lower volume of memory, in particular, for the big data including a large number of inputs (i.e., if the number of datasets is significantly increased), where the training and testing speed and time, computational resources, classification, and prediction are crucial, the neural-like structure of non-iterative models such as the successive geometric transformations model (SGTM) can be used. These methods usually provide a lower error value for the regression task. Ito decomposition (Kolmogorov–Gabor polynomial) can be used in combination with SGTM to extend the inputs of the SGTM [
42].
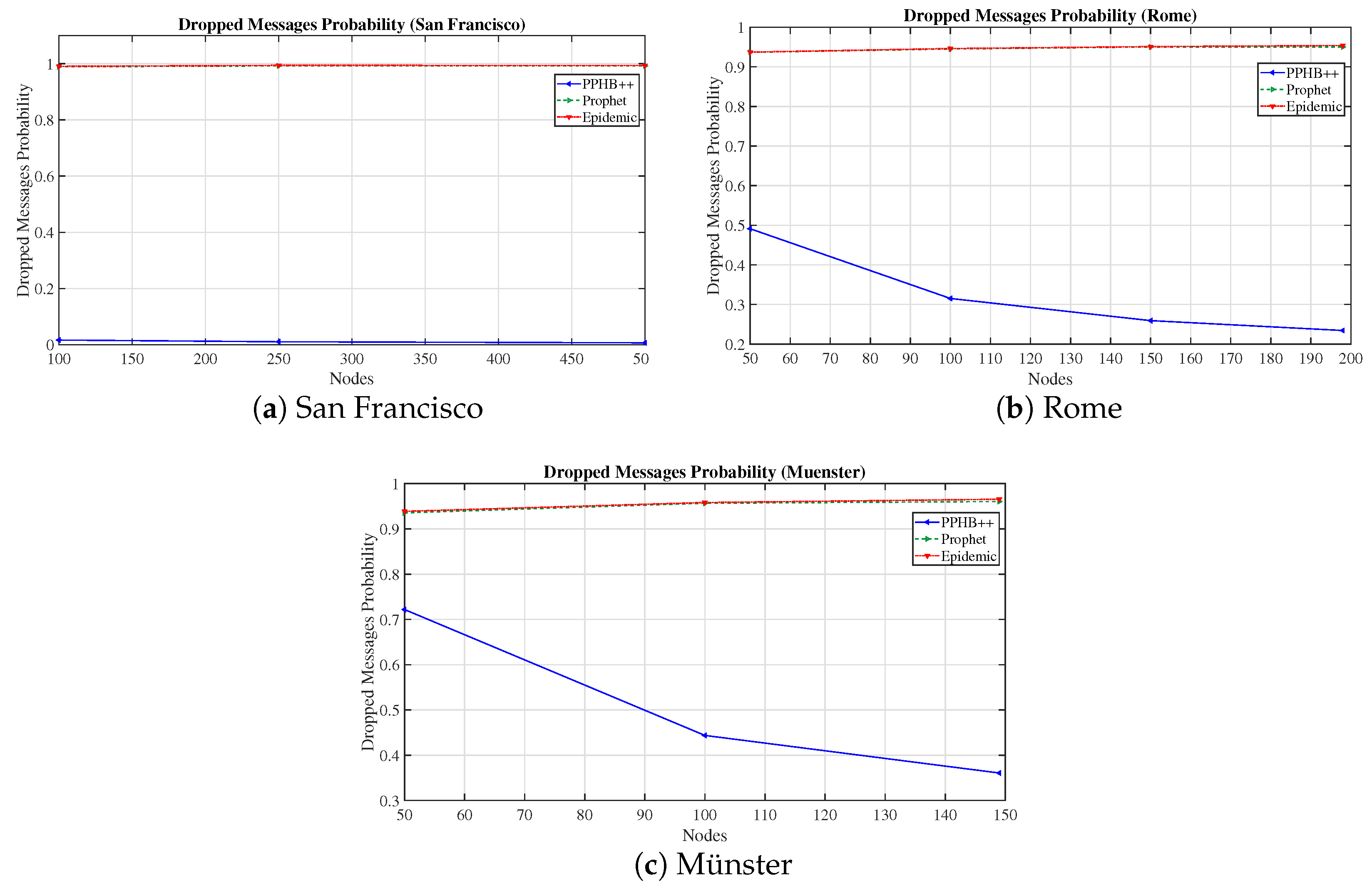
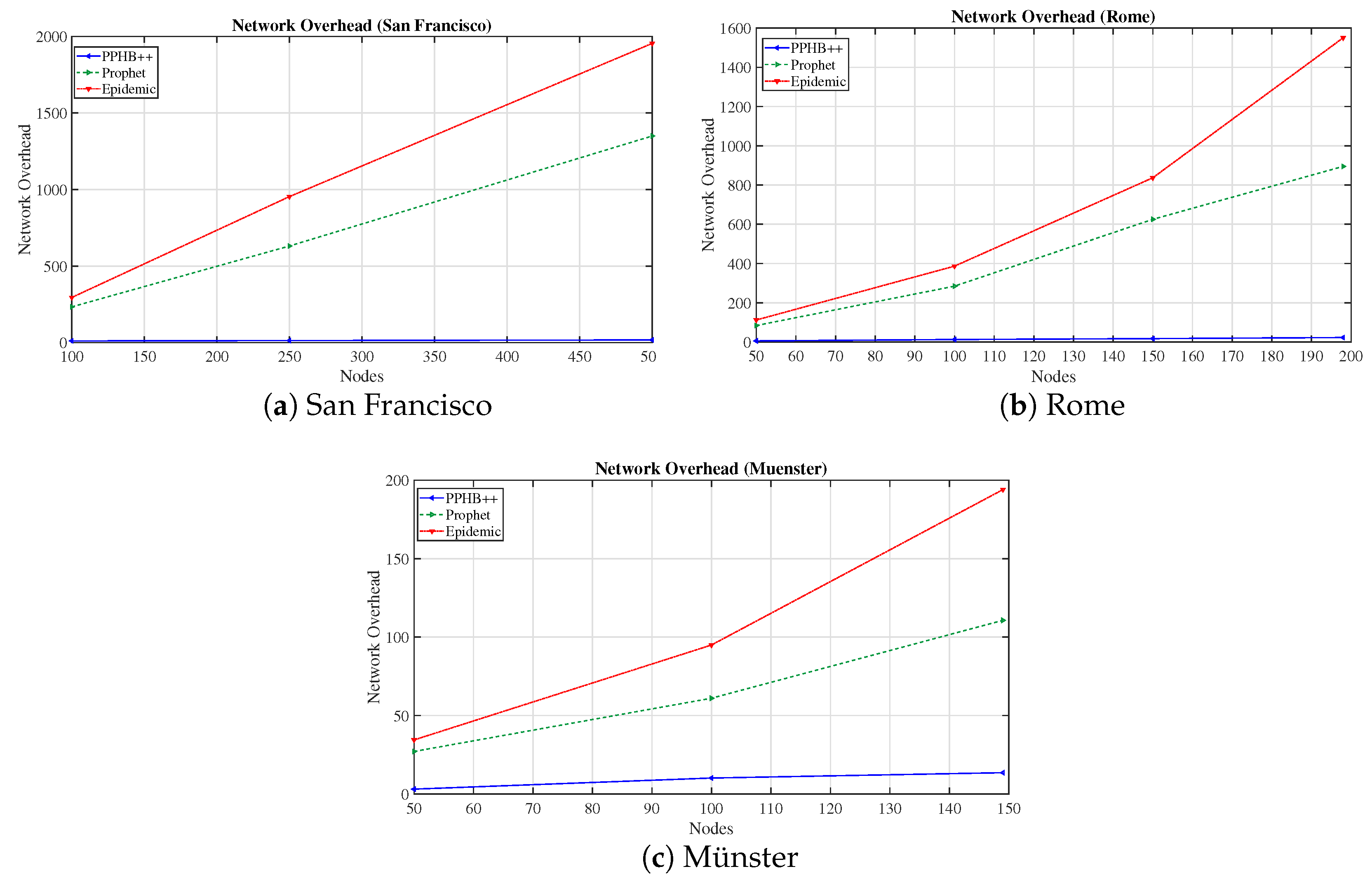
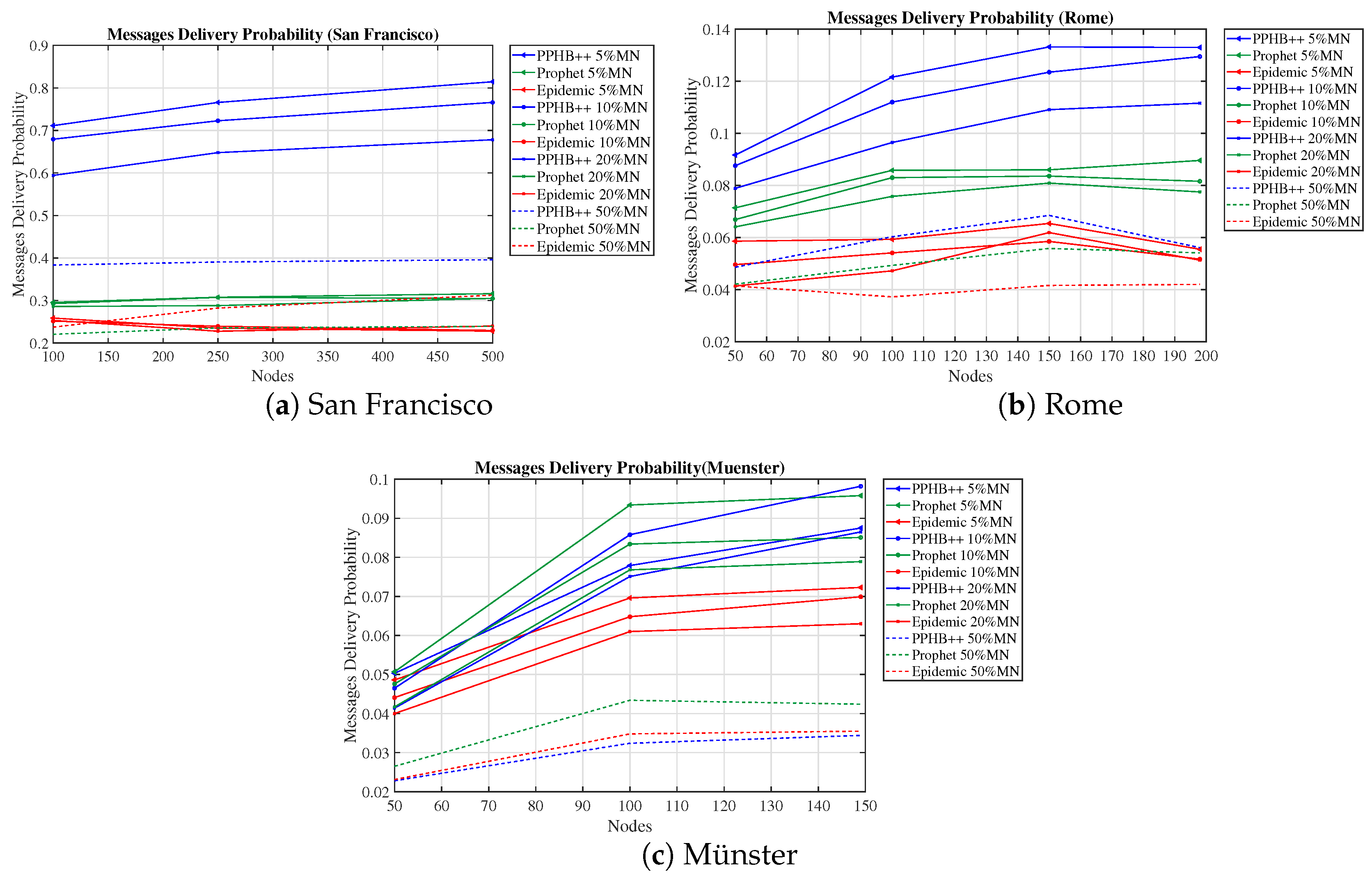
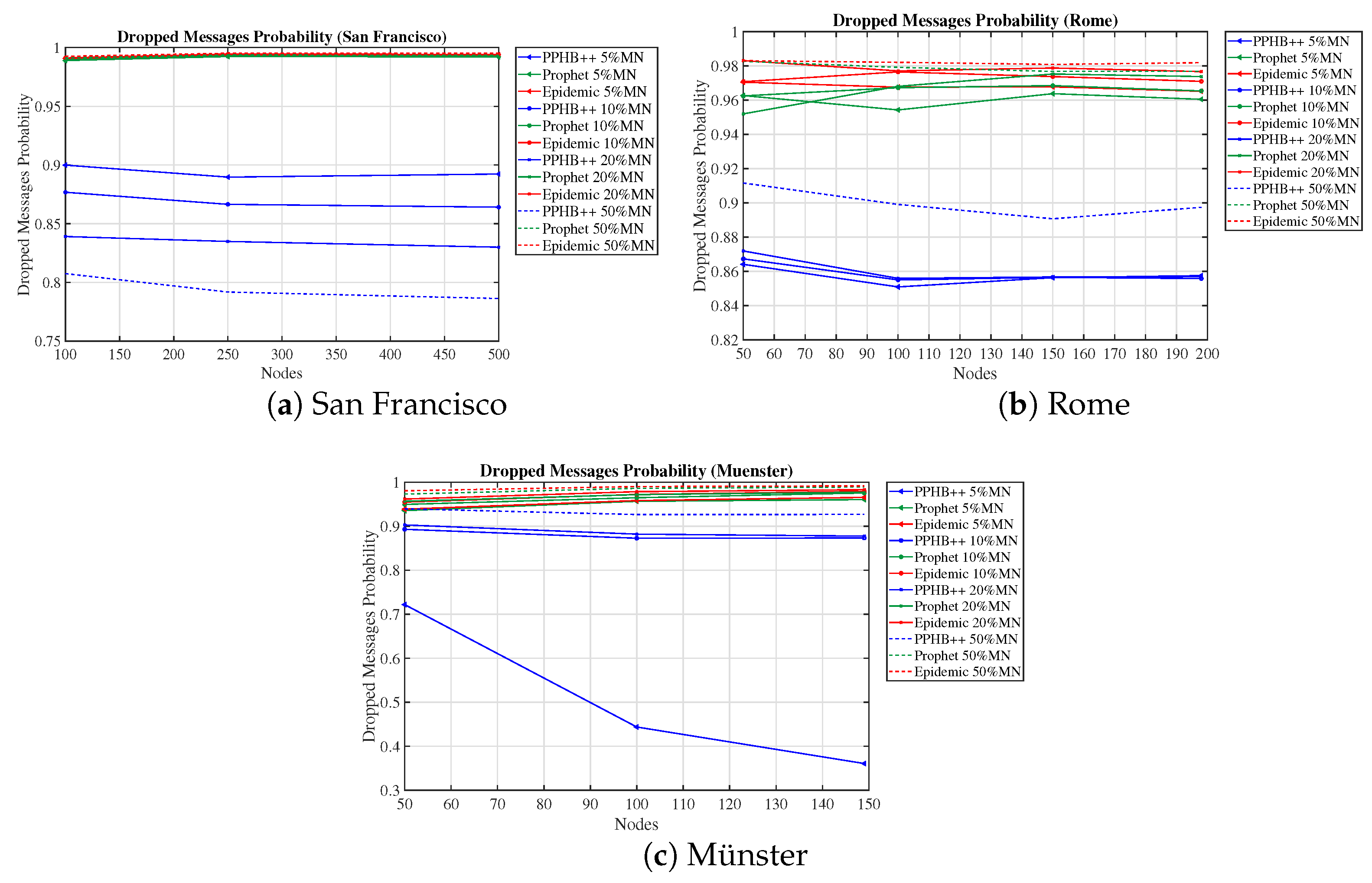
We evaluated the network performance in terms of MDP, DMP, NumN, NM, and NetO on three concrete datasets with PPHB++, Prophet, and Epidemic routing algorithms. The results show that PPHB++ has better MDP in San Francisco and Rome because of their free movement, and Prophet delivers a better MDP in the Münster dataset. PPHB++ is the best performer in terms of DMP and NetO, followed by the Prophet and Epidemic algorithms.
We also estimated the impact of malicious nodes on network performance. We studied three algorithms with the presence of different numbers of malicious nodes. Algorithm PPHB++ has the best performance in MDP, DMP, and NetO with malicious network nodes without restricting the nodes’ movement. When there are constraints on node paths, the Prophet algorithm only works better in MDP.
In the San Francisco scenarios, where there are more nodes in the network, they acted slightly differently in the presence of malicious nodes.
According to the results, each network parameter can be set efficiently to have the best performance according to the network’s conditions and needs and consider what percentage of network nodes may be malicious. Our comprehensive study shows that network performance influences parameters configured based on the applications and restrictions. Depending on the importance of the terms of performance in each application, the influencing parameters might be weighted to deliver the output. Using ML techniques for considering network behavior under various features, influencing parameters, and datasets representing a real-world application allowed us to extend the study by predicting different scenarios in a network significantly.
5.4. Comparison of ONE Default Setting with Optimized Parameters
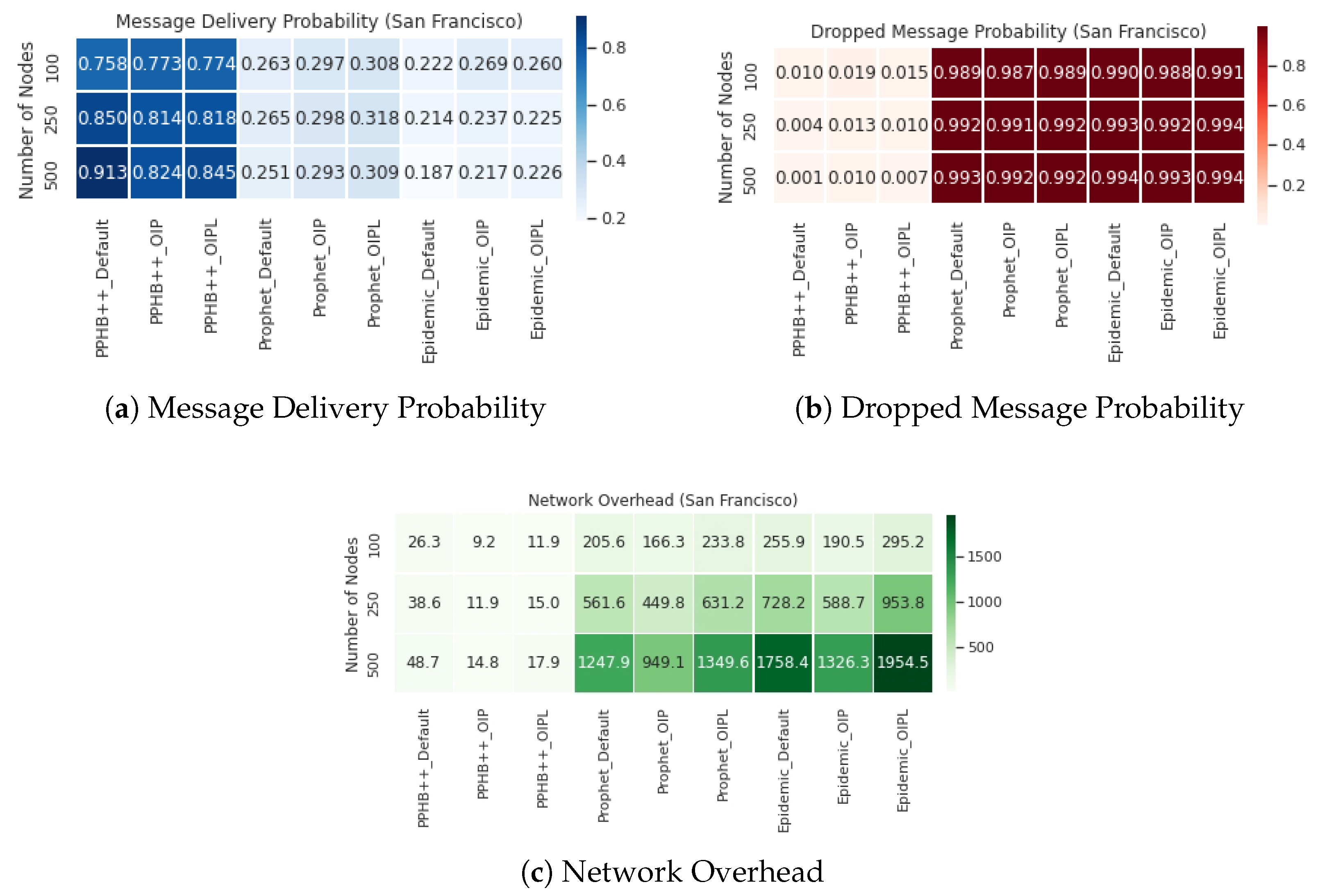
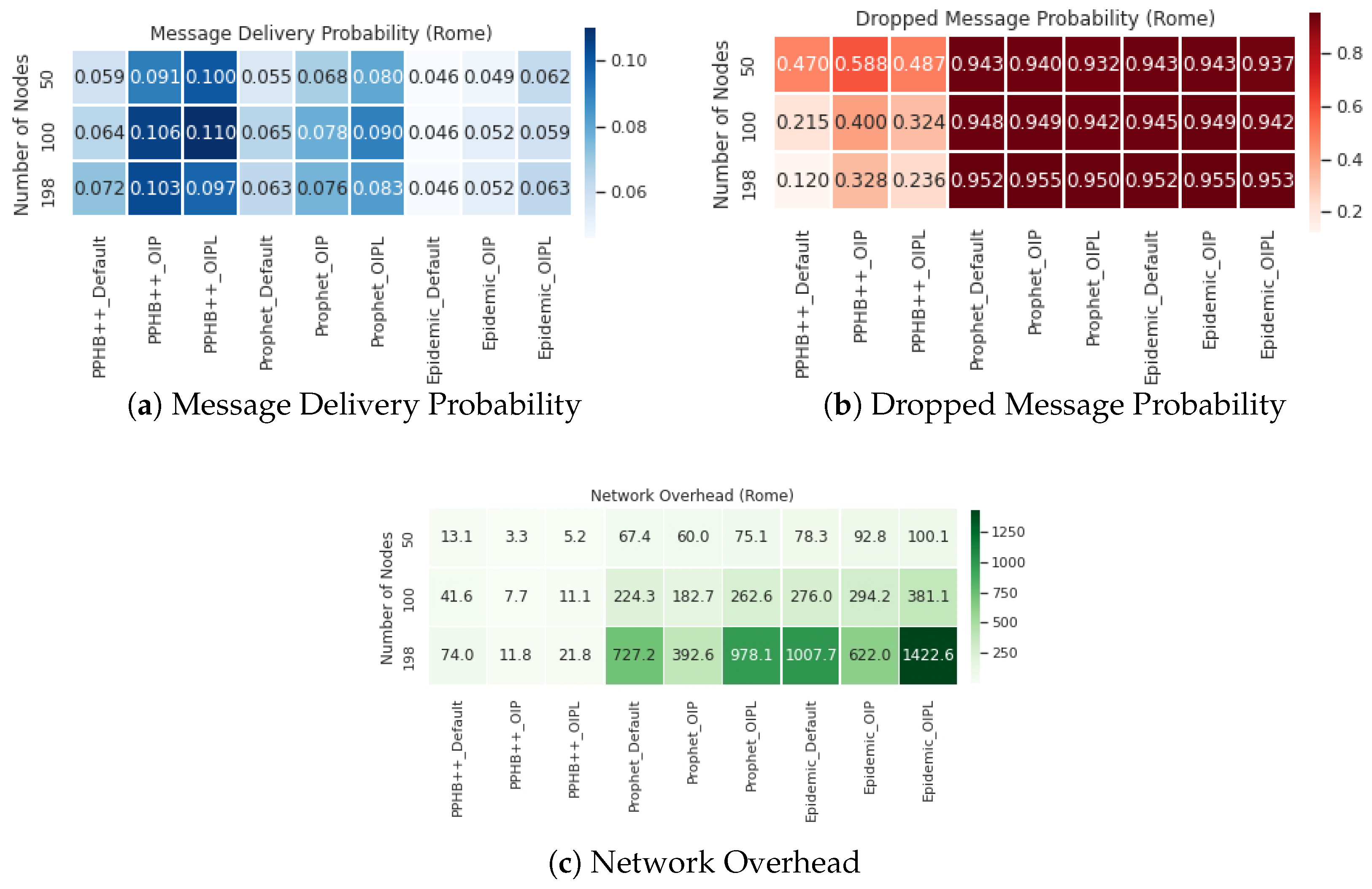
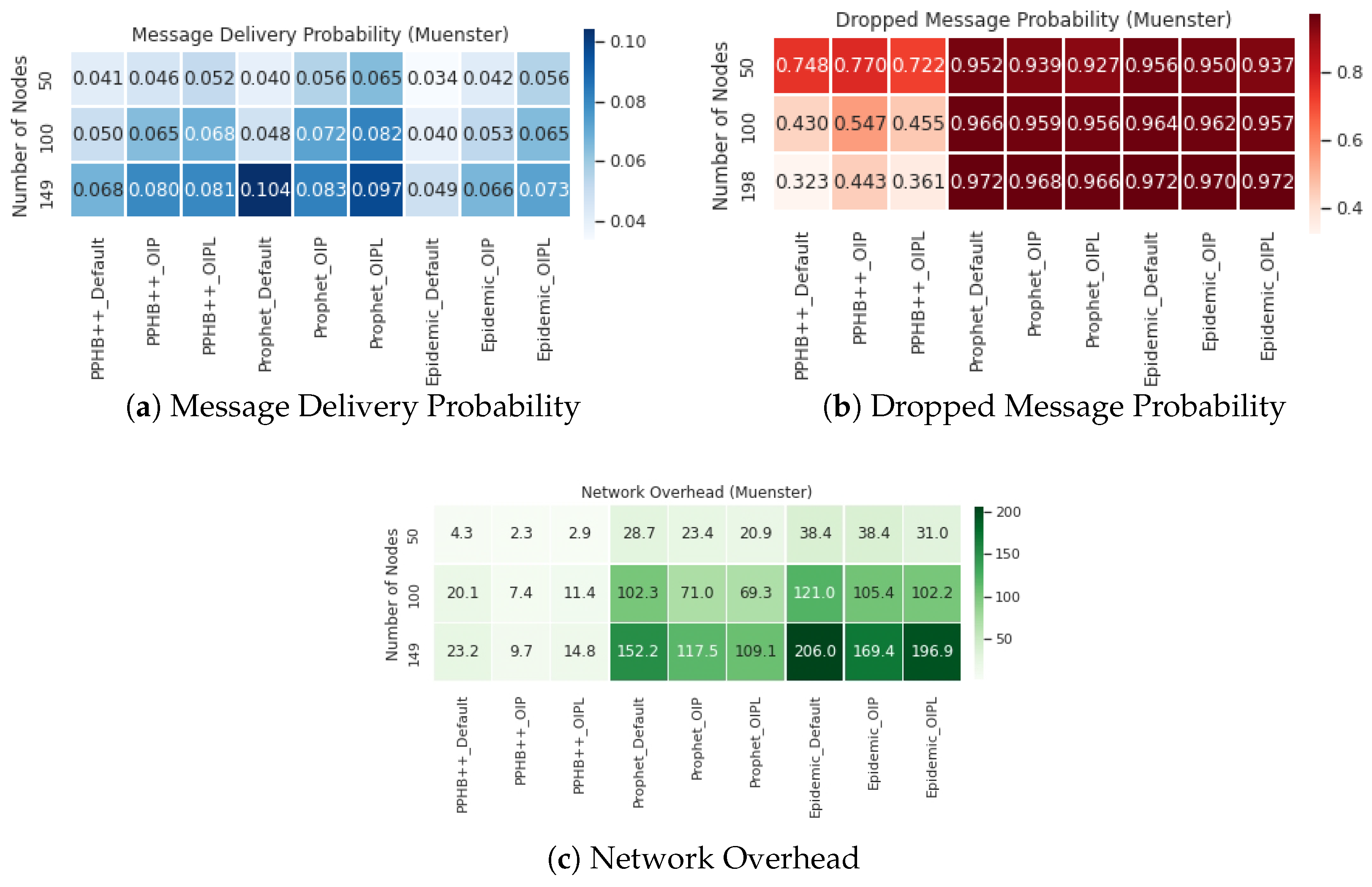
Figure 9,
Figure 10 and
Figure 11 present the results of ONE default setting, Optimized Influence Parameter (OIP), and Optimized Influencing Parameters with Limited resources (OIPL) under the specified conditions stated earlier. More details regarding these results are provided in
Appendix A. Furthermore, we have compared OIP and OIPL results with the default setting to calculate the network performance’s enhancement (if any). We performed this experiment and compared all influencing parameters for the San Francisco, Rome, and Münster datasets. Thus, the results are represented as Improved OIP Improved OIPL for MDP, DMP, NetO.
For the Prophet algorithm, MDP increased by an average of in San Francisco and in the Rome and Münster datasets. For the Epidemic algorithm, increasing the number of nodes in all conditions reduces the MDP at different rates; however, in general, MDP increased by an average of in San Francisco and in the Rome and Münster dataset. OIP and OIPL are significantly positive in average improvement in all datasets under the Epidemic algorithm. Although OIP for 250 nodes in San Francisco delivers the lowest MDP, no meaningful pattern is observed.
The impact of DMP for OIP and OIPL is negligible in the Prophet and Epidemic algorithms in all datasets. This effect under PPHB++ has quite the inverse negative impact on San Francisco and Rome, and it is, on average, an increase of in the Münster dataset.
The results indicate an improvement of NetO in all datasets and algorithms; however, the improvement in the PPHB++ algorithm is greater (for example, in the Rome dataset). Under PPHB++, NetO decreased by an average of for OIP, but it also experienced an average of for OIPL in San Francisco. It presents an average of decrease in the San Francisco dataset. For the Prophet algorithm, NetO decreased by an average of for OIP, but increased by an average of for OIPL in Rome. NetO decreased by an average of for OIP, but increased by an average of for OIPL in Rome for the Epidemic algorithm. NetO is decreased by an average of for Prophet and Epidemic algorithms in the Münster dataset. Analyzing the results shows that the presented solution influences MDP and NetO significantly in all three datasets and algorithms (there are some exceptions) and remains neutral for DMP.
6. Conclusions
In real-world applications, wearable devices, taxis, and buses might be the nodes of opportunistic networks to save-carry-forward a message from the source to the destination, particularly when facing a lack of infrastructure or sending an emergency alert from an injured involved in an accident to a hospital or rescue team. Albeit with various weights, NumMC, BuffS, MI, NumN, and NM influence the network’s performance. To explore the real-world applications’ restrictions and impact of resources on the network performance, we deployed three datasets that differed in features and structures to represent the characteristics of such networks. Extensive simulations and analyses are required to show the impact of each factor on the network’s performance. We found that the nodes and the respective features are the most significant influences on the network performance represented by MDP, DMP, and NetO. This means that NumN, NM, and NumMC have greater weights than BuffS and MI. In the real world, this is mapped to the type of node (taxi or bus), its speed (NM), and the route it follows. All these factors are impacted by the route and regulation features determined by the dataset represented by the algorithm used in the simulation.
In a vast network, this requires specific configuration and tests. Thus, we used regressions techniques of machine learning to predict the optimized parameters for both networks with(out) resource restrictions.
We showed that obtaining the optimized parameters in each scenario rather than general configuration improves the network performance under different routine algorithms (i.e., PPHB++, Prophet, and Epidemic). Applying the optimized parameters to the network, MDP improved by an average of in San Francisco and in Rome and Münster (Prophet algorithm). In the same manner, MDP was enhanced by an average of in San Francisco and in Rome and Münster (Epidemic algorithm). In all datasets, the impact of DMP is negligible for the Prophet and Epidemic algorithms. Still, it has an inverse negative impact on PPHB++ in San Francisco and Rome and increases by in the Münster dataset. NetO was improved across all datasets and algorithms, although the PPHB++ algorithm gained the most.
A dense network may improve the probability of delivering a message, but increase the NetO. We concluded that public transportation could be used in OppNets depending on the purpose of the application. However, care must be taken to choose the appropriate means (wearables/taxis/bus) depending on the purpose and structure of the environment (city). Our study showed that buses with lower NetO are appropriate in OppNets if the message is time-tolerant.
The results indicated that using taxis in modern texture cities with a higher network overhead (e.g., several taxis in the same area and direction), greater speed (NM), and fewer restrictions on driving are suitable.
The datasets’ features restrict our work in terms of data acquisition (two days) and node characterizations (limited by node density and mobility and 500 nodes). For future work, we plan to consider pedestrians included in our dataset. Therefore, we plan to implement an OppNet on several wearable devices deployed in real situations with true-to-life scenarios. In addition, we would like to compare these results with the simulation outcomes and improve the ML algorithms in terms of performance, speed, and time to train.