In-Season Predictions Using Chlorophyll a Fluorescence for Selecting Agronomic Traits in Maize
Abstract
1. Introduction
2. Results
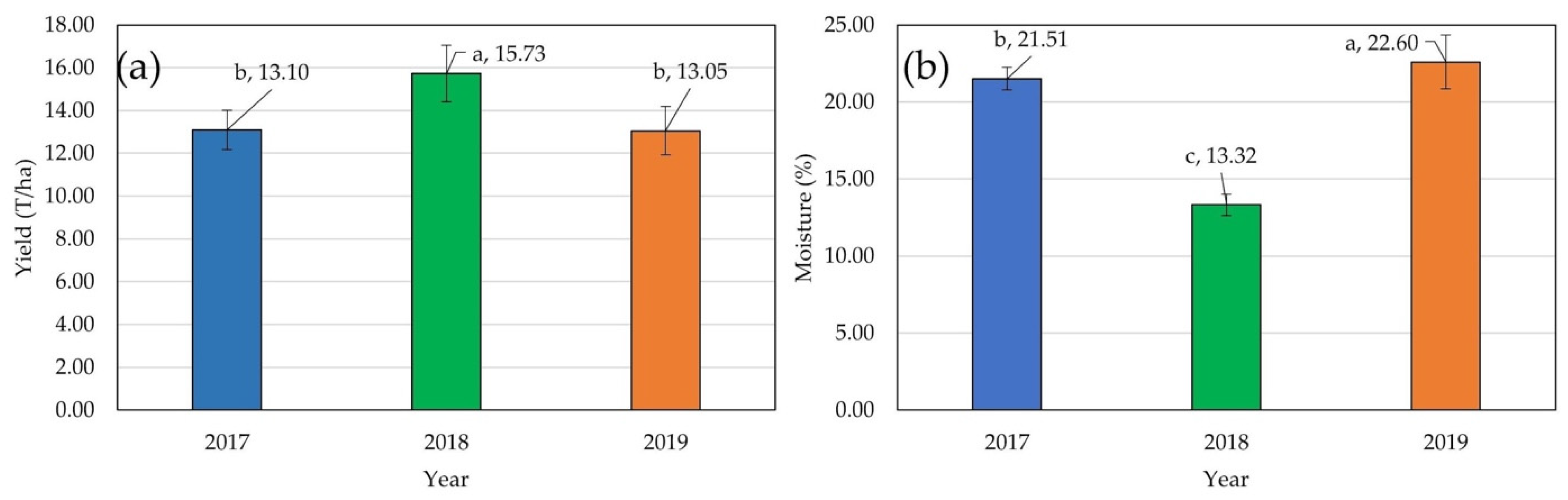
2.1. Mean Values and ANOVA for GY and GM, Fv/Fm, and PSIABS
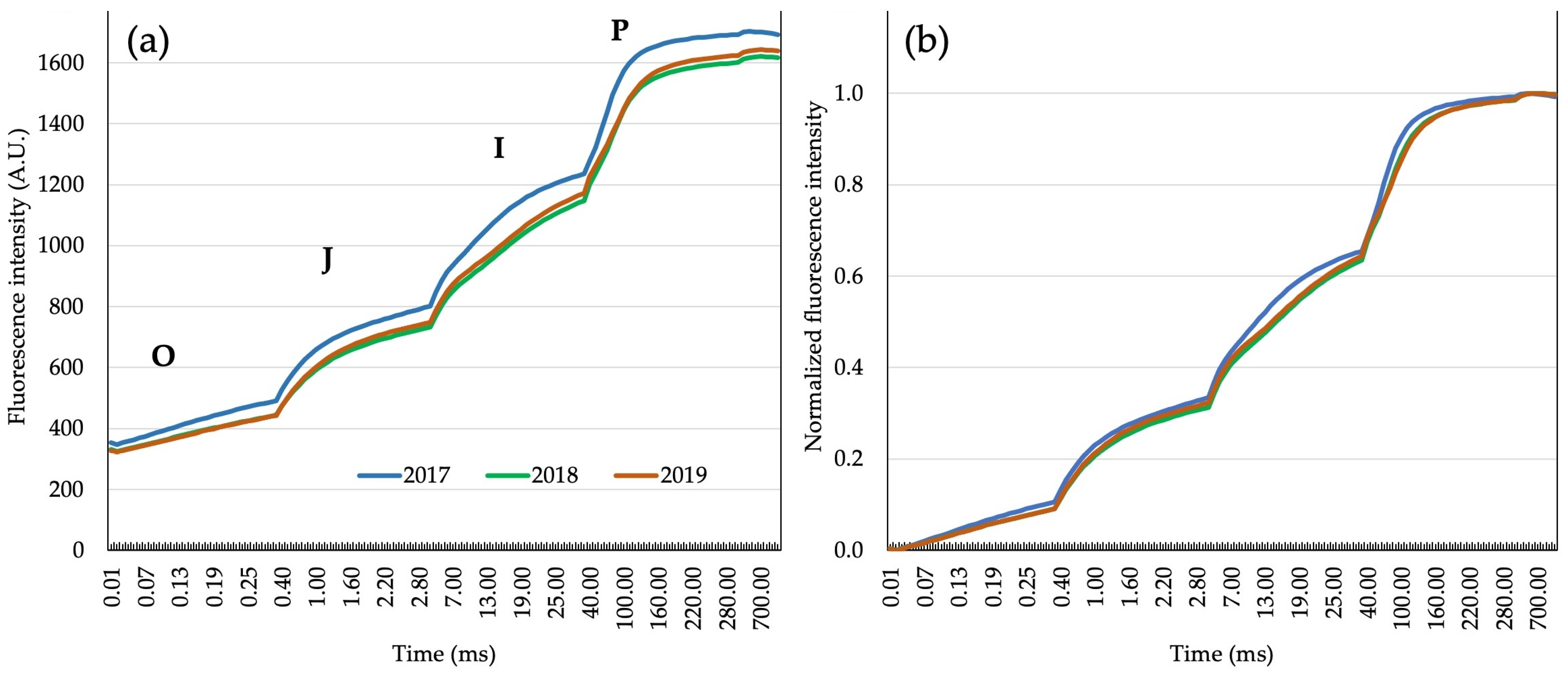
2.2. Plateaus of Fluorescence (OJIP)
2.3. Variance Components Estimated with Mixed Model and Trait Correlations
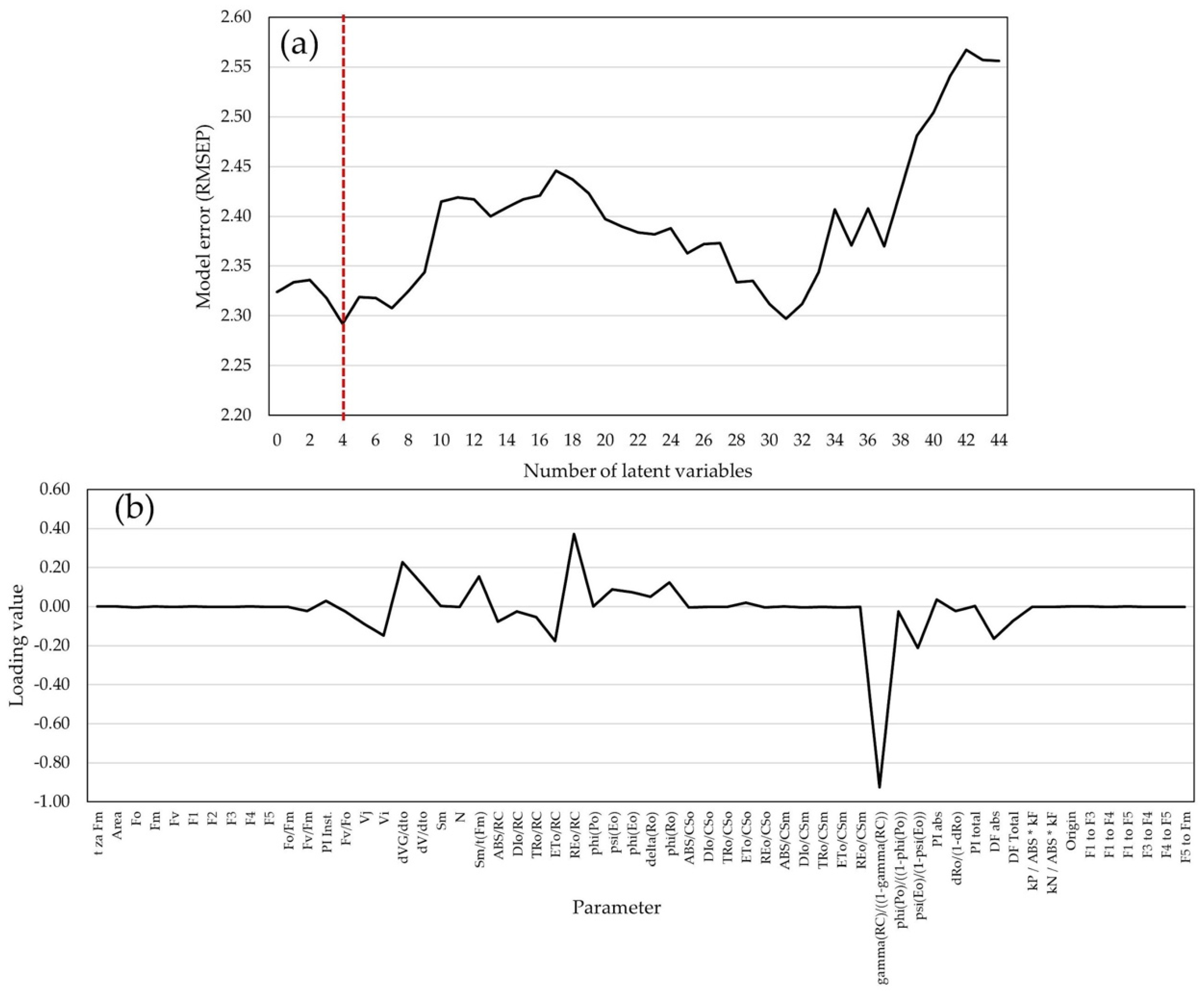
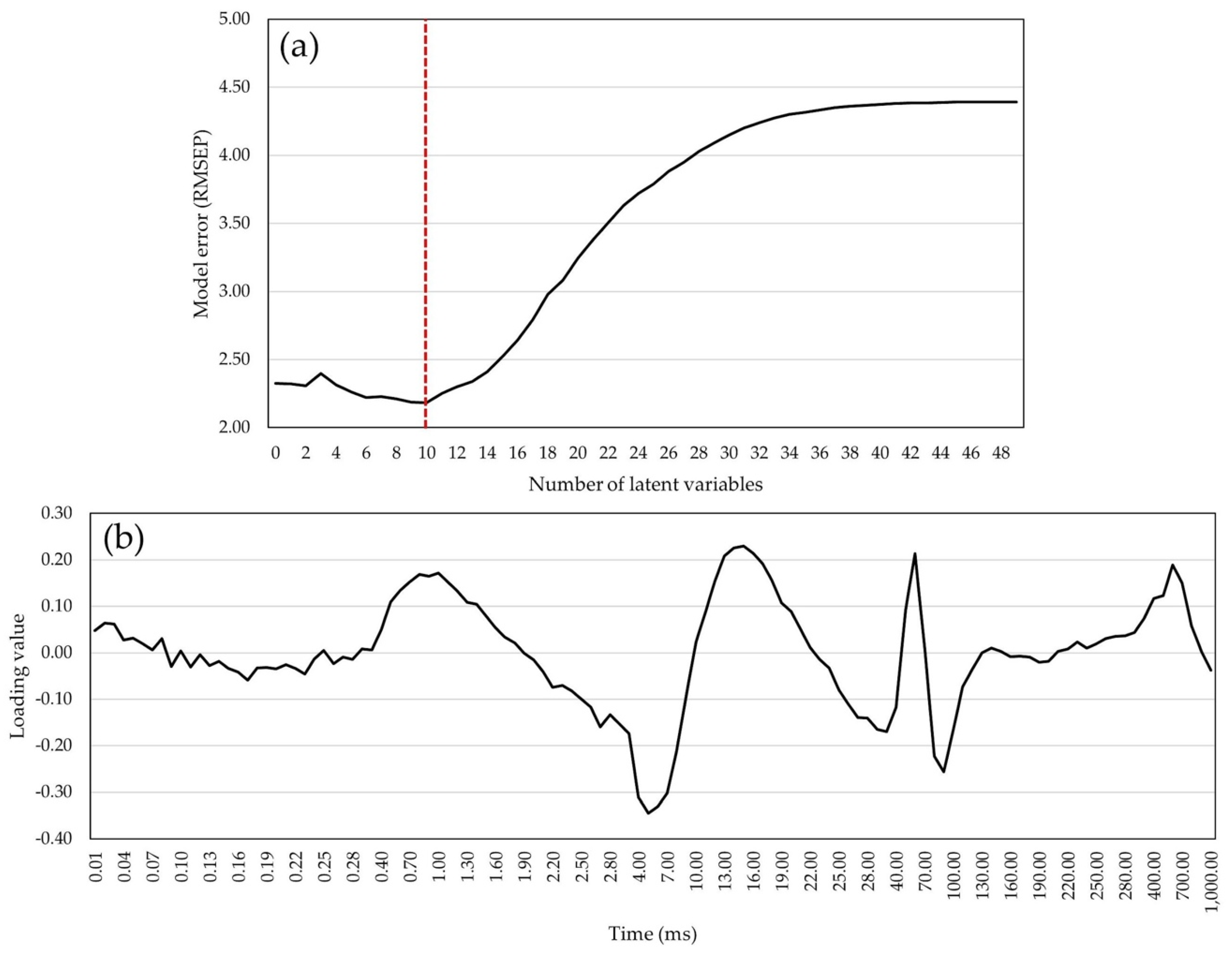
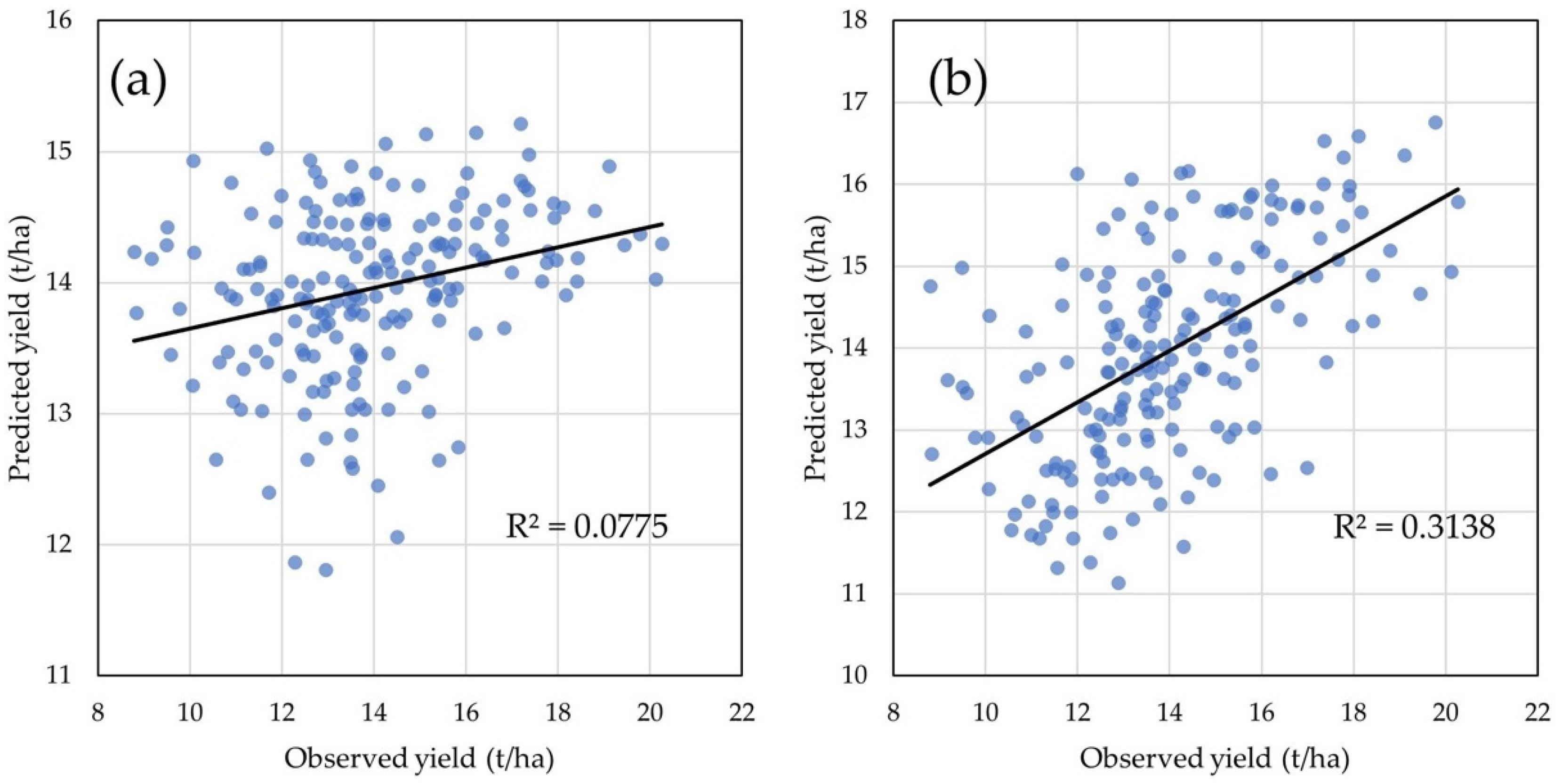
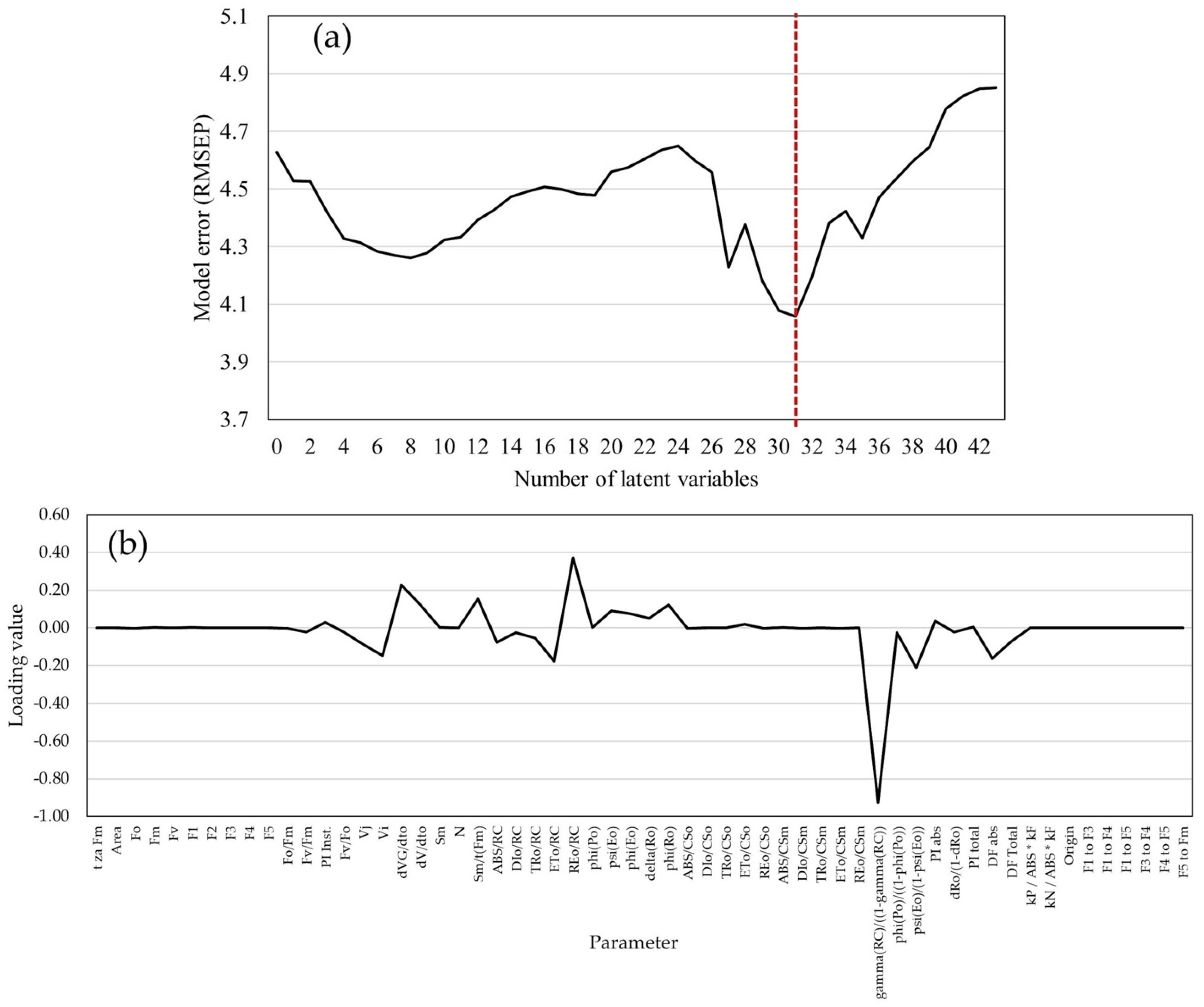
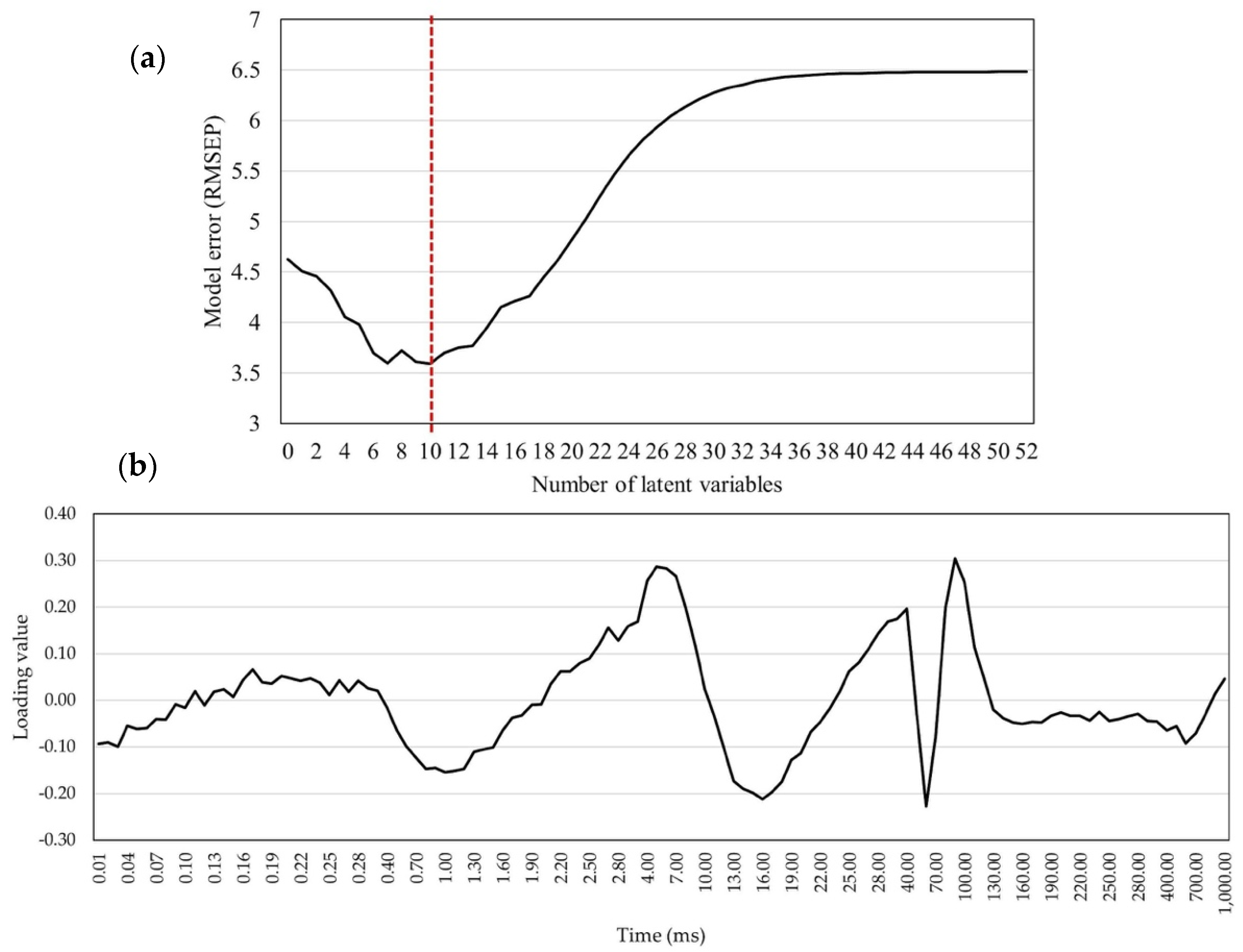
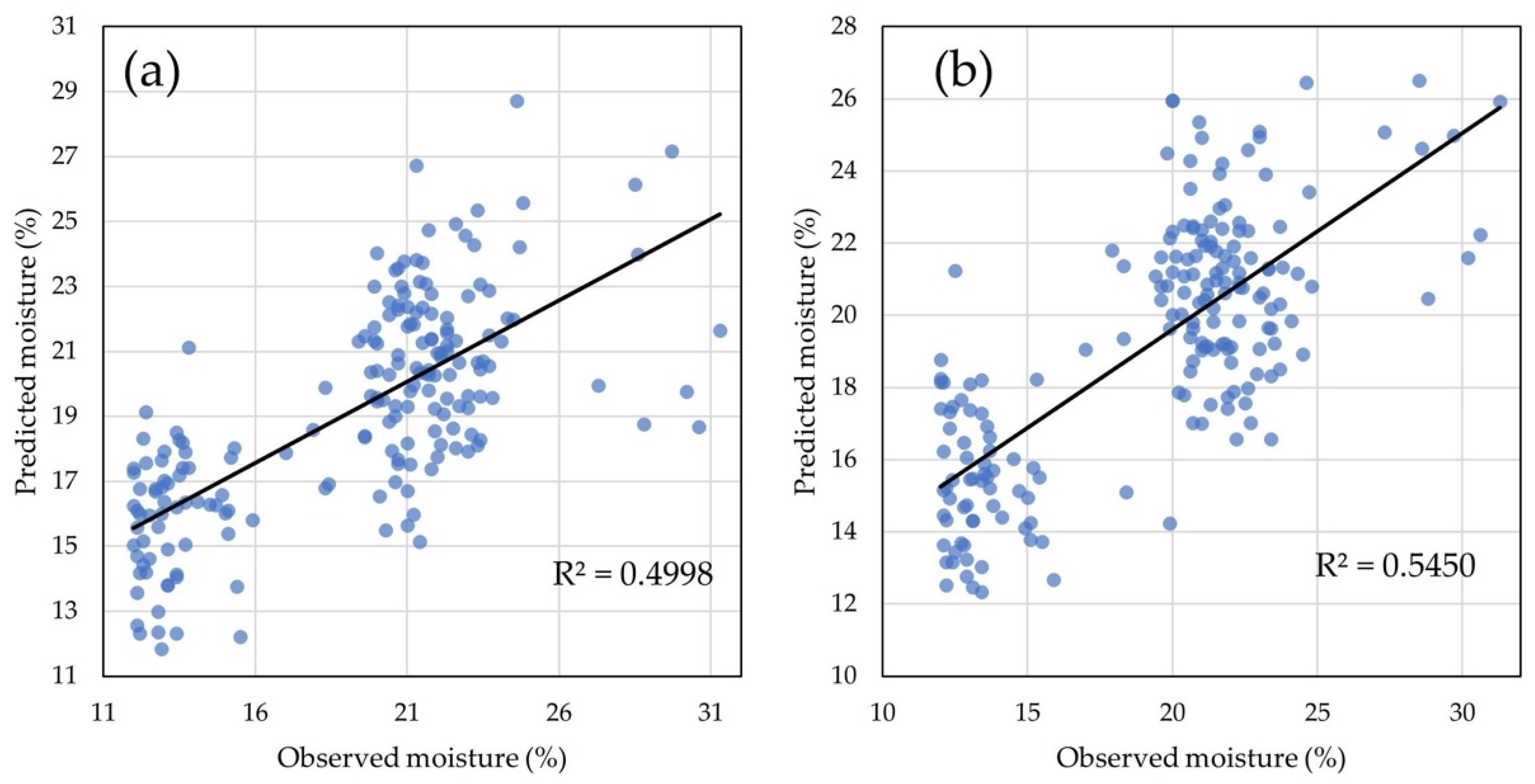
2.4. Statistical Models for GY and GM Predictions
2.5. Variance Components of Predicted Traits
3. Discussion
3.1. Agronomic Traits
3.2. Photosynthetic Efficiency Traits
3.3. GY Prediction Model Efficiency Analysis
3.4. GM Prediction Model Efficiency Analysis
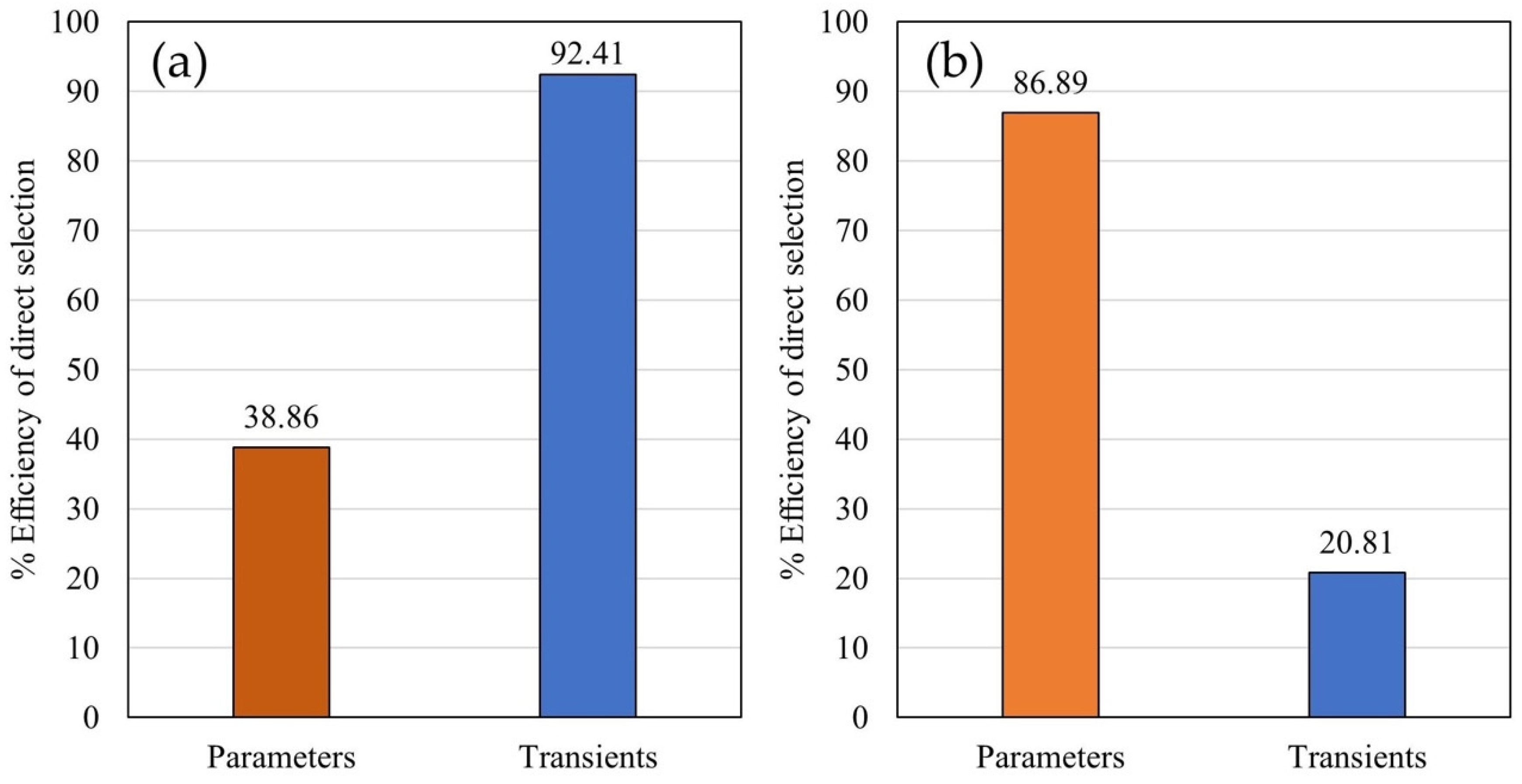
3.5. Indirect Selection Efficiency Analysis
3.6. Limitations of This Study
4. Materials and Methods
4.1. Plant Material and Experimental Design
4.2. Agrotechnical Practices and Grain Yield
4.3. Chlorophyll a Measurements
4.4. Predictive Statistic Models
4.5. Data Analysis and Model Development
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Troyer, A.F. Breeding widely adapted, popular maize hybrids. Euphytica 1996, 92, 163–174. [Google Scholar] [CrossRef]
- Lafitte, R.; Blum, A.; Atlin, G. Using secondary traits to help identify drought tolerant genotypes. In Breeding Rice for Drought-prone Environments; Fischer, K.S., Lafitte, R., Fukai, S., Atlin, G., Hardy, B., Eds.; IRRI: Los Baños, Philippines, 2003; pp. 37–48. [Google Scholar]
- Ziyomo, C.; Bernardo, R. Drought tolerance in maize: Indirect selection through secondary traits versus genomewide selection. Crop Sci. 2013, 53, 1269–1275. [Google Scholar] [CrossRef]
- Fellahi, Z.E.; Hannachi, A.; Bouzerzour, H. Analysis of direct and indirect selection and indices in bread wheat (Triticum aestivum L.) segregating progeny. Int. J. Agron. 2018, 1, 8312857. [Google Scholar]
- Edmeades, G.O.; Bolaños, J.; Chapman, S.C. Value of secondary traits in selecting for drought tolerance in tropical maize. In Developing Drought- and Low N-Tolerant Maize; Edmeades, G.O., Bänziger, M., Mickelson, H.R., Peña-Valdivia, C.B., Eds.; Proceedings of a Symposium; CIMMYT: El Batán, Mexico, 1996. [Google Scholar]
- Bänziger, M.; Edmeades, G.O.; Beck, D.; Bellon, M. Breeding for Drought and Nitrogen Stress Tolerance in Maize: From Theory to Practice; CIMMYT: Mexico City, Mexico, 2000. [Google Scholar]
- Cattivelli, L.; Rizza, F.; Badeck, F.W.; Mazzucotelli, E.; Mastrangelo, A.M.; Francia, E.; Mare, C. Drought tolerance improvement in crop plants: An integrated view from breeding to genomics. Field Crops Res. 2008, 105, 1–14. [Google Scholar] [CrossRef]
- Tembo, L.; Asea, G.; Gibson, P.T.; Okori, P. Indirect selection for resistance to Stenocarpella maydis and Fusarium graminearum and the prospects of selecting for high-yielding and resistant maize hybrids. Plant Breed. 2016, 135, 446–451. [Google Scholar] [CrossRef]
- Gheith, E.M.S.; El-Badry, O.Z.; Lamlom, S.F.; Ali, H.M.; Siddiqui, M.H.; Ghareeb, R.Y.; El-Sheikh, M.H.; Jebril, J.; Abdelsalam, N.R.; Kandil, E.E. Maize (Zea mays L.) productivity and nitrogen use efficiency in response to nitrogen application levels and time. Front. Plant Sci. 2022, 13, 941343. [Google Scholar] [CrossRef]
- Chapman, S.C.; Edmeades, G.O. Selection improves drought tolerance in tropical maize populations: II. Direct and correlated responses among secondary traits. Crop Sci. 1999, 39, 1315–1324. [Google Scholar] [CrossRef]
- Zaidi, P.H.; Maniselvan, P.; Sultana, R.; Yadav, M.; Singh, R.P.; Singh, S.B.; Dass, S.; Srinivasan, G. Importance of secondary traits in improvement of maize (Zea mays L.) for enhancing tolerance to excessive soil moisture stress. Cereal Res. Commun. 2007, 35, 1427–1435. [Google Scholar]
- Messmer, R.; Fracheboud, Y.; Bänziger, M.; Vargas, M.; Stamp, P.; Ribaut, J.M. Drought stress and tropical maize: QTL-by-environment interactions and stability of QTLs across environments for yield components and secondary traits. Theor. Appl. Genet. 2009, 119, 913–930. [Google Scholar] [CrossRef]
- Harrison, M.T.; Tardieu, F.; Dong, Z.; Messina, C.D.; Hammer, G.L. Characterizing drought stress and trait influence on maize yield under current and future conditions. Glob. Change. Biol. 2014, 20, 867–878. [Google Scholar] [CrossRef]
- Ertiro, B.T.; Olsen, M.; Das, B.; Gowda, M.; Labuschagne, M. Efficiency of indirect selection for grain yield in maize (Zea mays L.) under low nitrogen conditions through secondary traits under low nitrogen and grain yield under optimum conditions. Euphytica 2020, 216, 134. [Google Scholar] [CrossRef]
- Lee, E.A.; Tracy, W.F. Modern Maize Breeding. In Handbook of Maize; Bennetzen, J.L., Hake, S., Eds.; Springer: New York, NY, USA, 2009; pp. 141–160. [Google Scholar]
- Jung, C.; Müller, A. Flowering time control and applications in plant breeding. Trends Plant Sci. 2009, 14, 563–573. [Google Scholar] [CrossRef] [PubMed]
- McMillan, I.; Fairfull, R.W.; Quinton, M.; Friars, G.W. The effect of simultaneous selection on the genetic correlation. Theor. Appl. Genet. 1995, 91, 776–779. [Google Scholar] [CrossRef] [PubMed]
- Krause, G.H. Photoinhibition of photosynthesis. An evaluation of damaging and protective mechanisms. Physiol. Plant. 1988, 74, 566–574. [Google Scholar] [CrossRef]
- Guidi, L.; Lo Piccolo, E.; Landi, M. Chlorophyll fluorescence, photoinhibition and abiotic stress: Does it make any difference the fact to be a C3 or C4 species? Front. Plant Sci. 2019, 10, 174. [Google Scholar] [CrossRef]
- Strasser, R.J.; Govindjee. The Fo and the OJIP fluorescence rise in higher plants and algae. In Regulation of Chloroplast Biogenesis; Argyroudi-Akoyunoglou, J.H., Ed.; Plenum Press: New York, NY, USA, 1991. [Google Scholar]
- Schreiber, U.; Schliwa, U.; Bilger, W. Continuous recording of photochemical and non-photochemical chlorophyll fluorescence quenching with a new type of modulation fluorometer. Photosynth. Res. 1986, 10, 51–62. [Google Scholar] [CrossRef]
- Strasser, R.J.; Srivastava, A.; Tsimilli-Michael, M. The fluorescence transient as a tool to characterize and screen photosynthetic samples. In Probing Photosynthesis: Mechanism, Regulation & Adaptation; Yunus, M., Pathre, U., Mohanty, P., Eds.; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Boca Raton, FL, USA, 2000. [Google Scholar]
- Falkowski, P.G.; Wyman, K.; Ley, A.C.; Mauzerall, D. Relationship of steady state photosynthesis to fluorescence in eucaryotic algae. Biochim. Biophys Acta 1986, 849, 183–192. [Google Scholar] [CrossRef]
- Kolber, Z.S.; Prašil, O.; Falkowski, P.G. Measurements of variable chlorophyll fluorescence using fast repetition rate techniques: Defining methodology and experimental protocols. Biochim. Biophys Acta 1998, 1367, 88–110. [Google Scholar] [CrossRef]
- Olson, R.J.; Chekalyuk, A.M.; Sosik, H.M. Phytoplankton photosynthetic characteristics from fluorescence induction assays of individual cells. Limnol Ocean. 1996, 41, 1253–1263. [Google Scholar] [CrossRef]
- Brestic, M.; Zivcak, M. PSII fluorescence for measurement of drought and high temperature stress signal in crop plants: Protocols and applications. In Molecular Stress Physiology of Plants; Rout, G.R., Das, A.B., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 87–131. [Google Scholar]
- Murchie, E.H.; Lawson, T. Chlorophyll fluorescence analysis: A guide to good practice and understanding some new applications. J. Exp. Bot. 2013, 64, 3983–3998. [Google Scholar] [CrossRef]
- Maxwell, K.; Johnson, G.N. Chlorophyll fluorescence—A practical guide. J. Exp. Bot. 2000, 51, 659–668. [Google Scholar] [CrossRef]
- Baker, N.R. Chlorophyll fluorescence: A probe of photosynthesis in vivo. Annu. Rev. Plant Biol. 2008, 59, 89–113. [Google Scholar] [CrossRef] [PubMed]
- Guidi, L.; Calatayud, A. Non-invasive tools to estimate stress-induced changes in photosynthetic performance in plants inhabiting Mediterranean areas. Environ. Exp. Bot. 2014, 103, 42–52. [Google Scholar] [CrossRef]
- Kalaji, H.M.; Schansker, G.; Ladle, R.J.; Goltsev, V.; Bosa, K.; Allakhverdiev, S.I.; Brestic, M.; Bussotti, F.; Calatayud, A.; Dąbrowski, P.; et al. Frequently asked questions about in vivo chlorophyll fluorescence: Practical issues. Photosynth. Res. 2014, 122, 121–158. [Google Scholar] [CrossRef] [PubMed]
- Kalaji, H.M.; Schansker, G.; Brestic, M.; Bussotti, F.; Calatayud, A.; Ferroni, L.; Goltsev, V.; Guidi, L.; Jajoo, A.; Li, P.; et al. Frequently asked questions about chlorophyll fluorescence, the sequel. Photosynth. Res. 2017, 132, 13–66. [Google Scholar] [CrossRef]
- Guo, Y.; Tan, J. Recent advances in the application of chlorophyll a fluorescence from Photosystem II. Photochem. Photobiol 2015, 91, 1–14. [Google Scholar] [CrossRef]
- Ruban, A.V. Nonphotochemical chlorophyll fluorescence quenching: Mechanism and effectiveness in protecting plants from photodamage. Plant Physiol. 2016, 170, 1903–1916. [Google Scholar] [CrossRef]
- Stirbet, A.; Lazár, D.; Kromdijk, J.; Govindjee, G. Chlorophyll a fluorescence induction: Can just a one-second measurement be used to quantify abiotic stress responses? Photosynthetica 2018, 56, 86–104. [Google Scholar] [CrossRef]
- Nishiyama, Y.; Allakhverdiev, S.I.; Murata, N. A new paradigm for the action of reactive oxygen species in the photoinhibition of photosystem II. Biochim. Biophys. Acta Bioenerg. 2006, 1757, 742–749. [Google Scholar] [CrossRef]
- Gururani, M.A.; Venkatesh, J.; Tran, L.S.P. Regulation of photosynthesis during abiotic stress-induced photoinhibition. Mol Plant 2015, 8, 1304–1320. [Google Scholar] [CrossRef]
- Krause, G.H.; Weis, E. Chlorophyll fluorescence and photosynthesis: The basics. Annu. Rev. Plant Biol. 1991, 42, 313–349. [Google Scholar] [CrossRef]
- Öquist, G.; Chow, W.S.; Anderson, J.M. Photoinhibition of photosynthesis represents a mechanism for the long-term regulation of photosystem II. Planta 1992, 186, 450–460. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.; Sharopova, N.; Beavis, W.D.; Grant, D.; Katt, M.; Blair, D.; Hallauer, A. Expanding the genetic map of maize with the intermated B73 x Mo17 (IBM) population. Plant Mol. Biol. 2002, 48, 453–461. [Google Scholar] [CrossRef] [PubMed]
- Lepeduš, H.; Brkić, I.; Cesar, V.; Jurković, V.; Antunović, J.; Jambrović, A.; Brkić, J.; Šimić, D. Chlorophyll fluorescence analysis of photosynthetic performance in seven maize inbred lines under water-limited conditions. Period. Biol. 2012, 114, 73–76. [Google Scholar]
- Franić, M.; Galić, V.; Mazur, M.; Šimić, D. Effects of excess cadmium in soil on JIP-test parameters, hydrogen peroxide content and antioxidant activity in two maize inbreds and their hybrid. Photosynthetica 2017, 56, 660–669. [Google Scholar] [CrossRef]
- Gonzalo, M.; Holland, J.B.; Vyn, T.J.; McIntyre, L.M. Direct mapping of density response in a population of B73 x Mo17 recombinant inbred lines of maize (Zea mays L.). Heredity 2010, 104, 583–599. [Google Scholar] [CrossRef]
- Franić, M.; Mazur, M.; Volenik, M.; Brkić, J.; Brkić, A.; Šimić, D. Effect of plant density on agronomic traits and photosynthetic traits and photosynthetic performance in the maize IBM population. Poljoprivreda 2015, 21, 36–40. [Google Scholar] [CrossRef]
- Franić, M.; Jambrović, A.; Zdunić, Z.; Šimić, D.; Galić, V. Photosynthetic properties of maize hybrids under different environmental conditions probed by the chlorophyll a flurescence. Maydica 2019, 64, M25. [Google Scholar]
- Galić, V.; Mazur, M.; Šimić, D.; Zdunić, Z.; Franić, M. Plant biomass in salt-stressed young maize plants can be modelled with photosynthetic performance. Photosynthetica 2020, 58, 194–204. [Google Scholar] [CrossRef]
- Chen, X.; Mo, X.; Zhang, Y.; Sun, Z.; Liu, Y.; Hu, S.; Liu, S. Drought detection and assessment with solar-induced chlorophyll fluorescence in summer maize growth period over North China Plain. Ecol. Indic. 2019, 104, 347–356. [Google Scholar] [CrossRef]
- Wang, Y.; Leng, P.; Shang, G.; Zhang, X.; Li, Z. Sun-induced chlorophyll fluorescence is superior to satellite vegetation indices for predicting summer maize yield under drought conditions. Comput. Electron. Agric. 2023, 205, 107615. [Google Scholar] [CrossRef]
- Galic, V.; Franic, M.; Jambrovic, A.; Ledencan, T.; Brkic, A.; Zdunic, Z.; Simic, D. Genetic correlations between photosynthetic and yield performance in maize are different under two heat scenarios during flowering. Front. Plant Sci. 2019, 10, 566. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.; Latham, J.; Licht, M.; Wang, L. A data-driven crop model for maize yield prediction. Commun. Biol. 2023, 6, 439. [Google Scholar] [CrossRef] [PubMed]
- Barreto, C.A.V.; das Graças Dias, K.O.; de Sousa, I.C.; Ferreira Azevedo, C.; Campana Nascimento, A.C.; Moreira Guimarães, L.J.; Teixeira Guimarães, C.; Pastina, M.M.; Nascimento, M. Genomic prediction in multi-environment trials in maize using statistical and machine learning methods. Sci. Rep. 2024, 14, 1062. [Google Scholar] [CrossRef] [PubMed]
- Duvick, D.N. The contribution of breeding to yield advances in maize (Zea mays L.). Adv. Agron. 2005, 86, 83–145. [Google Scholar]
- Assefa, Y.; Prasad, P.V.V.; Carter, P.; Hinds, M.; Bhalla, G.; Schon, R.; Jeschke, M.; Paszkiewicz, S.; Ciampitti, I.A. A new insight into corn yield: Trends from 1987 through 2015. Crop. Sci. 2017, 57, 2799–2811. [Google Scholar] [CrossRef]
- Statistical Yearbook of the Republic of Croatia; Croatian Bureau of Statistics: Zagreb, Croatia, 2018.
- Wang, T.; Ma, X.; Li, Y.; Bai, D.; Liu, C.; Liu, Z.; Tan, X.; Shi, Y.; Song, Y.; Carlone, M.; et al. Changes in yield and yield components of single-cross maize hybrids released in China between 1964 and 2001. Crop. Sci. 2011, 51, 512–525. [Google Scholar] [CrossRef]
- Waqas, M.A.; Wang, X.; Zafar, S.A.; Noor, M.A.; Hussain, H.A.; Nawaz, M.A.; Farooq, M. Thermal stresses in maize: Effects and management strategies. Plants 2021, 10, 293. [Google Scholar] [CrossRef]
- Goltsev, V.N.; Kalaji, H.M.; Paunov, M.; Bąba, W.; Horaczek, T.; Mojski, J.; Kociel, H.; Allakhverdiev, S.I. Variable chlorophyll fluorescence and its use for assessing physiological condition of plant photosynthetic apparatus. Russ. J. Plant Physiol. 2016, 63, 869–893. [Google Scholar] [CrossRef]
- Strasser, R.J.; Govindjee. On the OJIP fluorescence transients in leaves and D1 mutants of Chlamydomonas reinhardtii. In Research in Photosynthesis; Murata, N., Ed.; Kluwer Academic: Dordrecht, The Netherlands, 1992; Volume II. [Google Scholar]
- Badr, A.; Brüggemann, W. Special issue in honour of Prof. Reto, J. Strasser—Comparative analysis of drought stress response of maize genotypes using chlorophyll fluorescence measurements and leaf relative water content. Photosynthetica 2020, 58, 638–645. [Google Scholar]
- Ahmad, I.; Ahmad, S.; Kamran, M.; Yang, X.N.; Hou, F.J.; Yang, B.P.; Ding, R.X.; Liu, T.; Han, Q.F. Uniconazole and nitrogen fertilization trigger photosynthesis and chlorophyll fluorescence, and delay leaf senescence in maize at a high population density. Photosynthetica 2021, 59, 192–202. [Google Scholar] [CrossRef]
- Gao, F.; Wang, G.Y.; Muhammad, I.; Tung, S.A.; Zhou, X.B. Interactive effect of water and nitrogen fertilization improve chlorophyll fluorescence and yield of maize. Agron. J. 2022, 115, 325–339. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, J.; Cui, Y.; Guan, Z.; Yang, L.; Tang, Q.; Sun, Y.; Yang, H.; Wen, X.; Mei, N.; et al. Effects of row spacing and planting pattern on photosynthesis, chlorophyll fluorescence, and related enzyme activities of maize ear leaf in maize–soybean intercropping. Agronomy 2022, 12, 2503. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, Y.; Yan, Y.; Hou, J.; Wang, H.; Luo, N.; Wei, D.; Meng, Q.; Wang, P. Mitigating heat impacts on photosynthesis by irrigation during grain filling in the maize field. J. Integr. Agric. 2023, 22, 2370–2383. [Google Scholar] [CrossRef]
- Yan, Y.; Hou, P.; Duan, F.; Niu, L.; Dai, T.; Wang, K.; Zhao, M.; Li, S.; Zhou, W. Improving photosynthesis to increase grain yield potential: An analysis of maize hybrids released in different years in China. Photosynth. Res. 2021, 150, 295–311. [Google Scholar] [CrossRef] [PubMed]
- Hallauer, A.R.; Carena, M.J.; Filho, J.B.M. Quantitative Genetics in Maize Breeding; Springer: New York, NY, USA, 2010. [Google Scholar]
- Yi, Q.; Álvarez-Iglesias, L.; Malvar, R.A.; Romay, M.C.; Revilla, P. A worldwide maize panel revealed new genetic variation for cold tolerance. Theor. Appl. Genet. 2021, 134, 1083–1094. [Google Scholar] [CrossRef]
- Mevik, B.H.; Wehrens, R. The pls package: Principal component and partial least squares regression in R. J. Stat. Softw. 2007, 18, 1–23. [Google Scholar] [CrossRef]
- Yu, S.; Zhang, N.; Kaiser, E.; Li, G.; An, D.; Sun, Q.; Chen, W.; Liu, W.; Luo, W. Integrating chlorophyll fluorescence parameters into a crop model improves growth prediction under severe drought. Agric. For. Meteorol. 2021, 303, 108367. [Google Scholar] [CrossRef]
- Spyroglou, I.; Rybka, K.; Maldonado Rodriguez, R.; Stefański, P.; Valasevich, N.M. Quantitative estimation of water status in field-grown wheat using beta mixed regression modeling based on fast chlorophyll fluorescence transients. A method for drought tolerance estimation. J. Agron. Crop Sci. 2021, 207, 589–605. [Google Scholar] [CrossRef]
- Spišić, J.; Šimić, D.; Balen, J.; Jambrović, A.; Galić, V. Machine learning in the analysis of multispectral reads in maize canopies responding to increased temperatures and water deficit. Remote Sens. 2022, 14, 2596. [Google Scholar] [CrossRef]
- Hammad, H.M.; Abbas, F.; Ahmad, A.; Bakhat, H.F.; Farhad, W.; Wilkerson, C.J.; Fahad, S.; Hoogenboom, G. Predicting Kernel Growth of Maize under Controlled Water and Nitrogen Applications. Int. J. Plant Prod. 2020, 14, 609–620. [Google Scholar] [CrossRef]
- Zhang, Z.; Ming, B.; Liang, H.; Huang, Z.; Wang, K.; Yang, X.; Wang, Z.; Xie, R.; Hou, P.; Zhao, R.; et al. Evaluation of maize varieties for mechanical grain harvesting in mid-latitude region, China. Agron. J. 2021, 113, 1766–1775. [Google Scholar] [CrossRef]
- Li, L.; Ming, B.; Gao, S.; Wang, K.; Hou, P.; Jin, X.; Chu, Z.; Zhang, W.; Huang, Z.; Li, H.; et al. A regional analysis model of maize kernel moisture. Agron. J. 2020, 113, 1467–1479. [Google Scholar] [CrossRef]
- Ni, P.; Anche, M.T.; Ruan, Y.; Dang, D.; Morales, N.; Li, L.; Liu, M.; Wang, S.; Robbins, K.R. Genomic prediction strategies for dry-down-related traits in maize. Front. Plant Sci. 2022, 13, 930429. [Google Scholar] [CrossRef] [PubMed]
- O’Neill, P.M.; Shanahan, J.F.; Schepers, J.S. Use of chlorophyll fluorescence assessments to differentiate corn hybrid response to variable water conditions. Crop. Sci. 2006, 46, 681–687. [Google Scholar] [CrossRef]
- Bernardo, R. Breeding for Quantitative Traits in Plants, 2nd ed.; Stemma Press: Woodbury, MN, USA, 2010. [Google Scholar]
- Troyer, A.F. Background of U.S. Hybrid Corn. Crop Sci. 1999, 39, 601–626. [Google Scholar] [CrossRef]
- Troyer, A.F. Development of hybrid corn and the seed corn industry. In Handbook of Maize: Genetics and Genomics; Bennetzen, J.L., Hake, S.C., Eds.; Springer: New York, NY, USA, 2009; pp. 87–114. [Google Scholar]
- Croatian Meteorological and Hydrological Service. Available online: https://meteo.hr/klima.php?section=klima_podaci¶m=k2_1&Godina (accessed on 10 November 2024).
- Strasser, R.J.; Tsimilli-Michael, M.; Srivastava, A. Analysis of the Chlorophyll a Fluorescence Transient. In Chlorophyll a Fluorescence: A Signature of Photosynthesis; Papageorgiou, G.C., Govindjee., Eds.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Wold, S.; Ruhe, A.; Wold, H.; Dunn, W.J., III. The Collinearity Problem in Linear Regression. The Partial Least Squares (PLS) Approach to Generalized Inverses. SIAM J. Sci. Stat. Comput. 1984, 5, 735–743. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Covarrubias-Pazaran, G. Genome-assisted prediction of quantitative traits using the r package sommer. PLoS ONE 2016, 11, e0156744. [Google Scholar] [CrossRef]

| Source of Variation | Df | MS | p | ||||
|---|---|---|---|---|---|---|---|
| GY | GM | GY | GM | ||||
| Genotype | 15 | 10.2 | 28.4 | <0.001 | *** | <0.001 | *** |
| Year | 2 | 148.1 | 1618.2 | <0.001 | *** | <0.001 | *** |
| Replication | 9 | 10.5 | 1.3 | <0.001 | *** | 0.132 | n.s. |
| Block | 9 | 4.4 | 2.2 | 0.094 | n.s. | 0.005 | ** |
| Genotype:Year | 30 | 3.9 | 9.2 | 0.065 | n.s. | <0.001 | *** |
| Error | 126 | 2.6 | 0.8 | ||||
| Source of Variation | Df | MS | p | ||||
|---|---|---|---|---|---|---|---|
| Fv/Fm | PIABS | Fv/Fm | PIABS | ||||
| Genotype | 15 | 0.00010 | 1.8 | <0.001 | *** | <0.001 | *** |
| Year | 2 | 0.00083 | 41.3 | <0.001 | *** | <0.001 | *** |
| Replication | 9 | 0.00014 | 1.1 | <0.001 | *** | <0.001 | *** |
| Block | 9 | 0.00006 | 0.6 | 0.046 | * | 0.026 | * |
| Genotype:Year | 30 | 0.00003 | 0.3 | 0.383 | n.s. | 0.493 | n.s. |
| Error | 126 | 0.00003 | 0.3 | ||||
| Components of Variance | GY | GM | Fv/Fm | PIABS |
|---|---|---|---|---|
| σ2 G | 0.553 | 1.296 | 5.88 × 10−6 | 0.120 |
| σ2 E | 2.124 | 25.335 | 1.02 × 10−5 | 0.622 |
| σ2 GxE | 0.307 | 2.209 | 7.17 × 10−5 | 0.003 |
| σ2 e | 2.593 | 0.795 | 2.97 × 10−5 | 0.272 |
| H2 | 0.64 ± 0.17 | 0.62 ± 0.17 | 0.70 ± 0.13 | 0.84 ± 0.07 |
| r | GY | GM | Fv/Fm | PIABS |
|---|---|---|---|---|
| GY | – | −0.49 *** | 0.06 | 0.16 * |
| GM | −0.10 ± 0.42 | – | 0.08 | −0.20 ** |
| Fv/Fm | 0.35 ± 0.37 | −0.61 ± 0.30 | – | 0.40 *** |
| PIABS | −0.24 ± 0.35 | −0.24 ± 0.19 | 0.76 ± 0.20 | – |
| Variance Component | Yield–Parameters | Moisture–Parameters | Yield–Transients | Moisture–Transients |
|---|---|---|---|---|
| σ2 G | 0.036 | 0.29686 | 0.080 | 0.032 |
| σ2 E | 0.191 | 8.053031 | 1.156 | 10.087 |
| σ2 GxE | 0.001 | 0.81675 | 0.137 | 1.650 |
| σ2 e | 0.233 | 4.19772 | 0.409 | 2.996 |
| H2 | 0.65 ± 0.16 | 0.32 ± 0.28 | 0.50 ± 0.23 | 0.03 ± 0.44 |
| rG | 0.44 ± 0.45 | 0.83 ± 1.05 | 0.97 ± 0.36 | 0.11 ± 0.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brkić, A.; Vila, S.; Šimić, D.; Jambrović, A.; Zdunić, Z.; Salaić, M.; Brkić, J.; Volenik, M.; Galić, V. In-Season Predictions Using Chlorophyll a Fluorescence for Selecting Agronomic Traits in Maize. Plants 2025, 14, 1216. https://doi.org/10.3390/plants14081216
Brkić A, Vila S, Šimić D, Jambrović A, Zdunić Z, Salaić M, Brkić J, Volenik M, Galić V. In-Season Predictions Using Chlorophyll a Fluorescence for Selecting Agronomic Traits in Maize. Plants. 2025; 14(8):1216. https://doi.org/10.3390/plants14081216
Chicago/Turabian StyleBrkić, Andrija, Sonja Vila, Domagoj Šimić, Antun Jambrović, Zvonimir Zdunić, Miroslav Salaić, Josip Brkić, Mirna Volenik, and Vlatko Galić. 2025. "In-Season Predictions Using Chlorophyll a Fluorescence for Selecting Agronomic Traits in Maize" Plants 14, no. 8: 1216. https://doi.org/10.3390/plants14081216
APA StyleBrkić, A., Vila, S., Šimić, D., Jambrović, A., Zdunić, Z., Salaić, M., Brkić, J., Volenik, M., & Galić, V. (2025). In-Season Predictions Using Chlorophyll a Fluorescence for Selecting Agronomic Traits in Maize. Plants, 14(8), 1216. https://doi.org/10.3390/plants14081216






