Simulating Net Ecosystem Productivity (NEP) in Mediterranean Pine Forests (Pinus brutia) During the 21st Century: The Effect of Leaf Area Index and Elevation
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. Stand Structure and Tree Measurements
2.3. Gas Exchange Measurements
2.4. Model Description
2.4.1. Primary Productivity
2.4.2. Soil Water Balance
2.4.3. Soil Respiration
2.5. Environmental Forcing Data
2.6. Model Evaluation and Simulations
3. Results
3.1. Model Evaluation
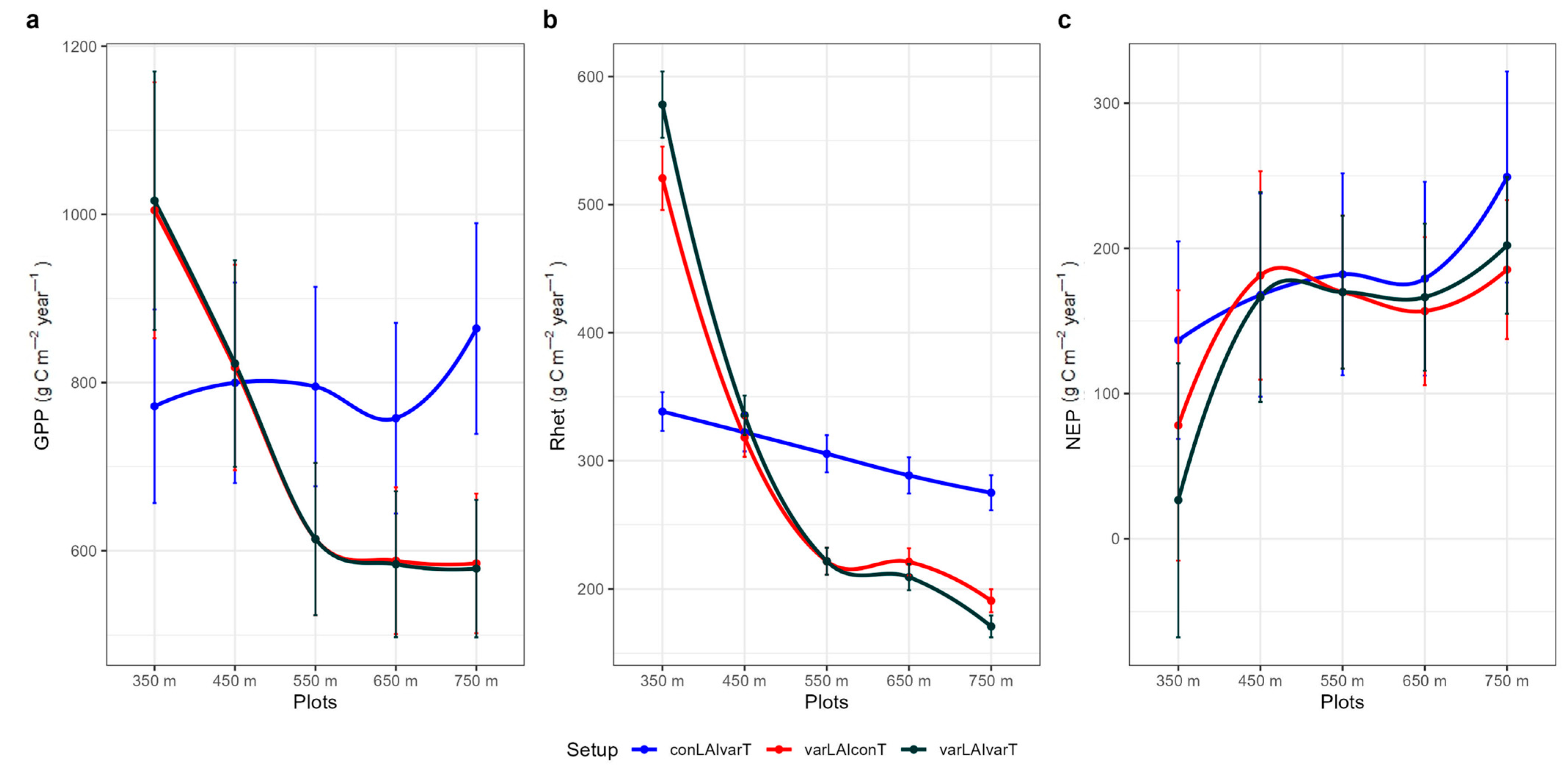
3.2. Simulation Experiment to Explore the Effects of LAI, Air Temperature and Increased CO2
3.3. Seasonal Variation of C-Fluxes Under Current and Future Conditions
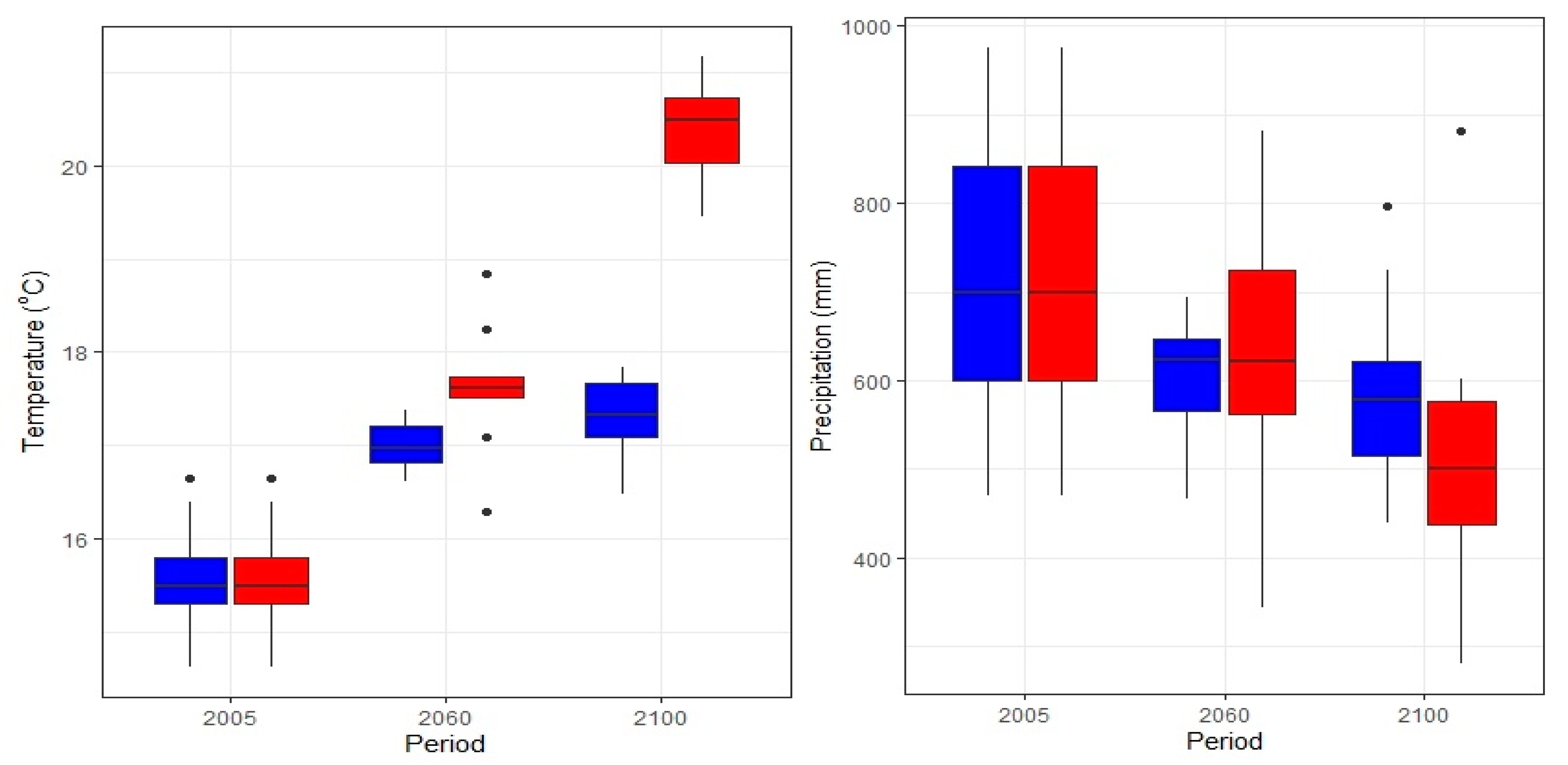
3.4. Annual C-Fluxes Under Current and Future Climate Conditions
4. Discussion
4.1. Model Verification
4.2. GPP
4.3. Soil Heterotrophic Respiration
4.4. NEP
4.5. Model Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Model Description
Appendix A.1.1. Primary Productivity
Appendix A.1.2. Soil Water Balance
| Soil Texture | Proportion of Clay and Sand | θr | θs | GMD | GSD |
|---|---|---|---|---|---|
| Coarse | 18% < clay and >65% sand | 0.025 | 0.403 | 0.4 | 5.3 |
| Medium | 18% < clay < 35% and ≥15% sand, or 18% < clay and 15% < sand < 65% | 0.01 | 0.439 | 0.3 | 7.4 |
| Medium Fine | <35% clay and <15% sand | 0.01 | 0.430 | 0.1 | 6.1 |
| Fine | 35% < clay < 60% | 0.01 | 0.520 | 0.07 | 14 |
| Very Fine | Clay > 60% | 0.01 | 0.614 | 0.007 | 15 |
Appendix A.1.3. Soil Heterotrophic Respiration
| Model | Random Effects | R2 Marginal | R2 Conditional | AIC | ||
|---|---|---|---|---|---|---|
| Rhet = | σ2 | τPlot | ICC | |||
| exp (Ts) | 0.22 | 0.11 | 0.34 | 0.017 | 0.352 | 149 |
| exp (Ts + θ) | 0.21 | 0.14 | 0.40 | 0.045 | 0.424 | 147 |
| exp (Ts) × θ | 0.21 | 0.14 | 0.40 | 0.040 | 0.421 | 152 |
| exp (Ts + Ts2) | 0.15 | 0.09 | 0.39 | 0.239 | 0.536 | 128 |
| exp (Ts + Ts2 + θ) | 0.10 | 0.16 | 0.61 | 0.328 | 0.738 | 100 |
| exp (Ts + Ts2) × θ | 0.11 | 0.15 | 0.58 | 0.304 | 0.710 | 109 |
| exp (Ts + Ts2 + θ + θ × Τs) | 0.10 | 0.17 | 0.63 | 0.341 | 0.754 | 100 |
| exp (Ts + Ts2 + θ + θ2) | 0.10 | 0.16 | 0.62 | 0.330 | 0.744 | 95 |
| exp (Ts + Ts2 + θ + θ × Τs + LAI) | 0.10 | 0.06 | 0.36 | 0.555 | 0.716 | 99 |
| exp (Ts + Ts2 + θ + θ2 + LAI) | 0.10 | 0.04 | 0.26 | 0.577 | 0.688 | 93 |
| exp (Ts + Ts2 + θ + θ × Τs) × LAI | 0.10 | 0.05 | 0.32 | 0.570 | 0.709 | 99 |
| exp (Ts + Ts2 + θ + θ2) × LAI | 0.10 | 0.03 | 0.23 | 0.587 | 0.684 | 93 |
Appendix A.2. Additional Information
| Plot | LAI (m2 m−2) | Soil Texture | Soil Depth (mm) | Elevation (m) | |
|---|---|---|---|---|---|
| Post-fire gradient | AMAL | 0.67 | Very Fine | 500 | 316 |
| PEV | 1.66 | Fine | 270 | 213 | |
| LML | 2.13 | Very Fine | 300 | 166 | |
| ACHL | 1.67 | Fine | 350 | 261 | |
| Elevation gradient | OLY1 | 4.26 | Fine | 200 | 350 |
| OLY2 | 2.08 | Fine | 250 | 450 | |
| OLY3 | 1.23 | Fine | 250 | 550 | |
| OLY4 | 1.23 | Fine | 200 | 650 | |
| OLY5 | 0.98 | Fine | 400 | 750 |
| Symbol | Description | Units |
|---|---|---|
| AW | Available soil water | mm |
| b | Function of soil texture | - |
| Ca | Partial pressure of CO2 in the atmosphere | Pa |
| Ci | Partial pressure of CO2 in the leaf | Pa |
| D | Vapor pressure deficit | Pa |
| eact | Actual vapor pressure | Pa |
| esat | Pressure of water vapor in saturated air | Pa |
| GPP | Gross Primary Productivity | g C m−2 day−1 |
| Iabs | Fraction of PAR absorbed by the canopy | umol quanta m−2 day−1 |
| K | Michaelis–Menten coefficient for photosynthesis | Pa |
| m′ | CO2 limitation factor for light-limited assimilation and electron transport capacity | - |
| m | CO2 limitation factor for light-limited assimilation | - |
| NEP | Net Ecosystem Productivity | g C m−2 day−1 |
| NPP | Net Primary Productivity | g C m−2 day−1 |
| Raut | Soil autotrophic respiration | mol CO2 m−2 day−1 |
| REW | Relative extractable water | - |
| Rex | Extraterrestrial radiation | MJ m−2 day−1 |
| Rhet | Soil heterotrophic respiration | mol CO2 m−2 day−1 |
| TK | Temperature | °K |
| Γ*Τ | Temperature-dependent photorespiratory compensation point | Pa |
| η* | Change in the viscosity of the water, relative to its value at 25 °C | - |
| θ | Soil water content | cm3 cm−3 |
| θfc | Soil water content at field capacity | cm3 cm−3 |
| θs | Water content of water-saturated soil | cm3 cm−3 |
| θwp | Soil water content at wilting point | cm3 cm−3 |
| φ0 | Intrinsic quantum yield efficiency | mol mol−1 |
| Ψe | Water potential at the maximum soil hydration | MPa |
| Ψi | Water potential | MPa |
| Symbol | Description | Units | Value |
|---|---|---|---|
| c* | Proportional to the unit carbon cost for the maintenance of electron transport | - | 0.41 |
| cL | Photosynthesis quantum efficiency parameter | - | 0.08718 |
| g | Gravitation constant | m s−2 | 9.80665 |
| Kc | Michaelis–Menten constants for carboxylation reactions | Pa | 39.97 |
| Ko | Michaelis–Menten constants for oxygenation reactions | Pa | 27,480 |
| L | Adiabatic lapse rate | °K m−1 | 0.0065 |
| Mc | Molecular mass of carbon | g mol−1 | 12.0107 |
| Mα | Molecular mass of dry air | kg mol−1 | 0.028963 |
| p0 | Atmospheric pressure at sea level | Pa | 101,325 |
| pO2 | Partial pressure of oxygen in the atmosphere at sea level | Pa | 21,000 |
| R | Universal gas constant | J mol−1 K−1 | 8.3145 |
| Density of the water | g cm−3 | 0.9982 | |
| β | Unit cost ratio | - | 146 |
| Γ* | Photorespiratory compensation point at 25 °C | Pa | 4.332 |
| ΔHKc | Activation energy for Kc | J mol−1 | 79,430 |
| ΔHKo | Activation energy for Ko | J mol−1 | 36,380 |
| ΔHΓ* | Activation energy for Γ* | Pa, J mol−1 | 23,400 |

References
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Carrara, A.; Janssens, I.A.; Curiel Yuste, J.; Ceulemans, R. Seasonal Changes in Photosynthesis, Respiration and NEE of a Mixed Temperate Forest. Agric. For. Meteorol. 2004, 126, 15–31. [Google Scholar] [CrossRef]
- Hadden, D.; Grelle, A. Changing Temperature Response of Respiration Turns Boreal Forest from Carbon Sink into Carbon Source. Agric. For. Meteorol. 2016, 223, 30–38. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A New Tool to Study the Temporal and Spatial Variability of Ecosystem–Scale Carbon Dioxide, Water Vapor, and Energy Flux Densities. Bull. Amer. Meteor. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Reichstein, M.; Bahn, M.; Ciais, P.; Frank, D.; Mahecha, M.D.; Seneviratne, S.I.; Zscheischler, J.; Beer, C.; Buchmann, N.; Frank, D.C.; et al. Climate Extremes and the Carbon Cycle. Nature 2013, 500, 287–295. [Google Scholar] [CrossRef]
- Fyllas, N.M.; Christopoulou, A.; Galanidis, A.; Michelaki, C.Z.; Dimitrakopoulos, P.G.; Fulé, P.Z.; Arianoutsou, M. Tree Growth-Climate Relationships in a Forest-Plot Network on Mediterranean Mountains. Sci. Total Environ. 2017, 598, 393–403. [Google Scholar] [CrossRef]
- Hikosaka, K.; Ishikawa, K.; Borjigidai, A.; Muller, O.; Onoda, Y. Temperature Acclimation of Photosynthesis: Mechanisms Involved in the Changes in Temperature Dependence of Photosynthetic Rate. J. Exp. Bot. 2006, 57, 291–302. [Google Scholar] [CrossRef] [PubMed]
- Dai, Y.; Dickinson, R.E.; Wang, Y.-P. A Two-Big-Leaf Model for Canopy Temperature, Photosynthesis, and Stomatal Conductance. J. Clim. 2004, 17, 19. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Ju, W.; Porcar-Castell, A.; Ye, S.; Zhang, Z.; Brümmer, C.; Urbaniak, M.; Mammarella, I.; Juszczak, R.; et al. Warmer Spring Alleviated the Impacts of 2018 European Summer Heatwave and Drought on Vegetation Photosynthesis. Agric. For. Meteorol. 2020, 295, 108195. [Google Scholar] [CrossRef]
- Flexas, J.; Diaz-Espejo, A.; Gago, J.; Gallé, A.; Galmés, J.; Gulías, J.; Medrano, H. Photosynthetic Limitations in Mediterranean Plants: A Review. Environ. Exp. Bot. 2014, 103, 12–23. [Google Scholar] [CrossRef]
- Warren, C.R.; Livingston, N.J.; Turpin, D.H. Water Stress Decreases the Transfer Conductance of Douglas-Fir (Pseudotsuga Menziesii) Seedlings. Tree Physiol. 2004, 24, 971–979. [Google Scholar] [CrossRef] [PubMed]
- Mittler, R.; Merquiol, E.; Hallak-Herr, E.; Rachmilevitch, S.; Kaplan, A.; Cohen, M. Living under a ‘Dormant’ Canopy: A Molecular Acclimation Mechanism of the Desert Plant Retama Raetam: Molecular Acclimation of Desert Plants. Plant J. 2001, 25, 407–416. [Google Scholar] [CrossRef]
- Munné-Bosch, S.; Alegre, L. Changes in Carotenoids, Tocopherols and Diterpenes during Drought and Recovery, and the Biological Significance of Chlorophyll Loss in Rosmarinus Officinalis Plants. Planta 2000, 210, 925–931. [Google Scholar] [CrossRef] [PubMed]
- Chaves, M.M. How Plants Cope with Water Stress in the Field? Photosynthesis and Growth. Ann. Bot. 2002, 89, 907–916. [Google Scholar] [CrossRef]
- Havaux, M. Stress Tolerance of Photosystem 11 in Vivo. Plant Physiol. 1992, 100, 9. [Google Scholar]
- Amthor, J.S. The Role of Maintenance Respiration in Plant Growth. Plant Cell Environ. 1984, 7, 561–569. [Google Scholar] [CrossRef]
- Piao, S.; Luyssaert, S.; Ciais, P.; Janssens, I.A.; Chen, A.; Cao, C.; Fang, J.; Friedlingstein, P.; Luo, Y.; Wang, S. Forest Annual Carbon Cost: A Global-Scale Analysis of Autotrophic Respiration. Ecology 2010, 91, 652–661. [Google Scholar] [CrossRef] [PubMed]
- Reich, P.B.; Tjoelker, M.G.; Machado, J.-L.; Oleksyn, J. Universal Scaling of Respiratory Metabolism, Size and Nitrogen in Plants. Nature 2006, 439, 457–461. [Google Scholar] [CrossRef]
- Tang, X.; Pei, X.; Lei, N.; Luo, X.; Liu, L.; Shi, L.; Chen, G.; Liang, J. Global Patterns of Soil Autotrophic Respiration and Its Relation to Climate, Soil and Vegetation Characteristics. Geoderma 2020, 369, 114339. [Google Scholar] [CrossRef]
- Luyssaert, S.; Inglima, I.; Jung, M.; Richardson, A.D.; Reichstein, M.; Papale, D.; Piao, S.L.; Schulze, E.-D.; Wingate, L.; Matteucci, G.; et al. CO2 Balance of Boreal, Temperate, and Tropical Forests Derived from a Global Database. Glob. Change Biol. 2007, 13, 2509–2537. [Google Scholar] [CrossRef]
- Conant, R.T.; Dalla-Betta, P.; Klopatek, C.C.; Klopatek, J.M. Controls on Soil Respiration in Semiarid Soils. Soil Biol. Biochem. 2004, 36, 945–951. [Google Scholar] [CrossRef]
- Bååth, E. Temperature Sensitivity of Soil Microbial Activity Modeled by the Square Root Equation as a Unifying Model to Differentiate between Direct Temperature Effects and Microbial Community Adaptation. Glob. Change Biol. 2018, 24, 2850–2861. [Google Scholar] [CrossRef]
- Orchard, V.A.; Cook, F.J. Relationship between Soil Respiration and Soil Moisture. Soil Biol. Biochem. 1983, 15, 447–453. [Google Scholar] [CrossRef]
- Grant, R.F.; Rochette, P. Soil Microbial Respiration at Different Water Potentials and Temperatures: Theory and Mathematical Modeling. Soil Sci. Soc. Am. J. 1994, 58, 1681. [Google Scholar] [CrossRef]
- Wallenstein, M.D.; Hall, E.K. A Trait-Based Framework for Predicting When and Where Microbial Adaptation to Climate Change Will Affect Ecosystem Functioning. Biogeochemistry 2012, 109, 35–47. [Google Scholar] [CrossRef]
- González-Ubierna, S.; Lai, R. Modelling the Effects of Climate Factors on Soil Respiration across Mediterranean Ecosystems. J. Arid. Environ. 2019, 165, 46–54. [Google Scholar] [CrossRef]
- Jarvis, P.; Rey, A.; Petsikos, C.; Wingate, L.; Rayment, M.; Pereira, J.; Banza, J.; David, J.; Miglietta, F.; Borghetti, M.; et al. Drying and Wetting of Mediterranean Soils Stimulates Decomposition and Carbon Dioxide Emission: The “Birch Effect”. Tree Physiol. 2007, 27, 929–940. [Google Scholar] [CrossRef]
- Ilstedt, U.; Nordgren, A.; Malmer, A. Optimum Soil Water for Soil Respiration before and after Amendment with Glucose in Humid Tropical Acrisols and a Boreal Mor Layer. Soil Biol. Biochem. 2000, 32, 1591–1599. [Google Scholar] [CrossRef]
- Rixon, A.J.; Bridge, B.J. Respiratory Quotient Arising from Microbial Activity in Relation to Matric Suction and Air Filled Pore Space of Soil. Nature 1968, 218, 961–962. [Google Scholar] [CrossRef]
- Janssens, I.A.; Lankreijer, H.; Matteucci, G.; Kowalski, A.S.; Buchmann, N.; Epron, D.; Pilegaard, K.; Kutsch, W.; Longdoz, B.; Grünwald, T.; et al. Productivity Overshadows Temperature in Determining Soil and Ecosystem Respiration across European Forests: Respiration Across European Forests. Glob. Change Biol. 2001, 7, 269–278. [Google Scholar] [CrossRef]
- Trumbore, S. Carbon Respired by Terrestrial Ecosystems-Recent Progress and Challenges: CARBON RESPIRED BY TERRESTRIAL ECOSYSTEMS. Glob. Change Biol. 2006, 12, 141–153. [Google Scholar] [CrossRef]
- Chambel, M.R.; Climent, J.; Pichot, C.; Ducci, F. Mediterranean Pines (Pinus Halepensis Mill. and Brutia Ten.). In Forest Tree Breeding in Europe: Current State-of-the-Art and Perspectives; Pâques, L.E., Ed.; Managing Forest Ecosystems; Springer: Dordrecht, The Netherlands, 2013; pp. 229–265. ISBN 978-94-007-6146-9. [Google Scholar]
- Isajev, V.; Fady, B.; Semerci, H.; Andonovski, V. EUFORGEN Technical Guidelines for Genetic Conservation and Use for European Black Pine (Pinus Nigra); Bioversity International: Rome, Italy, 2004; ISBN 978-92-9043-659-1. [Google Scholar]
- Jung, M.; Maire, G.L.; Zaehle, S.; Luyssaert, S.; Vetter, M.; Churkina, G.; Ciais, P.; Viovy, N.; Reichstein, M. Assessing the Ability of Three Land Ecosystem Models to Simulate Gross Carbon Uptake of Forests from Boreal to Mediterranean Climate in Europe. Biogeosciences 2007, 4, 647–656. [Google Scholar]
- Martínez-García, E.; Rubio, E.; García-Morote, F.A.; Andrés-Abellán, M.; Miettinen, H.; López-Serrano, F.R. Net Ecosystem Production in a Spanish Black Pine Forest after a Low Burn-Severity Fire: Significance of Different Modelling Approaches for Estimating Gross Primary Production. Agric. For. Meteorol. 2017, 246, 178–193. [Google Scholar] [CrossRef]
- Martin-Benito, D.; Kint, V.; del Río, M.; Muys, B.; Cañellas, I. Growth Responses of West-Mediterranean Pinus Nigra to Climate Change Are Modulated by Competition and Productivity: Past Trends and Future Perspectives. For. Ecol. Manag. 2011, 262, 1030–1040. [Google Scholar] [CrossRef]
- Sarris, D.; Christodoulakis, D.; Körner, C. Recent Decline in Precipitation and Tree Growth in the Eastern Mediterranean. Glob. Change Biol. 2007, 13, 1187–1200. [Google Scholar] [CrossRef]
- van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.-F.; et al. The Representative Concentration Pathways: An Overview. Clim. Change 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Intergovernmental Panel On Climate Change (IPCC). Climate Change 2022 – Impacts, Adaptation and Vulnerability: Working Group II Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, 1st ed.; Cambridge University Press: Cambridge, UK, 2023; ISBN 978-1-00-932584-4. [Google Scholar]
- Mariotti, A.; Pan, Y.; Zeng, N.; Alessandri, A. Long-Term Climate Change in the Mediterranean Region in the Midst of Decadal Variability. Clim. Dyn. 2015, 44, 1437–1456. [Google Scholar] [CrossRef]
- Zittis, G.; Almazroui, M.; Alpert, P.; Ciais, P.; Cramer, W.; Dahdal, Y.; Fnais, M.; Francis, D.; Hadjinicolaou, P.; Howari, F.; et al. Climate Change and Weather Extremes in the Eastern Mediterranean and Middle East. Rev. Geophys. 2022, 60, e2021RG000762. [Google Scholar] [CrossRef]
- Polade, S.D.; Gershunov, A.; Cayan, D.R.; Dettinger, M.D.; Pierce, D.W. Precipitation in a Warming World: Assessing Projected Hydro-Climate Changes in California and Other Mediterranean Climate Regions. Sci. Rep. 2017, 7, 10783. [Google Scholar] [CrossRef]
- Sazeides, C.I.; Christopoulou, A.; Fyllas, N.M. Coupling Photosynthetic Measurements with Biometric Data to Estimate Gross Primary Productivity (GPP) in Mediterranean Pine Forests of Different Post-Fire Age. Forests 2021, 12, 1256. [Google Scholar] [CrossRef]
- Kosmas, C.; Danalatos, N.G.; Gerontidis, S. The Effect of Land Parameters on Vegetation Performance and Degree of Erosion under Mediterranean Conditions. Catena 2000, 40, 3–17. [Google Scholar] [CrossRef]
- Christopoulou, A.; Sazeides, C.I.; Fyllas, N.M. Size-Mediated Effects of Climate on Tree Growth and Mortality in Mediterranean Brutia Pine Forests. Sci. Total Environ. 2022, 812, 151463. [Google Scholar] [CrossRef] [PubMed]
- Rinn, F. TSAP-Win: Time Series Analysis and Presentation for Dendrochronology and Related Applications–Version 4.81. User Reference. Heidelberg, Germany. 2011. Available online: http://www.rinntech.com (accessed on 23 October 2018).
- Stokes, M.A.; Smiley, T.L. An Introduction to Tree-Ring Dating; The University of Arizona Press: Tucson, AZ, USA, 1996. [Google Scholar]
- Mina, M.; Martin-Benito, D.; Bugmann, H.; Cailleret, M. Forward Modeling of Tree-Ring Width Improves Simulation of Forest Growth Responses to Drought. Agric. For. Meteorol. 2016, 221, 13–33. [Google Scholar] [CrossRef]
- ArchMiller, A.; Samuelson, L. Partitioning Longleaf Pine Soil Respiration into Its Heterotrophic and Autotrophic Components through Root Exclusion. Forests 2016, 7, 39. [Google Scholar] [CrossRef]
- Stocker, B.D.; Wang, H.; Smith, N.G.; Harrison, S.P.; Keenan, T.F.; Sandoval, D.; Davis, T.; Prentice, I.C. P-Model v1.0: An Optimality-Based Light Use Efficiency Model for Simulating Ecosystem Gross Primary Production. Geosci. Model Dev. 2020, 13, 1545–1581. [Google Scholar] [CrossRef]
- Brown, L.A.; Meier, C.; Morris, H.; Pastor-Guzman, J.; Bai, G.; Lerebourg, C.; Gobron, N.; Lanconelli, C.; Clerici, M.; Dash, J. Evaluation of Global Leaf Area Index and Fraction of Absorbed Photosynthetically Active Radiation Products over North America Using Copernicus Ground Based Observations for Validation Data. Remote Sens. Environ. 2020, 247, 111935. [Google Scholar] [CrossRef]
- DeLucia, E.H.; Drake, J.E.; Thomas, R.B.; Gonzalez-Meler, M. Forest Carbon Use Efficiency: Is Respiration a Constant Fraction of Gross Primary Production? Glob. Change Biol. 2007, 13, 1157–1167. [Google Scholar] [CrossRef]
- Tarboton, D.G. Rainfall-Runoff Processes; Utah State University: Logan, UT, USA, 2003. [Google Scholar]
- Benito Garzón, M.; González Muñoz, N.; Wigneron, J.-P.; Moisy, C.; Fernández-Manjarrés, J.; Delzon, S. The Legacy of Water Deficit on Populations Having Experienced Negative Hydraulic Safety Margin. Glob. Ecol. Biogeogr. 2018, 27, 346–356. [Google Scholar] [CrossRef]
- Wösten, J.H.M.; Lilly, A.; Nemes, A.; Le Bas, C. Development and Use of a Database of Hydraulic Properties of European Soils. Geoderma 1999, 90, 169–185. [Google Scholar] [CrossRef]
- Campbell, G.S. Soil Physics with BASIC: Transport Models for Soil-Plant Systems; Developments in Soil Science; Elsevier: Amsterdam, The Netherlands; New York, NY, USA, 1985; ISBN 978-0-444-42557-7. [Google Scholar]
- Deligöz, A.; Bayar, E.; Genç, M.; Karatepe, Y. Differences in Water Relations and Total Carbohydrate Content between Precommercially Thinned and Unthinned Pinus Nigra Subsp. Pallasiana Stands. J. For. Sci. 2021, 67, 125–133. [Google Scholar] [CrossRef]
- Tegos, A.; Efstratiadis, A.; Koutsoyiannis, D. A Parametric Model for Potential Evapotranspiration Estimation Based on a Simplified Formulation of the Penman-Monteith Equation; IntechOpen: London, UK, 2013; ISBN 978-953-51-1115-3. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. FAO Irrigation and Drainage Paper No.56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; Volume 56, pp. 26–40. [Google Scholar]
- Janssens, I.A.; Pilegaard, K. Large Seasonal Changes in Q10 of Soil Respiration in a Beech Forest: SHORT-TERM Q 10 OF SOIL RESPIRATION. Glob. Change Biol. 2003, 9, 911–918. [Google Scholar] [CrossRef]
- Xu, M.; Shang, H. Contribution of Soil Respiration to the Global Carbon Equation. J. Plant Physiol. 2016, 203, 16–28. [Google Scholar] [CrossRef]
- Balogh, J.; Pintér, K.; Fóti, S.; Cserhalmi, D.; Papp, M.; Nagy, Z. Dependence of Soil Respiration on Soil Moisture, Clay Content, Soil Organic Matter, and CO2 Uptake in Dry Grasslands. Soil Biol. Biochem. 2011, 43, 1006–1013. [Google Scholar] [CrossRef]
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using Lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Kuznetsova, A.; Brockhoff, P.B.; Christensen, R.H.B. lmerTest Package: Tests in Linear Mixed Effects Models. J. Stat. Softw. 2017, 82, 1–26. [Google Scholar] [CrossRef]
- Lüdecke, D. sjPlot: Data Visualization for Statistics in Social Science. R Package Version 2.8.17 2024. Available online: https://CRAN.R-project.org/package=sjPlot (accessed on 11 March 2025).
- Hadley, W. Ggplot2: Elegant Graphics for Data Analysis; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Giorgetta, M.; Jungclaus, J.; Reick, C.; Legutke, S.; Brovkin, V.; Crueger, T.; Esch, M.; Fieg, K.; Glushak, K.; Gayler, V.; et al. CMIP5 Simulations of the Max Planck Institute for Meteorology (MPI-M) Based on the MPI-ESM-LR Model: The Rcp85 Experiment, Served by ESGF. World Data Cent. Clim. 2012. [Google Scholar] [CrossRef]
- Giorgetta, M.; Jungclaus, J.; Reick, C.; Legutke, S.; Brovkin, V.; Crueger, T.; Esch, M.; Fieg, K.; Glushak, K.; Gayler, V.; et al. CMIP5 Simulations of the Max Planck Institute for Meteorology (MPI-M) Based on the MPI-ESM-LR Model: The Rcp45 Experiment, Served by ESGF. World Data Cent. Clim. 2012. [Google Scholar] [CrossRef]
- Xu, K.; Wang, X.; Liang, P.; An, H.; Sun, H.; Han, W.; Li, Q. Tree-Ring Widths Are Good Proxies of Annual Variation in Forest Productivity in Temperate Forests. Sci. Rep. 2017, 7, 1945. [Google Scholar] [CrossRef]
- Kagawa, A.; Sugimoto, A.; Maximov, T.C. 13CO2 Pulse-Labelling of Photoassimilates Reveals Carbon Allocation within and between Tree Rings. Plant Cell Environ. 2006, 29, 1571–1584. [Google Scholar] [CrossRef]
- Kozlowski, T.T. Carbohydrate Sources and Sinks in Woody Plants. Bot. Rev. 1992, 58, 107–222. [Google Scholar] [CrossRef]
- Ouyang, S.; Wang, X.; Wu, Y.; Jianxin Sun, O. Contrasting Responses of Net Primary Productivity to Inter-Annual Variability and Changes of Climate among Three Forest Types in Northern China. J. Plant Ecol. 2014, 7, 309–320. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, G.; Chen, Z.; Zhang, L.; Wang, Q.; Zhang, Y.; He, H.; Han, L.; Chen, S.; Han, S.; et al. Attribute Parameter Characterized the Seasonal Variation of Gross Primary Productivity (αGPP): Spatiotemporal Variation and Influencing Factors. Agric. For. Meteorol. 2020, 280, 107774. [Google Scholar] [CrossRef]
- Chirici, G.; Chiesi, M.; Fibbi, L.; Giannetti, F.; Corona, P.; Maselli, F. High Spatial Resolution Modelling of Net Forest Carbon Fluxes Based on Ground and Remote Sensing Data. Agric. For. Meteorol. 2022, 316, 108866. [Google Scholar] [CrossRef]
- Maseyk, K.; Grünzweig, J.M.; Rotenberg, E.; Yakir, D. Respiration Acclimation Contributes to High Carbon-Use Efficiency in a Seasonally Dry Pine Forest: Respiration Acclimation Under Drought. Glob. Change Biol. 2008, 14, 1553–1567. [Google Scholar] [CrossRef]
- Chen, S.; Zou, J.; Hu, Z.; Lu, Y. Climate and Vegetation Drivers of Terrestrial Carbon Fluxes: A Global Data Synthesis. Adv. Atmos. Sci. 2019, 36, 679–696. [Google Scholar] [CrossRef]
- Fibbi, L.; Moriondo, M.; Chiesi, M.; Bindi, M.; Maselli, F. Impacts of Climate Change on the Gross Primary Production of Italian Forests. Ann. For. Sci. 2019, 76, 59. [Google Scholar] [CrossRef]
- Gea-Izquierdo, G.; Nicault, A.; Battipaglia, G.; Dorado-Liñán, I.; Gutiérrez, E.; Ribas, M.; Guiot, J. Risky Future for Mediterranean Forests Unless They Undergo Extreme Carbon Fertilization. Glob. Change Biol. 2017, 23, 2915–2927. [Google Scholar] [CrossRef]
- Haverd, V.; Smith, B.; Canadell, J.G.; Cuntz, M.; Mikaloff-Fletcher, S.; Farquhar, G.; Woodgate, W.; Briggs, P.R.; Trudinger, C.M. Higher than Expected CO2 Fertilization Inferred from Leaf to Global Observations. Glob. Change Biol. 2020, 26, 2390–2402. [Google Scholar] [CrossRef]
- Keenan, T.; Maria Serra, J.; Lloret, F.; Ninyerola, M.; Sabate, S. Predicting the Future of Forests in the Mediterranean under Climate Change, with Niche- and Process-Based Models: CO2 Matters! Glob. Change Biol. 2011, 17, 565–579. [Google Scholar] [CrossRef]
- Kirschbaum, M.U.F. The Temperature Dependence of Soil Organic Matter Decomposition, and the Effect of Global Warming on Soil Organic C Storage. Soil Biol. Biochem. 1995, 27, 753–760. [Google Scholar] [CrossRef]
- Lloyd, J.; Taylor, J.A. On the Temperature Dependence of Soil Respiration. Funct. Ecol. 1994, 8, 315. [Google Scholar] [CrossRef]
- Ali, R.S.; Poll, C.; Kandeler, E. Dynamics of Soil Respiration and Microbial Communities: Interactive Controls of Temperature and Substrate Quality. Soil Biol. Biochem. 2018, 127, 60–70. [Google Scholar] [CrossRef]
- Zhao, C.; Miao, Y.; Yu, C.; Zhu, L.; Wang, F.; Jiang, L.; Hui, D.; Wan, S. Soil Microbial Community Composition and Respiration along an Experimental Precipitation Gradient in a Semiarid Steppe. Sci. Rep. 2016, 6, 24317. [Google Scholar] [CrossRef]
- Pietikainen, J.; Pettersson, M.; Baath, E. Comparison of Temperature Effects on Soil Respiration and Bacterial and Fungal Growth Rates. FEMS Microbiol. Ecol. 2005, 52, 49–58. [Google Scholar] [CrossRef] [PubMed]
- Tuomi, M.; Vanhala, P.; Karhu, K.; Fritze, H.; Liski, J. Heterotrophic Soil Respiration—Comparison of Different Models Describing Its Temperature Dependence. Ecol. Model. 2008, 211, 182–190. [Google Scholar] [CrossRef]
- Reichstein, M.; Rey, A.; Freibauer, A.; Tenhunen, J.; Valentini, R.; Banza, J.; Casals, P.; Cheng, Y.; Grünzweig, J.M.; Irvine, J.; et al. Modeling Temporal and Large-scale Spatial Variability of Soil Respiration from Soil Water Availability, Temperature and Vegetation Productivity Indices. Glob. Biogeochem. Cycles 2003, 17, 2003GB002035. [Google Scholar] [CrossRef]
- Chen, H.; Harmon, M.E.; Griffiths, R.P.; Hicks, W. Effects of Temperature and Moisture on Carbon Respired from Decomposing Woody Roots. For. Ecol. Manag. 2000, 138, 51–64. [Google Scholar] [CrossRef]
- Feng, X.; Uriarte, M.; González, G.; Reed, S.; Thompson, J.; Zimmerman, J.K.; Murphy, L. Improving Predictions of Tropical Forest Response to Climate Change through Integration of Field Studies and Ecosystem Modeling. Glob. Change Biol. 2018, 24, E213–E232. [Google Scholar] [CrossRef]
- Fierer, N.; Schimel, J.P.; Holden, P.A. Variations in Microbial Community Composition through Two Soil Depth Profiles. Soil Biol. Biochem. 2003, 35, 167–176. [Google Scholar] [CrossRef]
- Allard, V.; Ourcival, J.M.; Rambal, S.; Joffre, R.; Rocheteau, A. Seasonal and Annual Variation of Carbon Exchange in an Evergreen Mediterranean Forest in Southern France: CO2 Fluxes of A Mediterranean Forest. Glob. Change Biol. 2008, 14, 714–725. [Google Scholar] [CrossRef]
- Evrendilek, F.; Berberoglu, S.; Taskinsu-Meydan, S.; Yilmaz, E. Quantifying Carbon Budgets Of Conifer Mediterranean Forest Ecosystems, Turkey. Environ. Monit Assess 2006, 119, 527–543. [Google Scholar] [CrossRef] [PubMed]
- Maselli, F.; Papale, D.; Puletti, N.; Chirici, G.; Corona, P. Combining Remote Sensing and Ancillary Data to Monitor the Gross Productivity of Water-Limited Forest Ecosystems. Remote Sens. Environ. 2009, 113, 657–667. [Google Scholar] [CrossRef]
- Mollicone, D.; Matteucci, G.; Köble, R.; Masci, A.; Chiesi, M.; Smits, P.C. A Model-Based Approach for the Estimation of Carbon Sinks in European Forests. In Fluxes of Carbon, Water and Energy of European Forests; Valentini, R., Ed.; Ecological Studies; Springer: Berlin/Heidelberg, Germany, 2003; Volume 163, pp. 179–206. ISBN 978-3-642-07848-4. [Google Scholar]
- Carvalhais, N.; Reichstein, M.; Collatz, G.J.; Mahecha, M.D.; Migliavacca, M.; Neigh, C.S.R.; Tomelleri, E.; Benali, A.A.; Papale, D.; Seixas, J. Deciphering the Components of Regional Net Ecosystem Fluxes Following a Bottom-up Approach for the Iberian Peninsula. Biogeosciences 2010, 7, 3707–3729. [Google Scholar] [CrossRef]
- Chapin, F.S.; Matson, P.A.; Mooney, H.A. Principles of Terrestrial Ecosystem Ecology; Springer: New York, NY, USA, 2002; ISBN 978-0-387-95439-4. [Google Scholar]
- Zhang, Z.; Ju, W.; Li, X.; Cheng, X.; Zhou, Y.; Xu, S.; Liu, C.; Li, J. Joint Improvement on Absorbed Photosynthetically Active Radiation and Intrinsic Quantum Yield Efficiency Algorithms in the P Model Betters the Estimate of Terrestrial Gross Primary Productivity. Agric. For. Meteorol. 2024, 346, 109883. [Google Scholar] [CrossRef]
- Wang, H.; Prentice, I.C.; Keenan, T.F.; Davis, T.W.; Wright, I.J.; Cornwell, W.K.; Evans, B.J.; Peng, C. Towards a Universal Model for Carbon Dioxide Uptake by Plants. Nat. Plants 2017, 3, 734–741. [Google Scholar] [CrossRef]
- Fernández-Alonso, M.J.; Díaz-Pinés, E.; Ortiz, C.; Rubio, A. Disentangling the Effects of Tree Species and Microclimate on Heterotrophic and Autotrophic Soil Respiration in a Mediterranean Ecotone Forest. For. Ecol. Manag. 2018, 430, 533–544. [Google Scholar] [CrossRef]
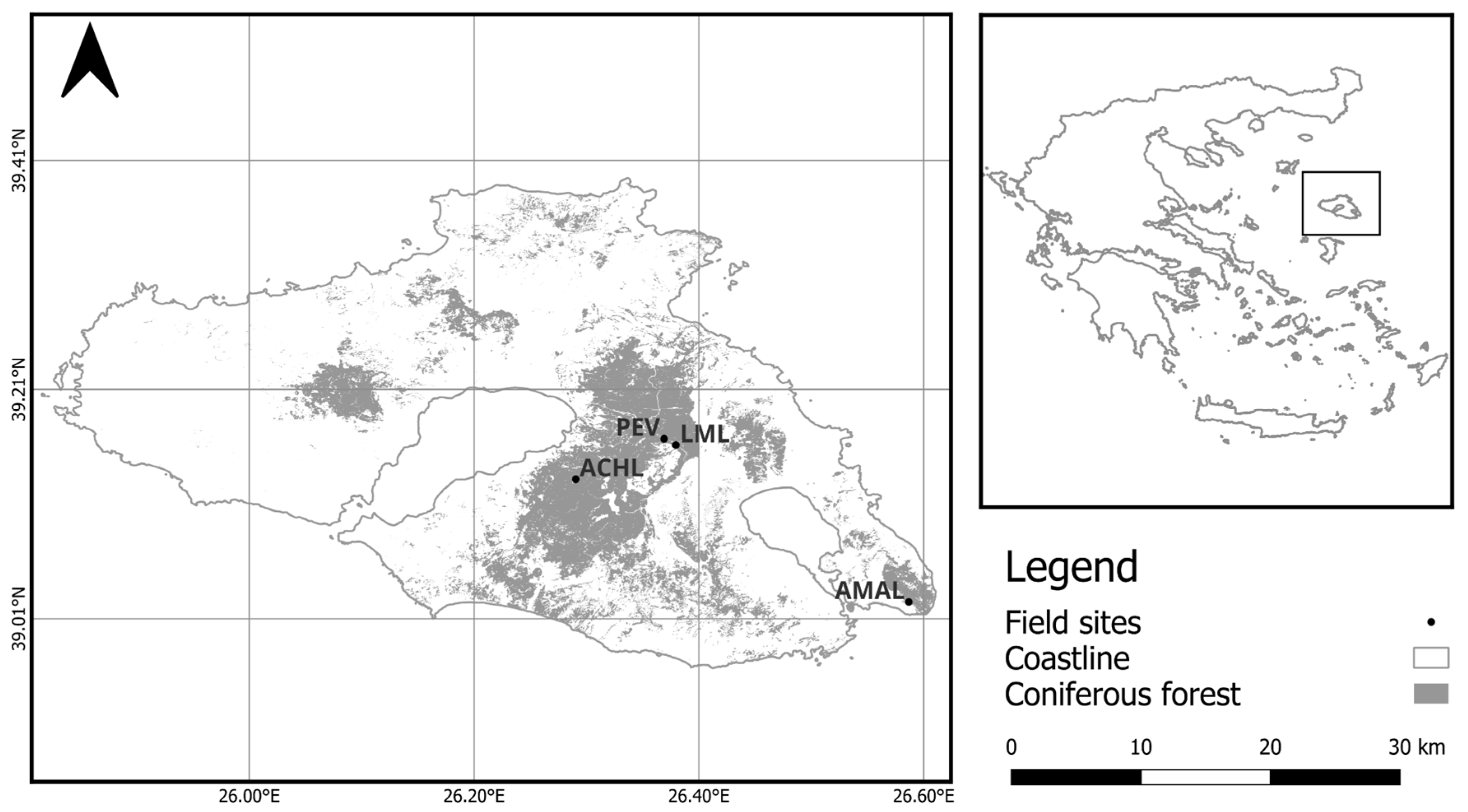
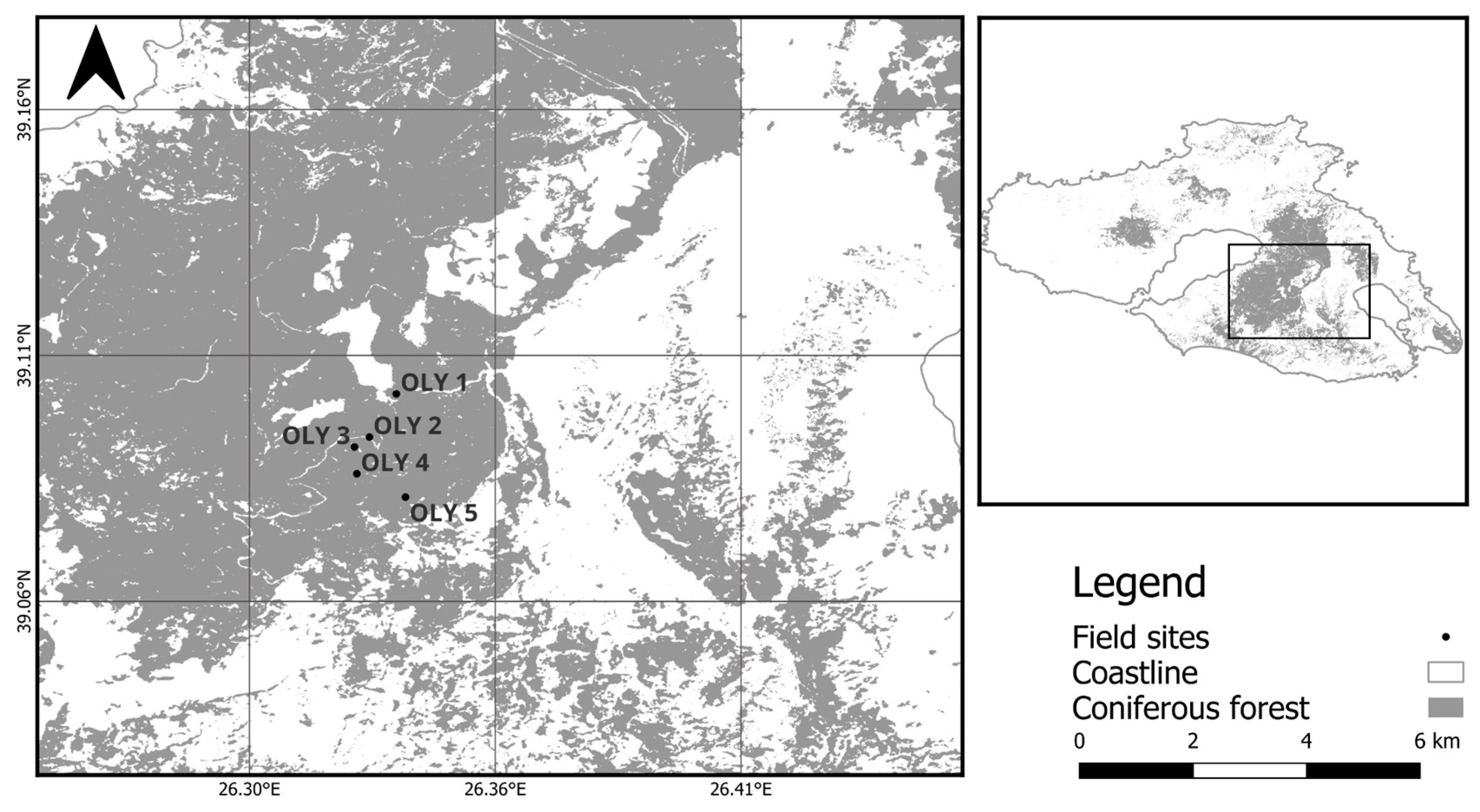

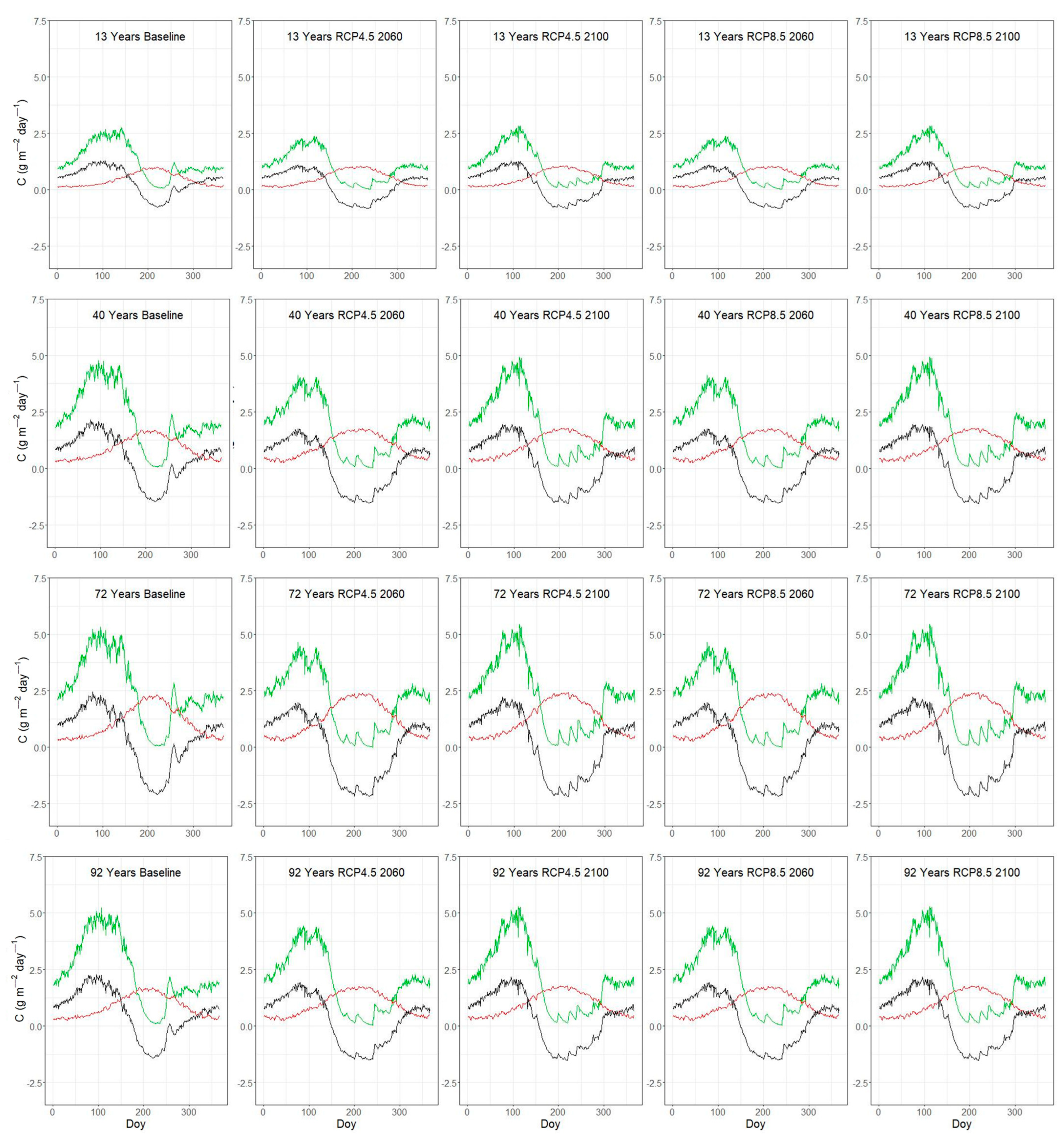
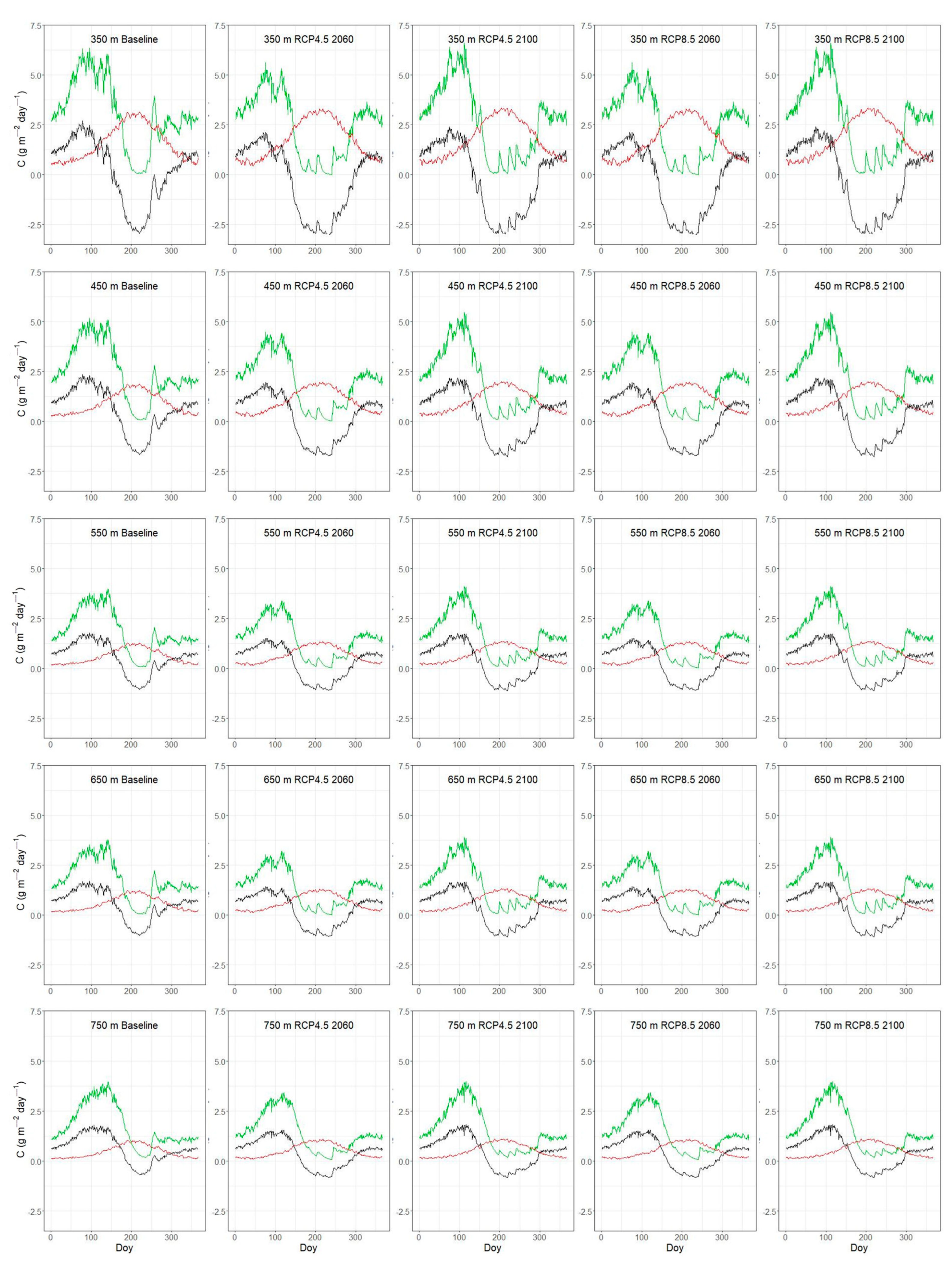
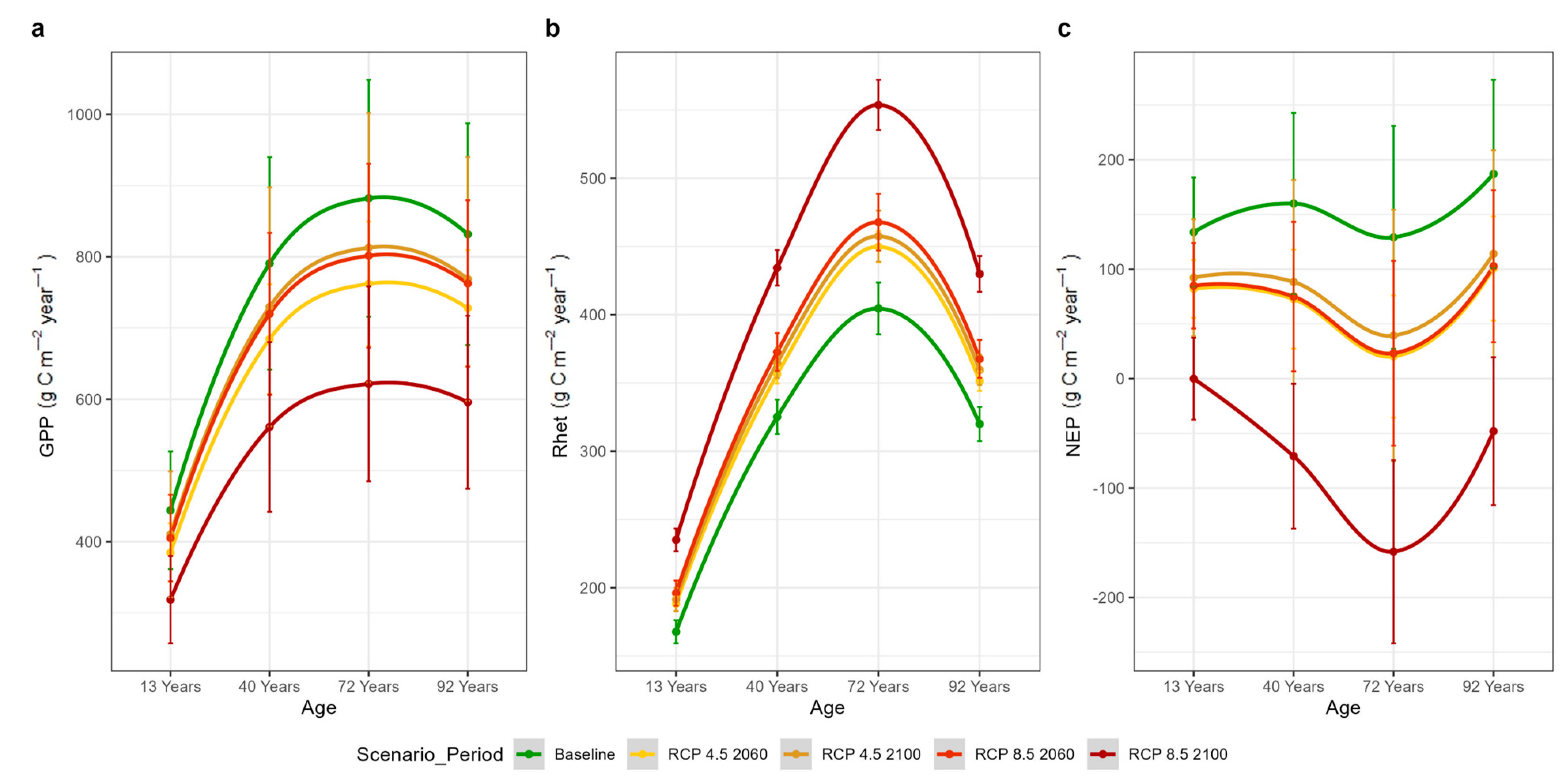

| Plot | Lat | Lon | Stand Age (y) | Elevation (m asl) | Inclination (%) | Orientation | LAI (m2 m−2) |
|---|---|---|---|---|---|---|---|
| AMAL | 39.02 | 26.59 | 13 | 316 | 10 | SE | 0.67 |
| PEV | 39.16 | 26.37 | 40 | 213 | 5 | SW | 1.66 |
| LML | 39.16 | 26.38 | 72 | 166 | 10 | SW | 2.13 |
| ACHL | 39.13 | 26.30 | 92 | 261 | 0 | - | 1.67 |
| OLY1 | 39.09 | 26.33 | 82 | 350 | 3 | NE | 4.26 |
| OLY2 | 39.09 | 26.33 | 95 | 450 | 7 | N | 2.08 |
| OLY3 | 39.09 | 26.33 | 96 | 550 | 5 | N | 1.23 |
| OLY4 | 39.08 | 26.33 | 64 | 650 | 7 | SE | 1.23 |
| OLY5 | 39.08 | 26.34 | 90 | 750 | 0 | - | 0.98 |
| Plot | Elevation (m) | TA | Tmin | Tmax | RHA | RHmin | RHmax | TsA | Tsmin | Tsmax |
|---|---|---|---|---|---|---|---|---|---|---|
| AMAL | 316 | 17.4 | 12.6 | 23.1 | 68.7 | 48.1 | 88.0 | |||
| PEV | 213 | 17.3 | 10.6 | 25.4 | 67.2 | 38.5 | 92.6 | |||
| LML | 166 | 16.6 | 9.2 | 24.7 | 70.8 | 44.8 | 91.5 | |||
| ACHL | 261 | 17.3 | 10.8 | 26.9 | 66.6 | 36.8 | 88.9 | |||
| OLY1 | 350 | 16.5 | 10.3 | 25.8 | 62.5 | 41.5 | 78.7 | 15.8 | 14.3 | 17.6 |
| OLY2 | 450 | 15.7 | 10.5 | 21.8 | 68.5 | 45.7 | 88.1 | 15.4 | 14.6 | 16.2 |
| OLY3 | 550 | 15.4 | 10.4 | 21.6 | 69.6 | 47.1 | 90.0 | 14.9 | 14.1 | 15.7 |
| OLY4 | 650 | 14.2 | 8.8 | 20.5 | 71.8 | 47.4 | 92.5 | 14.3 | 13.5 | 15.2 |
| OLY5 | 750 | 12.6 | 8.5 | 18.3 | 76.0 | 59.5 | 88.1 | 12.3 | 11.6 | 13.0 |
| RCP4.5 2060 | RCP4.5 2100 | RCP8.5 2060 | RCP8.5 2100 | |
|---|---|---|---|---|
| GPP (% change) | −13.2 | −7.7 | −8.8 | −28.8 |
| Rhet (% change) | 10.7 | 12.9 | 15.5 | 36.2 |
| NEP (% change) | −56 | −46.1 | −54.2 | −148 |
| RCP4.5 2060 | RCP4.5 2100 | RCP8.5 2060 | RCP8.5 2100 | |
|---|---|---|---|---|
| GPP (% change) | −13.8 | −7.6 | −8.5 | −28.3 |
| Rhet (% change) | 11.4 | 14.2 | 17 | 84 |
| NEP (% change) | −86 | −71.8 | −52.3 | −227.7 |
| Plots | NEP (g C m−2 s−1) | |
|---|---|---|
| Mean | SD | |
| 13 Years | 134 | ±50.0 |
| 40 Years | 160 | ±82.7 |
| 72 Years | 129 | ±101.8 |
| 92 Years | 187 | ±86.0 |
| 350 m a.s.l. | 52 | ±115.4 |
| 450 m a.s.l. | 188 | ±92.2 |
| 550 m a.s.l. | 185 | ±68.1 |
| 650 m a.s.l. | 180 | ±64.6 |
| 750 m a.s.l. | 216 | ±62.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sazeides, C.I.; Fyllas, N.M. Simulating Net Ecosystem Productivity (NEP) in Mediterranean Pine Forests (Pinus brutia) During the 21st Century: The Effect of Leaf Area Index and Elevation. Plants 2025, 14, 1090. https://doi.org/10.3390/plants14071090
Sazeides CI, Fyllas NM. Simulating Net Ecosystem Productivity (NEP) in Mediterranean Pine Forests (Pinus brutia) During the 21st Century: The Effect of Leaf Area Index and Elevation. Plants. 2025; 14(7):1090. https://doi.org/10.3390/plants14071090
Chicago/Turabian StyleSazeides, Christodoulos I., and Nikolaos M. Fyllas. 2025. "Simulating Net Ecosystem Productivity (NEP) in Mediterranean Pine Forests (Pinus brutia) During the 21st Century: The Effect of Leaf Area Index and Elevation" Plants 14, no. 7: 1090. https://doi.org/10.3390/plants14071090
APA StyleSazeides, C. I., & Fyllas, N. M. (2025). Simulating Net Ecosystem Productivity (NEP) in Mediterranean Pine Forests (Pinus brutia) During the 21st Century: The Effect of Leaf Area Index and Elevation. Plants, 14(7), 1090. https://doi.org/10.3390/plants14071090







