Developing the DSSAT-CERES-Millet Model for Dynamic Simulation of Grain Protein and Starch Accumulation in Foxtail Millet (Setaria italica) Under Varying Irrigation and Nitrogen Regimes
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Site
2.2. Field Experiments
2.2.1. Experimental Design
2.2.2. Measurements
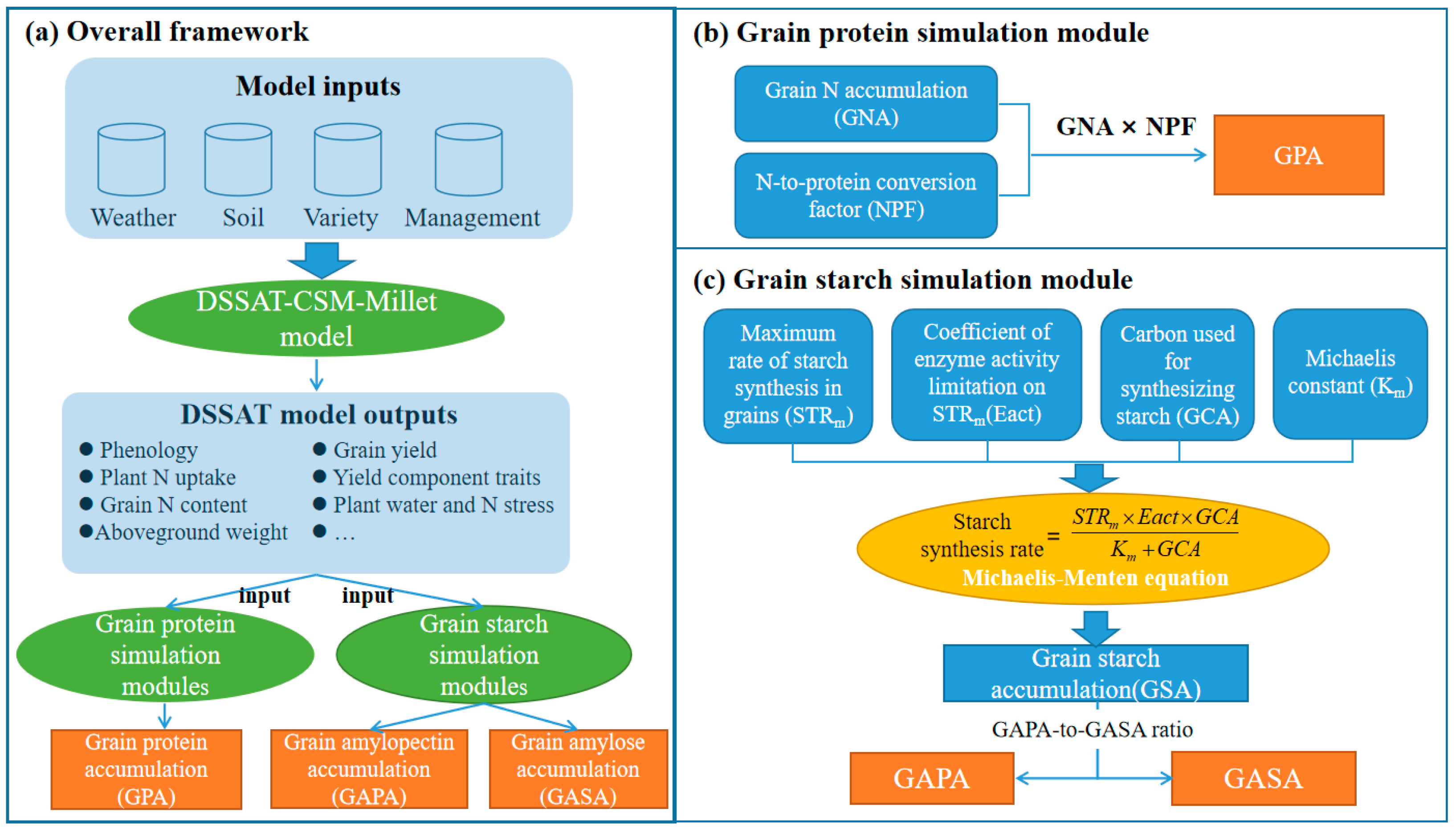
2.3. Models and Methods for Simulating Grain Protein and Starch Accumulation
2.3.1. Description of DSSAT-CERES-Millet
2.3.2. Description of Grain Protein Simulation Modules
2.3.3. Description of Grain Starch Simulation Modules
2.3.4. Model Calibration, Validation, and Evaluation
3. Results
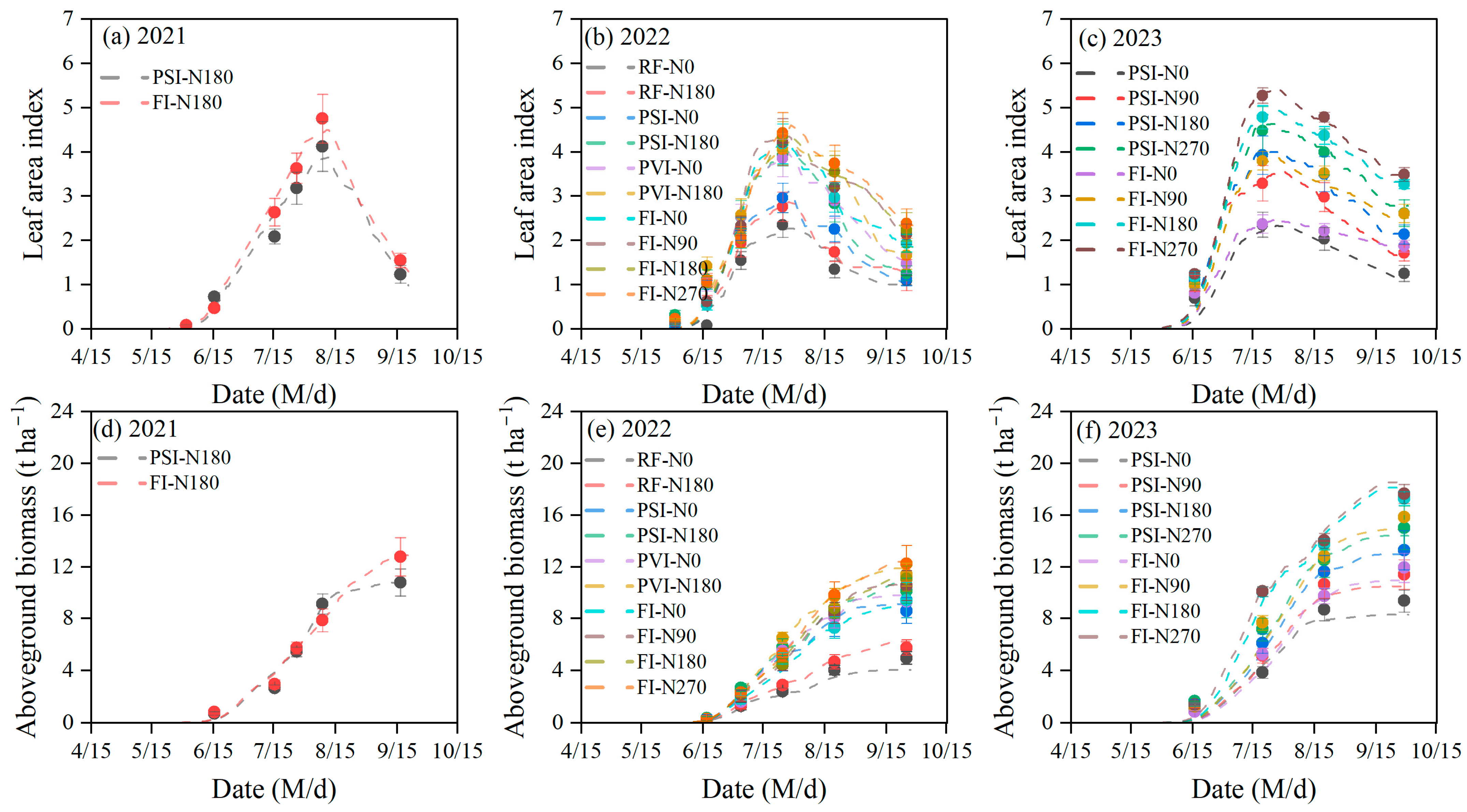
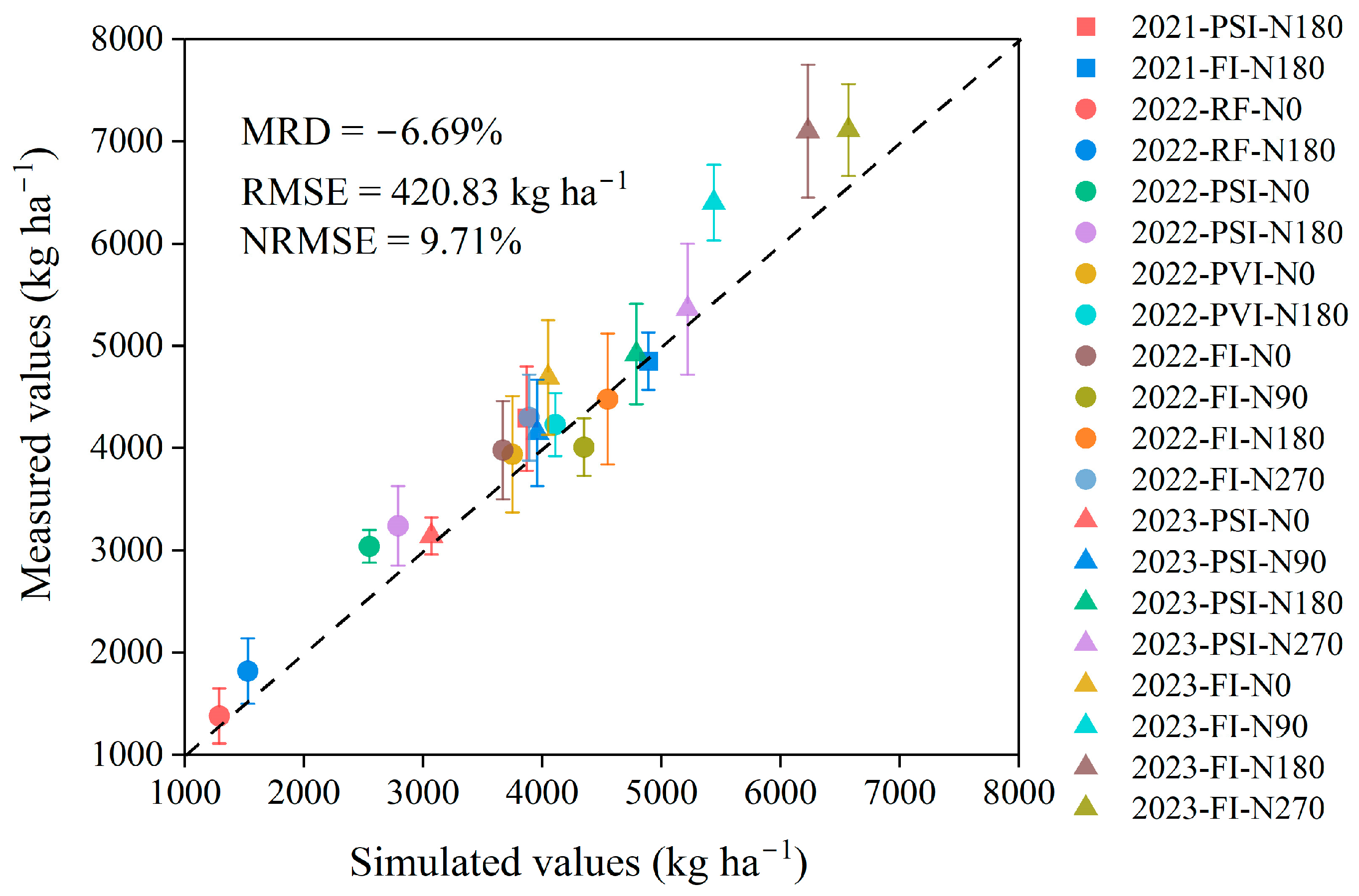
3.1. Performance of the DSSAT-CERES-Millet Model
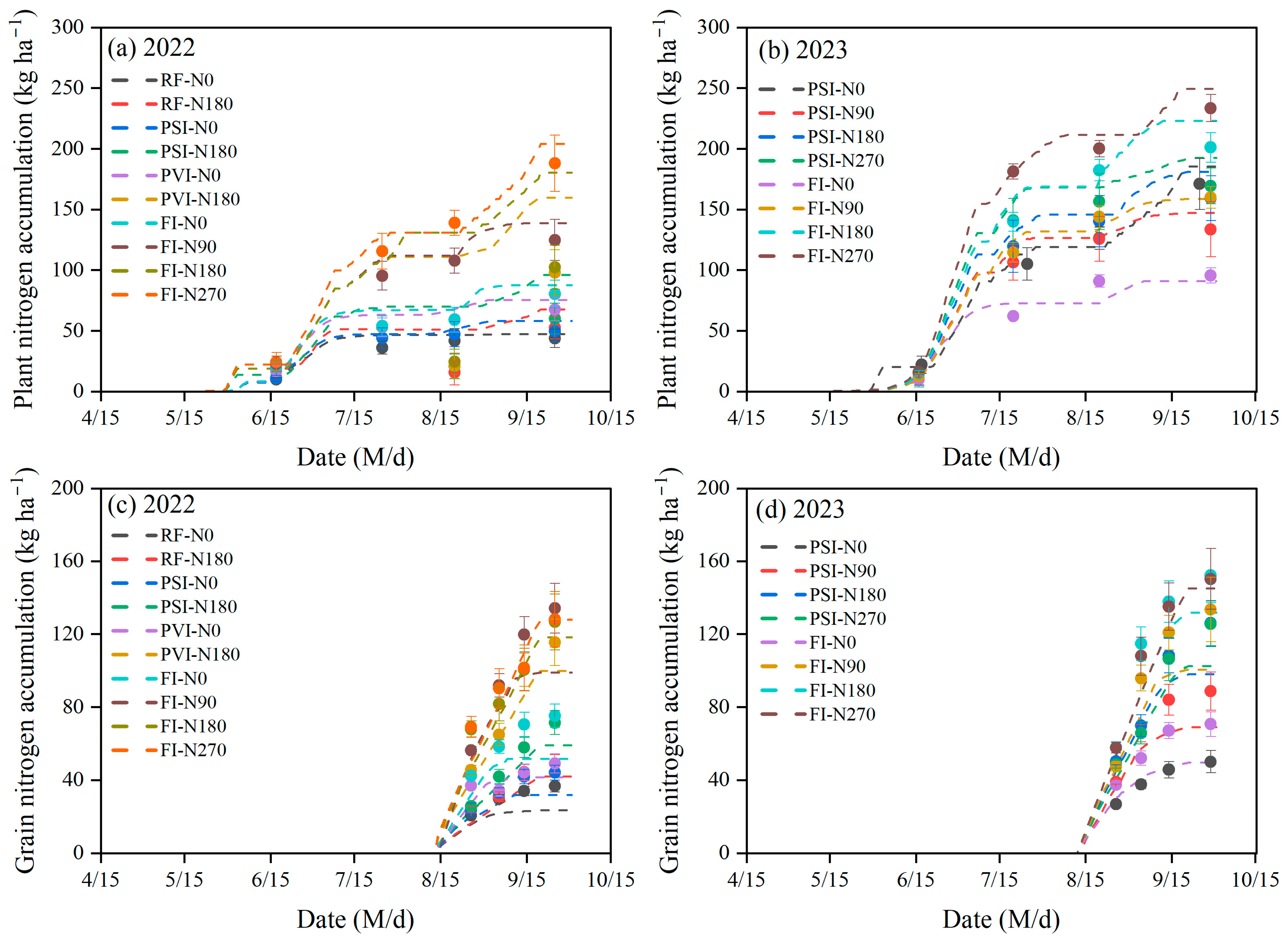
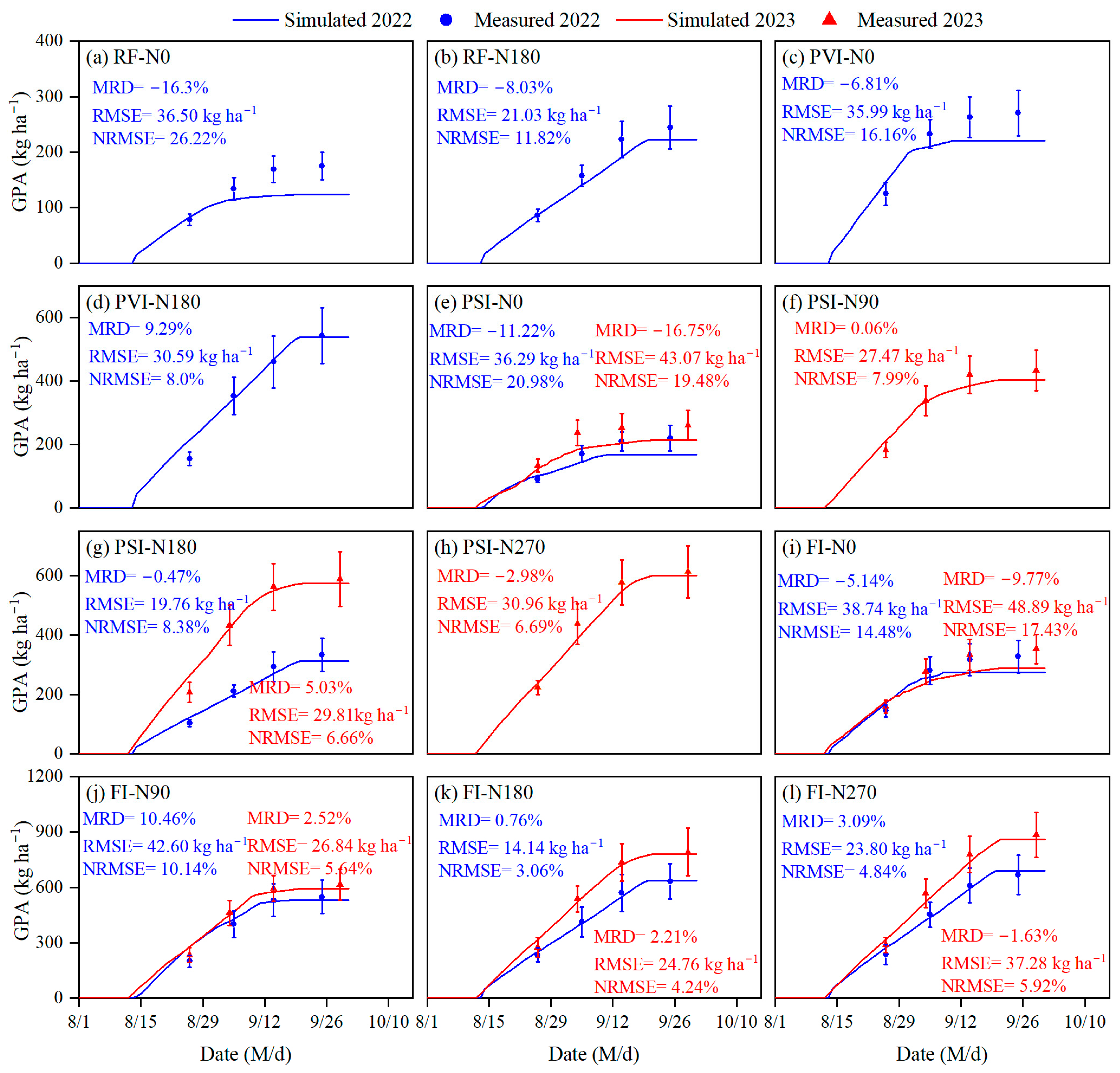
3.2. Simulation of Grain Protein Accumulation
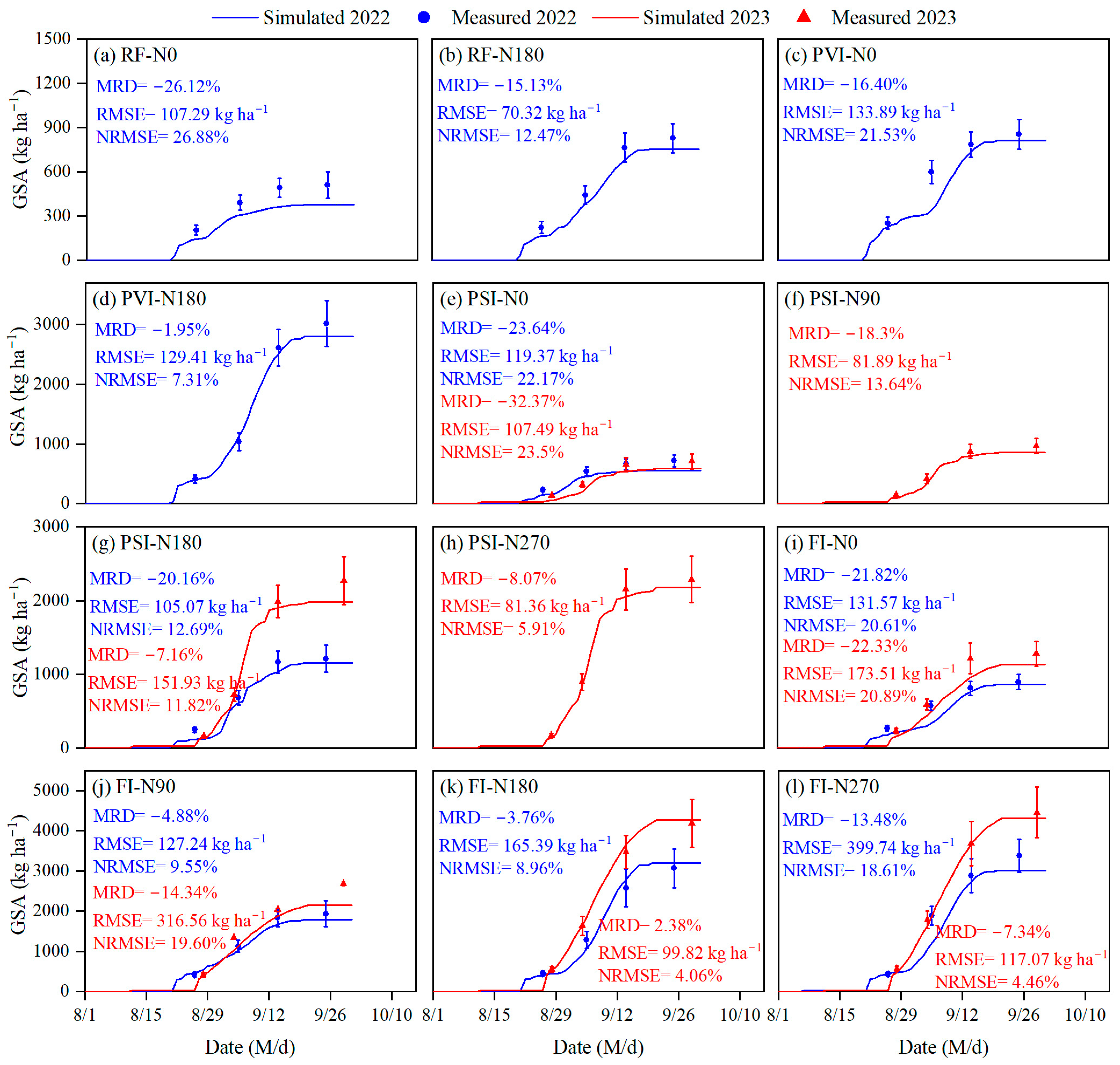
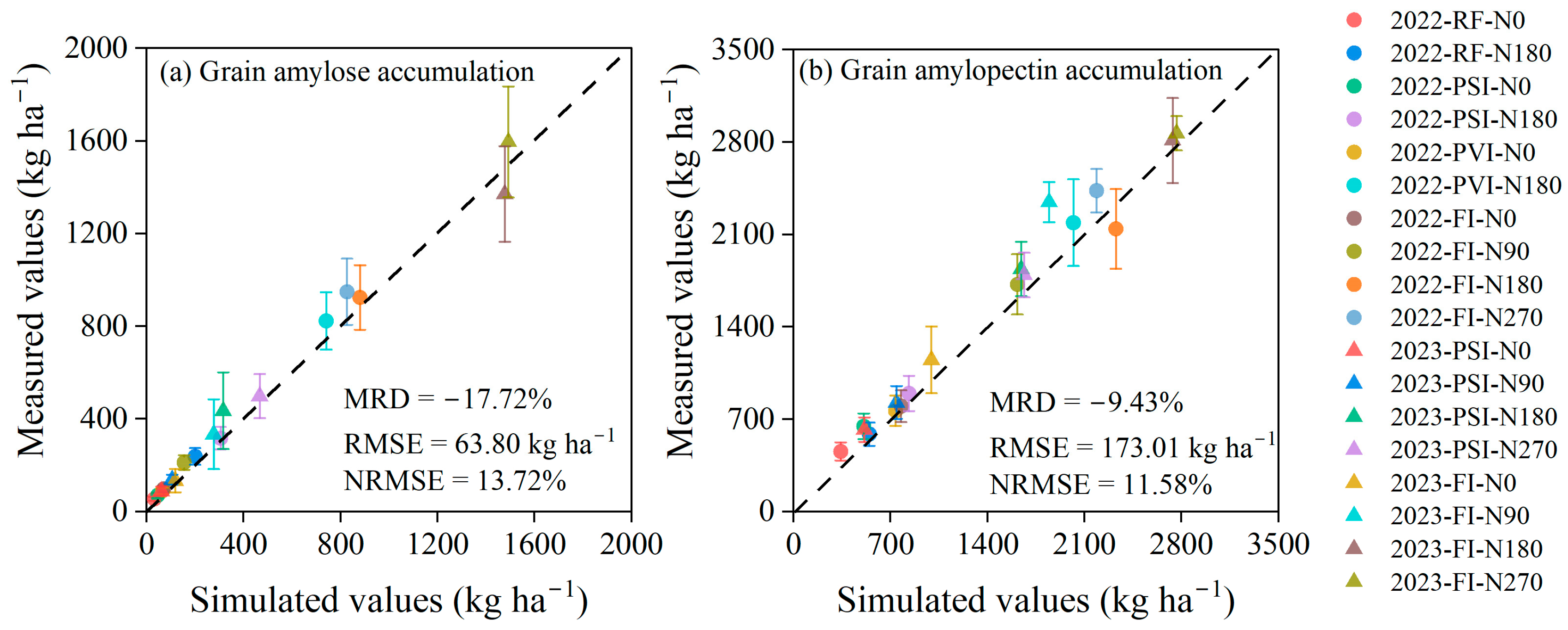
3.3. Simulation of Grain Starch Accumulation
4. Discussion
4.1. Performance of the DSSAT-CERES-Millet Model
4.2. Simulation of Grain Protein Accumulation
4.3. Simulation of Grain Starch Accumulation
4.4. Limitations of the Enhanced DSSAT-CERES-Millet Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Diao, X. Production and genetic improvement of minor cereals in China. Crop J. 2017, 5, 103–114. [Google Scholar] [CrossRef]
- Sharma, A.; Ceasar, S.A.; Pandey, H.; Devadas, V.S.; Kesavan, A.K.; Heisnam, P.; Vashishth, A.; Misra, V.; Mall, A.K. Millets: Nutrient-rich and climate-resilient crops for sustainable agriculture and diverse culinary applications. J. Food Compos. Anal. 2025, 137, 106984. [Google Scholar] [CrossRef]
- Hassan, Z.M.; Sebola, N.A.; Mabelebele, M. The nutritional use of millet grain for food and feed: A review. Agric. Food Secur. 2021, 10, 16. [Google Scholar] [CrossRef] [PubMed]
- Nie, T.; Li, J.; Jiang, L.; Zhang, Z.; Chen, P.; Li, T.; Dai, C.; Sun, Z.; Yin, S.; Wang, M. Optimizing Irrigation and Nitrogen Application to Enhance Millet Yield, Improve Water and Nitrogen Use Efficiency and Reduce Inorganic Nitrogen Accumulation in Northeast China. Plants 2024, 13, 3067. [Google Scholar] [CrossRef] [PubMed]
- Zheng, T.; Wang, S.; Wang, M.; Mao, J.; Xu, Y.; Ren, J.; Liu, Y.; Liu, S.; Qiao, Z.; Cao, X. Effect of Different Fertilizer Types on Quality of Foxtail Millet under Low Nitrogen Conditions. Plants 2024, 13, 1830. [Google Scholar] [CrossRef]
- Han, G.; Wang, J.; Zhao, H.; Wang, D.; Duan, Y.; Han, R.; Nie, M.E.; Zhao, L.; Du, H. Response of Quality and Yield of Foxtail Millet to Nitrogen and Zinc Application. Agriculture 2023, 13, 1731. [Google Scholar] [CrossRef]
- Hashemi, M.; Heidari, H.; Jahansouz, M.R.; Afshar, R.K. Evaluation of Yield and Quality of Sorghum and Millet as Alternative Forage Crops to Corn under Normal and Deficit Irrigation Regimes. Jordan J. Agric. Sci. 2014, 10, 699–715. [Google Scholar]
- Craufurd, P.Q.; Vadez, V.; Jagadish, S.V.K.; Prasad, P.V.V.; Zaman-Allah, M. Crop science experiments designed to inform crop modeling. Agric. For. Meteorol. 2013, 170, 8–18. [Google Scholar] [CrossRef]
- Matthews, R.B.; Rivington, M.; Muhammed, S.; Newton, A.C.; Hallett, P.D. Adapting crops and cropping systems to future climates to ensure food security: The role of crop modelling. Glob. Food Sec. 2013, 2, 24–28. [Google Scholar] [CrossRef]
- van Keulen, H.; Asseng, S. Simulation Models as Tools for Crop Management; Savin, R., Slafer, G.A., Eds.; Springer: New York, NY, USA, 2019; pp. 433–452. [Google Scholar]
- Zhou, S.; Ye, F.; Xia, D.; Liu, Z.; Wu, Y.; Chen, F. Climate change impacts assessment and developing adaptation strategies for rainfed foxtail millet in northern Shanxi, China. Agric. Water Manag. 2023, 290, 108575. [Google Scholar] [CrossRef]
- Guo, D.; Chen, C.; Guo, P.; Yuan, X.; Xing, X.; Ma, X. Evaluation of AquaCrop Model for Foxtail Millet (Setaria italica) Growth and Water Use with Plastic Film Mulching and No Mulching under Different Weather Conditions. Water 2018, 10, 836. [Google Scholar] [CrossRef]
- Akponikpè, P.B.I.; Gérard, B.; Michels, K.; Bielders, C. Use of the APSIM model in long term simulation to support decision making regarding nitrogen management for pearl millet in the Sahel. Eur. J. Agron. 2010, 32, 144–154. [Google Scholar] [CrossRef]
- Wang, S.; Zheng, M.; Yu, J.; Wang, S.; Copeland, L. Insights into the Formation and Structures of Starch–Protein–Lipid Complexes. J. Agric. Food Chem. 2017, 65, 1960–1966. [Google Scholar] [CrossRef]
- Qin, L.; Chen, G.; Chen, E.; Li, F.; Yang, Y.; Zhang, H.; Liu, Z.; Guan, Y. Effects of different ecological environments on the nutritional quality and starch characteristics of foxtail millet. J. China Agric. Univ. 2024, 29, 28–39. [Google Scholar]
- Dong, E.; Wang, Y.; Wang, J.; Liu, Q.; Huang, X.; Jiao, X. Effects of Nitrogen Fertilization Levels on Grain Yield, Plant Nitrogen Utilization Characteristics and Grain Quality of Foxtail Millet. Sci. Agric. Sin. 2024, 57, 306–318. [Google Scholar]
- Zhao, L.; Ma, K.; Zhang, L.; Tang, S.; Yuan, X.; Diao, X. Analysis of Agronomic Traits and Quality of Foxtail Millet Varieties in Different Ecological Regions. Crops 2022, 2, 44–53. [Google Scholar]
- Ji, W.; Osman, R.; Ma, J.; Jiang, X.; Wang, L.; Xiao, L.; Tang, L.; Cao, W.; Zhu, Y.; Liu, B.; et al. Improving Process-Based Modelling to Simulate the Effects of Low-Temperature Stress During Pre-Anthesis on the Quality Characteristics of Wheat Grains. Plant Cell Environ. 2025, 48, 1574–1593. [Google Scholar] [CrossRef] [PubMed]
- Guo, P.; Li, Y.; Li, B.; Xue, H.; Pan, Y.; Ding, M.; Li, X.; Liu, P.; Xu, S. The Progress for the Formation Simulation of Crop Quality. J. Inner Mongolia Univ. Natl. 2015, 5, 412–415. [Google Scholar]
- Nuttall, J.G.; O’Leary, G.J.; Panozzo, J.F.; Walker, C.K.; Barlow, K.M.; Fitzgerald, G.J. Models of grain quality in wheat—A review. Field Crops Res. 2017, 202, 136–145. [Google Scholar] [CrossRef]
- Thitisaksakul, M.; Jiménez, R.C.; Arias, M.C.; Beckles, D.M. Effects of environmental factors on cereal starch biosynthesis and composition. J. Cereal Sci. 2012, 56, 67–80. [Google Scholar] [CrossRef]
- Pan, J.; Zhu, Y.; Cao, W. Modeling plant carbon flow and grain starch accumulation in wheat. Field Crops Res. 2007, 101, 276–284. [Google Scholar] [CrossRef]
- Chen, J. Study on Rice Grain Starch and Protein Accumulation Simulation Model. Ph.D. Thesis, Nanjing Agricultural University, Nanjing, China, 2011. [Google Scholar]
- Ishigooka, Y.; Hasegawa, T.; Kuwagata, T.; Nishimori, M.; Wakatsuki, H. Revision of estimates of climate change impacts on rice yield and quality in Japan by considering the combined effects of temperature and CO2 concentration. J. Agric. Meteorol. 2021, 77, 139–149. [Google Scholar] [CrossRef]
- Cappelli, G.A.; Bregaglio, S. Model-based evaluation of climate change impacts on rice grain quality in the main European rice district. Food Energy Secur. 2021, 10, e307. [Google Scholar] [CrossRef]
- Liu, J.; Feng, H.; He, J.; Chen, H.; Ding, D. The effects of nitrogen and water stresses on the nitrogen-to-protein conversion factor of winter wheat. Agric. Water Manag. 2018, 210, 217–223. [Google Scholar] [CrossRef]
- Virmani, S.M.; Tandon, H.L.S.; Alagarswamy, G. Modeling the Growth and Development of Sorghum and Pearl Millet; Research Bulletin No. 12; ICRISAT: Patancheru, Andhra Pradesh, India, 1989. [Google Scholar]
- Hoogenboom, G.; Porter, C.H.; Shelia, V.; Boote, K.J.; Singh, U.; Pavan, W.; Oliveira, F.A.A.; Moreno-Cadena, L.P.; Ferreira, T.B.; White, J.W.; et al. Decision Support System for Agrotechnology Transfer (DSSAT) Version 4.8.5 (www.DSSAT.net); DSSAT Foundation: Gainesville, FL, USA, 2024. [Google Scholar]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Garba, M.; Kamara, A.Y.; Mohamed, A.M.L.; Tofa, A.I.; Mahamane, S.A.; Salissou, H.; Kapran, B.I.; Abdoulaye, T.; Garba, I.I. Assessing the effects of plant density and nitrogen on millet yield in Southern Niger using the CERES-millet model. CABI Agric. Biosci. 2024, 5, 20. [Google Scholar] [CrossRef]
- Liu, T.; Yang, X.; Batchelor, W.D.; Liu, Z.; Zhang, Z.; Wan, N.; Sun, S.; He, B.; Gao, J.; Bai, F.; et al. A case study of climate-smart management in foxtail millet (Setaria italica) production under future climate change in Lishu county of Jilin, China. Agric. For. Meteorol. 2020, 292–293, 108131. [Google Scholar] [CrossRef]
- Ullah, A.; Ahmad, I.; Ahmad, A.; Khaliq, T.; Saeed, U.; Habib-ur-Rahman, M.; Hussain, J.; Ullah, S.; Hoogenboom, G. Assessing climate change impacts on pearl millet under arid and semi-arid environments using CSM-CERES-Millet model. Environ. Sci. Pollut. Res. 2019, 26, 6745–6757. [Google Scholar] [CrossRef] [PubMed]
- Lancashire, P.D.; Bleiholder, H.; Boom, T.V.D.; Langelüddeke, P.; Stauss, R.; Weber, E.; Witzenberger, A. A uniform decimal code for growth stages of crops and weeds. Ann. Appl. Biol. 1991, 119, 561–601. [Google Scholar] [CrossRef]
- Sáez-Plaza, P.; Navas, M.J.; Wybraniec, S.; Michałowski, T.; Asuero, A.G. An Overview of the Kjeldahl Method of Nitrogen Determination. Part II. Sample Preparation, Working Scale, Instrumental Finish, and Quality Control. Crit. Rev. Anal. Chem. 2013, 43, 224–272. [Google Scholar] [CrossRef]
- Lin, C.; Chen, X.; Jian, L.; Shi, C.; Jin, X.; Zhang, G. Determination of grain protein content by near-infrared spectrometry and multivariate calibration in barley. Food Chem. 2014, 162, 10–15. [Google Scholar] [CrossRef] [PubMed]
- Chi, C.; Zou, Y.; Peng, X.; Yang, Y.; Chen, B.; He, Y.; Wang, H.; Weng, L. Measurement of starch gelatinization using a spectrophotometer. Food Hydrocoll. 2023, 144, 108956. [Google Scholar] [CrossRef]
- Greenwood, D.J.; Lemaire, G.; Gosse, G.; Cruz, P.; Draycott, A.; Neeteson, J.J. Decline in Percentage N of C3 and C4 Crops with Increasing Plant Mass. Ann. Bot. 1990, 66, 425–436. [Google Scholar] [CrossRef]
- Roskoski, R. Michaelis-Menten Kinetics. Reference Module in Biomedical Sciences; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Yang, J.; Zhang, J.; Wang, Z.; Zhu, Q.; Liu, L. Activities of enzymes involved in sucrose-to-starch metabolism in rice grains subjected to water stress during filling. Field Crops Res. 2003, 81, 69–81. [Google Scholar] [CrossRef]
- Dhaka, A.; Muthamilarasan, M.; Prasad, M. A comprehensive study on core enzymes involved in starch metabolism in the model nutricereal, foxtail millet (Setaria italica L.). J. Cereal Sci. 2021, 97, 103153. [Google Scholar] [CrossRef]
- He, J.; Dukes, M.D.; Jones, J.W.; Graham, W.D.; Judge, J. Applying GLUE for Estimating CERES-Maize Genetic and Soil Parameters for Sweet Corn Production. Trans. ASABE 2009, 52, 1907–1921. [Google Scholar] [CrossRef]
- Alhijawi, B.; Awajan, A. Genetic algorithms: Theory, genetic operators, solutions, and applications. Evol. Intell. 2024, 17, 1245–1256. [Google Scholar] [CrossRef]
- Jamieson, P.D.; Porter, J.R.; Wilson, D.R. A test of the computer simulation model ARCWHEAT1 on wheat crops grown in New Zealand. Field Crops Res. 1991, 27, 337–350. [Google Scholar] [CrossRef]
- Mohamed, A.M.L.; Jibrin, J.M.; Auwalu, B.M.; Garba, M.; Lawan, B.A. Application of Ceres-Millet model of DSSAT for simulating millet varieties under different sowing windows in Niger. J. Crop Improv. 2023, 37, 41–59. [Google Scholar] [CrossRef]
- Pandey, R.; Vengavasi, K.; Hawkesford, M.J. Plant adaptation to nutrient stress. Plant Physiol. Rep. 2021, 26, 583–586. [Google Scholar] [CrossRef]
- Yang, X.; Lu, M.; Wang, Y.; Wang, Y.; Liu, Z.; Chen, S. Response Mechanism of Plants to Drought Stress. Horticulturae 2021, 7, 50. [Google Scholar] [CrossRef]
- Chapagain, R.; Remenyi, T.A.; Harris, R.M.B.; Mohammed, C.L.; Huth, N.; Wallach, D.; Rezaei, E.E.; Ojeda, J.J. Decomposing crop model uncertainty: A systematic review. Field Crops Res. 2022, 279, 108448. [Google Scholar] [CrossRef]
- Jahangirlou, M.R.; Morel, J.; Akbari, G.A.; Alahdadi, I.; Soufizadeh, S.; Parsons, D. Combined use of APSIM and logistic regression models to predict the quality characteristics of maize grain. Eur. J. Agron. 2023, 142, 126629. [Google Scholar] [CrossRef]
- Johnson, K.A.; Goody, R.S. The Original Michaelis Constant: Translation of the 1913 Michaelis–Menten Paper. Biochemistry 2011, 50, 8264–8269. [Google Scholar] [CrossRef] [PubMed]
- Butterworth, P.J.; Bajka, B.H.; Edwards, C.H.; Warren, F.J.; Ellis, P.R. Enzyme kinetic approach for mechanistic insight and predictions of in vivo starch digestibility and the glycaemic index of foods. Trends Food Sci. Technol. 2022, 120, 254–264. [Google Scholar] [CrossRef]
- Schulze, W.X.; Altenbuchinger, M.; He, M.; Kränzlein, M.; Zörb, C. Proteome profiling of repeated drought stress reveals genotype-specific responses and memory effects in maize. Plant Physiol. Biochem. 2021, 159, 67–79. [Google Scholar] [CrossRef]
- Wang, X. Effects of Drought Stress at Booting Stage on Carbon Metabolism and Yield Formation of Japonica Rice in Cold Region. Ph.D. Thesis, Northeast Agricultural University, Harbin, China, 2020. [Google Scholar]
- Amoah, J.N.; Adu-Gyamfi, M.O.; Kwarteng, A.O. Unraveling the dynamics of starch metabolism and expression profiles of starch synthesis genes in millet under drought stress. Plant Gene 2024, 38, 100449. [Google Scholar] [CrossRef]
| Soil Layer (cm) | Texture (%) | BD (g/cm−3) | Ks (cm/h−1) | θFC (cm3/cm−3) | θWP (cm3/cm−3) | ||
|---|---|---|---|---|---|---|---|
| Sand | Silt | Clay | |||||
| 0~20 | 43.2 | 45.1 | 11.7 | 1.54 | 1.21 | 0.23 | 0.10 |
| 20~40 | 47.7 | 26.8 | 25.5 | 1.58 | 0.52 | 0.25 | 0.12 |
| 40~60 | 30.6 | 53.2 | 16.2 | 1.48 | 0.76 | 0.28 | 0.14 |
| 60~80 | 37.3 | 54.3 | 8.4 | 1.32 | 1.23 | 0.32 | 0.15 |
| 80~100 | 26.3 | 63.1 | 10.6 | 1.42 | 0.98 | 0.32 | 0.15 |
| Years | Treatments | N application Amount (kg/ha−1) | Total Irrigation Amount (mm) | Irrigation Time (Amount) of Each Irrigation Event |
|---|---|---|---|---|
| 2021 | PSI-N180 | 180 | 100 | 4/25 (100 mm) |
| FI-N180 | 180 | 280 | 4/25 (100 mm), 7/4 (60 mm), 8/4 (60 mm), 8/25 (60 mm) | |
| 2022 | RF-N0 | 0 | 0 | — |
| RF-N180 | 180 | 0 | — | |
| PSI-N0 | 0 | 100 | 4/21 (100 mm) | |
| PSI-N180 | 180 | 100 | 4/21 (100 mm) | |
| PVI-N0 | 0 | 220 | 4/21 (100 mm), 6/19 (60 mm), 7/18 (60 mm) | |
| PVI-N180 | 180 | 220 | 4/21 (100 mm), 6/19 (60 mm), 7/18 (60 mm) | |
| FI-N0 | 0 | 280 | 4/21 (100 mm), 6/19 (60 mm), 7/18 (60 mm), 8/3 (60 mm) | |
| FI-N90 | 90 | 280 | 4/21 (100 mm), 6/19 (60 mm), 7/18 (60 mm), 8/3 (60 mm) | |
| FI-N180 | 180 | 280 | 4/21 (100 mm), 6/19 (60 mm), 7/18 (60 mm), 8/3 (60 mm) | |
| FI-N270 | 270 | 280 | 4/21 (100 mm), 6/19 (60 mm), 7/18 (60 mm), 8/3 (60 mm) | |
| 2023 | PSI-N0 | 0 | 100 | 4/24 (100 mm) |
| PSI-N90 | 90 | 100 | 4/24 (100 mm) | |
| PSI-N180 | 180 | 100 | 4/24 (100 mm) | |
| PSI-N270 | 270 | 100 | 4/24 (100 mm) | |
| FI-N0 | 0 | 280 | 4/24 (100 mm), 6/10 (60 mm), 7/8 (60 mm), 8/27 (60 mm) | |
| FI-N90 | 90 | 280 | 4/24 (100 mm), 6/10 (60 mm), 7/8 (60 mm), 8/27 (60 mm) | |
| FI-N180 | 180 | 280 | 4/24 (100 mm), 6/10 (60 mm), 7/8 (60 mm), 8/27 (60 mm) | |
| FI-N270 | 270 | 280 | 4/24 (100 mm), 6/10 (60 mm), 7/8 (60 mm), 8/27 (60 mm) |
| Model/Module | Parameters | Description | Values |
|---|---|---|---|
| DSSAT–CERES-Millet model | P1 | Thermal time from seedling emergence to the end of the juvenile phase, during which the plant is not responsive to changes in the photoperiod; GDD (°C d) | 138.0 |
| P20 | Critical photoperiod, or the longest day length at which development occurs at the maximum rate; at values higher than P20, the rate of development is reduced; hours | 12.7 | |
| P2R | Extent to which phasic development leading to panicle initiation is delayed for each hour increase in the photoperiod above P20; GDD (°C d) | 32.0 | |
| P5 | Thermal time from the beginning of grain filling (3–4 days after anthesis) to physiological maturity; GDD (°C d) | 485.0 | |
| G1 | Scaler for the relative leaf size | 0.48 | |
| G4 | Scaler for partitioning of assimilates to the panicle (head) | 3.35 | |
| PHINT | Phyllochron interval; the interval between successive leaf tip appearances; GDD (°C d) | 41.0 | |
| Grain protein simulation module | NPF0 | The baseline value for the nitrogen-to-protein conversion factor | 5.83 |
| δ | The correction factor for NPF0 | 0.18 | |
| Grain starch simulation module | IGSA0 | The initial starch content in a single grain; mg per grain | 0.1 |
| ISTRm | Maximum starch accumulation rate of a single grain; mg/day−1 per grain | 1.2 | |
| Km | Michaelis constant; mg per grain | 0.7 | |
| GDDm | The accumulated temperature from anthesis to peak grain synthetic amylase activity; GDD (°C d) | 256 | |
| γ | Sensitivity coefficient of amylase activity to the accumulation of growing degree days after anthesis | 0.002 | |
| α | Scaling factor that determines how the natural logarithm of growing degree days influences the ratio of amylose accumulation relative to total starch | 0.4 | |
| β | Correction factor that adjusts the baseline ratio of amylose to total starch independent of heat accumulation and nitrogen stress effects | 2.1 |
| Year | Treatment | Leaf Area Index | Aboveground Biomass | ||||
|---|---|---|---|---|---|---|---|
| MRD (%) | RMSE | NRMSE (%) | MRD (%) | RMSE (t/ha−1) | NRMSE (%) | ||
| 2021 | PSI-N180 | −5.56 | 0.24 | 12.34 | −2.60 | 0.57 | 9.94 |
| FI-N180 | 4.37 | 0.20 | 8.79 | −6.03 | 0.43 | 7.08 | |
| 2022 | RF-N0 | 45.80 | 0.20 | 18.35 | −14.30 | 0.47 | 15.07 |
| RF-N180 | −22.42 | 0.24 | 16.69 | 7.55 | 0.24 | 8.23 | |
| PSI-N0 | −25.20 | 0.25 | 15.24 | 4.39 | 0.48 | 10.38 | |
| PSI-N180 | −21.60 | 0.35 | 14.02 | −9.03 | 0.38 | 6.92 | |
| PVI-N0 | −22.34 | 0.27 | 13.74 | 9.60 | 0.30 | 6.11 | |
| PVI-N180 | −21.91 | 0.28 | 12.35 | 3.33 | 0.31 | 5.27 | |
| FI-N0 | −15.00 | 0.21 | 10.41 | 0.21 | 0.41 | 8.67 | |
| FI-N90 | −16.85 | 0.22 | 10.65 | 5.81 | 0.21 | 4.07 | |
| FI-N180 | −19.77 | 0.23 | 10.07 | 2.60 | 0.13 | 2.48 | |
| FI-N270 | −18.54 | 0.19 | 8.27 | −2.87 | 0.10 | 1.65 | |
| 2023 | PSI-N0 | −22.25 | 0.30 | 16.96 | −22.23 | 0.94 | 14.34 |
| PSI-N90 | −15.09 | 0.33 | 13.43 | −28.45 | 1.06 | 12.87 | |
| PSI-N180 | −13.77 | 0.35 | 11.83 | −24.47 | 0.87 | 9.32 | |
| PSI-N270 | −12.66 | 0.42 | 12.53 | −25.41 | 1.10 | 10.52 | |
| FI-N0 | −15.38 | 0.28 | 14.06 | −28.92 | 1.01 | 12.67 | |
| FI-N90 | −19.40 | 0.39 | 12.95 | −26.46 | 1.27 | 11.71 | |
| FI-N180 | −15.97 | 0.42 | 11.21 | −18.62 | 1.00 | 8.17 | |
| FI-N270 | −14.67 | 0.40 | 9.72 | −13.86 | 0.88 | 6.26 | |
| Year | Treatment | Anthesis (Days After Sowing) | Maturity (Days After Sowing) | ||
|---|---|---|---|---|---|
| Measured | Simulated | Measured | Simulated | ||
| 2021 | PSI-N180 | 101 | 100 | 150 | 155 |
| FI-N180 | 99 | 100 | 154 | 155 | |
| 2022 | RF-N0 | 100 | 98 | 140 | 145 |
| RF-N180 | 102 | 98 | 141 | 145 | |
| PSI-N0 | 99 | 98 | 140 | 145 | |
| PSI-N180 | 100 | 98 | 142 | 145 | |
| PVI-N0 | 95 | 98 | 141 | 145 | |
| PVI-N180 | 98 | 98 | 144 | 145 | |
| FI-N0 | 96 | 98 | 140 | 145 | |
| FI-N90 | 97 | 98 | 142 | 145 | |
| FI-N180 | 98 | 98 | 145 | 145 | |
| FI-N270 | 98 | 98 | 144 | 145 | |
| 2023 | PSI-N0 | 102 | 101 | 148 | 152 |
| PSI-N90 | 100 | 101 | 150 | 152 | |
| PSI-N180 | 100 | 101 | 152 | 152 | |
| PSI-N270 | 103 | 101 | 152 | 152 | |
| FI-N0 | 98 | 101 | 151 | 152 | |
| FI-N90 | 102 | 101 | 154 | 152 | |
| FI-N180 | 100 | 101 | 153 | 152 | |
| FI-N270 | 103 | 101 | 154 | 152 | |
| Year | Treatment | Plant Nitrogen Accumulation | Grain Nitrogen Accumulation | ||||
|---|---|---|---|---|---|---|---|
| MRD (%) | RMSE (t/ha−1) | NRMSE (%) | MRD (%) | RMSE (t/ha−1) | NRMSE (%) | ||
| 2022 | RF-N0 | 14.55 | 6.13 | 18.66 | −29.75 | 9.80 | 32.39 |
| RF-N180 | −2.50 | 7.42 | 14.57 | −19.16 | 6.81 | 18.47 | |
| PSI-N0 | 5.64 | 4.98 | 13.04 | −21.28 | 8.60 | 24.30 | |
| PSI-N180 | −0.80 | 7.43 | 12.61 | −12.51 | 7.61 | 15.46 | |
| PVI-N0 | 2.40 | 8.37 | 16.92 | 13.96 | 8.39 | 20.45 | |
| PVI-N180 | 3.87 | 9.56 | 10.13 | −10.11 | 10.65 | 13.03 | |
| FI-N0 | 0.84 | 9.57 | 17.92 | −24.81 | 16.71 | 27.19 | |
| FI-N90 | 3.17 | 10.32 | 11.65 | −16.51 | 21.76 | 21.66 | |
| FI-N180 | 0.42 | 10.85 | 10.57 | −11.15 | 11.83 | 12.58 | |
| FI-N270 | 1.56 | 10.88 | 9.36 | −7.21 | 11.27 | 11.61 | |
| 2023 | PSI-N0 | 9.53 | 5.31 | 9.37 | −21.51 | 10.34 | 23.61 |
| PSI-N90 | 3.22 | 9.45 | 9.13 | −15.85 | 15.55 | 20.37 | |
| PSI-N180 | 8.35 | 13.65 | 11.55 | −10.74 | 17.57 | 18.02 | |
| PSI-N270 | 13.41 | 16.58 | 12.63 | −11.59 | 15.21 | 15.69 | |
| FI-N0 | 0.35 | 11.80 | 16.54 | −25.12 | 17.67 | 28.29 | |
| FI-N90 | −5.47 | 7.39 | 6.24 | −16.31 | 24.59 | 22.54 | |
| FI-N180 | 0.84 | 16.35 | 11.02 | −14.05 | 20.78 | 16.34 | |
| FI-N270 | 3.15 | 10.75 | 6.19 | −9.35 | 13.18 | 10.02 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Liu, Z.; Chen, F. Developing the DSSAT-CERES-Millet Model for Dynamic Simulation of Grain Protein and Starch Accumulation in Foxtail Millet (Setaria italica) Under Varying Irrigation and Nitrogen Regimes. Plants 2025, 14, 910. https://doi.org/10.3390/plants14060910
Zhou S, Liu Z, Chen F. Developing the DSSAT-CERES-Millet Model for Dynamic Simulation of Grain Protein and Starch Accumulation in Foxtail Millet (Setaria italica) Under Varying Irrigation and Nitrogen Regimes. Plants. 2025; 14(6):910. https://doi.org/10.3390/plants14060910
Chicago/Turabian StyleZhou, Shiwei, Zijin Liu, and Fu Chen. 2025. "Developing the DSSAT-CERES-Millet Model for Dynamic Simulation of Grain Protein and Starch Accumulation in Foxtail Millet (Setaria italica) Under Varying Irrigation and Nitrogen Regimes" Plants 14, no. 6: 910. https://doi.org/10.3390/plants14060910
APA StyleZhou, S., Liu, Z., & Chen, F. (2025). Developing the DSSAT-CERES-Millet Model for Dynamic Simulation of Grain Protein and Starch Accumulation in Foxtail Millet (Setaria italica) Under Varying Irrigation and Nitrogen Regimes. Plants, 14(6), 910. https://doi.org/10.3390/plants14060910





