Theoretical Analyses of Turgor Pressure and Expansive Growth Rate of Plant Cells During Water Deficit
Abstract
1. Introduction
1.1. Biophysical Perspective of Expansive Growth
1.2. Biophysical Equations Describing Expansive Growth
1.2.1. Rate of Water Uptake
1.2.2. Rate of Deformation of the Cell Wall
1.2.3. Rate of Change in the Turgor Pressure
1.3. Dimensionless Numbers and the Physical Interpretation of the Variables
1.4. Method
1.5. Overview
2. Analyses and Results
2.1. Turgor Pressure
2.2. Turgor Pressure When Lw and ϕp Change
- (a)
- P(t), Peq, and vs decrease when the rate of water uptake (Lw) decreases.
- (b)
- P(t) and Peq decrease, and vs increases, when the wall plastic deformation rate (ϕp) increases and Lw remains constant.
- (c)
- The same increase in ϕp produces a larger decrease in P(t) and Peq when Lw is smaller, and this produces a smaller increase in vs.
- (d)
- When Lw and/or ϕp decrease, tc increases. In general, changes in P(t) and v(t) take longer to complete when Lw is small.
2.3. Analyses of the Time Constant, tc
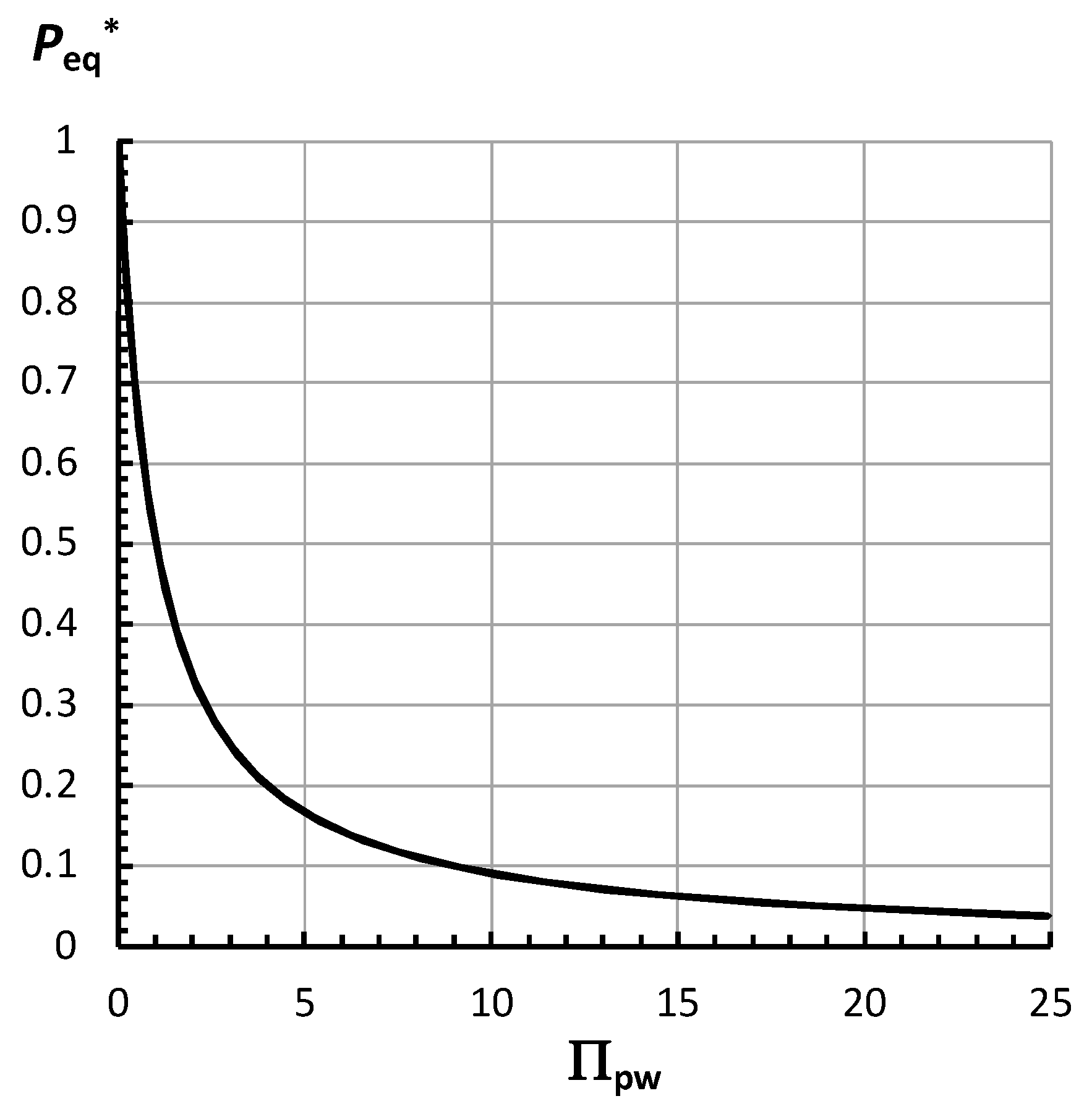
2.4. Analyses of the Equilibrium Turgor Pressure, Peq
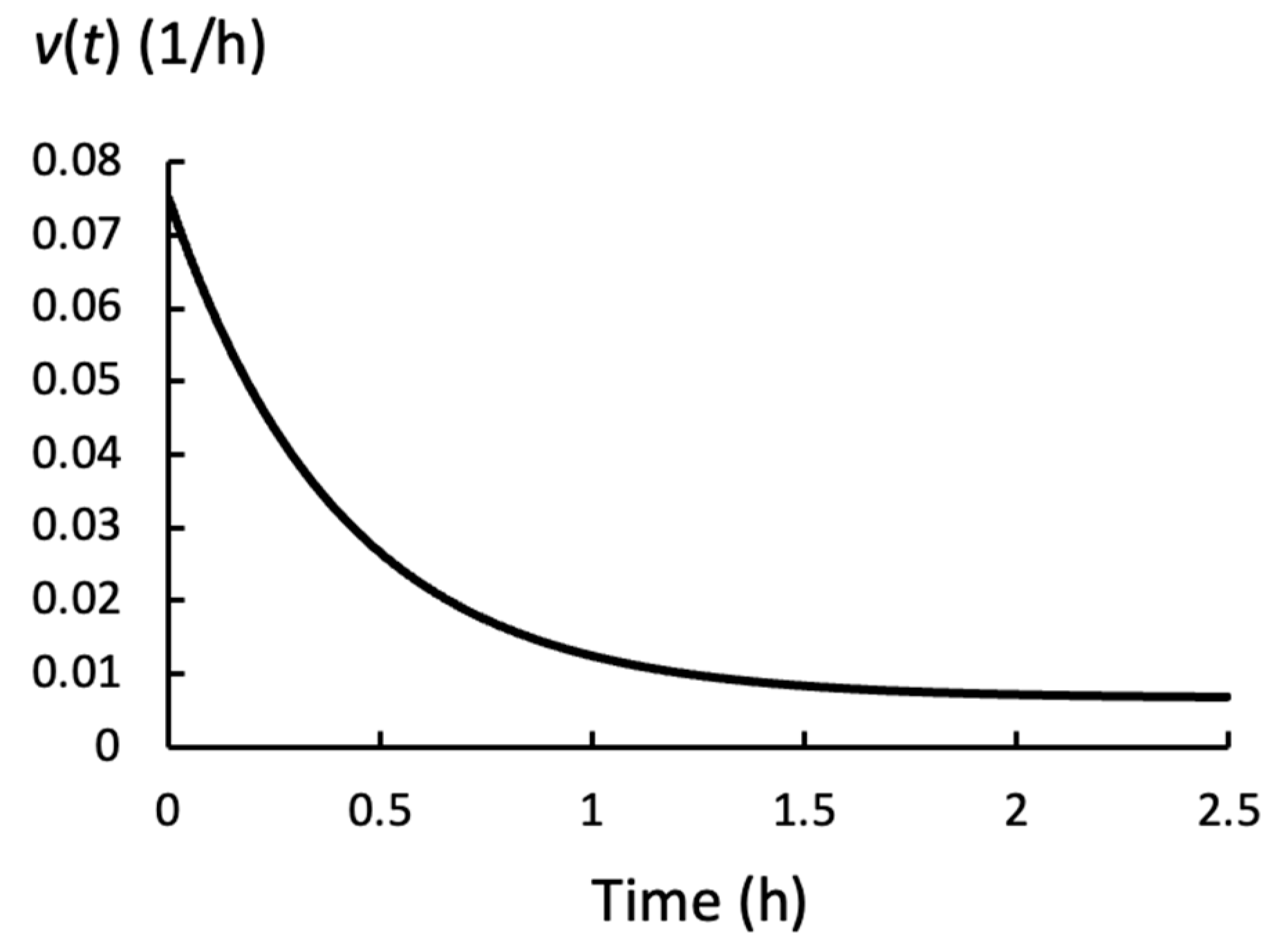
2.5. Growth Rate for Gradual Changes in P
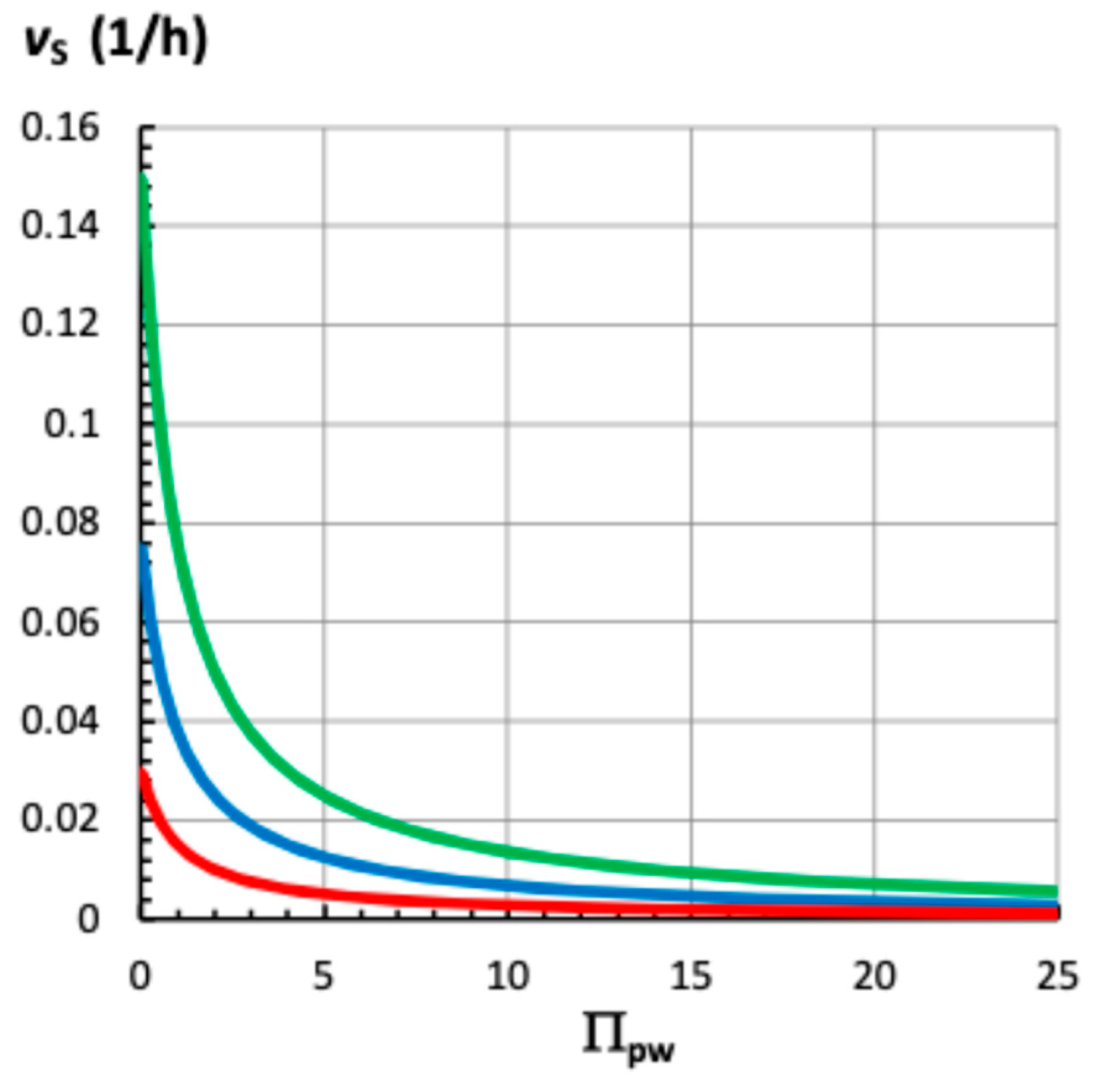
2.6. Steady Relative Growth Rate, vs, i.e., When P = Constant
3. Discussion
3.1. Turgor Pressure During Water Deficits
3.2. Expansive Growth During Water Deficit
3.3. Analyzing Expansive Growth During Water Deficits
3.4. Growth Rate and Turgor Pressure of Roots During Water Deficits
3.5. Growth Rate and Turgor Pressure of Maize Roots During Water Deficits
3.5.1. Passive Response
3.5.2. Active Response
3.5.3. Limitation of the “Lump” Parameter Method
3.6. Growth Rate of Roots and Shoots from Other Plants During Water Deficits
3.7. Transpiration and Apoplasm Pathway
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Definitions of Individual Variables (Units)
- A—area of the plasma membrane (m2)
- Lp—hydraulic conductivity of the plasma membrane (m h−1 MPa−1)
- L—relative hydraulic conductance of the plasma membrane (h−1 MPa−1)
- P—turgor pressure (MPa)
- t—time (h)
- V—volume (m3)
- v—relative rate of change in volume (h−1)
- ε—volumetric elastic modulus of the cell wall (MPa)
- ϕ—relative irreversible extensibility of the cell wall (h−1 MPa−1)
- π—osmotic pressure (MPa)
- Δπ—difference in osmotic pressure across the plasma membrane (MPa)
- Π—dimensionless parameter or dimensionless number (no units)
Appendix B. Derivation of Equation (7)
Appendix C. Derivation of Equation (8)
Appendix D. Using Equation (8) to Calculate Peq
Appendix E. Derivation of Equation (12)
References
- Boyer, J.S. Plant productivity and environment. Science 1982, 218, 443–448. [Google Scholar] [CrossRef]
- Fedoroff, N.V. The past, present and future of crop genetic modification. New Biotechnol. 2010, 27, 461–465. [Google Scholar] [CrossRef]
- Cao, Y.; Yang, W.; Ma, J.; Cheng, Z.; Zhang, X.; Liu, X.; Wu, X.; Zhang, J. An Integrated Framework for Drought Stress in Plants. Int. J. Mol. Sci. 2024, 25, 9347. [Google Scholar] [CrossRef] [PubMed]
- Şimşek, Ö.; Isak, M.A.; Dönmez, D.; Şekerci, A.D.; İzgü, T.; Kaçar, Y.A. Advanced Biotechnological Interventions in Mitigating Drought Stress in Plants. Plants 2024, 13, 717. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, T.C. Plant responses to water stress. Annu. Rev. Plant. Physiol. 1973, 24, 519–570. [Google Scholar] [CrossRef]
- Voothuluru, P.; Wu, Y.; Sharp, R.E. Not so hidden anymore: Advances and challenges in understanding root growth under water deficits. Plant Cell 2024, 36, 1377–1409. [Google Scholar] [CrossRef]
- Dumais, J. Mechanics and hydraulics of pollen tube growth. New Phytol. 2021, 232, 1549–1565. [Google Scholar] [CrossRef]
- Ali, O.; Cheddadi, I.; Landrein, B.; Long, Y. Revisiting the relationship between turgor pressure and plant cell growth. New Phytol. 2023, 238, 62–69. [Google Scholar] [CrossRef]
- Chaumont, F.; Tyerman, S.D. Aquaporins: Highly Regulated Channels Controlling Plant Water Relations. Plant Physiol. 2014, 164, 1600–1618. [Google Scholar] [CrossRef]
- Cosgrove, D.J. Structure and growth of plant cell walls. Nat. Rev. Mol. Cell Biol. 2024, 25, 340–358. [Google Scholar] [CrossRef]
- Ortega, J.K.E. Theoretical analyses of turgor pressure during stress relaxation and water uptake, and after changes in expansive growth rate when water uptake is normal and reduced. Plants 2023, 12, 1891. [Google Scholar] [CrossRef]
- Fox, R.W.; McDonald, A.T.; Pritchard, P.J. Introduction to Fluid Mechanics, 6th ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; John Wiley and Sons: Hoboken, NJ, USA, 1975; ISBN 978-0-471-43132-9. [Google Scholar]
- Dainty, J. Water relations of plant cells. Adv. Bot. Res. 1963, 1, 279–326. [Google Scholar]
- Lockhart, J.A. An analysis of irreversible plant cell elongation. J. Theor. Biol. 1965, 8, 264–275. [Google Scholar] [CrossRef] [PubMed]
- Ray, P.M.; Green, P.B.; Cleland, R. Role of turgor in plant cell growth. Nature 1972, 239, 163–164. [Google Scholar] [CrossRef]
- Ortega, J.K.E. Augmented equation for cell wall expansion. Plant Physiol. 1985, 79, 318–320. [Google Scholar] [CrossRef]
- Ortega, J.K.E.; Keanini, R.G.; Manica, K.J. Pressure probe technique to study transpiration in Phycomyces sporangiophores. Plant Physiol. 1988, 87, 11–14. [Google Scholar] [CrossRef]
- Ortega, J.K.E. Governing equations for plant cell growth. Physiol. Plant. 1990, 79, 116–121. [Google Scholar] [CrossRef]
- Ortega, J.K.E. Plant cell growth in tissue. Plant Physiol. 2010, 154, 1244–1253. [Google Scholar] [CrossRef]
- Geitmann, A.; Ortega, J.K.E. Mechanics and modeling of plant cell growth. Trends Plant Sci. 2009, 14, 467–478. [Google Scholar] [CrossRef]
- Ortega, J.K.E.; Welch, S.W.J. Mathematical models for expansive growth of cells with walls. Math. Model. Nat. Phenom. 2013, 8, 35–61. [Google Scholar] [CrossRef]
- Ortega, J.K.E. Dimensional analysis of expansive growth of cells with walls. Res. Rev. J. Bot. Sci. 2016, 5, 17–24. [Google Scholar]
- Ortega, J.K.E. Dimensionless number is central to stress relaxation and expansive growth of the cell wall. Sci. Rep. 2017, 7, 3016. [Google Scholar] [CrossRef] [PubMed]
- Ortega, J.K.E. Dimensionless numbers for plant biology. Trends Plant Sci. 2018, 23, 6–9. [Google Scholar] [CrossRef] [PubMed]
- Ortega, J.K.E. Dimensionless numbers to analyze expansive growth processes. Plants 2019, 8, 17. [Google Scholar] [CrossRef]
- Munoz, C.M.; Ortega, J.K.E. Dimensionless numbers to study cell wall deformation of stiff mutants of Phycomyces blakesleeanus. Plant Direct 2019, 3, e00195. [Google Scholar] [CrossRef]
- Ortega, J.K.E. The relationship between wall extensibility, hydraulic conductance, and turgor pressure during expansive growth. Plant Physiol. 2025, 197, kiaf135. [Google Scholar] [CrossRef]
- Cosgrove, D.J. Cell wall yield properties of growing tissue; evaluation by in vivo stress relaxation. Plant Physiol. 1985, 78, 347–356. [Google Scholar] [CrossRef]
- Hsiao, T.C.; Xu, L.-K. Sensitivity of growth of roots versus leaves to water stress: Biophysical analysis and relation to water transport. J. Exp. Bot. 2000, 51, 1595–1616. [Google Scholar] [CrossRef]
- Cosgrove, D.J. Analysis of the dynamic and steady-state responses of growth rate and turgor pressure to changes in cell parameters. Plant Physiol. 1981, 68, 1439–1446. [Google Scholar] [CrossRef]
- Sharp, R.E.; Silk, W.K.; Hsiao, T.C. Growth of the maize primary root at low water potential: Spatial distribution of expansive growth. Plant Physiol. 1988, 87, 50–57. [Google Scholar] [CrossRef]
- Spollen, W.G.; Sharp, R.E. Spatial distribution of turgor and root growth at low water potential. Plant Physiol. 1991, 96, 438–443. [Google Scholar] [CrossRef]
- Sharp, R.E.; Hsiao, T.C.; Silk, W.K. Growth of the maize primary root at low water potentials. II. Role of growth and deposition of hexose and potassium in osmotic adjustment. Plant Physiol. 1990, 93, 1337–1346. [Google Scholar] [CrossRef]
- Spollen, W.G.; Sharp, R.E.; Saab, I.N.; Wu, Y. Regulation of cell expansion in roots and shoots at low water potentials. In Water Deficits: Plant Responses from Cell to Community; Smith, J.A.C., Griffiths, H., Eds.; Bios Scientific Publishers: Oxford, UK, 1993; pp. 37–52. [Google Scholar]
- Sharp, R.E.; Poroyko, V.; Hejlek, L.G.; Spollen, W.G.; Springer, G.K.; Bohnert, H.J.; Nguyen, H.T. Root growth maintenance during water deficits: Physiology to functional genomics. J. Exp. Bot. 2004, 55, 2343–2351. [Google Scholar] [CrossRef]
- Westgate, M.E.; Boyer, J.S. Osmotic adjustment and the inhibition of leaf, root, stem and silk growth at low water potentials in maize. Planta 1985, 164, 540–549. [Google Scholar] [CrossRef] [PubMed]
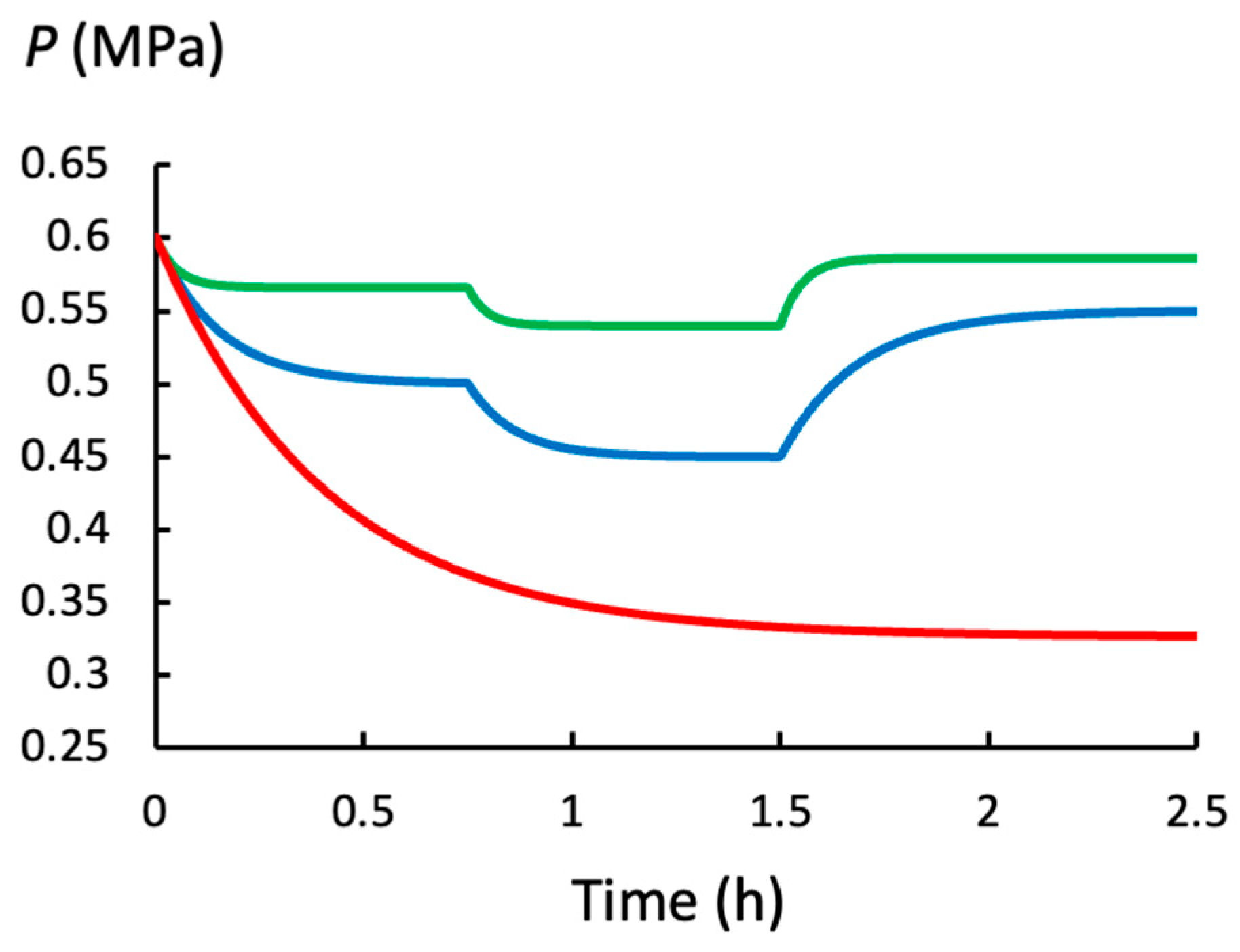

| Biophysical Variable (Units) | t < 0 | Time Intervals 0.0 h ≤ t < 0.75 h | 0.75 h ≤ t < 1.5 h | 1.5 h ≤ t < 2.5 h |
|---|---|---|---|---|
| Δπ (MPa) | 0.6 | 0.6 | 0.6 | 0.6 |
| PC (MPa) | --- | 0.3 | 0.3 | 0.3 |
| ε (MPa) | 9.0 | 9.0 | 9.0 | 9.0 |
| ϕp (h−1 MPa−1) | 0.0 | 0.25 | 0.50 | 0.10 |
| For Green Curve | ||||
| Lw (h−1 MPa−1) | 2.0 | 2.0 | 2.0 | 2.0 |
| Peq (MPa) | 0.60 | 0.566 | 0.540 | 0.586 |
| tc = (h) | --- | 0.049 | 0.044 | 0.053 |
| Πpw | --- | 0.125 | 0.25 | 0.05 |
| vs (h−1) | --- | 0.067 | 0.12 | 0.029 |
| For Blue Curve | ||||
| Lw (h−1 MPa−1) | 2.0 | 0.5 | 0.5 | 0.5 |
| Peq (MPa) | 0.60 | 0.500 | 0.450 | 0.550 |
| tc = (h) | --- | 0.148 | 0.111 | 0.185 |
| Πpw | --- | 0.5 | 1.0 | 0.2 |
| vs (h−1) | --- | 0.05 | 0.075 | 0.025 |
| For Red Curve | ||||
| t < 0 | 0.0 h ≤ t < 2.5 h | |||
| Lw (h−1 MPa−1) | 2.0 | 0.025 | ||
| Peq (MPa) | 0.60 | 0.327 | ||
| tc = (h) | --- | 0.40 | ||
| Πpw | --- | 10.0 | ||
| vs (h−1) | --- | 0.00675 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ortega, J.K.E. Theoretical Analyses of Turgor Pressure and Expansive Growth Rate of Plant Cells During Water Deficit. Plants 2025, 14, 3538. https://doi.org/10.3390/plants14223538
Ortega JKE. Theoretical Analyses of Turgor Pressure and Expansive Growth Rate of Plant Cells During Water Deficit. Plants. 2025; 14(22):3538. https://doi.org/10.3390/plants14223538
Chicago/Turabian StyleOrtega, Joseph K. E. 2025. "Theoretical Analyses of Turgor Pressure and Expansive Growth Rate of Plant Cells During Water Deficit" Plants 14, no. 22: 3538. https://doi.org/10.3390/plants14223538
APA StyleOrtega, J. K. E. (2025). Theoretical Analyses of Turgor Pressure and Expansive Growth Rate of Plant Cells During Water Deficit. Plants, 14(22), 3538. https://doi.org/10.3390/plants14223538






