Genetic Stability and Inbreeding in a Synthetic Maize Variety Based on a Finite Model
Abstract
1. Introduction
2. Results
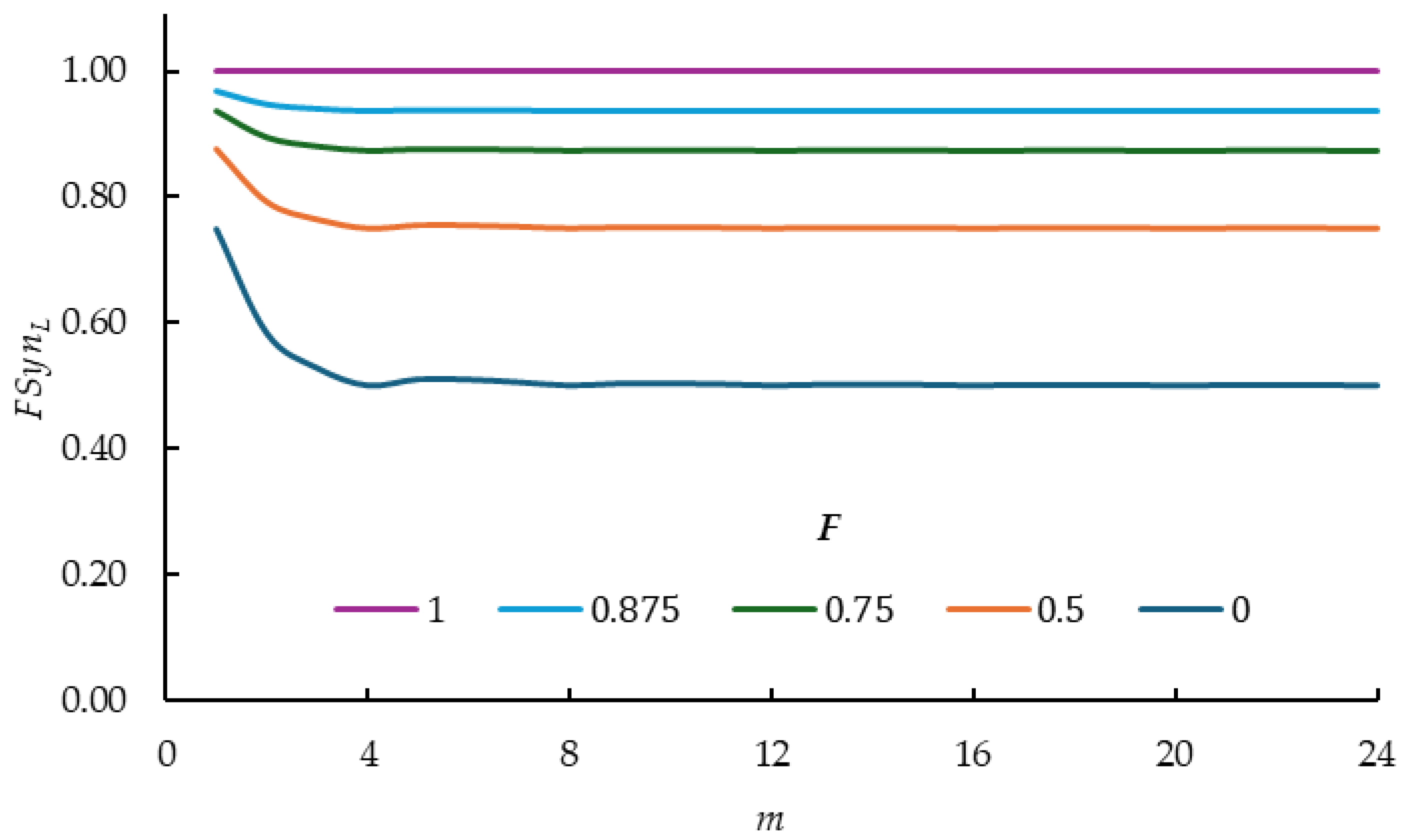
2.1. Inbreeding Coefficient
- (a)
- For each value the largest values occur when
- (b)
- increases when is larger
- (c)
- With values decrease as increases
- (d)
- From onwards values stabilize for each value and their relative performance at the five values are parallel to each other.
2.2. Genotype Retention Probability
- (a)
- For the objects A, B and C, there are different permutations: ABC, ACB, BAC, BCA, CAB and CBA.
- (b)
- For the objects A, B, A, there are different permutations: AAB, ABA, and BAA.
2.3. Probability of No Exclusion of Genes from the Sample
3. Discussion
4. Materials and Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Andrés-Meza, P.; Vázquez-Carrillo, M.G.; Sierra-Macías, M.; Mejía-Contreras, J.A.; Molina-Galán, J.D.; Espinosa-Calderón, A.; Gómez-Montiel, N.O.; López-Romero, G.; Tadeo-Robledo, M.; Zetina-Córdoba, P.; et al. Genotype-environment interaction on productivity and protein quality of synthetic tropical maize (Zea mays L.) varieties. Interciencia 2017, 42, 578–585. [Google Scholar]
- Andrés-Meza, P.; Sierra-Macías, M.; Mejía-Contreras, J.A.; Molina-Galán, J.D.; Espinosa-Calderón, A.; Gómez-Montiel, N.O.; Vázquez-Carrillo, M.G.; Leyva-Ovalle, O.R.; Tadeo-Robledo, M.; Cebada-Merino, M. Integración de sintéticos con líneas de maíz convertidas al carácter de alta calidad de proteína. Interciencia 2018, 43, 701–706. [Google Scholar]
- Ciancaleoni, S.; Negri, V. A method for obtaining flexible broccoli varieties for sustainable agriculture. BMC Genet. 2020, 21, 51. [Google Scholar] [CrossRef]
- Ibarra-Sánchez, A.; Rodríguez Pérez, J.E.; Peña Lomelí, A.; Villanueva-Verduzco, C.; Sahagún-Castellanos, J. General and Exact Inbreeding Coefficient of Maize Synthetics Derived from Three-Way Line Hybrids. Phyton-Int. J. Exp. Bot. 2022, 91, 33–43. [Google Scholar] [CrossRef]
- Sierra-Macías, M.; Andrés-Meza, P.; Gómez-Montiel, N.; Tadeo-Robledo, M. Yield and stability in synthetic maize varieties for the humid tropic in Mexico. J. Nat. Agric. Sci. 2021, 8, 1–7. [Google Scholar] [CrossRef]
- Wright, S. The Effects of Inbreeding and Crossbreeding on Guinea Pigs; USDA Bull. 1121; U.S. Government Publishing Office: Washington, DC, USA, 1922. [Google Scholar]
- Busbice, T. Predicting yield of synthetic varieties. Crop Sci. 1970, 32, 265–269. [Google Scholar] [CrossRef]
- Sierra-Macías, M.; Rodríguez-Montalvo, F.A.; Espinosa-Calderón, A.; Tadeo-Robledo, M.; Andrés-Meza, P.; Gómez-Montiel, N. Adaptabilidad de cruzas varietales de maíz en Veracruz y Tabasco. Rev. Mex. Cienc. Agrícolas 2023, 14, 327–337. [Google Scholar] [CrossRef]
- Kempthorne, O. An Introduction to Genetic Statistics; Wiley: New York, NY, USA, 1957; p. 545. [Google Scholar]
- Falconer, D.S. Introduction to Quantitative Genetics; John Wiley & Sons: New York, NY, USA, 1989; p. 438. [Google Scholar]
- Márquez-Sánchez, F. Inbreeding coefficient and mean prediction of maize of three-way lines hybrids. Maydica 2010, 55, 227–229. [Google Scholar]
- Masuka, B.; Magorokosho, C.; Olsen, M.; Atlin, G.N.; Bänziger, M.; Pixley, K.V.; Vivek, B.S.; Labuschagne, M.; Matemba-Mutasa, R.; Burguefio, J.; et al. Gains in maize genetic improvement in Eastern and Southern Africa Il. CIMMYT open-pollinated variety, breeding pipeline. Crop Sci. 2017, 57, 180–191. [Google Scholar] [CrossRef]
- Farid, M.; Musa, Y.; Nasarudolin, R.I. Selection of various synthetic maize (Zea mays L.) genotypes on drought stress condition. lOP Conf. ser. Earth Environ. Sci. 2019, 235, 012027. [Google Scholar] [CrossRef]
- Mengesha, W.; Menkir, A.; Meseka, S.; Bossey, B.; Afolabi, A.; Burgueño, J.; Crossa, J. Factor analysis to investigate genotype and genotype x environment interaction effects on pro-vitamin A content and yield in maize synthetics. Euphytica 2019, 215, 180. [Google Scholar] [CrossRef]
- De León-García de Alba, C. CP-Elvia 3, new white maize variety resistant to tar spot complex for Mexican subtropical areas. Rev. Mex. Fitopatol. 2020, 38, 485–490. [Google Scholar] [CrossRef]
- Arellano-Suarez, D.; Rodríguez-Pérez, J.E.; Peña-Lomelí, A.; Sahagún-Castellanos, J. Exact inbreeding coefficient of maize synthetic varieties derived from mixed lines and single crosses. Crop Breed. Appl. Biotechnol. 2020, 20, e31392047. [Google Scholar] [CrossRef]
| Reproductive Events ¶ | Progenies | Inbreeding Coefficients | |
|---|---|---|---|
| Genotypes | Average ¶ | ||||
|---|---|---|---|---|---|
| Genotypes | |||||
| Average | |||||
| 0.0000 | 0.5000 | 0.7500 | 0.8750 | 1.0000 | ||
|---|---|---|---|---|---|---|
| 1 | 1 | 0.75 | 0.88 | 0.94 | 0.97 | 1.00 |
| 2 | 2 | 0.58 | 0.79 | 0.90 | 0.95 | 1.00 |
| 3 | 3 | 0.53 | 0.76 | 0.88 | 0.94 | 1.00 |
| 4 | 0 | 0.50 | 0.75 | 0.88 | 0.94 | 1.00 |
| 5 | 1 | 0.51 | 0.76 | 0.88 | 0.94 | 1.00 |
| 6 | 2 | 0.51 | 0.75 | 0.88 | 0.94 | 1.00 |
| 7 | 3 | 0.51 | 0.75 | 0.88 | 0.94 | 1.00 |
| 8 | 0 | 0.50 | 0.75 | 0.88 | 0.94 | 1.00 |
| 9 | 1 | 0.50 | 0.75 | 0.88 | 0.94 | 1.00 |
| 10 | 2 | 0.50 | 0.75 | 0.88 | 0.94 | 1.00 |
| 11 | 3 | 0.50 | 0.75 | 0.88 | 0.94 | 1.00 |
| 12 | 0 | 0.50 | 0.75 | 0.88 | 0.94 | 1.00 |
| 13 | 1 | 0.50 | 0.75 | 0.88 | 0.94 | 1.00 |
| 14 | 2 | 0.50 | 0.75 | 0.88 | 0.94 | 1.00 |
| 15 | 3 | 0.50 | 0.75 | 0.88 | 0.94 | 1.00 |
| 16 | 0 | 0.50 | 0.75 | 0.88 | 0.94 | 1.00 |
| 17 | 1 | 0.50 | 0.75 | 0.88 | 0.94 | 1.00 |
| 18 | 2 | 0.50 | 0.75 | 0.88 | 0.94 | 1.00 |
| 19 | 3 | 0.50 | 0.75 | 0.88 | 0.94 | 1.00 |
| 20 | 0 | 0.50 | 0.75 | 0.88 | 0.94 | 1.00 |
| 21 | 1 | 0.50 | 0.75 | 0.88 | 0.94 | 1.00 |
| 22 | 2 | 0.50 | 0.75 | 0.88 | 0.94 | 1.00 |
| 23 | 3 | 0.50 | 0.75 | 0.88 | 0.94 | 1.00 |
| 24 | 0 | 0.50 | 0.75 | 0.88 | 0.94 | 1.00 |
| Genotypic Frequencies | ||||||
|---|---|---|---|---|---|---|
| 0.059 | ||||||
| 0.117 | ||||||
| 0.029 | ||||||
| 0.117 | ||||||
| 0.029 | ||||||
| 0.059 | ||||||
| 0.411 | ||||||
| 0.015 | ||||||
| 0.117 | ||||||
| 0.015 | ||||||
| 0.147 | ||||||
| 0.088 | ||||||
| 0.088 | ||||||
| 0.646 | ||||||
| Genotypic Frequencies | Number of Different Permutations (Equation (11)) | ||||||
|---|---|---|---|---|---|---|---|
| k | |||||||
| 0.0225 | |||||||
| 0.0016 | |||||||
| 0.0123 | |||||||
| 0.0671 | |||||||
| 0.0157 | |||||||
| 0.0532 | |||||||
| 0.0492 | |||||||
| 0.0104 | |||||||
| 0.0209 | |||||||
| 0.0291 | |||||||
| 0.0305 | |||||||
| 0.0270 | |||||||
| 0.0657 | |||||||
| 0.0580 | |||||||
| 0.0722 | |||||||
| 0.0734 | |||||||
| 0.1174 | |||||||
| 0.1316 | |||||||
| 0.1127 | |||||||
| 0.979 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Pérez, J.E.; Sahagún-Castellanos, J.; Peña-Lomelí, A.; Villanueva-Verduzco, C.; Arellano-Suarez, D. Genetic Stability and Inbreeding in a Synthetic Maize Variety Based on a Finite Model. Plants 2025, 14, 182. https://doi.org/10.3390/plants14020182
Rodríguez-Pérez JE, Sahagún-Castellanos J, Peña-Lomelí A, Villanueva-Verduzco C, Arellano-Suarez D. Genetic Stability and Inbreeding in a Synthetic Maize Variety Based on a Finite Model. Plants. 2025; 14(2):182. https://doi.org/10.3390/plants14020182
Chicago/Turabian StyleRodríguez-Pérez, Juan Enrique, Jaime Sahagún-Castellanos, Aureliano Peña-Lomelí, Clemente Villanueva-Verduzco, and Denise Arellano-Suarez. 2025. "Genetic Stability and Inbreeding in a Synthetic Maize Variety Based on a Finite Model" Plants 14, no. 2: 182. https://doi.org/10.3390/plants14020182
APA StyleRodríguez-Pérez, J. E., Sahagún-Castellanos, J., Peña-Lomelí, A., Villanueva-Verduzco, C., & Arellano-Suarez, D. (2025). Genetic Stability and Inbreeding in a Synthetic Maize Variety Based on a Finite Model. Plants, 14(2), 182. https://doi.org/10.3390/plants14020182







