Selecting High-Performing and Stable Pea Genotypes in Multi-Environmental Trial (MET): Applying AMMI, GGE-Biplot, and BLUP Procedures
Abstract
:1. Introduction
2. Results
2.1. Analysis of Variance, Variance Components, and Heritability
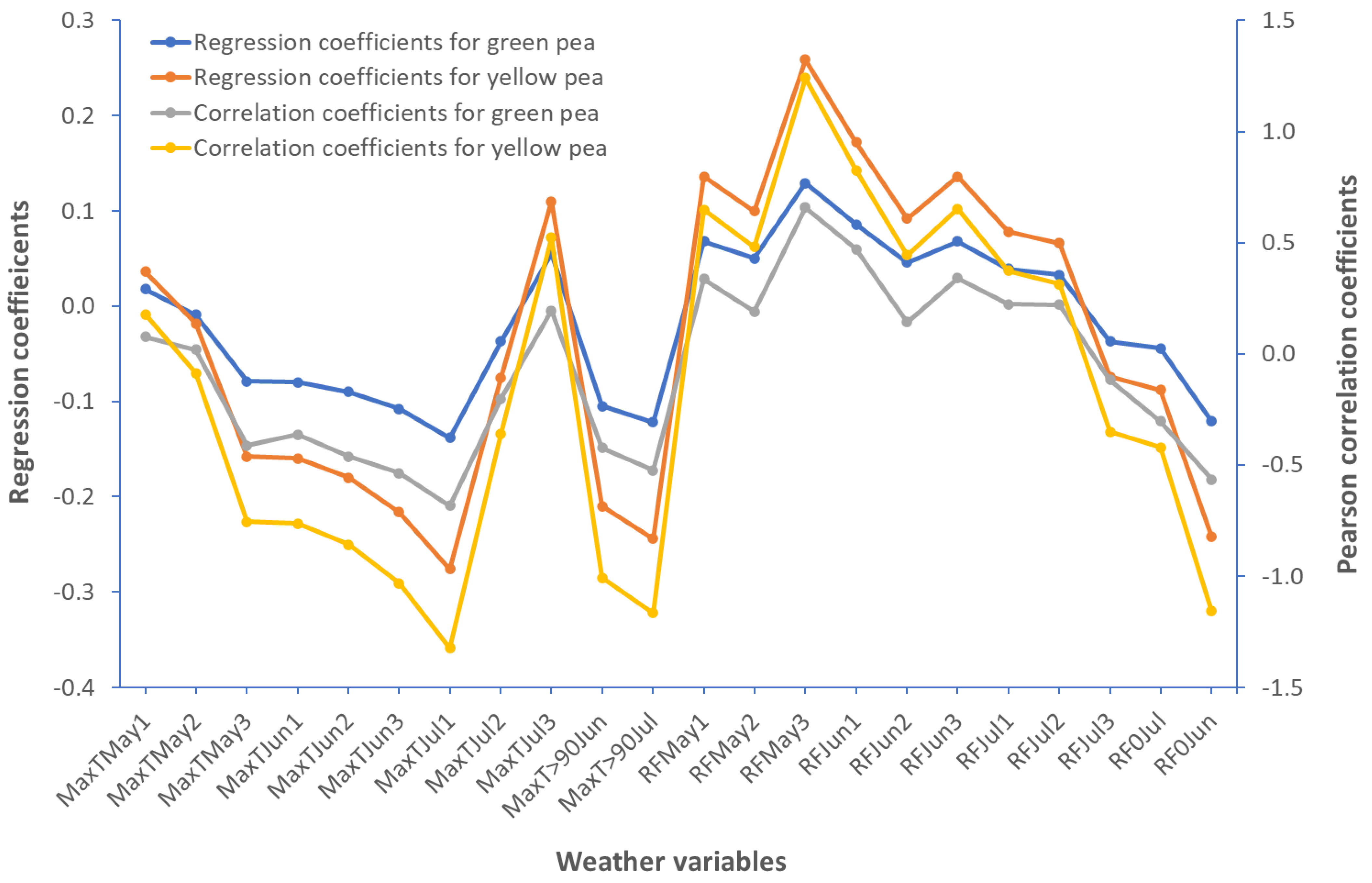
2.2. Weather and Pea Seed Yield
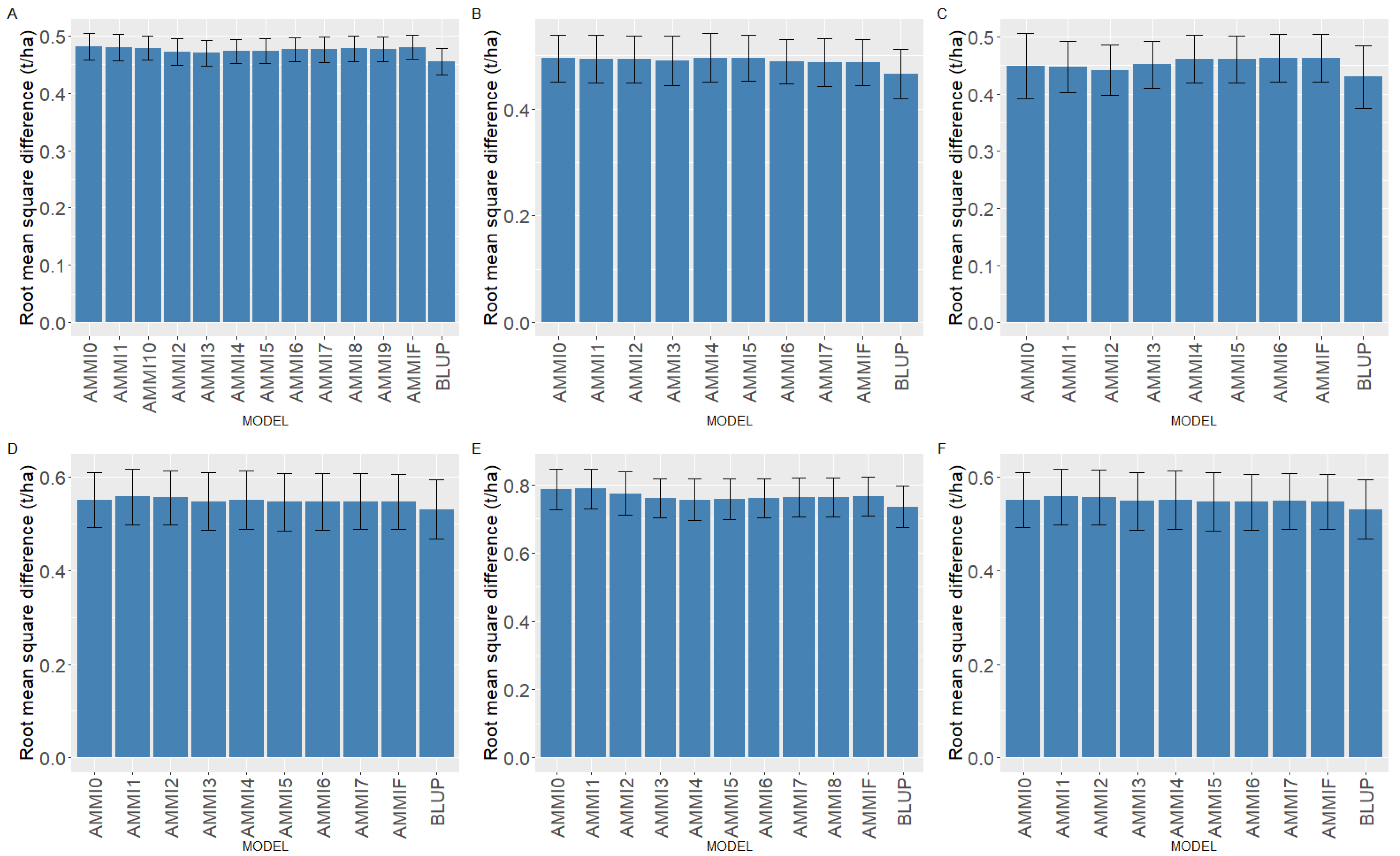
2.3. Comparison of BLUP and AMMI Family Models
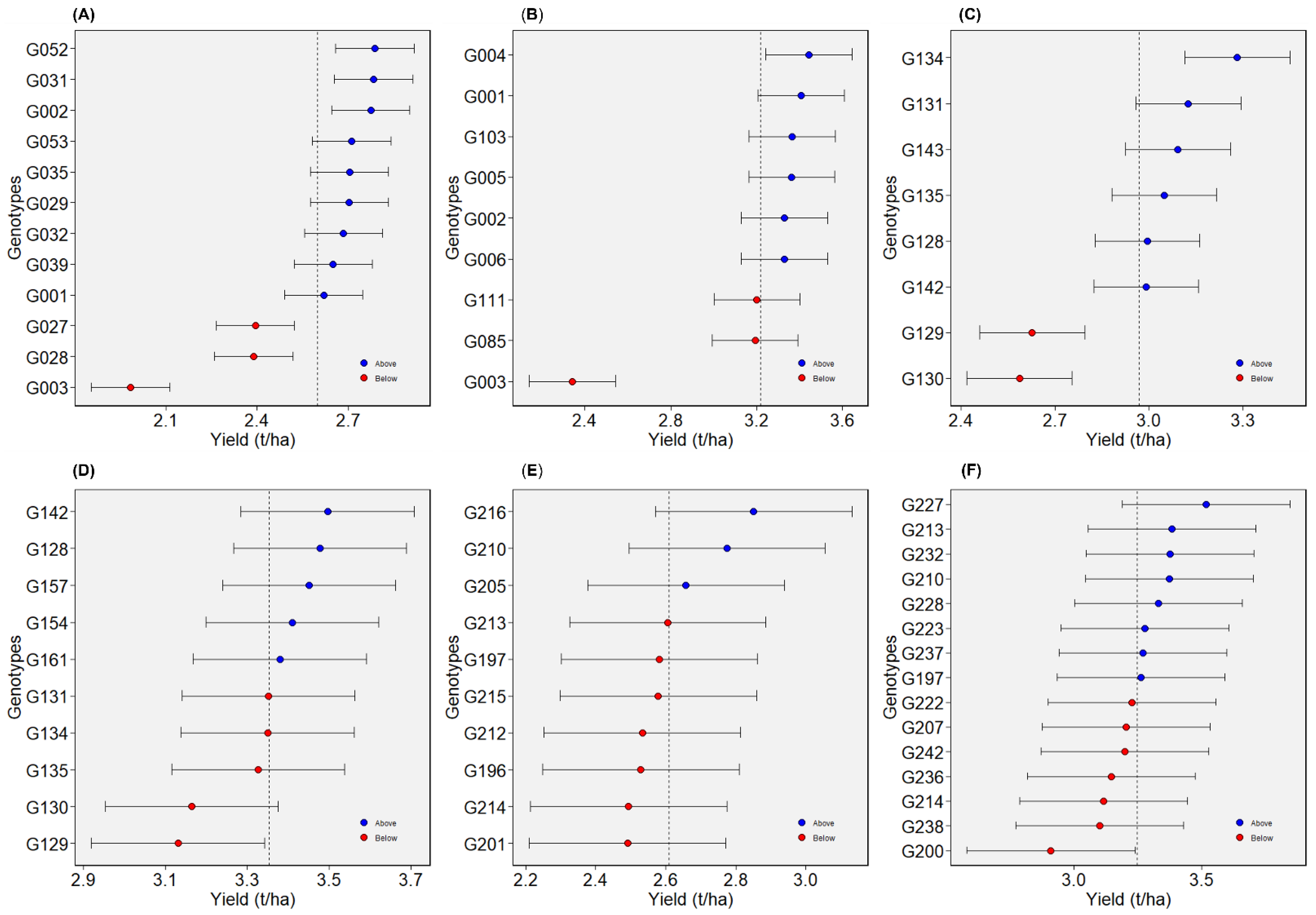
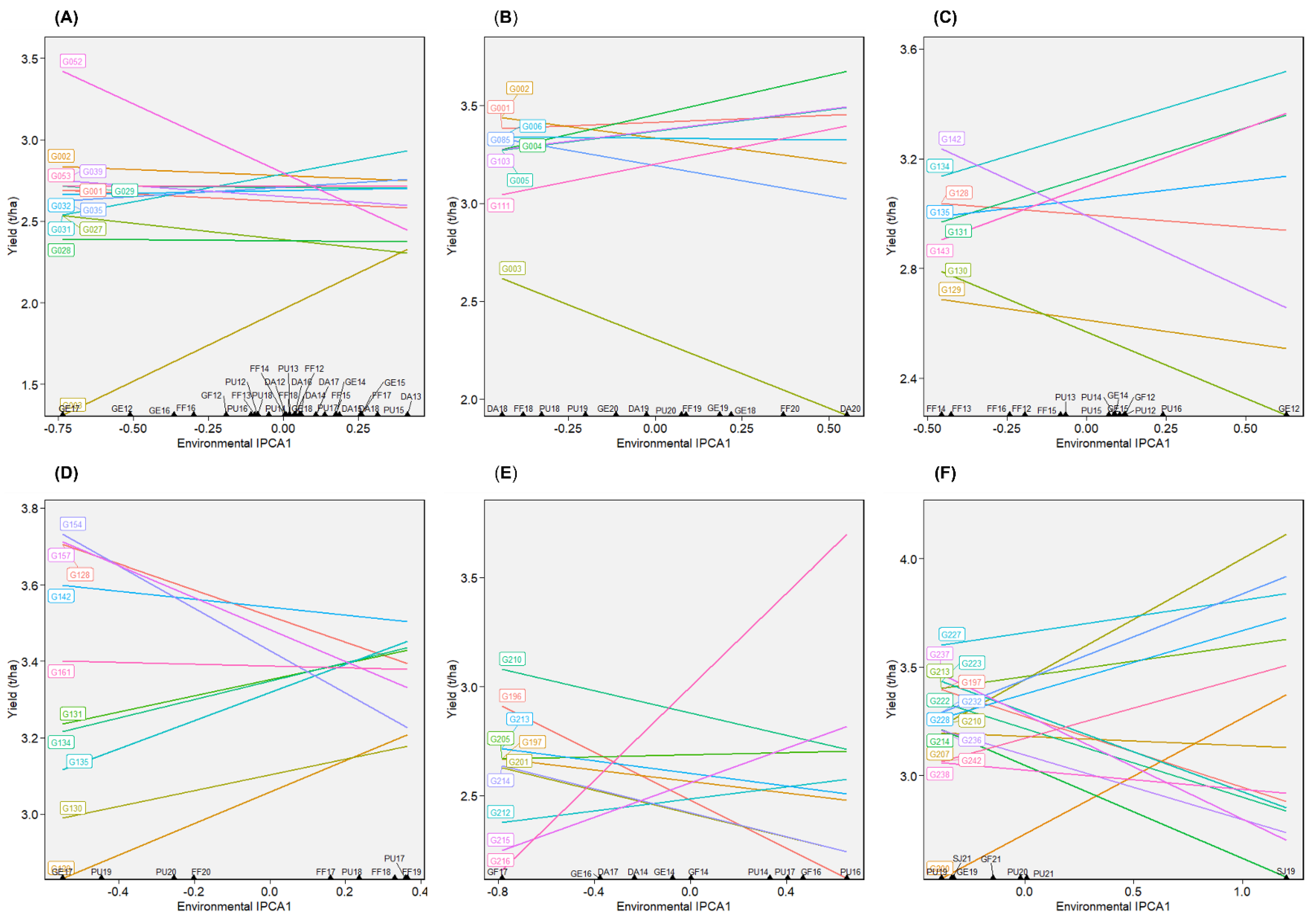
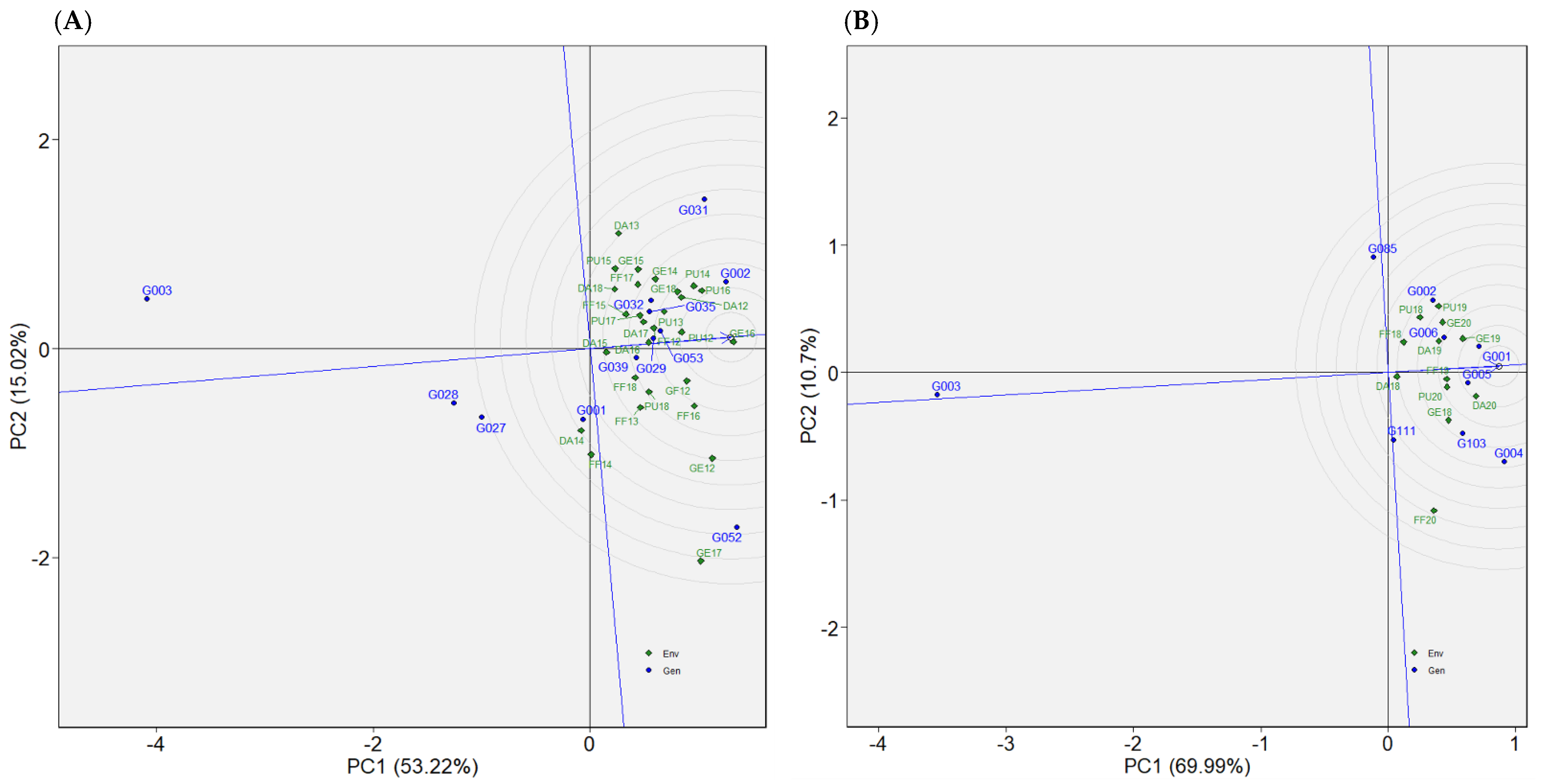
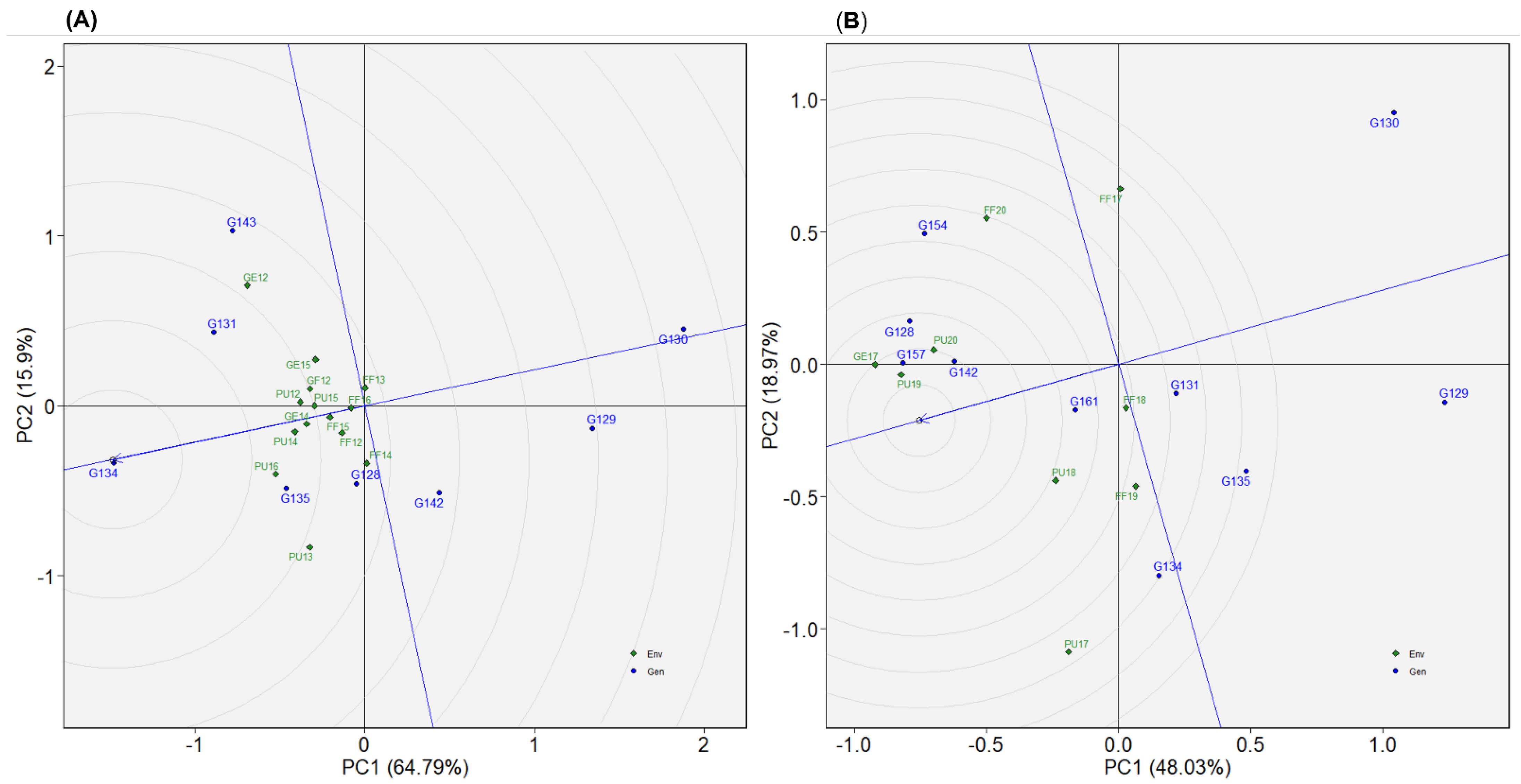
2.4. Selection for Overall Performance and Stability
2.4.1. Dataset 1: Green1218
2.4.2. Dataset 2: Green1820
2.4.3. Dataset 3: Yellow1216
2.4.4. Dataset 4: Yellow1720
2.4.5. Dataset 5: Winter1417
2.4.6. Dataset 6: Winter1921
3. Discussion
4. Materials and Methods
4.1. Yield Trial Datasets and Measured Traits
4.2. Data Analysis
4.3. Analysis of Weather Data
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Redden, B.; Leonfrorte, T.; Ford, R.; Croser, J.; Slattery, J. Pea (Pisum sativum) L. In Genetic Resources, Chromosome, Engineering, and Crop Improvement; Singh, R.J., Jauhar, P.P., Eds.; Taylor & Francis: Boca Raton, FL, USA, 2005. [Google Scholar]
- Daba, S.D.; Morris, C.F. Pea proteins: Variation, composition, genetics, and functional properties. Cereal Chem. 2022, 99, 8–20. [Google Scholar] [CrossRef]
- Yan, W.; Hunt, L.A.; Sheng, Q.; Szlavnics, Z. Cultivar evaluation and mega-environment investigation based on the GGE Biplot. Crop Sci. 2000, 40, 597–605. [Google Scholar] [CrossRef]
- Piepho, H.P.; Möhring, J.; Melchinger, A.E.; Büchse, A. BLUP for phenotypic selection in plant breeding and variety testing. Euphytica 2008, 161, 209–228. [Google Scholar] [CrossRef]
- Bernardo, R. Breeding for Quantitative Traits in Plants; Stemma Press: Woodbury, MN, USA, 2020. [Google Scholar]
- Leon, N.D.; Jannink, J.-L.; Edwards, J.W.; Kaeppler, S.M. Introduction to a special issue on genotype by environment interaction. Crop Sci. 2016, 56, 2081–2089. [Google Scholar] [CrossRef] [Green Version]
- Saltz, J.B.; Bell, A.M.; Flint, J.; Gomulkiewicz, R.; Hughes, K.A.; Keagy, J. Why does the magnitude of genotype-by-environment interaction vary? Ecol. Evol. 2018, 8, 6342–6353. [Google Scholar] [CrossRef] [PubMed]
- Olivoto, T.; Lúcio, A.D.C.; da Silva, J.A.G.; Marchioro, V.S.; de Souza, V.Q.; Jost, E. Mean performance and stability in multi-environment trials I: Combining features of AMMI and BLUP techniques. Agron. J. 2019, 111, 2949–2960. [Google Scholar] [CrossRef]
- Gauch, H.G.; Zobel, R.W. Predictive and postdictive success of statistical analyses of yield trials. Theor. Appl. Genet. 1988, 76, 1–10. [Google Scholar] [CrossRef]
- Gauch, H.G. Model selection and validation for yield trials with interaction. Biometrics 1988, 44, 705–715. [Google Scholar] [CrossRef]
- Spoorthi, V.; Ramesh, S.; Sunitha, N.C.; Vaijayanthi, P.V. Prediction of genotype performance for untested years based on additive main effects and multiplicative interaction and linear mixed models: An illustration using dolichos bean (Lablab purpureus (L.) Sweet) multiyear data. Ann. Appl. Biol. 2022, 180, 224–235. [Google Scholar] [CrossRef]
- Tack, J.B.; Holt, M.T. The influence of weather extremes on the spatial correlation of corn yields. Clim. Chang. 2016, 134, 299–309. [Google Scholar] [CrossRef]
- Bueckert, R.A.; Wagenhoffer, S.; Hnatowich, G.; Warkentin, T.D. Effect of heat and precipitation on pea yield and reproductive performance in the field. Can. J. Plant Sci. 2015, 95, 629–639. [Google Scholar] [CrossRef]
- Jiang, Y.; Davis, A.R.; Vujanovic, V.; Bueckert, R.A. Reproductive development response to high daytime temperature in field pea. J. Agron. Crop Sci. 2019, 205, 324–333. [Google Scholar] [CrossRef]
- Osorio, E.E.; Davis, A.R.; Bueckert, R.A. High temperatures disturb ovule development in field pea (Pisum sativum). Botany 2022, 100, 47–61. [Google Scholar] [CrossRef]
- Ray, D.K.; Gerber, J.S.; MacDonald, G.K.; West, P.C. Climate variation explains a third of global crop yield variability. Nat. Commun. 2014, 6, 5989. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lobell, D.B.; Field, C.B. Global scale climate–crop yield relationships and the impacts of recent warming. Environ. Res. Lett. 2007, 2, 014002. [Google Scholar] [CrossRef]
- Kukal, M.S.; Irmak, S. Climate-driven crop yield and yield variability and climate change impacts on the U.S. Great Plains agricultural production. Sci. Rep. 2018, 8, 3450. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Olivoto, T.; Lúcio, A. Metan: An R package for multi-environment trial analysis. Methods Ecol. Evol. 2020, 11, 783–789. [Google Scholar] [CrossRef] [Green Version]
- Gauch, H.G. A simple protocol for AMMI analysis of yield trials. Crop Sci. 2013, 53, 1860–1869. [Google Scholar] [CrossRef]



| Environments | Green Peas | Yellow Peas | Winter | |||
|---|---|---|---|---|---|---|
| Mean | CV | Mean | CV | Mean | CV | |
| DA2012 | 2.9 | 9.2 | 2.8 | 19.0 | ||
| DA2013 | 2.2 | 9.5 | ||||
| DA2014 | 0.9 | 11.2 | 1.2 | 19.2 | ||
| DA2015 | 1.5 | 9.5 | ||||
| DA2016 | 2.3 | 9.2 | ||||
| DA2017 | 1.5 | 10.2 | 1.1 | 19.8 | ||
| DA2018 | 0.9 | 11.4 | 2.1 | 19.4 | ||
| DA2019 | 2.0 | 9.8 | 1.3 | 22.4 | ||
| DA2020 | 2.3 | 10.7 | ||||
| FF2012 | 4.0 | 9.0 | 4.0 | 8.6 | ||
| FF2013 | 2.9 | 9.4 | 3.7 | 9.5 | ||
| FF2014 | 2.9 | 8.6 | 3.3 | 9.4 | ||
| FF2015 | 2.2 | 8.5 | 2.1 | 10.0 | ||
| FF2016 | 4.9 | 9.6 | 4.9 | 8.2 | ||
| FF2017 | 2.6 | 9.1 | 3.7 | 9.7 | ||
| FF2018 | 2.8 | 8.8 | 3.1 | 8.7 | ||
| FF2019 | 3.2 | 9.8 | 3.4 | 8.7 | ||
| FF2020 | 4.4 | 9.0 | 5.3 | 9.4 | ||
| FF2021 | 1.1 | 10.1 | 2.1 | 10.0 | ||
| GE2012 | 3.7 | 9.6 | 4.1 | 7.8 | ||
| GE2014 | 2.2 | 9.0 | 3.0 | 8.2 | 1.5 | 20.5 |
| GE2015 | 2.2 | 8.5 | 2.3 | 9.9 | ||
| GE2016 | 3.3 | 10.2 | 4.7 | 18.6 | ||
| GE2017 | 2.7 | 14.7 | 1.6 | 20.4 | ||
| GE2018 | 4.6 | 8.9 | ||||
| GE2019 | 3.9 | 9.4 | 4.0 | 18.3 | ||
| GE2020 | 3.5 | 9.6 | ||||
| GF2012 | 2.2 | 9.8 | 2.5 | 8.9 | 4.6 | 19.2 |
| PU2012 | 3.2 | 9.3 | 3.3 | 8.5 | 3.7 | 18.6 |
| PU2013 | 3.4 | 9.1 | 3.4 | 7.8 | 1.7 | 20.4 |
| PU2014 | 1.8 | 10.5 | 1.7 | 10.8 | 3.1 | 20.2 |
| PU2015 | 0.7 | 11.3 | 0.7 | 20.4 | ||
| PU2016 | 2.4 | 9.3 | 2.4 | 8.2 | 3.9 | 19.5 |
| PU2017 | 1.7 | 9.1 | 1.5 | 10.1 | 4.0 | 18.9 |
| PU2018 | 3.5 | 8.9 | 3.6 | 9.0 | 4.0 | 20.2 |
| PU2019 | 2.1 | 9.7 | 2.8 | 10.4 | 2.4 | 20.0 |
| PU2020 | 4.0 | 8.8 | 4.8 | 8.6 | 5.6 | 18.8 |
| PU2021 | 1.8 | 9.5 | 1.5 | 12.6 | ||
| Type | Environments | Number of Genotypes |
|---|---|---|
| Dataset 1: Green1218: Green peas | DA, FF, and PU (2012–2018), GE (2012, 2014–2018), GF (2012) | 12 |
| Dataset 2: Green1820: Green peas | DA, FF, GE, and PU (2018–2020) | 9 |
| Dataset 3: Yellow1216: Yellow peas | FF and PU (2012–2016), GE (2012, 2014, 2015), GF (2012) | 8 |
| Dataset 4: Yellow1720: Yellow peas | FF and PU (2017–2020) GE (2017) | 10 |
| Dataset 5: Winter1417: Winter peas | GF and PU (2014, 2016, 2017), DA (2014, 2017), GE (2014, 2016) | 10 |
| Dataset 6: Winter1921: Winter peas | PU (2019–2021), GE and SJ (2019, 2021) | 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daba, S.D.; Kiszonas, A.M.; McGee, R.J. Selecting High-Performing and Stable Pea Genotypes in Multi-Environmental Trial (MET): Applying AMMI, GGE-Biplot, and BLUP Procedures. Plants 2023, 12, 2343. https://doi.org/10.3390/plants12122343
Daba SD, Kiszonas AM, McGee RJ. Selecting High-Performing and Stable Pea Genotypes in Multi-Environmental Trial (MET): Applying AMMI, GGE-Biplot, and BLUP Procedures. Plants. 2023; 12(12):2343. https://doi.org/10.3390/plants12122343
Chicago/Turabian StyleDaba, Sintayehu D., Alecia M. Kiszonas, and Rebecca J. McGee. 2023. "Selecting High-Performing and Stable Pea Genotypes in Multi-Environmental Trial (MET): Applying AMMI, GGE-Biplot, and BLUP Procedures" Plants 12, no. 12: 2343. https://doi.org/10.3390/plants12122343
APA StyleDaba, S. D., Kiszonas, A. M., & McGee, R. J. (2023). Selecting High-Performing and Stable Pea Genotypes in Multi-Environmental Trial (MET): Applying AMMI, GGE-Biplot, and BLUP Procedures. Plants, 12(12), 2343. https://doi.org/10.3390/plants12122343







