An Overview of Key Factors Affecting Genomic Selection for Wheat Quality Traits
Abstract
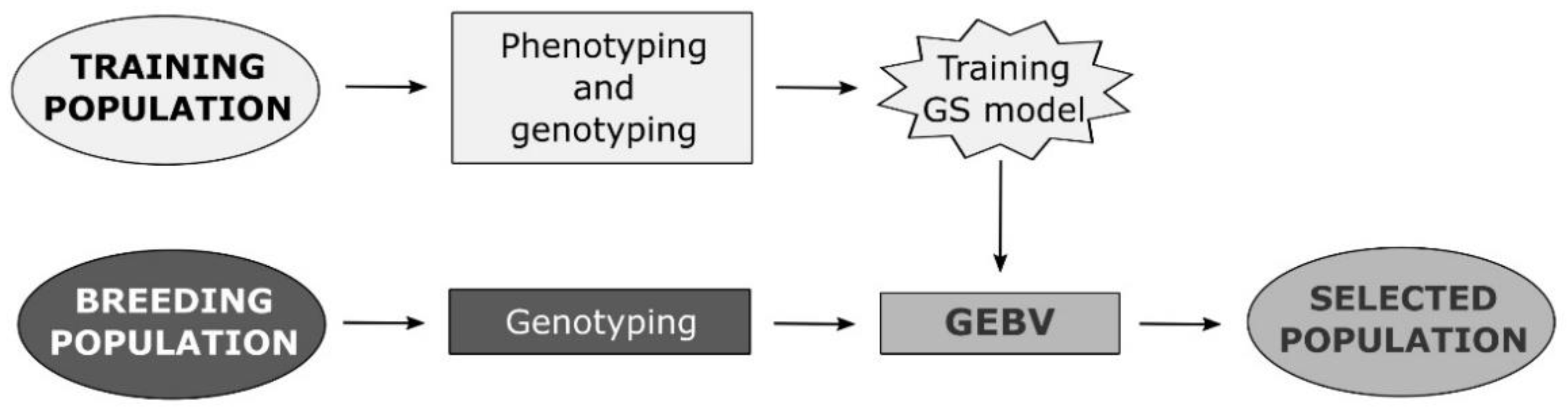
1. Introduction
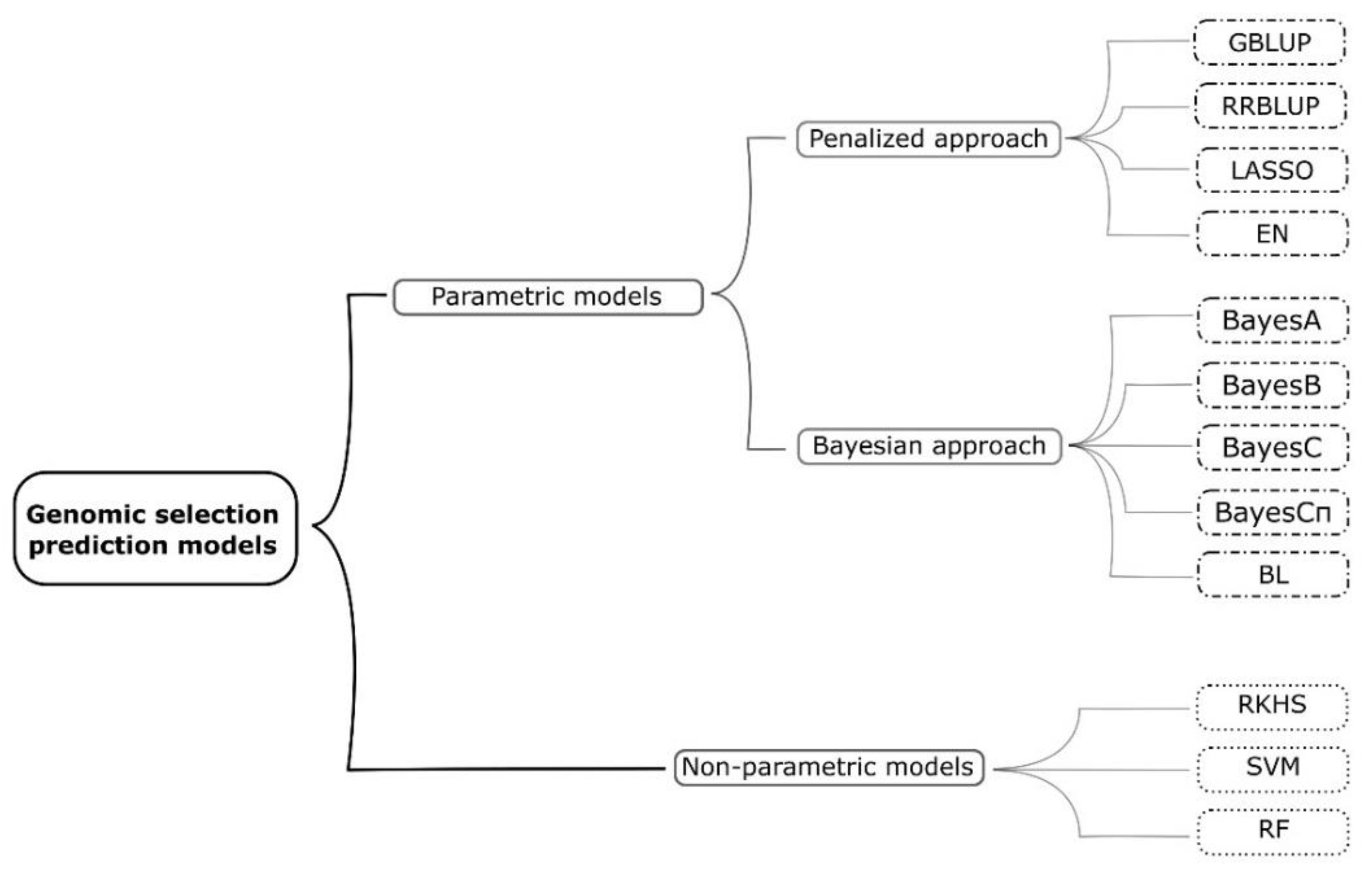
2. Genomic Selection and Prediction Models Used
3. Factors Affecting Prediction Accuracies of Genomic Selection in Wheat
4. Overview of Genomic Selection Research for Wheat Quality Improvement
4.1. Effect of Training Population Size
4.2. Relatedness of Training and Validation Population
4.3. Effect of Marker Density
4.4. Effect of Heritability of the Trait
4.5. Effect of Model Used
5. Multitrait Genomic Selection
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- CIMMYT. International Maize and Wheat Improvement Center. Available online: https://www.cimmyt.org/work/wheat-research/ (accessed on 16 March 2021).
- Shewry, P.R. Improving the protein content and quality of temperate cereals: Wheat, barley and rye. In Impacts of Agriculture on Human Health and Nutrition; Cakmak, I., Welch, R., Eds.; USDA, ARS, U.S. Plant, Soil and Nutrition Laboratory, Cornell University: Ithaca, NY, USA, 2004; Volume 2. [Google Scholar]
- Simmonds, N.W. The Relation between Yield and Protein in Cereal Grain. J. Sci. Food Agric. 1995, 67, 309–315. [Google Scholar] [CrossRef]
- Guzman, C.; Peña, R.J.; Singh, R.; Autrique, E.; Dreisigacker, S.; Crossa, J.; Rutkoski, J.; Poland, J.; Battenfield, S. Wheat Quality Improvement at CIMMYT and the Use of Genomic Selection on It. Appl. Transl. Genom. 2016, 11, 3–8. [Google Scholar] [CrossRef]
- Groos, C.; Robert, N.; Bervas, E.; Charmet, G. Genetic Analysis of Grain Protein-Content, Grain Yield and Thousand-Kernel Weight in Bread Wheat. Theor. Appl. Genet. 2003, 106, 1032–1040. [Google Scholar] [CrossRef]
- Payne, P.I.; Nightingale, M.A.; Krattiger, A.F.; Holt, L.M. The Relationship between HMW Glutenin Subunit Composition and the Bread-Making Quality Of British-grown Wheat Varieties. J. Sci. Food Agric. 1987, 40, 51–65. [Google Scholar] [CrossRef]
- Wieser, H. Chemistry of Gluten Proteins. Food Microbiol. 2007, 24, 115–119. [Google Scholar] [CrossRef] [PubMed]
- Grausgruber, H.; Oberforster, M.; Werteker, M.; Ruckenbauer, P.; Vollmann, J. Stability of Quality Traits in Austrian-Grown Winter Wheats. Field Crop. Res. 2000, 66, 257–267. [Google Scholar] [CrossRef]
- Robert, N.; Denis, J.B. Stability of Baking Quality in Bread Wheat Using Several Statistical Parameters. Theor. Appl. Genet. 1996, 93, 172–178. [Google Scholar] [CrossRef] [PubMed]
- Simmonds, N.W. Genotype (G), Environment (E) and GE Components of Crop Yields. Exp. Agric. 1981, 17, 355–362. [Google Scholar] [CrossRef]
- Crossa, J.; Beyene, Y.; Semagn, K.; Pérez, P.; Hickey, J.M.; Chen, C.; de los Campos, G.; Burgueño, J.; Windhausen, V.S.; Buckler, E.; et al. Genomic Prediction in Maize Breeding Populations with Genotyping-by-Sequencing. G3 Genes Genom. Genet. 2013, 3, 1903–1926. [Google Scholar] [CrossRef] [PubMed]
- Meuwissen, T.H.E.; Hayes, B.J.; Goddard, M.E. Prediction of Total Genetic Value Using Genome-Wide Dense Marker Maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef] [PubMed]
- de los Campos, G.; Naya, H.; Gianola, D.; Crossa, J.; Legarra, A.; Manfredi, E.; Weigel, K.; Cotes, J.M. Predicting Quantitative Traits with Regression Models for Dense Molecular Markers and Pedigree. Genetics 2009, 182, 375–385. [Google Scholar] [CrossRef] [PubMed]
- Crossa, J.; de los Campos, G.; Pérez, P.; Gianola, D.; Burgueño, J.; Araus, J.L.; Makumbi, D.; Singh, R.P.; Dreisigacker, S.; Yan, J.; et al. Prediction of Genetic Values of Quantitative Traits in Plant Breeding Using Pedigree and Molecular Markers. Genetics 2010, 186, 713–724. [Google Scholar] [CrossRef] [PubMed]
- Heffner, E.L.; Sorrells, M.E.; Jannink, J.L. Genomic Selection for Crop Improvement. Crop Sci. 2009, 49, 1–12. [Google Scholar] [CrossRef]
- Heslot, N.; Jannink, J.L.; Sorrells, M.E. Perspectives for Genomic Selection Applications and Research in Plants. Crop Sci. 2015, 55, 1–12. [Google Scholar] [CrossRef]
- Arruda, M.P.; Brown, P.J.; Lipka, A.E.; Krill, A.M.; Thurber, C.; Kolb, F.L. Genomic Selection for Predicting Fusarium Head Blight Resistance in a Wheat Breeding Program. Plant Genom. 2015, 8, 1–12. [Google Scholar] [CrossRef]
- Crossa, J.; Pérez, P.; Hickey, J.M.; Burgueño, J.; Ornella, L.; Cerón-Rojas, J.; Zhang, X.; Dreisigacker, S.; Babu, R.; Li, Y.; et al. Genomic Prediction in CIMMYT Maize and Wheat Breeding Programs. Heredity 2014, 112, 48–60. [Google Scholar] [CrossRef]
- Poland, J.; Endelman, J.B.; Dawson, J.; Rutkoski, J.; Wu, S.; Manes, Y.; Dreisigacker, S.; Crossa, J.; Sánchez-Villeda, H.; Sorrells, M.; et al. Genomic Selection in Wheat Breeding Using Genotyping-by-Sequencing. Plant Genom. 2012, 5, 103–113. [Google Scholar] [CrossRef]
- Rutkoski, J.; Benson, J.; Jia, Y.; Brown-Guedira, G.; Jannink, J.L.; Sorrells, M. Evaluation of Genomic Prediction Methods for Fusarium Head Blight Resistance in Wheat. Plant Genom. 2012, 5, 51–61. [Google Scholar] [CrossRef]
- Heffner, E.L.; Jannink, J.-L.; Sorrells, M.E. Genomic Selection Accuracy Using Multifamily Prediction Models in a Wheat Breeding Program. Plant Genom. 2011, 4, 65–75. [Google Scholar] [CrossRef]
- Ray, D.K.; Mueller, N.D.; West, P.C.; Foley, J.A. Yield Trends Are Insufficient to Double Global Crop Production by 2050. PLoS ONE 2013, 8, e66428. [Google Scholar] [CrossRef]
- Rutkoski, J.E.; Crain, J.; Poland, J.; Sorrells, M.E. Genomic Selection for Small Grain Improvement. In Genomic Selection for Crop Improvement: New Molecular Breeding Strategies for Crop Improvement; Varshney, R.K., Roorkiwal, M., Sorrells, M.E., Eds.; Springer International Publishing AG: Cham, Switzerland, 2017; pp. 99–130. [Google Scholar]
- Bernardo, R.; Yu, J. Prospects for Genomewide Selection for Quantitative Traits in Maize. Crop Sci. 2007, 47, 1082–1090. [Google Scholar] [CrossRef]
- Sorrells, M.E. Genomic selection in plants: Empirical results and implications for wheat breeding. In Advances in Wheat Genetics: From Genome to Field; Ogihara, Y., Takumi, S., Handa, H., Eds.; Springer Japan KK: Yokohama, Japan, 2015; pp. 401–409. [Google Scholar]
- Voss-Fels, K.P.; Cooper, M.; Hayes, B.J. Accelerating Crop Genetic Gains with Genomic Selection. Theor. Appl. Genet. 2019, 132, 669–686. [Google Scholar] [CrossRef] [PubMed]
- Desta, Z.A.; Ortiz, R. Genomic Selection: Genome-Wide Prediction in Plant Improvement. Trends Plant Sci. 2014, 19, 592–601. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Xu, Y.; Hu, Z.; Xu, C. Genomic Selection Methods for Crop Improvement: Current Status and Prospects. Crop J. 2018, 6, 330–340. [Google Scholar] [CrossRef]
- Zhang, H.; Yin, L.; Wang, M.; Yuan, X.; Liu, X. Factors Affecting the Accuracy of Genomic Selection for Agricultural Economic Traits in Maize, Cattle, and Pig Populations. Front. Genet. 2019, 10, 189. [Google Scholar] [CrossRef]
- Heffner, E.L.; Jannink, J.-L.; Iwata, H.; Souza, E.; Sorrells, M.E. Genomic Selection Accuracy for Grain Quality Traits in Biparental Wheat Populations. Crop Sci. 2011, 51, 2597–2606. [Google Scholar] [CrossRef]
- de los Campos, G.; Hickey, J.M.; Pong-Wong, R.; Daetwyler, H.D.; Calus, M.P.L. Whole-Genome Regression and Prediction Methods Applied to Plant and Animal Breeding. Genetics 2013, 193, 327–345. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef]
- Jannink, J.L.; Lorenz, A.J.; Iwata, H. Genomic Selection in Plant Breeding: From Theory to Practice. Brief. Funct. Genom. Proteom. 2010, 9, 166–177. [Google Scholar] [CrossRef]
- Gianola, D.; Van Kaam, J.B.C.H.M. Reproducing Kernel Hilbert Spaces Regression Methods for Genomic Assisted Prediction of Quantitative Traits. Genetics 2008, 178, 2289–2303. [Google Scholar] [CrossRef]
- van den Berg, I.; Meuwissen, T.H.E.; MacLeod, I.M.; Goddard, M.E. Predicting the Effect of Reference Population on the Accuracy of within, across, and Multibreed Genomic Prediction. J. Dairy Sci. 2019, 102, 3155–3174. [Google Scholar] [CrossRef] [PubMed]
- Habier, D.; Fernando, R.L.; Dekkers, J.C.M. The Impact of Genetic Relationship Information on Genome-Assisted Breeding Values. Genetics 2007, 177, 2389–2397. [Google Scholar] [CrossRef]
- Isidro, J.; Jannink, J.L.; Akdemir, D.; Poland, J.; Heslot, N.; Sorrells, M.E. Training Set Optimization under Population Structure in Genomic Selection. Theor. Appl. Genet. 2015, 128, 145–158. [Google Scholar] [CrossRef] [PubMed]
- Lorenzana, R.E.; Bernardo, R. Accuracy of Genotypic Value Predictions for Marker-Based Selection in Biparental Plant Populations. Theor. Appl. Genet. 2009, 120, 151–161. [Google Scholar] [CrossRef] [PubMed]
- Combs, E.; Bernardo, R. Accuracy of Genomewide Selection for Different Traits with Constant Population Size, Heritability, and Number of Markers. Plant Genome 2013, 6, 1–7. [Google Scholar] [CrossRef]
- Zhang, X.; Pérez-Rodríguez, P.; Semagn, K.; Beyene, Y.; Babu, R.; López-Cruz, M.A.; San Vicente, F.; Olsen, M.; Buckler, E.; Jannink, J.-L.L.; et al. Genomic Prediction in Biparental Tropical Maize Populations in Water-Stressed and Well-Watered Environments Using Low-Density and GBS SNPs. Heredity 2015, 114, 291–299. [Google Scholar] [CrossRef]
- Brauner, P.C.; Müller, D.; Molenaar, W.S.; Melchinger, A.E. Genomic Prediction with Multiple Biparental Families. Theor. Appl. Genet. 2020, 133, 133–147. [Google Scholar] [CrossRef]
- Edwards, S.M.K.; Buntjer, J.B.; Jackson, R.; Bentley, A.R.; Lage, J.; Byrne, E.; Burt, C.; Jack, P.; Berry, S.; Flatman, E.; et al. The Effects of Training Population Design on Genomic Prediction Accuracy in Wheat. Theor. Appl. Genet. 2019, 132, 1943–1952. [Google Scholar] [CrossRef]
- Heslot, N.; Yang, H.P.; Sorrells, M.E.; Jannink, J.L. Genomic Selection in Plant Breeding: A Comparison of Models. Crop Sci. 2012, 52, 146–160. [Google Scholar] [CrossRef]
- Lorenz, A.J.; Smith, K.P. Adding Genetically Distant Individuals to Training Populations Reduces Genomic Prediction Accuracy in Barley. Crop Sci. 2015, 55, 2657–2667. [Google Scholar] [CrossRef]
- Rutkoski, J.E.; Singh, R.P.; Huerta-Espino, J.; Bhavani, S.; Poland, J.; Jannink, J.-L.; Sorrells, M.E. Efficient Use of Historical Data for Genomic Selection: A Case Study of Stem Rust Resistance in Wheat. Plant Genome 2015, 8, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Bassi, F.M.; Bentley, A.R.; Charmet, G.; Ortiz, R.; Crossa, J. Breeding Schemes for the Implementation of Genomic Selection in Wheat (Triticum Spp.). Plant Sci. 2016, 242, 23–36. [Google Scholar] [CrossRef]
- Robertsen, C.; Hjortshøj, R.; Janss, L. Genomic Selection in Cereal Breeding. Agronomy 2019, 9, 95. [Google Scholar] [CrossRef]
- Norman, A.; Taylor, J.; Edwards, J.; Kuchel, H. Optimising Genomic Selection in Wheat: Effect of Marker Density, Population Size and Population Structure on Prediction Accuracy. G3 Genes Genom. Genet. 2018, 8, 2889–2899. [Google Scholar] [CrossRef] [PubMed]
- Meuwissen, T.H.E. Accuracy of Breeding Values of “unrelated” Individuals Predicted by Dense SNP Genotyping. Genet. Sel. Evol. 2009, 41, 35. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Zhao, Y.; Gowda, M.; Longin, C.F.H.; Reif, J.C.; Mette, M.F. Predicting Hybrid Performances for Quality Traits through Genomic-Assisted Approaches in Central European Wheat. PLoS ONE 2016, 11, e0158635. [Google Scholar] [CrossRef]
- Battenfield, S.D.; Guzmán, C.; Gaynor, R.C.; Singh, R.P.; Peña, R.J.; Dreisigacker, S.; Fritz, A.K.; Poland, J.A. Genomic Selection for Processing and End-Use Quality Traits in the CIMMYT Spring Bread Wheat Breeding Program. Plant Genom. 2016, 9, 1–12. [Google Scholar] [CrossRef]
- Michel, S.; Kummer, C.; Gallee, M.; Hellinger, J.; Ametz, C.; Akgöl, B.; Epure, D.; Löschenberger, F.; Buerstmayr, H. Improving the Baking Quality of Bread Wheat by Genomic Selection in Early Generations. Theor. Appl. Genet. 2018, 131, 477–493. [Google Scholar] [CrossRef]
- Crossa, J.; Jarquín, D.; Franco, J.; Pérez-Rodríguez, P.; Burgueño, J.; Saint-Pierre, C.; Vikram, P.; Sansaloni, C.; Petroli, C.; Akdemir, D.; et al. Genomic Prediction of Gene Bank Wheat Landraces. G3 Genes Genom. Genet. 2016, 6, 1819–1834. [Google Scholar] [CrossRef] [PubMed]
- Huang, M.; Cabrera, A.; Hoffstetter, A.; Griffey, C.; Van Sanford, D.; Costa, J.; McKendry, A.; Chao, S.; Sneller, C. Genomic Selection for Wheat Traits and Trait Stability. Theor. Appl. Genet. 2016, 129, 1697–1710. [Google Scholar] [CrossRef]
- Michel, S.; Ametz, C.; Gungor, H.; Epure, D.; Grausgruber, H.; Löschenberger, F.; Buerstmayr, H. Genomic Selection across Multiple Breeding Cycles in Applied Bread Wheat Breeding. Theor. Appl. Genet. 2016, 129, 1179–1189. [Google Scholar] [CrossRef]
- Hayes, B.J.; Panozzo, J.; Walker, C.K.; Choy, A.L.; Kant, S.; Wong, D.; Tibbits, J.; Daetwyler, H.D.; Rochfort, S.; Hayden, M.J.; et al. Accelerating Wheat Breeding for End-Use Quality with Multi-Trait Genomic Predictions Incorporating near Infrared and Nuclear Magnetic Resonance-Derived Phenotypes. Theor. Appl. Genet. 2017, 130, 2505–2519. [Google Scholar] [CrossRef] [PubMed]
- Michel, S.; Gallee, M.; Löschenberger, F.; Buerstmayr, H.; Kummer, C. Improving the Baking Quality of Bread Wheat Using Rapid Tests and Genomics: The Prediction of Dough Rheological Parameters by Gluten Peak Indices and Genomic Selection Models. J. Cereal Sci. 2017, 77, 24–34. [Google Scholar] [CrossRef]
- Haile, J.K.; N’Diaye, A.; Clarke, F.; Clarke, J.; Knox, R.; Rutkoski, J.; Bassi, F.M.; Pozniak, C.J. Genomic Selection for Grain Yield and Quality Traits in Durum Wheat. Mol. Breed. 2018, 38, 75. [Google Scholar] [CrossRef]
- Kristensen, P.S.; Jahoor, A.; Andersen, J.R.; Cericola, F.; Orabi, J.; Janss, L.L.; Jensen, J. Genome-Wide Association Studies and Comparison of Models and Cross-Validation Strategies for Genomic Prediction of Quality Traits in Advanced Winter Wheat Breeding Lines. Front. Plant Sci. 2018, 9, 69. [Google Scholar] [CrossRef] [PubMed]
- Lado, B.; Vázquez, D.; Quincke, M.; Silva, P.; Aguilar, I.; Gutiérrez, L. Resource Allocation Optimization with Multi-Trait Genomic Prediction for Bread Wheat (Triticum Aestivum L.) Baking Quality. Theor. Appl. Genet. 2018, 131, 2719–2731. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Zhao, D.; Chen, X.; Zhang, Y.; Wang, J. Use of Genomic Selection and Breeding Simulation in Cross Prediction for Improvement of Yield and Quality in Wheat (Triticum aestivum L.). Crop J. 2018, 6, 353–365. [Google Scholar] [CrossRef]
- Hu, X.; Carver, B.F.; Powers, C.; Yan, L.; Zhu, L.; Chen, C. Effectiveness of Genomic Selection by Response to Selection for Winter Wheat Variety Improvement. Plant Genom. 2019, 12, 180090. [Google Scholar] [CrossRef]
- Juliana, P.; Poland, J.; Huerta-Espino, J.; Shrestha, S.; Crossa, J.; Crespo-Herrera, L.; Toledo, F.H.; Govindan, V.; Mondal, S.; Kumar, U.; et al. Improving Grain Yield, Stress Resilience and Quality of Bread Wheat Using Large-Scale Genomics. Nat. Genet. 2019, 51, 1530–1539. [Google Scholar] [CrossRef]
- Kristensen, P.S.; Jahoor, A.; Andersen, J.R.; Orabi, J.; Janss, L.; Jensen, J. Multi-Trait and Trait-Assisted Genomic Prediction of Winter Wheat Quality Traits Using Advanced Lines from Four Breeding Cycles. Crop. Breed. Genet. Genom. 2019, 1, e1900010. [Google Scholar] [CrossRef]
- Kristensen, P.S.; Jensen, J.; Andersen, J.R.; Guzmán, C.; Orabi, J.; Jahoor, A. Genomic Prediction and Genome-Wide Association Studies of Flour Yield and Alveograph Quality Traits Using Advanced Winter Wheat Breeding Material. Genes 2019, 10, 669. [Google Scholar] [CrossRef] [PubMed]
- Michel, S.; Löschenberger, F.; Ametz, C.; Pachler, B.; Sparry, E.; Bürstmayr, H. Combining Grain Yield, Protein Content and Protein Quality by Multi-Trait Genomic Selection in Bread Wheat. Theor. Appl. Genet. 2019, 132, 2767–2780. [Google Scholar] [CrossRef]
- Ibba, M.I.; Crossa, J.; Montesinos-López, O.A.; Montesinos-López, A.; Juliana, P.; Guzman, C.; Delorean, E.; Dreisigacker, S.; Poland, J. Genome-Based Prediction of Multiple Wheat Quality Traits in Multiple Years. Plant Genom. 2020, 13, e20034. [Google Scholar] [CrossRef]
- Tsai, H.Y.; Janss, L.L.; Andersen, J.R.; Orabi, J.; Jensen, J.D.; Jahoor, A.; Jensen, J. Genomic Prediction and GWAS of Yield, Quality and Disease-Related Traits in Spring Barley and Winter Wheat. Sci. Rep. 2020, 10, 3347. [Google Scholar] [CrossRef] [PubMed]
- Charmet, G.; Storlie, E.; Oury, F.X.; Laurent, V.; Beghin, D.; Chevarin, L.; Lapierre, A.; Perretant, M.R.; Rolland, B.; Heumez, E.; et al. Genome-Wide Prediction of Three Important Traits in Bread Wheat. Mol. Breed. 2014, 34, 1843–1852. [Google Scholar] [CrossRef] [PubMed]
- Piepho, H.P.; Möhring, J. Computing Heritability and Selection Response from Unbalanced Plant Breeding Trials. Genetics 2007, 177, 1881–1888. [Google Scholar] [CrossRef] [PubMed]
- Ward, J.; Rakszegi, M.; Bedo, Z.; Shewry, P.R.; Mackay, I. Differentially Penalized Regression to Predict Agronomic Traits from Metabolites and Markers in Wheat. BMC Genet. 2015, 16, 19. [Google Scholar] [CrossRef]
| Reference | Quality Traits Examined 1 | Population Type and Size 2 | Platform and Number of Markers 2 | GS Prediction Model 3 | Factors Affecting Prediction Accuracy Examined 2 | Comparison to Other Types of Selection 2 | Single-Trait (ST) or Multitrait (MT) Analysis | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Selected Model | TP Size | TP/VP Relatedness | Marker Density | |||||||
| [30] | TW, PHS, FY, KH, LA-SRC, NaCO-SRC, Suc-SRC, H2O-SRC | 2 biparental populations (209/174 DHs) | 399 multiple platforms/574 DArTs | RRBLUP, BayesCπ | Yes | Yes | No | Yes | Yes (MAS and PS) | ST |
| [21] | TW, PHS, FY, FP, LA-SRC, NaCO-SRC, Suc-SRC, H2O-SRC, KH | 374 lines | 1158 DArTs | RRBLUP, BayesA, BayesB, BayesCπ | Yes | Yes | No | Yes | Yes (MAS and PS) | ST |
| [51] | TKW, TW, GPC, FY, FP, LV, KH, SDS sedimentation, mixograph and alveograph traits | 5520 lines | 3075 SNPs | RRBLUP, GAUSS, PLSR, EN, RF | Yes | Yes | No | No | Yes | ST |
| [53] | TKW, TW, GPC, KH, SDS sedimentation | 8416/2403 landrace accessions | ~23,000/~33,000 DArT SNPs | GBLUP | No | Yes | Yes | No | No | ST |
| [54] | TW, FY, FP, LA-SRC, NaCO-SRC, Suc-SRC, H2O-SRC, KH | 273 elite lines and cultivars | 3919/13,198 SNPs | RRBLUP, BRR, RKHS, EN | Yes | Yes | Yes | Yes | No | ST |
| [50] | TKW, TW, GPC, GC, SC, KH, Zeleny sedimentation | 135 inbred lines,1604 hybrids | 17,372 SNPs | RRBLUP, W-BLUP, BayesCπ | Yes | Yes | Yes | Yes | Yes (PS) | ST |
| [55] | GPC, PY | 659 lines | 9500 DArT SNPs | RRBLUP | No | Yes | Yes | No | No | ST |
| [56] | TKW, TW, GPC, FY, FP, SC, amylose content, FN, LV, LT, MIXT, KH, starch damage, viscosity, farinograph and extensograph traits | 2076 varieties and synthetic derivative lines | 51,208 SNPs | Multivariate model | No | No | No | No | No | ST + MT |
| [57] | GPC, farinograph, extensograph, and alveograph traits | 128 DHs | 6600 DArT SNPs | RRBLUP | No | No | No | No | No | MT |
| [58] | GPC, gluten index, alveograph traits | 170 varieties and advanced lines, 154 DHs | 9752/5153 SNPs | RRBLUP, GBLUP, BayesA, BayesB, BL, RKHS, MT-BayesA, MT-Matrix, MT-SI | Yes | No | Yes | Yes | No | ST + MT |
| [59] | TKW, TW, GPC, FN, Zeleny sedimentation | 635 lines (159 full-sib families) | 10,802 SNPs | GBLUP, BL | Yes | Yes | Yes | Yes | No | ST |
| [60] | TW, GPC, WGC, SV, alveograph and mixograph traits | 495 lines | 6655 SNPs | BRR, Bayes multivariate Gaussian model | No | Yes | No | No | No | ST + MT |
| [52] | GPC, farinograph and extensograph traits | 840 lines | 4598 DArT SNPs | RRBLUP, W-BLUP | Yes | No | No | No | Yes (MAS) | ST + MT |
| [61] | TKW, GPC, mixograph, farinograph, and extensograph traits | 57 cultivars and lines | 7588 SNPs | RRBLUP, BayesA BayesB, BL, BRR | Yes | No | No | No | No | ST + MT |
| [62] | TKW, GPC, SDS sedimentation | 282 DHs | 7426 SNPs | RRBLUP, BL, RF, RKHS | Yes | Yes | No | No | Yes (PS) | ST |
| [63] | TKW, TW, GPC, FY, FP, FS, LV, MIXT, KH, grain color, alveograph traits | 3485 lines | 78,606 SNPs | GBLUP, BayesB | Yes | No | Yes | Yes | No | ST |
| [64] | TKW, GPC, FN, Zeleny sedimentation | 1152 lines | 11,058 SNPs | GBLUP, Bayesian SNP-BLUP | Yes | Yes | Yes | No | Yes (MAS) | ST + MT |
| [65] | FY, alveograph traits | 635 lines (159 full-sib families) | 10,802 SNPs | GBLUP, BL | Yes | Yes | Yes | No | No | ST |
| [66] | GPC, PY, extensograph and farinograph traits | 480 lines | 7300 DArT SNPs | GBLUP, W-BLUP | Yes | No | No | No | No | ST + MT |
| [67] | TKW, TW, GPC, FP, LV, KH, SDS sedimentation, mixograph and alveograph traits | ~1400 lines | 78,606 SNPs before filtering * | BMTME, MTR | Yes | No | No | No | No | MT |
| [68] | GPC, Zeleny sedimentation | 1325 lines | 9290 SNPs | RRBLUP, BL | Yes | No | No | No | No | ST |
| Reference | Quality Traits Examined 1 | Heritability Type | Heritability Strength | Heritability Range | GS Prediction Accuracy Range 3 |
|---|---|---|---|---|---|
| [21] | PHS, GPC, TW, Suc-SRC, LA-SRC, KH, FY | broad-sense | high | 0.71–0.93 | 0.45–0.76 |
| [30] | TW, PHS, FY, KH, LA-SRC, NaCO-SRC, Suc-SRC, H2O-SRC | broad-sense | moderate—high | 0.67–0.95 | 0.27–0.74 |
| [51] | TKW, TW, GPC, FY, FP, SDS sedimentation, KH, LV, mixograph and alveograph traits | narrow-sense | moderate | 0.41–0.68 | 0.42–0.71 |
| [54] | TW, FY, FP, KH, LA-SRC, NaCO-SRC, Suc-SRC, H2O-SRC | alternative calculation for unbalanced data 2 | high | 0.75–0.95 | 0.31–0.67 |
| [50] | TKW, TW, GPC, GC, SC, KH, Zeleny sedimentation | broad-sense | moderate—high | 0.63–0.96 | 0.35–0.96 4 |
| [57] | GPC, farinograph, extensograph, and alveograph traits | alternative calculation for unbalanced data 2 | moderate—high | 0.69–0.83 | 0.16–0.61 4 |
| [59] | TKW, TW, GPC, FN, Zeleny sedimentation | narrow-sense | moderate—high | 0.56–0.81 | 0.2–0.79 |
| [60] | TW, GPC, WGC, SV, alveograph and mixograph traits | broad-sense | moderate | 0.36–0.64 | 0.24–0.43 4 |
| [52] | GPC, farinograph and extensograph traits | narrow-sense | moderate | 0.4–0.66 | 0.3–0.53 |
| [61] | TKW, GPC, mixograph, farinograph, and extensograph traits | broad-sense | high | 0.78–0.93 | 0.25–0.42 |
| [65] | FY, alveograph traits | narrow-sense | moderate—high | 0.38–0.72 | 0.3–0.79 |
| [68] | GPC, SC, Zeleny sedimentation | narrow-sense | low—moderate | 0.35–0.62 | 0.1–0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plavšin, I.; Gunjača, J.; Šatović, Z.; Šarčević, H.; Ivić, M.; Dvojković, K.; Novoselović, D. An Overview of Key Factors Affecting Genomic Selection for Wheat Quality Traits. Plants 2021, 10, 745. https://doi.org/10.3390/plants10040745
Plavšin I, Gunjača J, Šatović Z, Šarčević H, Ivić M, Dvojković K, Novoselović D. An Overview of Key Factors Affecting Genomic Selection for Wheat Quality Traits. Plants. 2021; 10(4):745. https://doi.org/10.3390/plants10040745
Chicago/Turabian StylePlavšin, Ivana, Jerko Gunjača, Zlatko Šatović, Hrvoje Šarčević, Marko Ivić, Krešimir Dvojković, and Dario Novoselović. 2021. "An Overview of Key Factors Affecting Genomic Selection for Wheat Quality Traits" Plants 10, no. 4: 745. https://doi.org/10.3390/plants10040745
APA StylePlavšin, I., Gunjača, J., Šatović, Z., Šarčević, H., Ivić, M., Dvojković, K., & Novoselović, D. (2021). An Overview of Key Factors Affecting Genomic Selection for Wheat Quality Traits. Plants, 10(4), 745. https://doi.org/10.3390/plants10040745








