Occupancy Grid and Topological Maps Extraction from Satellite Images for Path Planning in Agricultural Robots
Abstract
1. Introduction
2. Related Work
3. Agrobpp-Bridge: Agrob Vineyard Detector
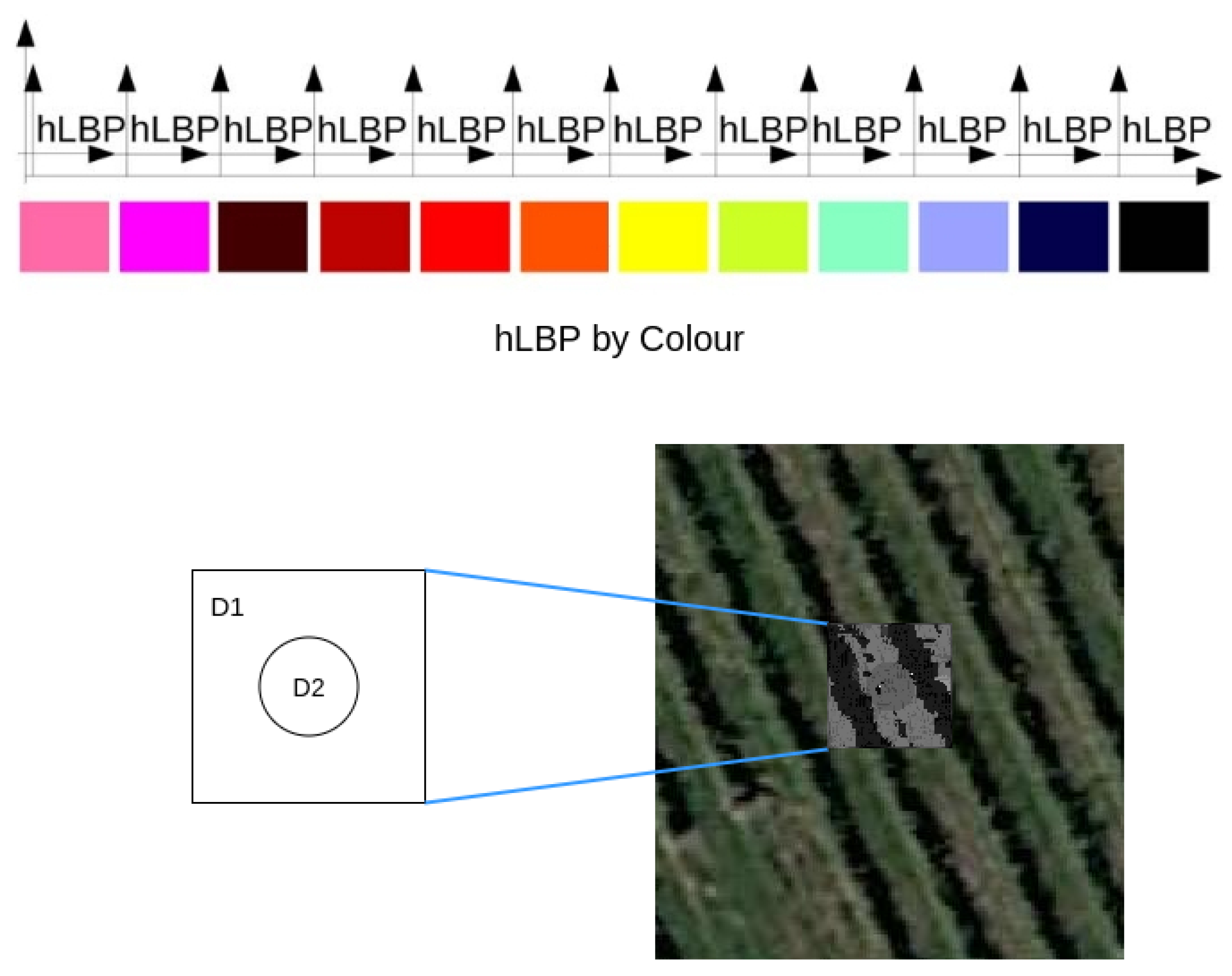
3.1. Segmentation Tool
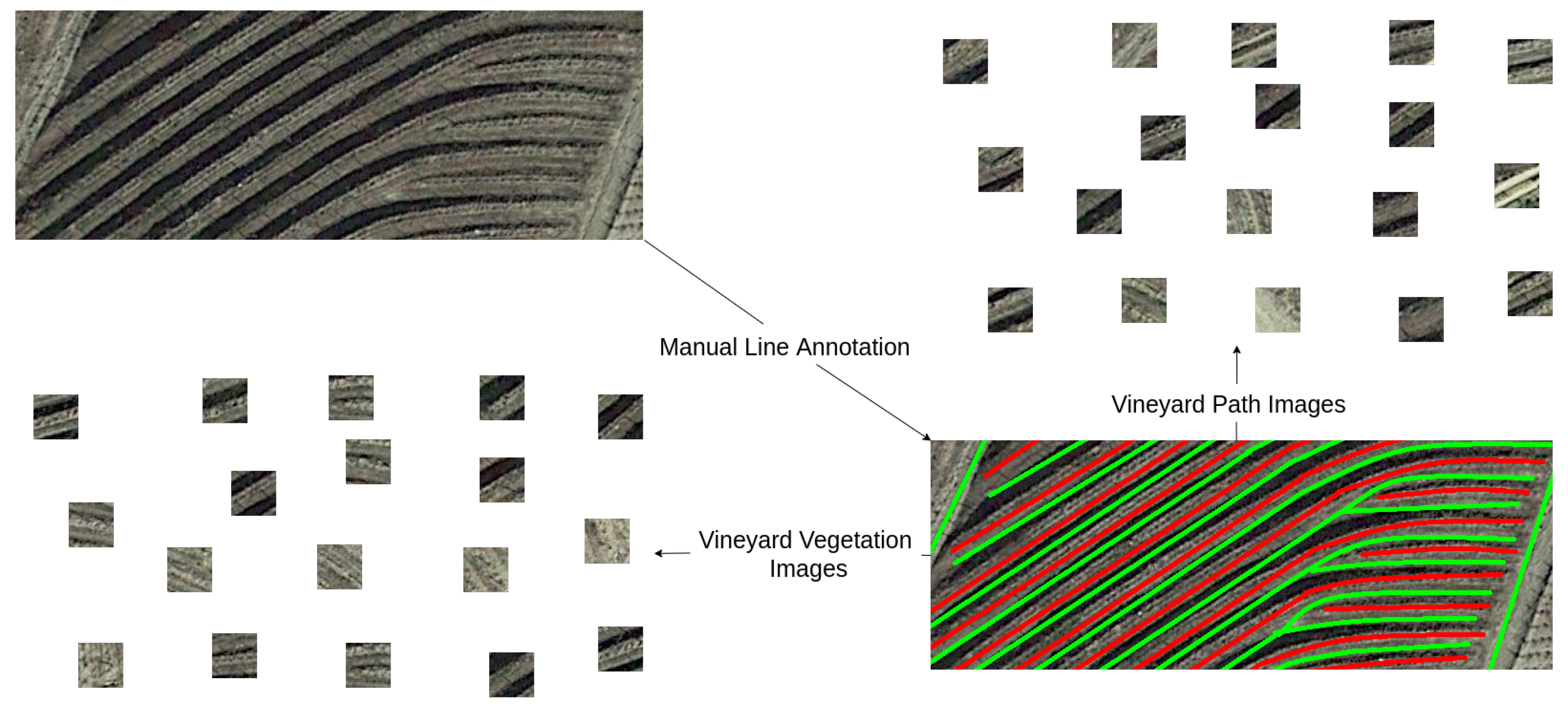
3.2. Annotation Tool
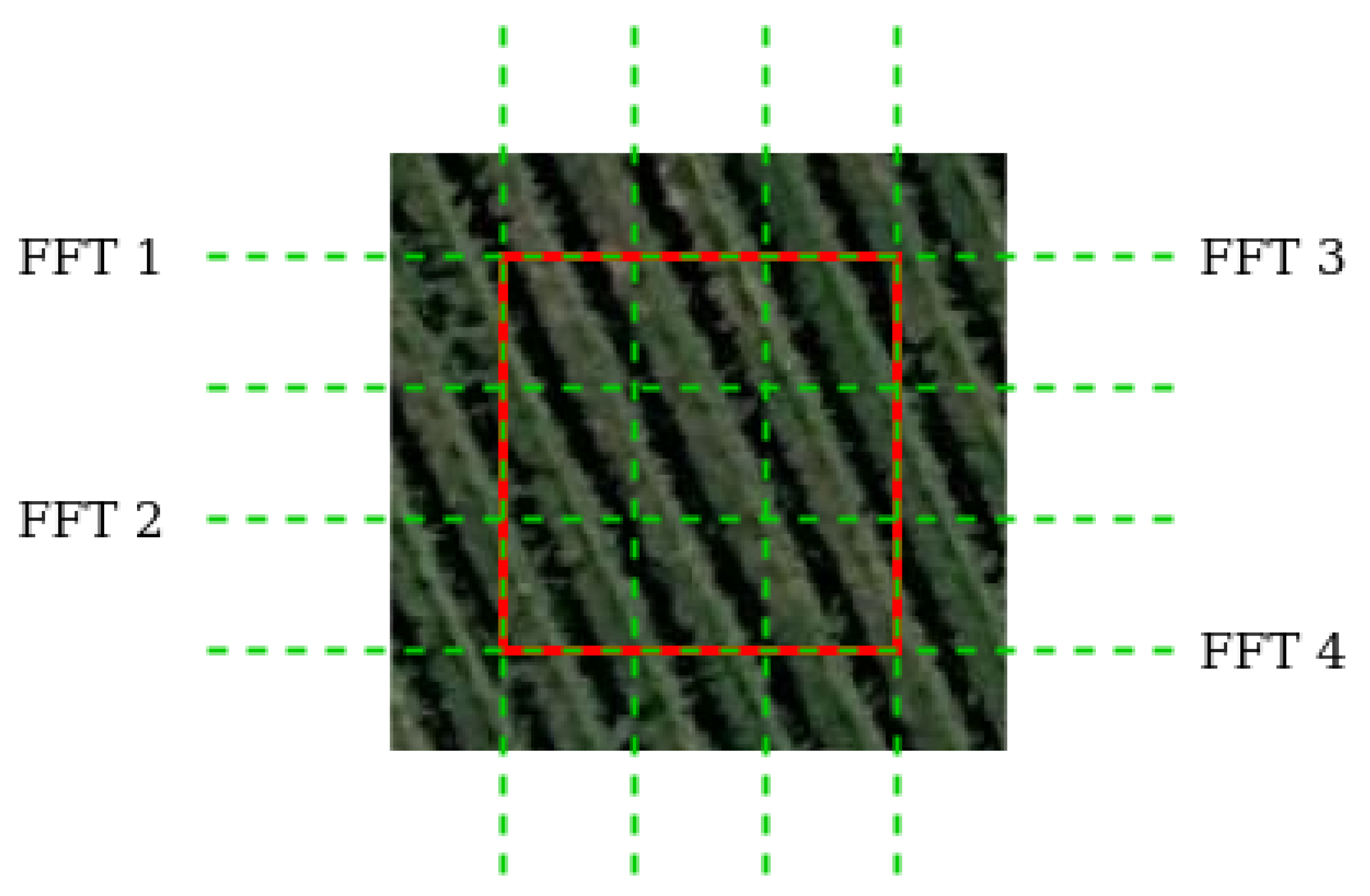
- Choose a column and a row of the selected image zone and calculate their FFTs.
- Choose the FFT with maximum magnitude value at the maximum index as this will be closer to the heading of the image.
- Calculate the distance between two lines: .
3.3. Segmentation Semantic Suite
4. AgRobPP-Bridge—AgRob Grid Map to Topologic
| Algorithm 1 A* algorithm [39] |
1: Add origin node to O (Open list) 2: Repeat 3: Choose nbest (best node) from O so that O 4: Remove nbest from O and add it to C (Closed list) 5: if nbest = target node then end 6: For all which are not in C do: if O then Add node x to O else if g(nbest) + c(nbest, x) < g(x) then Change parent of node x to nbest 7: until O is empty |
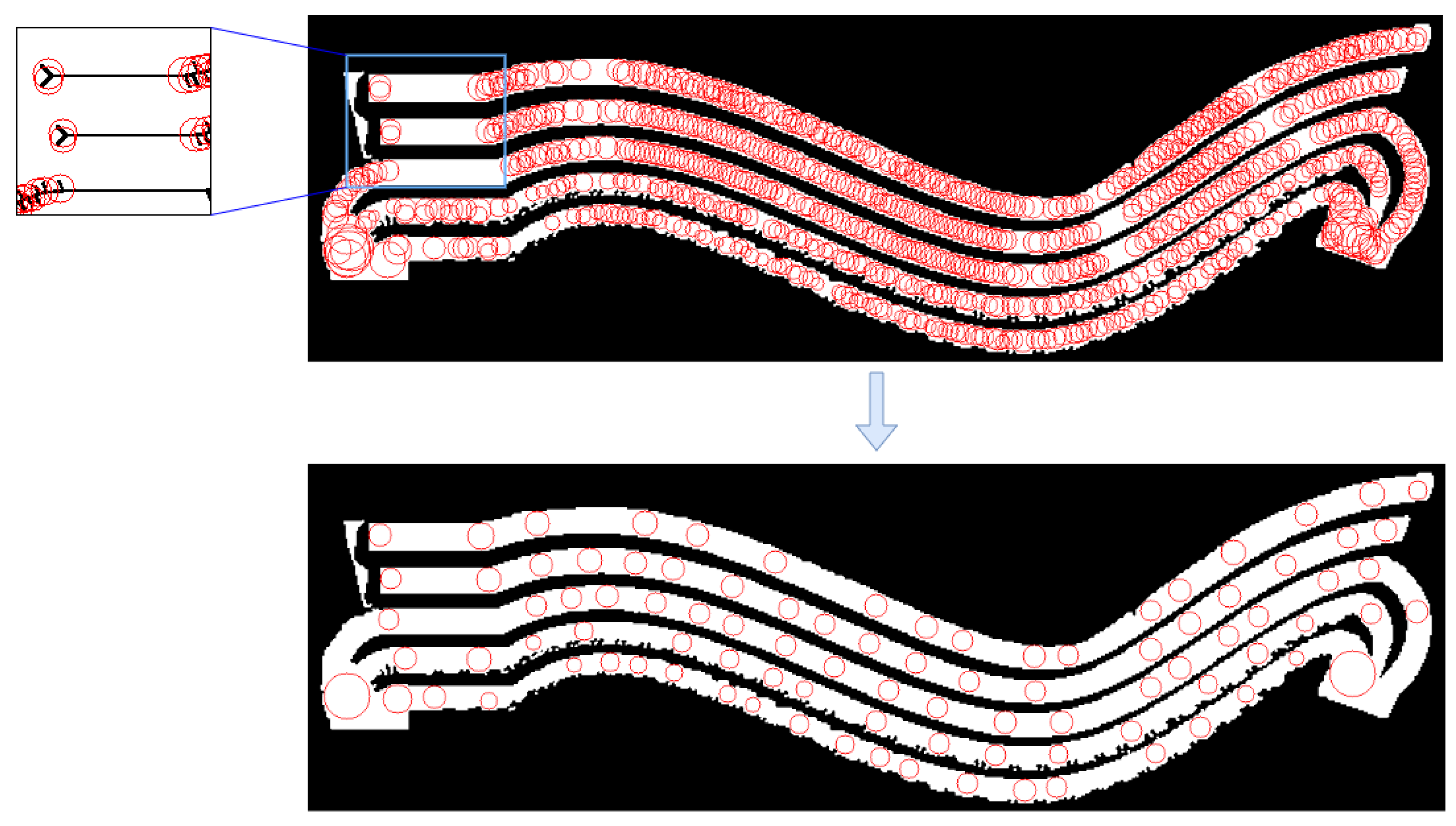
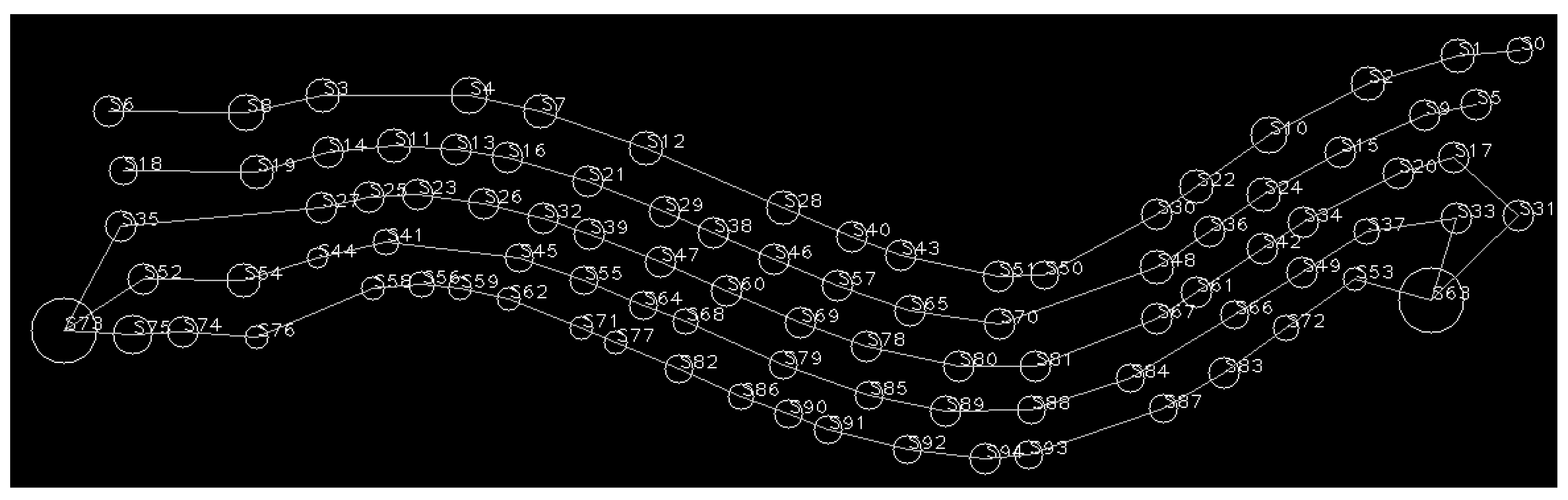
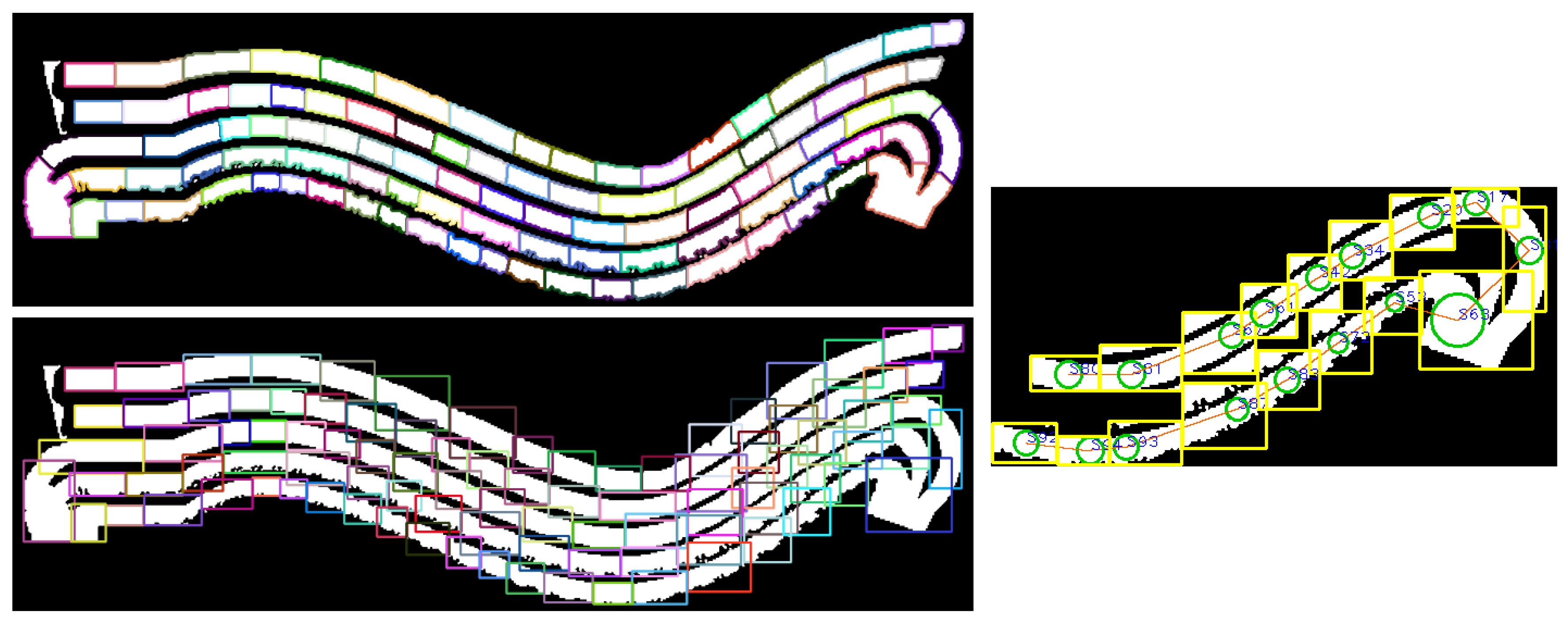
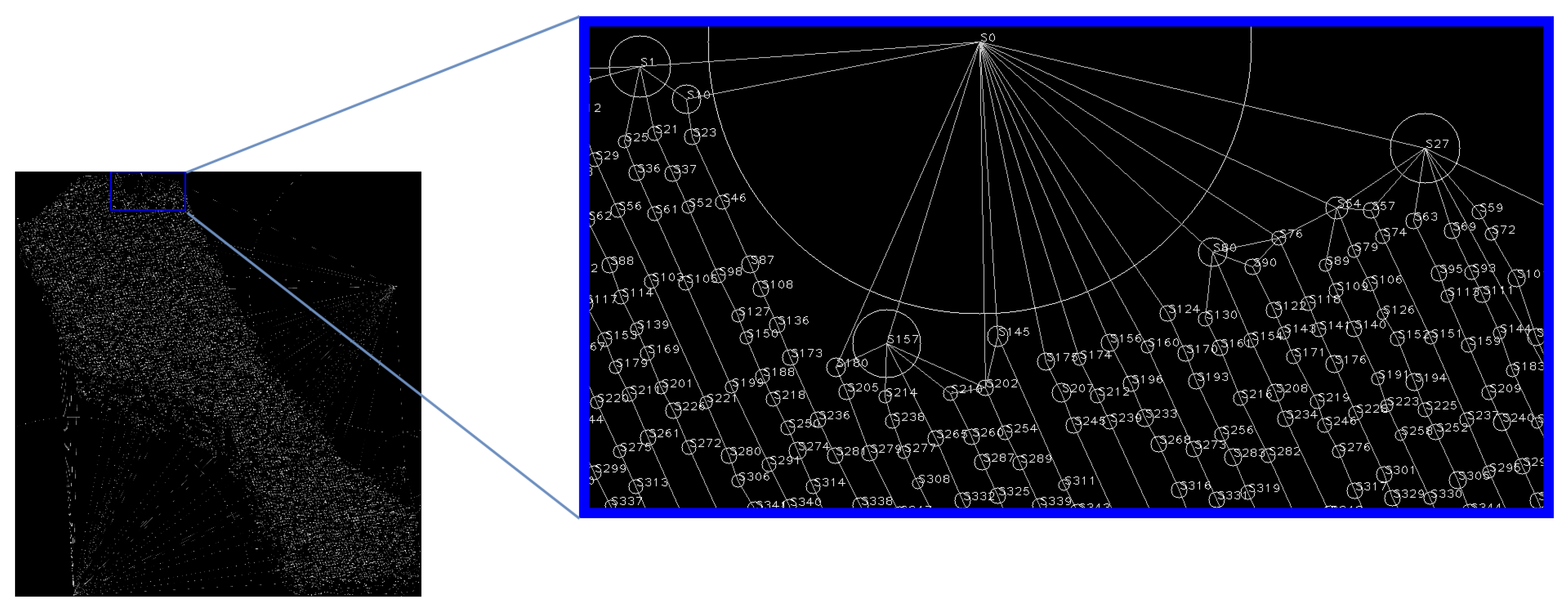
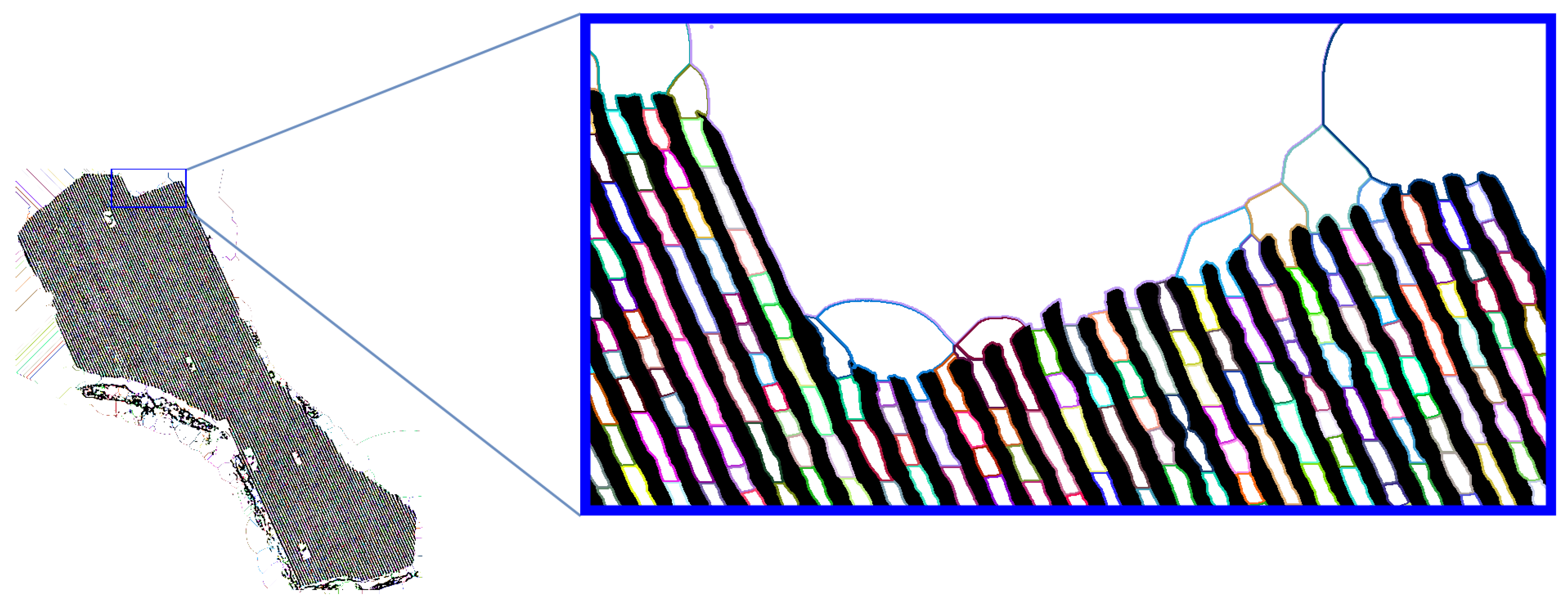
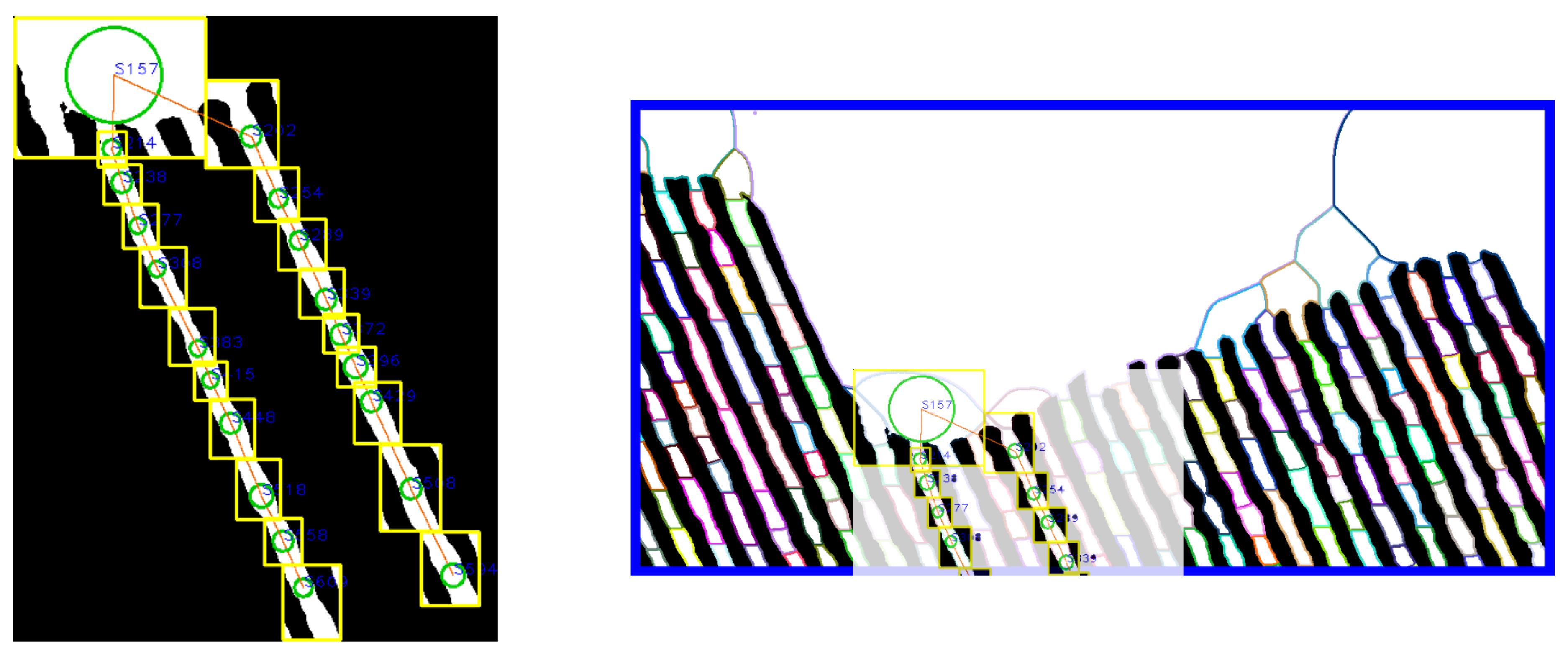
4.1. Voronoi Diagram Extraction
4.2. Topological Map Construction
4.3. Place Delimitation
5. Results
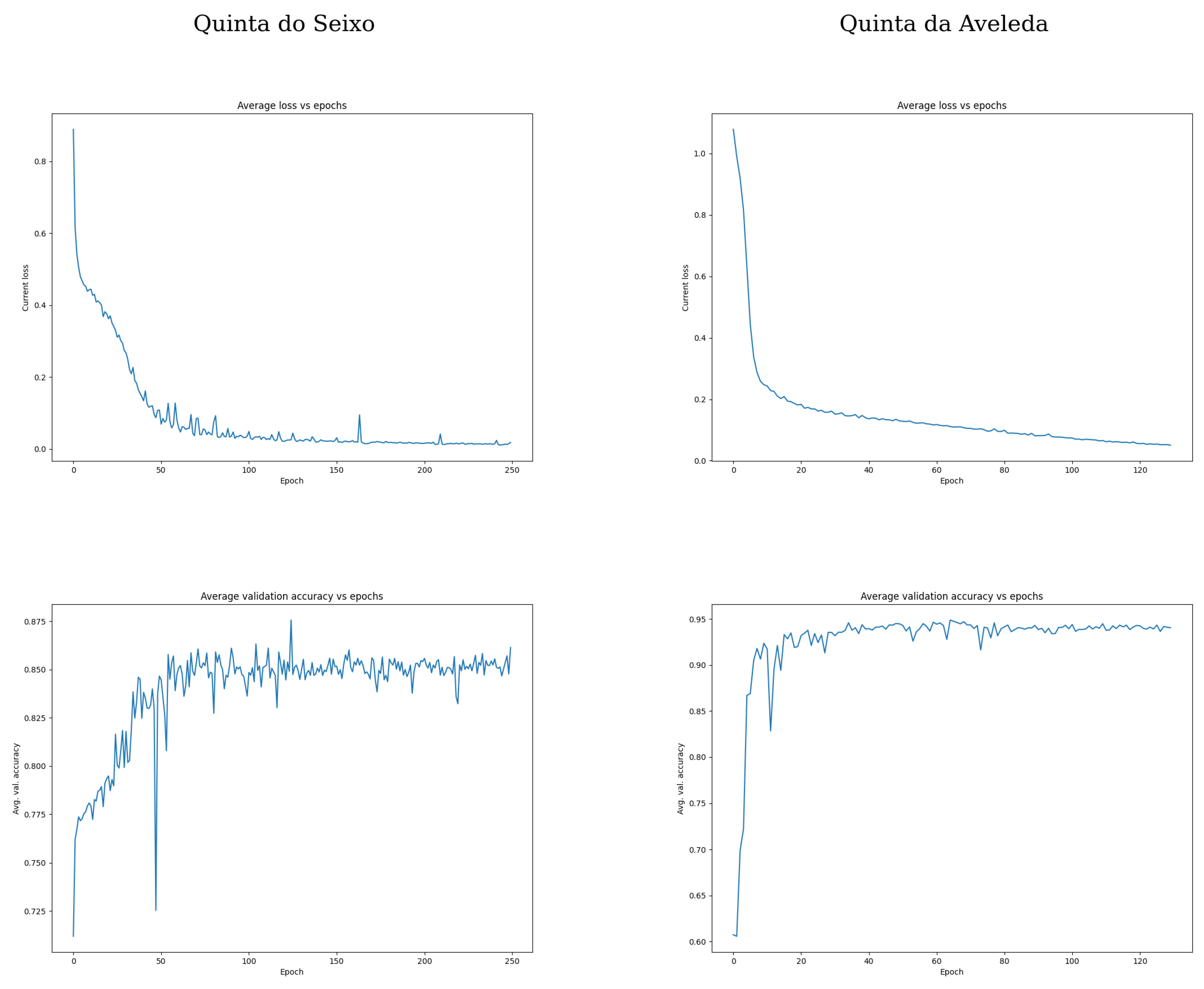
5.1. Agrob Vineyard Detector Results
5.2. Segmentation Semantic Suite Results
5.3. Agrob Grid Map to Topologic Results
5.4. Results Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SLAM | Simultaneous localization and mapping |
| LBP | Local binary patterns |
| SVM | Support vector machine |
| GNSS | Global navigation satellite systems |
| AgRobPP | Agricultural robotics path planning |
| LIDAR | Light detection and ranging |
| UAV | Unmanned aerial vehicle |
| ROS | Robot operating system |
| FFT | Fast Fourier transform |
| DFT | Discrete Fourier transform |
| DL | Deep learning |
| CNN | Convolutional neural network |
| CPU | Central processing unit |
| GPU | Graphical processing unit |
References
- Kitzes, J.; Wackernagel, M.; Loh, J.; Peller, A.; Goldfinger, S.; Cheng, D.; Tea, K. Shrink and share: Humanity’s present and future Ecological Footprint. Philos. Trans. R. Soc. B Biol. Sci. 2008, 363, 467–475. [Google Scholar] [CrossRef] [PubMed]
- Perry, M. Science and Innovation Strategic Policy Plans for the 2020s (EU,AU,UK): Will They Prepare Us for the World in 2050? Appl. Econ. Financ. 2015, 2, 76–84. [Google Scholar] [CrossRef]
- Leshcheva, M.; Ivolga, A. Human resources for agricultural organizations of agro-industrial region, areas for improvement. In Sustainable Agriculture and Rural Development in Terms of the Republic of Serbia Strategic Goals Realization within the Danube Region: Support Programs for the Improvement of Agricultural and Rural Development, 14–15 December 2017, Belgrade, Serbia. Thematic Proceedings; Institute of Agricultural Economics: Belgrade, Serbia, 2018; pp. 386–400. [Google Scholar]
- Rica, R.L.V.; Delan, G.G.; Tan, E.V.; Monte, I.A. Status of agriculture, forestry, fisheries and natural resources human resource in cebu and bohol, central philippines. J. Agric. Technol. Manag. 2018, 19, 1–7. [Google Scholar] [CrossRef]
- Robotics, E. Strategic Research Agenda for Robotics in Europe 2014–2020. Available online: Eu-robotics.net/cms/upload/topicgroups/SRA2020SPARC.pdf (accessed on 21 April 2018).
- Bietresato, M.; Carabin, G.; D’Auria, D.; Gallo, R.; Ristorto, G.; Mazzetto, F.; Vidoni, R.; Gasparetto, A.; Scalera, L. A tracked mobile robotic lab for monitoring the plants volume and health. In Proceedings of the 2016 12th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Auckland, New Zealand, 29–31 August 2016; pp. 1–6. [Google Scholar]
- Ristorto, G.; Gallo, R.; Gasparetto, A.; Scalera, L.; Vidoni, R.; Mazzetto, F. A Mobile Laboratory for Orchard Health Status Monitoring in Precision Frming. In Proceedings of the XXXVII CIOSTA & CIGR Section V Conference, Research and innovation for the Sustainable and Safe Management of Agricultural and Forestry Systems, Palermo, Italy, 13–15 June 2017. [Google Scholar]
- Mahmud, M.S.A.; Abidin, M.S.Z.; Mohamed, Z.; Rahman, M.K.I.A.; Iida, M. Multi-objective path planner for an agricultural mobile robot in a virtual greenhouse environment. Comput. Electron. Agric. 2019, 157, 488–499. [Google Scholar] [CrossRef]
- Iqbal, J.; Xu, R.; Sun, S.; Li, C. Simulation of an Autonomous Mobile Robot for LiDAR-Based In-Field Phenotyping and Navigation. Robotics 2020, 9, 46. [Google Scholar] [CrossRef]
- Fountas, S.; Mylonas, N.; Malounas, I.; Rodias, E.; Hellmann Santos, C.; Pekkeriet, E. Agricultural Robotics for Field Operations. Sensors 2020, 20, 2672. [Google Scholar] [CrossRef] [PubMed]
- Dos Santos, F.N.; Sobreira, H.; Campos, D.; Morais, R.; Moreira, A.P.; Contente, O. Towards a reliable robot for steep slope vineyards monitoring. J. Intell. Robot. Syst. 2016, 83, 429–444. [Google Scholar] [CrossRef]
- Santos, L.; Santos, F.; Mendes, J.; Costa, P.; Lima, J.; Reis, R.; Shinde, P. Path Planning Aware of Robot’s Center of Mass for Steep Slope Vineyards. Robotica 2020, 38, 684–698. [Google Scholar] [CrossRef]
- Seif, G. Semantic Segmentation Suite in TensorFlow. Available online: https://github.com/GeorgeSeif/Semantic-Segmentation-Suite (accessed on 15 July 2020).
- Raja, P.; Pugazhenthi, S. Optimal path planning of mobile robots: A review. Int. J. Phys. Sci. 2012, 7, 1314–1320. [Google Scholar] [CrossRef]
- Mac, T.T.; Copot, C.; Tran, D.T.; De Keyser, R. Heuristic approaches in robot path planning: A survey. Robot. Auton. Syst. 2016, 86, 13–28. [Google Scholar] [CrossRef]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef]
- Pivtoraiko, M.; Knepper, R.A.; Kelly, A. Differentially constrained mobile robot motion planning in state lattices. J. Field Robot. 2009, 26, 308–333. [Google Scholar] [CrossRef]
- Karaman, S.; Walter, M.R.; Perez, A.; Frazzoli, E.; Teller, S. Anytime Motion Planning using the RRT*. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shangai, China, 9–13 May 2011; pp. 1478–1483. [Google Scholar]
- Fernandes, E.; Costa, P.; Lima, J.; Veiga, G. Towards an orientation enhanced astar algorithm for robotic navigation. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; IEEE; pp. 3320–3325. [Google Scholar]
- Elhoseny, M.; Tharwat, A.; Hassanien, A.E. Bezier curve based path planning in a dynamic field using modified genetic algorithm. J. Comput. Sci. 2018, 25, 339–350. [Google Scholar] [CrossRef]
- Santos, L.C.; Santos, F.N.; Solteiro Pires, E.J.; Valente, A.; Costa, P.; Magalhães, S. Path Planning for ground robots in agriculture: A short review. In Proceedings of the 2020 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Ponta Delgada, Azores, Portugal, 15–17 April 2020; pp. 61–66. [Google Scholar]
- Mougel, B.; Lelong, C.; Nicolas, J. Classification and information extraction in very high resolution satellite images for tree crops monitoring. In Remote Sensing for a Changing Europe, Proceedings of the 28th Symposium of the European Association of Remote Sensing Laboratories, Istanbul, Turkey, 2–5 June 2008; IOS Press: Amsterdam, The Netherlands, 2009; pp. 73–79. [Google Scholar]
- Karakizi, C.; Oikonomou, M.; Karantzalos, K. Vineyard detection and vine variety discrimination from very high resolution satellite data. Remote Sens. 2016, 8, 235. [Google Scholar] [CrossRef]
- Rovira-Más, F.; Zhang, Q.; Reid, J.; Will, J. Hough-transform-based vision algorithm for crop row detection of an automated agricultural vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2005, 219, 999–1010. [Google Scholar] [CrossRef]
- Pérez-Ortiz, M.; Gutiérrez, P.A.; Peña, J.M.; Torres-Sánchez, J.; López-Granados, F.; Hervás-Martínez, C. Machine learning paradigms for weed mapping via unmanned aerial vehicles. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016; IEEE; pp. 1–8. [Google Scholar]
- Delenne, C.; Durrieu, S.; Rabatel, G.; Deshayes, M. From pixel to vine parcel: A complete methodology for vineyard delineation and characterization using remote-sensing data. Comput. Electron. Agric. 2010, 70, 78–83. [Google Scholar] [CrossRef]
- Smit, J.; Sithole, G.; Strever, A. Vine signal extraction—An application of remote sensing in precision viticulture. S. Afr. J. Enol. Vitic. 2010, 31, 65–74. [Google Scholar] [CrossRef]
- Poblete-Echeverría, C.; Olmedo, G.F.; Ingram, B.; Bardeen, M. Detection and segmentation of vine canopy in ultra-high spatial resolution RGB imagery obtained from unmanned aerial vehicle (UAV): A case study in a commercial vineyard. Remote Sens. 2017, 9, 268. [Google Scholar] [CrossRef]
- Nolan, A.; Park, S.; Fuentes, S.; Ryu, D.; Chung, H. Automated detection and segmentation of vine rows using high resolution UAS imagery in a commercial vineyard. In Proceedings of the 21st International Congress on Modelling and Simulation, Gold Coast, Australia, 29 November–4 December 2015; pp. 1406–1412. [Google Scholar]
- Comba, L.; Gay, P.; Primicerio, J.; Aimonino, D.R. Vineyard detection from unmanned aerial systems images. Comput. Electron. Agric. 2015, 114, 78–87. [Google Scholar] [CrossRef]
- Quinta do Seixo at Sogrape. Available online: https://eng.sograpevinhos.com/regioes/Douro/locais/QuintadoSeixo (accessed on 30 August 2020).
- Kuipers, B.; Byun, Y.T. A robot exploration and mapping strategy based on a semantic hierarchy of spatial representations. Robot. Auton. Syst. 1991, 8, 47–63. [Google Scholar] [CrossRef]
- Luo, R.C.; Shih, W. Topological map Generation for Intrinsic Visual Navigation of an Intelligent Service Robot. In Proceedings of the 2019 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 11–13 January 2019; pp. 1–6. [Google Scholar]
- Joo, K.; Lee, T.; Baek, S.; Oh, S. Generating topological map from occupancy grid-map using virtual door detection. In Proceedings of the IEEE Congress on Evolutionary Computation, Las Vegas, NV, USA, 11–13 January 2010; pp. 1–6. [Google Scholar]
- Thrun, S. Learning metric-topological maps for indoor mobile robot navigation. Artif. Intell. 1998, 99, 21–71. [Google Scholar] [CrossRef]
- Brunskill, E.; Kollar, T.; Roy, N. Topological mapping using spectral clustering and classification. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 3491–3496. [Google Scholar]
- Konolige, K.; Marder-Eppstein, E.; Marthi, B. Navigation in hybrid metric-topological maps. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3041–3047. [Google Scholar]
- Santos, F.N.; Moreira, A.P.; Costa, P.C. Towards Extraction of Topological maps from 2D and 3D Occupancy Grids. In Progress in Artificial Intelligence; Correia, L., Reis, L.P., Cascalho, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 307–318. [Google Scholar]
- Santos, L.; Santos, F.N.; Magalhães, S.; Costa, P.; Reis, R. Path Planning approach with the extraction of Topological maps from Occupancy Grid Maps in steep slope vineyards. In Proceedings of the 2019 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Porto, Portugal, 24–26 April 2019; pp. 1–7. [Google Scholar]
- Santos, L.; Santos, F.N.; Filipe, V.; Shinde, P. Vineyard Segmentation from Satellite Imagery Using Machine Learning. In Progress in Artificial Intelligence; Moura Oliveira, P., Novais, P., Reis, L.P., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 109–120. [Google Scholar]
- Ojala, T.; Pietikäinen, M.; Harwood, D. A comparative study of texture measures with classification based on featured distributions. Pattern Recognit. 1996, 29, 51–59. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, Y.F. One-against-all multi-class SVM classification using reliability measures. In Proceedings of the 2005 IEEE International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005; IEEE; pp. 849–854. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. (TIST) 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Caesars Palace, Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Jing, J.; Wang, Z.; Rätsch, M.; Zhang, H. Mobile-Unet: An efficient convolutional neural network for fabric defect detection. Text. Res. J. 2020. [Google Scholar] [CrossRef]
- Jegou, S.; Drozdzal, M.; Vazquez, D.; Romero, A.; Bengio, Y. The One Hundred Layers Tiramisu: Fully Convolutional DenseNets for Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Lau, B.; Sprunk, C.; Burgard, W. Improved updating of Euclidean distance maps and Voronoi diagrams. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 281–286. [Google Scholar]
- Map Puzzel Tool for Google Maps. Available online: http://www.mappuzzle.se/ (accessed on 2 July 2020).
- Espejo-Garcia, B.; Lopez-Pellicer, F.J.; Lacasta, J.; Moreno, R.P.; Zarazaga-Soria, F.J. End-to-end sequence labeling via deep learning for automatic extraction of agricultural regulations. Comput. Electron. Agric. 2019, 162, 106–111. [Google Scholar] [CrossRef]










| Classes | N° of Images | Train Images | Test Images | Confusion Matrix | Accuracy (%) | ||
|---|---|---|---|---|---|---|---|
| Path | Vegetation | ||||||
| Aveleda | Path | 537 | 457 | 80 | 72 | 8 | 93.4% |
| Vegetation | 684 | 582 | 102 | 4 | 98 | ||
| Seixo | Path | 607 | 516 | 91 | 81 | 10 | 84% |
| Vegetation | 523 | 445 | 78 | 17 | 61 | ||
| Classes | TP | FP | Accuracy (%) | F1-Score (%) | |
|---|---|---|---|---|---|
| Aveleda | Vineyard | 4,670,106 | 2,075,617 | 88.5 | 66.0 |
| Path | 32,389,277 | 2,734,308 | |||
| Seixo | Vineyard | 339,554 | 460,578 | 87.7 | 54.8 |
| Path | 3,658,598 | 100,345 |
| Classes | TP | FP | Accuracy (%) | F1-Score (%) | |
|---|---|---|---|---|---|
| Aveleda | Vineyard | 5,722,413 | 910,572 | 87.4 | 81.5 |
| Path | 7,361,845 | 2,244,559 | |||
| Background | 25,421,493 | 2,386,748 | |||
| Seixo | Vineyard | 311,261 | 216,800 | 73.3 | 64.3 |
| Path | 1,136,978 | 718,661 | |||
| Background | 2,005,063 | 323,685 |
| AgRob Vineyard Detector (SVM) | Semantic Segmentation Suite | |
|---|---|---|
| Training Time | Low | High |
| Testing Time | High | Low |
| Computational Resources | Medium | High |
| Precision | Medium-high | Medium-high |
| Annotation Process Complexity | Medium-low | High |
| Annotation Process Time | Medium | High |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, L.C.; Aguiar, A.S.; Santos, F.N.; Valente, A.; Petry, M. Occupancy Grid and Topological Maps Extraction from Satellite Images for Path Planning in Agricultural Robots. Robotics 2020, 9, 77. https://doi.org/10.3390/robotics9040077
Santos LC, Aguiar AS, Santos FN, Valente A, Petry M. Occupancy Grid and Topological Maps Extraction from Satellite Images for Path Planning in Agricultural Robots. Robotics. 2020; 9(4):77. https://doi.org/10.3390/robotics9040077
Chicago/Turabian StyleSantos, Luís Carlos, André Silva Aguiar, Filipe Neves Santos, António Valente, and Marcelo Petry. 2020. "Occupancy Grid and Topological Maps Extraction from Satellite Images for Path Planning in Agricultural Robots" Robotics 9, no. 4: 77. https://doi.org/10.3390/robotics9040077
APA StyleSantos, L. C., Aguiar, A. S., Santos, F. N., Valente, A., & Petry, M. (2020). Occupancy Grid and Topological Maps Extraction from Satellite Images for Path Planning in Agricultural Robots. Robotics, 9(4), 77. https://doi.org/10.3390/robotics9040077









