Interactive Robot for Playing Russian Checkers

Abstract

Human–robot interaction in board games is a rapidly developing field of robotics. This paper presents a robot capable of playing Russian checkers designed for entertaining, training, and research purposes. Its control program is based on a novel unsupervised self-learning algorithm inspired by AlphaZero and represents the first successful attempt of using this approach in the checkers game. The main engineering challenge in mechanics is to develop a board state acquisition system non-sensitive to lighting conditions, which is achieved by rejecting computer vision and utilizing magnetic sensors instead. An original robot face is designed to endow the robot an ability to express its attributed emotional state. Testing the robot at open-air multiday exhibitions shows the robustness of the design to difficult exploitation conditions and the high interest of visitors to the robot.

1. Introduction

Designing robots playing games with human opponents is a challenge. Among the earliest examples of playing robots dates back to the XVIII century when Wolfgang de Kempelen presented the first chess-playing robot called “The Turk” or “Automaton Chess Playing” [1,2]. This automaton consisted of a mechanical puppet costumed as a Turkish sorcerer seated at a chessboard, awaiting the challenges of living opponents. It was in fact not autonomous at all since the mechanical arm was operated by human hiding inside the machine. The first successful automaton “El Ajedrecista” was introduced in 1912 by Leonardo Torres y Quevedo [3]. El Ajedrecista was a true automaton built to play chess without the need for human guidance. Since then, no other examples of playing robots have been recorded until the digital revolution and the introduction of computers. Nowadays, the design of playing robots is strictly related to the use of advanced approaches of automated control, artificial intelligence and human–machine interface design.

Games that involve active interaction with physical media such as table tennis or pool require developing sophisticated automatic control algorithms rather than intelligent decision-making programs. Examples of such robots include a table tennis robot based on an industrial KUKA robot by J. Tebbe et al. [4], a self-learning table tennis robot by M. Matsushima et al. [5], an autonomous air hockey robot by M. Lakin [6], and a dual-armed pool robot by T. Nierhoff et al. [7]. Other games such as chess and Go do not necessarily need a physical implementation of a robotic player, but designing the decision-making algorithms for such games is an extremely difficult task. Examples of such game machines are the chess computer Deep Blue [8], capable of winning against a world chess champion Garry Kasparov, and AlphaGo [9], Google’s AI Program that beat the Chinese GoMaster Ke Jie. Nevertheless, it is proposed that the physical implementation of a robotic player in such games improves the user experience and the game attractiveness to human players [10]. Moreover, manipulating non-instrumented arbitrary-shaped pieces on a board in changing environmental conditions is a challenging task itself. In [11], the autonomous chess-playing system Gambit capable of playing physical board games against human opponents in non-idealized environments was presented. In [12], the authors presented a four degree-of-freedom chess-playing robotic manipulator based on a computer vision chess recognition system, whereas in [13,14], a Baxter robot was used to play chess in unconstrained environments by dynamically responding to changes. Other recent examples are the manipulator for Chinese chess presented in [15], the didactic robotic arm for playing chess using an artificial vision system described in [16], and the Chinese chess robotic system for the elderly using convolutional neural networks shown in [17]. Moreover, in [18], the implementation of collaborative robots for a chess-playing system that was designed to play against a human player or another robot was experimentally evaluated. In order to make the board game design easier and fully independent from lighting conditions, some authors propose using an array of Hall sensors for detecting pieces on the board [19]. It is also important that robots with advanced mimics can transmit non-verbal information to human players, which can be also used in gameplay [20,21].

In our work, we pursued a goal to implement a small-sized Russian checkers robot that would have a simple design and be capable of playing checkers on a flexible level. We created a robotic setup consisting of the Dobot 3-DoF manipulator with a custom magnetic-sensor checkers board, control electronics, and a laptop. We developed an original game algorithm using basic features of the renowned AlphaZero, which proved to be efficient in the game Go and then was extended to chess and other games [22]. The game difficulty level is easily selected by choosing the generation of the neural network controlling the move selection process in our algorithm. To our knowledge, this is the first successful attempt to utilize the AlphaZero approach to the Russian checkers game. We obtained an unsupervised self-learning program that was proven to improve its playing capabilities after a number of iterations in our experiment.

The main engineering finding of our research is utilizing Hall sensors instead of computer vision (CV). In table game applications, computer vision is a relatively common and sometimes overestimated solution suffering from sensitivity to light conditions and requiring proper calibration. Our solution utilizes the properties of the game which allows distinguishing the game state after a human player moves without using any special checker identification, using only binary information on the presence/absence of the checker on a field. Therefore, more reliable and robust magnetic sensors were used instead of computer vision.

As the main result, we created a highly transportable, friendly-designed robot, highly versatile in its playing skills. The main challenges in the reported work were creating a novel playing algorithm, reliable hardware, and combining them in a machine, and the aim of our project is conducting a number of studies in human–machine interaction, especially in using robots for education. While the popularity of such classical games as chess and checkers is threatened by video games, using robotized assistants can raise interest in table games among young players, and taking advantage of AI and the robotic environment, they might be very useful in teaching and training classical table games.

Briefly, the main contributions of our study are as follows:

• A novel checkers board with Hall sensors was designed, which allowed us to avoid CV implementation.
• Innovative hardware setup was designed including a control board and an animated face.
• A novel checkers game program was designed based on a deep learning approach inspired by AlphaZero algorithm.

The rest of the paper is organized as follows: Section 2 describes the robot setup and the experimental testbed. Section 3 presents the AlphaZero based algorithm allowing the robot to play Russian checkers. Finally, a discussion on our project in human–machine interaction (HMI) and conclusions are given in Section 4.

2. Robotic Setup

The checkers robot described in the paper has a simple design and contains the following components:

• Actuator (robotic arm);
• Control electronics;
• Checkers field module;
• Facial module (robot’s head);
• Laptop.

As the main mechanical part, the 3-DoF Dobot robotic arm with a repeatability of 0.2 mm was used, equipped with a pneumatic gripper for capturing and moving checkers. It is powered and controlled with an Arduino-based electronic unit. Two PCBs are used in the design: the control electronics module PCB and the checkers field PCB. Due to splitting the electronics into two independent physical parts, the checkers board can be replaced in the future without changing the control electronics module. The working area of the robotic arm is limited due to its compact size, so a 15 cm × 15 cm custom checkers board is used. Equipped with magnetic checker sensors, it is placed in front of the arm. The robot’s head is placed on a neck mounted on the robotic arm basement and has a face with 8 × 8 LED matrices for eyes and eyebrows for expressing a wide range of emotions: surprise, happiness, anger, etc. while remaining schematic enough to avoid the “uncanny valley” effect [23]. A laptop with Core i5 CPU and Win10 operational system running the checkers program is connected to the robot via UART COM-port emulator above USB protocol. 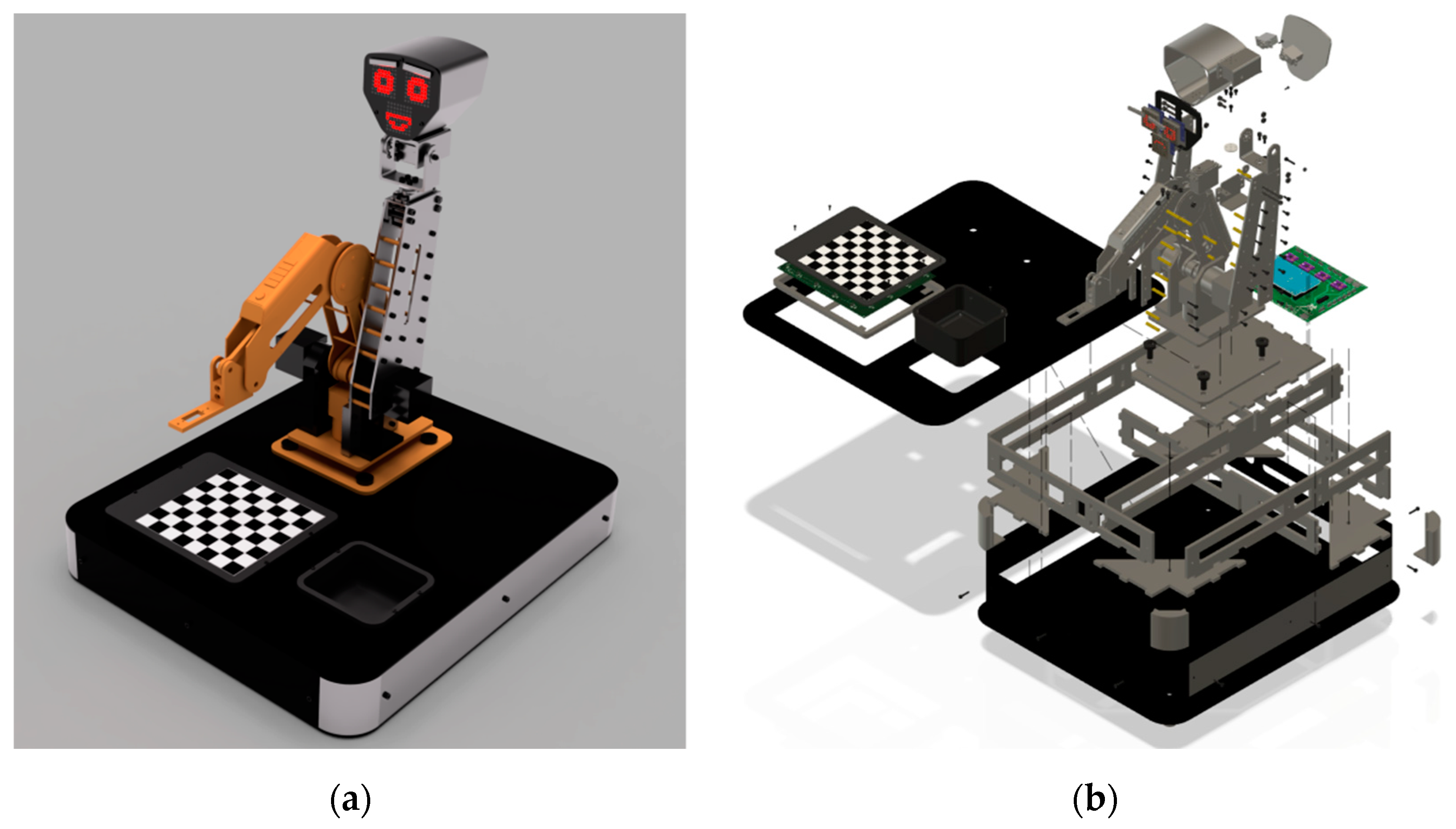Figure 1 shows the 3D model of the main parts of the robotic setup. The custom body details are made of Dibond composite panels. The body of the checkers robot consists of the following parts: a robotic arm and its platform, a rack for a control PCB, a rack for a checkers field PCB, a checkers field cover, a compartment for captured checkers, a robot head with a face. The checkers and some auxiliary mechanical parts are printed from PLA plastic using the 3D printer.

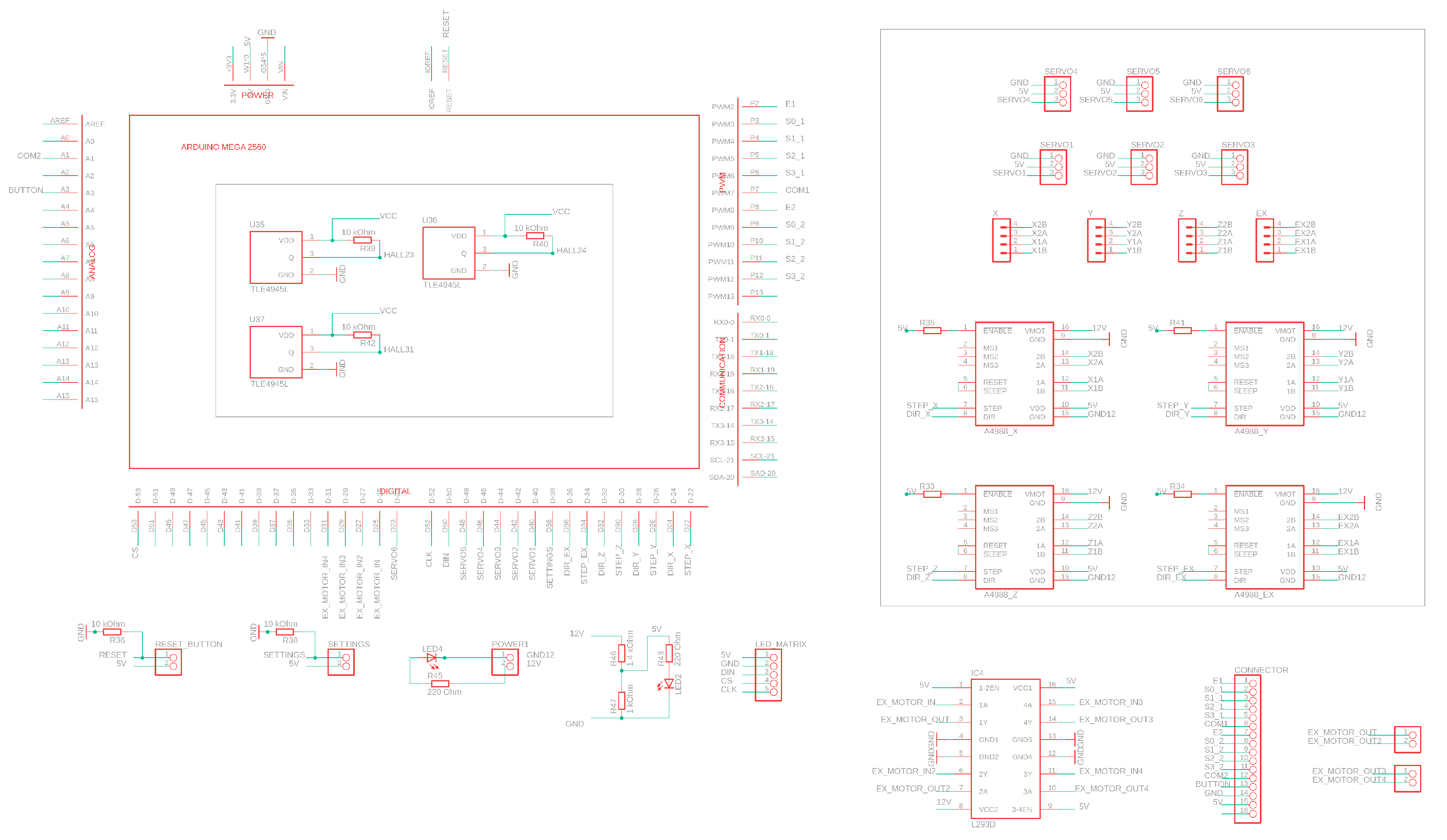
Figure A1 (see Appendix A) presents control electronics schematics for the checkers robot. The electronic unit uses three A4988 drivers for Nema 17 stepper motors and has a driver and a slot for an additional stepper motor. Additionally, the board controls two SG90 servo motors for the eyebrows and two MG996R servo motors for the robot neck. Two additional optional SG90 servo motors can be used for mounting a fingered gripper (not used in the current project). The Dobot original angle position sensors are not used. Instead, limit switches based on TLE4945L bipolar Hall sensors and neodymium magnets are used for more precise initial positioning. For object capturing, an air pump connected through an L293D driver with the microcontroller is used. The control board has three press buttons: reset, power, and settings. Two 8 × 8 LED matrices MAX7219 are connected to the control board for the robot eye imitation.

The board state is obtained via an array of hall sensors below black cells (see Figure A2). The human player confirms his/her move via pressing the button which enforces the microcontroller to read the state of all Hall sensors and transmit a data packet to the laptop. To ensure the proper power supply of all 32 Hall sensors, a power unit should provide at least 15 W.

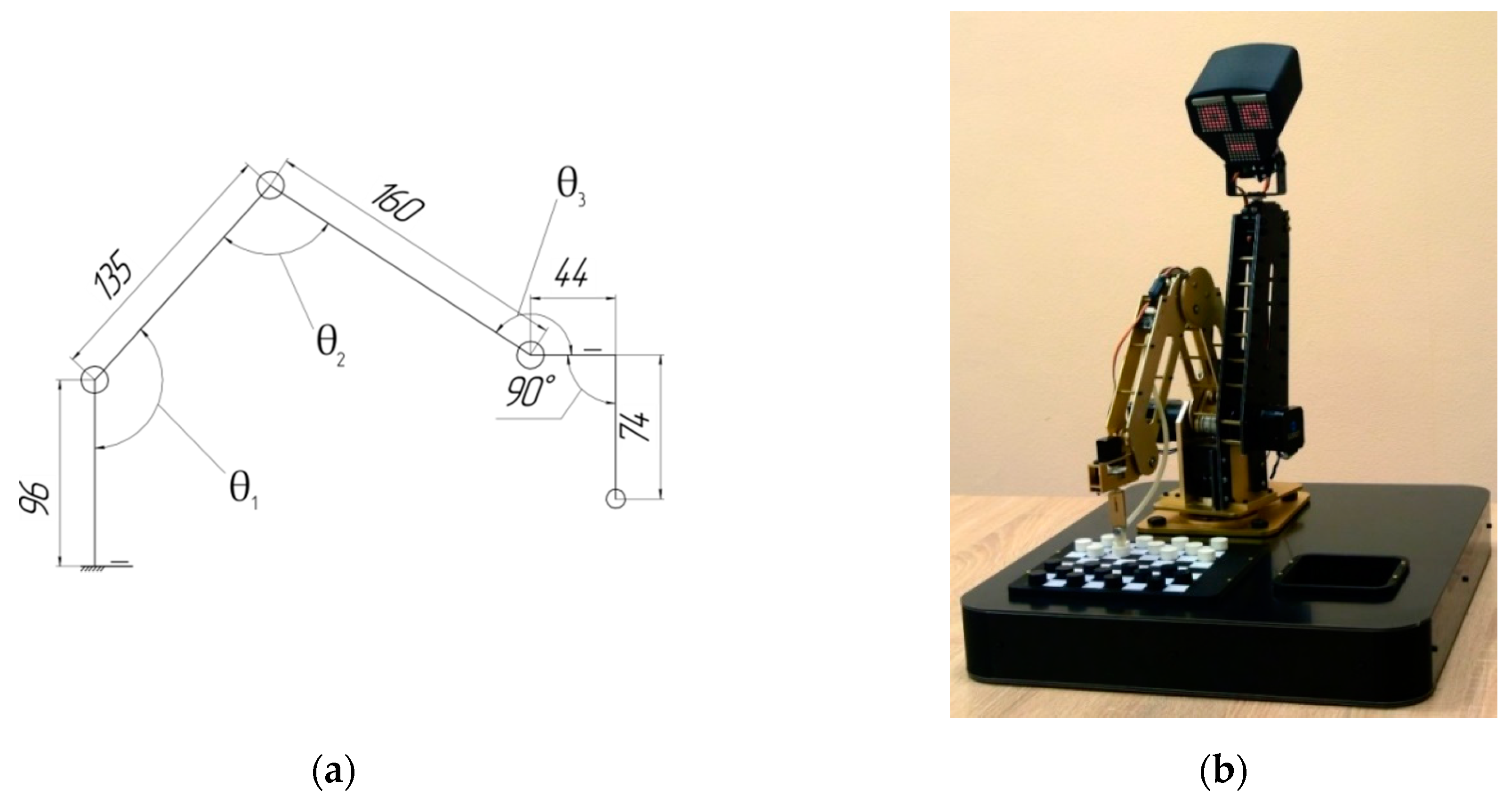
The trajectory of the arm is calculated by the robot controller, and then the robot moves the checker to the desired cell. Since there are no strong limitations for the speed of computation and the precision of the robot moves, the inverse kinematics problem can be solved directly on the controller. The solution utilizes the inverse Jacobian approach, briefly outlined as follows. The kinematic chain is depicted in Figure 2a, where the dependent angle ${\theta }_3=270°-{\theta }_1$ provides the platform where the end effector (pump nozzle) is mounted to be strictly horizontal. The angle ${\theta }_0$ is not shown in the figure since it stands for the rotation of the vertical axis of the robot basement.

Let $\mathrm{s}={\left(x,y,z\right)}^{\top }$ be the end effector position, and $\theta ={\left({\theta }_0,{\theta }_1,{\theta }_2\right)}^{\top }$ be the angular position vector. Then, the Jacobian matrix is computed as

$$J{\left(\theta \right)}_{ij}=\left(\frac{\partial s_i}{\partial {\theta }_j}\right).$$

Then, the dynamics for the forward kinematics is calculated as

$$\dot{\mathrm{s}}=J\left(\theta \right)\dot{\theta }.$$

Thus, the inverse kinematics dynamics can be calculated as

$${\Delta \theta }_n={\mathrm{J}}^{-1}\left({\mathrm{s}}^{*}-{\mathrm{s}}_n\right),$$

where ${\Delta \theta }_n$ is the increment of the current angle ${\theta }_{n+1}={\theta }_n+ {\Delta \theta }_n$ during the robot movement, and ${\mathrm{s}}^{*}$ is the desired position. The path is represented as the fastest trajectory for achieving the desired position ${\mathrm{s}}^{*}$. It is not necessary to provide any special path shape due to the absence of obstacles and singularities in the working field of the robot.

If, during its move, the robot captures an opponent’s checkers, then, at the end of its move, it successively picks up all the captured checkers and throws them into the special compartment representing a rectangular deepening in the robot basement. Figure 2b shows the robotic setup.

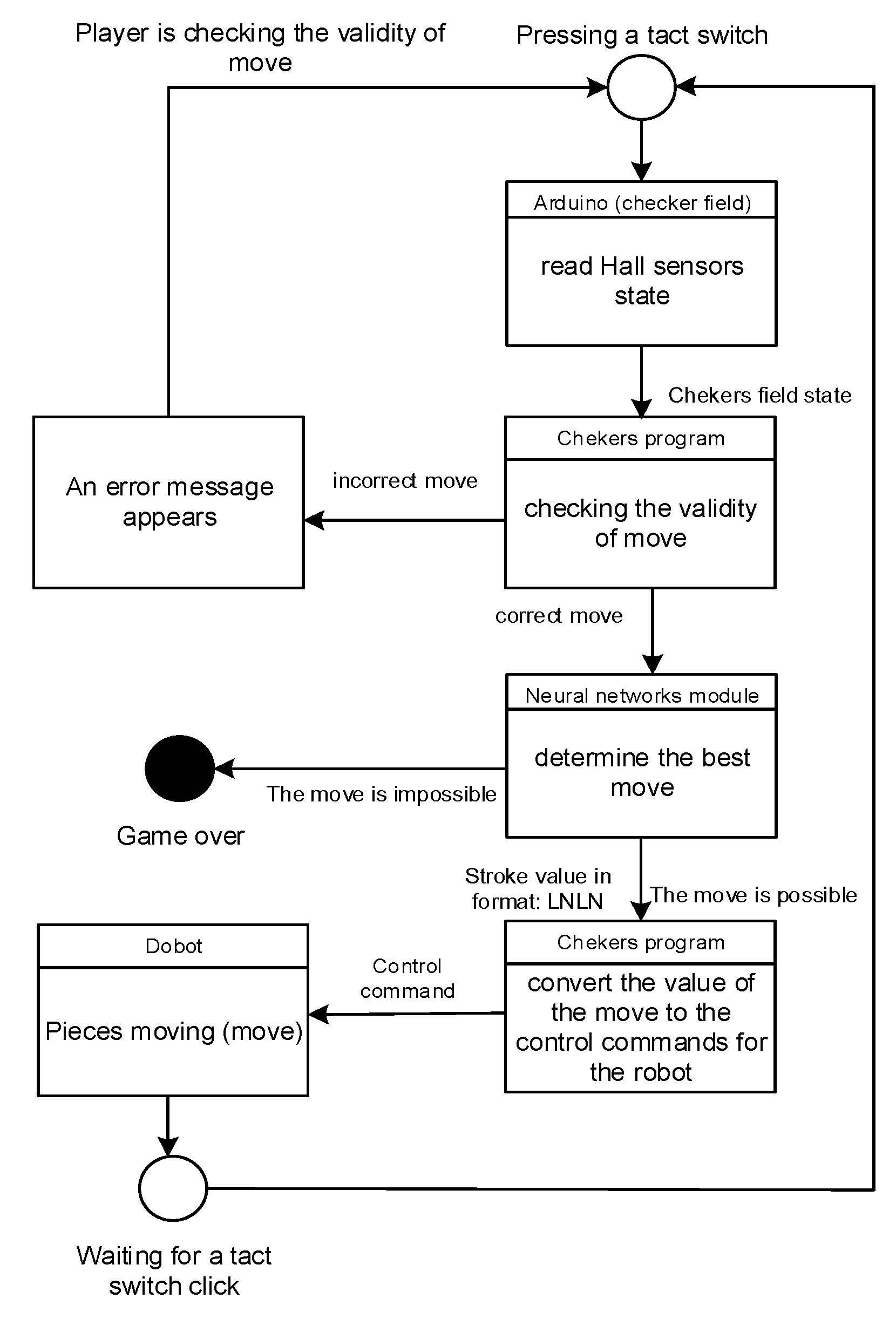
The program provides protection from improper moves. If the player performs a wrong move, the program interface warns with a sound and message. The player then needs to change the move and press the red button again.

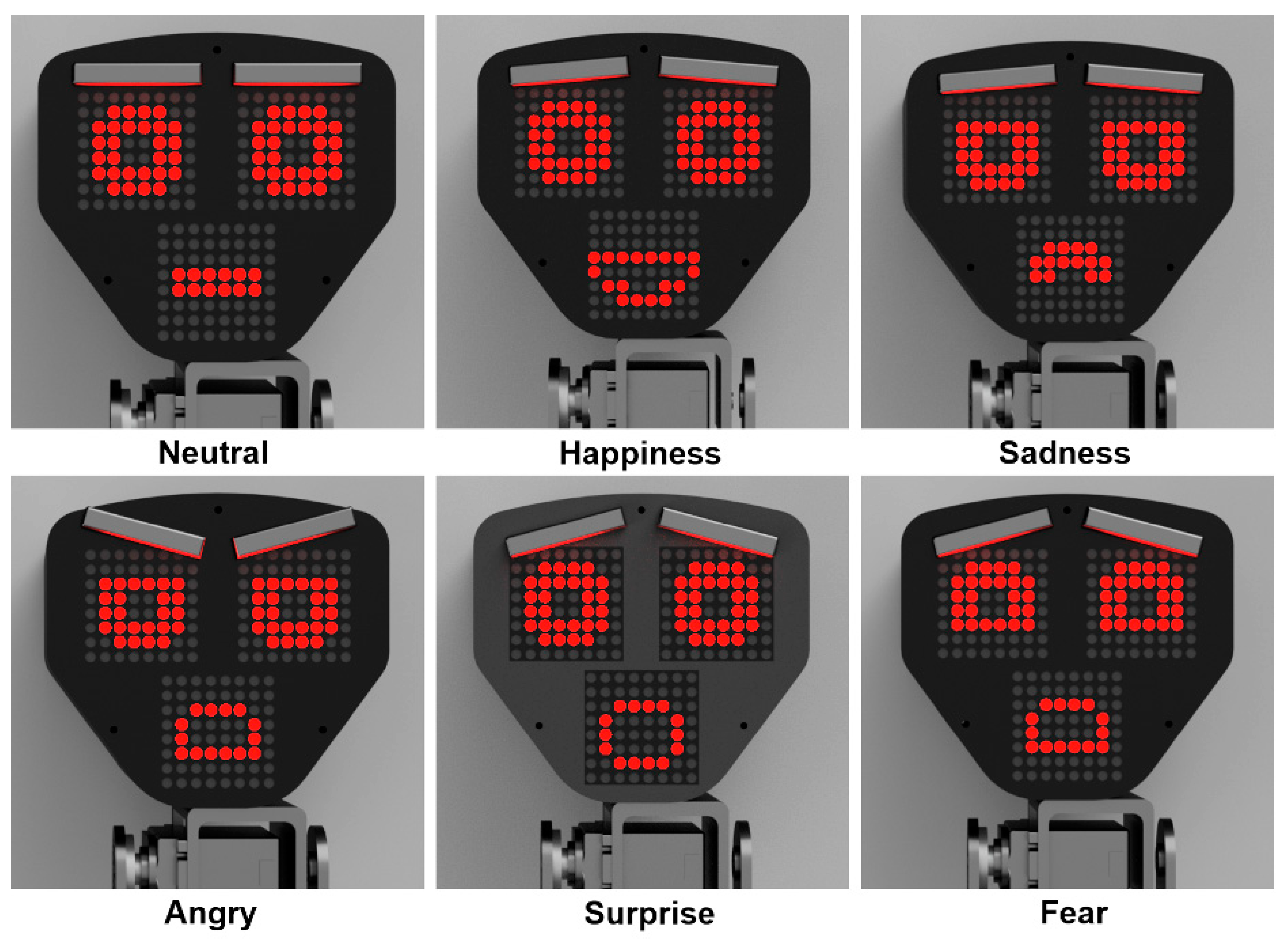
The variety of the robot’s facial expressions is depicted in Figure 3. The basic emotions programmed for the robot, following the famous concept of Ekman and Friesen, are: neutral, happy, sad, angry, surprise, fear, and disgust. The main facial features imitating emotional states follow FLOBI robot features [24].

The eyebrow servo motor positions and facial LED matrices images are controlled by the laptop, which also plays back a voice remarks attributed to the robot corresponding to its emotional state. For instance, when a robot captures an opponent’s checker, it imitates the emotion of “happiness” on its face and plays a voice commentary of the corresponding emotion; when a player breaks the rules, the robot simulates the emotion of anger on its face and plays a voice comment that the rules are violated. The control program for the robot running on the laptop is written based on a custom implementation of the AlphaZero program.

3. Algorithm for Playing Russian Checkers

This section presents the AlphaZero-based algorithm allowing the robot to play Russian checkers. This algorithm does not need any input data for training except the game rules, which is a special feature of AlphaZero-based programs, and no database of the games, possible tricks, or tactics existing for the game are required [25]. Therefore, we decided to base our algorithm on the ideas of AlphaZero. While a number of open-source checkers programs exist, these approaches are mostly obsolete, not as versatile and promising in a possible upgrade in the future.

3.1. Russian Checkers Rules

Russian checkers was chosen because this variant of the game is the most popular in Russia, and visitors at shows will be able to start the game without additional instructions. It is also important that Russian checkers is not a solved game, unlike English checkers [26].

Russian checkers is a board game for two players. The general rules of Russian checkers are similar to other versions of this game, such as English checkers, except for a few points. For clarity, we give a brief list of the rules used during the algorithm training.

• Simple checkers (“men”) move diagonally forward on one cell.
• Inverted checkers (“kings”) move diagonally on any free field both forward and backward.
• Capture is mandatory. Captured checkers are removed only after the end of the turn.
• Simple checker located next to the checker of the opponent, behind which there is a free field, transfers over this checker to this free field. If it is possible to continue capturing other checkers of the opponent, this capture continues until the capturing checker reaches the position from which the capture is impossible. A simple checker performs the capture both forwards and backwards.
• The king captures diagonally, both forward and backward, and stops on any available field after the checker is captured. Similarly, a king can strike multiple pieces of a rival and must capture as long as possible.
• The rule of “Turkish capture” is applied: during one move, the opponent’s checker can be captured only once. If during the capture of several checkers, the simple checker or king moves on a cell from which it attacks the already captured checker, the move stops.
• In multiple capture variants, such as one checker or two, the player selects the move corresponding to his/her own decision.
• The game may have a draw state. A draw occurs when both players have kings and during the last 15 moves no checkers have been attacked.
• White move first.

The checkers field has a size of 8 by 8 cells (64 cells). The white cell in the corner is on the right hand of each player; the cell coordinates are represented by a combination of a letter and a number.

3.2. Monte-Carlo Tree Search Algorithm

The AlphaZero algorithm contains two basic elements: the Monte Carlo Tree Search Algorithm (MCTS) and the neural network. The MCTS algorithm is a randomized decision tree search. Each node of a decision tree is a field state, and each edge is an action necessary to reach the corresponding state. In order to perform decision making, the algorithm simulates the game, during which the player moves from the root of the tree to the leaf.

The neural network estimates the probability of the current player winning $v$ and the probability of the current move choosing $P$, giving the information regarding which of the currently available moves is the most efficient. The MCTS algorithm uses these predictions ($P$ and $v$) to decide where to perform a more elaborate tree search.

Each tree edge contains four values: P, the number $N$ of the current edge visits, the total action value $W$, the expected reward for the current move Q, which is calculated as

$$Q(s,a)=\frac{W(s,a)}{N(s,a)}.$$

(1)

The structure of the decision tree is shown in Figure 4. The next move is made to maximize the action a_t = Q + U. A nonlinear parameter U is computed as

$$U(s,a)=c_{puct}P(s,a)\frac{\sqrt{{\displaystyle \sum _{b}N(s,b)}}}{1+N(s,a)}$$

(2)

where $c_{puct}$ controls the level of tree exploration,$\sum _{b}N\left(s,b\right)$ is the sum of visits in all parents of the current action. The term $U$ is added in order to prevent selecting the “best” moves in early simulations but to encourage tree research. However, over time, the parameter $Q$, which characterizes the overall quality of the move based on multiple wins and defeats, starts to play a leading role, while the role of the parameter $U$ decreases. This reduces the probability of choosing a potentially wrong action. As the result, MCTS computes a search probability vector $\pi$ which assigns a probability of playing the move proportional to the number of nodes visited:

π ∝ N(s,a)^(1/τ),

where τ is the “temperature” parameter controlling the degree of exploration. When τ is 1, the algorithm selects moves randomly taking into account the number of wins. When τ → 0, the move with the largest number of wins will be selected. Thus, τ = 1 allows exploration, and τ→ 0 does not. The activity diagram of MCTS is shown in Figure 5. When the search is complete, the move is selected by the algorithm randomly proportional to its probability $\pi$ found by MCTS.

3.3. Deep Neural Network

The proposed robot game algorithm uses the convolutional deep neural networks (DNN) with a parameter set θ.

To design it, input and output data are first determined. The input data are the field state. The field is a two-dimensional array 8 × 8, but only black cells are used in the game, and each black cell contains different types of data, as follows: empty cell (0), black checker (1), white checker (2), black king (3), white king (4). All checkers move diagonally.

The checkers board contains four areas depending on how many moves a checker can perform from it—see Figure 6. Each area of smaller size contains four fewer black cells and two more moves—see

Table 1. Summary field information on checkerboard areas.

Area	Black Cell Moves	Black Cells
I	7	14
II	9	10
III	11	6
IV	13	2

.

After calculating the data, we obtained 280 possible moves. This number is equal to the number of output neurons that get certain values as the result of the given field state classification. Regarding the state of the checkerboard, our algorithm takes into account not only the current state but also the previous states, dividing one state into two layers.

One layer contains information about the first player’s objects, and another one contains information about the objects of the second player. One additional layer provides information on which player is currently performing the action. The overall set of layers is shown in Figure 7.

The size of this set depends on how many states are stored in memory. If only the current state is considered, three layers are used, but with storing one more move the number of layers increases by two.

Training a DNN is performed after each game. At every move, the MCTS runs first estimating move probabilities π, and each pair (s, π) is recorded, and when the game is complete, its outcome z ∈ {−1, +1} is also recorded. Then, the DNN parameters θ are updated so as to minimize the objective function (up to the regularization term):

l = (z − v)² − π^⊤ logp

(3)

where $v$ and $p$ are values predicted by the DNN.

Initially, we had a completely empty, untrained network, so we could ignore network solutions and perform a tree search based on a random guess, updating only Q and N. After a huge number of preliminary simulations, we obtained a decision tree that works without the neural network directly. Then, we could teach the DNN by searching its set of parameters that match the Monte-Carlo search results as closely as possible. This DNN is close to the AlphaZero network proposed in [9,27].

3.4. Comparing Different Generations of DNN

We ran several tests of the program with similar neural network architecture, varying the size of the input data. Using these results, we analyzed the DNN learning efficiency on input data size. Eight different neural network architectures were generated. Each architecture had 6 residual layers containing 75 matching 4 × 4 filters. The architectures were different in the input data size, namely, how many past game states were stored. Thus, we had 8 variants of neural networks with the number of past states from 0 to 7, which corresponded to input data array sizes from 3 × 8 × 8 to 17 × 8 × 8.

Each network was trained until at least five generations of the network were produced. A new generation was formed when the learner’s agent defeated the current agent with coefficient 1.3, implying that the new version is potentially superior to the previous one. For each architecture, the results of the first five generations were examined. Within the same architecture, 20 games were played between each generation. Each generation received points calculated as the difference between the wins of this generation over another. These points qualitatively estimate the neural network performance. Figure 8 shows that DNN with 13 input layers performs the best.

Using a three-layer neural network, each subsequent generation is progressing, but as we see in the fifth generation, during training, the network can also decrease its performance despite the superiority of the previous version. This is particularly evident in the neural network with 9 input layers, where there was a perceptible failure because the learning process went in the wrong direction. Since the 4th generation, the network has started to grow qualitatively. This indicates that even an ill-trained neural network is capable of retraining and improving initial results. The curve of the neural network with 13 input layers shows that it asymptotically approaches the limit of its learning, and each new generation is progressing less than the previous.

It is difficult to confirm the explicit correlation of the input data with the accuracy of DNN training. In terms of training quality, the network with 13 input layers proved to be the best, which could potentially indicate the most appropriate amount of data for this configuration.

3.5. Comparing with Aurora Borealis

As a reference checkers program, we used a free version of Aurora Borealis [28]. This program is a well-known prize-winner of European and world championships and is one of the top ten best checkers programs. Its Russian checkers engine uses a database with approximately 110 thousand games. Maximum performance settings of the program were used for our test.

A number of matches were played between Aurora Borealis and 5th generation DNN with 17 input layers. Most of the matches were played according to the rules of blitz tournaments with a limit of 15 min per match, and several matches were played according to the classical rules with a 1 h limit. In about half of all matches, Aurora Borealis failed to find a move in the allotted time and was disqualified. The remaining half of the matches was predominantly won by Aurora Borealis.

The result of tests shows that the DNN-based program is much faster and more reliable but still needs additional learning to be able to compete on equal terms with top checkers programs. The speed is the extremely important parameter here due to the main purpose of designed robot.

3.6. Interaction between Checkers Program, Robot, and User

Figure 9 presents a diagram of the Russian checker robot algorithm. After the software module based on AlphaZero has received the data on checker field state, it produces the move and returns the corresponding command set to the robotic setup.

The program also produces an emotional state based on the current robot move quality estimation v (probability to win) given by the DNN. The correspondence between the robot’s emotional state, its attitude to the human player, and the game state is given in

Table 2. Emotional state of the robot.

Attitude to Human	Robot Move Estimation	Emotional State
positive	$v<0.6$	happiness
	$v\in \left[0.6;0.9\right]$	neutral
	$v>0.9$	sadness
negative	$v>0.8$	happiness
	$v\in \left[0.4;0.8\right]$	sadness
	$v<0.4$	anger

.

Two emotions (surprise and fear) are used in exceptional cases of $v$ in comparison to its previous value. The attitude is prescribed in the program settings and may be “positive” (benevolent) and “negative” (aggressive). When it is set to “positive”, the robot imitates that it empathizes with the human player and rejoices at the user’s good play. When the attitude is “negative”, the robot imitates its aggression and rivalry. The phrases corresponding to the emotional state are occasionally played back describing the robot’s state and giving value judgments on the game, such as: “Brilliant move!” or “Sorry, but I don’t think this move was good for you”. It also asks the user to make another move if the last user’s move was incorrect. The voice messages are transmitted through the laptop speakers or an external powerful speaker if the environment is too noisy—e.g., at exhibitions and shows. Servo motors in the robot neck tilt its head in the direction of the board when the robot makes a move and set the head in a vertical position when it waits for the opponent’s move or speaks a message. Eye LED matrices imitate pupil movements towards the board and the user, and follow the overall emotional expression—see Figure 3.

4. Discussion and Conclusions

In this paper, we presented a robot playing Russian checkers based on the AlphaZero algorithm. The checkers algorithm with 13 state layers recording the last five moves proved to achieve the best results among the tested versions. The robotic setup was built using the Dobot v.1.0 robotic arm with a custom checker board and successfully performed its task.

The reported robot participated in Geek Picnic 2019, Night of Museums 2019, and other exhibitions and public events in Saint Petersburg, Russia. Due to the use of Hall sensors instead of a computer vision system, it was independent from lighting conditions, which was especially valuable at events with rapidly changing, insufficient, and flashing light. It also made the design compact and non-expensive. On the other hand, using the digital Hall sensors turned out to be less robust to inaccurate piece localization than could be achieved with analog sensors.

The robot played a number of games with visitors at the abovementioned events. As a qualitative result, the robot gained the attention of visitors of all ages and showed itself as a well-recognized attraction. Adjusting the game difficulty level by selecting the generation of the DNN was proved as a reliable idea.

The ability of the robot to render a facial emotional state and its voice remarks were appreciated by many users since it brings better interactivity to the gameplay.

The robot was designed within the project on the human–machine interface (HMI). The main motivation of the work is as follows. While conventional interfaces for table games (Chess, Checkers, Go, etc.) between human players and computer belong mostly to a class of GUI-based solutions, a classical game design with physical pieces and a board can only be used in a robotized environment [29]. It is intuitively clear that physical interface (GUI or real board) may somehow affect the performance or psychosomatic state of players, but only recently the evidence of the latter phenomenon was obtained for chess game [30]. The authors show that this difference is caused by being familiar or not with playing chess with a computer. While training with a computer is an ordinary practice for many young players, these results indirectly indicate an importance of training in a physical environment as well.

The robot can not only serve as a manipulator for pieces, but it can also introduce some additional interactivity or stress factor for making the training process more versatile, which is especially valuable for young players. For example, it can help to improve their focus on the game, or train their stress resistance. Some recent results show successful examples of using robots in teaching handwriting, showing that a robotized environment may be used for developing an efficient teaching process [31].

In our future work, we will focus on the following aspects:

• Investigation of the robot application to teaching checkers game and its efficiency in various training aspects.
• Investigation of performance of checkers board with analog Hall sensors.
• Additional learning procedures for DNN and more elaborate comparison with existing checkers programs.

Additionally, we will perform a qualitative study on how apparent emotions make the game process more entertaining.