Adaptive Interval Type-2 Fuzzy Logic Control of a Three Degree-of-Freedom Helicopter
Abstract
1. Introduction
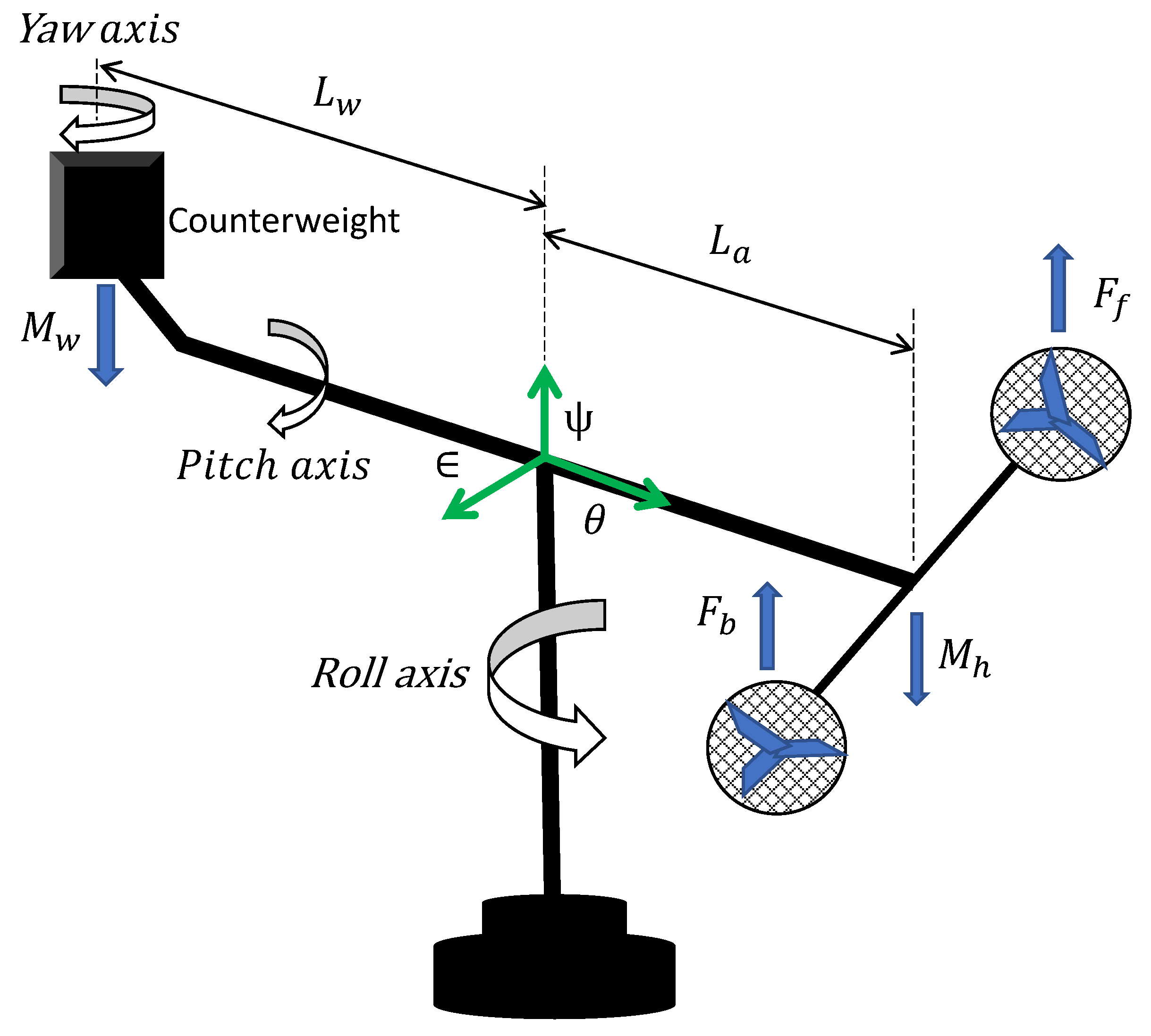
2. System Dynamics
- The roll angle (): The helicopter turns relative to the perpendicular axis (elevation angle). The total force exerted on the system is the aggregation of the thrusts caused by the propellers powered by the two engines and the moments exerted by the counterweight and the weight of the main beam.
- The pitch angle (): This is a movement which is due to the imbalance of forces between the pair of motors, or an inclination of one relative to the other, taking as a pivot the end of the arm which contains them.
- The yaw angle (): The forces acting on the axis of movement are due to the difference between the thrusts of the two motors.
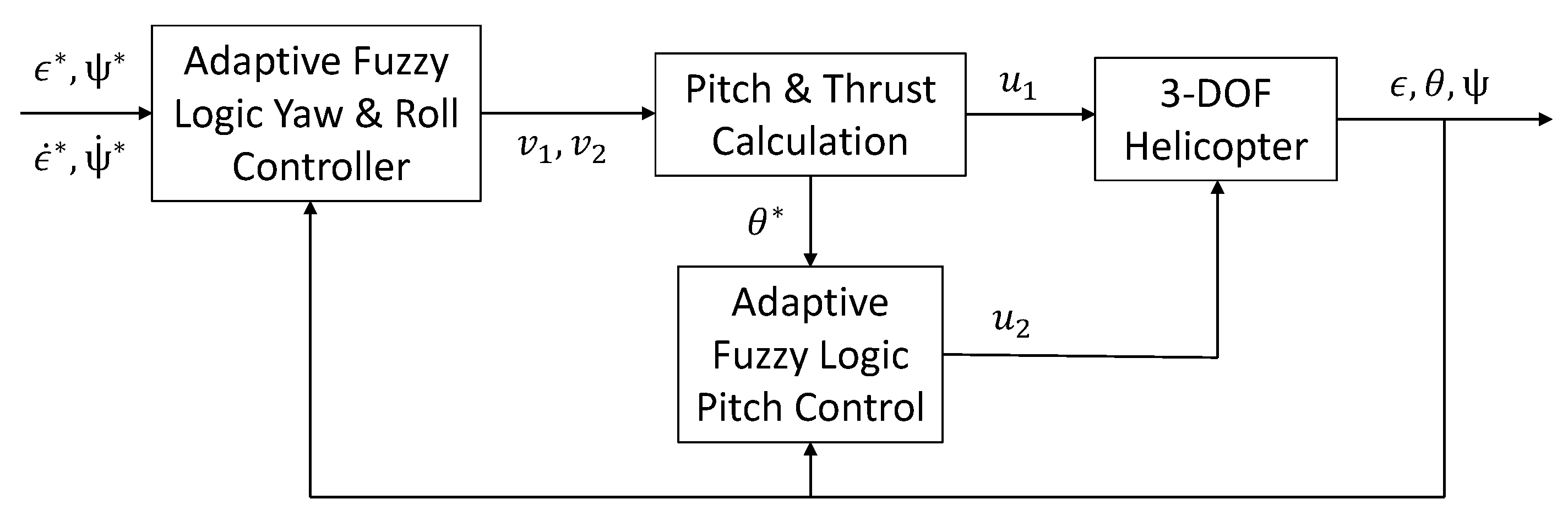
3. Adaptive Interval Type-2 Fuzzy Logic Control
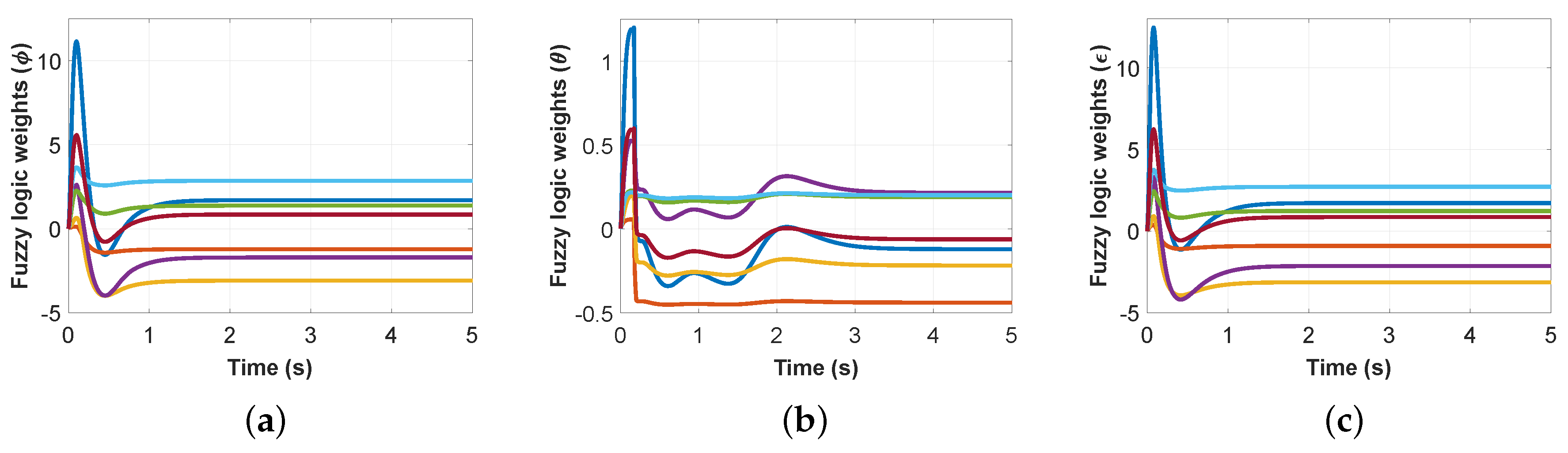
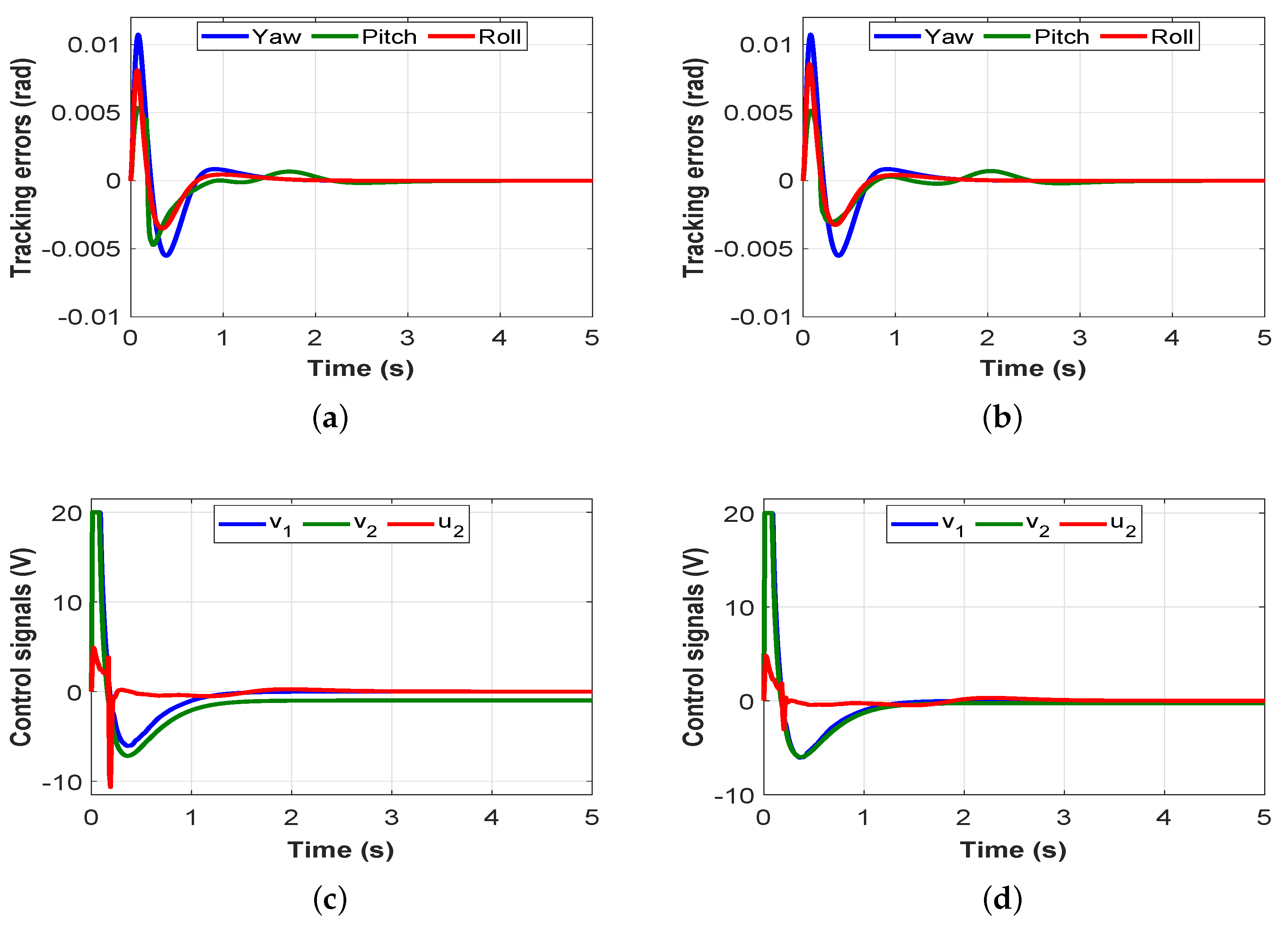
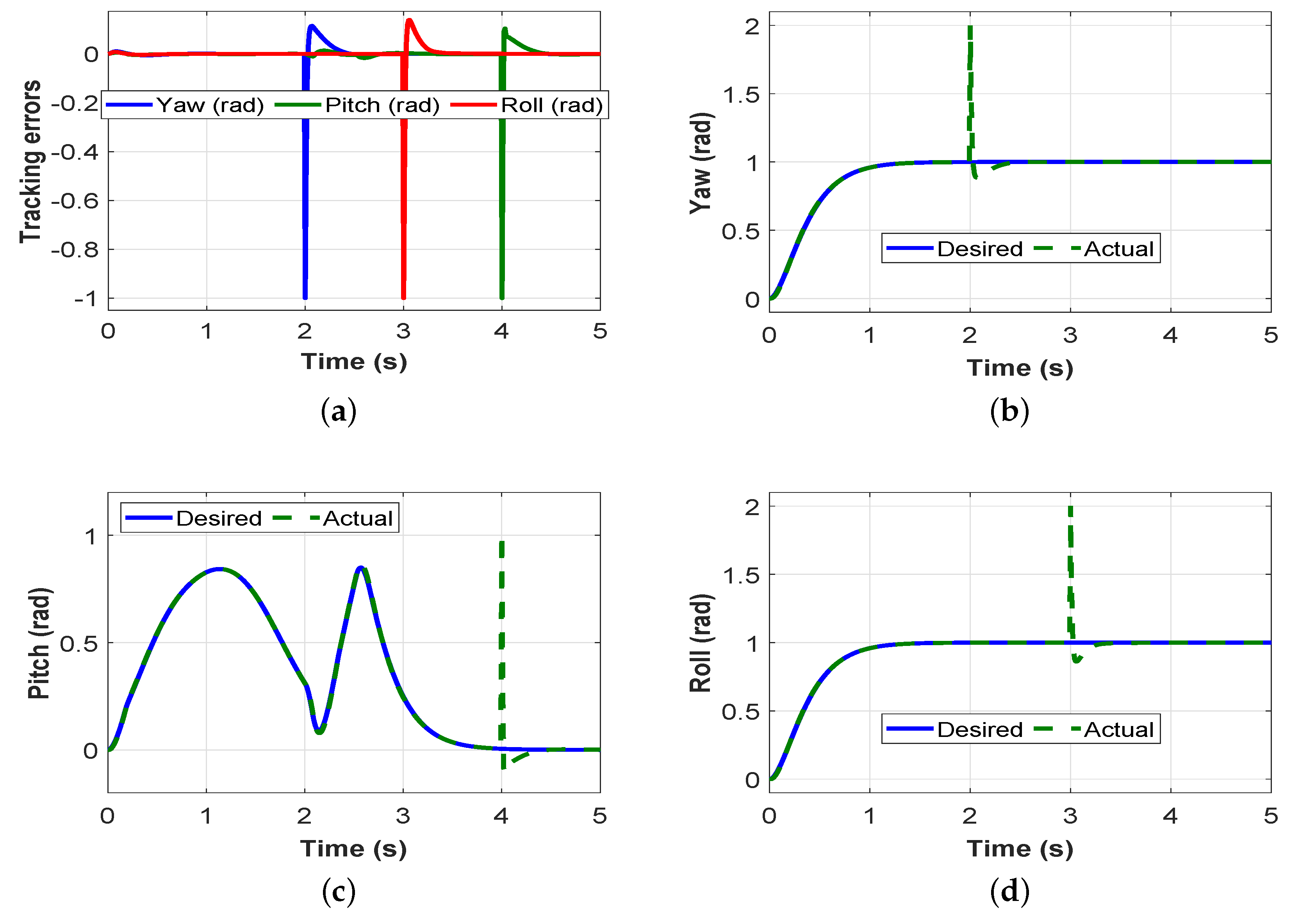
4. Results and Discussion
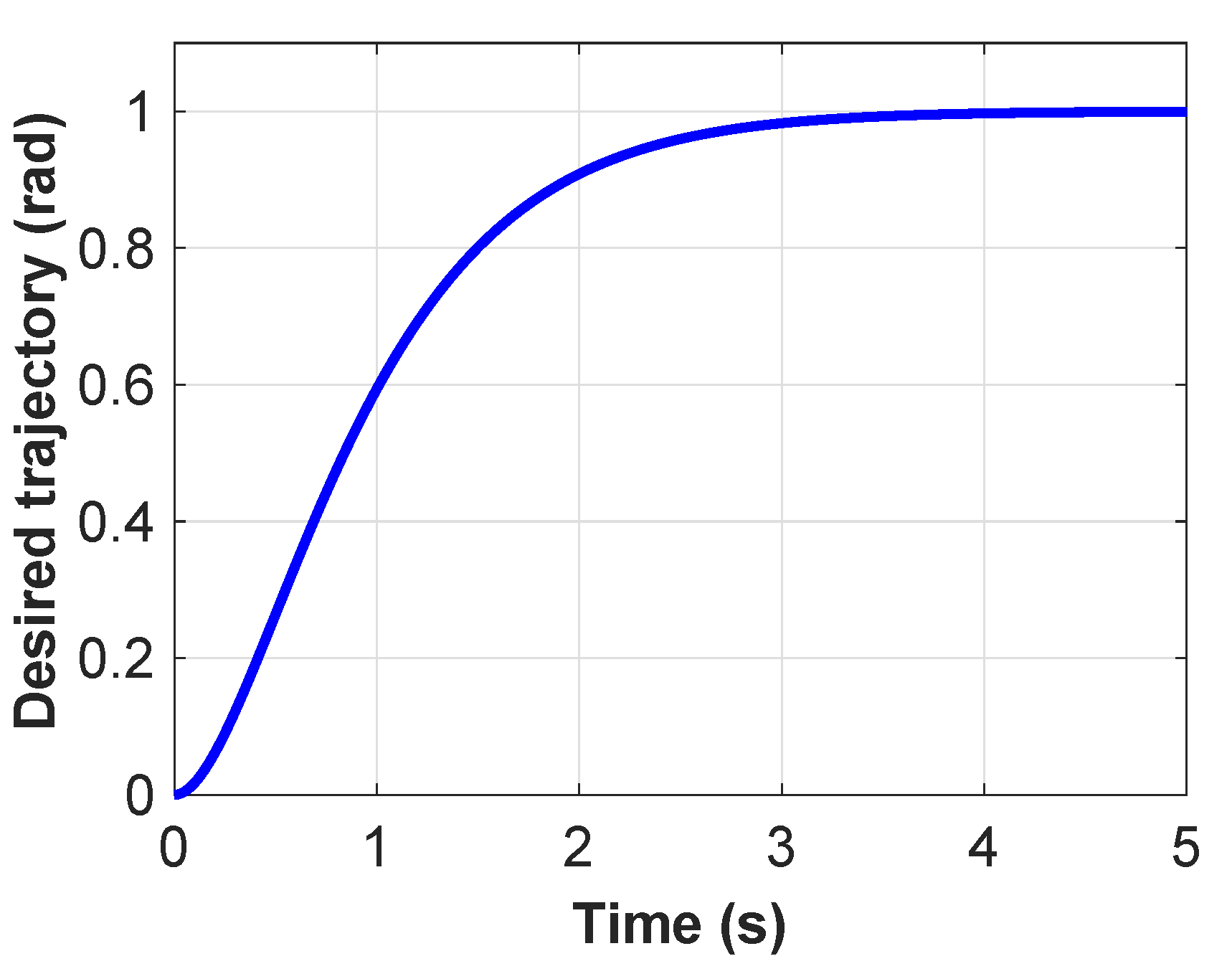
4.1. Setup
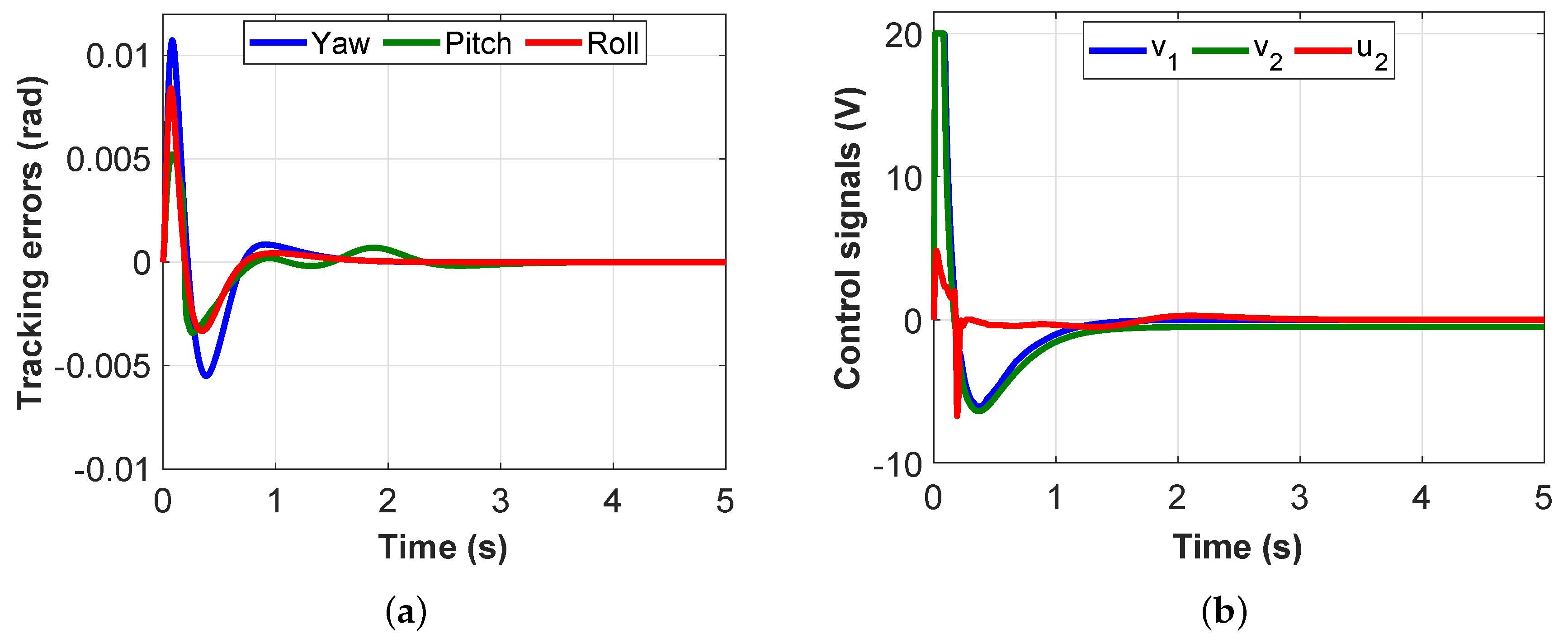
4.2. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Castaneda, H.; Plestan, F.; Chriette, A.; de Leon-Morales, J. Continuous Differentiator Based on Adaptive Second-Order Sliding-Mode Control for a 3-DOF Helicopter. IEEE Trans. Ind. Electron. 2016, 63, 5786–5793. [Google Scholar] [CrossRef]
- Guerrero-Sánchez, M.-E.; Hernández-González, O.; Lozano, R.; García-Beltrán, C.-D.; Valencia-Palomo, G.; López-Estrada, F.-R. Energy-Based Control and LMI-Based Control for a Quadrotor Transporting a Payload. Mathematics 2019, 7, 1090. [Google Scholar] [CrossRef]
- Dong, J.; He, B. Novel Fuzzy PID-Type Iterative Learning Control for Quadrotor UAV. Sensors 2019, 19, 24. [Google Scholar] [CrossRef] [PubMed]
- Mo, H.; Farid, G. Nonlinear and Adaptive Intelligent Control Techniques for Quadrotor UAV—A Survey. Asian J. Control 2019, 21, 989–1008. [Google Scholar] [CrossRef]
- Wang, B.; Yu, X.; Mu, L.; Zhang, Y. Disturbance observer-based adaptive fault-tolerant control for a quadrotor helicopter subject to parametric uncertainties and external disturbances. Mech. Syst. Signal Process. 2019, 120, 727–743. [Google Scholar] [CrossRef]
- Fu, M.; Zhang, T.; Ding, F. Adaptive Finite-Time PI Sliding Mode Trajectory Tracking Control for Underactuated Hovercraft with Drift Angle Constraint. IEEE Access 2019, 7, 184885–184895. [Google Scholar] [CrossRef]
- Li, Z.; Yu, J.; Xing, X.; Gao, H. Robust output-feedback attitude control of a three-degree-of-freedom helicopter via sliding-mode observation technique. IET Control Theory Appl. 2015, 9, 1637–1643. [Google Scholar] [CrossRef]
- Li, Z.; Liu, H.H.T.; Zhu, B.; Gao, H. Robust Second-Order Consensus Tracking of Multiple 3-DOF Laboratory Helicopters via Output Feedback. IEEE/ASME Trans. Mechatronics 2015, 20, 2538–2549. [Google Scholar] [CrossRef]
- Yan, K.; Chen, M.; Wu, Q.; Wang, Y. Adaptive flight control for unmanned autonomous helicopter with external disturbance and actuator fault. IEEE J. Eng. 2019, 2019, 8359–8364. [Google Scholar] [CrossRef]
- Yang, X.; Zheng, X. Adaptive NN Backstepping Control Design for a 3-DOF Helicopter: Theory and Experiments. IEEE Trans. Ind. Electron. 2020, 67, 3967–3979. [Google Scholar] [CrossRef]
- Chaoui, H.; Sicard, P. Adaptive Fuzzy Logic Control of Permanent Magnet Synchronous Machines with Nonlinear Friction. IEEE Trans. Ind. Electron. 2012, 59, 1123–1133. [Google Scholar] [CrossRef]
- Abdollahi, T.; Salehfard, S.; Xiong, C.; Ying, J. Simplified fuzzy-Padé controller for attitude control of quadrotor helicopters. IET Control Theory Appl. 2006, 12, 310–317. [Google Scholar] [CrossRef]
- Pounds, P.E.I.; Dollar, A.M. Stability of Helicopters in Compliant Contact Under PD-PID Control. IEEE Trans. Aerosp. Electron. Syst. 2014, 30, 1–6. [Google Scholar] [CrossRef]
- Liu, H.; Xi, J.; Zhong, Y. Nonlinear control of a quadrotor for attitude stabilization. IEEE Trans. Ind. Electron. 2017, 64, 5585–5594. [Google Scholar] [CrossRef]
- Huaman Loayza, A.S.; Pérez Zuñiga, C.G. Design of a Fuzzy Sliding Mode Controller for the Autonomous Path-Following of a Quadrotor. IEEE Lat. Am. Trans. 2019, 17, 962–971. [Google Scholar] [CrossRef]
- Kanieski, J.M.; Tambara, R.V.; Pinheiro, H.; Cardoso, R.; Gründling, H.A. Robust Adaptive Controller Combined with a Linear Quadratic Regulator Based on Kalman Filtering. IEEE Trans. Autom. Control. 2016, 61, 1373–1378. [Google Scholar] [CrossRef]
- Kiefer, T.; Graichen, K.; Kugi, A. Trajectory Tracking of a 3DOF Laboratory Helicopter Under Input and State Constraints. IEEE Trans. Control Syst. Technol. 2010, 18, 944–952. [Google Scholar] [CrossRef]
- Zhang, K.; Gao, X. Distributed tracking control of unmanned aerial vehicles under wind disturbance and model uncertainty. IEEE J. Syst. Eng. Electron. 2016, 27, 1262–1271. [Google Scholar] [CrossRef]
- Ma, H.; Liu, Y.; Li, T.; Yang, G. Nonlinear High-Gain Observer-Based Diagnosis and Compensation for Actuator and Sensor Faults in a Quadrotor Unmanned Aerial Vehicle. IEEE Trans. Ind. Inform. 2019, 15, 550–562. [Google Scholar] [CrossRef]
- Lyu, L.; Chen, C.; Hua, C.; Zhu, S.; Guan, X. Co-design of stabilization and transmission scheduling for wireless control systems. IEEE/IET Control Theory Appl. 2017, 11, 1767–1778. [Google Scholar] [CrossRef]
- El-Sousy, F.F.M.; El-Naggar, M.F.; Amin, M.; Abu-Siada, A.; Abuhasel, K.A. Robust Adaptive Neural-Network Backstepping Control Design for High-Speed Permanent-Magnet Synchronous Motor Drives: Theory and Experiments. IEEE Access 2019, 7, 99327–99348. [Google Scholar] [CrossRef]
- Chen, M.; Shi, P.; Lim, C.C. Adaptive Neural Fault-Tolerant Control of a 3-DOF Model Helicopter System. IEEE Trans. Syst. Man, Cybern. Syst. 2016, 46, 260–270. [Google Scholar] [CrossRef]
- Yan, K.; Chen, M.; Wu, Q.; Jiang, B. Extended state observer-based sliding mode fault-tolerant control for unmanned autonomous helicopter with wind gusts. IET Control Theory Appl. 2019, 13, 1500–1513. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, X.; Zhu, J. Online Performance-Based Adaptive Fuzzy Dynamic Surface Control for Nonlinear Uncertain Systems Under Input Saturation. IEEE Trans. Fuzzy Syst. 2019, 27, 209–220. [Google Scholar] [CrossRef]
- Noshadi, A.; Shi, J.; Lee, W.S.; Shi, P.; Kalam, A. System Identification and Robust Control of Multi-Input Multi-Output Active Magnetic Bearing Systems. IEEE Trans. Control. Syst. Technol. 2016, 24, 1227–1239. [Google Scholar] [CrossRef]
- Li, Y.; Jiu, M.; Sun, Q.; Dong, Q. An Adaptive Distributed Consensus Control Algorithm Based on Continuous Terminal Sliding Model for Multiple Quad Rotors’ Formation Tracking. IEEE Access 2019, 7, 173955–173967. [Google Scholar] [CrossRef]
- Kamalasadan, S.; Ghandakly, A.A. Multiple Fuzzy Reference Model Adaptive Controller Design for Pitch-Rate Tracking. IEEE Trans. Instrum. Meas. 2007, 56, 1797–1808. [Google Scholar] [CrossRef]
- Cajo, R.; Mac, T.T.; Plaza, D.; Copot, C.; De Keyser, R.; Ionescu, C. A Survey on Fractional Order Control Techniques for Unmanned Aerial and Ground Vehicles. IEEE Access 2019, 7, 66864–66878. [Google Scholar] [CrossRef]
- Song, Y.; He, L.; Zhang, D.; Qian, J.; Fu, J. Neuroadaptive Fault-Tolerant Control of Quadrotor UAVs: A More Affordable Solution. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1975–1983. [Google Scholar] [CrossRef]
- Khayamy, M.; Chaoui, H.; Oukaour, A.; Gualous, H. Adaptive Fuzzy Logic Control Mixing Strategy of DC/DC Converters in Both Discontinuous and Continuous Conduction Modes. J. Control Autom. Electr. Syst. 2016, 7, 274–288. [Google Scholar] [CrossRef]
- Chen, J.; Xu, C.; Wu, C.; Xu, W. Adaptive Fuzzy Logic Control of Fuel-Cell-Battery Hybrid Systems for Electric Vehicles. IEEE Trans. Ind. Inform. 2018, 14, 292–300. [Google Scholar] [CrossRef]
- Chaoui, H.; Gueaieb, W. Type-2 Fuzzy Logic Control of a Flexible-Joint Manipulator. J. Intell. Robot. Syst. 2008, 51, 159–186. [Google Scholar] [CrossRef]
- Soltanpour, M.R.; Otadolajam, P.; Khooban, M.H. Robust control strategy for electrically driven robot manipulators: Adaptive fuzzy sliding mode. IET Sci. Meas. Technol. 2015, 9, 322–334. [Google Scholar] [CrossRef]
- Chaoui, H.; Yadav, S. Adaptive Control of a 3-DOF Helicopter. J. Control Autom. Electr. Syst. 2020, 31, 94–107. [Google Scholar] [CrossRef]
- Chaoui, H.; Khayamy, M.; Aljarboua, A. Adaptive Interval Type-2 Fuzzy Logic Control for PMSM Drives with a Modified Reference Frame. IEEE Trans. Ind. Electron. 2017, 64, 3786–3797. [Google Scholar] [CrossRef]
- Liang, Q.; Mendel, J.M. Interval type-2 fuzzy logic systems: Theory and design. IEEE Trans. Fuzzy Syst. 2000, 8, 535–550. [Google Scholar] [CrossRef]
- Li, Z.; Liu, H.H.T.; Zhu, B.; Gao, H.; Kaynak, O. Nonlinear Robust Attitude Tracking Control of a Table-Mount Experimental Helicopter Using Output Feedback. IEEE Trans. Ind. Electron. 2015, 62, 5665–5676. [Google Scholar] [CrossRef]


| Parameter | Helicopter | Unit |
|---|---|---|
| Helicopter body mass () | 1.42 | (kg) |
| Counterweight mass () | 1.87 | (kg) |
| Distance between the elevation axis and the center of mass () | 0.66 | (m) |
| Distance between the lifting axis and the counterweight () | 0.66 | (m) |
| Distance between the pitch axis and each motor () | 0.17 | (m) |
| Gravitational constant (g) | 9.81 | (m·s) |
| Moment of inertia on the axis of roll () | 1.0348 | (kg·m) |
| Moment of inertia on the axis of pitch () | 0.0451 | (kg·m) |
| Moment of inertia on the axis of yaw () | 1.0348 | (kg·m) |
| Parameter | Gains |
|---|---|
| , , | 40, 12, 16 |
| , , | 25, 2.5, 3 |
| Sampling frequency () | 100 |
| Natural frequency () | 5 |
| Proposed Method | PID Control | Adaptive Control | Adaptive SMC | |
|---|---|---|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaoui, H.; Yadav, S.; Ahmadi, R.S.; Bouzid, A.E.M. Adaptive Interval Type-2 Fuzzy Logic Control of a Three Degree-of-Freedom Helicopter. Robotics 2020, 9, 59. https://doi.org/10.3390/robotics9030059
Chaoui H, Yadav S, Ahmadi RS, Bouzid AEM. Adaptive Interval Type-2 Fuzzy Logic Control of a Three Degree-of-Freedom Helicopter. Robotics. 2020; 9(3):59. https://doi.org/10.3390/robotics9030059
Chicago/Turabian StyleChaoui, Hicham, Sumit Yadav, Rosita Sharif Ahmadi, and Allal El Moubarek Bouzid. 2020. "Adaptive Interval Type-2 Fuzzy Logic Control of a Three Degree-of-Freedom Helicopter" Robotics 9, no. 3: 59. https://doi.org/10.3390/robotics9030059
APA StyleChaoui, H., Yadav, S., Ahmadi, R. S., & Bouzid, A. E. M. (2020). Adaptive Interval Type-2 Fuzzy Logic Control of a Three Degree-of-Freedom Helicopter. Robotics, 9(3), 59. https://doi.org/10.3390/robotics9030059







