On Using Inertial Measurement Units for Solving the Direct Kinematics Problem of Parallel Mechanisms
Abstract
1. Introduction
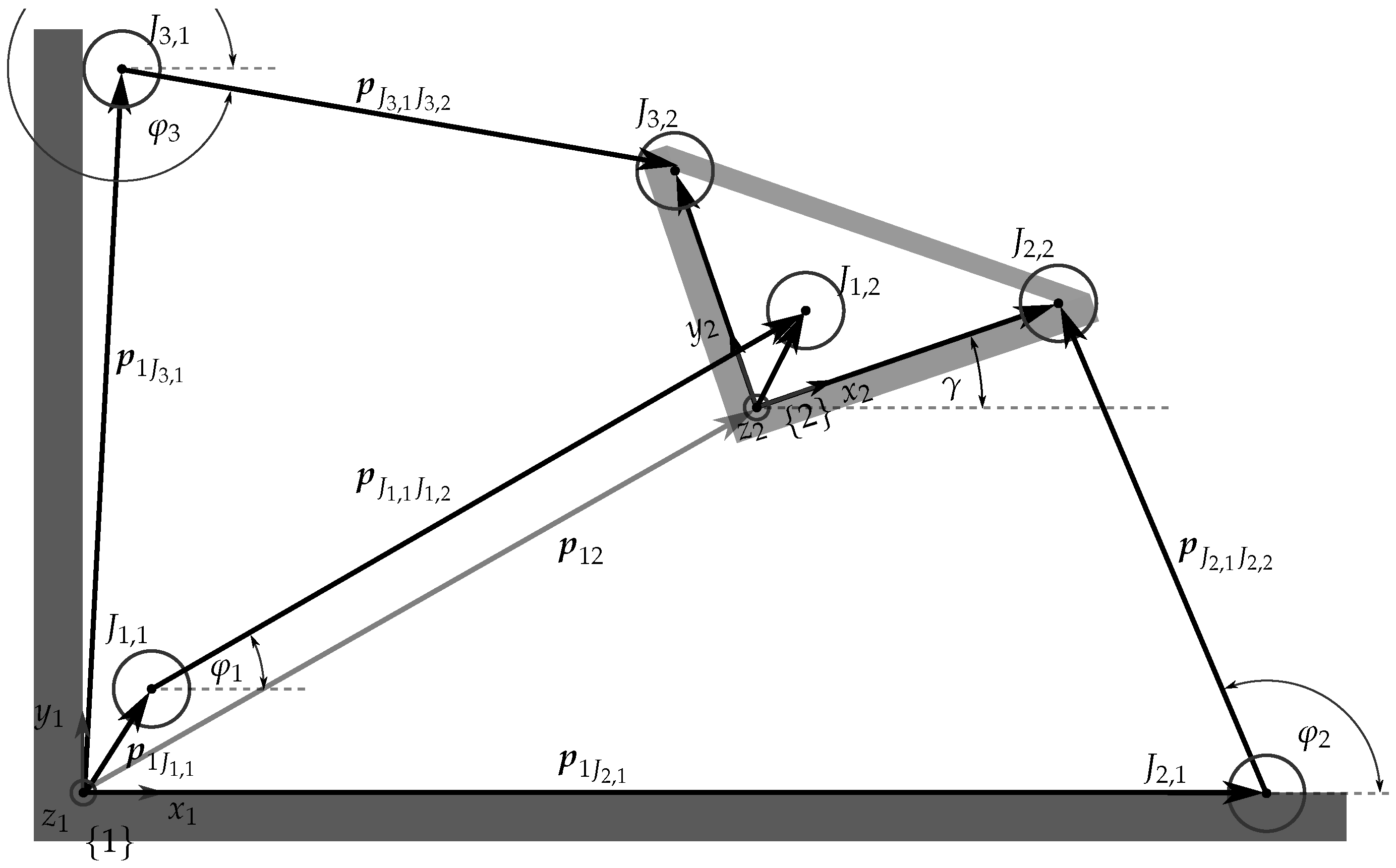
2. Direct Kinematics Solution for Planar 3-RPR Parallel Mechanisms
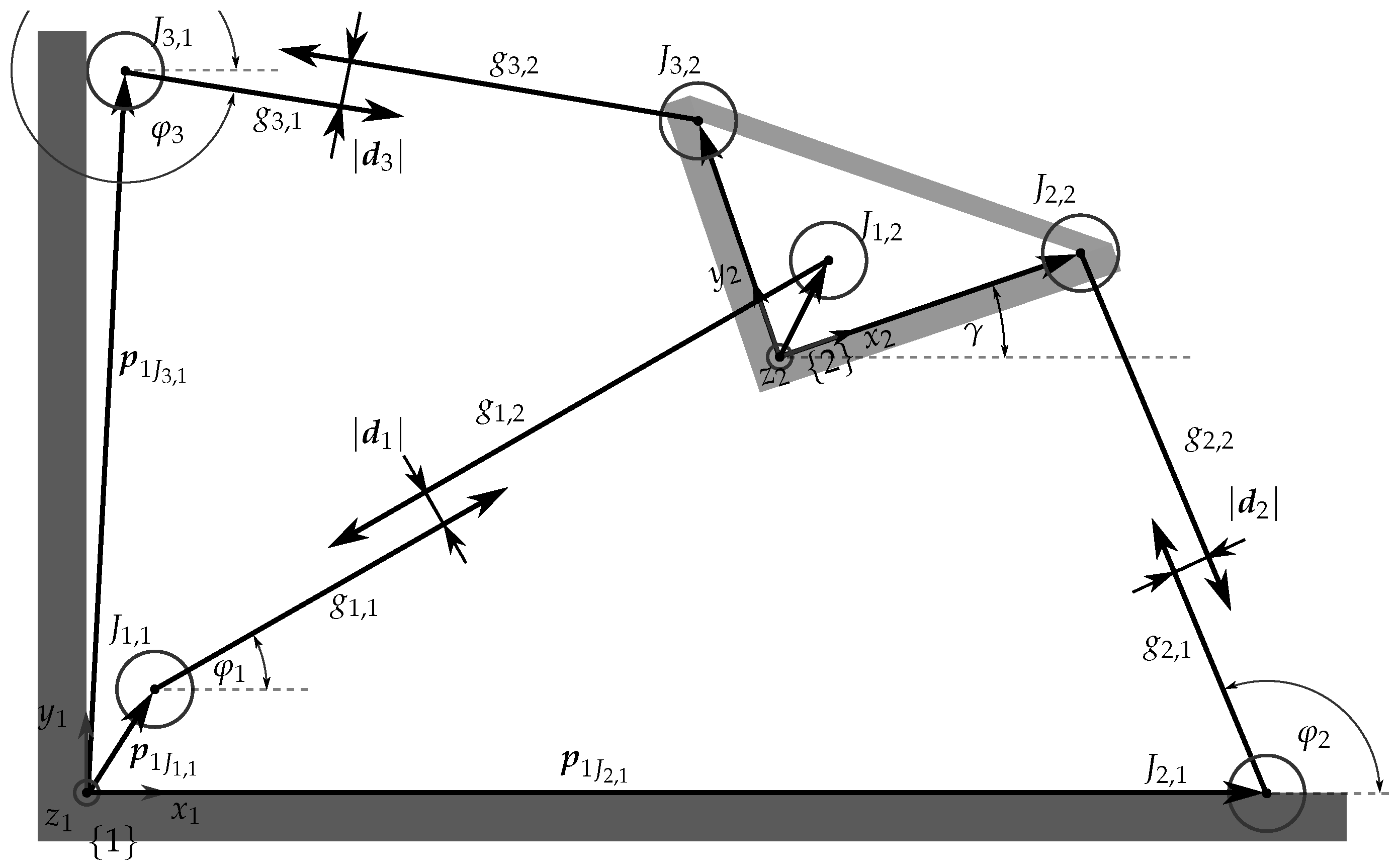
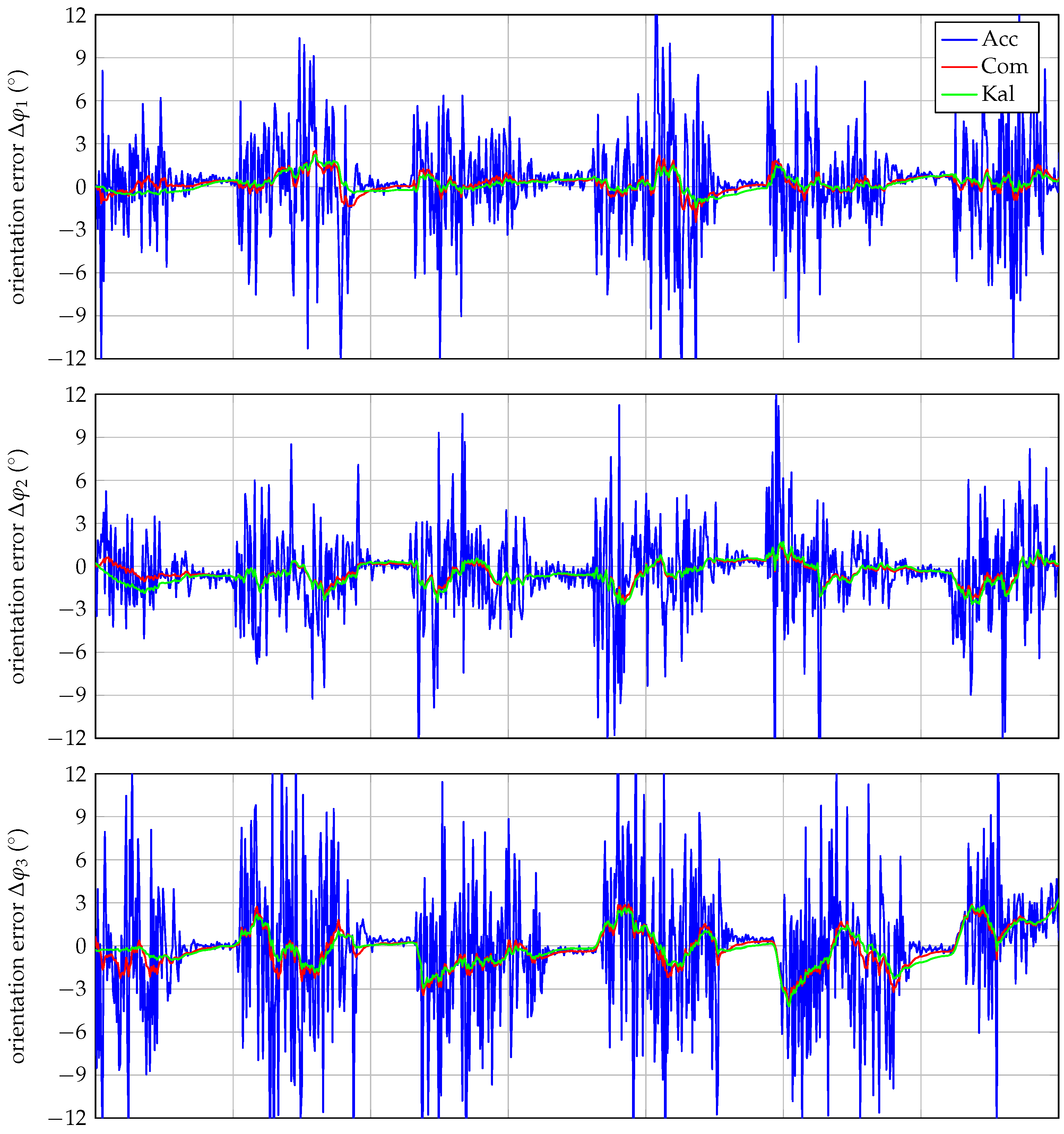
2.1. Robust Orientation Measurements
2.2. Robust Pose Calculations
2.2.1. Linear Least-Squares Formulation
2.2.2. Sensor Fusion
3. Experiment
3.1. Achievable Sampling Rates
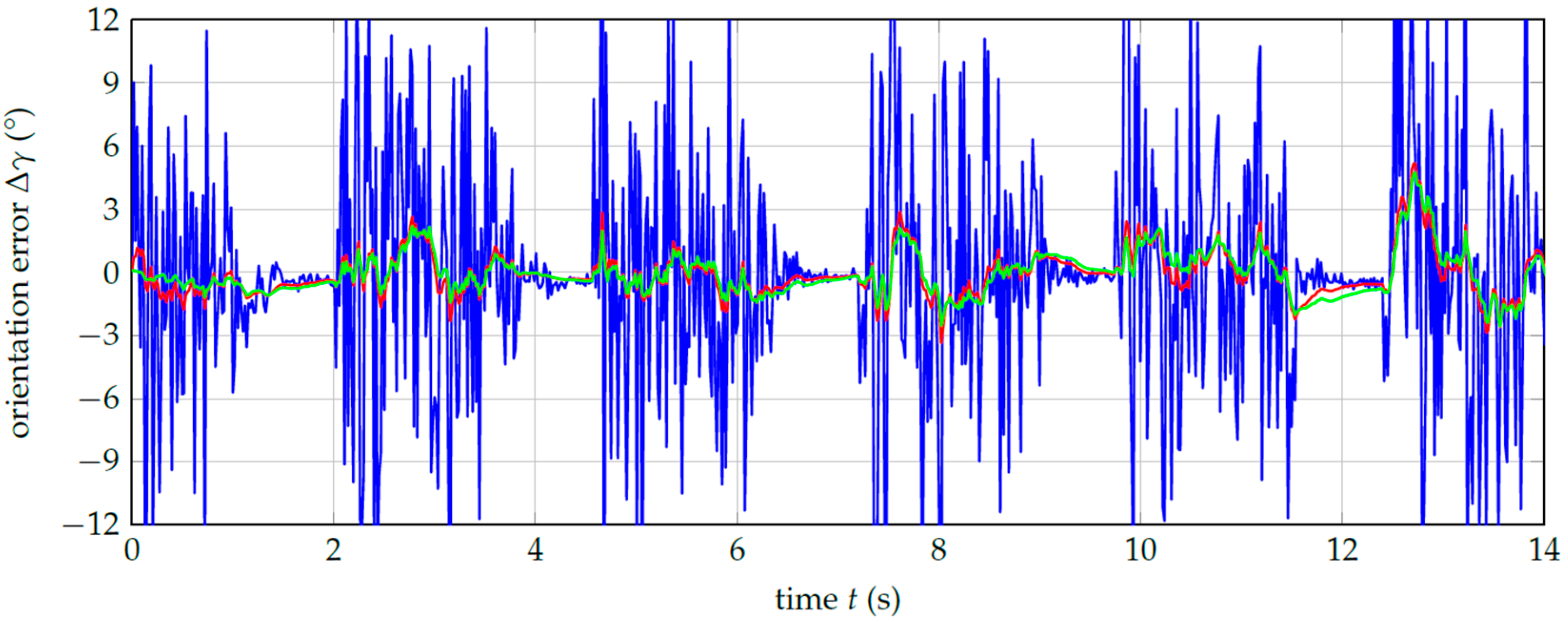
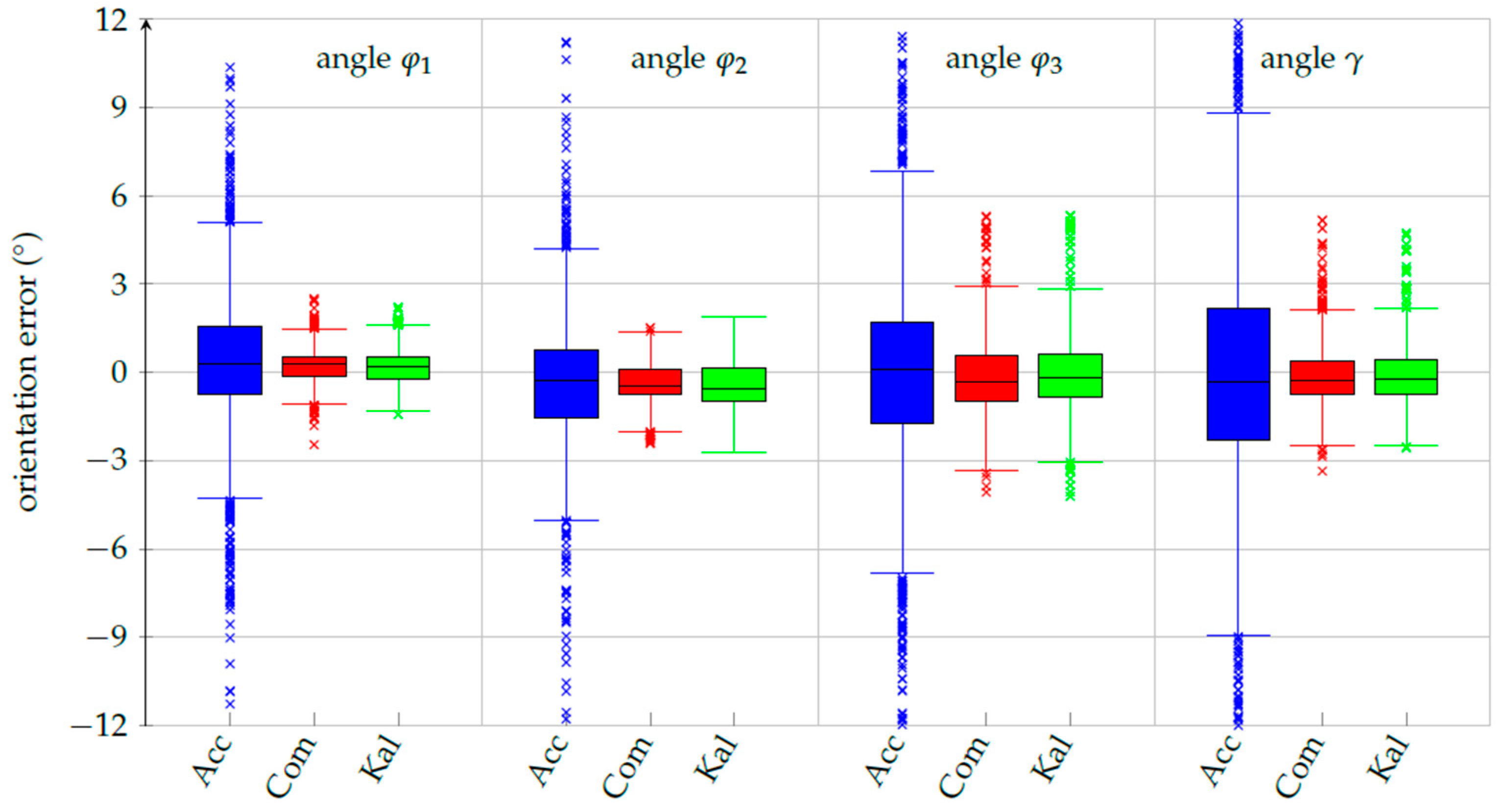
3.2. Robust Orientation Measurements
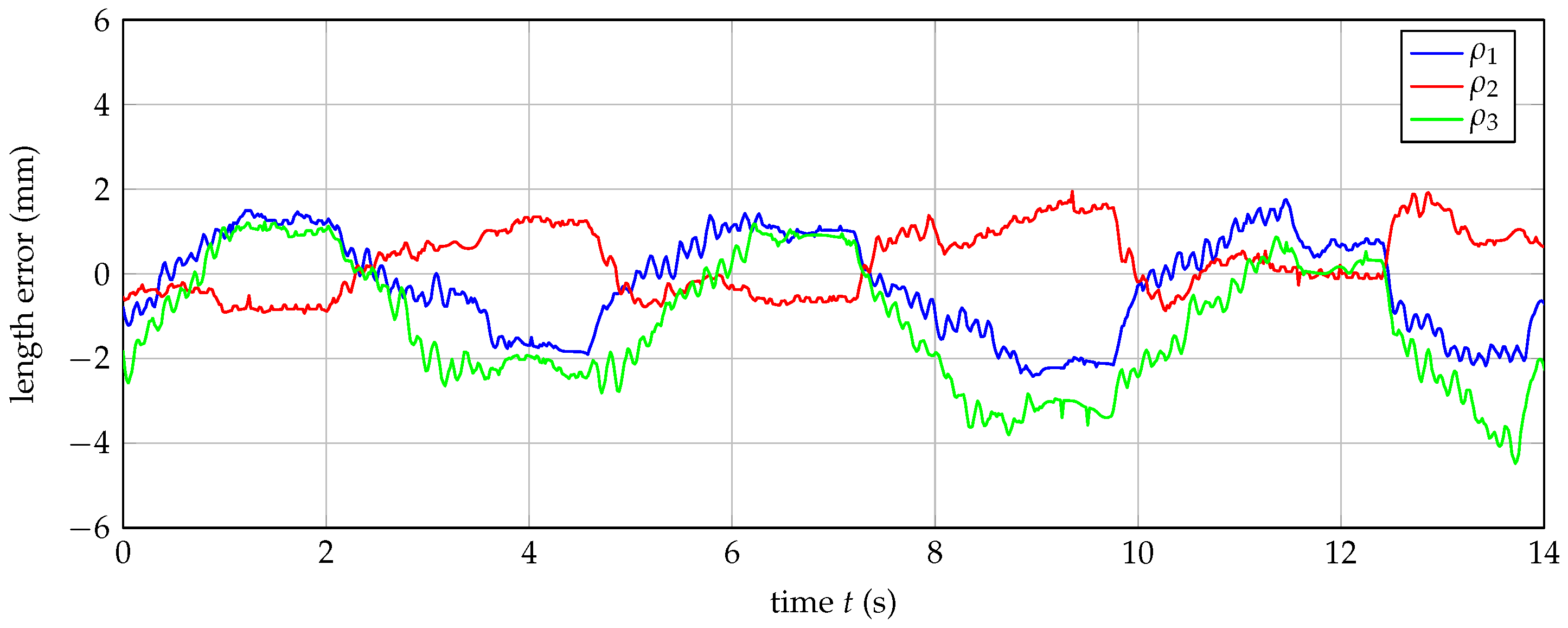
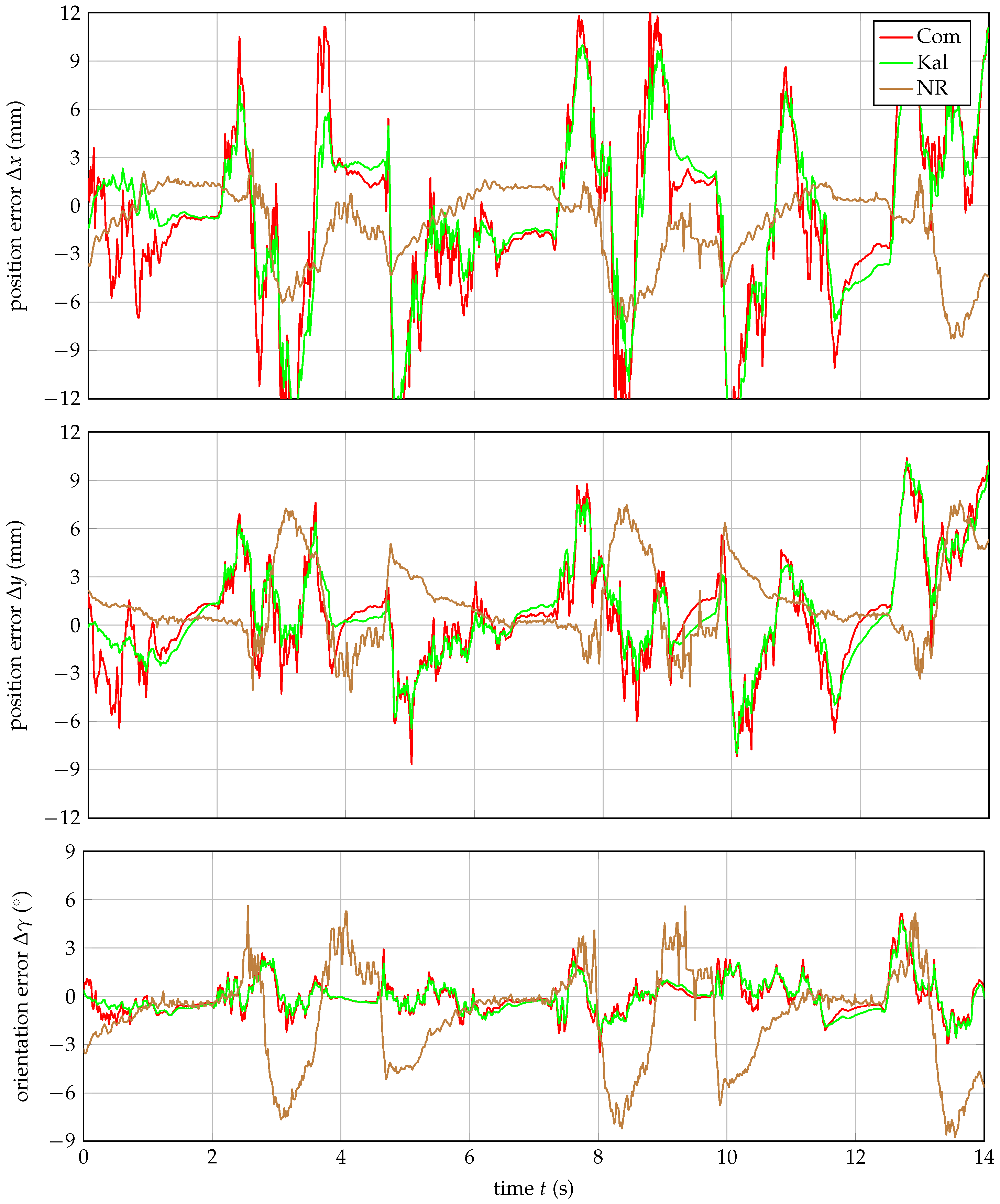
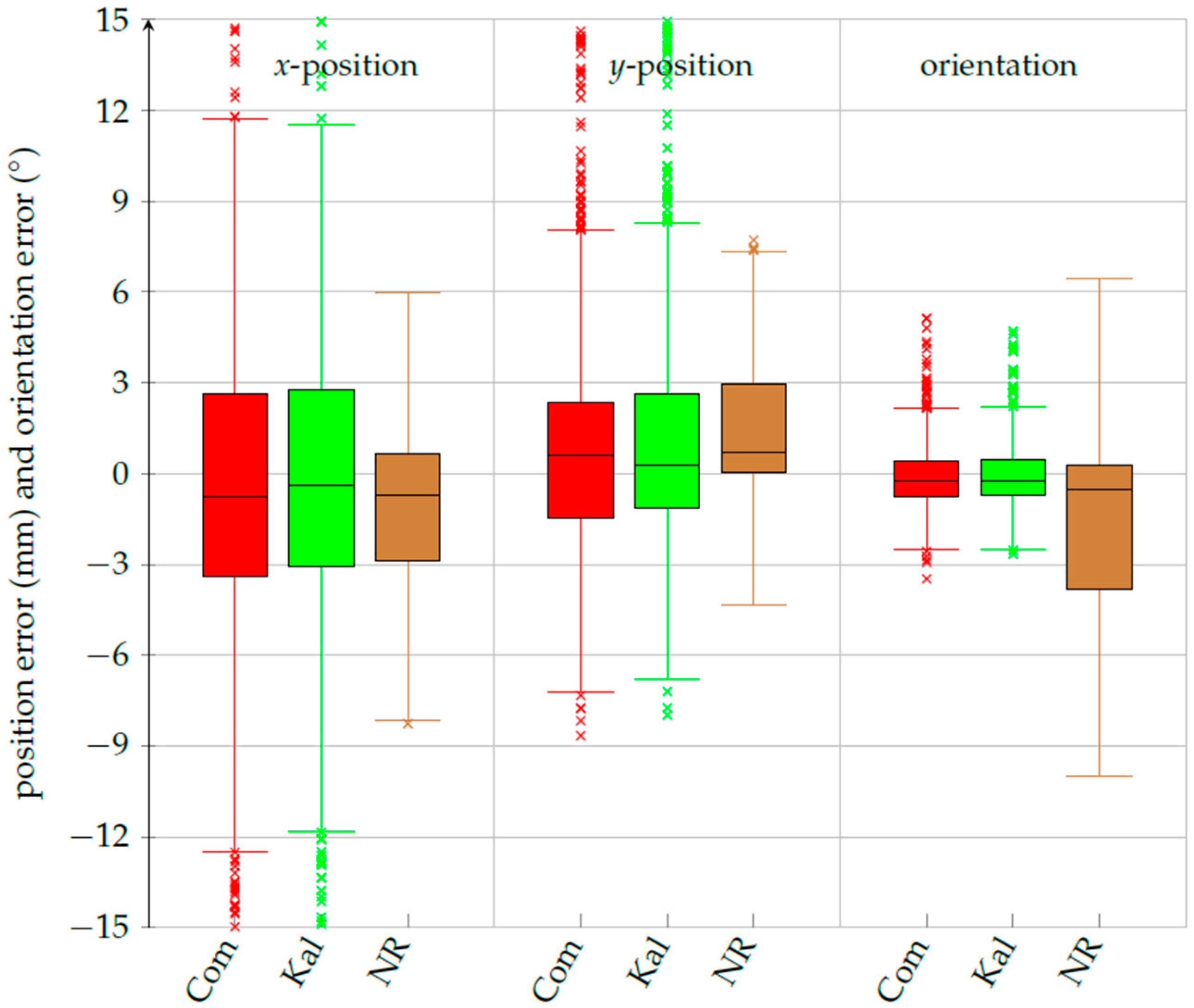
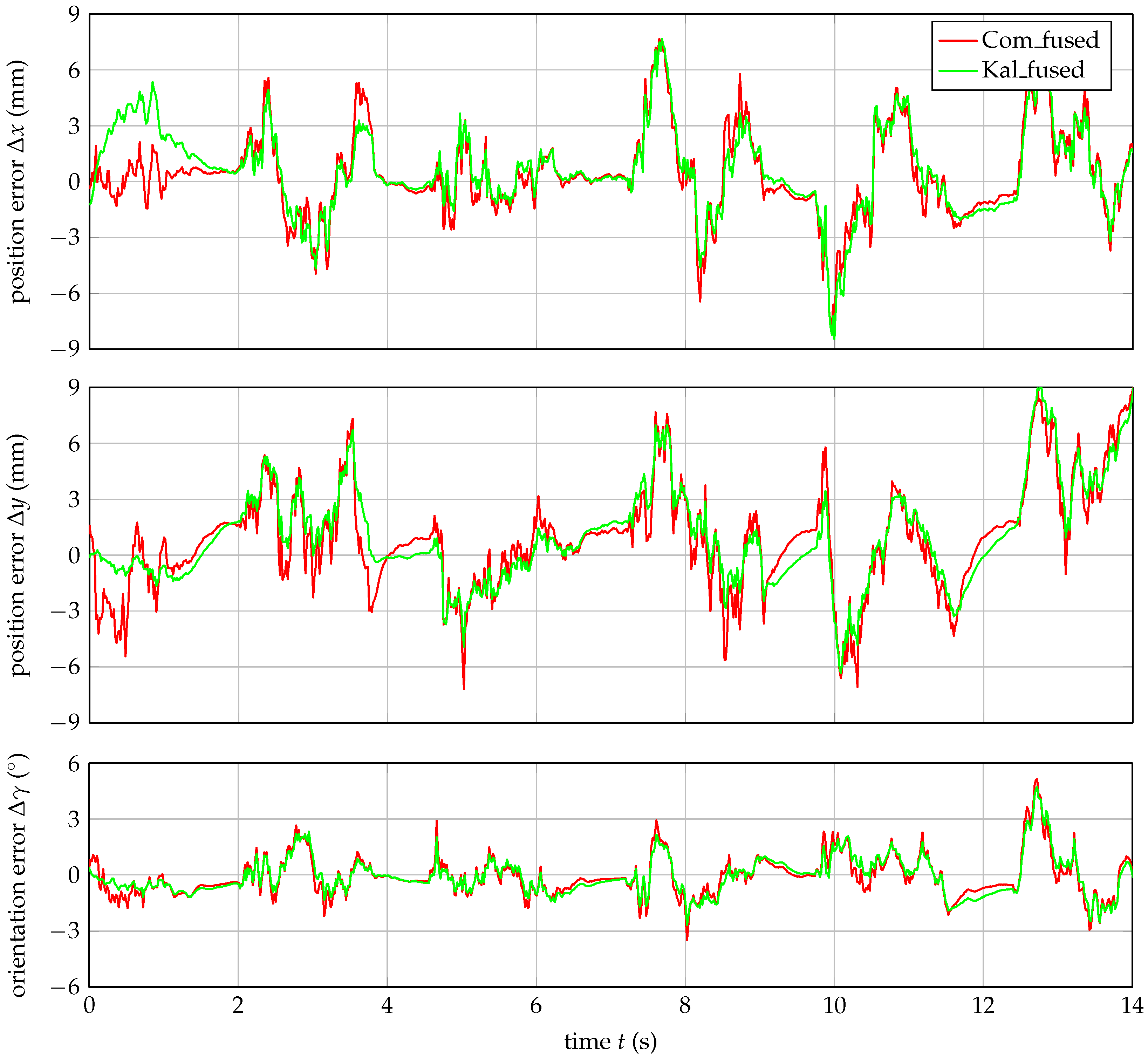
3.3. Robust Pose Calculations
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
References
- Hunt, K.H. Structural kinematics of in-parallel-actuated robot-arms. J. Mech. Transm. Autom. Des. 1983, 105, 705–712. [Google Scholar] [CrossRef]
- Lazard, D. Stewart platform and Gröbner basis. In Proceedings of the International Symposium on Advances in Robot Kinematics (ARK), Ferrare, Italy, 7–9 September 1992; pp. 136–142. [Google Scholar]
- Ronga, F.; Vust, T. Stewart platforms without computer? In Proceedings of the International Conference on Real Analytic and Algebraic Geometry, Trento, Italy, 21–25 September 1992; pp. 197–212. [Google Scholar]
- Lazard, D. On the representation of rigid-body motions and its application to generalized platform manipulators. In Computational Kinematics; Gladwell, G.M.L., Angeles, J., Hommel, G., Kovács, P., Eds.; Solid Mechanics and its Applications; Springer: Dordrecht, The Netherlands, 1993; Volume 28, pp. 175–181. [Google Scholar] [CrossRef]
- Mourrain, B. The 40 ‘generic’ positions of a parallel robot. In Proceedings of the International Symposium on Symbolic and Algebraic Computation (ISSAC), Kiev, Ukraine, 6–8 July 1993; pp. 173–182. [Google Scholar] [CrossRef]
- Raghavan, M. The Stewart platform of general geometry has 40 configurations. J. Mech. Des. 1993, 115, 277–282. [Google Scholar] [CrossRef]
- Raghavan, M.; Roth, B. Solving polynomial systems for the kinematic analysis of mechanisms and robot manipulators. ASME J. Mech. Des. 1995, 117, 71–79. [Google Scholar] [CrossRef]
- Husty, M.L. An algorithm for solving the direct kinematics of general Stewart-Gough platforms. Mech. Mach. Theory 1996, 31, 365–379. [Google Scholar] [CrossRef]
- Dietmaier, P. The Stewart-Gough platform of general geometry can have 40 real postures. In Advances in Robot Kinematics: Analysis and Control; Lenarčič, J., Husty, M.L., Eds.; Springer: Dordrecht, The Netherland, 1998; pp. 7–16. [Google Scholar] [CrossRef]
- Merlet, J.P. Solving the forward kinematics of a Gough-type parallel manipulator with interval analysis. Int. J. Robot. Res. 2004, 23, 221–235. [Google Scholar] [CrossRef]
- Porta, J.M.; Thomas, F. The forward kinematics of doubly-planar Gough-Stewart platforms and the position analysis of strips of tetrahedra. In Advances in Robot Kinematics 2018; Lenarčič, J., Parenti-Castelli, V., Eds.; Springer: Cham, Switzerland, 2019; pp. 124–132. [Google Scholar] [CrossRef]
- Gosselin, C.M.; Sefrioui, J.; Richard, M.J. Solutions polynomiales au problème de la cinématique directe des manipulateurs parallèles plans à trois degrés de liberté. Mech. Mach. Theory 1992, 27, 107–119. (In French) [Google Scholar] [CrossRef]
- Peisach, E.E. Determination of the position of the member of three-joint and two-joint four member Assur groups with rotational pairs. Machinowedenie 1985, 5, 55–61. (In Russian) [Google Scholar]
- Pennock, G.R.; Kassner, D.J. Kinematic analysis of a planar eight-bar linkage: Application to a platform-type robot. J. Mech. Des. 1992, 114, 87–95. [Google Scholar] [CrossRef]
- Wohlhart, K. Direct kinematic solution of the general planar Stewart platform. In Proceedings of the International Conference on Computer Integrated Manufacturing, Zakopane, Poland, 24–27 March 1992; pp. 403–411. [Google Scholar]
- Gosselin, C.; Merlet, J.P. The direct kinematics of planar parallel manipulators: Special architectures and number of solutions. Mech. Mach. Theory 1994, 29, 1083–1097. [Google Scholar] [CrossRef]
- Kong, X.; Gosselin, C. Forward displacement analysis of third-class analytic 3-RPR planar parallel manipulators. Mech. Mach. Theory 2001, 39, 1009–1018. [Google Scholar] [CrossRef]
- Collins, C.L. Forward kinematics of planar parallel manipulators in the Clifford algebra of ℙ2. Mech. Mach. Theory 2002, 37, 799–813. [Google Scholar] [CrossRef]
- Wenger, P.; Chablat, D. Kinematic analysis of a class of analytic planar 3-RPR parallel manipulators. In Computational Kinematics; Kecskeméthy, A., Müller, A., Eds.; Springer: Berlin, Germany, 2009; pp. 43–50. [Google Scholar] [CrossRef]
- Rojas, N.; Thomas, F. The forward kinematics of 3-RPR planar robots: A review and a distance-based formulation. IEEE Trans. Robot. 2011, 27, 143–150. [Google Scholar] [CrossRef]
- Dieudonne, J.E.; Parrish, R.V.; Bardusch, R.E. An Actuator Extension Transformation for a Motion Simulator and Inverse Transformation Applying Newton-Raphson’s Method; NASA Tech. Report TN D-7067; NASA Langley Research Center: Hampton, VA, USA, 1972.
- Liu, K.; Fitzgerald, J.M.; Lewis, F.L. Kinematic analysis of a Stewart platform manipulator. IEEE Trans. Ind. Electron. 1993, 40, 282–293. [Google Scholar] [CrossRef]
- Nguyen, C.C.; Zhou, Z.L.; Antrazi, S.S.; Campbell, C.E. Efficient Computation of Forward Kinematics and Jacobian Matrix of a Stewart Platform-Based Manipulator; IEEE of the Southeastcon: Williamsburg, VA, USA, 1991; pp. 869–874. [Google Scholar] [CrossRef]
- Merlet, J.P. Direct kinematics of parallel manipulator. IEEE Trans. Robot. Autom. 1993, 9, 842–846. [Google Scholar] [CrossRef]
- Boudreau, R.; Turkkan, N. Solving the forward kinematics of parallel manipulators with a genetic algorithm. J. Robot. Syst. 1996, 13, 111–125. [Google Scholar] [CrossRef]
- McAree, P.R.; Daniel, R.W. A fast, robust solution to the Stewart platform forward kinematics. J. Robot. Syst. 1996, 13, 407–427. [Google Scholar] [CrossRef]
- Yee, C.S.; Lim, K.B. Forward kinematics solution of Stewart platform using neural networks. Neurocomputing 1997, 16, 333–349. [Google Scholar] [CrossRef]
- Didrit, O.; Petitot, M.; Walter, E. Guaranteed solution of direct kinematic problems for general configurations of parallel manipulator. IEEE Trans. Robot. Autom. 1998, 14, 259–266. [Google Scholar] [CrossRef]
- Parikh, P.J.; Lam, S.S.Y. A hybrid strategy to solve the forward kinematics problem in parallel manipulators. IEEE Trans. Robot. 2005, 21, 18–25. [Google Scholar] [CrossRef]
- Liu, S.; Li, W.-L.; Du, Y.-C.; Fang, L. Forward kinematics of the Stewart platform using hybrid immune genetic algorithm. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Luoyang, China, 25–28 June 2006; pp. 2330–2335. [Google Scholar] [CrossRef]
- Rolland, L.; Chandra, R. Forward kinematics of the 6-6 general parallel manipulator using real coded genetic algorithms. In Proceedings of the IEEE/ASME Conference on Advanced Intelligent Mechatronics (AIM), Singapore, 14–17 July 2009; pp. 1637–1642. [Google Scholar] [CrossRef]
- Yang, C.; Zheng, S.; Jin, J.; Zhu, S.; Han, J. Forward kinematics analysis of parallel manipulator using modified global Newton-Raphson method. J. Cent. South Univ. Technol. 1996, 17, 1264–1270. [Google Scholar] [CrossRef]
- Rolland, L.; Chandra, R. The forward kinematics of the 6-6 parallel manipulator using an evolutionary algorithm based on generalized generation gap with parent-centric crossover. Robotica 2016, 34, 1–22. [Google Scholar] [CrossRef]
- Arai, T.; Cleary, K.; Nakamura, T. Design, analysis and construction of a prototype parallel link manipulator. In Proceedings of the IEEE/RSJ International Workshop on Intelligent Robots and Systems (IROS), Ibaraki, Japan, 3–6 July 1990; pp. 205–212. [Google Scholar] [CrossRef]
- Shi, X.; Fenton, R.G. Forward kinematic solution of a general 6 DOF Stewart platform based on three point position data. In Proceedings of the Eighth World Congress on the Theory of Machines and Mechanism, Prague, Czechoslovakia, 26–31 August 1991; pp. 1015–1018. [Google Scholar]
- R. Stoughton, R.; Arai, T. Optimal sensor placement for forward kinematics evaluation of a 6-DOF parallel link manipulator. In Proceedings of the IEEE/RSJ International Workshop on Intelligent Robots and Systems (IROS), Osaka, Japan, 3–5 November 1991; pp. 785–790. [Google Scholar] [CrossRef]
- Cheok, K.C.; Overholt, J.L.; Beck, R.R. Exact methods for determining the kinematics of a Stewart platform using additional displacement sensors. J. Robot. Syst. 1993, 10, 689–707. [Google Scholar] [CrossRef]
- Merlet, J.P. Closed-form resolution of the direct kinematics of parallel manipulators using extra sensors data. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Atlanta, GA, USA, 2–6 May 1993; pp. 200–204. [Google Scholar] [CrossRef]
- Jin, Y. Exact solution for the forward kinematics of the general Stewart platform using two additional displacement sensors. In Proceedings of the 23th ASME Biennial Mechanism Conference, Minneapolis, MN, USA, 11–14 September 1994; pp. 491–945. [Google Scholar]
- Nair, R.; Maddocks, J.H. On the forward kinematics of parallel manipulators. Int. J. Robot. Res. 1994, 13, 171–188. [Google Scholar] [CrossRef]
- Etemadi-Zanganeh, K.; Angeles, J. Real-time direct kinematics of general six-degree-of-freedom parallel manipulators with minimum-sensor data. J. Robot. Syst. 1995, 12, 833–844. [Google Scholar] [CrossRef]
- Han, K.; Chung, W.; Youm, Y. Local structurization for the forward kinematics of parallel manipulators using extra sensor data. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Nagoya, Japan, 21–27 May 1995; pp. 514–520. [Google Scholar] [CrossRef]
- Tancredi, L.; Merlet, J.P. Extra sensors data for solving the forward kinematics problem of parallel manipulators. In Proceedings of the 9th World Congress on the Theory of Machines and Mechanisms, Milan, Italy, 29 August–2 September 1995; pp. 2122–2126. [Google Scholar]
- Tancredi, L.; Teillaud, M.; Merlet, J.P. Forward kinematics of a parallel manipulator with additional rotary sensors measuring the position of platform joints. In Computational Kinematics; Merlet, J.P., Ravani, B., Eds.; Solid Mechanics and its Applications; Kluwer Academic Publishers: Dordrecht, The Netherland, 1995; Volume 40, pp. 261–270. [Google Scholar] [CrossRef]
- Han, K.; Chung, W.; Youm, Y. New resolution scheme of the forward kinematics of parallel manipulators using extra sensor data. ASME J. Mech. Des. 1996, 118, 214–219. [Google Scholar] [CrossRef]
- Innocenti, C. Closed-form determination of the location of a rigid body by seven in-parallel linear transducers. J. Mech. Des. 1998, 120, 293–298. [Google Scholar] [CrossRef]
- Parenti-Castelli, V.; Gregorio, R.D. Real-time computation of the actual posture of the general geometry 6-6 fully-parallel mechanism using two extra rotary sensors. J. Mech. Des. 1998, 120, 549–554. [Google Scholar] [CrossRef]
- Bonev, I.A.; Ryu, J.; Kim, N.J.; Lee, S.K. A simple new closed-form solution of the direct kinematics of parallel manipulators using three linear extra sensors. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Atlanta, GA, USA, 19–23 September 1999; pp. 526–530. [Google Scholar] [CrossRef]
- Parenti-Castelli, V.; Gregorio, R.D. Determination of the actual configuration of the general Stewart platform using only one additional sensor. J. Mech. Des. 1999, 121, 21–25. [Google Scholar] [CrossRef]
- Baron, L.; Angeles, J. The direct kinematics of parallel manipulators under redundant sensors. IEEE Trans. Robot. Autom. 2000, 16, 12–19. [Google Scholar] [CrossRef]
- Baron, L.; Angeles, J. The kinematic decoupling of parallel manipulators using joint-sensor redundancy. IEEE Trans. Robot. Autom. 2000, 16, 644–651. [Google Scholar] [CrossRef]
- Bonev, I.A.; Ryu, J. A new method for solving the direct kinematics of general 6-6 Stewart platforms using three linear extra sensors. Mech. Mach. Theory 2000, 35, 423–436. [Google Scholar] [CrossRef]
- Parenti-Castelli, V.; Gregorio, R.D. A new algorithm based on two extra-sensors for real-time computation of the actual configuration of the generalized Stewart-Gough manipulator. J. Mech. Des. 2000, 122, 294–298. [Google Scholar] [CrossRef]
- Bonev, I.A.; Ryu, J.; Kim, N.J.; Lee, S.K. A closed-form solution to the direct kinematics of nearly general parallel manipulators with optimally located three linear extra sensors. IEEE Trans. Robot. Autom. 2001, 17, 148–156. [Google Scholar] [CrossRef]
- Chiu, Y.J. Forward kinematics of a general fully parallel manipulator with auxiliary sensors. Int. J. Robot. Res. 2001, 20, 401–414. [Google Scholar] [CrossRef]
- Vertechy, R.; Dunlop, G.R.; Parenti-Castelli, V. An accurate algorithm for the real-time solution of the direct kinematics of 6-3 Stewart platform manipulators. In Advances in Robot Kinematics; Lenarčič, J., Thomas, F., Eds.; Solid Mechanics and Its Applications; Kluwer Academic Publishers: Dordrecht, The Netherland, 2002; Volume 40, pp. 369–378. [Google Scholar] [CrossRef]
- Vertechy, R.; Parenti-Castelli, V. Accurate and fast body pose estimation by three point position data. Mech. Mach. Theory 2007, 42, 1170–1183. [Google Scholar] [CrossRef]
- Vertechy, R.; Parenti-Castelli, V. Robust, fast and accurate solution of the direct position analysis of parallel manipulators by using extra-sensors. In Parallel Manipulators, Towards New Applications; Wu, H., Ed.; I-Tech Education and Publishing: Vienna, Austria, 2008; pp. 133–154. [Google Scholar]
- Merlet, J.P. Parallel Robots; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar] [CrossRef]
- Staicu, S. Power requirement comparison in the 3-RPR planar parallel robot dynamics. Mech. Mach. Theory 2009, 44, 1045–1057. [Google Scholar] [CrossRef]
- Chablat, D.; Jha, R.; Caro, S. A framework for the control of a parallel manipulator with several actuation modes. In Proceedings of the IEEE International Conference on Industrial Informatics (INDIN), Poitiers, France, 19–21 July 2016; pp. 190–195. [Google Scholar] [CrossRef]
- Moezi, S.A.; Rafeeyan, M.; Zakeri, E.; Zare, A. Simulation and experimental control of a 3-RPR parallel robot using optimal fuzzy controller and fast on/off solenoid valves based on the PWM wave. ISA Trans. 2016, 61, 265–286. [Google Scholar] [CrossRef]
- Schulz, S.; Seibel, A.; Schreiber, D.; Schlattmann, J. Sensor concept for solving the direct kinematics problem of the Stewart-Gough platform. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1959–1964. [Google Scholar] [CrossRef]
- Seibel, A.; Schulz, S.; Schlattmann, J. On the direct kinematics problem of parallel mechanisms. J. Robot. 2018, 2018, 2412608. [Google Scholar] [CrossRef]
- Schulz, S.; Seibel, A.; Schlattmann, J. Closed-form solution for the direct kinematics problem of planar 3-RPR parallel mechanisms. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 968–973. [Google Scholar] [CrossRef]
- Schulz, S.; Seibel, A.; Schlattmann, J. Performance of an IMU-based sensor concept for solving the direct kinematics problem of the Stewart-Gough platform. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 5055–5062. [Google Scholar] [CrossRef]
- Yun, X.; Lizarraga, M.; Bachmann, E.R.; McGhee, R.B. An improved quaternion-based Kalman filter for real-time tracking of rigid body orientation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 27–31 October 2003; pp. 1074–1079. [Google Scholar] [CrossRef]
- Mahony, R.; Hamel, T.; Pflimlin, J.M. Nonlinear complementary filters on the special orthogonal group. IEEE Trans. Autom. Control 2008, 53, 1203–1218. [Google Scholar] [CrossRef]
- Madgwick, S.O.H.; Harrison, A.J.L.; Vaidyanathan, R. Estimation of IMU and MARG orientation using a gradient descent algorithm. In Proceedings of the IEEE International Conference on Rehabilitation Robotics (ICORR), Zurich, Switzerland, 29 June–1 July 2011; pp. 179–185. [Google Scholar] [CrossRef]
- Valenti, R.G.; Dryanovski, I.; Xiao, J. Keeping a good attitude: A quaternion-based orientation filter for IMUs and MARGs. Sensors 2015, 15, 19302–19330. [Google Scholar] [CrossRef]
- Penrose, R. A generalized inverse for matrices. Math. Proc. Camb. Philos. Soc. 1955, 51, 406–413. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C++. The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Merlet, J.P. Direct kinematics of CDPR with extra cable orientation sensors: The 2 and 3 cables case with perfect measurement and sagging cables. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 6973–6978. [Google Scholar] [CrossRef]
- Merlet, J.P. An experimental investigation of extra measurements for solving the direct kinematics of cable-driven parallel robots. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 6947–6952. [Google Scholar] [CrossRef]
- Nieminen, T.; Kangas, J.; Suuriniemi, S.; Kettunen, L. An enhanced multiposition calibration method for consumer grade inertial measurement units applied and tested. Meas. Sci. Technol. 2010, 21, 10. [Google Scholar] [CrossRef]
- Du, S.; Sun, W.; Gao, Y. MEMS IMU Error Mitigation Using Rotation Modulation Technique. Sensors 2016, 16, 2017. [Google Scholar] [CrossRef] [PubMed]
- Syed, Z.F.; Aggarwal, P.; Goodall, C.; Niu, X.; El-Sheimy, N. A new multi-position calibration method for MEMS inertial navigation systems. Meas. Sci. Technol. 2007, 18, 1897–1907. [Google Scholar] [CrossRef]
- Fong, W.T.; Ong, S.K.; Nee, A.Y.C. Methods for in-field user calibration of an inertial measurement unit without external equipment. Meas. Sci. Technol. 2008, 19, 085202. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, Y.; Wu, W.; Wu, M.; Hu, X. Improved multi-position calibration for inertial measurement units. Meas. Sci. Technol. 2009, 21, 015107. [Google Scholar] [CrossRef]
- Schulz, S. Performance evaluation of a sensor concept for solving the direct kinematics problem of general planar 3-RPR parallel mechanisms by using solely the linear actuators’ orientations. Robotics 2019, 8, 72. [Google Scholar] [CrossRef]
- Schulz, S.; Seibel, A.; Schlattmann, J. Solution for the direct kinematics problem of the general Stewart-Gough Platform by using only linear actuators’ orientations. In Advances in Robot Kinematics 2018; Lenarčič, J., Parenti-Castelli, V., Eds.; Springer: Cham, Swizerland, 2019; pp. 124–132. [Google Scholar] [CrossRef]

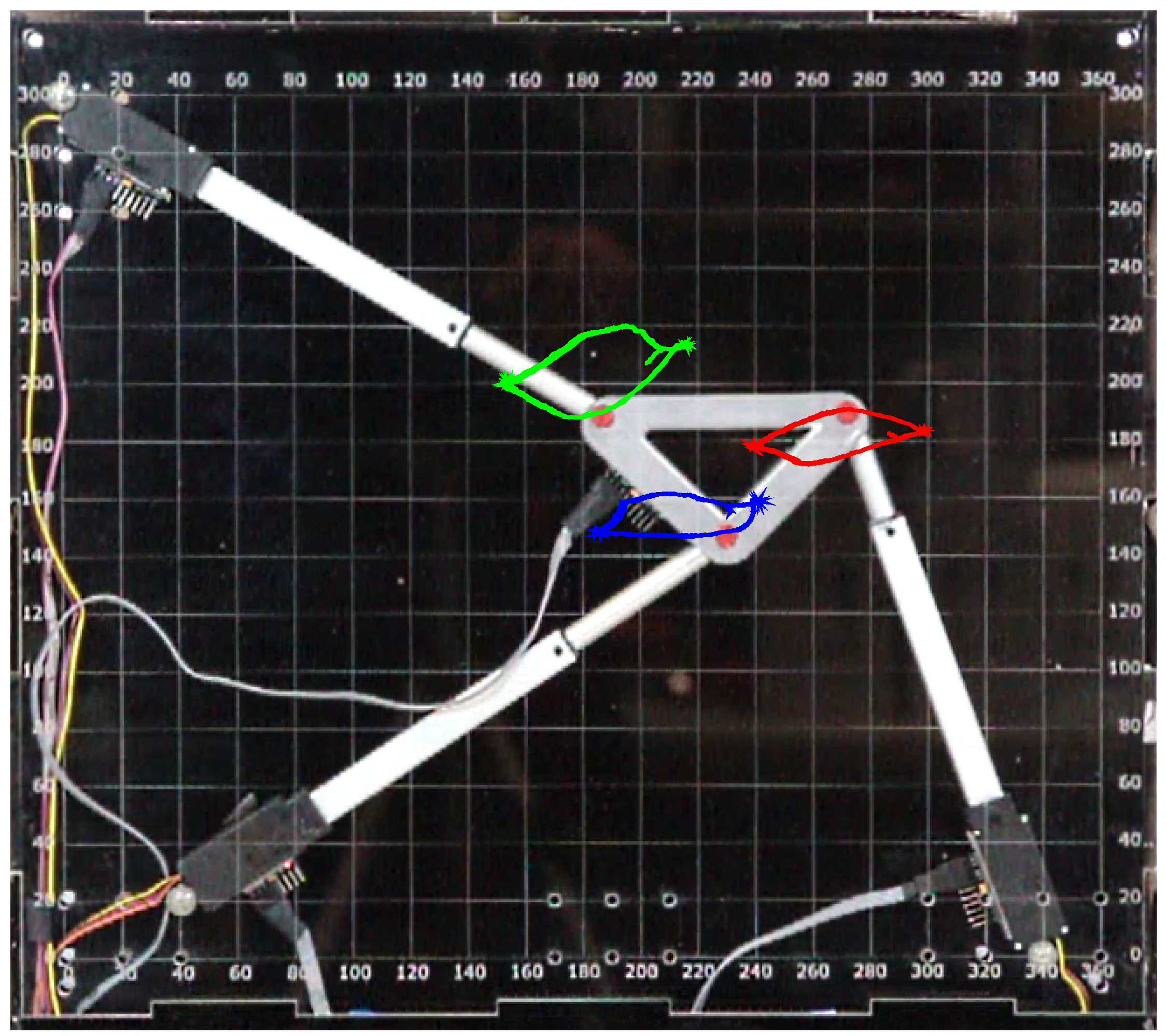
| Base Platform Joints | Manipulator Platform Joints | ||||
|---|---|---|---|---|---|
| No. | Included Calculation | Displayed Data | Sampling Rate |
|---|---|---|---|
| 1 | length measurement (3 lengths) | 4 | 399.71 Hz |
| 2 | orientation measurement (4 IMUs) | 16 | 71.27 Hz |
| 3 | #1 + length control | 4 | 293.88 Hz |
| 4 | #1 + #2 + length control | 16 | 57.85 Hz |
| 5a | #4 + raw angles | 5 | 70.95 Hz |
| 5b | #4 + orientation filtering (complementary filter) | 5 | 60.41 Hz |
| 5c | #4 + orientation filtering (Kalman filter) | 5 | 53.02 Hz |
| 6a | #5a + linear least-squares formulation | 4 | 46.20 Hz |
| 6b | #5b + linear least-squares formulation | 4 | 44.82 Hz |
| 6c | #5c + linear least-squares formulation | 4 | 40.82 Hz |
| 7 | #3 + Newton Raphson algorithm | 4 | 3.82 Hz |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schulz, S. On Using Inertial Measurement Units for Solving the Direct Kinematics Problem of Parallel Mechanisms. Robotics 2019, 8, 99. https://doi.org/10.3390/robotics8040099
Schulz S. On Using Inertial Measurement Units for Solving the Direct Kinematics Problem of Parallel Mechanisms. Robotics. 2019; 8(4):99. https://doi.org/10.3390/robotics8040099
Chicago/Turabian StyleSchulz, Stefan. 2019. "On Using Inertial Measurement Units for Solving the Direct Kinematics Problem of Parallel Mechanisms" Robotics 8, no. 4: 99. https://doi.org/10.3390/robotics8040099
APA StyleSchulz, S. (2019). On Using Inertial Measurement Units for Solving the Direct Kinematics Problem of Parallel Mechanisms. Robotics, 8(4), 99. https://doi.org/10.3390/robotics8040099






