Efficient Closed-Form Task Space Manipulability for a 7-DOF Serial Robot
Abstract
1. Introduction
1.1. Contribution
- a new parametrization of the state- and null space that results in concise IK expressions with symmetric structure in the individual components
- analytical closed-form expressions from task space to manipulability measure w.r.t. joint limits, which allow array operation in vector-optimized programming languages. Note that array operation is also called Vectorization in e.g., MATLAB. It refers to the exploitation of Single Instruction Multiple Data (SIMD) instructions of modern Central Processing Unit (CPUs) and allows to operate on multiple data points simultaneously.
- sensitivity analysis of manipulability in task space
- real-time capable application for evaluating the task space manipulability of the entire null space, for globally optimal redundancy resolution w.r.t. manipulability of single poses and full trajectories on SE(3)
1.2. Related Work
1.2.1. Performance Measures
1.2.2. Inverse Kinematics
1.2.3. Optimizing Manipulability
1.3. Outline
2. Problem Formulation
- Problem 1:
- Find a parametrization of the task- and null space that exploits the kinematic structure for concise expressions.
- Problem 2:
- Find closed-form expressions for all mappings from task space to manipulability that allow efficient array operation in vector-optimized programming languages.
- Problem 3:
- Let be the space of admissible joint configurations. Find an analytical expression of the range of the null space solutions , for which the inverse kinematics function results in an admissible joint configuration .
3. Technical Approach
3.1. Manipulability Measure
3.1.1. Reduction of First Joint
3.1.2. Reduction of Last Joint
3.1.3. Closed-Form Expression
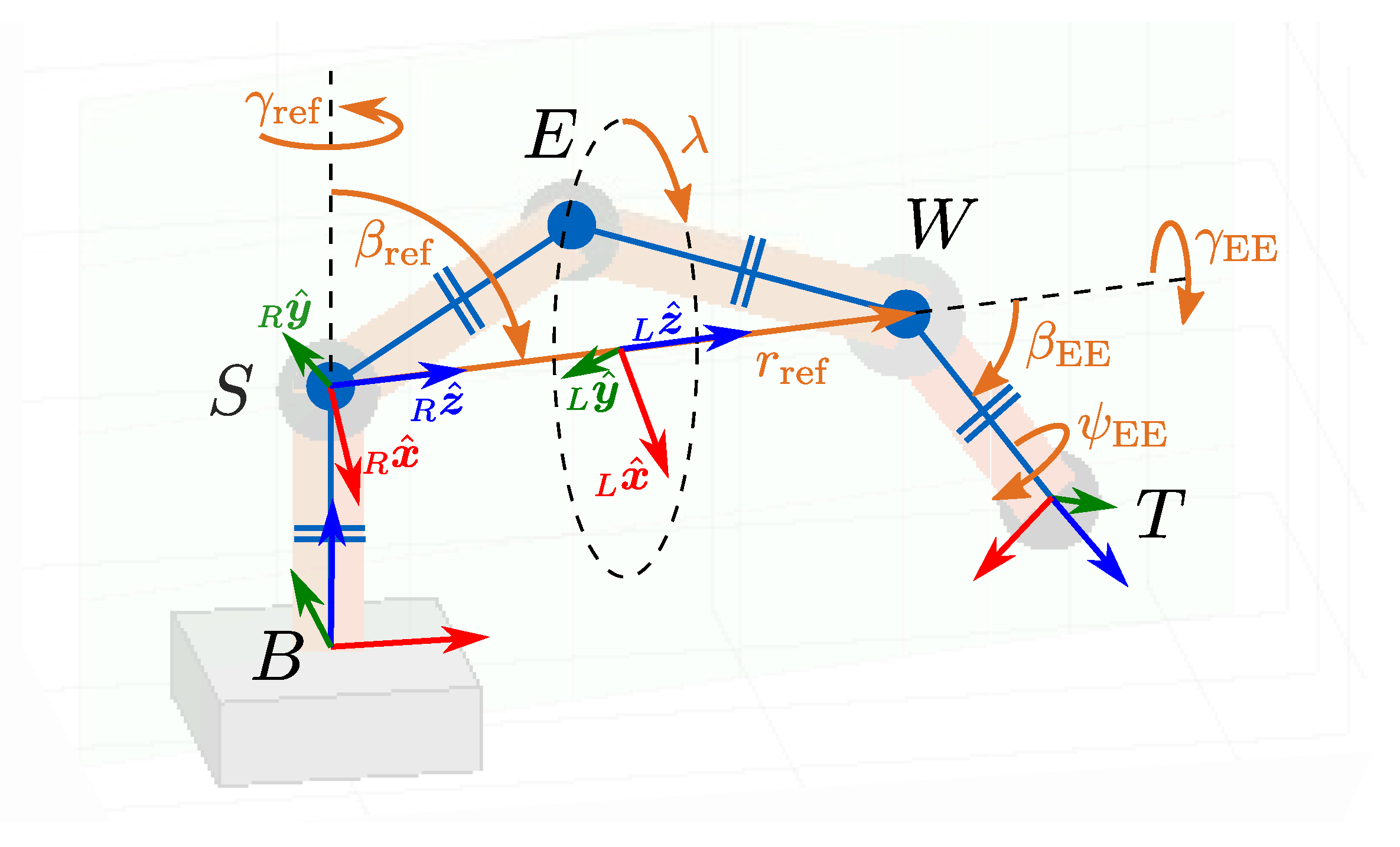
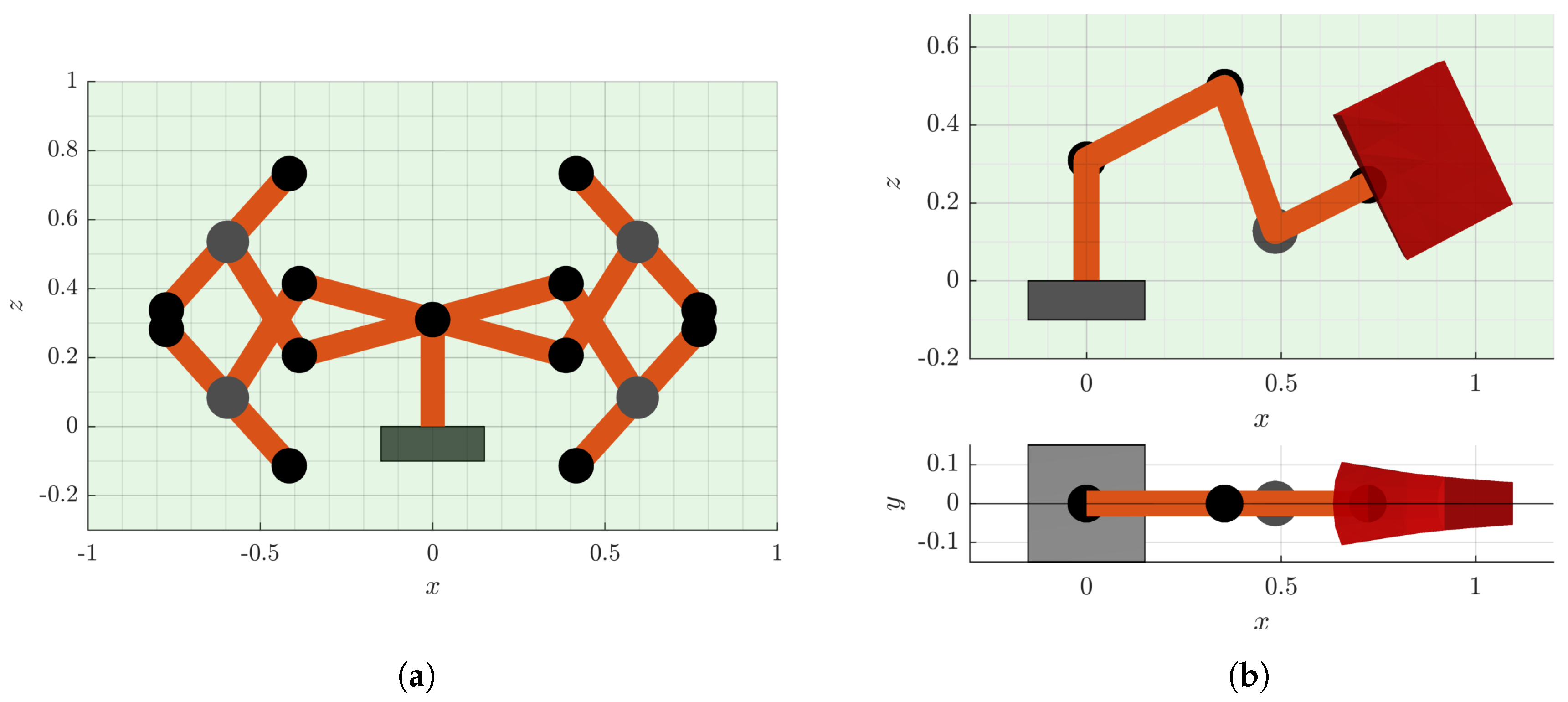
3.2. Task Space Parametrization
- PR1:
- uniquely define the null space parameter for the entire space of SE(3).
- PR2:
- result in a minimal number of parameters for the components of the IK vector map .
- PR3:
- allow direct application of the above-mentioned reductions.
3.2.1. Task Space Projection
3.2.2. Task Space Surjection
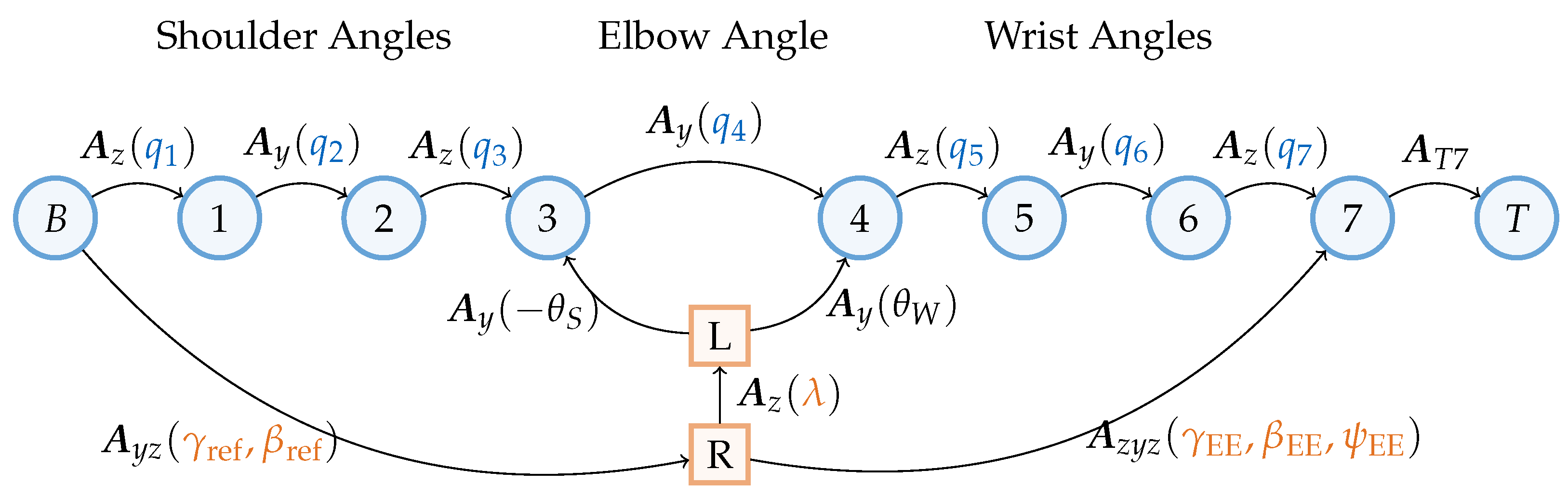
3.3. Inverse Kinematics
3.3.1. Manipulator Configuration
3.3.2. Elbow Angles
3.3.3. Shoulder Angles
3.3.4. Wrist Angles
3.3.5. Overview
3.4. Forward Kinematics
3.5. Admissible Parameter Space
3.5.1. Shoulder-Wrist Distance
3.5.2. Null Space Parameter
4. Results
4.1. Accuracy
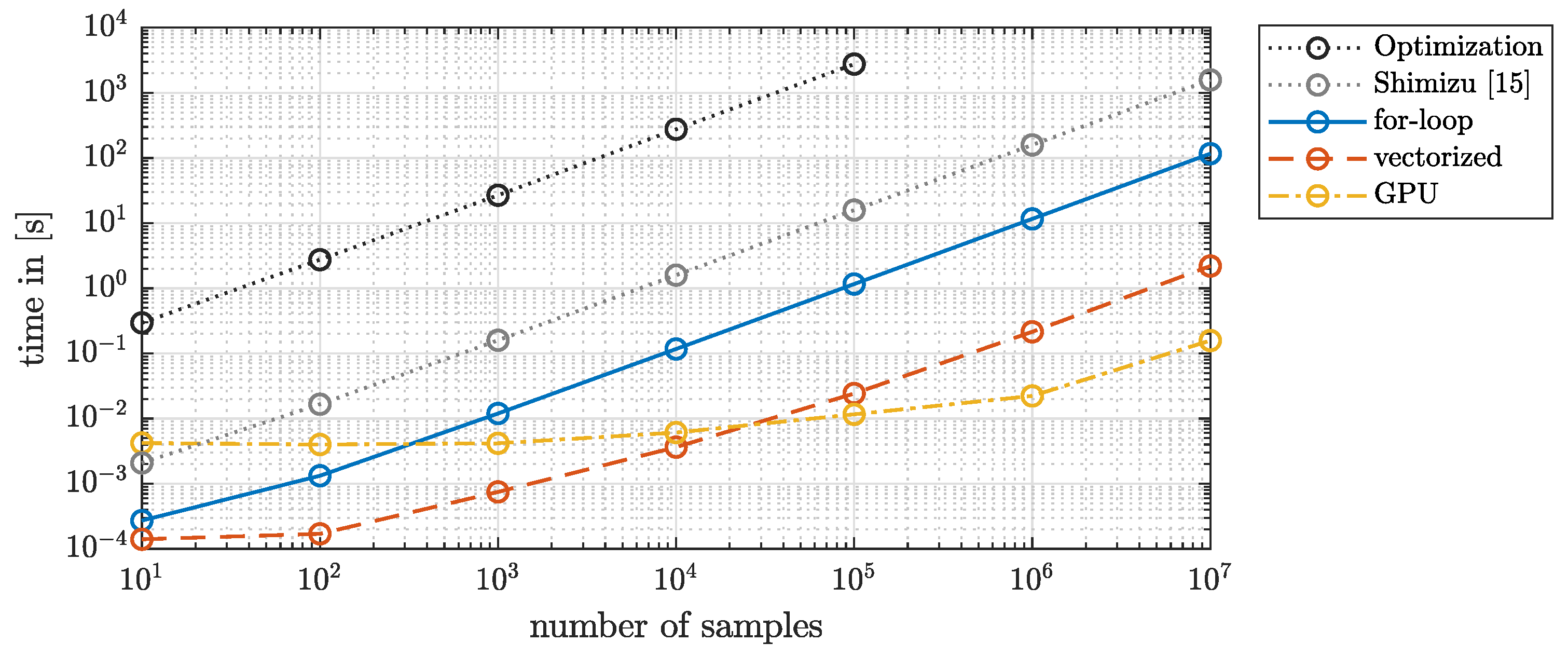
4.2. Run-Time Comparison
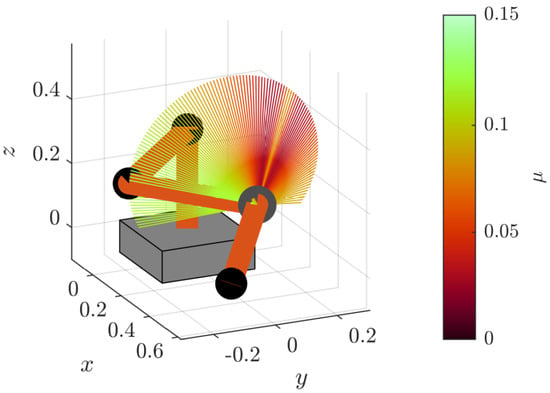
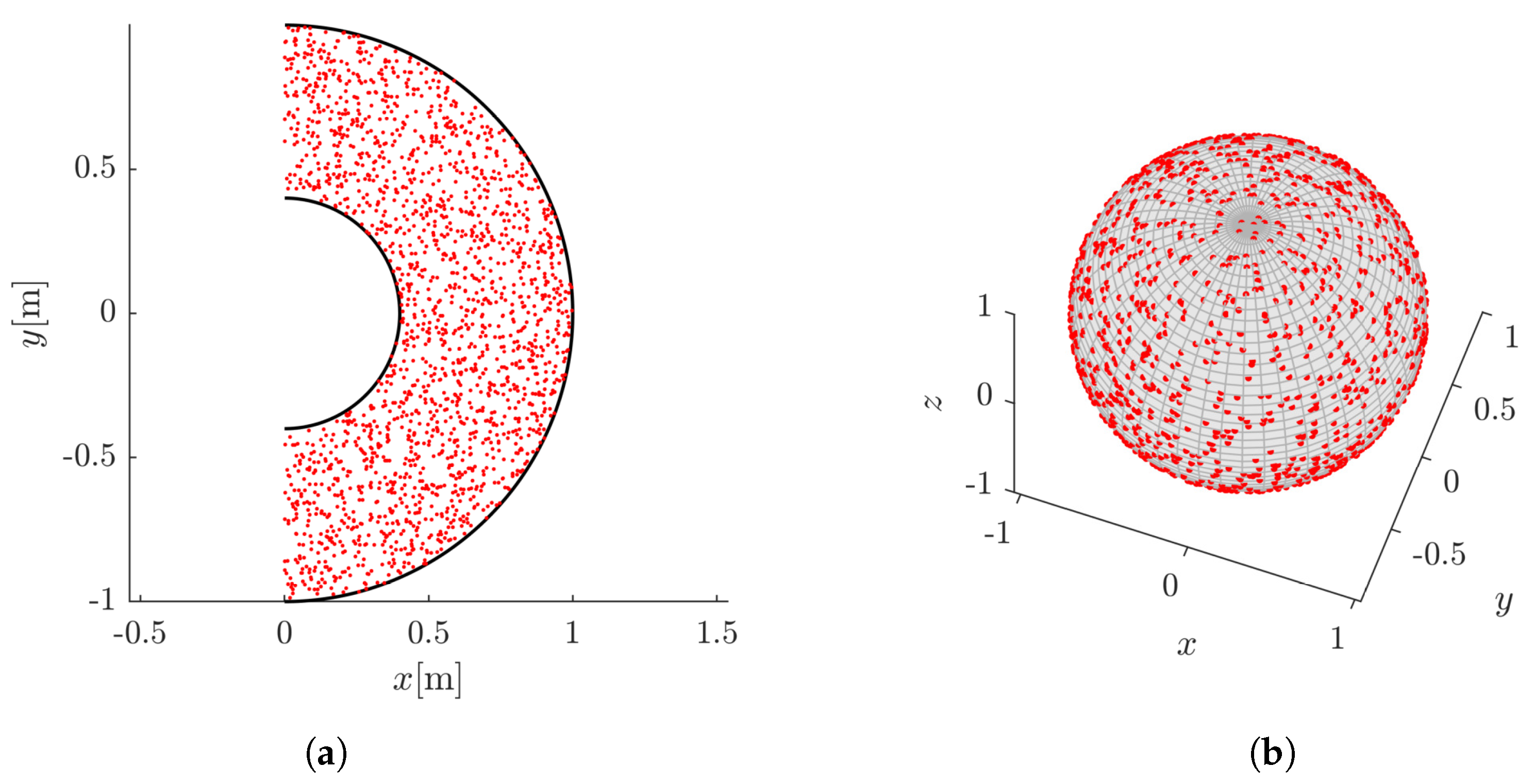
4.3. Sampling in Task Space
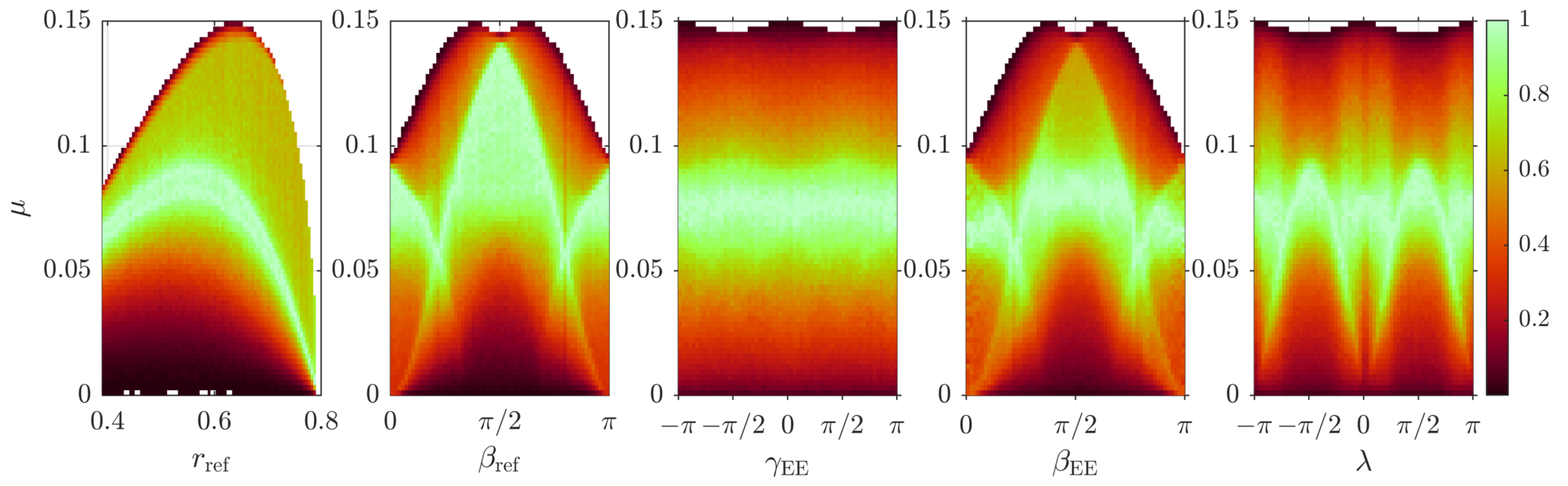
4.4. Parameter Sensitivity Analysis of Manipulability in Parameter Space
4.4.1. Translation Parameters and
4.4.2. Orientation Parameters and
4.4.3. Null Space Parameter
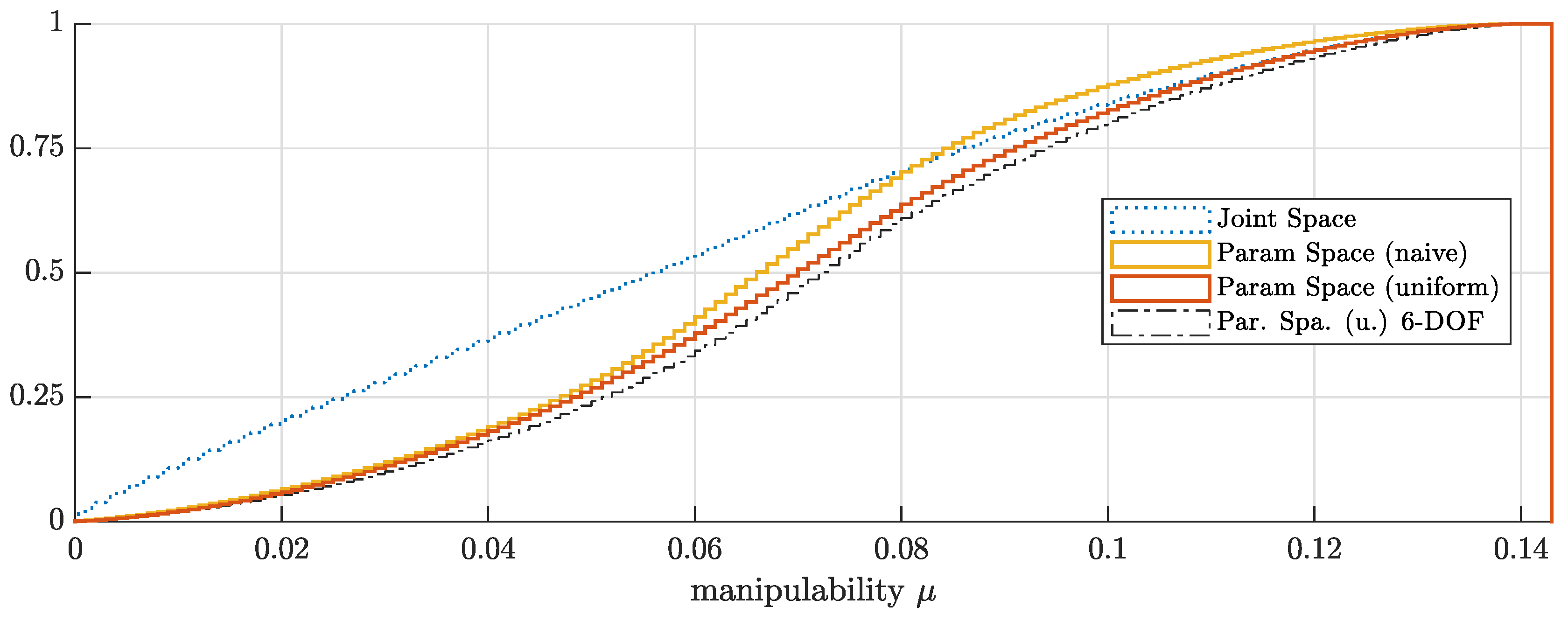
4.4.4. Discussion of Manipulability in Different Sampling Strategies
Naive vs. Uniformly Distributed Sampling
6-DOF vs. 7-DOF Kinematics
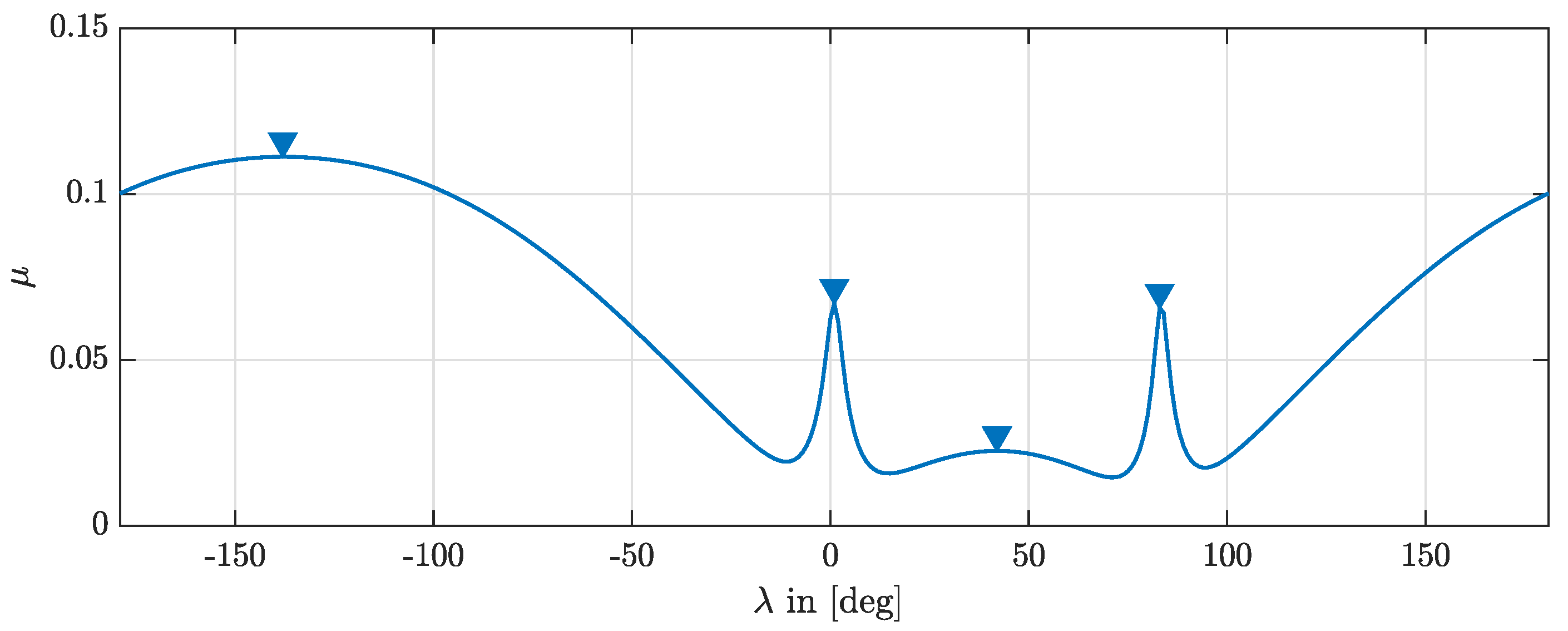
4.5. Number of Local Optima
5. Applications
5.1. Optimal Robot Placement
5.1.1. Best Overall Robot Configuration
5.1.2. Best Robot Configuration for Multiple Task Poses
5.1.3. Optimizing Robot Mounting Positions Regarding a Workspace Envelope
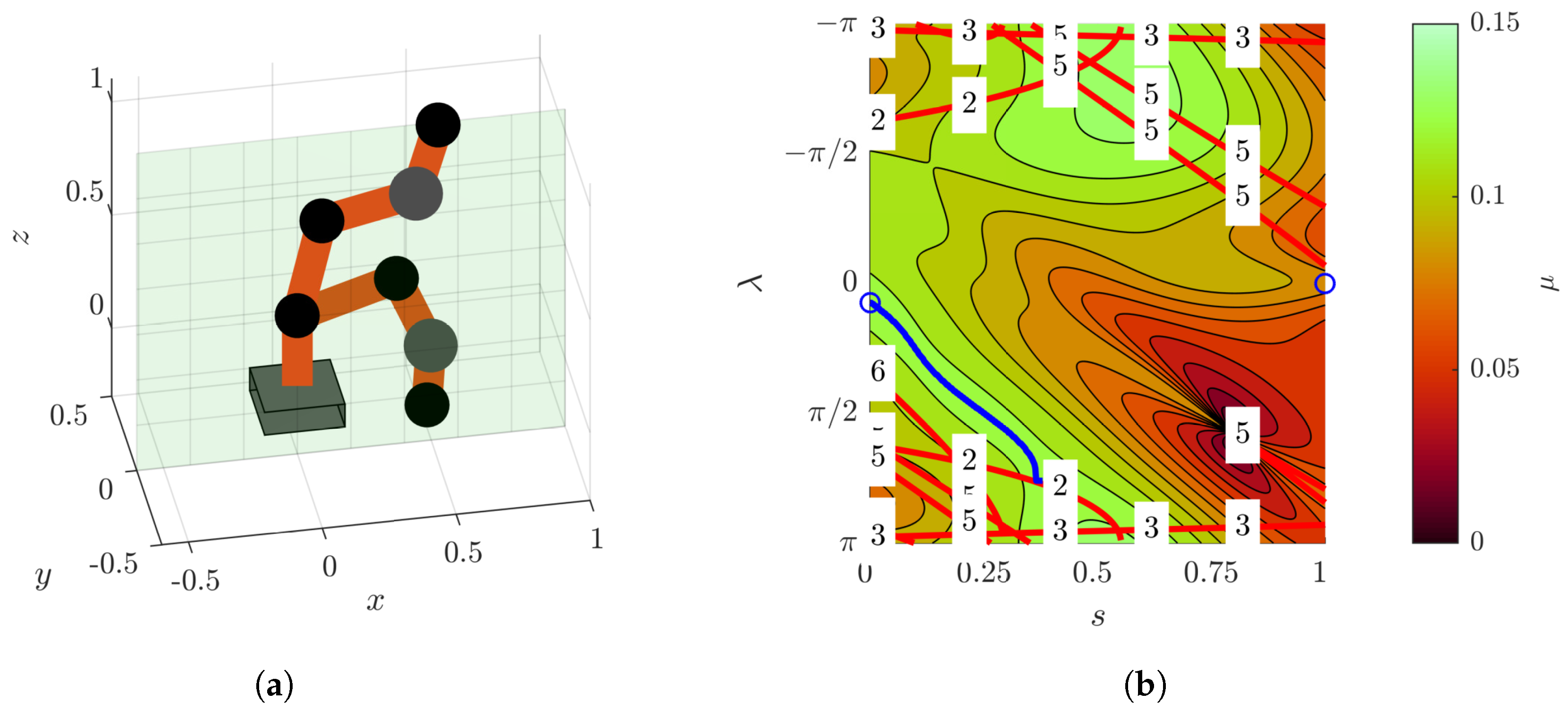
5.2. Redundancy Resolution
5.2.1. Redundancy Resolution for Global Manipulability Optima
5.2.2. Optimizing Null Space Solution of Given End-Effector Trajectory
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CDF | cumulative distribution function |
| CLIK | Closed-Loop Inverse Kinematic |
| CPU | Central Processing Unit |
| DOF | degree of freedom |
| FK | Forward Kinematic |
| GPU | Graphics Processing Unit |
| IK | Inverse Kinematic |
| M | Manipulability |
| probability density function | |
| PR | parameter requirements |
| SIMD | Single Instruction Multiple Data |
| S-R-S | Spherical-Revolute-Spherical |
| TCP | tool center point |
| TSP | Task Space Projection |
| TSS | Task Space Surjection |
Appendix A. Manipulability
Appendix B. Inverse Kinematic Functions from (43)
Appendix C. Absolute Valued Inverse Kinematics Functions from (55a)
Appendix D. Admissible Null Space Parameter Functions from (56)
References
- Yoshikawa, T. Manipulability of robotic mechanisms. Int. J. Rob. Res. 1985, 4, 3–9. [Google Scholar] [CrossRef]
- Yoshikawa, T. Dynamic manipulability of robot manipulators. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; pp. 1033–1038. [Google Scholar]
- Chiacchio, P.; Chiaverini, S.; Sciavicco, L.; Siciliano, B. Influence of gravity on the manipulability ellipsoid for robot arms. J. Dyn. Syst. Meas. Contr. 1992, 114, 723–727. [Google Scholar] [CrossRef]
- Chiacchio, P. A new dynamic manipulability ellipsoid for redundant manipulators. Robotica 2000, 18, 381–387. [Google Scholar] [CrossRef]
- Vahrenkamp, N.; Asfour, T.; Metta, G.; Sandini, G.; Dillmann, R. Manipulability analysis. In Proceedings of the 12th IEEE-RAS International Conference on Humanoid Robots (Humanoids 2012), Osaka, Japan, 29 November–1 December 2012; pp. 568–573. [Google Scholar]
- Waldron, K.J.; Schmiedeler, J. Kinematics. In Springer Handbook of Robotics, 2nd ed.; Siciliano, B., Khatib, O., Eds.; Springer: Cham, Switzerland, 2016; pp. 11–36. [Google Scholar]
- Jun, B.H.; Lee, P.M.; Kim, S. Manipulability analysis of underwater robotic arms on ROV and application to task-oriented joint configuration. J. Mech. Sci. Technol. 2008, 22, 887–894. [Google Scholar] [CrossRef]
- Abdel-Malek, K.; Yu, W.; Yang, J. Placement of Robot Manipulators to Maximize Dexterity. Int. J. Rob. Autom. 2004, 19, 6–14. [Google Scholar] [CrossRef]
- Wolovich, W.A.; Elliott, H. A computational technique for inverse kinematics. In Proceedings of the 23rd IEEE Conference on Decision and Control, Las Vegas, NV, USA, 12–14 December 1984; pp. 1359–1363. [Google Scholar]
- Colomé, A.; Torras, C. Closed-loop inverse kinematics for redundant robots: Comparative assessment and two enhancements. IEEE/ASME Trans. Mechatron. 2014, 20, 944–955. [Google Scholar] [CrossRef]
- Antonelli, G. Stability analysis for prioritized closed-loop inverse kinematic algorithms for redundant robotic systems. IEEE Trans. Rob. 2009, 25, 985–994. [Google Scholar] [CrossRef]
- Bjoerlykhaug, E. A Closed Loop Inverse Kinematics Solver Intended for Offline Calculation Optimized with GA. Robotics 2018, 7, 7. [Google Scholar] [CrossRef]
- Reiter, A.; Müller, A.; Gattringer, H. On Higher Order Inverse Kinematics Methods in Time-Optimal Trajectory Planning for Kinematically Redundant Manipulators. IEEE Trans. Ind. Inf. 2018, 14, 1681–1690. [Google Scholar] [CrossRef]
- Siciliano, B. Kinematic Control of Redundant Robot Manipulators: A Tutorial. J. Intell. Rob. Syst. 1990, 3, 201–212. [Google Scholar] [CrossRef]
- Shimizu, M.; Kakuya, H.; Yoon, W.K.; Kitagaki, K.; Kosuge, K. Analytical inverse kinematic computation for 7-DOF redundant manipulators with joint limits and its application to redundancy resolution. IEEE Trans. Rob. 2008, 24, 1131–1142. [Google Scholar] [CrossRef]
- Faria, C.; Ferreira, F.; Erlhagen, W.; Monteiro, S.; Bicho, E. Position-based kinematics for 7-DoF serial manipulators with global configuration control, joint limit and singularity avoidance. Mech. Mach. Theory 2018, 121, 317–334. [Google Scholar] [CrossRef]
- D’Souza, A.; Vijayakumar, S.; Schaal, S. Learning inverse kinematics. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Maui, HI, USA, 29 October–3 November 2001; Volume 1, pp. 298–303. [Google Scholar]
- Tejomurtula, S.; Kak, S. Inverse kinematics in robotics using neural networks. Inf. Sci. 1999, 116, 147–164. [Google Scholar] [CrossRef]
- Köker, R.; Öz, C.; Çakar, T.; Ekiz, H. A study of neural network based inverse kinematics solution for a three-joint robot. Rob. Autom. Syst. 2004, 49, 227–234. [Google Scholar] [CrossRef]
- Sariyildiz, E.; Ucak, K.; Oke, G.; Temeltas, H.; Ohnishi, K. Support Vector Regression based inverse kinematic modeling for a 7-DOF redundant robot arm. In Proceedings of the 2012 International Symposium on Innovations in Intelligent Systems and Applications, Trabzon, Turkey, 2–4 July 2012; pp. 1–5. [Google Scholar]
- Parker, J.K.; Khoogar, A.R.; Goldberg, D.E. Inverse kinematics of redundant robots using genetic algorithms. In Proceedings of the 1989 International Conference on Robotics and Automation (ICRA), Scottsdale, AZ, USA, 14–19 May 1989; pp. 271–276. [Google Scholar]
- KöKer, R. A genetic algorithm approach to a neural-network-based inverse kinematics solution of robotic manipulators based on error minimization. Inf. Sci. 2013, 222, 528–543. [Google Scholar] [CrossRef]
- Dereli, S.; Köker, R. A meta-heuristic proposal for inverse kinematics solution of 7-DOF serial robotic manipulator: Quantum behaved particle swarm algorithm. Artif. Intell. Rev. 2019, 1–16. [Google Scholar] [CrossRef]
- Kamrani, B.; Berbyuk, V.; Wäppling, D.; Feng, X.; Andersson, H. Optimal usage of robot manipulators. In Robot Manipulators; IntechOpen: London, UK, 2010. [Google Scholar]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Chan, T.F.; Dubey, R.V. A weighted least-norm solution based scheme for avoiding joint limits for redundant joint manipulators. Trans. Rob. Autom. 1995, 11, 286–292. [Google Scholar] [CrossRef]
- Dariush, B.; Hammam, G.B.; Orin, D. Constrained resolved acceleration control for humanoids. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taiwan, 18–22 October 2010; pp. 710–717. [Google Scholar]
- Dufour, K.; Suleiman, W. On integrating manipulability index into inverse kinematics solver. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 6967–6972. [Google Scholar]
- Jin, L.; Li, S.; La, H.M.; Luo, X. Manipulability optimization of redundant manipulators using dynamic neural networks. IEEE Trans. Ind. Electron. 2017, 64, 4710–4720. [Google Scholar] [CrossRef]
- Lee, S. Dual redundant arm configuration optimization with task-oriented dual arm manipulability. Trans. Rob. Autom. 1989, 5, 78–97. [Google Scholar] [CrossRef]
- Guilamo, L.; Kuffner, J.; Nishiwaki, K.; Kagami, S. Manipulability optimization for trajectory generation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Orlando, FL, USA, 15–19 May 2006; pp. 2017–2022. [Google Scholar]
- Rozo, L.; Jaquier, N.; Calinon, S.; Caldwell, D.G. Learning manipulability ellipsoids for task compatibility in robot manipulation. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 3183–3189. [Google Scholar]
- Jaquier, N.; Rozo, L.D.; Caldwell, D.G.; Calinon, S. Geometry-aware Tracking of Manipulability Ellipsoids. In Proceedings of the Proceedings Robotics: Science and Systems, Pittsburgh, PA, USA, 26–30 June 2018. [Google Scholar]
- Faroni, M.; Beschi, M.; Visioli, A.; Tosatti, L.M. A global approach to manipulability optimisation for a dual-arm manipulator. In Proceedings of the 2016 IEEE 21st International Conference on Emerging Technologies and Factory Automation (ETFA), Berlin, Germany, 6–9 September 2016; pp. 1–6. [Google Scholar]
- Zacharias, F.; Borst, C.; Wolf, S.; Hirzinger, G. The capability map: A tool to analyze robot arm workspaces. Int. J. Humanoid Rob. 2013, 10, 1350031. [Google Scholar] [CrossRef]
- Zlatanov, D.; Fenton, R.G.; Benhabib, B. Singularity analysis of mechanisms and manipulators via a velocity-equation model of the instantaneous kinematics. In Proceedings of the International Conference on Robotics and Automation (ICRA), San Diego, CA, USA, 8–13 May 1994; Volume 2, pp. 980–985. [Google Scholar]
- Staffetti, E.; Bruyninckx, H.; De Schutter, J. On the invariance of manipulability indices. In Advances in Robot Kinematics; Lenarčič, J., Thomas, F., Eds.; Springer: Dordrecht, The Netherlands, 2002; pp. 57–66. [Google Scholar]
- Gotlih, K.; Troch, I. Base invariance of the manipulability index. Robotica 2004, 22, 455–462. [Google Scholar] [CrossRef]
- Lee, S.; Bejczy, A.K. Redundant arm kinematic control based on parameterization. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Sacramento, CA, USA, 9–11 April 1991; pp. 458–465. [Google Scholar]
- Tondu, B. A closed-form inverse kinematic modelling of a 7R anthropomorphic upper limb based on a joint parametrization. In Proceedings of the 2006 6th IEEE-RAS International Conference on Humanoid Robots, Genova, Italy, 4–6 December 2006; pp. 390–397. [Google Scholar]
- Kreutz-Delgado, K.; Long, M.; Seraji, H. Kinematic analysis of 7-DOF manipulatorsiter. Int. J. Rob. Res. 1992, 11, 469–481. [Google Scholar] [CrossRef]
- Goldenberg, A.; Benhabib, B.; Fenton, R. A complete generalized solution to the inverse kinematics of robots. J. Rob. Autom. 1985, 1, 14–20. [Google Scholar] [CrossRef]
- Kuffner, J.J. Effective sampling and distance metrics for 3D rigid body path planning. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), New Orleans, LA, USA, 26 April–1 May 2004; pp. 3993–3998. [Google Scholar]
- Kuhlemann, I.; Jauer, P.; Ernst, F.; Schweikard, A. Robots with seven degrees of freedom: Is the additional DoF worth it? In Proceedings of the 2016 2nd International Conference on Control, Automation and Robotics (ICCAR), Hong Kong, China, 28–30 April 2016; pp. 80–84. [Google Scholar]
- Dixon, L.C.W. The Global Optimization Problem. An Introduction. Toward Global Optim. 1978, 2, 1–15. [Google Scholar]
- Fubini, G. Sugli integrali multipli. Rend. Acc. Naz. Lincei 1907, 16, 608–614. [Google Scholar]
- Chiacchio, P. Exploiting redundancy in minimum-time path following robot control. In Proceedings of the 1990 American Control Conference, San Diego, CA, USA, 23–25 May 1990; pp. 2313–2318. [Google Scholar]
- Chiu, S. Control of redundant manipulators for task compatibility. In Proceedings of the 1987 IEEE International Conference on Robotics and Automation (ICRA), Raleigh, NC, USA, 31 March–3 April 1987; Volume 4, pp. 1718–1724. [Google Scholar]
- Somani, N.; Rickert, M.; Gaschler, A.; Cai, C.; Perzylo, A.; Knoll, A. Task level robot programming using prioritized non-linear inequality constraints. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 430–437. [Google Scholar]
- Huber, G.; Wollherr, D. An Online Trajectory Generator on SE(3) for Human Robot Collaboration. Robotica 2019. accepted. [Google Scholar] [CrossRef]
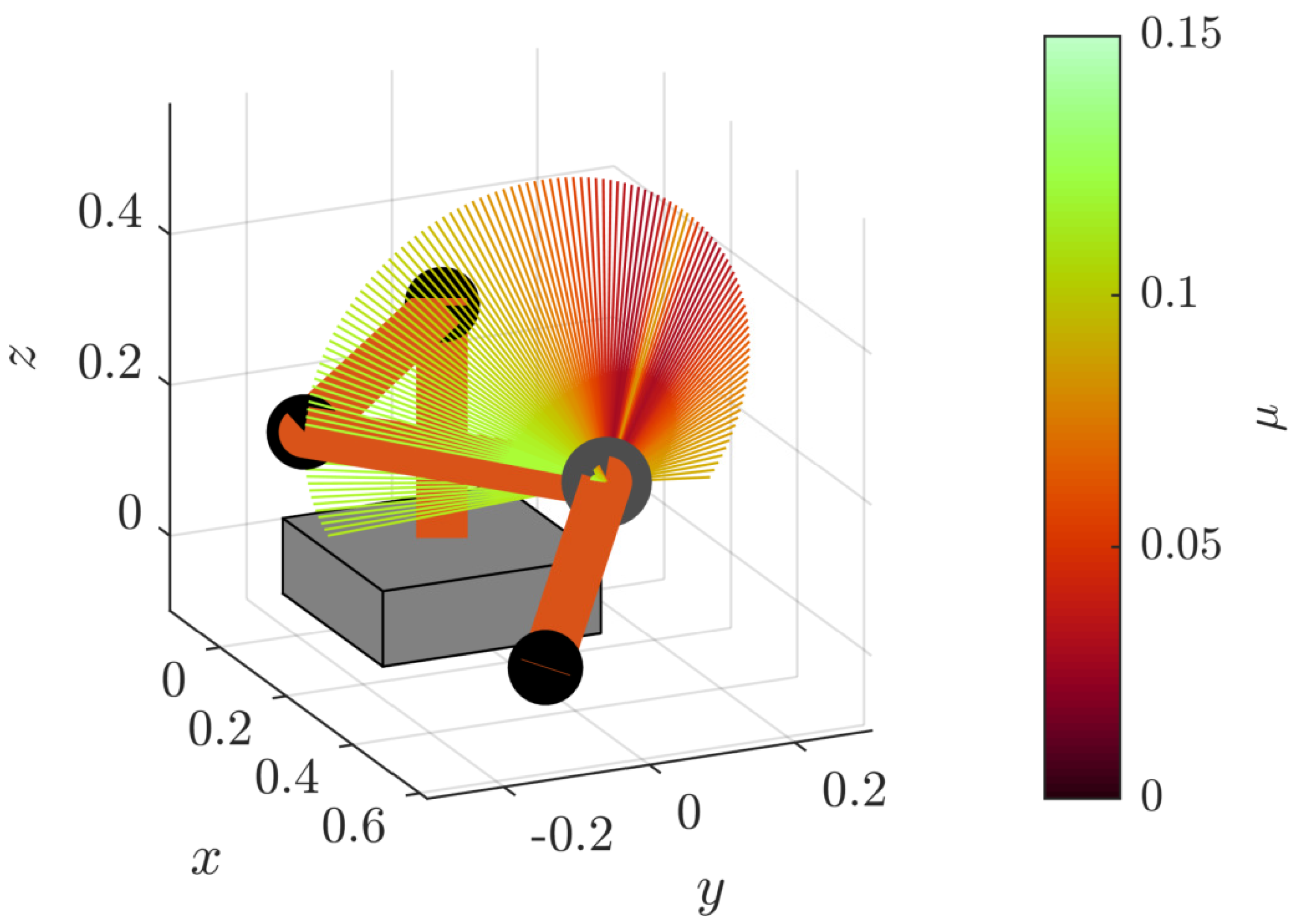

| # optima | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| percentage | 20% | 41% | 27% | 12% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huber, G.; Wollherr, D. Efficient Closed-Form Task Space Manipulability for a 7-DOF Serial Robot. Robotics 2019, 8, 98. https://doi.org/10.3390/robotics8040098
Huber G, Wollherr D. Efficient Closed-Form Task Space Manipulability for a 7-DOF Serial Robot. Robotics. 2019; 8(4):98. https://doi.org/10.3390/robotics8040098
Chicago/Turabian StyleHuber, Gerold, and Dirk Wollherr. 2019. "Efficient Closed-Form Task Space Manipulability for a 7-DOF Serial Robot" Robotics 8, no. 4: 98. https://doi.org/10.3390/robotics8040098
APA StyleHuber, G., & Wollherr, D. (2019). Efficient Closed-Form Task Space Manipulability for a 7-DOF Serial Robot. Robotics, 8(4), 98. https://doi.org/10.3390/robotics8040098