Reliable Real-Time Ball Tracking for Robot Table Tennis
Abstract
:1. Introduction
1.1. Contributions
1.2. Related Work
2. Reliable Real-Time Ball Tracking
2.1. Finding the Position of the Ball in an Image
| Algorithm 1 Finding the set of pixels of an object. |
| Input: A probability image , and a high and low thresholds and . Output: A set of object pixels O
|
2.2. Robust Estimation of the Ball Position
| Algorithm 2 Remove outliers by finding the largest consistent subset of 2D observations for stereo vision. |
| Input: A set of 2D observations and camera matrix pairs , and pixel error threshold . Output: A subset of maximal size without outliers.
|
3. Experiments and Results
3.1. Evaluation on a Simulation Environment
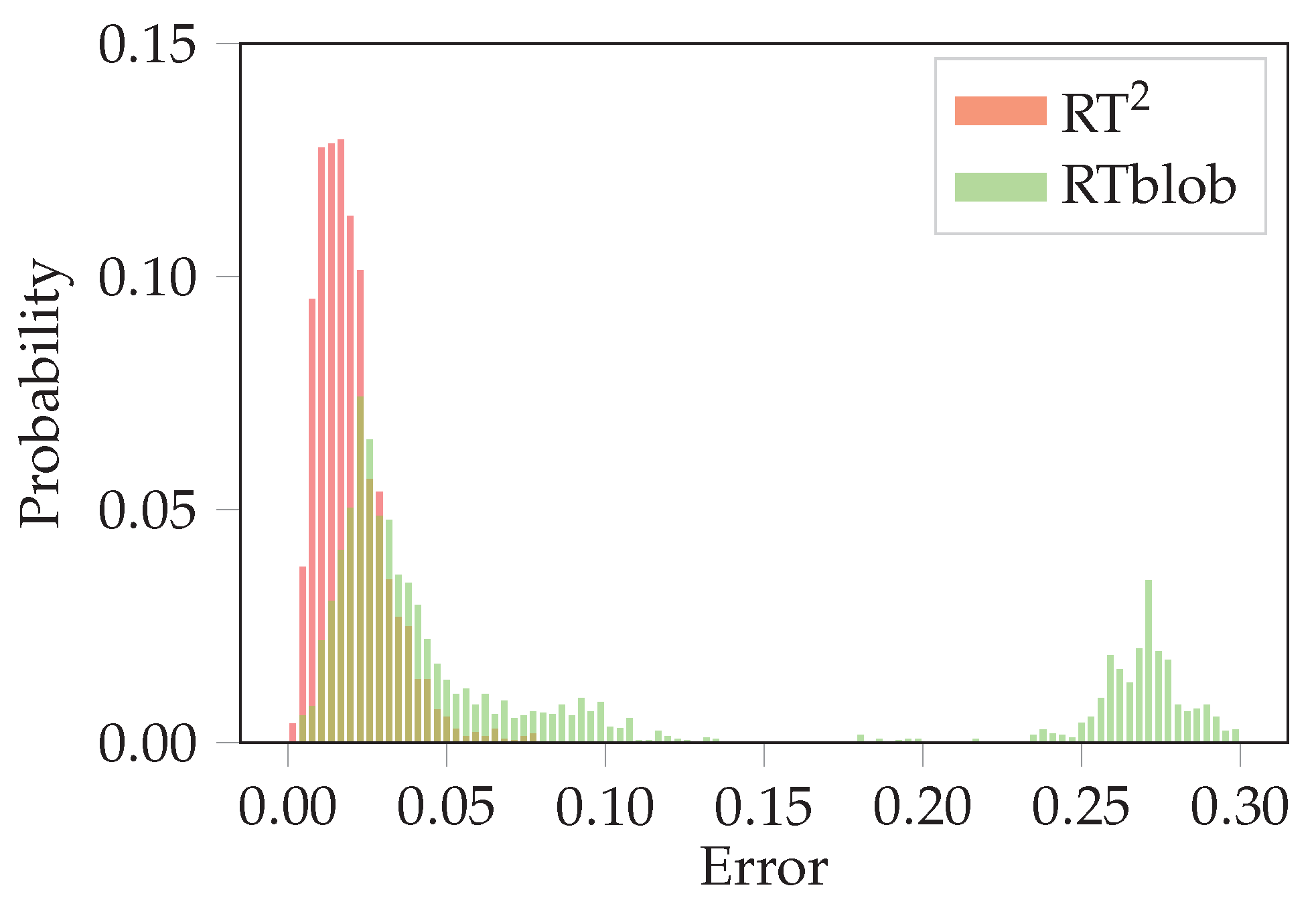
3.2. Evaluation on the Real Robot Platform
4. Conclusions and Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Campbell, M.; Hoane, A.J., Jr.; Hsu, F.H. Deep blue. Artif. Intell. 2002, 134, 57–83. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Kitano, H.; Asada, M.; Kuniyoshi, Y.; Noda, I.; Osawa, E. Robocup: The robot world cup initiative. In Proceedings of the first International Conference on Autonomous Agents (AGENTS ’97), Marina del Rey, CA, USA, 5–8 February 1997; pp. 340–347. [Google Scholar]
- Mülling, K.; Kober, J.; Peters, J. A biomimetic approach to robot table tennis. Adapt. Behav. 2011, 19, 359–376. [Google Scholar] [CrossRef]
- Gomez-Gonzalez, S.; Neumann, G.; Schölkopf, B.; Peters, J. Using probabilistic movement primitives for striking movements. In Proceedings of the International Conference of Humanoid Robots, Cancun, Mexico, 15–17 November 2016; pp. 502–508. [Google Scholar]
- Mülling, K.; Kober, J.; Kroemer, O.; Peters, J. Learning to select and generalize striking movements in robot table tennis. Int. J. Robot. Res. 2013, 32, 263–279. [Google Scholar] [CrossRef]
- Huang, Y.; Schölkopf, B.; Peters, J. Learning optimal striking points for a ping-pong playing robot. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 4587–4592. [Google Scholar]
- Lampert, C.; Peters, J. Real-time detection of colored objects in multiple camera streams with off-the-shelf hardware components. J. Real-Time Image Process. 2012, 7, 31–41. [Google Scholar] [CrossRef]
- Gomez-Gonzalez, S.; Neumann, G.; Schölkopf, B.; Peters, J. Adaptation and Robust Learning of Probabilistic Movement Primitives. arXiv 2018, arXiv:1808.10648. [Google Scholar]
- Open Source Implementation of the Ball Tracking System. Available online: https://gitlab.tuebingen.mpg.de/sgomez/ball_tracking (accessed on 20 October 2019).
- Seo, Y.; Choi, S.; Kim, H.; Hong, K.S. Where are the ball and players? Soccer game analysis with color-based tracking and image mosaick. In International Conference on Image Analysis and Processing; Springer: Berlin/Heidelberg, Germany, 1997; pp. 196–203. [Google Scholar] [Green Version]
- Tong, X.F.; Lu, H.Q.; Liu, Q.S. An effective and fast soccer ball detection and tracking method. In Proceedings of the International Conference on Pattern Recognition, Cambridge, UK, 26 August 2004; Volume 4, pp. 795–798. [Google Scholar]
- Chen, H.T.; Tien, M.C.; Chen, Y.W.; Tsai, W.J.; Lee, S.Y. Physics-based ball tracking and 3D trajectory reconstruction with applications to shooting location estimation in basketball video. J. Vis. Commun. Image Represent. 2009, 20, 204–216. [Google Scholar] [CrossRef]
- Pingali, G.; Opalach, A.; Jean, Y. Ball tracking and virtual replays for innovative tennis broadcasts. In Proceedings of the International Conference on Pattern Recognition, Barcelona, Spain, 3–7 September 2000; Volume 4, pp. 152–156. [Google Scholar]
- Liu, H.; Li, Z.; Wang, B.; Zhou, Y.; Zhang, Q. Table tennis robot with stereo vision and humanoid manipulator II: Visual measurement of motion-blurred ball. In Proceedings of the International Conference on Robotics and Biomimetics, Shenzhen, China, 12–14 December 2013; pp. 2430–2435. [Google Scholar]
- Li, H.; Wu, H.; Lou, L.; Kühnlenz, K.; Ravn, O. Ping-pong robotics with high-speed vision system. In Proceedings of the International Conference on Control Automation Robotics & Vision, Guangzhou, China, 5–7 December 2012; pp. 106–111. [Google Scholar]
- Chen, X.; Huang, Q.; Wan, W.; Zhou, M.; Yu, Z.; Zhang, W.; Yasin, A.; Bao, H.; Meng, F. A robust vision module for humanoid robotic ping-pong game. Int. J. Adv. Robot. Syst. 2015, 12, 35. [Google Scholar] [CrossRef]
- Huang, J.; Rathod, V.; Sun, C.; Zhu, M.; Korattikara, A.; Fathi, A.; Fischer, I.; Wojna, Z.; Song, Y.; Guadarrama, S.; et al. Speed/accuracy trade-offs for modern convolutional object detectors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single shot multibox detector. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2016; pp. 21–37. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Pohlen, T.; Hermans, A.; Mathias, M.; Leibe, B. Full-resolution residual networks for semantic segmentation in street scenes. arXiv 2017, arXiv:1611.08323. [Google Scholar]
- Heyden, A.; Pollefeys, M. Multiple view geometry. Emerging topics in computer vision; Prentice Hall PTR: Upper Saddle River, NJ, USA, 2005; pp. 45–107. [Google Scholar]
- Hodge, V.; Austin, J. A survey of outlier detection methodologies. Artif. Intell. Rev. 2004, 22, 85–126. [Google Scholar] [CrossRef]
- Chum, O. Two-View Geometry Estimation by Random Sample and Consensus. Ph.D. Thesis, Czech Technical University, Prague, Czech Republic, 2005. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Tordoff, B.; Murray, D.W. Guided sampling and consensus for motion estimation. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2002; pp. 82–96. [Google Scholar]
- Nasuto, D.; Craddock, J.B.R. Napsac: High noise, high dimensional robust estimation-it’s in the bag. In Proceedings of the British Machine Vision Conference, University of Cardiff, September 2002; pp. 458–467. [Google Scholar]
- Raguram, R.; Chum, O.; Pollefeys, M.; Matas, J.; Frahm, J.M. USAC: A universal framework for random sample consensus. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 2022–2038. [Google Scholar] [CrossRef] [PubMed]



| c | Probability of Outliers | |||||
|---|---|---|---|---|---|---|
| 1% | 5% | 10% | 25% | 50% | ||
| 4 | E | 0.71 cm | 0.85 cm | 0.84 cm | 0.79 cm | 4.67 cm |
| F | 0.1% | 0.5% | 2.0% | 9.7% | 37.7% | |
| 8 | E | 0.52 cm | 0.53 cm | 0.59 cm | 0.94 cm | 6.84 cm |
| F | 0.0% | 0.0% | 0.0% | 0.1% | 4.5% | |
| 15 | E | 0.35 cm | 0.36 cm | 0.37 cm | 0.41 cm | 4.72 cm |
| F | 0.0% | 0.0% | 0.0% | 0.0% | 0.02% | |
| 30 | E | 0.24 cm | 0.25 cm | 0.25 cm | 0.28 cm | 0.35 cm |
| F | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | |
| Cameras | 4 | 8 | 15 | 30 | 50 |
| Run time (ms) | 0.001 | 0.012 | 0.015 | 3.02 | 11.46 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomez-Gonzalez, S.; Nemmour, Y.; Schölkopf, B.; Peters, J. Reliable Real-Time Ball Tracking for Robot Table Tennis. Robotics 2019, 8, 90. https://doi.org/10.3390/robotics8040090
Gomez-Gonzalez S, Nemmour Y, Schölkopf B, Peters J. Reliable Real-Time Ball Tracking for Robot Table Tennis. Robotics. 2019; 8(4):90. https://doi.org/10.3390/robotics8040090
Chicago/Turabian StyleGomez-Gonzalez, Sebastian, Yassine Nemmour, Bernhard Schölkopf, and Jan Peters. 2019. "Reliable Real-Time Ball Tracking for Robot Table Tennis" Robotics 8, no. 4: 90. https://doi.org/10.3390/robotics8040090
APA StyleGomez-Gonzalez, S., Nemmour, Y., Schölkopf, B., & Peters, J. (2019). Reliable Real-Time Ball Tracking for Robot Table Tennis. Robotics, 8(4), 90. https://doi.org/10.3390/robotics8040090






