Tactile-Driven Grasp Stability and Slip Prediction
Abstract
1. Introduction
1.1. Types of Tactile Sensors
- In a piezo-resistive sensor [11], the resistance of the materials changes when a force is applied. The advantages of this sensor are its wide dynamic range in the measurements, the low cost of manufacturing it, its simple integration and its great durability, although it has low spatial resolution and can produce hysteresis.
- Capacitive sensor [12], in which the distance between two plates changes when a force is applied. Its advantages are good integration, high sensitivity, stability and its ability to sense normal and tangential forces. However, it can produce hysteresis too.
- Optical sensor, which uses a camera to measure the visual deformation of a pattern in an internal surface. The main advantage of this type of sensors is that it is immune to electromagnetic interferences, it has a quick response and high spatial resolution. The disadvantage is that it is usually large. One of the most known is the GelSight [13,14].
- Based on magnetic transduction [15]. This sensor measures changes in the flow density of a small magnet caused by the applied force. It stands for its high sensitivity, also for providing a good dynamic range and it can detect multi-direction deflections. Its response is linear and without hysteresis. Moreover, its manufacturing materials are robust.
- Barometric sensors, which measure the pressure of a contact from the deformation of a liquid or air contained inside the sensor, affecting the electric current registered by a set of electrodes. An example is the BioTac sensor [16] used in this work.
1.2. Tactile Data Processing
2. Related Works
3. Materials and Methods
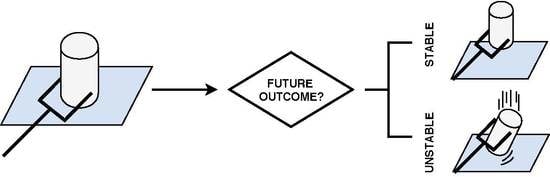
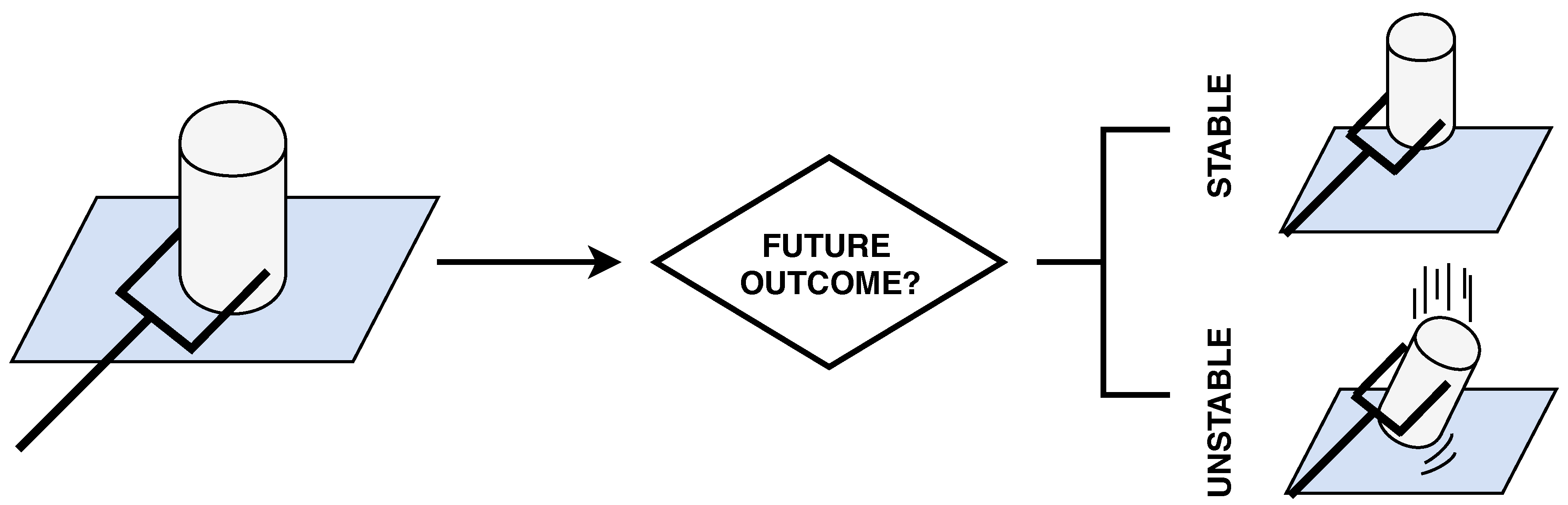
3.1. Problem Statement
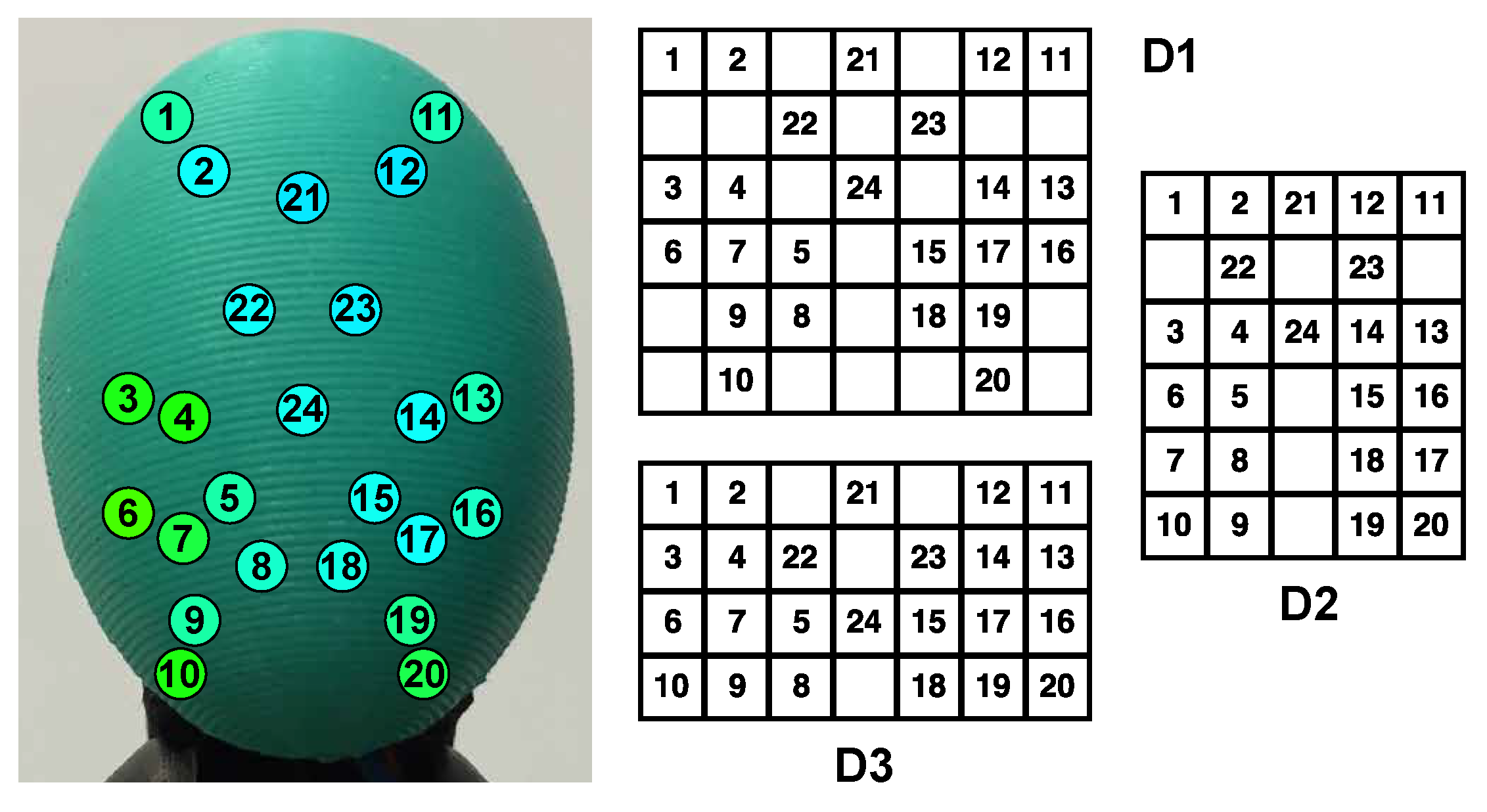
3.2. Tactile Sensor
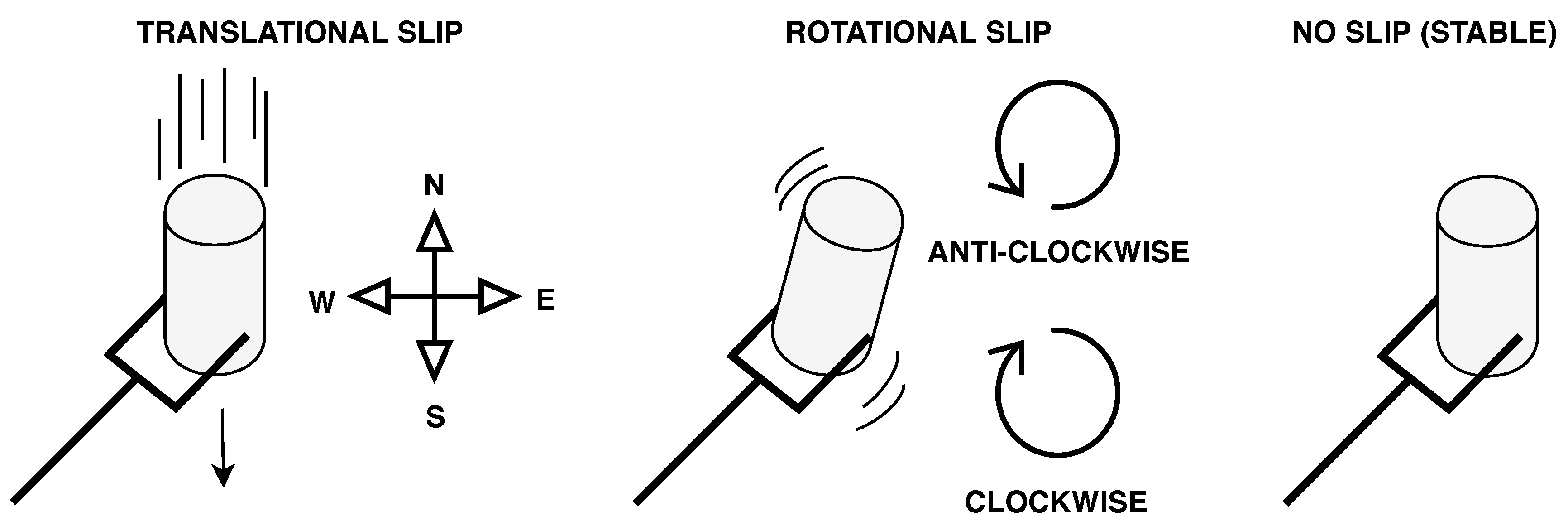
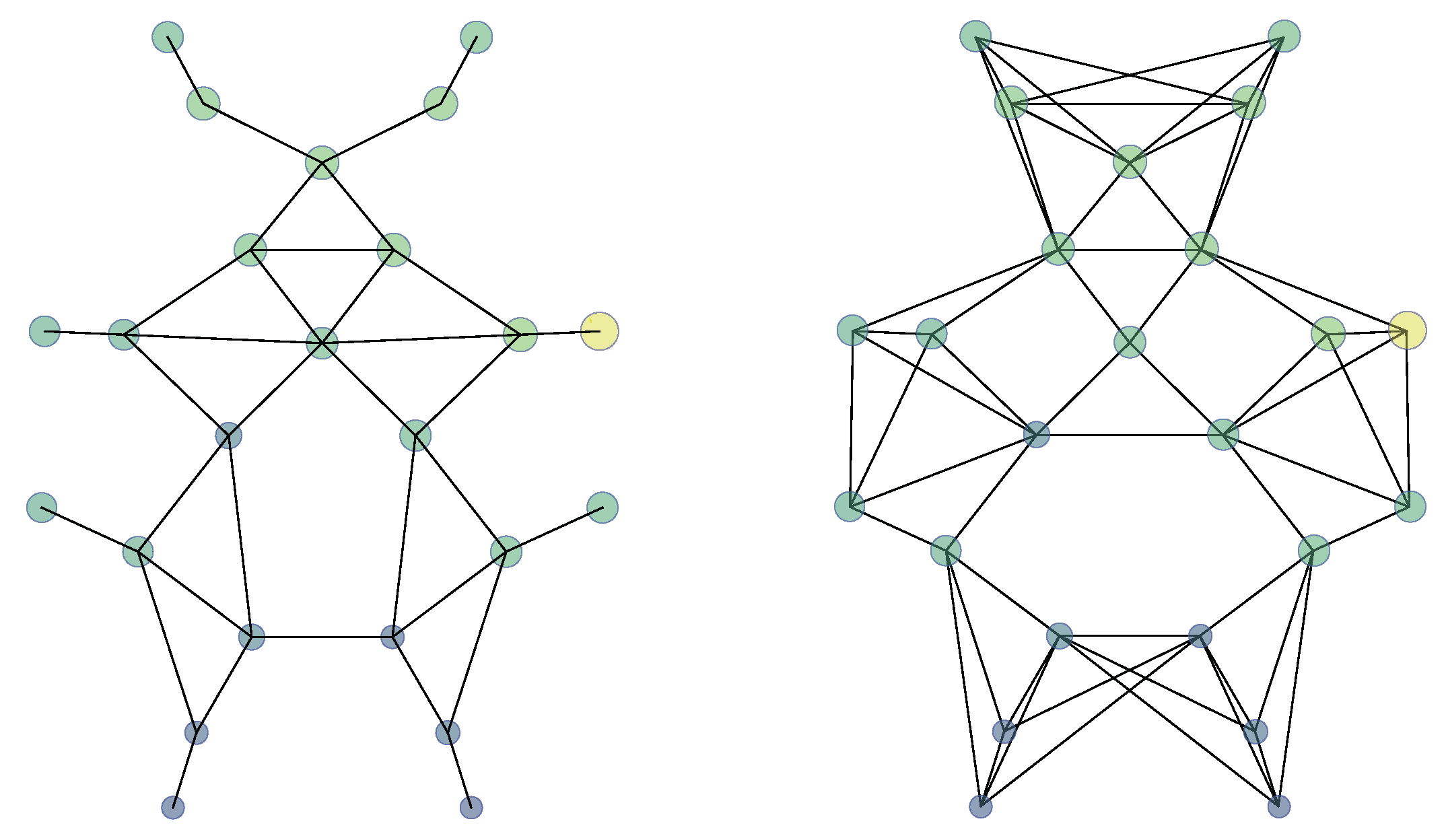
3.3. Data Interpretation
3.4. Learning Methods
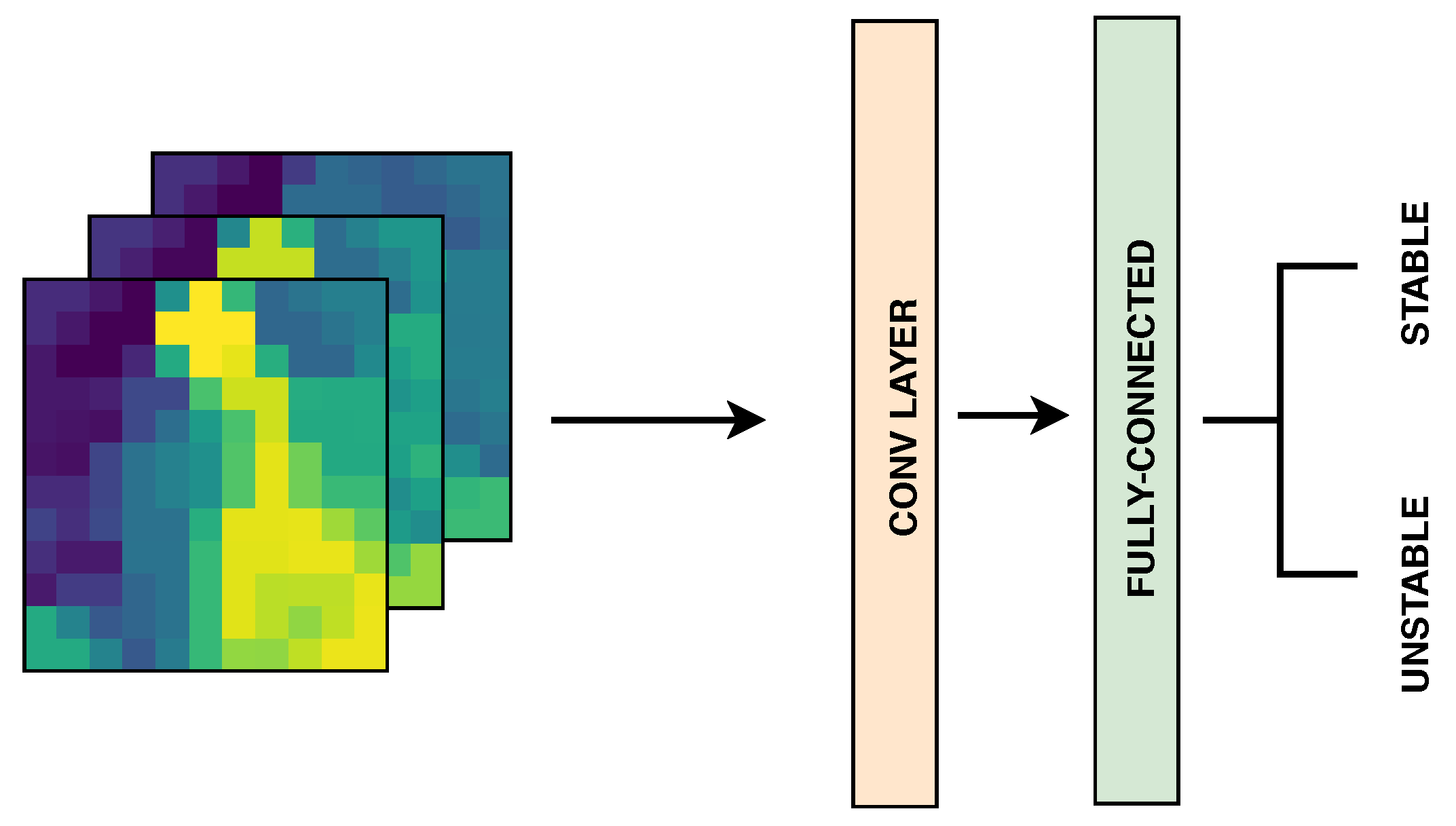
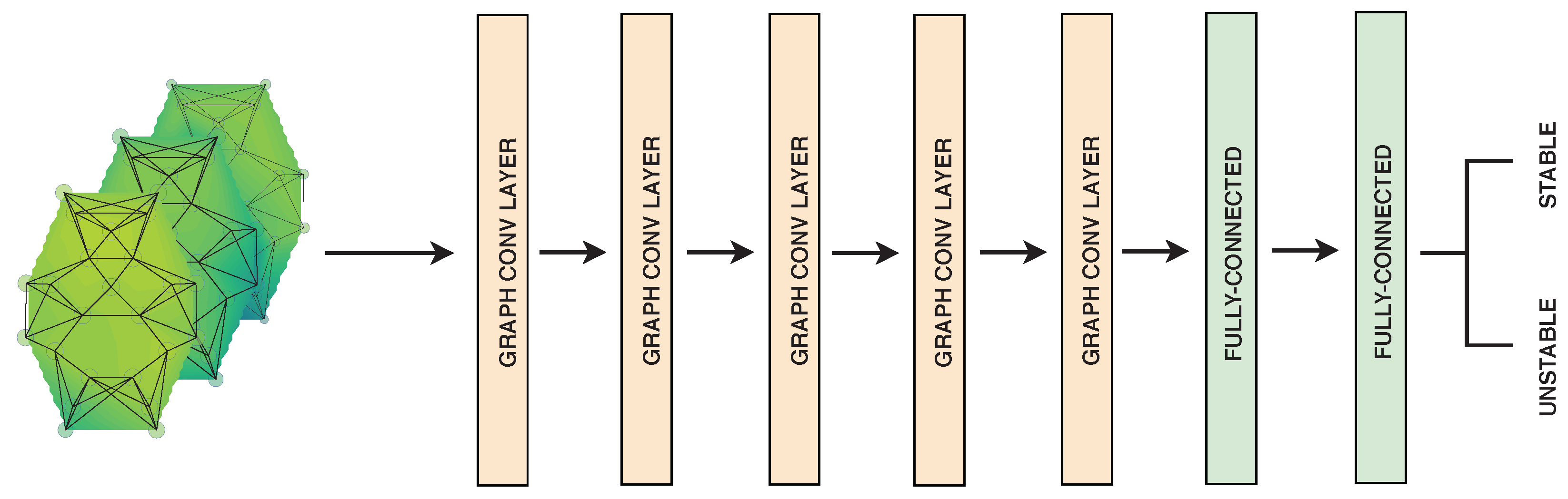
3.4.1. Deep Neural Networks for Static Data
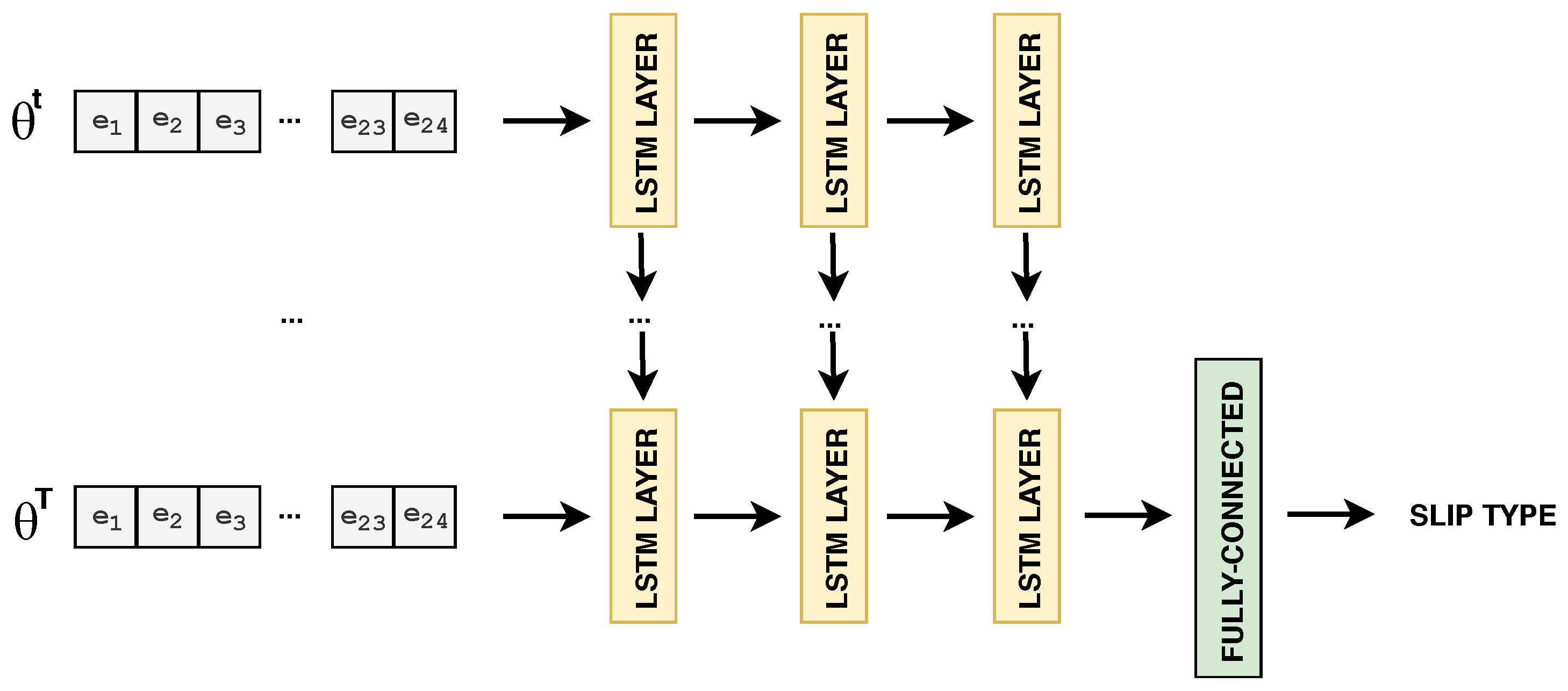
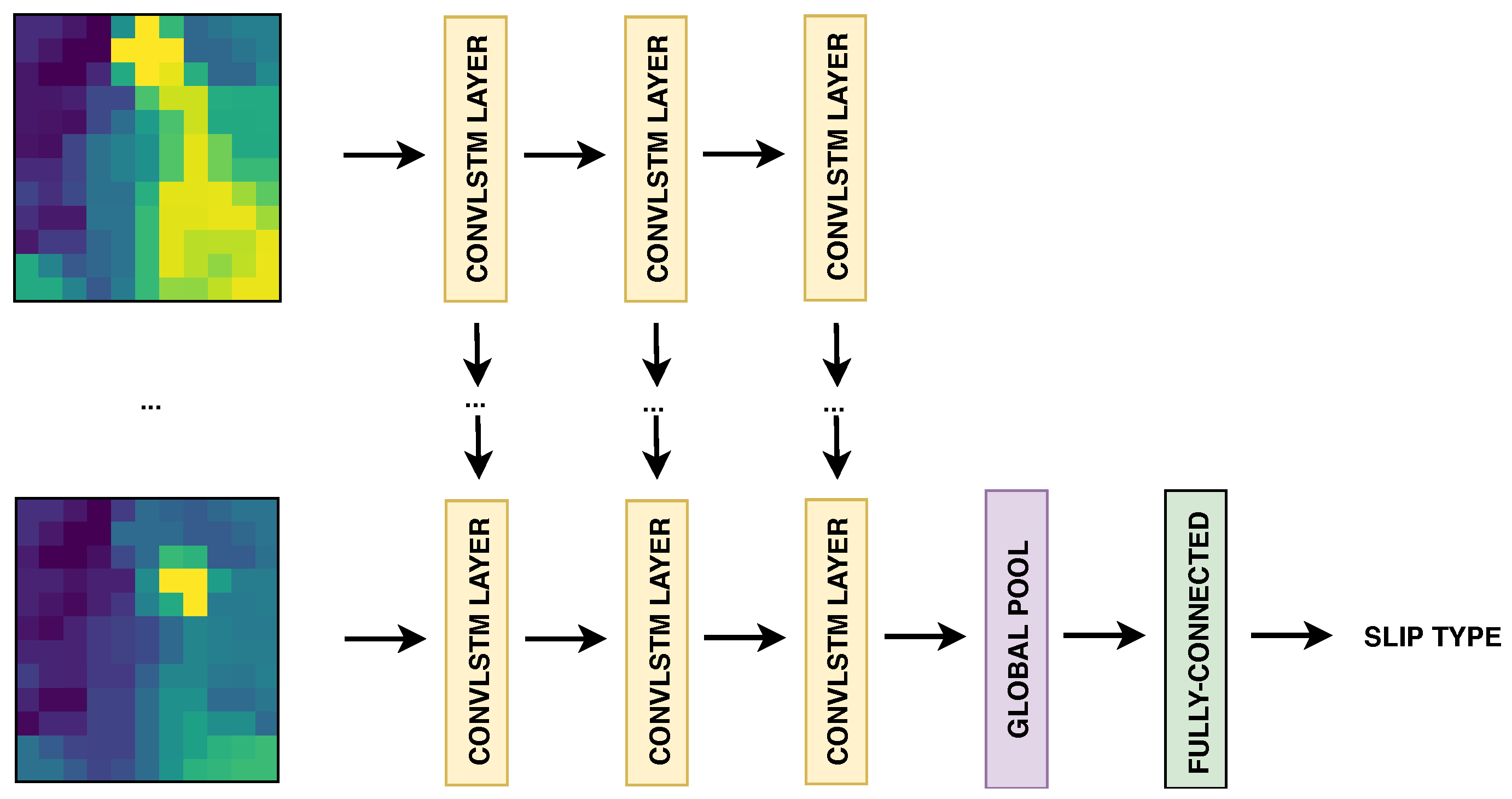
3.4.2. Deep Neural Networks for Temporal Sequences
4. Results and Discussion
4.1. Dataset and Training Methodology
- Grasp the object: the hand performed a three-fingered grasp that contacted the object, which was laying on a table.
- Read the sensors: a single reading was recorded then from each of the sensors at the same time.
- Lift the object: the hand was raised in order to lift the object and check the outcome.
- Label the trial: the recorded tactile readings were labelled according to the outcome of the lifting with two classes; stable, i.e., it is completely static or slip, i.e., either fell from the hand or it moves within it.
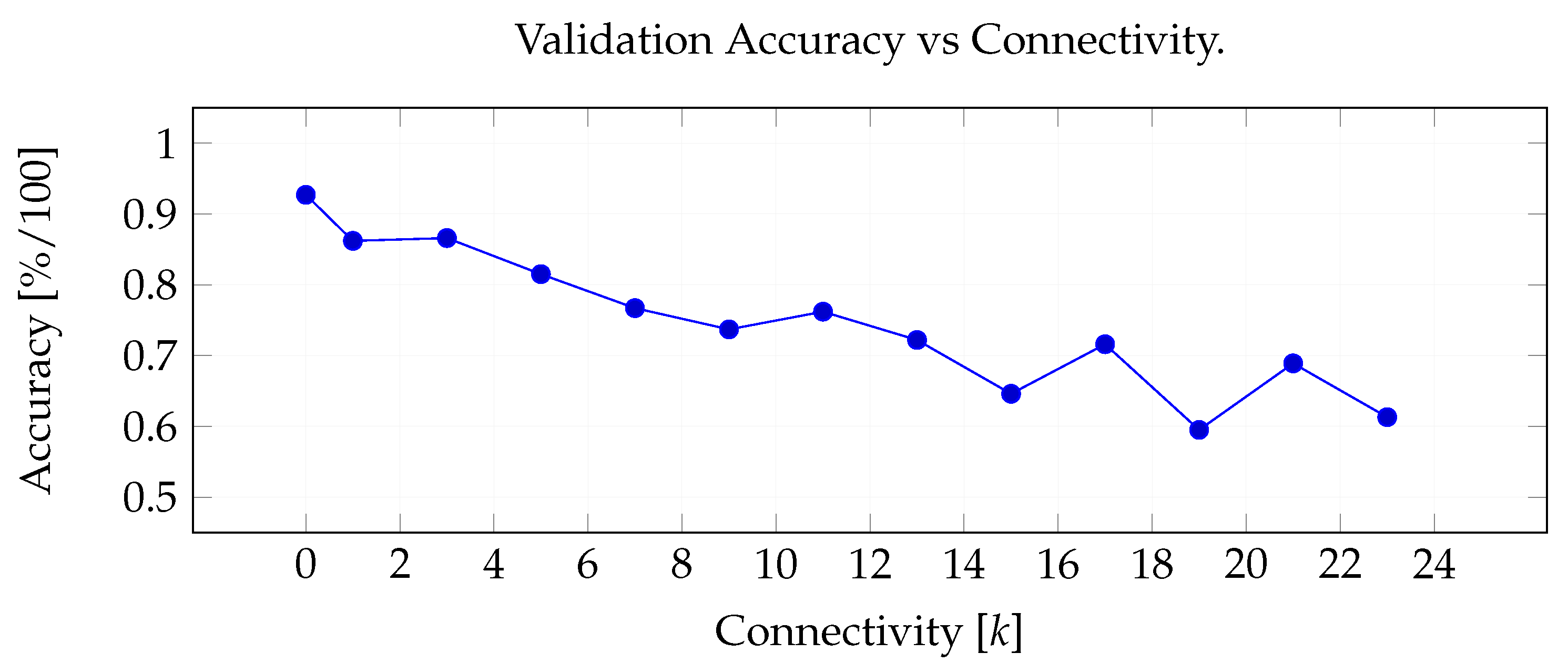
4.2. Tuning of Tactile Images and Tactile Graphs
4.3. CNN vs. GCN: Image vs. Graph
4.4. LSTM vs. ConvLSTM: 1D-Signal vs. 2D-Image Sequence
4.5. Limitations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kappassov, Z.; Corrales, J.A.; Perdereau, V. Tactile sensing in dexterous robot hands—Review. Robot. Auton. Syst. 2015, 74, 195–220. [Google Scholar] [CrossRef]
- Luo, S.; Bimbo, J.; Dahiya, R.; Liu, H. Robotic tactile perception of object properties: A review. Mechatronics 2017, 48, 54–67. [Google Scholar] [CrossRef]
- Kerzel, M.; Ali, M.; Ng, H.G.; Wermter, S. Haptic material classification with a multi-channel neural network. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), 2017, Anchorage, AK, USA, 14–19 May 2017; pp. 439–446. [Google Scholar] [CrossRef]
- Liu, H.; Sun, F.; Zhang, X. Robotic Material Perception Using Active Multimodal Fusion. IEEE Trans. Ind. Electron. 2019, 66, 9878–9886. [Google Scholar] [CrossRef]
- Schmitz, A.; Bansho, Y.; Noda, K.; Iwata, H.; Ogata, T.; Sugano, S. Tactile object recognition using deep learning and dropout. In Proceedings of the 2014 IEEE-RAS International Conference on Humanoid Robots, Madrid, Spain, 18–20 November 2014; pp. 1044–1050. [Google Scholar] [CrossRef]
- Velasco, E.; Zapata-Impata, B.S.; Gil, P.; Torres, F. Clasificación de objetos usando percepción bimodal de palpación única en acciones de agarre robótico. Rev. Iberoam. Autom. Inform. Ind. 2019. [Google Scholar] [CrossRef]
- Van Hoof, H.; Hermans, T.; Neumann, G.; Peters, J. Learning robot in-hand manipulation with tactile features. In Proceedings of the 2015 IEEE-RAS 15th International Conference on Humanoid Robots (Humanoids), Seoul, Korea, 3–5 November 2015; pp. 121–127. [Google Scholar] [CrossRef]
- Hang, K.; Li, M.; Stork, J.A.; Bekiroglu, Y.; Pokorny, F.T.; Billard, A.; Kragic, D. Hierarchical Fingertip Space: A Unified Framework for Grasp Planning and In-Hand Grasp Adaptation. IEEE Trans. Robot. 2016, 32, 960–972. [Google Scholar] [CrossRef]
- Calandra, R.; Owens, A.; Jayaraman, D.; Lin, J.; Yuan, W.; Malik, J.; Adelson, E.H.; Levine, S. More Than a Feeling: Learning to Grasp and Regrasp using Vision and Touch. IEEE Robot. Autom. Lett. 2018, 3, 3300–3307. [Google Scholar] [CrossRef]
- Yi, Z.; Zhang, Y.; Peters, J. Biomimetic tactile sensors and signal processing with spike trains: A review. Sens. Actuators A Phys. 2018, 269, 41–52. [Google Scholar] [CrossRef]
- Stassi, S.; Cauda, V.; Canavese, G.; Pirri, C.F. Flexible Tactile Sensing Based on Piezoresistive Composites: A Review. Sensors 2014, 14, 5296–5332. [Google Scholar] [CrossRef]
- Tiwana, M.I.; Shashank, A.; Redmond, S.J.; Lovell, N.H. Characterization of a capacitive tactile shear sensor for application in robotic and upper limb prostheses. Sens. Actuators A Phys. 2011, 165, 164–172. [Google Scholar] [CrossRef]
- Johnson, M.K.; Cole, F.; Raj, A.; Adelson, E.H. Microgeometry Capture Using an Elastomeric Sensor. ACM Trans. Graph. 2011, 30, 46:1–46:8. [Google Scholar] [CrossRef]
- Yuan, W.; Dong, S.; Adelson, E.H. GelSight: High-Resolution Robot Tactile Sensors for Estimating Geometry and Force. Sensors 2017, 17, 2762. [Google Scholar] [CrossRef] [PubMed]
- Alfadhel, A.; Kosel, J. Magnetic Nanocomposite Cilia Tactile Sensor. Adv. Mater. 2015, 27, 7888–7892. [Google Scholar] [CrossRef] [PubMed]
- Su, Z.; Fishel, J.; Yamamoto, T.; Loeb, G. Use of tactile feedback to control exploratory movements to characterize object compliance. Front. Neurorobot. 2012, 6, 7. [Google Scholar] [CrossRef] [PubMed]
- Delgado, A.; Corrales, J.; Mezouar, Y.; Lequievre, L.; Jara, C.; Torres, F. Tactile control based on Gaussian images and its application in bi-manual manipulation of deformable objects. Robot. Auton. Syst. 2017, 94, 148–161. [Google Scholar] [CrossRef]
- Zapata-Impata, B.S.; Gil, P.; Torres, F. Non-Matrix Tactile Sensors: How Can Be Exploited Their Local Connectivity For Predicting Grasp Stability? In Proceedings of the IEEE/RSJ IROS 2018 Workshop RoboTac: New Progress in Tactile Perception and Learning in Robotics, Madrid, Spain, 1–5 October 2018; pp. 1–4. [Google Scholar]
- Garcia-Garcia, A.; Zapata-Impata, B.S.; Orts-Escolano, S.; Gil, P.; Garcia-Rodriguez, J. TactileGCN: A Graph Convolutional Network for Predicting Grasp Stability with Tactile Sensors. arXiv 2019, arXiv:1901.06181. [Google Scholar]
- Kaboli, M.; De La Rosa T, A.; Walker, R.; Cheng, G. In-hand object recognition via texture properties with robotic hands, artificial skin, and novel tactile descriptors. In Proceedings of the 2015 IEEE-RAS 15th International Conference on Humanoid Robots (Humanoids), Seoul, Korea, 3–5 November 2015; pp. 1155–1160. [Google Scholar] [CrossRef]
- Kaboli, M.; Walker, R.; Cheng, G. Re-using prior tactile experience by robotic hands to discriminate in-hand objects via texture properties. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 2242–2247. [Google Scholar] [CrossRef]
- Luo, S.; Mou, W.; Althoefer, K.; Liu, H. Novel Tactile-SIFT Descriptor for Object Shape Recognition. IEEE Sens. J. 2015, 15, 5001–5009. [Google Scholar] [CrossRef]
- Yang, J.; Liu, H.; Sun, F.; Gao, M. Object recognition using tactile and image information. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO), Zhuhai, China, 6–9 December 2015; pp. 1746–1751. [Google Scholar] [CrossRef]
- Spiers, A.J.; Liarokapis, M.V.; Calli, B.; Dollar, A.M. Single-Grasp Object Classification and Feature Extraction with Simple Robot Hands and Tactile Sensors. IEEE Trans. Haptics 2016, 9, 207–220. [Google Scholar] [CrossRef]
- Gao, Y.; Hendricks, L.A.; Kuchenbecker, K.J.; Darrell, T. Deep learning for tactile understanding from visual and haptic data. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 536–543. [Google Scholar] [CrossRef]
- Li, J.; Dong, S.; Adelson, E. Slip Detection with Combined Tactile and Visual Information. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018. [Google Scholar]
- Zhang, Y.; Kan, Z.; Tse, Y.A.; Yang, Y.; Wang, M.Y. FingerVision Tactile Sensor Design and Slip Detection Using Convolutional LSTM Network. arXiv 2018, arXiv:1810.02653. [Google Scholar]
- Zapata-Impata, B.S.; Gil, P.; Torres, F. Learning Spatio Temporal Tactile Features with a ConvLSTM for the Direction Of Slip Detection. Sensors 2019, 19, 523. [Google Scholar] [CrossRef] [PubMed]
- Bekiroglu, Y.; Laaksonen, J.; Jorgensen, J.A.; Kyrki, V.; Kragic, D. Assessing Grasp Stability Based on Learning and Haptic Data. IEEE Trans. Robot. 2011, 27, 616–629. [Google Scholar] [CrossRef]
- Calandra, R.; Owens, A.; Upadhyaya, M.; Yuan, W.; Lin, J.; Adelson, E.H.; Levine, S. The Feeling of Success: Does Touch Sensing Help Predict Grasp Outcomes? arXiv 2017, arXiv:1710.05512. [Google Scholar]
- Lee, M.A.; Zhu, Y.; Zachares, P.; Tan, M.; Srinivasan, K.; Savarese, S.; Fei-Fei, L.; Garg, A.; Bohg, J. Making Sense of Vision and Touch: Learning Multimodal Representations for Contact-Rich Tasks. In Proceedings of the International Conference on Robotics and Automation (ICRA 2019), Montreal, QC, Canada, 20–24 May 2019. [Google Scholar]
- Schill, J.; Laaksonen, J.; Przybylski, M.; Kyrki, V.; Asfour, T.; Dillmann, R. Learning continuous grasp stability for a humanoid robot hand based on tactile sensing. In Proceedings of the 2012 4th IEEE RAS EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Rome, Italy, 24–27 June 2012; pp. 1901–1906. [Google Scholar] [CrossRef]
- Cockbum, D.; Roberge, J.; Le, T.; Maslyczyk, A.; Duchaine, V. Grasp stability assessment through unsupervised feature learning of tactile images. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 2238–2244. [Google Scholar] [CrossRef]
- Kwiatkowski, J.; Cockburn, D.; Duchaine, V. Grasp stability assessment through the fusion of proprioception and tactile signals using convolutional neural networks. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 286–292. [Google Scholar] [CrossRef]
- Reinecke, J.; Dietrich, A.; Schmidt, F.; Chalon, M. Experimental comparison of slip detection strategies by tactile sensing with the BioTac® on the DLR hand arm system. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 2742–2748. [Google Scholar] [CrossRef]
- Veiga, F.; van Hoof, H.; Peters, J.; Hermans, T. Stabilizing novel objects by learning to predict tactile slip. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 5065–5072. [Google Scholar] [CrossRef]
- Su, Z.; Hausman, K.; Chebotar, Y.; Molchanov, A.; Loeb, G.E.; Sukhatme, G.S.; Schaal, S. Force estimation and slip detection/classification for grip control using a biomimetic tactile sensor. In Proceedings of the 2015 IEEE-RAS 15th International Conference on Humanoid Robots (Humanoids), Seoul, Korea, 3–5 November 2015; pp. 297–303. [Google Scholar] [CrossRef]
- Heyneman, B.; Cutkosky, M.R. Slip classification for dynamic tactile array sensors. Int. J. Robot. Res. 2016, 35, 404–421. [Google Scholar] [CrossRef]
- Meier, M.; Patzelt, F.; Haschke, R.; Ritter, H. Tactile Convolutional Networks for Online Slip and Rotation Detection. In Proceedings of the 25th International Conference on Artificial Neural Networks (ICANN), Barcelona, Spain, 6–9 September 2016; Springer: Berlin, Germany, 2016; Volume 9887, pp. 12–19. [Google Scholar] [CrossRef]
- Dong, S.; Yuan, W.; Adelson, E.H. Improved GelSight Tactile Sensor for Measuring Geometry and Slip. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017. [Google Scholar]
- Wettels, N.; Santos, V.J.; Johansson, R.S.; Loeb, G.E. Biomimetic Tactile Sensor Array. Adv. Robot. 2008, 22, 829–849. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y. Convolutional Networks for Images, Speech, and Time-Series. In The Handbook of Brain Theory and Neural Networks; The MIT Press: Cambridge, MA, USA, 1995; Volume 3361, pp. 1–14. [Google Scholar]
- Calandra, R.; Owens, A.; Upadhyaya, M.; Yuan, W.; Lin, J.; Adelson, E.H.; Levine, S. The Feeling of Success: Does Touch Sensing Help Predict Grasp Outcomes? In Proceedings of the 1st Annual Conference on Robot Learning, Mountain View, CA, USA, 13–15 November 2017; Volume 78, pp. 314–323. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems 25 (NIPS 2012), Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1–9. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.k.; Woo, W.c. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. In Proceedings of the Advances in Neural Information Processing Systems 28 (NIPS 2015), Montreal, QC, Canada, 7–12 December 2015; pp. 802–810. [Google Scholar]
- BioTac SP Stability Set. Available online: https://github.com/3dperceptionlab/biotacsp-stability-set-v2 (accessed on 26 September 2019).
- BioTac SP Direction of Slip Set. Available online: https://github.com/yayaneath/BioTacSP-DoS (accessed on 26 September 2019).
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]



| Distribution | Accuracy | Precision | Recall | F1 |
|---|---|---|---|---|
| D1 (12 × 11) | 90.9 ± 1.5 | 90.4 ± 2.4 | 91.6 ± 2.4 | 91.0 ± 1.4 |
| D2 (6 × 5) | 89.6 ± 1.7 | 89.5 ± 2.8 | 89.9 ± 2.0 | 89.7 ± 1.5 |
| D3 (4 × 7) | 89.7 ± 1.3 | 89.7 ± 1.8 | 89.8 ± 2.6 | 89.7 ± 1.4 |
| Accuracy | Precision | Recall | F1 | |||||
|---|---|---|---|---|---|---|---|---|
| Pose | GCN | CNN | GCN | CNN | GCN | CNN | GCN | CNN |
| Palm 0 | 74.1 | 82.9 | 74.1 | 93.6 | 75.1 | 71.7 | 74.5 | 81.2 |
| Palm 90 | 75.1 | 70.8 | 78.5 | 85.8 | 70.9 | 51.5 | 74.5 | 64.3 |
| Palm 45 | 77.4 | 76.3 | 77.4 | 86.0 | 78.3 | 63.9 | 77.8 | 73.4 |
| Average | 75.5 | 76.5 | 76.6 | 88.4 | 74.7 | 61.8 | 75.6 | 72.6 |
| Accuracy | Precision | Recall | F1 | |||||
|---|---|---|---|---|---|---|---|---|
| Surface | ConvLSTM | LSTM | ConvLSTM | LSTM | ConvLSTM | LSTM | ConvLSTM | LSTM |
| Rigid & smooth | 82.6 ± 1.2 | 82.5 ± 2.0 | 80.9 ± 3.3 | 82.6 ± 3.7 | 82.3 ± 2.8 | 82.7 ± 6.7 | 81.1 ± 2.5 | 81.8 ± 4.3 |
| Rough | 73.5 ± 0.7 | 73.8 ± 2.0 | 72.0 ± 2.8 | 74.7 ± 4.2 | 73.7 ± 2.1 | 74.1 ± 7.9 | 72.5 ± 2.1 | 73.5 ± 4.1 |
| Little contact | 70.9 ± 1.9 | 72.4 ± 3.6 | 72.3 ± 4.0 | 75.5 ± 4.1 | 70.7 ± 6.6 | 72.8 ± 9.1 | 70.9 ± 4.9 | 72.7 ± 5.5 |
| Average | 75.5 ± 1.2 | 76.1 ± 2.4 | 75.0 ± 3.3 | 77.5 ± 4.0 | 75.4 ± 3.4 | 76.4 ± 7.8 | 74.7 ± 3.0 | 75.9 ± 4.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zapata-Impata, B.S.; Gil, P.; Torres, F. Tactile-Driven Grasp Stability and Slip Prediction. Robotics 2019, 8, 85. https://doi.org/10.3390/robotics8040085
Zapata-Impata BS, Gil P, Torres F. Tactile-Driven Grasp Stability and Slip Prediction. Robotics. 2019; 8(4):85. https://doi.org/10.3390/robotics8040085
Chicago/Turabian StyleZapata-Impata, Brayan S., Pablo Gil, and Fernando Torres. 2019. "Tactile-Driven Grasp Stability and Slip Prediction" Robotics 8, no. 4: 85. https://doi.org/10.3390/robotics8040085
APA StyleZapata-Impata, B. S., Gil, P., & Torres, F. (2019). Tactile-Driven Grasp Stability and Slip Prediction. Robotics, 8(4), 85. https://doi.org/10.3390/robotics8040085