1. Introduction
In recent years, the prices of industrial cobots (and robots) have dropped significantly. Due to this, not the cobot itself, but programming a cobot has become the biggest expense, since a specialized engineer is required [
1,
2]. Replacing that engineer with untrained workers (without programming skills) would reduce the cost of production, but then it must also become possible for these workers to program the cobots. In such a setting, where a cobot is collaborating with a human [
3,
4], it would be useful if the human could easily optimize the behavior of his cobot partner. To achieve this, cobots should be able to learn from knowledge given by untrained users, who need a natural and intuitive communication channel to transfer their human knowledge, which is interpreted by the cobot.
In this paper, learning is done using Reinforcement Learning (RL), where an agent learns new behaviors by performing actions in its environment, and optimizes its behavior based on rewards from this environment. More specifically, Interactive Reinforcement Learning (IRL) is used, where the reward signal of the RL agent is not only dependent on the environment and the state, but also on the advice from a human. IRL results in an optimal productivity because human and cobot work together, while the autonomy of the cobot increases over time and the workload of the human decreases. The advantage of using RL methods is that it remains possible to learn an assembly sequence, even when the complexity of the task increases, resulting in an enormous state-space. This in contrast with an exhaustive search, which in general only works efficiently for smaller assemblies. Currently, a problem with RL is that it requires many interactions with its environment before it can learn a valid policy. This problem is similar with IRL, because it often requires feedback from a human telling it how well the last action was perfomed, which means again many interactions. This way of teaching is not suited for industry, because it is not productive and no operator will want to give feedback for a long time.
We present a novel method that is a solution to the two problems outlined before. First, natural language is a natural and intuitive way of communicating information, because we use it as well for human–human teaching. The method presented here uses advice constraints translated from natural language to cope with the complexity of programming a robot. Second, interaction using advice constraints translated from natural language ensures that the advice only has to be given once, compared to the multiple feedback interactions, as stated before.
The constraint predicates are used to set up a potential function over the entire state space (PBRS). This potential function is used in a simulated environment to solve the interaction problem. A simulated environment makes it possible for the IRL agent to quickly “rehearse” the best assembly plan consistent with the given constraints. The method is based on the programming by demonstration principle, which leverages human advice to increase the learning speed of a cobot. This is the power of IRL: the operator can fill up knowledge gaps of the cobot using advice, while the RL agent is still able to learn tasks that the operator cannot advise on [
5] (e.g., too many possibilities for human to advise on the fastest assembly plan).
This paper focuses on the learning part of the RL agent, and not on the actual interaction between human and cobot. First, the experiments reveal that advice constraints, translated from natural language, is an efficient way of learning from human knowledge compared to two other communication models based on feedback strategies. Afterwards, a user study is performed to show that the IRL agent learns quickly enough to keep up with advice from users and is able to adapt online to a changing knowledge base.
The paper is structured as follows.
Section 2 starts with a summary of the related work.
Section 3 gives a short introduction on reinforcement learning principles.
Section 4 explains how the interaction and learning works.
Section 5 describes experiments, where the novel method of this work is compared to two other methods and tested in a user study.
2. Related Work
In recent years, a new kind of robot has been adopted in industry, the collaborative robot or cobot, which is a robot that can safely work in close proximity to humans. Therefore, it becomes possible to teach cobots by interaction, which has been investigated already. A programming paradigm that can be applied to leverage the knowledge of untrained workers is Programming by Demonstration (PbD). PbD is a programming paradigm in which a cobot is programmed by physically demonstrating to it what to do. PbD can be done on two different levels, namely trajectory and task level programming [
6]. On the
trajectory level [
7,
8,
9,
10,
11], a demonstration consists of a trajectory that is mapped onto a robot trajectory. Some applications already exist that do PbD on the trajectory level (e.g., Emika Franka Panda interface [
12]). On the
task level [
13,
14,
15,
16], demonstrations represent a skill as a sequence of symbolic actions. This paper focuses on the task level, where advice on the assembly will also be viewed as a demonstration.
Kramberger et al. [
17] used human demonstrations, in the form of a sequence of demonstrated actions, and generalized them to all possible valid action sequences. To generate all possible assembly sequences of 10 objects with certainty already requires more than 20 demonstrations. However, the problem is that larger assemblies (more objects) require more demonstrations. Mollard et al. [
18] also started from low-level demonstrations of the assembly task, and afterwards could extract a high-level relational plan of the task. The user is then able to use a GUI to correct the acquired knowledge by refining the high-level plans. The downside is that the user will need to learn how this GUI works, which results in a loss of intuitiveness. In addition, Senft et al. [
19] used human guidance in the field of social robotics to accelerate the learning speed of an agent. These methods require many demonstrations, which is preferably avoided in industry.
The field of reinforcement learning also already uses human knowledge to increase the learning speed. Using feedback [
20] has the advantage to reduce the sample complexity of the RL agent, resulting in fewer states that need to be visited. An improvement on this teaching method is using guidance [
21], where attention direction helps the human teacher to keep the exploration within a more useful portion of the state space. This is similar to an approach taken by G. Thomas et al. [
22], where RL policy learning is improved by using CAD information of the objects to more efficiently learn an assembly task. Their approach focuses on the trajectory level using knowledge from CAD models, while the work presented here focuses on the symbolic level using human knowledge. An additional increase in learning speed can be achieved by using contextual affordances [
23], where the system recognizes the context of the environment and alters the act ion set accordingly.
3. Reinforcement Learning
Reinforcement Learning (RL) [
24] is a learning paradigm in which an agent learns a behavior based on rewards received from interactions with its environment. The RL problem can be defined as a Markov Decision Process (MDP)
, where:
S represents all possible states of the environment and the agent;
A defines all possible actions;
T are the probabilities of the system transitioning from state to for some action a;
is the discount factor, and represents how important long-term rewards are; and
R represents the immediate reward that is given when an action a is taken in state s.
The goal of RL is to find a behavior or policy (
) that maximizes the expected discounted accumulated reward,
:
Temporal difference RL algorithms (e.g., Q-learning [
25]) learn behavior by approximating an action–value function, mapping state–action pairs to the expected discounted reward. In Q-learning, the goodness of an action
a in state
s at episode
t is represented by the fitness value
. Every time the situation
is encountered, a better estimate of the fitness value is calculated using the following rule:
where
is the learning rate, which is a measure of how much new knowledge overwrites the old knowledge. Knowledge is represented by an
table, where every state–action combination is saved with its corresponding fitness value.
3.1. Potential Based Reward Shaping
Reward shaping, derived from behavioral psychology [
26], is a method that employs prior knowledge to kick start the learning process. It uses additional intermediate rewards for completing part of a task. Hence, the additional reward
F is added to the original reward
R:
However, changing the original reward scheme may result in convergence to a suboptimal policy. Ng et al. [
27] showed that policy invariant reward shaping can be achieved if the shaping reward is of the form:
where
is a potential function over the state space. The fact that an interactive RL agent is used here means that the potential functions can change over time as well. On the other hand, Devlin [
28] showed that even dynamic potential-based reward shaping will result in policy invariance. The new update rule is of the form:
With this new update rule, the expected discounted accumulated reward becomes:
Most potential values in Equation (
6) cancel each other out, such that the only remaining potential value is
.
3.2. Hierarchical Reinforcement Learning (HRL)
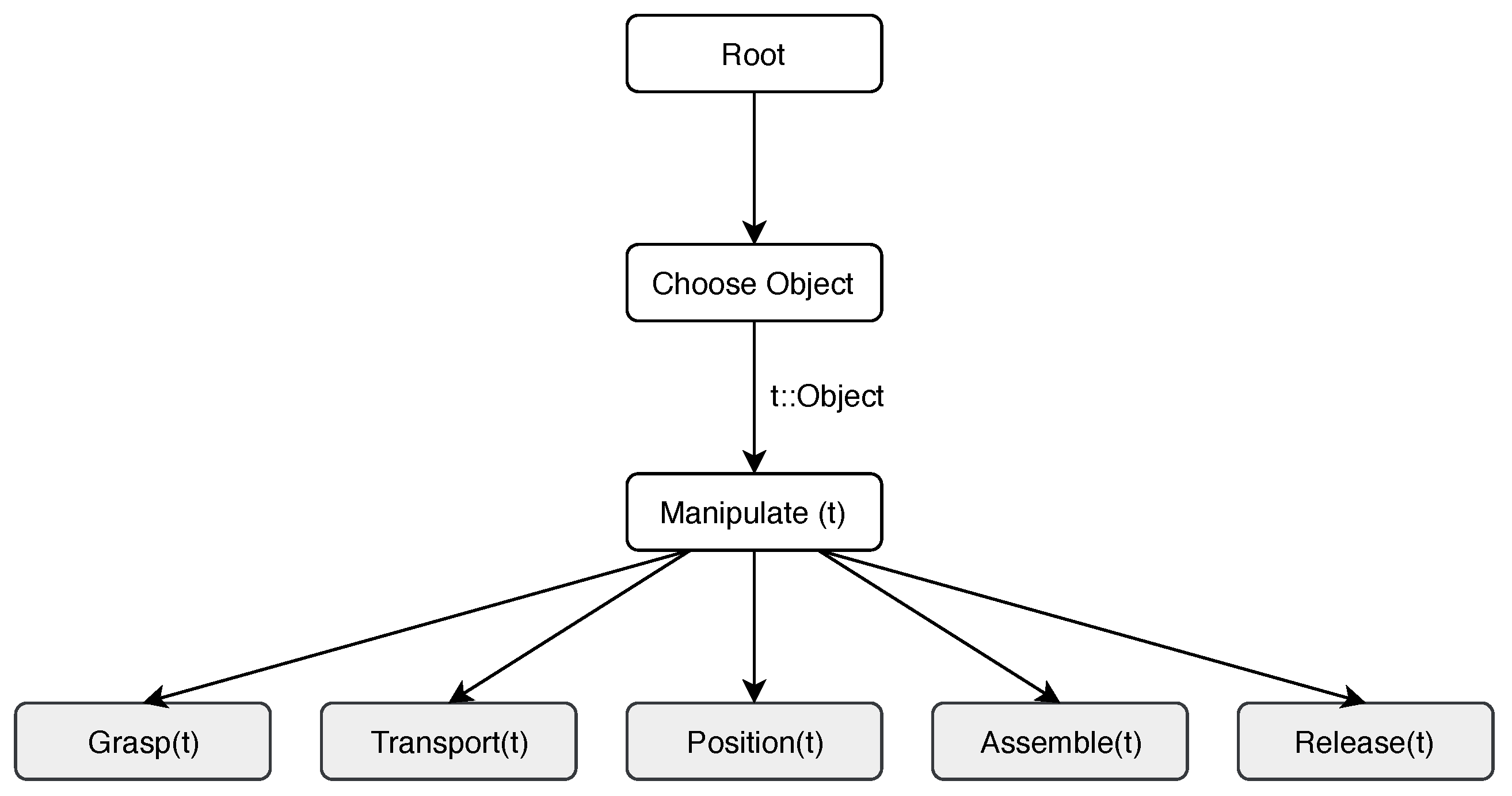
The actions required for an assembly process can be ordered in a two-level hierarchy. Top-level actions concern what object to handle next or, more specifically, the order in which objects are to be assembled. The bottom-level, on the other hand, focuses on what actions are required to assemble a specific object. This natural hierarchical structure of assemblies can be exploited to reduce the total solution space. The Hierarchical Reinforcement Learning (HRL) method used in this work is the MAXQ algorithm [
29], which decomposes the MDP M into a set of subtasks
, where
is the Root of the hierarchy (optimal policy for
is also an optimal policy for
M). The actions taken by
can be a primitive action or a composite action, which in turn can consist of primitive and/or composite actions. Take, e.g., the problem of stacking a blue block on top of a red block. The top level action would be the composite action
Choose_Next_Object(blue_block), which can contain subtasks with primitive actions
search(blue_block), and
Hold (wait for some seconds) and the composite action
Manipulate(blue_block). The composite subtask
Manipulate can use a set of five primitive actions (see
Section 4.1). The entire structure is best visualized in a task graph [
29] (
Figure 1). Here, Root represents subtask
of the task M,
is the subtask on the
Choose Object level and
is the
Manipulate subtask. This HRL method can also be extended with the PBRS principle described in the previous section, where the potential function is defined over all composite tasks (for the complete algorithm, see [
30]).
4. Human Knowledge Transfer System
As stated in the Introduction, the main goal of this work is to use human transferred knowledge to speed up a RL agent. To transfer knowledge to the system, a natural and intuitive communication channel is required, which can be achieved using advice constraints translated from natural language, because this is also used for human–human teaching. Compared to IRL feedback strategies, advice sentences in natural language will have a higher information density and will be applicable to more states at a time in the state space. Thus, one natural sentence can shape the solution space more compared to one interaction in a feedback interaction model (see
Section 5.1).
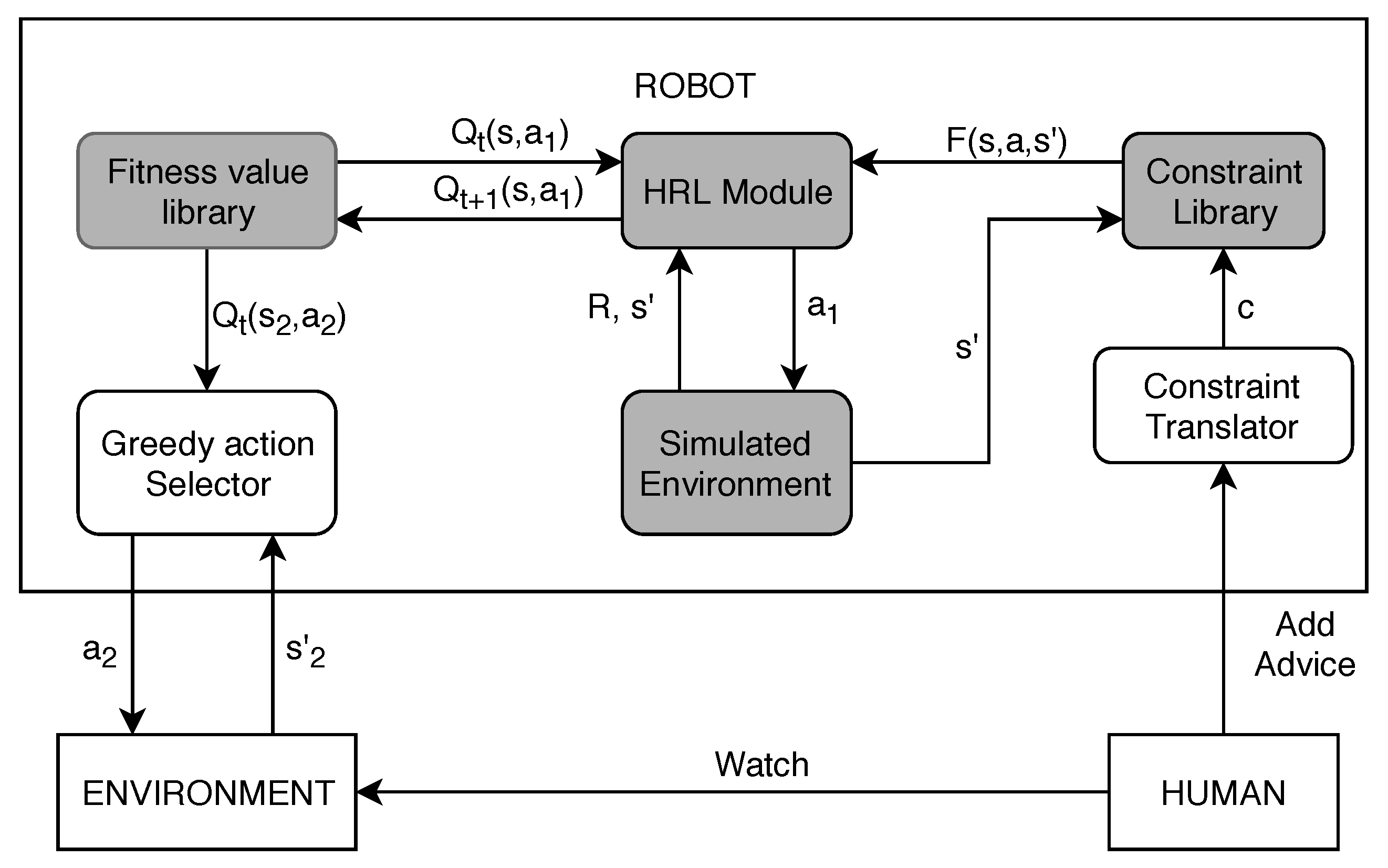
The architecture of the system, shown in
Figure 2, shows two different environments,
ENVIRONMENT and
Simulated Environment.
ENVIRONMENT represents the real world in which the cobot will perform the actual actions. It is this environment that the human watches and, if needed, gives additional guidance to the cobot.
Simulated Environment is an abstraction of the real environment, where only the objects required for the assembly are represented. This environment is meant for the HRL agent (
HRL Module) to learn a behavior that is consistent with the human advice. Learning a behavior in this industrial setting means that the robot learns to generate assembly plans that are consistent with the human given advice constraints. The fitness-values
are stored in a database, and can be used by
Greedy Action Selector to choose the actual actions the cobot will perform in the real world (represented by an action
taken in state
).
The HRL Module works by using the techniques of
Section 3. Performing an action
will pass the
Simulated Environment on to a new state
, with a corresponding reward
R indicating how well this action was. The shaping reward (PBRS)
is calculated using the constraints in the
Constraint Library (see
Section 3.1). The human can add new knowledge by verbally telling the agent the constraint in a natural language sentence, which gets translated in
Constraint Translator to a first-order logic predicate
c. All constraints considered here are precedence constraints (e.g., place the shaft before placing the pendulum).
4.1. Action Set
The actions used in this paper are ordered into a hierarchy (see
Figure 1). The low level primitive actions (bottom row of
Figure 1) used here are a subset of the Therblig action encoding [
31], which is a set of 18 fundamental actions, required for a worker to complete a task. The subset of actions are
Grasp(t),
Transport(t) (move object from point A to point B),
Position(t) (place the object in the required pose),
Assemble(t),
Release(t), and
Manipulate(t). The latter is the composite action that can be a sequence of the five lower level actions. The argument
t represents the object that is currently being manipulated.
When this paper mentions high level actions it means in what order Choose Object chooses the objects. Low level means how Manipulate(t) is built up using the five actions from a level lower. Three actions already have a pre-condition defined. Grasp(t) will only be able in states where the cobot is not holding an object. Release(t) and Transport(t) will only be possible in states where the cobot is holding the object.
4.2. State Representation
The fact that the RL agent here is a hierarchical learner with two levels means that also the states will be represented in two different ways. The top level aims at representing which objects are to be handled next. As a result, the state representation on this level will contain for every object in the assembly the state of the object. The state of a specific object can be either “default” (part is still in its starting position) or “finished” (part has been assembled). On the low level, the state should represent which steps are required to assemble a specific object. This can be done with just one value, assuming that only the current state is represented, and no previous states of the object. There are six possible values on this level, five possible actions, and one starting state (“default”). The entire state of a specific object can be represented by two values: (1) the state of the object; and (2) the value identifying the object.
4.3. Reward Signal
The only function of the reward signal (R) at this point is to make sure that the assembly plans are as short as possible, meaning that the goal needs to be achieved with as few actions as possible. This is accomplished by giving a negative reward () every time an action is taken. Additionally, the agent is also rewarded when it reaches the final state of an object (“finished”). An extra reward of 1 is given in this state, which results in a major improvement in convergence speed.
4.4. Potential Function
The potential function of state
s is calculated by evaluating constraint
i and summing over all constraints. Assuming there is a set of constraints
, the potential function is calculated as:
where,
with
w the weight given to the violated constraint. Thus, from
Section 3.1, we know that the fitness value, in a state that violates
, will be subtracted with a value
w. For now, all constraints get the same weight, but it is also possible to give lower weights to constraints that are less important.
4.5. Learning Rate
The fact that constraints can be added in an online fashion, means that the potential function
will change over time [
28]. Therefore, the learning rate will be reset after a new constraint has been added, to accelerate convergence to an optimal policy. The RL agent was tested with both a constant learning rate (
) and with a learning rate that resets. It showed that convergence with the constant learning rate was much slower when new advice was added. Thus, the learning rate will change according to [
32]:
where
is a parameter that counts how many times this state–action pair has been visited, and
. The first time a state–action pair is visited, the learning rate will be equal to 1, meaning that the old value of this pair will be entirely overwritten by the new value.
5. Experiments
Thus far, the presented IRL-PBRS method is capable of interpreting human advice, given as a list of logical predicates, aimed at focusing the solution space to a smaller and more useful part of the entire state space. Two main requirements were identified for a human knowledge transfer system. Firstly, the interaction between human and cobot should be as efficient as possible, meaning that the same information should be transferred while using the fewest interactions. Secondly, the transferred information should be interpreted quickly enough, which means the IRL agent should be able to find a valid assembly plan before new knowledge is given by the user.
The two experiments presented here aimed at examining whether these two requirements are satisfied by the IRL-PBRS method. The first experiment was a comparison between using advice as a communication model and using feedback as a communication model. The next section presents a user study, where participants were asked to advise a cobot on how to perform an assembly.
The benchmark used for both experiments was the Cranfield Benchmark Problem [
33], as shown in
Figure 3. The problem consists of the assembly of a pendulum, in which the placement of some pieces are a prerequisite for others, and for some pieces the order of placement is not important. It is assumed that the position of the objects is known in advance, as well as the trajectories linked with the actions on the objects.
5.1. Simulated Experiment
In this experiment, the IRL-PBRS method was compared to two other communication models. The communication models were compared based on two characteristics of efficient learning from communication: (1) how many interactions were required to get information across, or similarly how much could be learned from one interaction; and (2) how quickly it could adapt its behavior based on the information of an interaction. All of them use the same MaxQ algorithm, with the same state space. The only difference is that IRL-FB and IRL-FBWS methods use feedback instead of advice.
IRL-FB: IRL with only binary feedback (0 if the next action of the cobot is valid, otherwise). The human will only interact with the cobot when the next action is incorrect. The agent will also get a small punishment () for every action it takes.
IRL-FBWS: IRL with the same binary feedback, but the human can now suggest a better action if the next action of the cobot is invalid. The agent will also get a small punishment () for every action it takes.
IRL-PBRS: The method presented in this paper.
For this experiment, all knowledge was assumed to be present before learning starts (knowledge about the assembly did not change during the simulation), and the process was fully constrained, meaning that only one assembly sequence could satisfy the constraints. Hence, for the IRL-PBRS method, eight separate constraints were required. Similarly, for IRL-FB and IRL-FBWS, a human was simulated who interacted with the IRL agent. The simulated human was also assumed to have all knowledge before the simulation starts, and he did not change his knowledge during the simulation. To suggest a better next action in IRL-FBWS, the simulated human listed all valid next actions and suggested a random action from that list. If no actions were possible (e.g., if the agent were assembling the wrong object, any next action with that object would be invalid), then a random action was suggested. The IRL agent tried to converge to a valid assembly sequence, while still using the fewest actions to reach its goal (i.e., all objects are in their final position).
5.1.1. Results
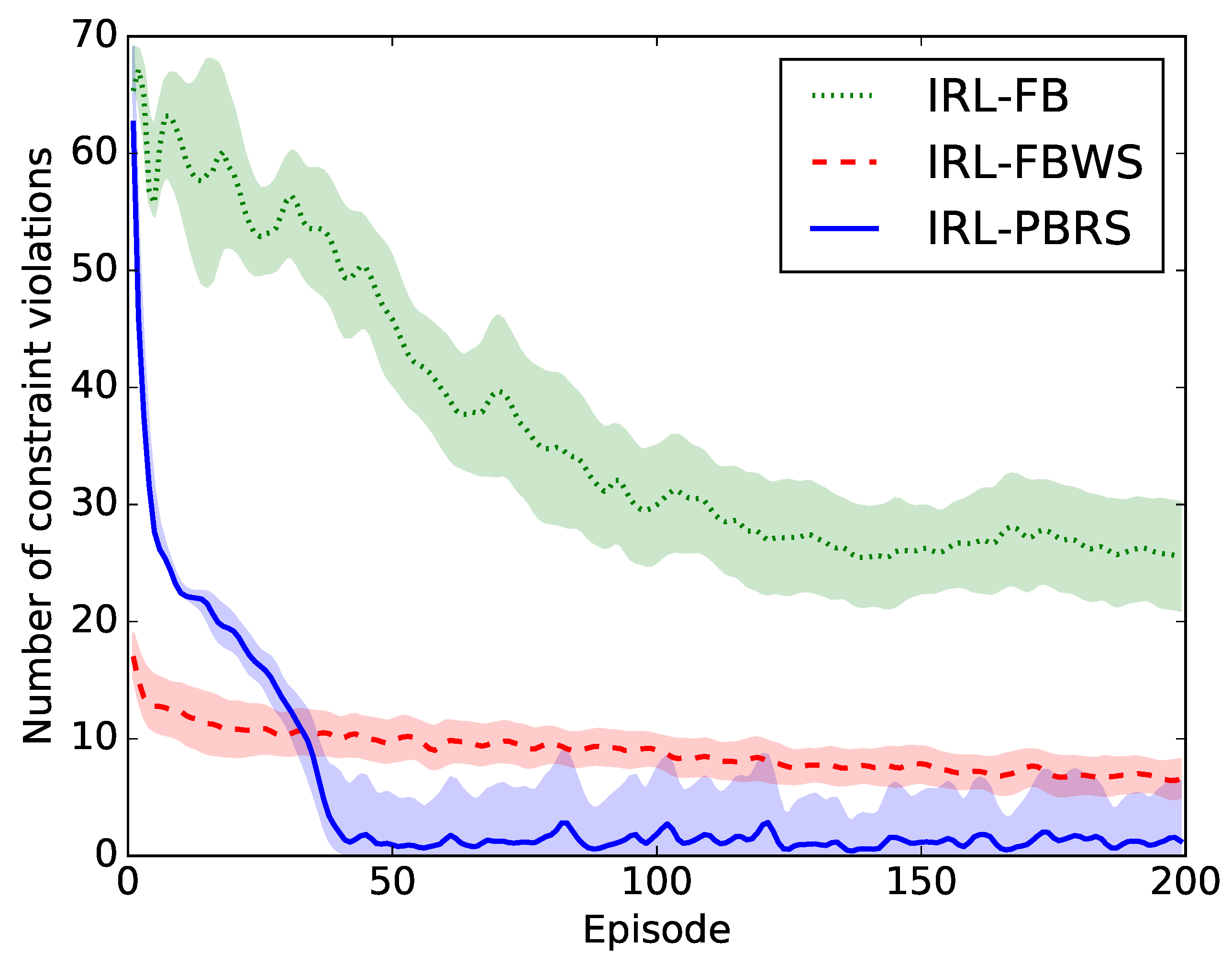
The compared results are shown in
Figure 4. An episode in this paper is defined as the agent performing the entire assembly once in the simulated environment and lasts on average
s. In the graph, for every action taken in an episode, a constraint violation of one is added if at least one constraint is violated in the resulting next state. This means, in the beginning, when the agent still takes too many actions, the number of violations can be a lot higher.
The result shows that IRL-FB (green) is not an option because it does not converge to a valid policy within a reasonable amount of time. IRL-FBWS (red) on the other hand converges more quickly, but still more slowly than IRL-PBRS.
5.1.2. Discussion
The slow convergence of the IRL-FB and IRL-FBWS methods is partly because of the MAX-Q algorithm, which only uses rewards to update the fitness function on the lowest level actions (bottom row of
Figure 1). This means that there is a step between learning actions of the higher level, because the fitness of high level actions is dependent on the fitness of the lower level actions. Nonetheless, IRL-FBWS is still able to converge more quickly because of the suggestions given by the user. In every state an action is taken, the agent gets feedback on how good that action was, plus a correctly suggested action if the current choice is invalid.
IRL-PBRS partly solves this problem by only applying the user advice on the level it is required. Thus, advice on a higher level (e.g., “place the green part after the blue parts”) will only have an influence on the potential function of the higher level. On the other hand, if the advice regards the actions on one specific object, (e.g., “position the gripper before grasping the blue block”), it will only be applied on the potential function of the lower level.
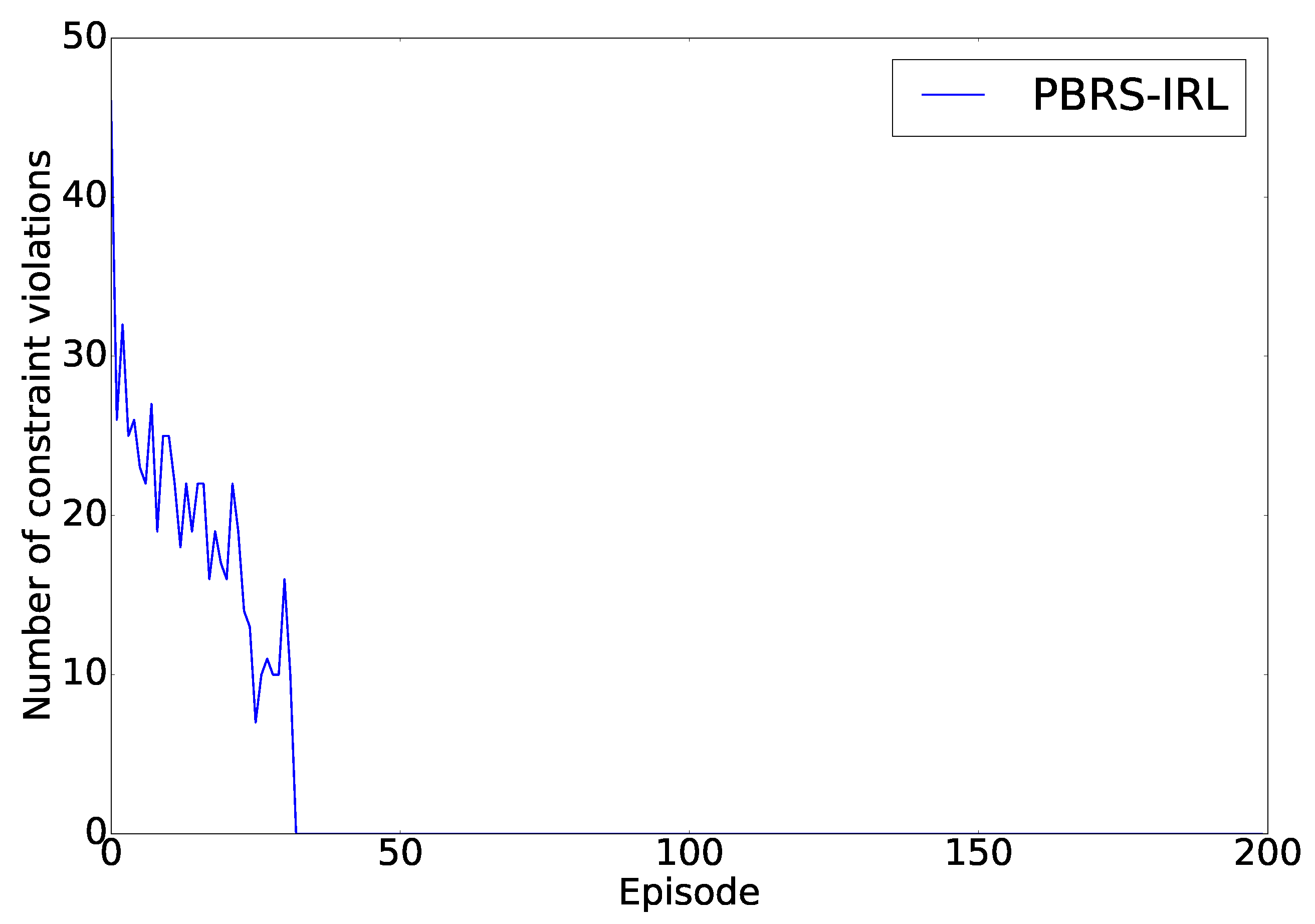
Note that the number of constraint violations never completely converge to zero. This is a consequence of the
-greediness of the action selection. In every state, the agent will normally take the action with the best fitness value, but it can also take a random action with a probability of 1%. This random action is required for exploration, but will result in the agent going in invalid states after the assembly has been learned. This can be seen in
Figure 5 where the number of constraint violations are shown as seen from the
Greedy action Selector. Here,
, thus, in every state, it will select the action with the highest fitness value, where these values are calculated in the
HRL Module. The figure shows that after the agent converges, after around 35 episodes, it will no longer generate assembly plans that contain constraint violations.
The figure also shows that at episode 0, the number of constraint violations is considerably higher for IRL-FB and IRL-PBRS, compared to IRL-FBWS. The reason of this behavior is a result of the suggested actions by the user. With IRL-FB and IRL-PBRS, the agent first has to learn by himself how to reach the goal as quickly as possible. IRL-FBWS on the other hand gets better suggestions from the human, thus it will know from the first episode that it has to assemble the object as quickly as possible. The initial convergence (until episode 100) of IRL-FB is also because the agent is learning a policy with fewer actions, but afterwards it converges at about the same speed as IRL-FBWS.
Lastly, since the cobot is meant to take some of the cognitive load from the human operator (minimize the number of required interactions), IRL-FB and IRL-FBWS would not be an adequate solution. IRL-FB requires around 28 interactions on average per episode and IRL-FBWS about four interactions per episode. Compared with the eight advice constraints (in total) required to fully constrain this assembly task, it becomes apparent that IRL-PBRS is a better way to transfer this kind of knowledge to an industrial cobot.
Hence, this experiment shows that the IRL-PBRS strategy will generate valid assembly plans more quickly than the other two communication models, and all this with the fewest interactions.
5.2. User Study
The presented method was also tested in a user study, to show that the IRL-PBRS method learns quickly enough to keep up with advice from humans and is able to adapt online to changing knowledge from the user, which means that the agent should converge to zero constraint violations similarly quickly as new constraints are given by the user. The study was performed using the Wizard of Oz (WOZ) method [
34], because the speech recognition software available was not robust enough. Thus, the focus was on the grey components of
Figure 2. The constraints are given in natural English language by the user, but now the experimenter plays the role of the
Constraint Translator.
The WOZ experiment was set up as shown in
Figure 6 (Video:
http://y2u.be/NMLs7GNWtkc). Participants were presented with a graphical programming interface (see
Figure 7) that contained a small manual of the advice they are allowed to give and a visual representation of the advice they already gave. All advice was in the form of temporal constraints on the objects, meaning which objects should precede which other objects in the assembly sequence. The assembly was not taking place in realtime, but the knowledge given by the user was visualized in the form of a precedence graph (see bottom left window in
Figure 7), where a line between two objects means that the object on the left should be assembled before the object on the right. The presented video shows the assembly being performed by the robot. The trajectories the robot follows for this assembly are programmed by the user, using a record and replay method, where the user demonstrates the trajectory once and the robot executes the identical trajectory.
After the participants were given a 5 min tutorial on the interface, they were asked to program two different assemblies. First, they were asked to program the assembly of a pyramid of blocks, which was a training exercise to let them get used to the interface. Afterwards, they were asked to program the assembly of the Cranfield Benchmark Problem. Only the results of this second assembly are reported here.
The goal in each assembly was to program the two assemblies as generally as possible. This means that they had to give enough constraints such that all assembly sequences not violating any of these constraints were still physically possible (under-constraining). However, not too much such that still valid assembly sequences were removed from the solution space (over-constraining). The interface shows a robot arm with a green background, indicating that the user was allowed to give additional advice. After an advice sentence was uttered, the background changed from green to grey, indicating that the advice was being interpreted. When the interpretation was finished the color changed back to green, indicating that the user could give additional advice. All constraints were added to the Constraint Library and taken into account at the time they were added (either between or during a learning episode).
Ten participants were invited for the study. They were fellow researchers between the ages of 23 and 47 (seven male and three female) with a technical background. All subjects gave their informed consent for inclusion before they participated in the study. The experiment was performed on an Intel® Core™ i7-7700.
5.2.1. Results
Table 1 shows the results of the user study. The table shows that users only needed 3–8 interactions to program the assembly of 9 objects, with a minimum of 34–89 episodes between interactions, depending on the interaction speed of the user. An interaction is defined as the user uttering one advice sentence (spoken natural language), but it can be translated to multiple constraints. The advice given by the user constrained the total number of assembly sequences that still satisfied the constraints. When the assembly was minimally constrained, while still physically assemblable, there were in total 840 possible assembly sequences. Participant 5 gave the most general advice, while Participants 4, 9 and 10 under-constrained the assembly. The rest of the participants over-constrained the assembly.
The table also shows also the maximum number of episodes required for the IRL-PBRS method to converge to a valid assembly plan. Convergence is defined as the episode in which 90% of the trials generate an assembly plan without advice violations. This value was chosen because of the epsilon greedy behavior of the IRL agent. In every state, there is a probability of 1% that the agent chooses a random next action, and this repeated for all objects. Of course, when the complexity of the task increases, so will the convergence time. However, this will not be as bad compared to, e.g., performing an exhaustive search.
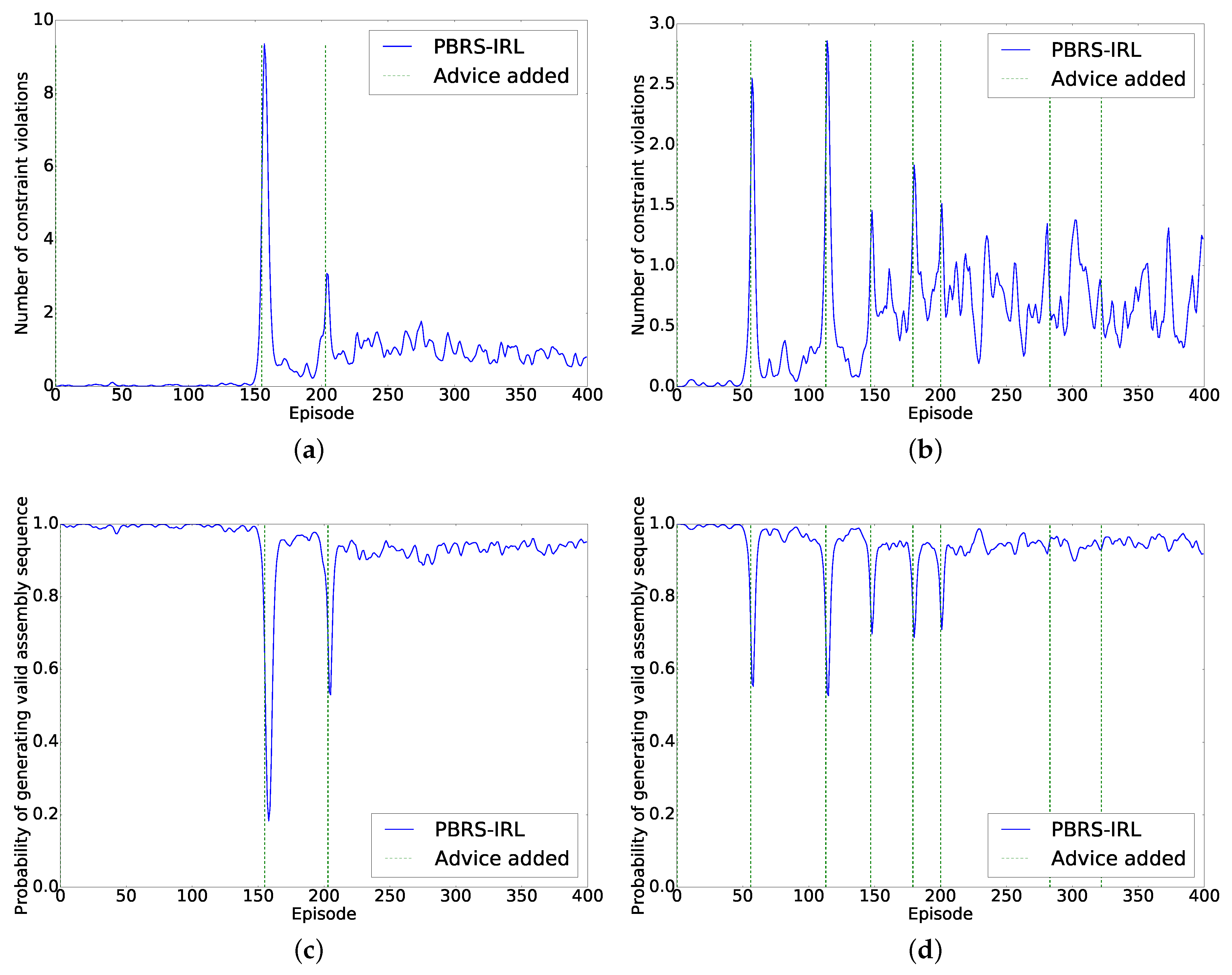
Figure 8 plots the number of constraint violations per episode for Participants 2 and 5, respectively, where the green dotted line indicates the episode at which a new constraint has been given. Their respective advice sentences are given in
Table 2.
5.2.2. Discussion
From the results in
Table 2, it becomes visible that not all participants interacted in the same way. First, in general, participants quickly understood how to advise the system. The over-constraining of most participants was because they did not immediately grasped the assembly. Possibly a better familiarity with the benchmark would have avoided this. Participant 5 under-constrained the assembly, but afterwards it became clear that he interpreted the GUI wrongly. In addition, Participants 9 and 10 under-constrained the assembly, because they interpreted the assembly differently and forgot to give one constraint.
Second, Participant 2 gave advice sentences with a higher information density (average of 10 constraints per interaction) compared to Participant 5 (average of 2.25 constraints per interaction). The difference in information density is visible in the episodes immediately after a constraint is added. The jump in number of constraint violations is higher for Participant 2 than for Participant 5. This is also slightly visible in the maximum number of episodes required until the agent converges, which is slightly higher for the users that used more complex advice sentences. Additionally, when looking at the total programming time, which is the time the user was able to interact with the robot (background of robot arm in the interface was green), the difference lies between 22 and 113 while the number of interactions is quite similar across all users, indicating that the main difference in programming time lies in thinking about the assembly and advice sentences. The total task time, which is the total programming time plus the time the experimenter took to interpret the constraints, averaged at around 110 s.
Participant 2 over-constrained the assembly compared to Participant 5. Nonetheless, after the agent converged, there is no real difference in average number of constraint violations for Participants 2 and 5, independently from the number of constraints given by the user (30 and 18, respectively). This shows the power of RL compared to, e.g., an exhaustive search, which will be more dependent on the number of constraints.
Another noteworthy point, visible with both participants, is that there was no spike in number of constraint violations when they added their first advice sentence, or when Participant 5 added the last two constraints. This is a result of what T. Dietterich [
29] defined as an
ordered GLIE policy, meaning the agent converges to a greedy policy that imposes an arbitrary fixed order
on the available actions and breaks ties in favor of the action that appears earliest in that order. Assembling the yellow object was an action that appeared earlier in the action order, thus initially the agent will choose this object anyways, independent of the constraints forcing it to do so. A similar reasoning applies to the last two constraints given by Participant 5. In the action order, the action to assemble the blue objects comes before the action to assemble the green object and the assembly of the purple object is also before the white object. Thus, the agent will always prefer a policy where blue is assembled before green and white is assembled before purple, in case there are no constraints forcing the opposite.
In conclusion, when comparing the maximum number of episodes required until convergence with the minimum number of episodes between interaction, it is clearly visible that the agent converges quickly enough to keep up with the advice given by users and is able to cope with changing knowledge from the user.
6. Conclusions
Reprogramming a cobot is a costly process, because a specialized engineer is required. An improvement would be if untrained workers could help a cobot to learn an assembly sequence by interaction in the form of advice. This paper investigates the most optimal communication model to transfer knowledge from a user and use that as knowledge for the cobot. The presented method (IRL-PBRS) is based on Interactive Reinforcement Learning (IRL), where a potential based reward shaping (PBRS) strategy is used to find the optimal assembly sequence without violating any advice from the user, where the advice is given in natural English sentences. The method is capable of receiving new advice in an interactive manner and use that to focus learning on a more useful part of the state space. The experiments show that the communication model based on advice constraints, translated from natural language, is more efficient, because it requires the fewest interactions while still converging more quickly than other communication models. In the user study, it is clear that the IRL-PBRS method learns quickly enough to keep up with user given advice and is able to cope with changing knowledge from the user.
Author Contributions
Conceptualization, J.D.W. and B.V.; methodology, J.D.W.; software, J.D.W.; validation, J.D.W. and A.D.B.; formal analysis, J.D.W.; investigation, J.D.W.; resources, J.D.W.; data curation, J.D.W.; writing—original draft preparation, J.D.W.; writing—review and editing, J.D.W., A.D.B., I.E.M., G.V.d.P., and B.V.; visualization, J.D.W.; supervision, B.V. and A.N.; project administration, B.V.; and funding acquisition, B.V.
Funding
This research was funded by SBO Yves and Flanders Make Proud (PROgramming by User Demonstration) and by the Flemish Government under the program ”Onderzoeksprogramma Artificiele Intelligentie (AI) Vlaanderen. Greet Van de Perre has an FWO postdoc and Albert De Beir a FWO PhD mandate.
Conflicts of Interest
The authors declare no conflict of interest. The funding sponsors had no role in the design of the study or interpretation of data; in the writing of the manuscript and in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| RL | Reinforcement Learning |
| IRL | Interactive Reinforcement Learning |
| PBRS | Potential Based Reward Shaping |
| HRL | Hierarchical Reinforcement Learning |
| WOZ | Wizard of Oz |
References
- Group, B.C. The Robotics Revolution: The Next Great Leap In Manufacturing. Available online: https://www.bcg.com/publications/2015/lean-manufacturing-innovation-robotics-revolution-next-great-leap-manufacturing.aspx (accessed on 16 December 2019).
- Kober, J.; Peters, J. Imitation and Reinforcement Learning. IEEE Robot. Autom. Mag. 2010, 17, 55–62. [Google Scholar] [CrossRef]
- El Makrini, I.; Elprama, S.A.; Van den Bergh, J.; Vanderborght, B.; Knevels, A.; Jewell, C.I.C.; Stals, F.; De Coppel, G.; Ravyse, I.; Potargent, J.; et al. Working with Walt: How a Cobot Was Developed and Inserted on an Auto Assembly Line. IEEE Robot. Autom. Mag. 2018, 25, 51–58. [Google Scholar] [CrossRef]
- El Makrini, I.; Merckaert, K.; De Winter, J.; Lefeber, D.; Vanderborght, B. Task allocation for improved ergonomics in Human-Robot Collaborative Assembly. Interact. Stud. 2019, 20, 103–134. [Google Scholar] [CrossRef]
- Kormushev, P.; Calinon, S.; Caldwell, D.G. Reinforcement Learning in Robotics: Applications and Real-World Challenges. Robotics 2013, 2, 122–148. [Google Scholar] [CrossRef]
- Skoglund, A. Programming by Demonstration of Robot Manipulators. Ph.D. Thesis, Orebro University, Orebro, Sweden, 2009. [Google Scholar]
- Aleotti, J.; Caselli, S. Robust trajectory learning and approximation for robot programming by demonstration. Robot. Auton. Syst. 2006, 54, 409–413. [Google Scholar] [CrossRef]
- Calinon, S. A tutorial on task-parameterized movement learning and retrieval. Intell. Serv. Robot. 2016, 9, 1–29. [Google Scholar] [CrossRef]
- Field, M.; Stirling, D.; Pan, Z.; Naghdy, F. Learning Trajectories for Robot Programing by Demonstration Using a Coordinated Mixture of Factor Analyzers. IEEE Trans. Cybern. 2016, 46, 706–717. [Google Scholar] [CrossRef] [PubMed]
- Melchior, N.A.; Simmons, R. Graph-based trajectory planning through programming by demonstration. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012; pp. 1929–1936. [Google Scholar]
- Zhu, Z.; Hu, H. Robot Learning from Demonstration in Robotic Assembly: A Survey. Robotics 2018, 7, 17. [Google Scholar]
- Emika Franka Panda Interface. Available online: https://www.franka.de/panda/ (accessed on 30 September 2019).
- Ahmadzadeh, S.R.; Paikan, A.; Mastrogiovanni, F.; Natale, L.; Kormushev, P.; Caldwell, D.G. Learning symbolic representations of actions from human demonstrations. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 3801–3808. [Google Scholar]
- Lambrecht, J.; Kleinsorge, M.; Rosenstrauch, M.; Krüger, J. Spatial Programming for Industrial Robots through Task Demonstration. Int. J. Adv.Robot. Syst. 2013, 10, 254. [Google Scholar] [CrossRef]
- Stenmark, M.; Topp, E.A. From Demonstrations to Skills for High-level Programming of Industrial Robots. In AAAI Fall Symposium Series 2016; AAAI Press: Palo Alto, CA, USA, 2016; pp. 75–78. [Google Scholar]
- Zhang, J.; Wang, Y.; Xiong, R. Industrial robot programming by demonstration. In Proceedings of the 2016 International Conference on Advanced Robotics and Mechatronics (ICARM), Macau, China, 18–20 August 2016; pp. 300–305. [Google Scholar]
- Kramberger, A.; Piltaver, R.; Nemec, B.; Gams, M.; Ude, A. Learning of assembly constraints by demonstration and active exploration. Ind. Robot Int. J. 2016, 43, 524–534. [Google Scholar] [CrossRef]
- Mollard, Y.; Munzer, T.; Baisero, A.; Toussaint, M.; Lopes, M. Robot programming from demonstration, feedback and transfer. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1825–1831. [Google Scholar]
- Senft, E.; Baxter, P.; Kennedy, J.; Lemaignan, S.; Belpaeme, T. Supervised autonomy for online learning in human-robot interaction. Pattern Recognit. Lett. 2017, 99, 77–86. [Google Scholar] [CrossRef]
- Knox, W.B.; Stone, P. Interactively Shaping Agents via Human Reinforcement: The TAMER Framework. In Proceedings of the Fifth International Conference on Knowledge Capture, Redondo Beach, CA, USA, 1–4 September 2009; pp. 9–16. [Google Scholar]
- Thomaz, A.L.; Breazeal, C. Reinforcement Learning with Human Teachers: Evidence of Feedback and Guidance with Implications for Learning Performance; AAAI Press: Palo Alto, CA, USA, 2006; Volume 1. [Google Scholar]
- Thomas, G.; Chien, M.; Tamar, A.; Ojea, J.; Abbeel, P. Learning Robotic Assembly from CAD. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 1–9. [Google Scholar] [CrossRef]
- Cruz, F.; Twiefel, J.; Magg, S.; Weber, C.; Wermter, S. Interactive reinforcement learning through speech guidance in a domestic scenario. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; pp. 1–8. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Introduction to Reinforcement Learning, 1st ed.; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Watkins, C. Learning From Delayed Rewards. Ph.D. Thesis, King’s College, Cambridge, UK, 1989. [Google Scholar]
- B.F. Skinner Foundation. The Behavior of Organisms: An Experimental Analysis; B.F. Skinner Foundation: Cambridge, MA, USA, 1938. [Google Scholar]
- Ng, A.Y.; Harada, D.; Russell, S.J. Policy Invariance Under Reward Transformations: Theory and Application to Reward Shaping. In Proceedings of the Sixteenth International Conference on Machine Learning, Bled, Slovenia, 27–30 June 1999; pp. 278–287. [Google Scholar]
- Devlin, S.; Kudenko, D. Dynamic Potential-based Reward Shaping. In Proceedings of the 11th International Conference on Autonomous Agents and Multiagent Systems, Valencia, Spain, 4–8 June 2012; Volume 1, pp. 433–440. [Google Scholar]
- Dietterich, T.G. Hierarchical Reinforcement Learning with the MAXQ Value Function Decomposition. J. Artif. Int. Res. 2000, 13, 227–303. [Google Scholar] [CrossRef]
- Gao, Y.; Toni, F. Potential Based Reward Shaping for Hierarchical Reinforcement Learning. In Proceedings of the 24th International Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015; pp. 3504–3510. [Google Scholar]
- Gilbreth, F.B.; Carey, E.G. Cheaper by the Dozen; Thomas Y. Crowell Company: New York, NY, USA, 1948. [Google Scholar]
- Even-Dar, E.; Mansour, Y. Learning Rates for Q-learning. J. Mach. Learn. Res. 2004, 5, 1–25. [Google Scholar]
- Collins, K.; Palmer, A.J.; Rathmill, K. The Development of a European Benchmark for the Comparison of Assembly Robot Programming Systems. In Robot Technology and Applications; Springer: Berlin/Heidelberg, Germany, 1985; pp. 187–199. [Google Scholar]
- Kelley, J.F. An Empirical Methodology for Writing User-Friendly Natural Language Computer Applications. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Boston, MA, USA, 12–15 December 1983; pp. 193–196. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).