1. Introduction
The compliance properties of industrial robots are very important for many industrial applications, such as automatic robotic assembly and material removal processes (e.g., machining and deburring). On the one hand, in robotic assembly, joint compliance can be useful for compensating dimensional errors in the parts to be assembled; on the other hand, in material removal processes, a low Cartesian compliance (high stiffness) of the end-effector is required. Indeed, still very few robots have been applied in this economically important application area [
1] mainly due to their low stiffness. Moreover, the compliance properties of robots appear very important in emerging fields such as flexible assembly systems [
2,
3] and collaborative robotics [
4].
From a static point of view, low stiffness causes imprecise products, due to the robot deflections during the robotic task. From a dynamic point of view, low frequency chatter vibrations [
5,
6,
7] can be induced when low-stiffness robots are used, with an impairment in the quality of the machined surface. Moreover, induced vibrations cause a reduction of tool life and can damage robot joint transmission.
In particular, the low joint stiffness of the robot is one of the main issues in using robotic machining instead of CNC machining. Indeed, it is well established in the literature (see, for example, [
8]) that the dominant contribution factor for a large displacement of the robot end-effector is joint compliance (mainly due to gear transmission elasticity), while link flexibility can be neglected. Moreover, the stiffness of an industrial robot is usually on the level of 10
6 N/m (with a base natural frequency of robot around 10 Hz), while a standard CNC machine has stiffness on the level of 10
8 N/m (with a base natural frequency of several hundred Hz or even more than 1000 Hz) [
5]. Sometimes, combinations of serial and parallel kinematic chains have been proposed to increase robot stiffness [
9].
The static force/torque-deformation experiments and identification are widely used to obtain the joint stiffness of industrial robots with good accuracy [
10]. During the static experiments, a set of forces/torques is applied to the robot end-effector (or to a single joint) in different robot configurations, while the displacement sensors (e.g., vision system, CMM, or laser sensors) measure the steady-state deformation of the end-effector. Therefore, the Cartesian stiffness of the robot can be calculated. Then, through the analytical relation between the joint and Cartesian stiffness based on the kinematic model of robot, many types of identification methods (e.g., least squares or genetic algorithms) can be employed to obtain the joint stiffness. Most of the works in the literature (e.g., see [
8,
11,
12,
13,
14]) neglect link flexibility and identify the joints’ rotational stiffness (modeled with linear rotational springs) using this method. In [
15], the robotic arm is modeled considering rigid links and three lumped rotational springs for each joint to take into account joint compliance, bearings compliance, and link deflections, which are all identified with the above method. In [
16], an analysis approach in which both joint and link stiffness are considered is presented.
It is worth mentioning that in [
13], the identified joint stiffnesses are then used in an analytical model, in which natural frequencies and mode shapes are validated through modal testing experiments. In particular, a good match is demonstrated between the first two experimental natural frequencies and related mode shapes and the corresponding ones predicted by the analytical model.
In [
17], experimental modal analysis is used to identify the joint and base stiffness of an industrial robot represented with a four-degrees-of-freedom (four-DOF) planar model.
In robotic processes, the directions along which the robot arm is compliant are very important. The stiffness matrix in the joint space does not directly give this information; moreover, for a serial robot, the stiffness matrix in the Cartesian space is not diagonal and it is configuration-dependent. This means that the force and deformation in the Cartesian space are coupled (e.g., a force applied in one direction will cause a deformation in all possible directions) and this can generate some counter-intuitive results. Moreover, due to the difference in compliance in different directions, machining accuracy can be different in different directions.
Since the end-effector of the robot, which is grasping a tool or an object, can be considered a rigid body mounted on the compliant robot, the basic ideas of the screw theory [
18] can be adopted to describe its motion.
In this paper, first, a novel method for the identification of robot stiffness is presented (
Section 2). It is based on the selective excitation of modes of vibration that chiefly involve only one joint. Since in this specific case modal stiffness coincides with joint stiffness, the latter can be identified from the measured natural frequency and the calculated value of moment of inertia. A serial six-DOF robot is considered (Omron Adept Viper s650), since it is representative of industrial robots used for a wide range of operations. Then, a new method for representing linear and rotational compliance using the concept of screw or Mozzi axis is presented (
Section 3). The proposed method is a useful tool to understand how the robot deforms with respect to the working surface, and to highlight the joints that give the largest contribution to robot compliance in specific configurations. Furthermore, robot configurations that place the Mozzi axis in the most favorable position with respect to the working surface can be found. Finally, the compliance properties of the tested robot are analyzed with the proposed method in different robot configurations (
Section 4), and conclusions are drawn.
2. Identification
2.1. Testing Equipment and Method
Stiffness (or compliance) properties of robot joints are usually measured by means of static tests [
13] carrying out measurements in the Cartesian space. Then, a mathematical model is used to correlate force vector
and deformation vector
in Cartesian space with the stiffness matrix
in the joint space.
is diagonal and the following equation holds [
8]:
where
is the Jacobian matrix that depends on robot configuration. Matrix
can be obtained from Equation (1) by least-square method considering some different configurations of the robot [
8,
13].
In this paper, a different approach based on modal testing is adopted. The basic idea is to excite modes of vibration dominated by the compliance of one joint and to identify stiffness (or compliance) from the measured modal frequency and the moment of inertia about the joint axis. The moment of inertia is calculated by means of the CAD (Computer Aided Design) model of the robot.
The equipment needed to carry out this kind of test is rather simple and cheap; it includes a hammer for modal testing, an accelerometer, and a data acquisition board. In the framework of this research, a PCB 086C01 hammer (with load cell sensitivity 0.2549 mV/N), a PCB 356A17 triaxial accelerometer (sensitivity 50.5 mV/(m/s2)) built by PCB Piezotronics, Inc., Depew, NY, USA, and a NI9234 data acquisition board were used built by National Instruments, Austin, TX, USA. After some preliminary tests, a sampling frequency of 1024 Hz and 2048 samples were selected. Measured signals were analyzed by means of ModalVIEW R2, a specific software for modal analysis.
Since motions of the base of the robot may have a negative effect on the quality of measurements, the robot was rigidly fastened to a large steel base (see
Figure 1) and an accelerometer was used to monitor residual base motions.
When a serial six-joint robot is loaded by a force applied on the end-effector, on the one hand, this force produces the largest moments about the first joints, and on the other hand, the rotations of the first joints due to compliance have the largest effect on end-effector positioning errors, due to the large lever arms [
19]. For these reasons, the present research is limited to the identification of the compliance properties of the first three joints of the robot. The last three joints are considered ideal revolute joints that contribute to define the pose of the end-effector, but are infinitely stiff. In the future, the method will be used to identify the compliance of all the joints, if the compliance of the wrist joints will appear relevant in some configurations.
Since in actual working conditions the joints of the robot are held in the desired configuration by the servomotors, the tests were carried out with the servomotors switched on. The identified stiffnesses are the result of the mechanical stiffness of the transmission plus the stiffness of the servo.
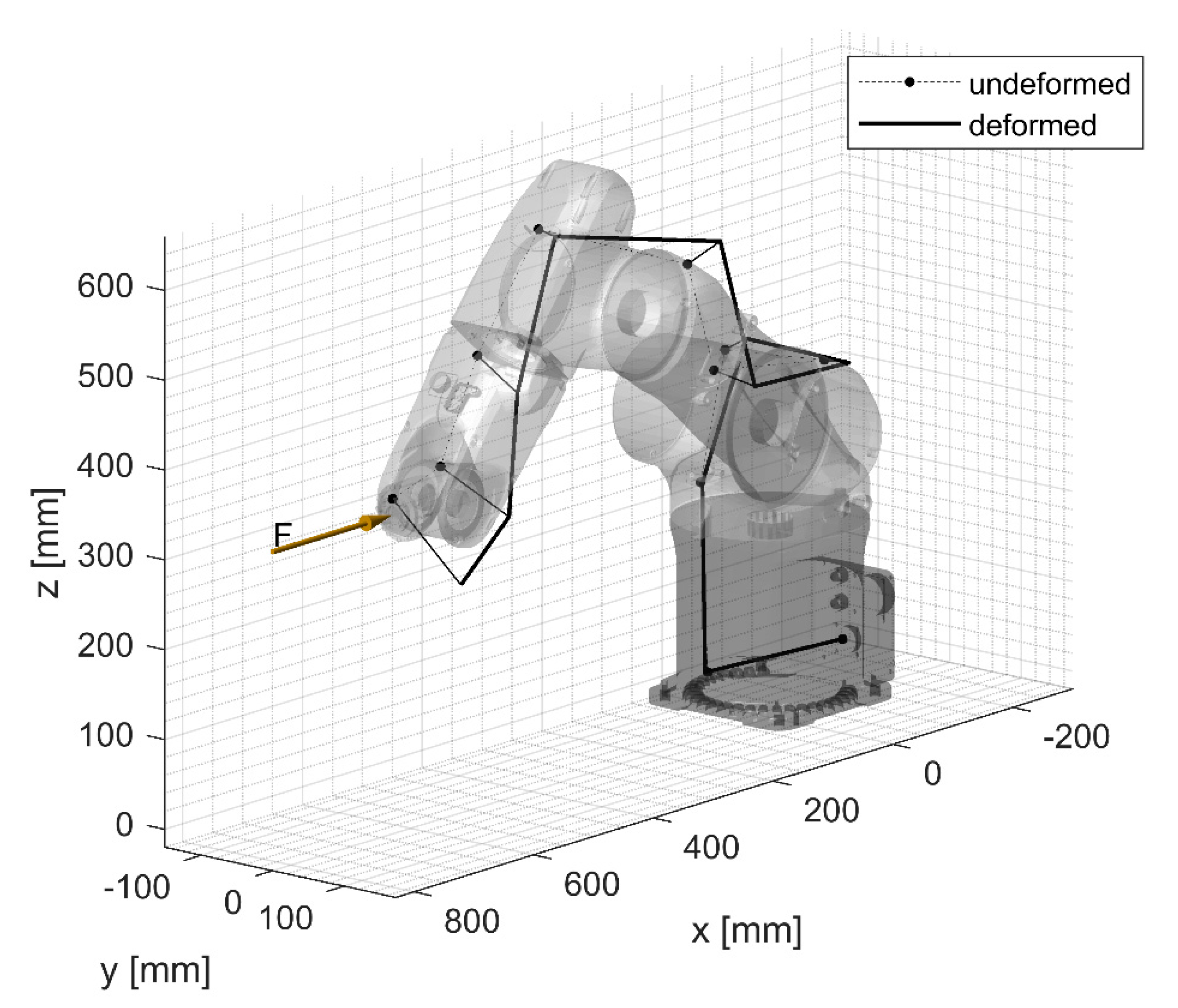
In order to identify the stiffnesses of the first three joints of the robot, three specific test conditions were defined (see
Table 1). The first condition, which is represented in
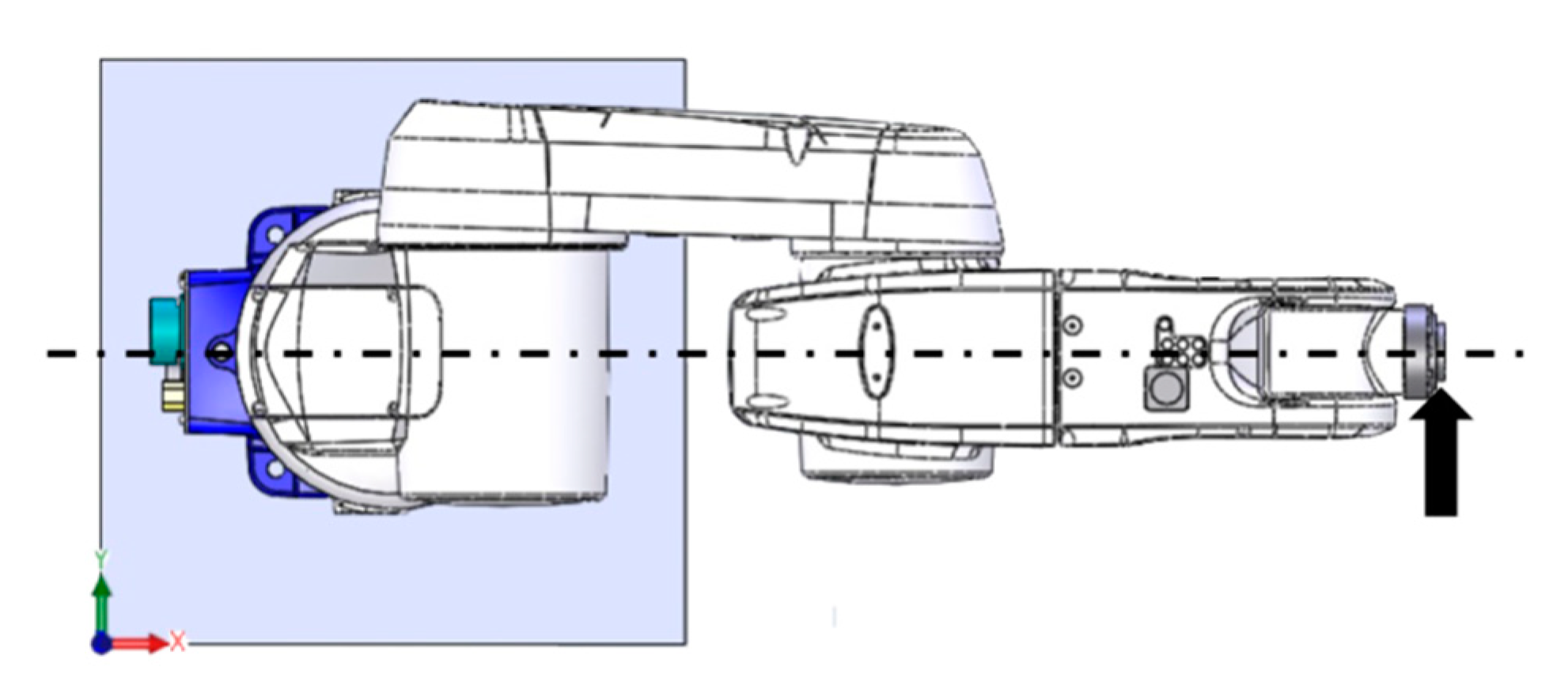
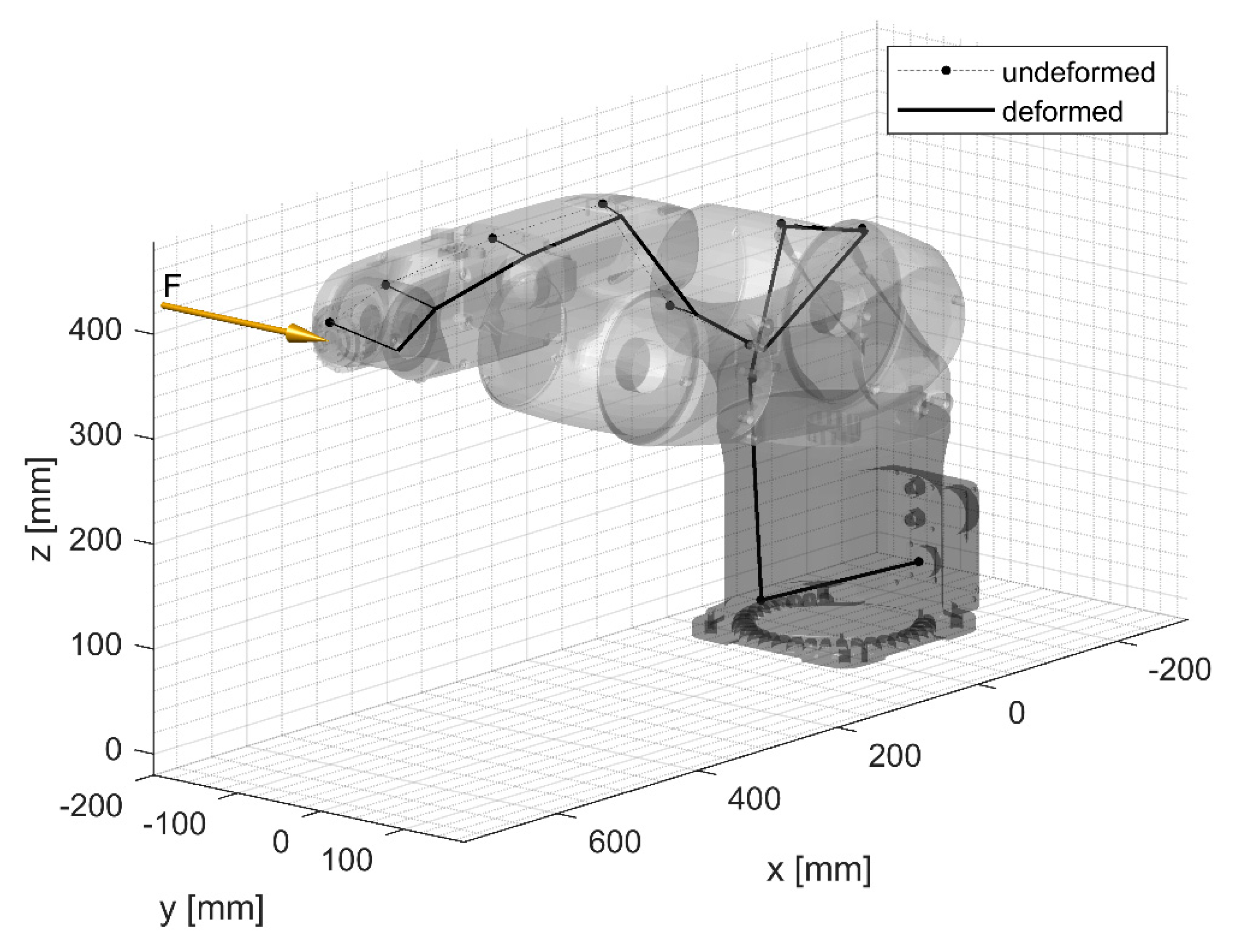
Figure 2, aimed to highlight the stiffness of the first joint. For this reason, the end-effector flange was excited by a lateral force (y direction) and joint rotations were set in order to achieve the maximum arm extension. In this configuration, the first mode of vibration should be dominated by the compliance of the first joint.
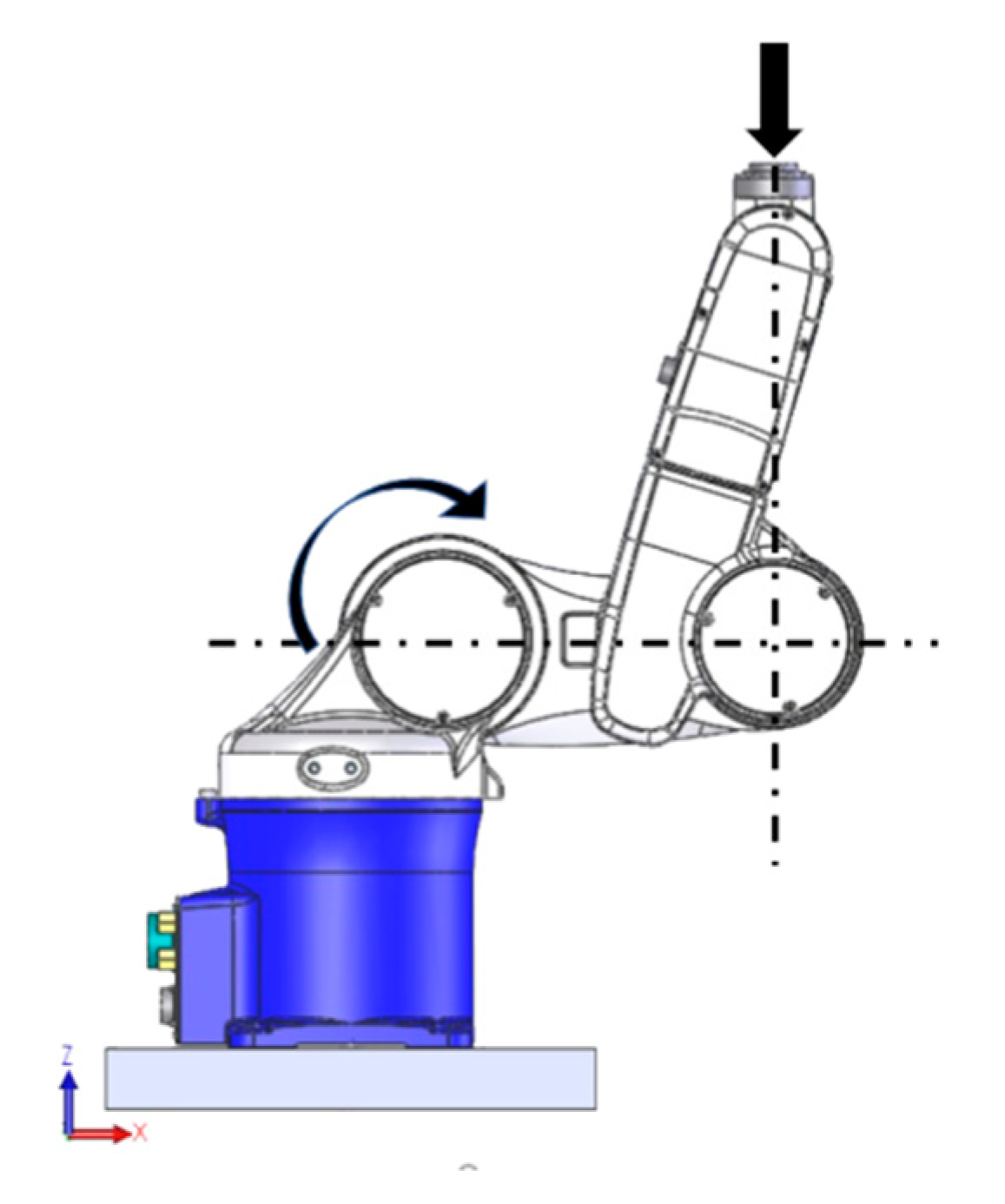
The second test condition (
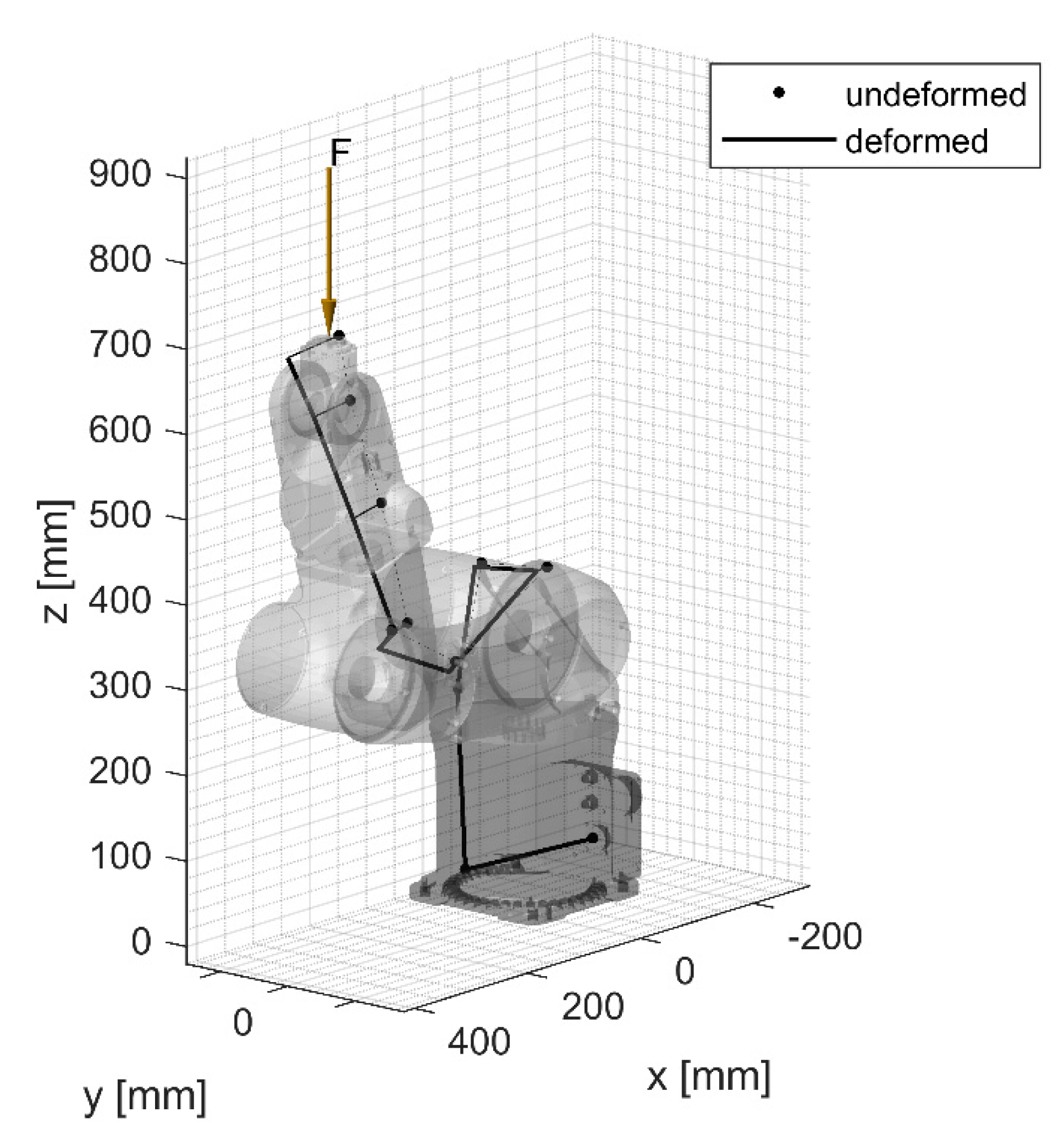
Figure 3) aimed to highlight the stiffness of joint 2. For this reason, the robot arm was configured with the approach axis of the end-effector pointing upwards and intersecting the axis of joint 3, and a vertical force was exerted by the hammer. Since in this test configuration the impact force intersected the axis of joint 3 and was parallel to the axis of joint 1, the compliances of these joints should not have influenced the fundamental mode of vibration.
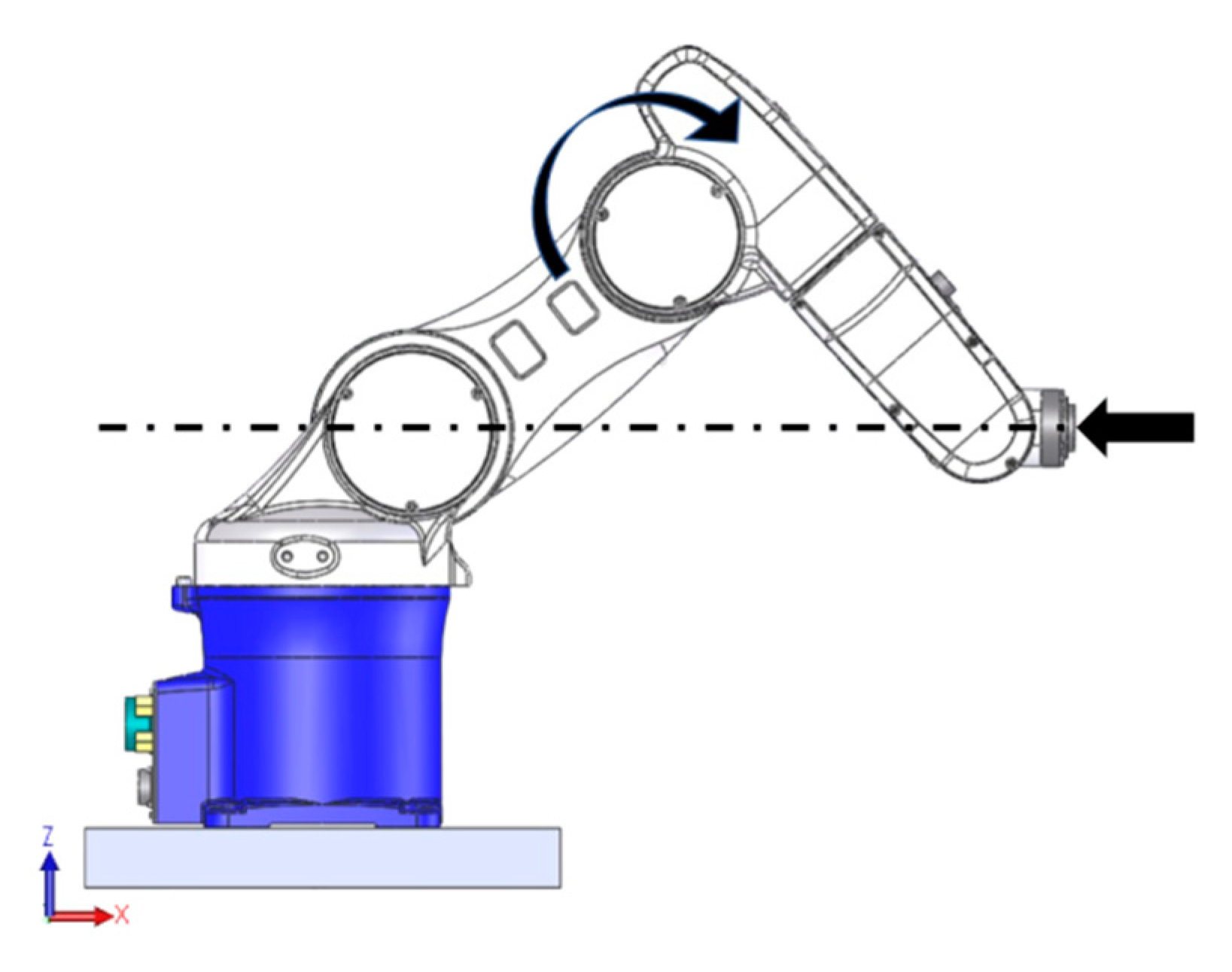
Figure 4 shows the third test configuration. In this case, the approach axis of the end-effector was aligned to the x axis and intersected both the axis of joint 2 and the axis of joint 1. Therefore, the fundamental mode of vibration excited by a hammer force in x direction should have been dominated by the stiffness of joint 3.
The tests were carried out with the modal analysis approach [
20], which is widely used in the fields of automotive engineering [
21,
22], aerospace engineering [
23], automatic machines [
24], and robotics [
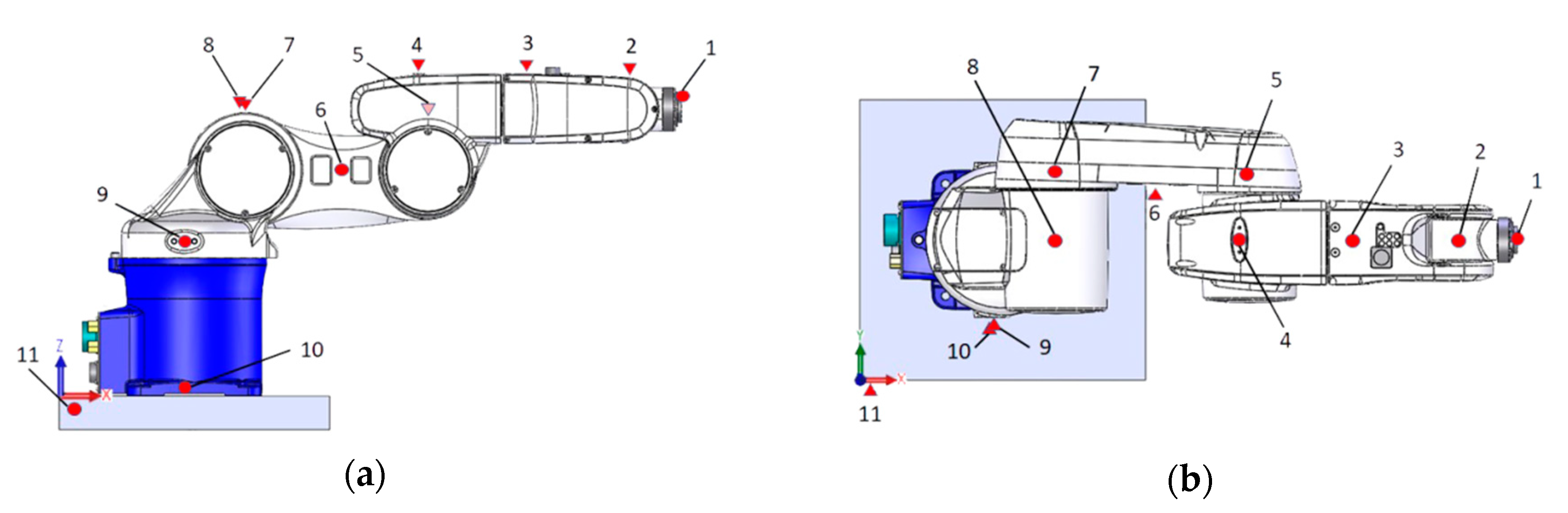
25]. A grid of measurement points was defined on the robot (see
Figure 5); points 10 and 11 were used to monitor base vibrations. In each test configuration, the hammer impact was always exerted on the end-effector flange in the defined direction, whereas the triaxial accelerometer was moved to the various grid points (rowing response approach). In this way, for each configuration, 33 frequency response functions (FRFs) were measured between the 3 acceleration components of the 11 grid points and the hammer impact force. In order to improve the repeatability and quality of measurements, each FRF was calculated averaging the results obtained with three hammer blows. Measured data were then processed with ModalVIEW in order to identify natural frequencies, modal dampings, and modal shapes.
2.2. Experimental Results
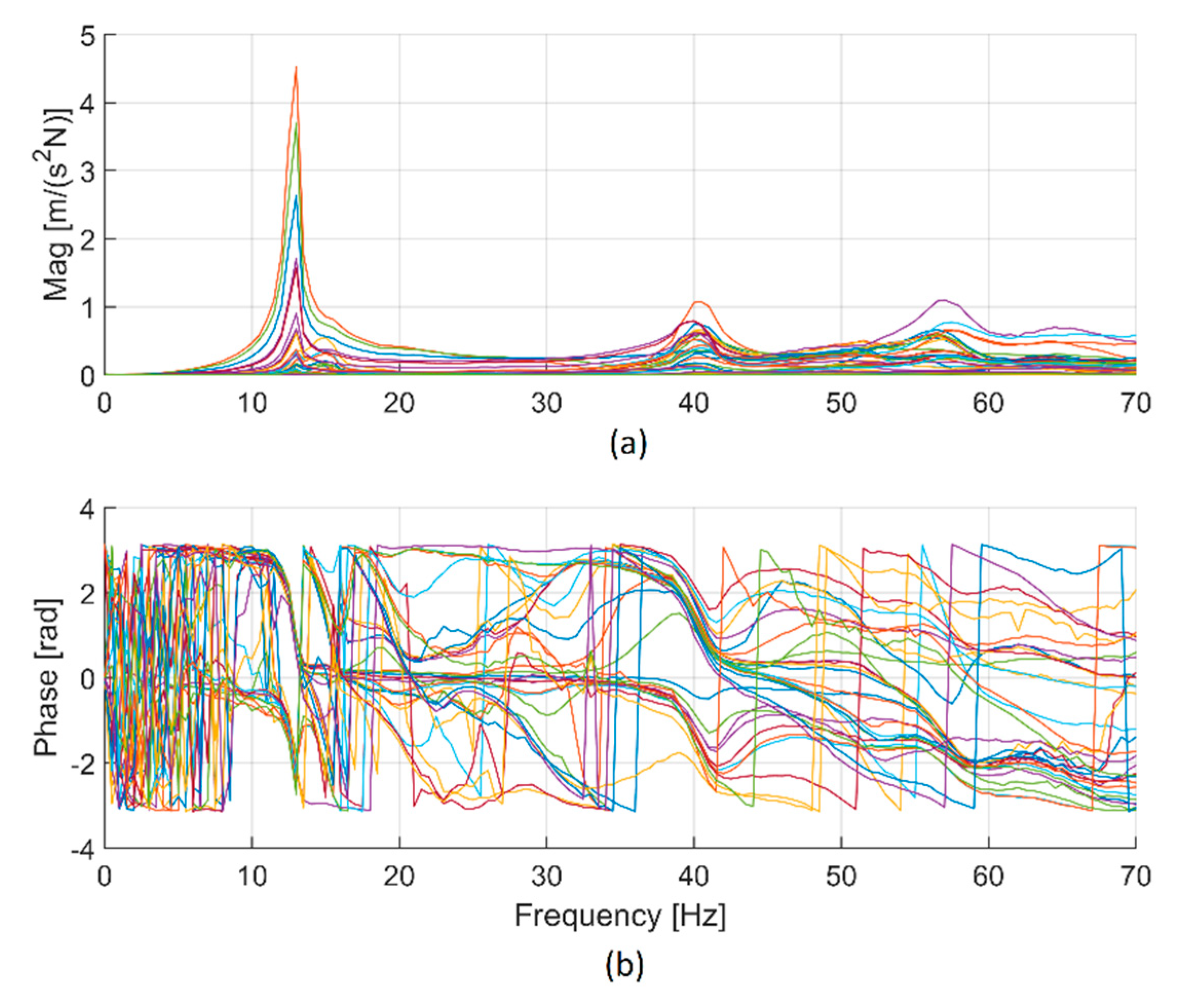
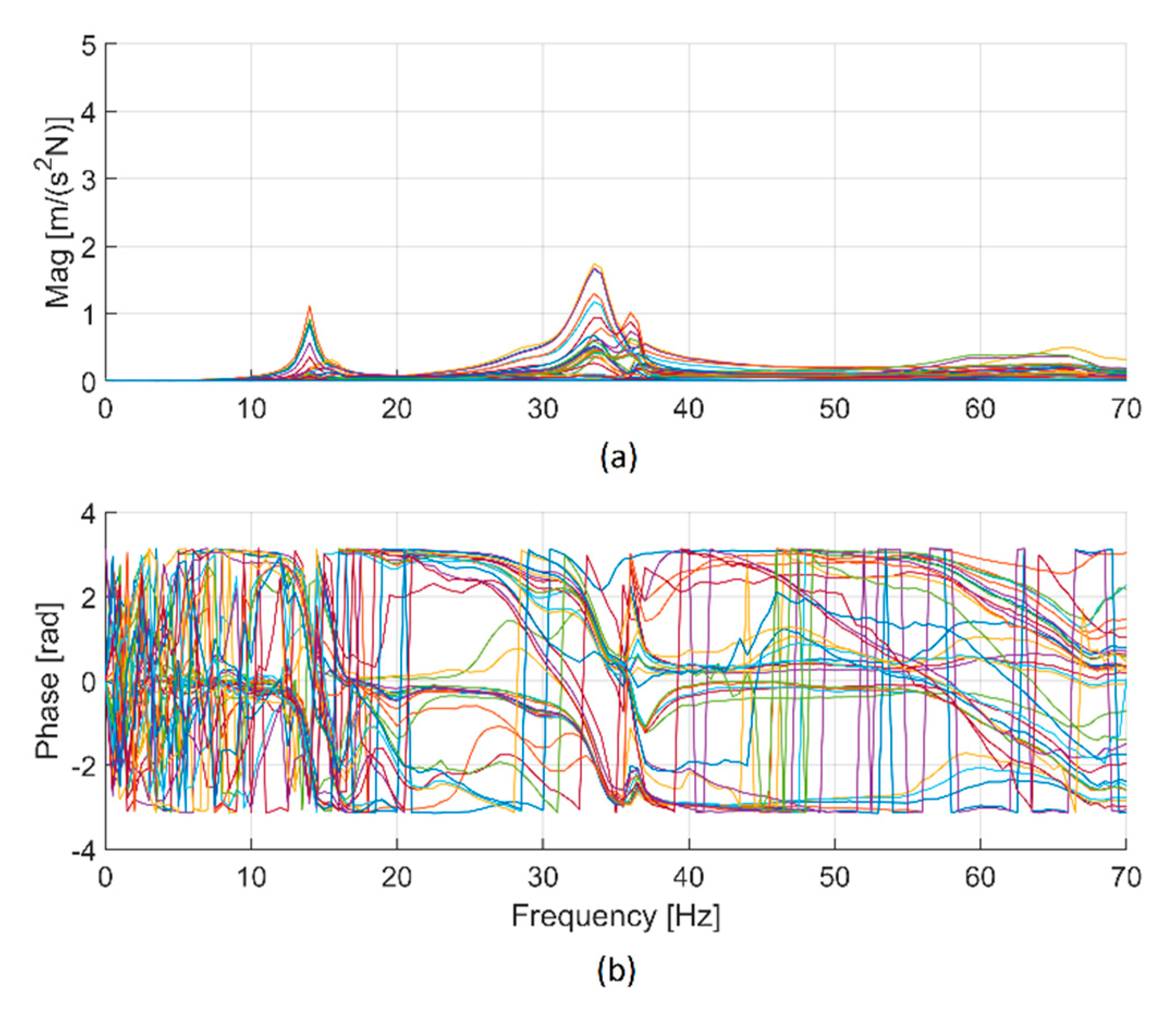
Figure 6 shows the overlay of FRFs measured in configuration 1. The modulus plot highlights the presence of the fundamental mode at about 13 Hz, and the phase plot corroborates this fact, showing large phase changes at the same frequency.
The identification, carried out with the algorithm Quick Fit of ModalVIEW, made it possible to find a natural frequency of 13.0 Hz, with a viscous damping ratio [
26] of 2.3%. The natural frequency is the main parameter needed to identify the stiffness of the joint, but the shape of the identified mode is important as well, since it makes possible the verification of the hypothesis that the selected joint dominates the mode of vibration. The mode of vibration corresponding to the natural frequency of 13.0 Hz is represented in
Figure 7; it is dominated by displacements in the x–y plane caused by the rotation of joint 1, and the contribution of the other joints and of link flexibility to this mode appears negligible. Therefore, the identified frequency is suited to identify the stiffness of joint 1.
The small resonance peaks at about 40 and 57 Hz in
Figure 6 are related to the excitation of higher-order modes that also involve the compliance of the other joints of the robot.
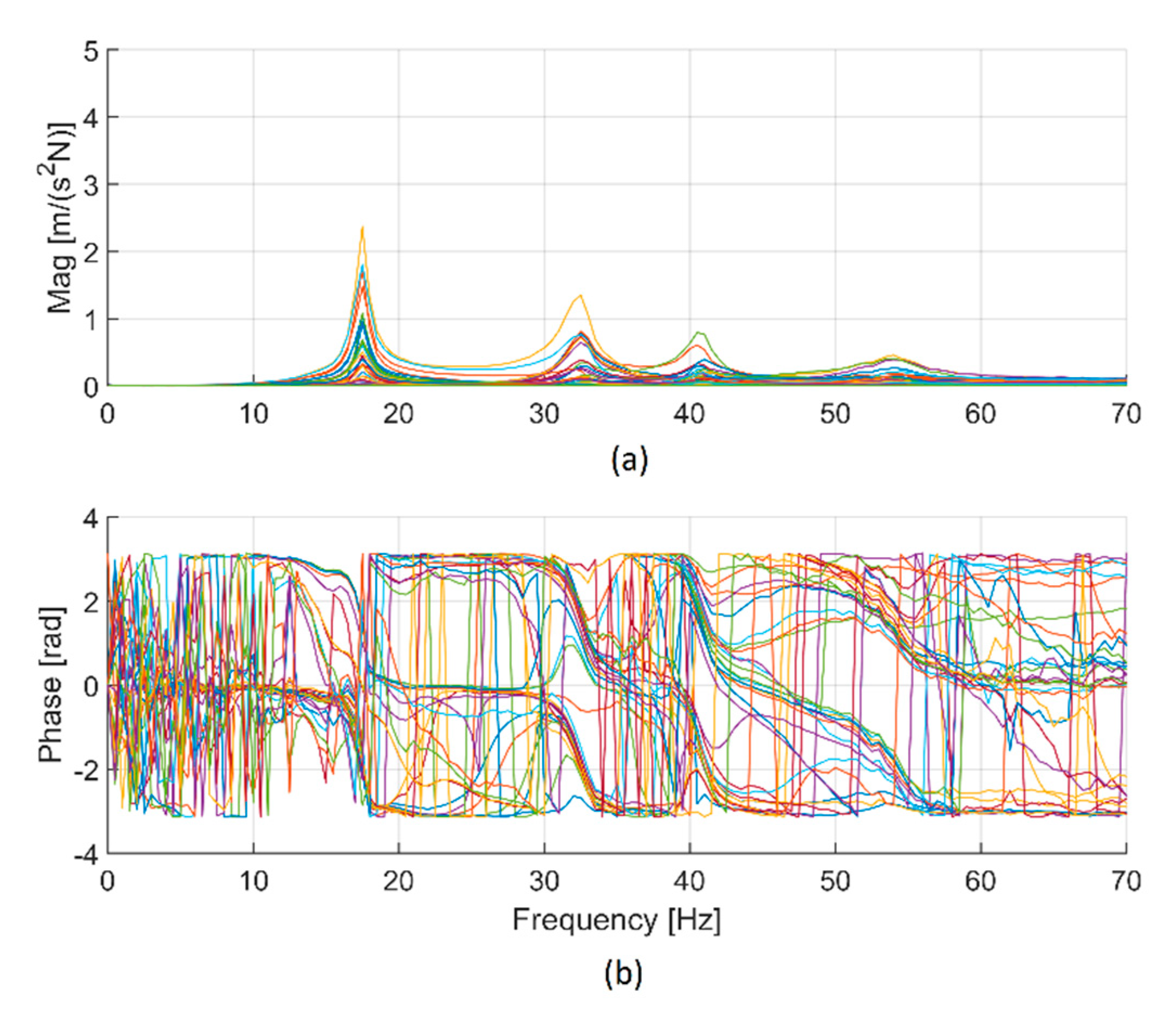
The results of the modal tests carried out in order to identify the compliance of joint 2 are presented in
Figure 8 and
Figure 9. The overlay of the measured FRFs shows the first peak at about 18 Hz. Modal analysis made it possible to identify a mode of vibration with natural frequency 17.5 Hz and viscous damping ratio of 1.9%. The shape of this mode of vibration (
Figure 9) is characterized by displacements dominated by the rotation of joint 2, therefore it is suited to identify the compliance of this joint.
The minor resonance peaks at about 32 and 40 Hz are related to the excitation of higher-order modes that also involve the compliance of the other joints of the robot.
Finally,
Figure 10 shows the FRFs measured in the third configuration, in order to identify the compliance of joint 3. Two resonance peaks appear. The first is at about 14 Hz and the second, which is the highest, is at about 33 Hz. Modal analysis results show that the first peak (the minor) corresponds to a mode dominated by the compliance of joint 2; this mode was excited since the hammer force did not intersect exactly the axis of joint 2. The mode at 33.5 Hz (with viscous damping ratio of 2.7%) is dominated by joint 3 compliance and is suited to identify the compliance of this joint (see
Figure 11).
It is worth noticing that the damping ratios of the selected modes are similar; this is a good clue that highlights that these modes chiefly involve the joints, which have similar transmissions and servos that are characterized by similar dissipation phenomena.
A linear vibrating system with N DOF is described by a system of coupled second-order differential equations in space coordinates. The modal approach transforms the N DOF vibrating system into N independent 1-DOF vibrating systems [
20,
27] governed by these equations:
where
are the modal mass, damping, and stiffness, respectively.
is the
modal coordinate and
is the modal force. The natural frequency is:
If robot vibrations are considered, in general, modal stiffness does not coincide with joint stiffness, because the modes of vibration involve rotation about several joints. However, if a mode exists that is dominated by rotation about joint , the modal stiffness is a good approximation of joint stiffness Therefore, joint stiffness can be calculated from Equation (3) with In this case, modal mass coincides with the moment of inertia of the robot about joint . These moments of inertia were calculated using the CAD model of the robot.
Since the manufacturer gives the total mass of the robot (28 kg) but does not give information about mass distribution, the total volume of the robot and of the various links were carefully calculated and the total mass was distributed to the links proportionally to their volumes. In the future, the calculated values will be checked with other methods.
The stiffnesses identified with the above-mentioned method are summarized in
Table 2; they are similar for the three joints and in agreement with literature values [
13].
2.3. Validation
In order to assess the validity of the identification method, the stiffness values of
Table 2 were implemented in a dynamic model of the robot and the first natural frequencies of the robot were calculated in a configuration (validation configuration) different from the configurations used for identification (see
Table 1 and
Figure 12).
Then, the robot was modally tested in the validation configuration and the first natural frequencies were experimentally identified. Hammer excitation was applied on the end-effector along three orthogonal directions of the end-effector coordinate system. It is worth noticing that the validation configuration was chosen in order to obtain modes of vibration that involved the compliance of various joints simultaneously.
The comparison between numerical and experimental values is shown in
Table 3. The three testing conditions (with different directions of excitation) essentially lead to the identification of the same natural frequencies. These frequencies are rather close to the numerical ones, with a maximum error of about 3 Hz in the natural frequency of the third mode.
3. Mathematical Model
When a structure (like a robot) has a polygonal open shape with an end locked to a very stiff structure and an end loaded by a static or dynamic force, the deformation of the loaded end can be studied considering the motion of a rigid body fixed to the loaded end of the structure. The basic concepts of rigid body mechanics can be adopted for describing this motion.
Giulio Giuseppe Mozzi del Garbo was an Italian mathematician who published in 1763 the book “Discorso matematico sopra il rotolamento dei corpi” (Mathematic Discourse on the Roll of Bodies) in which he stated that a generic differential spatial rigid motion can be considered a helical motion around a line, which is called the Mozzi axis [
27]. In other words, the rigid motion of a body is represented in every instant by rotation about and translation along the Mozzi axis, which is also known as the instantaneous screw axis. The direction of the Mozzi axis coincides with the instantaneous direction of the angular velocity vector. Afterwards, the ideas of Mozzi were developed by Cauchy in 1827, Poinsot in 1834, Chasles in 1878 [
28]. Ball in 1900 developed the modern screw theory introducing the concepts of twist and wrench [
29,
30]. A twist is the combination of a screw with a parallel linear velocity related to the angular velocity by the pitch of the screw; a wrench is a force acting along the screw combined with a torque related to the force by the pitch of the screw.
In recent years, the interest in the screw theory increased due to the discovery of possible applications in the fields of multibody dynamics [
31], vehicle dynamics [
32,
33,
34], vibration control [
35], and robotics. In robotics, the screw theory has been adopted for calculating Jacobians [
18], for decomposing the stiffness matrix [
36], and for finding its properties [
37,
38]: the twist-compliant axes and the wrench-compliant axes. A twist about a twist-compliant axis produces only a torque parallel to the rotation axis, whereas a wrench applied on a wrench-compliant axis produces a parallel linear deformation.
In the framework of this research, the concepts of screw theory will be used for a different purpose: the representation of the rotation and translation axis of the compliant motion of the end-effector caused by an external load. This information is very useful when the robot end-effector interacts with an object and the displacement caused by compliance may assist or counteract the performed operation. Sometimes the object is characterized by its own compliance, and in the near future, the same concepts will be adopted to represent the relative rotation and translation between the robot and the object.
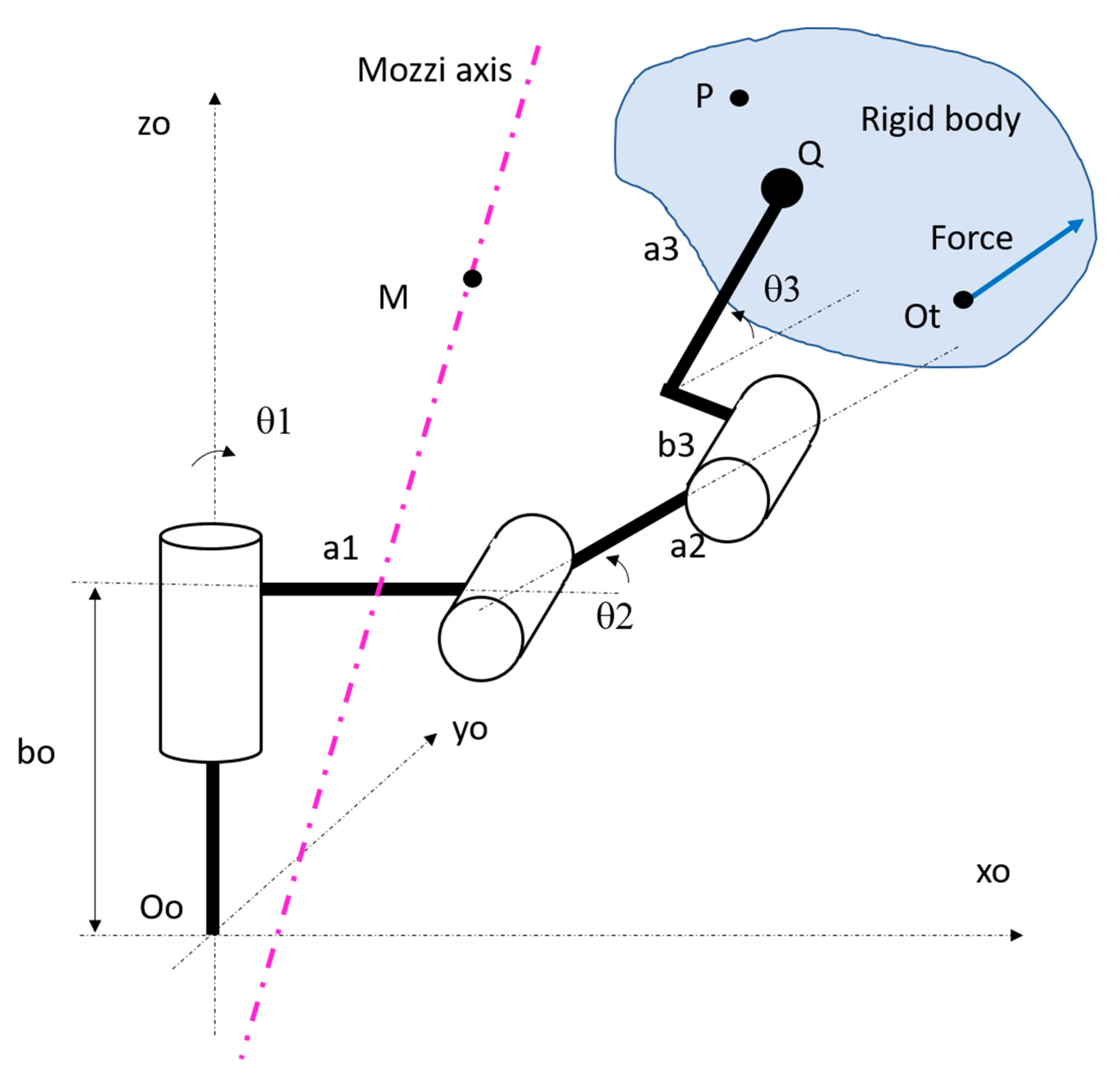
In order to accomplish this specific task, the basic concepts of Mozzi or screw axis are sufficient. In
Figure 13, a serial six-joint robot is represented. A fixed system of coordinates with origin
and axes
is established. Joint rotations are fixed but compliance is allowed in the first three joints. Point
is the center of the wrist. Since wrist joints are infinitely stiff, link 3, the wrist, the end-effector, and the tool grasped by the end-effector form a unique rigid body, which is used for Mozzi axis analysis. Point
is used for defining the external force on the tool, which causes robot arm deformation. It is worth noticing that if the compliance of some wrist joint were important, the rigid body would begin after the last compliant joint.
The linear velocity
of a point
belonging to the rigid body can be calculated using the equation of rigid body velocity:
where
is the linear velocity of a reference point belonging to the rigid body (wrist center
),
is the angular velocity vector, and
is the vector from
to
.
The linear velocity of point
can be expressed as a translation along the Mozzi axis plus a rotation about the Mozzi axis according to this equation:
where
is a scalar and
is a point on the Mozzi axis. If the two expressions of
are equated, the following result holds:
Velocity
in general has a component (
) parallel to
and a component (
) perpendicular to
, whereas the vector product is always perpendicular to
. Hence Equation (6) splits into the two equations:
The parallel component
, which coincides with the linear velocity along the Mozzi axis, can be calculated by means of the inner product:
where
is the unit vector of
The perpendicular component (
can be calculated by difference:
Moreover, for the perpendicular component, this equation holds:
The unknown of the system of Equations (7) and (11) is vector
, which defines the position of a point on the Mozzi axis. Since the angular velocity matrix is skew-symmetric [
18], there are infinite solutions for
that belong to a line; this line is the Mozzi axis. The solution of the system of (7) and (11) can be found using vector algebra as shown in [
18]:
where
is an arbitrary scalar parameter. Therefore, the position of a point along the Mozzi axis with respect to origin
is given by:
If all the vectors are projected on the fixed coordinate system, these scalar equations define the Mozzi axis:
When an interval of time
is considered, Equation (14) can be written in terms of differential displacements (
and rotations (
):
When differential displacements (and rotations () are calculated by means of Equation (1), Equation (15) can describe the Mozzi axis of a robot with a certain configuration and an assigned force vector
The representation of the compliance properties of the robot arm by means of the Mozzi axis has some advantages with respect to the representation based on the Cartesian stiffness matrix. First, the Mozzi axis gives a more intuitive and geometric interpretation of the phenomenon. Second, the Mozzi axis also suggests the origin of the compliance, since its proximity to a joint axis identifies this axis as the most compliant.
4. Mozzi Axis of the Tested Robot
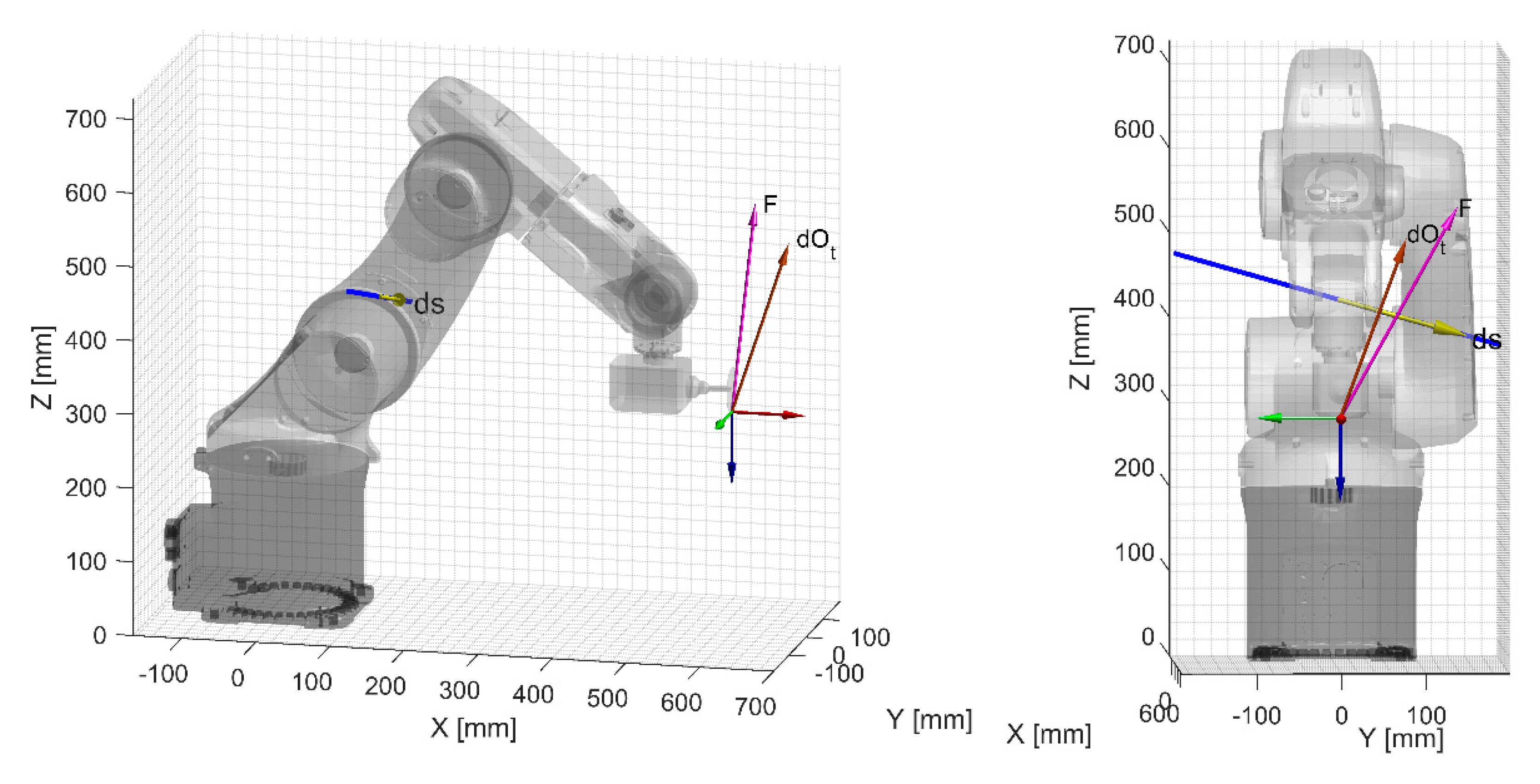
To show the potentialities of the Mozzi axis approach, multiple simulations, in two different scenarios, A and B, were performed. Both A and B configurations were excited by grinding forces along
,
, and
axes. The two configurations differed in the orientation of the grinding equipment. From a generic point of view, these configurations show how the Mozzi axis changes with a different position of the grinding forces with the same robot joint configuration. Finally, a real case machining scenario [
5] was simulated (
Figure 14).
In
Figure 15,
Figure 16 and
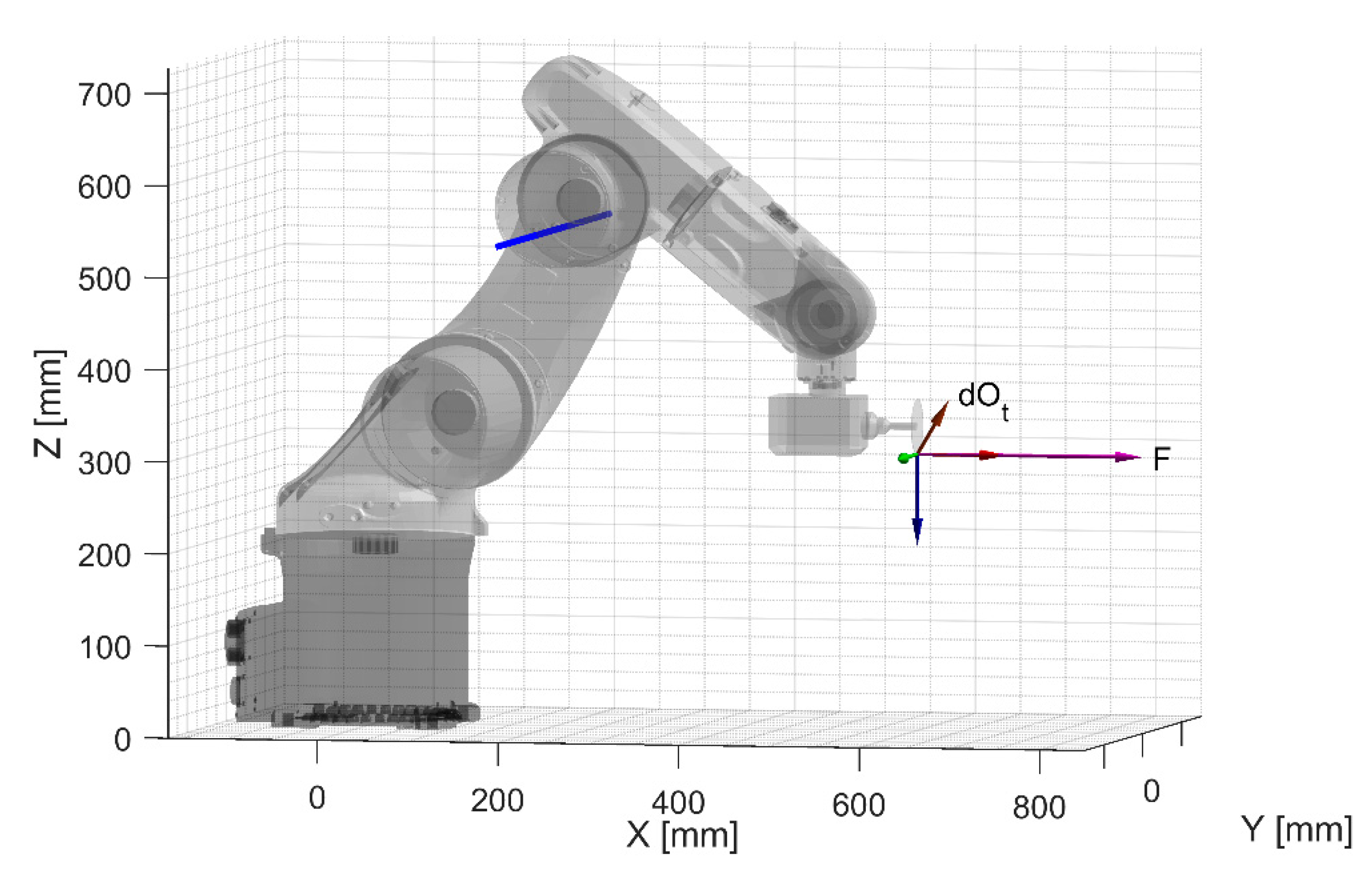
Figure 17, the robot is excited by a machining force that lies in the vertical plane perpendicular to the axes of joints 2 and 3. The rotation vector of the end-effector is parallel to the axes of joints 2 and 3, therefore the Mozzi axis has the same direction and passes at a distance from the robot base that depends on the compliances of joints 2 and 3. No translation along the Mozzi axis takes place. It is worth noticing that, since in
Figure 15 the force has a small lever arm with respect to joint 2, the motion of the end-effector is dominated by compliance of joint 3 and the Mozzi axis passes very close to the center of this joint. In
Figure 16 and
Figure 17, the vertical force exerts moments about both joint 2 and 3 and the Mozzi axis crosses the robot at an intermediate point.
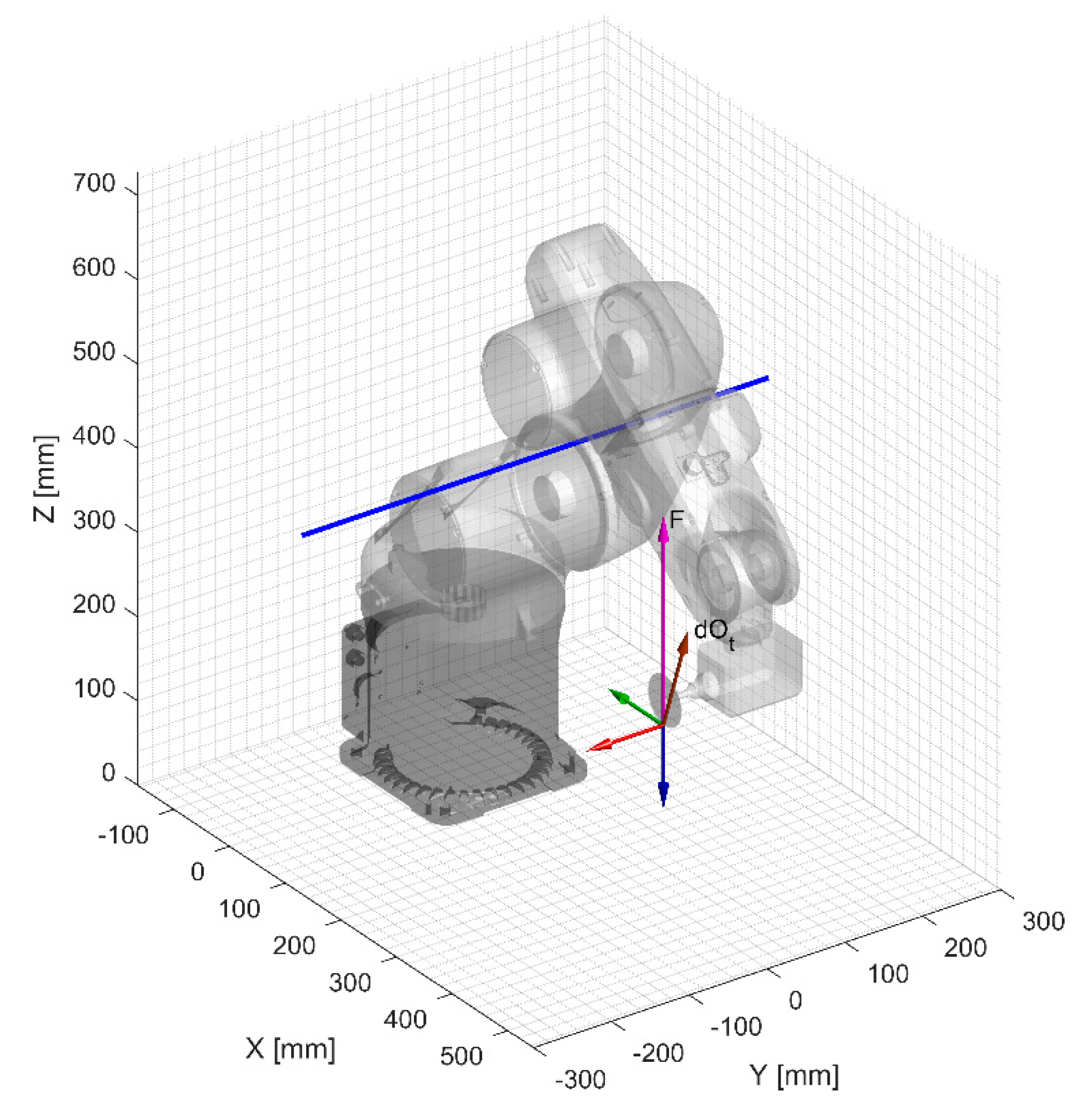
In
Figure 18 and
Figure 19, the robot is excited by machining forces parallel to the
axis. Since this axis is parallel to the joint 2 and 3 axes, the only joint that can comply to the machining force is joint 1, therefore the Mozzi axis is coincident with the axis of joint 1.
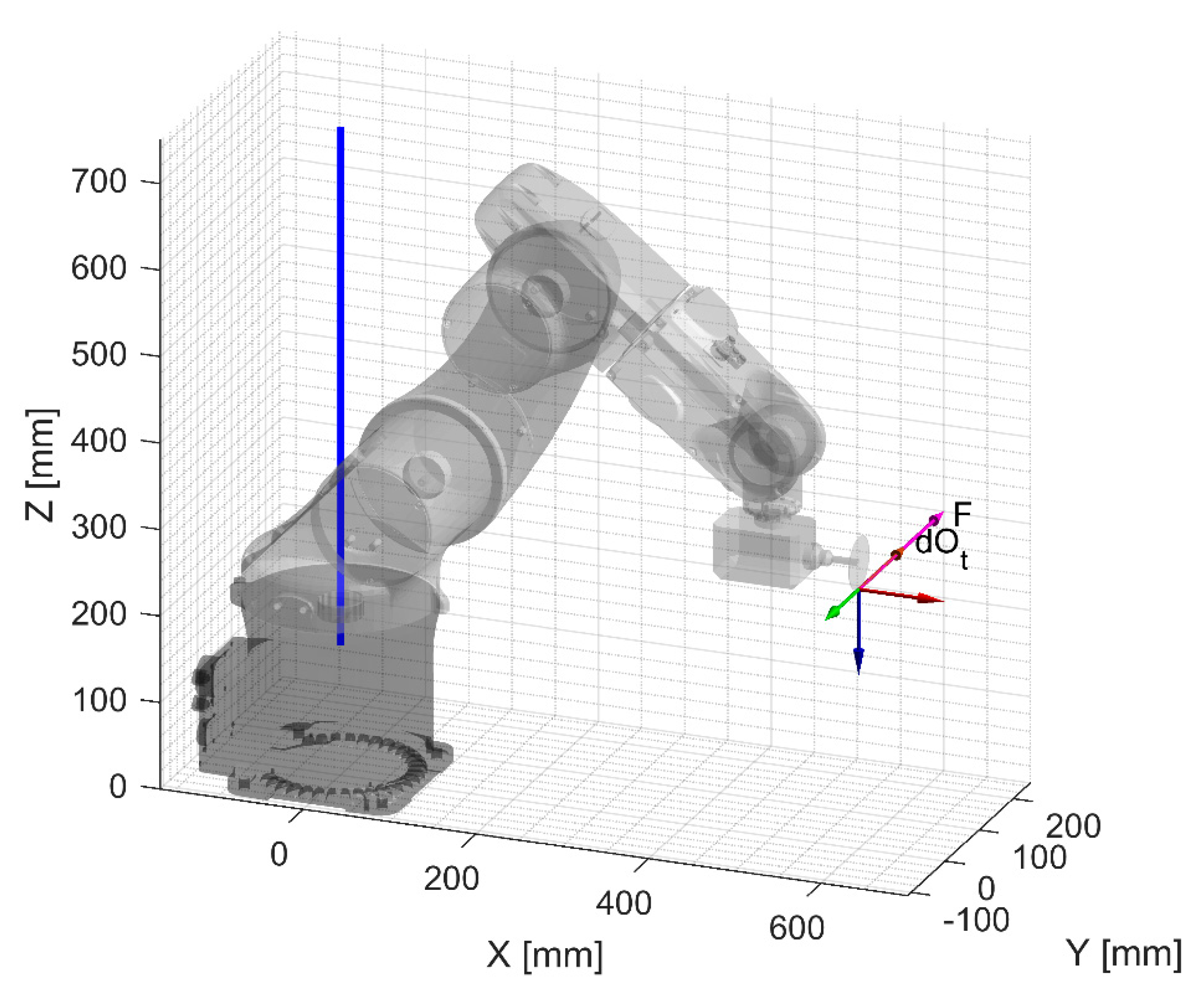
Figure 20 shows how the compliances of all the joints can combine together when excited by an eccentric force. Force
is applied parallel to the
axis on a plane perpendicular to the axes of joints 2 and 3, which does not intersect the axis of joint 1. Thus, it excites all the joints and the position of the Mozzi axis results from the combination of all joint compliances. The Mozzi axis is tilted with respect to plane
–
, and there is a displacement
along the axis as well.
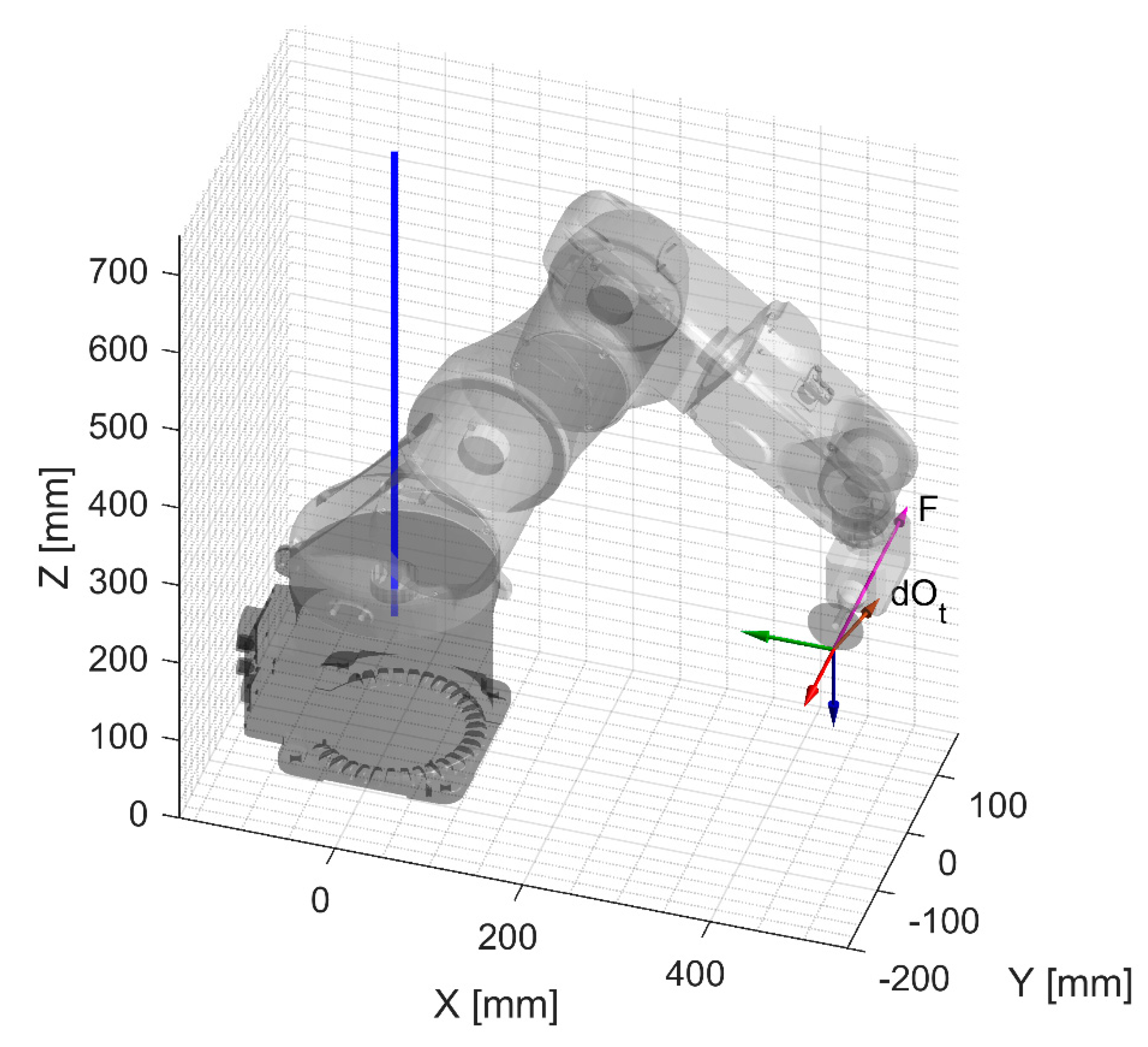
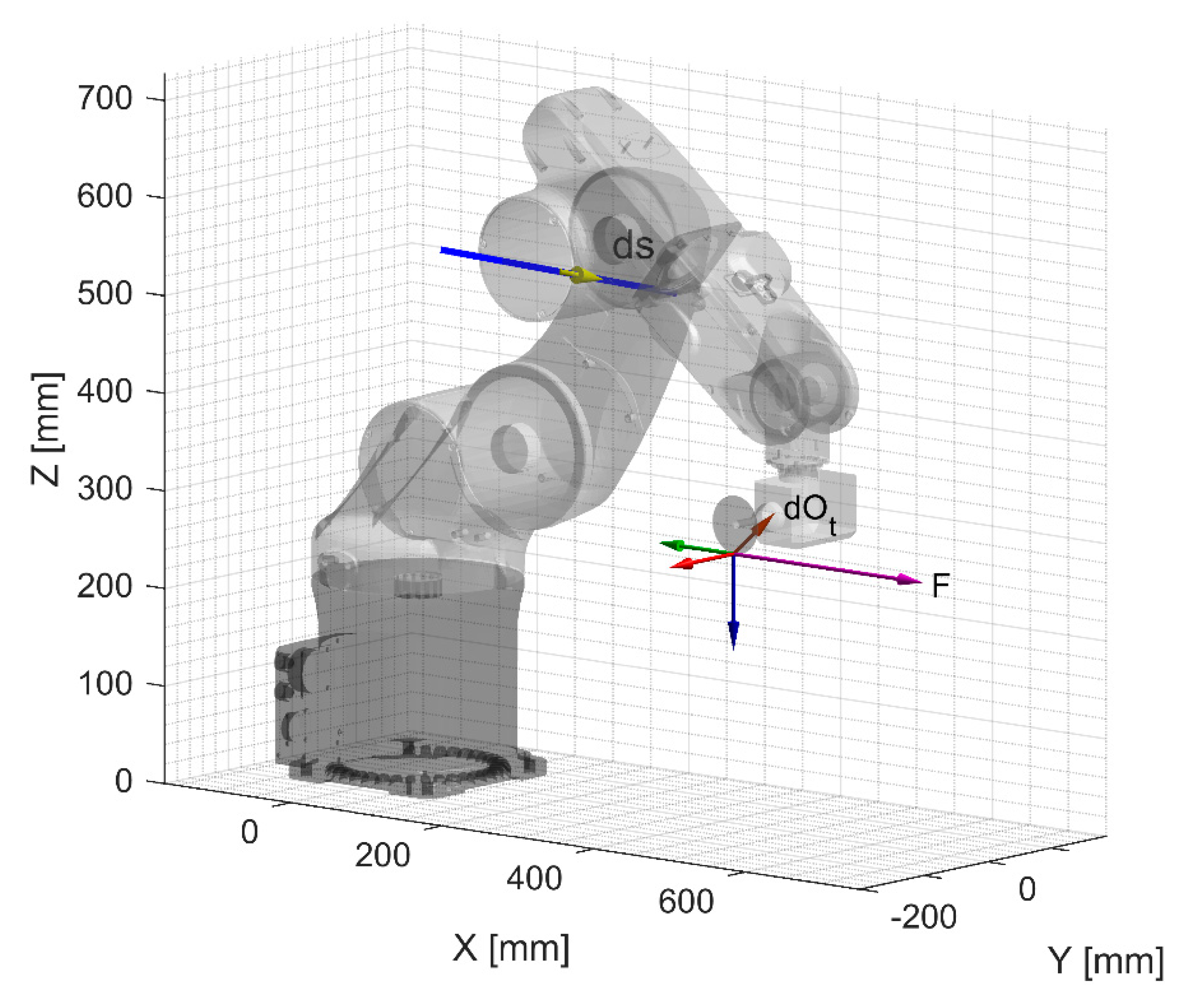
In
Figure 14, a real scenario simulation is shown. Force
lies on a plane parallel to the
–
plane and its direction is defined by the downmilling process described in [
5]. In this case, the Mozzi axis has a location similar to the one in
Figure 20: the main contribution to the end-effector movement is provided by the compliance of joints 2 and 3, but a small component of force
along the
axis results in a non-negligible compliance of joint 1. It is interesting to notice how the high lever arm with respect to joint 1 results in a significant compliance even with a small exciting force.
Another important aspect that can be highlighted by the seven figures is the direction of the Cartesian movement of the point of application of the force. This direction is perpendicular to the Mozzi axis when displacement along the axis is null and a combination of both rotational and sliding displacements in the general case. Moreover, the direction is not related to the direction of force , but it depends on the compliance of the joints. The only relation that can be found between the two vectors is that this movement is placed within the semispace defined by force vector .