Fault Diagnosis for UAV Blades Using Artificial Neural Network
Abstract
1. Introduction
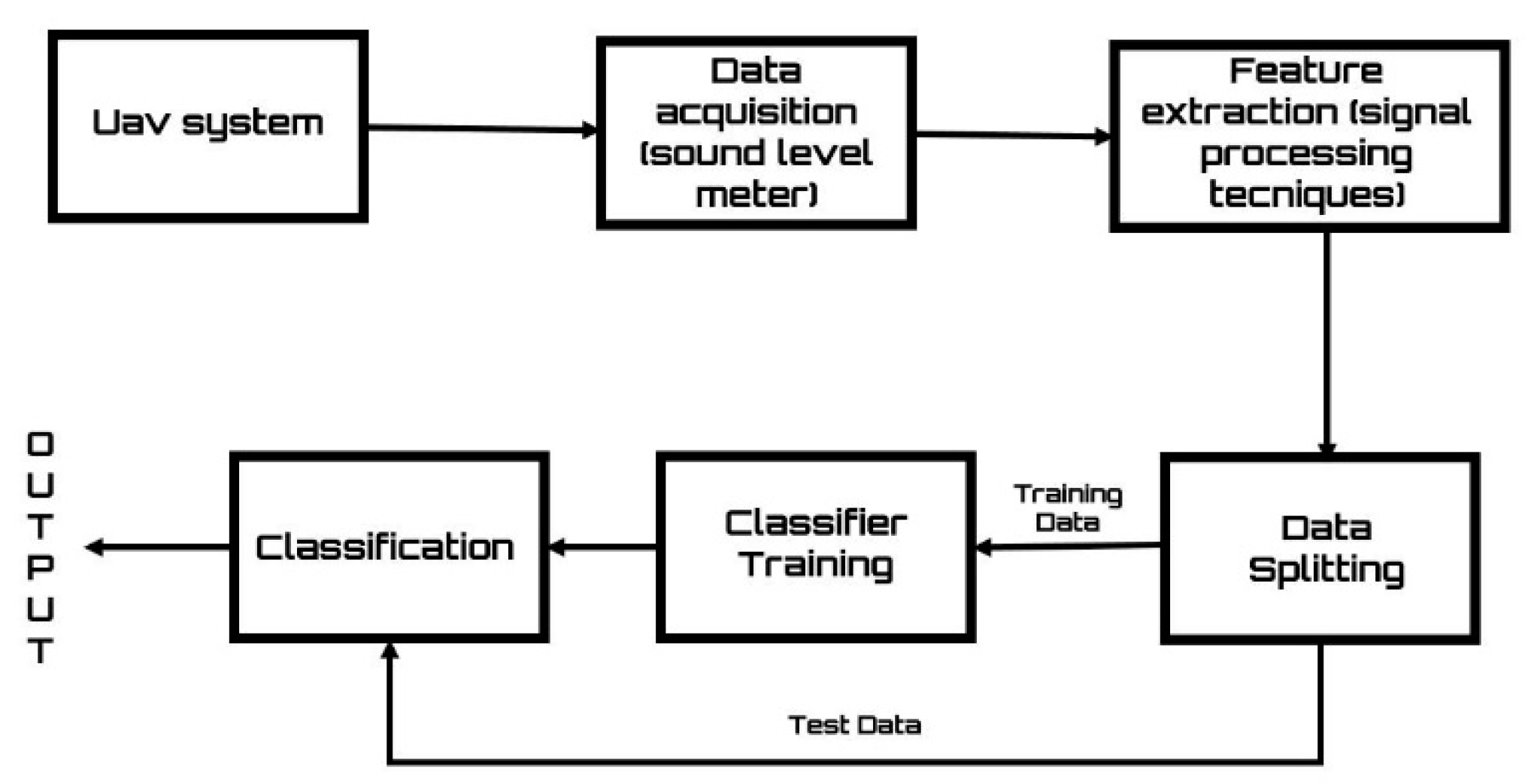
2. Materials and Methods
2.1. Unmanned Aerial Vehicle System
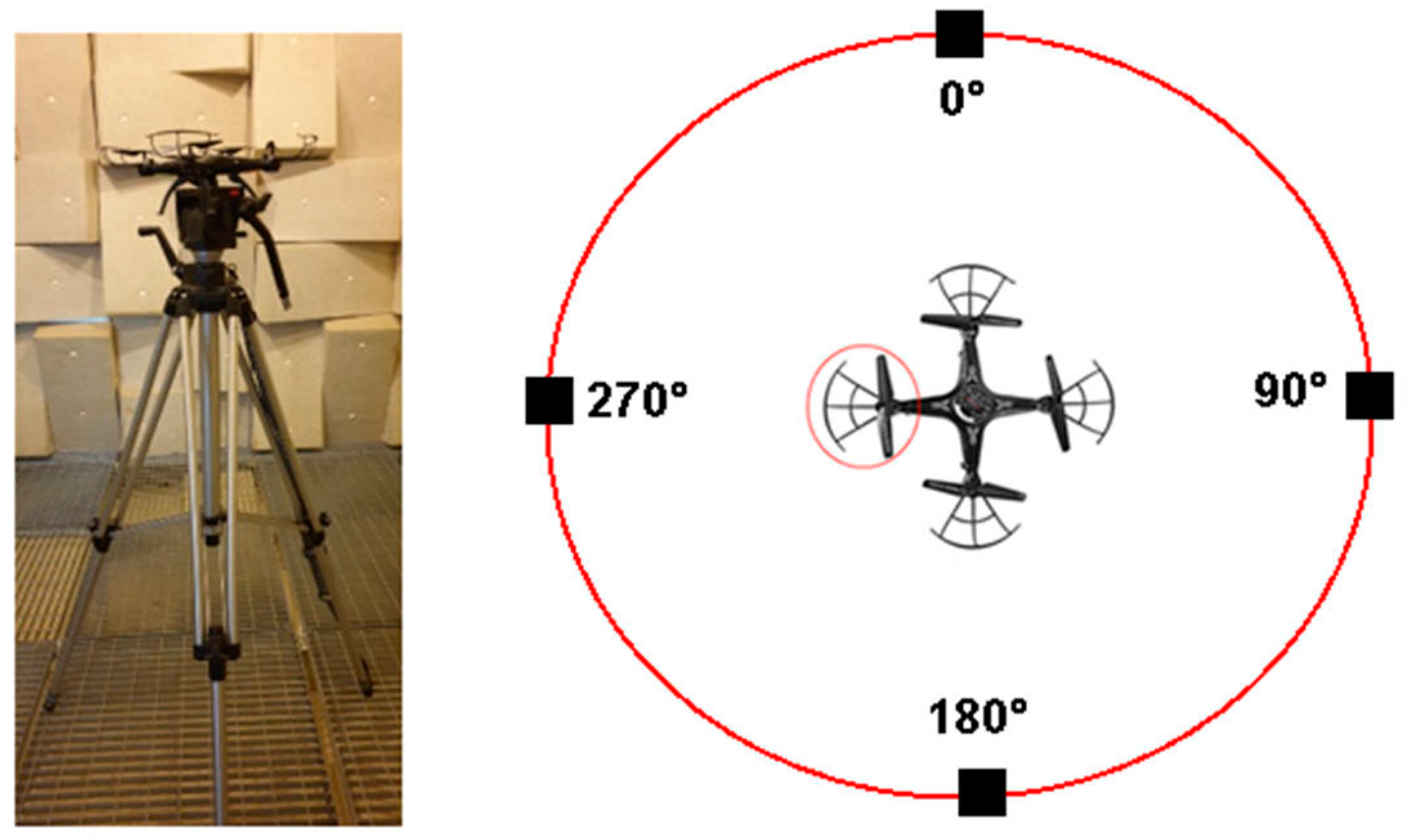
2.2. Data Acquisition
- Solo 01dB integrating sound level meter model of “Class 1”
- Class 1 calibrator to IEC 60942:2003
- Tripod
2.3. Feature Extraction
2.4. Data Splitting
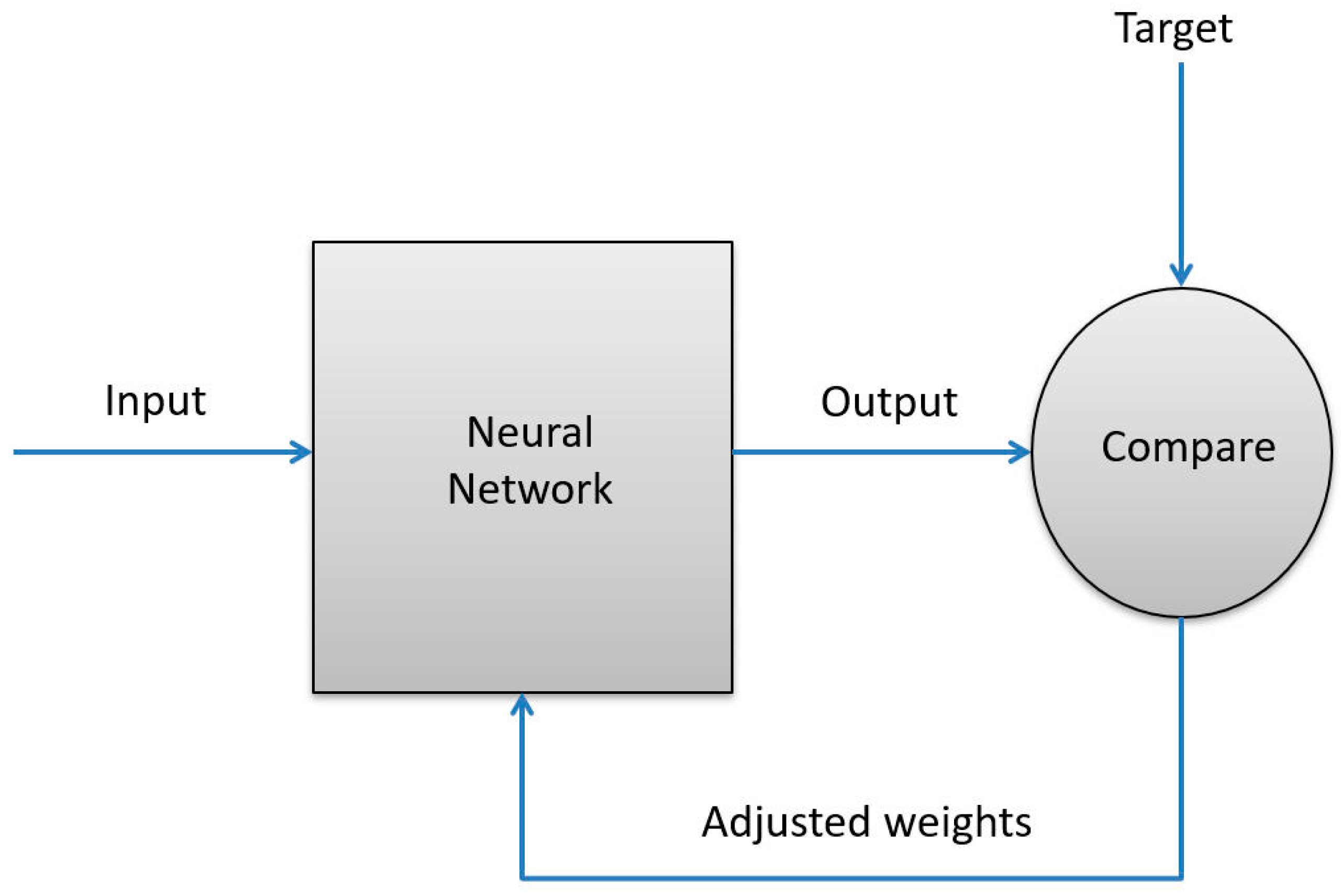
2.5. Classifier Training
- xi is the input
- y is the output
- µ is the learning rate
- f(x,w) is the current model prediction
2.6. Classification
3. Results and Discussion
3.1. Acoustic Measurements Analysis
3.2. Data Pre-Processing
3.3. Neural Network Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Valavanis, K.P.; Vachtsevanos, G.J. Handbook of Unmanned Aerial Vehicles; Springer: Dordrecht, The Netherlands, 2015; pp. 2993–3009. [Google Scholar]
- Newcome, L.R. Unmanned Aviation: A Brief History of Unmanned Aerial Vehicles; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2004. [Google Scholar]
- Gertler, J. US Unmanned Aerial Systems; Congressional Research Service (Library of Congress): Washington, DC, USA, 2012. [Google Scholar]
- Rao, B.; Gopi, A.G.; Maione, R. The societal impact of commercial drones. Technol. Soc. 2016, 45, 83–90. [Google Scholar] [CrossRef]
- Agrawal, K.; Shrivastav, P. Multi-rotors: A revolution in unmanned aerial vehicle. Int. J. Sci. Res. 2015, 4, 1800–1804. [Google Scholar]
- Gertler, J. Fault Detection and Diagnosis; Springer: London, UK, 2013; pp. 1–7. [Google Scholar]
- Marzat, J.; Piet-Lahanier, H.; Damongeot, F.; Walter, E. Model-based fault diagnosis for aerospace systems: A survey. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2012, 226, 1329–1360. [Google Scholar] [CrossRef]
- Yoon, S.; MacGregor, J.F. Fault diagnosis with multivariate statistical models part I: Using steady state fault signatures. J. Process Control 2001, 11, 387–400. [Google Scholar] [CrossRef]
- Ding, S.X. Model-Based Fault Diagnosis Techniques: Design Schemes, Algorithms, and Tools; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Simani, S.; Fantuzzi, C.; Patton, R.J. Model-based fault diagnosis techniques. In Model-Based Fault Diagnosis in Dynamic Systems Using Identification Techniques; Springer: London, UK, 2003; pp. 19–60. [Google Scholar]
- Glowacz, A. Acoustic based fault diagnosis of three-phase induction motor. Appl. Acoust. 2018, 137, 82–89. [Google Scholar] [CrossRef]
- Ma, S.; Cai, W.; Liu, W.; Shang, Z.; Liu, G. A Lighted Deep Convolutional Neural Network Based Fault Diagnosis of Rotating Machinery. Sensors 2019, 19, 2381. [Google Scholar] [CrossRef] [PubMed]
- Toliyat, H.A.; Nandi, S.; Choi, S.; Meshgin-Kelk, H. Electric Machines: Modeling, Condition Monitoring, and Fault Diagnosis; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Chen, J.; Patton, R.J. Robust Model-Based Fault Diagnosis for Dynamic Systems; Springer Science & Business Media: Berlin, Germany, 2012; Volume 3. [Google Scholar]
- Zedda, M.; Singh, R. Gas turbine engine and sensor fault diagnosis using optimization techniques. J. Propuls. Power 2002, 18, 1019–1025. [Google Scholar] [CrossRef]
- Nandi, S.; Toliyat, H.A. Fault diagnosis of electrical machines—A review. In Proceedings of the IEEE International Electric Machines and Drives Conference IEMDC’99 Proceedings (Cat. No. 99EX272), Seattle, WA, USA, 9–12 May 1999; pp. 219–221. [Google Scholar]
- Shen, L.; Tay, F.E.; Qu, L.; Shen, Y. Fault diagnosis using rough sets theory. Comput. Ind. 2000, 43, 61–72. [Google Scholar] [CrossRef]
- Rai, A.; Upadhyay, S.H. A review on signal processing techniques utilized in the fault diagnosis of rolling element bearings. Tribol. Int. 2016, 96, 289–306. [Google Scholar] [CrossRef]
- Nandi, S.; Toliyat, H.A.; Li, X. Condition monitoring and fault diagnosis of electrical motors—A review. IEEE Trans. Energy Convers. 2005, 20, 719–729. [Google Scholar] [CrossRef]
- Kankar, P.K.; Sharma, S.C.; Harsha, S.P. Fault diagnosis of ball bearings using continuous wavelet transform. Appl. Soft Comput. 2011, 11, 2300–2312. [Google Scholar] [CrossRef]
- Wang, M.H. A novel extension method for transformer fault diagnosis. IEEE Trans. Power Deliv. 2003, 18, 164–169. [Google Scholar] [CrossRef]
- Edwards, S.; Lees, A.W.; Friswell, M.I. Fault diagnosis of rotating machinery. Shock Vib. Dig. 1998, 30, 4–13. [Google Scholar] [CrossRef]
- Siddique, A.; Yadava, G.S.; Singh, B. A review of stator fault monitoring techniques of induction motors. IEEE Trans. Energy Convers. 2005, 20, 106–114. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; Zuo, M.J.; He, Z. Condition monitoring and fault diagnosis of planetary gearboxes: A review. Measurement 2014, 48, 292–305. [Google Scholar] [CrossRef]
- Gao, Z.; Ding, S.X.; Cecati, C. Real-time fault diagnosis and fault-tolerant control. IEEE Trans. Ind. Electron. 2015, 62, 3752–3756. [Google Scholar] [CrossRef]
- Fekih, A. Fault diagnosis and fault tolerant control design for aerospace systems: A bibliographical review. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 1286–1291. [Google Scholar]
- Guo, D.; Zhong, M.; Ji, H.; Liu, Y.; Yang, R. A hybrid feature model and deep learning based fault diagnosis for unmanned aerial vehicle sensors. Neurocomputing 2018, 319, 155–163. [Google Scholar] [CrossRef]
- Bondyra, A.; Gasior, P.; Gardecki, S.; Kasiński, A. Fault diagnosis and condition monitoring of uav rotor using signal processing. In Proceedings of the 2017 Signal Processing: Algorithms, Architectures, Arrangements, and Applications (SPA), Poznan, Poland, 20–22 September 2017; pp. 233–238. [Google Scholar]
- Marichal, G.; Del Castillo, M.; López, J.; Padrón, I.; Artés, M. An artificial intelligence approach for gears diagnostics in AUVs. Sensors 2016, 16, 529. [Google Scholar] [CrossRef]
- Xie, X.H.; Xu, L.; Zhou, L.; Tan, Y. GRNN Model for Fault Diagnosis of Unmanned Helicopter Rotor’s Unbalance. In Proceedings of the 5th International Conference on Electrical Engineering and Automatic Control; Springer: Berlin/Heidelberg, Germany, 2016; pp. 539–547. [Google Scholar]
- Li, C.; Sánchez, R.V.; Zurita, G.; Cerrada, M.; Cabrera, D. Fault diagnosis for rotating machinery using vibration measurement deep statistical feature learning. Sensors 2016, 16, 895. [Google Scholar] [CrossRef]
- Joshuva, A.; Sugumaran, V. Wind turbine blade fault diagnosis using vibration signals through decision tree algorithm. Indian J. Sci. Technol. 2016, 9, 1–7. [Google Scholar] [CrossRef]
- Gong, X.; Qiao, W. Simulation investigation of wind turbine imbalance faults. In Proceedings of the 2010 International Conference on Power System Technology, Hangzhou, China, 24–28 October 2010; pp. 1–7. [Google Scholar]
- Kusiak, A.; Verma, A. A data-driven approach for monitoring blade pitch faults in wind turbines. IEEE Trans. Sustain. Energy 2010, 2, 87–96. [Google Scholar] [CrossRef]
- Laouti, N.; Sheibat-Othman, N.; Othman, S. Support vector machines for fault detection in wind turbines. IFAC Proc. 2011, 44, 7067–7072. [Google Scholar] [CrossRef]
- Cohen, W.W. Fast effective rule induction. In Proceedings of the International Conference on Machine Learning, Tahoe City, CA, USA, 9–12 July 1995; pp. 115–123. [Google Scholar]
- Fürnkranz, J.; Widmer, G. Incremental reduced error pruning. In Proceedings of the Machine Learning Proceedings 1994, New Brunswick, NJ, USA, 10–13 July 1994; pp. 70–77. [Google Scholar]
- Godwin, J.L.; Matthews, P. Classification and detection of wind turbine pitch faults through SCADA data analysis. IJPHM Spec. Issue Wind Turbine PHM 2013, 4, 90. [Google Scholar]
- Baskaya, E.; Bronz, M.; Delahaye, D. Fault detection & diagnosis for small uavs via machine learning. In Proceedings of the 2017 IEEE/AIAA 36th Digital Avionics Systems Conference (DASC), St. Petersburg, FL, USA, 17–21 September 2017; pp. 1–6. [Google Scholar]
- Pourpanah, F.; Zhang, B.; Ma, R.; Hao, Q. Anomaly Detection and Condition Monitoring of UAV Motors and Propellers. In Proceedings of the 2018 IEEE SENSORS, New Delhi, India, 28–31 October 2018; pp. 1–4. [Google Scholar]
- de Jesus Rangel-Magdaleno, J.; Ureña-Ureña, J.; Hernández, A.; Perez-Rubio, C. Detection of unbalanced blade on UAV by means of audio signal. In Proceedings of the 2018 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 7–9 November 2018; pp. 1–5. [Google Scholar]
- Pechan, T.; Sescu, A. Experimental study of noise emitted by propeller’s surface imperfections. Appl. Acoust. 2015, 92, 12–17. [Google Scholar] [CrossRef]
- Miljković, D. Methods for attenuation of unmanned aerial vehicle noise. In Proceedings of the 2018 41st International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 21–25 May 2018; pp. 0914–0919. [Google Scholar]
- Kurtz, D.W.; Marte, J.E. A review of aerodynamic noise from propellers, rotors, and lift fans. Jet Propulsion Laboratory, California Institute of Technology. Tech. Rep. 1970, 32–1462. [Google Scholar]
- International Electrotechnical Commission. IEC 60942: 2003. Electroacoustics–Sound Calibrators; International Electrotechnical Commission: Geneva, Switzerland, 2003. [Google Scholar]
- UNI EN ISO 3745:2012. Acoustics. Determination of Sound Power Levels of Noise Sources using Sound Pressure Precision Methods for Anechoic and Hemi-Anechoic Rooms. Available online: https://www.iso.org/standard/45362.html (accessed on 1 June 2019).
- Patro, S.; Sahu, K.K. Normalization: A preprocessing stage. arXiv 2015, arXiv:1503.06462. [Google Scholar] [CrossRef]
- Anthony, M.; Bartlett, P.L. Neural Network Learning: Theoretical Foundations; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Møller, M. A scaled conjugate gradient algorithm for fast supervised learning. Neural Netw. 1993, 6, 525–533. [Google Scholar] [CrossRef]
- Ebrahimkhanlou, A.; Salamone, S. Single-sensor acoustic emission source localization in plate-like structures using deep learning. Aerospace 2018, 5, 50. [Google Scholar] [CrossRef]
- Wild, G.; Murray, J.; Baxter, G. Exploring civil drone accidents and incidents to help prevent potential air disasters. Aerospace 2016, 3, 22. [Google Scholar] [CrossRef]
- Heredia, G.; Caballero, F.; Maza, I.; Merino, L.; Viguria, A.; Ollero, A. Multi-unmanned aerial vehicle (UAV) cooperative fault detection employing differential global positioning (DGPS), inertial and vision sensors. Sensors 2009, 9, 7566–7579. [Google Scholar] [CrossRef]
- Sun, B.; Wang, J.; He, Z.; Zhou, H.; Gu, F. Fault Identification for a Closed-Loop Control System Based on an Improved Deep Neural Network. Sensors 2019, 19, 2131. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, F.; Zhu, A. Bearing Fault Diagnosis Based on a Hybrid Classifier Ensemble Approach and the Improved Dempster-Shafer Theory. Sensors 2019, 19, 2097. [Google Scholar] [CrossRef]
- Zhuang, Z.L.; Lv, H.C.; Xu, J.; Huang, Z.Z.; Qin, W. A Deep Learning Method for Bearing Fault Diagnosis through Stacked Residual Dilated Convolutions. Appl. Sci. 2019, 9, 1823. [Google Scholar] [CrossRef]
- Iannace, G.; Ciaburro, G.; Trematerra, A. Heating, Ventilation, and Air Conditioning (HVAC) Noise Detection in Open-Plan Offices Using Recursive Partitioning. Buildings 2018, 8, 169. [Google Scholar] [CrossRef]
- Leite, A.; Pinto, A.; Matos, A. A Safety Monitoring Model for a Faulty Mobile Robot. Robotics 2018, 7, 32. [Google Scholar] [CrossRef]
- Almeshal, A.; Alenezi, M. A Vision-Based Neural Network Controller for the Autonomous Landing of a Quadrotor on Moving Targets. Robotics 2018, 7, 71. [Google Scholar] [CrossRef]
- Papa, U.; Iannace, G.; Del Core, G.; Giordano, G. Sound power level and sound pressure level characterization of a small unmanned aircraft system during flight operations. Noise Vib. Worldw. 2017, 48, 67–74. [Google Scholar] [CrossRef]
- Leslie, A.; Wong, K.C.; Auld, D. Broadband noise reduction on a mini-UAV propeller. In Proceedings of the 14th AIAA/CEAS Aeroacoustics Conference (29th AIAA Aeroacoustics Conference), Vancouver, BC, Canada, 5–7 May 2008; p. 3069. [Google Scholar]
- Massey, K.; Gaeta, R. Noise measurements of tactical UAVs. In Proceedings of the 16th AIAA/CEAS Aeroacoustics Conference, Stockholm, Sweden, 7–9 June 2010; p. 3911. [Google Scholar]
- Christnacher, F.; Hengy, S.; Laurenzis, M.; Matwyschuk, A.; Naz, P.; Schertzer, S.; Schmitt, G. Optical and acoustical UAV detection. Int. Soc. Opt. Photonics 2016, 9988, 99880B. [Google Scholar] [CrossRef]
- Sadasivan, S.; Gurubasavaraj, M.; Sekar, S.R. Acoustic signature of an unmanned air vehicle exploitation for aircraft localisation and parameter estimation. Def. Sci. J. 2001, 51, 279–284. [Google Scholar] [CrossRef]
- Sinibaldi, G.; Marino, L. Experimental analysis on the noise of propellers for small UAV. Appl. Acoust. 2013, 74, 79–88. [Google Scholar] [CrossRef]
- Papa, U.; Iannace, G.; Del Core, G.; Giordano, G. Determination of sound power levels of a small UAS during flight operations. In Proceedings of the INTER-NOISE 2016—45th International Congress and Exposition on Noise Control Engineering: Towards a Quieter Future, Hamburg, Germany, 21–24 August 2016; pp. 216–226. [Google Scholar]



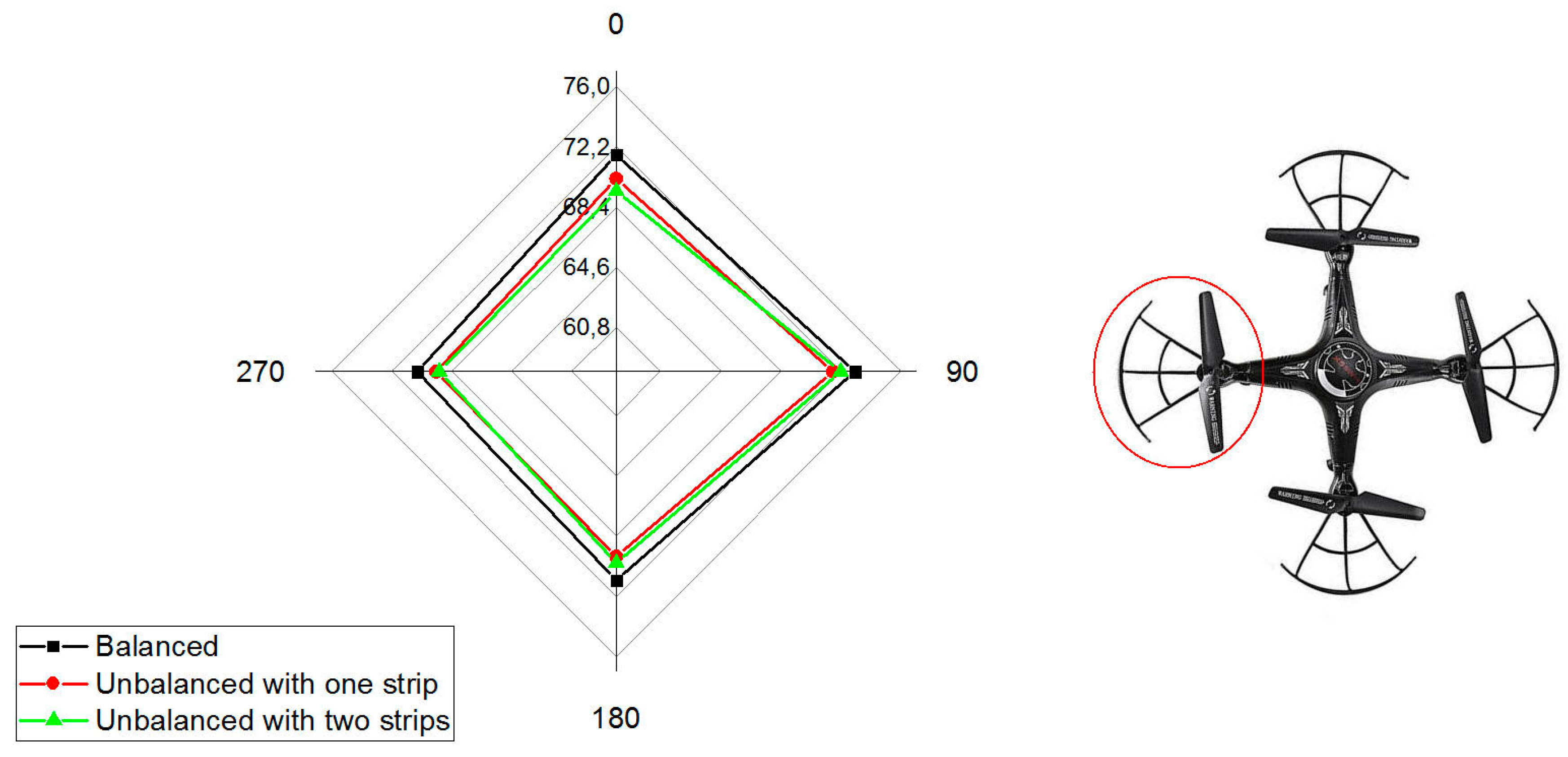
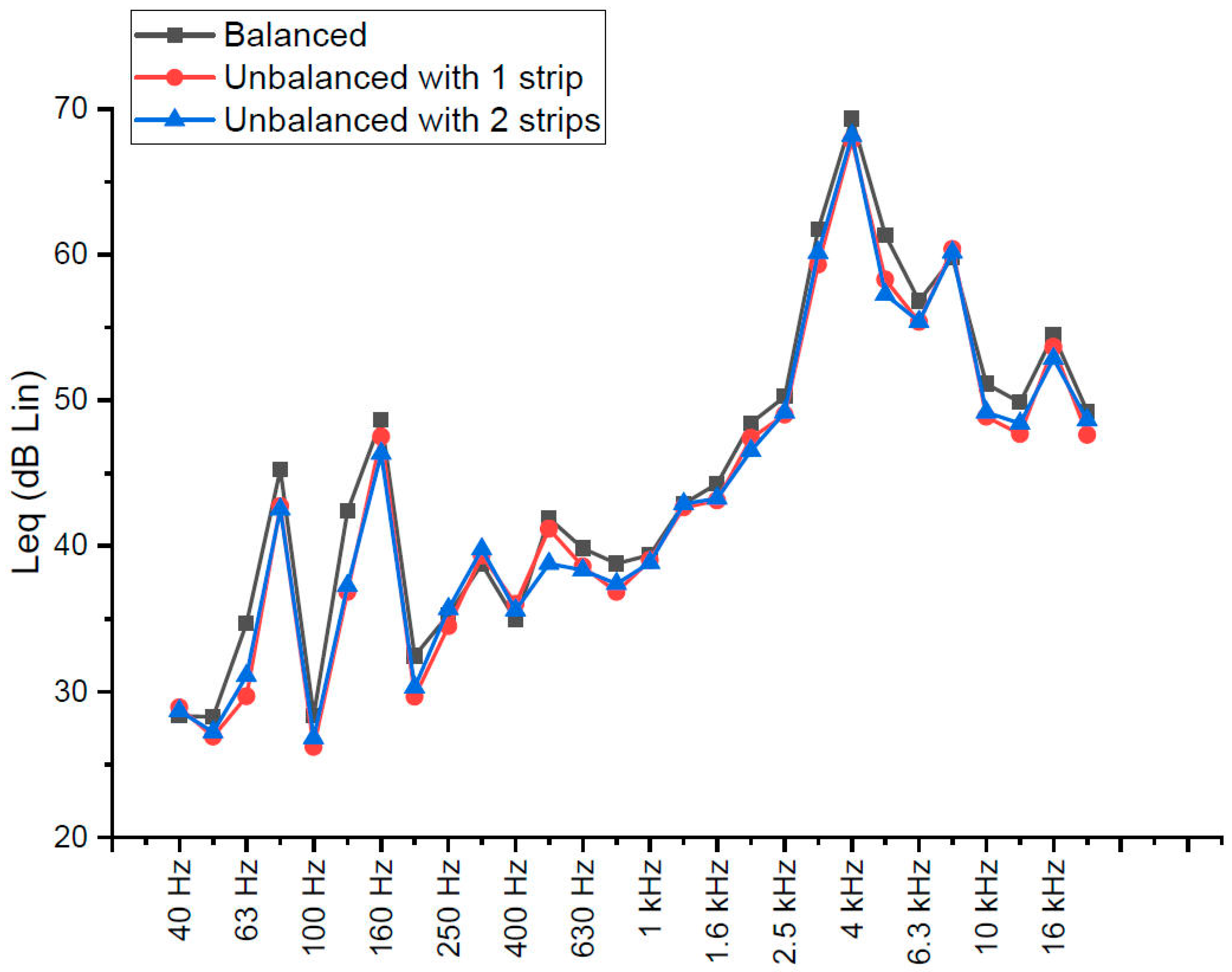

| Microphone Position | Balanced [dB Lin] | Unbalanced with 1 Strip [dB Lin] | Unbalanced with 2 Strips [dB Lin] |
|---|---|---|---|
| 0° | 71.7 | 70.2 | 69.4 |
| 90° | 73.1 | 71.7 | 72.2 |
| 180° | 71.2 | 69.7 | 70.1 |
| 270° | 70.6 | 69.4 | 69.2 |
| Balanced | Unbalanced with 1 Strip | Unbalanced with 2 Strips | |
|---|---|---|---|
| Number of samples | 243 | 287 | 317 |
| Time constant (ms) | 125 | 125 | 125 |
| Number of features | 31 | 31 | 31 |
| Number of Samples | % | |
|---|---|---|
| Starting Dataset | 847 | 100 |
| Train data | 594 | 70 |
| Test data | 253 | 30 |
| Predicted | ||||
|---|---|---|---|---|
| 0 | 1 | 2 | ||
| Actual | 0 | 71 | 1 | 0 |
| 1 | 1 | 83 | 2 | |
| 2 | 0 | 2 | 93 | |
| Class 0 | Class 1 | Class2 | |
|---|---|---|---|
| Sensitivity | 0.9861 | 0.9651 | 0.9789 |
| Specificity | 0.9945 | 0.9820 | 0.9873 |
| Balanced Accuracy | 0.9903 | 0.9736 | 0.9831 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iannace, G.; Ciaburro, G.; Trematerra, A. Fault Diagnosis for UAV Blades Using Artificial Neural Network. Robotics 2019, 8, 59. https://doi.org/10.3390/robotics8030059
Iannace G, Ciaburro G, Trematerra A. Fault Diagnosis for UAV Blades Using Artificial Neural Network. Robotics. 2019; 8(3):59. https://doi.org/10.3390/robotics8030059
Chicago/Turabian StyleIannace, Gino, Giuseppe Ciaburro, and Amelia Trematerra. 2019. "Fault Diagnosis for UAV Blades Using Artificial Neural Network" Robotics 8, no. 3: 59. https://doi.org/10.3390/robotics8030059
APA StyleIannace, G., Ciaburro, G., & Trematerra, A. (2019). Fault Diagnosis for UAV Blades Using Artificial Neural Network. Robotics, 8(3), 59. https://doi.org/10.3390/robotics8030059







