Proposed Smooth-STC Algorithm for Enhanced Coverage Path Planning Performance in Mobile Robot Applications

Abstract

Robotic path planning is a field of research which is gaining traction given the broad domains of interest to which path planning is an important systemic requirement. The aim of path planning is to optimise the efficacy of robotic movement in a defined operational environment. For example, robots have been employed in many domains including: Cleaning robots (such as vacuum cleaners), automated paint spraying robots, window cleaning robots, forest monitoring robots, and agricultural robots (often driven using satellite and geostationary positional satellite data). Additionally, mobile robotic systems have been utilised in disaster areas and locations hazardous to humans (such as war zones in mine clearance). The coverage path planning problem describes an approach which is designed to determine the path that traverses all points in a defined operational environment while avoiding static and dynamic (moving) obstacles. In this paper we present our proposed Smooth-STC model, the aim of the model being to identify an optimal path, avoid all obstacles, prevent (or at least minimise) backtracking, and maximise the coverage in any defined operational environment. The experimental results in a simulation show that, in uncertain environments, our proposed smooth STC method achieves an almost absolute coverage rate and demonstrates improvement when measured against alternative conventional algorithms.

1. Introduction

Robots have been employed in a diverse range of domains and systems; for example robotic systems have addressed the demands of: Cleaning (such as robotic vacuum cleaners), automated paint spraying, window cleaning, forest monitoring, and agriculture (where robotic control and monitoring systems are often implemented using geostationary positional satellite data), and in disaster areas and locations hazardous to humans (such as war zones and locations with restricted access) [1,2]. The broad range of robot applications has driven interest in optimising the operational efficacy of robots, to address this challenge, research into the coverage path planning (CPP) problem has gained significant traction. CPP describes an approach which is designed to determine the path that traverses all points in a defined operational environment (DOE) while avoiding static and dynamic (moving) obstacles within a defined operational area [3,4]. Further investigation has been concerned with an Iterative Structured Orientation Coverage, which is capable of handling complex environments [5], in an investigation of the current state of swarm robotics such as self-reconfigurable, modular, self-replicating, and swarm systems [6].

An typical application of CPP is an automatic robotic domestic vacuum cleaner which, when activated using CPP, can manoeuvre around a DOE (typically a room or on one level) to clean the area while avoiding static (moving) obstacles (such as furniture) or dynamic (moving) objects (such as a domestic animal) when traversing the DOE [7,8]. To solve this problem, it is necessary to build an algorithm to find optimal coverage path for the DOE; in studies addressing CPP (for example see Cao et al. [9]) basic standards for the robotic path coverage problem have been set (see Section 2).

In this paper, to overcome the outstanding limitations in current CPP applications (and obtain maximum coverage of the DOE) we propose a new Smooth-STC (SmSTC) algorithm based on the use of a spanning tree. Our proposed SmSTC model targets the identification of optimal paths while avoiding all obstacles, preventing (or at least minimising) backtracking, and maximising the coverage in any DOE. The experimental results in a simulation show that, in uncertain environments, our proposed smooth STC method achieves an almost absolute coverage rate and demonstrates improvement when measured against alternative conventional algorithms.

The remainder of this paper is structured as follows: Section 2 considers related research addressing the CPP problem. CPP in unknown environments is addressed in Section 3 with CPP environments considered in Section 4. Section 4.5 sets out the proposed SmSTC algorithm with the results and a discussion set out in Section 6 with an overview of potential future work. The paper closes with concluding observations.

2. Related Research

In considering the CPP problem a number of basic standards for the robotic path coverage problem have been identified; for example, see Cao et al. [9]; in practice it is not always possible to satisfy all the basic standards and there is frequently a ‘trade-off’ to reach an optimal domain-specific solution. The ‘trade-off’ is reflected in the current research where methods focus on certain ‘specific’ constraints.

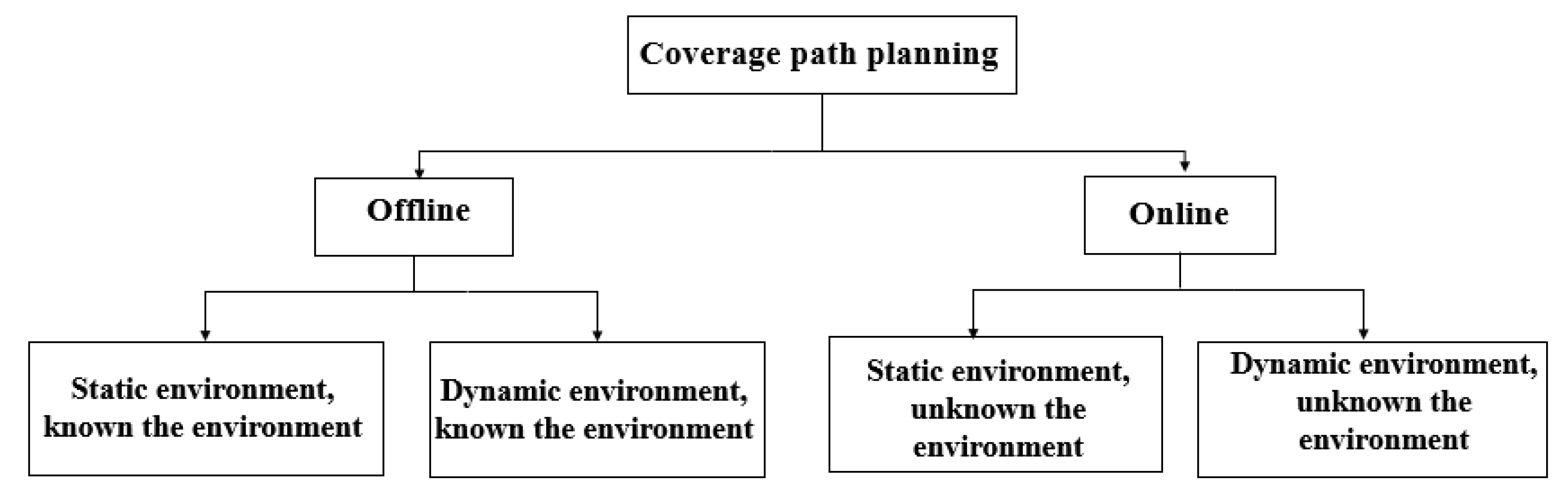
Over the past three decades, robotics research has mainly focused on solving the CPP and coverage path optimisation problems in both static environments (environments where obstacles do not move) and dynamic environments (environments in which there are both static and dynamic (moving) obstacles). The CPP problem may be approached in two ways: ’Classical’ and ’heuristic’ methods (also identified as artificial intelligence (AI)); each of the approaches demonstrates specific strengths and weaknesses [3,10]. In Figure 1 we present our graphical composite summary of the mainstream approaches to CPP, namely ’off-line’ and ’on-line’ methods; the classification tree is drawn from related research sources reviewed, principally [3,11].

CPP algorithms are categorised as ’on-line and ’off-line’, see Choset, 2001) [11]. Off-line algorithms assume that the working environment (the DOE) is known, therefore the path of the robot can be optimised. In contrast, on-line algorithms do not need to know the advance the DOE information, the operation of a robot is based on information collected from ‘real-time’ sensors which read and monitor the DOE and the location, shape, and size of the obstacles [12,13] thus providing a suitable path to provide complete coverage of the DOE. On-line algorithms are generally known as sensor-based coverage algorithms [3,14]. Moreover, dependent on the conditions of the DOE, it is possible to classify more detailed problems based on static environments or dynamic environments; in this paper, the authors consider static environments. Figure 1 shows a graphical representation of the coverage path planing problem.

A simple approach to solving the CPP problem is a random algorithm. For example, consider a cleaning robot where the cleaning is randomly executed without time restrictions, while the cleaning may be effective the algorithmic approach is not efficient or reliable [3,9,15]. For example, some commercial robots (such as Roomba by iRobot [7]) do not need to be equipped with complex sensors to enable location determination and calculation (of the coverage path) and are therefore more simple.

Nonetheless, in a large area or a three-dimensional space (such as an underwater or aerial DOE) the operational costs of the robot (in terms of both energy and time) can be very expensive and therefore in a ‘real-world’ application not feasible; therefore alternative approaches are required [15,16].

• First, it is necessary to divide the environment into small continuous areas where the robot can completely move without colliding with obstacles [17];
• In this way, there are algorithms such as Trapezoidal Decomposition, Boustrophedon Decomposition, BSA, and BA* just to name a few [18,19];
• All of them need to have a mechanism for linking domains to achieve optimal coverage; “backtracking” points are used with different algorithms to find the shortest path from the current location to those backtracking points. The greater the number of backtracking points, the larger the overlap area and the longer execution time for the robot. Moreover, the robot also requires a large enough memory to store all of the backtracking points.

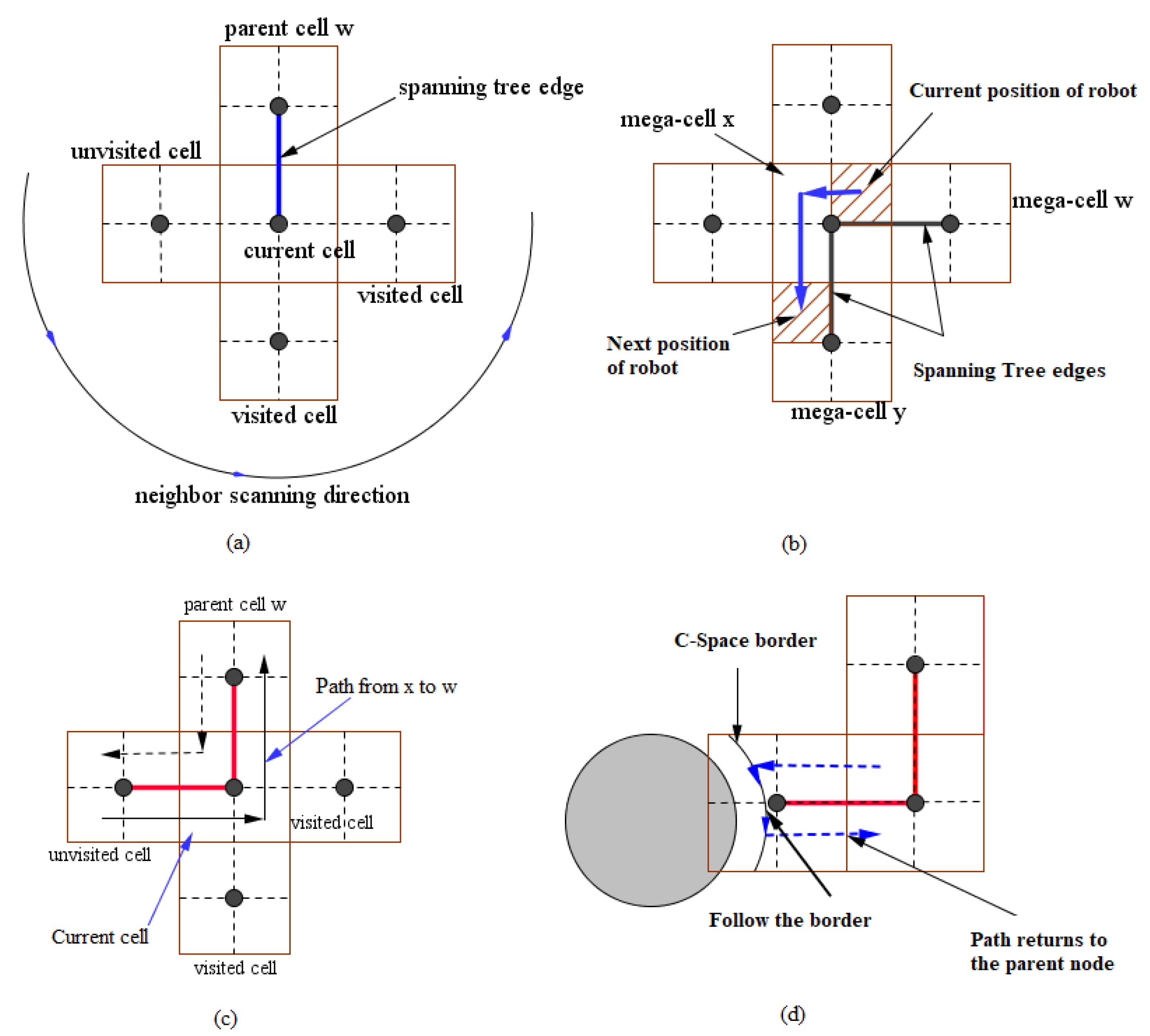
An alternative approach is to divide the environment into a grid of equal sized cells, the cells being equal to the size of the robot. The Spanning Tree Covering (STC) algorithm (see Section 3) is a significant example of this approach, it defines two types of cell: mega-cells and sub-cells that create a spanning tree between mega-cells and a path covered [by a robot] over the sub-cells by moving along the spanning tree. It has been proven to enable the coverage of the DOE with limited of no overlapping. However, the major limitation (of the STC algorithm) lies in the coverage area not being optimal. 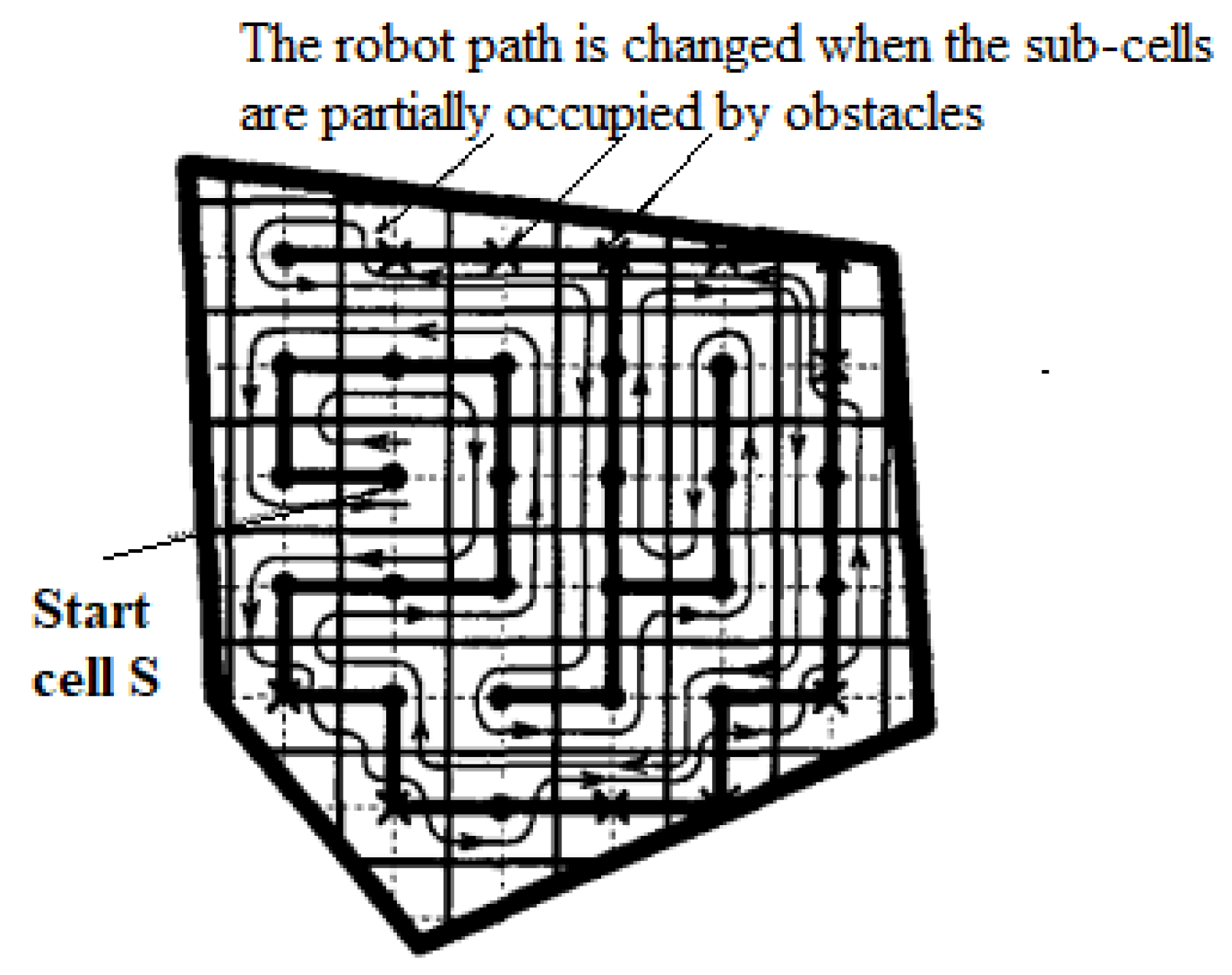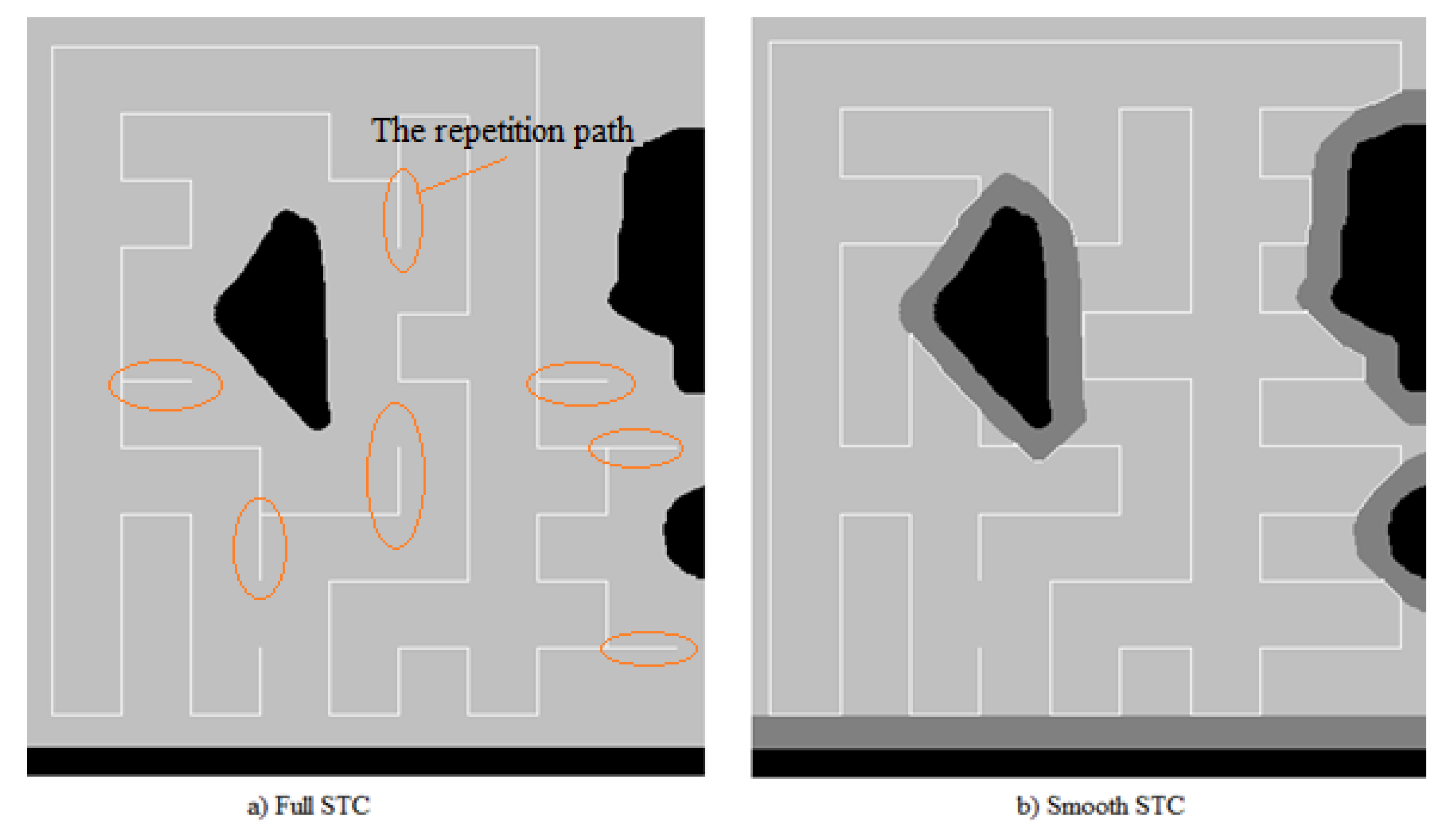Figure 2a demonstrates the limitations of the STC Algorithm; if a mega-cell is occupied by a part of an obstacle then the entire mega-cell is also seen as an obstruction occupied entirely by an obstacle, as such a robot will consider the entire cell an obstruction and fail to cover the cell area. Therefore, the DOE will not be entirely covered.

A proposed improvement in the STC algorithm is a Full-STC algorithm where a robot ignores only sub-cells occupied by obstacles. In this case, an overlap in DOE coverage is accepted in exchange for a large coverage area. The limitation of this algorithm is shown in Figure 2b. Depending on the shape and size of the obstruction, the cell coverage area also changes.

Research in [20] by Luo & Yang proposes a neural network based approach to CPP predicated on grid maps along with other recent improvements in 2008 [21] and 2015 [22]. The DOE is into grid cells (similar to sub-cells in STC) called neurons. The possibility nodes can carry activate values (free cell) or restrain values (fully occupied cell or partially occupied by obstacles). This approach is based on the neural propagation model (NPM) of Hodgkin-Huxley (1952) [23]; in the NPM the objective is to ensure high-positive neurons will be propagated to the entire environment while restrained neurons will only spread within a narrow range of its neighbours [21,24]. The robot determines the next position by selecting the proximity of the highest positive neuron. The drawback of STC algorithms is that all cells that occupied partly by obstacles are bypassed.

Our SmSTC method presented in this paper aims to address the limitations of the related research considered by targeting the identification of optimal paths while avoiding all obstacles, preventing (or at least minimise) backtracking, and maximising the coverage in any DOE. The SmSTC algorithm aims to address.

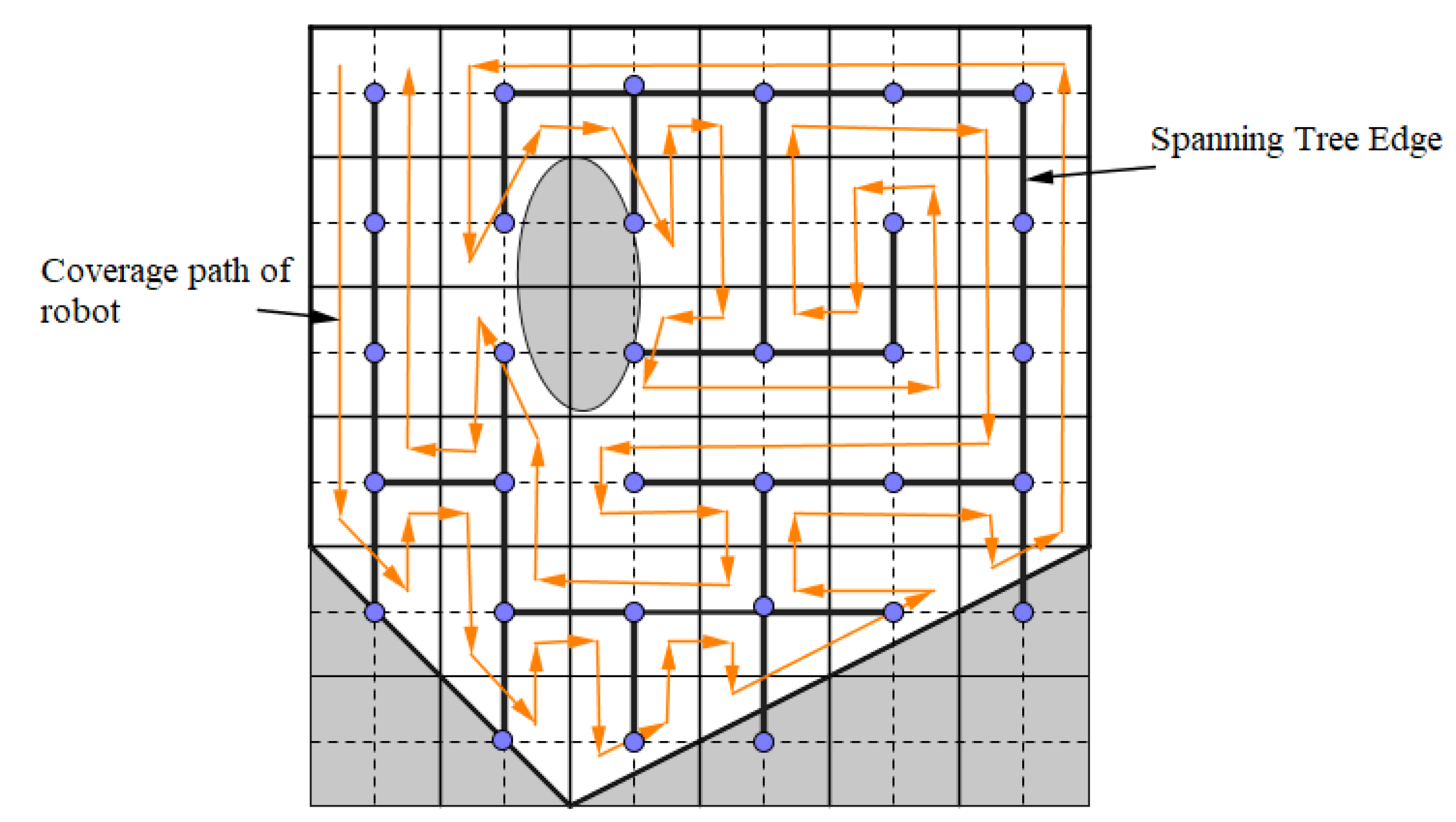
3. Robot Coverage Path Planning in Unknown Environments

In a static known environment, obstacles are fixed and the robot will anticipate environmental information before implementing coverage [25]. One of the classic methods to solve this problem is divide the DOE into non-overlapping sub-domains (cells) that contain no obstacles which called cell. These cells are easily covered with simple movements of robot like a zigzag line. Two cells are called adjacent if they share the same edge. An adjacent graph is used to represent the relationship between cells. The nodes represent the cells and the edges represent the links between the cells. The problem now is finding a path through all the nodes of the graph. 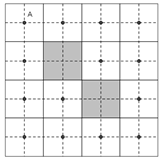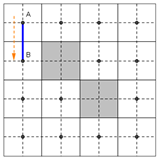(Figure 3 shows an adjacent graph for the algorithm).

Gabriely & Rimon (2002) [12] proposed the Spiral Spanning Tree Coverage (SSTC) algorithm which is an on-line algorithm in which the path of the robot was built in a spiral; two SSTC algorithms are introduced: SSTC and Full-STC. As with STC off-line, the entire grid is divided into mega-cells, each of them contains four robot size smaller cells. However, the robot is equipped with two additional sensors: a position-direction sensor and a sensor to detect obstacles [12,16]. Whenever the robot reaches a certain mega-cell that will be marked “visited" and against the new cells marked “unvisited”. The robot will scan the clockwise direction to find the first neighbourhood marked “unvisited” in order to create a spanning tree. The robot then moves to the right edge from the current cell to the selected neighbouring cell. The algorithm ends when the robot returns to its original position.

As with the off-line STC algorithm, SSTC will ignore the mega-cells that are partially or wholly occupied by obstacles; therefore, it still carries the limitations of STC. Along with the Full-STC algorithm, the SSTC algorithm ignores only the sub-cells occupied by obstacles and creates a pathway through the remaining free sub-cells. Figure 3 shows the path resulting from the use of the Full-STC algorithm.

4. Robot Coverage Path Planning Environments

In this section we address robotic coverage path planning environments and consider: (a) The conceptual cells of a robot, (b) the nodes in a mega cell and sub cells, (c) The C-Space in the world of the mobile robot, (d) the adjacent graph, (e) the connection edge between two nodes of two adjacent mega-cells, and (f) the input and output edges. In Section 4.5 we introduce our proposed Smooth-STC algorithm.

4.1. Conceptual Cells of the Robot

Similar to the STC algorithms, the grid division uses two cell types which are $D\times D$-sized sub-cells and $2D\times 2D$-sized mega-cell (D is the size of the robot). Each mega-cell will contain 4 sub-cells inside and Figure 4 shows two types of cell.

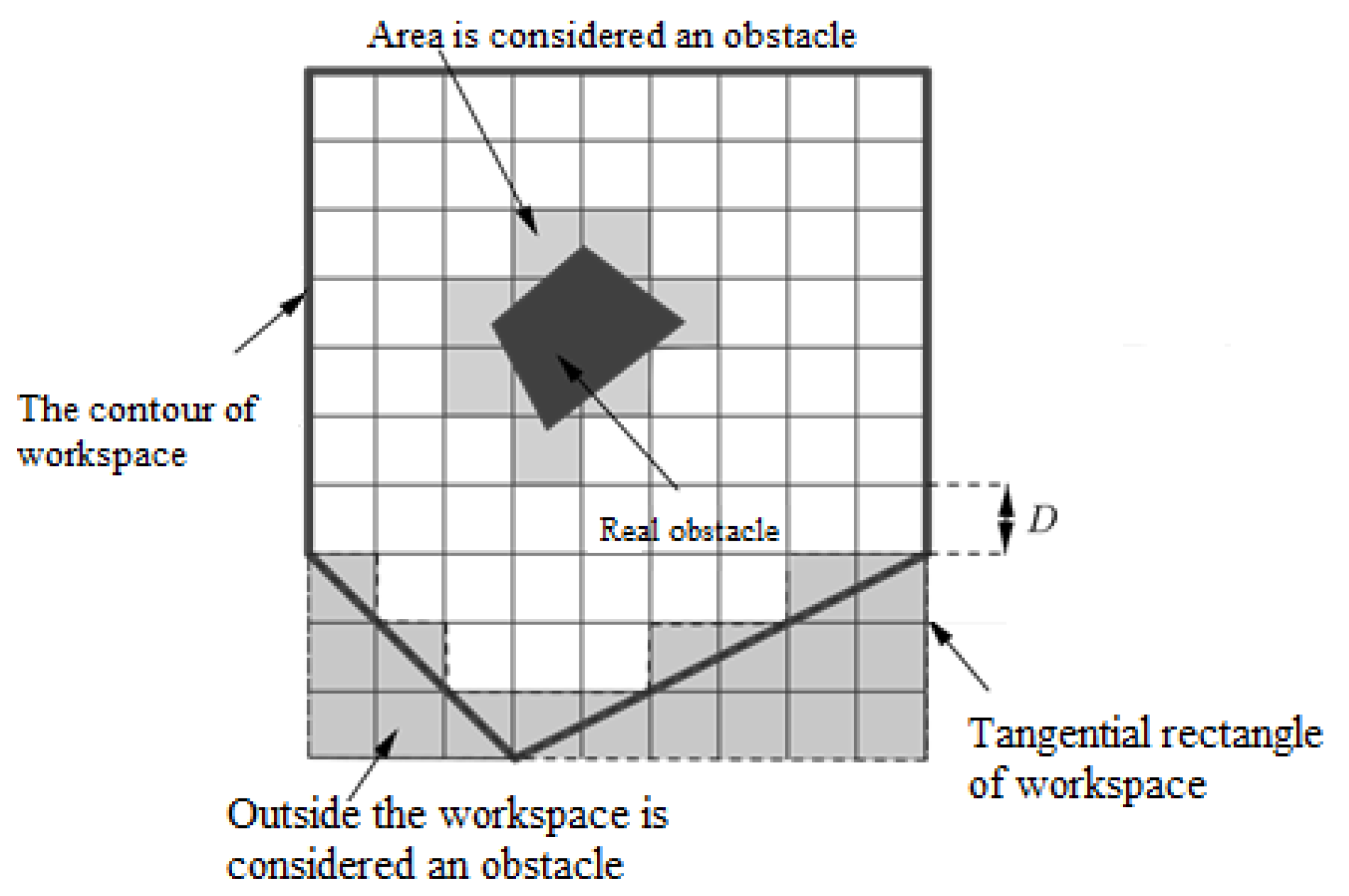
Assume Q is the workspace of robot. Consider Q performing in 2-dimensional space ($Q\subset {\mathbb{R}}^2$) and $Q_R$ is the smallest size rectangle that surrounds the Q. Assume $Q_R$ is the $2mD\times 2nD$-sized ($m,n\in {\mathbb{N}}^{*}$) in other words $Q_R$ is divided into $\left(m\times n\right)$ mxn mega-cells of $\left(2D\times 2D\right)$ size.

Suppose there are N obstructions in Q which are $O=\{O_1,O_2,\dots ,O_N\}$. Each obstruction $O_i$ can occupy whole or part of the sub-cell. Space outside the work area of $Q_R$ will be considered an obstacle. An illustration of this division is shown in Figure 5.

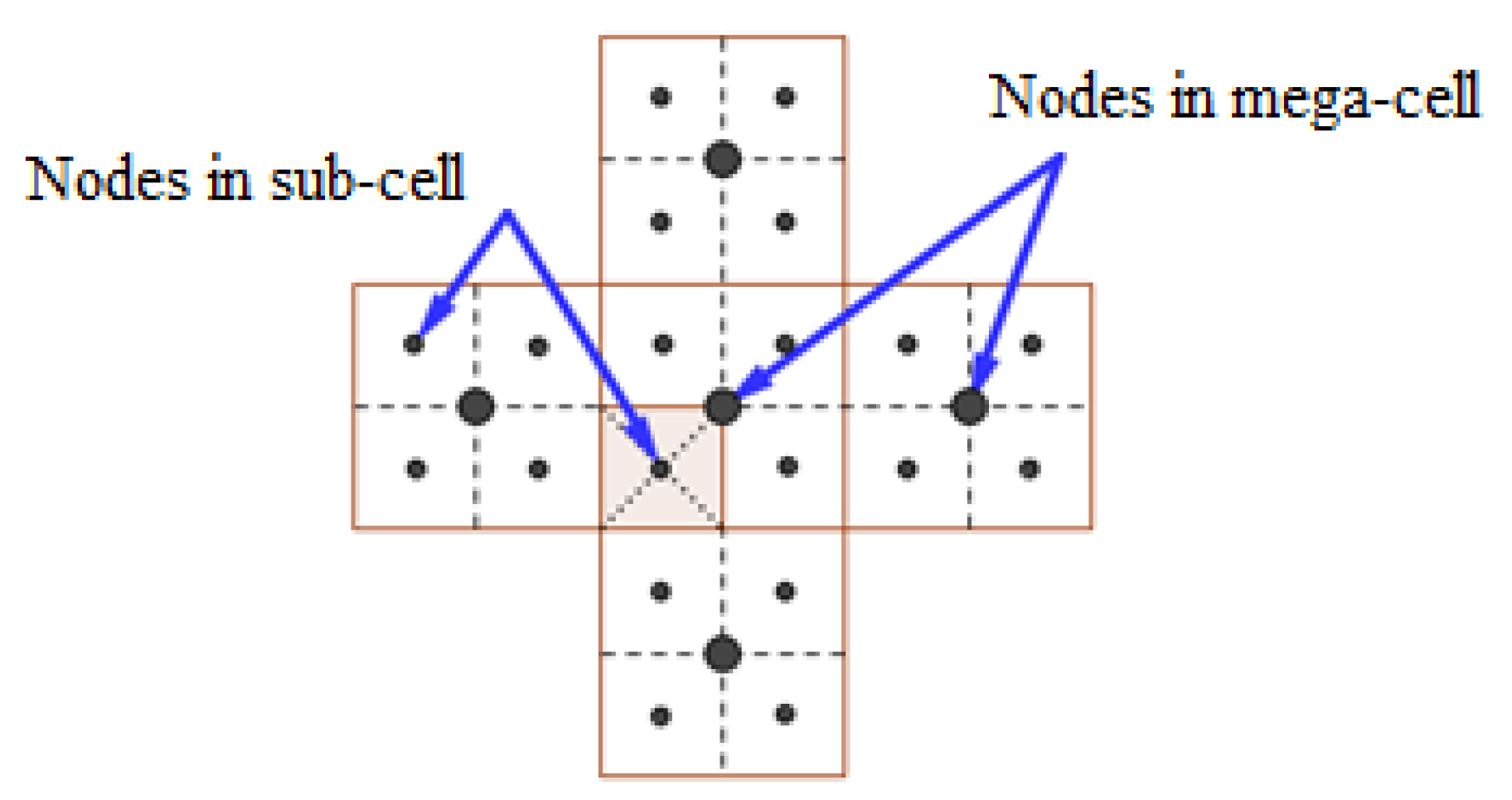
4.2. Nodes in a Mega Cell and Sub Cells

Each mega-cell will be characterised by a node located centrally in the cell, the same configuration will apply to each sub-cell. Figure 6 shows the location of the nodes in the centre of the cells. These nodes play an important role in creating the spanning tree of the SmSTC algorithm.

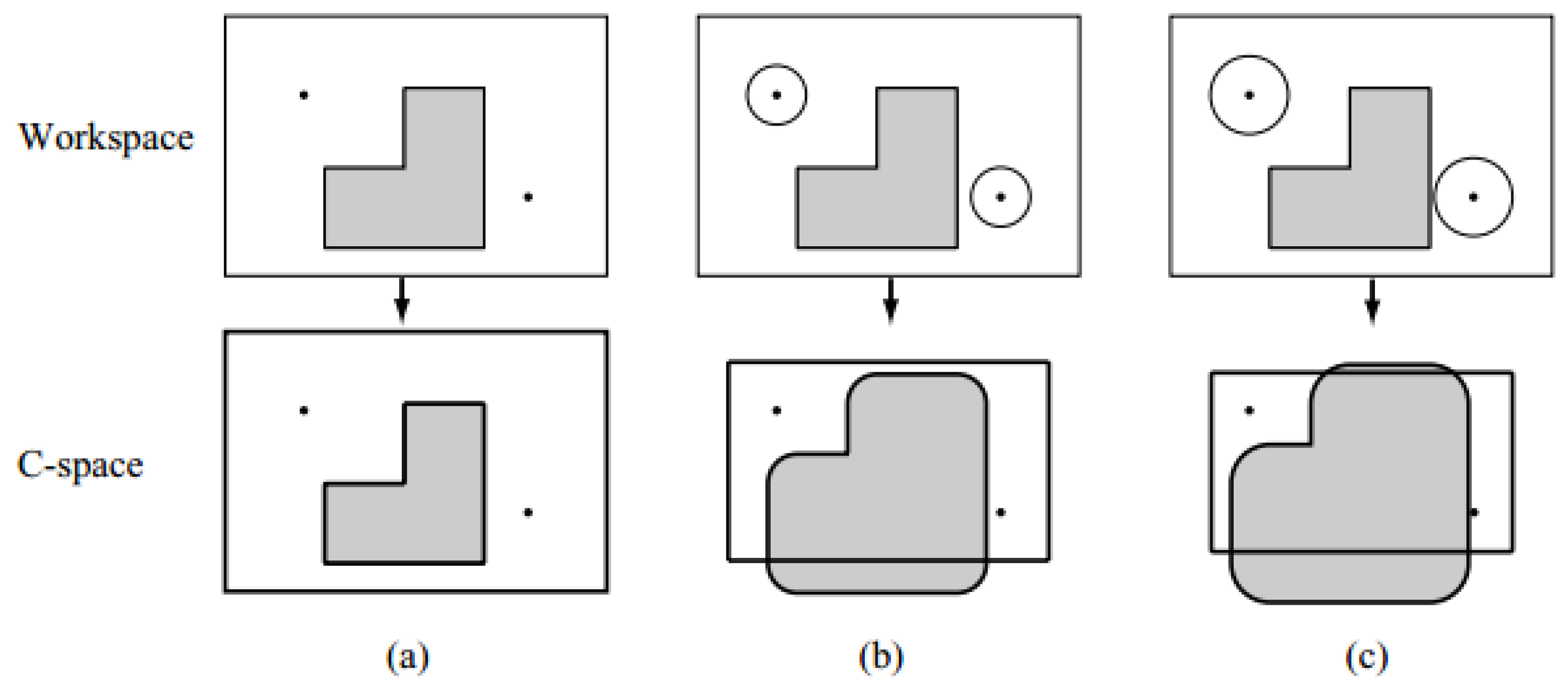
4.3. C-Space in the World of the Mobile Robot

The C-Space simply considers an object of any shape in this space (the DOE) as a point. Assume C is a C-Space where $q=\left(x,y\right)$ are points in the DOE occupied by the robot. $R\left(q\right)$ is a set of the q points. Obstructions $O_i$ in C-Space is a form in which robots intersect with a real obstacle $W{O}_i$ in the workspace ie: $O_i=\{q\in C|R\left(q\right)\cap W{O}_i\ne \varnothing \}$. The free space also known as the $C_o$ free space which is a set of areas in which robots do not intersect with any obstacles $W{O}_i$.

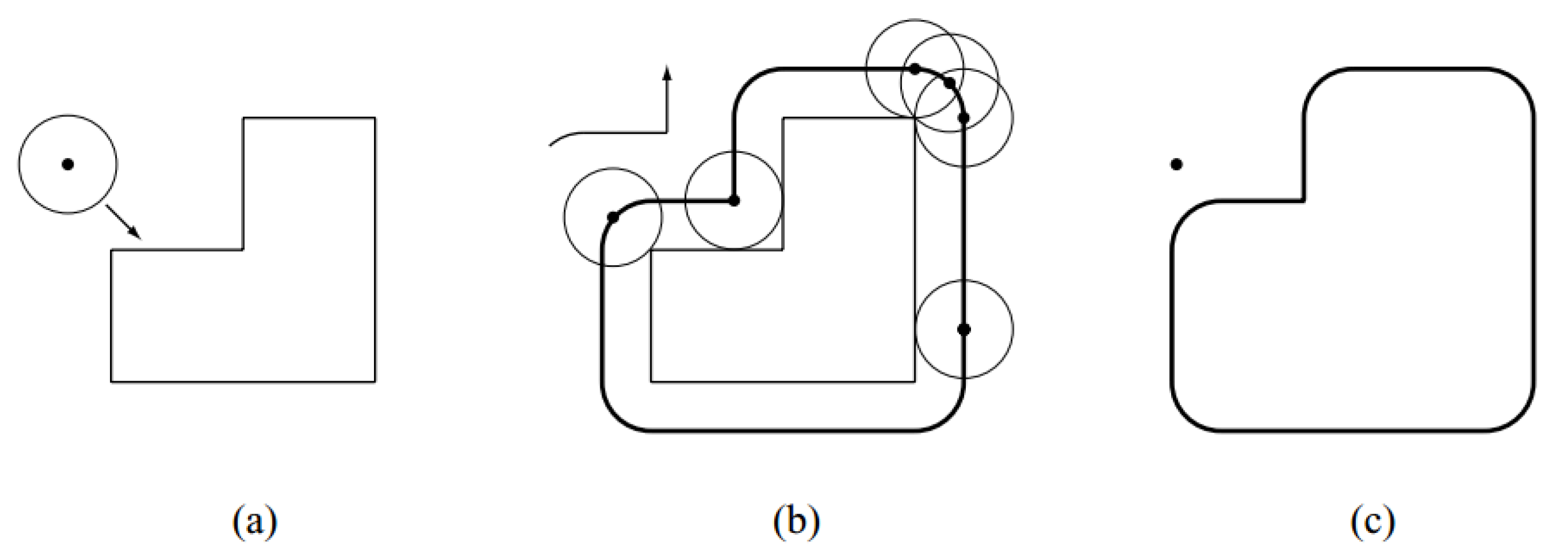
Considering a circular robot represented by a centre $\left(x,y\right)$ in space. Knowing the r radius of the robot can completely identify the set of points $q=(x,y)$ in the space occupied by the robot. $R_q=\{(x^{\prime },y^{\prime })|{(x-x^{\prime })}^2+{(y-y^{\prime })}^2\le r^2\}$. Suppose the workspace of robot has only one obstruction (see Figure 7). Figure 7b showing the robot moves around an obstacle to determine the shape of an obstacle in the C-Space. At that time, the robot can be viewed as a point in C-Space and it can move arbitrarily without affecting obstacles (Figure 7c). Depending on the size of each robot that the shape of the C-Space is different (see Figure 7).

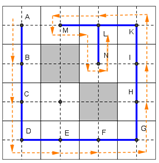
4.4. Adjacent Graph

An adjacent graph $G(V,E)$ has a set of vertices V which is the set of nodes in the mega-cells and E is the connections between the nodes in two adjacent mega-cells. Smooth-STC uses this graph to create a robot cover path.

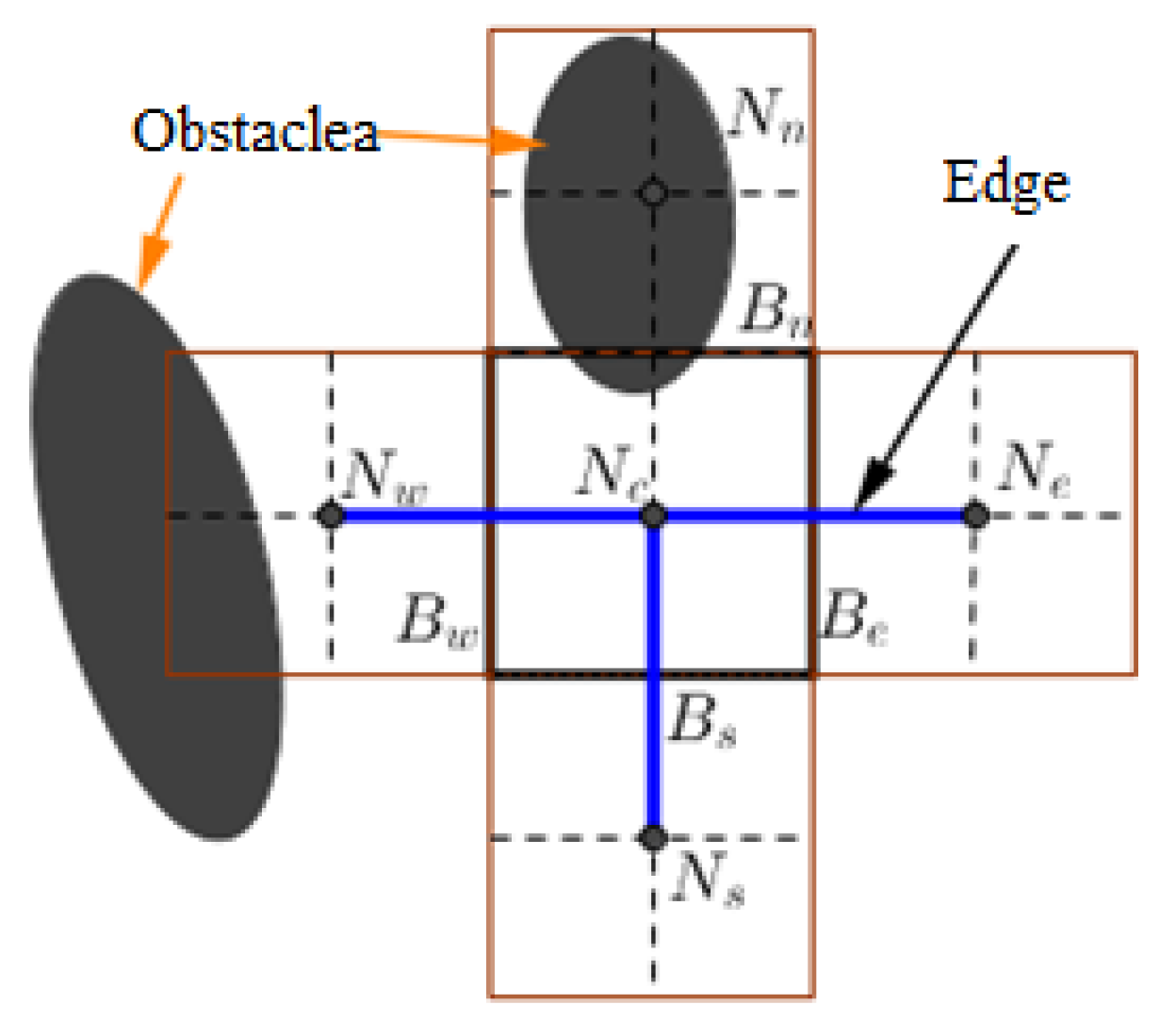
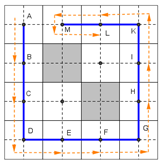
4.4.1. Connection Edge between Two Nodes of Two Adjacent Mega-Cells

Where the edge between two adjacent mega-cells is completely free, a connected edge between the corresponding nodes on the graph can be created and vice versa, then two nodes cannot be connected through this edge. Figure 8 shows the connections of adjacent mega-cells. Node $N_c$ can create the connect with nodes $N_e$, $N_s$ and $N_w$ because the common edges between them ($B_e$, $B_s$ and $B_w$) are free. With node $N_c$, it is not possible to create a connection to $N_n$ since the common edge $B_n$ is partially occupied by the obstacle. Figure 9 models this condition.

4.4.2. Input and Output Edges

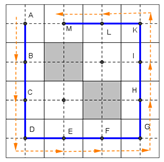
If node $N_i$ can create a connected edge $E_{ij}$ to an adjacent node $N_j$, that edge $E_{ij}$ is termed the input edge of node $N_j$ and output edge of node $N_i$. In our proposed SmSTC algorithm, completely free mega-cells may have either an input or an output edge. However, with mega-cells partly occupied by an obstacle, they only have an output edge (i.e., there is no input edge). Mega-cells completely occupied by obstacles of course there will be no connection edges. Figure 10 shows an example of the input and output edge.

4.5. Proposed Smooth-STC Algorithm

In the proposed algorithm to smooth the DOE and maximise the coverage area mega-cells partially occupied by obstacles are converted into a C-Space. The authors propose two types of SmSTC algorithms: Off-line and on-line.

4.5.1. Smooth-STC in a Known Environment

Environmental information is divided into n mega-cells 2D × 2D size $M_1,M_2,\dots ,M_n$ mega-cells and the starting cell position s of mega-cell $M_s$ is the starting point for the robot to traverse the DOE.

Algorithm 1: SmSTC_offline(G, s).

Input: a grid G includes n mega-cells $M_1,M_2,\dots ,M_n$ and a starting Cell s of MegaCell $M_s$ Output: A coverage path P that cover all reachable cells in G from s 1: T = $Create\_Spaning\_Tree(G,M_s)$ 2: P = $Coverage\_Step(s,T)$ 3: return P   Procedure $Creat\_Spaning\_Tree$ $(G,M_s):$ 1: T = tree consisting only the MegaCell $M_s$ 2: visit($M_s$): 3:      for each $MegaCellW$ adjacent to $M_s$ and not yet in T do 4:        add W and edge $\{M_s,W\}$ to T 5:        visit(W) 6:      end for   Procedure Coverage_Step(s, T): 1: $P\leftarrow \varnothing$ 2: current.Cell $\leftarrow s$, current.MegaCell $\leftarrow M_s$ 3: while $(\exists M_i\in G$ that ∃ edge {$M_i$, current.MegaCell} $\in T$: 4:    if $(\exists M_j\in G$ that ∃ edge {current.MegaCell,$M_j$} $\in T)$ then 5:        add path from current.Cell to next.Cell to P 6:        current.Cell $\leftarrow \mathit{next}.Cell$, current.MegaCell $\leftarrow MegaCell(\mathit{next}.Cell)$ 7:    else 8:        add path from current.Cell to Cell(last.MegaCell) to P 9:         current.MegaCell ← last.MegaCell, current.Cell $\leftarrow Cell(\mathit{last}.MegaCell)$

In the SmSTC off-line algorithm, a spanning tree is created in step 1 using DFS algorithm. However, depending on the characteristics of each mega-cell, the connection edge between nodes is different. The execution of the robot in step 2 started from a sub-cell of S. The robot performs the right-side spanning tree to move around the spanning tree and ensure complete coverage (Step 2.1). Whenever the centre of the robot is located on the boundary of the C-Space the robot will move on the boundary from right to left and returns to the previous mega-cell (Step 2). The algorithm stops when the robot returns to the original mega-cell S. Details of this algorithm are illustrated in Figure 11.

4.5.2. The SmSTC Algorithm in Unknown Environment

In the SmSTC on-line algorithm, robots will have on knowledge in advance relating to information in the DOE. They perform DOE coverage using sensors to detect obstructions. The SmSTC on-line algorithm continuously divides the working area into mega-cells and ignores the mega-cells completely occupied by obstacles. The remaining mega-cells will be used to create a graph called a spanning tree so that each node is the centre of the mega-cells and each side has the ability to connect the adjacent mega-cells.

SmSTC on-line Algorithm:

• Sensors: Position and direction sensors, detect obstacles in adjacent 4 mega-cell sensors.
• Input: Start $MegaCell{M}_s$.
• Recursive function: SmSTC ($w,x$), where $x\leftarrow$current.MegaCell, $w\leftarrow$parent.MegaCell$\left(x\right)$.
• Initialisation: SmSTC ($null,M_s$).

Algorithm 2: SmSTC($w,x$).

1: $x\leftarrow visited$.Cell 2: While ∃ unvisited.Cell do 3:     $y\leftarrow firstNeighbours\left(x\right)$ 4:      Build_Edge($x,y$) 5:     if y is free then 6:        $x\leftarrow$ Cell$\left(y\right)$ 7:     if y is not free then 8:        $accessEdge\leftarrow$ Build_C-Space_Contour$\left(y\right)$ 9:        x follow $accessEdge$ to return x 10:     SmSTC($x,y$) 11: if x is not $M_s$ then 12:      move to x

Each time the spanning tree is expanded, the robot divides the mega-cell into four sub-cells equal size for the robot. For every free mega-cell, the robot follow the path through each sub-cell surround the spanning tree. With mega-cells partially occupied by obstacles, robots perform calculations in C-Space. Here, it performs a new border movement of C-Space of that mega-cell. The algorithm stops, when all mega-cells are covered or robot returns to the start position. A mega-cell is called “unvisited” if one of its 4 sub-cells has not been covered and vice versa mega-cell will be called “visited”.

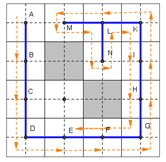
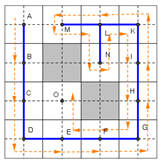
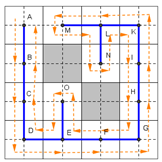
• Finding adjacent mega-cells in the counter-clockwise direction at step 2.1 ensures the path of robot when it encircles the spanning tree in a uniform direction (Figure 12a);
• At step 2.2 if x is completely free and the robot is located at a certain sub-cell of x and it can move to an “unvisited” mega-cell y;
• An edge of the spanning tree $\overrightarrow{xy}$ will be created from the mega-cell x to y. This edge will be treated as the output edge from x and the input edge in y. With the mega-cell x partially occupied, it only has input edges;
• The coverage is carried out in steps 2.3 and 2.4 for two abilities to be completely free or partially occupied by obstacles. If y is completely free then from the sub-cell position in x the robot can move to a certain sub-cell in y by moving along the right side of the $\overrightarrow{xy}$ edge (Figure 12b);
• Because y is not occupied by an obstacle, this coverage path is always guaranteed in one direction (step 2.3). If y is partially occupied by an obstacle, the robot needs to calculate the C-Space surrounding y (step 2.4);
• Assuming a robot with a circle of centre I that can see its movement as a movement of the centre I. At this point, the robot still follows the edge to enter the y until its centre I lies on the road. The boundary of the space C-Space moves centre I on this boundary from right to left of the $\overrightarrow{xy}$ edge, until the centre I is on the other side of edge $\overrightarrow{xy}$ then the robot follows the edge to return to x (Figure 12);
• Call recursively for the current node y and parent node x (step 2.4). If the current mega-cell $x_o$ has no neighbours marked as “unvisited” then $x_o$ is a leaf node when the robot will move back to the parent node (Figure 12c) or $x_o$ is the start node S. So, the robot has finished covering and the algorithm has ended. Figure 12 details the robot movement in the sub-cells of this algorithm.

5. Implementation

The implementation of algorithm is built using the programming Java language, the program interface uses Swing java library. With the SmSTC algorithm off-line, the robot has a priori information relating to the DOE. Therefore, before finding the path, the algorithm needs to build an optimal spanning tree that can use any tree traversal algorithm, DFS is an example of such an algorithm. A spanning tree is generated that allows the robot to perform coverage by following this tree. The authors used a stack to save information about the nodes after each robot visit.

• Push the start button in the stack, from the current node found node n which is the first unvisited neighbour in a anticlockwise order;
• If the n node is not empty, move the robot from the current node to node n. Mark the current button as the previous node of node n (setPreNode is the current node). Mark the n button as visited;
• If the next node n is empty, pop the current node off the stack.;
• The robot moves from the current node to the stack top button. Mark the previous node of the top of stack with the current node.
• This process repeats until stack is empty. The stack operation illustration is shown in

  Table 1. SmSTC algorithm off-line.

  S	A-B
  S	A-B-C
  	…	…
  S	A-B-C-D-E-F-G-H-I-K-L-M
  Pop M off the stack
  S	A-B-C-D-E-F-G-H-I-K-L
  Push N in stack
  S	A-B-C-D-E-F-G-H-I-K-L-N
  Pop N off the stack
  S	A-B-C-D-E-F-G-H-I-K-L
  Pop F off the stack
  S	A-B-C-D-E
  Push O in stack
  S	A-B-C-D-E-O
  	…	…
  Pop A off the stack
  S	Null
  	Finish

  .

6. Results and Discussion

In this section we present an evaluation of our SmSTC algorithm with the results obtained in experimental testing using simulation and in a ‘real-world’ environment. We have carried out a comparative analysis (using simulation) which compares the performance of our proposed approach with the other current approaches; Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17 show the relative performance of our SmSTC algorithm as compared to the alternative approaches. To evaluate our proposed method in a ‘real-world’ environment we conducted tests in the ‘Moc Chau’s hill forest’ (see Figure 18 and Figure 19) using a CIST* BK robot.

6.1. Simulation

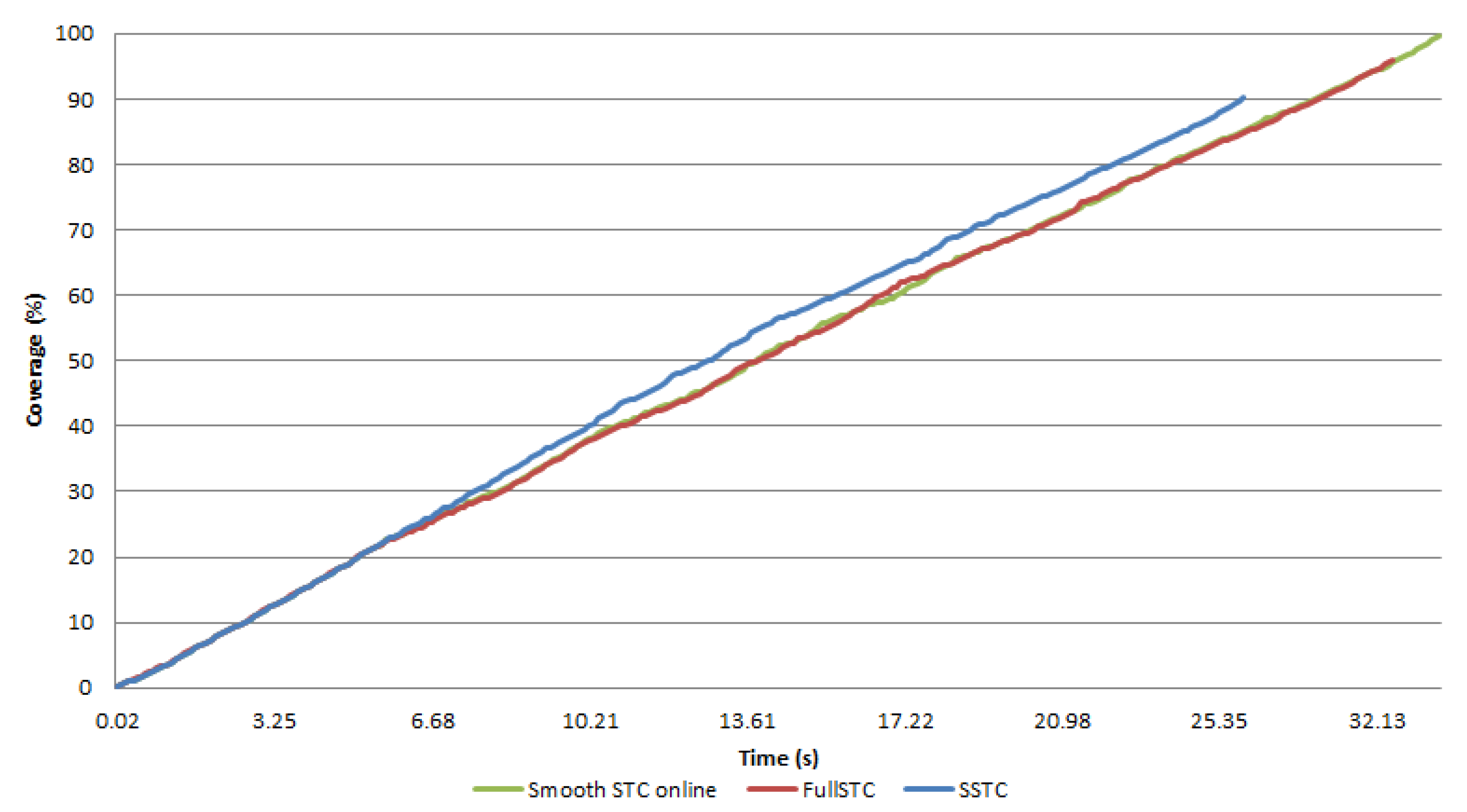
In simulation testing, our SmSTC algorithm used the same conditions and mapping in cell numbering nodes; the number of nodes used in testing is in the range 90–350. In testing we can adjust the number of nodes traversed by the robot along with the number and nature of the rules (in the knowledge-base) considered by our proposes system for both static and dynamic obstacles. For consistency, all experimental runs use the same size of robot, the same starting position, and the same starting time. Note: the coverage ratio and the relationship to time for the Smooth-STC on-line algorithm is greater than our SmSTC on-line and Full-STC algorithms as shown in Figure 13.

During the first 6 seconds (of an experimental run) the coverage rates of all algorithms are the similar, this is because during this time span there are no obstacles. From the 7th second differences have been identified: the runtime of SmSTC is shorter because of the shorter path travel distance resulting in reduced time to cover the DOE. The runtime for the Full STC and Smooth-STC algorithms are very similar; however, the coverage rate for the SmSTC is almost 100% while the coverage rate for the Full STC is only over 93%.

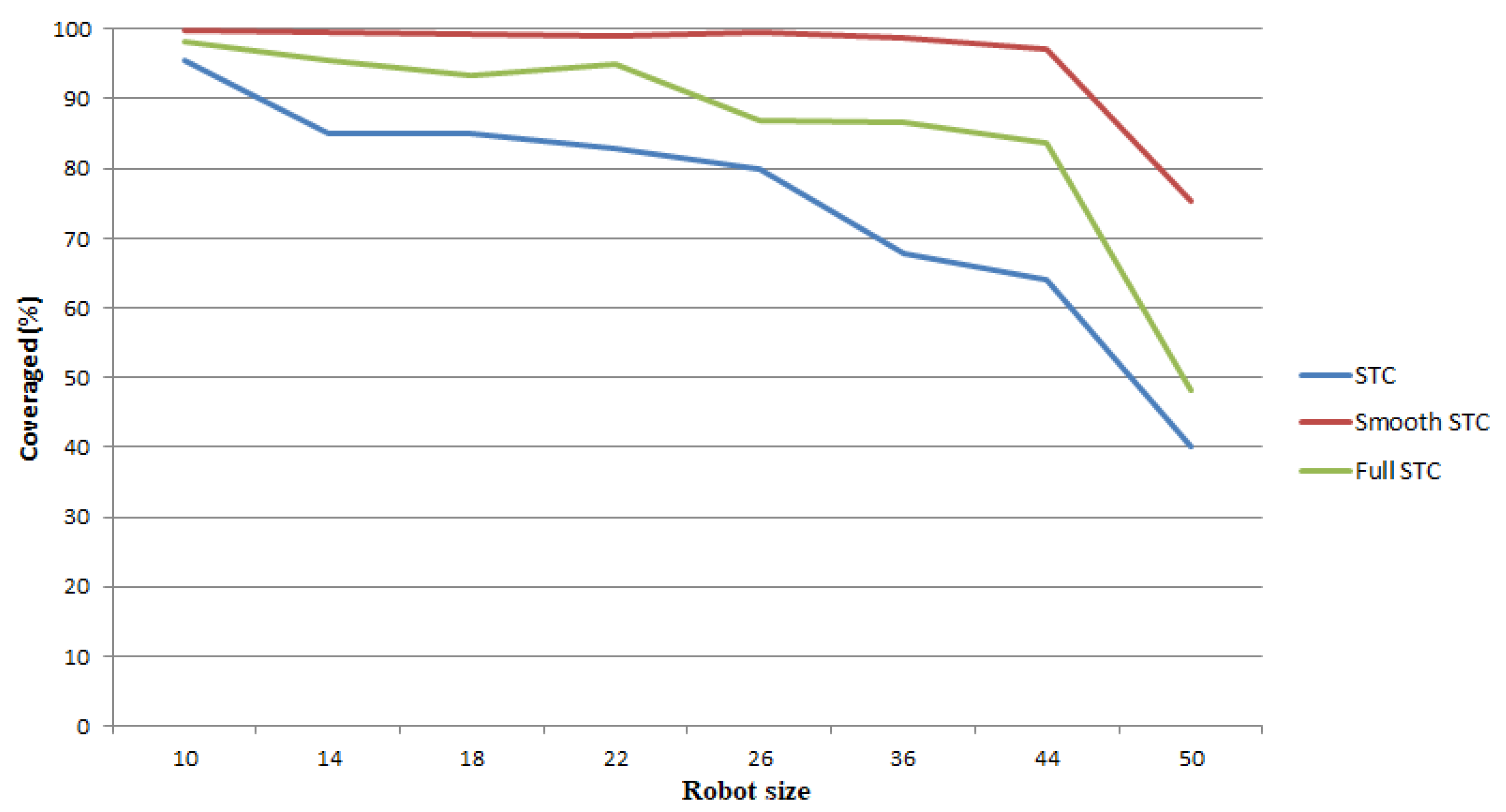
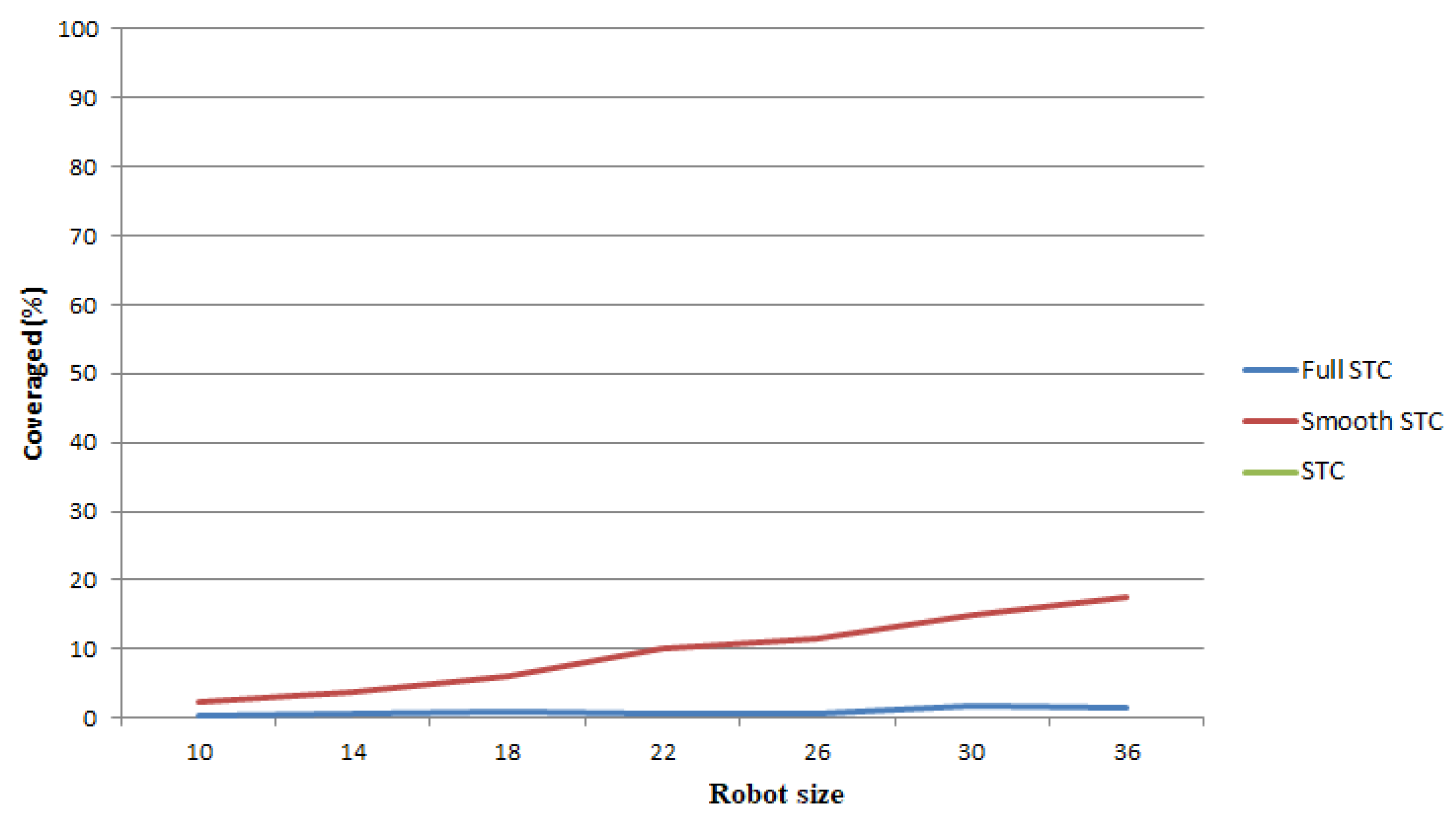
The influence of the robot size on the coverage ratio has been evaluated by gradually increasing the robot size. The results in Figure 14 show that the coverage ratio depends on the robot size, the larger the robot size the lower the ratio. This indicates that the SmSTC algorithm achieved coverage ratio close to 100% in most cases and this result is an improvement over the alternative algorithms considered; this is especially evident when the robot size is bigger. In the same map with the same complexity (when changing the size of the robot) the testing obtained the overlap area ratio of those algorithms as shown in Figure 15. The ratio of overlap area of SmSTC algorithm remains much larger than previous algorithms, the larger the robot size, the larger the repeating area. However, these overlap areas are mainly located around the obstructions. In fact, these areas have ‘stain’ density more than areas far away from obstacles. So repeating in these areas is also meant to be cleaner.

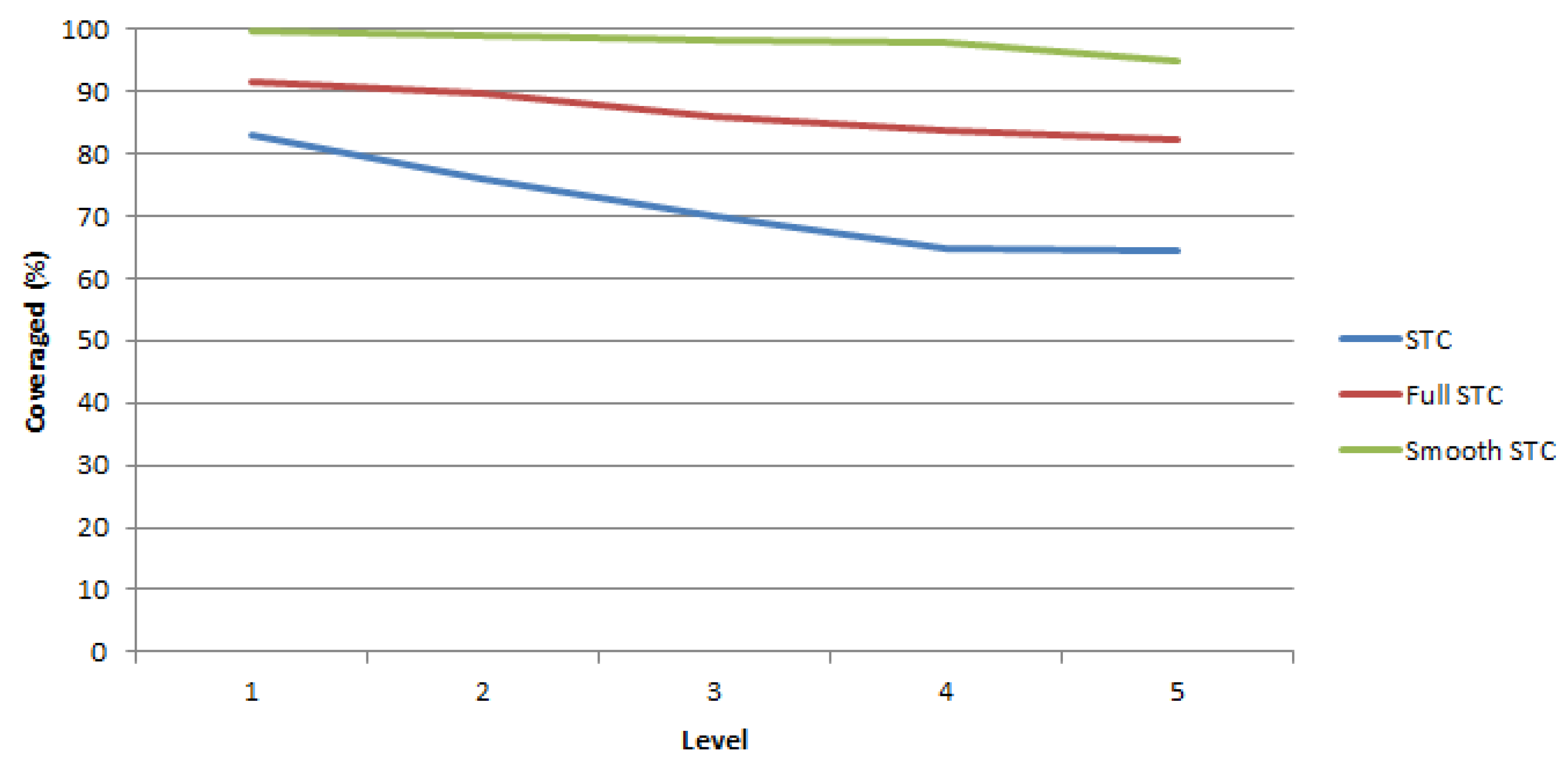
To compare the influence of the complexity of the DOE to the coverage area, the experimental testing evaluated the algorithms on maps with increasing complexity. The complexity of the map is objectively evaluated based on: (a) The number of obstacles in the environment, and (b) the shape of each obstacle. For a general robot with a size of 30, the experimental results are shown in Figure 16. The results results show that the higher the complexity of the environment, the better the STC and Full STC algorithms coverage. While our SmSTC always maintains a coverage of over 95% which demonstrates that SmSTC is effective in many different [DOE] environments. The proposed SmSTC algorithm generates a coverage path [for the robot] which avoids path repetition, minimises overlap, and avoids backtracking during the movement as shown in Figure 17. In testing, the Full STC algorithm made 7 turns in traversing the DOE while our SmSTC covered the DOE without any reversing or backtracking.

6.2. Evaluation in a ‘Real-World’ Environment

To evaluate the proposed approach a CIST* BK robot was deployed in the ‘Moc Chau’s hill forest’ as shown in Figure 18 and Figure 19. Testing demonstrated the efficacy of our proposed approach in uncertain ‘real-world’ environments (i.e., the ‘Moc Chau’s hill forest’) where the coverage path planning with the avoidance has been demonstrated under ‘real-world’ conditions such as shown in Figure 19.

In evaluating the proposed method in a ‘real-world’ environment our focus was to test the ability of a robot to achieve optimal path planning while avoiding static and dynamic obstacles. The CIST* BK robot has been implemented in square area (DOE) of 60 × 40 m in Moc Chau’s hill forest. All of the sensors (on the CIST* BK robot) have the same range and are capable of recognising free cell or cells containing: (a) Static obstacles such as flora (i.e., trees, plants, and bushes, (b) dynamic (moving) objects (such as animals), and (c) other obstacles. In practice the robot sensors automatically detect the dynamic operating environment (effectively the DOE) through 360 degrees (the right side, left side, the rear, and the front). For a discussion on the CPP, the cell structure, and the edges see Section 4 where the four directions for the cells are introduced.

To enhance the running time and performance (of the real robot) we have improved a robot design with its smart sensors to capture potential coverage paths while moving the fields in the ‘Moc Chau’s hill forest’. The experimental results shown that the proposed algorithm can be used in ‘real-world’ conditions to monitor agriculture in the ‘Moc Chau’s hill forest’. In the real experiments (over 15 runs) our SmSTC algorithm achieves an almost 98–100% coverage as shown in Figure 20, while there is some overlap in areas located around detected obstructions such overlap is dependent on the sensor’s identification in the ‘real’ situation. The results show that while the Full-STC and STC obtained at 83–88% and 81–85% respectively, it shows that the proposed SmSTC algorithm is effective in a variety of real environments.

6.3. Open Research Questions and Future Work

An outstanding open research question is the inclusion of input and output for the robot that helps ensure a continuous path in coverage for monitoring in the forest. However, it also makes the total turning angle of the robot increase sharply. Therefore, the rotation angle of the robot when moving through the area around the obstacle changes constantly. This increases the time and cost of energy, to overcome this, there must be solutions to smooth out the areas around the obstructions with smart camera and the senses of the robot.

In considering potential directions for future research we contemplate further investigation into the updating of the rules in the knowledge base. In addition, we plan to investigate combining various data sets from real experimental case studies using data tracking logs, we consider that such data may be useful in finding optimal solutions for of considered rules in inference of the proposed system performance together with a robotic knowledge.

7. Conclusions

The proposed SmSTC algorithm has addressed the significant issue of finding an optimal coverage path while avoiding backtracking and achieving maximum coverage of the DOE. Experimental results indicate that the addition of C-space technique combined with the proposed model helps the robot to traverse the DOE effectively while avoiding collisions when entering dangerous areas where obstructions are located.

Our proposed SmSTC algorithm achieves an almost 100% coverage but still has overlap in areas located around obstructions. However, in reality, there are often more stains around obstacles than areas far away from obstacles. Therefore, repeating these areas also means cleaning the surface. The proposed SmSTC algorithm achieves improved performance over the alternative algorithms considered and presents a useful ‘real-world’ approach to managing robotic operations in uncertain dynamic environments.