1. Introduction
Traumatic injury is a leading cause of death for people in the United States under the age of 65, responsible for approximately 79,000 yearly deaths in Americans that are 45 years old and younger [
1]. Per the U.S. Department of Transportation National Highway Traffic Safety Administration, when a first responder encounters a person who may have suffered a traumatic injury, the accepted standard operating procedure is to bring the cervical spine into the neutral position, then fit a stabilization unit to the patient [
2]. The goal is to minimize translation and rotation of the head in order to avoid aggravating spinal injuries during lifting or transport.
Classically, the prescribed methods for post-trauma stabilization include a two-fold strategy of fitting a cervical collar to the patient’s neck, followed by immobilizing the head of the patient utilizing some form of head supporting framework. However, recent work illustrating the contributions of cervical immobilization to patient mortality and morbidity have led to a concerted effort to explore the reduced use of a cervical collar in trauma situations [
3,
4,
5]. Cervical collars can restrict a patient’s airway, consume valuable first responder time to fit and secure, and raise intra-cranial pressure, which can be fatal in the event of an accompanying head injury. In fact, research performed in reference [
6] even purported to demonstrate that there is little to no effect on neurologic outcome from spinal immobilization, albeit in a limited study. However, there are still benefits to be gained through the use of some measure of stabilization for a patient who has suffered a traumatic injury. Should critical damage be present in the cervical spine, further motion could cause further injury or death. Research has shown that cranio-thoracic stabilization methods such as sandbags or stabilization blocks upon a stretcher can nearly completely stabilize the cervical spine, without the use of a cervical collar [
7]. This thus forms the basis for the necessity and function of the proposed head stabilization device.
The prior work on head stabilization for automated rescue applications has focused largely on the immobilization of the head of the injured person in quick drying foam to prepare for extraction by a team of mobile robots [
8]. While successful in the restriction of movement, the foam took several minutes to set, and must be cut away to remove the person’s head. Thus, while the method did achieve the goal of immobilization, the long setting time and the requirement of an outside person to cut away the foam serve to increase the transportation time required to get the injured person to an area where they can be treated by a medical professional. The MechaNek is another solution for head stabilization, in this case to protect the neck and head of NASCAR drivers through the use of an active cabling system fixed to a shoulder harness [
9]. However, as the focus is on active stabilization in crash scenarios, the goal of this system is to protect against large accelerations, not to maintain steady state stability of the head.
This paper presents a novel robotic head stabilization system, along with possible applications, a discussion on the design process and a demonstration of the system’s capabilities. In
Section 2, real-world applications of the device are described, followed by a mechanical design overview in
Section 3.
Section 4 details the controller design, and
Section 5 discusses the results of simulations featuring the chosen controller. Finally,
Section 6 contains experimental validation while
Section 7 concludes with the future work planned for the system.
2. Field Application
The proposed head stabilization device has potential both as a standalone robotic system that can be utilized in place of standard manual-placement head stabilization blocks and as a subsystem of a larger autonomous rescue platform. One study has found that the process of stabilizing a patient’s head following a traumatic injury with cervical collar and head stabilization blocks takes a first responder on average 5.64 min, ± 1.49 min [
10]. In addition, this requires the full attention of a first responder, possibly precluding them from performing other life-saving actions. The use of an autonomous head stabilization device can therefore free a medic in the critical first minutes of contact. In addition, through the proper controller design, the device can actively reject vibrations of the head with respect to the stretcher, helping to minimize any jostling or swaying while in transport. In the case of an autonomous rescue platform, the head stabilization unit can be integrated to assist in safely and securely transporting a rescued person to a medical staging area.
The expansion of the technological advances that form the basis of robotic autonomy has led to application of autonomous and semi-autonomous systems in many fields that previously exposed humans to significant risk. Among those explored is the search and rescue field, where the duties of first responders are performed or augmented by robots. Following cataclysmic disasters or combat, traumatic injuries are responsible for a large portion of the preventable fatalities [
11,
12]. Tasks that have already been successfully performed in the real-life scenarios include searching rubble for survivors, surveying damaged structures, and exploring irradiated sites [
13]. With robot autonomy, systems can be built that can be utilized to keep first responders out of harm’s way and to shift some of the burden off these brave men and women.
With respect to combat wounds, hemorrhage resulting from major trauma is believed to be the primary factor in as many as 80% of the potentially survivable fatalities [
14]. Several systems have been explored that are intended to be utilized in order to extract and transport an injured person away from a dangerous locale, including the Vecna Battlefield Extraction-assist Vehicle (BEAR) [
15], the Robotic Evacuation and Extraction Vehicles (REX/REV) developed by the US Army [
16], and the Combat Robotic Nursing Assistant (cRONA) from Hstar Technologies [
17], shown in
Figure 1. However, all of these systems lack a simply applied and easily initiated head support device. The head stabilization device presented in this work can be incorporated in the stretcher section of the transport units of the shown systems, or placed on the ground for stabilization and transportation by the humanoids. However, stemming from the lack of a comprehensive solution, the U.S. Army Medical Research and Material Command has recently re-initiated research into this space [
18]. Thus, the primary design influence for the head stabilization system derives from its inclusion on a novel robotic rescue robot.
While several form factors were considered for the presented head stabilization system, the current form factor was based on its implementation as a subsystem of the Semi-Autonomous Victim Extraction Robot (SAVER) [
19]. Pictured in
Figure 2, SAVER is a next-generation robotic rescue platform intended to remedy the shortcoming of previous attempts at building a rescue robot. It is designed to autonomously navigate to the location of an incapacitated person, and then utilize telemanipulated articulated arms to gently adjust the pose of the person. Once completed, the retraction unit traverses the declined stretcher bed and grasps the injured person by their underarms, while stabilizing the head and neck. Once secure, the retraction unit will gently pull the target on-board while the arms are used to ensure the body remains properly aligned. A passively-suspensioned tracked differential drive provides SAVER with the ability to overcome a variety of terrains while reducing vibration and shocks to the transported person as much as possible. Multi-modal vision, including Lidar, stereo, and thermal cameras provide both the autonomous navigation module as well as the human operator with a comprehensive visual data stream in order to locate the target as well as to avoid any obstacles. Furthermore, a two-way communications system allows trained medical professionals to provide first aid instruction as well as to help reduce any discomfort or anxiety the transported person may face should they regain consciousness while being transported by a robotic system. SAVER has the capability to function as a standalone system as well as a companion robot to first responders, thereby reducing the manpower required to transport injured patients to triage locations or field hospitals.
3. Electro-Mechanical Design
While designing the head stabilization system, there are several key goals to be met in order to ensure the proper operation of the device. The primary goal is that force be applied equally at by the support blocks in order to reduce discomfort and provide a secure and stable hold when restricting the motion of the head. Additionally, the device must be able to hold the head stable in the presence of outside disturbance, such as vibration during transport on an ambulance or autonomous robot. Finally, the system must be lightweight and low profile to facilitate easy transport, while also being reusable and easily sterilized.
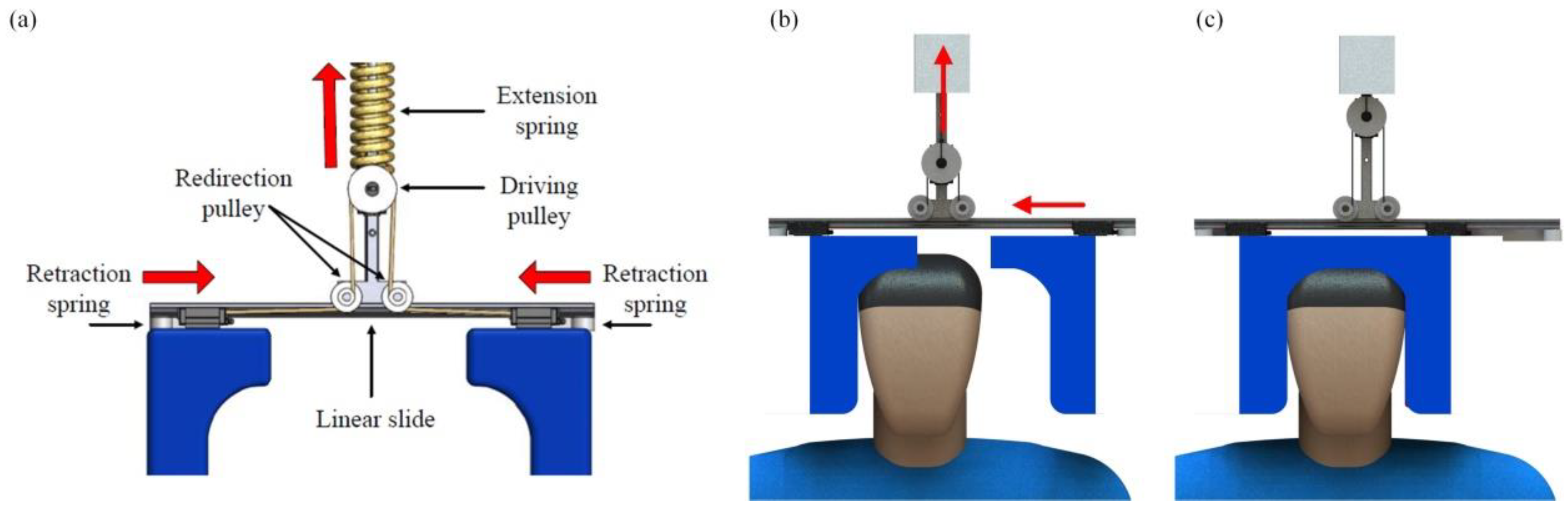
Based on the above requirements, a head support system was designed as shown in
Figure 3. The proposed system consists of a differential mechanism connected to two foam head support blocks. A major design goal for the subsystem was to have the two supporting blocks driven by a single actuator. Each block will maintain the freedom to reach an asymmetric final position, while applying constant force to hold the head steady without causing discomfort. The allowance of an asymmetric final position gives the device the ability to stabilize the head and neck in the position in which the patient is originally encountered or in the position in which it is manually placed by a trained emergency medical professional. In addition, the asymmetry helps the device to better accommodate patients wearing headgear or helmets, which is achieved in this case through the use of a differential mechanism. As defined by Hirose in reference [
20], a differential mechanism is capable of redistributing the input force between multiple output points inside the system.
The overall working of the mechanism can be explained as follows, a cable is routed between the driving pulley and the redirection pulleys and both ends of the cable are connected to the foam blocks. The driving pulley and the foam bock are capable of sliding on the frame such that when the driving pulley moves back from the frame, it pulls the foam blocks closer towards each other in order to secure the head of the injured person. The driving pulley was connected to a linear actuator through an extension spring forming a Series Elastic Actuator (SEA), thereby allowing simple PID-based force control to operate the head support blocks. As shown in
Figure 3, even if the head is encountered closer to one of the foam blocks, it will stop and not exert any force until the second one makes contact with the head, and thereby securing it in place. The mechanical design as well as force control of the proposed head support system is explained in detail in references [
21,
22]. Detailed experimentations described in reference [
22] showed that the incorporation of the linear actuator and the sliding differential pulley was both too slow and too large for practical implementation. Thus, it was determined that future designs required a rotary motor as well as a more compressed form factor in order to provide a workable design. Furthermore, while the PID controller implemented in reference [
22] met the stated control design goals, a more effective feedback controller for rejection of disturbances was desired. This objective is addressed in
Section 4. Pictured in
Figure 4 is the proof-of-concept device built to demonstrate the viability of the overall concept.
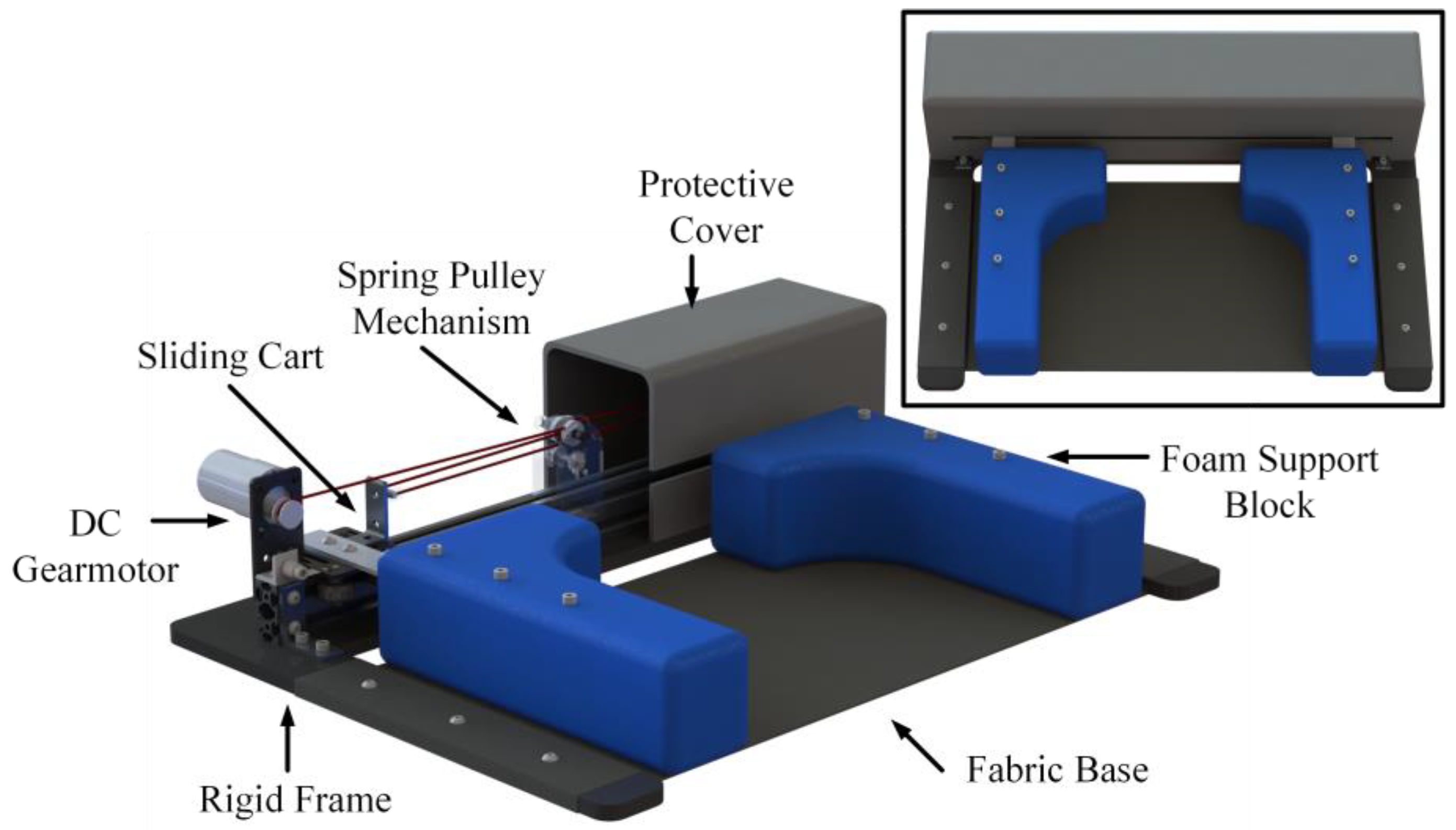
With the above goals as the guiding influence, the resultant mechanical design of the head stabilization device can be seen in
Figure 5. Two shaped medical-grade foam head blocks act to provide compliant support in direct contact with the head of the injured person. A rigid frame forms a low-profile structure to support the mechanical components as well as holding the fabric base piece upon which the head rests during stabilization. The treated nylon fabric base is held taut between the arms of the frame, and can both be easily disinfected and replaced as needed. The fabric used will be thin and compliant enough to ensure that it slides under a person’s head without need for large clearance, and provides a measure of compliance while supporting the head. A plastic cover protects the motor and moving parts as well as helps to prevent headwear or hair from becoming caught in the mechanism.
The two head support blocks are mounted on thin aluminum plates, which are then rigidly fixed to sliding carts. The carts are actuated via a cabling system, which allows for differential motion of the blocks. In case of the head support mechanism, this design ensures the stabilization force is apportioned equally between each of the foam pieces, and allows for the successful support of the head even if encountered in asymmetrical configurations. When such a case is encountered, one of the support blocks will make contact before the other. It follows that the differential mechanism ensures the block that made contact stops moving, without exerting any additional force, and the other block moves in to make contact. The system exerts force on the head only once both the head support blocks have made contact. This action is essential in providing a stable support without placing undue force upon the head and neck of an injured person, particularly when implemented by an autonomous rescue robot. While trained medical professionals have the skills to analyze an injury and determine whether re-aligning the cervical spine is safe, an autonomous robotic system is much better served in stabilizing in-situ as best as possible and maintaining the patient in that state until expert human medical attention is available.
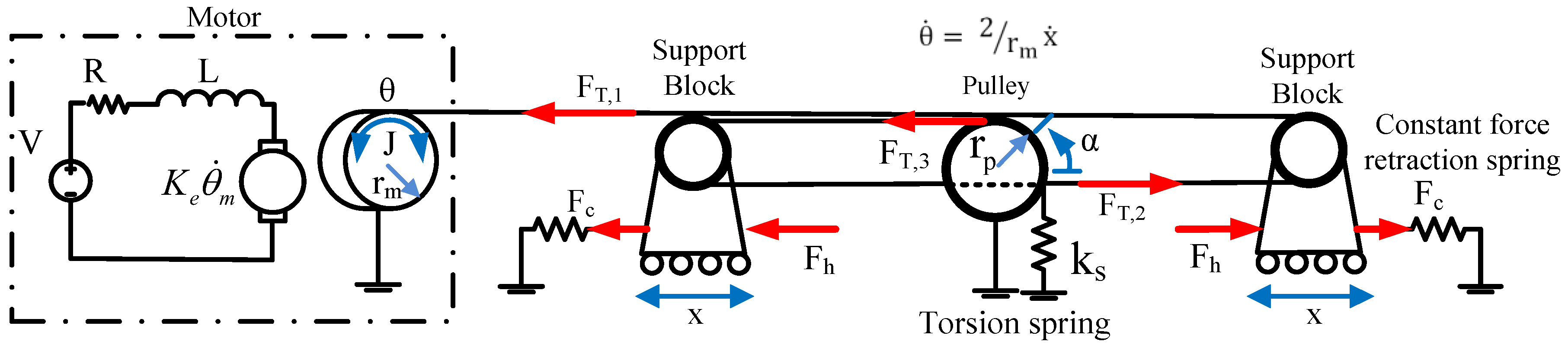
The cabling system that drives the motion of the two blocks is depicted in
Figure 6. The cable is driven using an electric motor, such that when the motor pulley rotates it reduces the total cable length in the system, pulling the two sliding carts close to each other. Additionally, two constant force springs are included to provide a constant retraction force. This ensures that as the motor feeds more cable into the system, the blocks move away from each other. Due to the differential design, if one cart makes contact, the second cart accelerates to travel at double the original speed inversely proportional to the motor pulley diameter,
, until contact is made with both foam supports. This can be shown by differentiating the total length of the cable and relating this to the change in position of the supporting block,
, such that
.
In the new design, the terminal end of the cable is wound about the spring pulley, and fixed to an extension spring, with a spring constant
, that is ground on the opposite side. Until an external force is applied to the system, this acts as a fixed cable termination (assuming the sliding carts’ motion is frictionless, as explained in
Section 4). Once the blocks make contact with the head, the spring extends by an amount
as the cable tension force increases to
. The extension of the spring allows the spring pulley to rotate by
, where
is the radius of the pulley. Therefore, by measuring the rotation of the pulley, the applied force can be mapped and thus utilized as the feedback for the controller. For the purpose of the experimental validation described in this work, a rotary potentiometer was used to measure the deflection of the spring. The only calibration needed was to estimate the relationship between the potentiometer readings and the spring deflection in degrees, which was linear for the required range of operation. By comparing the potentiometer readings with the zero deflection reading, the force exerted by the system could be determined in real-time during the head support applications.
4. System Modeling
Biomechanical studies performed in reference [
23] were utilized to determine the required stabilization force to be provided by the system. Based on the studies, to adequately restrict unwanted motion initiated by the patient and the environment, the desired force applied by the system is a net 20 N, with the force applied by each support block,
, equal to 10 N.
The effect of friction in the pulley system was taken into consideration while considering the model of the force applied to the head by the support blocks. The standard pulley friction model as found in the literature [
24] is given by
, where
is the coefficient of static friction between the pulley and cable,
is the cable wrap angle and
and
are the tension forces on either side of the pulley on the right support block. Similarly,
and
are the tension forces on either side of the pulley on the left support block. Based on the arrangement of the system as described in
Figure 6, the wrap angle for both sliding block pulleys is approximately
radians due to the motor and spring spool pulleys being larger in diameter than the redirection pulleys. The coefficient of friction for the ultra-high-molecular-weight polyethylene cable utilized in the system running on a metal pulley is less than 0.1. Thus, for the above specifications,
approached unity, rendering the effect of friction on the system negligible and the tension forces
, and
can be considered equal, and represented as
. This then results in the necessary tension force in the cable,
, being half of the sum of the support forces applied to the head (
) and against the constant force retraction spring (
) by a single block, such that
. Additionally, the tension force at the spring pulley is directly proportional to the rotation of the spring pulley due to the spring, resulting in
. Combining these two equations, along with the relation between the spring pulley and motor pulley rotation,
results in the direct coupling between the force and motor rotation,
. A set of free body diagrams depicting the forces applied to the motor, support blocks, and spring pulley is shown in
Figure 6.
The system can be modeled as an electro-mechanical system through the electrical and mechanical models for DC motors given below.
where V represents the armature voltage applied to the motor,
is the armature resistance,
denotes the armature inductance,
is the armature current, n represents the gear ratio,
is the electromotive force constant, and
denotes motor shaft velocity. The rotor position is equal to the motor pulley position multiplied by the gear ratio n, such that
. Additionally, the load torque is represented by
while J denotes the combined motor and gearbox inertia, and B is the motor and gearbox damping. The torque contributed by the spring displacement is
. Finally, the load torque is related to the armature current by the motor torque constant
. Using the three electromechanical motor equations and the relation between tension force and motor rotation, the resultant system transfer function is shown below in Equation (2).
It can be observed that the resultant system is a third order system due to the presence of the integration introduced when relating motor torque to angular position. The time constants of the electrical and mechanical systems are represented by
and
. As the electrical time constant is negligible relative to the mechanical time constant, its effects on the dynamic system can be ignored, thus resulting in the reduced order model in Equation (3).
where
,
, and
. The reduced order model simplifies the control of the system and helps to guarantee the stability of the controller introduced in the following section.
5. Controller Design
Ultimately, the goal in providing support of the head and neck of an injured person is to minimize any undue angular oscillations of the head with respect to the neck. This prevents further damage to the possibly damaged vertebrae. To this end, it is ideal that the controller maintaining the securing force on the head would act to reject outside oscillatory or impulsive disturbances that may be injected into the system. Possible sources of such disturbances include vibrations from rough terrain being traversed by a rescue robot, or vehicle dynamics imposed by robot locomotion modules or transport in an ambulance.
While model-based controllers are often used in such situations, the system as designed provides difficulties in accurately estimating a variety of model properties. The compliance of the foam support blocks introduces variable damping as well as spring elements that are difficult to ascertain, and may vary with compression. Furthermore, the effective mass in the system is provided by the head being stabilized, which will be different for each person being stabilized and is also dependent on factors such as headwear. Additionally, a conscious person with some degree of muscle control will require a lesser degree of stabilization than an unconscious patient, whose head will freely move in response to stimulus.
In pursuit of such a feedback controller, active disturbance rejection control (ADRC) is implemented for the system. Fully articulated by Han in reference [
25], the controller is at the intersection between classic PID control and modern model-based control theory. The key aspect is that the entire system, including external disturbances, is captured utilizing an extended state observer (ESO). Once so estimated, the disturbances can be compensated for, all without requiring any model specific knowledge of the system beyond assumption of a base canonical state space formulation. While the seminal work on ADRC features a nonlinear r state estimator and control law, the system presented here utilizes a linearized version (LADRC) [
26,
27]. In LADRC, the nonlinear estimator is replaced with a Luenberger observer and coupled with a proportional-derivative controller. Active disturbance rejection techniques have been used in the past for various applications such as for position control of very lightweight single-link flexible arms with large payload variations [
28], motion control for advanced mechatronics systems in various modes [
29], and vibration control of multimass resonant systems [
30]. The following section is a tutorial section for interested readers on the detailed implementation of LADRC for the proposed application.
As shown above, the head stabilization device can be represented as a second-order, single-input-single-output system, whose plant can be represented by . In this representation, a and b are unknown as they cannot be accurately modeled due to the presence of frictional effects and the compliance of the foam support blocks. However, some knowledge is present of the system, so b0 can be estimated such that b = b0 + berr. Further, while u is the known control input, is the unknown external disturbance, which includes signal noise, external impulses, and model estimation error, berr.
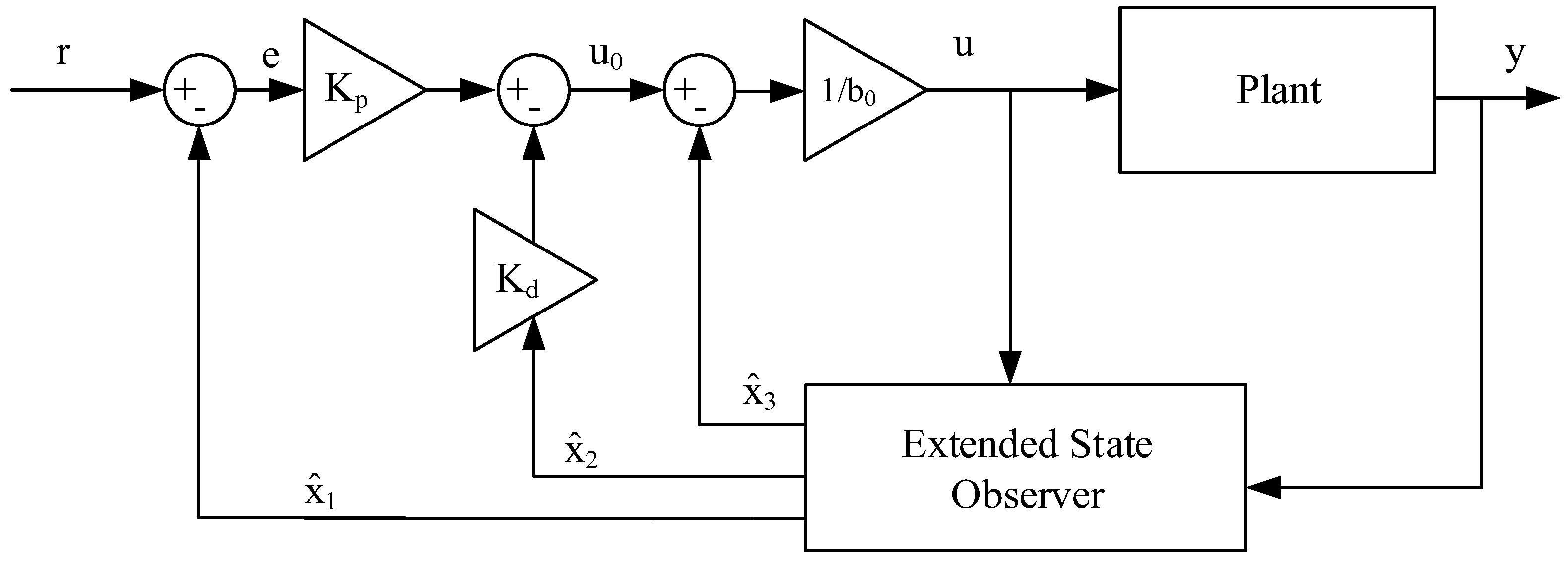
In the LADRC scheme diagrammed in
Figure 7, the state vector,
, contains the first and second order response of the system,
and
, as well as a third, augmented state,
, that encapsulates the plant’s behavior, inclusive of the external disturbance. Incorporating f into the plant enables the reduction of the second order system to the form shown in Equation (4).
If an estimation of
is determined through a state observer such as the Luenberger instituted in LADRC, the estimation,
, can be incorporated into the two step PD control law found in Equation (5).
Substituting into Equation (4), it can be seen that the control law is structured such that the system can be reduced to a unit gain double integrator control system [
26]:
In state space, this system is represented as Equation (7).
The system can then be estimated through the implementation of a Luenberger observer in Equation (8)
where
in the above representation,
represents individual Luenberger observer gains.
Through parametrization of the controller and observer gains [
26], stable gains are chosen for the control system. As Equation (6) can be approximated as the second order system,
, given the accuracy of the estimated disturbance, the control gains are chosen as
and
, where
and
are the desired closed loop natural frequency and damping, respectively. Further, these gains are chosen such that they correspond to real-valued negative poles for the closed loop system, ensuring the stability of the PD controller. When considering the Luenberger observer, the error dynamics of the estimated system are determined by the resultant matrix of (A-LC):
To guarantee the stability of the observer, the roots of must be in the left hand plane. For simplicity, the three poles can be placed at a common point,, representing the bandwidth of the observer. Equivalently, and thus , and, .
In order to effectively implement LADRC on a microcontroller, the observer was discretized using zero-order hold (ZOH) [
27]. Following discretization, the observer would be considered to be in the form of a “predictive discrete observer”, as shown in Equation (10).
where the subscript d represents the discretized version of a matrix. It can thus be understood that the predictive observer utilizes current state and system feedback to predict the future states of the system. However, low-sampling rates or communications delays may introduce error in the predictions and thus instability in the controller. As a method of proofing the observer against such instabilities, it can be configured as a “current observer” [
31], resulting in the discrete observer seen in Equation (11).
where
The discretized control law is thus represented by Equation (12).
While the PID gains are unchanged following the discretization of the system, the observer error dynamics vary, resulting in an updated observer gain matrix as determined by the discretized coefficient matrices and the desired observer natural frequency
, discretized such that
.
6. System Simulation
Before validating the performance of the proposed control technique on real hardware, its feasibility was tested in simulation and its performance was compared with a PID controller. The system pictured in
Figure 7 was simulated as a discrete time model in MATLAB. The plant of the system was modeled as a canonical second-order system of the form
. The system properties were estimated through the application of Nelder-Mead simplex optimization through the MATLAB fminsearch function, fitting the model to data collected when testing the proof-of-concept prototype in [
21].
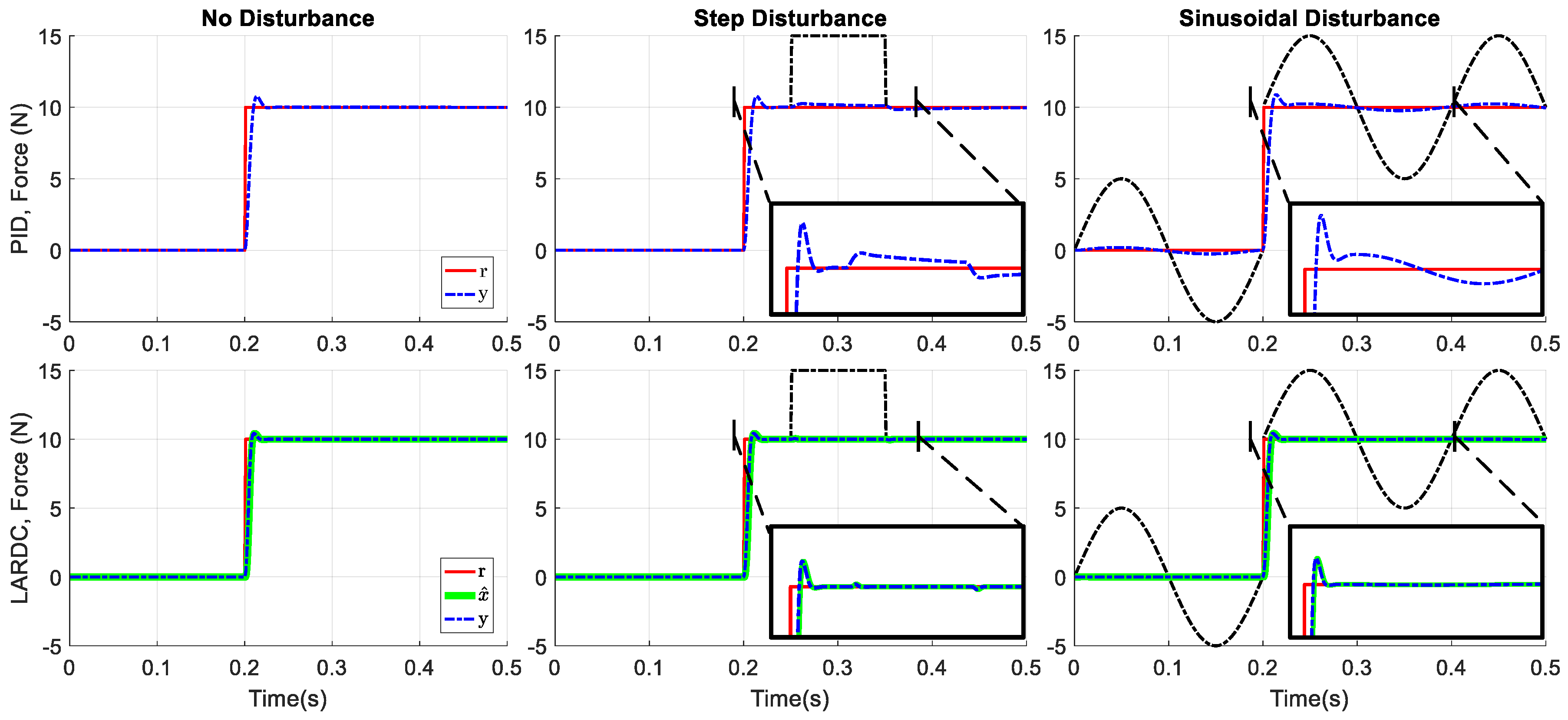
As a reference case, the simulation was tested both with a PID controller and with the LARDC controller. The first task was to verify the controllers’ response to a step input of 10 N occurring at 0.2 s, to verify that LARDC performs as well as the PID in absence of disturbance. In both cases, the controller outputs were passed through a saturation limit at the motor’s top speed. The two controllers can be seen to have almost identical rise times, and less than 10% overshoot. The results of this simulation are found in
Figure 8.
Following the validation of the control behavior in an undisturbed system, the controllers were tested in their rejection capabilities when correcting for both a momentary step disturbance of 5 N at 0.25 s, held for 0.1 s, and a sinusoidal disturbance with amplitude of 5 N and frequency of 30 Hz. While PID rejects the majority of the disturbance, the LADRC model shows even less deviation from the setpoint. The disturbance rejection abilities of LADRC are demonstrated when a sinusoidal disturbance is injected into the system as well.
The sum of the L1 norms of the error with relation to the setpoint for the PID and LADRC controllers are shown in
Table 1. The error values are corrected for the initial controller tracking by subtracting the error incurred with no disturbance. In the case of a step disturbance, LADRC provides almost complete rejection of the unwanted input. The PID controller, while tuned to have a nearly identical rise time as the LADRC, demonstrates good rejection behavior as well, but requires a non-trivial amount of time to recover completely from the disturbance. This improved steady state error minimization in the LARDC implementation derives from the removal of steady state error through the observed augmented state, rather than the necessity of including an integral term. When the system is injected with a sinusoidal disturbance, LADRC again demonstrates superior performance removing the effects of the injected disturbance signal, with a nearly sevenfold reduction in integral error over the duration of the simulation. This type of disturbance in more in line with the higher frequencies encountered when a vehicle travels over rough terrain.
The simulation results show that LADRC offers improved disturbance rejection behavior, without the necessity of including an integrator to the system. The superior operation justifies the use of LADRC as compared to a tuned PID controller, when building a physical prototype of the system for experimentation.
7. Experimental Validation
In order to validate the performance of the system, a physical prototype was fabricated, and experiments were conducted. For the rigid base, an acrylic frame was manufactured. A brushed DC gearmotor is the central actuator for the system, with a no load speed of 200 RPM and a stall torque of 1.2 N-m. The control system is implemented on the prototype utilizing an ARM Cortex-M4 microcontroller with a clock speed of 96 MHz. The prototype can be seen in
Figure 9. In order to provide a simulacrum for a human head, a weighted, to-scale foam model was utilized when conducting experiments. A 3-axis joystick was affixed to the neck in order to provide feedback on the roll, pitch and yaw of the head relative to the neck during stabilization, providing angular feedback with a maximum range of ±54°. A second ARM Cortex-M4 microcontroller ran concurrently in order to collect the angular data.
The disturbances seen by the system in the act of stabilizing the head of a rescued person during transport can be broadly categorized into three main modes. The first such disturbance would be due to the presence of a momentary unilateral force disturbance, e.g., caused by the motion of the prone person’s entire body, possibly due to centripetal force during a turn performed by the mobile robot. In this case, the desired behavior is to allow the translation of the body, neck, and head so as not to cause undue shear forces in the neck and possibly exacerbate any injuries. This disturbance mode is compensated for by the differential mechanism. In response to unilateral force, the entire block-head-block system will translate laterally in response to the disturbance, while maintaining constant force upon the head, due to the translation of the cable through the pulley system.
The second type of disturbance the system would encounter is a constant bidirectional force disturbance applied to each support block equally caused by a roll-inducing moment in the head, e.g., a conscious person turning their head. In such a case, the control system acts to maintain the commanded reference force, and in response to the increased force feedback would act to reduce the applied force at the support blocks. Finally, the third disturbance mode is due to low frequency oscillatory force induced by the motion of the platform upon the person and head stabilization device, such as a disturbance caused by the vibration of a vehicle on rough terrain. This disturbance mode contains elements of the other two, in that the oscillations can both cause full-body translations and induce head roll. In addition, out of phase oscillatory motion between the head and the body may be deleterious to the health of the patient. In such a case, the control system will act to reduce the force disturbances while maintaining the reference force, which in turn also acts to reduce the asynchronous oscillations between the head and body.
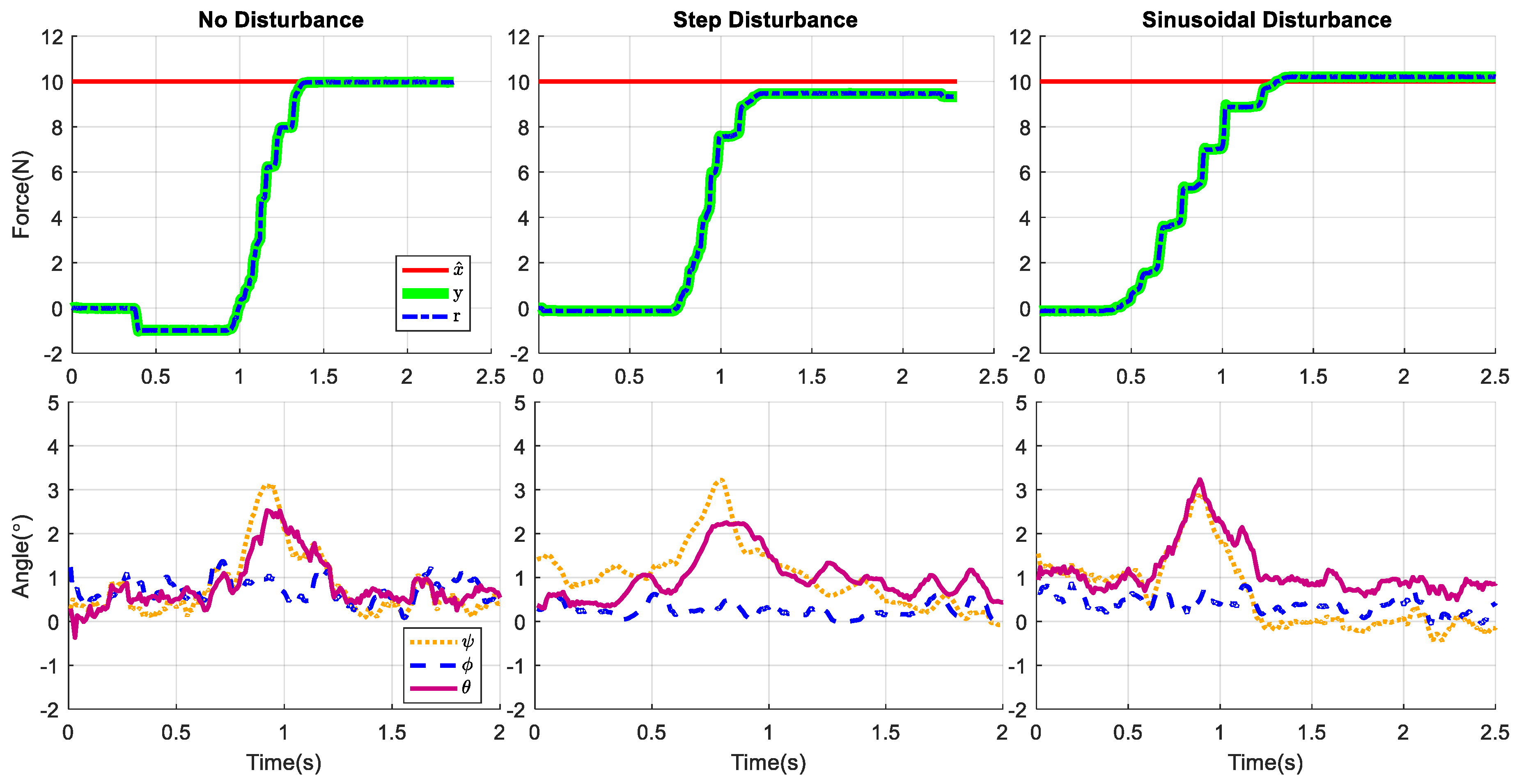
In order to prove the viability of the system, the ability of the system to reject the Type 1, 2 and 3 disturbances were validated experimentally. The first trial in
Figure 10 corresponds to a Type 1 error. The head stabilization device received a step input of 10 N, after which a unidirectional force was applied to the model head. There is no change in force feedback observed as the differential mechanism simply translates the system in the direction of the force. The estimated state feedback, the system feedback, the setpoint, and the Euler angles of the head model were simultaneously recorded. The controller exhibits critically damped behavior, desirable to minimize any impulses incurred when contacting with the patient head. The extended state observer shows excellent tracking behavior, with very little estimation error. Despite the application of significant force by the support blocks, the head shows minimal angular displacement. The roll (
), pitch (
) and yaw
angles had a maximum of 3.1°, 1.3°, and 2.5° respectively. The stepwise behavior of the system as force is applied is due to the gearing utilized to translate the rotation of the central shaft to the potentiometer. Future implementations of the system will seek to avoid this through the use of an optical encoder.
In the second trial shown in
Figure 10, the system’s ability to reject a bidirectional force applied at time t = 1.5 s is shown. To validate the rejection of a Type 3 disturbance by the system, the entire platform upon which the head stabilization unit, the head model, and the angular measurement device were placed was injected with a sinusoidal input with a frequency of approximately 5 Hz. The effect on the angular displacement of the unsupported head can be seen in
Figure 11. The disturbance was then repeated as the system attempted to stabilize the model head while data was recorded. The results of this experiment are shown in the third column of
Figure 10. For the force plots, the reference signal
, estimated output
and measured output
is shown. In addition, the roll (
), pitch (
) and yaw
angles of the weighted head model are also given. The disturbance rejection properties of the controller are again demonstrated, as the force disturbances are nearly fully minimized and the angular disturbances beyond those due to the initial impact were nearly completely reduced.
In summary, the experiments validate the performance of the system and establish its ability to stabilize the head and neck of an injured person during medical transport. When presented with both step and sinusoidal disturbances, the experimental results replicate the results predicted in the simulation of the control system and show that LADRC is an effective control system for the rejection of disturbances.