Non-Linear Lumped-Parameter Modeling of Planar Multi-Link Manipulators with Highly Flexible Arms
Abstract
1. Introduction
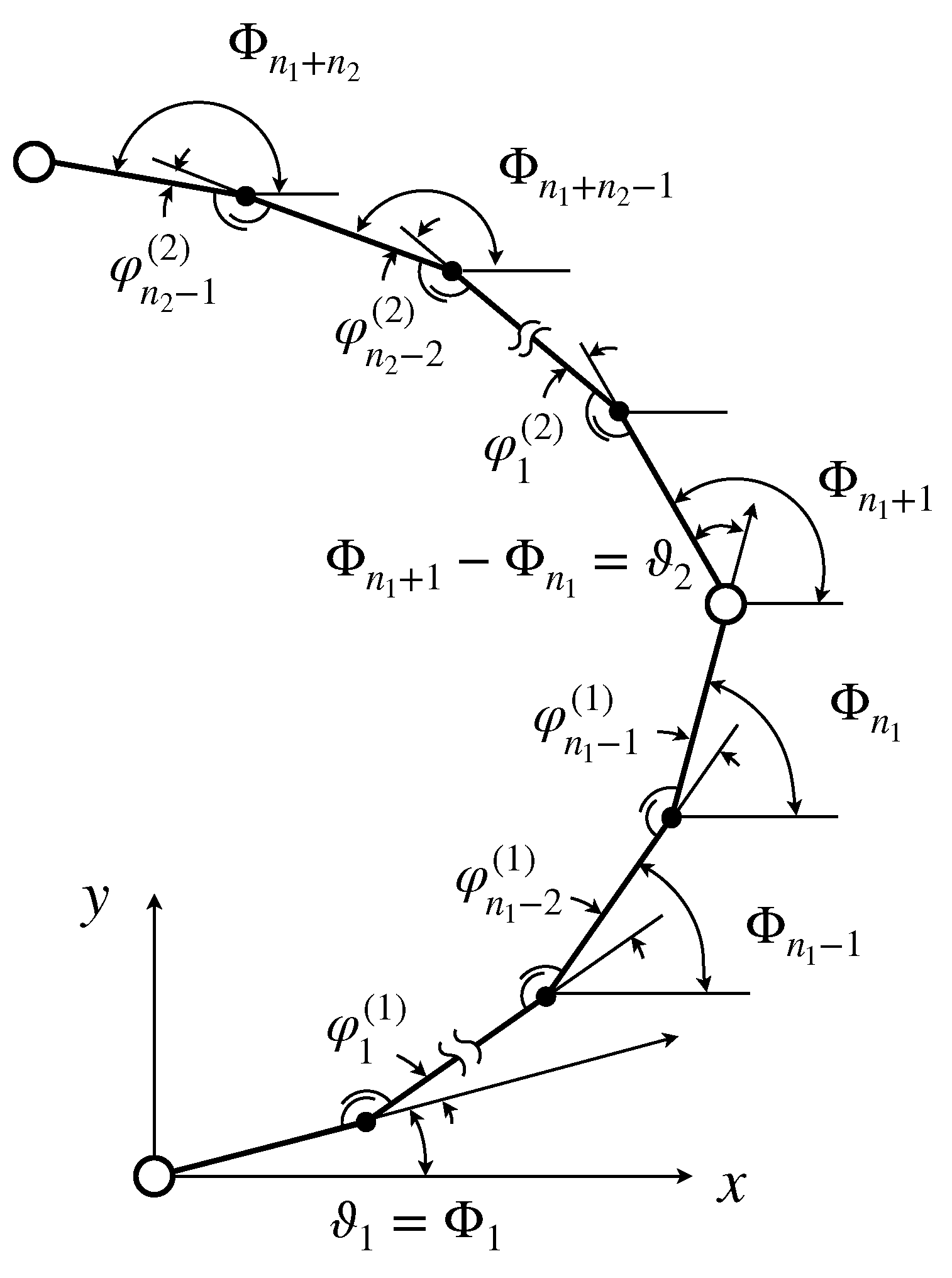
2. Dynamic Modeling of the Flexible Robot Manipulator
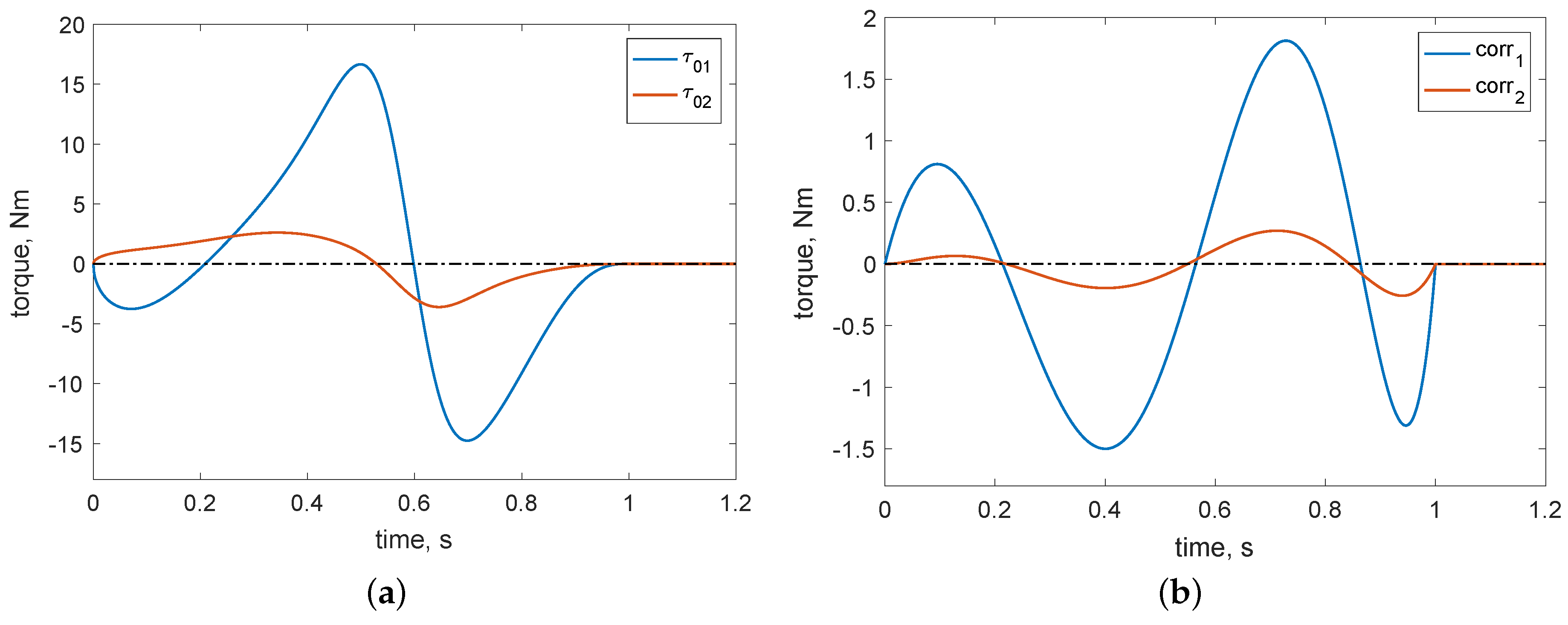
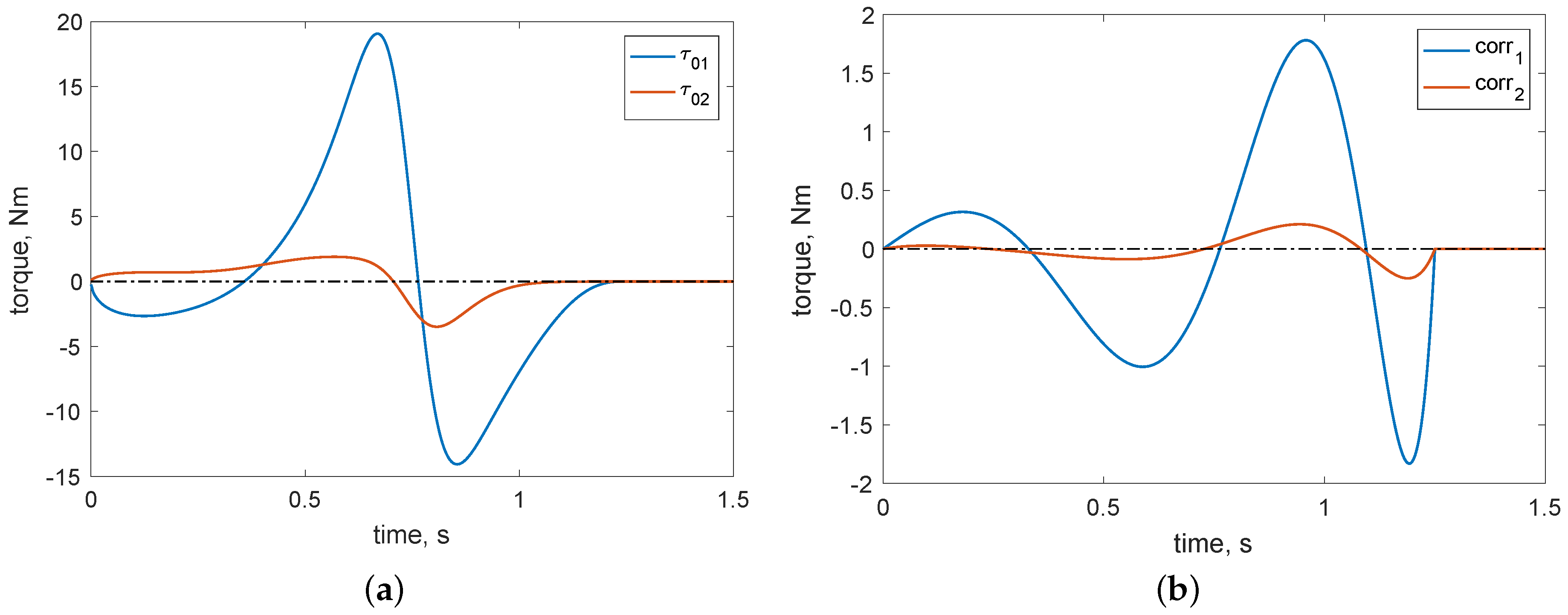
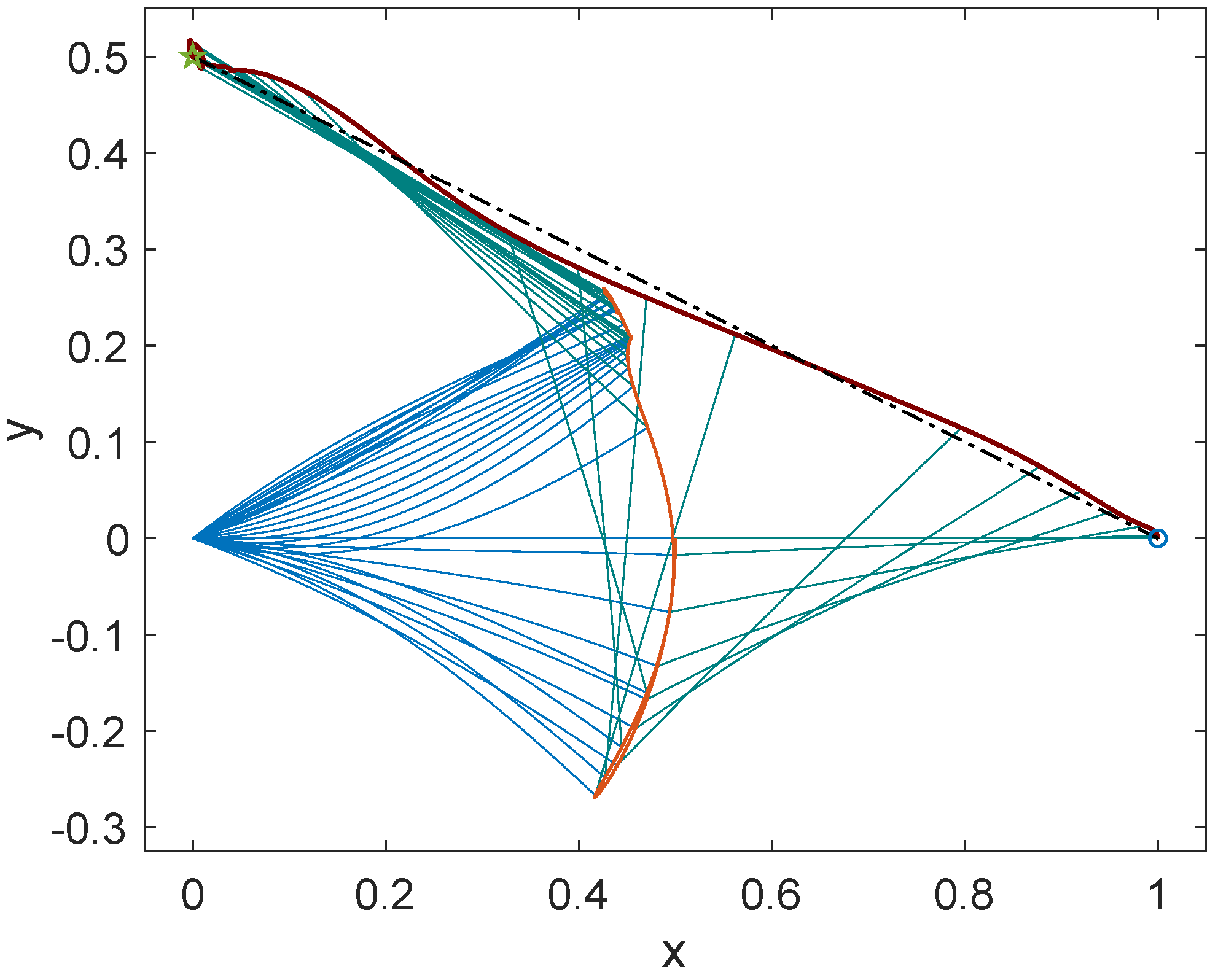
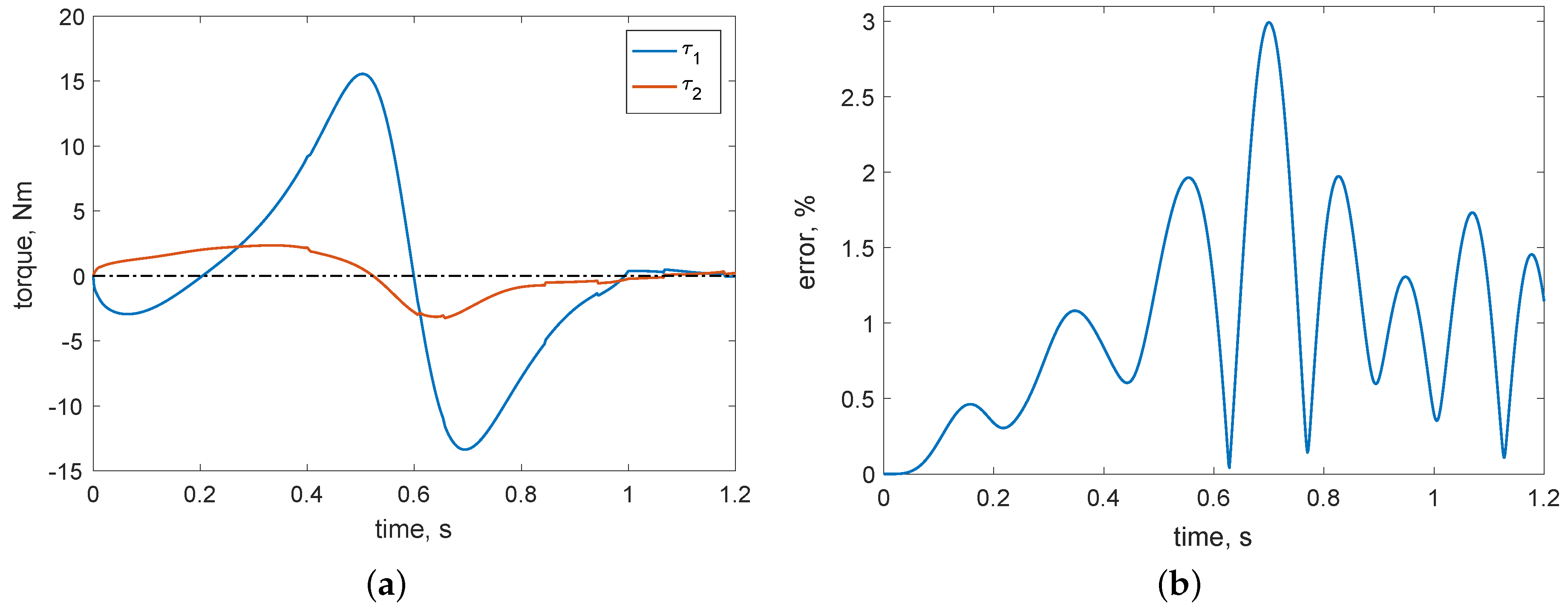
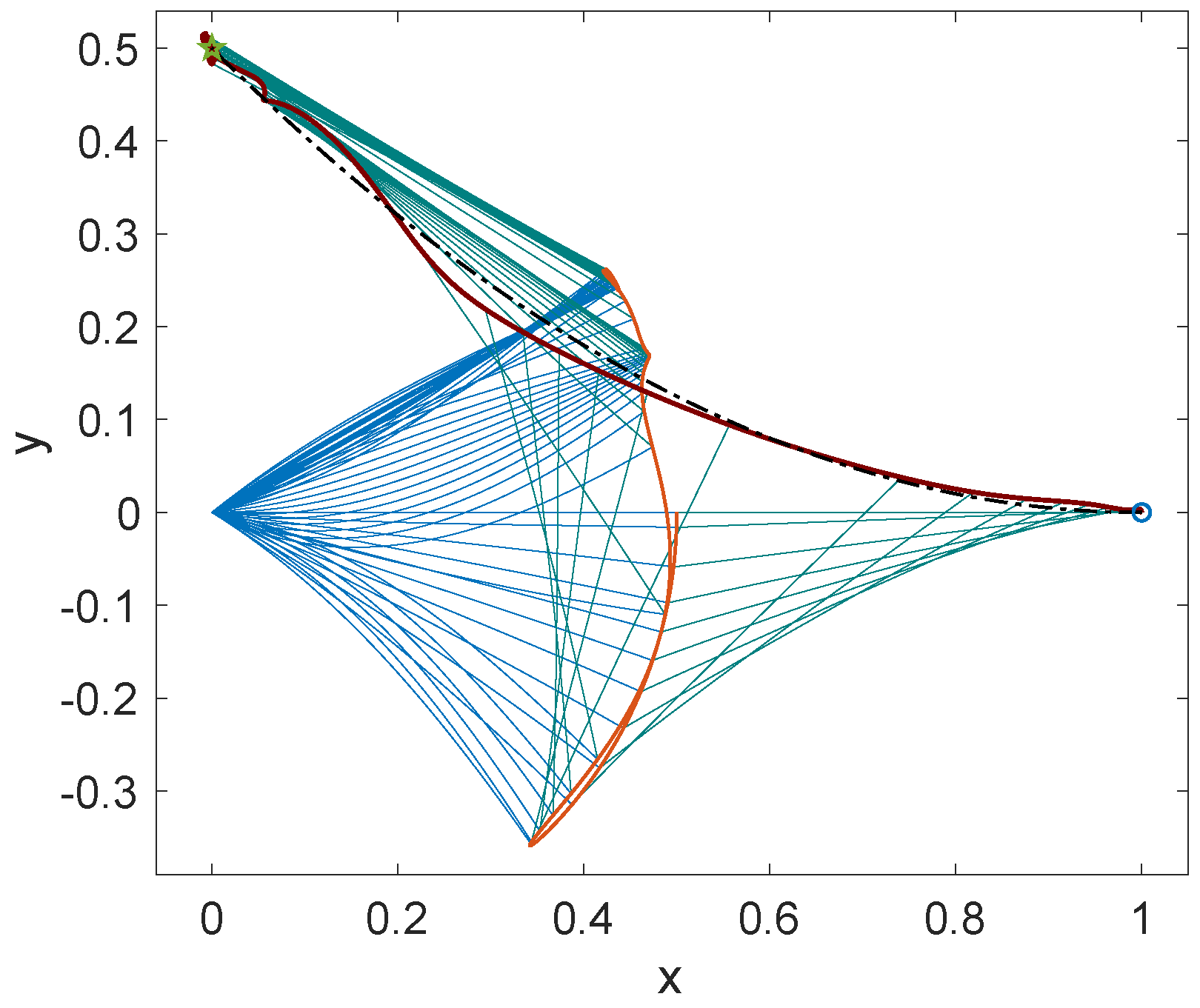
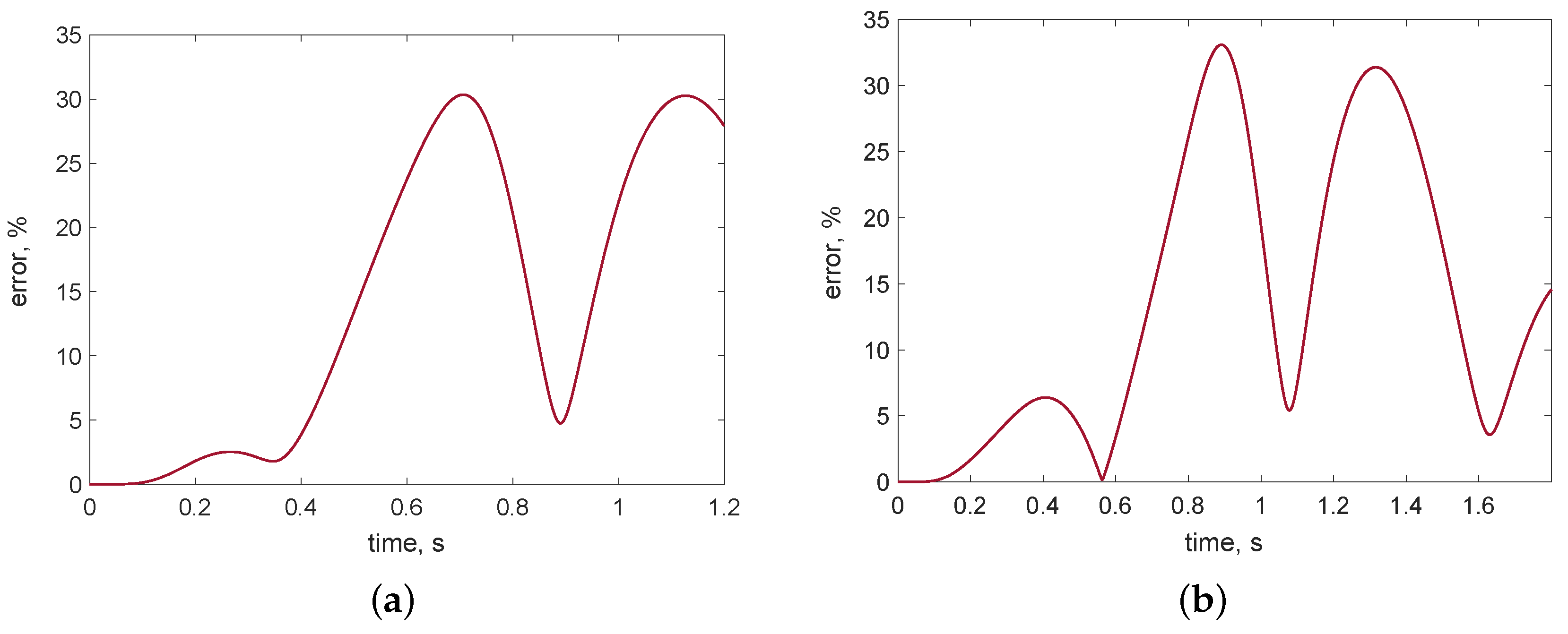
3. Numerical Examples for Some Trajectory-Tracking Cases
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cannon, R.H., Jr.; Schmitz, E. Initial experiments on the end-point control of a flexible one-link robot. Int. J. Robot. Res. 1984, 3, 62–75. [Google Scholar] [CrossRef]
- Tosunoglu, S.; Lin, S.H.; Tesar, D. Accessibility and controllability of flexible robotic manipulators. J. Dyn. Syst. Meas. Control 1992, 114, 50–58. [Google Scholar] [CrossRef]
- Sayahkarajy, M.; Mohamed, Z.; Mohd Faudzi, A.A. Review of modeling and control of flexible-link manipulators. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2016, 230, 861–873. [Google Scholar] [CrossRef]
- Önsay, T.; Akay, A. Vibration reduction of a flexible arm by time-optimal open-loop control. J. Sound Vib. 1991, 147, 283–300. [Google Scholar] [CrossRef]
- Meckl, P.; Seering, W. Experimental evaluation of shaped inputs to reduce vibration for a cartesian robot. J. Dyn. Syst. Meas. Control 1990, 112, 159–165. [Google Scholar] [CrossRef]
- Gregory, J.; Olivares, A.; Staffetti, E. Energy-optimal trajectory planning for robot manipulators with holonomic constraints. Syst. Control Lett. 2012, 61, 279–291. [Google Scholar] [CrossRef]
- Book, W.J. Controlled motion in an elastic world. J. Dyn. Syst. Meas. Control 1993, 115, 252–261. [Google Scholar] [CrossRef]
- Katzschmann, R.K.; Marchese, A.D.; Rus, D. Autonomous object manipulation using a soft planar grasping manipulator. Soft Robot. 2015, 2, 155–164. [Google Scholar] [CrossRef] [PubMed]
- Antman, S.S. Kirchhoff’s problem for nonlinearly elastic rods. Q. Appl. Math. 1974, 32, 221–240. [Google Scholar] [CrossRef]
- Steigmann, D.J.; Faulkner, M.G. Variational theory for spatial rods. J. Elast. 1993, 33, 1–26. [Google Scholar] [CrossRef]
- Greco, L.; Cuomo, M. Consistent tangent operator for an exact Kirchhoff rod model. Contin. Mech. Thermodyn. 2015, 27, 861–877. [Google Scholar] [CrossRef]
- Altenbach, H.; Bîrsan, M.; Eremeyev, V.A. Cosserat-type rods. In Generalized Continua from the Theory to Engineering Applications; Springer: Vienna, Austria, 2013; pp. 179–248. [Google Scholar]
- Eugster, S.R.; Hesch, C.; Betsch, P.; Glocker, C. Director-based beam finite elements relying on the geometrically exact beam theory formulated in skew coordinates. Int. J. Numer. Methods Eng. 2014, 97, 111–129. [Google Scholar] [CrossRef]
- Della Corte, A.; dell’Isola, F.; Esposito, R.; Pulvirenti, M. Equilibria of a clamped Euler beam (Elastica) with distributed load: Large deformations. Math. Models Methods Appl. Sci. 2017, 27, 1391–1421. [Google Scholar] [CrossRef]
- Spagnuolo, M.; Andreaus, U. A targeted review on large deformations of planar elastic beams: Extensibility, distributed loads, buckling and post-buckling. Math. Mech. Solids 2018. [Google Scholar] [CrossRef]
- Giorgio, I.; Della Corte, A.; Del Vescovo, D. Modelling flexible multi-link robots for vibration control: Numerical simulations and real-time experiments. Math. Mech. Solids 2017. [Google Scholar] [CrossRef]
- Low, K.H. Solution schemes for the system equations of flexible robots. J. Field Robot. 1989, 6, 383–405. [Google Scholar] [CrossRef]
- Du, H.; Lim, M.; Liew, K. A nonlinear finite element model for dynamics of flexible manipulators. Mech. Mach. Theory 1996, 31, 1109–1119. [Google Scholar] [CrossRef]
- Wang, Y.; Huston, R.L. A lumped parameter method in the nonlinear analysis of flexible multibody systems. Comput. Struct. 1994, 50, 421–432. [Google Scholar] [CrossRef]
- Šalinić, S. An improved variant of Hencky bar-chain model for buckling and bending vibration of beams with end masses and springs. Mech. Syst. Signal Process. 2017, 90, 30–43. [Google Scholar] [CrossRef]
- Yoshikawa, T.; Hosoda, K. Modeling of flexible manipulators using virtual rigid links and passive joints. Int. J. Robot. Res. 1996, 15, 290–299. [Google Scholar] [CrossRef]
- Konno, A.; Uchiyama, M. Vibration suppression control of spatial flexible manipulators. Control Eng. Pract. 1995, 3, 1315–1321. [Google Scholar] [CrossRef]
- Garcea, G.; Trunfio, G.A.; Casciaro, R. Mixed formulation and locking in path-following nonlinear analysis. Comput. Methods Appl. Mech. Eng. 1998, 165, 247–272. [Google Scholar] [CrossRef]
- Livesley, R. The equivalence of continuous and discrete mass distributions in certain vibration problems. Q. J. Mech. Appl. Math. 1955, 8, 353–360. [Google Scholar] [CrossRef]
- Leckie, F.A.; Lindberg, G.M. The effect of lumped parameters on beam frequencies. Aeronaut. Q. 1963, 14, 224–240. [Google Scholar] [CrossRef]
- Duncan, W.J. A critical examination of the representation of massive and elastic bodies by systems of rigid masses elastically connected. Q. J. Mech. Appl. Math. 1952, 5, 97–108. [Google Scholar] [CrossRef]
- Dell’Isola, F.; Bucci, S.; Battista, A. Against the fragmentation of knowledge: The power of multidisciplinary research for the design of metamaterials. In Advanced Methods of Continuum Mechanics for Materials and Structures; Springer: Singapore, 2016; pp. 523–545. [Google Scholar]
- Jawed, M.K.; Novelia, A.; O’Reilly, O.M. A Primer on the Kinematics of Discrete Elastic Rods; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Zhang, H.; Wang, C.M.; Challamel, N. Buckling and vibration of Hencky bar-chain with internal elastic springs. Int. J. Mech. Sci. 2016, 119, 383–395. [Google Scholar] [CrossRef]
- Alibert, J.J.; Della Corte, A.; Seppecher, P. Convergence of Hencky-type discrete beam model to Euler inextensible elastica in large deformation: Rigorous proof. In Mathematical Modelling in Solid Mechanics; Springer: Singapore, 2017; pp. 1–12. [Google Scholar]
- Alibert, J.J.; Della Corte, A.; Giorgio, I.; Battista, A. Extensional Elastica in large deformation as Γ-limit of a discrete 1D mechanical system. Z. Angew. Math. Phys. 2017, 68. [Google Scholar] [CrossRef]
- Battista, A.; Della Corte, A.; dell’Isola, F.; Seppecher, P. Large deformations of 1D microstructured systems modeled as generalized Timoshenko beams. Z. Angew. Math. Phys. 2018, 69. [Google Scholar] [CrossRef]
- Khakalo, S.; Balobanov, V.; Niiranen, J. Modelling size-dependent bending, buckling and vibrations of 2D triangular lattices by strain gradient elasticity models: Applications to sandwich beams and auxetics. Int. J. Eng. Sci. 2018, 127, 33–52. [Google Scholar] [CrossRef]
- De Luca, A.; Mattone, R.; Oriolo, G. Control of underactuated mechanical systems: Application to the planar 2R robot. In Proceedings of the 35th IEEE Conference on Decision and Control, Kobe, Japan, 13 December 1996; IEEE: Piscataway, NJ, USA, 1996; Volume 2, pp. 1455–1460. [Google Scholar]
- De Luca, A.; Oriolo, G. Trajectory planning and control for planar robots with passive last joint. Int. J. Robot. Res. 2002, 21, 575–590. [Google Scholar] [CrossRef]
- De Luca, A.; Mattone, R.; Oriolo, G. Stabilization of an underactuated planar 2R manipulator. Int. J. Robust Nonlinear Control IFAC-Affil. J. 2000, 10, 181–198. [Google Scholar] [CrossRef]
- Mohamed, Z.; Martins, J.; Tokhi, M.; Da Costa, J.S.; Botto, M. Vibration control of a very flexible manipulator system. Control Eng. Pract. 2005, 13, 267–277. [Google Scholar] [CrossRef]
- Singhose, W.; Singer, N.; Seering, W. Comparison of command shaping methods for reducing residual vibration. In Proceedings of the European Control Conference, Rome, Italy, 5–8 September 1995; pp. 1126–1131. [Google Scholar]
- De Luca, A.; Caiano, V.; Del Vescovo, D. Experiments on Rest-to-rest Motion of a Flexible Arm. In Experimental Robotics VIII; Springer: Berlin, Germany, 2003; pp. 338–349. [Google Scholar]
- Pepe, G.; Carcaterra, A.; Giorgio, I.; Del Vescovo, D. Variational Feedback Control for a nonlinear beam under an earthquake excitation. Math. Mech. Solids 2016, 21, 1234–1246. [Google Scholar] [CrossRef]
- Boscariol, P.; Gasparetto, A. Model-based trajectory planning for flexible-link mechanisms with bounded jerk. Robot. Comput.-Integr. Manuf. 2013, 29, 90–99. [Google Scholar] [CrossRef]
- Boscariol, P.; Gasparetto, A. Optimal trajectory planning for nonlinear systems: Robust and constrained solution. Robotica 2016, 34, 1243–1259. [Google Scholar] [CrossRef]
- Turco, E. Discrete is it enough? The revival of Piola–Hencky keynotes to analyze three-dimensional Elastica. Contin. Mech. Thermodyn. 2018. [Google Scholar] [CrossRef]
- Rubinstein, D. Dynamics of a flexible beam and a system of rigid rods, with fully inverse (one-sided) boundary conditions. Comput. Methods Appl. Mech. Eng. 1999, 175, 87–97. [Google Scholar] [CrossRef]
- Wang, C.M.; Zhang, H.; Gao, R.P.; Duan, W.H.; Challamel, N. Hencky bar-chain model for buckling and vibration of beams with elastic end restraints. Int. J. Struct. Stab. Dyn. 2015, 15. [Google Scholar] [CrossRef]
- Dell’Isola, F.; Giorgio, I.; Pawlikowski, M.; Rizzi, N.L. Large deformations of planar extensible beams and pantographic lattices: Heuristic homogenization, experimental and numerical examples of equilibrium. Proc. R. Soc. A 2016, 472. [Google Scholar] [CrossRef]
- Turco, E.; dell’Isola, F.; Cazzani, A.; Rizzi, N.L. Hencky-type discrete model for pantographic structures: Numerical comparison with second gradient continuum models. Z. Angew. Math. Phys. 2016, 67. [Google Scholar] [CrossRef]
- Altenbach, H.; Eremeyev, V.A. On the constitutive equations of viscoelastic micropolar plates and shells of differential type. Math. Mech. Complex Syst. 2015, 3, 273–283. [Google Scholar] [CrossRef]
- Cuomo, M. Forms of the dissipation function for a class of viscoplastic models. Math. Mech. Complex Syst. 2017, 5, 217–237. [Google Scholar] [CrossRef]
- Dietrich, L.; Lekszycki, T.; Turski, K. Problems of identification of mechanical characteristics of viscoelastic composites. Acta Mech. 1998, 126, 153–167. [Google Scholar] [CrossRef]
- De Wit, C.C.; Olsson, H.; Astrom, K.J.; Lischinsky, P. A new model for control of systems with friction. IEEE Trans. Autom. Control 1995, 40, 419–425. [Google Scholar] [CrossRef]
- Buechner, S.; Schreiber, V.; Amthor, A.; Ament, C.; Eichhorn, M. Nonlinear modeling and identification of a dc-motor with friction and cogging. In Proceedings of the Industrial Electronics Society, IECON 2013-39th Annual Conference of the IEEE, Vienna, Austria, 10–13 November 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 3621–3627. [Google Scholar]
- Dawson, D.M.; Abdallah, C.T.; Lewis, F.L. Robot Manipulator Control: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Greco, L.; Cuomo, M.; Contrafatto, L.; Gazzo, S. An efficient blended mixed B-spline formulation for removing membrane locking in plane curved Kirchhoff rods. Comput. Methods Appl. Mech. Eng. 2017, 324, 476–511. [Google Scholar] [CrossRef]
- Cazzani, A.; Malagù, M.; Turco, E. Isogeometric analysis of plane-curved beams. Math. Mech. Solids 2016, 21, 562–577. [Google Scholar] [CrossRef]
- Niiranen, J.; Balobanov, V.; Kiendl, J.; Hosseini, S. Variational formulations, model comparisons and numerical methods for Euler–Bernoulli micro-and nano-beam models. Math. Mech. Solids 2017. [Google Scholar] [CrossRef]

| Link 1 | 113.65 | −590.40 | 102.40 | 210.97 | 3612.9 | −3800.3 | −0.00178 |
| Link 2 | −0.1364 | 105.65 | −780.47 | 1570.4 | −848.80 | −108.65 | −0.01214 |
| Link 1 | 0.8090 | 1.114 | −11.239 | −1.681 | 1.297 | 19.485 | 14.592 | −6.116 | −15.732 |
| Link 2 | 0.2139 | −1.434 | 2.659 | 0.0668 | −9.700 | 10.966 | 3.453 | −5.661 | −0.2856 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giorgio, I.; Del Vescovo, D. Non-Linear Lumped-Parameter Modeling of Planar Multi-Link Manipulators with Highly Flexible Arms. Robotics 2018, 7, 60. https://doi.org/10.3390/robotics7040060
Giorgio I, Del Vescovo D. Non-Linear Lumped-Parameter Modeling of Planar Multi-Link Manipulators with Highly Flexible Arms. Robotics. 2018; 7(4):60. https://doi.org/10.3390/robotics7040060
Chicago/Turabian StyleGiorgio, Ivan, and Dionisio Del Vescovo. 2018. "Non-Linear Lumped-Parameter Modeling of Planar Multi-Link Manipulators with Highly Flexible Arms" Robotics 7, no. 4: 60. https://doi.org/10.3390/robotics7040060
APA StyleGiorgio, I., & Del Vescovo, D. (2018). Non-Linear Lumped-Parameter Modeling of Planar Multi-Link Manipulators with Highly Flexible Arms. Robotics, 7(4), 60. https://doi.org/10.3390/robotics7040060






