1. Introduction
Shoenflies’ motions are rigid-body displacements obtained by combining spatial translations and rotations around axes with a fixed direction. They constitute a 4-dimensional (4-D) subgroup, named Shoenflies’ subgroup, of the 6-D displacement group [
1,
2]. Since the set of rotation-axis’ directions is a bi-dimensional space, the set of Shoenflies’ subgroups is a bi-dimensional space, too. Many industrial manipulations (e.g., pick-and-place on a conveyor belt) require displacements that belong to only one Schoenflies’ subgroup and can be accomplished by particular 4-degrees-of-freedom (4-DOF) manipulators, named Shoenflies-motion generators (SMGs) [
3].
The serial robot SCARA, presented in 1981, is the most known SMG, but many alternative serial architectures can be conceived [
3]. The main drawback of serial architectures is the need of actuating joints that connect mobile links, which brings to increase the mobile masses and, simultaneously, to reduce the dynamic performances. Parallel architectures can solve this issue and parallel SMGs have been presented (see, for instance [
4,
5,
6,
7,
8,
9,
10,
11,
12]), too. Most of the proposed parallel SMGs feature four limbs (e.g., [
5,
6,
7,
9,
12]) and one actuator per limb located on the base. Other parallel SMGs are simply obtained by adding a double Cardan shaft (i.e., a limb of
RUPUR type), which connects the base to the platform, in a translational parallel manipulator.
The main drawback of parallel SMGs is their complex multi-loop structure that drastically reduces their workspace, usually brings cumbersome kinematics and control algorithms, and, often, does not allow a full rotation of the end effector (platform). Nevertheless, adopting two-limbed (i.e., single-loop) architectures with serial [
4,
13] or hybrid [
8,
11] limbs with two actuators per limb reduces the structure complexity while keeping the actuators on the base. Some design tricks [
14,
15] can yield end-effector’s full rotations, and some architectures [
12,
13] can give the possibility of decoupling position and orientation (decoupled kinematics), which allows simpler and more intuitive control strategies. Moreover, not-overconstrained architectures [
4] make it possible to avoid jamming without using small tolerances during manufacturing.
The first author has recently proposed a novel not-overconstrained parallel SMG of type
CRS-
RRC [
13]. Such SMG features a single-loop architecture with actuators on the base and a simple decoupled kinematics. Here, firstly, an organic review of the previous results on this SMG is presented; then, its design is addressed by considering its kinetostatic performances. This design procedure will yield a realistic 3D model that solves all the manufacturing doubts with simple and cheap solutions.
The paper is organized as follows.
Section 2 and
Section 3 state the notations and review the previous results presented in [
13,
16].
Section 4 addresses the analysis of the kinetostatic performances and the design based on them.
Section 5 discusses the results and
Section 6 draws the conclusions.
2. Notations and Background
Figure 1 shows the SMG of type
CRS-
RRC presented in [
13]. The axes of the R and C pairs are all parallel. The platform is connected to the base through two limbs: one of type
CRS and the other of type
RRC. The actuated C pair of the
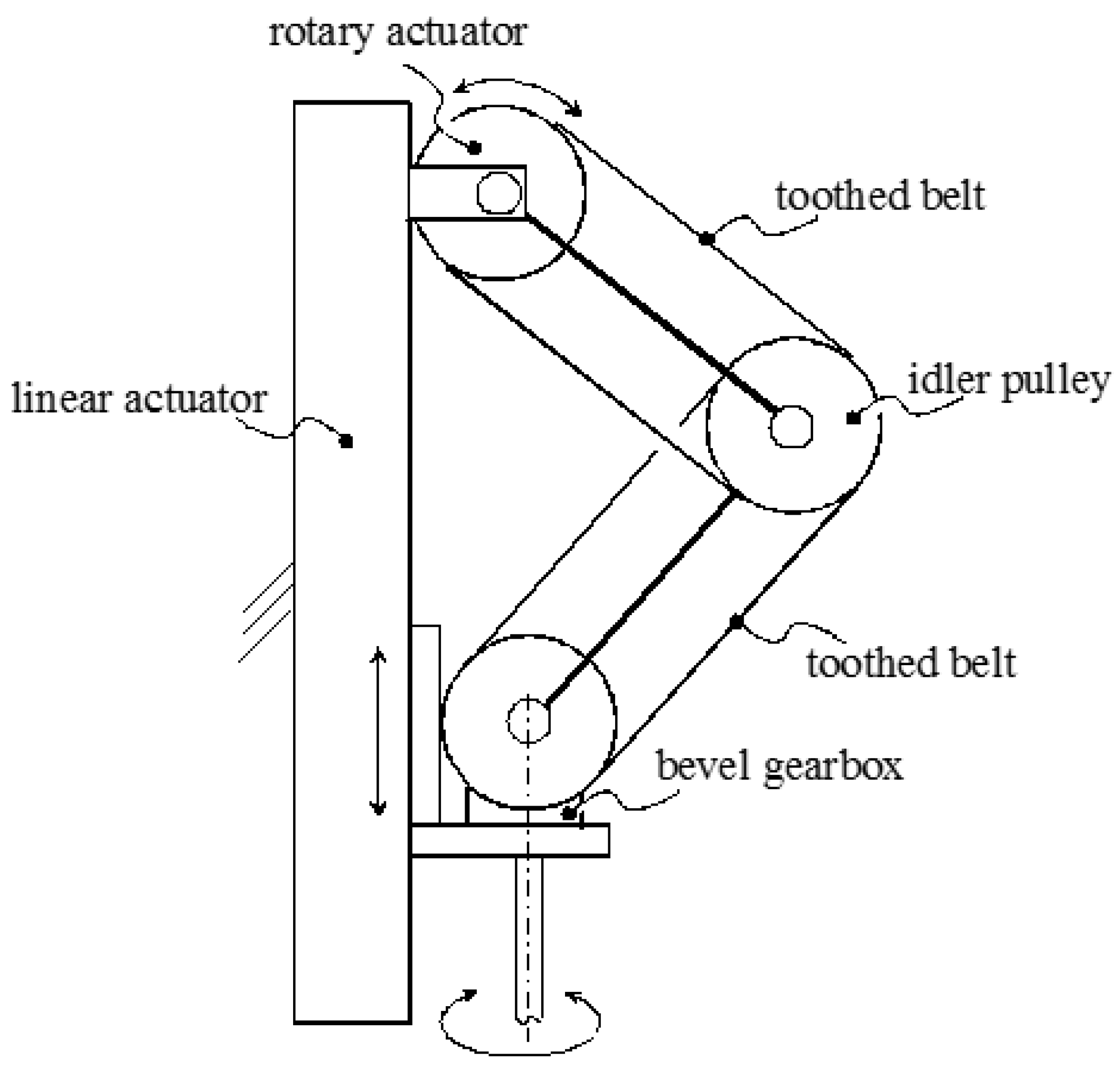
CRS limb is obtained by mean of a PR chain with the sliding direction of the P pair parallel to the axis of the R pair. Such a kinematic chain can be actuated by keeping the motors on the base and using commercial components as shown in
Figure 2. Also, the second actuated R pair of the
RRC limb can be moved from the base by simply using a toothed-belt transmission.
With reference to
Figure 1, O
bx
by
bz
b is a Cartesian reference fixed to the base; the direction of the z
b coordinate axis is the same as the R and C pair axes. In the platform, a
p is the constant distance of the center of the S pair from the axis of the passive C pair and is equal to the length of the segment A
pA
2. O
p is the reference point of the platform, and h is the length of the segment A
pO
p. The coordinates, (x
p, y
p, z
p)
T, of O
p, measured in O
bx
by
bz
b, locate the position of the platform; whereas, the angle, φ, between the segment A
pA
2 and a line parallel to x
b and passing through A
p uniquely determines the platform orientation. In the
CRS limb, point B
2 lies on the axis of the actuated C pair and is fixed to the output link of the C pair. The linear variable of the actuated C pair is the signed distance, d, of B
2 from O
b. The plane parallel to the x
by
b plane and passing through B
2 intersects the axis of the passive R pair at D
2, the axis of the passive C pair at A
p, and the axis parallel to the z
b axis and passing through the center of the S pair at A
2. a
3 and a
4 are the lengths of the segments B
2D
2 and D
2A
2, respectively; whereas, θ
3 and θ
4 are the angular variable of the actuated C pair and the joint variable of the passive R pair, respectively. The point A
p is fixed to the platform. In the
RRC limb, the actuated-joint variables are θ
1 and θ
2. The x
by
b plane intersects the axis of the R pair adjacent to the base at B
1, the axis of the other R pair at D
1, and the axis of the passive C pair at A
1. a
0, a
1 and a
2 are the lengths of the segments O
bB
1, B
1D
1 and D
1A
1, respectively. The
RRC limb constrains the platform to perform Schoenflies motions with rotation axis parallel to the z
b axis; whereas, the
CRS limb controls the coordinate z
p of point O
p through its linear variable, d, and, independently, the platform orientation through its angular variable, θ
3.
According to these notations, the 4-tuples
q = (θ
1, θ
2, θ
3, d)
T and
κ = (x
p, y
p, z
p, φ)
T collect the actuated-joint (input) variables and the platform-pose (output) variables, respectively. The inspection of
Figure 1 yields the following closure equations
If
q is assigned (direct position analysis (DPA)), Equation (1a–c) yield a unique platform position; whereas, Equation (1d) yields two platform orientations (i.e., the DPA has two solutions that share the same platform position). Vice versa, if
κ is assigned (inverse position analysis (IPA)), Equation (1c) yields only one value for d; whereas, Equation (1a,b,d) yield at most four values for (θ
1, θ
2, θ
3) which can be computed through explicit formulas (see [
13] for the proof and the formulas), that is, the IPA has at most four solutions which share the same value of d.
The time derivatives of Equation (1a–d) yield
where m
x = x
p + a
p cos φ − a
3 cos θ
3 and m
y = y
p + a
p sin φ − a
3 sin θ
3.
Since the
RRC limb forbids the platform to perform displacements that do not belong to the above-mentioned Schoenflies’ subgroup, the studied SMG has no constraint singularities
2 and
uniquely identifies the platform twist. As a consequence, Equation (2a–d) are sufficient to relate the platform twist to the actuated-joint rates,
, that is, they are the instantaneous input-output relationship (InI/O).
The InI/O of a manipulator is a linear mapping between platform twists and actuated-joint rates whose coefficient matrices (Jacobians) only depend on the configuration of the manipulator. The configurations (singularities) where these Jacobians have not full rank make the linear mapping not bijective and have relevant kinetostatic implications [
17,
18,
19,
20,
21].
According to the above-deduced InI/O, if
is assigned,
is always uniquely determined, but
is not determined when the segments A
2D
2 and A
2A
p are aligned (i.e., a parallel singularity
3 occurs). In addition, if
is assigned, only two geometric conditions make one or more actuated-joint rates undetermined (i.e., a serial singularity
4 occurs): (i) the 2-tuple
is not determined when the segments A
1D
1 and D
1B
1 are aligned, and (ii)
is not determined when the segments A
2D
2 and D
2B
2 are aligned.
3. Workspace Analysis
According to the adopted notations, the geometric constants of the
CRS-
RRC SMG, which affect the SMG behavior, are a
0, a
1, a
2, a
3, a
4, a
p, and h (
Figure 1). Two of the authors, in [
16], analyzed some workspace characteristics of this SMG. Such analysis brought to size some of those constants. This section summarizes and reviews the results deduced in [
16].
If the two actuated R pairs of the
RRC limb and the linear variable, d, of the actuated C pair are locked (i.e., by keeping z
p and A
1 fixed), the segments B
2A
p (=O
bA
1 =
), B
2D
2 (=a
3), D
2A
2 (=a
4), and A
pA
2 (=a
p) behave like frame, input link, coupler, and follower, respectively, of a four-bar linkage. θ
3 and φ are input and output variables, respectively, of this four-bar linkage, and the singularities of this four-bar correspond to the above-identified parallel singularity and serial singularity (ii). If this four-bar satisfies Grashof’s law [
22] and A
pA
2 is the shortest bar, the platform can perform a complete rotation (i.e., the angle φ has no limitation). Nevertheless, only a double-crank four-bar can guarantee a full control of the platform rotation.
Let
p and
p denote the position vector (
A1–
Ob) and its magnitude (=
), respectively. From an analytic point of view, the four-bar is a double-crank (i.e., the platform can perform a complete rotation fully controlled by θ
3) if and only if
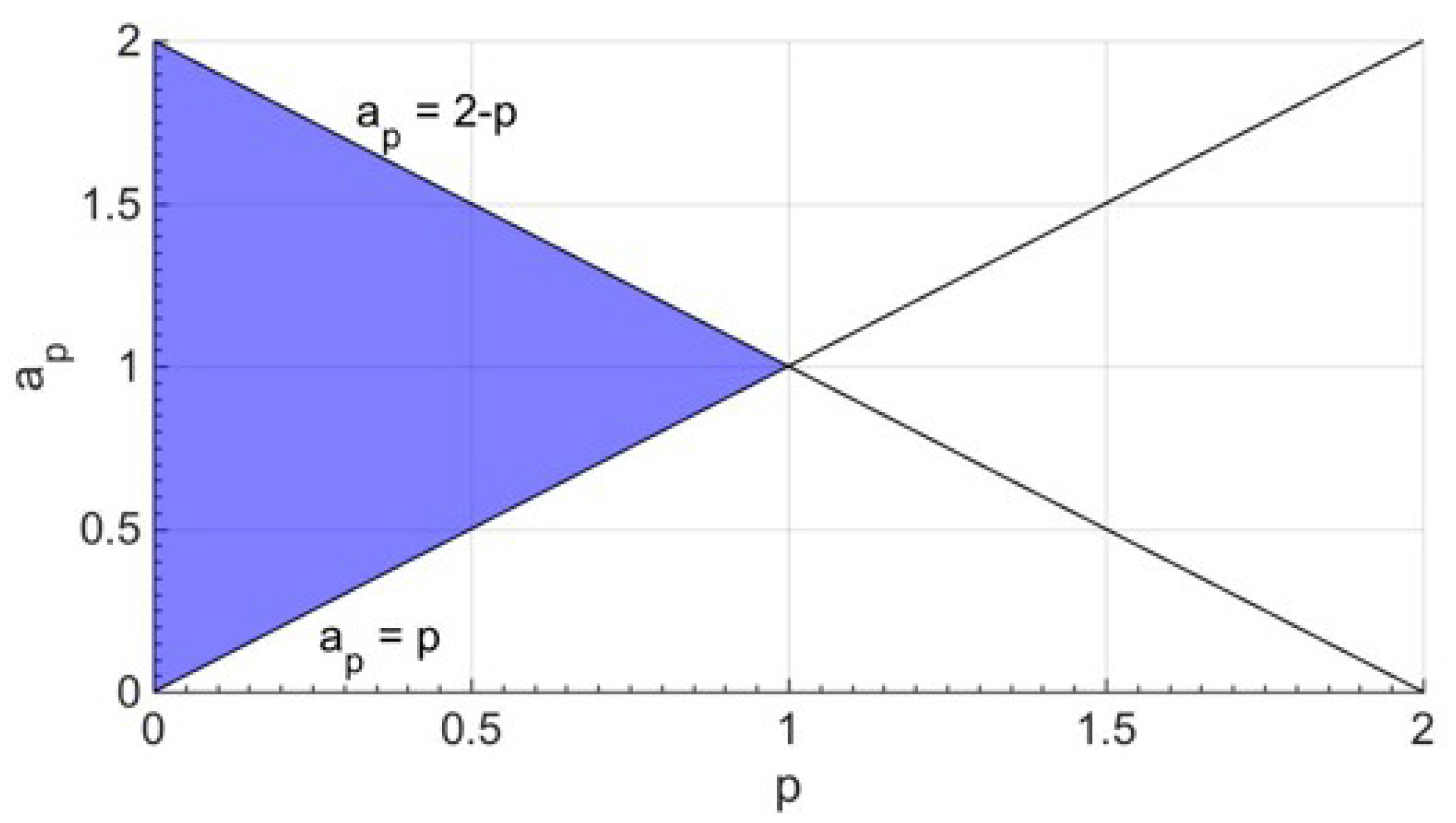
Inequalities (3a,b) impose that the platform can perform a full rotation and condition (3c) make the four-bar linkage double-crank.
Since there is no reason to have a
3 different from a
4 and a possible scaling factor does not affect the analysis, the choice a
3 = a
4 = 1 length unit (l.u.) is adopted. With this assumption, inequality (3b) become |a
p −
p| ≥ 0 and is identically satisfied; whereas, inequality (3a) and condition (3c) become
The blue area of
Figure 3 indicates the values of the 2-tuple (
p, a
p) that satisfy inequalities (4).
Figure 3 shows that the maximum value,
pGr, that
p can assume depends only on a
p: when the values of a
p increase,
pGr increases for a
p ≤ 1 and, then, decreases for a
p > 1. The maximum value of
pGr is 1 l.u. and is obtained with a
p = 1 l.u. Since p
Gr is the radius (see
Figure 1) of the circle centered at O
b that is the region (double-crank region) where A
1 must be located to have a double-crank linkage, the choice a
p = 1 l.u. is adopted to maximize the double-crank region.
Let Δd (=d
max − d
min) be the maximum linear stroke of the actuated C pair. The reachable workspace [
23] referred to O
p is a right cylinder with height Δd, whose cross section is the intersection between two circles: one centered at O
b with radius a
3 + a
4 + a
p and the other centered at B
1 with radius a
1 + a
2. The cross section of the reachable workspace is maximized if the smaller circle is located inside the other, that is, if
or
In addition, if such section contains the double-crank region, the dexterous workspace [
23] referred to O
p is maximum, and it is equal to a right circular cylinder obtained by translating the double-crank region along the z
b axis of Δd. This condition is satisfied if
At the border of the double-crank region (i.e., for p = pGr), the four-bar linkage can still make the platform perform a complete rotation, but the linkage encounters two times the parallel singularity condition during the platform rotation. Since the integrity of parallel manipulators can be preserved only by keeping them work out and far from parallel singularities, a safe free-from-singularity dexterous workspace requires p << pGr.
Outside the double-crank region (i.e., for
p >
pGr), the four-bar linkage does not satisfy Grashof’s law any longer; as a consequence, it can only be a rocker-rocker four-bar linkage and the rotation range, Δφ, of the platform is limited.
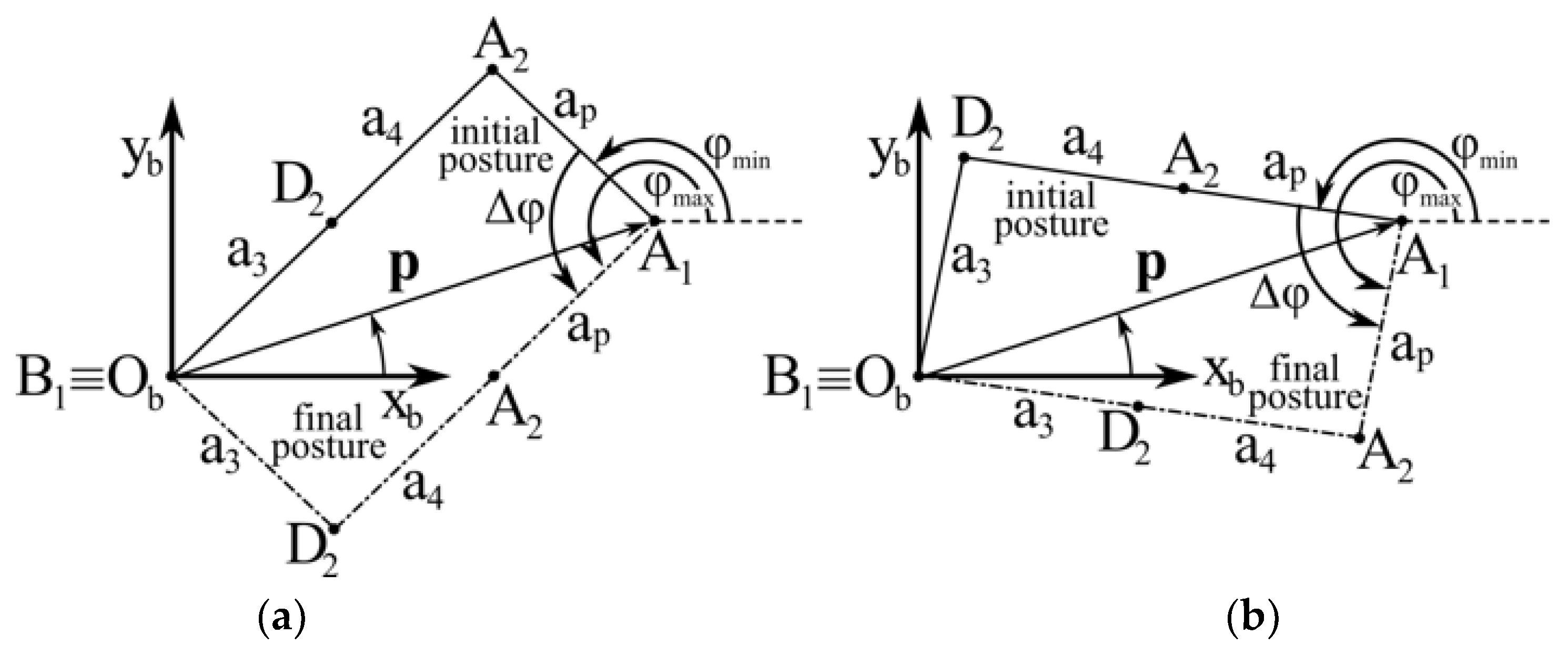
Figure 4 shows the above-defined not-Grashof four-bar linkage at the configurations corresponding to the extreme values of φ. In a rocker-rocker four-bar, the whole Δφ is swept by moving from a serial singularity (ii) to a parallel singularity (
Figure 4a) or vice versa (
Figure 4b). In both the cases, Δφ does not change, but the configurations the mechanism passes through are different. The analysis of
Figure 4 gives the following simple analytic formula for Δφ
Formula (7) highlights that Δφ depends only on p (i.e., the direction of the position vector
p does not affect Δφ) and decreases when p increases. This symmetry with respect to the z
b axis and the fact that the decrease of Δφ with the increase of p is not sharp [
16] make wide regions of the reachable workspace that are out of the double-crank region usable for manipulation tasks that need not a complete platform rotation.
4. Kinetostatic-Performance Analysis and Dimensional Synthesis
The previous sections brought to choose a
3 = a
4 = a
p = 1 l.u. All the other geometric constants (i.e., a
0, a
1, a
2, and h) can be used to match the adoption of a useful workspace adequate to industrial tasks with satisfactory kinetostatic properties. Even though the
CRS-
RRC SMG can perform some tasks outside the above-defined dexterous workspace, the choice of the useful workspace has to take into account the generality of the industrial tasks of an SMG. Consequently, in this case, the useful workspace is chosen as a right circular cylinder with axis passing through O
b (see
Figure 1) and radius,
puw, that satisfies the condition
puw <<
pGr, which makes it coincide with a safe free-from-singularity dexterous workspace.
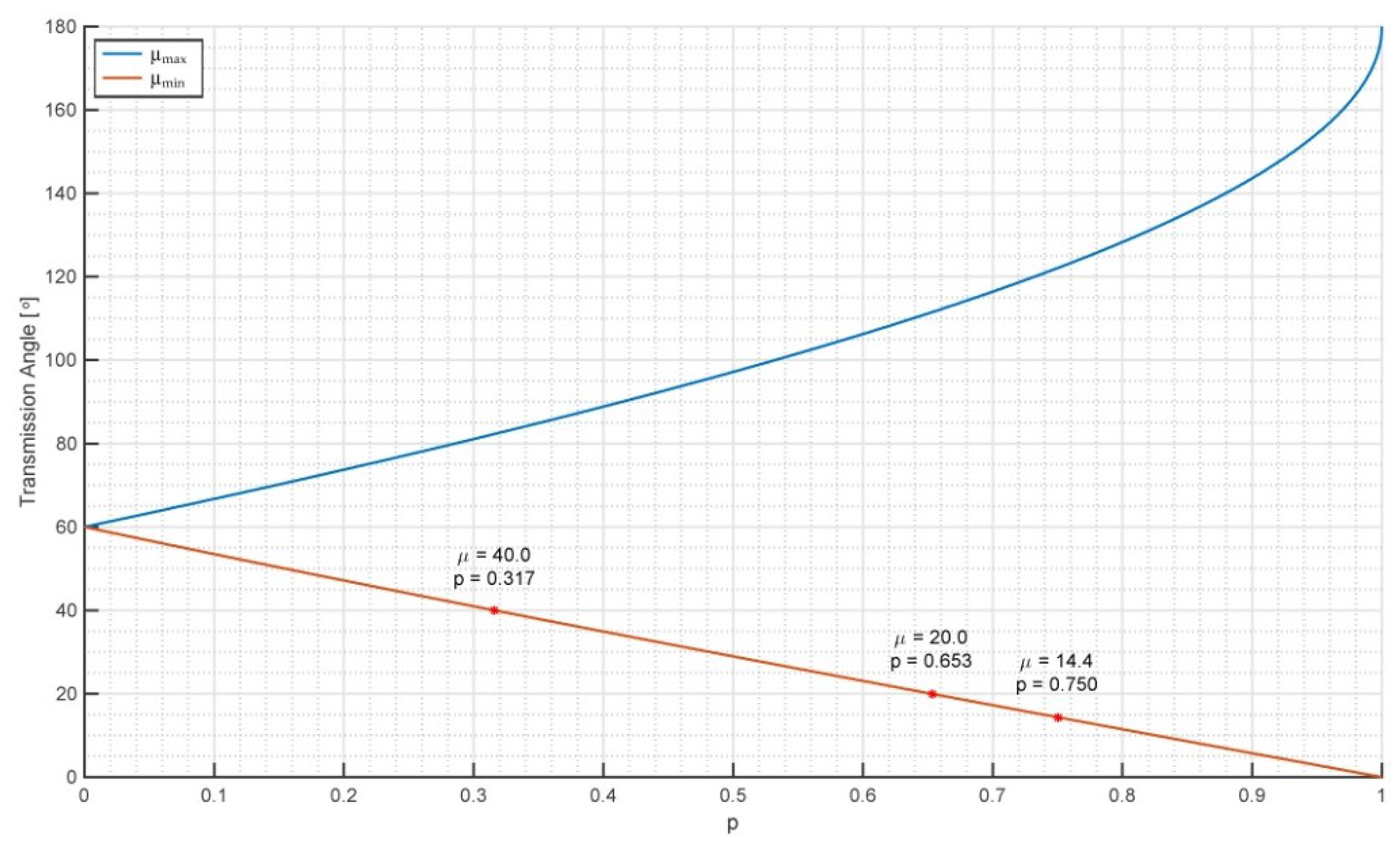
The determination of
puw can be done by imposing that the transmission angle [
22,
24], μ, of the above-defined four-bar linkage has an acceptable value during the platform rotation. In general, tasks that require the application of relevant forces to the gripper during motion (e.g., machining tasks like drilling) need values of |μ − 90| (°) lower than 50° and low friction in the kinematic pairs. Other manipulation tasks with reduced force interaction can accept |μ − 90| values lower than 70°; whereas, when force interaction is not present (e.g., pick-and-place tasks) |μ − 90| could be even larger than 70°. The formulas (see [
24]) that give the minimum, μ
min, and the maximum, μ
max, transmission angles, when particularized to the studied case, become (μ ∈ [0°, 180°])
which, for a
3 = a
4 = a
p = 1 l.u., give the diagrams of
Figure 5.
Figure 5 shows that |μ − 90| ≤ 50° corresponds to
p = 0.317 and |μ − 90| ≤ 70° corresponds to
p = 0.653; whereas, for
p = 0.75, |μ − 90| exceeds 70° only in a small neighborhood of μ
min which is equal to 14.4°.
Since SMGs are mainly employed in pick-and-place tasks, the choice puw = 0.75 is adopted by confining the force interaction tasks in region with p ≤ 0.653 or with p ≤ 0.316 according to the type of task.
A commercial SMG is the pickstar YS02N of Kawasaki [
25]. Its useful workspace is a right circular cylinder with a base radius of 300 mm and a height of 200 mm. Hereafter, this right circular cylinder is chosen as useful workspace for the dimensional synthesis of the
CRS-
RRC SMG. This choice together with the previous choice
puw = 0.75 yield 1 (l.u.) = 400 mm, that is, a
3 = a
4 = a
p = 400 mm.
Figure 6 shows the region of the x
by
b plane swept by the above-defined four-bar linkage with a
3 = a
4 = a
p = 400 mm when point A
1 is moved along the x
b axis from O
b (i.e., A
1 = (0, 0)) to the border of the useful workspace (i.e., A
1 = (300, 0) mm). The whole region swept by the four-bar when the direction of the motion of A
1 changes can be obtained by making the region highlighted in
Figure 6 rotate around O
b in the x
by
b plane. Such rotation yields a circle with a radius of 700 mm. Consequently, by taking into account the physical sizes of the links, the choice a
0 = 800 mm is adopted in order to avoid interferences between the frame and the four-bar during motion.
4.1. Measure of the Kinetostatic Performances
The matrix form of system (2) (i.e., of the InI/O) is
with
Kinetostatic performances of manipulators can be evaluated by using indices built by using the Jacobians
Jk and
Jq of Equation (9). Two of these indices are the “conditioning index” (CI) [
26] of the matrix
J = (
Jq)
−1Jk, which is defined as the inverse of the condition number of
J, and its average value on the useful workspace, named “global conditioning index” (GCI). The computation of the CI and GCI needs that the entries of the Jacobians
Jk and
Jq be homogeneous [
9,
27,
28,
29]. Jacobian homogenization can be obtained with the introduction of a characteristic length, λ, through a change of variables [
27], even though which λ should be used is an open problem.
In the studied case, the introduction of the new homogeneous variables
and
into Equation (9) yields
where
Jh = (
Jqh)
−1Jkh with
Jh is a homogeneous Jacobian with dimensionless entries. The condition number, χ, of
Jh is, by definition,
where
stands for any matrix norm of the argument, if the Frobenius norm [
21] is adopted
. Consequently, the conditioning index, CI = 1/χ, depends both on the SMG configuration and on the geometric constants a
1 and a
2 that have not been determined, yet. The CI ranges from 0, at parallel singularities to 1 at isotropic configurations (i.e., SMG configurations where
Jh is proportionate to the identity matrix), which are the farthest from parallel singularities. The CI is a local index that measures the kinetostatic performance of the SMG at a configuration; whereas, the GCI (i.e., its average value on the useful workspace) gives a score to the kinetostatic performance of the SMG and could be used to compare different manipulators.
Optimizing the kinetostatic performances of a manipulator by using the CI and the GCI means determining the available geometric constants (in this case, a1 and a2) so that the minimum value, CImin, of the CI and the GCI are as high as possible for that architecture. Such optimization is presented in the following subsection.
4.2. Dimensional Synthesis
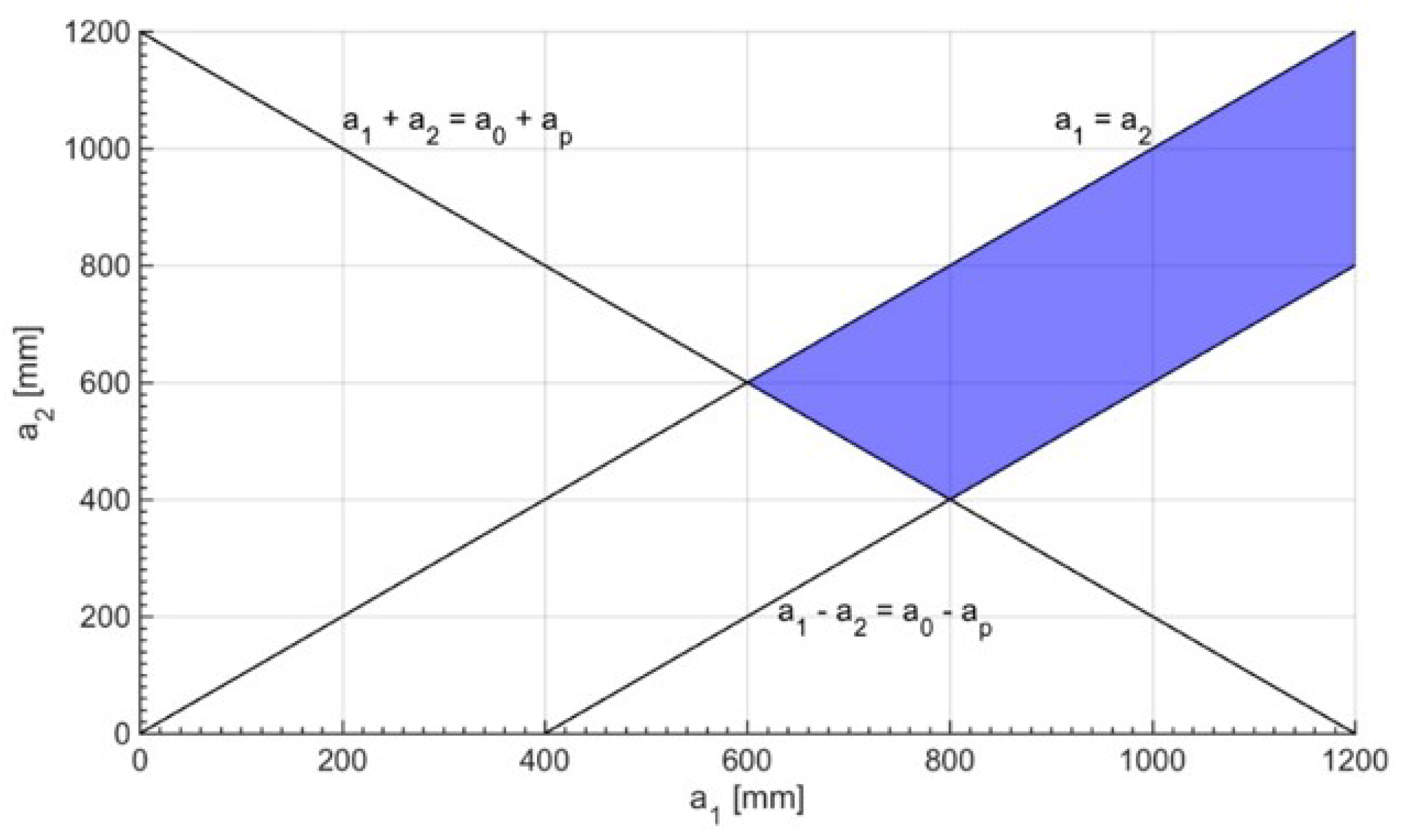
The admissible values of a
1 and a
2 must satisfy inequalities (6a,b) with a
0 = 800 mm and
pGr = a
p = 400 mm. Moreover, a reasonable choice for the
RRC limb would be a
2 ≤ a
1. All these inequalities are satisfied in the region highlighted in blue of
Figure 7.
By setting λ = 400 mm (i.e., equal to the length of a
p, a
3 and a
4 and to the arithmetic mean of the diameter and the height of the useful workspace), a numerical algorithm has been used to compute the GCI and the CI
min referred to the useful workspace for each admissible values of (a
1, a
2). The results of these computations are shown in
Figure 8.
The analysis of the GCI values displayed in
Figure 8a reveals that the maximum GCI is equal to 0.48795 and is obtained with a
1 = 869 mm and a
2 = 469 mm, which correspond to CI
min = 0.28682 (
Figure 8b). Also,
Figure 8a shows that the maximum GCI falls in a smooth region (more or less flat) which allows large variation of (a
1, a
2) with small reductions of the GCI.
On the other side, the analysis of the CI
min values displayed in
Figure 8b reveals that the maximum CI
min is equal to 0.29806 and is obtained with a
1 = 993 mm and a
2 = 593 mm, which correspond to GCI = 0.4763 (
Figure 8a). Moreover,
Figure 8b shows that also the maximum CI
min falls in a smooth region (more or less flat). These results bring to choose a
1 = 950 mm and a
2 = 600 mm which correspond to a good compromise with GCI = 0.482 and CI
min = 0.29743 that are values near enough to their maxima. The chosen values of a
1 and a
2 yield the minimum CI values at each A
1 position inside the useful workspace shown in
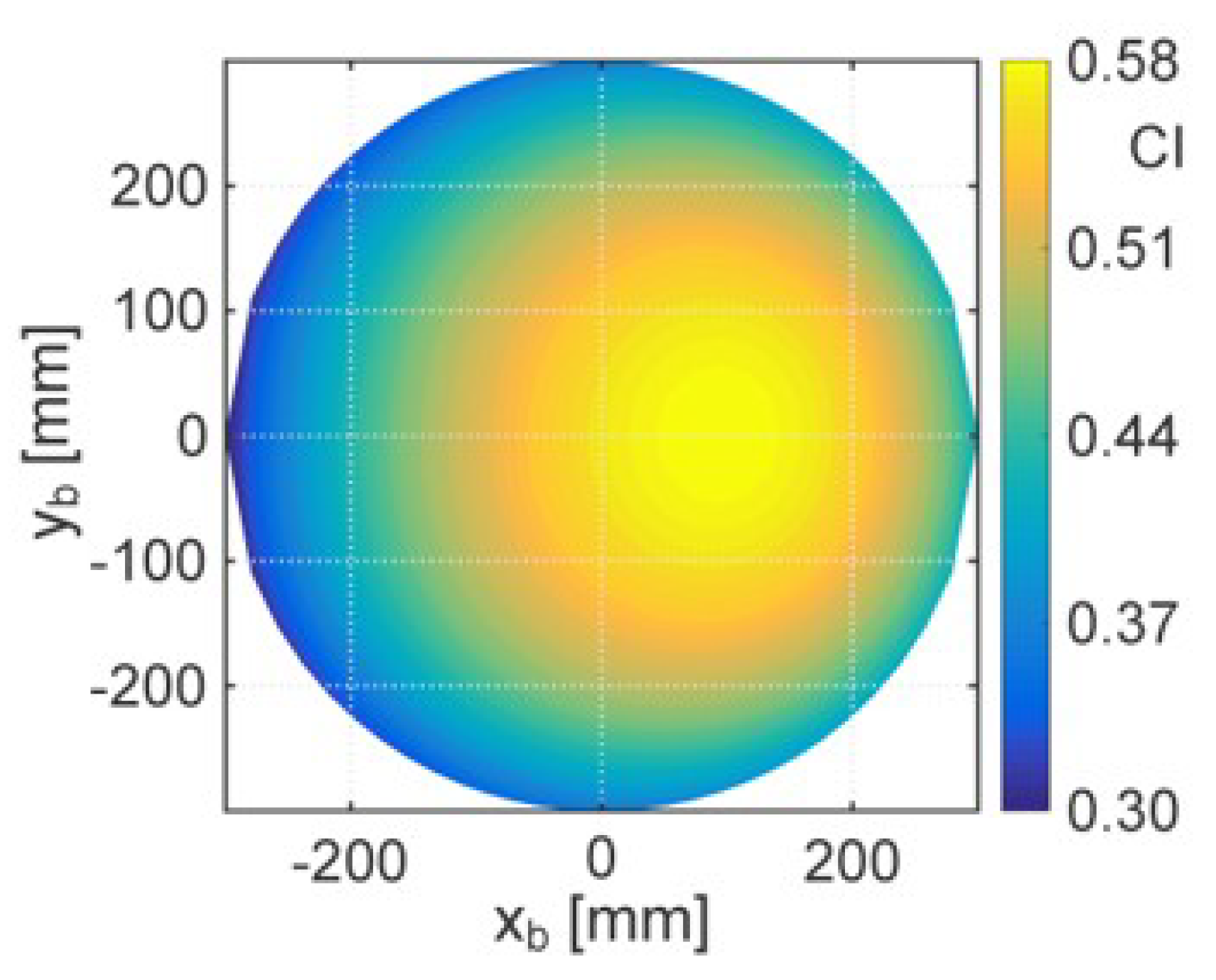
Figure 9.
Figure 9 highlights that most of the useful workspace has CI ≥ 0.45, which makes the CI distribution acceptable.
4.3. The 3D Model
The dimensional synthesis, with useful workspace assigned as a right circular cylinder with a radius of 300 mm and a height of 200 mm, brought to choose the following values of the geometric constants: a
0 = 800 mm, a
1 = 950 mm, a
2 = 600 mm, a
3 = 400 mm, a
4 = 400 mm, and a
p = 400 mm.
Figure 10 shows the region of the x
by
b plane swept by the
RRC limb, with a
0 = 800 mm, a
1 = 950 mm, and a
2 = 600 mm, when point A
1 is moved on the whole circular boundary of the useful workspace and the limb is assembled in either of the two assembly modes the IPA identifies [
13]. The analysis of
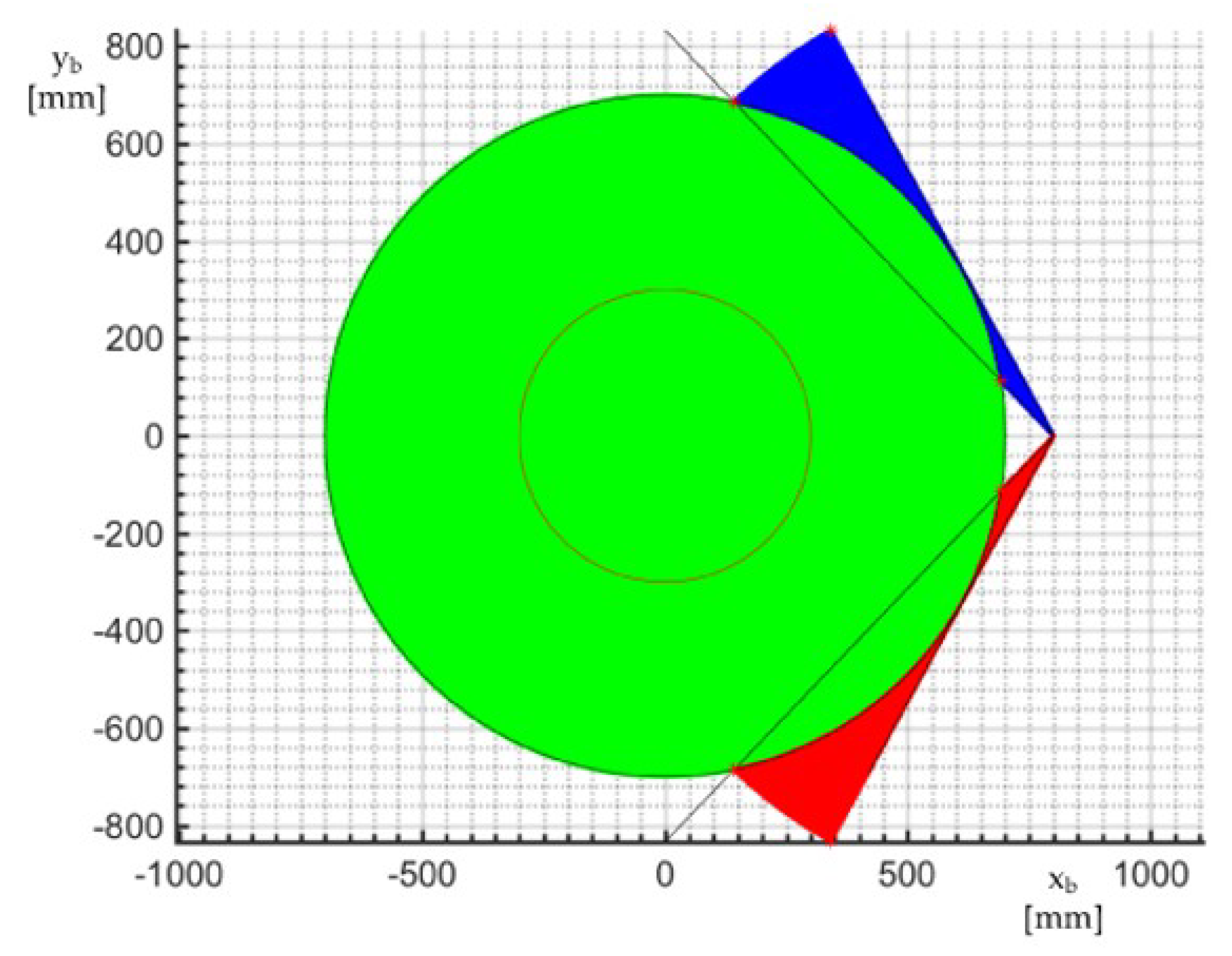
Figure 10 highlights that no link interference occurs with the chosen geometric data. By combining
Figure 6 and
Figure 10 the overall region of the x
by
b plane that is swept by both the limbs is obtained.
Figure 11 shows such region.
In order to solve all the doubts about the actual feasibility of the machine, a CAD model of the
CRS-
RRC SMG has been built with the chosen geometric data.
Figure 12 shows the 3D view (
Figure 12a) and the lateral view (
Figure 12b) of this model. Such model has an L-shaped base, only commercial actuators that are all mounted on the base, rolling bearings in all the R pairs to avoid jamming of the above-defined four-bar linkage at low transmission angles, a spherical roller bearings that implements the S-pair constraint
5, and a linear ball bearing that implements the constraint of the passive C-pair. The bevel gearbox and the toothed belts (
Figure 2 and
Figure 12) are commercial products, too.
5. Summary of the Results and Discussion
The kinematic analysis [
13] of the
CRS-
RRC SMG showed that both the DPA and IPA are solvable with simple and explicit formulas, and that platform’s translation and rotation are decoupled. Therefore, the control algorithms are easy to implement and require very low computation time, which makes it possible to build a fast online control system.
The above-reviewed workspace analysis (see also Ref. [
16]) highlighted that the reachable workspace has axially-symmetric properties. In particular, a safe free-from-singularity dexterous workspace, which is a right circular cylinder, is easy to identify in a wider region of the reachable workspace where the platform can perform complete rotations. Moreover, parallel singularities occur only for two known platform orientations and, in the reachable workspace, they are located on a circle that is the boundary of the dexterous workspace. Thus, the platform can pass through the parallel-singularity locus simply by changing its orientation and, if necessary, can accomplish particular tasks in region where the platform rotation is bounded.
The kinetostatic analysis based on the transmission angle and the conditioning index revealed that the machine can be so dimensioned that the GCI and the CImin are acceptable in a useful workspace, equal to those of commercial SMGs, with transmission angles adequate to the generality of industrial tasks.
The CAD model of the CRS-RRC SMG showed that its manufacture needs only commercial components. This result proves the actual feasibility of the machine with cheap production processes. Moreover, it highlights that the L-shaped base when fixed on a rotating frame allows an easy way for setting up the machine with respect to different machining planes (e.g., belt conveyors).