High Performance Motion-Planner Architecture for Hardware-In-the-Loop System Based on Position-Based-Admittance-Control
Abstract
:1. Introduction
- Cost effectiveness, in fact it allows one to reduce the number of costly in-field tests and use these only for advanced development stages of the system.
- Repeatability and variety of test conditions, difficult to reproduce in an actual environment.
- Safety and accuracy, due to the possibility of integrating hard to predict and simulate parts of the system, like human beings, complex actuators, sensors and the like. Moreover, potentially dangerous conditions and system failures can be simulated in a safe way.
- Concurrent systems engineering, since HIL offers development teams the possibility of working on their hardware or control algorithms without losing sight of integration issues, allowing testing at different levels of completion and coordination of the whole system.
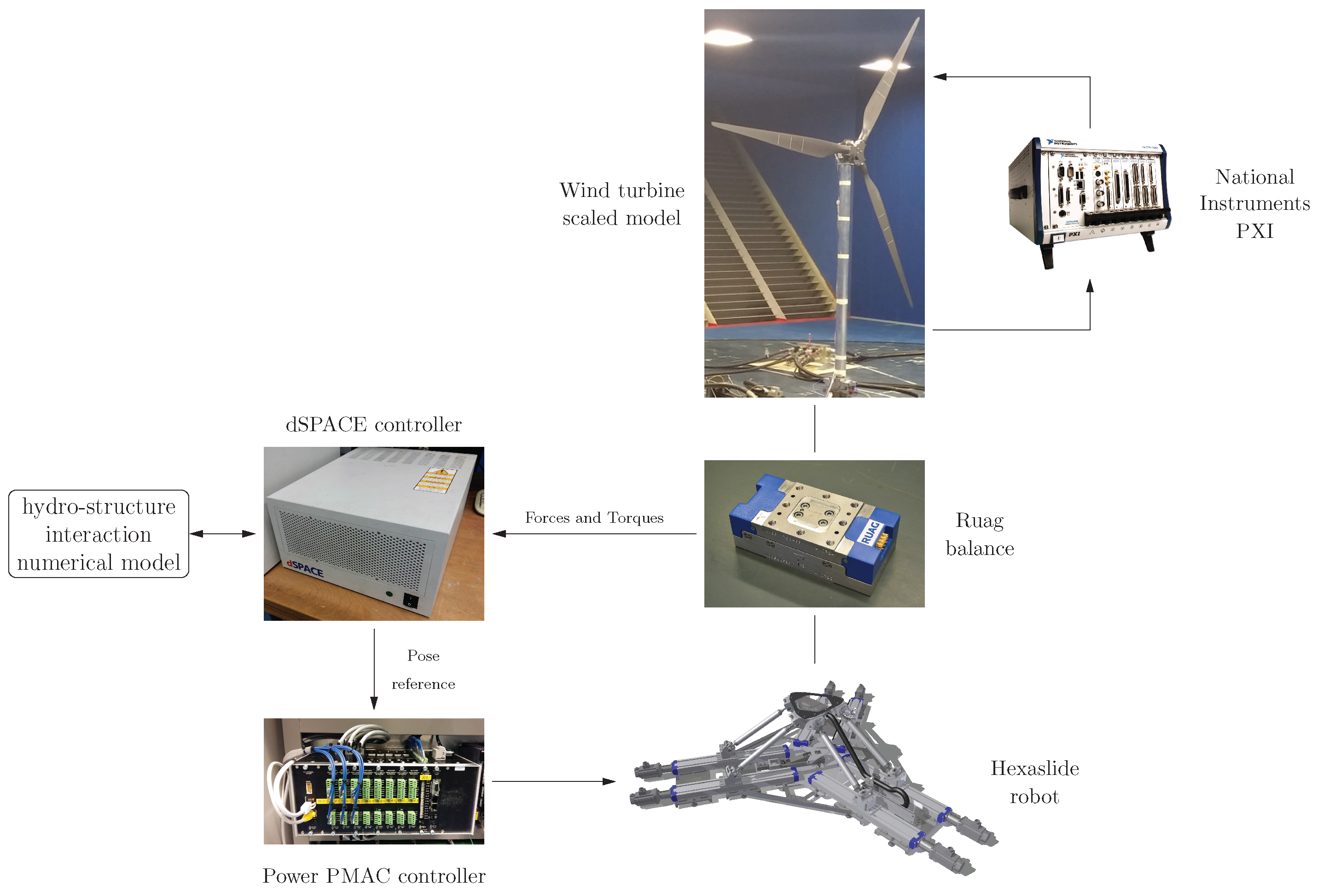
2. The HIL System
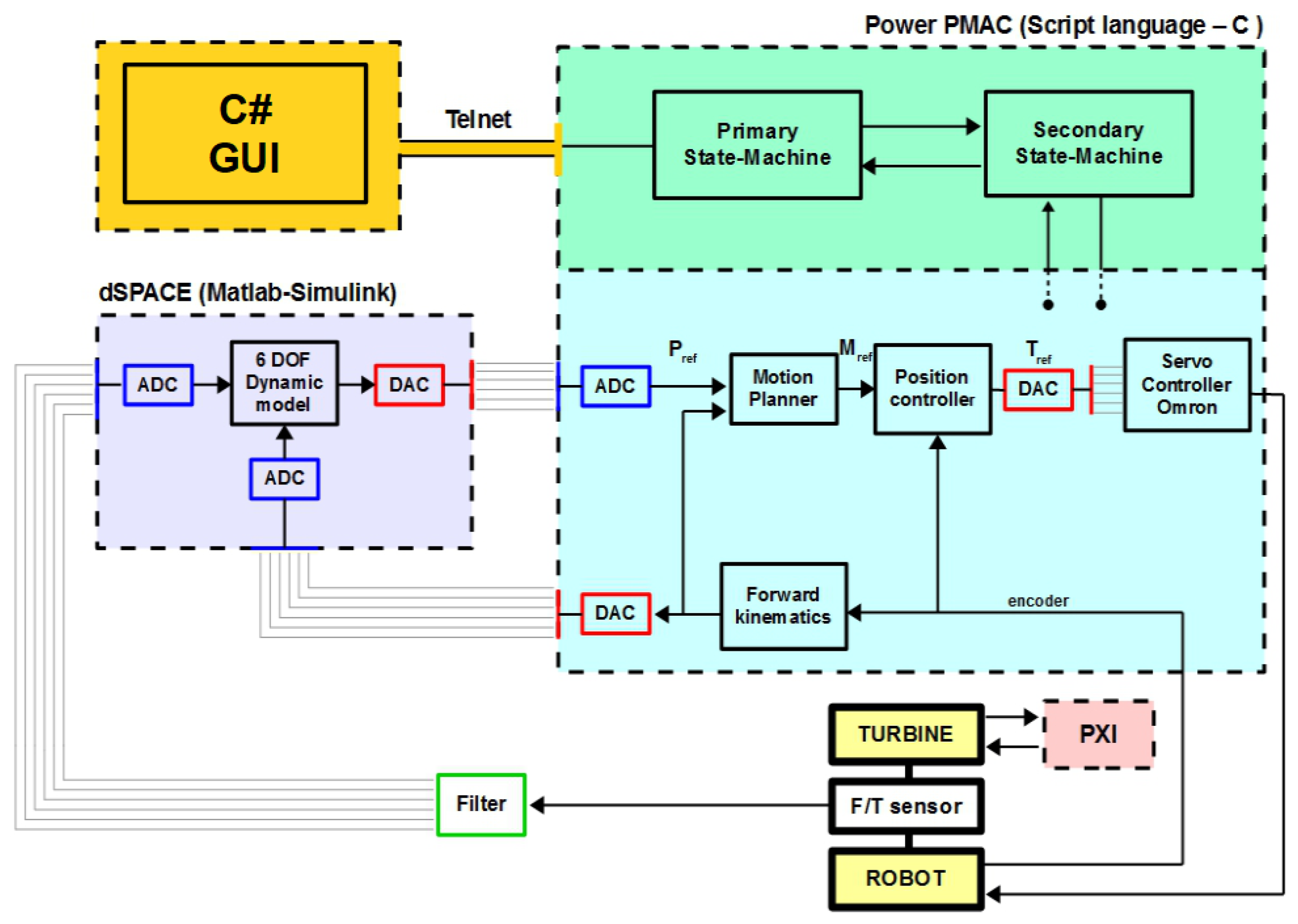
3. Control Architecture
Real Time Pose Estimation
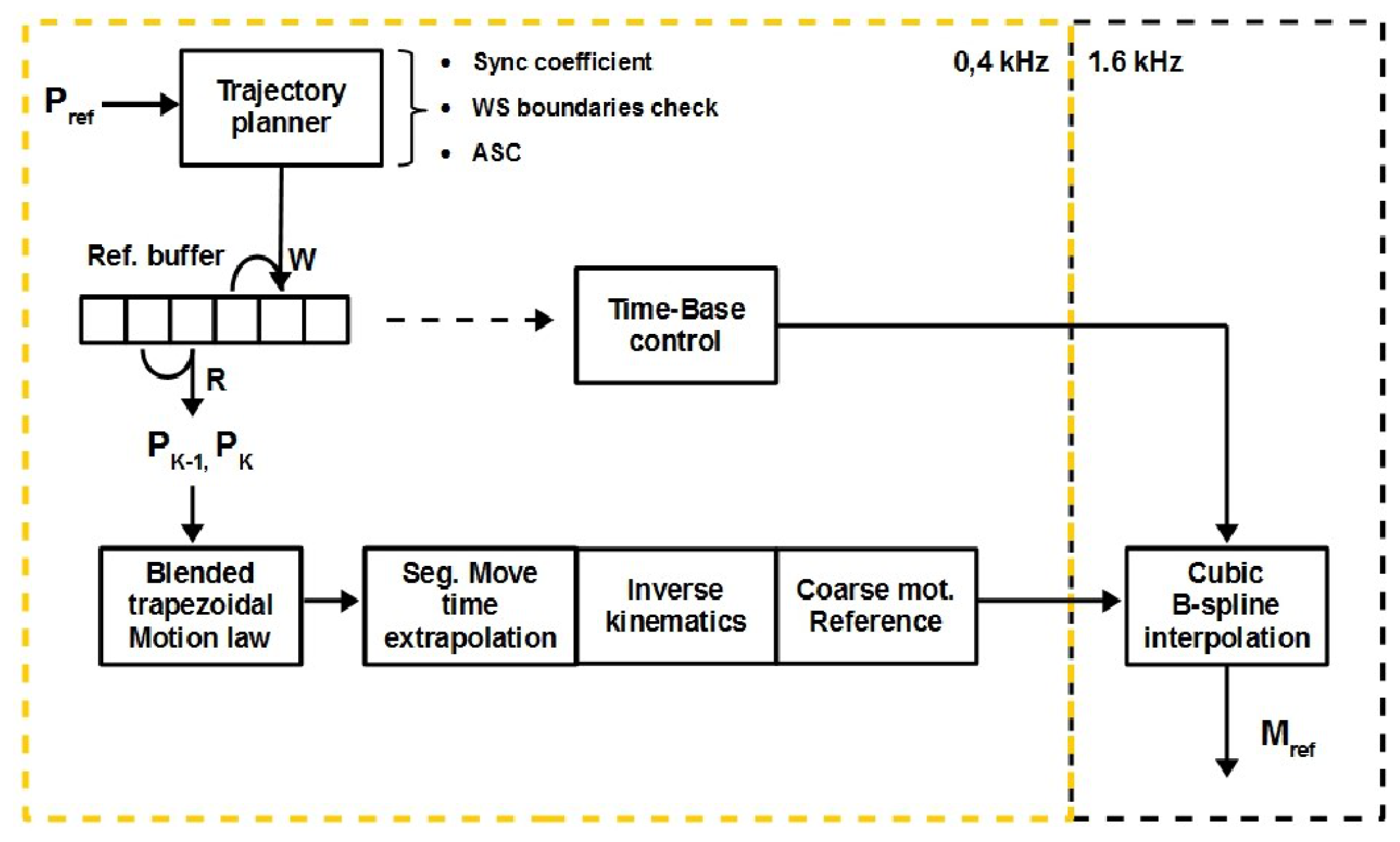
4. Motion Planner
4.1. High Level Algorithms
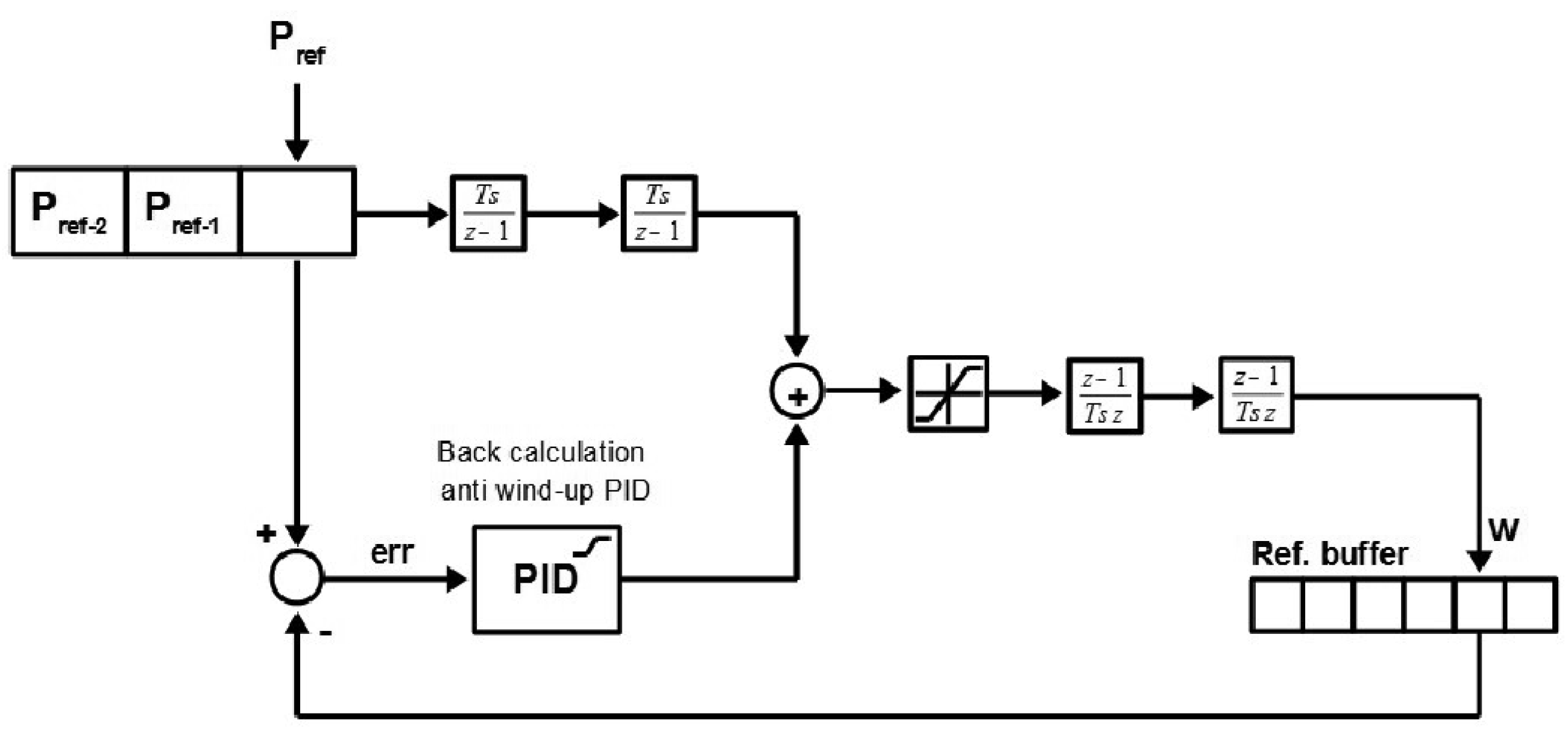
4.1.1. Synchronization Coefficient
4.1.2. Workspace Boundaries Check
4.1.3. Acceleration Saturation Control (ASC)
4.2. Medium Level Algorithms
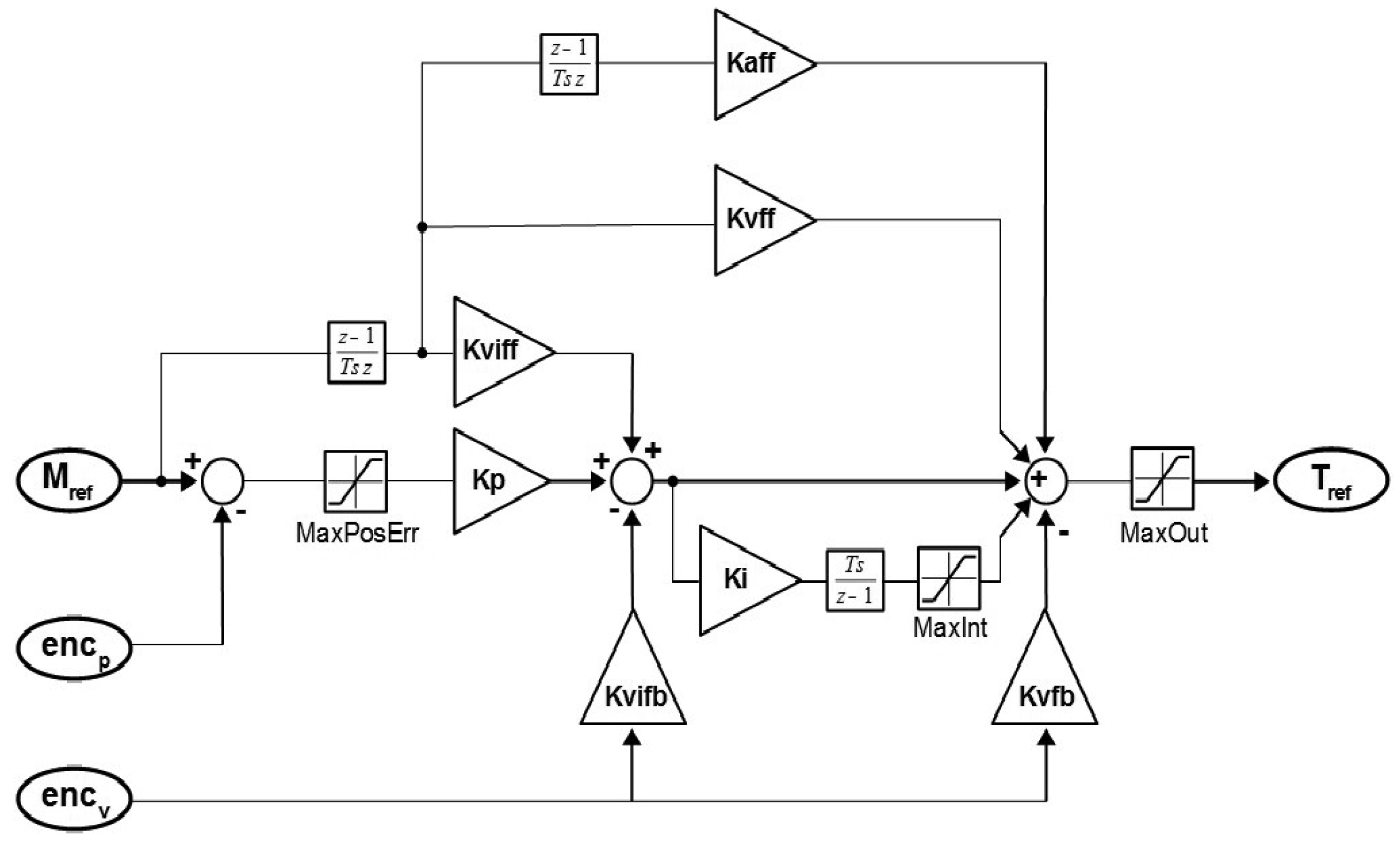
4.3. Low Level Algorithms
5. Experimental Setup and Results
- Two real-time script language PLCs manage the robot’s state machine. The first of these initializes all the robot parameters and the setup variables at the machine booting. Subsequently it runs the primary machine state. This routine checks for any errors, manages the change of state required by the user according to the current state of the robot and activates the secondary state machine. The latter is operated by the second real-time PLC and executes the request of state change forwarded by the primary machine state. It further manages the current state and the corresponding tasks, permits the debug procedure towards the user and executes the numerical forward kinematics C routine in order to transmit the real-time estimated pose.
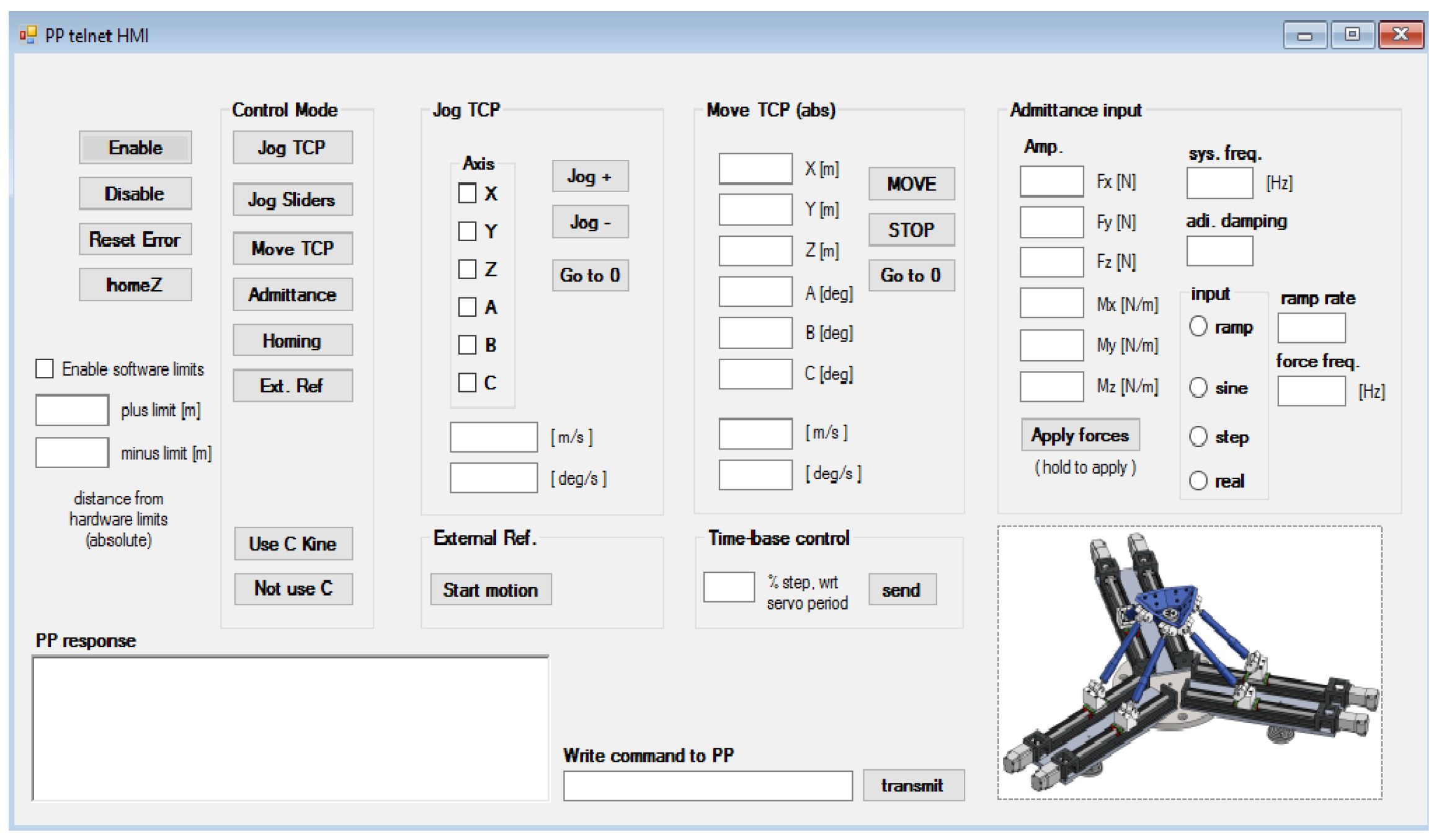
- All the commands by the users are transmitted to the primary state machine through a GUI written in C# and connected, via the Telnet protocol, to the Power PMAC variables saved in a shared memory.
- Non real-time PLC language scripts manage the tasks relative to the operating modes. The more computationally demanding routines are written in C and executed by the main PLC with precise timing. Among these are the workspace safety limiting algorithms, acceleration saturation control, time-base control, signal processing and buffer management. Other tasks carried out by the main PLC are the debug procedure towards the state machine, the start/stop tasks of the motion program and the handling of possible exceptions.
- The motion program is in the bottom level of this software architecture. This is the task with the highest priority executed between the servo interrupts. This routine deals with the motion curve generation, trajectory blending, segmentation time extrapolation, inverse kinematics and the accurate interpolation.
- Underneath the motion program, the servo loops manage the signals coming from the encoders and transform the actuator position references into analogical torque commands which are transmitted to the Omron amplifiers via the DACs.
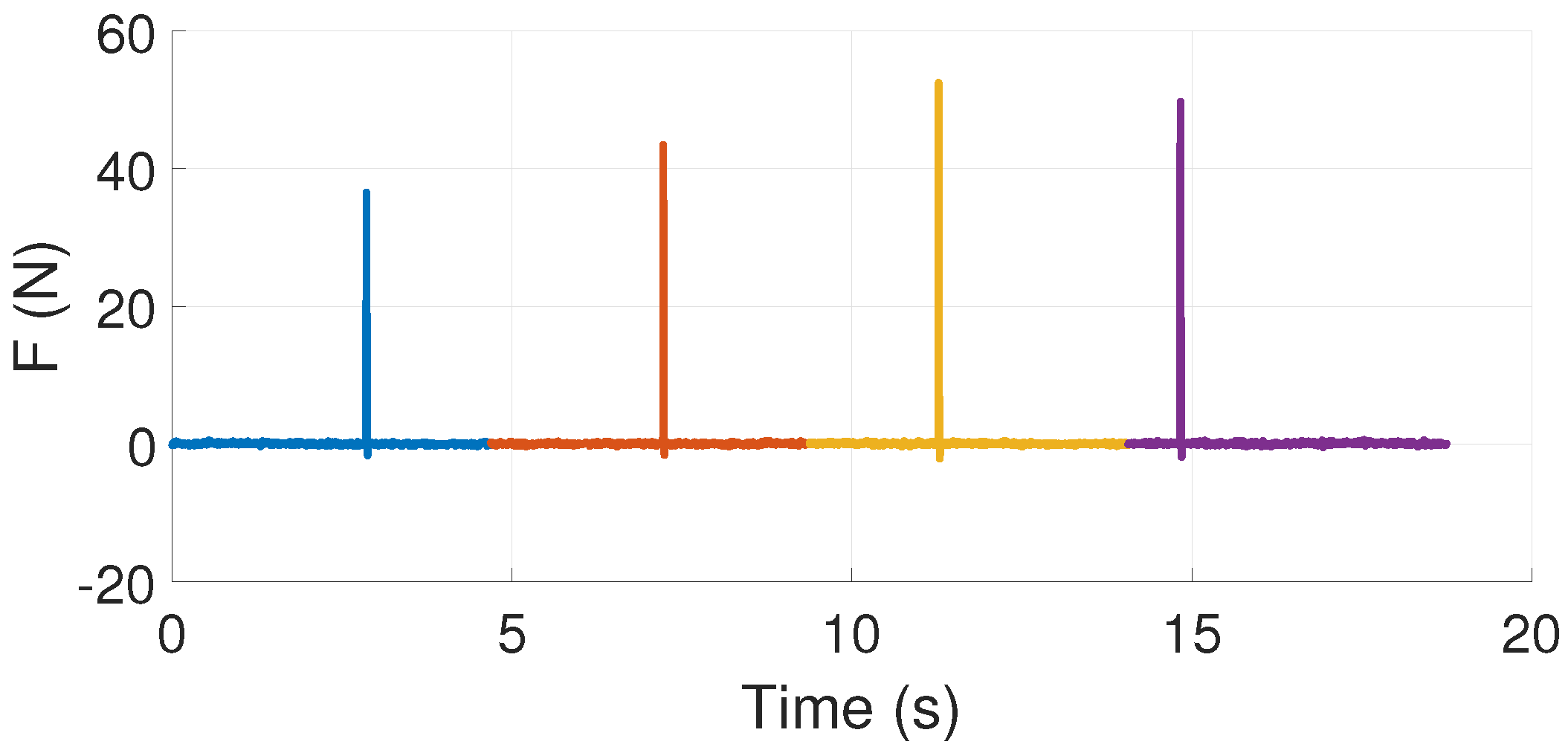
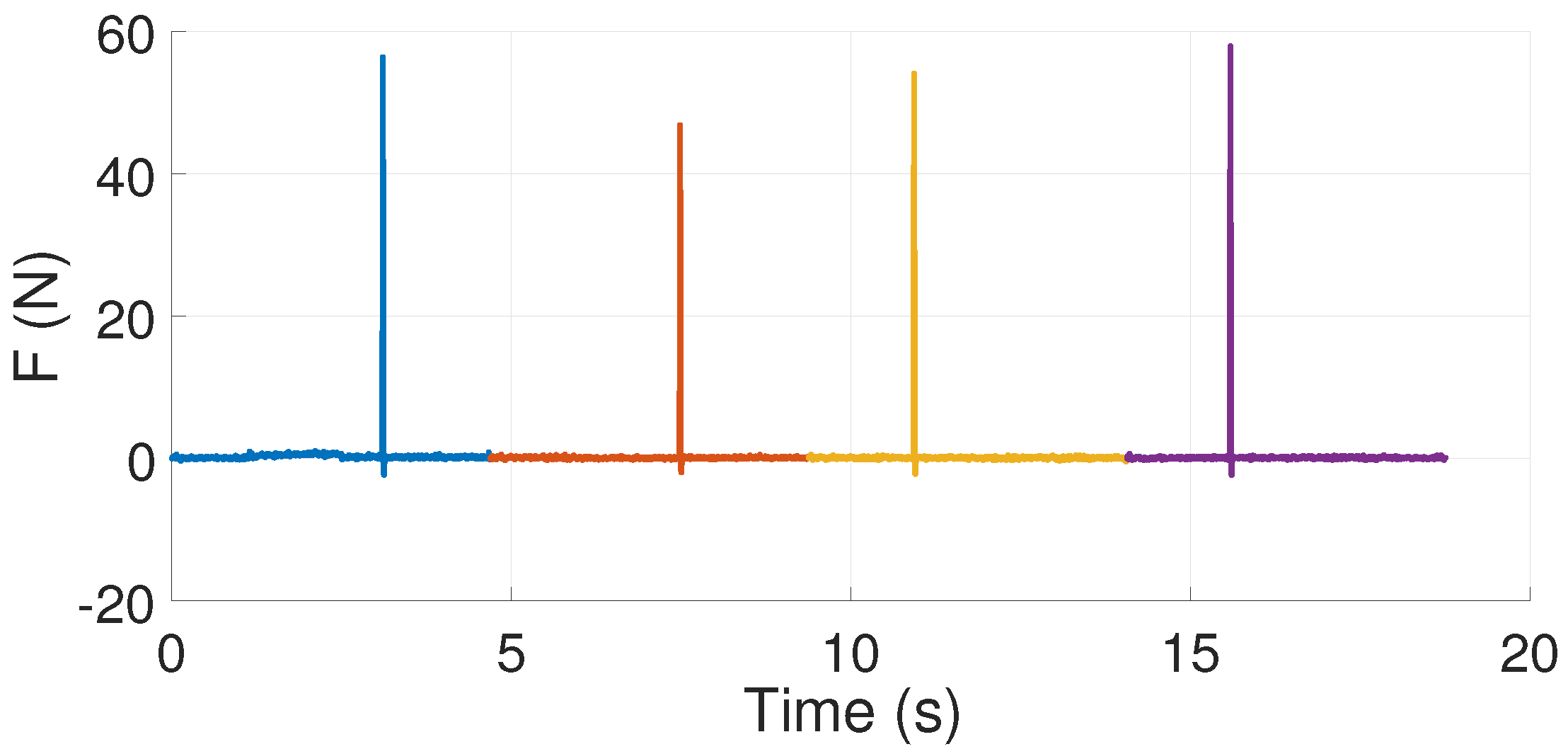
5.1. Experimental Tests
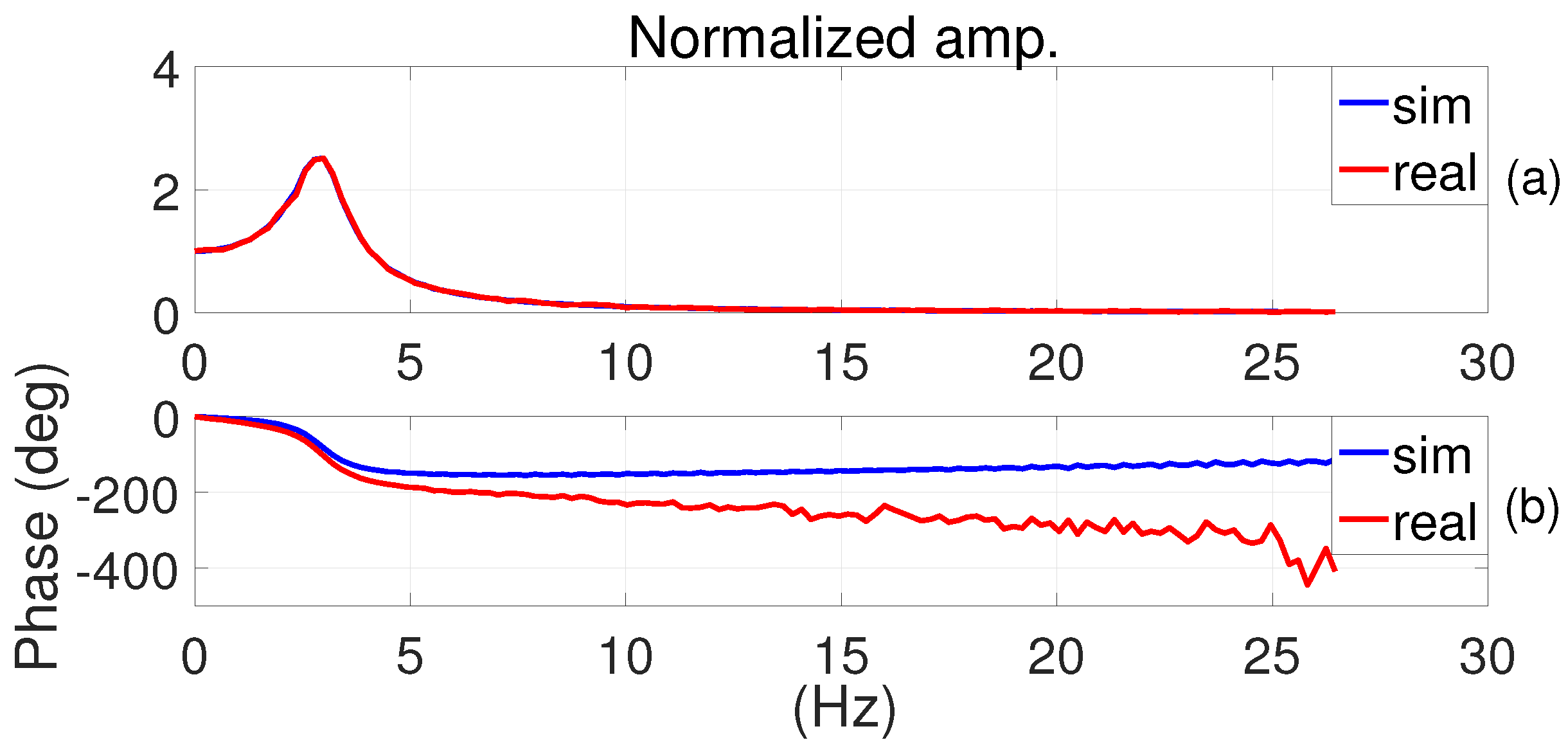
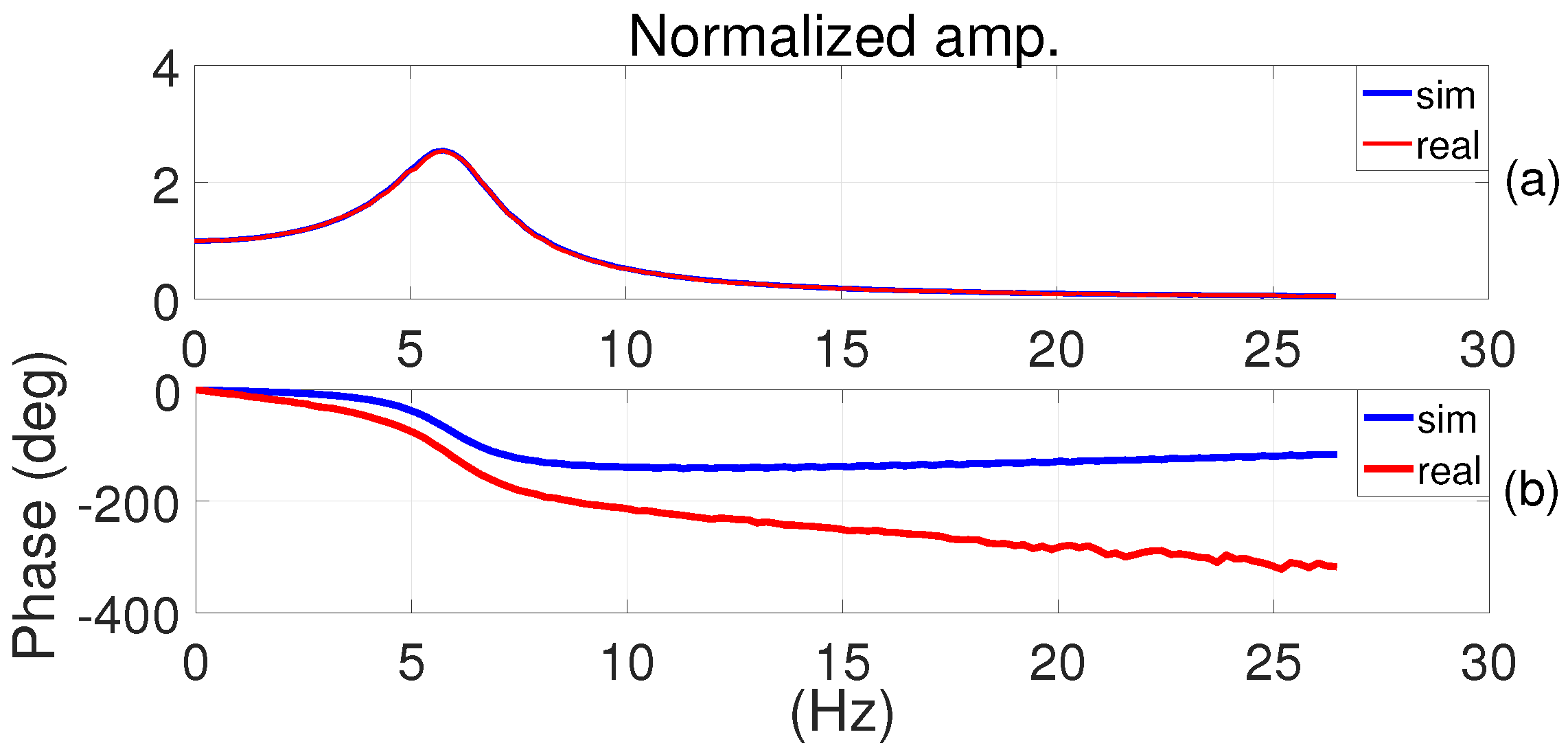
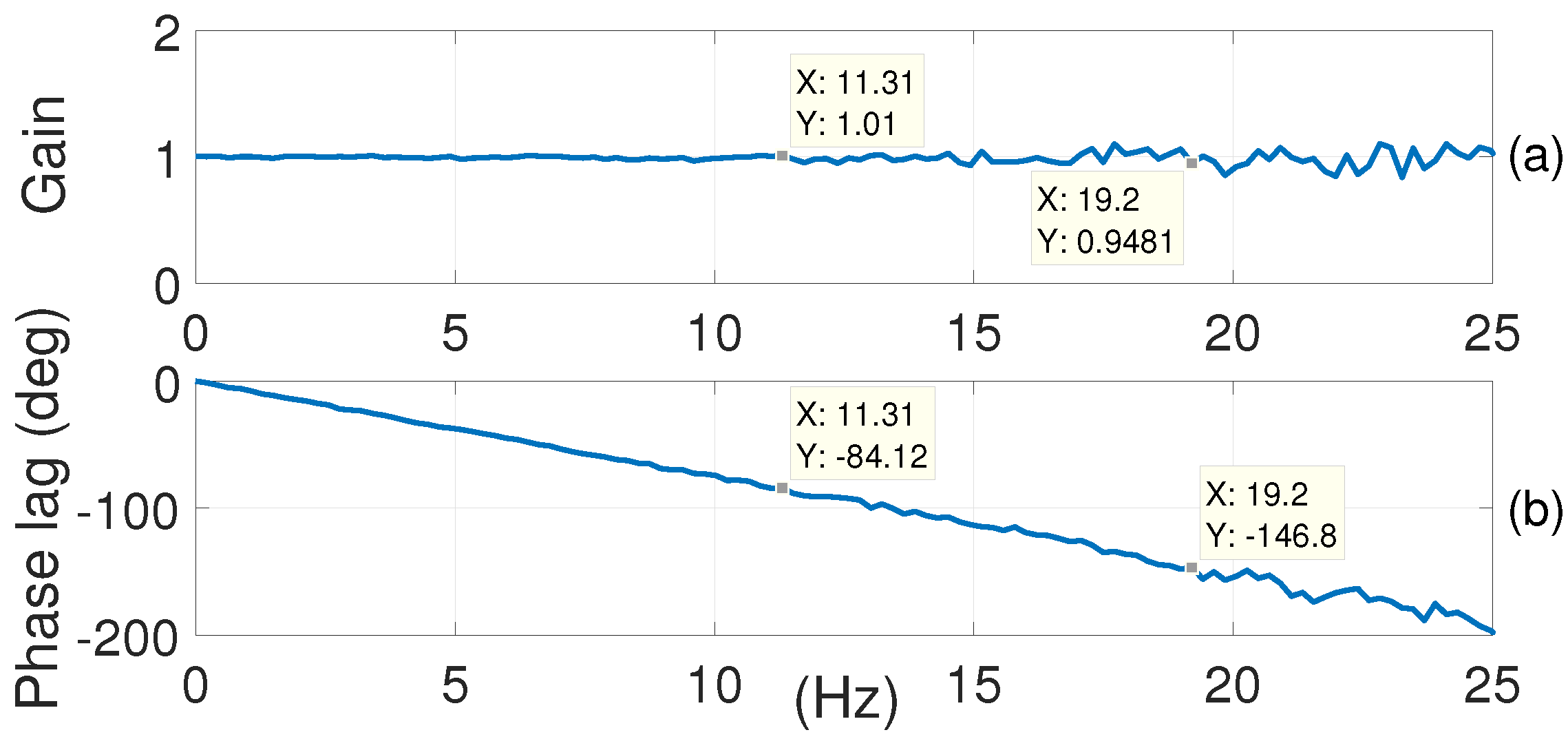
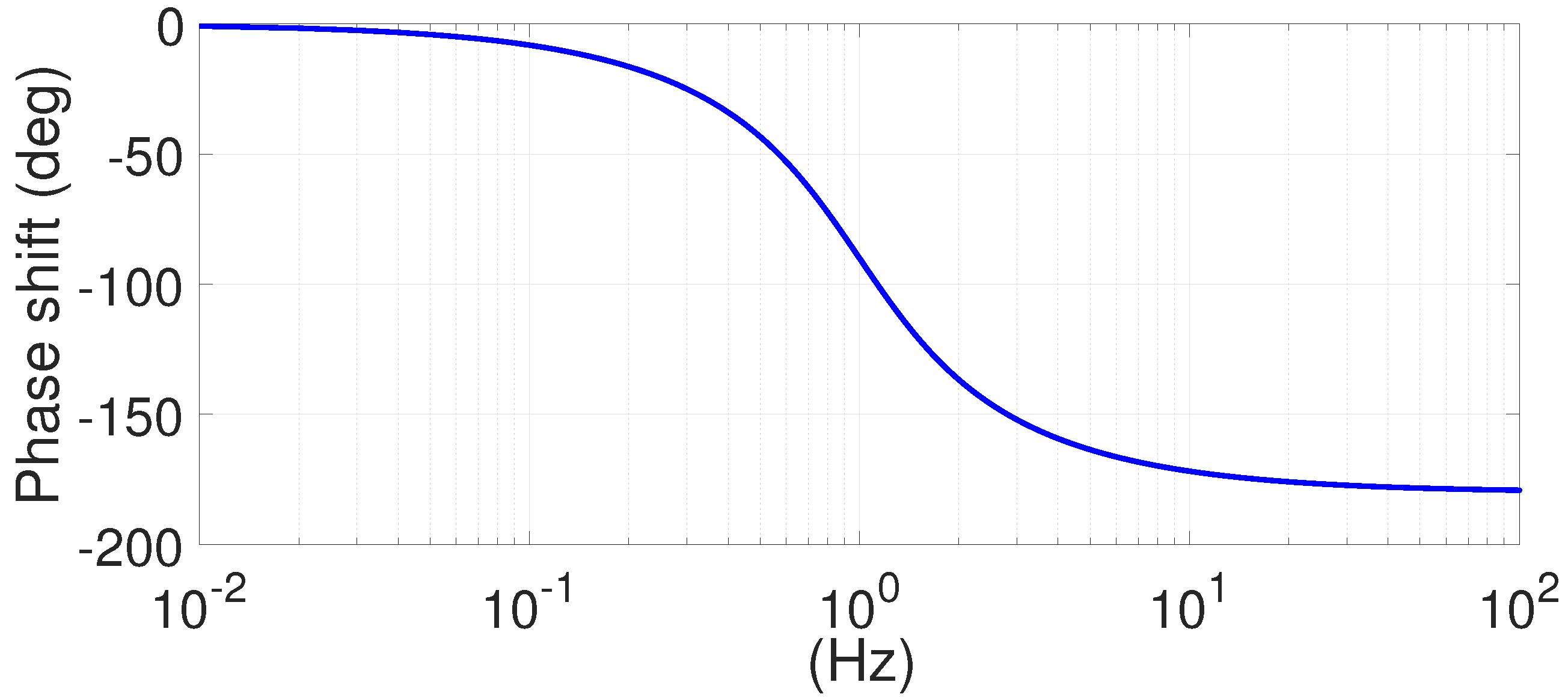
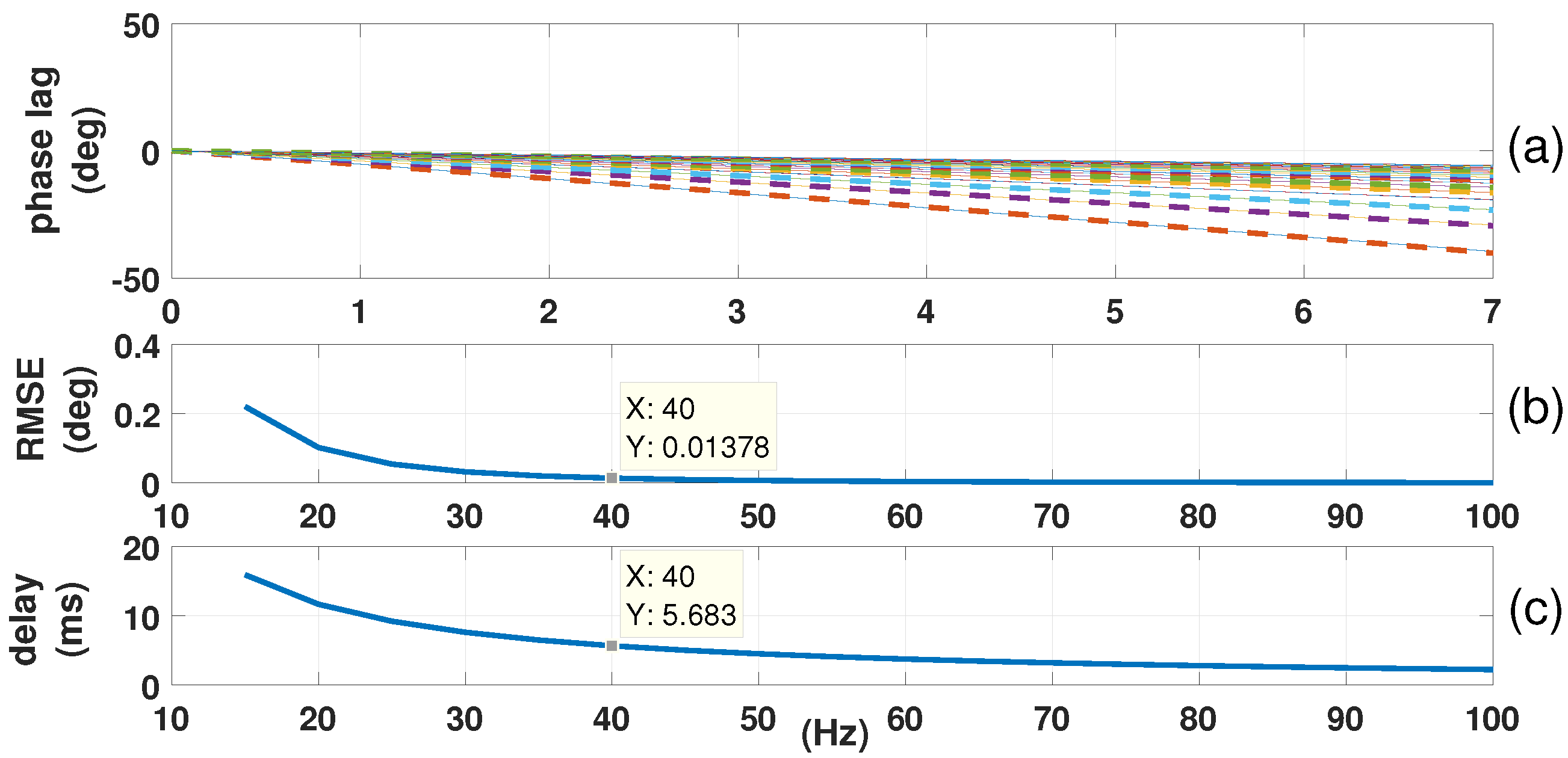
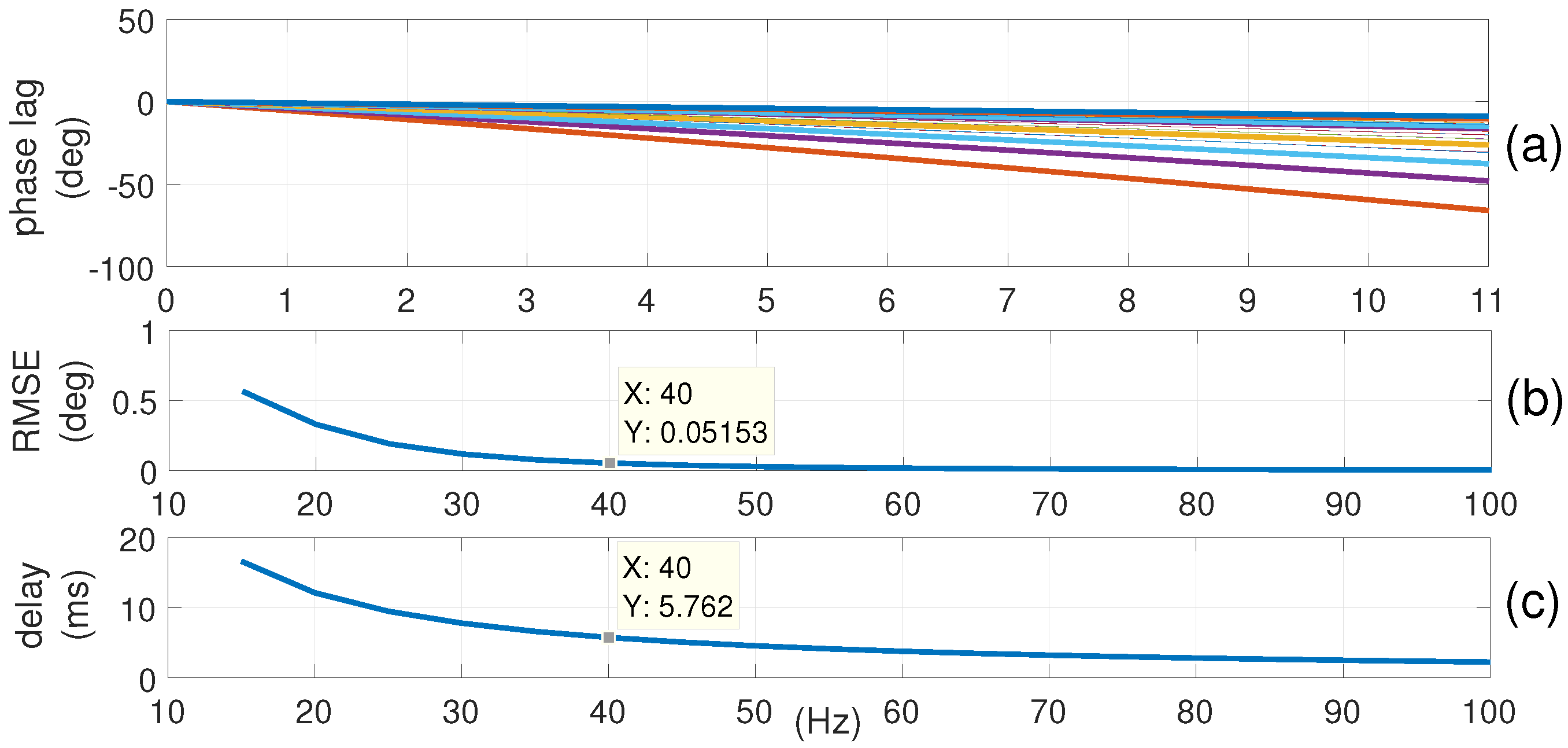
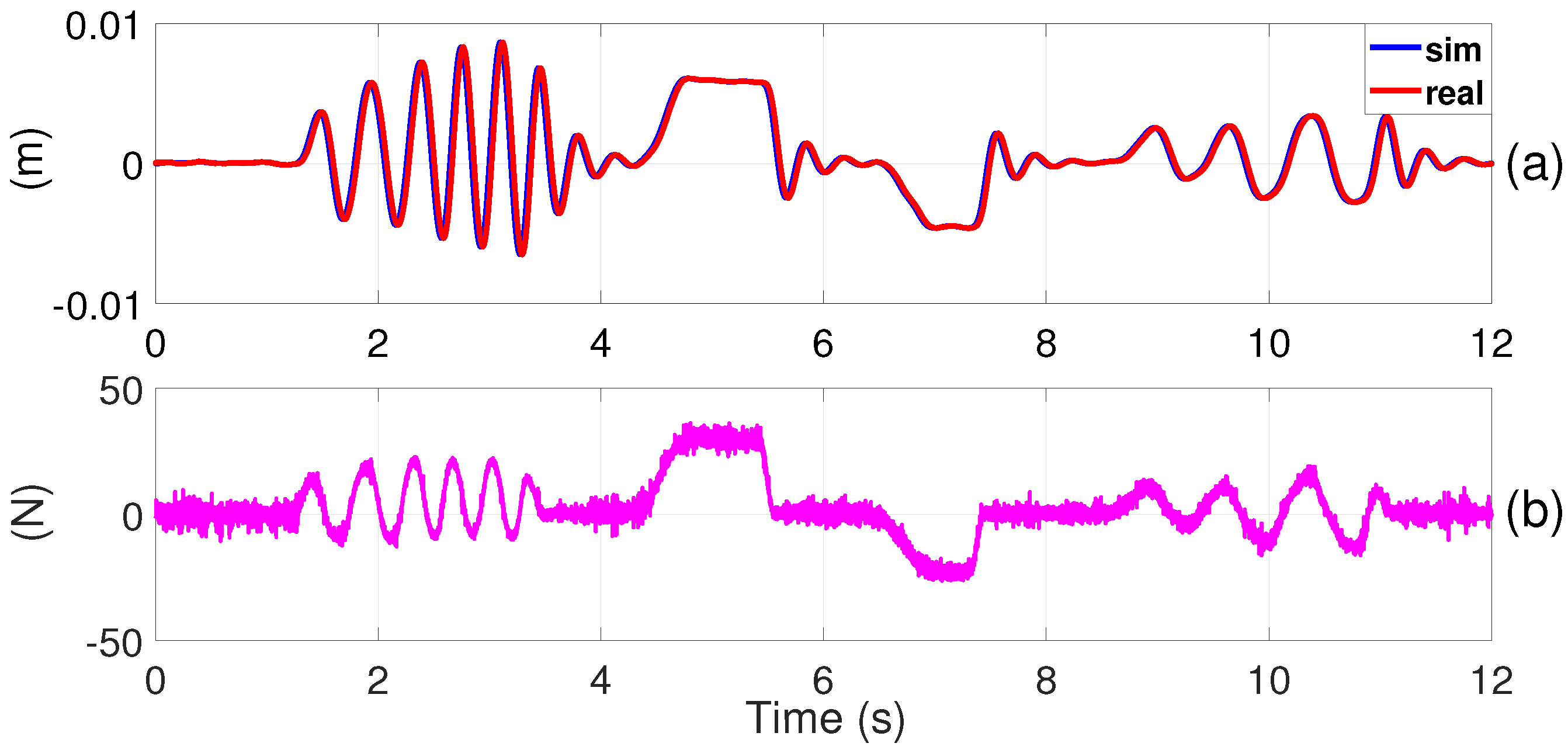
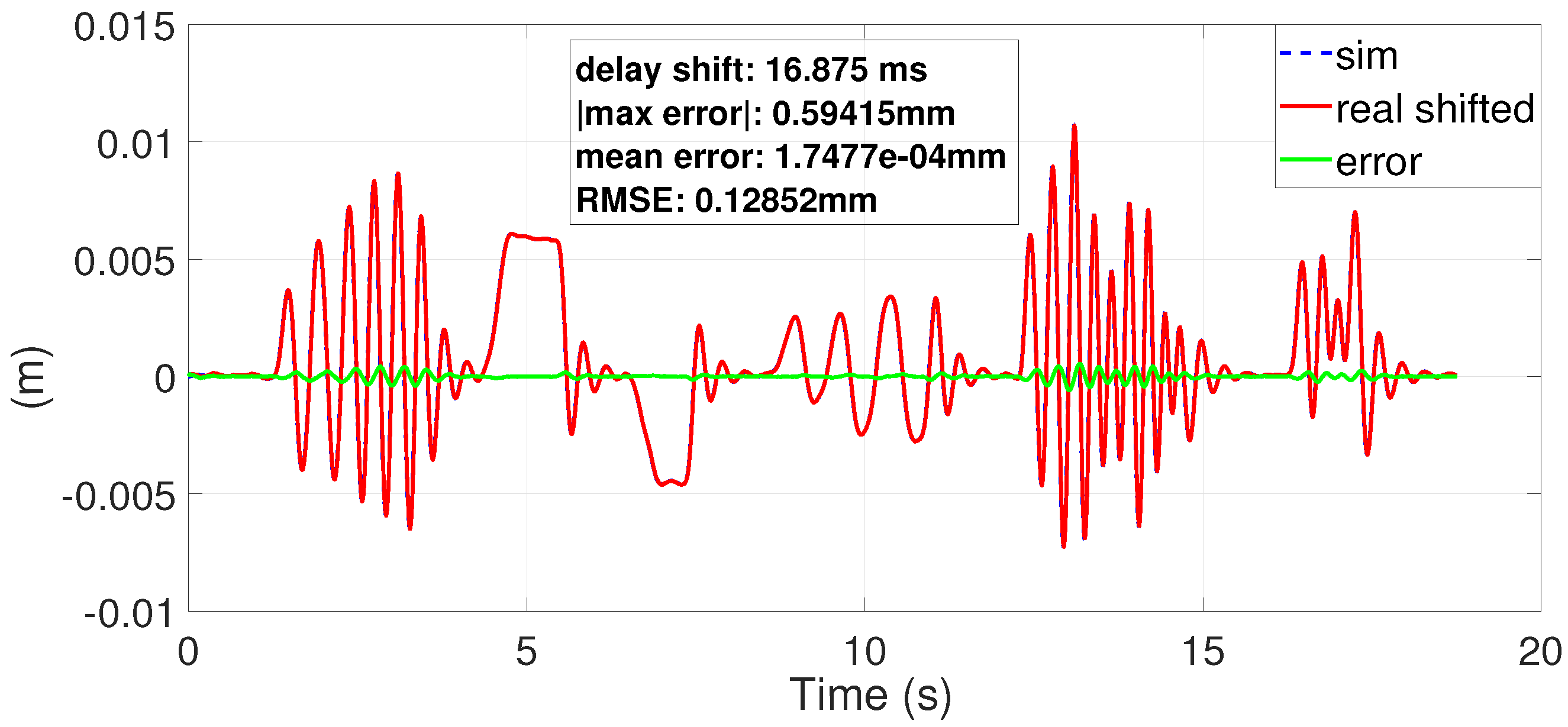
5.2. Results and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fathy, H.K.; Filipi, Z.S.; Hagena, J.; Stein, J.L. Review of hardware-in-the-loop simulation and its prospects in the automotive area. In Proceedings of the SPIE, San Diego, CA, USA, 13–17 August 2006; Volume 1001. [Google Scholar]
- Carignan, C.; Scott, N.; Roderick, S. Hardware-in-the-loop simulation of satellite capture on a ground-based robotic testbed. In Proceedings of the 12th International Symposium on Artificial Intelligence, Robotics and Automation in Space (iSAIRAS), Montreal, QC, Canada, 17–19 June 2014. [Google Scholar]
- DeMore, L.A.; Mackin, P.; Swamp, M.; Rusterholtz, R. Improvements in flight table dynamic transparency for hardware-in-the-loop facilities. In Proceedings of the SPIE, Orlando, FL, USA, 12 July 2000; Volume 4027, pp. 101–112. [Google Scholar]
- Nunez, P.; Jones, R.; Shoop, S. High-Fidelity Ground Platform and Terrain Mechanics Modeling for Military Applications Involving Vehicle Dynamics and Mobility Analysis; Technical Report; Army Tank Automotive Research Development and Engineering Center: Warren, MI, USA, 2004. [Google Scholar]
- Isermann, R.; Schaffnit, J.; Sinsel, S. Hardware-in-the-loop simulation for the design and testing of engine-control systems. Control Eng. Pract. 1999, 7, 643–653. [Google Scholar] [CrossRef]
- Brünger-Koch, M. Motion parameter tuning and evaluation for the DLR automotive simulator. In Proceedings of the Driving Simulator Conference–North America 2005 (DSC NA CD-ROM), Orlando, FL, USA, 30 November–2 December 2005. [Google Scholar]
- Silvestri, M.; Confalonieri, M.; Andrea, F. Piezoelectric actuators for micro positioning stages in automated machines: Experimental characterization of open loop implementations. FME Trans. 2017, 45, 331–338. [Google Scholar] [CrossRef]
- Bayati, I.; Belloli, M.; Bernini, L.; Fiore, E.; Giberti, H.; Zasso, A. On the Functional Design of the DTU10 MW Wind Turbine Scale Model of LIFES50+ Project. J. Phys. Conf. Ser. 2016, 753, 052018. [Google Scholar] [CrossRef]
- Bayati, I.; Belloli, M.; Facchinetti, A.; Giappino, S. Wind tunnel tests on floating offshore wind turbines: A proposal for hardware-in-the-loop approach to validate numerical codes. Wind Eng. 2013, 37, 557–568. [Google Scholar] [CrossRef]
- Anglani, N.; Bossi, M.; Quartarone, G. Energy conversion systems: The case study of compressed air, an introduction to a new simulation toolbox. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012; pp. 32–38. [Google Scholar]
- Bayati, I.; Belloli, M.; Bernini, L.; Giberti, H.; Zasso, A. Scale model technology for floating offshore wind turbines. IET Renew. Power Gener. 2017, 11, 1120–1126. [Google Scholar] [CrossRef]
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Hansen, M.H.; Blasques, J.P.A.A.; Gaunaa, M.; Natarajan, A. The DTU 10-MW Reference Wind Turbine. Available online: http://orbit.dtu.dk/files/55645274/The_DTU_10MW_Reference_Turbine_Christian_Bak.pdf (accessed on 31 January 2018).
- Giberti, H.; Ferrari, D. A novel hardware-in-the-loop device for floating offshore wind turbines and sailing boats. Mech. Mach. Theory 2015, 85, 82–105. [Google Scholar] [CrossRef]
- Bayati, I.; Belloli, M.; Ferrari, D.; Fossati, F.; Giberti, H. Design of a 6-DoF robotic platform for wind tunnel tests of floating wind turbines. Energy Procedia 2014, 53, 313–323. [Google Scholar] [CrossRef]
- Fiore, E.; Giberti, H. Optimization and Comparison between two 6-DoF Parallel Kinematic Machines for HIL Simulations in Wind Tunnel; EDP Sciences: Les Ulis, France, 2016; Volume 45. [Google Scholar]
- Ferrari, D.; Giberti, H. A genetic algorithm approach to the kinematic synthesis of a 6-DoF parallel manipulator. In Proceedings of the 2014 IEEE Conference on Control Applications (CCA), Juan Les Antibes, France, 8–10 October 2014; pp. 222–227. [Google Scholar]
- Fiore, E.; Giberti, H.; Ferrari, D. Dynamics modeling and accuracy evaluation of a 6-DoF hexaslide robot. In Nonlinear Dynamics; Springer: Berlin/Heidelberg, Germany, 2016; Volume 1, pp. 473–479. [Google Scholar]
- Heinrichs, B.; Sepehri, N.; Thornton-Trump, A. Position-based impedance control of an industrial hydraulic manipulator. IEEE Control Syst. 1997, 17, 46–52. [Google Scholar] [CrossRef]
- Lawrence, D.A. Stability and transparency in bilateral teleoperation. IEEE Trans. Robot. Autom. 1993, 9, 624–637. [Google Scholar] [CrossRef]
- Shen, G.; Tang, Y.; Zhao, J.; Lu, H.; Li, X.; Li, G. Jacobian free monotonic descent algorithm for forward kinematics of spatial parallel manipulator. Adv. Mech. Eng. 2016, 8. [Google Scholar] [CrossRef]
- D’Antona, G.; Davoudi, M.; Ferrero, R.; Giberti, H. A model predictive protection system for actuators placed in hostile environments. In Proceedings of the 2010 IEEE Instrumentation Measurement Technology Conference, Austin, TX, USA, 3–6 May 2010; pp. 1602–1606. [Google Scholar]




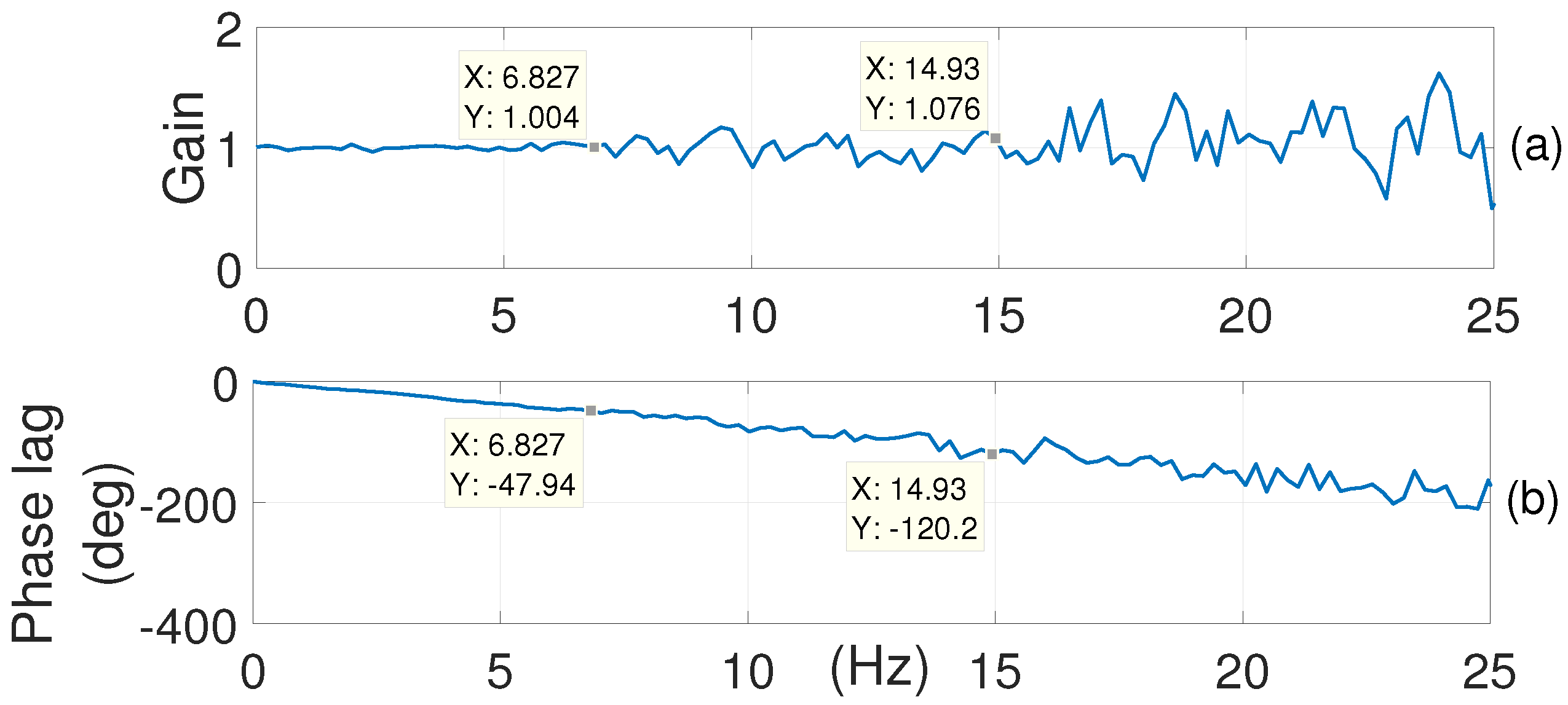
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
La Mura, F.; Todeschini, G.; Giberti, H. High Performance Motion-Planner Architecture for Hardware-In-the-Loop System Based on Position-Based-Admittance-Control. Robotics 2018, 7, 8. https://doi.org/10.3390/robotics7010008
La Mura F, Todeschini G, Giberti H. High Performance Motion-Planner Architecture for Hardware-In-the-Loop System Based on Position-Based-Admittance-Control. Robotics. 2018; 7(1):8. https://doi.org/10.3390/robotics7010008
Chicago/Turabian StyleLa Mura, Francesco, Giovanni Todeschini, and Hermes Giberti. 2018. "High Performance Motion-Planner Architecture for Hardware-In-the-Loop System Based on Position-Based-Admittance-Control" Robotics 7, no. 1: 8. https://doi.org/10.3390/robotics7010008
APA StyleLa Mura, F., Todeschini, G., & Giberti, H. (2018). High Performance Motion-Planner Architecture for Hardware-In-the-Loop System Based on Position-Based-Admittance-Control. Robotics, 7(1), 8. https://doi.org/10.3390/robotics7010008





