On the Development of Learning Control for Robotic Manipulators

Abstract

Learning control for robotic manipulators has been developed over the past decade and to the best of the authors’ knowledge, it is still in its infant development stage; the authors believe that it will become one of the most promising directions in the control area in robotic manipulators. Learning control in robotic manipulators is mainly used to address the issue that the friction at the joints of robotic mechanisms and other uncertainties may exist in the dynamic models, which are very complex and may even be impossible to model mathematically. In this paper, the authors review and discuss the learning control in robotic manipulators and some issues in learning control for robotic manipulators are also illustrated. This review is able to give a general guideline for future research in learning control for robotic manipulators.

1. Introduction

Robotic manipulators have been used in many industries. However, most of the control systems that are used nowadays include traditional PID (proportional–integral–derivative) control, computed torque control, and other nonlinear model-based controls. In academia, learning control in robotic manipulators has been intensively studied in the past years. 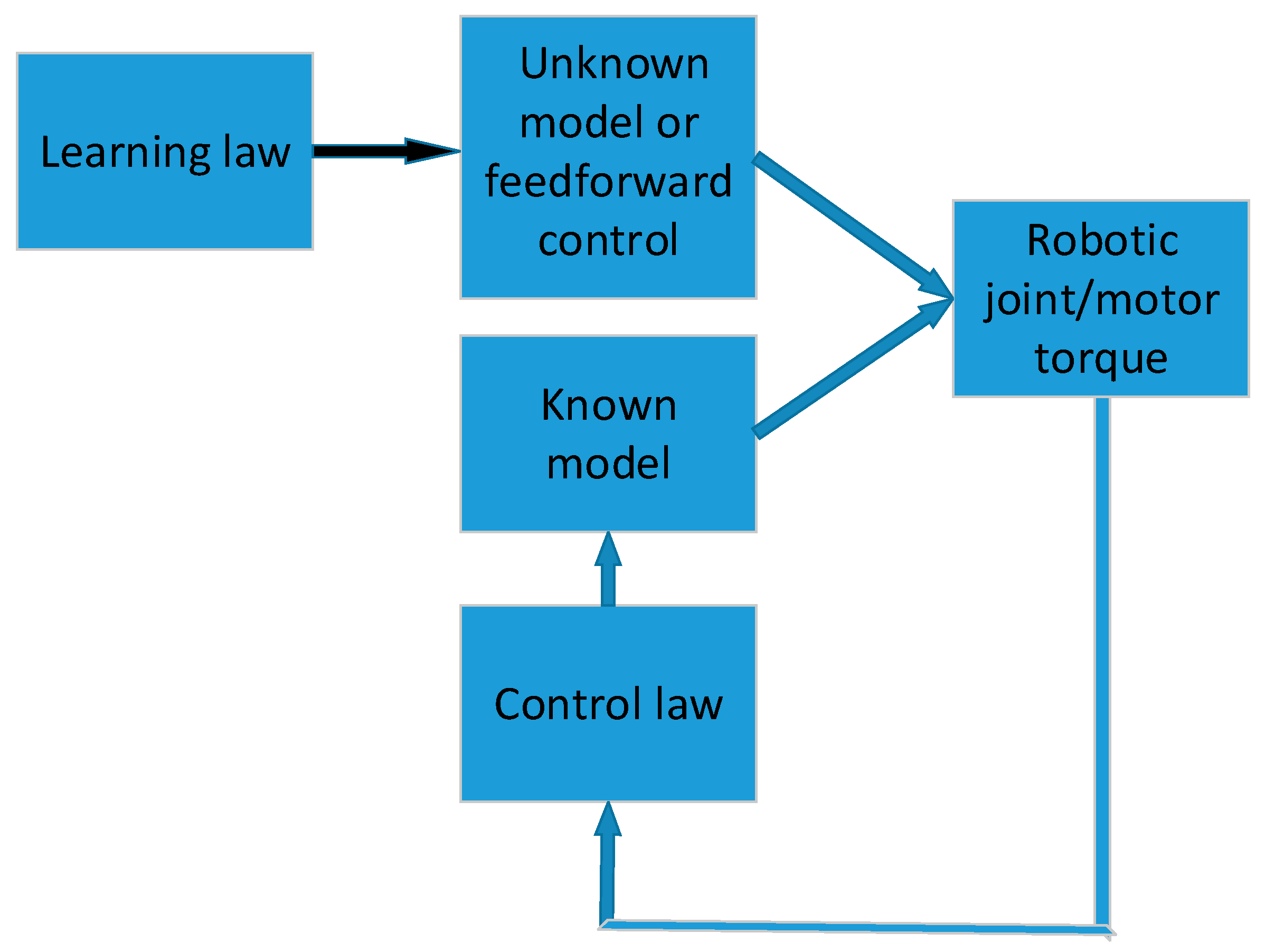However, learning control is rarely used in industries nowadays due to its control structure complexity, expenses, and other reasons [1,2].

Learning control in robotic manipulators is mainly used to address the issue that the friction at the joints of robotic mechanisms, to correct, for example, high frequency vibrations caused by elasticity in the joints, as well as other uncertainties, may exist in the dynamic models, which are very complex and may even be impossible to model mathematically. Friction at joints is nonlinearly dependent on joint velocity and sometimes also dependent on joint position [3]. The main idea behind the leaning control approach is to develop a control approach so that it is not necessary to model those uncertainties mathematically, but to learn them. Furthermore, it is noticed that in most of the industrial robots, they have the characteristics of the reference trajectory being repeated over a specified operation. The motivation for the development of learning control in robotics is that in some cases where pre-planning is not impossible, adaptive control or other other types are not good enough to handle this kind of situation, rather, learning control can then be used in this scenario. Also, one of the characteristics in learning controls is that it is permitted to fail as compared to, for example, adaptive control, where it is not permitted to fail. Learning control will become prevalent in robotics compared to other methods since in the future, robots will need to learn by themselves rather than through pre-planning by users every time. Since learning control in robotic manipulators has been investigated in the last decade, the authors believe that it is necessary to give a review on the learning control for robotic manipulators in order to provide a general summary and guideline for the upcoming research in the learning control of robotic manipulators.

One of the commonly used approaches and ideologies in designing a learning control system for robotic manipulators is to make full use of available information on the robotic dynamic models and then learn what cannot be modelled (e.g., friction). Put in another way, one usually partitions the dynamic of the robotic manipulators into two parts: modelled and un-modelled. We use the knowledge and information from the modelled system to learn and update the can-not-be-modelled system.

Learning control for robotic manipulators is quickly developed after the development of the adaptive control of robotic manipulators. The most significant advantage of using the learning control in robotic manipulators is that it is not necessary to model the complex models and uncertainties (e.g., friction at joints) mathematically. However, there is a limitation in using the learning control in robotic manipulators, which is that the robotic manipulators need to have repeated motions so that those complex models can be learned by the learning control system; luckily, the fact of the matter is that most robotic manipulators nowadays used in the manufacturing plants have a repetitive motion characteristic. Although the authors believe that the most important contributions have been cited and included, it is possible that the authors here are unware of some works.

The organization of this paper is as follows: Section 2 briefly presents general learning control and its background; learning control in robotic manipulators is presented and reviewed in Section 3; finally, the conclusion is given in Section 4.

2. Learning Control

In traditional control systems, there is a feedback loop which is used to compare the output with the desired value and create a difference, which is then given to the controller. Normally, we can adjust control parameters in order to achieve a better control performance. Keep in mind that the above mentioned loop is only produced on the condition that we know every parameter in the robotic manipulator system dynamics. However, when parameters in the robotic system change with respect to time and are not predictable, the traditional control system as mentioned above is not quite as effective anymore. Under this situation, we can employ adaptive control. To extend it further, if there are unmodelled dynamics (e.g., friction at joints are hard to model or sometimes even impossible to model), one can then resort to the learning control scheme. The learning control scheme will then be useful to compensate for the remaining unmodelled effects after one performs the parameter identification. For example, after the adaptive control scheme conducts the identification of unknown parameters in a model, the learning algorithm will be used to further minimize the trajectory-following errors. A basic learning control concept is shown in Figure 1.

3. Learning Control in Robotic Manipulators

The early development of learning control for robotic manipulators can be traced back to [4], where the author proposed the method of trial and correction of the reference function to address the problem of the tremendous computation effort of the computed torques. Through repeating a trial and correction process, the reference function that is able to realize the ideal pattern of the trajectory can therefore be determined. Details can be referred to [4]. The stability of the proposed control algorithm was also verified. Following this, several typical learning control schemes were proposed. For example, following a similar approach to that in [4], a learning strategy for robotic mechanisms is developed in [5] for the case of repeated trials of a trajectory. Through adequate learning, random trajectories that are within the velocity and torque limits of the robotic arm can therefore be carried out with bounded errors. In [6,7], a learning control principle is put forward for linear and nonlinear dynamical systems based on a PID-type iterative process and is applied to a trajectory tracking control for robotic mechanisms. The convergence of the proposed control system was also proved. Following the above studies, the learning control for robotic manipulators has been developed intensively.

3.1. Iterative Learning Control and Its Variants

In [8,9], a notion named the “betterment process” is put forward in order to offer a learning ability of automatic-construction of a better control input to MIMO robotic systems. The betterment process has an iteration law that automatically produces an actuator input better than the previous one through employing previous data under the condition that the desired output response is provided. This process has an iterative learning system so that the current input (to joint actuators) is formed of the previous input and an error term that exhibits the difference between the previous motion path and the specified ideal motion path. In [10], direct iterative learning control is developed in a way that a uniform convergence of error is guaranteed. The conditions on the convergence of the control system are determined. The proposed control system was applied to the trajectory control of a robotic manipulator and obtained decent outcomes. The proposed control system in [10] set a foundation of servo theory.

In [11], the author developed a kind of PI-based learning control algorithm that does not utilize the velocity signals derivative geared to the robotic mechanisms motion control. The author illustrates the robustness of the learning control w.r.t. initialization errors. It is found that by incorporating a forgetting factor to the iterative learning principle, a robustness performance where trajectories move toward a desired neighborhood and stay in it can be guaranteed. In [12], the authors illustrate a robust adaptive learning control technique for robotic mechanisms tracking problems in task space. The learning control can reach zero tracking error regardless of external disturbances and modelling uncertainties. The control algorithm is also convergent. Since the algorithm is designed in the task space, inverse kinematics are not required.

In [13], the authors presented an adaptive iterative learning control for a two-DOF planar robotic mechanism with uncertainties and revolute joints in Cartesian space for path tracing. The proposed controller has a PD system and a learning feedforward term, and it can be used to anticipate the ideal actuator torque. Based on the Lyapunov approach, the developed control system is proved as stable. In [14], the issue in the process of developing an iterative learning control system for the trajectory tracking of robotic mechanisms that have external disturbances with conducting repetitive works and with no knowledge of the velocity measurement is demonstrated. To handle this issue, the authors put forward a velocity observer that contains an iterative form which is used to recreate the velocity signal. By assuming that the disturbances are repetitive and employing a Lyapunov-like positive definite sequence, the designed control is shown to be asymptotically stable and the observation error is also shown to be asymptotically stable.

In [15], a precision tracking control approach for robotic mechanisms is illustrated. To address the problem of the nonlinear and coupled dynamics in robotic mechanisms and the transmission error, the authors employed a nonparametric statistical learning technique that can achieve the data-driven iterative compensation of torque and motor reference. Transmission error is managed through separate learning modules. The developed technique is able to use both a timed trajectory measurement and untimed contour inspection. In [16], by incorporating model-based with iterative learning control, a technique is developed for the purpose of having high-quality direct-drive robotic systems motion control in repetitive works. The model-based segment is mainly used for compensating for the nonlinear terms and coupled dynamics of the robotic system. The authors employ an approach, which is on the basis of a batch-adaptive control, to approximate the model parameters. The remaining dynamics of the robotic system after the compensation from the model-based segment are determined through employing the frequency response function measurements. The developed learning control is applied to a spatial serial direct-drive robot mechanism, and the experimental results indicate that a substantial improvement of the motion control performance in every single joint has been achieved.

In [17], an optimization-based iterative learning control technique is briefly presented for arbitrary nonlinear robotic mechanisms with n-DOF in a closed-loop configuration. The designed learning technique has two steps which are executed at each iteration. Model correction is first solved through dealing with the torque and joint angular position measurements. The resulting correction is subsequently employed in the model inversion step for the purpose of computing a reference update via solving an optimization problem. The designed technique is tested in a 6-DOF robot mechanism. In [18], the author illustrates an adaptive iterative learning control scheme that is formed on the basis of an estimation process by employing a Kalman filter and the optimization of a quadratic criterion. It is observed that through including the measurement disturbance, the resulting iterative learning control filters are iteration-varying. After experimental studies on an ABB industrial robotic manipulator, it is observed that an improvement in the trajectory tracing on the motor-side of the robotic manipulator is achieved and also the designed adaptive and model-based iterative learning control scheme provides better results than that of a conventional iterative learning control scheme with constant gains.

In [19], based on the studies in [20,21], the authors illustrate how the adaptive learning control system developed in [22] can be further used in robot mechanisms that are driven by non-salient-pole permanent magnet synchronous motors. Unstructured uncertain dynamics of the robotic system that has rotational joints and uncertainties in stator resistances of the synchronous motors are considered. In [23], the authors designed an adaptive iterative learning control technique for uncertain robot mechanisms. It differs from other learning techniques in that the uncertain parameters are approximated in the time domain, while repetitive disturbances are determined and compensated for thereafter in the iteration domain. The developed adaptive iterative learning control technique is a combination of traditional adaptive control and iterative learning control. The designed learning control scheme is tested by a planar 2-DOF (degrees of freedom) serial mechanism.

In [24], an output-based adaptive iterative learning control technique for a 2-DOF robot mechanism is developed. Through employing the output-based adaptive iterative learning control, the tracking performance can therefore be improved iteratively with smaller values of observer-controller gains based on the condition that the system traces the same task iteratively. The output-based adaptive iterative learning control technique joins the PD control system with an adaptive segment which can update uncertain velocity signal parameters iteratively via the linear observer output. Based on the Lyapunov online switching system, tracking errors convergence is guaranteed. In [25], an iterative learning control that is formed on the basis of the passivity for 2-DOF robotic mechanisms with antagonistic bi-articular muscles is developed. The iterative learning control scheme is designed by resorting to the Arimoto-type iterative learning control presented in [26]. The closed-loop system’s convergence is analyzed on the basis of passivity. The designed controller is robust in that the parameters of the accurate models are not needed for the input torque. Details can be referred to in [25].

In [27], the authors simply applied the iterative learning control to an underwater robotic system to address the issue that the parameter approximation of hydrodynamic coefficients of the underwater robotic system is unsuited to establish the feedforward control inputs due to the difficulty in modeling and approximating the hydrodynamic terms. The advantages of the iterative learning control are illustrated by the experimental results. In [28], the authors employed the model-free feedback-assisted iterative learning control scheme for the purpose of the path tracking of a 6-DOF mechanism. The iterative learning control scheme is used to produce the feedforward control signal and the direct feedback control is used to produce the feedback control signal. The developed control scheme can conduct accurate trajectory tracking via iterative learning. Due to the scheme being model-free, the singularity issue is avoided, which usually arises in the traditional Jacobean-based visual servo system. Through experimental studies, it is observed that the designed control system is robust to image noise.

In [29], a new indirect iterative learning control scheme is developed for a robot mechanism that conducts repeat operations and has non-Gaussian disturbances. A performance index regarding the entropy of the tracking error and the related optimization technique are employed for estimating the control system local parameters. The authors compared a developed learning control scheme to a traditional iterative learning controller, and it was proved that the developed learning control scheme is stable. The developed learning control technique is tested in the robot trajectory tracking. In [30], the authors employed the model-based iterative learning control technique for the purpose of improving the tracking accuracy for an industrial serial robotic manipulator that has elasticity. In order to minimize the predicted tracking error in the next iteration, the iterative learning control scheme refreshes the robotic manipulator’s reference trajectory iteratively. The tracking error is anticipated through a model of the closed-loop dynamics of the robotic manipulator, and the model contains the variation of servo resonance frequency and the first resonance frequency along the trajectory. Through experiments, it is found that the tracking error of the robotic manipulator is reduced.

In [31], an iterative learning control technique that is composed of feedforward learning controls and hybrid feedback PD-PID (P refers to proportional, I refers to integral, D refers to derivative) controls is proposed for a two-link flexible robotic mechanism. The PID is used to restrain linkage vibrations via the end-points acceleration feedback and the PD (P refers to proportional, D refers to derivative) is used to guarantee the hubs to trace the desired trajectory via the hub angle and joint velocity feedback. By incorporating the iterative learning control scheme to the feedforward path to anticipate the desired torque, the input tracking and vibration suppression of the robotic system can be successfully accomplished. The proposed learning control technique is demonstrated as robust through the payload variation effect studies. In [32], the authors developed backstepping adaptive iterative learning control through integrating the merits of adaptive iterative learning control, the backstepping design approach, and the fuzzy neural network function estimation attribute for a robotic mechanism that conducts repetitive works. The purpose of employing the fuzzy neural network as a fuzzy neural learning segment is to compensate for the unknown certainty equivalent control system, and the purpose of employing the iterative learning control is to compensate for the uncertainties. Based on the Lyapunov technique, it is proved that the tracking error converges to zero.

In [33], a hybrid iterative learning control technique geared to restrain vibrations and the track input for a flexible robotic mechanism is designed based on a collocated PD with iterative learning control. The collocated PD control that uses the hub-angle and hub-velocity feedback is used to manipulate the mechanism motions. By incorporating the iterative learning control with acceleration feedback and the genetic algorithm, which is used to optimize the learning parameters, the vibration of the mechanism is suppressed. The designed learning control technique is used in a 1-DOF flexible robotic mechanism with and without loads. In [34], the author developed adaptive iterative learning control on the basis of the mathematical model and identified a model for a 1-DOF flexible robotic mechanism to address the issue that the flexible mechanism vibrates with a low frequency. Since the flexible mechanism is nonlinear and time-varying, in order to satisfy the control system design requests, an adaptive nonlinear autoregressive with exogenous input model is determined through employing the input/output experimental data. It is found that adaptive iterative learning control developed by employing the identified adaptive nonlinear autoregressive with exogenous input model outperforms the adaptive iterative learning control developed by employing the mathematical model.

In [35], the authors designed a new type of feedback controller for robot mechanisms with random communication delays through incorporating the optimal P-type iterative learning controller concept and a minimum tracking error entropy control scheme. In the process of controller development, it is treated as an optimization problem that has a performance index and constraint. More precisely, the performance index indicates the concept of the closed-loop tracking error minimum entropy control. In [36], a wavelet series-based learning control technique is designed to address the tracking controls of a robotic mechanism. Wavelet series estimation is employed for estimating the ideal and real path of the robotic mechanism and converting these values into a number of wavelet coefficients. A learning control scheme is developed in the wavelet domain which pushes the real output technique’s wavelet coefficients to the corresponding wavelet coefficients of the ideal path, and in this way, the tracking of the robotic mechanism can be accomplished. Through experiments, it is observed that the learning control scheme designed in the wavelet domain can effectively cope with the uncertainties in a robotic mechanism.

In [37], an adaptive iterative learning control method is designed to cope with the uncertain parameters and other disturbances for a rigid robotic mechanism for the purpose of tracing trajectories. The designed control system is based on incorporating the PD control and an iterative segment. The control system is proved to be stable by resorting to the Lyapunov method. Later in [38], the proposed adaptive iterative learning control is tested on a five degrees-of-freedom serial mechanism. However, an issue is found that the learning process needs to be stopped after some iterations in order to not make the noise effect increase. In [39], the issue of developing iterative learning control with a forgetting factor for path tracing for robotic mechanisms that have external disturbances and conducting repetitive works without needing to have the precise knowledge of the robotic systems structure model or robotic system parameters is investigated. The merit of the designed control scheme is that it not only applies to robotic mechanisms that have model uncertainties, but also applies to entirely unknown robotic systems. The stability of the designed learning control is proved by resorting to the Lyapunov method. Details can be referred to in [39].

In [40], iterative learning control for a planar 2-DOF serial mechanism with revolute joints is put forward on the basis of the finite dimensional input subspace. The designed control system can achieve tracking purpose, even without knowing the error signals’ time derivatives or mechanism’s dynamics exact information. However, it is noticed that the learning process has to be stopped in the experimental study after certain trails due to gradual gathering of the motor noises and the starting resetting errors. In [41], a nonlinear iterative learning control for MIMO robotic mechanisms is developed. An algorithm that can guarantee the errors of trajectory-tracing to be confined by a specified error norm is designed. The control system is tested by a PUMA 6-DOF serial mechanism with revolute joints. In [42], a hybrid iterative learning control system for a 4-DOF robot mechanism that is used in CNC machine tools is developed. The control system consists of a nonlinear saturated PID with desired gravity compensation and PD-based iterative learning control. The purpose of the PID system is to maintain local stability of the robot mechanism, and the purpose of the PD-based iterative learning control system is to provide robustness to parameter variations and dynamic uncertainties. The system is proved stable by employing the Lyapunov approach. In [43], an iterative learning control system is designed on the basis of PD control and a switching type control system for the purpose of the repetitive control of robotic mechanisms with only revolute joints. The proposed control system is developed with no a priori information of the dynamic parameters. However, the control structure is quite complex and also the control parameters contain a sign function. In [44], the authors investigate nonlinear iterative learning control with sampled-data feedback for robotic mechanisms. This control system can be used in a robotic mechanism that has more than 6-DOF due to the existence of a sampled-data feedback system. The stability of the control system is also studied.

It is noted that in classical iterative learning control, some postulates are required, although recently, some iterative learning control algorithms are reported so that these postulates can be relaxed. Details can be referred to in [45].

3.2. Repetitive Learning Control and Its Variants

In [46], a repetitive control method is developed, and in it, the manipulated variables are able to follow the cyclic reference instructions through pinpointing the generator for cyclic signals in the closed-loop. The error convergence condition for linear systems is determined based on the small gain theorem and a synthesized algorithm based on the Kalman Filter is illustrated. The designed control system is proved as stable by employing the passivity theorem, and finally, the proposed control system is tested on the trajectory control for a simple three-linkage robotic manipulator. In [47], a modified version of the learning control system in [8,9] is designed through modifying the input based on the position error to address the problem that the measured signals of the velocity and acceleration variables can be easily subject to a noise effect. It is observed that through employing the modified learning control strategy here, the robot motion is able to approach the desired one and experiments also demonstrated that the robotic mechanism is able to polish the curved surface of an object. The modified learning approach can be applied to the force control of robotic mechanisms.

In [48], a discrete learning control algorithm which uses the error of state variables of the system that comprises the position and velocity error for manipulating robotic manipulators is designed and illustrated. The condition for position convergence is then determined, and the proposed control system is tested by a PUMA-560 robot and the end results demonstrate the effectiveness of the designed control system. In [49], an algorithm utilizes path following errors for improving feedforward commands to a robot. The strategy in robot learning is formed on the basis of explicit modeling of the robotic system and employs an inverse of the robotic system model as one learning operator that handles the trajectory errors. Through experimental studies, it is observed that an accurate robotic system model betters the path learning performance, and the learning algorithm does not make a dent on reducing the need for an accurate model in robotic system control.

In [50], an adaptive learning principle that is used for the purpose of identification and controlling the robot manipulators is proposed. The function estimate is produced through combining the product of a predefined kernel with an influence function approximate. The learning principle updates the function approximate through updating the influence function approximate. The goal is to determine and compensate for a nonlinear disturbance function. The designed control system is proved as stable under certain assumptions. In [51], task level learning (i.e., a technique to learn via practice) is briefly discussed. The author programs a robotic system to juggle a ball through hitting it up with a paddle. The robotic system employs a binary vision to trace the ball. The task level learning has a model of performance errors at the task level in the process of practice, and employs this model to process the task-level orders. Its study sets a foundation for memory-based approaches for task level learning.

In [52], the authors demonstrate the exponential convergence for a group of learning control algorithms of robotic mechanisms. The learning technique identifies the robotic inverse dynamic function through making the robotic system perform tasks over and over again. Based on the functional persistence of excitation and also functional uniform complete observability, it is observed that under the situation where a training task is chosen for the robotic system that is persistently exciting, the learning controls are globally and exponentially stable. In [53,54], iterative learning impedance control is presented for robotic mechanisms. Through employing the developed learning control technique, the learning performance can therefore be specified by a reference model and reference trajectory. The learning control system can learn and then make the closed-loop dynamics to follow the target impedance response when one repeats the actions. The developed learning impedance control is tested by a SCARA (Selective Compliance Assembly Robot Arm) robot. In [55], adaptive learning control is developed through introducing the learning control to an adaptive controller for the purpose of coping with periodic uncertainties with known periods for a 2-DOF planar robot mechanism with time-varying uncertainties. Based on the Lyapunov technique, the proposed control system illustrated that the tracking errors are able to be converged successfully.

In [56], the authors illustrate a frequency-domain technique to develop learning control systems in order to reach the desired repetitive action in a robotic system. The technique employs two independent filters for the purpose of generating a quick improvement in a specified bandwidth and at the same time refraining potential destabilizing dynamic effects that could interfere with learning convergence. The learning strategy is added in parallel to a feedback control system for the purpose of improving the performance. The designed learning control system is tested for tracing repetitive trajectories of robotic mechanisms, and through experiments, it is observed that the developed learning technique is able to avoid the unstable occurrence. In [57], the authors propose a robust learning control method for robotic mechanisms through synthesizing learning and robust controls. The nonlinear learning control technique is applied to the structured system uncertainties and the variable structure control technique (i.e., robust control technique) is applied to the unstructured uncertainties in order to guarantee that the system is able to maintain a globally and asymptotically stable nature. Through combining the learning and robust controls, the designed controller is able to achieve a certain performance to which it is hard to achieve if one only employs learning control or only employs variable structure control.

In [58], a learning control scheme for robotic mechanisms is proposed by assuming that the desired path trajectory is cyclic. The dynamic model of the robotic mechanism is treated as uncertain and having additive disturbances. In the process of developing the learning control system, the robust control segment presented in [59] is jointed with a nonlinear learning control segment for the purpose of compensating for the uncertain dynamics of the robotic system. The direct Lyapunov method is employed during the learning control system development to ensure that the tracking error approach is zero. In [60], the authors utilize the (m, m)-Padé approximants in implementing repetitive learning control for asymptotically tracing the joint position of robotic mechanisms that have uncertain dynamics and cyclic position reference signals. The control design technique produces linear learning control systems which generalizes the PID to the case of periodic references to the point where the long-term instability problems in traditional repetitive learning control schemes because of disturbance noises can be avoided. In [20], the authors investigate the tracking control issue for induction motor servo drives with uncertainties. Through assuming that the reference profile of the rotor angle is periodic of a known period, a robust adaptive learning control scheme that can be adaptive w.r.t. the uncertain rotor resistance is developed to learn the periodic disturbance signal through determining the truncated approximation Fourier coefficients.

In [22], the issue of developing an output error feedback-based adaptive learning control scheme for robotic mechanisms that have revolute joints and also possess uncertain dynamics is studied. The reference signals that are tracked are treated as smooth and periodic with a known period. Based on the Fourier series expansion, an output error feedback learning control scheme is proposed that can learn the input reference signals through determining the Fourier coefficients. In [61], an adaptive switching learning PD control technique is put forward for path tracing for robotic mechanisms in a repeat working mode. Since the designed learning control scheme is formed on the basis of combining the feedback PD control scheme and the feedforward learning control scheme with the input torque profile from the preceding iteration, the new developed learning control scheme is able to offer an improved tracing performance when the iteration increases. The developed learning control is proved as stable by employing the Lyapunov approach.

In [62], a repetitive learning control for robotic mechanisms is illustrated. The trajectory tracking performance is illustrated through employing the designed control scheme and the designed repetitive learning control scheme is applied to a PUMA robotic system. The authors made a comparison between the traditional PD control, computed torque control, and decentralized control. It is found that the designed repetitive learning control generates a better tracking performance and produces a minimum tracking error compared to the other controls. In [63], the authors gave a demonstration on how a learning-based estimate is employed for the purpose of having asymptotic tracking under the situation where nonlinear disturbances exist. Since the learning-based controller approximate produced from the Lyapunov stability analysis, the authors further illustrated how Lyapunov-based design approaches are used to reject elements of the unknown and un-periodic dynamics. More precisely, a hybrid adaptive learning control system is developed for the dynamics of robotic mechanisms. Through the experiment on a two-link robotic mechanism, it is observed that the performance of the link tracking is improved at every single period of the desired trajectory, and this is all because of the learning estimate mitigating action.

In [64], the authors developed a quasi-sliding mode-based repetitive learning control technique to handle robotic mechanisms that are MIMO (multiple-input multiple-output) nonlinear and continuous-time with matching perturbations. The developed learning control scheme can reject cyclic exogenous disturbances and can also track cyclic reference trajectories. Through conducting the comparison with the traditional variable structure control for a planar 2-DOF mechanism with revolute joints, it is observed that the quasi-sliding mode-based repetitive learning control technique is able to avoid the chattering, whereas the traditional variable structure control approach cannot under the situation of handling the cyclic exogenous disturbances. In [65], the authors illustrated the issues in terms the stability conditions of the hybrid control system developed in [66], which is designed through combining repetitive learning control and model-based adaptive control. For the purpose of relaxing the stability conditions, an improved hybrid control scheme on the basis of the control system is developed in [66]. The designed learning control system is proved as stable based on the Lyapunov approach, and the proposed learning control system is applied to a two-link robotic mechanism.

In [67], an experiment is conducted to justify an adaptive dominant type hybrid adaptive and learning control system for obtaining accurate path tracing of a cyclic desired trajectory for robotic mechanisms. The learning control system is designed by combining the model-based adaptive, repetitive learning, and PD controls. The designed control system employs only one vector to approximate unknown parameters of the dynamics, and it does not require too much computational power and is easy to use in real robotic mechanism applications. Through applying the control system to a four-link robotic mechanism, it is observed that the position tracking error can reach zero. In [68], adaptive learning PD control is proposed for serial mechanisms with only revolute joints for the purpose of tracing a periodic output reference, but the limitation is that it is assumed that the robotic parameter bounds are already known. The control structure contains a PD segment and a learning segment, which is used to approximate the joint reference input. Similarly, in [69], adaptive nonlinear PD learning control is developed for a 2-DOF serial robotic mechanism with revolute joints for tracing trajectories. The control system has a PD system and a learning system. In [70], a type of adaptive repetitive learning control scheme is developed for the trajectory tracking of uncertain robot mechanisms. By introducing a Lyapunov-like function, the developed technique only needs the system to start from the last stop position, and the initial repositioning is not needed anymore. Through employing the saturated learning principle, zero-error tracking can be accomplished via compensating for the repetitive disturbance torque. Also, it is observed that the iterative trajectories will eventually approach the desired ones.

In [71], the author presents and discusses the differences among repetitive controls, betterment learning methods, and adaptive learning methods on the basis of integral transforms. The stability performances of adaptive learning algorithms on the basis of integral transforms are illustrated.

It is observed that most of the above studies employed a similar pattern. The difference is mainly in the approach of illustrating stability, convergence, and performances.

3.3. Reinforcement Learning Control

In [72], the difference between centralized and decentralized reinforcement learning for the learning control of a planar 2-DOF robotic mechanism with revolute joints is demonstrated. It is observed that the decentralized reinforcement learning did not focus on the scalability issue. Also, reinforcement learning updates presume perfect knowledge of the task model, which is usually unavailable in actual situations. In [73], a framework for learning about the operational space control of robotic mechanisms is briefly presented, and the concept of reinforcement learning via reward-weighted regression is also put forward. The developed learning control scheme is mainly used for immediate reward problems, for example, locating an optimal result for determining redundancy in the operational space control of robotic systems.

In [74], the tracking performance of reinforcement learning control for a two link robotic mechanism that has parameter variations and external disturbances is studied. Robustness performances in the aspect of error and control efforts are compared by employing different parameterized function estimators. It is observed that using the continuous action in the fuzzy inference system is able to result in a better performance when compared to the discrete action in neural network machine function estimators.

A comparison study of iterative learning control with reinforcement learning control and iterative learning control with repetitive learning control can be referred to in [75,76], respectively. The authors here will not reiterate it anymore.

A brief comparative table with the advantages and drawbacks of the above methods is illustrated in

Table 1. A brief comparative table.

	Advantages	Drawbacks	Application in Robotics and Its Characteristics
Reinforcement learning control	More flexible in terms of repetition	Usually requires strict exploration mechanisms	Learning by trial & error. Involve function approximation, and it has curse of dimensionality.
Repetitive Learning Control	Simple implementation and little performance dependency on system parameters	Usually needs repetitive process	Relying on the internal model.
Iterative Learning Control	Be able to compensate for exogenous signals	Usually needs repetitive reference trajectory	Starting from the same initial conditions at every iteration.

.

4. Conclusions

In this manuscript, the learning control in robotic manipulators is reviewed and discussed and typical issues in learning control that are used in robotic manipulators are also illustrated. Learning control for robotic manipulators has been developed over the past decade and to the best of the authors’ knowledge, it is still in its early development stage. The authors believe that it is necessary to conduct a complete review on the learning control for robotic manipulators, which can provide general information and a guideline for the upcoming research in this field. It is observed that most of the studies used a similar pattern. The difference is mainly in the approach of illustrating stability, convergence, and performances. The authors also believe that combining learning control with the artificial intelligence for robotic mechanisms will become one of the future research topics in the robotic control area.

Since the most reliable and intelligent control system ever encountered is the human internal control system, learning control design through simulating human internal control and nervous systems for robot manipulators is worth exploring so as to make the control system more intelligent. The authors believe the combination of the mechatronic design approach and learning control design approach for robotic manipulators also has great potential for future enhancements. One of the applications of the learning control approach could be addressing safety issues such as those found in robotic-based manufacturing industries.

As an extra note, it is known that unmanned aerial vehicles (UAV) have been developed in the past years and used in many areas, such as sporting shooting, search and rescue, farming, border patrol, reconnaissance, and in the transportation of large objects, but there are still many issues that are waiting to be solved. Factors such as speed, reliability, safety, navigation and mapping capability, and fully autonomous capability are most of our concerns, and these are all directly or indirectly related with the synthesized control algorithm used in the flying robots. To the best of the authors’ knowledge, learning control has not really been maturely used in the flying robots, and the authors believe that it will be used in the flying robots in the near future. Most of the flying robots/drones use the adaptive control algorithm, particularly the model reference adaptive control algorithm (MRAC) to control the speed of the propellers in order to control the pitch, roll, and yaw motions, i.e., to control the voltage of the motors of the propellers. The challenge that one faces in the control system is how to construct a synthesized control algorithm that allows the flying drones to achieve the desired output and motions while handling the unexpected disturbances from the environment, for example, gusts of wind or payload variation situations if the drones are used to transport different objects. The applications and issues of learning control in flying robots have yet to be explored and will hopefully be discovered in the coming years.