Synthetic Aperture Computation as the Head is Turned in Binaural Direction Finding
Abstract
:1. Introduction
2. Angle (Lamda) between the Auditory Axis and the Direction to an Acoustic Source
| is the angle between the auditory axis and the direction to the acoustic source; | |
| is the distance between the ears (the length of the line LR); and | |
| is the difference in the acoustic ray path lengths from the source to the left and right ears as a proportion of the length (). |
| is the acoustic transmission velocity in air (e.g., 330 ms−1); and | |
| is the difference in arrival times of sound received at the ears. |
| is the uncertainty in the estimate of arrival time difference ; and | |
| is the rate of change of with respect to . |
3. Synthetic Aperture Audition
3.1. Horizontal Auditory Axis
3.2. The effect of an Inclined Auditory Axis
4. Remarks
5. Summary
Acknowledgments
Conflicts of Interest
Appendix A. Trigonometrical Relationships in an Auditory System
| is the angle between the auditory axis (the straight line that passes through both ears) and the direction to an acoustic source; | |
| is the lateral (longitudinal) angle to a source of sound to the right of the direction in which ahead is facing; | |
| is the vertical (latitudinal) angle below the horizontal (with respect to the direction the head is facing) to an acoustic source; and | |
| is the inclination of the auditory axis to the right across the head. |
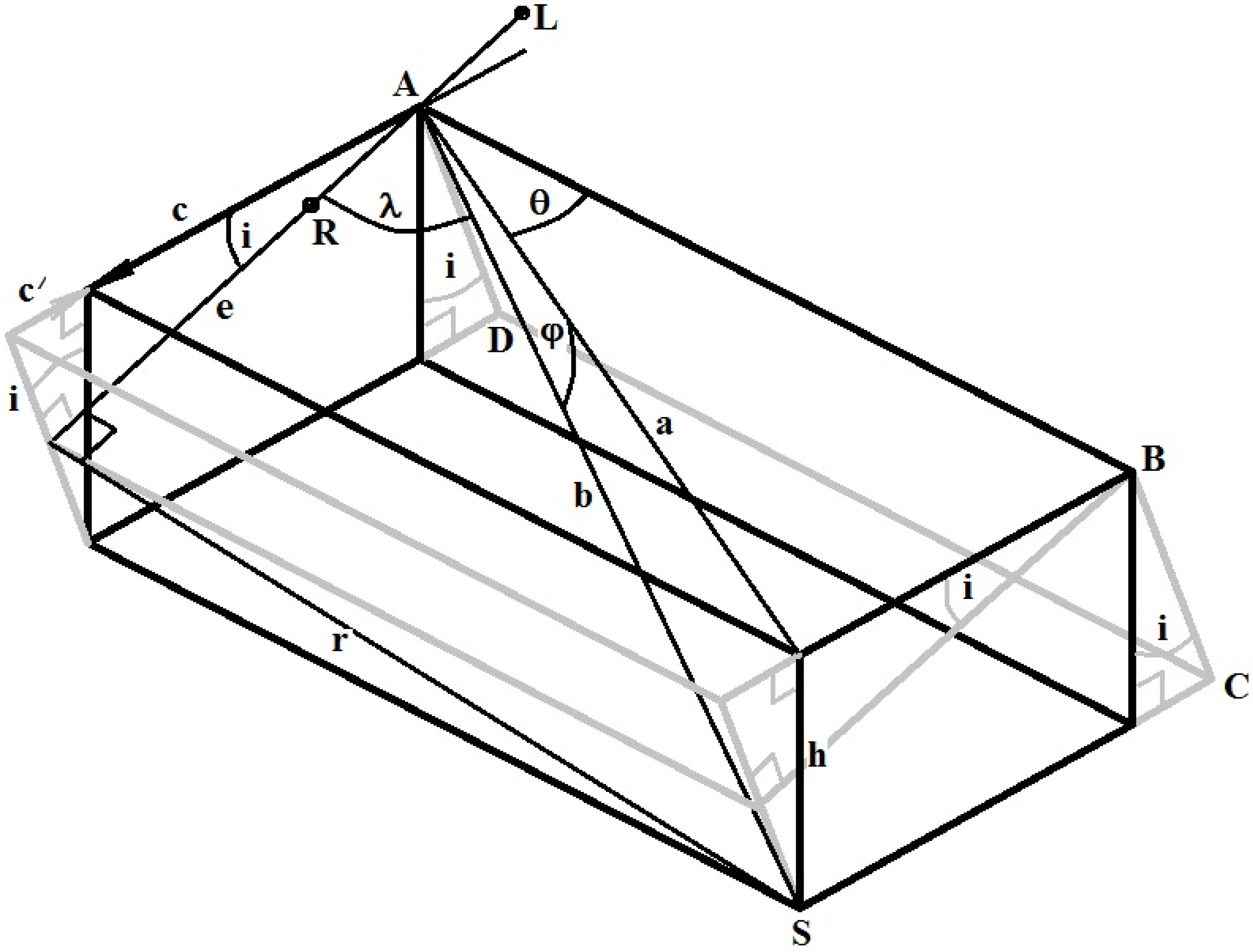
Appendix A.1. The Angle as a Function of Angles:, and :
Appendix A.2. The Angle when = 90° as a Function of Angles: and i
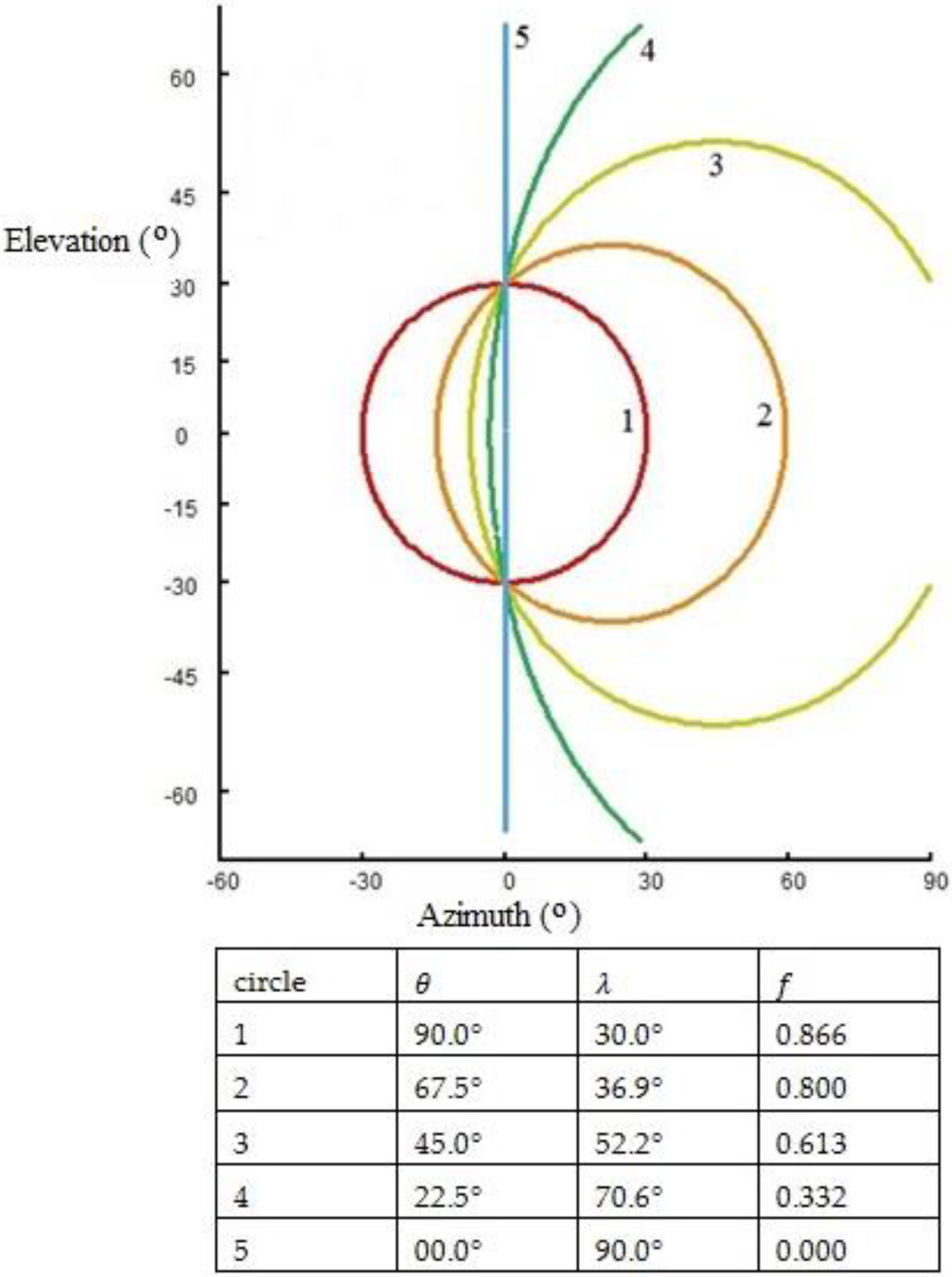
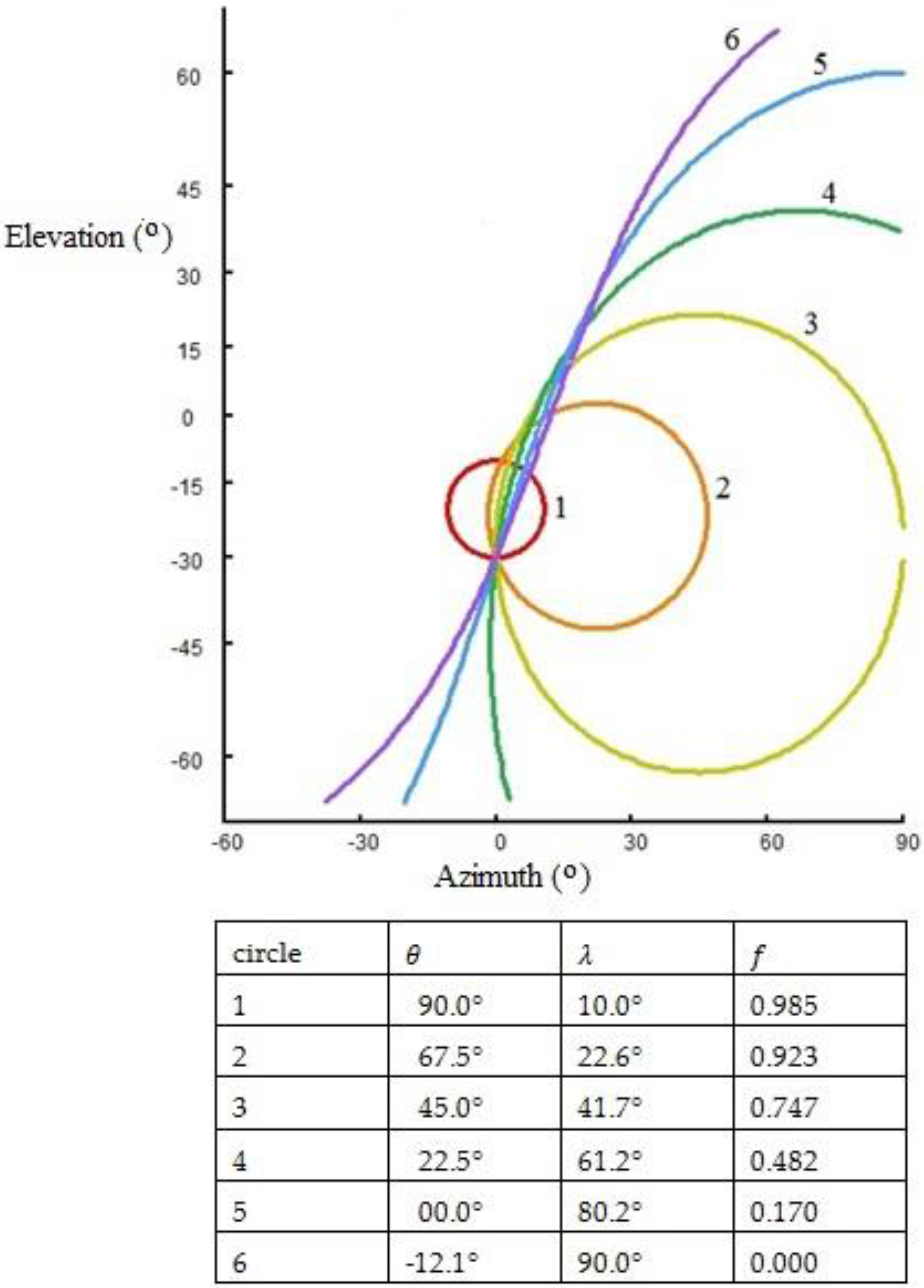
Appendix B. Lamda Circle Plots in a Virtual Field of Audition for Display in Mercator Projection
- ;
- ; and
- is the azimuthal orientation of head with respect to some datum, e.g., grid/magnetic north, and north latitude and east longitude are positive.
- (to convert colatitude to latitude); and
- varies by say one degree between and radians.
- ; and
- is the slope of the auditory axis across the head (downslope to the right is positive).
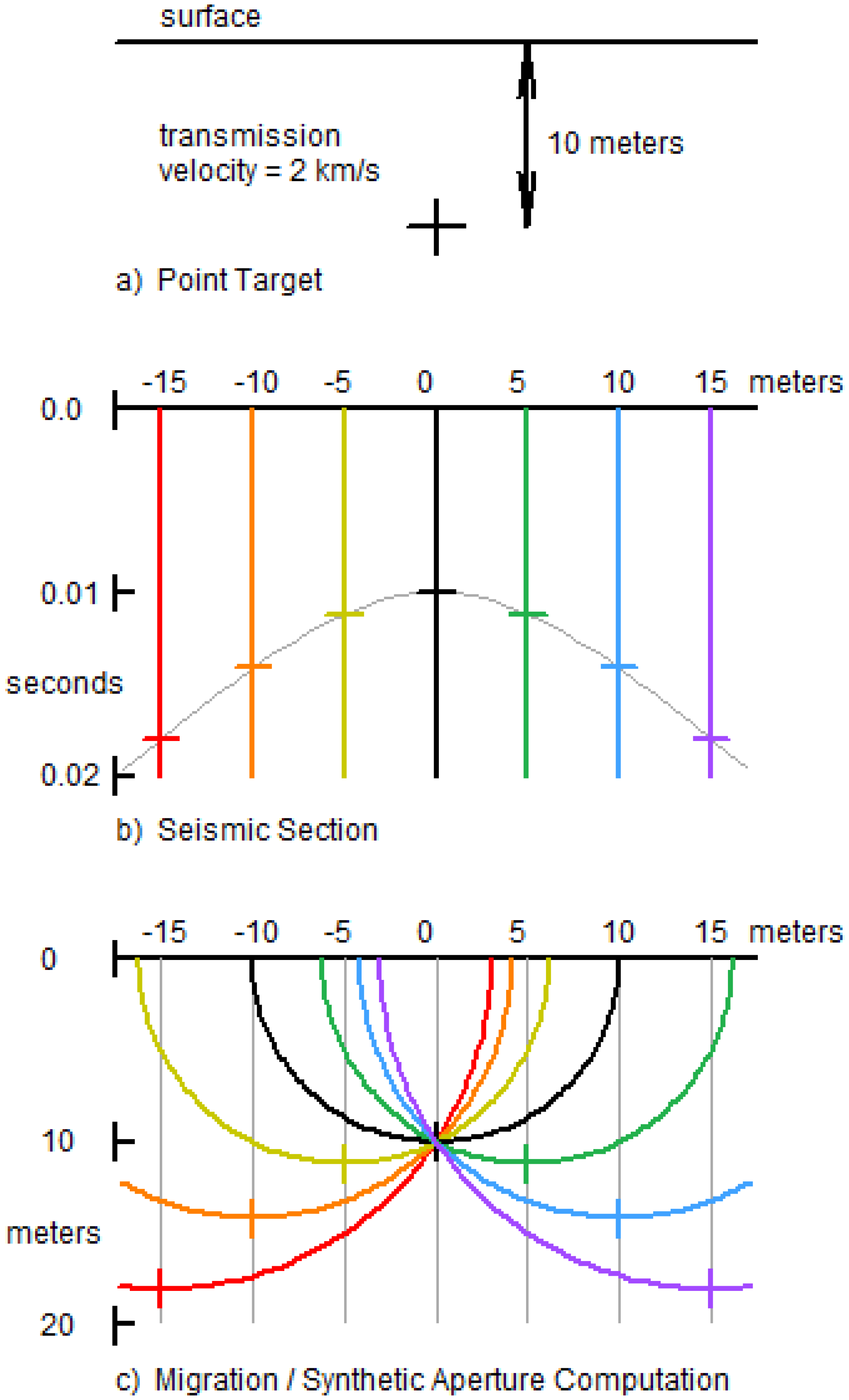
Appendix C. Synthetic Aperture Computation in Migration
References
- Wallach, H. The role of head movement and vestibular and visual cues in sound localisation. J. Exp. Psychol. 1940, 27, 339–368. [Google Scholar] [CrossRef]
- Pace, N.G.; Gao, H. Swathe seabed classification. IEEE J. Ocean. Eng. 1988, 13, 83–90. [Google Scholar] [CrossRef]
- Tamsett, D. Characterisation and classification of the sea-floor from power-spectra of side-scan sonar traces. Mar. Geophys. Res. 1993, 15, 43–64. [Google Scholar] [CrossRef]
- Mills, A.W. On the minimum audible angle. J. Acoust. Soc. Am. 1958, 30, 237–246. [Google Scholar] [CrossRef]
- Brughera, A.; Danai, L.; Hartmann, W.M. Human interaural time difference thresholds for sine tones: The high-frequency limit. J. Acoust. Soc. Am. 2013, 133, 2839. [Google Scholar] [CrossRef] [PubMed]
- Wightman, F.L.; Kistler, D.J. The dominant role of low frequency interaural time differences in sound localization. J. Acoust. Soc. Am. 1992, 91, 1648–1661. [Google Scholar] [CrossRef] [PubMed]
- Sayers, B.M.A.; Cherry, E.C. Mechanism of binaural fusion in the hearing of speech. J. Acoust. Soc. Am. 1957, 36, 923–926. [Google Scholar] [CrossRef]
- Jeffress, L.A.A. A place theory of sound localization. J. Comp. Physiol. Psychol. 1948, 41, 35–39. [Google Scholar] [CrossRef] [PubMed]
- Colburn, H.S. Theory of binaural interaction based on auditory-nerve data. 1. General strategy and preliminary results in interaural discrimination. J. Acoust. Soc. Am. 1973, 54, 1458–1470. [Google Scholar] [CrossRef] [PubMed]
- Kock, W.E. Binaural localization and masking. J. Acoust. Soc. Am. 1950, 22, 801–804. [Google Scholar] [CrossRef]
- Durlach, N.I. Equalization and cancellation theory of binaural masking-level differences. J. Acoust. Soc. Am. 1963, 35, 1206–1218. [Google Scholar] [CrossRef]
- Licklider, J.C.R. Three auditory theories. In Psychology: A Study of a Science; Koch, S., Ed.; McGraw-Hill: New York, NY, USA, 1959; pp. 41–144. [Google Scholar]
- Perrett, S.; Noble, W. The effect of head rotations on vertical plane sound localization. J. Acoust. Soc. Am. 1997, 102, 2325–2332. [Google Scholar] [CrossRef] [PubMed]
- Wightman, F.L.; Kistler, D.J. Resolution of front-back ambiguity in spatial hearing by listener and source movement. J. Acoust. Soc. Am. 1999, 105, 2841–2853. [Google Scholar] [CrossRef] [PubMed]
- Iwaya, Y.; Suzuki, Y.; Kimura, D. Effects of head movement on front-back error in sound localization. Acoust. Sci. Technol. 2003, 24, 322–324. [Google Scholar] [CrossRef]
- Kato, M.; Uematsu, H.; Kashino, M.; Hirahara, T. The effect of head motion on the accuracy of sound localization. Acoust. Sci. Technol. 2003, 24, 315–317. [Google Scholar] [CrossRef]
- McAnally, K.I.; Russell, L.M. Sound localization with head movement: Implications for 3-D audio displays. Front. Neurosci. 2014, 8, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Roffler, S.K.; Butler, R.A. Factors that influence the localization of sound in the vertical plane. J. Acoust. Soc. Am. 1968, 43, 1255–1259. [Google Scholar] [CrossRef] [PubMed]
- Batteau, D. The role of the pinna in human localization. Proc. R. Soc. Lond. B Biol. Sci. 1967, 168, 158–180. [Google Scholar] [CrossRef] [PubMed]
- Middlebrooks, J.C.; Makous, J.C.; Green, D.M. Directional sensitivity of sound-pressure levels in the human ear canal. J. Acoust. Soc. Am. 1989, 86, 89–108. [Google Scholar] [CrossRef] [PubMed]
- Rodemann, T.; Ince, G.; Joublin, F.; Goerick, C. Using binaural and spectral cues for azimuth and elevation localization. In Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 2185–2190.
- Norberg, R.A. Independent evolution of outer ear asymmetry among five owl lineages; morphology, function and selection. In Ecology and Conservation of Owlss; Newton, I., Kavanagh, J., Olsen, J., Taylor, I., Eds.; CSIRO Publishing: Victoria, Australia, 2002; pp. 229–342. [Google Scholar]
- Norberg, R.A. Occurrence and independent evolution of bilateral ear asymmetry in owls and implications on owl taxonomy. Phil. Trans. Roy. Soc. Lond. Ser. B. 1977, 280, 375–408. [Google Scholar] [CrossRef]
- Norberg, R.A. Skull asymmetry, ear structure and function, and auditory localization in Tengmalmt Owl, Aegolius funereus (Linne). Phil. Trans. Roy. Soc. Lond. Ser. B. 1978, 282, 325–410. [Google Scholar] [CrossRef]
- Lollmann, H.W.; Barfus, H.; Deleforge, A.; Meier, S.; Kellermann, W. Challenges in acoustic signal enhancement for human-robot communication. In Proceedings of the ITG Conference on Speech Communication, Erlangen, Germany, 24–26 September 2014.
- Takanishi, A.; Masukawa, S.; Mori, Y.; Ogawa, T. Development of an anthropomorphic auditory robot that localizes a sound direction. Bull. Cent. Inf. 1995, 20, 24–32. (In Japanese) [Google Scholar]
- Matsusaka, Y.; Tojo, T.; Kuota, S.; Furukawa, K.; Tamiya, D.; Nakano, Y.; Kobayashi, T. Multi-person conversation via multi-modal interface—A robot who communicates with multi-user. In Proceedings of 16th National Conference on Artificial Intelligence (AAA1–99), Orlando, Florida, 18–22 July 1999; pp. 768–775.
- Ma, N.; Brown, G.J.; May, T. Robust localisation of multiple speakers exploiting deep neural networks and head movements. In Proceedings of INTERSPEECH 2015, Dresden, Germany, 6–10 September 2015; pp. 3302–3306.
- Schymura, C.; Winter, F.; Kolossa, D.; Spors, S. Binaural sound source localization and tracking using a dynamic spherical head model. In Proceedings of the INTERSPEECH 2015, Dresden, Germany, 6–10 September 2015; pp. 165–169.
- Winter, F.; Schultz, S.; Spors, S. Localisation properties of data-based binaural synthesis including translator head-movements. In Proceedings of the Forum Acusticum, Krakow, Poland, 7–12 September 2014.
- Bustamante, G.; Portello, A.; Danes, P. A three-stage framework to active source localization from a binaural head. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 5620–5624.
- May, T.; Ma, N.; Brown, G. Robust localisation of multiple speakers exploiting head movements and multi-conditional training of binaural cues. In Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 2679–2683.
- Ma, N.; May, T.; Wierstorf, H.; Brown, G. A machine-hearing system exploiting head movements for binaural sound localisation in reverberant conditions. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 2699–2703.
- Nakadai, K.; Lourens, T.; Okuno, H.G.; Kitano, H. Active audition for humanoids. In Proceedings of the 17th National Conference Artificial Intelligence (AAAI-2000), Austin, TX, USA, 30 July–3 August 2010; pp. 832–839.
- Cech, J.; Mittal, R.; Delefoge, A.; Sanchez-Riera, J.; Alameda-Pineda, X. Active speaker detection and localization with microphone and cameras embedded into a robotic head. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots (Humanoids), Atlanta, GA, USA, 15–17 October 2013; pp. 203–210.
- Deleforge, A.; Drouard, V.; Girin, L.; Horaud, R. Mapping sounds on images using binaural spectrograms. In Proceedings of the European Signal Processing Conference, Lisbon, Portugal, 1–5 September 2014; pp. 2470–2474.
- Nakamura, K.; Nakadai, K.; Asano, F.; Ince, G. Intelligent sound source localization and its application to multimodal human tracking. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 143–148.
- Yost, W.A.; Zhong, X.; Najam, A. Judging sound rotation when listeners and sounds rotate: Sound source localization is a multisystem process. J. Acoust. Soc. Am. 2015, 138, 3293–3310. [Google Scholar] [CrossRef] [PubMed]
- Kim, U.H.; Nakadai, K.; Okuno, H.G. Improved sound source localization in horizontal plane for binaural robot audition. Appl. Intell. 2015, 42, 63–74. [Google Scholar] [CrossRef]
- Rodemann, T.; Heckmann, M.; Joublin, F.; Goerick, C.; Scholling, B. Real-time sound localization with a binaural head-system using a biologically-inspired cue-triple mapping. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 860–865.
- Portello, A.; Danes, P.; Argentieri, S. Acoustic models and Kalman filtering strategies for active binaural sound localization. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 137–142.
- Sun, L.; Zhong, X.; Yost, W. Dynamic binaural sound source localization with interaural time difference cues: Artificial listeners. J. Acoust. Soc. Am. 2015, 137, 2226. [Google Scholar] [CrossRef]
- Zhong, X.; Sun, L.; Yost, W. Active binaural localization of multiple sound sources. Robot. Auton. Syst. 2016, 85, 83–92. [Google Scholar] [CrossRef]
- Stern, R.; Brown, G.J.; Wang, D.L. Binaural sound localization. In Computational Auditory Scene Analysis; Wang, D.L., Brown, G.L., Eds.; John Wiley and Sons: Hoboken, NJ, USA, 2005; pp. 1–34. [Google Scholar]
- Nakadai, K.; Okuno, H.G.; Kitano, H. Robot recognizes three simultaneous speech by active audition. In Proceedings of the ICRA/IEEE International Conference on Robotics and Automation, Taipel, Taiwan, 14–19 September 2003; pp. 398–405.
- Lurton, X. Seafloor-mapping sonar systems and Sub-bottom investigations. In An Introduction to Underwater Acoustics: Principles and Applications, 2nd ed.; Springer: Berlin, Germany, 2010; pp. 75–114. [Google Scholar]
- Claerbout, J.F. Imaging the Earth’s Interior; Blackwell Science Ltd.: Oxford, UK, 1985. [Google Scholar]
- Yilmaz, O. Seismic Data Processing; Society of Exploration Geophysics: Tulsa, OK, USA, 1987. [Google Scholar]
- Scales, J.A. Theory of Seismic Imaging; Colarado School of Mines, Samizdat Press: Golden, CO, USA, 1994. [Google Scholar]
- Biondi, B.L. 3D Seismic Imaging; Society of Exploration Geophysics: Tulsa, OK, USA, 2006. [Google Scholar]
- Cutrona, L.J. Comparison of sonar system performance achievable using synthetic aperture techniques with the performance achievable with conventional means. J. Acoust. Soc. Am. 1975, 58, 336–348. [Google Scholar] [CrossRef]
- Cutrona, L.J. Additional characteristics of synthetic-aperture sonar systems and a further comparison with nonsynthetic-aperture sonar systems. J. Acoust. Soc. Am. 1977, 61, 1213–1217. [Google Scholar] [CrossRef]
- Oliver, C.; Quegan, S. Understanding Synthetic Aperture Radar Images; Artech House: Boston, MA, USA, 1998. [Google Scholar]
- Bellettini, A.; Pinto, M.A. Theoretical accuracy of synthetic aperture sonar micro navigation using a displaced phase-center antenna. IEEE J. Ocean. Eng. 2002, 27, 780–789. [Google Scholar] [CrossRef]
- Hagen, P.E.; Hansen, R.E. Synthetic aperture sonar on AUV—Making the right trade-offs. J. Ocean Technol. 2011, 6, 17–22. [Google Scholar]
- Griffin, D.R. Listening in the Dark; Yale University Press: New York, NY, USA, 1958. [Google Scholar]
- Chesterman, W.D.; Clynick, P.R.; Stride, A.H. An acoustic aid to sea-bed survey. Acustica 1958, 8, 285–290. [Google Scholar]
- Au, W.W.L. The Sonar of Dolphins; Springer: New York, NY, USA, 1993. [Google Scholar]
- Au, W.W.L.; Simmons, J.A. Echolocation in dolphins and bats. Phys. Today 2007, 60, 40–45. [Google Scholar] [CrossRef]
- Dawkins, R. Chapter 2—Good design. In The Blind Watchmaker; Penguin Books: London, UK, 1986. [Google Scholar]
- Tamsett, D.; McIlvenny, J.; Watts, A. Colour sonar: Multi-frequency sidescan sonar images of the seabed in the Inner Sound of the Pentland Firth, Scotland. J. Mar. Sci. Eng. 2016, 4, 26. [Google Scholar] [CrossRef]
- Dutch, S. Rotation on a Sphere. 1999. Available online: https://www.uwgb.edu/dutchs/MATHALGO/sphere0.htm (accessed on 14 February 2017).


© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamsett, D. Synthetic Aperture Computation as the Head is Turned in Binaural Direction Finding. Robotics 2017, 6, 3. https://doi.org/10.3390/robotics6010003
Tamsett D. Synthetic Aperture Computation as the Head is Turned in Binaural Direction Finding. Robotics. 2017; 6(1):3. https://doi.org/10.3390/robotics6010003
Chicago/Turabian StyleTamsett, Duncan. 2017. "Synthetic Aperture Computation as the Head is Turned in Binaural Direction Finding" Robotics 6, no. 1: 3. https://doi.org/10.3390/robotics6010003
APA StyleTamsett, D. (2017). Synthetic Aperture Computation as the Head is Turned in Binaural Direction Finding. Robotics, 6(1), 3. https://doi.org/10.3390/robotics6010003





