Abstract
This paper discusses a strategy by which a robotic hand can use the physical properties of a fabric to pinch the fabric. Pinching may be accomplished by using a wiping motion, during which the movement and deformation of a deformable object occur simultaneously. The wiping motion differs from the displacement of a deformable object. During the wiping motion, there is contact, but no relative movement, between the manipulator and the object, whereas, during displacement, there is both contact and relative movement between the object and the floor. This paper first describes wiping motion and distinguishes wiping slide from wiping deformation by displacement of the internal points of an object. Wiping motion is also shown to be an extended scheme of pushing and sliding of rigid objects. Our strategy for pinching a fabric is accomplished with a combination of wiping deformation and residual deformation of the fabric under unloaded conditions. Using this strategy, a single-armed robotic hand can pinch both surfaces of the fabric without handover motion.
1. Introduction
Over the past several decades, many studies have analyzed deformable object manipulation [1]. One type utilized industrially is fabric manipulation; however, processes to handle messy deformable objects have not yet been automated in certain industries, including the apparel, linen supply, and medical services industries. Although dexterous fabric handling is easy for humans, it is much more difficult for robotics. In addition, descriptions of deformable object manipulation have not been as clear and systematic as descriptions of rigid body manipulation.
Specific implements have utilized methods of deformable object manipulation in fabric handling. These include an end-effector with pins to grasp single piles from a stack of fabrics [2] and a robotic pneumatic hand to grasp fabrics, with the acquisition points on the fabrics detected by visual perception [3]. A robotic system for unfolding of fabrics on a floor via visual and touch sensing was shown to pinch the corner edge of a fabric to unfold it [4]. In addition, a robotic hand with three fingers and a palm has been used to pick up one fabric from a stack of fabrics [5]. Fabric grasping may be accomplished using a rotational hand, which could roll up the fabric with two rotational wheels on the fingertips [6]. In addition, a visual system can be used to detect grasping points for messy fabrics [7]. A gripper based on two passively turning fingers and a simple on-off pneumatic drive mechanism was used experimentally to grasp pieces of furs from a mixed bundle [8]. Indirect simultaneous positioning of an extensible fabric has been demonstrated and simulated using Proportional-Integral-Derivative (PID) control for desired locations [9]. Control of a few manipulated points was shown to regulate several positioned points to their desired locations [10,11], and a dual-armed robotic system has been proposed for dressing activity [12]. Furthermore, the folding motion of clothes using a robotic laundry system [13] and a visual perception for grasping/folding messy fabrics [14] has been assessed. Recently, a specialized gripper for garments [15] and a tactile sensor for identification of fabrics [16] have been developed. These manuscripts represented an importance of force sensing for fabric handling.
Deformable object manipulation can be subdivided into various basic tasks. For example, a system based on hierarchical control was constructed to handle a flat fabric on a table [17]. That hand was able to grasp, unfold, and flatten the fabric using vision and force/torque sensors, but these tasks have not yet been described using mathematical formulations. We have also analyzed the stability of deformable object manipulation [18]. Displacement of deformable objects can include both the movement and deformation of the object, allowing both to be controlled simultaneously. Although we analyzed the stability of one-dimensional systems from the viewpoint of simultaneous control, we did not focus on concrete descriptions and examples.
This paper describes a as a task in which motion and deformation of a deformable object occur simultaneously. In previous research [19,20], we proposed the concept of wiping motion, and showed preliminary experimental results. In this paper, we investigate the concept via mechanical analyses and several experiments including these results. First, we define wiping motion as a type of fabric handling. Second, we describe a wiping motion, and distinguish from by displacement of the internal points of a moving object. We also show that wiping motion is an extension of pushing and sliding motions described for rigid object manipulation. Next, we use physical models to analyze the mechanism of wiping deformation, using a uniform belt-like fabric as a specimen, and we clarify the effectiveness of rigid bending and the static coefficient of friction in wiping deformation. Finally, we introduce a strategy of fabric pinching as an example of a wiping motion. Our strategy for pinching a fabric consists of a combination of wiping deformation and residual deformation of the fabric under unloaded conditions. Using this strategy, a single-armed robotic hand can pinch both surfaces of the fabric without handover motion.
2. Wiping Motion
2.1. Classification of Fabric Handling
This section classifies fabric handling to clearly define wiping motion. Based on handling processes by humans, the setting process of a fabric can be divided into four basic motions (Figure 1):
- (a)
- Wiping motion: a human hand in contact with a fabric displaces and deforms a fabric on a floor (Figure 1a). No slippage between the hand and the fabric occurs during displacement.
- (b)
- Pinching motion: a human hand pinches the fabric to move it (Figure 1b).
- (c)
- Unfolding motion: while pinching a fabric, humans often slide their fingertips along the fabric surface (Figure 1c). Humans also handle fabric hems dextrously during unfolding.
- (d)
- Placing motion: humans place the unfolded fabric on a floor (Figure 1d).

Figure 1.
Human operations in moving a fabric. (a) Wiping motion; (b) Pinching motion; (c) Unfolding motion; (d) Placing motion.
Humans dextrously handle fabrics using combinations of these basic motions. This paper describes wiping motion, in which the movement and deformation of a deformable object occur simultaneously. Wiping motion using a deformable object is defined as a task in which there is contact, but no relative movement, between the manipulator and the object. In contrast, during displacement of the object, there is both contact and relative movement between the object and the floor.
2.2. Description of Wiping Motion
This section describes the wiping motion of a deformable object. Multiple fingers handle a deformable object, assuming that each area of contact between a fingertip and the object is a point contact. If is the position vector of the point on the i-th fingertip (), is the position vector of the point on the surface of a deformable object at the initial state, before displacement, then is the position vector of the point fixed on the floor during a displacement. The numbers of vectors and coincide with the respective numbers of fingertips. These position vectors have the same origin.
Figure 2 shows a sample task of two manipulators moving in one dimension, where the i-th and j-th fingers () handle a deformable object on a floor. To better view the fingers, they are shown separately. In this example, we assume that the deformable object is thin and without shear; thus, the initial conditions of these points satisfy the equations (Figure 2a):
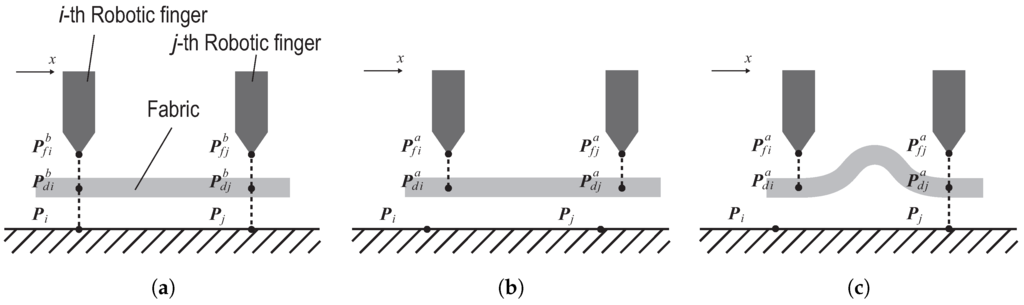
Figure 2.
Representation of a wiping motion during displacement. (a) Initial condition; (b) Wiping slide; (c) Wiping deformation.
The manipulators displace the object from a location satisfied by Equation (1). We assume that position vectors and are moving to points and , respectively, during displacement. Motions that satisfy the following equations during displacement are referred to collectively as the of a deformable object:
Based on this concept, wiping motions differ from traditional path-tracking tasks. During the latter, there is relative movement between the fingers and the object, but not between the object and the floor, during displacement:
In this paper, we assume that the thin deformable object being manipulated is shaped like a rigid object; hence, a wiping motion can be classified as the displacement of the internal given points of the object during manipulations. We assumed that and are vectors at two given points of the object at the initial state, before a displacement. We also assumed that points and are moving to positions and , respectively, after the displacement. A wiping motion that satisfies the following conditions for any two points in the deformable object is referred to as a (Figure 2b):
The conditions in Equation (4) can be satisfied during rigid object manipulation. During graspless manipulation of a rigid object, this motion is referred to as a sliding and a pushing motion [21,22,23]. If a wiping motion does not satisfy the conditions of Equation (4) (e.g., the object becomes deformed during displacement), the wiping motion is referred to as (Figure 2c). This does not occur during rigid object manipulation. Hence, the wiping motion we describe is an extension of the pushing and sliding motions of rigid objects.
According to Equation (4), most wiping motions can be categorized as wiping deformations because one part of manipulated deformable objects such as hems and edges of fabrics may deform during displacement. In practice, wiping motions with no relative movements among the fingertips during displacements are referred to as wiping slide motions; hence this wiping slide motion satisfies the following equation for any i-th and j-th fingertips during the displacements described by Equation (2):
That is, a wiping motion in which there is relative movement among the fingertips during the displacement described by Equation (2) is referred to as a wiping deformation.
3. Pinching of Fabrics Using Wiping Deformation
3.1. Strategy
In this section, we physically analyze wiping motion and show that wiping deformation is useful for handling deformable objects. As an example of wiping deformation, we utilize the pinching motion of fabrics. There are two ways to pinch fabrics (Figure 3). A robotic gripper that pinches a fabric utilizes a pinching method, in which the robotic fingers are in contact with one side of the surface (Figure 3a) [5,24]. To unfold fabrics in air without a handover motion after pinching the fabrics, however, the robotic hand should pinch both sides of the fabric (see Figure 1c,b). Handover motions may be generally accomplished using a multi-armed robotic hand, which is difficult to control. Using wiping deformation, a single-armed robotic hand can pinch both sides of a fabric. A single-armed robotic hand system can pinch a fabric using a four-step pinching strategy (Figure 4):
- (a)
- Using a gripper, a robotic hand presses on an edge of the fabric,
- (b)
- The hand moves the gripper to wrinkle the fabric,
- (c)
- The hand moves up the fabric,
- (d)
- The gripper pinches the edge of the fabric.
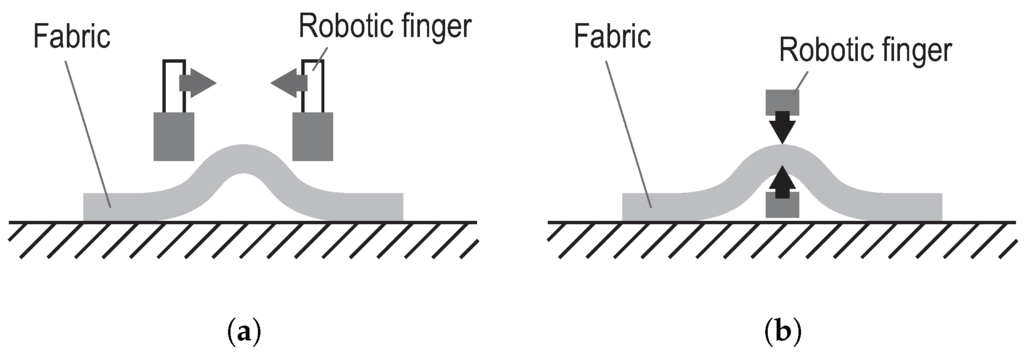
Figure 3.
Pinching of a fabric by robotic fingers. (a) With one side of the surface; (b) With both sides of the surface.
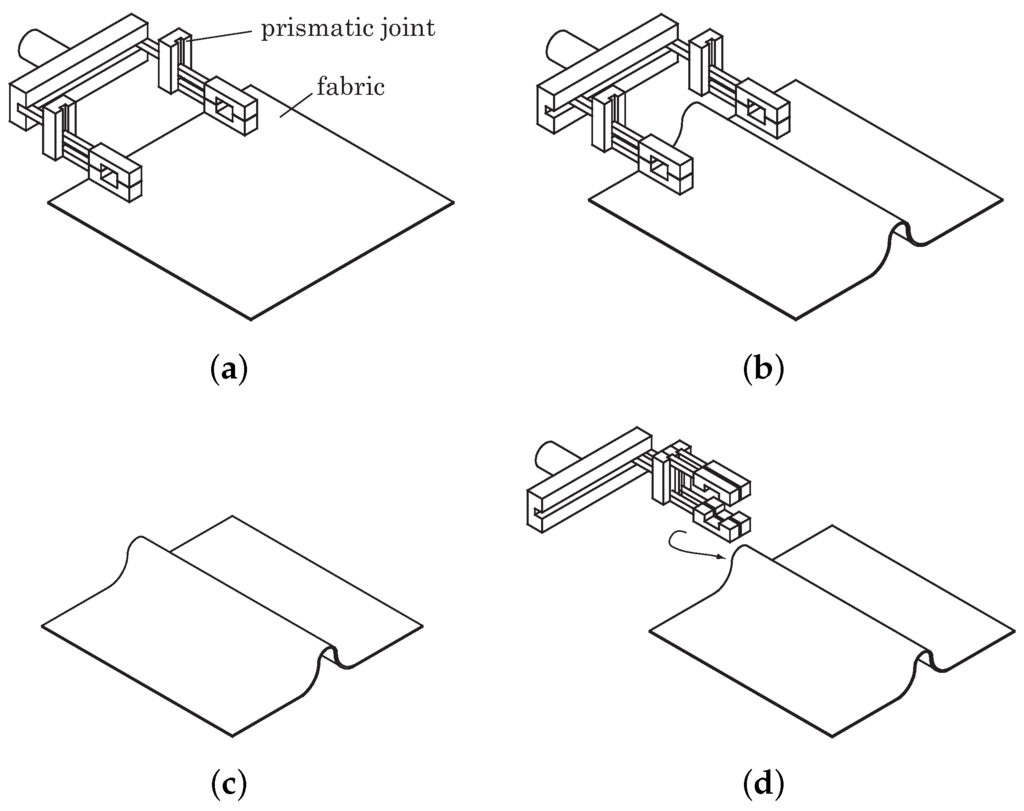
Figure 4.
Strategy of fabric pinching. (a) Using a gripper, a robotic hand presses on an edge of the fabric; (b) The hand moves the gripper to wrinkle the fabric; (c) The hand moves up the fabric; (d) The gripper pinches the edge of the fabric.
Step (b) represents wiping deformation. In step (c), there is residual deformation of the fabric so that the shape of the pinched area is maintained. Although the example shown in the figure uses one hand with four prismatic joints, a gripper with two prismatic joints can pinch the fabric using this procedure if the arm has many degrees of freedom.
3.2. Mechanical Analyses of the Wiping Deformation
In this section, we analyze mechanically how to wrinkle a fabric on a flat floor using wiping deformation. For simplicity, this analysis assumes that two robotic fingers, the i-th and j-th fingers, manipulate a fabric with a belt-like shape on a flat floor. To make a simple pinching area of a fabric on a floor by a parallel gripper, these analyses will be enough available. Figure 5 shows the dominant forces that make wrinkles in our model. Both fingers press the fabric with normal force to generate frictional force. The i-th finger moves to deform the fabric. The fabric beneath the i-th finger slips on the floor and the fabric beneath the j-th finger does not slip on the floor. In addition, no slippage between the each hand and the fabric occurs during manipulation. In this strategy the definitions of working deformation as presented in Section 2.2 are satisfied.
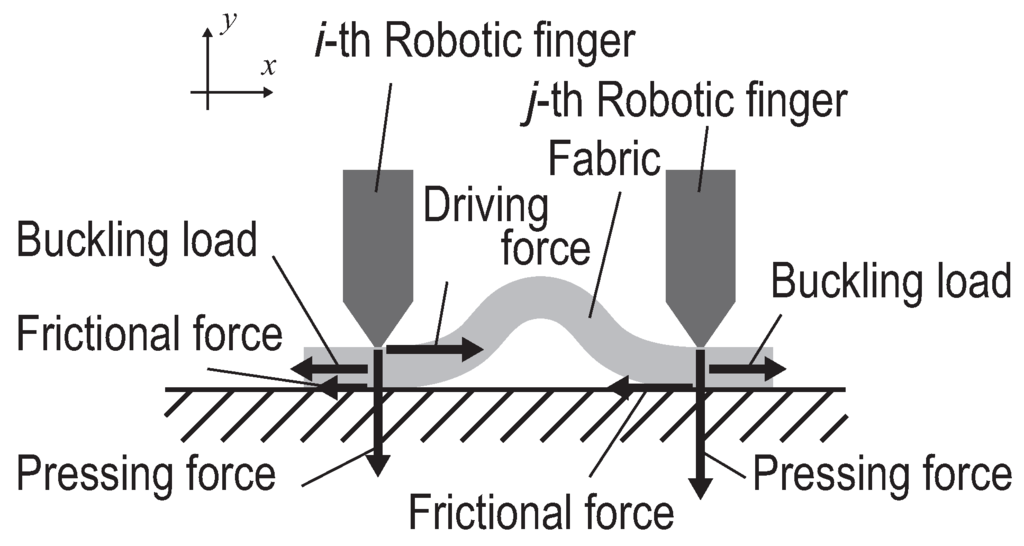
Figure 5.
Formation of a wrinkle by robotic fingers.
Fingers and fabrics are modeled as masses, as shown in Figure 6. We also consider the gravitational forces on these masses. The i-th finger generates sufficient external force to make the wrinkle. Let and be the horizontal and normal components, respectively, of the external force. The wrinkle is generated by buckling distortion of the fabric. The maximum static frictional force between the i-th finger and the fabric can be represented by the equation:
where , and g are the coefficient of static friction between the finger and the fabric, the mass of the i-th finger and the acceleration of gravity, respectively. The maximum static frictional force between the fabric and the floor can be represented by the equation:
where and are the coefficient of static friction between the fabric and the floor and mass of the fabric, respectively. To generate a wrinkle, the i-th finger must move along the fabric horizontally without slippage, but there must be slippage between the fabric and the floor. Therefore, the horizontal driving force is satisfied by the following conditions:
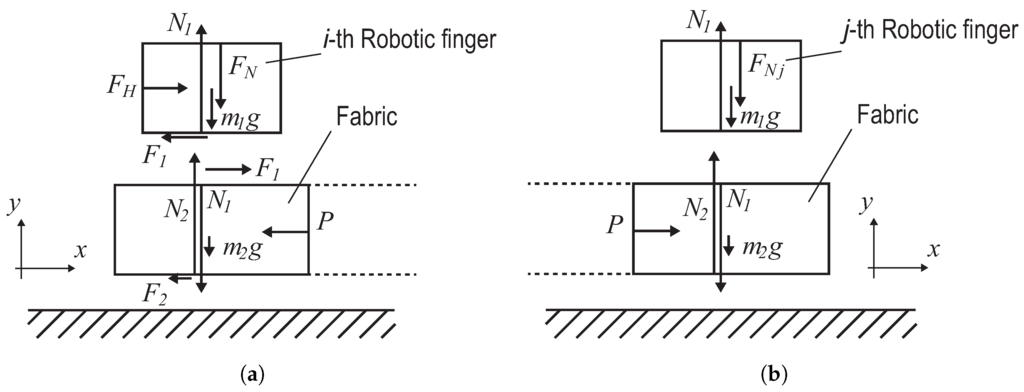
Figure 6.
Physical model of wiping motion. (a) Sliding motion by the i-th finger; (b) Pressing motion by the j-th finger.
Based on Equations (6)–(8), the friction coefficients and should be satisfied by the following conditions:
The inequality should therefore be satisfied, at least in this manipulation. In addition, the driving force needs to overcome the sum of the buckling load P and the frictional force of the fabric:
with the frictional force being equal to in this situation. We assumed that the bending moment of the wrinkle can be summarized as the buckling load of a uniform beam fixed at both ends. The buckling load P can be described as:
where L is the length of the wrinkle and K is the bending rigidity of the fabric, which represents the product of Young’s modulus and the second moment of area of the fabric; . The units for K in this paper are gf·cm. Buckling analysis can also be applied to the handling of plain paper in the manipulation of a deformable object [25].
The j-th finger presses on the fabric to fix it on the floor. The j-th finger therefore is satisfied by the equation:
where is the pressing force of the j-th finger. This analysis assumed that the masses of the i-th and j-th fingers were identical. Equation (12) shows that a pressing force is required to be large enough to hold the fabric onto the floor; however, if Equation (9) is satisfied, a wrinkle must be generated during wiping deformation. According to Equation (9), the frictional coefficients of the manipulated object are significant for this strategy. In these analyses, we assumed that there is no unexpected disturbance during the manipulation. The manipulated fingertips may slip on the fabric surface by unexpected disturbances if the condition of Equation (9) is satisfied. The fingertip’s slippage on the object by the disturbances will decrease the working precision.
3.3. Making a Pinching Area Using Residual Deformation
In this section, we derive the length needed to maintain a stable shape, such that the frictional force of its weight is equal to the sum of fabric bending moments generated by the wrinkle (Figure 7). The maximum force of static friction is dependent on the weight of the fabric [26], as shown in the equation:
where ρ is the weight per unit area of the fabric, is the length of the contacting area, and w is the width of the fabric. Thus, the length needed to counterbalance the buckling load P must satisfy the inequality: ; hence,
where is the bending rigidity of the fabric in Kawabata’s Evaluation System (KES) [27,28], a standard method of measuring the physical parameters of fabrics that has been used to identify fabrics in computer graphics [29,30]. The units of are gf·cm/cm, thus satisfying the equation: .
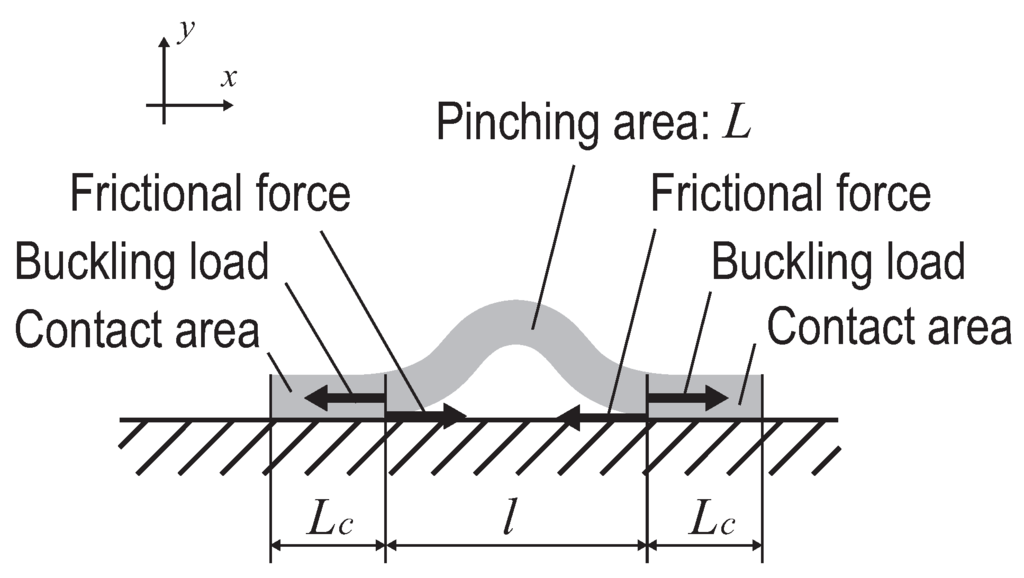
Figure 7.
Making a pinching area using residual deformation.
As shown in Figure 7, the buckling load P is generated at both ends of the wrinkle so that the following entire length is required to generate a wrinkle of length L under unloaded conditions:
These formulations did not include deformation volume or the nonlinearity and variations of physical parameters.
4. Experiments
4.1. Robotic Hand
Based on the above results, we constructed a robotic hand consisting of two grippers, each of which could move independently in both vertical and horizontal directions. Thus, this hand had four degrees of freedom (Figure 8). Two grippers moving vertically could pinch a fabric, whereas their horizontal movement could wrinkle the fabric to create a pinching area. Silicon rubbers were mounted onto the bottom of each gripper to improve the frictional force. The horizontal and vertical joints were composed of two ball screws and two trapezoidal screws, respectively. Each joint also was composed of individual DC motors. The prototype robotic hand was mounted onto a scalar arm (made by Mitsubishi Electric, Tokyo, Japan) with four degrees of freedom. To realize easily the pressing motion and wiping deformation, we utilized a scalar arm with parallel grippers in this system. The hand wrinkled the fabric using the following four-step strategy:
- (a)
- Using the bottoms of the grippers, the robotic hand pressed the fabric,
- (b)
- The hand wrinkled the fabric by moving the two grippers horizontally,
- (c)
- The hand moved up,
- (d)
- The system finished the sequence.
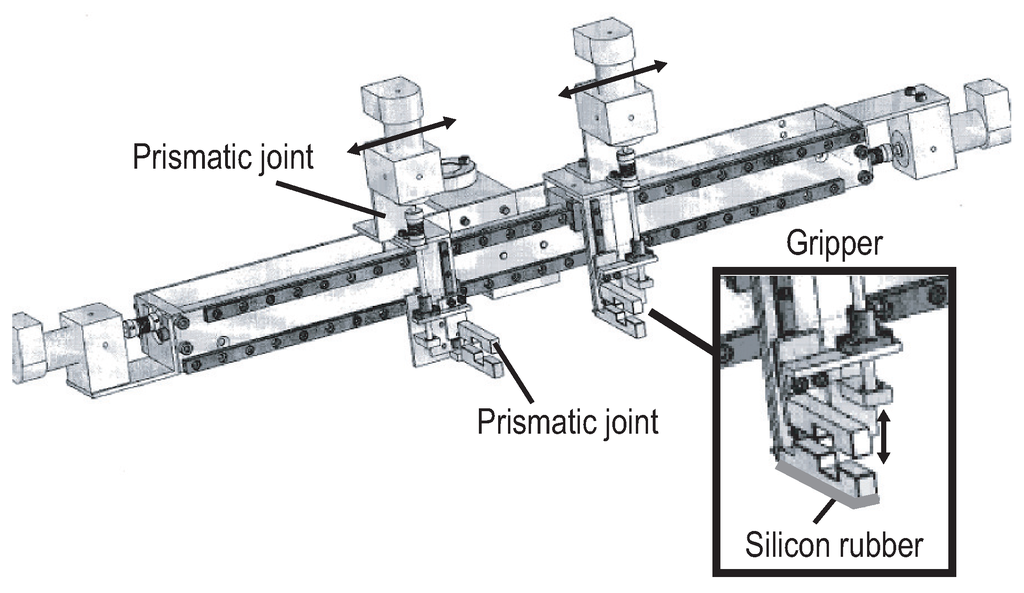
Figure 8.
Prototype of a robotic hand.
In our system, we have to measure physical properties of the fabric such as frictional coefficients and bending rigidity according to Equations (9) and (12) in advance. The robotic hand did not require the force profile if the hand pressed the fabric appropriately based on these properties; hence, we did not implement any force sensors in our prototype. To improve the working precision, we should check the contact conditions using several tactile sensing techniques during the manipulation. We will implement force sensors to our robotic fingertips in future.
4.2. Investigation of Buckling
Equations (14) and (15) indicate that the conditions under which a wrinkle could maintain its shape during residual deformation depend on the bending rigidity of the fabric, the weight per unit area of the fabric, the length of the wrinkle, and the maximum coefficient of static friction between the fabric and the floor. In this section, we experimentally evaluated the validity of our analysis of buckling load using a cotton handkerchief (Table 1), with the superscript asterisks indicating the parameters measured by KES. The coefficient of friction between the handkerchief and the silicon rubber mounted onto the robotic fingers was measured, as was that between the handkerchief and the floor, a chloroethylene board. The values of these coefficients of friction were larger than those measured by KES.

Table 1.
Physical properties of specimen.
Based on Equation (15), we calculated that, for a wrinkle of 6.0 cm, the length of the cotton handkerchief required for its weight to maintain a stable shape in an unloaded condition was 14.8 cm. We confirmed the validity of our analyses using specimens of lengths 10 cm, 15 cm, and 20 cm. These specimens were belt-like shaped pieces of cotton, of width 3.0 cm. Under these conditions, Equation (11) determined that the buckling loads P of these specimens were 0.14 gf. That is, the horizontal force required to realize the wiping deformation for fabrics would be of gram-force order. The robotic hand in Figure 8 wrinkled these specimens using wiping deformation. If l is the distance between the fingertips after wrinkling the specimens, then length l was set at 3.0 cm, 4.0 cm, and 5.0 cm for an initial length L of 6.0 cm (see Figure 7). The robotic hand was slowly moved up after wrinkling the specimens.
Table 2 shows the percentages of success rates of the experimental wiping deformation, with 10 trials for each condition. Success was defined as maintenance of the shape of the wrinkle after moving the hand, while failure was defined as a distortion of the shape of the wrinkle, due to an inability to stand up under its own weight. We found that, although both successes and failures occurred for specimens 15 cm in length, all trials of 20 cm long specimens were successes. These results indicate that 15 cm is the criterion for buckling analysis. The length was strongly dependent on the coefficient of friction , with the latter tending to vary relative to the surrounding environment. Equation (15) shows that the length should be more than 14.8 cm when is 1.07, but should be more than 15.4 cm if is 1.00. Based on Equations (14) and (15), a wrinkle can be made under unloaded conditions.

Table 2.
Success rates in wiping deformation.
In addition, we experimentally evaluated the validity of our buckling analysis for other fabrics. Table 3a shows physical properties of three specimens, two cottons and a polyester textile. The superscript asterisk in Table 3a indicates the parameters measured by KES. The coefficients of friction between the textiles and the floor, a wood board were measured to estimate the entire length in these experiments. Based on Equation (15), we calculated the length of the textiles required for its weight to maintain a stable shape in an unloaded condition for a wrinkle of 6.0 cm. These specimens were belt-like shaped pieces of cotton, of width 2.0 cm.
Table 3b shows the percentages of success rates of the experimental wiping deformation, with 10 trials for each condition. Success was defined as maintenance of the shape of the wrinkle after moving the hand, while failure was defined as a distortion of the shape of the wrinkle, due to an inability to stand up under its own weight as stated in the previous experiments. The lines in Table 3b indicated that we did not experiment under these conditions. We found that, although experimental results for two cottons were as we almost expected, the entire length of polyester textile was smaller than the estimated one. Based on Equation (15), this estimation was strongly dependent on the coefficient of friction and the bending rigidity . Using a longer specimen, there may be a tendency that the non-uniformity of physical properties of the fabric influenced the entire length .
4.3. Fabric Pinching by a Single-Armed Robotic Hand
Our strategy for pinching a fabric consists of a combination of wiping deformation and residual deformation of the fabric under unloaded conditions. Using this strategy, a single-armed robotic hand can pinch both surfaces of a fabric without handover motion. The hand in Figure 8 pinches the fabric using the following steps:
- (a)
- The system visually detects a candidate area for pinching,
- (b)
- Using its fingertips, the robotic hand presses the fabric,
- (c)
- The hand wrinkles the fabric by shutting two grippers horizontally,
- (d)
- The hand opens the grippers,
- (e)
- The hand moves up,
- (f)
- The hand inserts grippers under the fabric,
- (g)
- The hand shuts the grippers vertically to pinch the fabric,
- (h)
- The system finishes the sequence.
Figure 9 shows successive images of the pinching motion. As a fabric specimen, we used a rectangular cotton handkerchief, measuring 450 mm × 430 mm; its physical properties are shown in Table 1. In step (a), a stereovision system detected the edge of the fabric. In step (c), the grippers made a pinching area, whereas, in step (d), the grippers partially released this area. These steps resulted in hysteresis for bending rigidity of the fabric. In general, bending rigidities of fabrics have hysteresis properties against the flexures. With hysteresis, the bending rigidity may become smaller for stable shapes depending on how to inflect the fabric; hence, based on Equation (14), the creation of a pinching area can be changed by the hysteresis effect. That is, this effect of hysteresis may be considered a dexterous manipulation by a robotic hand. We will evaluate the success rate of pinching should be investigated including this effect of hysteresis in future. In this experiment, the length of the pinching area L was set at 60 mm and the distance between the two fingers after wiping deformation l was set at 30 mm.

Figure 9.
Pinching motion for a fabric by a single-armed robotic hand. (a) The system visually detects a candidate area for pinching; (b) Using its fingertips, the robotic hand presses the fabric; (c) The hand wrinkles the fabric by shutting two grippers horizontally; (d) The hand opens the grippers; (e) The hand moves up; (f) The hand inserts grippers under the fabric; (g) The hand shuts the grippers vertically to pinch the fabric; (h) The system finishes the sequence.
5. Discussion
5.1. Minimum Entire Length of a Manipulated Fabric
Based on Equation (15), the entire length of the fabric is described as a function of the length L. This equation has one local minimum when . At the local minimum, the minimum entire length of the fabric can be calculated as:
The pinching length at the can be described as:
These equations indicate that the lengths and depend on the bending rigidity of the fabric, the weight per unit area of the fabric, and the maximum coefficient of static friction between the fabric and the floor.
5.2. Applicability to Other Thin Deformable Objects
In this section, we discuss the applicability of our pinching strategy to other thin deformable objects, such as plain paper and plastic film. Table 4 shows physical parameters measured by KES of a cotton handkerchief, a piece of plain paper, and a piece of plastic film used in food packaging. This table also shows the minimum entire length and the pinching area calculated by Equations (16) and (17). and were smallest for the cotton handkerchief; thus, a robotic hand can easily pinch this fabric using our pinching strategy. The size of the hand required for pinching depends on these lengths and ; however, a smaller-sized hand would be required in industrial settings. Therefore, length L should be smaller than length . In our previous single-armed robotic hand, the assumed length of the pinching area L was 60 mm. Pinching by our wiping motion requires careful determination of the coefficient of static friction .

Table 4.
Applicability of residual deformation.
6. Conclusions
This paper discussed a pinching strategy of a fabric by a robotic hand based on the physical properties of the fabric. We described as a task in which the motion and deformation of a deformable object occurred simultaneously. Wiping motion of a deformable object was defined as a task in which there was contact, but no relative movement, between manipulators and the object; combined with contact, plus relative movement, between the object and the floor, during the displacement of the object. First, we described wiping motion and distinguished from caused by the displacement of internal points of an object. We also showed that wiping motion was an extension scheme of pushing and sliding of rigid objects. We physically analyzed planar wiping deformation in terms of buckling load and residual deformation under unloaded conditions, as physical properties of a fabric. We finally demonstrated that a single-armed robotic hand could pinch both surfaces of a fabric, using our pinching strategy, without handover motion.
In this paper, we measured the physical properties of manipulated fabrics in advance to estimate the entire length of the fabrics. We also assumed that a robot hand with prismatic joints handled a uniform belt-like fabric on a flat floor. The approach will be very useful for a number of fields such as apparel and linen supply industries. We will apply sensing techniques using vision and tactile sensors to improve the precision of the manipulation. Our strategy required that all fingers had to press the fabric with normal force to generate frictional force during manipulation. We will expand our system to a complex robotic hand with angular grippers and more than three fingertips to realize generalized manipulations. In the future, we will also consider how to move the robotic fingers to make a pinching area using other physical properties such as the hysteresis for the flexure.
Acknowledgments
This research was partly supported by funding from the Research for Promoting Technological Seeds in Japan Science and Technology Agency.
Author Contributions
Mizuho Shibata came up with the idea and physical analyses for Wiping motion. He performed the experiments to investigate the analyses. Shinichi Hirai discussed the result and thoroughly revised the paper. Mizuho Shibata wrote the paper. All authors discussed and interpreted the results, and, agreed about the conclusions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Taylor, P.M. Sensory Robotics for the Handling of Limp Materials; Springer: Berlin, Germany, 1990. [Google Scholar]
- Parker, J.K.; Dubey, R.; Paul, F.W.; Becker, R.J. Robotic Fabric Handling for Automation Garment Manufacturing. J. Eng. Ind. 1983, 105, 21–26. [Google Scholar] [CrossRef]
- Torgerson, E.; Paul, F.W. Vision Guided Robotic Fabric Manipulation for Apparel Manufacturing. In Proceedings of the IEEE International Conference on Robotics and Automation, Raleigh, NC, USA, 31 March–3 April 1987.
- Ono, E.; Kita, N.; Sakane, S. Strategy for unfolding a fabric piece by cooperative sensing of touch and vision. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Pittsburgh, PA, USA, 5–9 August 1995.
- Ono, E.; Takase, K. On Better Pushing for Picking a Piece of Fabric from Layers. In Proceedings of the IEEE/RSJ International Conference on Robotics and Biomimetics, Sanya, China, 15–18 December 2007.
- Kabaya, T.; Kakikura, M. Service Robot for Housekeeping Clothing Handling. J. Robot. Mechatron. 1998, 10, 252–257. [Google Scholar]
- Hamajima, K.; Kakikura, M. Planning Strategy for Task Untangling Laundry Isolating Clothes from a Washed Mass. J. Robot. Mechatron. 1998, 10, 244–251. [Google Scholar]
- Fahantidis, N.; Doulgeri, Z. A Gripper for Grasping Non-Rigid Material Pieces out of a Bundle. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Takamatsu, Japan, 30 October–5 November 2000.
- Hirai, S.; Wada, T. Indirect Simultaneous Positioning of Deformable Objects with Multi Pinching Fingers Based on Uncertain Model. Robotica 2000, 18, 3–11. [Google Scholar] [CrossRef]
- Kita, Y.; Saito, F.; Kita, N. A deformable model driven visual method for handling clothes. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004.
- Yamazaki, K. A Method of Grasp Point Selection from an Item of Clothing Using Hem Element Relations. Adv. Robot. 2014, 29, 13–24. [Google Scholar] [CrossRef]
- Tamei, T.; Matsubara, T.; Rai, A.; Shibata, T. Reinforcement Learning of Clothing Assistance with a Dual-Arm Robot. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Bled, Slovenia, 26–28 October 2011.
- Miller, S.; Berg, J.; Fritz, M.; Darrell, T.; Goldberg, K.; Abbeel, P. A Geometric Approach to Robotic Laundry Folding. Int. J. Robot. Res. 2012, 31, 249–267. [Google Scholar] [CrossRef]
- Maitin-Shepard, J.; Cusumano-Towner, M.; Lei, J.; Abbeel, P. Cloth grasp point detection based on multiple-view geometric cues with application to robotic towel folding. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010.
- Le, T.; Jilich, M.; Landini, A.; Zoppi, M.; Zlatanov, D.; Molfino, R. On the Development of a Specialized Flexible Gripper for Garment Handling. J. Autom. Control Eng. 2013, 1, 255–259. [Google Scholar] [CrossRef]
- Denei, S.; Maiolino, P.; Baglini, E.; Cannata, G. On the development of a tactile sensor for fabric manipulation and classification for industrial applications. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015.
- Paraschidis, K.; Fahantidis, N.; Vassiliadis, V.; Petridis, V.; Doulgeri, Z.; Petrou, L.; Hasapis, G. A Robotic System for Handling Textile Materials. In Proceedings of the IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995.
- Shibata, M.; Hirai, S. Soft Object Manipulation by Simultaneous Control of Motion and Deformation. In Proceedings of the IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006.
- Shibata, M.; Ota, T.; Hirai, S. Wiping Motion for Deformable Object Handling. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009.
- Shibata, M.; Ota, T.; Endo, Y.; Hirai, S. Handling of Hemmed Fabrics by a Single-Armed Robot. In Proceedings of the IEEE International Conference on Automation Science and Engineering, Washington, DC, USA, 23–26 August 2008.
- Maeda, Y.; Kijimoto, H.; Aiyama, Y.; Arai, T. Planning of graspless manipulation by multiple robot fingers. In Proceedings of the IEEE International Conference on Robotics and Automation, Seoul, Korea, 21–26 May 2001.
- Lynch, K.; Mason, M. Stable Pusing: Mechanics, Controllability, and Planning. Int. J. Robot. Res. 1996, 17, 485–503. [Google Scholar]
- Terasaki, O.; Hasegawa, T. Intelligent manipulation of sliding operations with parallel two-fingered grippers. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 26–30 July 1993.
- Taylor, P.M.; Pollet, D.M.; Abbott, P.J.W. The Influence of Environmental Conditions on Automated Fabric Handling. J. Robot. Mechatron. 1998, 10, 258–263. [Google Scholar]
- Nishimura, K.; Nakagawa, M.; Kawasaki, H. Mechanism and Control of a Page-Turning Robot. ASME Robot. Manuf. Autom. 1985, PED-15, 269–276. [Google Scholar]
- Dourmashkin, P. Classical Mechanics MIT 8.01 Course Notes; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Kawabata, S.; Niwa, M. Fabric Performance in Clothing Manufacture. J. Text. Inst. 1989, 80, 19–50. [Google Scholar] [CrossRef]
- Harwood, R.J.; Weedall, P.J.; Carr, C. The use of the Kawabata Evaluation System for product development and quality control. J. Soc. Dyers Colour. 1990, 106, 64–68. [Google Scholar] [CrossRef]
- Eberhardt, B.; Weber, A.; Strasser, W. A Fast, Flexible, Particle-System Model for Cloth Draping. IEEE Comput. Graph. Appl. 1996, 16, 52–59. [Google Scholar] [CrossRef]
- Eischen, J.W.; Deng, S.; Clapp, T.G. Finite-Element Modeling and Control of Flexible Fabric Parts. IEEE Comput. Graph. Appl. 1996, 16, 71–80. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).