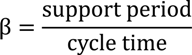Design Issues for Hexapod Walking Robots
Abstract
:1. Introduction
2. State of Art Overview
2.1. Early Designs

2.2. Recent Developments

| Main Characteristics | Main Performance | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Robot Name | Mass (Kg) | Length (cm) | Width (cm) | Height (cm) | Total DoFs | Max Speed (m/s) | Gait/Mobility | Power (W) | Year | Application Tasks |
| Ambler | 2700 | 500 | 500 | 700 | 12 | 0.007 | Wave Free | 1900 | 1989 | Planetary exploration |
| ASV | 3200 | 520 | 240 | 300 | 15 | 1.0 | Wave Free | 26000 | 1989 | Navigate on uneven terrains |
| Hannibal | 2.7 | 35 | NA | 20 | 19 | 0.04 | Wave Free | NA | 1989 | Planetary exploration |
| Tum | 23 | 80 | 40 | 100 | 18 | 0.3 | Wave | 500 | 1991 | Hexapod following biological principles |
| Biobot | 11 | 58 | 14 | 23 | 18 | NA | NA | NA | 2000 | Locomotion over rough terrain |
| Hamlet | 13 | 40 | 28 | 40 | 18 | 0.1 | Wave Free | 52 | 2001 | Testing force and position control |
| Rhex | 7 | 53 | 20 | 15 | 6 | 0.55 | Wave Free | 100 | 2001 | Hexapod with reduced actuators |
| Sprawlita | 0.27 | 16 | NA | NA | 12 | 0.35 | Wave | NA | 2002 | Robots inspired to cockroaches |
| Lauron III | 18 | 50 | 30 | 80 | 18 | 0.4 | Wave Free | NA | 1999–2003 | Testing a hierarchical walk controller |
| Genghis | 1 | 40 | 15 | NA | 12 | 0.04 0.12 | Wave Free | NA | 2004 | Developing of a reactive controller |
| Aqua II | 16.5 | 64 | 44 | 13 | 6 | 0.7 1 | Land Water | 200 | 2010 | Underwater hexapod robot |
| Bill-Ant-p | 2.3 | 47 | 33 | 16 | 22 | 0.004 | Wave | 25 | 2005 | Biologically inspired legged robot |
| Gregor I | 1.2 | 30 | 9 | 4 | 16 | 0.03 | NA | 25 | 2006 | Robot inspired on cockroaches. |
| Athelete | 850 | 2.75 | 2.75 | 2 | 36 | 2.78 0.016 | Wheleed Wave | NA | 2006 | Navigate on rough soil of on the Moon |
| RiSe | 2.8 | 41 | NA | NA | 12 | NA | Wave | NA | 2006 | Hexapod climbing robots |
| Comet IV | 2120 | 280 | 330 | 250 | 24 | 0.278 | Wave | 20600 | 2009–2011 | Hexapod for multitasks on outdoor environment |
| CR200 | 600 | 250 | 200 | 130 | 18 | 0.5 | Wave | 20000 | 2013 | Walk either on land or underwater in the turbulent surf zone |
| Mantis | 1900 | 420 | 220 | 280 | 18 | NA | Wave | 42000 | 2013 | Entertainment |
2.3. Hexapod Robots’ Performance Indices
- Duty factor
- Froude number
- Specific resistance
- Stability margin
- The duty factor β [42] is defined as:
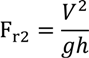
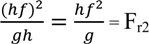
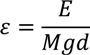
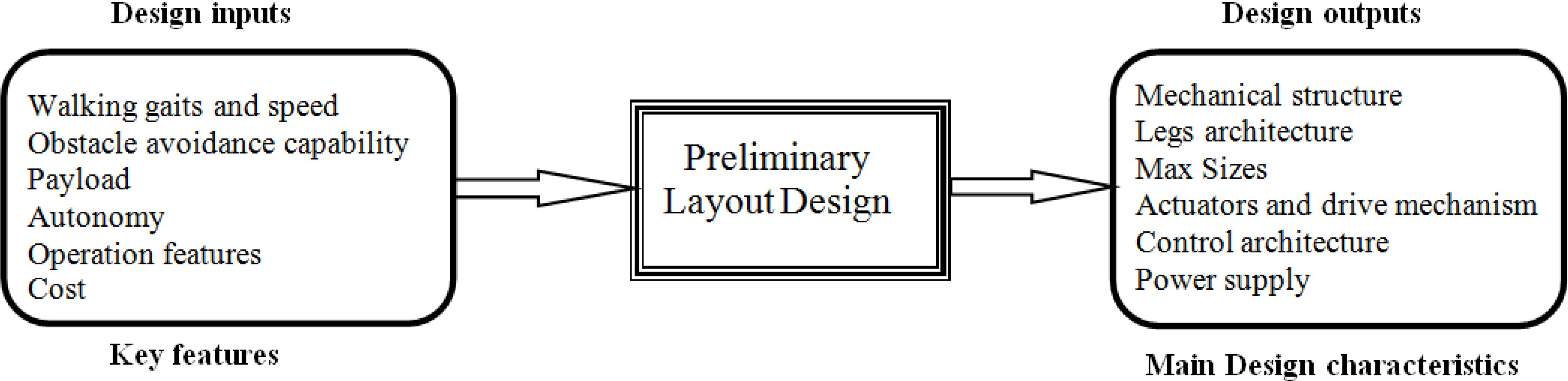
3. Design Considerations
- the mechanical structure of robot body;
- leg architecture;
- max sizes;
- actuators and drive mechanisms;
- control architecture;
- power supply;
- walking gaits and speed;
- obstacle avoidance capability;
- payload;
- autonomy;
- operation features;
- cost.
| Importance of Key Features | Value |
|---|---|
| Not important to project success | 1 |
| Somewhat important to project success | 2 |
| Fairly important to project success | 3 |
| Very important to project success | 4 |
| Critical to project: design driver | 5 |
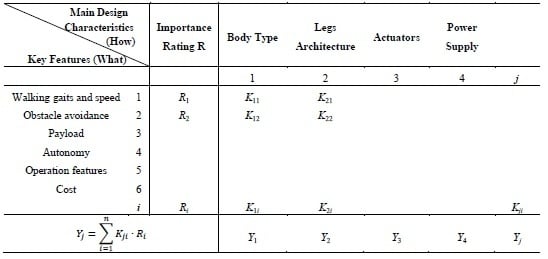
| Main Design Characteristics (How) | Importance Rating R | Body Type | Legs Architecture | Actuators | Power Supply | |||
|---|---|---|---|---|---|---|---|---|
| Key Features (What) | ||||||||
| 1 | 2 | 3 | 4 | j | ||||
| Walking gaits and speed | 1 | R1 | K11 | K21 | ||||
| Obstacle avoidance | 2 | R2 | K12 | K22 | ||||
| Payload | 3 | |||||||
| Autonomy | 4 | |||||||
| Operation features | 5 | |||||||
| Cost | 6 | |||||||
| i | Ri | K1i | K2i | Kji | ||||
Yj = 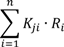 | Y1 | Y2 | Y3 | Y4 | Yj | |||
| Engineering Solution Satisfies the Requirement | Value |
|---|---|
| By itself | 9 |
| In conjunction with one or two factors | 3 |
| In conjunction with many other factors | 1 |
| Does not satisfy the requirements | 0 |
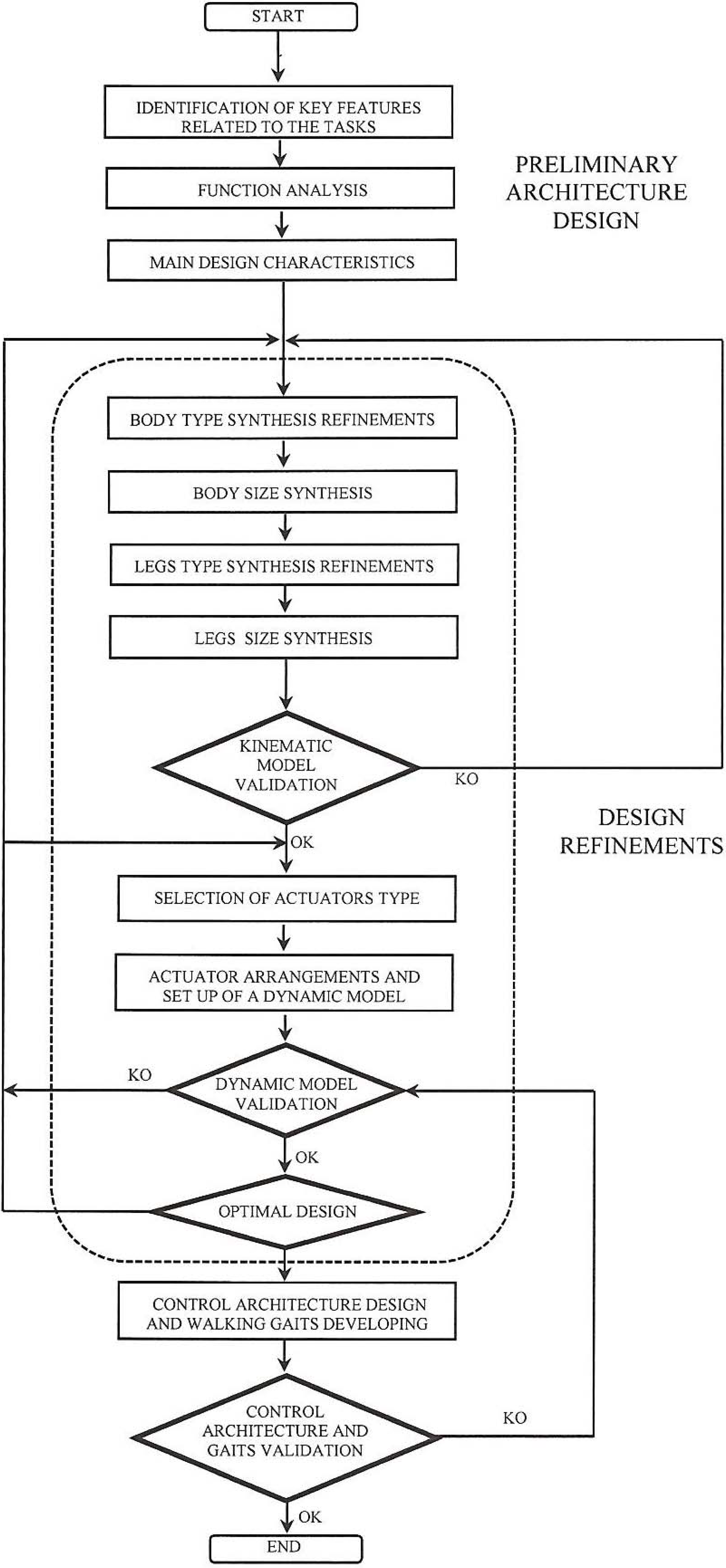
3.1. Robot Body Architecture
3.2. Kinematic Architectures of Legs
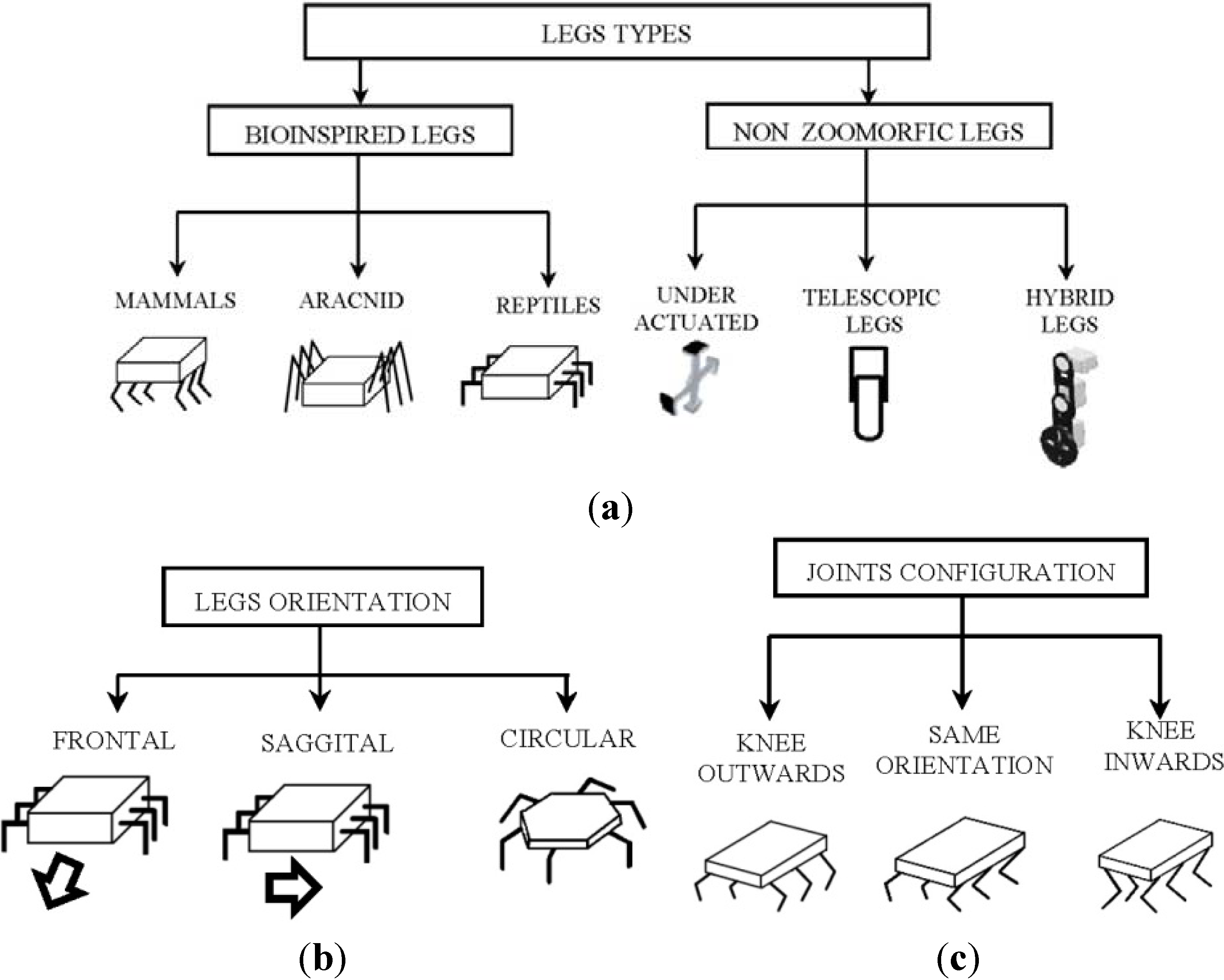
3.2.1. Actuator Types
3.2.2. Actuators Arrangements
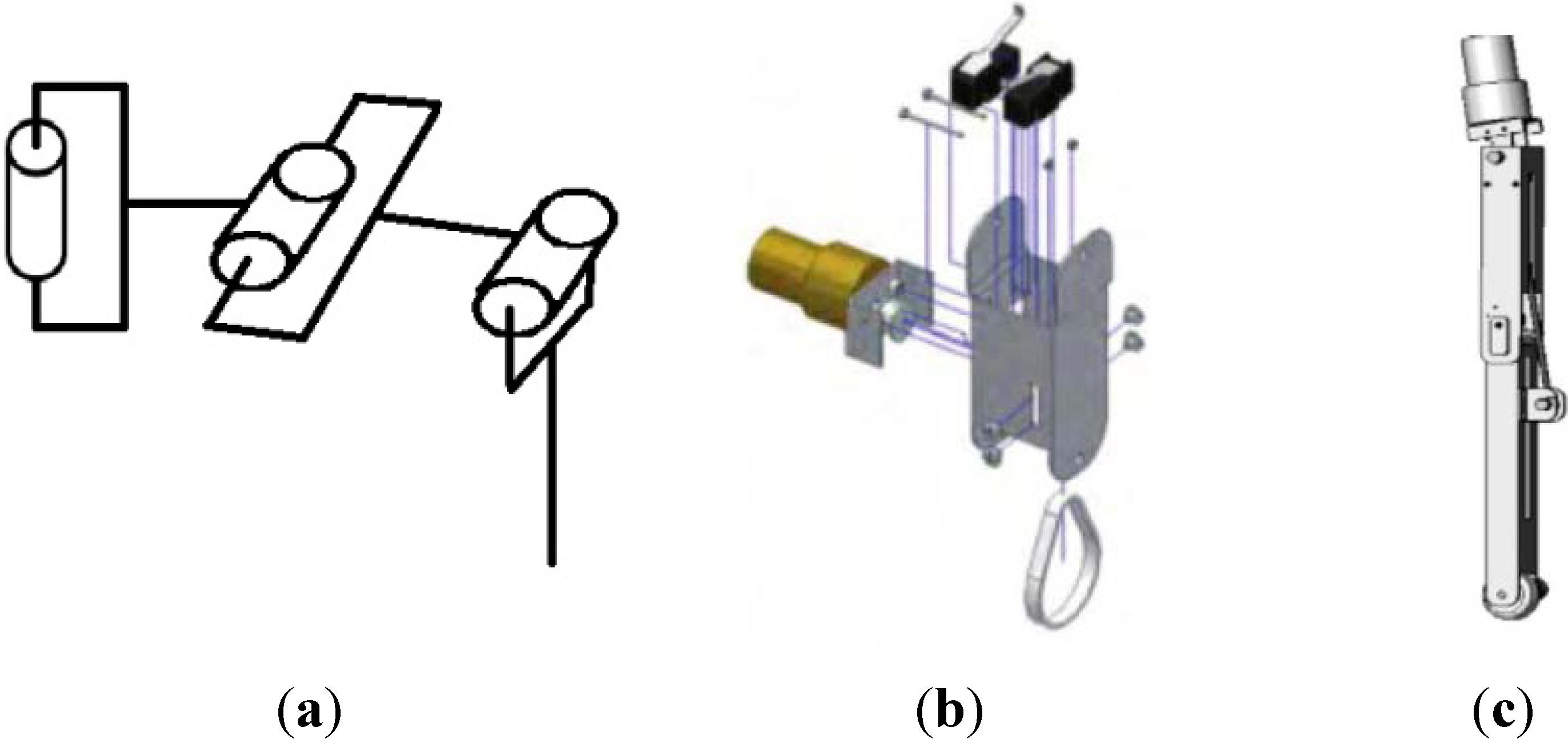
3.3. Modeling Issues
3.4. Optimal Design
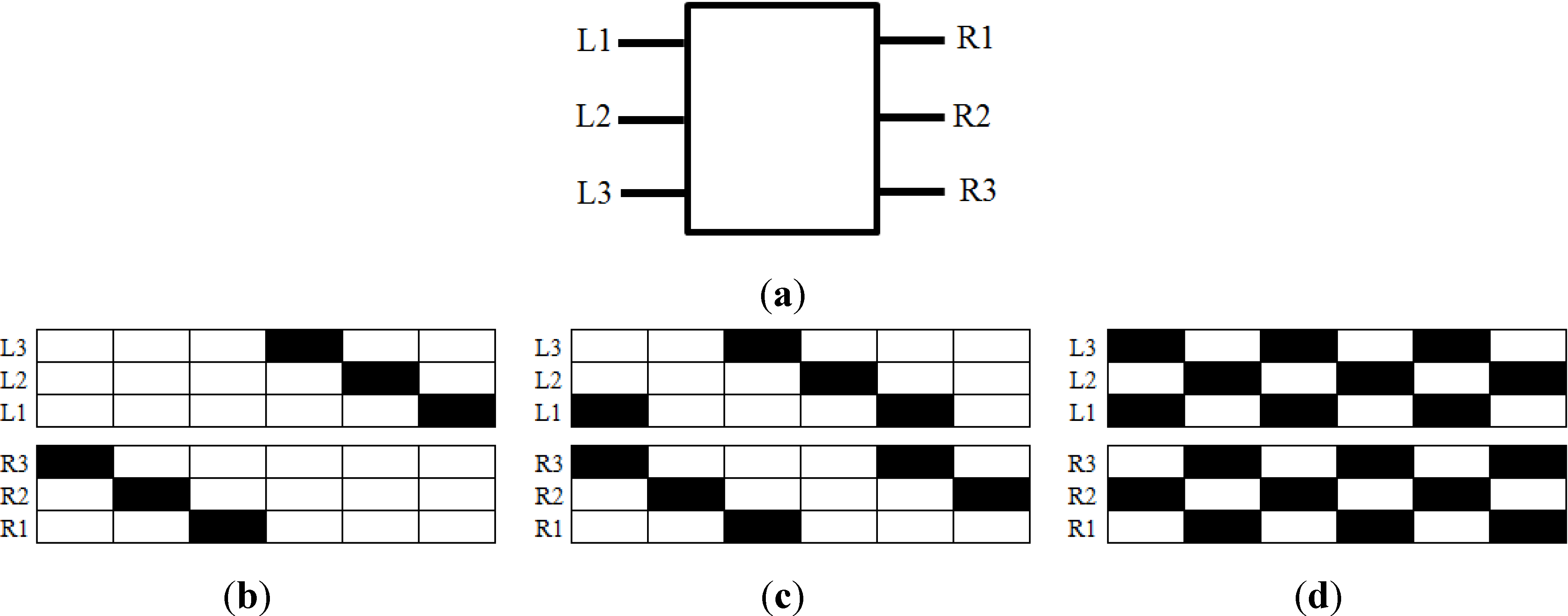
X X i = 1,…,N
3.5. Hexapod Walking Robot Control
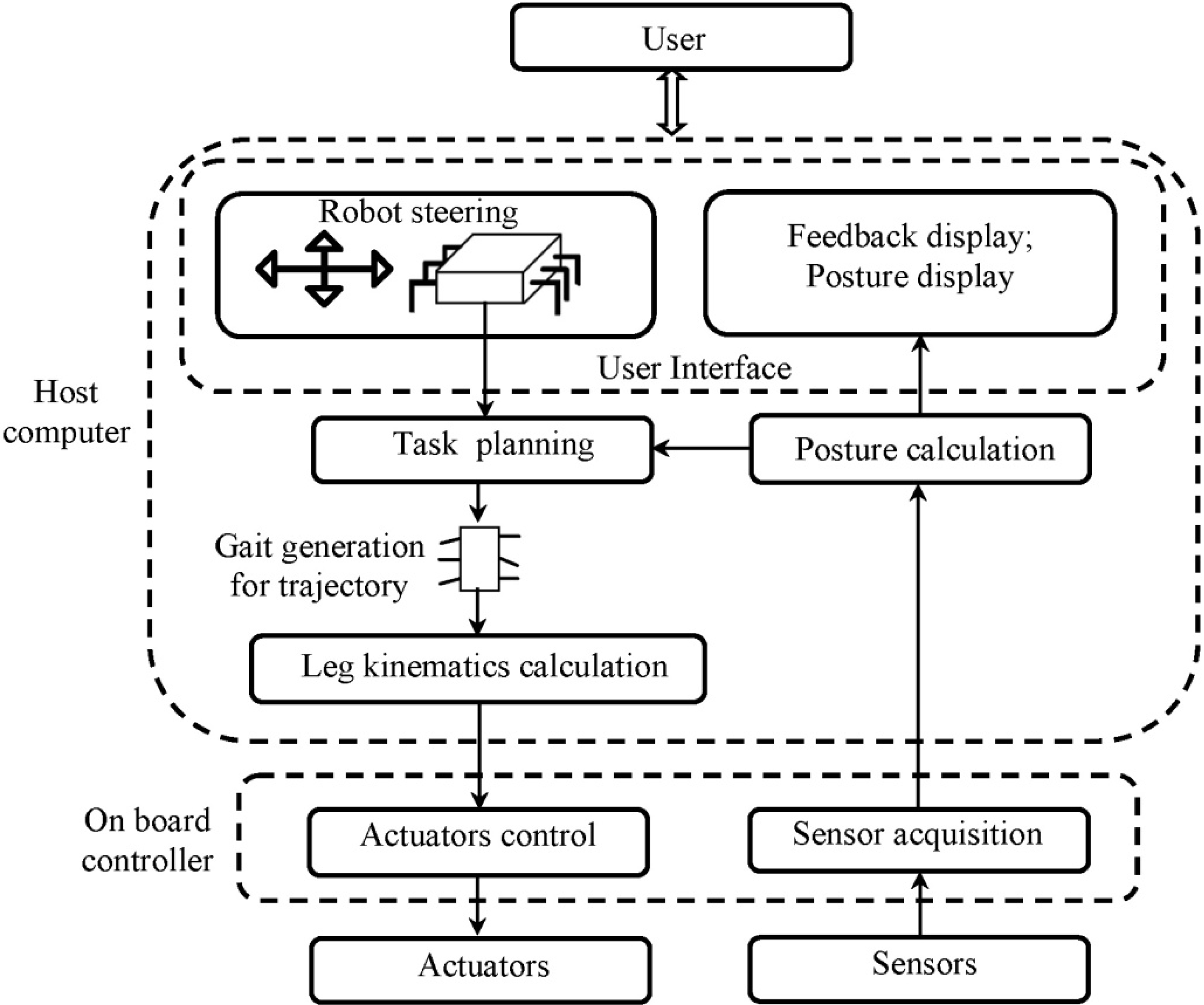
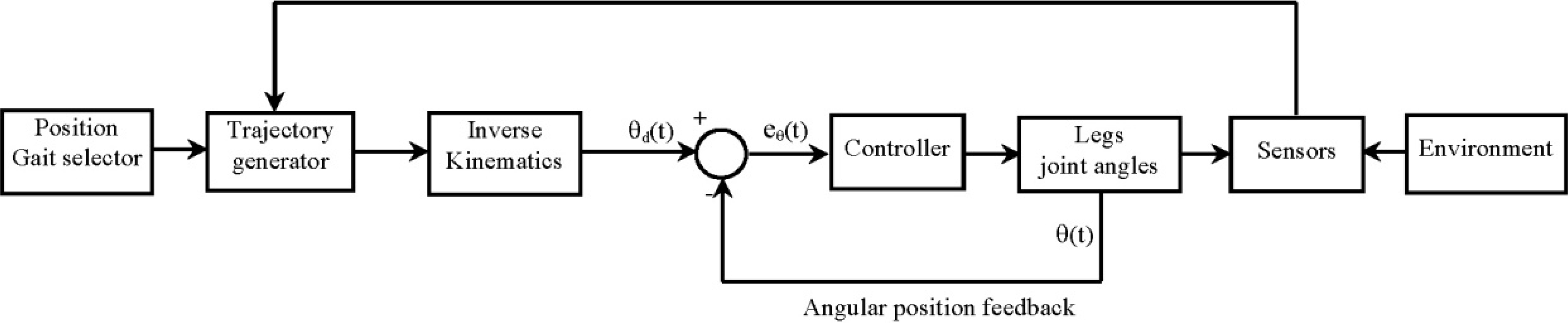
3.6. Gait Planning
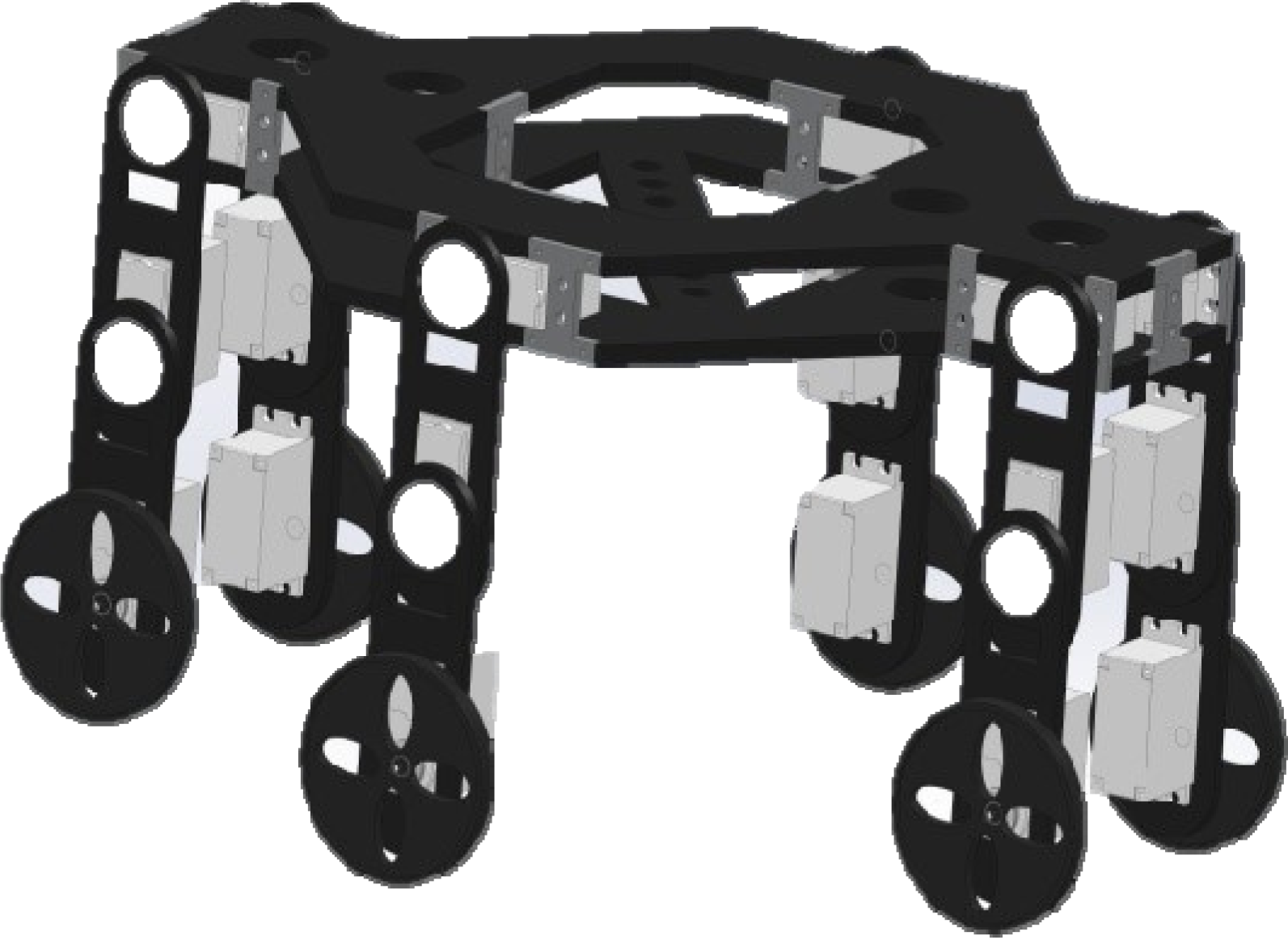
4. A Case of Study for Preliminary Lay-Out Design
- low cost ( <1000 Euros);
- user-friendly operation, also for non-expert users (e.g., architects);
- possibility to negotiate a large variety of obstacles, such as
- -
- a step with maximum height of 60 mm;
- -
- a crest with maximum width of 100 mm and maximum height of 60 mm;
- -
- a ditch with a maximum width of 60 mm;
- the robot must be able to move inside archaeological and/or architectural sites by carrying surveying devices and by avoiding damage of the surface and other parts of the site;
- the robot can be operating wirelessly, in environments that cannot be reached or that are unsafe for human operators;
- operating speed on regular terrain should be >0.1 m/s on regular terrain and ≥0.01 m/s on uneven terrains as based on previous experience in architectonical survey.
| Main Design Characteristics (How) | Rating of Importance R | Body Type | Legs Type Synthesis | Actuators | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rectangular Shape | Hexagonal Shape | Configuration | Orientation | Knee | Electrical | Pneumatic | Hydraulics | |||||||||||
| Mammalian Legs | Reptile Legs | Spider Legs | Hybrid Legs | Sagittal | Frontal | Circular | Outwards | Same Orientation | Inwards | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||||
| Walking speed | ||||||||||||||||||
| Regular terrain ≥ 0.1 m/s | 1 | 5 | 3 | 3 | 1 | 1 | 1 | 9 | 3 | 9 | 3 | 3 | 3 | 3 | 9 | 3 | 3 | |
| Uneven terrain ≥ 0.01 m/s | 2 | 3 | 3 | 3 | 1 | 1 | 1 | 3 | 3 | 9 | 3 | 3 | 3 | 3 | 9 | 3 | 3 | |
| Low Cost | ||||||||||||||||||
| Cost ≤ 1000 Euro | 3 | 5 | 3 | 3 | 3 | 3 | 3 | 3 | 1 | 1 | 1 | 1 | 1 | 1 | 9 | 1 | 1 | |
| Use of commercial components | 4 | 4 | 3 | 1 | 9 | 9 | 9 | 9 | 3 | 3 | 3 | 3 | 3 | 3 | 9 | 3 | 1 | |
| Obstacle avoidance | ||||||||||||||||||
| Step Hmax ≥ 60 mm | 5 | 4 | 3 | 3 | 9 | 1 | 1 | 9 | 1 | 3 | 3 | 3 | 9 | 1 | 1 | 1 | 1 | |
| Crest Hmax ≥ 60 mm W ≥ 100 mm | 6 | 4 | 3 | 3 | 9 | 1 | 1 | 9 | 1 | 3 | 3 | 3 | 9 | 1 | 1 | 1 | 1 | |
| Ditch Wmax ≥ 100 mm | 7 | 4 | 3 | 3 | 9 | 1 | 1 | 9 | 1 | 3 | 3 | 3 | 9 | 1 | 1 | 1 | 1 | |
| Operation | ||||||||||||||||||
| Wireless | 8 | 5 | 3 | 3 | 3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 9 | 1 | 1 | |
| Omnidirectional Steering | 9 | 4 | 3 | 3 | 1 | 3 | 3 | 3 | 3 | 3 | 9 | 3 | 3 | 3 | 3 | 3 | 3 | |
| Autonomy ≥ 1 h | 10 | 5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 9 | 0 | 0 | |
| Walking Gait | ||||||||||||||||||
| Tripod gait | 11 | 3 | 9 | 9 | 3 | 3 | 3 | 9 | 3 | 3 | 3 | 3 | 3 | 3 | 1 | 1 | 1 | |
| Metachronal gait | 12 | 3 | 9 | 3 | 3 | 3 | 3 | 3 | 9 | 3 | 3 | 3 | 3 | 3 | 1 | 1 | 1 | |
| Free gaits | 13 | 1 | 3 | 3 | 1 | 1 | 1 | 9 | 3 | 1 | 1 | 1 | 3 | 3 | 1 | 1 | 1 | |
| Ground clearance > 15 cm | 14 | 3 | 9 | 3 | 9 | 3 | 1 | 3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Load carrying capacity ≥ 0.5 kg | 15 | 5 | 3 | 3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 3 | 3 | 3 | |
Yj = 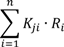 | 218 | 174 | 242 | 126 | 120 | 294 | 122 | 174 | 150 | 126 | 200 | 104 | 292 | 95 | 87 | 87 | ||
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chàvez-Clemente, D. Gait Optimization for Multi-legged Walking Robots, with Application to a Lunar Hexapod. Ph.D. Thesis, Stanford University, California, CA, USA, 2011. [Google Scholar]
- Carbone, G.; Ceccarelli, M. Legged robotic systems. In Cutting Edge Robotics; Kordic, V., Lazinica, A., Merdan, M., Eds.; InTech: Vienna, Austria, 2005; pp. 553–576. [Google Scholar]
- Cigola, M.; Pelliccio, A.; Salotto, O.; Carbone, G.; Ottaviano, E.; Ceccarelli, M. Application of robots for inspection and restoration of historical sites. In Proceedings of the International Symposium on Automation and Robotics in Construction of the Conference, Ferrara, Italy, 11–14 September 2005; p. 37.
- Jun, B.H.; Shim, H.; Kim, B.; Park, J.Y.; Baek, H.; Yoo, S.; Lee, P.M. Development of seabed walking robot CR200. In Proceedings of the OCEANS’13 MTS/IEEE of the Conference, San Diego, CA, USA, 23–26 September 2013; pp. 1–5.
- Georgiades, C. Simulation and Control of an Underwater Hexapod Robot. M.D. Thesis, McGill University, Montreal, QC, Canada, 2005. [Google Scholar]
- Bares, J.; Hebert, M.; Kanade, T.; Krotkov, E.; Mitchell, T.; Simmons, R.; Whittaker, W. Ambler: An autonomous rover for planetary exploration. IEEE Comput. 1989, 26, 6–18. [Google Scholar]
- Preumont, A.; Alexandre, P.; Doroftei, I.; Goffin, F. A conceptual walking vehicle for planetary exploration. Mechatronics 1997, 7, 287–296. [Google Scholar]
- Bartholet, T.; Crawson, R. Robot Applications for Nuclear Power Plant Maintenance; EPRI Report-NP-3941, Research Report Center: Palo Alto, CA, USA, 1985. [Google Scholar]
- Oku, M.; Yang, H.; Paio, G.; Harada, Y.; Adachi, K.; Barai, R.; Nonami, K. Development of hydraulically actuated hexapod robot COMET-IV-The 1st report: System design and configuration. In Proceedings of the 2007 JSME Conference on Robotics and Mechatronics, Akita, Japan, 26–28 May 2007.
- Gregorio, P.; Ahmadi, M.; Buehler, M. Design, control, and energetics of an electrically actuated legged robot. Syst. Man Cybern. B IEEE Trans. 1997, 27, 626–634. [Google Scholar] [CrossRef]
- Schneider, A.; Schmucker, U. Force sensing for multi-legged walking robots: Theory and experiments part 1: Overview and force sensing. In Mobile Robotics, Moving Intelligence; Buchli, J., Ed.; Pro Literatur Verlag ARS: Germany; Austria, 2006; pp. 125–174. [Google Scholar]
- Peternella, M.; Salinari, S. Simulation by digital computer of walking machine control system. In Proceedings of the 5th IFAC Symposium on Automatic Control in Space of the Conference, Genova, Italy, June 1973.
- Okhotsimski, D.; Platonov, A. Control algorithm of the walking climbing over obstacles. In Proceedings of the 3rd International Joint Conference on Artificial Intelligence, Stanford, CA, USA, 20 August 1973.
- Gurfinkel, V.; Gurfinkel, E.; Devjanin, E.; Efremov, E.; Zhicharev, D.; Lensky, A.; Schneider, A.; Shtilman, L. Investigation of robotics. In Six-legged Walking Model of Vehicle with Supervisory Control; Nauka Press: Moscow, Russia, 1982; pp. 98–147. [Google Scholar]
- McGhee, R. Control of legged locomotion systems. In Proceedings of the 18th Automatic Control Conference, San Francisco, CA, USA, 3–8 December 1977; pp. 205–215.
- Raibert, M. Legged Robots that Balance; MIT Press: Cambridge, London, 1986; pp. 180–201. [Google Scholar]
- Byrd, J.; de Vries, K. A six-legged telerobot for nuclear applications development. Int. J. Robot. Res. 1990, 9, 43–52. [Google Scholar] [CrossRef]
- Efimov, V.; Kudriasev, M.; Titov, A. Investigation of robotics systems. In A Physical Similar of Motion Walking Apparatus; Nauka Press: Moscow, Russia, 1982; pp. 86–91. [Google Scholar]
- Song, S.M.; Waldron, K. Machines that Walk: The Adaptive Suspension Vehicle; MIT Press: Cambridge, London, 1989; pp. 283–299. [Google Scholar]
- Akozono, J.; Iwasaki, M.; Asakura, O. Development on a walking robot for underwater inspection. In Proceedings of the International Conference on Arabidopsis Research (ICAR’ 89), Columbus, OH, USA, 13–15 June 1989.
- Brooks, R.A. A robot that walks; emergent behaviors from a carefully evolved network. Neural Comput. 1989, 1, 253–262. [Google Scholar] [CrossRef]
- Bares, J.; Hebert, M.; Kande, T.; Krotkov, E.; Mitchell, T.; Simmons, R.; Whittaker, W. Ambler: An autonomous rover for planetary exploration. IEEE Comput. 1989, 22, 18–26. [Google Scholar] [CrossRef]
- Angle, C.A.; Brooks, R.A. Small planetary rovers. In Proceedings of the IEEE International Workshop on Intelligent Robots and Systems, Ibaraki, Japan, 3–6 July 1990; pp. 1–5.
- Pfeiffer, F.; Eltze, J.; Weidermann, H. Six-legged technical walking considering biological principles. Robot. Autom. 1995, 14, 223–232. [Google Scholar] [CrossRef]
- Nelson, G.M.; Quinn, R.D.; Bachmann, R.J.; Flannigan, W.C.; Ritzmann, R.E.; Watson, J.T. Design and simulation of a cockroach-like hexapod robot. In Proceedings of the 1997 IEEE International Conference on Robotics and Automation, Albuquerque, NM, USA, 25 April 1997; pp. 1106–1111.
- Delcomyn, F.; Nelson, M.E. Architectures for a biomimetic hexapod robot. Robot. Auton. Syst. 2000, 30, 5–15. [Google Scholar] [CrossRef]
- Fielding, M.R.; Dunlop, R.; Damaren, C.J. Hamlet: Force/Position controlled hexapod walker—Design and systems. In Proceedings of the IEEE Conference on Control Applications, Mexico City, Mexico, 5–9 September 2001; pp. 984–989.
- Saranli, U.; Buehler, M.; Koditschek, D.E. RHex—A simple and highly mobile hexapod robot. Int. J. Robot. Res. 2001, 20, 616–631. [Google Scholar] [CrossRef]
- Roennau, A.; Heppner, G.; Pfozter, L.; Dillman, R. Lauron V: Optimized leg configuration for the design of a bio-inspired walking robot. In Proceedings of the 16th International Conference on Climbing and Walking Robots and the Support Technologies for Mobile Machines, Sydney, Australia, 14–17 July 2013; pp. 563–571.
- Arena, P.; Fortuna, L.; Frasca, M.; Patanè, L.; Pavone, M. Implementation and experimental validation of an autonomous hexapod robot. In Proceedings of the IEEE International Symposium on Circuits and Systems, Kos, Greece, 21–24 May 2006.
- Cham, J.G.; Bailey, S.A.; Clark, J.E.; Full, R.J.; CutKosky, M.R. Fast and robust: Hexapedal robots via shape deposition manufacturing. Int. J. Robot. Res. 2002, 21, 869–882. [Google Scholar] [CrossRef]
- Lewinger, W.A.; Branicky, M.S.; Quinn, R.D. Insect-inspired, actively compliant hexapod capable of object manipulation. In Proceedings of the 8th International Conference on Climbing and Walking Robots (CLAWAR’ 2005), London, UK, 13–15 September 2005; pp. 65–72.
- Kennedy, B.; Okon, A.; Aghazarian, H.; Garrett, M.; Huntsberger, T.; Magnone, L.; Robinson, M.; Townsend, J. The lemur II-Class robots for inspection and maintenance of orbital structures: A system description. In Proceedings of the 8th International Conference on Climbing and Walking Robots (CLAWAR’ 2005), London, UK, 13–15 September 2005; pp. 1069–1076.
- Showalter, M. Hexapod Work Space and Walking Algorithm; VDM Verlag: Saarbrücken, Germany, 2009; pp. 20–34. [Google Scholar]
- Hauser, T.; Bretl, K.; Latombe, J.C.; Harada, W. Motion planning for legged robots on varied terrain. Int. J. Robot. Res. 2008, 27, 1325. [Google Scholar] [CrossRef]
- Georgiadis, C.; German, A.; Hogue, A.; Liu, H.; Prahacs, C.; Ripsman, A.; Sim, R.; Torres, L.A.; Zhang, P.; Buehler, M.; Dudek, G.; Jenkin, M.; Milios, E. AQUA: An aquatic walking robot. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Sendai, Japan, 28 September–2 October, 2004.
- Kang, H.; Shim, H.; Jun, B.H.; Lee, P.M. Design of underwater link and joint for the development of multi-legged underwater robot CR200. In Proceedings of the MTS/IEEE OCEANS 2012, Yeosu, Korea, 21–24 May 2012; pp. 1–6.
- Asbeck, A.T.; Kim, S.; McClung, A.; Parness, A.; Cutkosky, M.R. Climbing walls with microspines. In Proceedings of the IEEE International Conference Robotics and Automation, Orlando, FL, USA, 15–19 May 2006.
- Nonami, K.; Huang, Q.J. Humanitarian mine detection six-legged walking robot COMET-II with two manipulators. In Proceedings of the 4th International Conference on Climbing and Walking Robots (CLAWAR’ 2001), Karlsruhe, Germany, 24–26 September 2001; pp. 989–996.
- Mantis homepage. Available online: http://www.mantisrobot.com (accessed on 24 March 2014).
- Genta, G. Introduction to the Mechanics of Space Robots; Springer: Berlin, Germany, 2012; pp. 381–423. [Google Scholar]
- Song, S.M.; Choi, B.S. The optimally stable ranges of 2n-Legged wave gaits. IEEE Trans. Syst. Man Cybern. B 1990, 20, 888–902. [Google Scholar] [CrossRef]
- Alexander, R. McN. Exploring Biomechanics—Animals in Motion; W.H. Freeman Press: New York, NY, USA, 1992. [Google Scholar]
- Alexander, R. McN. The gait of bipedal and quadrupedal animals. Int. J. Robot. Res. 1984, 3, 49–59. [Google Scholar] [CrossRef]
- Gabrielli, G.; von Karman, T. What price speed—Specific power required for propulsion of vehicles. Mech. Eng. 1950, 72, 775–781. [Google Scholar]
- McGhee, R.B.; Frank, A.A. On the stability properties of quadruped creeping gaits. Math. Biosci. 1968, 3, 331–351. [Google Scholar] [CrossRef]
- Messuri, D.A.; Klein, C.A. Automatic body regulation for maintaining stability of a legged vehicle during rough-terrain locomotion. IEEE J. Robot. Autom. 1985, 1, 132–141. [Google Scholar] [CrossRef]
- Zielinska, T. Autonomous walking machines, discussion of the prototyping problems. Bulletin of the Polish academy of sciences. Tech. Sci. 2010, 58, 443–451. [Google Scholar]
- Rashid, M.Z.A.; Aras, M.S.M.; Radzak, A.A.; Kassim, A.M.; Jamali, A. Development of hexapod robot with manoeuvrable wheel. Int. J. Adv. Sci. Tech. 2012, 49, 119–136. [Google Scholar]
- Ding, X.; Wang, Z.; Rovetta, A.; Zhu, J.M. Locomotion analysis of hexapod robot. In Climbing and Walking Robots; In Tech: Rijeka, Croatia, 2010; pp. 291–310. [Google Scholar]
- Lee, T.T.; Liao, C.M.; Chen, T.K. On the stability properties of hexapod tripod gait. IEEE J. Robot. Autom. 1988, 4, 427–434. [Google Scholar] [CrossRef]
- Waldron, K.J.; McGhee, R.B. The adaptive suspension vehicle. IEEE Control Syst. Mag. 1986, 6, 7–12. [Google Scholar] [CrossRef]
- Wang, X.J. A Study of Locomotion and Force Planning for Multilegged Walking Robots. Ph.D. Thesis, Huazhong University of Science & Technology, Wuhan, China, 2005; pp. 95–100. [Google Scholar]
- Preumont, A.; Alexadre, P.; Ghuys, D. Gait analysis and implementation of a six leg walking machine. In Proceedings of the Fifth International Conference on Advanced Robotics. Robots in Unstructured Environments (ICAR’ 91), Pisa, Italy, 19–22 June 1991; Volume 2, pp. 941–945.
- Takahashi, Y.; Arai, T. Development of multi-limb robot with omnidirectional manipulability and mobility. In Proceedings of the 2000 IEEE-RSJ International Conference on Intelligent Robots and Systems, Takamatsu, Japan, 31 October–5 November 2000; Volume 3, pp. 2012–2017.
- Chu, S.K.-K.; Pang, G.K.-H. Comparison between different models of hexapod robot in fault-tolerant gait. IEEE Trans. Syst. Man Cybern. 2002, 32, 752–756. [Google Scholar] [CrossRef]
- Silva, M.F.; Tenreiro Machado, J.A. A historical perspective of legged robots. J. Vib. Control 2007, 13, 1447–1486. [Google Scholar] [CrossRef]
- Billah, M.M.; Ahmed, M.; Farhana, S. Walking hexapod robot in disaster recovery developing algorithm for terrain negotiation and navigation. In New Advanced Technologies; Lazinica, A., Ed.; In Tech: Rijeka, Croatia, 2010. [Google Scholar]
- Nava Rodríguez, N.E.; Carbone, G.; Ceccarelli, M.; Moreno Lorente, L.E. Design evolution of cassino hexapod robot. In Proceedings of the 10th Biennial ASME Conference on Engineering Systems Design and Analysis ESDA2010, Istanbul, Turkey, 12–14 July 2010.
- Endo, G.; Hirose, S. Study on Roller-Walker: System integration and basic experiments. Robot. Autom. 1999, 3, 2032–2037. [Google Scholar] [CrossRef]
- Nonami, K.; Barai, R.K.; Irawan, A.; Daud, M.R. Hydraulically Actuated Hexapod Robots; Springer: London, UK, 2014; pp. 78–104. [Google Scholar]
- Conrad, J.M.; Mills, J.W. The history and future of stiquito: A hexapod insectoid robot. In Artificial Life Models in Hardware; Springer: London, UK, 2009; pp. 1–20. [Google Scholar]
- Rahnejat, H. Multi-body dynamics: Historical evolution and application. J. Mech. Eng. Sci. 2000, 214, 149–173. [Google Scholar] [CrossRef]
- Salmi, S.; Halme, A. Implementing and testing a reasoning-based free gait algorithm in the six-legged walking machine MECANT. Control Eng. Pract. 1996, 4, 487–492. [Google Scholar] [CrossRef]
- Silva, M.F.; Tenreiro Machado, J.A. A Kinematic and dynamic performance analysis of artificial legged systems. Robotica 2008, 26, 19–39. [Google Scholar]
- De Santos, P.G.; Garcia, E.; Ponticelli, R.; Armada, M. Minimizing energy consumption in hexapod robots. Adv. Robot. 2009, 23, 681–704. [Google Scholar] [CrossRef]
- Grace, A. Optimization Toolbox User’s Guide; The MatlabWorks Inc.: Denver, CO, USA, 1992. [Google Scholar]
- Vanderplaats, G. Numerical Optimization Techniques for Engineers Design; McGraw-Hill: NewYork, NY, USA, 1984. [Google Scholar]
- Eldar, Y.C. Minimax estimation of deterministic parameters in linear models with a random model matrix. IEEE Trans. Signal Process. 2006, 54, 601–612. [Google Scholar] [CrossRef]
- Medanic, J.; Andjelic, M. Minimax solution of the multiple-target problem. IEEE Trans. Autom. Control 1972, 17, 597–604. [Google Scholar] [CrossRef]
- Franklin, G.F. Feedback Control of Dynamic Systems; Addison-Wesley Longman Publishing Co.: Boston, MA, USA, 2002. [Google Scholar]
- Collins, J.J.; Stewart, I. Hexapodal gaits and coupled nonlinear oscillator models. Biol. Cybern. 1993, 68, 287–298. [Google Scholar] [CrossRef]
- Song, S.M.; Waldron, K.J. An analytical approach for gait study and its applications on wave gaits. Int. J. Robot. Res. 1987, 6, 60–71. [Google Scholar] [CrossRef]
- Ferrell, C. Robust Agent Control of an Autonomous Robot with Many Sensors and Actuators; MIT AI Lab: Cambridge, MA, USA, Technical Report 1443; 1993; pp. 1–100. [Google Scholar]
- McGhee, R.B.; Iswandhi, G.I. Adaptive locomotion of a multilegged robot over rouch terrain. IEEE Trans. Syst. Man Cybern. 1979, 9, 176–182. [Google Scholar] [CrossRef]
- Shih, T.; Tsai, C.S.; Her, I. Comparison of alternative gaits for multiped robots with severed legs. Int. J. Adv. Robot. Syst. 2012, 9, 1–8. [Google Scholar]
- Silva, M.F.; Tenreiro Machado, J.A.; Lopes, A.M. Quasi-periodic Gaits in Multi-legged Robots. In Proceedings of the 5th International Conference on Climbing and Walking Robots and the Support Technologies for Mobile Machines (CLAWAR’ 2002), Paris, France, 25–27 September 2002; pp. 733–740.
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley Longman Publishing Co.: Upper Saddle River, NJ, USA, 1989; pp. 110–130. [Google Scholar]
- Kosko, B. Neural Networks and Fuzzy Systems: A Dynamical Systems Approach to Machine Intelligence; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1992; pp. 179–193. [Google Scholar]
- Gonzalez de Santos, P.; Garcia, E.; Estremera, J. Quadrupedal Locomotion: An Introduction to the Control of Four-Legged Robots; Springer: London, UK, 2006. [Google Scholar]
- Carbone, G.; Ceccarelli, M. A mechanical design of a low-cost easy-operation anthropomorphic wheeled leg for walking machines. Int. J. Robot. Manag. 2004, 9, 3–8. [Google Scholar]
- Carbone, G.; Shrot, A.; Ceccarelli, M. Operation strategy for a low-cost easy-operation cassino hexapod. Appl. Bionics Biomech. 2007, 4, 149–156. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tedeschi, F.; Carbone, G. Design Issues for Hexapod Walking Robots. Robotics 2014, 3, 181-206. https://doi.org/10.3390/robotics3020181
Tedeschi F, Carbone G. Design Issues for Hexapod Walking Robots. Robotics. 2014; 3(2):181-206. https://doi.org/10.3390/robotics3020181
Chicago/Turabian StyleTedeschi, Franco, and Giuseppe Carbone. 2014. "Design Issues for Hexapod Walking Robots" Robotics 3, no. 2: 181-206. https://doi.org/10.3390/robotics3020181
APA StyleTedeschi, F., & Carbone, G. (2014). Design Issues for Hexapod Walking Robots. Robotics, 3(2), 181-206. https://doi.org/10.3390/robotics3020181