Preliminary Design and Testing of Brush.Q: An Articulated Ground Mobile Robot with Compliant Brush-like Wheels

Abstract

Recent advances in mobile robotics have emphasized the need for systems capable of operating in unstructured environments, combining obstacle negotiation, stability, and adaptability. This study presents the preliminary design and testing of Brush.Q, an articulated ground robot featuring a novel structure distinct from existing wheel-legged robots, equipped with compliant brush-like wheels composed of multiple spokes. The main contribution is the experimental analysis of suspension capability across different wheel geometric profiles, combined with the assessment of obstacle-climbing performance. A simplified prototype was constructed to evaluate the effects of wheel rotation direction, spoke number, and spoke tapering. Results show that reducing the number of spokes improves obstacle-climbing at the expense of suspension, while higher spoke count and compliant geometry enhance suspension and stability. Spoke tapering improves obstacle climbing in the backward-facing configuration but consistently reduces suspension. Overall, these findings highlight the critical role of wheel geometry and the potential for reconfigurable spoked wheels to enhance adaptability and versatility in unstructured terrains.

1. Introduction

In recent years, mobile robotics has advanced rapidly, driven by the demand for autonomous systems able to operate in complex and unstructured environments. Applications such as infrastructure inspection, surveillance, and search and rescue require robots capable of traversing uneven terrains while navigating obstacles and maintaining stability on irregular surfaces [1]. Traditional locomotion approaches include wheels, legs, and tracks and each present trade-offs as follows: wheeled robots offer energy efficiency and mechanical simplicity but struggle with vertical obstacles; legged robots deliver superior adaptability but at the cost of increased complexity and energy consumption; tracked robots provide enhanced stability but often suffer from reduced maneuverability in confined spaces. To address these challenges, hybrid locomotion systems that combine different modalities have emerged. Among these, wheel-legged robots are particularly promising; they integrate wheel-like motion with leg mechanisms for enhanced obstacle negotiation. One reference design for this family of robots is RHex [2], a compliant legged hexapod robot known for its robust, highly mobile locomotion across rugged terrain using full-rotation leg spokes. Within wheel-legged robotics, designs fall into the following two main categories [3]: non-transformable wheels, which maintain fixed geometry, and transformable wheel, which can reconfigure their structure depending on the terrain. Transformable wheel-legged robots, such as the OmniWheg [4], FUHAR [5], and TurboQuad [6], allow the active adjustment of wheel-leg geometry to overcome obstacles. However, they often come at the cost of added mechanical complexity, weight, and control demands. In contrast, non-transformable wheel-leg designs can retain simplicity and reliability while also taking advantage of passive compliance. One example is Whegs [7], which stands for Wheel-Legs, representing a non-transformable wheel-leg hexapod robot inspired by cockroaches gait. The system features multiple compliant spokes that function as both propulsion and suspension elements, enabling adaptability to irregular terrain. Stability is a critical aspect for wheel-legged robots, as they must balance rolling dynamics with legged support to maintain robust contact and posture over uneven surfaces. Recent studies have explored rolling-based locomotion for wheeled quadrupeds using centroidal dynamics [8] and horizontal stability control frameworks [9], showing how integrated whole-body motion planning, compliance, and terrain-adaptive control can improve stability and adaptability on rough, unknown terrain. Some wheel-legged robots also feature articulated body structures; for instance, certain designs use a body flexion joint to improve stability and obstacle-climbing capabilities [10]. However, such joints typically do not provide significant gains in maneuverability. A notable example is the Advanced Security Guard (ASGUARD) [11], which integrates a passive compliant spine to boost traction on uneven terrain but does not deliver enhanced agility. More recent locomotion strategies enhance adaptability to an unstructured environment with an articulated or continuum body structure such as the FRESE robot family [12]. Lizard [13] features a cable-driven origami flexible spine to improve turning and obstacle-climbing capabilities. Ai et al. [14] presented a soft robot with a pneumatically actuated flexible body and wheel-legs, capable of moving across diverse terrains and climbing steps.

Table 1. Comparison of wheel and structure characteristics of various wheel-legged robots.

Robot	Wheel Type	Wheel Structure	Body Structure
RHex [2]	Non-trasformable	C-shaped single leg	Rigid
OmniWheg [4]	Trasformable	4-lobe	Rigid
FUHAR [5]	Trasformable	6-lobe	Rigid
TurboQuad [6]	Trasformable	2-lobe	Rigid
Whegs I [7]	Non-trasformable	Straight-curved 3-spoke	Rigid
Whegs II [10]	Non-trasformable	Straight-curved 3-spoke	Articulated
ASGUARD [11]	Non-trasformable	Straigth 5-spoke	Articulated
FRESE I [12]	Non-trasformable	5-spoke	Articulated
FRESE II [12]	Non-trasformable	5-spoke	Continuum
FRESE III [12]	Non-trasformable	5-spoke	Articulated
FRESE IV [12]	Non-trasformable	5-spoke	Continuum
Lizard [13]	Non-trasformable	Curved 3-spoke	Continuum
Crawling soft robot [14]	Non-trasformable	8-spoke	Continuum
Wheel-legged Mobile Robot [15]	Non-trasformable	Straight-curved 3-spoke	Articulated

summarizes the state-of-the-art references discussed, providing a more comprehensive comparison of their wheel and body structure characteristics. The wheel type concerns the capability that allows the active adjustment of the wheel–leg geometry, and it distinguishes wheels into transformable and non-transformable. The wheel structure classifies the wheel according to its topology, specifically based on the number and the shape of the components that constitute it [3]. The term leg is used when the wheel either has, or acquires through transformation, the typical shape of a single leg rotating about the wheel center. The term lobe applies only to transformable wheels, as in this case, the outermost wheel circle is split into different segments through a rotational motion of the individual parts. The term spoke is used when the wheel is composed of elements that protrude radially from the wheel’s center. Regarding the structure of the robot body, it is defined as rigid when the robot consists of a single module, articulated when it is composed of multiple rigid modules connected through discrete joints, and continuum when it consists of a flexible body capable of continuous deformation.

Wheel-legged robots offer a promising solution for mobility over unstructured terrain. Research to date has primarily focused on the experimental evaluation of their obstacle-climbing capabilities, a key requirement for navigating such environments. This ability refers to the robot’s capacity to overcome obstacles taller than its wheel radius. While the wheel radius represents the theoretical geometric maximum height for a conventional wheel, in practice, the maximum height for vertical steps may be slightly lower due to contact and traction constraints. Li et al. [15] proposed a mathematical model to assess the obstacle-climbing performance of multi-spoked wheel geometries, also highlighting the influence of wheel rotation direction.

In addition to obstacle climbing, suspension capability is critical for mobility on unstructured terrain, allowing the robot to absorb irregularities and maintain wheel-ground contact. Maintaining contact ensures stability and traction. At the same time, oscillations and shocks transmitted to the chassis can affect structural integrity and component durability.

To our knowledge, no studies have compared different wheel geometries in wheel-legged robots with respect to suspension performance. This work experimentally analyzes high-frequency vibrations resulting from wheel interaction with terrain obstacles lower than the wheel radius, while also assessing obstacle-climbing performance for a comprehensive comparison of wheel designs. A prototype was constructed and tested to evaluate the obstacle-climbing and suspension capabilities of various wheels. This framework provides guidance for selecting wheels for generic wheel-legged robots operating on unstructured terrain.

The analysis also forms the basis for wheel selection for the articulated ground mobile robot proposed in this study, Brush.Q, which is equipped with compliant brush-like wheels composed of multiple spokes and featuring a novel structure, different from existing wheel-legged robot configurations. The preliminary design of Brush.Q is presented.

The main contributions of this work are twofold as follows:

• Functional design of Brush.Q: A novel articulated wheel-legged robot equipped with compliant brush-like wheels, featuring a compact modular architecture that minimizes chassis exposure to obstacles and enhances adaptability to unstructured terrain.
• Systematic experimental analysis of wheel suspension: Evaluation of different wheel geometries through prototype testing to characterize high-frequency vibrations and assess suspension performance. Obstacle-climbing capabilities are also measured, but the core innovation lies in quantifying and understanding wheel suspension behavior, providing a basis for future wheel selection in wheel-legged robots.

The paper is organized as follows: Section 2, Materials and Methods, describes the preliminary design of Brush.Q, its structure, and the different types of brush-like wheels, as well as the prototype and the evaluation procedure used for obstacle-climbing and suspension analysis; Section 3, Results and Discussion, presents and analyzes the experimental findings; and Section 4 details the conclusions and outlines future work.

2. Materials and Methods

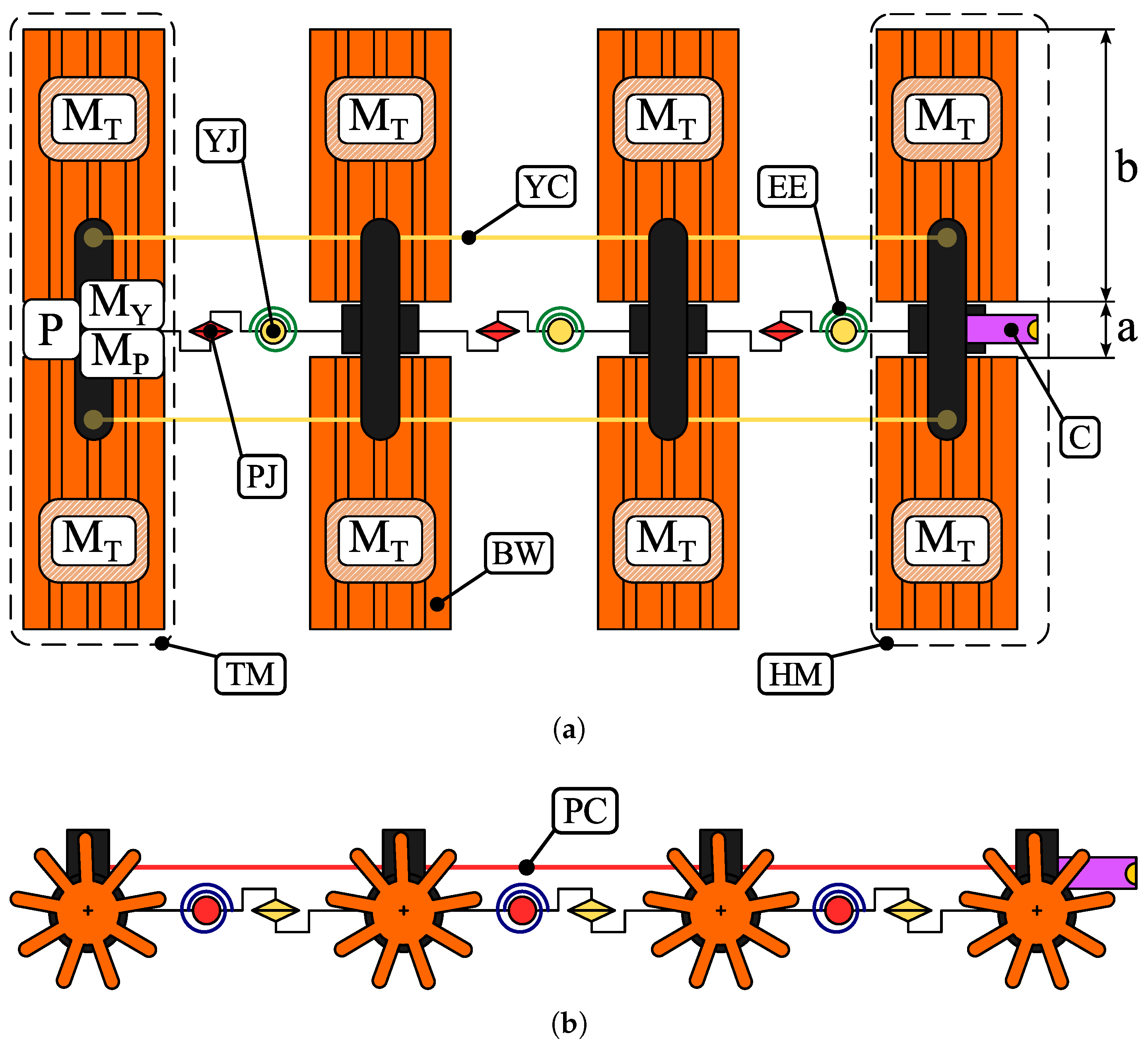
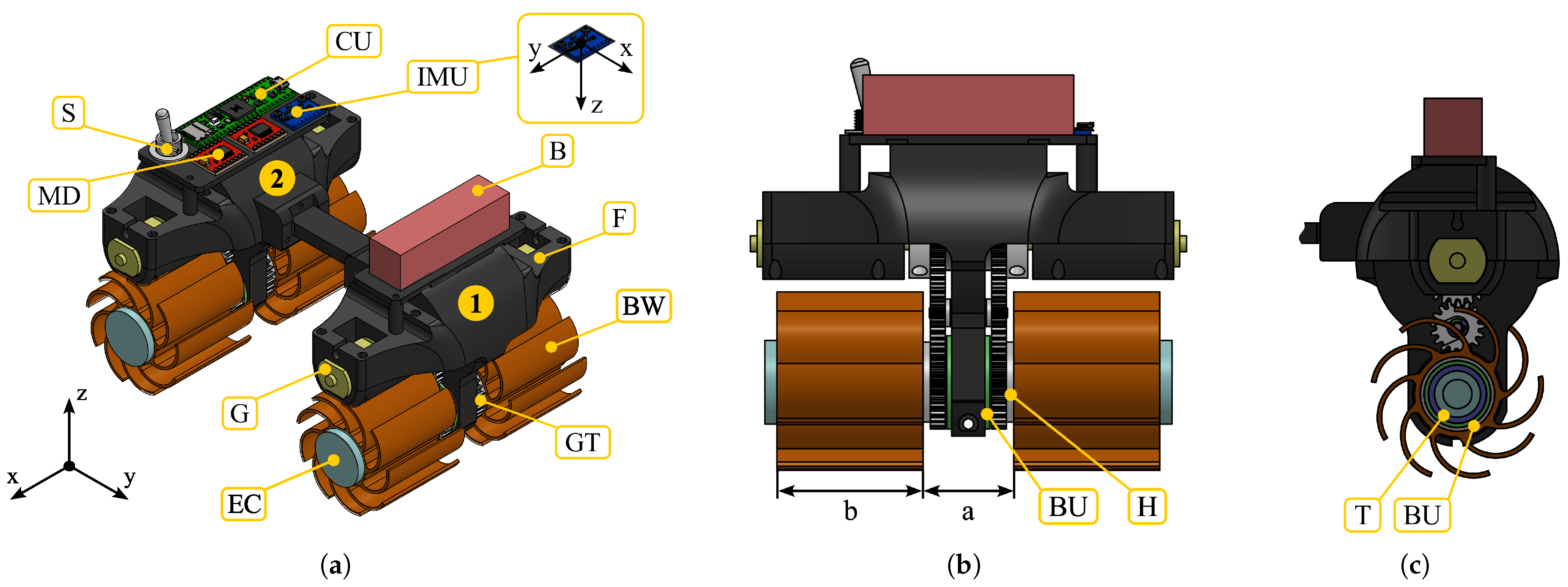
2.1. Functional Design: Mechanical Architecture

Wheel-legged robots are typically based on an architecture consisting of a central body with wheels mounted on either side. The robot body is typically enclosed, pseudo-rectangular in shape, and houses the motors, transmission system, electronics, sensors, and battery. Moreover, its front and rear faces usually feature a semicircular geometry, allowing the robot to overcome discontinuities encountered between the two wheels. This configuration offers the advantages of protecting the internal components and allowing the robot to perform self-righting maneuvers. However, despite certain geometric precautions, there remains the possibility that centrally located obstacles obstruct robot motion. In the proposed design, each wheel occupies the majority of the robot’s track width, thereby minimizing the exposure of the central chassis. As a result, obstacles encountered along the midline are more likely to be engaged by the wheels rather than impacting the body, reducing the risk of immobilization. This design choice therefore enhances obstacle-crossing capability and reduces failure cases associated with chassis–ground interference. Figure 1 illustrates the functional design of Brush.Q, a mobile robot equipped with brush-like compliant wheels and a flexible articulated structure to improve mobility and adaptability to complex and unstructured environments. The brush-like wheels (BW) consist of multiple spokes that exhibit passive compliance due to their geometric profile. These characteristics enhance the robot’s ability to adapt to uneven terrain and to overcome obstacles. Each brush wheel is driven by an integrated actuator (M_T), without the need for external transmission components, resulting in architecture more reliable, efficient and compact. The wheels have a transverse footprint, indicated as b in the Figure, which is significantly larger than the chassis width, indicated as a. The articulated structure connects the four modules of the robot, each equipped with two wheels, through a series of yaw (YJ) and pitch (PJ) joints, equipped with elastic elements (EE), which improve mobility and obstacle negotiation capabilities. Elastic elements can be understood as a pair of tension or compression springs symmetrically positioned with respect to the robot’s longitudinal axis, or as a torsional spring located along the joint axis. The structure is underactuated and controlled by two actuators via a cable-driven system. The cables are anchored to the head (HM) and tail (TM) modules of the robot. The actuator (M_Y) controls the yaw joints via a pair of cables (YC), enabling steering, while the pitch actuator (M_P) controls the pitch joints (PJ) via the lift cable (PC) to raise the robot off the ground. The tail module also carries the payload (P), including the battery and onboard electronics, so that it remains grounded while the robot is lifted. The head module houses the vision system (C), which supports the execution of the robot’s tasks.

Compared to existing wheel-legged robots, Brush.Q introduces several key innovations. Its brush-like wheels, composed of multiple flexible C-shaped spokes, are inspired by the semicircular legs of RHex, providing passive compliance that adapts to uneven terrain and reduces chassis oscillations. In contrast, Whegs uses fewer fixed compliant spokes, limiting passive suspension and the ability to overcome obstacles. Transformable wheel robots such as OmniWheg, FUHAR, and TurboQuad actively adjust wheel-leg geometry via articulated lobes, increasing mechanical complexity and control requirements. Robots with articulated or continuum body structures, such as ASGUARD, FRESE, Lizard, and Crawling soft robot, further enhance terrain adaptability, often at the cost of increased mechanical complexity and control requirements. Brush.Q integrates its flexible wheels into a compact articulated chassis, where the wheels occupy most of the track width, minimizing central chassis exposure to obstacles. By combining passive compliance, modularity, and a simple mechanical architecture, Brush.Q provides a balance between adaptability and construction simplicity, distinguishing it from previous wheel-legged robots in both structural design and functional approach.

2.2. Brush-like Wheels

Brush-like wheels represent the primary element of adaptability of Brush.Q to unstructured environments, even more so than its articulated structure. They consist of multiple spokes evenly distributed around the rotation axis. The number of spokes directly influences ride smoothness as follows: reducing the number of spokes increases vertical hub oscillations during transitions between spokes, whereas a larger number of spokes distributes contact with the terrain more evenly, improving stability [7]. In addition, spoke geometry and radial thickness affect both obstacle-climbing and suspension capabilities, the latter being defined as the ability to reduce chassis oscillations in the presence of terrain irregularities.

The wheel design is inspired by RHex, whose semicircular legs with a constant radius of curvature $\rho$ provide passive compliance essential for adaptation to uneven terrain and for reducing chassis oscillations, as seen in Figure 2a. However, single-spoke designs have the following limitations: locomotion on flat surfaces can be less smooth, and vertical hub oscillations increase stress on components, reducing ride smoothness.

Both spoke shape and number strongly influence obstacle-climbing performance. Modeling studies in the literature [15] investigated spokes derived from the basic semicircular leg geometry, showing that certain profiles introduce a preferential direction for obstacle crossing, while reducing the number of spokes increases the maximum obstacle height that can be overcome. Although the analyzed leg geometry is not exactly C-shaped, the results indicate that both spoke shape and spoke count are key factors affecting locomotor capability.

RHex mitigates vertical oscillation effects through a tripod gait, in which at least three legs remain in contact with the ground at all times, ensuring static and dynamic stability, continuous traction, and uniform load distribution even on irregular terrain. Similar strategies are employed in Whegs, where tripod gait helps stabilize movement despite a reduced number of simultaneously active legs. In general, spoke compliance can further attenuate vertical hub motion.

In this study, the analysis is extended to an innovative brush-like wheel with a high number of semicircular spokes inspired by RHex legs, whose geometry also functions as an integrated suspension. The following three variants are compared: a wheel with nine spokes, Figure 2b; a wheel with three spokes, Figure 2c; and a wheel with three tapered spokes, Figure 2d, to evaluate both obstacle-climbing and suspension capabilities. The key geometric parameters of interest, which will be reported for the prototype, are outlined as follows: radius of curvature of the spoke $\rho$; hub radius r; outer wheel radius R; spoke thickness s; $\theta$, defined as the angular separation between spokes; and $\gamma$, defined as the central angle between the attachment points of the tapered blades on the hub. For the tapered blade, s varies along its length and depends on $\alpha$, the angle between the line from the wheel center to the blade tip and the point on the blade being considered. Notably, the hub has a non-reduced diameter such as RHex and equal to r, allowing the integration of the motor within the wheel and enabling a compact design in which the wheels occupy the majority of the robot’s track width.

2.3. Prototyping

Given that the focus of this paper is the wheel subsystem of Brush.Q, a simplified prototype was constructed to assess the obstacle-climbing and suspension performance of the various wheel designs. The schematic design of the prototype is shown in Figure 3. The prototype measures 204 mm in length (along the y-axis), 135 mm in width (along the x-axis), and 137 mm in height (along the z-axis).

The prototype consists of two modules rigidly connected to each other, each equipped with two brush wheels (BW). Each of the four wheels is actuated by its own gearmotor (G) as follows: a 163-RPM Mini Econ Gear Motor for the wheels of the head module (1), and an 81-RPM Mini Econ Gear Motor for those of the tail module (2), with the specified values corresponding to the no-load speed of the respective gearmotors. The wheels are driven by the gear motors through a two-stage spur gear transmission (GT) with a unit transmission ratio, chosen to preserve the output torque of the gear motor while avoiding excessive radial encumbrance of the gears. Each wheel is mounted via an interference fit onto its hub (H), which is manufactured as a single part with the spur gear which is coaxial with the wheel. The hub rotates freely with respect to an aluminum tube (T), clamped to the robot frame (F), thanks to a pair of plain bearings (BU). The axial positioning of the wheel is ensured by an end cap (EC), inserted into the tube through an interference fit. The wheels have a transverse width, 2b, of 98 mm and an inter-wheel spacing, a, of 30 mm, which corresponds to 76% of the total track width of the robot (2b + a). The battery (B), rated at 12 V, is located on the head module. The tail module hosts the following robot control electronics: the switch (S) required to power the robot, the microcontroller unit (CU, Teensy 4.1) that controls the two dual-motor drivers (MD, TB6612FNG) regulating the input power to the gearmotors, and the inertial measurement unit (IMU, GY-521) used to measure the robot’s linear accelerations and angular velocities. The IMU includes a 3-axis accelerometer and a 3-axis gyroscope, with typical noise levels of approximately $400\mathsf{\mu }\mathrm{g}/\sqrt{\mathrm{Hz}}$ for the accelerometer and ${0.005}^{\circ }/\mathrm{s}/\sqrt{\mathrm{Hz}}$ for the gyroscope. Its sampling frequency is around 1 kHz with a stability of $\pm 1\%$. The reference frame used for evaluating vertical acceleration is also indicated for the IMU. The robot frame, the gears, and the end caps were 3D-printed in Tough PolyLactic Acid (Tough PLA), while the brush wheels were fabricated in Thermoplastic Polyurethane (TPU) 82A (shore hardness 82A, tensile strength 40 MPa, and elongation at break 650%), providing high flexibility and shock absorption. Figure 4 shows the four types of wheels that were manufactured, outlined as follows: the circular wheel, chosen as the reference conventional wheel; the nine-spoke wheel; the three-spoke wheel; and the tapered three-spoke wheel. All wheels have an outer radius $R=60$ mm. The spoked wheels share a common hub radius $r=30$ mm. The nine-spoke ($\theta =40$°) and three-spoke ($\theta =120$°) wheels feature the same spoke thickness $s=1.5$ mm, whereas the tapered three-spoke version is manufactured with a tapering angle ($\gamma =40$°). Wheel replacement does not require disassembling the entire axle as the wheels can be easily slid off the hub.

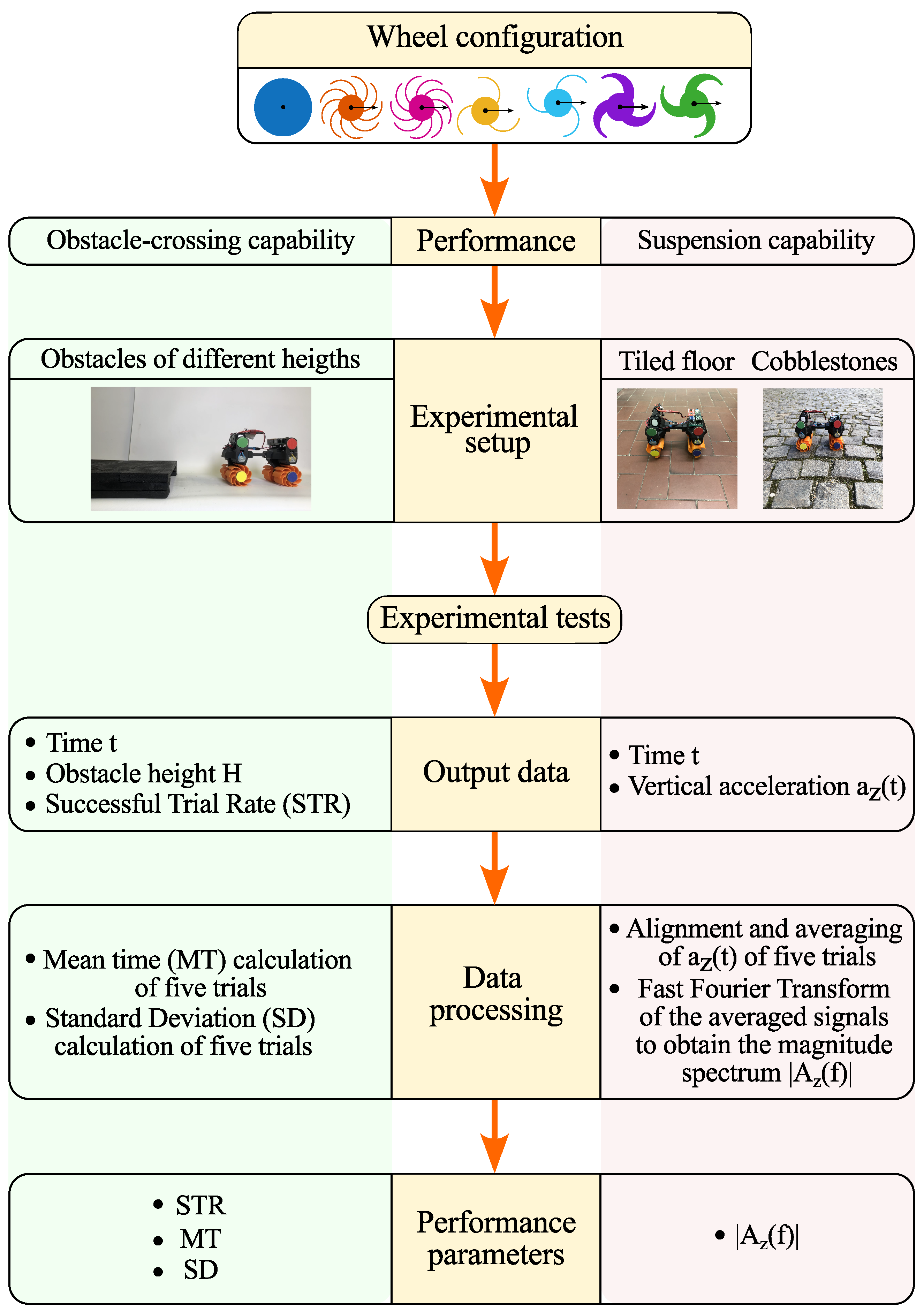
2.4. Experimental Tests

The experimental tests aimed to evaluate the suspension and obstacle-climbing capabilities of the different wheels considered. The following three parameters were analyzed as potentially affecting wheel behavior:

• The number of spokes.
• The wheel rotation direction.
• The cross-sectional profile of the spoke along the radial direction.

The combination of these parameters results in a set of configurations summarized in Figure 5. The designation of each configuration, except for the conventional circular wheel, indicates the number of spokes (zero for the circular wheel configuration) and the direction of motion, which refers to the orientation of the C-shaped spokes. Specifically, when the first contact point with the ground lies on the upper surface of the spoke, the configuration is referred to as forward-facing (FF), whereas when the first contact point coincides with the spoke tip, it is referred to as backward-facing (BF). The variation of the spoke thickness was analyzed only for the three-spoke wheel configuration.

2.4.1. Obstacle-Climbing Capability

The obstacle-climbing capability refers to a robot’s ability to overcome obstacles with heights greater than its wheel radius, heights that a conventional wheel would normally be unable to handle. To experimentally evaluate the obstacle-climbing capability of the different wheels, a test setup was constructed using rectangular obstacles of varying heights (Figure 6). Each obstacle was created by stacking a series of wooden boards fixed to the surface of a table. The heights tested were 16 mm (0.53R), 33 mm (1.1R), 47 mm (1.57R), and 51 mm (1.7R), where R is the wheel radius and is 30 mm. The obstacle heights were chosen by combining the available wooden board thicknesses of 4, 14, 16, and 17 mm. The first height value (0.53R) corresponds approximately to the maximum practical height that a conventional circular wheel can overcome on a vertical step, based on preliminary observations. Subsequent heights correspond to the combinations of the thicknesses of the available material.

The experiments evaluated the climbing ability of the circular wheel and the spoked wheels in different configurations. Each configuration was defined by a specific number of spokes and a rotation direction. For each configuration, five trials of up to 10 s were performed. A trial was considered successful if the robot neither tipped over nor became stuck, and if all four wheels rested stably on top of the obstacle. Trials were excluded from the evaluation if the wheel hub became lodged beneath the top board of the obstacle, as this outcome was influenced by the arbitrary initial angular position.

The robot was tested starting from rest at an initial distance of 10 cm from the obstacle. Before activation, the robot’s wheels were synchronized at arbitrary angular positions relative to each other, meaning that the spokes were aligned along the wheels’ axial direction to ensure uniform initial contact with the ground. This procedure minimizes the risk of lateral tipping, which occurs when the robot encounters an obstacle with only one wheel. This effect is more pronounced for wheels with fewer spokes, as the contact between the wheel and the ground is more discontinuous. The robot was operated in open-loop velocity control at an input of 81 rpm. After the acceleration transient and just before the obstacle, it reached a speed of approximately 2.5 cm/s.

To evaluate the experimental influence of the wheels alone, it was important to minimize the frontal surface of the obstacle in order to reduce the effect of rear-wheel traction, which can push the front wheels against a vertical obstacle and facilitate climbing even if the wheels are not geometrically suited.

2.4.2. Suspension Capability

The suspension capability of a robot is generally defined as its ability to reduce chassis oscillations caused by terrain irregularities, maintain wheel ground contact to ensure traction and stability, and absorb shocks by attenuating the impact forces transmitted to the chassis and internal components. In this study, we focus on a specific aspect of this capability as follows: the analysis of high-frequency vibrations arising from wheel ground interactions while traversing obstacles smaller than the wheel radius. Although these vibrations occur at frequencies higher than the primary chassis oscillations, they play a crucial role in assessing the robot’s structural response and the durability of components.

To assess the suspension capability of the wheels, time-domain vertical acceleration signals (${\mathrm{a}}_{\mathrm{z}}$ see the IMU reference frame indicated in Figure 3) were acquired using the IMU sensor with a sampling frequency of 260 Hz and a full scale range of $\pm 8$ g (where g is the gravitational acceleration 9.81 $\mathrm{m}/{\mathrm{s}}^2$) and then logged on a SD card. The robot was tested on two types of terrain as follows: a regular surface, the tiled floor (Figure 7a), used as a reference; and an irregular surface, cobblestones (Figure 7b). Five trials were conducted for each wheel configuration on both terrains, with each trial lasting 10 s. The robot was placed in a sufficiently flat area and was operated in open-loop velocity control. In this case as well, before each trial, the wheels were synchronized to an arbitrary angular position.

The data were then processed to obtain a representative frequency spectrum for the different cases. For each terrain and configuration, five signals were acquired. The signal were aligned, superimposed and averaged point by point, obtaining a statistically representative signal for each configuration and terrain.

Subsequently, the Fast Fourier transform (FFT) of the averaged signals was computed and normalized by the number of samples (N). To compare different configurations on the same terrain, each spectrum was truncated at a common maximum frequency of $77$ Hz, corresponding to the minimum Nyquist frequency among all the averaged signals of the various configurations (for the mathematical derivations, see Appendix A). A qualitative frequency-domain analysis of the vertical acceleration signals was therefore carried out by varying one parameter at a time while keeping the others fixed.

To assess the suspension effect of the wheels under the various configurations, the high-frequency components of the acceleration signals were analyzed based on a fixed frequency threshold, common to all configurations and to both terrains. This threshold was not derived from the literature values but was pragmatically defined to qualitatively separate the low-frequency components—corresponding to the theoretical rotation frequency (1.33 Hz) and the spoke-passing frequencies ($3.99$ Hz for the three-spoke wheel and 11.97 Hz for the nine-spoke wheel)—from the faster oscillations associated with the suspension system dynamics. Although this approach is qualitative, it enables a coherent and meaningful comparison among the different wheel configurations for each terrain. In the absence of a standardized reference in the literature, the threshold separating low- and high-frequency components was set at 30 Hz, an arbitrary but conservative value that exceeds twice the maximum blade-passing frequency (11.97 Hz). In this way, the components above this threshold represent the dynamic behavior of the wheels and the suspension capability of the system. Figure 8 summarizes the steps used to evaluate the obstacle-overcoming and suspension capabilities of the different wheels.

3. Results and Discussion

3.1. Obstacle-Climbing Capability Results

Figure 9 reports the experimental results related to obstacle-climbing capability as follows: the successful trial rate (STR) for the five trials conducted at the different obstacle heights H, expressed as a scaled value of the wheel radius for each configuration. To allow comparison between configurations with the same STR, both the mean time (MT) and the corresponding standard deviation (SD) of the five trials are reported. For each trial, the time interval between the moment the front wheels approach the obstacle and the moment all wheels are stably positioned on top of it is measured. The mean time (MT) is defined as the average of these time intervals over the five trials. The standard deviation (SD) quantifies the variability of the time intervals with respect to the mean time. In practice, a configuration better suited for obstacle-climbing requires less time, as it relies primarily on shape-based coupling, determined by wheel geometry, rather than force-based interaction with the obstacle’s frontal surface. This behavior is due to the flexibility of the spokes, which deform upon frontal contact with the obstacle, facilitating the engagement of the subsequent spoke. Furthermore, as noted above, a higher number of spokes improves frontal grip, particularly for the leading module, which benefits from the push of the following module to increase deformation, contact force, and thus traction on the frontal surface.

From the experimental data of obstacle-climbing capability of the different wheel configurations, the following conclusions can be drawn:

• Circular wheel behavior: The circular wheel (7) can overcome only the smallest obstacle, with a height of 0.53R.
• Effect of wheel rotation direction: Regardless of the number of spokes, the backward-facing configurations (2), (4), and (6) outperform the corresponding forward-facing configurations (1), (3), and (5) in terms of both STR and MT. This is attributed to favorable shape-based engagement and reduced interference with the obstacle.
• Influence of the number of spokes: Configurations with three spokes, both forward-facing (3, 5) and backward-facing (4, 6), generally outperform the corresponding nine-spoke configurations. The lower number of spokes enables these wheels to overcome taller obstacles. Moreover, even when the STR is equal, as observed for configurations (2), (4), and (6) at a height of 1.57R, the MT consistently favors the three-spoke configurations (Figure 10a–c).
• Effect of spoke stiffness: For a given number of spokes, tapering the spokes to increase stiffness allows the wheel to overcome higher obstacles. With the same robot weight, stiffer spokes raise the wheel height above the ground, allowing the wheel to surmount taller obstacles (Figure 10c). At the same time, the increased stiffness limits the bending of the spoke during contact with the obstacle, thereby facilitating its traversal.
• Stability considerations: Although three-spoke configurations achieve higher obstacle-climbing capability, they are also more unstable: with three spokes, there are fewer simultaneous contact points and a lower contact frequency with the ground, causing the body to oscillate more and increasing the risk of tipping. With nine spokes, the greater number of distributed contacts maintains robot stability even if some spokes are not perfectly synchronized. Therefore, at equal angular velocity, loss of angular synchronization between the wheels increases the likelihood of lateral tipping (Figure 11).
• Statistical considerations: For a given wheel configuration, both MT and SD increase with the obstacle height, consistent with the increasing difficulty for the wheel to overcome taller obstacles. As noted earlier, for the same obstacle height and wheel rotation direction, MT consistently favors the three-spoke configurations. SD values are nearly zero for an obstacle height of 0.53R for all configurations and remain below one except for the forward-facing configurations (3) and (5) at an obstacle height of 1.57R, where SD equals 3.07 s and 1.71 s, respectively. This result further highlights the favorable shape-based engagement and reduced obstacle interference characteristic of the backward-facing configurations.

3.2. Comparison of Obstacle-Climbing Capability with Other Wheel-Legged Designs

It is interesting to compare the obstacle-climbing capability of the prototype with several non-transformable wheel-legged designs for which experimental data are available in the literature. The comparison focuses on the three-spoke tapered wheels in the backward-facing configuration, which demonstrated the best performance in the prototype. The results are summarized in the

Table 2. Comparison of obstacle-climbing capability of different non-transformable wheel-legged designs.

Robot	Body Structure	Max Height (R)
Tapered 3-spoke wheel prototype	Rigid	1.7
RHex [2]	Rigid	1.25
Whegs I [7]	Rigid	1.5
Whegs II [10]	Articulated	1.38
FRESE IV [12]	Continuum	3.6
Lizard [13]	Continuum	2.4
Crawling soft robot [14]	Continuum	2.2

. Here, R represents the radius of the wheel-leg for each robot; to allow consistent comparison between robots of different sizes, the maximum obstacle height cleared by each robot is expressed in multiples of its respective wheel radius.

The three-spoke wheel design presented in this study achieves a maximum scalable height of 1.7R, higher than Whegs I (1.5R) and Whegs II (1.38R). Although Whegs II reaches slightly lower obstacles, its articulated body may offer better adaptability on irregular terrain.

Continuum robots (Frese IV, Lizard and Crawling soft robot) can scale significantly taller obstacles (3.6R, 2.4R, and 2.2R, respectively) due to their flexibility, but this comes with more complex design requirements and control, which may limit practical use.

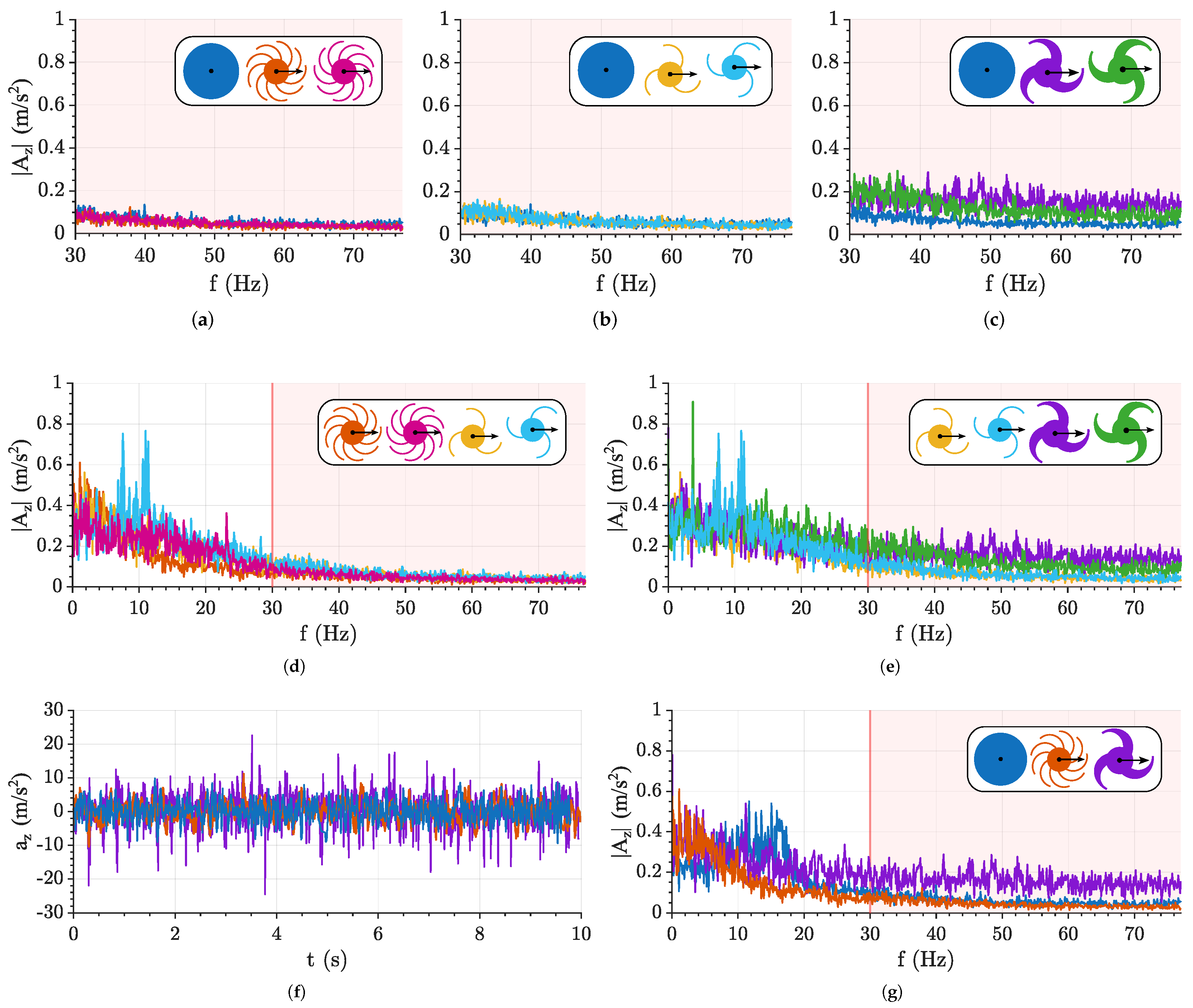
3.3. Suspension Capability Results

Figure 12a–e shows comparisons of the frequency spectra for the various configurations, while Figure 12f,g presents the time-domain acceleration signals and frequency spectra of the most significant configurations on the tiled floor.

Figure 13a–e shows comparisons of the frequency spectra for the various configurations, while Figure 13f,g shows the time-domain acceleration signals and frequency spectra of the most significant configurations on the cobblestone.

From the experimental data of the suspension capability of the different wheel configurations, the following qualitative conclusions can be drawn:

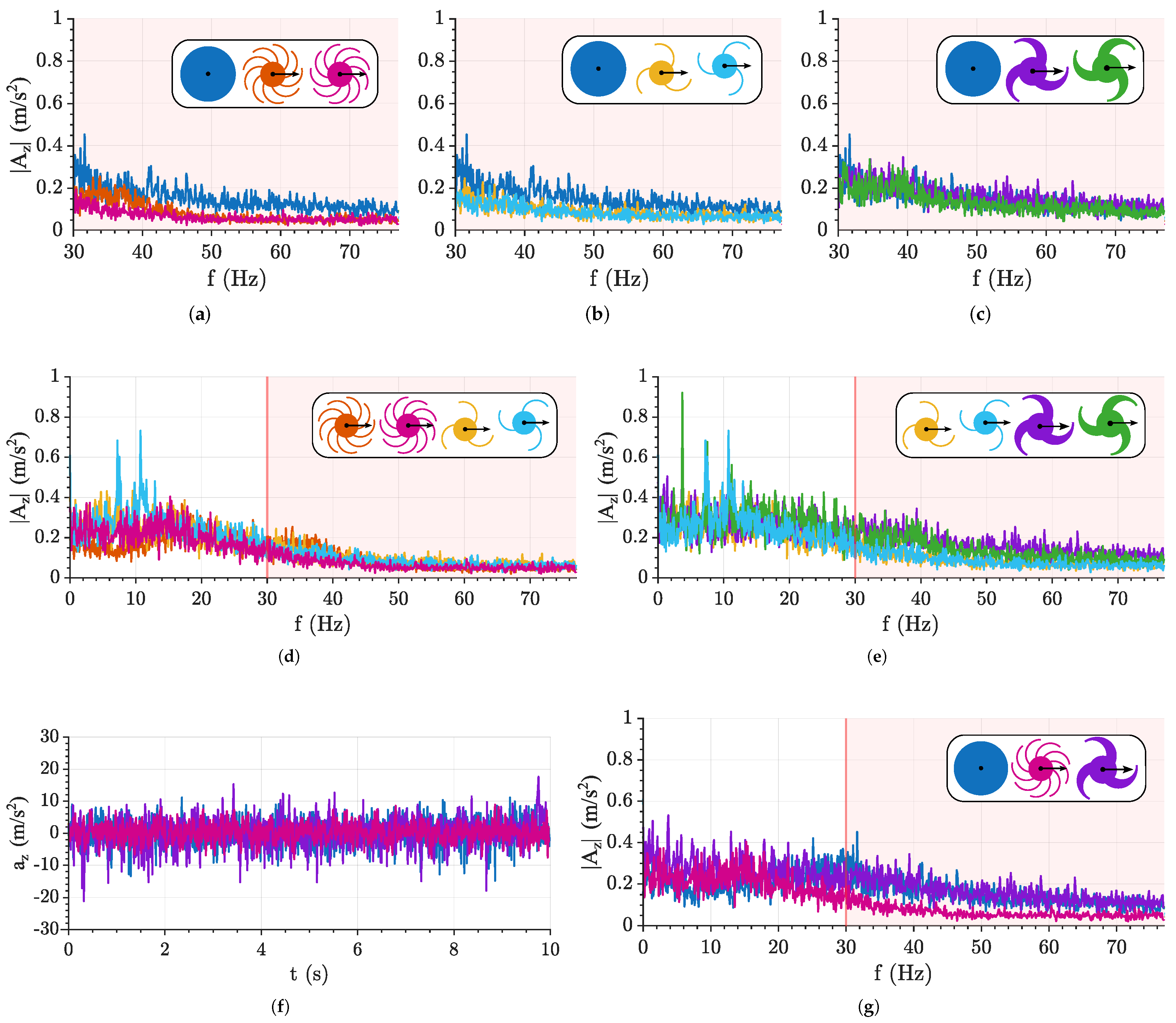
• Tiled floor: The circular wheel, together with the nine-spoke forward-facing wheel, exhibits the best suspension capability, with the latter being slightly superior (Figure 12a,g). The wheel rotation direction does not appear to be a significant parameter (Figure 12a,b), except for the tapered three-spoke wheel (Figure 12c), where the forward-facing configuration appears to yield worse results, e.g., it exhibits higher vibration levels at higher frequencies. The number of spokes highlights an advantage for the nine-spoke wheel (Figure 12d) because the contact with the ground is more continuous. The tapering of the three-spoke wheel further reduces suspension capability due to the increased stiffness (Figure 12e). In summary, the circular wheel and the nine-spoke forward-facing wheel are the best-performing configurations, whereas the tapered three-spoke wheel is the worst-performing one, as indicated by the acceleration peaks in (Figure 12f).
• Cobblestones: On this terrain, the circular wheel performs the worst (Figure 13a,g) because its shape does not adapt well to irregularities. The nine-spoke wheel, on the other hand, maintains consistently good capabilities (Figure 13a,f). Wheel rotation direction has little impact overall, except for a slight degradation in the forward-facing configurations of the three- and nine-spoke wheels (Figure 13a,b), which becomes more noticeable for the tapered three-spoke wheel (Figure 13c). Regarding the number of spokes, three-spoke wheels show reduced capability (Figure 13d), with further degradation for the tapered profile (Figure 13e). In summary, the nine-spoke forward-facing wheel is the best-performing configuration, while the circular wheel and the tapered three-spoke wheel are the worst, as shown by the acceleration peaks in Figure 13f.

3.4. Performance Overview

Table 3. Qualitative assessment of different wheel configuration capabilities. Arrows indicate the direction of wheel motion and colors are used for visual distinction only.

Configuration
Obstacle-climbing capability	Very low	Medium	Low	High	Low	Very high	Very Low
Suspension capability	Very high	Very high	Medium	High	Very low	Low	Very high

provides a qualitative overview of the obstacle-overcoming and suspension capabilities associated with each wheel configuration. The experimental campaign highlights the following key outcomes:

• The circular wheel consistently exhibits the lowest capabilities, confirming its limited suitability for operation on unstructured or irregular terrains.
• The wheel rotation direction has a measurable impact on both capabilities, with a clear improvement when transitioning from the forward-facing to the backward-facing configuration.
• A reduction in the number of spokes leads to a degradation in suspension capability, while concurrently enhancing obstacle-climbing capability, independently of the rotation direction.
• A variation in the spoke thickness, considered in this context as a tapering of the spoke profile, does not affect the obstacle-climbing capability in the forward-facing configuration, while it leads to a noticeable improvement in the backward-facing configuration. However, profile tapering consistently reduces the suspension capability for both rotation directions.

Overall, the findings indicate that all three design parameters, wheel rotation direction, number of spokes, and spoke tapering, significantly influence wheel behavior. While rotation direction strongly affects obstacle-climbing, it requires repositioning the robot, which may not be feasible in constrained environments. In contrast, modifying the number of spokes or the spoke tapering can achieve substantial improvements in both obstacle traversal and suspension without moving the robot. This highlights the potential for a reconfigurable spoked wheel design that enhances adaptability and versatility in unstructured terrains while minimizing operational constraints.

4. Conclusions and Future Works

This study investigated the preliminary design and testing of an articulated ground mobile robot, Brush.Q, composed of four modules, each equipped with two compliant brush-like wheels. These wheels are multi-spoked and feature passive compliance and a novel structural design distinct from existing wheel-legged robot configurations. Beyond the presentation of this preliminary yet innovative design, the main contribution of the work lies in the experimental analysis of the suspension capability of spoked wheels with different geometric profiles. Combined with the evaluation of obstacle-climbing performance, the study provides a comprehensive comparison of different wheel designs.

A simplified prototype, consisting of two rigidly connected modules, was constructed and tested to evaluate the obstacle-climbing and suspension capabilities of various wheels. This framework provides guidance for selecting wheels for generic wheel-legged robots operating on unstructured terrain and highlights which wheel configurations perform best under specific conditions.

The following three design parameters were identified as influencing wheel behavior: the number of spokes, the wheel rotation direction, and the radial cross-sectional profile of the spokes. Several wheel geometries were investigated, including a conventional circular wheel, a nine-spoke wheel, a three-spoke wheel, and a tapered three-spoke wheel. The obstacle-climbing capability was evaluated using obstacles of increasing height, while suspension performance was assessed through the spectral analysis of vertical acceleration signals measured by an IMU on both regular and irregular terrains.

The results demonstrate the limited suitability of conventional circular wheels for unstructured environments and confirm the critical role of wheel geometry in overall robot performance. Reducing the number of spokes improves obstacle-climbing capability but degrades suspension performance and lateral stability, whereas a higher spoke count enhances both suspension and stability. Wheel rotation direction significantly affects performance, with backward-facing configurations consistently outperforming forward-facing ones across all wheel types. Spoke tapering improves obstacle climbing in the backward-facing configuration but reduces suspension. Overall, all three parameters significantly influence wheel behavior, and modifying spoke geometry emerges as a practical strategy to enhance adaptability without requiring robot reorientation. These findings highlight the potential benefits of incorporating a reconfigurable spoke-wheel mechanism, enabling the robot to leverage the advantages of different wheel configurations under varying conditions.

The conducted analysis can be extended to different terrains and obstacle conditions, providing guidance for future research. At present, the study focuses exclusively on the wheel subsystem of the robot. A more comprehensive performance assessment, including quantitative indicators such as stability, energy efficiency, and steering flexibility, will be conducted once the complete Brush.Q prototype is realized, which represents a key future work. Additionally, the design and development of a reconfigurable wheel mechanism represent a crucial direction for further study, aiming to fully exploit the advantages of various wheel geometries and enhance the robot’s adaptability and versatility in unstructured environments. Potential application scenarios include search and rescue operations, inspection and detection tasks, and exploration in complex or hazardous terrains, where obstacle negotiation and suspension performance are critical.