A Chain Rule-Based Generalized Framework for Efficient Dynamic Analysis of Complex Robotic Systems

Abstract

System representation via computational graphs has become a cornerstone of modern machine learning, underpinning the gradient-based training of complex models. We have previously introduced the Partial Lagrangian Method—a divide-and-conquer approach that decomposes the Lagrangian into link-wise components—to derive and evaluate the equations of motion for robot systems with dynamically changing structures. That method leverages the symbolic expressiveness of computational graphs with automatic differentiation to streamline dynamic analysis. In this paper, we advance this framework by establishing a principled way to encode time-dependent differential equations as computational graphs. Our approach, which augments the state vector and applies the chain rule, constructs fully time-independent graphs directly from the Lagrangian, eliminating the erroneous time-derivative embeddings that previously required manual correction. Because our transformation is derived from first principles, it guarantees graph correctness and generalizes to any system governed by variational dynamics. We validate the method on a simple serial-link robotic arm, showing that it faithfully reproduces the standard equations of motion without graph failure. Furthermore, by compactly representing state variables, the resulting computational graph achieves a seven-fold reduction in evaluation time compared to our prior implementation. The proposed framework thus offers a more intuitive, scalable, and efficient design and analysis of complex dynamic systems.

1. Introduction

Computational graphs are powerful tools, especially in machine learning, for representing complex models and their input–output relationships. They enable efficient gradient computation and capture intricate dependencies among variables [1,2,3]. In robotics, the use of computational graphs is rapidly expanding, with applications in control system design [4,5,6] and constraint management via graph structures [7,8]. Furthermore, efficiently handling graph structures is a crucial technology in robotics—such as in UAV (Unmanned Aerial Vehicle) and MSV (Marine Surface Vehicle) path planning—and graph-based theoretical designs enable swarm control and collision avoidance among individual robots [9,10]. This study applies computational graphs to differential equations with time-dependent states with the aim of leveraging the powerful representational capacity of automatic differentiation inherent in computational graphs for analyzing the equations of motion of robotic systems.

When considering the implementation of dynamics in a robotic system, the Featherstone’s algorithms based on the RNEA (Recursive Newton–Euler Algorithm) and ABA (Articulated-Body Algorithm) are known to be extremely efficient. If the system’s structure is fully specified in advance, these methods represent the optimal choice for dynamics computation in robotics. However, we focus on scenarios where the robot’s configuration can change flexibly and its internal structure is not fixed. To address this, we have developed an approach that dynamically constructs the equations of motion using computational graphs. Our method builds on the analytically derived Lagrangian equations of motion, allowing rapid extension or modification of the system’s dynamics whenever its configuration evolves [11,12,13].

We have investigated the potential of computational graphs for representing robotic system dynamics, as their ability to map one-to-one with symbolic expressions and support automatic differentiation makes them highly capable of representing differential equations. Our proposed Partial Lagrangian Method, founded on a divide-and-conquer paradigm, lets us design and analyze each subgraph to understand force transmission [11]. It also allows us to model system branching and dynamic structural changes by connecting or separating those subgraphs. From a graph-theoretic standpoint, this approach opens up new avenues of analysis that were not apparent in traditional differential-equation formulations. By embedding the Lagrangian into the graph and using automatic differentiation, we automatically derived equations of motion, enabling both the design and analysis of robotic systems. Conventional graph-based representations of differential equations, however, struggle with time-dependent states, hindering accurate modeling and analysis.

Traditionally, computational graphs have been used to analyze various physical phenomena. For example, their use in gravitational-wave analysis has been reported [14] as well as in computational fluid dynamics [15]. With rapid advances in AI, computational-graph frameworks and their underlying automatic-differentiation techniques have matured, leading to the widespread adoption across diverse fields [16,17,18]. Despite these applications, the field of robotics has yet to establish a scheme for applying computational graphs to the design and analysis of robotic systems. Furthermore, directly applying traditional robotics approaches to computational graphs can introduce invalid connections within the graph. To address this, we propose a method for transforming the equations of motion so that no theoretically incorrect connections can arise. By describing the system according to our proposed scheme, the correct equations of motion can be expressed directly as a computational graph. By combining our previously proposed Partial Lagrangian Method with the present approach, even the equations of motion for complex, structurally reconfigurable robotic systems can be represented as computational graphs easily and without error.

The main contributions of this study are outlined below:

• A generalized framework for solving differential equations with time-evolving states using computational graphs and the chain rule.
• Demonstration of the framework’s effectiveness in robotic systems, showcasing its ability to handle complex dynamics and time-dependent relationships.
• Insights into the implications of our approach for future research in dynamic systems and computational graph-based analysis.

The remainder of this paper is organized as follows. Section 2 details our proposed method, including the chain-rule transformation of differential equations. Section 3 applies the method to robotic systems, highlighting its effectiveness for time-varying states. Section 4 analyzes computational costs and identifies minimal components of the equations of motion for a divide-and-conquer strategy. Finally, Section 5 concludes and outlines directions for future work.

2. Methods

We propose a framework for designing and analyzing robotic systems using computational graphs, which is a paradigm widely adopted in machine learning. In particular, we introduce a method that leverages automatic differentiation to concisely formulate the equations of motion for multi-degree-of-freedom systems. Automatic differentiation systematically computes exact derivatives by traversing computational graphs, enabling the efficient differentiation of complex, multivariate functions [19,20]. Building on this foundation, we have developed an approach that partitions the computational graph via a divide-and-conquer strategy applied to the Lagrangian equations of motion for robotic systems [21,22]. This strategy allows us to handle changes in a robot’s degrees of freedom—such as those arising from extension or disassembly—without compromising computational efficiency.

A key feature of our method is the automatic embedding of differential relationships into the computational graph. By simply specifying the system’s Lagrangian, AD constructs the full computational graph of the dynamics. Consequently, users are relieved from manually expanding intricate motion equations and need only provide the Lagrangian (i.e., the system’s energy) to generate the equations of motion.

2.1. Problems with Embedding Time-Derivative Relationships in Computational Graphs

While computational graphs facilitate analytical operations via automatic differentiation, their underlying purely algebraic structure can present challenges when handling dynamic behaviors like complex control flow or time-varying systems.

For instance, embedding a time-varying system relationship like Euler’s method into a computational graph is a straightforward way to represent a time-derivative relationship for a state variable.

$$\begin{array}{c}\hfill \theta =\dot{\theta }dt+{\theta }_{old}\to \dot{\theta }={\displaystyle \frac{d\theta }{dt}}\end{array}$$

(1)

This definition integrates the $\theta$-$\dot{\theta }$ dependency into the graph so that chain-rule analysis becomes possible.

Despite enabling differentiation, this embedding introduces unintended couplings during automatic differentiation. Consider differentiating the Lagrangian

$$L=\frac{1}{2}I{\dot{\theta }}^2-\frac{1}{2}k{\theta }^2$$

first with respect to $\dot{\theta }$ and then with respect to time:

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dt}}{\displaystyle \frac{\partial L}{\partial \dot{\theta }}}={\displaystyle \frac{d}{dt}}{\displaystyle \frac{\partial }{\partial \dot{\theta }}}\left({\displaystyle \frac{1}{2}}I{\dot{\theta }}^2-{\displaystyle \frac{1}{2}}k{\theta }^2\right)=I\ddot{\theta }\end{array}$$

(2)

where I and k denote the moment of inertia and stiffness, respectively, and we assume $\theta =0$ at the equilibrium. Crucially, $\theta$ and $\dot{\theta }$ must be independent so that the potential-energy term does not affect the partial derivative with respect to $\dot{\theta }$.

If instead the time-derivative relation is embedded as above, the same differentiation yields

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dt}}{\displaystyle \frac{\partial L}{\partial \dot{\theta }}}={\displaystyle \frac{d}{dt}}{\displaystyle \frac{\partial }{\partial \dot{\theta }}}\left({\displaystyle \frac{1}{2}}I{\dot{\theta }}^2-{\displaystyle \frac{1}{2}}k{\theta }^2\right)& \to {\displaystyle \frac{d}{dt}}{\displaystyle \frac{\partial }{\partial \dot{\theta }}}\left({\displaystyle \frac{1}{2}}I{\dot{\theta }}^2-{\displaystyle \frac{1}{2}}k{(\dot{\theta }dt+{\theta }_{old})}^2\right)\hfill \\ \hfill & ={\displaystyle \frac{d}{dt}}\left(I\dot{\theta }-k(\dot{\theta }dt+{\theta }_{old})dt\right)\hfill \\ \hfill & =I\ddot{\theta }-\underset{\mathrm{Unnecessary}\mathrm{terms}}{\underbrace{k(\ddot{\theta }d{t}^2+2\dot{\theta }dt+{\theta }_{old})}}\hfill \end{array}$$

(3)

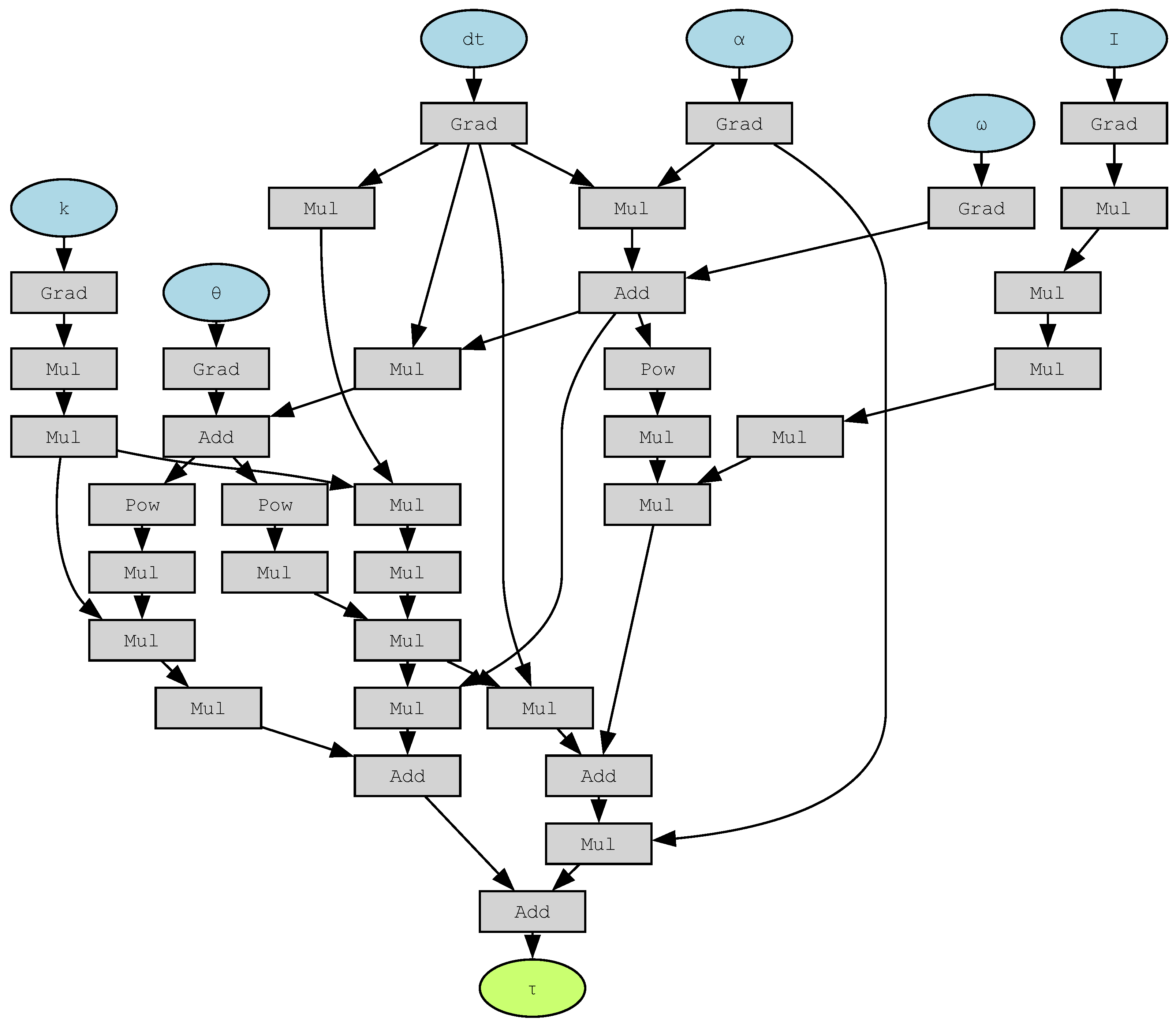
which contains clearly unnecessary terms. These spurious contributions arise because variables that should be independent become coupled in the graph. Consequently, a mismatch appears between the algebraic graph definition and the analytical operations performed by automatic differentiation. Figure 1 shows the computational graph generated directly from Equation (3).

To avoid this issue, we define and differentiate the kinetic energy K and the potential energy P separately without constructing the full Lagrangian subgraph. In particular, the velocity-derivative term in Lagrange’s equation can be written as

$${\displaystyle \frac{d}{dt}}{\displaystyle \frac{\partial L}{\partial \dot{\theta }}}={\displaystyle \frac{d}{dt}}{\displaystyle \frac{\partial K}{\partial \dot{\theta }}}.$$

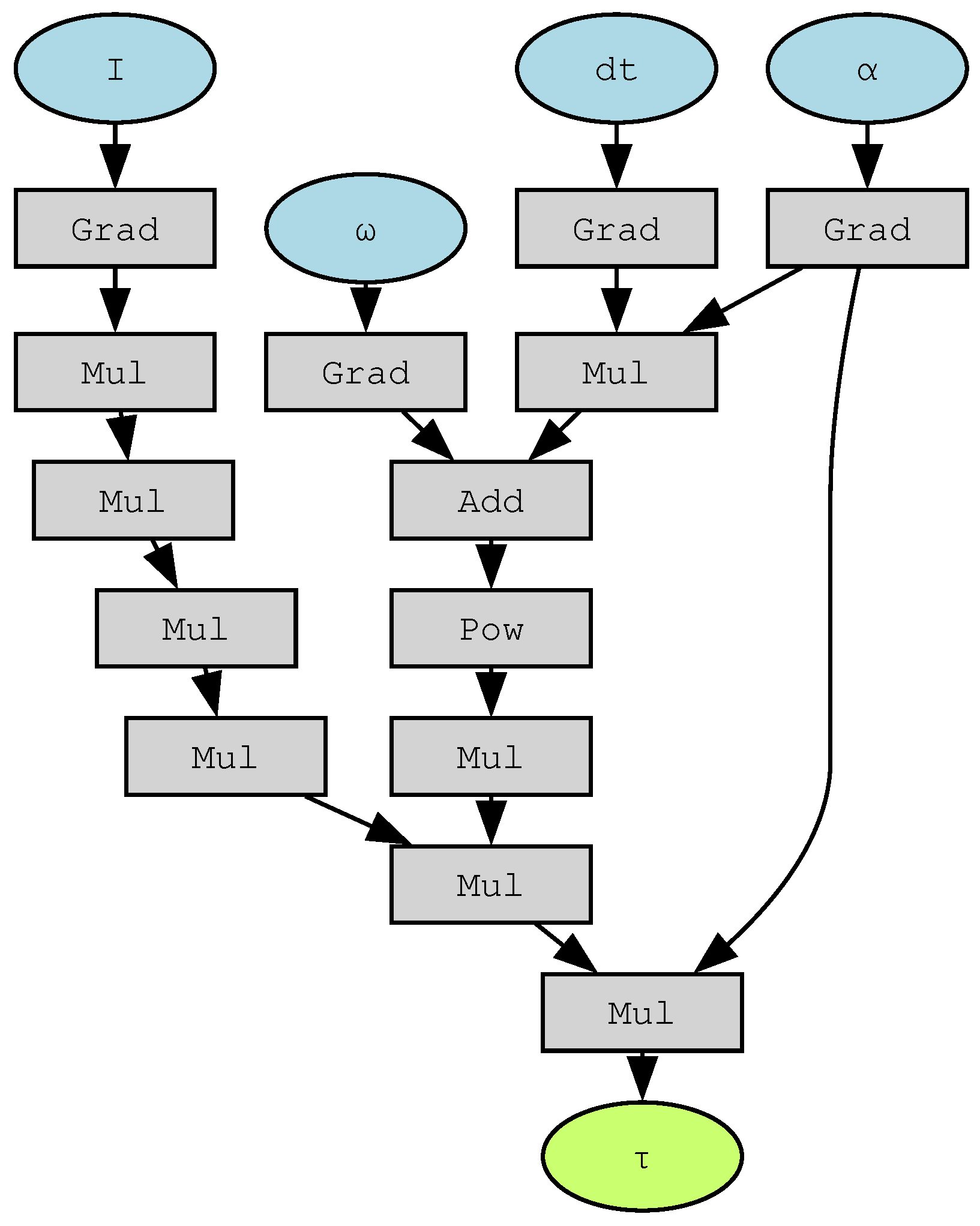
Figure 2 depicts the resulting computational graph. Because P is excluded from this definition, no spurious connections arise, and the calculation remains correct. In our prior work, this approach yielded mathematically equivalent equations of motion and posed no problems for robotic-system design and analysis.

While this workaround avoids erroneous connections in practice, it disregards the theoretical unity of the Lagrangian formulation and is not fundamental. To address the root cause, we propose in the next section a chain-rule-based transformation of differential equations that preserves theoretical consistency while eliminating unnecessary graph couplings.

2.2. Eliminating Differential Relationships from Computational Graphs Using the Chain Rule

The root of the problem resides in the need to embed explicit time-derivative relationships of state variables into the computational graph. Computational graphs themselves are defined algebraically, whereas automatic differentiation performs analytical operations on those algebraic expressions. This duality introduces spurious couplings when state variables are intended to remain independent.

To overcome this issue, we propose a formulation of differential equations that exploits the chain rule in tandem with an augmented state-variable vector. The chain rule is a fundamental operation for differentiating composite functions [23,24]. By computing the gradient in the vector field spanned by the state variables and contracting it with their known time derivatives, we can resolve the embedding problem in a fully equivalent manner.

Let the expanded state vector

$$\mathit{x}={\left[{\theta }_1,\dots ,{\theta }_n,{\dot{\theta }}_1,\dots ,{\dot{\theta }}_n\right]}^T$$

have dimension $2n$. Denote this extended state $\mathit{x}\in {\mathbb{R}}^{2n}$. For any scalar function $y\left(\mathit{x}\right)$, its time derivative can be written as

$$\begin{array}{c}\hfill \dot{y}={\displaystyle \frac{dy}{dt}}={\displaystyle \frac{\partial y}{\partial \mathit{x}}}·{\displaystyle \frac{d\mathit{x}}{dt}}=\left({\nabla }_{\mathit{x}}y\right)·\dot{\mathit{x}},\end{array}$$

(4)

where

$${\nabla }_{\mathit{x}}:={\displaystyle \frac{\partial }{\partial \mathit{x}}}=\left[\frac{\partial }{\partial {\theta }_1},\dots ,\frac{\partial }{\partial {\theta }_n},\frac{\partial }{\partial {\dot{\theta }}_1},\dots ,\frac{\partial }{\partial {\dot{\theta }}_n}\right].$$

In (4), the left-hand side corresponds to a time-dependent graph, while the right-hand side admits a time-independent construction whenever $\dot{\mathit{x}}$ is known. Crucially, in initial-value problems, $\dot{y}$ is unknown but $\dot{\mathit{x}}$ is prescribed by the dynamics.

This transformation offers three principal advantages when representing differential equations as computational graphs:

• Time-derivative dependencies of the parameters need not be explicitly embedded in the graph.
• The independence of ${\theta }_i$ and ${\dot{\theta }}_i$ is inherently preserved.
• The term ${\nabla }_{\mathit{x}}y$ corresponds directly to a gradient computation, allowing immediate evaluation via automatic differentiation.

By applying only simple algebraic manipulations and incorporating the state vector, we can eliminate all explicit time dependence from the equations of motion. Because computational graphs must be built from algebraic expressions, this transformation yields an optimal equation-of-motion form for direct graph embedding. Moreover, the same procedure applies generally to any system that admits a Lagrangian formulation.

As an illustrative example, consider the inertial term in Lagrange’s equation:

$${\displaystyle \frac{d}{dt}}{\displaystyle \frac{\partial L}{\partial \dot{\theta }}}=\left({\nabla }_{\mathit{x}}{\displaystyle \frac{\partial L}{\partial \dot{\theta }}}\right)·\dot{\mathit{x}}=\underset{=0}{\underbrace{\left({\displaystyle \frac{\partial }{\partial \theta }}{\displaystyle \frac{\partial L}{\partial \dot{\theta }}}\right)\dot{\theta }}}+\underset{\mathrm{Obtained}\mathrm{graph}}{\underbrace{\left({\displaystyle \frac{\partial }{\partial \dot{\theta }}}{\displaystyle \frac{\partial L}{\partial \dot{\theta }}}\right)\ddot{\theta }}}=I\ddot{\theta }$$

Applying our chain-rule transformation yields the computational graph shown in Figure 3. Although this graph is built from the full Lagrangian L, it remains free of any potential-energy interference and is fully time-independent.

By eliminating unnecessary time-dependent connections, the resulting graph is simpler, reducing both computational cost and memory usage, and enhancing the performance of automatic differentiation [25,26,27].

3. Results

Generalized Analysis of Robotic Arm Mechanics

In our prior work, we used computational graphs to analyze robotic systems. However, during implementation, we embedded the Lagrange equations by handling the kinetic energy K and potential energy P separately instead of directly using the full Lagrangian L. We applied a divide-and-conquer strategy by decomposing L into partial Lagrangians $L_i$ for each degree of freedom, which provided an abstract, system-level view. Nevertheless, discrepancies in the implementation of velocity and time derivatives prevented us from employing these abstracted partial Lagrangians $L_i$ directly.

By removing these implementation-specific constraints, our computational-graph approach to the equations of motion naturally extends to general differential equations. In particular, we have generalized the algebraic construction of computational graphs while preserving the analytical independence inherent in variationally derived equations.

To demonstrate the generality and validity of the proposed method, we consider the equations of motion for a robotic arm with n degrees of freedom. The standard Lagrangian formulation is

$$\begin{array}{c}\hfill \mathit{\tau }={\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{\partial L}{\partial \dot{\mathit{\theta }}}}\right)-{\displaystyle \frac{\partial L}{\partial \mathit{\theta }}}\end{array}$$

(5)

Rewriting this in a time-independent form gives

$$\begin{array}{c}\hfill \mathit{\tau }={\displaystyle \frac{d}{d\mathit{x}}}\left({\displaystyle \frac{\partial L}{\partial \dot{\mathit{\theta }}}}\right)·{\displaystyle \frac{d\mathit{x}}{dt}}-{\displaystyle \frac{\partial L}{\partial \mathit{\theta }}}=\left({\nabla }_{\mathit{x}}{\displaystyle \frac{\partial L}{\partial \dot{\mathit{\theta }}}}\right)·\dot{\mathit{x}}-{\displaystyle \frac{\partial L}{\partial \mathit{\theta }}}\end{array}$$

(6)

The key step is to replace explicit time derivatives with gradients over the state space $\mathit{x}$ and the known state derivatives $\dot{\mathit{x}}$, thereby eliminating time-differentiation operators from the computational graph.

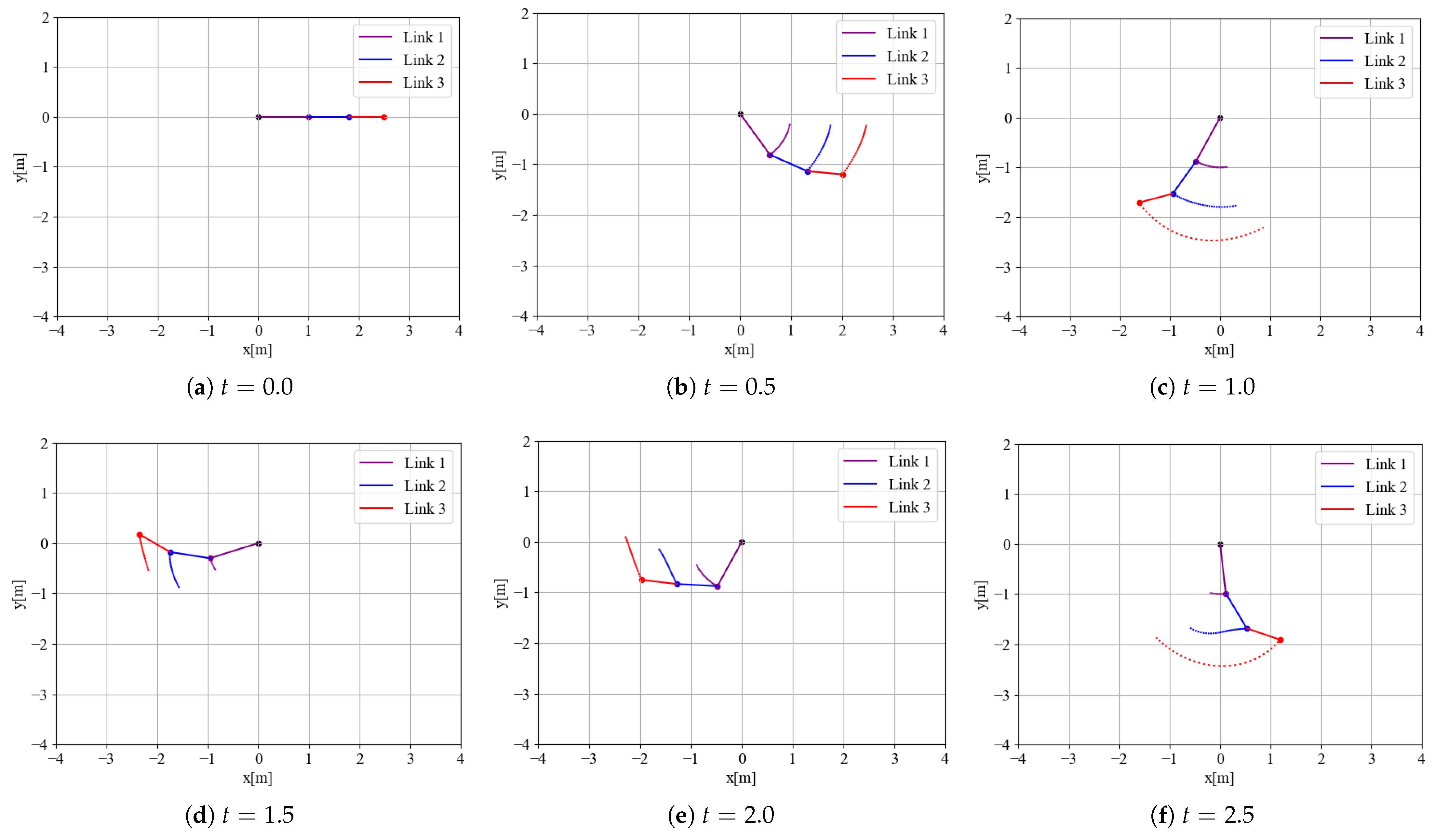
We validate our approach on a three-link manipulator modeled as a triple pendulum in free fall, facilitating comparison with existing results [28,29,30]. Using a fourth-order Runge–Kutta integrator, we simulate the motion by automatically generating the equations of motion via the proposed computational graph. Figure 4 presents snapshots of the manipulator’s configuration at selected time points.

The model used in Figure 4 consists of link 1 (purple) with mass 1.0 and length 1.0; link 2 (blue) with mass 0.8 and length 0.8; and link 3 (red) with mass 0.7 and length 0.7. The viscous damping at all joints was set to 0.1. For this simple simulation, only gravity was assumed. However, previous research has confirmed that even when joint actuation forces or external loads are applied, the forward dynamics and control systems implemented through computational graphs operate correctly.

The close agreement between our computational-graph-based simulation and established analytical methods confirms that the equations of motion are generated correctly via automatic differentiation and validates the proposed framework for robotic-system design and analysis.

4. Discussion

4.1. Validation of the Computational-Graph-Based Construction of Equations of Motion

The equations of motion can be generated automatically by constructing a computational graph in the form of Equation (4) and applying automatic differentiation. In our prior implementation, we needed to manually verify the correctness of graph connections and used ad hoc transformations to eliminate errors. By instead formulating the graph according to Equation (4), we can theoretically guarantee an error-free topology. To validate this, we compare the trajectories produced by our computational-graph-derived equations of motion with those from the MuJoCo physics simulator (Mujoco, DeepMind Technologies Ltd., London, UK) rather than a physical robot. The same physical parameters as in the previous section are used for this comparison.

The behavior analysis results obtained with the physics simulator are shown in Figure 5. Figure 5 shows screenshots of the simulator at each time step. Compared with these results, the computational graph in Figure 4 is shown to construct valid equations of motion, and the forward dynamics analysis using the Runge–Kutta method also functions appropriately.

In conventional physics simulators, the equations of motion are treated as opaque numerical integrators, and their underlying analytical structure is lost. In contrast, our approach encodes these equations in a computational graph, preserving all symbolic dependencies. This representation not only underlies the Runge–Kutta integration used in our experiments but also makes it possible to derive impedance-control laws directly from the graph’s structure. By leveraging the modular decomposition of the Partial Lagrangian Method, we can furthermore perform theoretical analyses of how each link’s force is transmitted to its joints when the system topology changes. Indeed, in prior work, we adaptively formulated the equations of motion for branched mechanisms using the Partial Lagrangian Method and analyzed their dynamic behavior with the same computation-graph-based framework introduced here.

4.2. Acceleration of Analysis Using Computational Graphs

Simplifying the computational graph greatly reduces complexity as system degrees of freedom increase. Here, we compare three implementations on the three-link manipulator from Section 3.

Table 1. Details of the computational speed test. Each value represents the computation time for a single step, and the mean and variance are calculated over 1000 iterations.

	Calculation Time (Average ± S.D.)	Note
Definition of Lagrange equation: ${\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{\partial L}{\partial \dot{\theta }}}\right)$	$51.7\pm 9.62$ ms	Incorrect result due to unnecessary terms
Our previous method: ${\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{\partial K}{\partial \dot{\theta }}}\right)$	$43.8\pm 8.03$ ms	Accurate results by symptomatic treatment
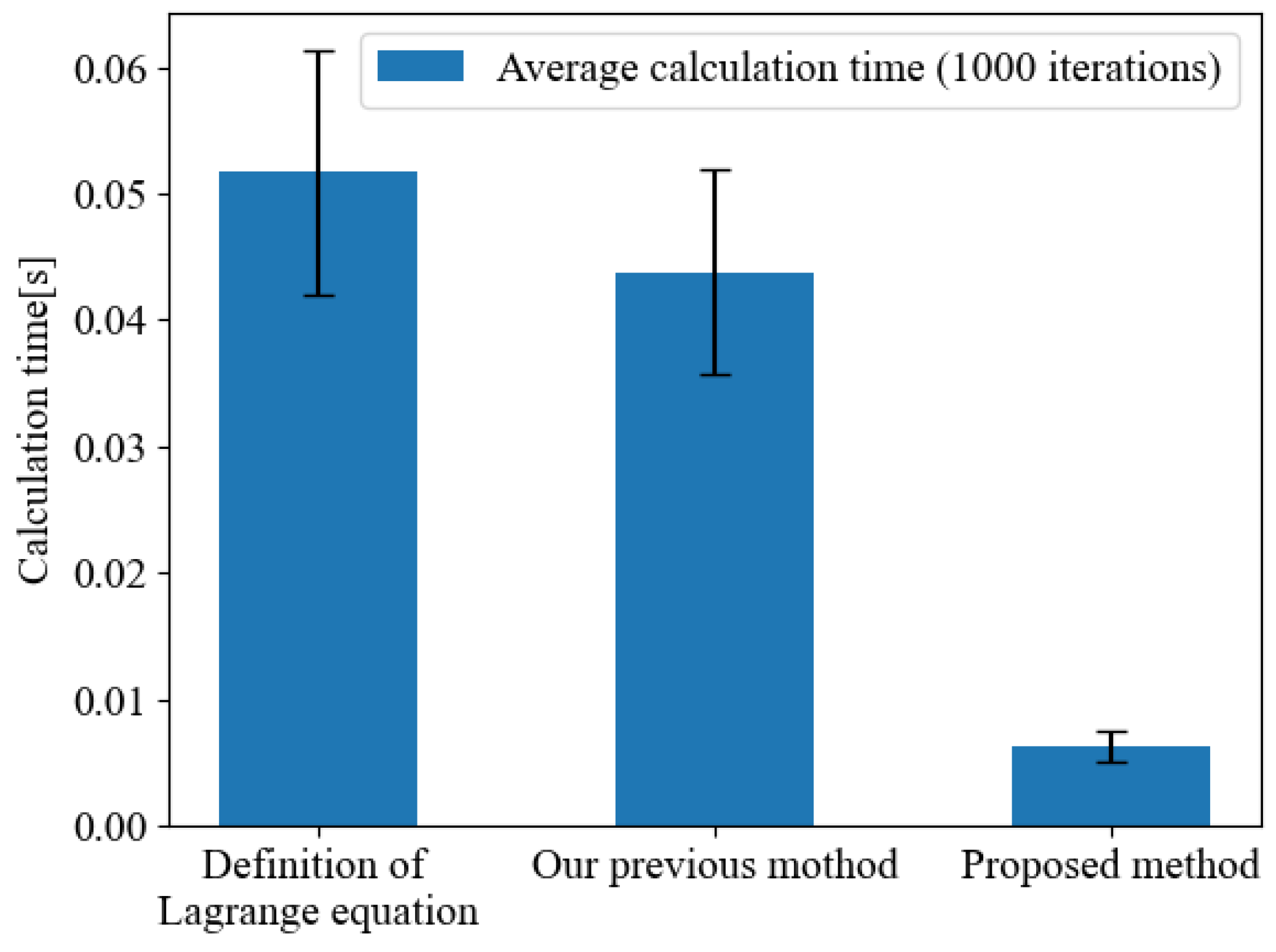
Proposed method: $\left({\nabla }_{\mathit{x}}{\displaystyle \frac{\partial L}{\partial \dot{\theta }}}\right)·\dot{x}$	$6.29\pm 1.15$ ms	Accurate results with broad applicability

and Figure 6 report the mean and standard deviation of single-step computation times over 1000 iterations for the following:

• Direct implementation of $\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)$ (“by-definition”);
• Our previous ad hoc method $\frac{d}{dt}\left(\frac{\partial K}{\partial \dot{\theta }}\right)$;
• The proposed chain-rule formulation $\left({\nabla }_{\mathit{x}}\frac{\partial L}{\partial \dot{\theta }}\right)·\dot{\mathit{x}}$.

Note that the by-definition approach produces incorrect results due to unremoved, unnecessary terms.

In the ad hoc method (middle column), the computation time decreases only by eliminating the unnecessary terms present in the by-definition graph. The proposed method (right column) achieves a substantial speed-up by removing the need to embed time derivatives into the graph, thereby reducing the number of graph edges.

As degrees of freedom n grow, the cost of connecting time-derivative relationships scales approximately as $\mathcal{O}\left(n^2\right)$. By contrast, our algebraically simplified graph has no explicit time derivatives or crossing dependencies, suggesting an $\mathcal{O}\left(n\right)$ complexity. Thus, the proposed method not only generalizes computational-graph-based solvers for differential equations but also delivers significant reductions in computational complexity.

4.3. Affinity with Decomposition by Partial Lagrangian Method

We previously introduced the Partial Lagrangian Method as a divide-and-conquer approach for formulating and analyzing Lagrangian equations of motion [11]. In this method, the total Lagrangian is split into link-wise components, thereby partitioning the computational graph and streamlining the derivation of the equations of motion. For each link i, we define a partial Lagrangian

$$L_i=K_i-P_i,$$

so that summing over all links recovers the standard Lagrangian:

$$L=K-P=\sum _i{K}_i-\sum _i{P}_i=\sum _i(K_i-P_i)=\sum _i{L}_i.$$

This decomposition permits multi-degree-of-freedom systems to be handled via smaller, independent computational graphs.

Automatic differentiation applied to these partial Lagrangians achieves an optimally efficient form. Since each subgraph is independent, the contribution to the equations of motion can be written as

$$\begin{array}{c}\hfill \left({\nabla }_{\mathit{x}}{\displaystyle \frac{\partial L}{\partial \dot{\theta }}}\right)·\dot{x}=\sum _i\underset{\begin{array}{c}\mathrm{Minimal}\mathrm{component}\mathrm{of}\\ \mathrm{Equation}\mathrm{of}\mathrm{motion}\\ \mathrm{for}\mathrm{divide-and-conquer}\end{array}}{\underbrace{\left[\left({\nabla }_{\mathit{x}}{\displaystyle \frac{\partial L_i}{\partial \dot{\theta }}}\right)·\dot{x}\right]}}\end{array}$$

(7)

The Partial Lagrangian Method and the rapid computational graph processing technique proposed in this work exhibit strong synergy. Unlike our earlier ad hoc approach—which used kinetic energy K in place of the full Lagrangian—the current method constructs a correct computational graph directly from L. This aligns with our guiding philosophy: by abstractly modeling a robotic system and delegating implementation details to the computational graph, we enable a more intuitive design and analysis of robot dynamics.

5. Conclusions

In this paper, we proposed a chain-rule-based framework for casting differential equations into computational graphs. By systematically removing redundant time-derivative dependencies, our method constructs fully time-independent graphs that both generalize the solution of differential equations and dramatically reduce computational complexity as the number of degrees of freedom grows. We validated its effectiveness and efficiency on the equations of motion for a three-link manipulator, confirming significant speed-ups without sacrificing accuracy.

Since the proposed method is theoretically formulated, our scheme for embedding the equations of motion into computational graphs is applicable to any robotic system that can be expressed in Lagrangian form. This enables, in conjunction with our prior Partial Lagrangian Method, the implementation of robotic-system extensions within a computational graph framework and the design and analysis of these systems from a graph-theoretic perspective.

The proposed approach is readily extendable to a wide range of differential-equation-driven problems in robotics, physics, and engineering. By abstracting system dynamics within a computation-graph paradigm, it offers a more intuitive and scalable route to understanding and solving complex dynamic systems.

In particular, this paper proposes a method for representing robotic systems as computational graphs by focusing on the Lagrange equations of motion. From a graph-structural perspective, the Lagrangian—as a second-order differential equation—manifests its formulaic structure in the computational graph’s depth. Conversely, the Hamiltonian—as a system of first-order differential equations—is expected to be captured not through depth but through parallelism within the graph. Because such a representation could yield a more compact graph and accelerate computation, future work will pursue the construction of a Hamiltonian computational graph.