Event-Based Closed-Loop Control for Path Following of a Purcell’s Three-Link Swimmer

Abstract

Purcell’s three-link swimmers, characterised by segments connected through one-degree-of-freedom joints, exhibit a difficulty in following precise paths. This is attributed to their motion primitives, which do not inherently generate displacement in a singular, predictable direction. To overcome this limitation, this paper proposes a closed-loop control strategy on the basis of event-based control. This control approach enables the robot to perform a specific motion primitive when the deviation from the desired trajectory exceeds a predefined threshold. In other words, an asynchronous strategy is used to adjust the motion of the swimmer, thereby ensuring tracking of the desired path with a limited error. The effectiveness of this closed-loop control strategy is demonstrated through experiments with a motor-driven 30 cm-length prototype. These tests show that this event-based control strategy allows the swimmer to follow specific paths with a tracking error of less than 30% of its length.

1. Introduction

With promising potential for diverse applications, autonomous swimming robots are set to revolutionise aquatic environments. They can assist with surveillance and protection around marine infrastructure, perform vital search and rescue missions, and even handle maintenance operations within complex pipe systems [1,2]. Inspired by the movements of biological swimmers like eels and water snakes, a leading approach in this field involves articulated snake-like robots, which navigate intricate underwater environments with remarkable adaptability. Snake-like robots intended for these applications can already be found in the literature [3,4], demonstrating the practical viability of this approach. These bio-inspired systems offer significant advantages through their undulating movement, which adapts to irregular shapes while minimising environmental disturbance in sensitive ecological environments and confined spaces.

Within this broader context of snake-like swimming robots, the Purcell’s swimmer represents a fundamental model designed to simulate the behaviour of biological swimmers in fluid environments. Originally intended for navigation at low Reynolds number ($Re$) regimes, where fluid dynamics are dominated by viscous forces rather than inertial ones, this system was introduced by Edward M. Purcell as the simplest swimmer capable of navigating these regimes [5]. The Purcell’s swimmer consists of three segments and two joints, making it a simplified version of more complex snake-like robots. This design allows it to achieve net movement by rotating its lateral segments in asymmetric sequences, known as motion primitives or gaits, which define their angular positions.

Research in viscosity-dominated regimes has established a solid theoretical foundation for understanding the behaviour of the swimmer, with its kinematics and dynamics being the most widely studied aspects. Researchers have extensively developed and analysed two-dimensional dynamic models, investigating various parameters that influence swimmer displacement. These studies have explored critical aspects such as swimmer geometry [6,7,8], motion primitives [9], and its asymmetry and stability [10]. Complementing two-dimensional approaches, other research efforts have focused on three-dimensional models of swimmers [11,12]. Some studies have taken a more generalised approach, first examining the dynamics of N-link systems and then attempting to approximate these models to sperm cell swimmers, with specific attention to the three-link case [13]. Concerning motion primitives, the literature presents traditional gaits such as square and circular configurations, which have been implemented and comparatively analysed in several studies [11,14]. Additionally, researchers have proposed innovative methodologies for designing novel motion primitives, as documented in a range of publications [7,9,15,16,17,18,19,20,21].

Regarding actuator types for rotating lateral links, the literature predominantly features two primary approaches: motorised systems and magnetic field-based actuation. Motorised prototypes have been extensively explored, with two notable servomotor-actuated swimmers developed in [14,22]. Another motorised prototype was introduced in [23], although experimental results were not presented. Magnetic field-based actuation represents an alternative approach, with significant research focused on magnetic Purcell’s swimmers. Researchers have comprehensively investigated these systems in studies such as [24,25,26,27]. A particularly noteworthy experimental contribution was the creation and testing of a magnetic prototype spanning a few centimetres, as detailed in [26].

Complementing these actuator strategies, some researchers have conducted mathematical analyses exploring the implications of passive and active elastic joints [23,28], providing additional theoretical insights into swimmer locomotion mechanisms. Moreover, ionic polymer-metal composites (IPMCs) have emerged as innovative materials for developing and simulating advanced swimming mechanisms. In [29], researchers explored the potential of IPMCs in designing a three-link Purcell’s swimmer, demonstrating the versatility of this material in biomimetic locomotion systems. Building upon this approach, a recent work successfully fabricated an IPMC-based Purcell’s swimmer prototype in which the joints were fabricated by this material, offering experimental results that validate the design [30].

While Purcell’s swimmer has shown promise in viscosity-dominated environments, there exists a notable gap in understanding its behaviour and applications in inertia-dominated regimes ($Re>1$). Extending this concept beyond its original theoretical framework is crucial for its practical application in marine environments, where higher $Re$ are typical. Despite its simple design, the Purcell’s swimmer offers significant potential for real-world applications. Its long and slender design makes it an ideal tool for specialised subsea inspections, such as around offshore wind farms. This allows it to reach remote and confined underwater spaces that are otherwise inaccessible by conventional methods, much like other articulated robotic systems [3]. In broader aquatic settings such as lakes, reservoirs, and shallow seas, these robots, equipped with appropriate tools and sensors, could aid in ecological inspections, habitat monitoring, or even rescue missions for trapped species. In the same way as snake-like robots, their biologically mimetic behaviours enable them to blend seamlessly with the surrounding environment [31].

Nevertheless, effective deployment in these applications requires trajectory-following capabilities, which remain relatively unexplored for Purcell’s swimmers. Notably, in [32], the author identifies distinct gaits, described as piecewise functions, enabling the swimmer to trace square and circular trajectories through an open-loop control strategy that eliminates the need for feedback mechanisms. Complementing this research, an open-loop control approach is proposed in [14], which focuses on estimating swimmer displacement and rotation primitives. The study further advanced the understanding of trajectory generation by analytically determining the optimal number of primitive repetitions required to achieve the desired movement path. Despite this, no closed-loop control strategies have been applied to the Purcell’s swimmer for the purpose of following given trajectories. Furthermore, its unique locomotion, driven by specific motion primitives, requires that any control strategy explicitly account for these fundamental gaits to achieve effective navigation.

Given the characteristics of this robot, event-based control is a suitable closed-loop strategy for enhancing its path-following performance. This approach includes various methods that reduce resource use by executing control actions only when needed. Among these, event-triggered control has the widest adoption, whereby control updates occur when a system-dependent condition, such as a state or output error, exceeds a threshold [33,34]. Conversely, self-triggered control predicts the subsequent triggering instant based on the present state, thereby reducing the necessity for continuous monitoring. This feature is particularly advantageous in systems with limited sensing or computational resources. More recently, adaptive and learning-based event-triggered control has emerged as a promising direction, enabling controllers to adjust triggering conditions in real time based on environmental disturbances or system uncertainties, thereby improving robustness in dynamic settings [35]. Each approach has its own set of trade-offs in terms of implementation complexity, performance, and resource efficiency, making them suitable for different classes of systems and application domains. Several examples of application of event-based methods in controlling other categories of mobile robots can be found in [36,37], as well as robotic arms in [38,39].

In this context, the aim of this paper is twofold. Firstly, it involves the kinematic and dynamic study of the swimmer, alongside the fabrication of a 30 cm-length motor-driven prototype. Secondly, it proposes an event-based closed-loop control strategy for path following. This strategy employs a threshold-based logical condition that considers both position error and its rate of change to initiate new events. Its operation switches between translation and rotation primitives based on trajectory error, allowing real-time path correction when the swimmer deviates from the target path. Moreover, experimental validation using the motor-driven prototype confirmed the effectiveness of the strategy.

Thus, the main contributions of this paper, all contextualised within inertia-dominated environments, include the following:

• The design, modelling, and fabrication of a three-link Purcell’s swimmer prototype;
• The proposal and experimental validation of a closed-loop control strategy for path following.

This document is organised as follows. Section 2 provides the definition and kinematic modelling of a Purcell’s swimmer, alongside the theoretical movement of the classical swimmer and the basis of event-based control. Section 3 outlines the methodology employed in this work, detailing the mechanical design of the fabricated motor-driven Purcell’s swimmer prototype, the dynamic modelling of such swimmers, and the designed control strategy for path following. The results of both simulations and experiments are presented and discussed in Section 4. Finally, conclusions and future works are drawn in Section 5.

2. Background

This section is devoted to the description of a Purcell’s swimmer concerning its geometry and kinematics, followed by the fundamentals of event-based control.

2.1. Generalities of Purcell’s Swimmers

2.1.1. Geometry and Kinematics

The Purcell’s swimmer consists of three links connected by one degree-of-freedom (DOF) joints, as illustrated in Figure 1. The segments are designated from 0 to 2, being their lengths $l_0$, $l_1$, and $l_2$, while the rotational joints are designated as $j_1$ and $j_2$. A ratio calculated by $\eta =l_0/l$ relates the lengths of the links, being l the total length of the swimmer. The lateral links will be supposed of equal length.

The angular position of i-link with respect to the global X axis is represented by ${\theta }_i$. The rotation of the lateral links is dictated by a motion primitive (or gait), a function that defines the angles ${\varphi }_1$ and ${\varphi }_2$ over time. These local gait angles are related to the global angular positions through the following equations: ${\theta }_1={\varphi }_1-{\theta }_0$ and ${\theta }_2={\varphi }_2+{\theta }_0$.

The literature presents several motion primitives, often categorised into those for translation and those for rotation. Translation primitives enable the swimmer to advance along the X axis of its body-fixed reference frame, whereas rotation primitives induce a rotation of the central segment about the Z axis. Furthermore, these primitives are typically designated according to their graphical representation in the ${\varphi }_1$ and ${\varphi }_2$ plane. Among the translation primitives identified in the literature, this work employs the most frequently utilised one, known as the square primitive, as depicted in Figure 2a. Regarding the rotation primitive, a gait exhibiting a double-square form with central symmetry about the origin of the coordinate system has been adopted, as illustrated in Figure 2b. Their mathematical definitions can be found in Appendix A.

When assessing the dynamics of the swimmer, the angles ${\varphi }_1$ and ${\varphi }_2$ fully define the movement of links $l_1$ and $l_2$ relative to the central link. However, the central link position is undetermined. Considering the mathematical development in [30] and defining the position of the centre of i-link as ${\mathbf{X}}_i={\left[x_i{y}_i{\theta }_i\right]}^T$, the linear and angular velocities of the links can be expressed as follows [8,17,22]:

$${\dot{\mathbf{X}}}_i={\mathbf{A}}_i{\dot{\mathbf{X}}}_0+{\mathbf{B}}_i\dot{\mathbf{\Phi }}$$

(1)

where $\mathbf{\Phi }={\left[{\varphi }_1{\varphi }_2\right]}^T$, with $i=\{0,1,2\}$, referring subscript 0 to the central link of the Purcell’s swimmer. Matrices ${\mathbf{A}}_i$ and ${\mathbf{B}}_i$, defined in [17,30], vary depending on the link for which velocity is being calculated. Further details can be found in Appendix B.1.

Regarding the acceleration of i-link, it can be obtained through the derivative of ${\dot{\mathbf{X}}}_i$ and can be expressed, in matrix form, as follows:

$${\ddot{\mathbf{X}}}_i={\mathbf{C}}_i{\ddot{\mathbf{X}}}_0+{\mathbf{D}}_i{\dot{\mathbf{X}}}_0+{\mathbf{E}}_i\ddot{\mathbf{\Phi }}$$

(2)

being matrices ${\mathbf{C}}_i$, ${\mathbf{D}}_i$, and ${\mathbf{E}}_i$ defined in Appendix B.2.

Moreover, the squared velocity will be used to calculate environment forces, so its expression should be also obtained. The squared velocity of i-link can be expressed, in terms of the velocity of the central link and the gait angles, as follows:

$${\dot{\mathbf{X}}}_i^2={\mathbf{G}}_i{\dot{\mathbf{X}}}_0^2+{\mathbf{H}}_i{\dot{\mathbf{X}}}_0+{\mathbf{K}}_i{\dot{\mathbf{\Phi }}}^2$$

(3)

where matrices ${\mathbf{G}}_i$, ${\mathbf{H}}_i$, and ${\mathbf{K}}_i$ are also detailed in Appendix B.1.

2.1.2. Classical Results

The Purcell’s swimmer was initially conceived to navigate in viscosity-dominated environments. This implies that the dynamic model of the swimmer only takes into account the viscous forces present in the interaction between the fluid and the swimmer, resulting in a straightforward model that has been outlined in previous studies and facilitated the analysis of its movement in these environments [30,40].

The findings indicate that classical motion primitives, such as the aforementioned square, generate a net displacement of the swimmer along the X axis, thereby enabling forward movement in the fluid environment. The displacement of the midpoint of the central segment of the swimmer along each of its axes, as well as the rotation of the central segment, are shown in Figure 3 for a millimetre-length swimmer. As is evident, despite a larger X-displacement, non-null movement along the Y axis and rotation of the central segment are observed. This suggests that, by repeatedly applying the square primitive, the swimmer will move forward on the X axis while deflecting slightly on the Y axis. This hypothesis is supported by Figure 4, which depicts the $XY$ trajectory of the swimmer in the same conditions as Figure 3.

On another note, it is possible to achieve a rotation of the central segment of the swimmer to modify its orientation by considering other types of primitives, such as the bi-square primitive that was introduced above. The results subsequent to the implementation of this gait are also plotted in Figure 3. Similar to the square motion primitive, the bi-square gait produces non-null net motion along the other axes, thus resulting in the deviation of the swimmer in both the X and Y directions during the application of the primitive.

With regard to the trajectory of the Purcell’s swimmer, Figure 4 illustrates how the central segment traces a loop or figure-eight trajectory while implementing the square gait. This trajectory, which is characteristic of such a swimmer within viscosity-dominated environments, has been obtained both theoretically and experimentally [14,41].

2.2. Generalities of Event-Based Control

The event-driven control, as the name suggests, is based on the activation of a controller when an event occurs, that is, the triggering of an event determines the calculation of the control action [42]. An event is usually triggered by a logical condition that, in a generic form, can be expressed as follows:

$$(\mathrm{logical}\mathrm{condition}\mathrm{IS}\mathrm{true})\mathrm{OR}(h_{without}\ge h_{max})$$

(4)

This event-based condition determines that an event occurs when the logical condition becomes true or when the elapsed time without triggering the event, $h_{without}$, is equal or higher than a set time period, $h_{max}$. This condition has two terms: an asynchronous term (on the left), involving the logical condition, and a synchronous part (on the right), which is a safety condition that triggers the event. The safety condition is included to trigger the event when the logical condition never becomes true.

A basic scheme of an event-based controller would include a controller, the system, a sensor, and an event detector. The controller receives data from the event detector when a new event takes place, while the controller calculates the control action and sends it to the system. Finally, the sensor measures the system output every sampling period, $h_{sensor}$, and sends it to the event detector, in order to evaluate the logical condition. Concerning the activation of each element, the sensor and event detector are activated periodically in order to detect if a new event occurs. On the contrary, the controller is only active when the event detector registers an event.

The event-triggering condition defined in the event detector and the activation of each element will determine the functioning of the control loop. The main criteria to define the event-triggering condition can be found in [42,43,44], of which the three most commonly used are as follows:

• Immediate triggering, which means that the data are read or sent to the next element in the control loop just when it arrives.
• Periodic triggering, whereby the data are read or sent at every sampling period h.
• Logical condition-based triggering, which employs several criteria, such as threshold and absolute deadband, to initiate events. In the threshold condition, for example, an event occurs when the measured data surpass a specific fixed value, represented by $\mathsf{\Delta }$.

3. Methodology

This section deals with the methodology followed throughout this work. Firstly, details of the prototype design are given, followed by the description of the dynamic model of such a swimmer and the definition of the control strategy for path following.

3.1. Purcell’s Swimmer Prototype

The Purcell’s swimmer prototype fabricated in this work, shown in Figure 5, is composed of two parts, namely, the floating and submerged parts, which have different functions. On the one hand, the submerged part corresponds to the three segments that make up the swimmer, where the central one is immobile and the lateral links can rotate thanks to the actuators, DC motors in this case. The connection between the lateral segments and the motor shaft is done by an intermediate component and plastic screws. Due to geometrical constraints, the lateral segments can only rotate within the range $-\pi /2<{\varphi }_i<\pi /2$ rad. The three segments were designed with rectangular cross-section for better manufacturing.

The floating section, however, not only ensures a constant depth of the swimmer segments during experiments but also incorporates a sealed housing. This housing protects all electronic components and other elements susceptible to water damage. A press-fitted cover on the housing contains several markers used for tracking the movement of the robot during the experiments. The key electrical components are as follows:

• DC motors and driver: the lateral segments are rotated by 6 V low-power micro metal gearmotors from Pololu Robotics and Electronics(Pololu Corporation, Las Vegas, NV, USA).These motors, detailed in

  Table 1. Technical specifications of DC motors used for the prototype.

  Technical Specifications	Value	Units	Technical Specifications	Value	Units
  Rated voltage	6	V	Rated torque	0.7	kg·cm
  Gear ratio	100.37:1	-	Rated speed	90	rpm
  Speed at no load	155	rpm	Instantaneous torque	1.5	kg·cm
  Current at no load	60	mA

  , feature a 100:1 gearbox and a built-in incremental encoder. A Toshiba TB6612FNG driver (Toshiba Electronic Devices & Storage Corporation, Tokyo, Japan) powers these DC motors.
• Microcontroller: an Arduino Nano 33 IoT (Arduino AG, Lugano, Switzerland) serves as microcontroller, managing all its movements and functionalities. Its WiFi+Bluetooth module, along with its numerous digital pins (usable for interrupts) and pulse width modulation (PWM) pins, made it suitable for this application.
• Batteries: two 3.7 V batteries provide power to the robot.
• LEDs and buttons: several LEDs and push buttons were also included inside and outside the housing of the robot for diverse purposes. External indicators allow to switch the robot on/off, change or identify its operating mode, and check the WiFi connection status. Internally, push buttons function as limit switches, essential for initialising the motor position.

Concerning materials, the prototype housing, the lateral links, and the mechanical parts were mainly fabricated with polylactic acid (PLA), a material used for additive manufacturing in 3D printers, although tough resin was also used for the fabrication of certain pieces that required better mechanical properties.

The choice of segment lengths in Purcell’s swimmer has been the subject of prior optimisation studies, where the lateral segments were sized relative to the central segment and a specific motion primitive under viscosity-dominated conditions. These studies aimed to maximise metrics such as relative displacement, efficiency, or both, per cycle. In the present work, the length of the central link was fixed at 40.5 mm due to mechanical constraints: the DC motors were housed within this segment, and the distance between them could not be reduced. However, the overall length of the swimmer could still be adjusted by modifying the length of the lateral segments, offering greater design flexibility.

For the experiments conducted in this work, a greater length was chosen for the lateral segments (147.64 mm). This decision was mainly driven by the need to achieve larger absolute displacements, thus facilitating the observation, quantification, and swimmer motion analysis in the experimental setup. Furthermore, at this scale, factors such as the resolution of motion capture systems, interaction with the surrounding medium, and the physical limitations of the test bench make it more practical to work with a larger swimmer. Finally, a longer segment length also contributes to greater robustness of the system against small inaccuracies in fabrication or control, thereby improving the reproducibility of the experiments.

3.2. Modelling of a Purcell’s Swimmer

This section begins with some preliminaries regarding initial hypotheses and notation. Next, the environmental forces that arise from the interaction between the swimmer and the fluid are introduced. Finally, the dynamic model of Purcell’s three-link swimmer is developed.

3.2.1. Preliminaries

Let consider the following assumptions [45]:

• The fluid is viscid, incompressible, and irrotational in the inertial frame.
• The swimmer incorporates a floatation element designed to maintain the underwater components at a constant depth.
• The flow field is defined by a constant, irrotational fluid velocity.
• Boundary effects are considered negligible.
• The swimmer navigates within an inertia-dominated regime.

Let us consider the following notation: the fluid velocities in X and Y axes are denoted as $V_{f,x}$ and $V_{f,y}$, respectively; $V_{r,x,i}$ and $V_{r,y,i}$ are the relative linear velocities of i-link with respect to the fluid in X and Y directions; ${\dot{V}}_{r,x,i}$ and ${\dot{V}}_{r,y,i}$ represent the relative linear accelerations of i-link; and relative angular velocity and acceleration of i-link are denoted as ${\dot{\Theta }}_{r,i}$ and ${\ddot{\Theta }}_{r,i}$, respectively.

3.2.2. Environment Interaction

The interaction between swimming objects and fluid environments leads to the appearance of forces that oppose to the movement. Mainly, two types of hydrodynamic forces can be found in these regimes: added-mass (or virtual-mass) forces and drag (or viscous) forces. Hereafter, these forces will be described considering their application to a Purcell’s three-link swimmer.

The added-mass forces are opposed to the movement of the swimmer and represent the effective mass of the fluid that surrounds the swimmer and must be accelerated with it. These forces depend on the relative acceleration of the swimmer through the following expression [45,46]:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \left[\begin{array}{c}{f}_{a,x,i}\\ f_{a,y,i}\\ {\tau }_{a,i}\end{array}\right]=& -\left[\begin{array}{ccc}{c}_{a,i}^{\Vert }cos{\theta }_i& -c_{a,i}^{\perp }sin{\theta }_i& 0\\ c_{a,i}^{\Vert }sin{\theta }_i& c_{a,i}^{\perp }cos{\theta }_i& 0\\ 0& 0& c_{a,i}^{\circ }\end{array}\right]\left[\begin{array}{c}{\dot{V}}_{r,x,i}\\ {\dot{V}}_{r,y,i}\\ {\ddot{\Theta }}_{r,i}\end{array}\right]\hfill \end{array}\end{array}$$

(5)

where $f_{a,x,i}$, $f_{a,y,i}$, and ${\tau }_{a,i}$ are the added-mass forces in the X and Y axes and the generated torque, respectively. The added-mass coefficients of the i-link in the tangential and perpendicular direction have been named as $c_{a,i}^{\Vert }$ and $c_{a,i}^{\perp }$, respectively, while the added-mass torque coefficient is defined by $c_{a,i}^{\circ }$. These coefficients only depend on the body geometry [47].

The relative acceleration of the swimmer can be obtained, for each link, as follows [45]:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \left[\begin{array}{c}{\dot{V}}_{r,x,i}\\ {\dot{V}}_{r,y,i}\\ {\ddot{\Theta }}_{r,i}\end{array}\right]=& \left[\begin{array}{ccc}cos{\theta }_i& sin{\theta }_i& 0\\ -sin{\theta }_i& cos{\theta }_i& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{\ddot{x}}_i\\ {\ddot{y}}_i\\ {\ddot{\theta }}_i\end{array}\right]+{\dot{\theta }}_i\left[\begin{array}{ccc}-sin{\theta }_i& cos{\theta }_i& 0\\ -cos{\theta }_i& -sin{\theta }_i& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{c}{\dot{x}}_i-V_{f,x}\\ {\dot{y}}_i-V_{f,y}\\ {\dot{\theta }}_i\end{array}\right]\hfill \end{array}\end{array}$$

(6)

Notice that the influence of the flow field is incorporated in Equation (6) by subtracting the fluid velocity from the swimmer velocity, which is a common and straightforward method for modelling the effect of ocean currents on underwater robots [48,49].

Substituting this expression into (5), leads to the following:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \left[\begin{array}{c}{f}_{a,x,i}\\ f_{a,y,i}\\ {\tau }_{a,i}\end{array}\right]=& -\left[\begin{array}{ccc}{c}_{a,i}^{\Vert }{cos}^2{\theta }_i+c_{a,i}^{\perp }{sin}^2{\theta }_i& \left(c_{a,i}^{\Vert }-c_{a,i}^{\perp }\right)sin{\theta }_{i}cos{\theta }_i& 0\\ \left(c_{a,i}^{\Vert }-c_{a,i}^{\perp }\right)sin{\theta }_{i}cos{\theta }_i& c_{a,i}^{\Vert }{sin}^2{\theta }_i+c_{a,i}^{\perp }{cos}^2{\theta }_i& 0\\ 0& 0& c_{a,i}^{\circ }\end{array}\right]\left[\begin{array}{c}{\ddot{x}}_i\\ {\ddot{y}}_i\\ {\ddot{\theta }}_i\end{array}\right]\hfill \\ \hfill -& \dot{{\theta }_i}\left[\begin{array}{ccc}-\left(c_{a,i}^{\Vert }-c_{a,i}^{\perp }\right)sin{\theta }_{i}cos{\theta }_i& c_{a,i}^{\Vert }{cos}^2{\theta }_i+c_{a,i}^{\perp }{sin}^2{\theta }_i& 0\\ -c_{a,i}^{\Vert }{sin}^2{\theta }_i-c_{a,i}^{\perp }{cos}^2{\theta }_i& \left(c_{a,i}^{\Vert }-c_{a,i}^{\perp }\right)sin{\theta }_{i}cos{\theta }_i& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{c}{\dot{x}}_i-V_{f,x}\\ {\dot{y}}_i-V_{f,y}\\ {\dot{\theta }}_i\end{array}\right]\hfill \end{array}\end{array}$$

(7)

In order to simplify the equation, the matrices will be denoted as follows:

$${\mathbf{M}}_i=\left[\begin{array}{ccc}{c}_{a,i}^{\Vert }{cos}^2{\theta }_i+c_{a,i}^{\perp }{sin}^2{\theta }_i& \left(c_{a,i}^{\Vert }-c_{a,i}^{\perp }\right)cos{\theta }_{i}sin{\theta }_i& 0\\ \left(c_{a,i}^{\Vert }-c_{a,i}^{\perp }\right)cos{\theta }_{i}sin{\theta }_i& c_{a,i}^{\perp }{cos}^2{\theta }_i+c_{a,i}^{\Vert }{sin}^2{\theta }_i& 0\\ 0& 0& c_{a,i}^o\end{array}\right]$$

$${\mathbf{N}}_i=\left[\begin{array}{ccc}-\left(c_{a,i}^{\Vert }-c_{a,i}^{\perp }\right){\dot{\theta }}_{i}cos{\theta }_{i}sin{\theta }_i& c_{a,i}^{\Vert }{\dot{\theta }}_i{cos}^2{\theta }_i+c_{a,i}^{\perp }{\dot{\theta }}_i{sin}^2{\theta }_i& 0\\ -c_{a,i}^{\perp }{\dot{\theta }}_i{cos}^2{\theta }_i-c_{a,i}^{\Vert }{\dot{\theta }}_i{sin}^2{\theta }_i& \left(c_{a,i}^{\Vert }-c_{a,i}^{\perp }\right){\dot{\theta }}_{i}cos{\theta }_{i}sin{\theta }_i& 0\\ 0& 0& 0\end{array}\right]$$

And the equation of added-mass forces for i-link can be written as follows:

$${\mathbf{F}}_{a,i}=-{\mathbf{M}}_i{\ddot{\mathbf{X}}}_i-{\mathbf{N}}_i\left({\dot{\mathbf{X}}}_i-{\mathbf{V}}_f\right)$$

(8)

where ${\mathbf{F}}_{a,i}={\left[f_{a,x,i}{f}_{a,y,i}{\tau }_{a,i}\right]}^T$ and ${\mathbf{V}}_f={\left[V_{f,x}{V}_{f,y}0\right]}^T$.

The drag or viscous forces typically consist of two components, encompassing both linear and nonlinear effects: the linear effects depend only on the relative velocity of each link, while the nonlinear ones depend on the squared relative velocity.

The linear drag forces can be obtained from the resistive force theory (RFT) by means of the following expression:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \left[\begin{array}{c}{f}_{v,x,i}^I\\ f_{v,y,i}^I\\ {\tau }_{v,i}^I\end{array}\right]=& -\left[\begin{array}{ccc}{c}_{v,i}^{\Vert }cos{\theta }_i& -c_{v,i}^{\perp }sin{\theta }_i& 0\\ c_{v,i}^{\Vert }sin{\theta }_i& c_{v,i}^{\perp }cos{\theta }_i& 0\\ 0& 0& c_{v,l}^{\circ }\end{array}\right]\left[\begin{array}{c}{V}_{r,x,i}\\ V_{r,y,i}\\ {\dot{\Theta }}_{r,i}\end{array}\right]\hfill \end{array}\end{array}$$

(9)

being $f_{v,x,i}^I$ and $f_{v,y,i}^I$ the linear drag forces, ${\tau }_{v,i}^I$ the linear drag torque, $c_{v,i}^{\Vert }$ and $c_{v,i}^{\perp }$ the drag coefficients of the i-link in the tangential and perpendicular direction, respectively (both common to linear and nonlinear effects), and $c_{v,l}^{\circ }$ the drag torque parameter for linear effects. The relative velocity can be obtained, for each link, as follows [45]:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \left[\begin{array}{c}{V}_{r,x,i}\\ V_{r,y,i}\\ {\dot{\Theta }}_{r,i}\end{array}\right]=& \left[\begin{array}{ccc}cos{\theta }_i& sin{\theta }_i& 0\\ -sin{\theta }_i& cos{\theta }_i& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{\dot{x}}_i-V_{f,x}\\ {\dot{y}}_i-V_{f,y}\\ {\dot{\theta }}_i\end{array}\right]\hfill \end{array}\end{array}$$

(10)

Simplifying terms and joining forces and velocities in matrices, the total drag forces and torque can be calculated through the following [8]:

$${\mathbf{F}}_{v,i}^I=-{\mathbf{R}}_i^I\left({\dot{\mathbf{X}}}_i-{\mathbf{V}}_f\right)$$

(11)

where ${\mathbf{F}}_{v,i}^I={\left[f_{v,x,i}^I{f}_{v,y,i}^I{\tau }_{v,i}^I\right]}^T$ and ${\mathbf{R}}_i^I$, which is called the resistance tensor, is defined by the following:

$${\mathbf{R}}_i^I=\left[\begin{array}{ccc}{c}_{v,i}^{\perp }{sin}^2{\theta }_i+c_{v,i}^{\Vert }{cos}^2{\theta }_i& \left(c_{v,i}^{\Vert }-c_{v,i}^{\perp }\right)cos{\theta }_{i}sin{\theta }_i& 0\\ \left(c_{v,i}^{\Vert }-c_{v,i}^{\perp }\right)cos{\theta }_{i}sin{\theta }_i& c_{v,i}^{\perp }{cos}^2{\theta }_i+c_{v,i}^{\Vert }{sin}^2{\theta }_i& 0\\ 0& 0& c_{v,l}^{\circ }\end{array}\right]$$

Concerning nonlinear drag forces, they depend on the squared velocity of the swimmer unlike linear ones, and they can be calculated as follows [45]:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \left[\begin{array}{c}{f}_{v,x,i}^{II}\\ f_{v,y,i}^{II}\\ {\tau }_{v,i}^{II}\end{array}\right]=& -\left[\begin{array}{ccc}{c}_{v,i}^{\Vert }\mathrm{sgn}\left(V_{r,x,i}\right)cos{\theta }_i& -c_{v,i}^{\perp }\mathrm{sgn}\left(V_{r,y,i}\right)sin{\theta }_i& 0\\ c_{v,i}^{\Vert }\mathrm{sgn}\left(V_{r,x,i}\right)sin{\theta }_i& c_{v,i}^{\perp }\mathrm{sgn}\left(V_{r,y,i}\right)cos{\theta }_i& 0\\ 0& 0& c_{v,nl}^{\circ }\end{array}\right]\left[\begin{array}{c}{\dot{V}}_{r,x,i}^2\\ {\dot{V}}_{r,y,i}^2\\ {\ddot{\Theta }}_{r,i}^2\end{array}\right]\hfill \end{array}\end{array}$$

(12)

where $f_{v,x,i}^{II}$ and $f_{v,y,i}^{II}$ are the nonlinear drag forces, ${\tau }_{v,i}^{II}$ is the nonlinear drag torque, and $c_{v,nl}^{\circ }$ is the drag torque parameter for nonlinear effects. Substituting the squared relative velocity and expressing in matrix form, the nonlinear drag forces can be obtained as follows:

$${\mathbf{F}}_{v,i}^{II}=-{\mathbf{R}}_i^{II}{\left({\dot{\mathbf{X}}}_i-{\mathbf{V}}_f\right)}^2$$

(13)

where ${\mathbf{F}}_{v,i}^{II}={\left[f_{v,x,i}^{II}{f}_{v,y,i}^{II}{\tau }_{v,i}^{II}\right]}^T$ and matrix ${\mathbf{R}}_i^{II}$ is defined as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathbf{R}}_i^{II}=\left[\begin{array}{ccc}{c}_{v,i}^{\Vert }\mathrm{sgn}\left(V_{r,x,i}\right)cos{\theta }_{i}cos2{\theta }_i+c_{v,i}^{\perp }\mathrm{sgn}\left(V_{r,y,i}\right)sin{\theta }_{i}sin2{\theta }_i& c_{v,i}^{\Vert }\mathrm{sgn}\left(V_{r,x,i}\right)cos{\theta }_{i}sin2{\theta }_i-c_{v,i}^{\perp }\mathrm{sgn}\left(V_{r,y,i}\right)sin{\theta }_{i}cos2{\theta }_i& 0\\ c_{v,i}^{\Vert }\mathrm{sgn}\left(V_{r,x,i}\right)sin{\theta }_{i}cos2{\theta }_i-c_{v,i}^{\perp }\mathrm{sgn}\left(V_{r,y,i}\right)cos{\theta }_{i}sin2{\theta }_i& c_{v,i}^{\Vert }\mathrm{sgn}\left(V_{r,x,i}\right)sin{\theta }_{i}sin2{\theta }_i+c_{v,i}^{\perp }\mathrm{sgn}\left(V_{r,y,i}\right)cos{\theta }_{i}cos2{\theta }_i& 0\\ 0& 0& c_{v,nl}^{\circ }\end{array}\right]\end{array}\end{array}$$

3.2.3. Dynamic Model

Considering an inertia-dominated regime, both added-mass and drag forces must be taken into account in the environment interaction. According to second Newton law, the force balance for each link is given by the following:

$$m{\ddot{\mathbf{X}}}_0=\sum _{i=0}^2\left({\mathbf{F}}_{a,i}+{\mathbf{F}}_{v,i}^I+{\mathbf{F}}_{v,i}^{II}\right)$$

(14)

being m the mass of the robot [45]. Recalling expressions (8), (11), and (13) and substituting them into (14), the force balance equation can be rewritten as follows:

$$m{\ddot{\mathbf{X}}}_0=\sum _{i=0}^2\left[-{\mathbf{M}}_i{\ddot{\mathbf{X}}}_i-{\mathbf{N}}_i\left({\dot{\mathbf{X}}}_i-{\mathbf{V}}_f\right)-{\mathbf{R}}_i^I{\dot{\mathbf{X}}}_i-{\mathbf{R}}_i^{II}{\left({\dot{\mathbf{X}}}_i-{\mathbf{V}}_f\right)}^2\right]$$

(15)

Substituting the expressions of ${\dot{\mathbf{X}}}_i$, ${\dot{\mathbf{X}}}_i^2$, and ${\ddot{\mathbf{X}}}_i$ and solving for ${\ddot{\mathbf{X}}}_0$, the acceleration of the centre of the central link can be estimated as follows:

$${\ddot{\mathbf{X}}}_0={\displaystyle \frac{{\mathbf{P}}_D{\dot{\mathbf{X}}}_0+{\mathbf{Q}}_D\dot{\mathbf{\Phi }}+{\mathbf{Q}}_{DD}\ddot{\mathbf{\Phi }}+{\mathbf{N}}_i{\mathbf{V}}_f-{\sum }_{i=0}^2{\mathbf{R}}_i^{II}{\left({\mathbf{A}}_i{\dot{\mathbf{X}}}_0+{\mathbf{B}}_i\dot{\mathbf{\Phi }}-{\mathbf{V}}_f\right)}^2}{{\mathbf{P}}_{DD}}}$$

(16)

where the matrices are defined as follows:

$${\mathbf{P}}_D=-\sum _{i=0}^2\left[{\mathbf{M}}_i{\mathbf{D}}_i+\left({\mathbf{N}}_i+{\mathbf{R}}_i^I\right){\mathbf{A}}_i\right]$$

$${\mathbf{P}}_{DD}=\sum _{i=0}^2\left(m+{\mathbf{M}}_i{\mathbf{C}}_i\right)$$

$${\mathbf{Q}}_D=-\sum _{i=0}^2\left({\mathbf{N}}_i+{\mathbf{R}}_i^I\right){\mathbf{B}}_i$$

$${\mathbf{Q}}_{DD}=-\sum _{i=0}^2{\mathbf{M}}_i{\mathbf{E}}_i$$

3.3. Control Strategy for Path Following

This section details the closed-loop control strategy for path following, specifically addressing the control problem associated with Purcell’s swimmers.

3.3.1. Control Problem Formulation

In the reviewed literature, only primitives for translation and rotation of the centre of the central link of the Purcell’s swimmer have been found. This implies that any movement that the swimmer needs to make or any trajectory to be followed must be performed by executing such gaits.

Following straight paths with no inclination, while seemingly simple, is challenging because translation gaits inherently cause drift along the Y axis. Similarly, complex curved paths with varying curvatures and dimensions cannot be followed by relying solely on X-axis movement. The persistent Y-axis drift further complicates trajectory tracking, causing the swimmer to progressively deviate from its intended path. It is also important to note that all primitives must be executed completely from start to finish, meaning the swimmer must wait for one gait to conclude before initiating another. Finally, external factors like environmental disturbances or inertia can cause the swimmer to deviate from its path more significantly or earlier than anticipated during experiments.

Given this context, a closed-loop control strategy should be proposed that overcomes all these issues. The requirements that the designed control strategy should have are as follows:

• To correct deviations of the path followed by the robot with respect to the desired one in order to compensate possible drifts.
• To allow switching between different types of primitives.

Among the existing control strategies, event-based control allows the control action to be modified according to the fulfilment of a logical condition, so that it is possible to change, in this way, the motion primitive to be applied to the swimmer. Other control strategies provide control laws that do not allow to change the motion primitive, which is not useful for this application. Several examples of application of event-based methods in controlling other categories of mobile robots can be found in [36,37], as well as robotic arms in [38,39].

In this case, the logical condition of the event-driven control depends on the tracking error and its derivative to keep the robot on its path. If the error exceeds a set threshold, the motion primitive is adjusted to correct the trajectory and reduce deviations from drift or disturbances. This control also facilitates the use of the two types of primitives seen above: one when the tracking error is below the threshold, and the other when it is exceeded. Moreover, a key advantage is that the strategy allows for waiting for the current primitive to complete before recalculating the tracking error and deciding if a gait modification is needed.

3.3.2. Proposed Control Strategy

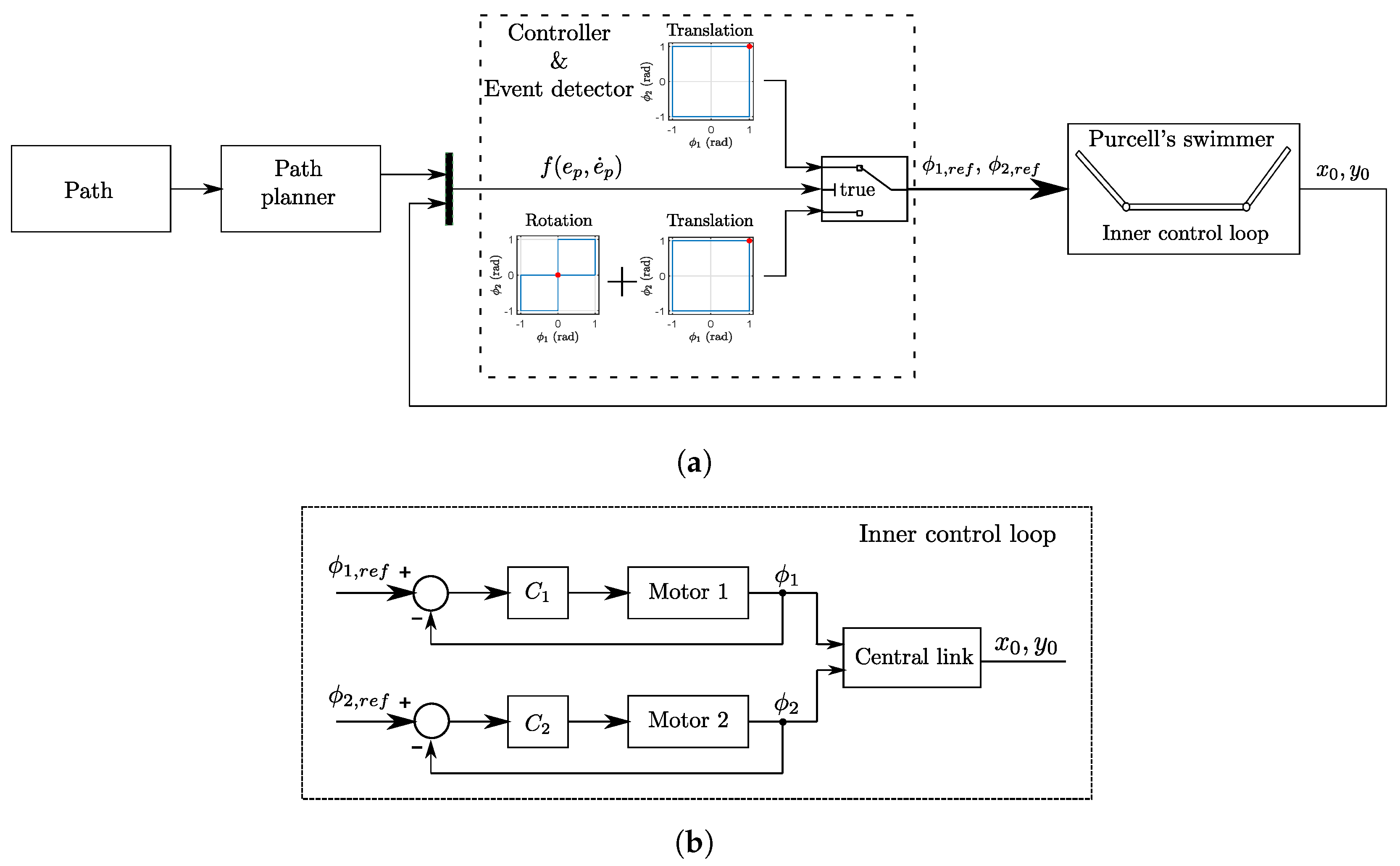
The proposed strategy for tracking a trajectory with the Purcell’s swimmer is an event-based control according to the scheme shown in Figure 6, where the triggering of the logical condition depends on two variables: the tracking error, better known as position error ($e_p$), and its derivative (${\dot{e}}_p$). Basically, the strategy consists of implementing a motion primitive for translation, when the swimmer is following or approaching the path, combined with the execution of a primitive for rotation, when it is further than a fixed distance and it is moving away from the trajectory. In other words, the proposed strategy switches between translation and rotation primitives depending on a logical function of $e_p$ and ${\dot{e}}_p$.

The first issue to be considered is the type of path, namely, straight or curved, to be followed by the swimmer. Due to the fact that the swimmer is only able to move in a rectilinear direction, the curvature of the path is important because, if the path is curved, it should be divided into a certain number of straight segments so that the swimmer can follow it. The number of segments into which the curved path is divided will depend on the precision desired for the movement of the swimmer. This task will be performed by the path planner.

Secondly, the event detector takes part and evaluates the following triggering condition:

$$f(e_p,{\dot{e}}_p)=\left(\right(|e_p|\ge \mathsf{\Delta })\mathrm{AND}({\dot{e}}_p>0))\mathrm{OR}\mathrm{new}\mathrm{segment}$$

(17)

where $\mathsf{\Delta }$ is the threshold. According to condition (17), a new event will occur when any of the following situations is met:

• The absolute value of $e_p$ is equal or higher than $\mathsf{\Delta }$ and its derivative is positive. In this situation, the event detector analyses if the swimmer is moving away from the trajectory, and both conditions concerning $e_p$ and ${\dot{e}}_p$ must be true for a new event to be detected. Should any of the aforementioned conditions not be met, that is, the swimmer is in proximity to the trajectory and within the threshold ($|e_p|<\mathsf{\Delta }$) or if it is approaching the trajectory, thus leading to a reduction in error (${\dot{e}}_p<0$), then any event occurs. The event triggering condition uses the error term ($e_p$) to ensure the robot remains within the specified $\mathsf{\Delta }$ of the trajectory. However, successive applications of rotation primitives, though necessary, can induce slight deviations that may cause the swimmer to drift significantly. By considering the derivative of the error (${\dot{e}}_p$), the strategy can opt to maintain translational movement when the swimmer is outside $\mathsf{\Delta }$ but approaching the trajectory, allowing it to naturally converge and re-enter the defined limits without unnecessary and potentially detrimental rotational adjustments.
• A new segment of the path must be followed, in order to redirect the swimmer to the direction of the new segment. This situation is necessary for those paths that are composed of multiple straight segments, such as compound or curved paths divided into straight segments.

The data sent to the event detector are the position of the centre of the central link of the swimmer in the $XY$ plane (${\mathbf{X}}_0$), and the event detector calculates the position error $e_p$ as the perpendicular distance between ${\mathbf{X}}_0$ and the path. Given that all the motion primitives have the same duration ($T_g$), the logical condition is evaluated periodically, after a motion primitive finishes. If the logical condition is not met, the controller proceeds with executing the translation primitive, as it assumes that the orientation of the swimmer is adequate and, therefore, the swimmer follows the desired path. On the contrary, if the logical condition is met, the controller applies a rotation primitive to adjust the swimmer orientation and rectify its motion in accordance with the desired path.

For comparison purposes and to validate the control strategy, both the tracking error and the mean square error (MSE) have been taken as performance indices, where the latter was given by the following definition:

$$\mathrm{MSE}={\displaystyle \frac{1}{n}}\sum _{k=1}^n{e}_{p,k}^2$$

(18)

where n is the number of samples.

In between two events, any data are sent to the controller. Nevertheless, the lateral links of the Purcell’s swimmer should be rotating at every instant, as they are implementing the motion primitive. To solve this, two control loops have been considered, as shown in Figure 6. The outer loop (Figure 6a) is the event-based controller, and determines the primitive that the swimmer should implement to follow the trajectory. The inner loop (Figure 6b) is a proportional-derivative (PD) controller that works at every instant to control the rotation of the lateral links, to ensure that the swimmer is implementing a motion primitive.

Concerning the inner control loop, the position of each of the DC motors was firstly identified as a second order system defined as follows:

$$G_p\left(s\right)={\displaystyle \frac{K}{s(\tau s+1)}}$$

(19)

being $\tau$ and K the time constant and the DC gain, respectively.

Secondly, a PD controller of the following form:

$$C\left(s\right)=K_P\left(1+T_{D}s\right)$$

(20)

where $K_P$ and $T_D$ are the proportional and the derivative time constants, respectively, was tuned using the root locus method to a settling time of about 0.5 s with no overshoot as design specifications for a step response of $\pi /2$ rad because of the geometrical constraints of the lateral links. The parameters of the system and the controller are indicated in

Table 2. Identification and controller parameters for both actuators of the motor-driven prototype. M1 refers to the motor that rotates segment $l_1$, while M2 rotates $l_2$.

Parameters	M1	M2
K	0.2935	0.2730
$\tau$	0.0655	0.068
$K_P$	19.5	20.0
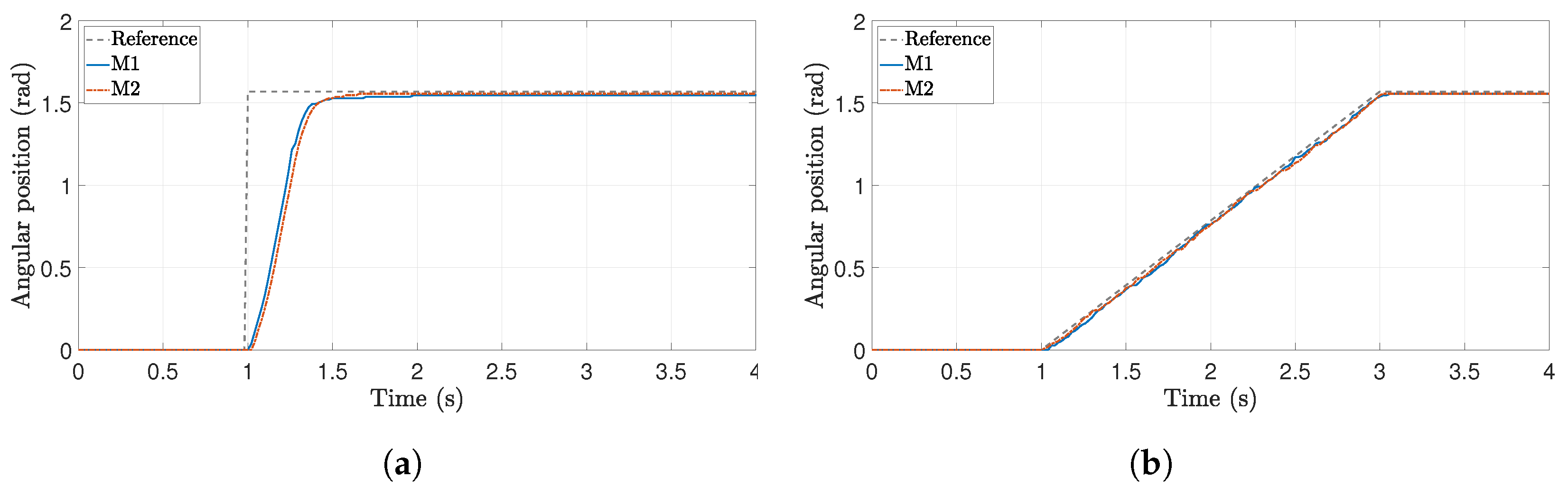
$T_D$	0.02	0.02

, where M1 and M2 refer to the motor that rotates $l_1$ and $l_2$, respectively. The responses of both motors applying the PD controllers are shown in Figure 7a, for a step reference, and in Figure 7b, for a ramp one. As can be observed, the design specifications are fulfilled.

4. Results

This section covers the results obtained in both simulations and experiments carried out with the motor-driven prototype.

4.1. Simulations

To conduct open-loop simulations of the Purcell’s swimmer, dynamic model (14) was simulated in MATLAB ^® in its R2022b version by solving the differential equation through the Runge–Kutta method. The simulation parameters indicated in

Table 3. Parameters used for motor-driven prototype simulations and experiments.

Water		Swimmer		Gaits
Parameter	Value	Parameter	Value	Parameter	Value
Density ($\rho$)	1000 kg/m3	Total length (l)	335.78 mm	Amplitude ($ϵ$)	$\pi$/3 rad
Dynamic viscosity ($\mu$)	1.002 · ${10}^{-3}$ kg/m·s	Relation between links ($\eta$)	0.1206	Period ($T_g$)	4 s
		Mass of the robot (m)	0.479 kg

were considered for the fluid, geometry of the swimmer, and motion primitives. In addition, the drag coefficients were estimated through COMSOL Multiphysics^® version 5.5 as detailed in [50], while the added-mass coefficients were approximated to those of a slender body, defined as follows [47]:

$$c_{a,i}^{\Vert }=0;c_{a,i}^{\perp }={\displaystyle \frac{1}{4}}\pi \rho l_i^2;c_{a,i}^{\circ }={\displaystyle \frac{1}{128}}\pi \rho l_i^4$$

The added mass of a slender body in the longitudinal direction, i.e., X axis, can be neglected in comparison to the body mass, so the added mass coefficient in this direction was approximated to zero [45,47].

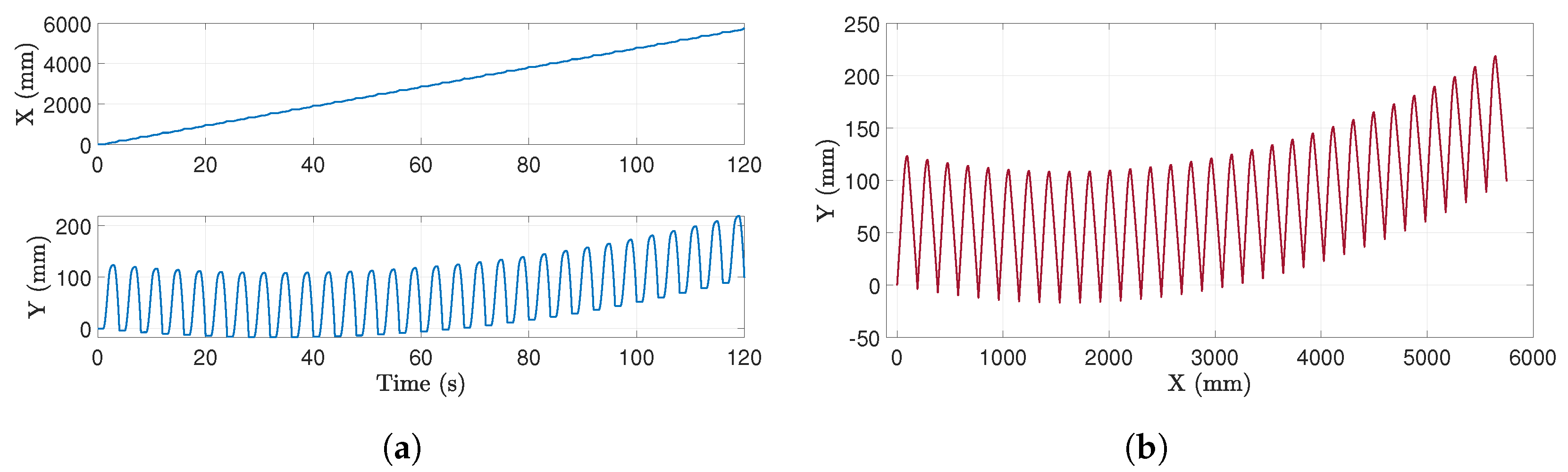
The simulation results implementing the clockwise square gait are shown in Figure 8, where the displacement in X and Y axes and the trajectory followed by the centre of the central link have been plotted. The data in Figure 8a corroborate the idea that a positive net displacement on the X axis is consistently achieved. The total displacement achieved is $5.75$ m along the X axis, while the displacement with a single gait repetition is $0.19$ m. Additionally, an oscillatory motion along the Y axis, typical of motion primitives, is evident. The amplitude of these oscillations, which is dependent on the dimensions of the swimmer, attains approximately $0.12$ m in this case, aligning with its dimensions.

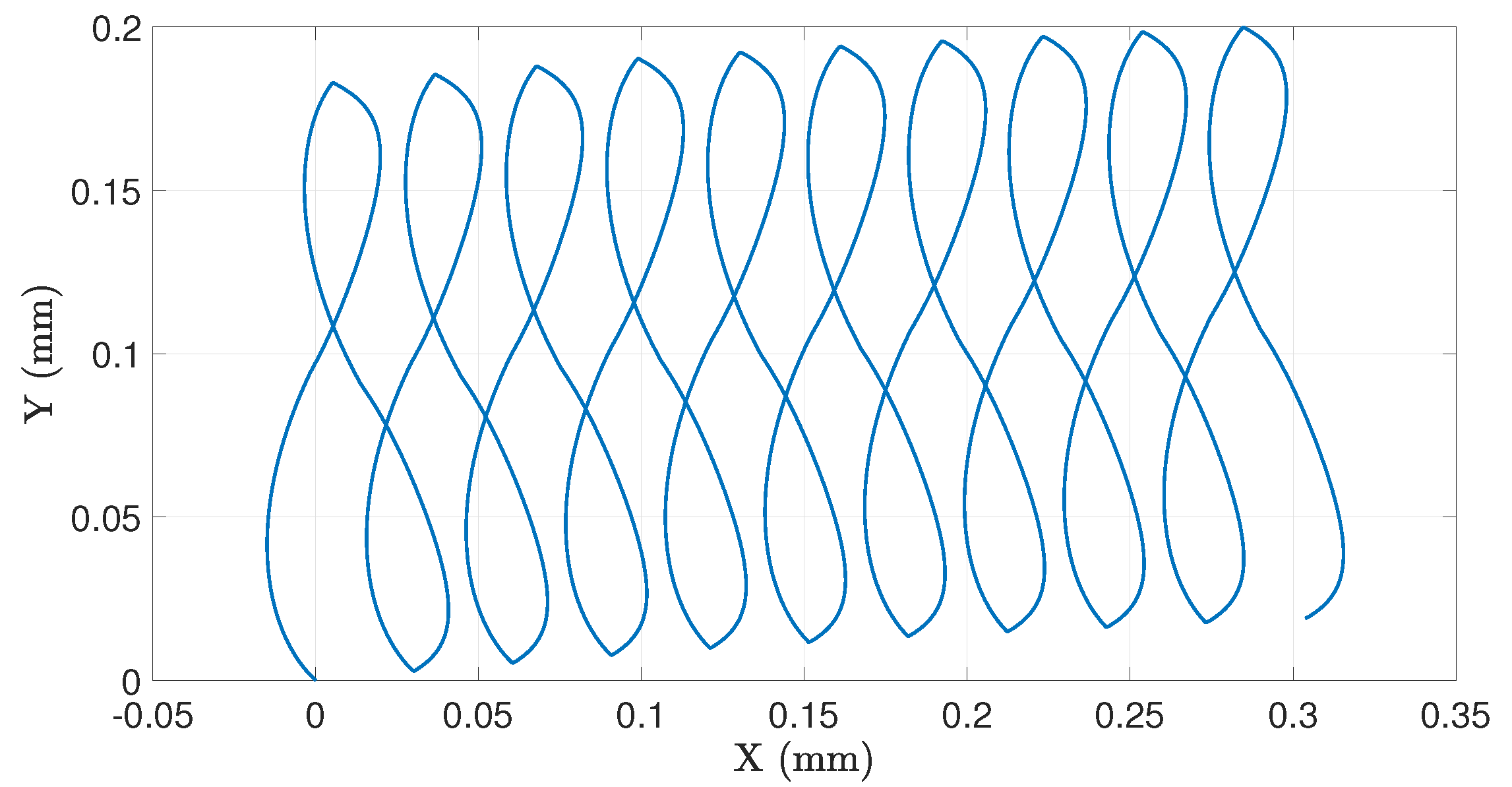
Concerning the trajectory observed in Figure 8b, it deviates from that characteristic of viscosity-dominated regimes. Under these conditions, the swimmer typically traces distinctive figure-eight loops (as depicted in Figure 4). In the present case, however, the loops exhibit a greater spatial extent and fail to close upon completion of the motion primitive, resulting in a trajectory resembling a sawtooth pattern.

Finally, it is evident from Figure 8b that the mean trajectory deviates from the $Y=0$ axis instead of following a straight line. This behaviour is consistent with results observed in viscosity-dominated regimes, which were considered in the development of the closed-loop path following strategy. For this specific experiment, the final positive Y-axis drift amounts to 10 cm, although the direction and magnitude of the drift vary throughout the simulation period.

In order to assess how external disturbances (specifically, the presence of a uniform flow field) affect the displacement and trajectory of the swimmer, several open-loop simulations under different fluid velocities and directions were conducted. The results are presented in Figure 9 and

Table 4. Comparison of the simulation results considering different fluid velocities and directions.

${\mathit{V}}_{\mathit{f},\mathit{x}}$ (m/s)	${\mathit{V}}_{\mathit{f},\mathit{y}}$ (m/s)	$\mathsf{\Delta }{\mathit{x}}_0$ (mm)	Reduction in $\mathsf{\Delta }{\mathit{x}}_0$ with Respect to Reference Case	$\mathsf{\Delta }{\mathit{y}}_0$ (mm)	Amplitude of Y Oscillations (mm)
0	0	5749.8	-	99.09	120
$-0.01$	0	4703.7	18.2%	1165.8	119–152
0	$-0.01$	5522.6	4.0%	$-440.3$	111–132
$-0.01$	$-0.01$	4483.1	22.0%	623.1	122–137

. A noticeable impact of the fluid flow on the net displacement and trajectory of the swimmer is shown in Figure 9 in comparison with Figure 8b, with the extent and direction of the deviation depending on the orientation of the flow relative to the motion of the swimmer. Notably, although the selected fluid velocity ($0.01$ m/s) may appear small in absolute terms, it is considerably high when compared to the size and mass of the swimmer. Nevertheless, the characteristic sawtooth-shaped trajectory remains qualitatively preserved in all cases, indicating that the locomotion pattern is robust to moderate flows.

Table 4 shows a comparison of the displacement and amplitude of oscillations between the case with null fluid velocity and the simulations performed. Focusing on the displacement along the X-axis (since the applied primitive corresponds to translation), it can be observed that, in all cases where $V_f\ne 0$, the net X-displacement decreases compared to the reference case ($V_f=0$), with reductions ranging from 4% to 22%. Regarding the Y-axis, the displacement increases consistently across all flow conditions, indicating that the swimmer deviates more significantly when exposed to external disturbances. Moreover, the amplitude of the characteristic sawtooth oscillations in the Y direction also increases, from values around 120 mm in the reference case to up to 152 mm under flow. These findings highlight the importance of implementing closed-loop control strategies to effectively regulate the trajectory of the swimmer and compensate for deviations caused by environmental disturbances.

4.2. Experiments

The experimental procedures and findings derived from testing the motor-driven prototype are covered in this section.

4.2.1. Types of Experiments

This section details the experimental procedures performed with the motor-driven prototype. Specifically, two distinct categories of experiments were conducted:

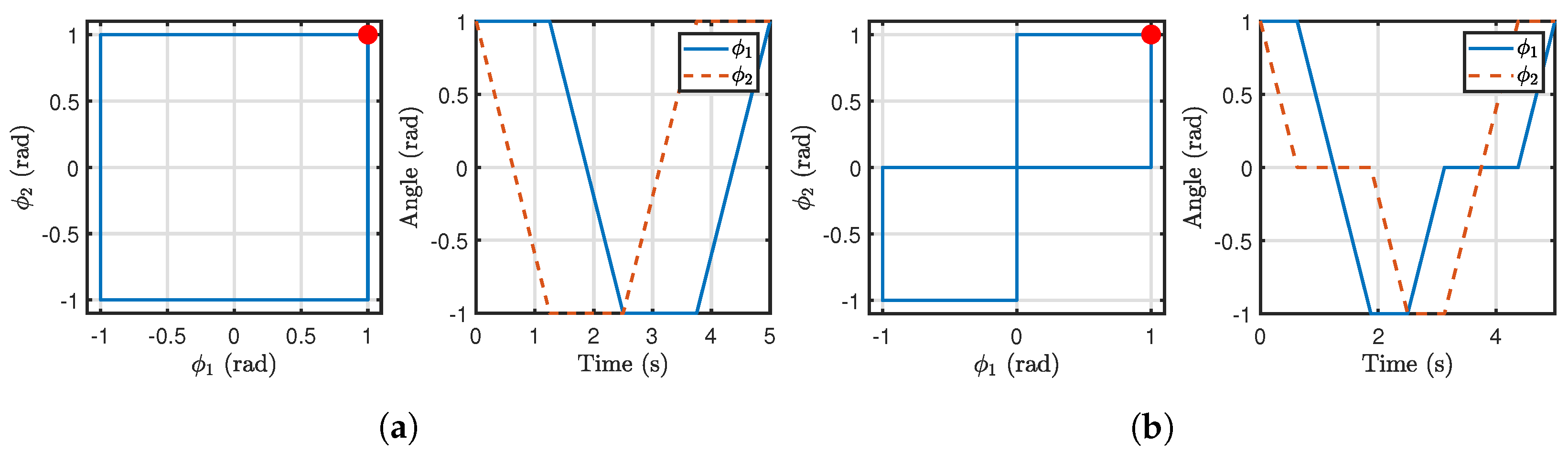
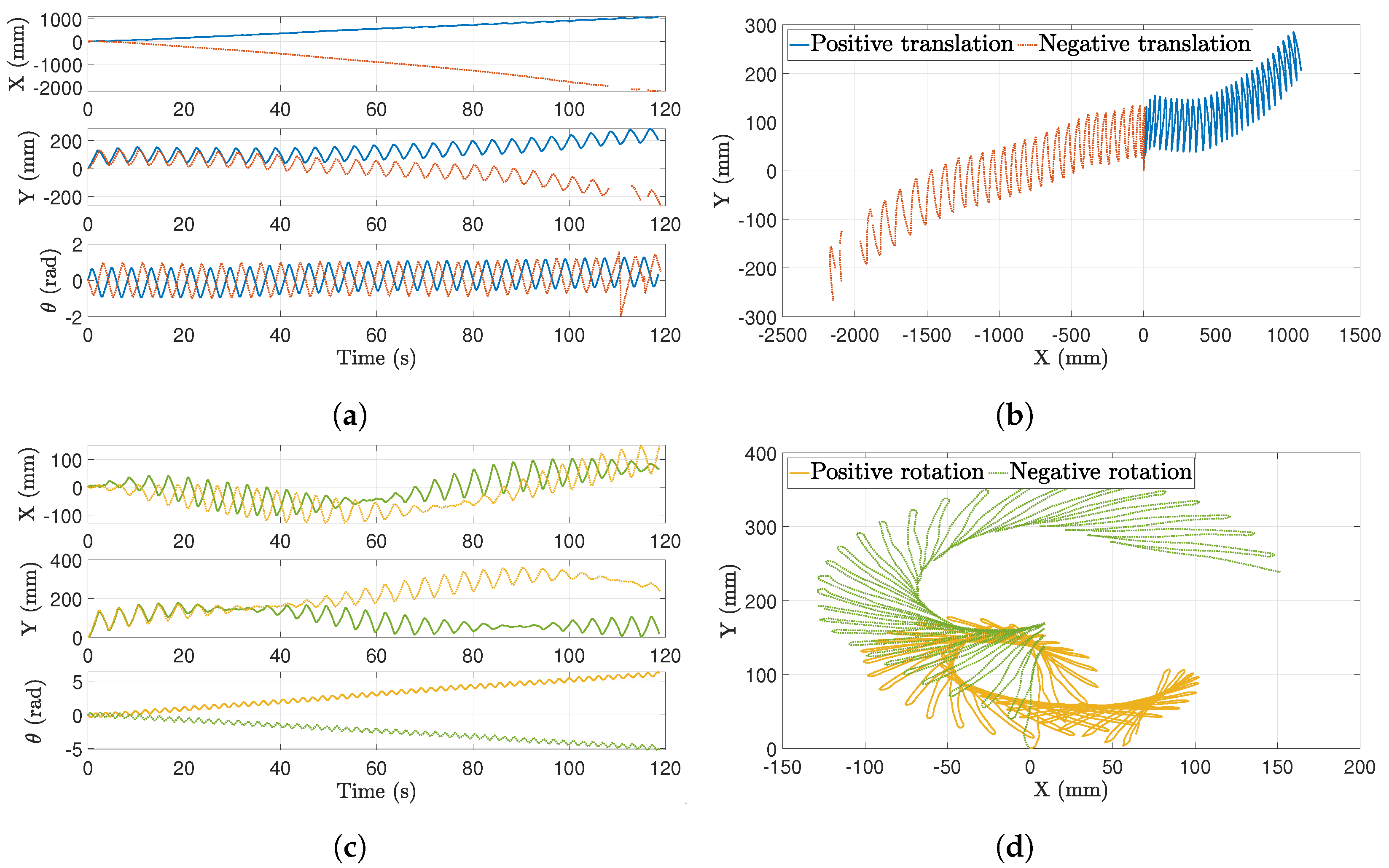
• Open-loop experiments: The first experiments carried out with the motor-driven prototype consisted of implementing the translation and rotation primitives that will be used for path following, with the aim of verifying that the direction of the swimmer displacement corresponds to that observed in simulations. Specifically, the square and bi-square primitives from Figure 2 were implemented for translation and rotation, respectively, applying them in clockwise or counterclockwise to obtain displacements in different directions. Hereafter, the translation primitives that provide positive displacement in X axis will be named as positive translation primitives, while those that produce a counterclockwise increase in the swimmer orientation will be called positive rotation primitives, and vice versa. These gaits were repeatedly applied a total of 30 times.
• Closed-loop experiments: The second type of experiments were carried out to verify the validity of the path following control algorithm. The square and bi-square motion primitives were implemented for translation and rotation of the robot, respectively. Concerning the path to be followed, three types of straight paths were considered to check that the robot was able to follow the trajectories, which were as follows:

  (a)

  A simple trajectory with no inclination, where the robot only has to change direction if it deviates.

  (b)

  A 45° inclined trajectory, for which the robot has to make an initial turn and position itself in the same direction as the path to be followed, and then implement the path following control algorithm in the same way as for the trajectory with no inclination.

  (c)

  A path consisting of two straight segments through a combination of the two previous ones, i.e., a first inclined segment and a second segment with zero slope, in order to check the transition from one segment to the other at different angles of inclination.

4.2.2. Equipments

Figure 10 shows the setup used for the experiments with the motor-driven prototype. As can be observed, it consists of the following:

• A pool filled with water, as observed in Figure 10a. Due to the dimensions of the prototype, it was necessary to carry out the experiments in a large tank that would allow the robot to move without any possible interference from nearby walls. To this end, the facilities at the University of Castilla-La Mancha (Spain) were used, specifically a pool measuring approximately $3\times 5$ metres, large enough to allow the robot to move freely. The height of the pool, approximately 1 m, is also suitable so that the bottom does not interfere with the rotation of the lateral segments of the swimmer when the pool is fully or partially filled.
• A motion capture system to detect the position of the robot at each stage of the experiment. For this purpose, a four-camera system from Qualisys (Qualisys AB, Gothenburg, Sweden) was deployed, as visualised in Figure 10a, which is capable of detecting the position of the markers placed in the prototype cover, as seen in Figure 10b. The software that allows to capture, visualise and record the position of the markers in real time is Qualisys Track Manager (QTM). The acquired position can also be sent in real time to other softwares, such as LabVIEW or MATLAB^®, facilitating the development of closed-loop experiments. In this case, LabVIEW 2020 was used to communicate with the robot in real time.
• A computer to run QTM version 2020.3 and LabVIEW 2020 softwares as seen in Figure 10c. In addition, the computer was used to process the data collected in the experiments using MATLAB^®, which was also installed on the computer.

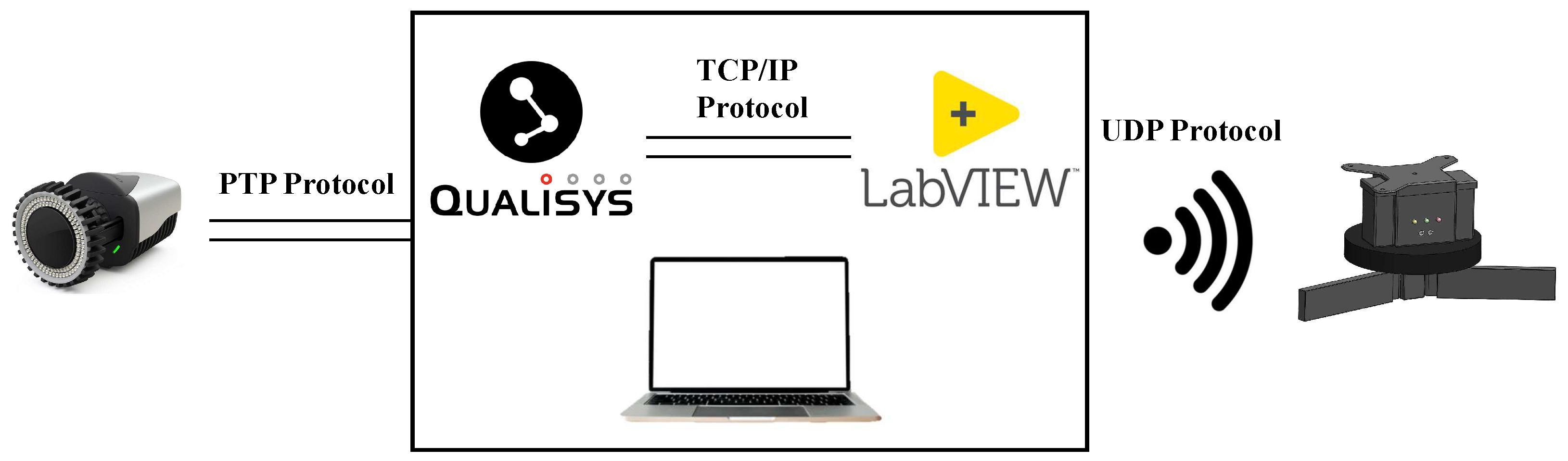
A communication protocol was developed to enable closed-loop experiments and transmit the position of the robot, as detected by the motion capture system, to the robot. This protocol, represented in Figure 11, consisted of three phases: cameras-QTM, QTM-LabVIEW, and LabVIEW-Arduino. Firstly, the cameras communicated with the QTM software using the precision time protocol (PTP) and an Ethernet connection. Then, QTM communicated in real time with LabVIEW via the transmission control protocol/internet protocol (TCP/IP). Lastly, the communication between the computer and the robot was done through LabVIEW. To do this, it was necessary to integrate the exchange of data with both QTM and the robot in the same LabVIEW file. This communication was performed through the user data protocol (UDP) via WiFi.

To ensure reliable communication, a crucial step was selecting the optimal frequency for data exchange between QTM and LabVIEW. A 10 Hz frequency was chosen to prevent data loss or buffer accumulation, which could lead to the control strategy operating incorrectly. Higher frequencies tested resulted in communication delays due to LabVIEW processing limitations. Thus, 10 Hz proved to be the maximum viable frequency for these specific experiments to avoid such drawbacks and ensure the correct execution of the control strategy.

4.2.3. Motion Primitives Experiments

The linear and angular displacements over time of the central link for the four primitives implemented in these experiments are plotted in Figure 12, while the net displacements are tabulated in

Table 5. Experimental net displacement for translation and rotation gaits, extracted from Figure 12.

Gait	$\mathsf{\Delta }{\mathit{x}}_0$ (mm)	$\mathsf{\Delta }{\mathit{x}}_0$/gait (mm)	$\mathsf{\Delta }{\mathit{y}}_0$ (mm)	$\mathsf{\Delta }{\mathit{y}}_0$/gait (mm)	$\mathsf{\Delta }{\mathit{\theta }}_0$ (rad)	$\mathsf{\Delta }{\mathit{\theta }}_0$/gait (rad)
Positive translation	1091.50	36.38	204.95	6.83	0.33	0.011
Negative translation	$-2149.95$	$-71.67$	$-268.25$	$-8.94$	0.48	0.016
Positive rotation	64.18	2.14	19.19	0.64	6.24	0.208
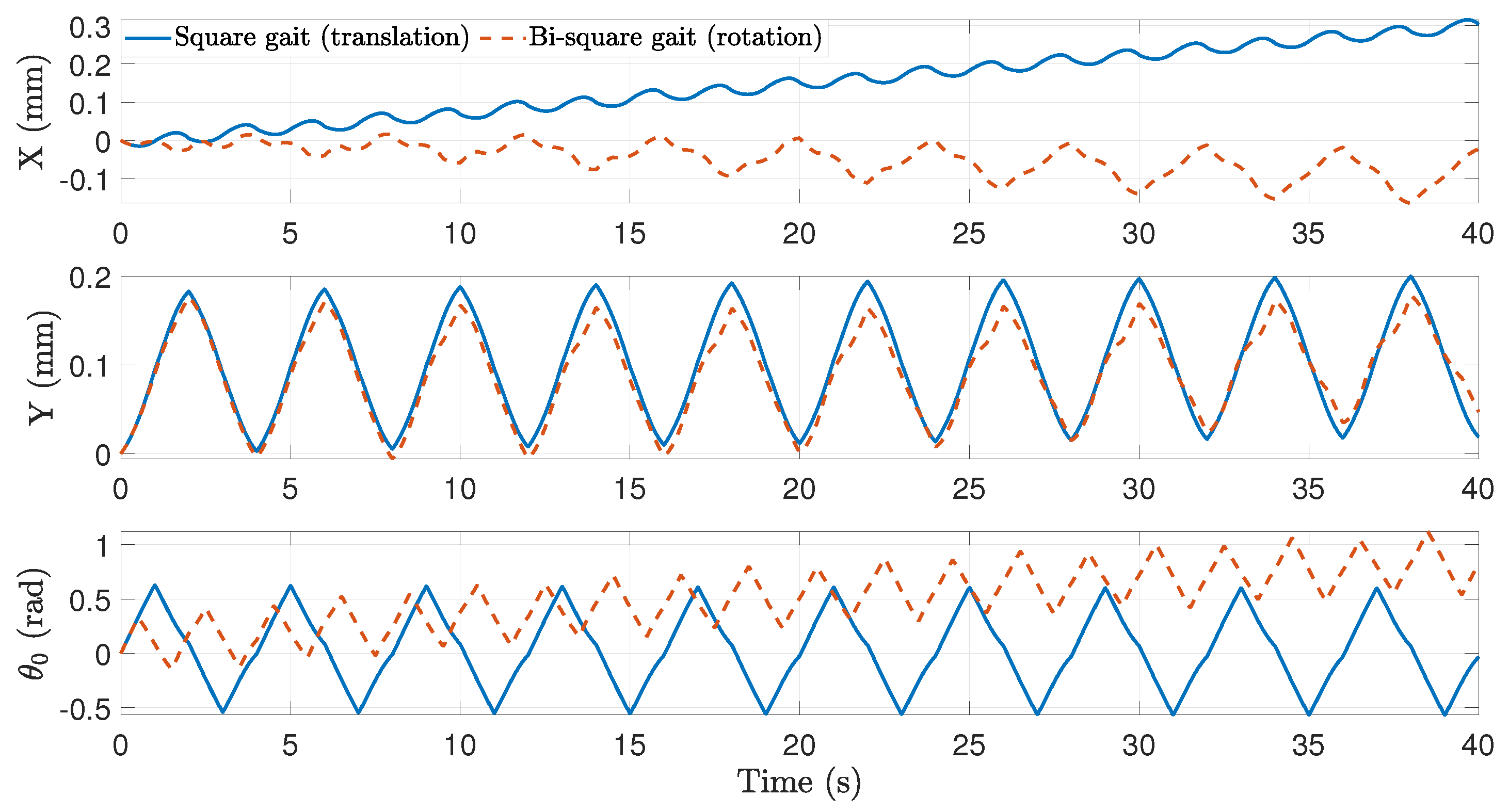
Negative rotation	151.50	5.05	238.55	7.95	$-4.94$	$-0.16$

. Similar to the simulations results, the swimmer does not trace the eight-shape loop of the viscosity-dominated case. Instead, the trajectory followed by the centre of the central link is composed of upward and downward movements similar to a sawtooth pattern, as already observed in simulations. The amplitude of these movements, although it differs throughout the experiments, achieved approximately 10 cm and is consistent with the dimensions of the swimmer.

In the case of the translation primitives shown in Figure 12a,b, it can be observed that the direction of the displacement in the X axis coincides with that obtained with the simulated model, i.e., the primitive for positive translation coincides with that applied theoretically, which is the clockwise square gait, while the primitive for negative translation is the counterclockwise square gait. Moreover, it can be seen that, in both cases, there is a drift in the Y axis, as already observed in the simulations, as well as a slight change in the orientation of the central segment.

However, the amplitude of the displacement is not consistent with the model or between the experiments themselves: since the primitives are the same but applied in opposite directions, it would be expected that the displacements would be also the same, but in opposite directions. Nevertheless, this is not reflected in the results, where it can be seen that the robot moves twice as much in the X axis with the negative translation primitive than with the positive translation gait (see Table 5). This asymmetry could be likely caused by small fabrication inaccuracies in the prototype, particularly a non-uniform mass distribution across the swimmer, which may shift the centre of mass and lead to direction-dependent inertial effects. Such asymmetries are difficult to avoid in physical implementations, especially at this scale, and are amplified under open-loop conditions where no corrective feedback is applied. These results highlight the limitations of open-loop execution and motivate the use of a closed-loop strategy to correct trajectory deviations caused by structural imbalances or external disturbances.

Regarding the rotation primitives, whose results are illustrated in Figure 12c,d, it can be seen that the positive rotation primitive causes a positive change of orientation of the central segment of the robot, and the opposite occurs for the negative rotation primitive. As for the amplitude of the angular displacement, in this case it is similar for both primitives, around 5–6 rad in absolute values. It is also observed that there is a drift in X and Y axes, positive in both cases and of greater amplitude for the negative rotation primitive.

In view of the results obtained for the translation and rotation primitives, it is worth clarifying the following:

• With respect to the translation primitives, the above results do not affect path following, since the control strategy should be able to correct the direction of the robot movement regardless of how far it moves in the $XY$ plane and its angular position. What is important in this case is that there is a net displacement in the X axis that is greater than that in the other axes.
• For rotation primitives, considering the dimensions of the robot and the angular displacement achieved, the drifts in X and Y axes can be neglected and will not affect, to a large extent, path following experiments.

4.2.4. Path Following Experiments

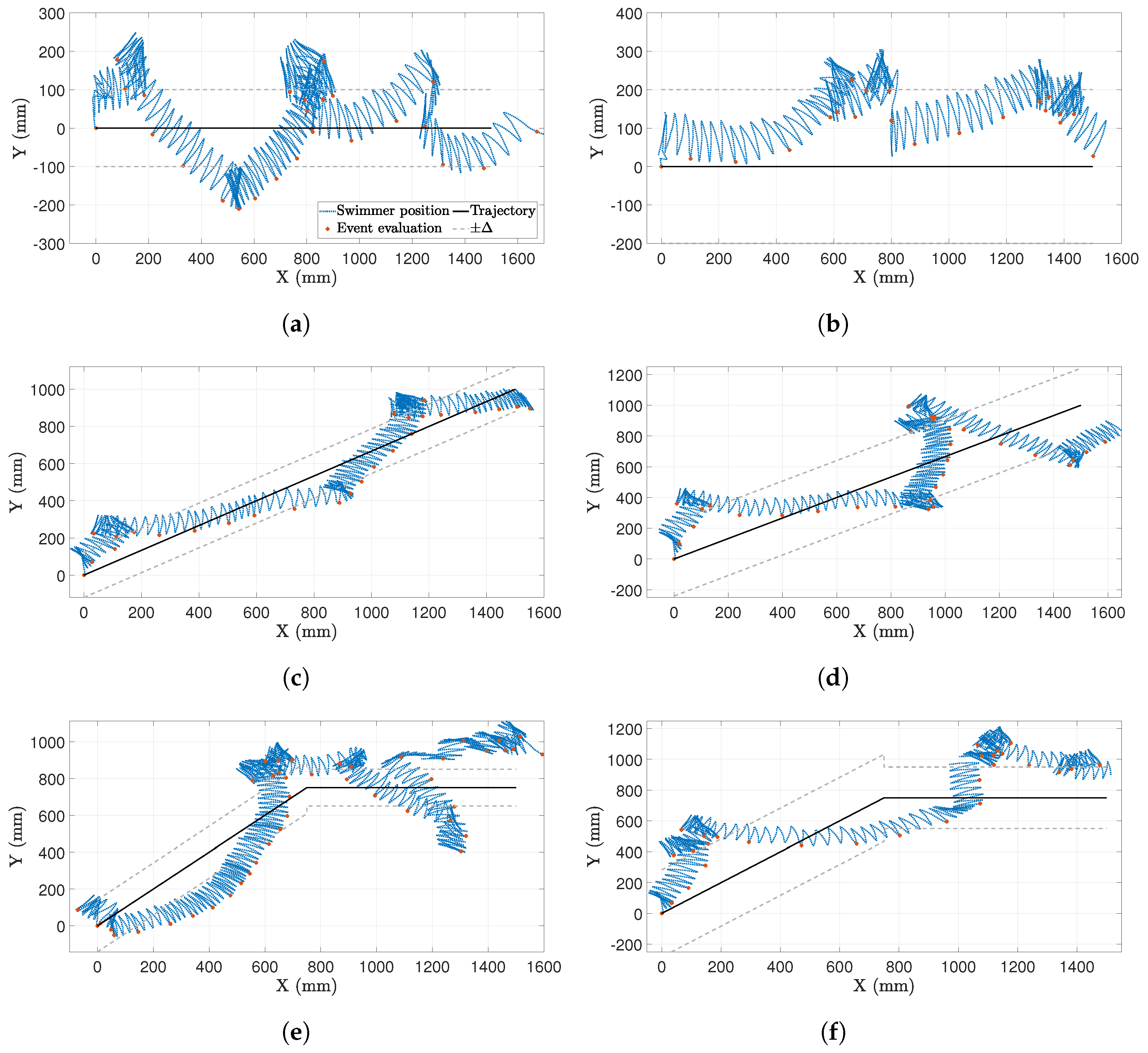
The results of the closed-loop experiments are depicted in Figure 13, where the swimmer trajectory has been represented in blue colour and the red marks correspond to the event detector activation. Evidently, this was not performed after the completion of each gait. These and other modifications to the original strategy were conducted and are indicated below:

• To optimise data exchange between the interacting elements, the control strategy evaluation was not performed after each individual gait execution. Instead, it was determined to wait until four repetitions of the motion primitives were completed, to prevent saturation of the information exchange between the motion capture system and the robot.
• Two threshold values were considered for the experiments: ${\mathsf{\Delta }}_1=l/3.35=100$ mm and ${\mathsf{\Delta }}_2=l/1.68=200$ mm, which will also be referred to as case 1 and 2, respectively. The rationale for selecting these specific threshold values stems from the observed deviations in both simulations and physical experiments. The Y-axis drift per motion primitive exhibits variability between these two contexts. In simulations, this drift ranges from $0.1$ mm in the middle of the simulations to $10.41$ mm at the end, suggesting a maximum potential cumulative drift of $41.64$ mm over four consecutive primitive executions, as planned for the experiments. Notably, the experimental open-loop application of the square primitive reveals even larger deviations, reaching up to 11 mm per primitive, which extrapolates to 44 mm over four repetitions. Consequently, selecting a threshold below 44 mm would likely trigger a new control event and necessitate the application of the rotation primitive at each evaluation of the control strategy. Consequently, thresholds exceeding this critical value, specifically ranging from approximately two to five times the 44 mm-drift, were chosen to avoid excessive and potentially destabilising activation of the rotation primitive.

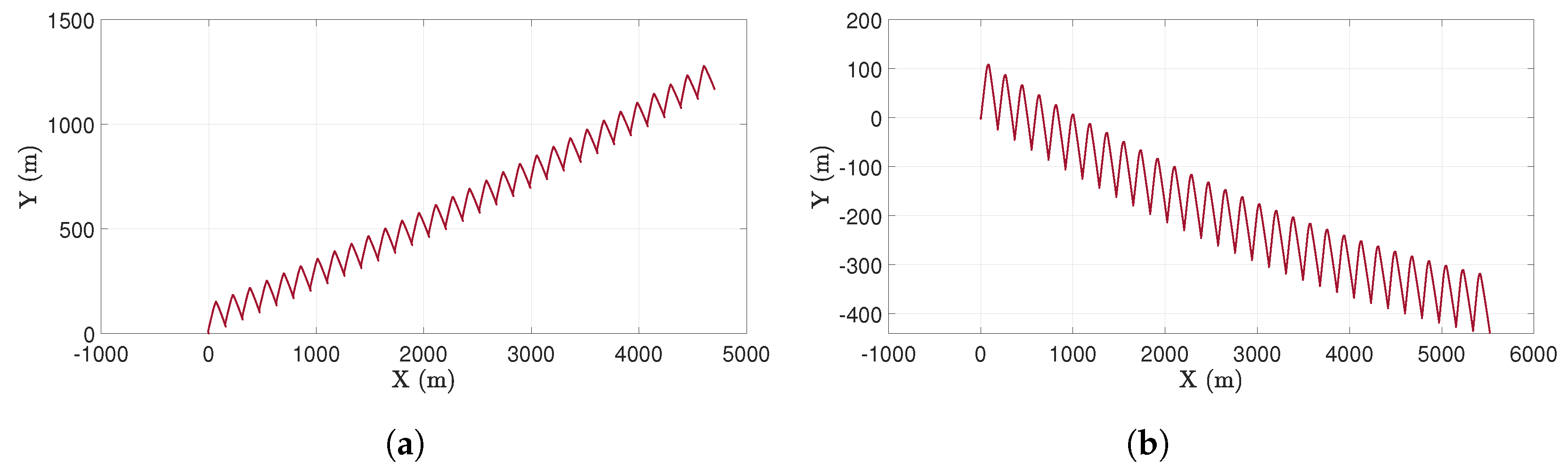
Figure 13 shows case 1 results in left column and case 2 in the right column. As can be observed, the following conclusions can be drawn:

• Path with no inclination (Figure 13a,b): The results indicate that a lower $\mathsf{\Delta }$ led to a higher frequency of robot rotations. This is attributed to the earlier exceedance of $\mathsf{\Delta }$, necessitating more frequent reorientations towards the desired path. Specifically, case 1 (Figure 13a) exhibited a total of four rotations, whereas case 2 (Figure 13b) involved three rotations. The second rotation in case 2 was required because the initial reorientation was insufficient to maintain the trajectory of the swimmer, leading to further deviation and a subsequent need for correction (evident in the X range of 600–800 mm in Figure 13b).
• Inclined path (in Figure 13c,d): The robot successfully followed the inclined path for both $\mathsf{\Delta }$ values, with highly similar trajectories observed in both cases. However, in case 2 (Figure 13d), the swimmer executed one additional rotation compared to case 1. This supplementary rotation occurred near the end of the trajectory due to a deviation away from the desired path. For the remaining rotations along the inclined paths, their timing was notably consistent across both $\mathsf{\Delta }$ values.
• Combined path (see Figure 13e,f): The swimmer exhibited superior performance in case 2, as depicted in Figure 13f. Initially, the robot rotated at the beginning of the first inclined segment to align its angular orientation and achieve a slope comparable to the desired trajectory. Subsequently, it continued with translational motion until $e_p$ exceeded $\mathsf{\Delta }$, at which point it rotated again to reduce the deviation. For the majority of the path, the swimmer remained within the $\pm \mathsf{\Delta }$ error bounds until a deviation occurred in the final zero-slope segment, prompting a further rotation to move downwards towards the intended trajectory. Case 1 (Figure 13e) showed unexpected results, with significant swimmer deviation in the range $1000<X<1300$ mm, and, although corrective rotations were implemented, the deviation remained considerable. Nevertheless, the robot achieved complete path tracking. The final zero-slope segment involved multiple rotations due to the swimmer orientation exceeding $\pi$/2 rad while targeting a 0 rad slope, requiring repeated adjustments.

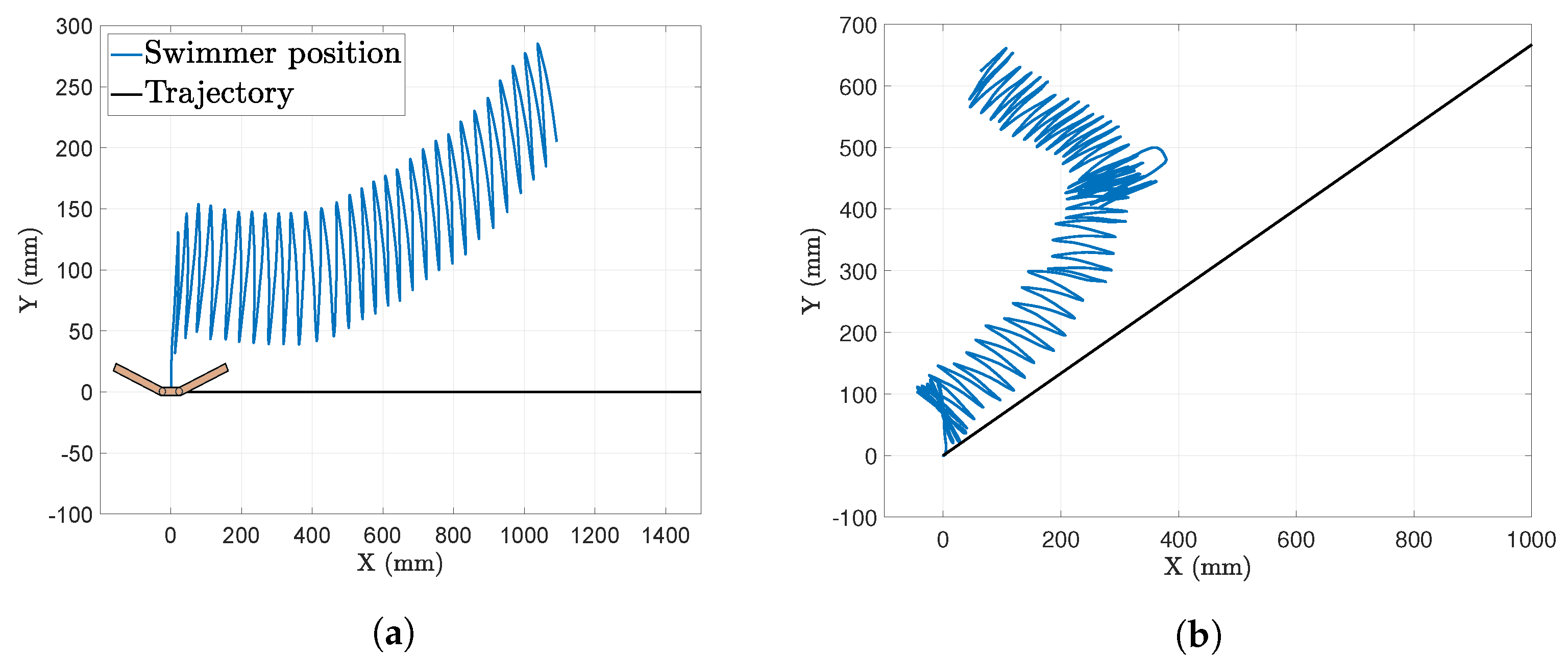
For comparison purposes, open-loop experiments for not inclined and inclined paths were also performed (the combined path was not tested because of the poor results obtained for the inclined one). The results are shown in Figure 14. As can be seen, the swimmer deviated to a large extent from the desired path, so closed-loop control is essential to reduce deviation.

A schematic of the robot with its actual dimensions has been included in Figure 14a to show the amplitude of the robot movement compared to its size. It is worth noting that, at first glance, the amplitude of the Y-movements appears to be much larger than the size of the robot, but there are two factors that influenced this. On the one hand, the inertia of the robot helped it to move further, so the movements were wider than those observed in the simulations. The upward motion of the robot involved a sequential rotation of its links, first one and then the other, with a similar sequence occurring during downward motion. This coordinated rotation of both links in each vertical movement cycle resulted in a larger amplitude of displacement along the Y axis.

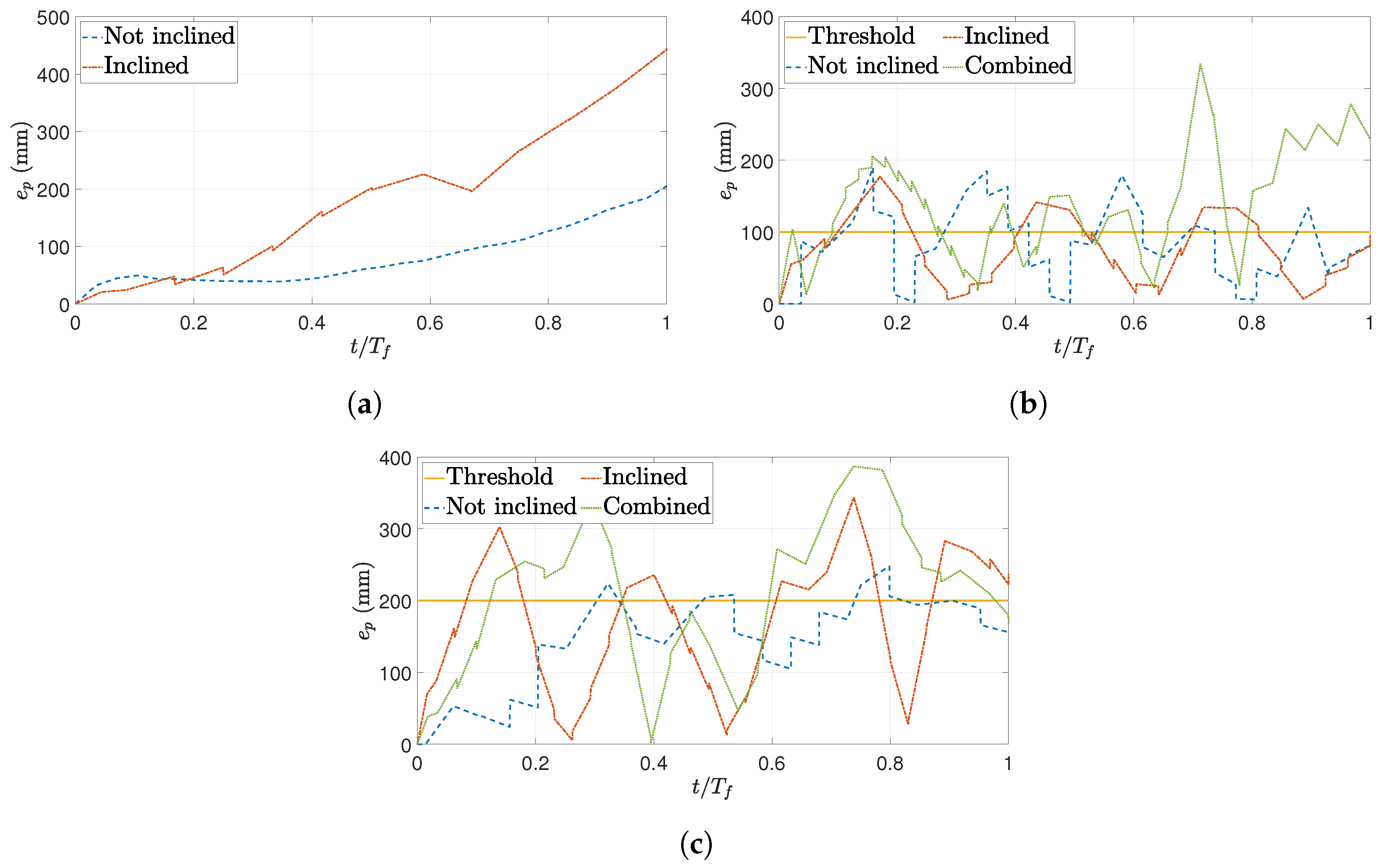
With regard to $e_p$, it has been calculated for each path, for open- and closed-loop, and for each $\mathsf{\Delta }$, and the results are plotted in Figure 15. The time axis has been normalised to $t/T_f$, with $T_f$ being the final time of the experiment, to improve result visualisation. As can be observed, $e_p$ for open-loop tracking (see Figure 15a) increases progressively until the end of the experiment, as expected from the results shown in Figure 14. Regarding the closed-loop tracking (see Figure 15b,c), it is evident that, for both values of $\mathsf{\Delta }$, the robot detected that the threshold had been exceeded and changed its direction of movement to reduce the error. Therefore, the results indicate that, when $e_p$ increases above $\mathsf{\Delta }$, it immediately decreases again towards values below the threshold. For the case 1 (see Figure 15b), an increase of the error well above the threshold is observed for $t/T_f\approx 0.7$, which corresponds to the deviation experienced by the swimmer in the range $1000<X<1300$ mm in Figure 13e.

For a better comparison, the MSE for each experiment has been calculated and tabulated in

Table 6. MSE ($\times {10}^3$) calculated for each path followed by the motor-driven prototype for two values of threshold ($\mathsf{\Delta }$).

Path	Open-Loop	Closed-Loop
		${\mathsf{\Delta }}_{\mathbf{1}}=\mathbf{100}$ mm	${\mathsf{\Delta }}_{\mathbf{2}}=\mathbf{200}$ mm
Not inclined	9.32	9.05	22.76
Inclined	54.55	6.37	30.30
Combined	-	21.03	47.79

. The data reveal a direct correlation between the $\mathsf{\Delta }$ value and the MSE across all paths, with the lowest $\mathsf{\Delta }$ yielding the smallest MSE and thus minimal trajectory deviation. For the path with no inclination, only minor differences are observed between the MSE of the open-loop control and the smallest $\mathsf{\Delta }$. This is likely attributable to the shorter duration of the open-loop experiment, which does not cover the entirety of the path (as evident in Figure 14a, where the final displacement is approximately 1100 mm compared to the total path length of 1500 mm). To sum up, it can be concluded that path following is more accurate for lower $\mathsf{\Delta }$ values in the proposed control strategy.

4.3. Discussion

This section includes a brief discussion with a comparison between the simulated and experimental results of the motor-driven prototype.

Several similarities can be found regarding the open-loop experiments and the simulations. First of all, the amplitude of the swimmer movement on the Y axis during the implementation of a motion primitive is similar for both cases (around 10 cm in experiments and 12 cm in simulations), and the loops that the swimmer performs in the $XY$ plane when navigating through viscosity-dominated environments are not observed in any of the results, showing instead a sawtooth pattern.

However, regarding the results, several differences are found in their magnitude. Firstly, the displacement in X is almost six times greater in the simulations than in the experiments, indicating that, for a single repetition of the primitive, the swimmer displaces 19 cm and 3.6 cm in simulations and experiments, respectively. Secondly, differences are also observed in the Y-drift, indicating that the swimmer deviates 10 cm in simulations and 20.5–26.8 cm in experiments, that is, the difference between both ranges from 2.05 to 2.68 times. Thus, the simulations show a larger longitudinal displacement along the X axis, but the experiments reveal a greater Y-drift.

In light of the presented results, several factors were identified that may have influenced the differences between simulations and experiments. Firstly, although the size of the pool should have minimised confinement effects, the enclosed environment might have introduced unaccounted-for forces in the dynamic model. Wall proximity could have influenced robot motion, and fluid oscillations from wall interactions might have affected displacement. Moreover, while maintaining constant depth and protecting electronics, the float itself could have influenced robot dynamics through unmodelled water surface drag forces.

Regarding the dynamic model, although the drag coefficients had been calculated via COMSOL Multiphysics^® simulations, they could have deviated from actual values, impacting environmental drag forces and the swimmer displacement. Concerning added-mass coefficients, these were derived from theoretical expressions and might not have accurately reflected real-world values. Discrepancies would have affected added-mass forces and, consequently, the robot motion. Furthermore, the complexity of the model and MATLAB^® implementation could have introduced minor discrepancies. Finally, the idealised representation of the fluid environment and hydrodynamic forces within the dynamic model omitted potentially relevant effects. As an example, the oscillatory motion of the swimmer caused the float to sway, resulting in its partial submersion in the fluid, which may have increased the drag.

In the area that the path-following control strategy concerns, the results have shown its effectiveness. However, alternatives or improvements could be proposed in terms of the triggering condition or the implementation of the strategy. Given the dissimilarities between simulation results and experimental data under the conditions explored in this work, it is inadvisable to employ model-dependent triggering criteria like linear predictor-based deadband and model-based approaches for path following. These methods, relying on inaccurate model predictions, would likely yield unsatisfactory control performance. However, promising alternative triggering strategies could be developed using absolute or integral deadband criteria, which assess the rate of deviation from the trajectory by comparing current and past data points.

For enhanced implementation, minimising communication delay and packet loss in the tracking system is crucial for accurate path following. Ideally, the robot should receive its position immediately after each primitive execution via fast communication. A significant advancement would be utilising the onboard positioning system of the robot, eliminating the reliance on external cameras for position detection and transmission.

5. Conclusions

This paper has presented a closed-loop control strategy for path following of Purcell’s three-link swimmers on the basis of event-based control. The strategy has been validated through experiments with a 30 cm-length motor-driven Purcell’s swimmer prototype within an inertia-dominated regime. The theoretical modelling of the Purcell’s swimmer was undertaken, succeeded by a description of the fabricated prototype. Following this, the simulations and experiments conducted were detailed, culminating in a discussion of the findings.

A comparison between simulation and experimental outcomes indicated both similarities and differences. Notably, both approaches showed consistent swimmer direction and overall displacement along the X axis. Furthermore, the extent of upward and downward motion observed in Y direction displayed a sawtooth pattern and similar amplitudes, aligning with the physical dimensions of the prototype. The trajectory followed by the swimmer showed differences from the ideal case at low Reynolds number ($Re$) conditions (viscosity-dominated regimes), as the eight-shape loops were not traced in this case.

Concerning experimental results, the prototype managed to displace and rotate in the desired directions with translation and rotation primitives, respectively. The closed-loop strategy was tested experimentally for path following with two values of threshold ($\mathsf{\Delta }$) and three types of straight paths, comparing with the open-loop alternative by means of the mean square error (MSE). The results showed that the strategy is appropriate for this type of swimmer, as it was able to follow all path types. Moreover, MSE results showed that, the smaller the $\mathsf{\Delta }$, the more accurate the tracking.

Future research should focus on refining experimental conditions by minimising communication delays and integrating onboard positioning systems to improve path-following accuracy. Additionally, exploring the robot performance with diverse and more intricate trajectories would be a valuable direction for future investigation. Moreover, future implementations may also incorporate adaptive mechanisms to improve the response to external disturbances. In particular, the integration of adaptive thresholds or disturbance observers could be explored to improve control robustness in environments with variable flow conditions or near-wall effects. In addition, future work may consider the integration of intelligent control techniques, such as fuzzy logic or neural networks, to enhance adaptability in the presence of unmodelled dynamics.