Abstract
This study presents the design, fabrication, and clinical validation of a lightweight, body-powered prosthetic index finger actuated via metacarpophalangeal (MCP) joint motion. The proposed system incorporates an underactuated, cable-driven mechanism combining rigid and compliant elements to achieve passive adaptability and embodied intelligence, supporting intuitive user interaction. Results indicate that the prosthesis successfully mimics natural finger flexion and adapts effectively to a variety of grasping tasks with minimal effort. This study was conducted in accordance with ethical standards and approved by the Institutional Review Board (IRB), Project No. 670161, titled “Biologically-Inspired Synthetic Finger: Design, Fabrication, and Application.” The findings suggest that the device offers a viable and practical solution for individuals with partial hand loss, particularly in settings where electrically powered systems are unsuitable or inaccessible.
1. Introduction
Limb loss is a global health concern, affecting over 552 million individuals, with over one million new amputations reported each year [1,2]. Among upper-limb amputations, index finger amputations are the most common, comprising approximately 27.27% of all cases [3]. The index finger plays a crucial role in fine motor control, including precision grip, object manipulation, and coordinated hand movements. Its loss significantly limits the performance of daily tasks and often results in emotional distress and decreased social participation [4,5]. These functional and psychosocial consequences underscore the broader impact of finger amputation on quality of life. As such, there is a pressing need for prosthetic solutions that are accessible, comfortable, and capable of restoring finger function in a practical and user-centered manner.
Recent advances in active prosthetic technologies have led to sophisticated devices incorporating motors, sensors, and control systems that offer precise and versatile finger movements [6,7,8]. However, these systems remain expensive, bulky, and complex to maintain, which significantly limits their accessibility, particularly in low-resource settings or for users with limited technical support. Despite their functional capabilities, active prostheses often impose additional cognitive and physical burdens on users. In contrast, body-powered prostheses provide a lightweight, energy-independent alternative that is generally recognized for its durability, simplicity, and affordability [9,10]. Yet, most existing body-powered designs fail to replicate the natural kinematics of the human finger, especially in cases of partial amputation, where the metacarpophalangeal (MCP) joint is preserved but the proximal interphalangeal (PIP) and distal interphalangeal (DIP) joints are missing [11]. This shortcoming limits their ability to restore intuitive and coordinated finger motion in such users.
Underactuated mechanisms have gained increasing attention in prosthetic hand and finger design, due to their ability to reduce actuator complexity while enabling adaptive, compliant interaction with objects [12,13]. By leveraging mechanical compliance, these systems can conform to various geometries without requiring individual actuation for each joint. This design philosophy holds particular promise for finger prostheses, where size, weight, and energy constraints are critical [14]. However, there remains a lack of focused research on prosthetic fingers that specifically utilize motion from a preserved metacarpophalangeal (MCP) joint to restore the functionality of the index finger, an important consideration in partial finger amputations. The main challenge lies in mechanically coupling a single MCP input to achieve coordinated flexion of PIP and DIP joints [15,16]. Previous designs have often relied on complex linkage systems or have intended for full-hand prostheses, making them less suitable for targeted applications [17]. As a result, it remains an open question whether a simple, body-powered, and underactuated mechanism can achieve the necessary biomechanical functionality and adaptability in everyday tasks.
To address this gap, the present study introduces a novel prosthetic index finger actuated exclusively by motion at the preserved MCP joint. The primary objective is to design, fabricate, and evaluate a compact and anatomically accurate underactuated mechanism capable of restoring coordinated flexion of the PIP and DIP joints. The proposed system employs a cable-driven architecture that exploits mechanical compliance and underactuation to produce adaptive and intuitive motion, without the need for electronic components. Special attention is given to ergonomic integration, mechanical simplicity, and user comfort to ensure long-term usability and acceptance in daily life. Emphasis is placed on ergonomic integration, mechanical simplicity, and material comfort to promote long-term usability and user acceptance.
This work makes several key contributions to the field of prosthetic finger design. First, it presents a novel mechanism that converts MCP joint motion into coordinate and lifelike flexion of the PIP and DIP joints, achieving an angular range of motion close to that of the natural human finger. Second, the mechanism exhibits effective passive adaptation during grasping tasks, enabled by its compliant and underactuated cable-driven architecture. Third, clinical evaluation with a partial finger amputee demonstrates the system’s ease of use, minimal learning curve, and psychosocial benefits, including enhanced self-confidence and reduced social stigma. Finally, the proposed design offers a lightweight, maintenance-free, and cost-effective alternative to motorized prostheses, making it particularly suitable for users in low-resource environments.
Together, the contributions of this study address a critical gap in prosthetic design by introducing a new approach that integrates mechanical efficiency with user-centered functionality. It proposes a design paradigm for body-powered and underactuated finger prostheses that emphasizes simplicity, adaptability, and clinical viability. The core of this work aligns with the research question: Can a body-powered and underactuated prosthetic finger, driven by only MCP joint motion, restore natural, adaptive and ergonomic finger movement through a mechanically efficient and clinically viable design?
2. Biomechanical Modeling
To achieve our goal of building a prosthetic finger, a deep understanding of human hand anatomy is required to replicate its biomechanics behaviors and functionalities, as shown in Figure 1a. Next, biomechanical perspectives need to be briefly explained viz. the bones and joints, the stabilization system, and actuation. The concept of the proposed mechanism is described as follows.
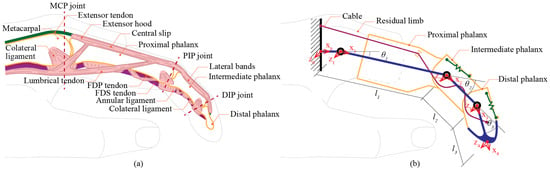
Figure 1.
(a) Anatomy and physiology of the finger, and (b) schematic diagram of the proposed prosthetic finger. Yellow indicates the phalangeal bones, blue denotes the kinematic links of the prosthetic system, purple represents the flexor tendons, and green highlights the extensor tendon and extension-assisting elements.
2.1. Bones and Joints
Each finger consists of one metacarpal bone and three phalanges, known as proximal, intermediate, and distal. Between each pair of adjacent bones is a physical connection called a joint. A real human finger joint functions as a rolling joint with 3D complex mating surfaces. This leads to a highly complex motion. Each finger basically is composed of three main joints: MCP, PIP, and DIP. Both PIP and DIP joints are modeled as one DOF joint, while the MCP joint is modeled as two DOFs. Side to side motion of the finger is known as the abduction and adduction. The twisting motion around the axis of a metacarpal bone is considered a passive feature of the MCP joint.
To build a compatible body-powered prosthetic finger (Figure 1b), the proposed prosthetic finger mechanism is designed to be fitted on the residual limb where the MCP joint is still functioning. Its core structure comprises three artificial rigid bodies, corresponding to the proximal, intermediate, and distal phalanges. These artificial phalanges are designed to maintain a length identical to the original finger, ensuring a natural range of motion and biomechanical behavior. In the proposed design, the artificial PIP and DIP are implemented as revolute joints. This configuration allows the prosthetic finger to exhibit flexion and extension movements with equivalent DOFs. The prosthesis is also fabricated using lightweight and strong components.
2.2. Joint Stabilization
Herein, tough bands of fibrous tissues (ligaments) are attached to two adjacent bones on both sides. Among these tissues, there are two crucial components called collateral ligaments located on the lateral sides of each finger and hand joint. The collateral ligaments stabilize and manipulate the range of motion (ROM) of each finger joint, constrained by the length of the ligaments. Their function also prevents excessive sideways bending of each joint. During off-plane bending of the finger, the collateral ligaments become taut but relax when it returns to its residual position. On the palmar side of the finger, thick ligaments formed at the base of joints are named volar plates. These volar plates are attached to both sides of the bones. Their functionality is to prevent the finger from being able to overextend (hyperextend) or dislocate.
Our design intends to employ angular contact bearings at such joints to handle the bending moments known as collateral ligaments. Stoppers are designed on the dorsal side of the artificial phalanges to avoid hyperextension, serving as volar plates.
3. Structural Design
3.1. Underactuatd Mechanism
Human motion is generated by the contraction of muscles. The connection between the bones and muscles is made by tendons. The human hand has two groups of tendons: extensor and flexor tendons. Flexor tendons bend the fingers. Extensor counterparts are a response to finger straightening. The corresponding muscle groups located in the forearm originate from both motions. On the dorsal side of the finger bones, the extensor tendons are divided into two layer-webs, which are in place at the beginning of the intermediate phalanges (central slip) and the distal phalanges (lateral bands).
The extensor tendons and forearm muscles are known as the extensor digitorum. The dorsal side of the finger phalanges is directly wrapped by the extensor digitorum tendon. Its functionality works as a braking system. At this point, the lateral bands split into two small ligaments across the PIP joint, regulating the braking torques based on the different postures of the finger. Even though the lateral bands serve as branches of the extensor tendons when the finger straightens, the two small branches shift their function to increase flexion torques at the PIP joint. Consequently, flexor tendons are being pulled while the extensor tendons are being stretched. This action enables the two small ligaments to pass downwards to the rotation axis. The central slip, like the lateral bands, splits into three ligaments: two small ligaments across the MCP joint and one at the center serving as the extensor digitorum. The central slip, therefore, helps bend the MCP joint due to the two small ligaments that travel along the rotation axis. One pair of its branches connect two small ligaments of the lateral bands, at the palmar side of the MCP joint. The tendon branches located here are connected to small intrinsic muscles, known as the lumbrical muscles, functioning as flexor tendons at the MCP joints, bending the PIP and DIP joints via the extensor hood mechanism.
Flexor tendons comprise two sets of tendons, namely the flexor digitorum superficialis (FDS) and flexor digitorum profundus (FDP), actuating the two characteristics of finger retraction. The FDP tendon (the fusiform muscle) is situated deep within the anterior (flexor) compartment of the wrist. These tendons are attached to the distal phalanges of the fingers at the base of the palmar surface. The rolling of the fingers at the MCP, DIP, and PIP joints is its primary purpose. The anterior compartment of the forearm contains a superficial muscle known as the FDS tendon. This muscle’s primary function is to roll the fingers at the PIP and MCP joints.
From an engineering perspective, muscles function as actuators that generate contraction forces while tendons serve as transmission components, delivering torque to each finger joint. Muscles are separated into two types: extrinsic and intrinsic muscles. The former, large muscle groups, directly connect to the central branch of both flexor and extensor tendons. However, the latter, small muscle groups, are often found between two adjacent metacarpal bones. During various hand activities, passive reflex-mediated compliance at finger joints can be achieved by these intrinsic muscles.
A layer of synovial membrane, wrapped around tendons, is called a tendon sheath, preventing the adherence of tendons to the surrounding structures. The inner layer produces lubricant, known as synovial fluid, allowing tendons to slide smoothly during contraction of the muscles. The synovial fluid protects tendons from friction of the surrounding joints and repeated pressure. The human finger has only one tendon sheath (common digital). The common digital tendon sheath separates both the FDP and FDS tendons from the surrounding area.
In mechanical engineering, different pulley systems have been applied to transmit power through cables. In biomechanics, pulley-like structures that stabilize the flexor tendons of the hand and wrist are formed by cruciate and annular ligaments. Cruciate ligaments are pairs of fibrous ligaments arranged and crossed in an X-shape. Their crossing pattern compresses the tendon sheaths against the underlying bone to avoid sheath collapse and expansion during digital motion. Annular ligaments are ring-shaped fibrous channels, which hold the tendons in place to prevent it from bowstringing. Annular ligaments are located on the top of the volar plates of MCP, DIP, and PIP joints as well as at the centers of the proximal and intermediate phalanges. In contrast, the crossed pulleys are located between the annular ligaments at the proximal and intermediate phalanges.
Further, we propose a design of one underactuated DOF prosthetic finger that relies on the flexion motion of the residual proximal phalanx. The cable system begins at the base of the prosthetic finger. Cable routing is strategically designed to follow a circular path, thus maximizing the moment and torque applied to the mechanism, and ultimately terminating at the distal phalanx. The circular path serves as cruciate ligaments and annular ligaments. The cable path is engineered to function like tendon sheaths, slipping over low friction surfaces like PTFE sheets. The mechanism also incorporates linear springs at PIP and DIP joints. These springs are crucial in reducing the complexity of the cable system and actuator requirements, as they provide the necessary passive tension for finger extension.
3.2. DH-Parameters
To understand the correlation of motion, the human finger can be considered as a serial connection of rigid links, which can be expressed through Denavit–Hartenberg (DH) parameters. The position of the fingertip with respect to the base is described as follows:
4. Fabrication
As shown in Figure 2, the proposed body-powered prosthetic finger driven by MCP motion was successfully fabricated. The proposed mechanism was integrated via both orthosis and prosthesis. Our proposed mechanism incorporated both rigid and compliant properties, allowing it to adapt to the environment while maintaining strength and stability akin to soft robotic systems [18]. A digital workflow was utilized, including computer-aided design program (Fusion 360) and digital fabrication to handle the complex geometry of the biological data and mechanism. All rigid components were fabricated using tough UV photosensitive resin and a 3D SLA printer with a resolution of 19 × 24 µm. As for the prosthetic section, it contained three 3D printed artificial phalanges (proximal, intermediate, and distal) and two joints (PIP and DIP).
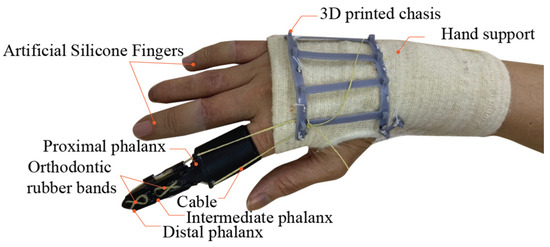
Figure 2.
The proposed fabricated prosthetic finger fitted on an amputee’s hand.
The interface between the artificial proximal phalanx and the residual limb was surrounded with a soft, 1 mm thick layer to fit the highly 3D complex organ without discomfort. At the joints, full ceramic deep groove ball bearings (CE 623) were installed in both the artificial proximal phalanx and intermediate phalanx due to their low tare weight, high durability, and extreme smooth-running. The integration of ceramic ball bearings and housings stabilize the joints, ensuring in-plane like motion similar to the function of collateral ligaments. A high-strength cable, with Φ 0.75 mm and 39 kg tensile strength, was utilized. Moreover, the cable’s high flexibility contributed to the smooth operation of the transmission system along a narrow bend path.
The cable route, laid in the 3D complex space, was successfully managed and fabricated using a digital workflow. Parallel cable pulling, unlike biomechanics, was applied with an insertion at the distal phalanx to increase stability. To minimize friction, 0.5 mm thick PTFE sheets were applied along the cable’s circular path as low-friction interfaces. Orthodontic rubber bands were located on the dorsal side at PIP (Φ 5/16″ 3.5 oz) and DIP joints (Φ 5/16″ 2.5 oz) to replicate the gliding mechanism of the extensor hood and assist in finger extension.
A 3D printed chassis was individually customized and sewn onto a hand support (Tubigrip® Feel free, Mölnlycke Health Care, Mölndal, Sweden) to accurately match the dorsal metacarpal bone. The hand support was fabricated from medical grade cotton using spiral knitting technology to enhance structural support and comfort. Thus, the pressure profile led to a perfect fit, preventing skin irritation and discomfort. Moreover, it improved the stability of the hand and wrist, thereby mitigating fatigue and further injury in long term usage. The 3D printed chassis was secured in position and could be bent without interference of biomechanics. The transmitted forces efficiently passed through the rigid metacarpal bones, providing more strength.
5. Mathematical Model
In the body-powered prosthetic finger, the variables (a function of time) and parameters are listed in Table 1 and Table 2, respectively.

Table 1.
State variables in the body-powered prosthetic finger.

Table 2.
Parameters in the body-powered prosthetic finger.
In our model, the fixed length of the cable constrains the system and controls its motion. Visualize an imaginary circle (Figure 3) with its origin at the cable’s endpoint on the dorsal side (0, 0) while the MCP joint is located at coordinates (d, −h). The length of an imaginary kinematic link, parallel to (), is measured from the MCP joint to the point where the first cable channel intersects the artificial proximal phalanx, denoting it as (). The length of the perpendicular projection is (p). As the residual limb moves, the length of the cable changes, creating a difference (∆d) between the end of the cable, fixed to the 3D-printed chassis, and the first cable channel on the artificial proximal phalanx. To simplify cable management, the section between the cable end and the first cable channel is kept within a 2D plane. The magnitude of ∆d is calculated as the difference in the cable length at any from the straightened state (l0). The increase in cable length can be represented accordingly:
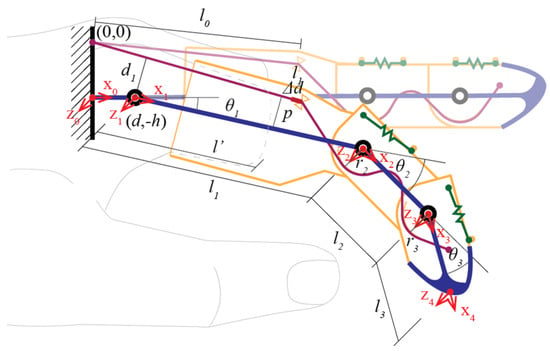
Figure 3.
Notation of the proposed prosthetic finger.
Since the cable length must remain constant, any extension in length must be compensated by an equivalent shortening. The decrease in cable length is influenced by two segments as follows:
where r2 and r3 denote the shortened arc length at PIP and DIP joints, respectively. In this case, r2 = r3 = r, as in the fabricated hardware, yielding the following:
The proposed body-powered prosthetic finger is designed to effectively perform everyday tasks, such as typing and grasping, which require the synchronization of joint movements. In the prosthetic finger, the actuator is controlled by the angular motion of and provides force to drive the underactuated 1-DOF mechanism (Figure 4). Both movement and force in the mechanism follow this relationship, indicating that the angular acceleration is dependent on both the mass moment of inertia and the applied torque:
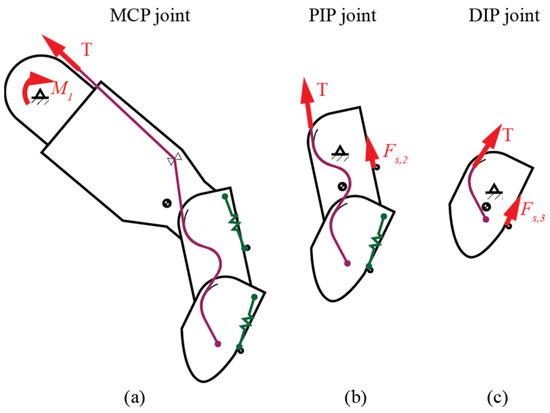
Figure 4.
Schematic representation of the active force: (a) MCP joint, (b) PIP joint, and (c) DIP joint.
To ensure consistent cable tension (T), uniform load distribution, negligible cable mass, and minimal friction are considered assumptions. The weight of the residual limb and the prosthetic mechanism is considered insignificant and ignored. The moment generated by the residual limb at the MCP pivot () drives the angular motion of the joint:
For both PIP and DIP joints, the governing equations are similar due to the circular path contact characteristics:
The spring force generated by the orthodontic rubber bands can be described by the following relationship:
To improve the stability of the prosthetic mechanism, orthodontic rubber bands are applied on the dorsal side of the PIP and DIP joints. The thickness of the orthodontic rubber bands is negligible compared to their stretch length, allowing calculations to be performed in 2D. To analyze the elastic behavior, imagine the elastic bands unfolded in a 2D plane. The total length of each band is split into four equal sections with an imaginary horizontal line through the center of the poles. Each section is influenced by a curved section wrapped around the rubber pole and a tangent section. The tangent segment represents one leg of a right-angled triangle, with (Cn) as the hypotenuse and (rpole) as the adjacent leg. The hypotenuse (Cn) is half the distance between the centers of the rubber poles, expressed as follows:
where () and () define the constant lengths of the cable sections and () defines the varied arc lengths due to joint angular motion. Thus, the length of the elastic bands can be derived, using this formula:
As observed, the spring sections act as non-linear torsional springs, leading to tension at the PIP and DIP joints:
Due to consistent T, the second derivative differential equation for angular motion can be determined, yielding:
6. Simulation
Designing a biomechanical finger that closely mimics human function often results in a complex mechanical system composed of multiple joints and links. In the proposed design, the finger is constructed as a planar mechanism using conventional revolute joints and geometrically complex links. In recent years, physics simulation has advanced significantly due to increased computational power [19,20,21]. These advancements include improved solving algorithms [22,23], better data handling capabilities, and enhanced performance. Collectively, they enable more realistic and accurate multi-domain simulations. Furthermore, the rise in parallel computing has allowed the real-time simulations of complex dynamic systems, which facilitates faster design iterations, performance evaluations, and optimization of prosthetic fingers [24].
In this study, Matlab® Simscape (R2023b), a multi-physics simulation environment, was employed for modeling, simulation testing, and iterative design refinement [25]. The physics underlying the proposed prosthetic finger were modeled using a bond graph approach. To manage complexity, a graphical block-diagram framework [26] was adopted, which is considered effective for such simulations [27,28]. The bond graph modeling approach complements block diagrams [29] by enabling effective connection between components using across and through variables that represent both physical domains and signal transmission.
The prosthetic finger’s physical domain was modeled as a system of multiple rigid bodies and a cable-driven actuation system. Simulation setup included components such as the solver configuration, world frame, mechanism configuration, and belt–cable properties blocks, which defined the mathematical solver, gravitational settings, and cable characteristics. To solve the system’s differential equations, the ODE45 solver [30,31], a variable-step numerical integrator based on the DormandPPrince method, was used.
In the multi-body dynamics section, file solid blocks were used to import 3D models and define their inertial properties. Belt–cable end blocks set the start and end positions of the cable, while pulley blocks guided the cable path. Revolute joint blocks allowed rigid bodies to rotate dynamically around specified axes, and torsional springs were modeled via these joints to represent elastic effects. Additionally, rigid transform blocks were employed to implement fixed joints between the residual limb and the prosthetic mechanism, as well as to manage positional relationships across the rigid body and cable domains. All these blocks were organized within subsystems and masked, as shown in Figure 5, allowing for efficient system management and reuse.
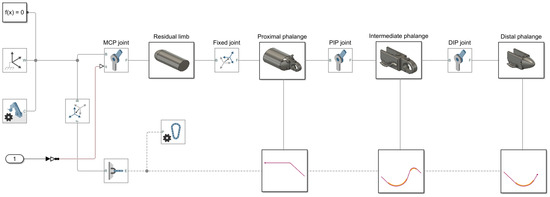
Figure 5.
A bond graph model of the proposed prosthetic finger.
7. Results
In Figure 6a, the MCP joint serves as the principal actuator, initiating movement across the finger’s kinematic chain during the free-motion phase. The numerical illustrates and :
where can be used to determine the tip position via transformation matrices and DH parameters, as outlined in the kinematic diagram (Figure 1b). The approximated closed-form position of the tip can be defined as follows:
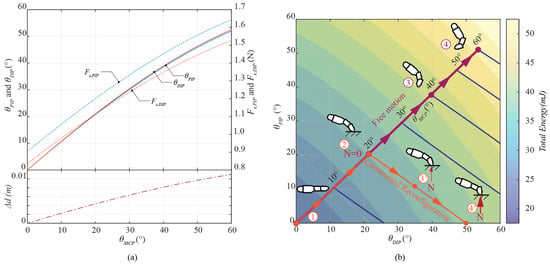
Figure 6.
Free motion driven by MCP joint: (a) motion relation, and (b) energy balance.
The total angle is given by . Combining both the elastic elements and the cable demonstrates the compliant behavior characteristics of soft robots at each finger joint. This combination allows the underactuated grasping fingers to automatically adjust to the shape of the objects they are grasping. To determine whether our mechanism functions properly and mimics the natural motion of a human finger, ROM is a key metric used. According to the data, the measured ROM for MCP, PIP, and DIP joints [32] is as follows:
Extension: −39.97°, −14.95°, and −16.96°, respectively.
Flexion: 62.29°, 72.55°, and 45.51°, respectively.
In our hardware, stoppers at the PIP and DIP joints limit extension to 0°, which aligns with the theoretical range when the is at 0°. Given that the ROM for the MCP joint has a flexion limit of 62.29°, our evaluation will focus on a range of from 0° to 60°. At full flexion, the mechanism creates angular movements of 54° and 53° at both PIP and DIP joints, respectively. The proposed mechanism generates a total angular range of 168°, which is close to the measured human range of 180.35°, indicating a deviation of only 6.85%. It is important to note that, for each fixed MCP configuration, the PIP and DIP joints naturally converge to a minimum-energy configuration. This behavior is indicative of a self-stabilizing mechanism, which promotes synchronized joint motion without requiring individual actuation. The corresponding tendon force distribution is also illustrated in Figure 6a. These outcomes suggest that the proposed mechanism successfully replicates the natural motion of a human finger.
As illustrated in Figure 6b, when user flexes the residual MCP joint, the prosthetic finger responds by following the free-motion trajectory (Path 1–2–3–4) at minimum energy equilibrium until the distal phalanx contacts an external constraint. Following Equation (6), this contact converts the system from underactuated to fully actuated, making the distal phalanx slide along the contact surface. Under such conditions, the MCP joint drives the system along a constrained motion path, shown in Figure 6b as Path 2–3′–4′. Upon reaching full extension at the PIP joint ( = 0), further movement is restricted by a mechanical end stop. Notably, as the system performs along this constrained path, the fingertip contact force increases progressively. At this limited position, the tension in the drive tendon exerts a dominant influence on the resulting contact force, thereby enhancing the finger’s capacity for stable surface interaction and effective object manipulation.
To test the performance of our prosthetic finger, grasping and manipulation experiments were conducted using 31 objects [33], following the grasping styles, categorized in human hand taxonomy [34,35]. Experiments focused on 14 specific postures, in which the index finger played a primary role. During tests, a female participant with limb loss wearing our prosthetic finger manipulated various objects and pressed buttons. The mechanism’s movement is controlled by the motion of the user’s hand, with feedback provided visually and through tactile sensation. The experiment demonstrated a series of grasping; the grasped objects were carried out without any problems. The prosthetic finger was able to perform a wide range of natural and seamless grasping postures. The grasps achieved during the tests covered most common grasping types (Figure 7). This outcome suggests that matching the prosthetic finger’s kinematics to those of a human hand is key for seamless functionality without requiring adaptation.
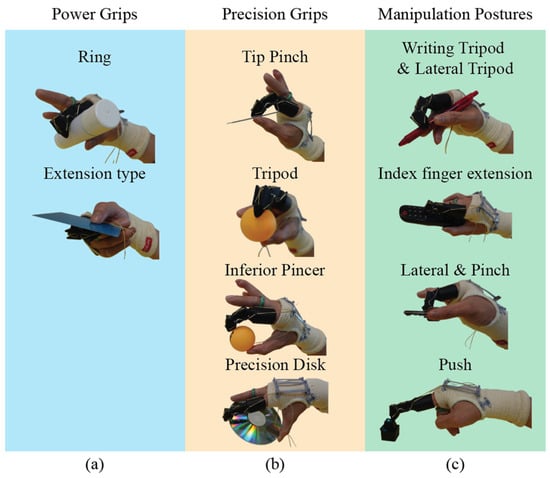
Figure 7.
Grasp taxonomy performed by the proposed mechanism: (a) power grips, (b) precision grips, and (c) manipulation postures.
User feedback on the prosthetic finger is collected through “like”, “wish”, and “wonder” categories (Table 1), using methods from the Stanford Design School. The user feedback indicates positive interactions with the prosthetic finger, with the mechanism operating smoothly and naturally, requiring no additional adaptation. According to Table 3, users are likely to adopt the technology due to its esthetics, functionality, ease of use, durability, reliability, comfort, and fit. In terms of psychological impact, the feedback shows an increase in user confidence and self-esteem. While the prosthetic finger has many positive aspects, there is room for improvement in ease of wearing, maintenance, fit, and output amplification.

Table 3.
Feedback on the proposed prosthetic finger collected from user testing, categorized by “Like”, “Wish”, and “Wonder”.
8. Discussion
This study explored the design, fabrication, and clinical validation of a body-powered, underactuated prosthetic index finger actuated via MCP joint motion. The primary objective was to develop a functional and accessible prosthesis that combines mechanical simplicity with biomechanical realism. The resulting device integrates a compliant, tendon-driven actuation mechanism within a compact 16 g structure, facilitating intuitive operation and user comfort.
The incorporation of both rigid and soft elements enabled passive adaptation to diverse object geometries and promoted embodied intelligence, allowing the finger to passively adapt to diverse object geometries and respond naturally to external forces without requiring precise user control or feedback systems. This characteristic, often lacking in rigid or powered alternatives, was central to the device’s ability to perform common tasks with low cognitive demand for spontaneous interaction with the environment. This passive compliance reduces the cognitive load for the user and enhances the device’s ability to perform common grasping and manipulation tasks seamlessly. Such behavior closely mimics natural human reflexes and biomechanics, particularly in unstructured or dynamic situations.
Clinical testing with a real user demonstrated promising outcomes. The participant was able to perform key grasping and manipulation activities effectively. User feedback confirmed that the prosthesis operated smoothly with minimal learning curve. Importantly, the user reported enhanced confidence, psychological well-being, and a reduction in social self-consciousness due to the prosthesis’s natural appearance and motion. These findings are consistent with the broader literature, emphasizing the significance of psychosocial factors in prosthetic adoption.
The integration of orthotic support within the design additionally contributed to hand and wrist stabilization, reducing fatigue and supporting prolonged daily use. Material selection, including the use of medical-grade cotton lining and PTFE interface layers—enhanced user comfort by reducing friction and improving breathability during extended wear.
Although the current study focuses specifically on the index finger, the proposed underactuated, body-powered design can be extended to other fingers experiencing similar symptoms, particularly the loss of PIP and DIP joints while preserving MCP function. The modular nature of the cable-driven mechanism and the passive compliance system enables adaptability with only minor modifications, such as adjusting linkage lengths, joint stiffness, and spring tension to accommodate anatomical differences. It is acknowledged that each finger plays a distinct functional role in grasping tasks. For example, the thumb requires opposition and multidirectional articulation, while the little finger exhibits a more limited flexion range and contributes to grip stabilization. In future iterations, these factors need to be considered. In our work, the index finger was selected as the initial focus due to its critical role in grasping, pointing, and fine manipulation. Future work may explore adaptation across all digits to support a wider range of prosthetic needs.
Despite the promising results, several limitations remain in this study. First, the grasping force generated by the prosthetic finger is currently limited to under 1 kg, primarily due to the low output force from the residual MCP joint and the rigid profile of the fingertip. Integrating a soft, high-friction fingertip could enhance contact stability and increase effective load capacity. Second, although the prosthesis offers intuitive motion, the force transmission remains direct and non-amplified. Future iterations may explore the incorporation of an adaptive mechanical advantage within the 3D-printed chassis, sewn onto the hand support, to amplify either force or motion based on task requirements. Additionally, the current design cannot be independently worn by users with unilateral amputation, as it requires assistance for proper fitting. In future developments, we aim to address this usability barrier by introducing a self-wearable mechanism, facilitating autonomous use and improving accessibility.
9. Conclusions
This study presented a lightweight, body-powered underactuated prosthetic finger actuated by MCP joint motion. The 16 g design successfully mimics natural finger flexion and adapts to various grasping tasks with minimal effort. Clinical evaluations confirmed its functional performance, while participant feedback emphasized comfort and ease of use. Future work will focus on broader clinical trials, refinement of the mechanical design, and the integration of a multi-finger prosthetic system to further enhance functionality.
Author Contributions
Conceptualization, W.C. and R.C. (Ratchatin Chancharoen); methodology, W.C.; software, W.C.; validation, W.C.; formal analysis, W.C. and R.C. (Ratchatin Chancharoen); investigation, W.C.; resources, W.C., R.C. (Ratchatin Chancharoen) and G.P.; data curation, W.C.; writing—original draft preparation, W.C., C.S., R.C. (Ratchatin Chancharoen), R.C. (Ronnapee Chaichaowarat), N.A. and G.P.; writing—review and editing, W.C., C.S., R.C. (Ratchatin Chancharoen), R.C. (Ronnapee Chaichaowarat), N.A. and G.P.; visualization, W.C.; supervision, R.C., N.A. and G.P.; project administration, W.C. and G.P.; funding acquisition, W.C., C.S., R.C. (Ratchatin Chancharoen), N.A. and G.P. All authors have read and agreed to the published version of the manuscript.
Funding
Research supported by National Research Council of Thailand (NRCT) and Faculty of Engineering, Chulalongkorn University, grant O1100.670161.
Informed Consent Statement
Ethical approval for this study was obtained from the Research Ethics Review Committee for Research Involving Human Participants (Group I), Chulalongkorn University. The study, titled “Bio-Inspired Synthetic Finger: Design, Fabrication, and Applications,” received approval under Certificate of Approval (COA) No. 017/68, Study Reference No. 670161, 23 August 2024.
Data Availability Statement
The data supporting the findings of this study are publicly accessible at https://github.com/worathris/A-Body-Powered-Underactuated-Prosthetic-Finger-Driven-by-MCP-Joint-Motion (accessed on 30 July 2025).
Acknowledgments
The authors would like to thank Naruephon Hengkratok for his advice on the fundamentals of the human hand and medical resources.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Owings, M. Ambulatory and Inpatient Procedures in the United States, 1996; US Department of Health and Human Services, Centers for Disease Control and Prevention: Atlanta, GA, USA, 1998. [Google Scholar]
- Sarvestani, A.S.; Azam, A.T. Amputation: A ten-year survey. Trauma Mon. 2013, 18, 126–129. [Google Scholar] [CrossRef]
- Yuan, B.; Hu, D.; Gu, S.; Xiao, S.; Song, F. The global burden of traumatic amputation in 204 countries and territories. Front. Public Health 2023, 11, 1258853. [Google Scholar] [CrossRef]
- Kristjansdottir, F.; Dahlin, L.B.; Rosberg, H.E.; Carlsson, I.K. Social participation in persons with upper limb amputation receiving an esthetic prosthesis. J. Hand Ther. 2020, 33, 520–527. [Google Scholar] [CrossRef]
- Skoff, H.; Skoff, H. The Psychological and Somatic Consequences of Digital Amputation. Plast. Reconstr. Surg.-Glob. Open 2022, 10, E4387. [Google Scholar] [CrossRef]
- Ahmad, N.; Thomas, G.N.; Gill, P.; Chan, C.; Torella, F. Lower limb amputation in England: Prevalence, regional variation and relationship with revascularisation, deprivation and risk factors. A retrospective review of hospital data. J. R. Soc. Med. 2014, 107, 483–489. [Google Scholar] [CrossRef]
- Behrendt, C.-A.; Sigvant, B.; Szeberin, Z.; Beiles, B.; Eldrup, N.; Thomson, I.A.; Venermo, M.; Altreuther, M.; Menyhei, G.; Nordanstig, J. International variations in amputation practice: A VASCUNET report. Eur. J. Vasc. Endovasc. Surg. 2018, 56, 391–399. [Google Scholar] [CrossRef] [PubMed]
- Staats, T. The rehabilitation of the amputee in the developing world: A review of the literature. Prosthet. Orthot. Int. 1996, 20, 45–50. [Google Scholar] [CrossRef]
- Carey, S.L.; Stevens, P.M.; Highsmith, M.J. Differences in Myoelectric and Body-Powered Upper-Limb Prostheses: Systematic Literature Review Update 2013–2016. J. Prosthet. Orthot. 2017, 29, P17–P20. [Google Scholar] [CrossRef]
- Hughes, W.; Goodall, R.; Salciccioli, J.D.; Marshall, D.C.; Davies, A.H.; Shalhoub, J. Editor’s Choice–Trends in lower extremity amputation incidence in European Union 15+ countries 1990–2017. Eur. J. Vasc. Endovasc. Surg. 2020, 60, 602–612. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.Y.; Lee, S.H.; Leigh, J.H.; Nam, H.S.; Hwang, E.Y.; Lee, J.Y.; Han, S.; Lee, G. Functional improvement by body-powered 3D-printed prosthesis in patients with finger amputation: Two case reports. Medicine 2022, 101, e29182. [Google Scholar] [CrossRef]
- Chungsangsatiporn, W.; Chancharoen, R. A Bio-Inspired Robotic Finger: Mechanics and Control. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023; pp. 4562–4567. [Google Scholar]
- Belter, J.T.; Segil, J.L.; Sm, B. Mechanical design and performance specifications of anthropomorphic prosthetic hands: A review. J. Rehabil. Res. Dev. 2013, 50, 599–618. [Google Scholar] [CrossRef] [PubMed]
- Carey, S.L.; Lura, D.J.; Highsmith, M.J. Differences in myoelectric and body-powered upper-limb prostheses: Systematic literature review. J. Rehabil. Res. Dev. 2015, 52, 247–262. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, P.; Li, T. Topology Optimization of Compliant Grippers Based on Stress Constraints. J. Mech. Robot. 2025, 17, 061001. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Y.; Pancheri, F.; Lueth, T.C. Larg: A lightweight robotic gripper with 3-d topology optimized adaptive fingers. IEEE/ASME Trans. Mechatron. 2022, 27, 2026–2034. [Google Scholar] [CrossRef]
- Kim, H.; Park, Y.; Bae, J. Optimized design of a body-powered finger prosthesis using fingertip trajectories based on polar coordinate analysis. J. Mech. Sci. Technol. 2020, 34, 387–399. [Google Scholar] [CrossRef]
- Sithiwichankit, C.; Chancharoen, R. Advanced Stiffness Sensing through the Pincer Grasping of Soft Pneumatic Grippers. Sensors 2023, 23, 6094. [Google Scholar] [CrossRef]
- Bauer, C.W.; Davoudi, Z.; Balantekin, A.B.; Bhattacharya, T.; Carena, M.; De Jong, W.A.; Draper, P.; El-Khadra, A.; Gemelke, N.; Hanada, M. Quantum simulation for high-energy physics. PRX Quantum 2023, 4, 027001. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Gao, R.X.; Zhang, F. Hybrid physics-based and data-driven models for smart manufacturing: Modelling, simulation, and explainability. J. Manuf. Syst. 2022, 63, 381–391. [Google Scholar] [CrossRef]
- Tang, S.; Chen, L.; He, K.; Xia, J.; Fan, L.; Nallanathan, A. Computational intelligence and deep learning for next-generation edge-enabled industrial IoT. IEEE Trans. Netw. Sci. Eng. 2022, 10, 2881–2893. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovský, P. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl.-Based Syst. 2023, 259, 110011. [Google Scholar] [CrossRef]
- Khodadadi, N.; Abualigah, L.; El-Kenawy, E.-S.M.; Snasel, V.; Mirjalili, S. An archive-based multi-objective arithmetic optimization algorithm for solving industrial engineering problems. IEEE Access 2022, 10, 106673–106698. [Google Scholar] [CrossRef]
- Huang, J.-C.; Zeng, G.-Q.; Geng, G.-G.; Weng, J.; Lu, K.-D.; Zhang, Y. Differential evolution-based convolutional neural networks: An automatic architecture design method for intrusion detection in industrial control systems. Comput. Secur. 2023, 132, 103310. [Google Scholar] [CrossRef]
- Pozzi, M.; Achilli, G.M.; Valigi, M.C.; Malvezzi, M. Modeling and simulation of robotic grasping in simulink through simscape multibody. Front. Robot. AI 2022, 9, 873558. [Google Scholar] [CrossRef]
- Zeb, K.; Ali, S.M.; Khan, B.; Mehmood, C.A.; Tareen, N.; Din, W.; Farid, U.; Haider, A. A survey on waste heat recovery: Electric power generation and potential prospects within Pakistan. Renew. Sustain. Energy Rev. 2017, 75, 1142–1155. [Google Scholar] [CrossRef]
- Attar, H.; Abu-Jassar, A.T.; Amer, A.; Lyashenko, V.; Yevsieiev, V.; Khosravi, M.R. Control system development and implementation of a CNC laser engraver for environmental use with remote imaging. Comput. Intell. Neurosci. 2022, 2022, 9140156. [Google Scholar] [CrossRef]
- Lee, J.; Leung, V.; Lee, A.-H.; Huang, J.; Asbeck, P.; Mercier, P.P.; Shellhammer, S.; Larson, L.; Laiwalla, F.; Nurmikko, A. Neural recording and stimulation using wireless networks of microimplants. Nat. Electron. 2021, 4, 604–614. [Google Scholar] [CrossRef]
- Maluf, A.S.; Sagawa, J.K.; Borges, R.F. Toward the use of bond graphs for manufacturing control: Comparison of existing models. Int. J. Adv. Manuf. Technol. 2022, 121, 2841–2865. [Google Scholar] [CrossRef]
- Shampine, L.F.; Reichelt, M.W. The matlab ode suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Ahmed, W.K. Advantages and disadvantages of using MATLAB/ode45 for solving differential equations in engineering applications. Int. J. Eng. 2013, 7, 25–31. [Google Scholar]
- Ngeo, J.G.; Tamei, T.; Shibata, T. Continuous and simultaneous estimation of finger kinematics using inputs from an EMG-to-muscle activation model. J. Neuroeng. Rehabil. 2014, 11, 122. [Google Scholar] [CrossRef]
- Choi, Y.S.; Deyle, T.; Chen, T.; Glass, J.D.; Kemp, C.C. A list of household objects for robotic retrieval prioritized by people with ALS. In Proceedings of the 2009 IEEE International Conference on Rehabilitation Robotics, Kyoto, Japan, 23–26 June 2009; pp. 510–517. [Google Scholar]
- Cutkosky, M.R. On grasp choice, grasp models, and the design of hands for manufacturing tasks. IEEE Trans. Robot. Autom. 1989, 5, 269–279. [Google Scholar] [CrossRef]
- Feix, T.; Romero, J.; Schmiedmayer, H.-B.; Dollar, A.M.; Kragic, D. The grasp taxonomy of human grasp types. IEEE Trans. Hum.-Mach. Syst. 2015, 46, 66–77. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).