Optimizing Path Planning for Automated Guided Vehicles in Constrained Warehouse Environments: Addressing the Challenges of Non-Rotary Platforms and Irregular Layouts
Abstract
1. Introduction
1.1. Problem Background
1.2. Problem Definition
1.3. Related Work
1.3.1. Classical Multi-Agent Path Finding Problem
1.3.2. Multi-Agent Path Finding for Large Agents (LA-MAPF)
1.3.3. Search-Based Solvers
- -based algorithms: Algorithms of this class include with k-agent search space, Operator Decomposition, Independence Detection, , and others. The main drawback of this class of algorithms is a lack of scalability due to the large search space.
- CBS-based algorithms: Conflict-Based Search (CBS) algorithms form a class of two-level search strategies. The low-level search is used to find a path for a single agent, and the high-level search is used for conflict resolution for paths obtained during the low-level search. This class includes CBS that is complete and optimal [21], ECBS (Enhanced CBS), a bounded-suboptimal variant of CBS [22], and EECBS (Explicit Estimation CBS), yet another bounded-suboptimal variant of CBS [23].
- Prioritized algorithms: The main idea of prioritizing planning algorithms is to select random agent ordering and find a minimum cost path for each agent according to the chosen priority [12]. If, at some moment, the path for agent cannot be constructed in such a way that it has no collisions with the path of agents with higher priority, then new ordering is selected, and the search is restarted. The adaptation of CBS to prioritized planning, named Conflict-Based Search with Priorities (CBSwP), and Priority-Based Search (PBS) are proposed in [24].
1.3.4. Multi-Label
- The ‘stay at the target’ approach prohibits other agents from entering the target location, which limits the number of simultaneously processed orders with the same destination to one.
- Disappearing at the target avoids the first problem, but some agents can block the path for the agent that leaves the target location. In both cases, additional heuristics or modifications should be added to algorithms.
1.3.5. Windowed Approach
1.3.6. MAPF Extensions
- Kinematic constraints: In the classical case, all agents in MAPF occupy a single vertex of the graph, but in real-world scenarios, each vertex of the graph has Euclidean coordinates, and agents may be prohibited from being in some pair of vertices due to their geometrical shapes or shapes of the attached loads. Any-angle SIPP was proposed by Yakovlev et al. [27] to deal with multiple agents of identical circular shape. Further research in this direction includes MC-CBS [18], a generalized version of CBS, and TP-SIPPwRT [28], an adaptation of Token Passing [19] that uses SIPPwRT as low-level search and takes kinematic constraints into account. MAPF-POST [29] adds a post-processing step where robot kinematics are considered.
- Rotations as separate actions: Standard MAPF operates only with graph vertices, and robot direction is not considered. Honig et al. [30] proposed an execution framework where robot rotations are used to model the rotation time and explicitly achieve more accurate plans. This approach also allows the consideration of kinematic constraints and finding collisions when the robot is planned to make a rotation near another robot or obstacle. However, this increases the search space because each robot’s position is now encoded with location and direction. On the other hand, as discovered in [20], rotations as separate actions can improve the throughput of ECBS-T and PP.
- k-Robustness: To deal with unexpected events that delay plan execution, Artzmon et al. [31] proposed the k-robust MAPF plan: a plan that can be executed even if a limited number of delays occur and adopted some MAPF solvers to use the k-Robustness constraint. This is achieved by redefining vertex conflict in such a way that if the agents share the same cell in within fewer than time steps, then these agents conflict with each other. This approach increases computational time compared to non-robust variants and increases the failure rate for prioritized planning algorithms but can produce higher throughput for some instances [20]. In addition, we should point out that k-Robustness implies that there are no edge conflicts.
1.3.7. Lifelong MAPF
- Reducing the problem to one-shot MAPF: If all the tasks are known beforehand, optimal or near-optimal solvers can generate a complete solution considering all tasks and agent interactions. Once a new navigation task is assigned, the new problem should be solved again in an offline setting. A further extension of this idea is replicating agents that receive new tasks (Online Independence Detection [32]) or reusing the previous search results.
- Decoupled (single-agent) frameworks: The idea is not new and quite simple. Agents plan their paths one after another, avoiding collision with already planned paths. Examples of such an approach are Cooperative [12], Token Passing (TP) and Token Passing with Tasks Swaps (TPTS) [19], and Token Passing using SIPP (TP-SIPPwRT) [28]. For this purpose, paths are stored in a global reservation system consisting of space-time cells. Each agent needs to reserve a cell at some time step to be available to move there and every cell can be reserved at most by one agent.
- Windowed solvers (Bounded-Horizon Planning): Another approach is based on constructing collision-free paths only for a limited number of steps w using any of the MAPF algorithms. Replanning is triggered after steps or when some new tasks are added to the system. Windowed solvers are faster than their complete version but generate longer paths. Examples of algorithms in this category are Windowed Hierarchical Cooperative () [12], and Rolling-Horizon Collision Resolution (RHCR) [26]. Varambally et al. [20] presented an execution framework called Rolling-Horizon Collision-Resolution and Execution (RHCRE), which combines RHCR with an Action-Dependency Graph. In this way, they achieved the same robustness guarantees as single-agent frameworks. They overcame the inaccuracies in the general assumptions of the MAPF problem, such as one-step actions and unpredictable delays. The ADG also allows for replanning during execution, which means that agents do not need to wait during replanning.
1.3.8. Action Dependency Graph
2. Materials and Methods
2.1. Environment and Equipment
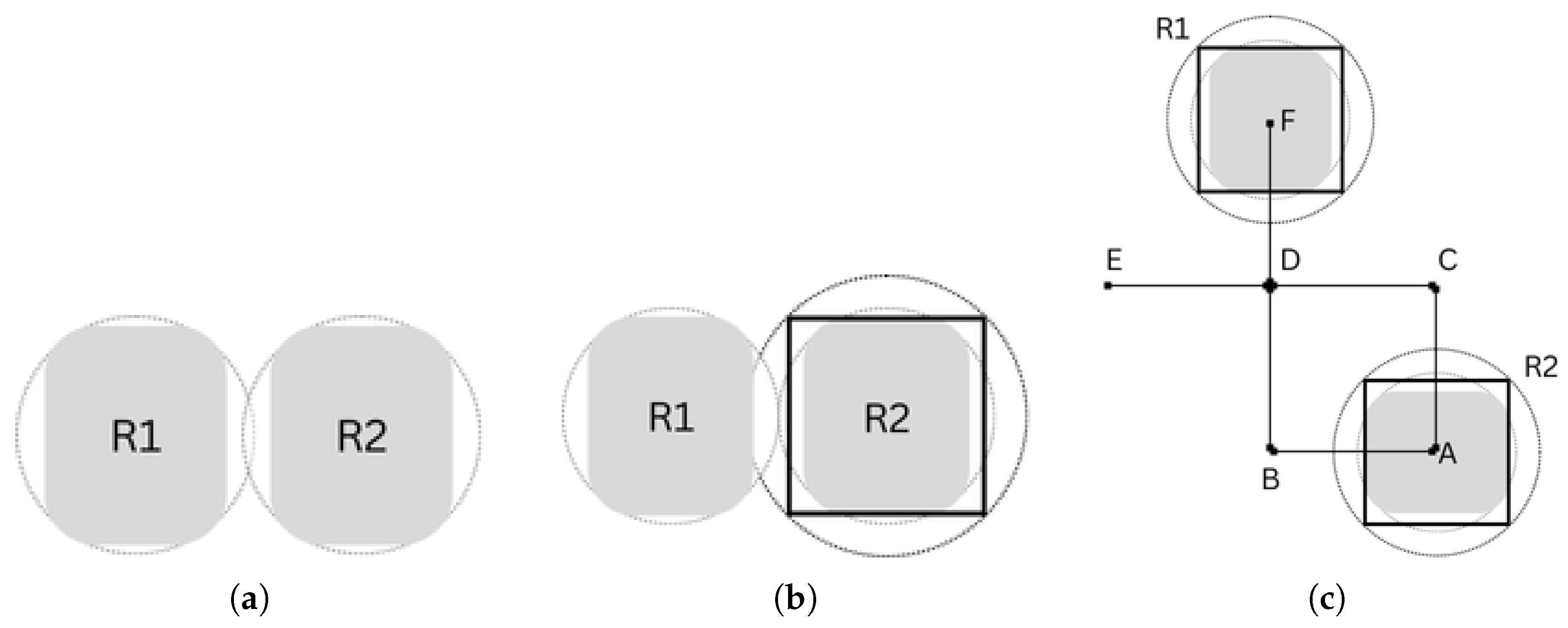
- Robot Dimensions: Each robot measures 798 mm in length and 666 mm in width and has a turning diameter of 872 mm. These dimensions are critical for navigating tight spaces and performing precise maneuvers.
- Lack of Rotary Platform: The robots are not equipped with a rotary platform, meaning that rotations require additional space and careful path planning to avoid collisions, especially when the load is attached to the robot.
- Safety sensors at the front: The robot has a 3-D camera, meaning forward movement is preferred, but backward movement is also possible.
- Shelf Dimensions: The shelves used in the warehouse measure 800 mm by 800 mm. Their size must be considered when planning paths and rotations, particularly in constrained areas.
- Storage Point Spacing: The distance between shelf storage points is 900 mm. This spacing affects how robots navigate between shelves and pick up or drop off loads.
- External Obstacles: The warehouse environment includes various external obstacles, such as columns, barriers, and walls. These obstacles prevent an even distribution of storage locations and necessitate flexible path planning to accommodate narrow passages, sometimes as small as 20–30 cm.
- Turn Restrictions: In specific locations, external obstacles prohibit the robot from turning with a shelf, requiring alternative strategies for maneuvering in these areas.
- Flexible Shelf Pickup: The system must accommodate the ability to pick up shelves at designated storage points and any arbitrary location within the warehouse map. This flexibility is crucial for efficient operation and recovery scenarios.
2.2. MAPF Problem Setup
2.3. Adaptation of MAPF Algorithms to the Problem
| Algorithm 1 Modified windowed CBSwP |
Input: Start states, goals sequences, loads, movement graphs, window T Result: MAPF joint plan
|
2.4. MAPF-POST Adaptation for Problem Conditions
- Task Assignment: Assigning tasks to robots considering the workload at picking stations.
- Task Sequence Optimization: Optimizing the order of task execution, e.g., reordering tasks during execution or assigning additional newly arrived tasks.
- Predicting Future Tasks: Anticipating the next racks whose tasks can be taken up.
| Algorithm 2 General scheme of pathfinding and motion planning using MAPF-POST |
|
2.5. Dynamical Obstacle Handling
3. Results
3.1. Experiment 1: One-Shot MAPF
- Every agent was randomly assigned to a rack, and with probability, the rack was chosen to be on the robot or at a location.
- The initial placement of the robots was generated to avoid collisions between robots and racks. However, this does not guarantee that the problem is solvable. For this experiment, we were only interested in the percentage of unsolvable configurations to show later that this number does not really matter in the lifelong version.
- Tasks were assigned to the first , where , representing the number of drop-off locations.
- Sequences of goals were constructed:
- -
- If a robot had an assigned task and the rack was already on the robot, the sequence contained two goals: one for visiting the drop-off location and another for moving the rack to its storage location.
- -
- If a robot had an assigned task and the rack was not already on the robot, the sequence contained three goals: picking up the rack from the storage location, moving the rack to the drop-off location, and returning the rack to its storage location.
- -
- If a robot had no assigned task, the sequence contained one goal for moving the rack to its storage location or parking the robot on the assigned rack’s storage location.
3.2. Experiment 2: Lifelong MAPF
- Increment the step and update agents’ positions according to the previously constructed plan.
- Add a new task.
- Remove completed tasks and attach containers from robots if necessary.
- Update task queues for the agents. Tasks were processed in the order they were added:
- -
- If the task shares a goal location with at least other tasks assigned to robots, skip this task and process the next one.
- -
- If the rack is already assigned to a robot and the robot has no tasks, add this task to the robot’s task queue and continue to the next task.
- -
- If the rack is already assigned to a robot and the robot has tasks for this rack, add this task if the rack is already on the robot and the robot has only one task. Otherwise, ignore this task.
- -
- If the rack is not yet assigned, choose the nearest robot without an assigned rack and add this task to that robot.
- Regenerate goal sequences. At this point, each robot with an assigned rack will have one of the following goal sequences:
- -
- Pick-up location → Drop-off location → Storage location (if the assigned rack was not already on the robot and the robot had one task in the queue);
- -
- Drop-off location → Drop-off location → Storage location (if the assigned rack was on the robot and the robot had two tasks in the queue);
- -
- Drop-off location → storage location (if the assigned rack was on the robot and the robot had one task in the queue);
- -
- Storage location (if the assigned rack was on the robot and the robot had no tasks);
- Paths were replanned if a new task was added or if h steps had passed since the last replanning step.
- If a solution was found, the paths were updated. Otherwise, the previously constructed paths were executed, and the execution was terminated if there had been w steps without successful replanning.
3.3. Real Warehouse Evaluation
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mas, I.; Kitts, C. Centralized and decentralized multi-robot control methods using the cluster space control framework. In Proceedings of the 2010 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Montreal, QC, Canada, 6–9 July 2010; pp. 115–122. [Google Scholar] [CrossRef]
- Wu, W.; Tong, S. Adaptive Fuzzy Distributed Optimal FTC for Nonlinear Multiagent Systems Based Multiplayer Differential Game. IEEE Trans. Fuzzy Syst. 2025, 33, 657–668. [Google Scholar] [CrossRef]
- Kaminka, G.A.; Erusalimchik, D.; Kraus, S. Adaptive multi-robot coordination: A game-theoretic perspective. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 328–334. [Google Scholar] [CrossRef]
- Manko, S.V.; Diane, S.A.K.; Krivoshatskiy, A.E.; Margolin, I.D.; Slepynina, E.A. Adaptive control of a multi-robot system for transportation of large-sized objects based on reinforcement learning. In Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), Moscow and St. Petersburg, Russia, 29 January–1 February 2018; pp. 923–927. [Google Scholar] [CrossRef]
- Sui, S.; Chen, C.L.P.; Tong, S. Command Filter-Based Predefined Time Adaptive Control for Nonlinear Systems. IEEE Trans. Autom. Control 2024, 69, 7863–7870. [Google Scholar] [CrossRef]
- Brooks, R. Planning Is Just a Way of Avoiding Figuring out What to Do Next; Technical Report; MIT Artificial Intelligence Laboratory: Cambridge, MA, USA, 1987. [Google Scholar]
- Sun, D.; Liao, Q. A Reactive Approach to Handling Multirobot Collision Based on p-Norm Approximation. IEEE Trans. Ind. Electron. 2024, 71, 9265–9275. [Google Scholar] [CrossRef]
- Garg, K.; Zhang, S.; So, O.; Dawson, C.; Fan, C. Learning safe control for multi-robot systems: Methods, verification, and open challenges. Annu. Rev. Control 2024, 57, 100948. [Google Scholar] [CrossRef]
- Cui, Y.; Zhang, Z.; Min, B.; Zheng, C.; Shen, J.; Huang, T. Byzantine-Resilient Impulsive Control for Bipartite Consensus of Heterogeneous Multiagent Systems. IEEE Trans. Circuits Syst. Regul. Pap. 2024, 1–13. [Google Scholar] [CrossRef]
- Ballotta, L.; Talak, R. Safe Distributed Control of Multi-Robot Systems With Communication Delays. IEEE Trans. Veh. Technol. 2025, 1–14. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Xiao, H. Multi-robot system task allocation mechanism for smart factory. In Proceedings of the 2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 24–26 May 2019; pp. 587–591. [Google Scholar] [CrossRef]
- Silver, D. Cooperative Pathfinding. In Proceedings of the AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment, Online, 11–15 October 2021; Volume 1, pp. 117–122. [Google Scholar] [CrossRef]
- Cui, Y.; Chen, J.; Lin, H.; Shu, Z.; Huang, T. Cooperative Multi-AAV Path Planning for Discovering and Tracking Multiple Radio-Tagged Targets. IEEE Trans. Syst. Man Cybern. Syst. 2025, 55, 2463–2475. [Google Scholar] [CrossRef]
- Barták, R.; Švancara, J.; Vlk, M. A Scheduling-Based Approach to Multi-Agent Path Finding with Weighted and Capacitated Arcs. In Proceedings of the 17th International Conference on Autonomous Agents and MultiAgent Systems, Stockholm, Sweden, 10–15 July 2018; pp. 748–756. [Google Scholar]
- Wilde, B.D.; Ter Mors, A.W.; Witteveen, C. Push and Rotate: A Complete Multi-agent Pathfinding Algorithm. J. Artif. Intell. Res. 2014, 51, 443–492. [Google Scholar] [CrossRef]
- Chan, S.H.; Stern, R.; Felner, A.; Koenig, S. Greedy Priority-Based Search for Suboptimal Multi-Agent Path Finding. In Proceedings of the International Symposium on Combinatorial Search, Prague, Czech Republic, 14–16 July 2023; Volume 16, pp. 11–19. [Google Scholar] [CrossRef]
- Stern, R.; Sturtevant, N.; Felner, A.; Koenig, S.; Ma, H.; Walker, T.; Li, J.; Atzmon, D.; Cohen, L.; Kumar, T.K.; et al. Multi-Agent Pathfinding: Definitions, Variants, and Benchmarks. In Proceedings of the International Symposium on Combinatorial Search, Guangzhou, China, 26–30 July 2021; Volume 10, pp. 151–158. [Google Scholar] [CrossRef]
- Li, J.; Surynek, P.; Felner, A.; Ma, H.; Kumar, T.K.S.; Koenig, S. Multi-Agent Path Finding for Large Agents. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–February 2019; Volume 33, pp. 7627–7634. [Google Scholar] [CrossRef]
- Ma, H.; Li, J.; Kumar, T.K.S.; Koenig, S. Lifelong Multi-Agent Path Finding for Online Pickup and Delivery Tasks. arXiv 2017, arXiv:1705.10868. [Google Scholar] [CrossRef]
- Varambally, S.; Li, J.; Koenig, S. Which MAPF Model Works Best for Automated Warehousing? In Proceedings of the International Symposium on Combinatorial Search, Vienna, Austria, 21–23 July 2022; Volume 15, pp. 190–198. [Google Scholar] [CrossRef]
- Sharon, G.; Stern, R.; Felner, A.; Sturtevant, N. Conflict-Based Search For Optimal Multi-Agent Path Finding. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 19–21 May 2021; Volume 26, pp. 563–569. [Google Scholar] [CrossRef]
- Barer, M.; Sharon, G.; Stern, R.; Felner, A. Suboptimal Variants of the Conflict-Based Search Algorithm for the Multi-Agent Pathfinding Problem. In Proceedings of the International Symposium on Combinatorial Search, Gugangzhou, China, 26–30 July 2021; Volume 5, pp. 19–27. [Google Scholar] [CrossRef]
- Li, J.; Ruml, W.; Koenig, S. EECBS: A Bounded-Suboptimal Search for Multi-Agent Path Finding. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 35, pp. 12353–12362. [Google Scholar] [CrossRef]
- Ma, H.; Harabor, D.; Stuckey, P.J.; Li, J.; Koenig, S. Searching with Consistent Prioritization for Multi-Agent Path Finding. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 7643–7650. [Google Scholar] [CrossRef]
- Grenouilleau, F.; Hoeve, W.J.V.; Hooker, J.N. A Multi-Label A* Algorithm for Multi-Agent Pathfinding. In Proceedings of the International Conference on Automated Planning and Scheduling, Guangzhou, China, 7–12 June 2021; Volume 29, pp. 181–185. [Google Scholar] [CrossRef]
- Li, J.; Tinka, A.; Kiesel, S.; Durham, J.W.; Kumar, T.K.S.; Koenig, S. Lifelong Multi-Agent Path Finding in Large-Scale Warehouses. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 35, pp. 11272–11281. [Google Scholar] [CrossRef]
- Yakovlev, K.; Andreychuk, A. Any-Angle Pathfinding for Multiple Agents Based on SIPP Algorithm. In Proceedings of the International Conference on Automated Planning and Scheduling, Pittsburgh, PA, USA, 18–23 June 2017; Volume 27, pp. 586–594. [Google Scholar] [CrossRef]
- Ma, H.; Hönig, W.; Kumar, T.K.S.; Ayanian, N.; Koenig, S. Lifelong Path Planning with Kinematic Constraints for Multi-Agent Pickup and Delivery. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 7651–7658. [Google Scholar] [CrossRef]
- Hoenig, W.; Kumar, T.K.; Cohen, L.; Ma, H.; Xu, H.; Ayanian, N.; Koenig, S. Multi-Agent Path Finding with Kinematic Constraints. In Proceedings of the International Conference on Automated Planning and Scheduling, London, UK, 12–17 June 2016; Volume 26, pp. 477–485. [Google Scholar] [CrossRef]
- Honig, W.; Kiesel, S.; Tinka, A.; Durham, J.W.; Ayanian, N. Persistent and Robust Execution of MAPF Schedules in Warehouses. IEEE Robot. Autom. Lett. 2019, 4, 1125–1131. [Google Scholar] [CrossRef]
- Atzmon, D.; Stern, R.; Felner, A.; Wagner, G.; Barták, R.; Zhou, N.F. Robust Multi-Agent Path Finding and Executing. J. Artif. Intell. Res. 2020, 67, 549–579. [Google Scholar] [CrossRef]
- Švancara, J.; Vlk, M.; Stern, R.; Atzmon, D.; Barták, R. Online Multi-Agent Pathfinding. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 7732–7739. [Google Scholar] [CrossRef]
- Andreychuk, A.; Yakovlev, K.; Atzmon, D.; Stern, R. Multi-Agent Pathfinding with Continuous Time. Artif. Intell. 2019, 305, 103662. [Google Scholar] [CrossRef]
- Berndt, A.; Van Duijkeren, N.; Palmieri, L.; Keviczky, T. A Feedback Scheme to Reorder a Multi-Agent Execution Schedule by Persistently Optimizing a Switchable Action Dependency Graph. arXiv 2020, arXiv:2010.05254. [Google Scholar] [CrossRef]
- Honig, W.; Preiss, J.A.; Kumar, T.K.S.; Sukhatme, G.S.; Ayanian, N. Trajectory Planning for Quadrotor Swarms. IEEE Trans. Robot. 2018, 34, 856–869. [Google Scholar] [CrossRef]
- Phillips, M.; Likhachev, M. SIPP: Safe interval path planning for dynamic environments. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 5628–5635. [Google Scholar] [CrossRef]



| Success Avg. time Avg. CT nodes Avg. sum of costs Solution not found Search timeout | 96.4% 2 ms 10 282 3.6% - | 96.4% 3 ms 32 284 3.6% - | 96.4% 9 ms 132 286 3.6% - | 96.4% 34 ms 391 286 3.6% 0.03% | |
| Success Avg. time Avg. CT nodes Avg. sum of costs Solution not found Search timeout | 94% 3 ms 20 339 6% - | 94% 5 ms 78 341 6% - | 94% 36 ms 533 345 6% - | 93.9% 126 ms 1441 345 6% 0.1% | |
| Success Avg. time Avg. CT nodes Avg. sum of costs Solution not found Search timeout | 91.4% 4 ms 42 386 8.6% - | 91.4% 14 ms 253 390 8.6% - | 91.4% 109 ms 1682 393 8.6% 0.7% | 91.1% 324 ms 4009 394 8.6% 3.3% |
| Success Avg. time Avg. CT nodes Avg. sum of costs Solution not found Search timeout | 95.9% 2 ms 10 282 4.1% - | 95.9% 3 ms 29 284 4.1% - | 95.9% 10 ms 138 286 4.1% - | 95.8% 22 ms 278 287 4.2% 0.06% | |
| Success Avg. time Avg. CT nodes Avg. sum of costs Solution not found Search timeout | 93.9% 3 ms 20 351 6.1% - | 93.9% 6 ms 89 354 6.1% - | 93.9% 106 ms 1513 358 6.1% - | 93.5% 288 ms 3435 358 6.1% 0.4% | |
| Success Avg. time Avg. CT nodes Avg. sum of costs Solution not found Search timeout | 91.1% 4 ms 42 419 8.9% - | 91.1% 22 ms 350 424 8.9% - | 90.5% 579 ms 7806 427 8.9% 0.63% | 87.7% 914 ms 11160 420 8.9% 3.43% |
| Makespan Service Time Runtime (s) | 3221 1098 1.32 | 3225 852 2.05 | 3229 607 1.68 | 3234 364 1.53 | 3248 126 1.68 | |
| Makespan Service Time Runtime (s) | 2215 584 2.29 | 2215 337 2.65 | 2247 111 2.12 | 2567 34 1.82 | 3058 30 1.82 | |
| Makespan Service Time Runtime (s) | 1859 385 4.18 | 1864 152 3.0 | 2074 38 3.41 | 2557 30 2.06 | 3056 27 1.82 | |
| Makespan Service Time Runtime (s) | 1736 318 3.88 | 1958 99 3.12 | 2067 34 2.62 | 2559 28 2.25 | 3059 27 3.12 |
| Initially solvable instances (out of 200) | 183 | 189 | 190 | 191 | 193 | 194 | 200 |
| Successful runs | 2% | 95% | 100% | 100% | 100% | 100% | 100% |
| Avg. Task Execution Time | Avg. Delivery Time | Avg. Operator Interaction Time | |
|---|---|---|---|
| One operator experiment | 91.25 s | 62.375 s | 10.420 s |
| Retrospective data | 137.649 s | 61.670 s | 36.698 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pikulin, P.; Lishunov, V.; Kułakowski, K. Optimizing Path Planning for Automated Guided Vehicles in Constrained Warehouse Environments: Addressing the Challenges of Non-Rotary Platforms and Irregular Layouts. Robotics 2025, 14, 39. https://doi.org/10.3390/robotics14040039
Pikulin P, Lishunov V, Kułakowski K. Optimizing Path Planning for Automated Guided Vehicles in Constrained Warehouse Environments: Addressing the Challenges of Non-Rotary Platforms and Irregular Layouts. Robotics. 2025; 14(4):39. https://doi.org/10.3390/robotics14040039
Chicago/Turabian StylePikulin, Pavlo, Vitalii Lishunov, and Konrad Kułakowski. 2025. "Optimizing Path Planning for Automated Guided Vehicles in Constrained Warehouse Environments: Addressing the Challenges of Non-Rotary Platforms and Irregular Layouts" Robotics 14, no. 4: 39. https://doi.org/10.3390/robotics14040039
APA StylePikulin, P., Lishunov, V., & Kułakowski, K. (2025). Optimizing Path Planning for Automated Guided Vehicles in Constrained Warehouse Environments: Addressing the Challenges of Non-Rotary Platforms and Irregular Layouts. Robotics, 14(4), 39. https://doi.org/10.3390/robotics14040039









