Design and Evaluation of a Dual-Bendable, Compressible Robotic Guide Sheath for Heart Valve Interventions

Abstract

Structural heart interventions require precise navigation through tortuous and dynamic cardiac anatomies. However, current guide sheaths often lack sufficient maneuverability for positioning additional catheters. To address these limitations, this paper presents the design and evaluation of a robotic guide sheath with a dual-bendable, compressible tip. The sheath is capable of navigating complex cardiac anatomies for multiple valve interventions. The system consists of a soft continuum sheath tip driven by tendons, a laser-cut compact motorized actuation bed, and a joystick-controlled tendon actuation mechanism. A constant-curvature kinematic model maps actuation inputs to tip bending in 3D, while a custom software interface enables real-time control. Mechanical evaluation (tension, maximum bending, and contraction tests) demonstrated low actuation tension requirements (0.78 N), a wide bending range (from 80° to 90°), and promising tip compressibility (average 5 mm). Trajectory-following tests showed good accuracy, with an average error of 3.34 mm. Catheter guidance trials further validated the sheath’s ability to navigate to the right atrium and guide additional catheters effectively. This work presents a proof-of-concept robotic guide sheath with enhanced maneuverability and adaptability, establishing a foundation for future integration of sensing, automation, and clinical applications.

1. Introduction

Heart valve diseases, including regurgitation, stenosis, and atresia, are pathological conditions that compromise unidirectional blood flow through the chambers of the heart, often resulting in heart failure or other life-threatening complications [1,2,3]. Although open heart surgery remains the standard treatment for repair or replacement, it carries a high operative risk, long recovery times, and considerable healthcare costs, particularly for elderly patients or those with clinical complications [4]. In the last decade, minimally invasive transcatheter procedures have emerged as a safer alternative, allowing percutaneous delivery of valve implants or repair devices via vascular access under imaging guidance [5,6,7]. Clinically, steerable guide sheaths, such as FlexCath steerable sheath from Medtronic (Minneapolis, MN, USA) [8], are often used to provide a delivery pathway and positioning support for other catheters [9,10]. They are particularly valuable in addressing anatomical access challenges, for example by compensating for the offset between the inferior vena cava and the tricuspid annulus [11]. However, the current generation of manual sheaths has several limitations: (1) substantial radiation exposure for clinicians during fluoroscopy-guided procedures; (2) restricted dexterity and lack of independent torsional control at the tip; (3) difficulty navigating tortuous anatomical pathways without contacting tissue; and (4) lack of standardization, with interventionalists required to master multiple device designs from different manufacturers depending on the procedure [12,13,14]. These factors hinder the broader adoption and accessibility of minimally invasive valve interventions, especially in resource-limited healthcare systems [15].

Robotic technology has been integrated into sheath guidance to overcome the limitations of manual systems, offering enhanced precision, stability, and operator safety [16]. Commercial platforms such as the Sensei, Magellan systems (Auris Surgical Robotics, Silicon Valley, CA, USA) and V-CAS Deflect (Stereotaxis, St. Louis, MO, USA) have been applied in cardiac interventions, enabling remote navigation of balloons, stents, and other devices through steerable sheaths [16,17]. These systems employ teleoperation workstations that allow the operator to control the sheath from outside the radiation field. However, despite their clinical utility, current commercial solutions, while mainly used for catheter ablation of fibrillation and mapping, remain constrained in their applicability to the wider spectrum of structural and valve interventions.

Compared with the extensively studied robotic catheter systems, research on robotic sheath systems remains relatively limited. Nonetheless, sheath design can draw significant inspiration from advances in continuum robot technologies developed for other minimally invasive procedures. Representative studies are summarized in

Table 1. Representative Studies on Robotic Sheath Systems.

Reference	Tip Material	Actuation	DoF	BA (°)	ID (mm)	Application
Chautems et al. [19]	Spring + magnets	Magnetic	2	150	3.0	Ablations
Kong et al. [22]	Backbone	Tendon	2	120	3.2	Transnasal surgery
Qi et al. [20]	Nitinol tube	Tendon	1	25	2.4	Single-port surgery
Wang et al. [23]	Backbone	Precurved tubes	2	79	2.2	Single-port surgery
Wang et al. [21]	Laser-cut hypotube	Tendon	1	120	7.6	Valve interventions
Sridhar et al. [24]	McKibben muscles	Pneumatic	2	68	6.0	Valve interventions
This work	Resin	Tendon	3	90	6.0	Valve interventions

Acronyms: BA, bending angle; ID, inner diameter. DoF refers specifically to the tip’s degrees of freedom, excluding general sheath translation and rotation; ‘Bending angle’ indicates the maximum bending angle reported in each study; ‘Inner diameter’ specifies the lumen size, serving as a reference for the largest catheter the sheath can accommodate. If not explicitly reported, the catheter’s outer diameter may be used as an alternative reference.

. In general, the actuation strategies reported in the literature can be categorized into three main types: magnetic, tendon/cable-driven, and pneumatic or hydraulic actuation [18]. Magnetic actuation has been applied to enhance the manipulability of sheath tips. For example, Chautems et al. [19] developed a magnetically actuated sheath that enables more intuitive control by steering a flexible distal segment with external magnetic fields. This approach allows remote actuation without onboard motors, though the achievable forces and workspace are constrained by field strength and system setup. Tendon-driven actuation remains the most widely adopted method. Laser-cut tube tips have been employed as the bending segment [20,21], although this configuration generally provides only a single bending degree of freedom (DoF). Backbone-based tips can achieve higher dexterity with multiple bending DoFs [22], but their range of motion is still limited by material and mechanical constraints. Building on this concept, concentric tube mechanisms have been innovatively integrated into sheaths; for instance, Wang et al. [23] demonstrated tip deflection in both the X and Y directions by rotating two precurved tubes inside the sheath. However, this method also suffers from a restricted bending range. Beyond tendon and concentric designs, soft continuum approaches have also been explored. Sridhar et al. [24] proposed a pneumatically actuated soft steerable sheath, which offers inherent compliance and safety advantages. Nevertheless, the prototype exhibited only a small bending range, highlighting the ongoing trade-off between flexibility, force generation, and workspace in sheath actuation.

In summary, while tendon-driven and soft robotic structures have been widely studied, research on robotic sheath systems for cardiac valve interventions remains limited. Existing robotic sheaths for such interventions typically offer 1–2 DoFs, limiting their maneuverability. Inspired by continuum robot techniques, we hypothesize that a tendon-driven soft tip could present a promising solution for achieving both higher DoFs and larger bending angles. Such a design could enhance maneuverability, reduce dependence on additional steerable catheters, and broaden applicability across multiple valve interventions.

In this work, we present the design, development, and validation of a dual-bendable, compressible robotic guide sheath for heart valve interventions. The sheath tip is modeled as a continuum structure with notched patterns and fabricated using soft materials. Combined with tendon-driven actuation, it provides 3-DoF motion, consisting of two bending DoFs and one contraction DoF. A compact motorized actuation bed with uniform tendon tension is connected to a joystick-controlled interface, enabling remote operation. The kinematic model is based on the constant-curvature assumption. First, the single-bending case is analyzed to establish the mapping from actuation space to task space. Using vector superposition, the dual-bending case is then formulated as an extension of the single-bending model, yielding the full kinematic representation. System performance was evaluated through mechanical testing, trajectory-following experiments, and catheter guidance trials. The results demonstrate the potential of the robotic sheath for navigation in complex cardiovascular interventions, establishing a strong foundation for future clinical applications. The contributions are summarized below:

• Hybrid tendon-driven soft tip: A novel sheath tip combining tendon-driven actuation with a soft, compressible structure, providing enhanced maneuverability with two bending DoFs and one contraction DoF.
• Dual-bending kinematic model: An efficient model built from the single-bending case using vector superposition, reducing computational complexity while accurately capturing motion.
• Comprehensive validation: Evaluated through mechanical testing, trajectory-following experiments, and catheter guidance trials, demonstrating improved dexterity and applicability for cardiac interventions.

2. Materials and Methods

The overview of the robotic guide sheath is shown in Figure 1. It consists of four main parts: a sheath tip, a long shaft (main cannula), an actuation system, and a joystick controller (DualSense wireless controller, PlayStation 5, Sony, Minato, Tokyo, Japan). The operating principle is straightforward: moving the joystick sends signals to the actuation system, which pushes or pulls the tendons through the cannula to shape the tip and create different guiding paths.

2.1. Guide Sheath Tip Design

The sheath tip was designed as a soft, tendon-driven, multi-DoF bending structure, adaptable to different clinical applications and capable of reproducing the curvature required for various valve intervention paths. The geometry was modeled in Fusion 360 (Autodesk, San Rafael, CA, USA), as shown in Figure 1A. The bending joint was created using notch patterns (width a: 3 mm; spacing between notches b: 6 mm) cut along the tip. Because the pattern is uniform, the bending curvature remains constant. To enable bidirectional bending, the same notch pattern was added to the opposite side. To further increase dexterity, an additional set of notch patterns, offset by c (3 mm), was placed on the perpendicular plane, creating two orthogonal bidirectional bending joints. To achieve a large bending angle, high-tensile polyethylene tendons (diameter: 0.5 mm, Young’s modulus: 3 GPa) were used to actuate the joints. Accordingly, four tendon routes (hole diameter d: 1 mm) were added along each notch pattern and uniformly distributed around the cross-sectional plane of the tip. The tendons were fixed at the distal tip using a routing block and pre-tensioned to eliminate slack before integration with the actuation system.

The sheath tip dimensions and tendon channel positions were refined by selecting from several prototype designs, inspired by previous research [25,26,27]. The inner diameter of the sheath tip was designed as e (6.0 mm), allowing it to accommodate interventional catheters smaller than 17 Fr, such as the Commander delivery system (Edwards Lifesciences Inc., Irvine, CA, USA) for valve replacement and the Jotec vascular stent graft system (JOTEC GmbH, Hechingen, Germany) for endovascular aneurysm repair. The overall tip measures 25 mm in length, with an outer diameter of 10 mm.

The sheath tip was fabricated using SLA 3D printing (Formlabs Inc., Somerville, MA, USA) at $50\mathsf{\mu }\mathrm{m}$ layer resolution. The initial objective was to obtain a flexible yet robust material able to actuate and sustain in the complex geometries of the four heart chambers. For this reason, three resin formulations were evaluated after consultations with several technicians and professionals: Tough 2000 resin [28] for stiffness, Flexible 80A resin [29] for compliant bending, and Elastic 50A [30] for enhanced flexibility. Flexible 80 A was selected as the final material for the most general surgical applications of the tip, due to its ideal trade-off between the two desired properties. Post-processing of the tips included isopropyl alcohol rinsing and UV curing to achieve optimal mechanical properties. In addition, Flexible 80A is marketed as a medical-grade material and is claimed with ISO 10993 [31] and USP Class VI certifications for certain contact durations (e.g., long-term skin, short-term mucosal exposure) [32]. These qualifications make the chosen resin material biocompatible for internal surgeries.

Because the tip is relatively soft, pulling all four tendons together allows the tip to retract, introducing a third DoF. This variable length provides finer control when navigating curves or folds in the heart, complementing the bending DoFs and reducing the risk of trauma or vessel damage.

2.2. Actuation System

The wireframe of the actuation system is shown in Figure 1B. Four brushless DC (BLDC) motors with integrated encoders (Suzhou Micro Actuator Technology Co., Suzhou, China) were used to drive the tendons. These motors offer high precision and fast response, reducing mechanism latency in control. They were powered by a 24 V DC supply, and communication with the controller was established via a USB-to-CAN bus adapter, enabling minimal-delay control and real-time encoder feedback. Each motor is paired with a 3D-printed spool (10 mm diameter) and tendon guide that anchor a tendon and converts rotational motion into linear displacement. The spools were sized to accommodate the required tendon pull range and the angular travel needed for maximum bending. To ensure uniform bending in multi-tendon configurations, the spools and motors were mounted symmetrically, and each motor’s control signal was mapped in the controller to coordinate paired tendon motion for smooth curvature generation. The tendons from the sheath tip were routed through a 3D-printed cannula, enclosed by PTFE tubes from the distal module to the actuation bed, minimizing friction and ensuring consistent force transmission. The cannula is supported by three stands.

All components were assembled on an actuation bed. The bed was designed as a compact platform fabricated from 8 mm cast acrylic sheets, cut using a CO₂ laser cutter (Epilog Fusion Edge), ensuring precise alignment of BLDCs, spools, and tendon guides.

2.3. Remote Control Interface

To reduce radiation exposure to the operator, the sheath was teleoperated using the joystick controller connected to a host computer. The joystick [33] served as the primary input device for the control system, which was implemented on macOS (Apple Silicon). Communication between the joystick and the computer was established via Bluetooth using Apple’s IOKit and IOBluetooth frameworks. Controller inputs were processed in C++23 and Python 3.14 with the hidapi and python-can libraries, which interfaced with a USB-to-CAN adapter within the Qt Creator 16 environment. The system operated at a target frequency of 50 Hz, consistent with other tendon-driven robotic platforms. Communication over USB-to-CAN at 1 Mbps introduced less than 3 ms of transmission and interface delay, as typically observed in commercial CAN adapters. Including sensor processing, control computation, and actuation response, the total end-to-end latency was approximately 25 ms, which remains well within the clinically safe range (<100 ms) reported for teleoperation systems [34].

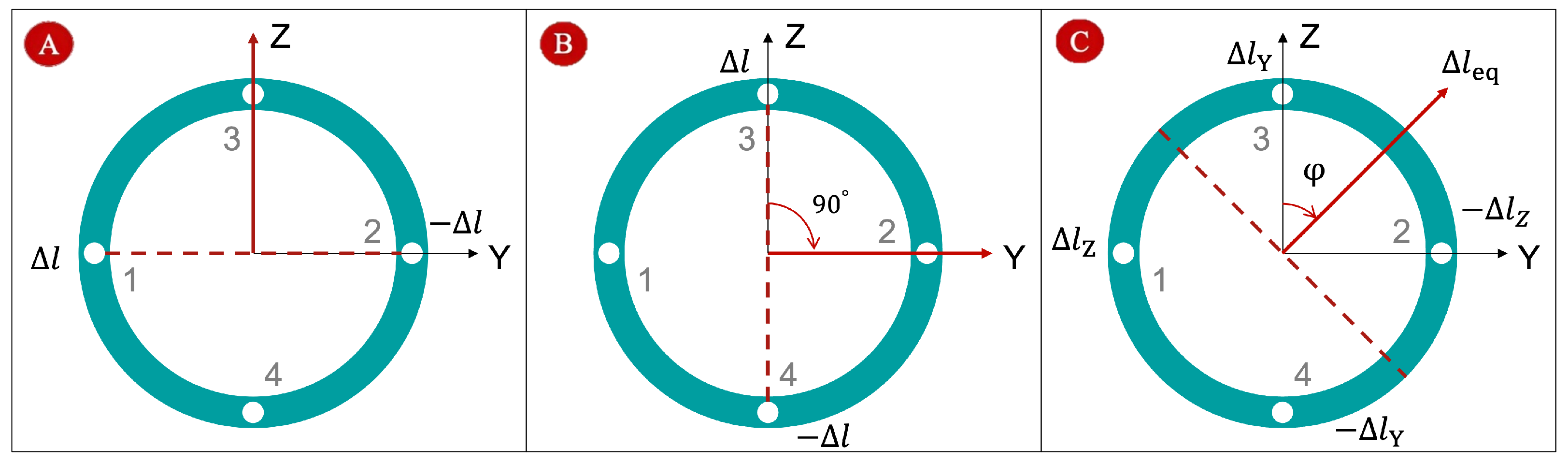
Each directional button on the controller (Figure 2) was mapped to a coordinated motor action (Figure 3): pressing left pulled Motor 1 while releasing Motor 4 to bend the tip left, pressing right reversed this motion, and the up and down buttons controlled Motors 2 and 3 in the same paired fashion for vertical bending. An additional “contraction” button was added to pull simultaneously the four motors, retracting the tip. The code ensured opposing tendons were always slightly tensioned to avoid slack, using current control to hold position when no movement was commanded. Final refinement in the code replaced velocity commands with incremental position control, observed to be more efficient during the evaluation phase, so each button press adjusted the tip angle by a fixed step, providing smooth, precise, and repeatable motion. Safety measures included software-defined travel limits, current limits, and an emergency stop command.

During operation, the system continuously logged command signals, encoder feedback, and joystick inputs for later performance analysis. The modular software architecture supports future integration of autonomous navigation, haptic feedback, and additional sensing modalities without requiring major code redesign.

2.4. Kinematic Modeling

The bending section of the sheath was modeled using the constant-curvature assumption, as described in Section 2.1. A single bend involves only one curvature, making the kinematics and tendon-actuation relationships straightforward. By first analyzing the single-bending case, the analysis can then be extended to the double-bending case through superposition or sequencing of curvatures.

2.4.1. Single-Bending Case

We first consider the single-bending case. Kinematics can typically be divided into three spaces: actuation, configuration, and task space [35]. The actuation space describes the motor angles that drive tendon movements. When a spool rotates by an angle $\varphi$ (in radians), it pulls a tendon wrapped around it, producing a linear displacement:

$$\Delta l=r_{\mathrm{s}}\varphi$$

(1)

where $\Delta l$ is the change in tendon length; $r_{\mathrm{s}}$ is the radius of the spool. For antagonistic tendons positioned on opposite sides of the catheter’s circumference, the difference in tendon lengths induces bending of the sheath.

The configuration space describes the geometric bending of the sheath segment, modeled as a circular arc under the constant-curvature assumption [36]. To account for tendon geometry, we first analyze the paths of the inner, outer, and centerline arcs in the X-Y plane (Figure 4A). The relevant parameters are:

• ${\theta }_{\mathrm{z}}$: Bending angle about Z axis, defined between the tangents at the base and the tip of the section, with its vertex fixed at the center of curvature;
• L: Length of the bending segment (i.e., the length of the centerline);
• $L_1$: Length of the outer tendon;
• $L_2$: Length of the inner tendon;
• r: Radius of curvature of the centerline;
• h: Radial offset (distance between a pair of tendons).

Based on arc geometry, we make the following assumptions:

• The outer tendon follows a longer path with radius;
• The inner tendon follows a shorter arc with radius;
• The centerline of the catheter lies at radius r.

From these assumptions, the tendon lengths are:

$$L_1=(r+h/2){\theta }_{\mathrm{z}}$$

(2)

$$L_2=(r-h/2){\theta }_{\mathrm{z}}$$

(3)

The difference in tendon lengths gives:

$$L_1-L_2=h{\theta }_{\mathrm{z}}\Rightarrow {\theta }_{\mathrm{z}}=(L_1-L_2)/h$$

(4)

Combining Equations (1) and (4) yields the mapping from configuration space to actuation space:

$${\theta }_{\mathrm{z}}=2\Delta l/h=2r_{\mathrm{s}}\varphi /h$$

(5)

The task-space coordinates are shown in Figure 4B. They define the tip’s position in task space, ${[x,y,z]}^{\mathrm{T}}$, relative to the base O of the bending segment. Given ${\theta }_{\mathrm{z}}$, the centerline radius of curvature can be calculated from the sheath’s arc length L:

$$r=L/{\theta }_{\mathrm{z}}$$

(6)

Using circular-arc geometry, the tip coordinates for bending in the X–Y plane are:

$$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{c}rsin{\theta }_{\mathrm{z}}\\ r(1-cos{\theta }_{\mathrm{z}})\\ 0\end{array}\right]$$

(7)

This completes the mapping from motor rotation, through bending, to the 2D spatial location of the sheath tip. If bending occurs in both X–Y and X–Z planes, the motions can be superposed to obtain the 3D tip position, as detailed next.

2.4.2. Two-Bending Case

Figure 5A illustrates the first bending scenario, where tendon 1 is pushed and tendon 2 is pulled by the same displacement $\Delta l$. The red dashed line represents the bending plane, and the red arrow indicates the bending direction. When tendon 3 is pushed and tendon 4 is pulled by $\Delta l$, the sheath bends in the X–Z plane (Figure 5B). To analyze this, we rotate the coordinate system about the X axis by −90°. In the rotated frame, the bending occurs about the Z axis, allowing us to apply the single-bending method from Section 2.4.1. The resulting tip position can then be transformed back to the original coordinates:

$$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\\ 0& -1& 0\end{array}\right]\left[\begin{array}{c}rsin{\theta }_{\mathrm{z}}\\ r(1-cos{\theta }_{\mathrm{z}})\\ 0\end{array}\right]=\left[\begin{array}{c}rsin{\theta }_{\mathrm{z}}\\ 0\\ -r(1-cos{\theta }_{\mathrm{z}})\end{array}\right]$$

(8)

Figure 5C shows the general case, where two pairs of tendons drive bending simultaneously: $\Delta l_{\mathrm{Z}}$ for X–Y bending and $\Delta l_{\mathrm{Y}}$ for X–Z bending. The tendon displacements in orthogonal planes can be treated as vector components. Using vector superposition, the effective bending displacement $\Delta l_{\mathrm{eq}}$ and bending-plane orientation $\phi$ are computed as:

$$\Delta l_{\mathrm{eq}}=\sqrt{{\Delta l_{\mathrm{Y}}}^2+{\Delta l_{\mathrm{Z}}}^2}$$

(9)

$$\phi =arctan(\Delta l_{\mathrm{Y}},\Delta l_{\mathrm{Z}})$$

(10)

Here, $\Delta l_{\mathrm{eq}}$ represents the magnitude of the equivalent displacement, and $\phi$ defines the orientation of the bending plane relative to the original coordinate system. Equivalently, this deformation can be modeled as a single tendon acting along the direction $\phi$ with an effective displacement $\Delta l_{\mathrm{eq}}$. This approach provides a straightforward way to handle two simultaneous bending patterns using the single-bending formulation. Using Equations (5) and (6), the equivalent bending angle ${\theta }_{\mathrm{eq}}$ and bending radius $r_{\mathrm{eq}}$ can be calculated. The resulting tip position, after rotating the coordinate system about the X axis by $-\phi$, is:

$$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& cos\phi & sin\phi \\ 0& -sin\phi & cos\phi \end{array}\right]\left[\begin{array}{c}{r}_{\mathrm{eq}}sin{\theta }_{\mathrm{eq}}\\ r_{\mathrm{eq}}(1-cos{\theta }_{\mathrm{eq}})\\ 0\end{array}\right]=\left[\begin{array}{c}{r}_{\mathrm{eq}}sin{\theta }_{\mathrm{eq}}\\ r_{\mathrm{eq}}cos\phi (1-cos{\theta }_{\mathrm{eq}})\\ -r_{\mathrm{eq}}sin\phi (1-cos{\theta }_{\mathrm{eq}})\end{array}\right]$$

(11)

Finally, note that pulling all four tendons simultaneously shortens the sheath tip, which reduces the arc length L. This contraction DoF can be incorporated by updating L in the kinematic calculations.

2.4.3. Further Consideration for Tendons and Joint Stiffness

Accounting for the elasticity of tendons and the stiffness of joints, the relationship between tendon displacement and bending angle becomes:

$${\theta }^{*}=\left({\displaystyle \frac{\Delta L}{d}}\right)\left({\displaystyle \frac{1}{1+\frac{k_e}{k_t}}}\right)$$

(12)

where $k_e$ is the elastic stiffness of the catheter material; $k_t$ is the tendon stiffness. This correction improves the model’s predictive abilities under real-world loading conditions [37].

2.5. Experimental Setup

The overview of the experimental setup is shown in Figure 6. The system validation process was designed to assess its intrinsic features, functions, positioning accuracy, and overall feasibility. Tension and maximum bending tests were performed to determine the minimum tension required to actuate the tip and its maximum bending range. Contraction tests verified the tip’s contraction capability, while trajectory-following tests evaluated positioning accuracy. Finally, sheath guidance and phantom tests assessed the feasibility of catheter guidance and anatomical navigation. All tests were conducted on a bench setup where the catheter was mounted to a fixed base with the actuation bed and control system connected to the host computer. The Aurora NDI electromagnetic tracking system (Northern Digital Inc., Waterloo, ON, Canada) was employed for all experiments, which provided six-DoF tip measurements in real time. EM sensors were placed at the end of the shaft and the tip of the catheter to capture the two directional positions for real-time tracking and respective orientation analysis. The PS5 DualSense controller served as the operator actuation instrument for all experiments, using the final position and current-control software function described in Section 2.3.

2.5.1. Tension Test Setup

The first experiment measured the minimum tendon tension required to initiate sheath tip movement and evaluated whether the motors could provide sufficient force. This was done by gradually increasing motor currents from zero using the current control function described in Section 2.3, while tip motion was detected with the NDI tracking system. The goal of this test was to quantify the relationship between commanded motor current and the resulting actuation force, thereby defining the safe operating tension range of the system. Tendon tension for each motor was calculated using the following function:

$$F={\displaystyle \frac{I{K}_t}{r_{\mathrm{s}}}}$$

(13)

where F is the tension in the wire (N); I is the motor current (A); $K_t$ is the torque constant of the motor (Nm/A).

2.5.2. Maximum Bending Test Setup

The maximum achievable bending angle was determined by gradually increasing motor displacement from the neutral position until either mechanical binding occurred or material deformation was observed at the tip. The corresponding bending angles were recorded using the NDI tracking system for both vertical and horizontal bending axes. These measurements defined the physical limits of the catheter tip and were implemented in the control software as travel limits to prevent hardware damage during operation.

2.5.3. Contraction Test Setup

The functionality of the contraction button, described in the interface section, was tested by pressing button X on the joystick. This command caused all motors to rotate simultaneously in their respective pulling directions, contracting the entire catheter tip (Figure 7). Six trials were conducted. The contraction distance was confirmed using the EM tracker system. This experiment was designed to measure the maximum range of the contraction DoF.

2.5.4. Trajectory-Following Test Setup

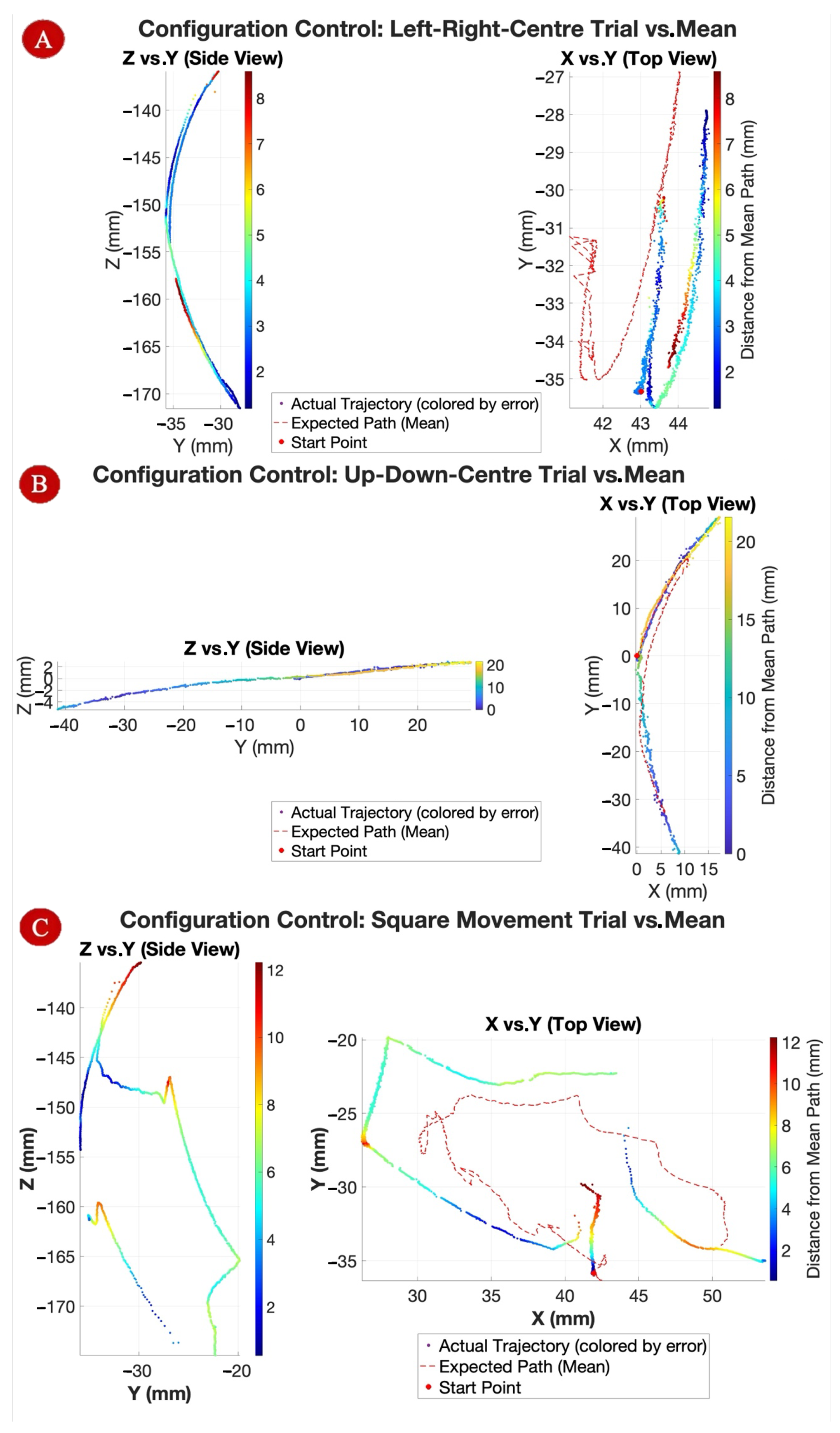
To evaluate the tip positioning precision, the Aurora NDI tracking system was used to record 3D coordinates of the sheath tip under both static and dynamic conditions. For static tests, the tip was actuated to a set of predetermined positions, activating one motor at the time to have the tip move along the four main directions of the two planes (left and right horizontally/up and down vertically) with each location held for several seconds to measure positional stability. For dynamic tests, the tip followed predefined trajectories in multiple planes replicating motions necessary in clinical scenarios: a right-left-centre movement, an up-down-centre movement, and a 360-degree (“Square”) movement. The experiment was performed 5 times per each motion (Figure 8), and measured paths were compared to commanded ones to calculate mean absolute errors. This allowed assessment of repeatability, responsiveness, and the effect of cable compliance on positioning accuracy.

2.5.5. Sheath Guidance Test Setup

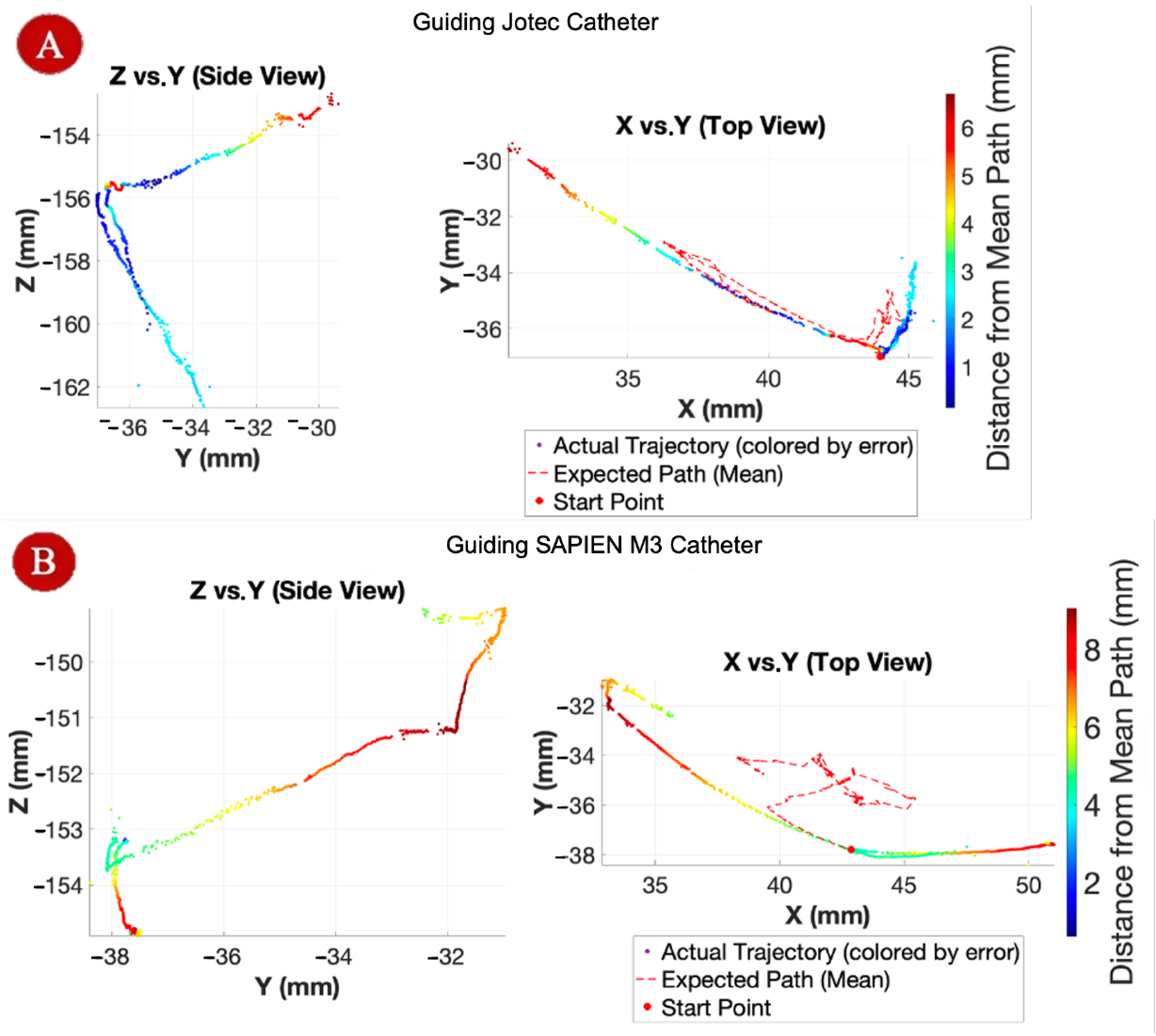
To evaluate sheath guidance under realistic operating conditions, different cardiac interventional catheters were placed inside the main cannula of the guide sheath and tested with the proposed system. The first catheter (Figure 9A) was the Jotec vascular stent graft system (JOTEC GmbH, Hechingen, Germany), designed for endovascular aneurysm repair (EVAR) [38]. The second catheter (Figure 9B) was the SAPIEN M3 dock catheter (Edwards Lifesciences Inc., Irvine, CA, USA), a docking system for mitral valve replacement [39], which represents one of the primary target procedures of this design. Bending tests were performed to assess whether the soft sheath tip provided sufficient stiffness to deflect the inserted catheters.

2.5.6. Phantom Navigation Test Setup

Anatomical navigation capability was tested in a custom PLA 3D-printed heart phantom for sheath navigation (Figure 10). The heart model, adapted from an echocardiography e-learning module by the University of Groningen (licensed under CC Attribution-NonCommercial-ShareAlike), is anatomically accurate. The test was designed to replicate the geometry of human cardiac chambers and access pathways to the mitral valve. Operators guided the sheath from the insertion point (inferior vena cava) to the valve region using the joystick controller in position-and-current control mode.

3. Results

3.1. Tension Test Results

The results of the tension test are shown in Figure 11.

Table 2. Summary of Input Current, Corresponding Tip Displacement, and Calculated Tendon Tension for Each Motor.

	Current (A)	Displacement (mm)	Tension (N)
Motor 1	0.11	0.38	0.66
Motor 2	0.11	0.46	0.66
Motor 3	0.11	0.22	0.66
Motor 4	0.13	0.49	0.78

summarizes the input currents, measured displacements, and calculated tendon tensions. Motion became detectable between 110–130 mA, with displacement first observed at 0.11 A for Motors 1–3 and 0.13 A for Motor 4. Using a torque constant $K_{\mathrm{t}}$ = 0.06 N·m/A and a spool radius $r_{\mathrm{s}}$ = 10 mm, the corresponding tendon tensions were calculated as 0.66 N for Motors 1–3 and 0.78 N for Motor 4. Variations between motors likely reflect differences in cable path friction, pre-tension, and sheath resistance, with earlier saturation in Motors 1 and 3 suggesting lower resistance or pre-tension. These values represent the minimum force required to actuate the sheath tip. All motors were able to provide sufficient force to overcome static and mechanical resistance, ensuring consistent tip bending.

3.2. Maximum Bending Test Results

The maximum bending angle test quantified the sheath tip’s physical bending limits under single-motor actuation in each of the four principal directions. Each motor was actuated independently until either the maximum displacement was reached or the motor’s internal torque limit caused motion to stop. NDI measurements and the kinematic model from Section 2.4 were used to calculate bending angles from tendon displacements $\Delta l$ through Equation (1) and obtained using a spool radius of 0.01 m and the measured motor rotation angles $\varphi$ of 1.536 rad (Motor 1), 1.396 rad (Motor 2), 1.484 rad (Motor 3), and 1.571 rad (Motor 4). The motor rotation angles, expressed in radians, were estimated from the EM data path arcs. Applying the constant-curvature relation (Equation (5)), with an antagonistic tendon spacing h = 0.01 m yielded bending angles of 88.3 ± 2°, 80.3 ± 2°, 84.8 ± 2°, and 90.0 ± 2° for Motors 1 through 4, respectively (

Table 3. Summary of the Maximum Bending Angle Achieved by Each Motor.

	Motor Rotation (°)	$\mathit{\Delta }\mathit{l}$ (m)	Bending Angle (°)
Motor 1	88	0.0140	88.3 ± 2
Motor 2	80	0.0157	80.3 ± 2
Motor 3	85	0.0148	84.8 ± 2
Motor 4	90	0.0154	90.0 ± 2

). The calculation error margin of ±2° was primarily due to non-uniform tendon resistance and interpolation error in the EM tracking data. These results demonstrated a maximum bending angle of 90° in one direction (Motor 4 actuation on the horizontal plane), while the other three directions reached bending angles of 80–88°. Although not exceeding 90° in every direction, these values represent sufficient bending capacity to enable navigation within the four cardiac chambers. These values will be enhanced with the introduction of a gearbox mechanism that will enhance the motor’s capabilities and therefore the bending ranges produced by the tip’s trajectory.

3.3. Contraction Test Results

NDI measurements along the Z-axis showed smooth and continuous motion across six trials, with contraction beginning shortly after 2 s and reaching a peak displacement of 17 mm at approximately 10 s (Figure 12). The mean trajectory displayed a consistent slope during both contraction and release, peaking around 5 mm with a standard deviation of ±1 mm, indicating a controlled elastic response and mechanical stability. A small hysteresis loop was observed at about 11 s after peak contraction, likely due to tendon guide friction and elastic energy storage within the catheter structure.

Although the final trajectories showed slight variations, all trials resulted in an average shortening of 15% of the segment length. The discrepancies are attributed to differences in tendon pre-tension between trials, frictional hysteresis in the tendon–sheath routing, and minor asymmetries in channel stiffness from the 3D-printed structure. Additionally, accumulated tendon elongation between trials contributed to gradual shifts in the neutral pose. These effects, while introducing minor off-axis deviations, did not prevent consistent overall contraction behaviour. Overall, the tip consistently returned to its original position in all trials, confirming full elastic recovery without permanent deformation. These findings demonstrate that the robotic sheath can withstand complete contraction cycles while maintaining precise recovery, a critical capability for rapid catheter repositioning in clinical use.

3.4. Trajectory-Following Test Results

The joystick control validated the system’s ability to produce consistent, directional tip motion when actuating each motor independently. The tip bent predictably in the four principal directions-left, right, up, and down, with minimal unintended motion, confirming effective tendon guidance and torque transfer through the sheath shaft.

The 3D trajectories recorded by the NDI system (Figure 13) demonstrated smooth, continuous tip motion across all three configuration tasks, confirming suitability for complex 3D positioning maneuvers. The Up–Down–Center path exhibited the most uniform curvature, while the Square path showed increased irregularities toward the end, attributed to tendon slackening or torque saturation of Motor 1. During nominal planar bending, one coordinate ideally remains zero; however, due to asymmetries in tendon pre-tension and routing, small off-axis displacements (<2 mm) were observed, leading to measurable errors in x, y, and z. Standard deviation in the Square path reached ±8 mm in later trials, whereas other motions remained within ±2.5 mm of predicted paths.

Static positioning trials across multiple target points produced a mean absolute positioning error of 2.81 mm (SD = 0.93 mm), with positional drift during 10 s holds remaining below 0.5 mm. Dynamic tests following a predefined path showed a mean tracking error of 3.34 mm, with overshoot during sharp directional changes averaging 1.15 mm before correction. The errors could be attributed to four primary factors: (i) friction and hysteresis within the tendon–sheath transmission, (ii) backlash and compliance in the actuation path, (iii) the absence of closed-loop feedback, and (iv) discretization effects from stepwise command inputs. Notably, the first two factors also reflect the inherent limitations of the constant curvature model approximation. These values fall within the typical positioning error range (≈1–5 mm) reported for tendon-driven continuum or catheter-based robotic systems [40,41,42]. While definitive clinical tolerances must ultimately be established through in-vivo studies and clinician trials, the system’s level of accuracy is consistent with the performance of prior systems used in cardiac navigation and is therefore considered acceptable for early-stage validation. Further improvements could focus on: (a) optimized tendon routing with increased curvature radii and fixed guides, (b) the introduction of low-friction liners together with calibrated pre-tension and anti-backlash mechanisms, (c) a friction–hysteresis compensation strategy employing inverse feedforward augmented with integral action, and (d) integration of closed-loop, image-based correction using a Jacobian-based PID controller with higher update rates and jerk-limited trajectory profiles.

Repeatability across repeated dynamic trials was high, with a standard deviation of 0.69 mm between corresponding trajectory points, confirming that the position-and-current control strategy maintained consistent tip placement despite tendon compliance. The constant-curvature kinematic model remained valid for multi-input scenarios, with measured trajectories aligning closely with vector sums of single-direction motions. These results confirm that both independent and coordinated joystick control are feasible, precise, and repeatable for catheter tip positioning.

3.5. Sheath Guidance Test Results

The results of the sheath guidance test are shown in Figure 14. When guiding the Jotec catheter, the sheath tip followed smooth, continuous paths with deviations generally within 2–3 mm, with occasional localized peaks of up to 6 mm, attributed to temporary tendon slack during sharp directional changes. In contrast, guidance of the SAPIEN M3 catheter resulted in larger deviations of up to 9 mm, with noticeable overshoot loops in the top-view plots, likely caused by accumulated slack and non-uniform torque transfer during complex multi-directional bending. Despite these disturbances, the system consistently re-stabilized and returned to the intended trajectory, confirming its ability to accommodate multi-axis motion demands while guiding real clinical tools.

3.6. Phantom Navigation Test Results

The sheath tip was navigated in the anatomical phantom models to assess its adaptability for clinically relevant navigation. Within the phantom, the tip was inserted through the inferior vena cava and successfully advanced to the right atrium, demonstrating the capability to perform the intervention motions required for the intended procedure. These results confirm the system’s suitability for anatomical navigation, while also indicating that further miniaturization will improve compatibility across a wider range of anatomical models and real operating scenarios.

4. Discussion

The tendon-driven robotic sheath system met its primary functional objectives, achieving smooth and controlled actuation across four independent motors. Tendon tensions of 0.66–0.78 N were sufficient to initiate and sustain bending. Feasibility and configuration control tests confirmed accurate and repeatable motion in both independent and multi-axis scenarios, with mean spatial errors around 3.34 mm. The measured motion fully complied with the constant-curvature kinematic model. Elastic recovery was demonstrated in contraction–recoil trials, with minimal hysteresis and negligible residual error (0.03 mm) while maximum bending angle tests achieved the target 90° curvature without structural damage. Guidance trials with commercial devices confirmed system compatibility, though stiffer instruments highlighted the need for higher motor torque.

However, all experiments were conducted under static bench and phantom conditions, which do not replicate the dynamic motion of a beating heart. In future applications using pulsatile heart simulators or in vivo models, compensation for cardiac motion would be achieved through image-guided navigation. Fluoroscopy provides continuous real-time visualization during transcatheter interventions and enables synchronization of catheter motion with the cardiac cycle. When combined with automated image tracking, it can form a closed-loop feedback system that dynamically counteracts cardiac motion.

Other limitations identified during testing included motor snapping under high-load conditions, consistent structural stability of the PLA shaft, EM tracking noise (±1 mm), and scale incompatibility with one phantom model. Despite these constraints, the overall performance supports the system’s suitability for precise and adaptable navigation in interventional cardiology. The platform is also inherently scalable: tendon routing, sheath diameter, and bending segment length can be modularly adjusted to accommodate both pediatric and adult anatomies. Downsizing the actuation module would enable use in smaller vessels, whereas larger lumen configurations could support adult-scale catheters and therapeutic tools.

Overall, the system’s modular design and mechanical adaptability provide a foundation for clinical translation. Further iterations will integrate real-time imaging feedback and closed-loop control to enhance precision and safety in dynamic cardiac environments.

5. Conclusions and Future Work

This paper presented the design, development, and experimental validation of a soft tendon-driven robotic guide sheath system for potential use in cardiac valve interventions. Unlike previous tendon-driven or concentric-tube designs, the proposed system uniquely integrates tendon actuation with a compressible soft body, enabling bidirectional bending and active shortening within confined cardiac chambers while maintaining lumen stability. The system reliably generated sufficient tendon tension for actuation, achieved repeatable independent motions, and executed complex multi-axis trajectories through coordinated joystick control. The catheter tip reached bending angles from 80° to 90°, meeting clinical navigation requirements for procedures such as transcatheter mitral valve repair and right atrial access. Contraction test confirmed robust elastic recovery, and successful guidance of commercial catheters demonstrated mechanical compatibility with existing interventional tools. While limitations such as motor torque saturation and scale incompatibility in phantom models were identified, the prototype achieved its primary objective of joystick-controlled, clinically relevant actuation. Overall, these findings establish the platform as a viable, low-cost foundation for future refinement and clinical translation.

Future development will focus on integrating a tendon force-sensing system to enable real-time feedback for improved safety and control precision. Motor torque capacity will be increased through spool geometry optimisation and the addition of a gearbox to support higher-load actuation without failure. Clinician-led user studies will be conducted to evaluate the control interface, assess system intuitiveness, and guide targeted refinements. The prototype will be also miniaturised to match standard clinical catheter dimensions, enabling validation in anatomically accurate, soft-tissue phantom models and eventual in vivo–like testing under fluoroscopic imaging. Longer-term objectives include implementing intelligent path-planning algorithms based on machine learning to enable adaptive and potentially autonomous navigation.