High Fidelity Real-Time Optimization of Multi-Robot Lines Processing Shared and Non-Deterministic Material Flows

Abstract

Multi-robot ensembles comprising several manipulators are commonly used in industrial settings to process non-deterministic flows of items loaded by an upstream source onto a shared transportation system. After the execution of a given task, the robots regularly deposit the items on a common output flow, which conveys the semi-finished material towards the downstream portion of the plant for further processing. The productivity and reliability of the entire process, which is affected by the plant layout, by the quality of the adopted scheduling and task assignment algorithms, and by the proper balancing of the input and output flows, may be degraded by random disturbances and transient conditions of the input flow. In this paper, a highly accurate event-based simulator of this kind of system is used in conjunction with a rollout algorithm to optimize the performance of the plant in all operating scenarios. The proposed method relies on a simulation of the plant that comprehensively considers the dynamic performance of the manipulators, their actual motion planning algorithms, the adopted scheduling and task assignment methods, and the regulation of the material flows. The simulation environment is built upon computationally efficient maps able to predict the execution time of the tasks assigned to the robots, considering all the determining factors, and on a representation of the manipulators themselves as finite state automata. The proposed formalization of the line balancing problem as a Markov Decision Process and the resulting rollout optimization method are shown to substantially improve the performance of the plant, even in challenging situations, and to be well suited to real-time implementation even on commodity hardware.

1. Introduction

In advanced manufacturing environments, the use of multi-robot ensembles constitutes a natural way of compounding the benefits obtainable by single manipulators. Typically, given productivity requirements that exceed the capabilities of a robotic device otherwise deemed suitable for the intended application, the introduction of a sufficient number of manipulators is perceived as an adequate solution, under the assumption of linearly scaling overall production rates. However, in contrast with single robot plants, multi-robot production lines are characterized by the interaction of several agents that operate in a shared environment. Notably, the composition of these interactions can generate emerging features which cannot be easily predicted in advance or modeled analytically. As a result, contrary to expectations based on rules of thumb, the efficient utilization of the robots becomes challenging even in apparently straightforward cases. This is especially true when the environment itself is not deterministic, and thus introduces additional uncertainty within the system.

Multi-robot ensembles have been treated in the current literature in a variety of applications, as surveyed, for example, in [1,2]. Regardless of the specific applications, these reviews highlight that, in very general terms, optimal coordination between the robots is in principle desirable; in practice, however, modeling difficulties, high computational costs, and limited communication bandwidth typically mandate—in the face of real-time constraints—approximate and not strictly optimal solutions to the cooperation problem. Accordingly, decentralized algorithms with low computational and communication requirements appear to be favored for the management of multi-robot systems.

Multi-robot systems appear in a wide range of possible applications that may variously involve mobile, aerial, or fixed-base industrial robots; given these marked specificities, it is clear that different subfields may benefit from suitably tailored optimization approaches. A typical case of clear industrial interest, on which this work focuses, is constituted by multi-robot lines dedicated to various operations such as assembly, sorting, ordering, or packaging. Commonly, such a line is constituted by several robots that operate on a shared transportation system, which suitably feeds the manipulators with the required inputs. The robots first process the items, and then regularly deposit them on a common output stream. The latter finally conveys the items towards a downstream section of the plant, which is dedicated to further operations such as packaging or palletizing. One key function of the robots is the generation of a deterministic output stream as required by the downstream machinery, which is thus effectively decoupled and insulated from the irregularities affecting the upstream item source.

Even within this more specialized focus, it is apparent that the overall multi-robot assembly is a complex system amenable to very different kinds of optimizations; performance improvements in such an application may be systematically pursued using either top-down or bottom-up approaches. The former starts with an overall, more abstract conception of the robot ensemble, focusing first on issues such as coordination and task assignment. The latter, on the contrary, begins with the maximization of the performance of each single manipulator through strategies that involve its suitable mechatronic design, the adoption of advanced control systems, and the development of optimized motion planning algorithms.

Ad hoc improvements of specific aspects of the multi-robot plant operation are also possible; their effectiveness, moreover, should not be discounted, especially given the fact that sizable gains may be obtained with relatively modest engineering effort.

This kind of plant has therefore been considered in the existing scientific literature from a variety of points of view and at different levels of sophistication, effectively reflecting the multiple facets of the application.

At a first, fundamental level, the basic formulas typically used in industrial settings for the sizing of this kind of plant are illustrated in [3]; a simplified simulation environment is furthermore proposed as a more advanced design tool able to assess the effects of some design choices that are otherwise usually neglected by the simple analytical relationships.

Possible layouts of a two-conveyor plant are discussed in [4], where two main variants, the co-flow and the counterflow one, are identified; in the former the input and output streams have the same direction, whereas in the latter they move opposite to each other. The counterflow configuration is noted to offer higher stability, but also for being covered by existing patents; additionally the co-flow variant is often preferable as it enables a more convenient disposition of the upstream and downstream systems. The selection of the best configuration of the input and output streams is a clear example of a simple ad hoc optimization that may nonetheless lead to large performance gains.

Beyond the qualitative choice of the plant layout, a related quantitative parameter that affects the plant performance is the item flow rate, i.e., the productivity of the upstream source. Its importance is highlighted, e.g., in [5], where the appropriate value for this parameter is determined through a Monte Carlo method enabled by a plant simulator that considers stochastically generated incoming items. Already from these selected papers, it appears that simulation-based computational approaches are required to evaluate and improve the performance of this type of system, and that conversely closed-form mathematical models, while useful for initial sizing, are ultimately unable to accurately predict the actual operation of the plant.

As already mentioned, a third element concurring in the determination of the performance of the plant is constituted by the task assignment and scheduling strategies. Specifically, task assignment performs the association of tasks with individual robots, while the scheduling algorithm sequences the assigned tasks. This is the aspect on which most of the existing literature focuses, since it is the one most tightly associated with the concept itself of multi-robot system. The methods presented in the literature regarding these algorithms are classifiable into two broad categories: one based on heuristic rules, the other relying on the formulation and solution of optimization problems. Examples of the former approach are presented in [6,7], while the latter is taken in [8,9], where Mixed Integer Linear Programming (MILP) is used both to optimize the conveyor velocities and to generate scheduling and task assignment solutions over a rolling horizon. A similar modeling methodology is described in [10], where the high computational cost of solving the MILP problem exactly is noted; as a remedy, an Iterated Local Search approximate solution method is used. In Ref. [11] a game theoretic approach is adopted to enhance the collaboration between the manipulators, while in Ref. [12] a conceptually similar problem, i.e., the harvesting of agricultural products with a mobile platform equipped with several robotic arms, is treated using extensions of graph coloring.

A middle course between the heuristic and the optimizing approaches is charted in [13,14], where scheduling and task assignment are performed for each robot according to a specific rule, such as First In First Out (FIFO), Last In Last Out (LIFO), or Shortest Processing Time (SPT), with the overall mix selected using a metaheuristic optimization process. As noted in Ref. [15], which uses reinforcement learning to determine the optimal mix of scheduling strategies assigned to the robots operating on a single conveyor belt, a detailed physics-based simulation of the plant is not strictly required, and indeed may even be harmful insofar as it introduces excessive computational costs. The typical strategy adopted in this and other works is therefore based on discrete event simulations in order to capture the plant-level dynamics while abstracting away the lower-level behavior of the robots. In doing so, however, a simplified model of the manipulators is adopted, thus reducing the accuracy of the event-based simulation. Nonetheless, high computational efficiency is required in all those cases in which the input stream is not deterministic: indeed, in such a situation it is not possible to rely on precomputed scheduling and task assignment solutions; rather these have to be computed in real time, reacting to the stochastically evolving environment.

This work considers a plant in which multiple robots must process items carried by an input stream and subsequently deposit them on a separate output stream. The input stream conveys the items to be processed, while the output one contains regularly organized deposit positions that need to be filled. In this type of plant the overall goal is the simultaneous maximization of the production rate and reliability. This in practice means that the robots should process all the incoming items and deposit positions while working as close as possible to full utilization. Considering specifically the literature dedicated to these kinds of plants, it emerges clearly that an important issue to be faced in these multi-robot systems is the appropriate balancing of the production inputs (namely the items) and of the deposit positions, not only globally, but also locally for each manipulator. Indeed, to operate properly, the robot requires both available items and reachable deposit positions; if these conditions are not met, idle waiting necessarily occurs. Notably, the higher effectiveness of the counterflow configuration is attributable to the fact that, at steady state, at the one end of the line many items are available to fill the few remaining deposit positions, while at the other end, the reverse situation (of abundant deposit positions for the leftover items) manifests itself. On the contrary, in co-flow plants both types of production inputs (items and deposit positions) are abundant at the inlet section, but moving downstream become increasingly scarce, scattered, and non-overlapping in time as a result of the operations performed by the upstream robots. This difficulty, which is always present also at steady state, is exacerbated during transient conditions and by random disturbances that affect the upstream production system. Accordingly, it is noted, e.g., in [8,9,10] that suitable management of the transportation systems is crucial to obtain good performance in all conditions. In general, it may be conservatively assumed that the production rate or profile of the upstream item source is a given quantity, and that the velocity of the input transportation system must be set accordingly; in contrast, the speed of the output one can be more readily acted upon in order to optimize the behavior of the plant.

Note that the need to properly balance the input and output flows is not present in the case of multi-robot plants characterized by a single transportation system and deposit positions that are fixed and always available to the robots. This configuration leads to a structurally simpler, yet interesting problem that already displays a dynamic character and is accordingly amenable to treatments based on dynamic programming or related techniques (such as reinforcement learning) used to determine the optimal scheduling sequence [16].

These works, regardless of the specific approach, highlight that the choice of a specific control or management input affects the future evolution of the state of the overall system; the optimization should therefore consider the ramifications of each decision, and not only its immediate consequences. Dynamic programming and reinforcement learning explicitly address this property of the system; alternatively, this same fundamental feature is reflected in those approaches—among the reviewed ones—that rely on rolling horizon scheduling solutions. All these approaches, despite their differences, implicitly or explicitly emphasize that the ability to simulate the dynamic trajectory of the entire system is of crucial importance.

Low simulation fidelity is, however, a commonly occurring limitation in the reviewed works: while the actual capabilities of the robots are expressed in terms of their cycle times, these are not considered as a function of the task and robot properties, but in various ways as a random variable [17], as an average value to which waiting times are added [6,7,10], as a single fixed value [8,9], or as a quantity obtained considering a limited number of parameters such as the robot maximum velocity [5,15]; these parameters must be conservatively set as they do not account for the actual configuration-dependent dynamic properties of the robot. This limitation is characteristic of a high-level perspective that, focusing on plant-level optimizations, treats each single robot as an abstract device that performs a given operation in a given time. This kind of approach, however, overlooks the fact that, as already introduced, the overall performance optimization for the entire multi-robot system may occur at different levels, ideally covering the mechanical design of the robots, their control, then the motion planning algorithms, and only at last the overall system dynamics. In particular, at the level of motion planning several sophisticated algorithms have been proposed specifically with the aim of minimizing the execution times of a given trajectory, considering not only its geometry, but also the specific kinematic and dynamic properties of the robot [18,19,20,21,22,23]. These algorithms enable the robot to execute the needed motions as quickly as possible, effectively maximizing its productivity. Their relevance for the optimization of the overall multi-robot plant performance is thus quite evident.

At the same time these techniques emphasize that there is no single task execution time actually representative of the capabilities of the robot. In fact, when a single cycle time is assumed, there are two main possibilities: either to consider a maximum cycle time, which underestimates the productivity of the robot, or to select the average one. The latter choice provides a good estimate of the robot capabilities, but leads to scheduling solutions that in many cases assign unfeasible tasks, with consequent degradation of the performance of the plant.

Ideally, the top-down and bottom-up optimization approaches should eventually converge to broadly similar and equally comprehensive solutions; however, the present literature review reveals a gap in this regard, as no existing work simultaneously addresses both high- and low-level issues in a unified framework. This paper aims to fill this gap, and therein lie its main contributions. The different perspectives of robot- and plant-level optimizations may indeed be bridged together using task time maps, which, through pre-evaluation, allow for accurately and efficiently quantifying the performance of a single robot as a specific function of its dynamic capabilities, of the individual task properties, and of the optimizing algorithms used for motion planning.

Task time maps have been proposed in the existing literature mainly for two reasons, the first of which is to determine in an efficient way which operation is to be prioritized among several competing alternatives, typically favoring the one that can be accomplished in the shortest amount of time. The second reason emerges when considering operations on continuously moving objects, such as those transported by conveyors or rotating tables; in this context, the task time map can be used to efficiently solve the optimal intercept or rendezvous problem, that is the problem of finding the shortest time and the corresponding location at which the manipulator may meet its target [24,25]. In a previous work [26], the authors have developed task time maps using neural networks, taking into account the geometric motion planning algorithm, the trajectory optimization method, and the dynamic model of the robot; conceptually analogous examples can however be found in the existing literature that implement the task time map as a simpler lookup table [27], which has the advantage of run-time efficiency at the expense of typically higher memory requirements.

In this paper, the task time map concept is leveraged to develop an accurate, efficient, and flexible event-based dynamic simulation of a multi-robot plant operating on two continuously moving streams: the input one conveying the unprocessed items, and the output one carrying deposit positions to be deterministically filled. As the adopted task time maps are application-specific, the simulator is entirely representative of the lower-level hardware and software layers responsible for motion planning, control, and execution. The plant-level dynamics are therefore simulated without sacrificing accuracy and with high computational efficiency. An abstract model of the robot is, in particular, described and shown to be consistent with the detailed, physical view of the manipulators and the transportation systems.

First of all, thanks to its high computational efficiency, the event-based simulator allows the implementation of a real-time algorithm for the maximization of the productivity and reliability of the plant. In particular, the output flow management problem is formalized as a Markov Decision Process (MDP), which is then approximately solved online using a rollout algorithm. Moreover, the simulator allows a highly accurate analysis of the effects of different design choices, such as the number of robots, also in relation to varying characteristics of the upstream production system. In summary, the main contributions of the paper are as follows:

• An efficient yet accurate event-based dynamic simulation of a multi-robot plant operating on two continuously moving input and output streams;
• The analysis of the effects of different non-idealities on the plant productivity and reliability;
• The formalization of the output stream management problem as an MDP, with the subsequent implementation of a rollout algorithm suitable for real-time application.

The paper is structured as follows: in Section 2 the simulation strategy and the rollout algorithms are presented; in Section 3 the results obtained from the application of the proposed methods to simulated case studies are illustrated and discussed; finally Section 4 collects the main conclusions of this work, together with some suggestions concerning future research directions.

2. Methods

As represented in Figure 1, the kind of plant considered in this work features a series of robots operating on two distinct input and output transportation systems (e.g., conveyor belts), an upstream production facility, and some postprocessing equipment placed downstream. The plant is therefore conceptually divided in three main sections:

• The upstream sources of items and deposit positions;
• The downstream postprocessing machinery;
• The multi-robot assembly interposed between the two.

The focus of this work is mostly placed on the middle section, i.e., on the multi-robot system. Within this plant section one transportation system—the input one—is placed at the outlet of the upstream production facility, which generates the items and hence the input stream. The output transportation system is (materially or virtually) loaded at regular intervals with empty deposit positions that are to be filled by the robots; the output stream then terminates at the inlet section of the downstream machinery, which accepts the sorted items and proceeds with their further processing.

Figure 1. Schematic representation of the kind of multi-robot plant considered in this work.

Figure 1. Schematic representation of the kind of multi-robot plant considered in this work.

The main task of the robots is to perform, on the fly, some operation on the items, and then transfer them from the input to the output stream. The robots are introduced within the overall setup not only to execute a given operation (such as cleaning, assembly, painting, labeling, or sorting), but also to effectively decouple the upstream production system from the downstream processing and packaging machinery. The upstream and downstream sections cannot be coupled directly owing to the discrepancies between the inputs required by the latter and the outputs provided by the former. Concerning the upstream production system, it can be stated that it may assume different characteristics according to the specific industrial application. Some processes require a transportation system that moves at fixed velocity (e.g., to guarantee all items an equal exposure time to some desired condition). Others, on the contrary, may tolerate varying velocity input streams, slowly adapting the upstream production rate to the velocity of the associated transportation system. Another classification relates to the type of production, which may occur continuously or in batches. Finally some production processes are deterministic, generating regularly spaced input flows, while others are affected by stochastic variations. This work focuses mostly on the more challenging cases of upstream productions characterized by batches and random disturbances. As regards the downstream section, it can be assumed that it needs to receive correctly arranged items, but also that it is able to process them independently of their arrival rate (up to a certain limit). An important function of the manipulators, then, is to rearrange the items in such a way that the downstream machines can operate properly.

Even within the limits of the above description of the plant, many configurations and variants can be easily conceived during the design phase. These variants emerge in relation to factors such as the following:

• The dimensions of the items;
• The pattern with which they are generated;
• Their required arrangement on the output stream;
• The productivity of the upstream machinery;
• The number and type of the robots;
• The physical size and the operating speeds of the transportation systems;
• The spatial arrangement of the input and output flows;
• The adopted task assignment and scheduling algorithms.

Many of these properties are related to each other, and should be accordingly sized during the initial design of the plant. For example, the item size will condition the dimensions of the transportation systems and of the robots; the number of manipulators is selected according to their performance and to the productivity of the upstream source; the input and output patterns of the items will affect the nominal speeds of the transportation systems. As shown in the next subsection, these notions can be turned into straightforward mathematical relationships applicable during the first sizing of the multi-robot assembly.

The upfront quantification of the impact of other necessary design and management choices is, however, far more difficult. Examples of these choices concern the methods for scheduling and task assignment, or techniques for manipulating the velocity of the input and output streams. Other effects that are often neglected during the sizing and design phases are those related to disturbances and to transient conditions occurring at startup time and also as a result of fluctuations of the upstream production rate.

These limitations can however be overcome by more accurate simulations of the system; one of the goals of this work is therefore the development of a simulation environment for the plant, able to account for its different variants. As presented in the following discussion, a plant simulator is useful not only during the design, but also for the development of an online management system that optimizes the productivity and reliability of the system through real-time forecasts of its likely evolution in different scenarios. For such a use, however, it is evident that both accuracy and computational efficiency are of paramount importance; these are achieved at the same time through suitable task time maps, which provide an abstract model of each manipulator that still takes into account its real capabilities, as determined by its actual dynamics and by the selected motion planning algorithms.

2.1. Base Concepts on Multi-Robot Plant Sizing

The specifications needed for the preliminary sizing of the plant are as follows:

• The dimensions of the items;
• The assumed pattern with which they enter the input stream;
• Their desired arrangement on the output stream;
• The maximum achievable productivity $P_{source,ub}$ of the upstream item source.

The width of the two transportation systems can be selected according to the item size and pattern information, forming also an overall estimate of the required dimensions of the robot workspace. After the definition of a suitable robot model, it becomes possible to construct its task time maps (see, e.g., [26]). The average cycle time of the robot, ${\overline{T}}_{cyc}$, is then estimated by summing the mean execution times of the elementary tasks that constitute the complete work cycle. Finally the characteristic productivity ${\overline{P}}_{rbt}$ of the robot is obtained as the inverse of its average cycle time: ${\overline{P}}_{rbt}={\overline{T}}_{cyc}^{-1}$.

The number of robots $n_{rbt}$ is next determined according to the inequality:

$$\begin{array}{c}\hfill n_{rbt}\ge {\displaystyle \frac{P_{source,ub}}{{\overline{P}}_{rbt}}}.\end{array}$$

(1)

To avoid overlapping items, their spacing $\Delta L_{item}$ on the input stream should be greater than their characteristic length $L_{item}$; considering that their entrance occurs through a number $n_{feeder}$ of feeding systems arranged along the width of the input stream, the required velocity ${\dot{x}}_{b,in}$ of the latter can be estimated in relation to the production rate of the upstream source. In particular, the maximum attainable input velocity ${\dot{x}}_{b,in,ub}$ must satisfy the inequality:

$$\begin{array}{c}\hfill {\dot{x}}_{b,in,ub}\ge {\displaystyle \frac{P_{source,ub}{L}_{item}}{n_{feeder}}}.\end{array}$$

(2)

With items to be deposited on the output streams on a number $n_{row}$ of rows, the maximum attainable velocity ${\dot{x}}_{b,out,ub}$ must obey a similar relationship:

$$\begin{array}{c}\hfill {\dot{x}}_{b,out,ub}\ge {\displaystyle \frac{P_{source,ub}{L}_{item}}{n_{row}}}.\end{array}$$

(3)

These estimates are useful to give a first idea of the likely operating point of the plant.

2.2. Motion Planning and Task Time Mapping

As described in greater detail in a previous work by the authors [26], a typical optimizing motion planning pipeline for a single robot having $n_{dof}$ degrees of freedom is constituted by a geometric trajectory planner (GTP) and by a task time optimizer (TTO). In most cases of practical interest, the GTP may be represented as a higher order function G that accepts $n_{dof}$-dimensional position and velocity boundary conditions ${\mathit{p}}_{\mathit{s}}$, ${\mathit{v}}_{\mathit{s}}$, ${\mathit{p}}_{\mathit{f}}$, ${\mathit{v}}_{\mathit{f}}$ and yields a curve $\gamma \subset {\mathbb{R}}^{n_{dof}}$, itself a function of parameter $u\in [u_{lb},u_{ub}]$. The TTO function H accepts $\gamma$ and the desired velocity boundary conditions to yield the parametrization of u as a function of time t that minimizes the trajectory execution time. Since the execution of a trajectory corresponds to an elementary task, the TTO provides as an additional output the minimal task execution time $T_{task}$. Overall, given an implementation of the GTP and of the TTO, $T_{task}$ is a function of the boundary conditions: $T_{task}=T_{task}({\mathit{p}}_{\mathit{s}},{\mathit{v}}_{\mathit{s}},{\mathit{p}}_{\mathit{f}},{\mathit{v}}_{\mathit{f}})$. As explained in greater detail in [26], a task time map ${\widehat{T}}_{task}$ is any function of the same inputs that provides $T_{task}$, with some tolerance; in practice, to be of any use the evaluation cost of ${\widehat{T}}_{task}$ should be lower than that associated with $T_{task}$. A typical implementation of ${\widehat{T}}_{task}$ relies on lookup tables, even though more sophisticated function approximation techniques may be used.

As already introduced, the task time map can be used to compute the optimal time and location at which the robot should intercept a moving target, and it may be used also to efficiently implement time-based scheduling rules.

In a plant of the kind considered in this work, the input and output streams are continuously moving. As a result, the motion cycle of each robot should be divided into the following elementary tasks:

• Item intercept motion: the robot positions itself above the item to be operated on, matching its velocity;
• Item tracking motion: the item is followed by the robot, processed, and grasped;
• Deposit position intercept motion: the robot positions its payload above the deposit position, matching its velocity;
• Deposit position tracking motion: the robot follows the deposit position, on which it releases the processed item.

As shown in Figure 2, the tracking motions may moreover be split into the following phases:

• Descent: the robot, while matching the transportation system speed, lowers its end effector to the level of the target;
• Following: the robot continues to follow its target, performing the intended operation;
• Ascent: to avoid collisions with other items on the transportation system, the robot continues to match the speed of its target while gaining a suitable altitude;
• Deceleration: if needed due to the absence of new potential tasks, the robot brings itself to a halt.

Figure 2. Half-cycle trajectory, with its constitutive phases, including the optional stop. The arrow indicates the initial velocity.

Figure 2. Half-cycle trajectory, with its constitutive phases, including the optional stop. The arrow indicates the initial velocity.

Application-specific task time maps should be created for each of the elementary tasks; once the maps are available, it is straightforward to quantify the average productivity of the chosen manipulator as required by the sizing relationships reported above.

At run time, moreover, given an item or a deposit position traveling with a given velocity along the input or output stream, the repeated evaluation of the task time map allows the real-time solution of the optimal intercept problem [26], without the need to invoke the much more computationally expensive GTP and TTO; this in turn allows the definition of the instant and of the location at which the robot may first reach its target. A qualitative illustration of this process is provided by the two panels of Figure 3; in the top one (Figure 3a) a spatial view of the problem is shown, with the initial position ${\mathit{p}}_{tgt,0}$ of the moving target, the initial position ${\mathit{p}}_{rbt,0}$ of the robot, and the intercept location ${\mathit{p}}_{intercept}$ that coincides with the robot’s position ${\mathit{p}}_{rbt,f}$ at the end of the intercept trajectory. The bottom panel (Figure 3b) represents the computation needed to obtain the longitudinal component $x_{intercept}$ of ${\mathit{p}}_{intercept}$: accordingly its vertical axis reports time t, while the horizontal axis represents the longitudinal displacement of the target. The time–displacement law of the moving target is assumed to be a known function $t_{tgt}$; the function $t_{rbt}$ is obtained from the task time map, and represents the travel time of the robot. The intersection between these functions yields the intercept location and time.

The present paper does not claim novelty concerning task time mapping, as the concept (as highlighted in the literature review) has already been used by other researchers in different forms and in relation to various robotic applications. Advanced techniques for task time mapping, moreover, have already been treated by the authors in [26], where all the main concepts summarized in this subsection have been treated in much greater detail, using the same general terminology but focusing on single-robot applications. A novelty of the present paper lies in the proposed use of the task time maps in industrial multi-robot systems, to aid their management and to enable their fast and accurate real-time simulation. Such simulations, as will be shown, can then be used in an online optimization of the plant performance. To rigorously reach that result, however, several other potential issues must be preliminarily considered and adequately treated, as explained in the following subsections.

2.3. Coordination Between Manipulators and Transportation Systems

In cases where the transportation systems are operated at variable speed, a suitable strategy for coordination with the manipulators is needed. Indeed, the optimal intercept problem is solved at scheduling time considering the current speed of the input or output stream, with subsequent variations being capable of inducing excessive errors during the task execution. To solve this problem, during a given operation the displacement of the transportation system is to be used in lieu of time as the independent coordinate of the manipulator’s motion. As a result, the motions of the two remain synchronized, also in the event of accelerating or decelerating input and output streams.

From the description above, it is clear that under this strategy the tracking motion will be performed properly as long as the intercept operation is correctly defined. Concerning this matter, recall that, as already discussed, the definition of the intercept task occurs in three stages. At first the task time ${\widehat{T}}_{task}$ and the intercept positions are defined by the scheduler; then the GTP generates the curve $\gamma \left(u\right)$; finally the TTO computes the parametrization $u\left(t\right)$ and the minimal task time $T_{task}\approx {\widehat{T}}_{task}$. The scheduled task time ${\widehat{T}}_{task}$ is enforced through minor modifications to the optimal solution provided by the TTO. To maintain the synchronization between the robot and the conveyor, the following reparametrization is considered:

$$\begin{array}{ccc}\hfill X_{task}& =& {\dot{x}}_b\left(t_0\right){\widehat{T}}_{task}\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill \tau & =& \Delta x_b\left(t\right){\displaystyle \frac{{\widehat{T}}_{task}}{X_{task}}},\hfill \end{array}$$

(5)

in which $\Delta x_b$ is the instantaneous transportation system displacement since the task was scheduled, $X_{task}$ is the displacement assigned for the execution of the task, ${\dot{x}}_b\left(t_0\right)$ is the actual speed of the targeted stream at scheduling time $t_0$, and $\tau$ is a pseudo-time parameter that coincides with t if the stream velocity does not vary. The evaluation of the motion law u as a function of $\tau$ then allows the robot to move directly in relation to the advancement of the transportation system. Notably, for $\Delta x_b=X_{task}$ the intercept motion terminates.

In the case of non-null initial and final velocities, a question arises about the correct velocity boundary conditions that must be assigned to the optimization problem yielding $u\left(\tau \right)$. Without loss of generality in the following it is assumed that the transportation systems are aligned to the global x axis. The geometric path, at its extremities, is required to have a geometric velocity aligned to the input or output stream. Under the just introduced synchronizing reparametrization it is possible to write the following equations:

$$\begin{array}{ccc}\hfill \gamma \left(t\right)& =& \gamma \left(u\left(\tau (\Delta x_b\left(t\right))\right)\right)\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill \dot{\gamma }\left(t\right)& =& {\gamma }_u{u}_{\tau }{\tau }_{\Delta x_b}{\dot{x}}_b,\hfill \end{array}$$

(7)

where $\dot{\gamma }$ denotes the time derivative of $\gamma$; ${\gamma }_u$, $u_{\tau }$, and ${\tau }_{\Delta x_b}$, on the other hand, represent derivatives with respect to the subscripted variable.

Let the $n_{dof}$ dimensional vector $\mathit{i}={\left[\begin{array}{c}1,0,\dots ,0\end{array}\right]}^{\top }$ represent the direction of the transportation systems; it is necessary to ensure that at the initial instant the velocity along the curve matches that of the robot, which is determined by the exit conditions of the previous task, and is therefore also aligned to the transportation system and initially equal to $v_{rbt,0}\mathit{i}$. Using the fact that ${\tau }_{\Delta x_b}={\widehat{T}}_{task}/X_{task}$, the following can be written:

$$\begin{array}{cc}\hfill {\mathit{i}}^{\top }\dot{\gamma }\left(t_0\right)& ={\mathit{i}}^{\top }{\gamma }_u\left(u_{lb}\right)u_{\tau }\left(0\right){\tau }_{\Delta x_b}\left(0\right){\dot{x}}_b\left(t_0\right)=v_{rbt,0}\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\mathit{i}}^{\top }\dot{\gamma }\left(t_f\right)& ={\mathit{i}}^{\top }{\gamma }_u\left(u_{ub}\right)u_{\tau }\left({\widehat{T}}_{task}\right){\tau }_{\Delta x_b}\left(X_{task}\right){\dot{x}}_b\left(t_f\right)={\dot{x}}_b\left(t_f\right).\hfill \end{array}$$

(9)

Equations (8) and (9) can be solved for the conditions to be imposed on $u_{\tau }$ to obtain the desired velocity boundary conditions independently of the evolution of the transportation system’s velocity:

$$\begin{array}{cc}\hfill u_{\tau }\left(0\right)& ={\displaystyle \frac{v_{rbt,0}}{{\mathit{i}}^{\top }{\gamma }_u\left(u_{lb}\right){\dot{x}}_b\left(t_0\right)}}{\displaystyle \frac{X_{task}}{{\widehat{T}}_{task}}}\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill u_{\tau }\left({\widehat{T}}_{task}\right)& ={\displaystyle \frac{1}{{\mathit{i}}^{\top }{\gamma }_u\left(u_{ub}\right)}}\hfill \end{array}$$

(11)

Summing up, even when considering transportation systems moving with a priori unknown variable velocities, the coordination problem is well posed given only the velocities of the target stream and of the robot observed at the scheduling time $t_0$.

A last issue to be solved is related to positive accelerations of the transportation system, which induce a corresponding acceleration of the robot that may potentially lead to torque saturation and thus degraded motion control performance. A straightforward remedy lies in limiting the input or output stream acceleration proportionally to its current velocity. Note that the transportation system deceleration does not pose this problem, as it increases the time available for task completion and reduces the velocities, accelerations, and torques required of the robot. Under the proposed scheme for coordination between the robots and the transportation systems, the latter’s acceleration should satisfy the following inequalities:

$$\begin{array}{c}\hfill {\ddot{x}}_{b,lb}\le {\ddot{x}}_b\le min({\ddot{x}}_{b,ub},\alpha {\dot{x}}_b),\end{array}$$

(12)

where ${\ddot{x}}_{b,lb}$ and ${\ddot{x}}_{b,ub}$ are the transportation system minimum and maximum acceleration values, and $\alpha$ is a positive constant tuned to prevent excessive requests placed on the manipulators.

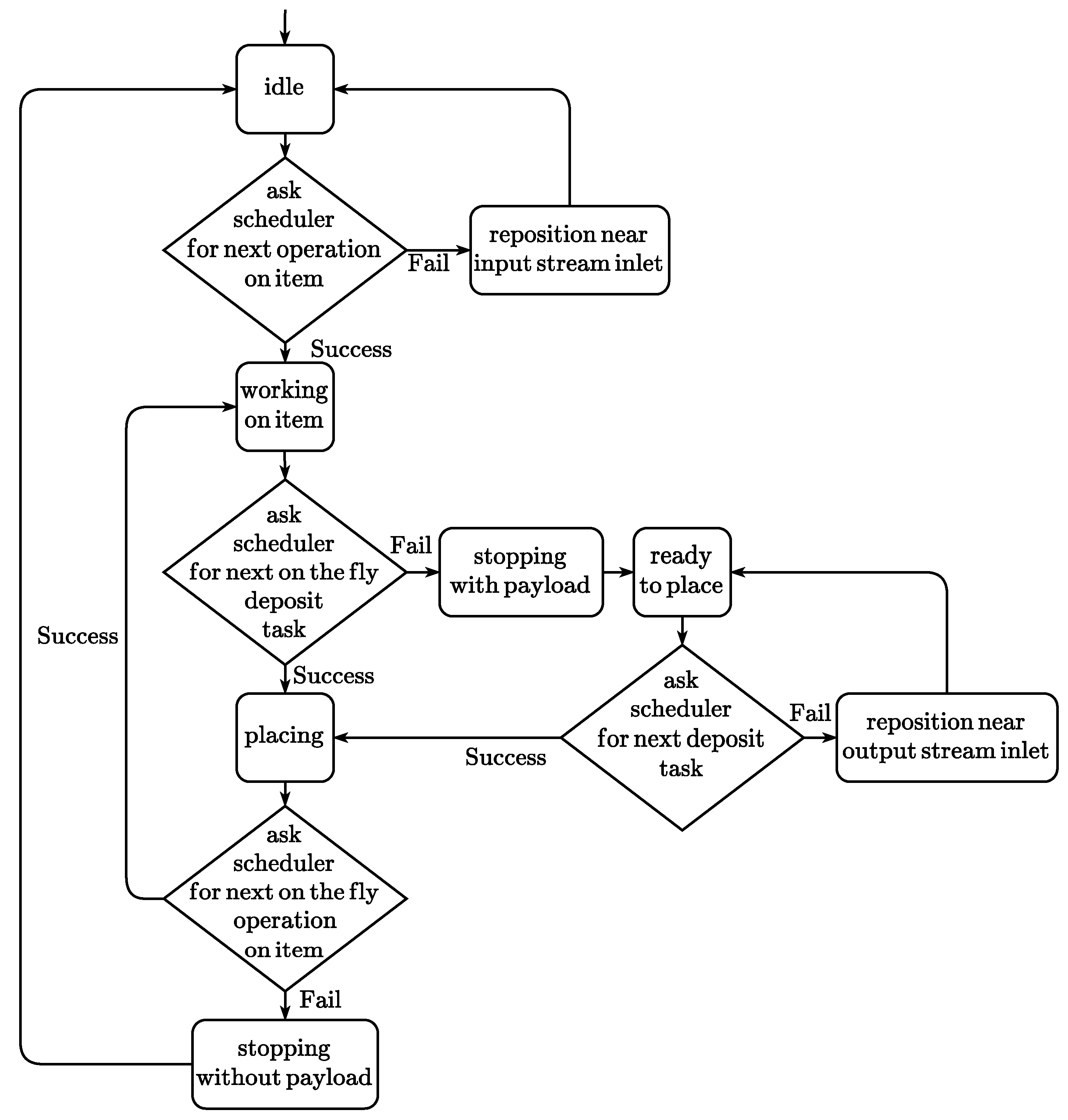
2.4. Manipulator Finite State Machine

As already discussed, from the point of view of plant-level dynamics the task time maps capture by their construction all the functionally relevant characteristics of the robot and of its tasks. Indeed, their generation technique ensures that they take into account the shape of the workspace, the geometry of the executed trajectories, and also, through the task time optimization algorithm, the maximum dynamic performance of the robot and of its actuation systems.

Once the map is available, then, it is possible to develop—for simulation purposes—an abstract model of the robot and of its task-specific software, while still taking into account all the factors that determine its actual performance. These are in fact conveniently expressed as execution times that depend on the individually configured task.

In particular, the details of the manipulator’s kinematics and dynamics, the inner working of the geometric trajectory planner and the specificities of the task time optimizer can be safely ignored, as they are accounted for within the information provided by the task time maps. Thanks to them, therefore, the robot can be modeled and simulated as a simple finite state automaton, with state transitions occurring at times dictated by the actual performance of the physical device. Several finite state machines, one for each manipulator, can then be combined to perform a highly efficient yet accurate event-based simulation of the multi-robot plant. A simplified state machine for the robot is depicted in Figure 4.

After a first initialization phase, the robot enters in the idle state; its gripping device is empty, and the robot consequently requests to the scheduler a new task on unprocessed items. If the scheduling is successful, the robot enters in the working state; otherwise, after a short waiting interval during which new requests on the scheduler are inhibited, it returns to the idle state. After performing the operation, the robot picks the item and becomes ready to place. The assignment of a new place operation is requested to the scheduler, so that the robot may deposit the processed item on the output stream; if the scheduler successfully answers, the robot enters in the placing state, otherwise it returns, after a short delay, in the ready to place state. After the completion of the place operation the robot has performed a full work cycle, and becomes again idle.

The state machine illustrated above is able to represent tasks in which the trajectories of the robot start and terminate at rest, i.e., with null velocities. A more complex situation arises when no stops between tasks are performed if not strictly necessary. In general, in the presence of a steady flow of items and deposit positions the robot does not need to halt its motion and instead can perform its work cycle in a continuous movement. On the other hand if the scheduler fails (e.g., because at some instant no items or deposit targets are available) the robot should bring its motion to a standstill, repositioning to a convenient location while waiting for the arrival of the required target. The finite state machine depicted in Figure 5 represents an operation of this kind. There it can be seen that the scheduler is invoked to assign four different kinds of tasks:

• Tasks on items that start with the robot at rest;
• Deposit tasks that start with the robot at rest;
• On-the-fly tasks on items, with initial velocities that result from the preceding task;
• On-the-fly deposit tasks, with initial velocities that result from the preceding task.

Other state transitions do not require the intervention of the scheduler; it is the robot itself that performs them as appropriate. Of note is the fact that when the scheduler selects a task it should consider not only its feasibility, but also the feasibility of a further stopping maneuver that must follow the operation whenever the scheduling of the next one fails.

Figure 5. Finite state machine for the simulation of a robot executing on-the-fly tasks.

Figure 5. Finite state machine for the simulation of a robot executing on-the-fly tasks.

2.5. Discrete Event Simulation

Given the above-described coordination strategy between the robot and the conveyors, the task time maps, and the robot finite state machine, it is possible to devise an event-based simulation of the multi-robot plant. The aim is to capture the emergent behavior of the system at a low computational cost and without loss of accuracy. A continuous time simulation, featuring not only the scheduling and planning modules but also the motion control systems, would clearly require the integration of ordinary differential equations to track the evolution of the physical state of the robots.

One of the main aims of this work is, on the contrary, the development of a lightweight simulation that faithfully captures the overall behavior of the system. The authors propose therefore an event-based framework in which the events are as follows:

• The entrance of items and empty deposit positions within the system;
• The exit of unprocessed items and deposit positions from the system;
• The state transitions of the robots;
• The update of the velocity or acceleration set-points assigned to the transportation systems;
• An optional and arbitrarily triggered observation event.

Due to several factors, the transportation systems are necessarily characterized by slowly changing velocities; in fact, their dynamic behavior is constrained by the following:

• Their large mass and low stiffness;
• The need to avoid sliding motions between themselves and the items they carry;
• The need to allow the robots to properly coordinate with them, as illustrated in Section 2.3.

A high-level conveyor manager therefore needs to update the velocity or acceleration set-point at a frequency $f_b$ in the order of 0.1 Hz; the actual motion controller can then extrapolate the slowly updated set-point to generate a finely sampled reference signal.

At the same time, the average frequency of the other events, which are related to the robot state transitions, can be expected to be roughly proportional to the upstream source productivity.

From the description of the robot state machine and of the coordination strategy between the manipulator and the transportation systems, it is apparent that the state transitions of the former are for the most part triggered by the transportation system’s displacements. Under the reasonable assumption of input and output streams moving with irreversible motion, it is possible to invert the relationship between time and the displacement of the transportation system. It is therefore possible to determine the time instant at which the next event will occur. In particular, knowing the kinematics of the transportation systems and their residual displacement associated with each robot task (i.e., the displacement remaining before the completion of the robot’s task), the time–displacement relationship is inverted to enable the comparison between the residual task execution times $\delta t_{res,rbt,k}$ (with $k=1,2,\dots ,n_{rbt}$) allocated to the operations of the robots, even when these operate on different target streams.

This simulation scheme, being compatible with the full evaluation of the dynamics of both robots and transportation systems, can economically and faithfully highlight the evolution of the global plant state. Let $f_{obs}$ be the frequency of the observation event. Then the residual time before the occurrence of a given event can be computed as follows:

$$\begin{array}{ccc}\hfill \delta t_{res,rbt,min}& =& min(\delta t_{res,rbt,1},\delta t_{res,rbt,2},\dots ,\delta t_{res,rbt,n_{rbt}})\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill \delta t_{res,b}& =& \mathrm{rem}(t_{sim},f_b^{-1})\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill \delta t_{res,obs}& =& \mathrm{rem}(t_{sim},f_{obs}^{-1}),\hfill \end{array}$$

(15)

where $\delta t_{res,rbt,min}$, $\delta t_{res,b}$, and $\delta t_{res,obs}$ indicate the residual times to the next events related, respectively, to the robots, to the transportation systems, and to the observation.

The adaptive time step yielding the event-based simulation is then computed as follows:

$$\begin{array}{c}\hfill \delta t_{sim}=min\left(\delta t_{res,rbt,min},\delta t_{res,b},\delta t_{res,obs}\right).\end{array}$$

(16)

Suppose at this point that the observation event is triggered at a higher or lower temporal resolution; it would then be possible to resolve more or less finely the actual motions of the robots and of the conveyors; however, the sequence of significant events would remain exactly the same. Even without the observation events, the simulation of the plant remains accurate as far as the evolution of the robot state machines and of the input and output streams is concerned.

2.6. Scheduling and Task Assignment Rules

Concerning task assignment, the two most widely implemented heuristics are the decentralized and the cyclic ones. According to the former, a new task is assigned to the manipulators independently of the other robots, using a given scheduling rule; when the latter is adopted, on the other hand, each item or empty deposit position is cyclically assigned to a specific manipulator as soon as it enters the system.

The most common heuristic rules for scheduling are based on position; some, such as FIFO and LIFO, prioritize the processing of an item or of a deposit position based on their location within the robot’s workspace; on the other hand, a rule such as the Nearest Target Next (NTN) considers the distance between a target and the instantaneous position of the robot’s end effector. The availability of a task time map allows the adoption of further time-based scheduling methods, such as the Shortest Processing Time (SPT), the Longest Processing Time (LPT), or the Second Shortest Sorting Time (SSST) [28] rules.

Within the context of this work, scheduling and task assignment algorithms based on optimization problems are not considered due to their high computational cost, which usually precludes their online application and leads to poor scalability with the plant size. As a result, focus has been placed on heuristic techniques; the following ones have been implemented: FIFO, LIFO, LPT, and SPT, both in their cyclic and decentralized versions. Each manipulator may be assigned an individually selected rule; moreover, the processing of the input and output streams may happen for each robot according to different scheduling and task assignment rules.

Note that despite the fact that some heuristics are not time-based, the task time maps are used also within their implementations to solve the intercept problem, properly configuring the task and guaranteeing its actual feasibility.

2.7. Rollout Algorithm for Input and Output Stream Balancing

The motion of the input and output streams can be manipulated to affect the flows of items and deposit positions, with the aim of improving the overall performance of the plant. Without loss of generality, in this work the focus is placed specifically on the output conveyor, under the conservative assumption that the input conveyor is managed according to the needs of the upstream item source. In particular, assuming a given upstream productivity, the velocity of the input transportation system must be high enough to guarantee adequate spacing between the items.

The deposit positions are generated in regular patterns at one end of the output conveyor, independently of its velocity. On the other hand, the position of the items is affected by random disturbances, and by random fluctuations of the upstream item source productivity.

Given the variety of possible plant configurations, the non-deterministic character of the input flows, and the intertemporal nature both of the plant state evolution and of the control goal (namely the maximization of the long-term reliability and productivity of the line), the output flow management problem has been formulated as a Markov Decision Problem (MDP) and solved using a rollout algorithm enabled by the efficient event-based plant simulator.

An MDP is characterized by a dynamic and stochastic environment whose evolution happens by discrete transitions following each other according to a probability distribution, itself conditioned by the current state and by the action selected by the decision agent:

$$\begin{array}{c}\hfill P_{s{s}^{\prime }}^a=\mathbb{P}\left\{S_{t+1}=s^{\prime }|S_t=s,A_t=a\right\}.\end{array}$$

(17)

$P_{s{s}^{\prime }}^a$ is the probability of the next state $S_{t+1}$ being equal to $s^{\prime }$ given that the current state $S_t$ is s and the current action $A_t$ is a. At each state transition a reward signal $R_t$ is disbursed; the expected value of the reward depends once again on the current state–action pair:

$$\begin{array}{c}\hfill R_s^a=\mathbb{E}\left\{R_t|S_t=s,A_t=a\right\};\end{array}$$

(18)

The MDP is solved when the agent is able to select for each state s the optimal action $a_{opt}$ that maximized in expectation the return $G_t$, i.e., the sum of future rewards, discounted by the rate $g\in (0,1)$:

$$\begin{array}{c}\hfill G_t=\sum _{k=0}^{\infty }{g}^k{R}_{t+k}.\end{array}$$

(19)

The explicit definition of the distribution $P_{s{s}^{\prime }}^a$, required by traditional dynamic programming algorithms, can be avoided by using methods based on the simulation of the process. As broadly outlined in [29], offline simulation can be used in conjunction with reinforcement learning methods to encode within a parametric approximator the match between a generic state s and the corresponding optimal action. When online projections are feasible, once a base policy has been fixed a rollout algorithm can be alternatively deployed to compare the truncated returns ${\widehat{G}}_t$ which result from each different action available at the current time.

With respect to the specific application here considered, the action is constituted by the acceleration value assigned to the output transportation system for the duration of the time interval $\delta t_b=f_b^{-1}$; after the acceleration phase, the base policy is to keep the conveyor velocities at a constant value for the remainder of the forward projection, which terminates at time $t+T_{rollout}$. To define the reward $R_t$, the following quantities were considered:

• The total number at time t of correctly processed deposit positions, denoted by $n_{out}\left(t\right)$;
• The total number at time t of items lost at the end of the input stream, denoted by $n_{in,lost}\left(t\right)$;
• The total number at time t of empty deposit positions lost at the end of the output stream, denoted by $n_{out,lost}\left(t\right)$.

• The reward is in particular computed as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill R_t=& w_1(n_{out}(t+\delta t_b)-n_{out}\left(t\right))+\hfill \\ \hfill & w_2(n_{in,lost}(t+\delta t_b)-n_{in,lost}\left(t\right))+\hfill \\ \hfill & w_3(n_{out,lost}(t+\delta t_b)-n_{out,lost}\left(t\right)).\hfill \end{array}\end{array}$$

(20)

In Equation (20), $w_1$ is a positive weight, whereas $w_2$ and $w_3$ are negative. As the forward projection of the rollout algorithm is necessarily truncated, no discounting of future rewards is adopted ($g=1$). The truncated return may therefore be evaluated as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\widehat{G}}_t=& w_1(n_{out}(t+T_{rollout})-n_{out}\left(t\right))+\hfill \\ \hfill & w_2(n_{in,lost}(t+T_{rollout})-n_{in,lost}\left(t\right))+\hfill \\ \hfill & w_3(n_{out,lost}(t+T_{rollout})-n_{out,lost}\left(t\right)).\hfill \end{array}\end{array}$$

(21)

The intuitive meaning of each weight $w_j$ becomes clear if the associated factor is considered. In particular:

• $w_1>0$ provides an incentive for higher production of finished products;
• $w_2<0$ penalizes the loss of items at the end of the input stream;
• $w_3<0$ penalizes the incomplete filling of the deposit positions.

In a typical application it is useful to set $|w_3| > |w_2|$, as items can usually be recirculated, whereas defects of the output stream are more difficult to trace and rectify. Moreover, if the production rate of the upstream productive system is insensitive to what happens within the downstream multi-robot plant, the parameter $w_1$ can be set to zero; the remaining weights are sufficient to ensure that the return function has its maximum when the entire production is processed correctly.

Regarding the rollout horizon $T_{rollout}$, it may be stated that its selection depends on the degree of accuracy with which the behavior of the upstream source can be modeled and predicted; shorter forecasts may be in particular more effective in cases characterized by greater uncertainty. This issue is treated in greater detail in Section 3.3, where a simple sensitivity analysis is presented in relation to a specific application case study.

A minimal action set has been finally defined as

$$\begin{array}{c}\hfill A=\left\{a_a,a_b,a_c\right\}=\left\{({\ddot{x}}_{b,out}=0),({\ddot{x}}_{b,out}=min(\alpha {\dot{x}}_{b,out},{\ddot{x}}_{out,ub})),({\ddot{x}}_{b,out}={\ddot{x}}_{b,out,lb})\right\}.\end{array}$$

(22)

In accordance to Inequality (12), ${\ddot{x}}_{b,out,ub}$ and ${\ddot{x}}_{b,out,lb}$ each correspond to the upper (positive) and lower (negative) bounds on the output transportation system acceleration values, while ${\dot{x}}_{b,out}$ represents its instantaneous velocity. Whenever the truncated returns corresponding to each action cannot be differentiated, the positive acceleration action is selected to introduce a bias towards the maximization of the plant production rate.

A comprehensive overview of the proposed simulation and optimization framework has now been presented; its novel aspects may be revisited. It can be remarked that the core of the present work is constituted by the overall simulator for the treated multi-robot system. While no particular aspect can be singled out as completely unprecedented, the proposed approach effectively bridges an existing gap between robot-level motion planning fidelity and plant-level management, offering, as will be demonstrated in the following section, a computationally feasible solution suitable for real-time optimization of the plant operating point.

To this end, a simple rollout algorithm to balance the input and output flows is proposed; to the best of the authors’ knowledge, this kind of algorithm applied to such a plant is a further novelty. At the same time, it represents only one among several possibilities enabled by the simulator; its development is meant mainly to showcase the capabilities and potentialities offered by the event-based dynamic model of the plant.

3. Results and Discussion

3.1. Case Study Description

To test the methods proposed in the preceding section, the following case study has been considered: a two-conveyor co-flow pick and place packaging line tended by identical 4-DOF five-bar robots capable of Shoenflies motion (namely three translations plus one rotation around the vertical axis). Each robot is of the kind described in detail and theoretically analyzed in [26]; having been used by the authors also for experimental activities [30,31], the possibility of fully controlling the manipulators with good accuracy is well established. The task time maps for the robots were implemented as lookup tables to minimize run time costs, considering the elementary tasks described in Section 2.2 and a maximum velocity for the moving target of 0.5 ms⁻¹. From the task time maps an average pick and place cycle time of ${\overline{T}}_{cyc}=1.21 \mathrm{s}$ was inferred; a maximum cycle time of ${\overline{T}}_{cyc,max}=2.15 \mathrm{s}$ was also estimated.

As already remarked in Section 1, if a single cycle time is adopted as a simplifying assumption, $T_{cyc,max}$ is the only choice that guarantees the feasibility of all the scheduled tasks. However, it is clear that doing so leads to a large penalty in terms of the productivity achieved by each robot. In the considered case, in fact, the characteristic productivity of the robot can be estimated at ${\overline{P}}_{rbt}=0.826 \mathrm{Hz}$ on the basis of ${\overline{T}}_{cyc}$, whereas it would be reduced to a much lower $0.4651$ $\mathrm{Hz}$ in a scheduling system that takes into account just $T_{cyc,max}$ instead of the more complete information provided by the task time maps.

The plants described in the following case studies were sized according to the relationships presented in Section 2.1. The number $n_{row}$ of rows on the output conveyor was set equal to one, which is the most challenging alternative given that it makes higher velocities necessary; the number of feeders associated with the input stream has been set on the other hand to $n_{feeder}=3$. The characteristic item length is $L_{item}=25 \mathrm{mm}$; accordingly, the nominal spacing on the input stream has been conservatively set to $\Delta L_{item,in}=75 \mathrm{mm}$, while the spacing between deposit positions on the output conveyor is fixed at $\Delta L_{item,out}=62.5 \mathrm{mm}$. While in a real-life scenario the number of robots would be selected according to the peak productivity of the item source, in the following simulations the opposite was carried out, fixing $P_{source,ub}=n_{rbt}{\overline{P}}_{rbt}$; as will be shown in the following, this choice allows for conveniently scaling up the plant as $n_{rbt}$ increases.

For illustration purposes, a two-robot plant is represented in Figure 6; larger plants can be obtained by adding further equally spaced robots. In the figure the conveyors and manipulators are represented with their actual dimensions, with the distance between adjacent robots having been chosen to avoid the possibility of collision between them; the useful portions of the robot workspaces are represented by the shaded areas. The items may be loaded onto the input conveyor randomly, with variable orientation. The robots should pick the items and place them with regular spacing on the output conveyor, on which both empty deposit positions and sorted items are depicted. 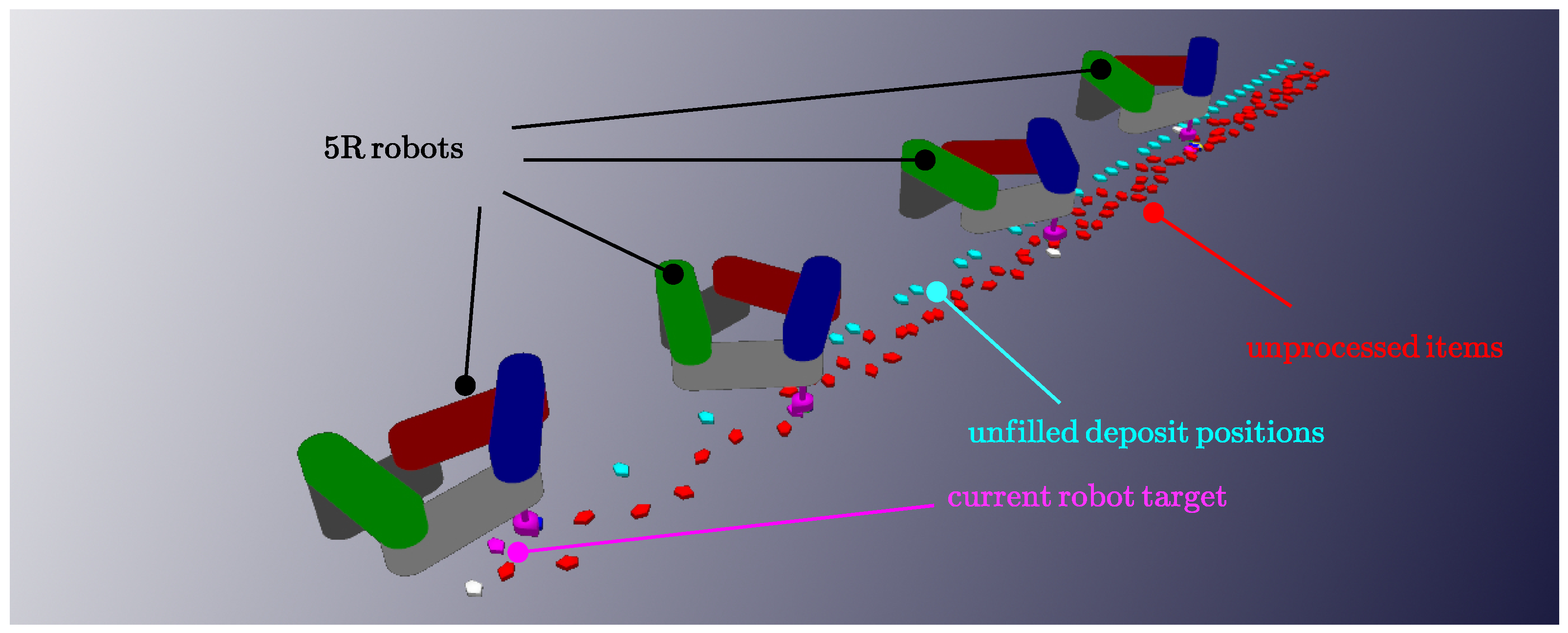Figure 7 reports moreover a single frame extracted from a minimalistic OpenGL animation of the robots and of the streams of unprocessed items and still available deposit positions. This kind of visualization tool was used to inspect in detail the simulation of the plant, and to gain additional qualitative insight into its operation.

For each simulation run, at every event the following primary indicators are collected:

• The number $n_{out}$ of correctly filled deposit positions;
• The number $n_{in,lost}$ and $n_{out,lost}$ of items and of deposit positions lost at the end of the input and output streams;
• The utilization rate $U_k$ of the $k^{th}$ robot (with $\mathit{U}$ denoting the vector collecting $U_1,U_2,\dots ,U_{n_{rbt}}$);
• The velocity ${\dot{x}}_{b,out}$ of the output stream;
• The instantaneous productivity $P_{source}$ of the upstream item source.

Figure 6. Two-robot plant; distances in millimeters. The global and local references axes are indicated with red (along x) and green (along y) arrows.

Figure 6. Two-robot plant; distances in millimeters. The global and local references axes are indicated with red (along x) and green (along y) arrows.

Figure 7. OpenGL rendering of the main elements of the multi-robot assembly: manipulators, unprocessed items (red), and available deposit positions (cyan).

Figure 7. OpenGL rendering of the main elements of the multi-robot assembly: manipulators, unprocessed items (red), and available deposit positions (cyan).

From these quantities other derived indicators are computed, such as the average source productivity ${\overline{P}}_{source}$, the net productivity $P_{out}$, and reliabilities $R_{in}$ and $R_{out}$ associated with the processing of the items and of the deposit positions. At the end time $T_f$ of a simulation run, the net productivity and the reliability indicators are defined as follows:

$$\begin{array}{cc}\hfill P_{out}& ={\displaystyle \frac{n_{out}\left(T_f\right)}{T_f}}\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill R_{in}& =100\left(1-{\displaystyle \frac{n_{in,lost}\left(T_f\right)}{n_{out}\left(T_f\right)}}\right)\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill R_{out}& =100\left(1-{\displaystyle \frac{n_{out,lost}\left(T_f\right)}{n_{out}\left(T_f\right)}}\right)\hfill \end{array}$$

(25)

Moving average versions $P_{out,ma}$, $R_{in,ma}$, $R_{out,ma}$ of the same quantities may also be straightforwardly defined.

The utilization rate of the robot is calculated considering that the device is either in states not related to production (null utilization), working at full speed as dictated by the optimizing motion planner (unitary utilization), or working at scaled down velocities (fractional utilization). The latter case occurs when, due to low availability of incoming items or deposit positions, the optimal intercept happens at the edges of the workspace, at a time higher than the one strictly needed to perform the motion. The time interval $\delta t_b$ is set equal to $0.10 \mathrm{s}$ to balance the opposing needs of attaining suitably granular conveyor velocity levels and sufficiently discernible rollout scenarios.

3.2. Constant Nominal Speed Simulations

In the following subsection, to establish a few base cases, some simulations that do not rely on the rollout algorithm are presented at first. All feature four robots, and conveyors moving at speeds set at their nominal values: $v_{in}=\Delta L_{item,in}{P}_{source,ub}/n_{feeder}=82.1 \mathrm{mm}{\mathrm{s}}^{-1}$ and $v_{out}=\Delta L_{item,out}{P}_{source,ub}/n_{row}=205.2 \mathrm{mm}{\mathrm{s}}^{-1}$.

Case (1a) is characterized by a regular, undisturbed input stream; the only transient conditions are those that occur during the startup. Case (2a) features random disturbances in the input stream, but no transient conditions except for the startup one. Case (3a) includes an upstream production system that works in batches of 1000 pieces each. At the end of each batch the production rate decreases to a low value and is then subject to a gradual ramp-up as the new batch commences. Case (4a), finally, is characterized both by batch production and by random disturbances. The above-mentioned cases use a simple FIFO scheduling with cyclic task assignment, both for the pick and for the place operations. Cases (1b), (2b), (3b), and (4b) replicate the conditions of cases (1a), (2a), (3a), and (4a), respectively, but are characterized by decentralized FIFO task assignment. Considering one of the more challenging cases (case (4a)), Figure 8 reports the entire time history of two key quantities, namely the upstream productivity $P_{source}$ and the losses $n_{out}$ of deposit positions. It can be clearly seen that the losses occur mainly during the startup transient and in correspondence with the batch changes, with new steady-state conditions being subsequently re-established.

The main global results for all cases described so far are reported in

Table 1. Constant speed simulation, cyclic FIFO scheduling.

	Case (1a)	Case (2a)	Case (3a)	Case (4a)
$n_{out}$	3852	3851	3597	3598
$n_{in,lost}$	0	0	0	0
$n_{out,lost}$	54	55	309	309
$R_{in}[\%]$	100.00	100.00	100.00	100.00
$R_{out}[\%]$	98.60	98.57	91.41	91.41
${\overline{P}}_{source}\left[{\mathrm{s}}^{-1}\right]$	3.2836	3.2836	3.0781	3.0780
$P_{out}$	3.2097	3.2092	2.9973	2.9983
${\mathit{U}}_{\mathit{average}}[\%]$	$[96, 96, 93, 95]$	$[96, 96, 93, 95]$	$[91, 90, 90, 89]$	$[91, 90, 90, 89]$

and

Table 2. Constant speed simulation, decentralized FIFO scheduling.

	Case (1b)	Case (2b)	Case (3b)	Case (4b)
$n_{out}$	3848	3846	3590	3591
$n_{in,lost}$	0	0	0	0
$n_{out,lost}$	57	57	313	312
$R_{in}[\%]$	100.00	100.00	100.00	100.00
$R_{out}[\%]$	98.52	98.52	91.28	91.31
${\overline{P}}_{source}\left[{\mathrm{s}}^{-1}\right]$	3.2836	3.2836	3.0706	3.0706
$P_{out}$	3.2064	3.2050	2.9914	2.9925
${\mathit{U}}_{\mathit{average}}[\%]$	$[99, 98, 97, 79]$	$[99, 98, 97, 80]$	$[99, 94, 90, 70]$	$[99, 94, 90, 71]$

.

From the tables it can be seen that at constant speed all the items are processed correctly, but some deposit positions remain unfilled. This is generally undesirable, since the unprocessed items may be recirculated, whereas the unfilled deposit positions correspond to defects in the finished product (such as incompletely filled boxes) and may also cause the downstream machinery to malfunction. In cases (1a), (2a), (1b), and (2b) the loss of deposit positions is associated with the startup transient; for cases (3a), (4a), (3b), and (4b), considerable losses occur during the batch changes, when the productivity of the upstream item source substantially drops. Random disturbances affect only minimally the performance of the plant, confirming the robustness and effectiveness of the robots against this kind of non-ideality.

Decentralized task assignment, finally, appears to perform marginally worse than the cyclic counterpart in terms of overall process reliability; its most important downside is however related to the utilization pattern of the robots. Indeed, in cases (1a) and (2a), where the upstream production rate is constant, it can be seen that all the robots operate at high utilization levels. In cases (3a) and (4a), on the other hand, the average utilization drops due to the lower production rate during batch change transients; however, the overall workload remains equally spread among the four robots. Conversely, in cases (1b) and (2b) the first three robots work almost at saturation, while the average utilization of the last one is a much lower 80%. The situation in cases (3b) and (4b) is even worse: due to reduced average upstream productivity, the first two robots work at complete saturation, leaving a lower workload to the remaining two, whose utilization reaches 90% and 70% only. This uneven utilization may lead to different mean time to failure for the robots, complicating maintenance and repair operations.

To better illustrate this aspect, contrast, e.g., case (4a), where on average the robots operate at 90 ± 1% utilization rate, with case (4b), in which the utilization averages to a slightly lower 88.5% with a peak of 99% on the first manipulator. Assuming that the mean time to failure of the robot is inversely proportional to its utilization rate, it may be concluded that under decentralized scheduling the average frequency of maintenance events is almost 10% higher. This moreover neglects the fact that maintenance programmed under the assumption of uniformly utilized (and thus worn) robots involves the repair of the entire ensemble at a single servicing downtime. On the contrary if the wear is uneven, two cases may present themselves: either all robots are repaired in the same way regardless of the different levels of damage (thus replacing still functional parts), or a specific maintenance routine is prescribed for each manipulator (further increasing the frequency of the plant downtimes).

3.3. Four-Robot Plant with Rollout Conveyor Management

The simulations performed in this subsection use the rollout algorithm described in Section 2.7. All the following cases feature batch production and random disturbances. To enable comparison with the preceding cases, FIFO scheduling with cyclic task assignment is used. To assess the effects of the rollout termination time $T_{rollout}$, the following cases are considered:

• Case (5a): $T_{rollout}=20 \mathrm{s}$;
• Case (5b): $T_{rollout}=40 \mathrm{s}$;
• Case (5c): $T_{rollout}=60 \mathrm{s}$;
• Case (5d): $T_{rollout}=80 \mathrm{s}$.

For these cases the weights appearing in Equation (21) are set to $w_1=0$, $w_2=-1$, $w_3=-5$. The reason for this choice is as follows: the loss of unfilled deposit positions is more heavily penalized compared to the loss of items that may be easily recirculated; furthermore, there is no need to incentivize a high production rate using $w_1$ as in the considered case the upstream productivity is not influenced by the actions taken by the rollout agent. In the considered scenario, the goal is to achieve $n_{out,lost}\left(T_f\right)=0$, with $n_{in,lost}\left(T_f\right)$ as low as possible. The overall results are reported in

Table 3. Four-robot plant with rollout management of the output conveyor.

	Case (5a)	Case (5b)	Case (5c)	Case (5d)
$T_{rollout}\left[\mathrm{s}\right]$	20	40	60	80
$n_{out}$	3186	3360	3393	3365
$n_{in,lost}$	413	231	202	228
$n_{out,lost}$	13	0	0	1
$R_{in}[\%]$	87.04	93.13	94.05	93.22
$R_{out}[\%]$	99.59	100.00	100.00	99.97
${\overline{P}}_{source}\left[{\mathrm{s}}^{-1}\right]$	3.0707	3.0797	3.0895	3.0922
$P_{out}$	2.6548	2.8000	2.8273	2.8042
${\mathit{U}}_{\mathit{average}}[\%]$	$[80, 82, 84, 87]$	$[85, 87, 86, 86]$	$[88, 87, 88, 87]$	$[88, 88, 87, 87]$

.

A rollout window of $20 \mathrm{s}$ appears insufficient to achieve the desired result, as there is a loss of deposit positions even with a high number of discarded items. Case (5b), on the other hand, achieves a desirable result of no loss of deposit positions, with a moderate loss of items. Even better results are obtained in case (5c), which further reduces the number of lost items at the price of a higher computational cost. Case (5d), which is characterized by the highest $T_{rollout}$, is less favorable than cases (5b) and (5c); this might be explained by the fact that the rollout simulations project forward the instantaneously observed upstream production rate, and do not assume anything about the future trends. Accordingly, after a certain point longer and longer forward predictions may lose accuracy and lead to the selection of the wrong action.

3.4. N-Robot Plants with Rollout Conveyor Management

In this subsection plants with rollout conveyor management characterized by different numbers of manipulators are considered:

• Case (6): $n_{rbt}=5$;
• Case (7): $n_{rbt}=6$;
• Case (8): $n_{rbt}=7$;
• Case (9): $n_{rbt}=8$.

As the upstream source productivity scales up, the batch sizes $n_{batch}$ are correspondingly increased to induce a similar number of batch change transients and to consequently enable a fair comparison between plants of different sizes.

As observable in Figure 9, one remarkable property of the algorithm is its ability to find a suitable steady-state value for ${\dot{x}}_{b,out}$, which moreover is appropriately adjusted during the transient conditions. In particular, Figure 9a shows the productivity profile assigned to the upstream item source, whereas Figure 9b represents the output conveyor velocities. From

Table 4. Plants of different sizes, with rollout management of the output conveyor.

	Case (6)	Case (7)	Case (8)	Case (9)
$T_{rollout}\left[\mathrm{s}\right]$	40	40	40	40
$n_{rbt}$	5	6	7	8
$n_{out}$	4228	4838	5505	6088
$n_{in,lost}$	267	551	785	1095
$n_{out,lost}$	0	0	0	0
$R_{in}[\%]$	93.68	88.61	85.74	82.01
$R_{out}[\%]$	100.00	100.00	100.00	100.00
${\overline{P}}_{source}\left[{\mathrm{s}}^{-1}\right]$	3.8495	4.6129	5.3730	6.1251
$P_{out}$	3.5230	4.0317	4.5871	5.0733
${\mathit{U}}_{\mathit{average}}[\%]$	$[87, 88, 89, 88, 88]$	$[87, 87, 87, 88,87, 87]$	$[86, 87, 87, 87, 86, 86, 86]$	$[85, 86, 85, 86, 85, 85, 85, 85]$

it can be seen that the overall performance in terms of reliability decreases as the number of robots increases. This may be explained by a few factors: first of all, the speed of the transportation systems increases, reducing the time window during which an item or a deposit position remains within the reach of the manipulator. Secondly, the greater length of the transportation systems increases delays within the system; thirdly, due to the operation of more robots, it may be expected that the downstream manipulators work with more rarefied and scattered targets, decreasing the chance of having items and deposit positions available at the same time.

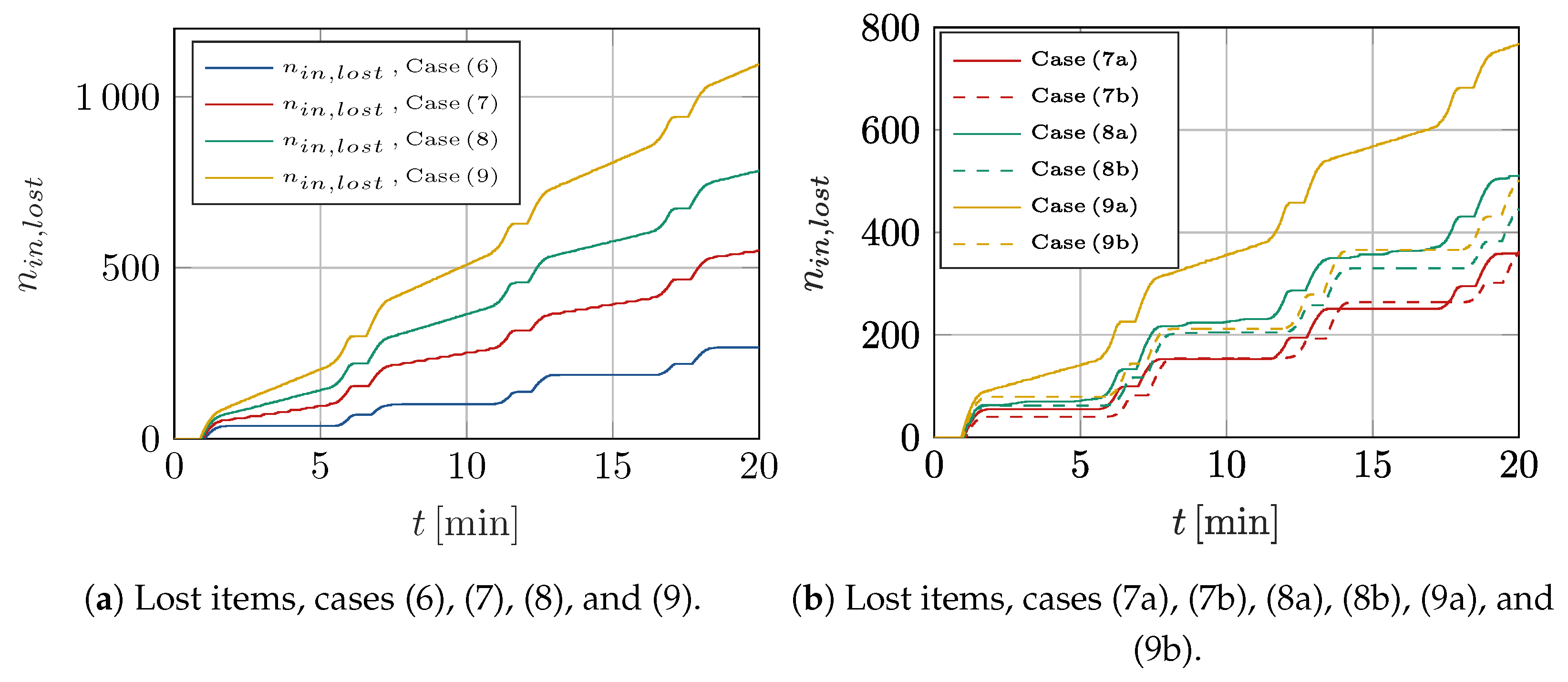
A further factor may be related to the fact that the average cycle time calculated over the entire task time map is not representative of the task time distribution conditioned by the actual operating point of the plant, which progressively shifts as the number of robots increase. Analyzing more in detail (see Figure 10a) the time history of the indicators $n_{in,lost}$ and $n_{out,lost}$ for cases (6), (7), (8), and (9), it is evident that for plant (7), even in steady-state conditions, there is a roughly uniform trickle of lost items; these losses become increasingly marked for plants (8) and (9). This suggests that the productivity of the upstream item source cannot be linearly scaled with the number of the robots. Variants with lowered peak upstream productivities were therefore analyzed. In particular, compared to cases (7), (8), and (9), a 5% reduction was applied to yield cases (7a), (8a), and (9a). Cases (7b), (8b), and (9b) were analogously obtained considering a 10% reduction. The time history of the lost items is reported in Figure 10b; it can be seen that case (7a) achieves zero losses in steady-state conditions, while case (8a) still displays some minor losses. Considering variants of case (9), it can be seen that the upstream productivity is still unacceptable in case (9a) and more appropriate in case (9b).

The global results for cases (7a), (7b), (8b), and (9b) are reported in

Table 5. Cases (7a), (7b), (8b), and (9b).

	Case (7a)	Case (7b)	Case (8b)	Case (9b)
$n_{out}$	4764	4474	5205	5960
$n_{in,lost}$	359	362	445	501
$n_{out,lost}$	0	0	0	0
$R_{in}[\%]$	92.46	91.91	91.45	91.59
$R_{out}[\%]$	100.00	100.00	100.00	100.00
${\overline{P}}_{source}\left[{\mathrm{s}}^{-1}\right]$	4.3816	4.1516	4.8378	5.5145
$P_{out}$	3.9697	3.7283	4.3371	4.9667
${\mathit{U}}_{\mathit{average}}[\%]$	$[85, 85, 86, 86, 86, 86]$	$[77, 80, 81, 79, 82, 85]$	$[80, 82, 82, 81, 81, 82, 83]$	$[83, 83, 83, 83, 84, 83, 83, 84]$

. First of all it can be seen that also in these cases the rollout algorithm is able to obtain the desired complete filling of the deposit positions. It can also be observed that the reduction in the upstream source productivity from case (7a) to case (7b) has a negative effect, as it reduces the number of processed outputs without increasing the reliability of the plant. Conversely, plant (9b) operates significantly better than plant (9): its output productivity is almost unchanged, with a considerably lower loss of discarded items. This analysis suggests that in plants where the upstream productivity can be to some extent regulated, the selection of the optimal value may lead to substantial benefits in terms of reliability.

Figure 11 reports a synthetic overview of the relationship between productivity and input processing reliability for the larger plants with six, seven, or eight robots. It can be seen that, in general, productivity increases with the number of robots: indeed, cases (7), (7a), and (7b) form a first cluster, cases (8), (8a), and (8b) a second one, and cases (9), (9a), and (9b) a third. The ability to reach high input processing reliability depends on the proper tuning of the input productivity. In fact, case (9b), with eight robots, achieves a reliability very close to those of the smaller plants of cases (8b) and (7a), On the contrary, in the case of excessive input productivity the reliability of larger plants is more markedly lowered. It should be remarked that regardless of the achieved $P_{out}$ and $R_{in}$, in all these cases the output reliability $R_{out}$ is equal to 100%.

3.5. Robustness Against Transient Conditions

To ascertain the robustness of the rollout algorithm against the disturbances introduced by different kinds of transient conditions, case (10) was devised. The plant is configured as in case (7a), with $n_{rbt}=6$ and $T_{rollout}=40$; the difference lies in the fact that the upstream productivity drops have been randomized and made more frequent.

The main results are reported in Figure 12. In particular, Figure 12a shows on separate axes the upstream source’s productivity profile and the output conveyor velocity as calculated by the rollout algorithm. Figure 12b displays the time history of $n_{out}$, $n_{out,lost}$, and $n_{in,lost}$. It can be seen that, as desired, $n_{out,lost}$ remains zero for the entire simulation run. The input reliability $R_{in}$, on the other hand, reaches a value of 85.4%. This result, which is worse than the comparable case (7a), is attributable to the fact that the plant is scarcely able to reach steady-state conditions due to the much more irregular upstream production.

3.6. Online Applicability of the Rollout Algorithm

The real-time applicability of the proposed method is conditional on the rollout forward projection being performed within the deadline set by $\delta t_b$. Accordingly, it is not an intrinsic property of the algorithm, but depends on many different factors.

Considering key features of the algorithm the following aspects should be highlighted:

• Increasing the above-mentioned parameter $\delta t_b$ relaxes the deadline, giving more time to perform the rollout computations;
• Variations of $T_{rollout}$ induce proportional variations in the computational cost;
• Considering a larger number $n_a$ of possible actions again scales the computation time linearly; however, if $n_a$ remains moderate, this negative effect could be entirely negated by straightforward parallelization, with each rollout scenario simulated by a separate core.

The computational costs are however affected also by the plant configuration. For example, computation time may be expected to increase with the number $n_{rbt}$ of robots. More subtly, the task assignment strategy has a considerable influence over computational costs, which are dominated by the scheduling activities. In particular cyclic task assignment restricts the possible tasks considered by the scheduler as a given manipulator becomes available; on the contrary, with decentralized task assignment, the scheduler has to discriminate among a considerably larger number of potential next tasks. For the same reason more rarefied input and output flows, characterized by a higher ratio between velocity and production rate, result in a lower number of items or deposit positions inside the system at any instant of time, leading to a reduced scheduling burden.

Despite these caveats, it may be stated that the proposed method in its current implementation is entirely suitable for real-time use in many cases of practical interest. To substantiate this claim, the computational costs of running a rollout scenario for $T_{rollout}=40 \mathrm{s}$ for the plants considered in cases (6), (7), (8), and (9) have been recorded.

The simulation tool has been written in C++ and tested on a machine having the specifications detailed below:

• CPU: Intel^®Core™i7-8750H processor 2.2 GHz (9 MB cache, up to 4.1 GHz, 6 cores);
• RAM: 32 GB DDR4 SO-DIMM, 2400 MHz.

Figure 13 reports the computational cost for the three rollout scenarios; the first corresponds to the action $a_a$ (null acceleration), the second to action $a_b$ (positive acceleration followed by constant velocity), the third to action $a_c$ (negative acceleration followed by constant velocity). It may be seen that even for the largest plant (Figure 13d) each rollout computation is performed in less than 30 ms; excluding the occasional spikes, a typical computation time is around 13 ms. The other plants (Figure 13a–c) require progressively lower computation times as the number of robots decreases. This analysis highlights the high computational efficiency of the simulation framework, and in particular confirms that, with a reasonable configuration, the online application of the rollout algorithm is quite feasible. It is notable that for all considered cases, the computational cost starts at a low value, and gradually ramps up; this is attributable to the fact that during the simulation the input conveyor progressively fills up, and the robots start to operate one after the other. Other variations in computation times are strongly correlated with the variations of upstream productivity, which increase or reduce the number of items inside the system.

Figure 13. CPU times associated with the three rollout scenarios executed in Cases (6), (7), (8), and (9). The three considered actions $a_a$, $a_b$, and $a_c$ correspond, respectively, to constant, increased, and decreased velocity of the output transportation system.

Figure 13. CPU times associated with the three rollout scenarios executed in Cases (6), (7), (8), and (9). The three considered actions $a_a$, $a_b$, and $a_c$ correspond, respectively, to constant, increased, and decreased velocity of the output transportation system.

3.7. Qualitative Comparison with Alternative Techniques

While a direct, quantitative comparison with other optimization techniques proposed in the current literature would be desirable, its actual feasibility is questionable. This is due to a few key differences, whose brief exploration may at least yield a qualitative contrast between the proposed framework and the already existing ones.

First of all, some of the reviewed works, such as [12,14,15,16], feature only one transportation system, and consider fixed and always available deposit stations; as such, the main issue arising within the kind of plant treated in this work—namely the balancing of the input and output streams—is entirely absent. Others, such as [8,9], do consider this aspect, but the adopted formalization does not include configuration-dependent task execution times, nor the actual robot-level motion planning, and not even the actual shape of the workspace. Moreover, unphysical finite-amplitude discontinuities in the transportation system velocities are allowed. These simplifications are introduced due to the need of casting the scheduling problem in a standard mathematical form, that can be then treated by known solving algorithms. As a result, however, the actual feasibility of the obtained solutions is far from being guaranteed.

Real-time application does not appear to be a focus of those works, while it has been explicitly addressed in this paper. The computational costs of those competing approaches are moreover superlinear with respect to the number of robots, whereas the proposed method has been shown to scale with relative ease to larger plants. In particular, as already discussed, linear increases in computation times can be expected with the number of robots and of the available actions. The computational efficiency problem has been addressed in [10], which still suffers, however, from excessively simplified modeling of the actual multi-robot plant. The approach proposed in this paper, on the other hand, has been developed taking into account all the lower-level issues that must be addressed to ensure the proper functioning of the entire plant. A 100% reliability of the output stream processing has moreover been shown in multiple challenging conditions that feature random disturbances and unpredictable batch changes. Depending on the actual configuration of the plant, this has been obtained at the expense of a lowered input stream processing reliability; even higher performance, where a greater portion of the input stream is achieved, is thus conceivable. It is nonetheless remarkable that a simple tuning of the optimization parameters straightforwardly leads to a specific outcome (namely the complete filling of the deposit positions) that in most practical applications is highly sought after and not always easily obtained.

The advantages of the proposed approach can be summarized as follows:

• Computational efficiency and scalability;
• Compatibility with the lower-level hardware and software layers;
• Straightforward tuning of the main optimization algorithm parameters to achieve specific production goals.

4. Conclusions

This paper presented a high-fidelity event-based simulation framework for multi-robot plants consisting of industrial manipulators that operate on shared input and output flows of items. The consistency between the event-based simulation and a more detailed physical model of the plant is achieved thanks to accurate, dynamics-based, and pre-evaluated task time maps that associate each operation of the robots with their actual execution time. This kind of simulation strategy is characterized by high computational efficiency, which enables the forward projection of the plant state in real time: in plants of up to eight robots, a 40 s forecast can typically be performed in less than 20 ms on commodity hardware. These forward projection capabilities form the basis for rollout algorithms aimed at the maximization of the plant performance.

The paper evaluates the effectiveness of the proposed simulation framework optimizing a production plant where the input flow is randomly scattered over the transportation system and subject to transient distribution, as it occurs in batch production. To address the primary issue in this type of plant, specifically managing the output stream in the presence of highly irregular input flows, a rollout method was employed. In this situation, where the absence of defects in the final production is required and the input flow can be recirculated, the proposed method can ensure a 100% reliable output stream processing.

An effect that was highlighted, even though not thoroughly treated, is that the upstream source productivity can be only approximately scaled linearly with the number of robots; using experimental tuning, it was found that minor adjustments lead to a considerably lowered proportion of recirculated inputs. More in general, the simulation framework can be used for a highly detailed sizing of the plant.

Building on the achieved results, several research directions may be pursued in the future. The first is the comparison of the rollout method with a Q-learning algorithm aimed at the solution of the same problem; this may lead to further gains in computational efficiency by substituting the forward simulations with the evaluation of a pre-trained neural network, and to the learning of more complex control sequences that further improve the reliability of the plant. A second future topic concerns plants in which the upstream productivity may be adjusted, at least slowly, to fully saturate the multi-robot assembly while guaranteeing good reliability. This may be straightforwardly achieved by incorporating the utilization rates of the robots and the rate of item loss as indicators of low, excessive, or appropriate saturation of the system. Finally, a further topic of additional research may concern the dynamic selection of combinations of task assignment and scheduling rules, or conversely the development of efficient scheduling optimization strategies.