Sampling-Based Path Planning and Semantic Navigation for Complex Large-Scale Environments ^†

Abstract

This article proposes a multi-agent path planning and decision-making solution for high-tempo field robotic operations, such as search-and-rescue, in large-scale unstructured environments. As a representative example, the subterranean environments can span many kilometers and are loaded with challenges such as limited to no communication, hazardous terrain, blocked passages due to collapses, and vertical structures. The time-sensitive nature of these operations inherently requires solutions that are reliably deployable in practice. Moreover, a human-supervised multi-robot team is required to ensure that mobility and cognitive capabilities of various agents are leveraged for efficiency of the mission. Therefore, this article attempts to propose a solution that is suited for both air and ground vehicles and is adapted well for information sharing between different agents. This article first details a sampling-based autonomous exploration solution that brings significant improvements with respect to the current state of the art. These improvements include relying on an occupancy grid-based sample-and-project solution to terrain assessment and formulating the solution-search problem as a constraint-satisfaction problem to further enhance the computational efficiency of the planner. In addition, the demonstration of the exploration planner by team MARBLE at the DARPA Subterranean Challenge finals is presented. The inevitable interaction of heterogeneous autonomous robots with human operators demands the use of common semantics for reasoning across the robot and human teams making use of different geometric map capabilities suited for their mobility and computational resources. To this end, the path planner is further extended to include semantic mapping and decision-making into the framework. Firstly, the proposed solution generates a semantic map of the exploration environment by labeling position history of a robot in the form of probability distributions of observations. The semantic reasoning solution uses higher-level cues from a semantic map in order to bias exploration behaviors toward a semantic of interest. This objective is achieved by using a particle filter to localize a robot on a given semantic map followed by a Partially Observable Markov Decision Process (POMDP)-based controller to guide the exploration direction of the sampling-based exploration planner. Hence, this article aims to bridge an understanding gap between human and a heterogeneous robotic team not just through a common-sense semantic map transfer among the agents but by also enabling a robot to make use of such information to guide its lower-level reasoning in case such abstract information is transferred to it.

1. Introduction

1.1. Motivation

The past decade has seen significant advancements in robotic exploration solutions for large-scale environments owing to the maturity of certain path-planning solutions such as sampling and graph-based path planners. In a recent attempt to bring together field-robotics researchers in this research area, the DARPA Subterranean (SubT) Challenge [1] aimed at developing robotic solutions to rapidly explore, map, and search austere underground environments. Autonomous underground exploration is critical for obtaining rapid situational awareness and to enhance the accessibility of the environment in disaster situations. The subterranean environments like man-made tunnel systems, natural cave networks, abandoned subway stations, etc., pose significant risk to humans in terms of harsh terrain, poor visibility, extremely narrow passages, intermittent or no communications, and no GPS availability, just to name a few. One prominent example is the Tham Luang cave rescue operation, where 12 soccer players went missing and were eventually rescued after a week from the partially flooded cave, 4 km from the cave’s mouth. Another incident is the Quecreek Mine rescue, where 9 mine workers were trapped underground in the dark for over 77 h until rescued after a challenging rescue operation. Beyond Earth, the subsurface exploration of other planets such as Mars is an active frontier in space exploration. There are 200 lunar and 2000 martian cave-related features reported by the scientific community [2]. Deep planetary caves could be a very likely candidate to harbor life due to their radiation shielding and shielding from cosmic rays. Moreover, exploring these subsurface voids could be a means to knowing the geological history and volcanic processes on other planets. All such applications require autonomy solutions to not only be theoretically sound by themselves but also to be suited for high-tempo operational environments with special focus on limitations and interactions of various components of the overall system.

Path planning is a vital component of a modern autonomous robotic system design. Typically, this component leverages perception information to generate paths in a vehicle’s state space in order to navigate it to parts of an environment that are of interest given a set of mission objectives. The perception information can be obtained as raw or processed sensor data such as occupancy grid, distance field, pointcloud, semantic map, depth image, etc. In case of a human-supervised heterogeneous team of robots, an ideal solution should not only respect diversity in mobility constraints but also cognitive constraints. In order to reduce workload on supervising humans during high-tempo field-robotics operations, the robotic fleet should be smart enough to carry out a mission autonomously on its own in a coordinated way. In cases where human cognition can improve the mission’s efficiency, the information transfer and utilization should be inclusive of human cognition and workload limitations. To further elaborate, an air vehicle, for instance, can treat any physical object as an obstacle, hence it can rather rely on a distance field mapping solution. In contrast, a ground robot needs a different mapping solution to assess positive and negative terrain obstacles. By bringing a heterogeneous robotic team together with a human in the loop, in addition to inter-robot alignment sensitivity and high communication bandwidth requirements for transfer, a geometric map information quickly becomes unintuitive to supervising humans for large-scale environments to an extent where even setting a 3D goal point on these maps during high-tempo missions is an additional burden on human cognition. This article proposes a sampling-based path-planning solution for a heterogeneous robotic team and builds a semantic reasoning framework in it to enable comprehensive human-supervised autonomy.

1.2. Robotic Exploration Problem

This article, more specifically, deals with the problem of robotic exploration of large-scale unstructured environments with special emphasis on deployability of solutions during high-tempo field operations. This section introduces some of the requirements of this problem inspired by the DARPA Subterranean Challenge. This research assumes that the minimal sensor stack on each of the robots includes a 360° 3D LiDAR and an Inertial Measurement Unit (IMU) for localization and mapping. 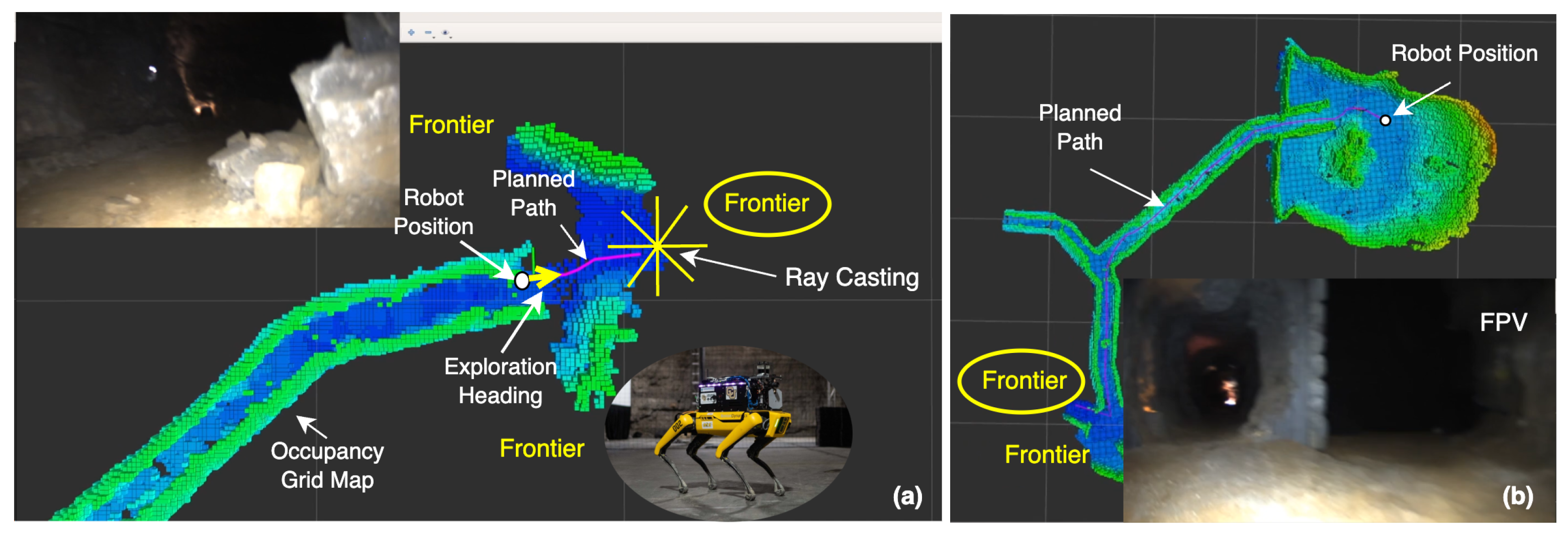The primary objective of an exploration problem is to make progress towards the frontiers of an environment map. This map is generated as a robot moves through the environment and can be obtained in various forms such as an occupancy grid, pointcloud, and distance field. Planning paths towards potential map frontiers enables a robot to expand the map in a feedforward fashion. A frontier in this article refers to a point on an explored map such that if occupied by a robot, a sufficient amount of volumetric gain is explored. Volumetric gain is proportional to the number of rays hitting the unexplored areas of a map if these rays are casted from the LiDAR sensor mounted on the robot. Sensors are assumed to be symmetrical; therefore, the volumetric gain is considered agnostic to robot orientation. However, sensor extrinsics relative to the robot are taken into account during ray casting. The concept of frontiers and ray casting for volumetric gain calculation is shown in Figure 1.

An important metric for efficient exploration is the amount of map volume explored in a unit of time. A more efficient exploration can be achieved if multiple robots are used to explore non-overlapping sections of an environment. Moreover, if these robots are heterogeneous in nature, the diversity in mobility can be leveraged to further improve the exploration efficiency. An aerial robot, for instance, is better adapted to explore vertical and elevated structures, a legged robot can traverse stairs, and wheeled robots, though most limited in mobility, can carry the most amount of payload of the former two. Therefore, an acceptable exploration solution should be able to handle multiple types of robots. Another important ingredient to a large-scale mission success of this kind is the ability of autonomy algorithms to respect human cognition and feedback in order to communicate and coordinate with supervising humans. Moreover, efforts should be made so that the exploration solution is less needy of communication bandwidth required to carry out multi-agent coordination.

This article aims at proposing an exploration solution that is well suited to be used for coordinated exploration of quadrotor air and wheeled and legged ground vehicles while respecting human cognition and feedback in the loop. Figure 2 shows robots used by the team MARBLE at the DARPA Subterranean Challenge. Emphasis has been put on taking care of the practical limitations such as communication bandwidth constraints, inter-robot map alignment errors, and portability and scalability of the solution. Figure 3 shows a block diagram of system-level integration which fits the solutions proposed in this article. For the higher-level system-integration overview, interested readers are referred to team MARBLE’s previously published articles [3,4].

1.3. Existing Literature

Robotics exploration for field applications root primarily from two approaches: frontier-based planning and sampling-based planning. The concept of frontier-based planning was first introduced by Yamauchi et al. [5,6]. In a typical frontier-based approach, an occupancy map is first processed to find the physical boundaries between seen and unseen parts of an environment known as frontiers. In case of an occupancy grid map, this boundary can be obtained in the form of large enough clusters of seen voxels adjacent to unseen voxels. Methods such as the ones proposed in [7,8,9,10] take this idea further, providing some performance comparisons and implementation on MAVs. The approach has been extended to multi-robot exploration as well [11]. Initially, the frontier-based method to exploration has been used to navigate to the nearest frontier, but later works incorporate objectives such as minimizing the velocity change into the problem [12]. While various adaptations of the method exist varying greatly in implementation, there are a few commonly faced challenges with this method. Such an approach often times lacks the distinction between reachable and non-reachable frontiers, until a path is planned toward each of them. Other common challenges faced by such an approach are large solution space and myopic one-step look-ahead decision-making. One of the planners used at the SubT challenge is called TARE [13,14]. The planner follows the frontier-based approach while reducing the computational complexity by proposing a two-tier approach. Dense data is maintained locally to a robot to generate a detailed path, which is appended to a coarse path obtained at the global environment scale. Another exploration solution proposed by a SubT challenge team also follows the concept of computing frontiers [15,16]. The method uses a pointcloud visibility approach [17] to calculate the boundary between known and unknown space. Hybrid A* is used for local planning, while long-distance planning relies on parse topometric graphs. An Occupancy Homogeneous Map is used to compute a height map, which is part of the planner cost function. In order to carry out multi-robot coordination, a multi-agent SLAM solution known as Wildcat SLAM [18] is used by the authors to compute global maps on each of the robots.

A sampling-based approach creates a representation of an environment parallel to the geometric SLAM map. This representation is obtained in the form of a graph by sampling the environment [19,20]. The frontiers in this approach are typically the graph vertices that are close to the boundary between seen and unseen parts of the environment. Sampling allows us to obtain a discrete set of paths to choose from, and the path that best satisfies the pre-set exploration objective is the solution to the path-planning problem. These approaches are better suited to plug-n-play different objectives and objectives formulations, which makes the solution search conveniently portable without needing to modify the underlying search algorithm [21]. Since a sampling-based approach provides a finite set of potential paths to choose from, optimization constraints are also easier to impose compared with a frontier-based method, which optimizes over a significantly large solution space. In this article, we leverage this fact extensively to improve the scalability of the planner. Reference [22] introduces the concept of Next-Best-View (NBV) planning, where a series of covering views are calculated to improve the coverage of an unknown environment. The concept is extended to the indoor exploration problem by [19], which uses Rapidly Exploring Random Trees (RRTs) to sample the environment and follow an optimal path in a receding horizon way so that the information gain can be maximized. A commonly known challenge with such approaches is that it is oftentimes not computationally feasible to sample a large-scale environment at once. Moreover, these environments are broken down into several sections, such as small and big room, narrow passages, and such. Therefore, it is undesirable for a robot to target a long-range goal when the exploration should be focused on nearby areas first to improve the overall exploration rate. To rectify such issues, there has been a recent development by Dang et. al. [23] that proposes the use of RRTs* in the local neighborhood of the robot while simultaneously building a global roadmap in the form of a graph. This representation is attractive because it does not sample the whole environment at once and also provides a sense of the range of paths to the solution-search algorithm. Our sampling strategy is an extension of this bifurcation approach to sampling. Limited literature exists on the use of sampling-based approaches to explore complex subterranean environments. These complex 3D environments pose some of the extreme field-robotics challenges, which call for a tightly coupled system design where one subsystem has to be designed by keeping in view the performance and limitations of other connected subsystems. Some of the challenges that the path planner has to be aware of in these environments include adverse terrain, negative and positive obstacles, collapses and closed passages, intermittent communication with other robots and supervising human team, varying scale in different sections of the environment, multi-robot map misalignment and map drifts, heterogeneous robots relying on different perception schemes, etc. The literature on other teams’ entries in the DARPA Subterranean Challenge [15,24,25,26,27] highlight these challenges and lessons learnt from attempting to solve them. The following subsections highlight the contributions brought by ScanPlan with respect to the existing literature.

1.3.1. Terrain Assessment

Terrain assessment is essential to planning collision-free paths for mobile ground robots. One of the SubT challenge’s sampling-based planners that uses the bifurcation approach for sampling relies on using high-resolution depth images to compute a grid-based elevation map using [28] in the local neighborhood of the robot and then segmenting this map to extract terrain features such as ramps, stairs, rails, and rough terrain using [29]. Since this terrain-assessment technique is computationally expensive and only used to generate a local map, the path planner would run into issues with global reachability awareness. Consequently, the road-map graph is built with an over-optimistic view of the terrain wherever the terrain information is not available. For instance, one of the problems faced by the authors [23] is that the robot would occasionally run into bad terrain and had to be backtracked to recompute feasibility. This also makes repeated rewiring of the graph necessary, which, in addition to backtracking, is slow to perform. This method being computationally expensive can only provide local terrain awareness. Another terrain-assessment method used by a belief-aware planning architecture [26,30] generates a multi-layer map to include other robots, communication nodes, and other environment obstacles. Positive obstacles are detected using ground segmentation [31], settling-based collision checks [32] for long ranges, and by applying local ground plane-relative step filters over short ranges. Negative obstacles are calculated using surface discontinuities in a pointcloud. Our terrain-assessment method is similar to the settling-based collision-check method, but we do not perform explicit ground segmentation to create an elevation map. The method is an on-demand method to check for traversabilty, hence it is more suitable for the planners that rely on sampling. Moreover, the proposed strategy performs collision checks at the occupancy grid resolution, which allows us to obtain the traversability information at all times anywhere on the explored map, not just locally, in a computationally feasible way. In our demonstrations, with Boston Dynamics Spot and Clearpath Husky, we used a coarser 0.15 m voxel size for our maps, obtained through a slightly modified version of OctoMap [33], feasible in large subterranean environments.

1.3.2. Solution-Search

Robotic applications have long been relying on multi-objective optimization approaches where performance is a function of user-defined gains [8,34,35,36,37]. For instance, existing solution-search methods [38] for the sampling-based exploration planners formulate an objective function as a combination of volumetric gain, exploration heading, and other necessary variables penalized by penalty gains. Since the subterranean environments vary greatly in structure and size, the tuning of gains to find a sweet spot is a cumbersome and environment-dependent process. Moreover, in this example specifically, the volumetric gain calculation is too expensive to be performed over all possible solutions obtained post-sampling. This research proposes to solve the solution-search problem in a constraint-satisfaction fashion. This approach targets various sections of the feasible solution space to obtain a good-enough solution in terms of exploration metrics such as volumetric gain and separation from teammate position histories instead of optimizing for a single objective function parametrized by penalty gains. This improves the computational efficiency of the planner while also making the performance less dependent on the gains tuning. In our simulation comparisons, with a recent sampling-based planner, we showed that our planner resulted in a significant drop in the number of expensive volumetric gain calculations that are needed to be performed to carry out an exploration mission. Moreover, the planner resulted in being scalable for various environment scales, which is evident by its success in the DARPA Subterranean Challenge.

1.3.3. Multi-Agent Coordination

A common approach to multi-robot coordination in field-robotics applications is to share maps among the teammate robots and use the merged map for planning on any individual robot [15,39,40,41]. This approach, though having a great potential of maximizing global coverage, comes with some pre-requisites. In practice, it is extremely challenging to find an exact transform between origins of multiple robots. Several optimization techniques have been proposed to carry out multi-robot SLAM [42,43] to obtain a coherent environment map from the information coming from different robots. A multi-robot, multi-sensor SLAM solution called Large-scale Autonomous Mapping and Positioning (LAMP) [44] is used for mapping and localization in perceptually degraded environments. A multi-modal solution [45] is used to perform SLAM onboard the robots by one of the SubT challenge teams. These methods come with their own burden on the system integration. Moreover, going from the map sharing technique to coordination often times not only implies sharing the frontiers between different agents but also the occupancy/traversability information. Therefore, unless the maps are very closely aligned, the reachability information becomes fairly corrupted over a long distance. In a heterogeneous robotic system, robots may rely on different types of maps, for instance, a quadrotor UAV generating a distance-field map while a ground robot relies on an elevation map. Transferring and merging robot-specific data types does not result in a scalable and portable system design overall and makes coordination challenging in practice. Another concern related to the graph-based bifurcation approach is that unlike a frontier-based method that directly reacts to any changes in the map, a parallel representation of the environment is built in the form of a graph, where each graph edge represents a traversable path segment. Consequently, any modification and augmentation in the map has to be reflected in the graph for the planner to make informed decisions. In case of dynamic obstacles, it implies modifying edges and nodes in the graph based on the map changes, whereas in case of multi-robot coordination, any new pieces of maps from other robots merged into the planning robot’s map have to be explicitly sampled and included in the graph. Recently, a solution is proposed that creates subgraphs from submaps of the individual robots and merges them to form a global graph [46]. Our work emphasizes the use of individual maps for path planning while biasing the solution search based on the position histories from other robots. This method provides a simpler solution to achieve inter-robot coordination while keeping the traversability decoupled from coordination in order to make the planner robust to map mis-alignments. Also, the position-history data structure is very commonly generated on each kind of robot by widely known SLAM systems. This allows different kinds of robots to have their own planning maps while communicating and coordinating using the common data structure. The idea of using position histories for multi-agent coordination is further developed to include environment semantics for the semantic navigation work proposed by this article in Section 3.

1.3.4. Semantic Navigation

Traditional dense sampling-based approaches have been successfully demonstrated by many to solve motion-planning tasks. However, the recent literature shows that a motion-planning problem, especially in a large-scale environment, can be represented as a higher-level problem. An example of this is [47], where authors use this concept to prevent wastage of state space samples by combining denser lower-level search with a semantic-level decision tree for longer-term maneuver planning. Ref. [48] is another example, where authors used higher-level cues in the form of terrain semantics to guide sampling and graph-based search strategies. Moreover, ref. [49] demonstrates a machine learning-based navigation strategy that leverages semantic information in environment modeling of feature space. Another type of literature on this topic uses semantic cues to improve localization accuracy, such as [50], which uses visual semantics with light-weight high-definition maps for position refinement. The later half of our article builds on the DARPA SubT sampling-based planner to propose a semantic navigation solution so that the higher-level environment cues can be used to minimize the need for high-resolution large-scale geometric maps for multi-robot planning.

1.4. Contributions

This article brings two key contributions to the area of robotic exploration of large-scale unstructured environments.

(1) A sampling-based path planner is proposed and developed to carry out autonomous robotic exploration of complex subterranean environments. The planner uses a bifurcation approach to sample the environment. This approach implies sampling the local neighborhood of a robot using Rapidly Exploring Random Trees (RRTs*) and then building a sparse roadmap graph using these samples for global awareness. (a) This article proposes a sample-and-project solution to terrain assessment that works directly on occupancy grid maps without a need of building an explicit elevation map of an environment. This function serves as the collision function for the path planner. (b) Secondly, a constraint satisfaction strategy is proposed to find an appropriate exploration solution. Multiple objective functions and search strategies are arranged hierarchically so that more preferable solution subsets are searched before the rest. This helps bring down the computational complexity of the planner, especially during replan ticks where exhaustive search is not required to find an appropriate solution. Moreover, the dependency on the gain tuning is relieved compared with the optimization strategy, where a linear combination of costs is optimized over. (c) Further, a multi-robot coordination solution is proposed as part of the solution search that leverages position histories rather than geometric maps to carry out the coordination. The position histories or routes taken by various robots on a team form a light-weight data structure while providing necessary information for the other robots to reason over, therefore reducing the communication bandwidth required to carry out the coordination. Moreover, the proposed coordination strategy brings the idea of having a robot move away from the position histories of other robots in order to carry out efficient exploration. Since the SLAM maps are not merged in the process, the proposed solution is less prone to inter-robot map misalignments. Contribution 2 of this article extends on this notion of carrying out multi-agent coordination. (d) Lastly, the path-planning solution is thoroughly field tested in environments ranging from school buildings and urban environments to man-made tunnels, cave networks, and abandoned subway stations. The planner provided the primary autonomy infrastructure to the DARPA Subterranean Challenge’s third-place finisher, team MARBLE.

(2) The sampling-based planner is extended to introduce a novel Partially Observable Markov Decision Process (POMDP)-based multi-agent coordination solution. In addition to challenges associated with bandwidth overload and inter-robot map mis-alignment, a shared SLAM map is fairly counter-intuitive to supervising humans. In practice, during high-tempo mission scenarios, it is also not convenient for a supervising human to quickly set a goal point for a robot on a SLAM map such as an occupancy grid or a pointcloud. Setting these goal points is often times mission critical and serves as one of the important features to leverage human cognition in the loop. While building and sharing semantic maps has been proposed in the literature as a way to overcome these challenges, the robotic algorithms have evolved over time to be more suited to using SLAM maps rather than compressed semantic maps to carry out the lower-level decision-making such as planning feasible paths. To this end, this article proposes a solution that not only relies on building and sharing semantic maps across various agents but also, unlike the existing literature, provides a way to leverage that semantic map information on a robot to guide its exploration towards semantics of interest while still having the robot plan on its own geometric SLAM map. Hence, the solution is respectful of communication and cognition constraints of both humans and robots in a heterogeneous multi-agent setup.

Contribution 1 of this article is published in part as a conference paper [51]. This article provides an elaborated literature review and description as well as builds on that contribution to further propose the semantic reasoning strategy for multi-agent exploration.

1.5. Outline

The rest of this article is organized as follows. Section 2 presents the sampling-based exploration and coordination planner that has been powering the autonomy stack for team MARBLE in the DARPA Subterranean Challenge, this is mentioned as Contribution 1 in Section 1.4. Further, Section 3 builds on the sampling-based planner and proposes a semantic reasoning solution for improved coordination amongst a supervised team of robots. Section 4 concludes the discussion and suggests some of the potential future directions.

2. Sampling-Based Planner for Autonomous Subterranean Exploration

Robotic exploration of subterranean environments is a classic example of a high-tempo field operation. Such operations require solutions that can operate beyond controlled lab environments, a few requirements for which include robustness, scalability, portability, and computational feasibility. This section presents ScanPlan, the path-planning and coordination solution that powered the autonomy stack of team MARBLE’s entry in the DARPA Subterranean Challenge. All fleet robots, i.e., quadrotor air and wheeled and legged ground robots, used this planner to explore unstructured underground environments in a coordinated way. Special emphasis has been put on the practical feasibility of the solution in outside-lab field environments while designing the solution. Although quadrotor UAVs were not deployed in SubT challenge finals, the planner is designed to cater for UAV needs as well through slight modifications such as using a different collision function. Since collision information for a UAV can conveniently be obtained using Euclidean distance fields (EDFs), the discussion in this article is focused on wheeled and legged ground robots. The SubT planner explained in this section is available at an open-source repository (https://github.com/arpg/scan_plan (accessed on 17 October 2025)).

2.1. Problem Setup and Preliminaries

Before introducing the proposed algorithm, we first outline the notation used throughout this work. The path planner’s objective is to generate a path $p^{\mathrm{goal}}:[0,1]\to {\mathbb{R}}^3$ in three-dimensional Euclidean space, starting from the robot’s current location to enable exploration of an unknown environment. At any point during the mission, the planner relies on several sources of information for decision-making. $p^{\mathrm{hist}}:[0,1]\to {\mathbb{R}}^3$ represents the position history of the robot as a path to its current position from the start. For multi-robot coordination, the position histories of other robots on the team are also considered, with the position history of the ith robot being $p_i^{\mathrm{hist}}:[0,1]\to {\mathbb{R}}^3$. The planner follows a bifurcation strategy, i.e., it samples the local environment neighborhood of a robot using RRTs* to construct a tree and then selects representative samples from this tree to build a graph that serves as a sparse global roadmap. Thus, at any moment, the robot can either move toward one of the tree leaves (local planning) or follow a frontier from the global graph (global planning). The global graph is therefore useful when all paths from the local tree fail to yield sufficient information gain, or when returning to base or reaching a human-defined goal. For a detailed overview of the bifurcation approach, we refer interested readers to [23,52]. For the sake of simplicity, in this work, trees and graphs are distinguished as local and global data structures respectively. All candidate solutions to the exploration problem are denoted by the following two sets. The set ${\mathcal{P}}^L$ represents all shortest local paths that start from the robot and end at the tree leaves and ${\mathcal{P}}^G$ is a set of all shortest global paths starting from the robot and ending at the graph frontiers. We use linear interpolation to extract paths between tree or graph vertices, and all candidate solutions follow the standard definition of a path.

The planner operates on a labeled occupancy grid map $\mathcal{M}:{\mathbb{R}}^3\to \mathcal{L}$, which assigns each 3D query point a label from the set $\mathcal{L}$. For legged robots, the label set is $\mathcal{L}=\{‘\mathrm{occupied}’,‘\mathrm{unknown}’,‘\mathrm{free}’,‘\mathrm{stair}’\}$ while for wheeled robots the set is $\mathcal{L}=\{‘\mathrm{occupied}’,‘\mathrm{unknown}’,‘\mathrm{free}’,‘\mathrm{rough}’\}$. Roughness is defined as the deviation of the surface normal vector from its ideal orientation within a voxel. This quantity is estimated using high-resolution pointcloud data obtained directly from depth sensor measurements [4]. A voxel is classified as ‘rough’ if it is occupied and its surface roughness exceeds a pre-defined threshold. This labeling is only utilized by wheeled robots, which require fine-grained surface information for the traversability assessment. Given a map $\mathcal{M}$, a query robot position $\mathit{q}\in {\mathbb{R}}^3$ and range, field-of-view, and resolution of all the sensors used for mapping, the volumetric gain is calculated using ray-casting followed by calculating the number of unknown voxels that are hit by all rays. Formally, the volumetric gain function is expressed as ${\mathcal{G}}^V\left(\mathit{q}\right):{\mathbb{R}}^3\to \mathbb{R}$. In this study, we assume the use of symmetrical sensors for mapping, making the volumetric gain agnostic to the robot’s orientation. Further, successive points of a query path can be used to estimate the robot’s heading along the path. The sets

$$\begin{array}{cc}\hfill {\mathcal{P}}^{LV}& =\{p:p\in {\mathcal{P}}^L\mathrm{and}{\mathcal{G}}^V\left(p\left(1\right)\right)\ge v_{\mathrm{thresh}}^g\}\mathrm{and}\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill {\mathcal{P}}^{GV}& =\{p:p\in {\mathcal{P}}^G\mathrm{and}{\mathcal{G}}^V\left(p\left(1\right)\right)\ge v_{\mathrm{thresh}}^g\}\hfill \end{array}$$

(2)

represent all local and global paths that lead to the areas of at least the threshold volumetric gain $v_{\mathrm{thresh}}^g\in \mathbb{R}$, respectively. Similarly, the local and global paths that lead to areas of at least a set amount of separation from the teammate position histories are given by the sets

$$\begin{array}{cc}\hfill {\mathcal{P}}^{LS}& =\{p:p\in {\mathcal{P}}^L\mathrm{and}{\mathcal{D}}^S(p\left(1\right),p_1^{\mathrm{hist}},\dots ,p_n^{\mathrm{hist}})\ge s_{\mathrm{thresh}}^d\}\mathrm{and}\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\mathcal{P}}^{GS}& =\{p:p\in {\mathcal{P}}^G\mathrm{and}{\mathcal{D}}^S(p\left(1\right),p_1^{\mathrm{hist}},\dots ,p_n^{\mathrm{hist}})\ge s_{\mathrm{thresh}}^d\}\hfill \end{array}$$

(4)

respectively. The function ${\mathcal{D}}^S$ is defined as

$$\begin{array}{c}\hfill {\mathcal{D}}^S(p\left(1\right),p_1^{\mathrm{hist}},\dots ,p_n^{\mathrm{hist}})=\underset{i\in \{1,2,\dots ,n\}}{\min }\underset{t\in [0,1]}{\min }\parallel p_i^{\mathrm{hist}}\left(t\right)-p\left(1\right)\parallel ,\end{array}$$

which is the shortest distance between the end point of a candidate path and the closest position history path from teammate robots. In our practical setup, we set $s_{\mathrm{thresh}}^d$ to be equal to 2 times the range of the mapping sensors. In this configuration, paths that belong to either ${\mathcal{P}}^{LS}$ or ${\mathcal{P}}^{GS}$ are guaranteed to lead the robot toward areas that are not mapped by any of the teammate robots. The planner aims to solve the constraint-satisfaction problem so that the solution lies in one of the following sets in the order of preference, ${\mathcal{P}}^{LV}\cap {\mathcal{P}}^{LS}$, ${\mathcal{P}}^{GV}\cap {\mathcal{P}}^{GS}$, ${\mathcal{P}}^{LV}$, or ${\mathcal{P}}^{GV}$. This architecture separates our work from the existing literature on exploration path planners, which primarily focuses on the optimization of objectives and constraints parametrized by some penalty gains. The ScanPlan architecture returns the solution once a good-enough path is available that is acceptable for exploration, reducing latency and computational load, which can worsen with existing planners as the scale of the exploration environment grows. The following subsections detail the three main pieces of the ScanPlan design as some of the contributions brought by the proposed exploration solution.

2.2. Terrain Assessment

An efficient generative model is required to classify environment samples as collision-free or otherwise. For unmanned aerial vehicles (UAVs), collision evaluation is naturally performed using Euclidean distance fields, whereas for ground vehicles, a sample is considered collision-free when the terrain beneath the pose is deemed traversable.

The proposed terrain-assessment framework leverages the fact that traversability checks are only necessary along the footprints of sampled nodes and the straight-line path segments connecting them. To evaluate a linear path segment between two vertices, each interpolated pose along the segment is sequentially tested for collision until all poses are verified as collision-free, or until an under-collision pose is encountered. Each pose corresponds to a rectangular footprint parameterized by the robot’s width and length, oriented along the direction of the path segment. The heading associated with the pose is obtained such that the rectangular geometry is aligned with the straight-line query path segment.

Given a query pose, this rectangular footprint is projected downward along the negative z-axis for a fixed projection distance $\Delta h^{\mathrm{proj}}\in \mathbb{R}$. Three successive checks are then performed:

• Projection Consistency: If a portion of the footprint fails to intersect any occupied voxel within the projection distance $\Delta h^{\mathrm{proj}}$, the number of successful projections is recorded. When the percentage of successful projections falls below a prescribed threshold, the terrain beneath the pose is classified as non-traversable.
• Stair Detection: If the above projection test succeeds and some of the intersected voxels are labeled as ‘stair’, the pose is directly marked and returned as collision-free.
• Elevation Consistency: For all ground voxels within the footprint, the maximum elevation difference is computed. If the maximum elevation difference exceeds a threshold $\Delta h^{\mathrm{elev}}\in \mathbb{R}$, the pose is marked as under-collision.

For the legged platform (Boston Dynamics Spot), an OctoMap resolution of 0.15 m proved effective in the DARPA SubT challenge to capture obstacles that were potentially non-traversable. This resolution enabled the generation of occupancy grid maps spanning over an hour-long mission, thereby providing computationally lightweight yet global terrain awareness. During field demonstrations, stair voxels were identified using an open-source labeling package [53]. For wheeled platforms (Clearpath Husky), higher-resolution pointclouds were used to assign a surface-roughness value to each voxel in the OctoMap. Traversability checks were then performed at the same map resolution, combining both elevation checks and mean roughness values of ground voxels to determine collision status.

Figure 4 illustrates the terrain-assessment process for several representative query poses, highlighting collision-free and under-collision cases based on elevation change and surface roughness. Algorithm 1 summarizes the terrain-assessment method in pseudo-code.

Algorithm 1 Terrain assessment for a query pose

1: ${\mathit{x}}^{\mathrm{pos}}\leftarrow \mathrm{input}\mathrm{query}\mathrm{pose}’\mathrm{s}\mathrm{position}\mathrm{in}{\mathbb{R}}^3$  2: $x^{\mathrm{head}}\leftarrow \mathrm{input}\mathrm{query}\mathrm{pose}’\mathrm{s}\mathrm{heading}\mathrm{in}{\mathbb{S}}^1$  3: ${\mathcal{P}}^{\mathrm{rect}}\leftarrow \mathrm{all}{\mathbb{R}}^3\mathrm{points}\mathrm{at}\mathrm{OctoMap}\mathrm{resolution}\mathrm{contained}\mathrm{in}$ $\mathrm{rectangle}\mathrm{that}\mathrm{is}\mathrm{centered}\mathrm{at}{\mathit{x}}^{\mathrm{pos}}\mathrm{and}\mathrm{aligned}\mathrm{with}$ $x^{\mathrm{head}}\mathrm{parallel}\mathrm{to}\mathrm{the}\mathrm{x}\text{-}\mathrm{y}\mathrm{plane}\mathrm{of}\mathrm{the}\mathrm{world}\mathrm{frame}$  4: $h_{\min }^{\mathrm{elev}}\leftarrow +\inf$, $h_{\max }^{\mathrm{elev}}\leftarrow -\inf$, $h^{\mathrm{proj}}\leftarrow {\mathit{x}}_z^{\mathrm{pos}}-\Delta h^{\mathrm{proj}}$  5: $n^{\mathrm{succ\_projs}}\leftarrow 0$, $n^{\mathrm{stair\_voxels}}\leftarrow 0$, $l^{\mathrm{vox}}\leftarrow \mathrm{voxel}\mathrm{length}$  6: for ${\mathit{p}}^{\mathrm{rect}}\in {\mathcal{P}}^{\mathrm{rect}}$ do  7:    while ${\mathit{p}}_z^{\mathrm{rect}}>h^{\mathrm{proj}}$ do  8:      ${\mathit{p}}_z^{\mathrm{rect}}={\mathit{p}}_z^{\mathrm{rect}}-l^{\mathrm{vox}}$  9:      if $\mathcal{M}\left({\mathit{p}}^{\mathrm{rect}}\right)\ne ‘\mathrm{occupied}’$ then 10:         continue 11:      end if 12:      $n^{\mathrm{succ\_projs}}++$ 13:      if $\mathcal{M}\left({\mathit{p}}^{\mathrm{rect}}\right)==‘\mathrm{stair}’$ then 14:         $n^{\mathrm{stair\_voxels}}++$ 15:      end if 16:      if ${\mathit{p}}_z^{\mathrm{rect}}>h_{\max }^{\mathrm{elev}}$ then 17:         $h_{\max }^{\mathrm{elev}}={\mathit{p}}_z^{\mathrm{rect}}$ 18:      else if ${\mathit{p}}_z^{\mathrm{rect}}<h_{\min }^{\mathrm{elev}}$ then 19:         $h_{\min }^{\mathrm{elev}}={\mathit{p}}_z^{\mathrm{rect}}$ 20:      end if 21:    end while 22: end for 23: if $n^{\mathrm{succ\_projs}}<n_{\mathrm{threshold}}^{\mathrm{succ\_projs}}$ then 24:    return false 25: else if $n^{\mathrm{stair\_voxels}}\ge n_{\mathrm{threshold}}^{\mathrm{stair\_voxels}}$ then 26:    return false 27: else if $h_{\max }^{\mathrm{elev}}-h_{\min }^{\mathrm{elev}}\le \Delta h_{\mathrm{threshold}}^{\mathrm{elev}}$ then 28:    return true 29: else 30:    return false 31: end if

2.3. Solution-Search

The objective of the solution-search module is to identify a feasible path that belongs to one of the preferred sets ${\mathcal{P}}^{LV}\cap {\mathcal{P}}^{LS}$ or ${\mathcal{P}}^{GV}\cap {\mathcal{P}}^{GS}$, in the order of priority. If neither set contains a valid path, the next best alternative path is selected from ${\mathcal{P}}^{LV}$ or ${\mathcal{P}}^{GV}$. To evaluate candidate paths, two cost functions are defined for a given path $p^{\mathrm{cand}}$.

$$\begin{array}{cc}\hfill J^{\alpha }& =c_0{\mathcal{D}}^P(p^{\mathrm{hist}},p^{\mathrm{cand}})-c_1|{\theta }^{\mathrm{explore}}-{\theta }_{\mathrm{mean}}^{\mathrm{cand}}|\hfill \\ \hfill & -c_2|h^{\mathrm{explore}}-h_{\mathrm{mean}}^{\mathrm{cand}}|,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill J^{\beta }& =-c_1|{\theta }^{\mathrm{explore}}-{\theta }_{\mathrm{mean}}^{\mathrm{cand}}|-c_2|h^{\mathrm{explore}}-h_{\mathrm{mean}}^{\mathrm{cand}}|\hfill \\ \hfill & +c_3{\mathcal{G}}^V\left(p^{\mathrm{cand}}\left(1\right)\right)+c_4{\mathcal{D}}^S(p^{\mathrm{cand}}\left(1\right),p_1^{\mathrm{hist}},\dots ,p_1^{\mathrm{hist}}),\hfill \end{array}$$

(6)

where $c_0,\dots ,c_4\in \mathbb{R}$ are the tuning gains, ${\theta }_{\mathrm{mean}}^{\mathrm{cand}}\in \mathbb{S}$ and $h_{\mathrm{mean}}^{\mathrm{cand}}\in \mathbb{R}$ represent the mean heading and height along $p^{\mathrm{cand}}$, respectively, and ${\theta }^{\mathrm{explore}}\in \mathbb{S}$ and $h^{\mathrm{explore}}\in \mathbb{R}$ are the exploration heading and the height, respectively. ${\theta }^{\mathrm{explore}}$ is calculated by taking the mean heading of the recent few points of $p^{\mathrm{hist}}$. The function ${\mathcal{D}}^P$ computes the mean of the minimum distance between two paths relative to the second one as

$$\begin{array}{c}\hfill {\mathcal{D}}^P(p^{\mathrm{hist}},p^{\mathrm{cand}})={\int }_0^1{t}_1·\underset{t_2\in [0,1]}{\min }\left|\right|p^{\mathrm{hist}}\left(t_1\right)-p^{\mathrm{cand}}\left(t_2\right)\left|\right|d{t}_1.\end{array}$$

The first cost function, $J^{\alpha }$, rewards paths that promote deeper exploration into the environment while penalizing deviations in heading and elevation. Because it avoids volumetric-gain computation, $J^{\alpha }$ provides a lightweight heuristic for rapid local decision-making. The second cost function, $J^{\beta }$, offers a more comprehensive evaluation of the search’s objective, incorporating volumetric gain and inter-robot separation to favor paths that both expand unexplored volume and maintain teammate spatial separation of position histories.

Step 1: Local Search The search begins by selecting the local path $p^l\in {\mathcal{P}}^L$ that minimizes $J^{\alpha }$. This path is then checked for sufficient volumetric gain and separation from teammate position histories using (2) and (4). In typical large-scale exploration missions, it is reasonable to make an educated guess that the collision-free path that minimizes $J^{\alpha }$ is the solution to the exploration problem. The exceptions to this assumption are the cases where the robot runs out of local areas with satisfactory amount of volumetric gain, or if the environment section is geometrically too complex, such as a mechanical workshop or a junction where most of the outlets are already explored. While the volumetric gain maximization has been the primary objective of the planners proposed in the literature so far, heading toward a bigger and open area rather than a smaller and tighter passage is seldom fruitful in a typical search-and-rescue operation. Although our proposed planner ends up weighing volumetric gain in some scenarios, it is not the primary concern of the planner. Therefore, the first step ensures that as long as the robot is headed toward a good-enough area, it is better to keep going instead of adopting a greedy strategy in terms of the volumetric gain. Consequently, we save significant computation time during most replan iterations. Only one volumetric gain check is required if a solution is found at this step, saving us from applying that operator on hundreds of candidate paths. This process is mentioned in lines 1–4 of Algorithm 2.

Step 2: Comprehensive Local Search If no solution could be found at the first step, a more thorough search is performed. A conventional approach to optimize for the volumetric gain and exploration heading is to form an objective function from the combination of the multiple objectives parametrized by penalty gains. The scale of an environment under exploration could be massive and can vary significantly during the run, for instance, an open cavern can lead to a very constrained passage. This means that the solution space, or the choice of paths, can vary significantly qualitatively during the mission. This variation makes it challenging to tune the gains that are agnostic to the environment type. Our approach targets the subsets in the space of potential solutions to find a solution so that the preferred potential solutions are checked before the rest. This helps make the solution search less dependent on the tuning gains. To this end, the second step in the solution search involves minimizing the cost function $J^{\beta }$ for all $p^l\in {\mathcal{P}}^L$ while sorting the solutions in sets ${\mathcal{P}}^{LV}\cap {\mathcal{P}}^{LS}$ and ${\mathcal{P}}^{LV}$. If at least one solution belonging to the former set is found, the minimum cost solution from that set is the solution to the exploration problem. Otherwise, the minimum cost solution from the latter set is saved if it is non-empty and global search is performed. This process is highlighted by Algorithm 3 and lines 5–8 of Algorithm 2.

Step 3: Global Search and Final Arbitration To perform the global solution search, all paths $p^g\in {\mathcal{P}}^G$ are first sorted in sets ${\mathcal{P}}^{GV}\cap {\mathcal{P}}^{GS}$ and ${\mathcal{P}}^{GV}$. If the former set is non-empty, then the exploration solution is a path in that set that is either leading to the most recent frontier or the frontier that has the least distance from the robot, depending on which of the two has the least path length. However, if the set ${\mathcal{P}}^{GV}\cap {\mathcal{P}}^{GS}$ is empty then the solution with the maximum ${\mathcal{D}}^S\left(p^g\right)$ from set ${\mathcal{P}}^{GV}$ is kept and compared with the local solution that was saved earlier to output a final solution. In the case when either ${\mathcal{P}}^{LV}$ or ${\mathcal{P}}^{GV}$ is empty, the saved solution from the non-empty set is returned. However, if both sets are empty, the minimum $J^{\alpha }$ local path, that was calculated during the first step, is returned to encourage the robot to keep moving even when no useful solution exists among the sampled paths. The only scenario in which the solution search does not return a path is if no collision-free paths can be sampled around the robot at the time instant when no global frontier has sufficient volumetric gain, i.e., sets ${\mathcal{P}}^L$ and ${\mathcal{P}}^{GV}$ are empty. If the sampling is dense enough, the former is a rare event which in our experience only happened when the robot was trapped with obstacles from all sides or when the localization drift in extremely narrow passages deteriorated the map, causing phantom occupied voxels to appear around the robot. Improving map uncertainties is, however, outside the scope of this work. The global planning algorithm and final steps of the solution search are shown in Algorithm 4 and lines 9–19 of Algorithm 2, respectively. 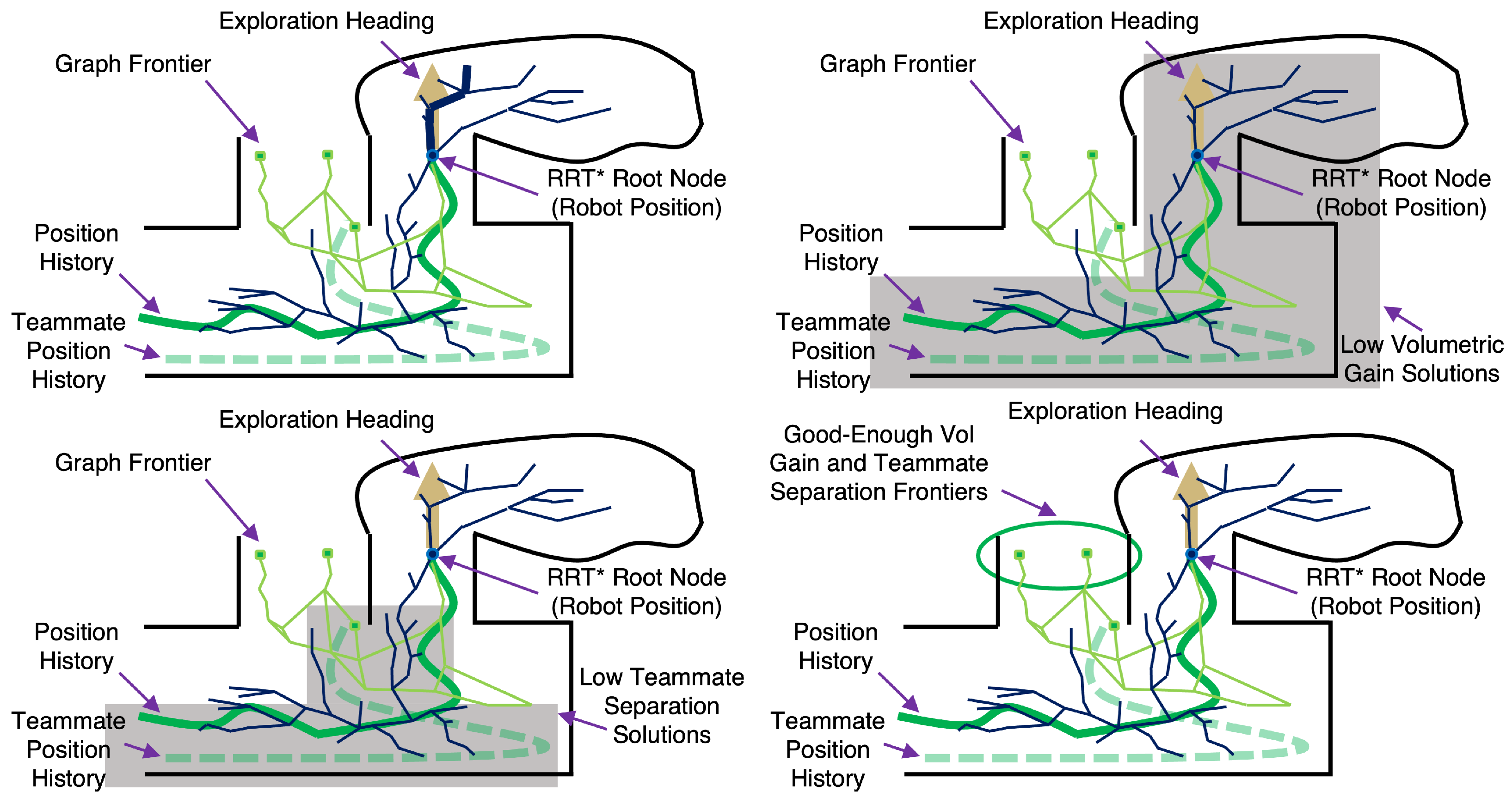Figure 5 and Figure 6 show two example scenarios for the search problem.

Algorithm 2 ScanPlan solution search

1: $p_{\alpha }^l\leftarrow$$p^{\mathrm{cand}}\in {\mathcal{P}}^L$ costing minimum $J^{\alpha }$  2: if ${\mathcal{G}}^V\left(p_{\alpha }^l\right)\ge v_{\mathrm{thresh}}^g$ and ${\mathcal{D}}^S\left(p_{\alpha }^l\right)\ge s_{\mathrm{thresh}}^g$ then  3:    return $p_{\alpha }^l$  4: end if  5: $p_{\beta }^l\leftarrow$PlanLocally()  6: if $p_{\beta }^l$ is non-empty and ${\mathcal{D}}^S\left(p_{\beta }^l\right)\ge s_{\mathrm{thresh}}^g$ then  7:    return $p_{\beta }^l$  8: end if  9: $p^l\leftarrow p_{\beta }^l$ 10: $p^g\leftarrow$PlanGlobally() 11: if $p^g$ is non-empty and ${\mathcal{D}}^S\left(p^g\right)\ge s_{\mathrm{thresh}}^g$ then 12:    return $p^g$ 13: else if $p^l$ is empty and $p^g$ is empty then 14:    return $p_{\alpha }^l$ 15: else if $p^g$ is empty or ($p^l$ is non-empty and ${\mathcal{D}}^S\left(p^l\right)\ge {\mathcal{D}}^S\left(p^g\right)$) then 16:    return $p^l$ 17: else if $p^l$ is empty or ($p^g$ is non-empty and ${\mathcal{D}}^S\left(p^g\right)\ge {\mathcal{D}}^S\left(p^l\right)$) then 18:    return $p^g$ 19: end if

Algorithm 3 PlanLocally(). Returns a path in ${\mathcal{P}}^{LV}\cap {\mathcal{P}}^{LS}$ or ${\mathcal{P}}^{LV}$ in the order of preference

1: $J_{\min }^{\beta }\leftarrow +\inf$  2: $p^{\mathrm{res}}\leftarrow \mathrm{none}$  3: $\mathrm{success}\leftarrow \mathrm{false}$  4: for $p_l\in {\mathcal{P}}^L$ do  5:    if ${\mathcal{G}}^V\left(p^l\right)\ge v_{\mathrm{thresh}}^g$ and ${\mathcal{D}}^S\left(p^l\right)\ge s_{\mathrm{thresh}}^d$ and $\sim \mathrm{success}$ then  6:      $J_{\min }^{\beta }\leftarrow J^{\beta }\left(p^l\right)$, $p^{\mathrm{res}}\leftarrow p^l$, $\mathrm{success}\leftarrow \mathrm{true}$  7:    else if $J^{\beta }\left(p^l\right)\ge J_{\min }^{\beta }$ then  8:      continue  9:    else if (${\mathcal{G}}^V\left(p^l\right)\ge v_{\mathrm{thresh}}^g$ and ${\mathcal{D}}^S\left(p^l\right)\ge s_{\mathrm{thresh}}^d$) or (${\mathcal{G}}^V\left(p^l\right)\ge v_{\mathrm{thresh}}^g$ and $\sim \mathrm{success}$) then 10:      $J_{\min }^{\beta }\leftarrow J^{\beta }\left(p^l\right)$, $p^{\mathrm{res}}\leftarrow p^l$ 11:    end if 12: end for 13: return $p^{\mathrm{res}}$

Algorithm 4 PlanGlobally(). Returns a path in ${\mathcal{P}}^{GV}\cap {\mathcal{P}}^{GS}$ or ${\mathcal{P}}^{GV}$ in the order of preference

1: ${\mathcal{P}}^{GV}\leftarrow \varnothing$, ${\mathcal{P}}^{GVS}\leftarrow \varnothing$  2: for $p^g\in {\mathcal{P}}^G$ do  3:    if ${\mathcal{G}}^V\left(p^g\right)\ge v_{\mathrm{thresh}}^g$ and ${\mathcal{D}}^S\left(p^g\right)\ge s_{\mathrm{thresh}}^d$ then  4:      ${\mathcal{P}}^{GVS}\leftarrow {\mathcal{P}}^{GVS}\cup \left\{p^g\right\}$  5:    else if ${\mathcal{G}}^V\left(p^g\right)\ge v_{\mathrm{thresh}}^g$ then  6:      ${\mathcal{P}}^{GV}\leftarrow {\mathcal{P}}^{GV}\cup \left\{p^g\right\}$  7:    end if  8: end for  9: if ${\mathcal{P}}^{GVS}$ is empty then 10:    return path $p^g\in {\mathcal{P}}^{GV}$ with maximum ${\mathcal{D}}^S\left(p^g\right)$ 11: end if 12: $p_r^g\leftarrow$ path from ${\mathcal{P}}^{GVS}$ leading to most recent frontier 13: $p_c^g\leftarrow$ path from ${\mathcal{P}}^{GVS}$ leading to closest frontier 14: if PathLength($p_r^g$) ≥ PathLength($p_c^g$) then 15:    return $p_c^g$ 16: else 17:    return $p_r^g$ 18: end if

2.4. Dynamic Obstacles

To ensure robust operation in real-world environments, the planner must account for dynamic obstacles and map changes that occur during execution. In the proposed approach, this adaptability is achieved by continuously validating the consistency between the global graph representation and the underlying occupancy map (OctoMap). Previous sampling-based planners for subterranean exploration typically assume a static environment, where graph edges are considered permanently traversable once created. In contrast, our method explicitly tracks graph edge traversability to reflect any potential environmental changes. Each edge in the graph is labeled as either occupied or unoccupied. Initially, all newly generated edges are marked unoccupied. While the robot executes a planned path, the planner continuously monitors the planned path for potential collisions using the latest occupancy information. If a collision is detected, indicating that the environment has changed since the edge was last validated, the algorithm triggers a replan. In case a collision is encountered, all edges in the neighborhood of the robot are checked for collisions and are marked accordingly and a replan is triggered. All of the occupied edges in the graph are constantly checked and re-validated at every replan, since they are typically not large in number. However, in order to reduce the computational burden, the validation of all neighborhood edges, regardless of their occupancy, is performed only if a planned path is under collision. Every time the graph is used to plan a path, the occupied edges are ignored during the graph search.

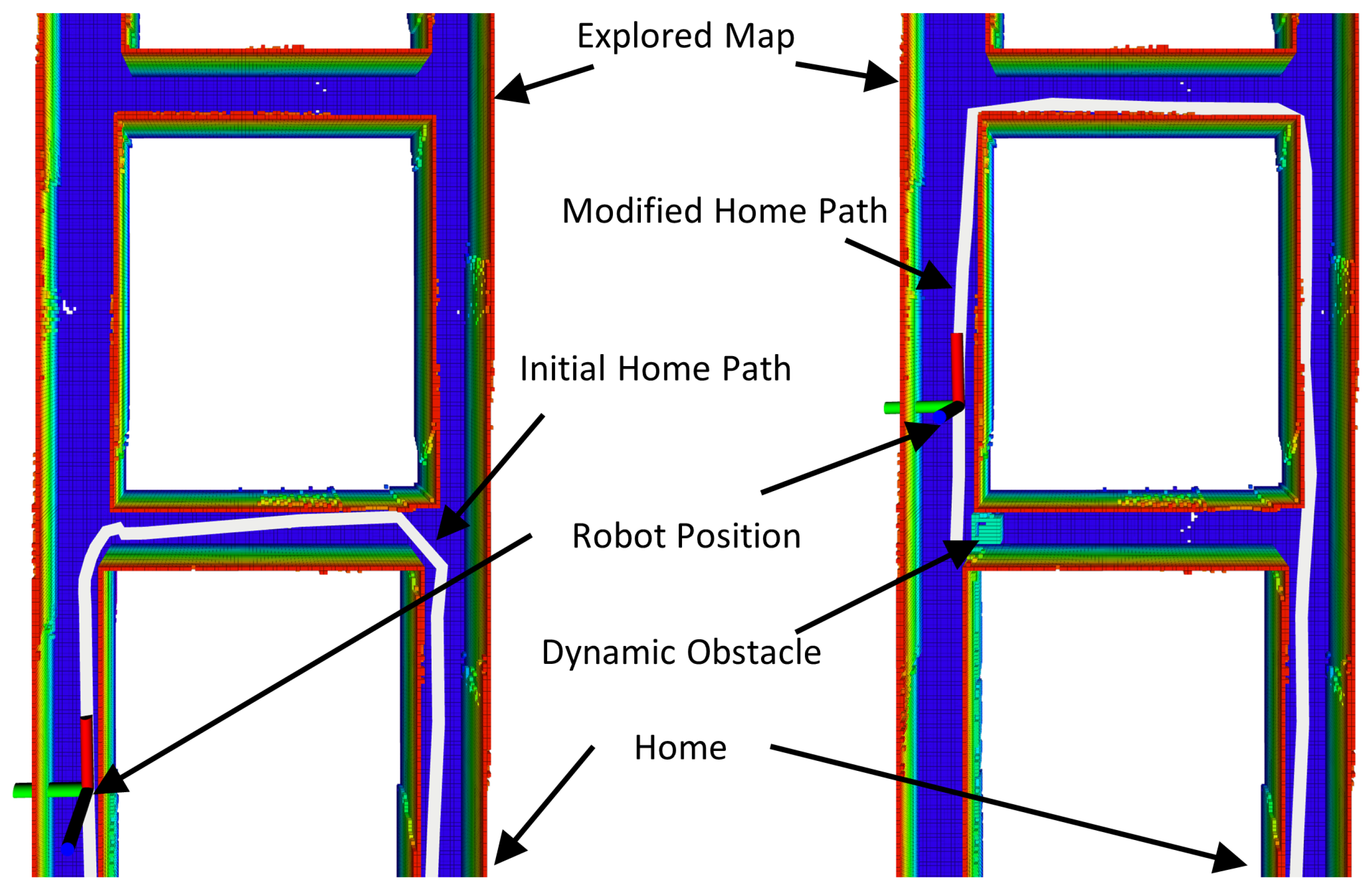
Figure 7 illustrates this process: the initially planned path to home becomes blocked after it is planned, prompting the robot to detect the change, update the corresponding graph edges, and successfully compute an alternate collision-free path.

2.5. Results

The performance of the proposed planner is evaluated in simulations followed by field deployments at the DARPA SubT challenge final event. The following two subsections discuss these results.

2.5.1. Performance Comparison

We run our simulation comparison against team CERBERUS’s GBPlanner [23]. This planner most closely resembles ours from the DARPA SubT teams in that it uses the local and global planning bifurcation approach. The planner uses an RRT-based local planner that intensively runs volumetric gain calculations on the tree to find an optimal solution. Coupled with frequent global re-plannings, the planner leaves a performance dip that ScanPlan is able to improve on.

The performance of the planner is evaluated in an environment which is composed of a constrained set of corridors and multi-way intersections. This environment is shown as the right section of a simulated room-and-pillar mine in Section 5 of [23]. The robot used for the comparison trials is Super Mega Bot [54] equipped with a horizontal 16-channel Velodyne LiDAR sensor for mapping. The overview of this simulation setup is shown in Figure 8. In a typical exploration planner, volumetric gain calculations dominate other planner computations in terms of the computational time. Despite the actual mapping sensor resolution being dense, the previously proposed graph-based planners have to be used with significantly scaled-down resolution parameters for the sensor model. This is because of the high number of volumetric gain calculations that are required to reach a solution for such planners. In many scenarios, assuming a coarse sensor model will not result in an accurate estimate of the volumetric gain; for instance, a sensor model with low horizontal resolution may not be able to report any volumetric gain in narrow passages when the actual mapping sensor is perceiving a useful amount of unexplored volume. Moreover, as shown in our previous work [10], a robot, especially a UAV, may need to be equipped with multiple mapping sensors for better vertical awareness of the volumetric gain in addition to horizontal, adding to the volumetric gain calculation burden. Our planning solution aims at finding a good-enough solution while not necessarily optimizing over the whole set of potential solutions in every iteration. If a solution is found at the first step of the solution-search process, only one volumetric gain check is required. The effect of such a strategy is depicted in Figure 9. Five simulation trials were performed for each of the three different planner configurations: ScanPlan with a high-resolution sensor model, GBplanner with a high-resolution sensor model, and GBPlanner with a low-resolution sensor model. The sensor field of view is set to 360° horizontal × 30° vertical. Furthermore, the low-resolution and high-resolution sensor models imply that the sensor resolution parameters are set to 5° and 1°, respectively. In comparison to ScanPlan, the GBPlanner can be seen to be struggling to keep up with the exploration performance when the sensor resolution increases because of the large number of volumetric gain computations that it needs to perform at every iteration. The simulations are run on an Intel i7DNBE computer, and the path follower is a PD controller with maximum forward speed and yaw rate set to 0.75 m/s and 1.0 rad/s, respectively.

In addition to the above comparison, a dynamic obstacle avoidance test is performed separately by confining the robot to a small section of the same environment. The robot is first set to explore and then commanded to plan home. On its way back home, we blocked a passage that was initially open, and the robot can be seen to plan an alternate path once the dynamic obstacle appears in the map. Figure 7 depicts this experiment.

2.5.2. Field Demonstrations

The planner is demonstrated to competitively perform at the DARPA SubT challenge final event, earning team MARBLE third place in the international challenge. The SubT challenge aimed at developing technologies to rapidly map, navigate, and search underground environments. These environments are expected to span kilometers, with a versatile nature of challenges such as constrained passages, vertical shafts, complex layouts, multiple levels, dust and fog to hamper vision, puddles, rubble, dripping water, and concrete to block communications, just to name a few. In rescue operations concerning these types of environments, it is vital for the robots to be self-sufficient with their autonomy because communications with a human operator may not be possible at all or could cost their attention or valuable time. The challenge was divided into three sub-domains, tunnel systems, urban underground, and cave networks, which have been the respective focus of the three preliminary circuit events conducted by DARPA. The final event held inside the Louisville Mega Cavern at Kentucky in September 2021 included all three types of the underground environments. The environment was divided into so-called sectors to highlight the depth of the environment explored. Team MARBLE participated in the challenge with two legged robots, D01 and D02, and two wheeled robots, H01 and H02, built on Boston Dynamics Spot and Clearpath Husky platforms, respectively. A 64-channel Ouster OS1 LiDAR was used as the primary mapping sensor on each robot. The total mission time allocated to each team was an hour. The subterranean environment meticulously built by the challenge officials would split into urban, tunnel, and cave environments, which were interconnected deeper into the course. Runs for D02 and H01 ended at the 1 h time-out mark as commanded by the DARPA officials, while D01 ended up having a slip-and-fall and H02’s computer went out due to excessive vibrations during the run. Figure 10 shows final OctoMaps generated individually by all four robots. The first robot that was sent into the course by team MARBLE was D02, followed by D01, H02, and H01. While D02 contributed the most to the overall exploration by exploring most of the cave and urban sections, D01 complemented it by exploring the tunnel section of the environment. The wheeled robots, H01 and H02, were constrained by the terrain they could traverse for a large part of the exploration mission. Therefore, the role of H01 and H02 was limited to carrying and dropping communication hardware. They can be seen to redundantly explore areas with relatively flat terrain such as the initial parts of the urban and tunnel sections. Figure 11 shows the volumetric gain explored by each of the robots while also showing the times when a robot was going home and when the planner was intervened on a robot by a higher-level mission management command. These planner interventions were primarily commanded to stop a robot and let another robot pass in case of a potential inter-robot collision, or to teleoperate a robot. The former was triggered autonomously when two robots would come close to each other. While teleoperation was deemed necessary in some cases, often limited by the available communication strength, a robot was never teleoperated due to a planner failure or to improve the volumetric gain but to complement autonomy with human-level cognition and intelligence. We only had teammate separation as soft constraints in our planner. While legged robots had their own local collision avoidance as well, the higher-level human–robot interaction component would automatically preemptively command robots to stop when they were in proximity in the order of priority. Interested readers are referred to [55] for details on the component. Figure 11c shows one instance where D01 teleoperation was initiated during the mission. The robot could be seen to have a path that was not only leading it toward an area of sufficient volumetric gain on its own map but was also guiding the robot to a new area that none of the other robots had visited. However, human-led mission strategies evolve rapidly during such rescue missions depending on when and what piece of information is available to them. Since it seemed to be of a higher value to explore tunnel systems first by that robot, the human supervisor manually drove the robot through the very beginning of the tunnel environment to move it past one of the teammate position histories. From there onward, the planner took over and continued exploration. Figure 11 highlights the activity in blue on D01’s explored volume plot, close to 20 and 30 min marks. Nevertheless, such instances show the robustness of the planner to such human collaboration. Furthermore, Figure 11a shows an instance of the planner dealing with a negative obstacle, i.e., a subway platform. Figure 11b shows an instance of the robot planning away from the teammate position histories, implying multi-robot coordination.

Table 1. Summary of ScanPlan parameters used at the DARPA SubT challenge finals.

Parameter	Description	Value
$v_{\mathrm{thresh}}^g$	Volumetric gain threshold	100 m3
$s_{\mathrm{thresh}}^d$	Preferred teammate separation	5 m
$\Delta h^{\mathrm{proj}}$	Ground plane search distance	2.5 m
$c_0$	Tuning gain (position history distance)	0.1
$c_1$	Tuning gain (exploration heading)	10
$c_2$	Tuning gain (exploration height)	0
$c_3$	Tuning gain (volumetric gain)	2 × ${10}^{-4}$
$c_4$	Tuning gain (teammate separation)	500

shows a list of ScanPlan parameters used for the field demonstrations at the SubT challenge finals. Additionally, to calculate volumetric gain, a sensor model with a field of view of 360° (horizontal) and 33° (vertical) and range of 5 m is used. The local planning is performed in a 20 m × 20 m rectangular area around the robot’s position. For terrain-assessment projections, we used 0.3 m (width) × 0.6 m (height) for Spot-based robots and 0.55 m (width) × 0.85 m (height) for Husky-based robots.

Videos of all four robots simultaneously exploring the complex subterranean environment at the SubT challenge final event are posted online (https://youtu.be/oDMKiYRQPow (accessed on 17 October 2025), https://youtu.be/OkmVQVSHaGI (accessed on 17 October 2025)).

3. Semantic Navigation for Complex Environments

Dense perception information such as pointclouds or occupancy grid maps are well suited to plan feasible paths for individual robots. However, many practical high-tempo robotic missions, for instance a subterranean exploration, require the use of compressed and lightweight perception information to be transmitted among different agents due to communication bandwidth limitations and human cognition and workload constraints. This section proposes a solution to generate a probabilistic semantic map on a robot and to leverage ScanPlan, presented in the previous section, to make use of such a semantic map to bias a robot’s exploration towards a desired goal region under uncertainty.

For large-scale complex environments, such as subterranean environments, communication and coordination among a heterogeneous set of robots and human operators are critical to the success of the exploration operations. Merging maps across robotic agents and using the combined map for planning on all individual robots is a common way to achieve multi-robot coordination. However, broadcasting large amounts of data resulting from occupancy grid, pointcloud or distance field maps is oftentimes not a feasible option given communication bandwidth constraints faced by robotic teams in large-scale environments. Moreover, when sent to humans, the above-mentioned environment representations are not convenient to infer situational awareness from, since they do not naturally lend themselves to higher-level abstraction. Another common challenge faced by the supervising human is to set a desired waypoint for the path planner on an unintuitive occupancy grid or pointcloud map, especially because the waypoint is typically commanded as a point in the 3D space. Efforts have been made to rectify these issues by representing a given environment in the form of a 3D scene graph [56,57,58,59]. The literature concerns capturing semantic aspects of an environment at multiple levels of abstraction. While such a high-level abstraction is useful for conceptual understanding of an environment, especially for a human in the loop, the robot path-planning solutions are most effective when used with metric information and dense geometric primitives such as points, lines, planes, and voxels in a global coordinate frame. Typically, a metric map contains all the geometric features necessary for safe navigation of a robot in its surroundings, and a semantic map comprises high-level features that model human concepts about places, objects, shapes, and their relationships [60], for instance, “a chair is in a room”. A large amount of semantic mapping literature uses metric maps to add semantic information on top of them [59,61,62,63]. In our mapping method, the metric information consists of (1) the position history of a robot that is obtained from the pose graph of an off-the-shelf onboard localization system LIO-SAM [64] and (2) the shortest path lengths between semantic regions obtained from the sampling-based graph planner presented in Section 2. The position history is labeled with semantic labels, resulting in a light-weight semantic map.

In the current state of robotic planning and the perception literature, it is unclear how robots can carry out their decision-making effectively while simultaneously interacting with humans and other robots in a way that respects their cognition and other communication and operational constraints. Therefore, the primary contribution of our work lies in integrating high-level concepts of the environments, such as objects and places, in the navigation stack. This work lies in the paradigm of semantic navigation [65].

This section is an effort to bridge the gap between human understanding and robot decision-making. More deliberately, the proposed work enables a robot to use a lower-level environment representation to satisfy mainstream planning and exploration objectives and to guide its exploration using semantic cues from a higher-level semantic map in case it needs to interact with a human operator or other robots, for instance, if going to a goal region is desired. The idea is for the robots to use their individual occupancy-grid maps that are generated onboard for planning while interacting with human operators and other robots only through light-weight common-sense semantic maps. To this end, we build on ScanPlan architecture to generate a so-called semantic map in real time onboard a robot carrying out an autonomous exploration mission. Three semantic labels are used, namely junction, room, and corridor, where one of the contributions of this work lies in the idea of generating probabilistic semantic maps. According to the world model categorization presented in [66], the structure of this map is closest to a topological map with semantic labels attached to the map. The framework proposed in this section can conveniently be extended to a wide variety of labels such as landmarks. A large amount of literature in common-sense 3D scene reconstruction [63,66] uses a finite set of discrete semantic labels to represent an environment. This assumption, however, breaks for many exploration missions, especially when the environment is unknown beforehand. Certain parts of a junction in a subterranean environment could look like a room to the classifier. Similarly, an office environment could have objects such as coffee maker, microwave, etc., that are common to a kitchen space. Since classifiers are commonly trained on the available data from known environments, a better intuition about an unknown environment can be obtained if each region in a semantic map is represented by a probability distribution of known labels instead of categorically labeling the regions. Some efforts have been made in the past to combine landmark-based maps with other sources of information to improve topological uncertainties [67]. We label regions in a semantic map as a probability distribution of the semantic labels. Additionally, we propose a POMDP-based technique to bias exploration of a robot towards a goal semantic region. It is oftentimes desired for a robot to plan over another robot’s map, for instance, to go to an unexplored frontier seen by another robot or if a human operator sets a goal point for the planner on another robot’s map. In either case, the relative non-zero transform between origins and maps of multiple robots makes it challenging for the planner to plan a path to the goal region. Since, in our framework, only semantic maps are transferred among robots and human operators, the goal is defined in terms of a semantic region. We propose a particle filter technique to first localize the robot on a semantic map sent by another robot or a human operator. A single-step POMDP is then solved at every replan iteration to bias the exploration of the underlying sampling-based planner to make progress towards the desired goal region.

To streamline the overall structure of this work, we follow the setup that is depicted in Figure 12. In this setup, a robot explores an unknown environment using a sampling-based planner relying on an incrementally built OctoMap [33] for perception. During exploration, the robot also builds a semantic map by labeling its position history with observation probabilities and other useful information such as the shortest path lengths from each map region to another. This semantic map information is sent to a human operator supervising the exploration mission. The human operator then selects a goal semantic region and forwards the map information to another robot, which undertakes the job of biasing its exploration towards the operator-defined goal semantic region. This setup accurately reflects many different operational scenarios for an exploration mission of a large-scale complex environment involving coordination between heterogeneous systems, especially with a human in the loop. For instance, one of the important applications of this setup is to direct a robot to an unexplored area that is previously observed but found inaccessible by another robot due to its geometry or other reachability-related constraints. The literature on the recent DARPA SubT challenge highlights many similar operational challenges thanks to coordination, communication, and human cognition and workload-related constraints that are faced during large-scale exploration missions.

3.1. Problem Setup

The problem is broken down into two sub-problems, as shown in Figure 12, i.e., semantic map generation and decision-making.

The semantic map generation implies breaking down a robot’s position history into equidistant segments and labeling them with the useful probability distributions to represent the state and observation models (Section 3.2). Therefore, a state of the system, which is represented by a position history segment, can be formally written as,

$$\begin{array}{c}\hfill \mathit{s}=\{p^{\mathrm{hist}}\left(t^s\right)\in {\mathbb{R}}^3:0\le t_{\mathrm{start}}^s\le t^s\le t_{\mathrm{end}}^s\le 1\},\end{array}$$

where the distance $\left|\right|p^{\mathrm{hist}}\left(t_{\mathrm{start}}^s\right)$ - $p^{\mathrm{hist}}\left(t_{\mathrm{end}}^s\right)\left|\right|$ is a fixed constant $\Delta d^s$ for all states. A collection of such states is the state space $\mathcal{S}=\{s_1,s_2,\dots ,s_n\}$, where $t_{\mathrm{start}}^{s,i+1}$, the start time index of $s_{i+1}$, is greater than $t_{\mathrm{end}}^{s,i}$, the end time index of $s_i$, and n being the total number of states. Larger $\Delta d^s$ produces a more compressed map at the expense of higher observation uncertainty. A semantic map is a collection of regions where each region is defined by a state $s\in \mathcal{S}$ augmented with the probability distribution of semantic labels (semantic information) and the shortest path lengths to every other state (metric information). The state space of the POMDP problem is therefore given by $\mathcal{S}$.

The second sub-problem, semantic decision-making, takes in an already-generated semantic map and a goal state. A particle filter approach is first used to localize a robot on the semantic map (Section 3.5), and then a POMDP-based controller is applied to guide the sampling-based action generation in the direction of the set goal state (Section 3.7). It is assumed that the robot responsible for carrying out the decision-making does not receive any pre-built map information from other agents except a semantic map; therefore, the underlying behavior of the robot is to explore its local occupancy grid map. Hence, the set of possible actions at any point in time is given by all the local and global paths, with sufficient volumetric gain, generated by the sampling-based planner, i.e., $\mathcal{A}={\mathcal{P}}^{LV}\cup {\mathcal{P}}^{GV}$ from Section 2. Finally, the observation space is defined as a set of environment labels based on the place geometry. In this work, $\mathcal{O}=\{‘\mathrm{corridor}’,‘\mathrm{junction}’,‘\mathrm{room}’\}$. A simplified block diagram for the semantic reasoning solution is shown in Figure 13.

3.2. Mapping and Observation Model

As the robot moves through an environment, horizontal 2D laser scans are used to infer observations at regular distance intervals. These intervals are kept as small as the sensor and inference rate supports in order to collect as many observations as possible, which is eventually helpful in bringing down the observation uncertainty. Spatial intervals are used instead of temporal to avoid redundant observations in case a robot stops for too long. Distance-based clustering is then used to generate a map region, i.e., a map region is created every time the robot travels a fixed distance $\Delta d^s$. Hence, each map region spans a collection of observations that define the observation probability distribution for the POMDP problem. For a map state ${\mathit{s}}_t\in \mathcal{S}$ with $n_o^s$ total number of observations and a kth observation given by ${\mathit{o}}^k\in \mathcal{O}$, the observation distribution is calculated as

$$\begin{array}{c}\hfill P\left({\mathit{o}}_t\right|{\mathit{s}}_t)\propto \sum _{k=0}^{n_o^s}({\mathit{o}}^k=={\mathit{o}}_t),\end{array}$$

(7)

where ${\mathit{o}}_t\in \mathcal{O}$.

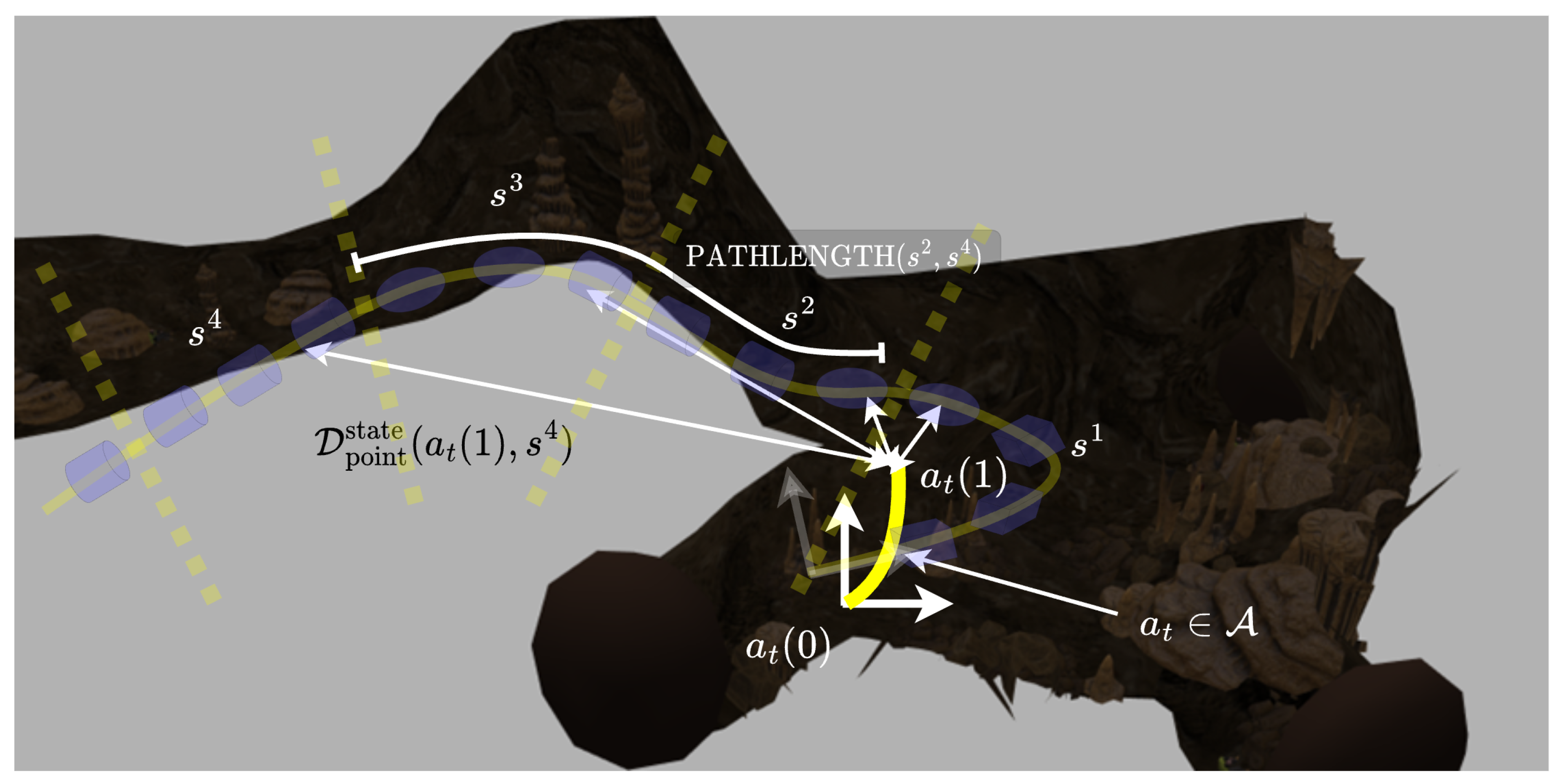
Another important table of quantities that is generated during the semantic map generation process is PathLength$({\mathit{s}}_t,{\mathit{s}}_{t+1}):\mathcal{S}\times \mathcal{S}\to {\mathbb{R}}^3$, which represents the shortest path length between any given pair of states ${\mathit{s}}_t$ and ${\mathit{s}}_{t+1}$. The global graph generated by the sampling-based planner is used to calculate the shortest paths, and the origin of each map state is considered to be its representative point to determine the shortest path from and to that particular state. This information is updated frequently to capture any new potentially shorter paths found as the planning graph builds up. This table of shortest path lengths factors later in determining the state transition likelihood during the decision-making part of the problem. Figure 14 shows the position history segmentation and observation distribution generation.

3.3. State Transition Model

Transition to a next state is determined by two characteristics of an action path: path length and end point. The action path length determines how far the robot is more likely to have traveled (in terms of path length), and the end point determines the final position of the robot should the action path be followed. Accounting for uncertainties potentially induced by the error between robot’s own frame and the frame in which the received semantic map is originally generated, the state transition probability can be written as,

$$\begin{array}{c}\hfill P\left({\mathit{s}}_{t+1}\right|{\mathit{s}}_t,{\mathit{a}}_t)=P_1\left({\mathit{s}}_{t+1}\right|{\mathit{s}}_t,{\mathit{a}}_t)P_2\left({\mathit{s}}_{t+1}\right|{\mathit{a}}_t),\end{array}$$

where $P_1\left({\mathit{s}}_{t+1}\right|{\mathit{s}}_t,{\mathit{a}}_t)\propto \mathcal{N}(0,{\sigma }_1^s)$ is a normal distribution of PathLength$({\mathit{s}}_t,{\mathit{s}}_{t+1})$ − PathLength$\left({\mathit{a}}_t\right)$ and $P_2\left({\mathit{s}}_{t+1}\right|{\mathit{a}}_t)\propto \mathcal{N}(0,{\sigma }_2^s)$ is a normal distribution of ${\mathcal{D}}_{\mathrm{point}}^{\mathrm{path}}({\mathit{a}}_t\left(1\right),{\mathit{s}}_{t+1})$. Here, PathLength is the path length of an input path and ${\mathcal{D}}_{\mathrm{point}}^{\mathrm{path}}$ is the shortest Euclidean distance between a point and a path. The latter is shown in Figure 15.

3.4. Place Classification

The place classification problem refers to inferring an observation $o\in \mathcal{O}$ from an onboard LiDAR’s pointcloud data. Each of our robots that was used for the DARPA Subterranean Challenge has been equipped with a horizontally mounted 3D Ouster LiDAR. This hardware configuration is assumed throughout this article (Section 1). Pointcloud from the LiDAR is first converted to a laser scan signal on which shape analysis is performed to obtain rotation invariant single-valued features [68,69]. Figure 16 shows the block diagram of the place classification process. Let M be a set of all possible laser scans containing range measurements, a feature maps a laser scan $\mu \in M$ to a real value, i.e., $f^{\mu }:\mu \to \mathbb{R}$. Inspired by [69], two sets of features are extracted from a laser scan. The first set of features is calculated using the range measurements, and the second is computed using the polygonal approximation of the laser scan signal given by Cartesian coordinates. The first set of features is as follows: (1) mean difference between the range of consecutive laser beams, (2) standard deviation of the differences between the range of consecutive laser beams, (3) mean difference between the range of consecutive beams considering a maximal possible value, (4) standard deviation of the differences between the length of consecutive range-limited beams, (5) mean beam length, (6) standard deviation of beam lengths, (7) number of gaps in a scan (a gap appears when absolute difference between consecutive beams is higher than a set threshold). The third and fourth subset of features were calculated by limiting ranges to 5, 10, 15,…, 50. The seventh subset of features was calculated by setting the threshold for gap identification as 1, 2, 3,…, 20, 25, 30, 35,…, 50.

Given the polygonal approximation of a laser scan as a set of Cartesian coordinates in ${\mathbb{R}}^2$ of all the beams in the sensor frame, the following properties of the polygon constitute the second set of features: (1) area, (2) perimeter, (3) seven invariants calculated from central moments, (4) normalized feature of compactness, (5) normalized feature of eccentricity, (6) form factor, (7) circularity defined as ${\displaystyle \frac{{\mathrm{perimeter}}^2}{\mathrm{area}}}$. Therefore, the dimension of a full feature vector comes out to be $1+1+10+10+1+1+26+1+1+7+1+1+1+1$ = 63.

OpenCV [70] implementation is used to train a Support Vector Machine (SVM) model with three types of output labels: ‘corridor’, ‘room’, ‘junction’. A polynomial kernel of degree 4 is used with SVM type set to n-class classification. The dataset is collected by tele-operating a robot around in CU Boulder’s Engineering Center building. This building is structurally complex, with an abundance of rooms, corridors, and junctions of varying shapes and sizes. Some of the laser scan examples are shown in Figure 17. The data is entirely hand-labeled. A laser scan is labeled as ‘junction’ when it has corners showing a multi-corridor junction. This category of training data is mostly dominated by 4-way and 2-way intersections inside the building. A laser scan is labeled as ‘corridor’ if it is taken inside a hallway with no clear corners that could represent intersections. The label ‘room’ corresponds to laser scans from inside classrooms and lobbies. These laser scans are the most unstructured because of typical presence of studying desks, chairs and glass panes.

The train-to-test data ratio was set to 85%, with total rooms, corridors, and junctions in the data-set being 1691, 4709, and 2729, respectively. The overall accuracy of the trained model on train and test data came out to be 99.6649% and 97.8817%, respectively. The confusion matrices for both train and test data are shown in

Table 2. Confusion matrix for SVM place classification for train and test data (format train, test test dataset).

Actual\Predicted	Corridor	Room	Junction
corridor	1466, 223	0, 1	0, 1
room	8, 5	3916, 751	18, 11
junction	0, 3	0, 8	2352, 366

. The ROS C++ code for place classification is available on a public Git repository (https://github.com/arpg/place_detector_ros (accessed on 17 October 2025)).

Table 3. Precision, Recall, and F1 scores for each class in the test dataset.

Class	Prediction	Recall	F1
corridor	0.9654	0.9911	0.9781
room	0.9882	0.9791	0.9836
junction	0.9683	0.9708	0.9695
Macro-Averaged	0.9739	0.9804	0.9771

summarizes the Precision, Recall, and F1 scores on the test dataset for the SVM classification model.

3.5. Localization and Belief Update

In order to explore towards a goal state of a semantic map received from other robots, the receiver robot first has to localize itself on the map. This localization is probabilistic, i.e., robot’s position on a semantic map is given by a probability distribution called belief. Belief at time t is written as ${\mathit{b}}_t=P\left({\mathit{s}}_t\right|{\mathit{o}}_{0:t})$, where ${\mathit{o}}_{0:t}$ represents the history of observations up until time t. The belief update is performed every meter of Euclidean distance traveled by the robot, and path traversed by the robot between successive belief updates is treated as action ${\mathit{a}}^{\mathrm{bu}}$, i.e.,

$$\begin{array}{c}\hfill {\mathit{a}}^{\mathrm{bu}}=\{p^{\mathrm{hist}}\left(t^s\right)\in {\mathbb{R}}^3:0\le t_{i-1}^{\mathrm{bu}}\le t^s\le t_i^{\mathrm{bu}}\le 1\},\end{array}$$

where $t_{i-1}^{\mathrm{bu}}$ and $t_i^{\mathrm{bu}}$ are the successive time instants at which belief update is performed. Particle filter is then used to update the belief using place classification observations and state transition and observation models defined above.

The belief is initialized as a uniform distribution, i.e., with an equal number of particles for every state. At belief update, N particles are drawn at random according to the belief distribution ${\mathit{b}}_t$. The path segment ${\mathit{a}}^{\mathrm{bu}}$ traversed by the robot since the last belief update step is recorded. More specifically, the path length of $a^{\mathrm{bu}}$, its end point ${\mathit{a}}^{\mathrm{bu}}\left(1\right)$, and PathLength$({\mathit{s}}^i,{\mathit{s}}^j)$ are used to calculate the state transition probability distribution. Each particle is propagated by drawing a sample from the importance distribution $P({\mathit{s}}_{t+1}\mid {\mathit{s}}_t,{\mathit{a}}^{\mathrm{bu}})$. Each propagated particle is then assigned a weight according to the observation likelihood $P({\mathit{o}}_{t+1}\mid {\mathit{s}}_{t+1})$ using (7). Finally, the particles are drawn at random according to the distribution of weights to output the posterior. It can be noted that the quantities PathLength$({\mathit{s}}^i,{\mathit{s}}^j)$ and $P({\mathit{o}}_{t+1}\mid {\mathit{s}}_{t+1})$ are calculated during semantic map generation on the sender robot.

3.6. Reward Function

Loosely speaking, the goal of this function is to reward the robot to move closer to the goal semantic. The location of the goal semantic region (or goal state), however, is defined relative to the origin of the robot that has generated the map in the first place. The robot performing decision-making over the received semantic map can potentially have a misaligned origin relative to the origin of the sender robot. This origin error makes it challenging to locate the goal state relative to the robot carrying out the decision-making, and this information is essential to evaluate a reward for the robot to drive towards the goal state. 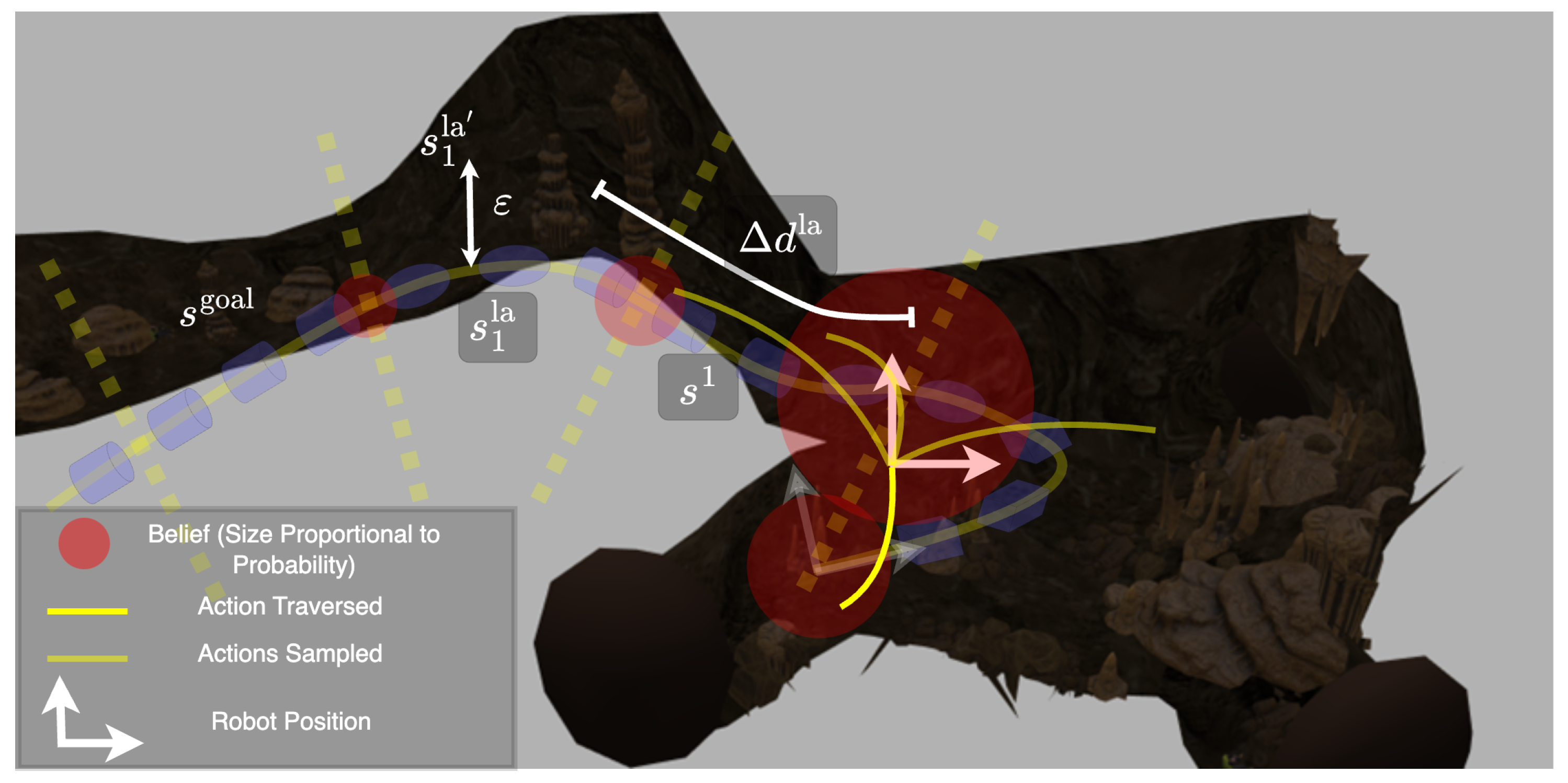The inspiration for this reward is derived from a path-following control method typically used in robotics application [71,72]. This method calculates a look-ahead, or a carrot point, on a planned path, which is a fixed distance away from the robot. The control actions are then generated such that the robot is attracted to the look-ahead point at all times. Following this idea, each state in the semantic map is assigned a look-ahead state. A look-ahead state ${\mathit{s}}_t^{\mathrm{la}}\in \mathcal{S}$ is defined as a state within a look-ahead path length $\Delta d^{\mathrm{la}}\in \mathbb{R}$ of current state ${\mathit{s}}_t$ of the robot that has minimum path length to the goal state. Formally,

$$\begin{array}{c}\hfill {\mathit{s}}_t^{\mathrm{la}}={\mathrm{argmin}}_s\left(\mathrm{P}\mathrm{A}\mathrm{T}\mathrm{H}\mathrm{L}\mathrm{E}\mathrm{N}\mathrm{G}\mathrm{T}\mathrm{H}(\mathit{s},{\mathit{s}}^{\mathrm{goal}})\right)\mathrm{such}\mathrm{that}\mathrm{P}\mathrm{A}\mathrm{T}\mathrm{H}\mathrm{L}\mathrm{E}\mathrm{N}\mathrm{G}\mathrm{T}\mathrm{H}({\mathit{s}}_t,\mathit{s})<\Delta d^{\mathrm{la}},\end{array}$$

where $\Delta d^{\mathrm{la}}>\Delta d^s$ to facilitate the robot’s progress towards the goal state. In order to calculate the reward function, the map states are first corrected for the error between the origins of the receiver robot and the robot carrying out the decision-making. This correction is performed every time the reward function is calculated and the robot performs an action generation step. Each state ${\mathit{s}}_t\in \mathcal{S}$ is transformed into ${\mathit{s}}_t^{\prime }$, where

$$\begin{array}{c}\hfill {\mathit{s}}_t^{\prime }=\{p^{\mathrm{hist}}\left(t^s\right)+{\mathbf{\epsilon }}_t^{\mathrm{map}}\in {\mathbb{R}}^3:0\le t_{\mathrm{start}}^s\le t^s\le t_{\mathrm{end}}^s\le 1\}\end{array}$$

and

$$\begin{array}{c}\hfill {\mathbf{\epsilon }}_t^{\mathrm{map}}={\mathit{x}}_t^{\mathrm{pos}}-\sum _{\mathit{s}\in \mathcal{S}}\left(0.5{\mathit{b}}_t\left(s\right)(\mathit{s}\left(0\right)+\mathit{s}\left(1\right))\right),\end{array}$$

(8)

where $\mathit{s}\left(0\right)$ and $\mathit{s}\left(1\right)$ are the end points of the path representing a state $\mathit{s}\in \mathcal{S}$ and ${\mathit{x}}_t^{\mathrm{pos}}$ is the current position of the robot carrying out the decision-making with respect to its own map. The error represents the translational offset between ${\mathit{x}}_t^{\mathrm{pos}}$ and the robot’s expected position on the semantic map. The average of $\mathit{s}\left(0\right)$ and $\mathit{s}\left(1\right)$ is taken as a means to reduce the output variance of error since the semantic map is discretized and $\mathit{s}$ can span a long path. Figure 18 depicts the look-ahead states and error calculations. The reward function is simply the distance between the end point of an action and the error-corrected look-ahead state.

$$\begin{array}{c}\hfill \mathcal{R}({\mathit{s}}_t,{\mathit{a}}_t)={\mathcal{D}}_{\mathrm{point}}^{\mathrm{path}}({\mathit{a}}_t\left(1\right),{\mathit{s}}_t^{{\mathrm{la}}^{\prime }})\end{array}$$

The error is treated to be translational in this work, as noted in (8). Since the probabilistic robot position on both the occupancy and semantic maps is available, more advanced error correction methods can be applied as future work of this research. In this work, the highly probable look-ahead states are close to the actual robot position, i.e., $\Delta d^{\mathrm{la}}$ is reasonably small; therefore, the translational error formulation provides a good approximation to the actual map error.

3.7. POMDP-Based Control

The control problem is solved using the single-step POMDP solution. At each planner replan tick, new paths are sampled from current robot position. This set of feasible paths can vary significantly from the set sampled at the previous replan tick. A single-step POMDP is solved with the action space set to the most recently sampled actions, i.e., $\mathcal{A}={\mathcal{P}}^{LV}\cup {\mathcal{P}}^{GV}$. The optimal value for belief ${\mathit{b}}_t$ is given by,

$$\begin{array}{c}\hfill U^{*}\left({\mathit{b}}_t\right)=\underset{\mathit{a}\in \mathcal{A}}{\max }\sum _{\mathit{s}\in \mathcal{S}}{\mathit{b}}_t\left(\mathit{s}\right)\mathcal{R}(\mathit{s},\mathit{a}).\end{array}$$

(9)

The solution to the problem is, therefore, the path that results in this optimal value. This path is eventually followed by the robot to bias the robot exploration towards the goal semantic state.

3.8. Results

Semantic reasoning-enabled ScanPlan is programmed on MARBLE Spot and tested in CU Boulder’s Engineering Center (EC) building. The building’s architecture is fairly complex, making it an ideal environment for testing. From a bird’s eye view, corridors, junctions, and rooms make up the building. However, artifacts such as open classroom doors, water fountains, trash bins, and printing stations alongside the corridors and unpredictable locations and shapes of study desks and cafeterias inside rooms add plenty of noise to the place detection. Moreover, these corridors, junctions, and room are not straightforwardly placed relative to each other. Figure 19 shows the relevant section of the EC environment. The robot is first manually teleoperated in the highlighted section of the map shown in Figure 19. This teleoperation is only intended to serve as a replacement to the ScanPlan exploration planner for the purpose of these experiments but is not essential to the closed-loop robotic operation. We used an open-source ROS package pointcloud_to_laserscan [73] to convert a pointcloud from the onboard Ouster LiDAR to a 2D laser scan with angle increment of 1° and minimum and maximum ranges of 0.01 m and 7.5 m, respectively. One semantic map node was constructed every 5 m, where the minimum distance between two semantic cues (interval between two successive inference from laser scans) was ensured to be 1 m. Four semantic maps constructed from this environment are also shown in Figure 20. It can be noted that the semantic maps are probabilistic, i.e., each region in a semantic map is represented by a probability distribution instead of a single deterministic observation. These maps only show the most probable observation at each region. The robot is then reset to act like the receiver robot, i.e., the robot is fully rebooted including all of the sensing, localization, mapping, and planning modules. One of the semantic maps, saved earlier, is then loaded with 5 degrees of yaw origin error added to the map relative to the new robot origin. The red semantic map region shown in Figure 21 is set as the goal, and the robot is set to autonomously explore. Four progress snapshots are shown in Figure 21 along with the belief and locations of the look-ahead states. In reality, the EC environment extends beyond the bounds shown in the above-mentioned figures. This in fact provides a significant amount of opportunities for the robot to go astray while exploring. However, the tests show that the robot was able to explore fairly closely to the semantic map to reach the user-defined goal state successfully. The effectiveness of the proposed decision-making algorithm can be inferred from the fact that the robot was able to bias its exploration towards a user-defined goal in a complex environment without any prior knowledge of the environment other than an abstract semantic map.

4. Conclusions and Future Work

This article brings contributions to the area of autonomous exploration of large-scale unstructured environments. With special emphasis on practicality of the solutions for high-tempo field operations, this article pushes frontiers of the existing literature by proposing solutions that have been the autonomy stack backbone of team MARBLE, third-place finisher of the DARPA Subterranean (SubT) Challenge. Initially, a sampling-based planner is proposed to explore complex subterranean environments. Meanwhile, collision check on aerial vehicles is performed using a readily available Euclidean Signed Distance Fields (ESDF) mapping scheme, and a sample-and-project-based terrain-assessment solution is proposed to be inclusive of ground vehicles. This terrain-assessment solution works directly on an occupancy grid map without the need to create an explicit high-resolution elevation map when not required, for instance, in the case of a legged robot. To solve the solution-search problem, a hierarchical approach is proposed, which targets different subsets of sampled paths to find an appropriate exploration solution in a constraint-satisfaction manner. Exploration objectives and respective search subsets are arranged in a hierarchical fashion in the order of preference based on computational complexity and desirability of the solution. This approach resulted in being minimally sensitive to the tuning gains and better computation times than an existing sampling-based planner also successfully demonstrated at the SubT challenge. This article further emphasized the use of light-weight data structures inclusive of different robot types to carry out multi-robot coordination. To this end, the use of position histories is first proposed and demonstrated at the SubT challenge. This approach adds another constraint to the solution-search problem to prefer solutions that are taking a robot away from the position histories of teammate robots. This solution is demonstrated to be capable of carrying out coordination without the need to merge different types of maps among a heterogeneous robotic team. The method resulted in being less sensitive to inter-robot map misalignments and less needy of communication bandwidth compared with the map-merging solution to coordination. While naively biasing the solution search away from teammate position histories provided a resilient solution with acceptable level of coordination at the SubT challenge, the approach had room for improvement. In order for the coordination solution to be optimal, it should support directed search in addition to merely moving away from position histories. This directed search may be required if moving to a goal point is desired that is not on an individual robot’s explored map, for instance, if this goal point is set by a supervising human or it is a frontier shared by another robot. Moreover, an efficient coordination solution should respect both human cognition and robot capabilities in the loop. To this end, a semantic mapping and decision-making solution is proposed. The primary contribution of this work is to use individual robot maps for exploration while biasing this exploration towards desired semantics on a semantic map, which is assumed to be the only data structure shared between human and robotic agents. The approach is demonstrated to be successful in a complex indoor environment under map-misalignment uncertainty.

The future potential of the work presented in this article primarily lies in the improvements that can be brought to semantic reasoning methods and models. Topological and semantic mapping is not a new concept to the robotics community. However, the relevant methods that exist so far are either concerned with improved semantic mapping or using graph search-like approaches to planning over the semantic map at a high level. As emphasized in this article, while a higher-level semantic map is ideal to infer situational awareness from, robotic decision-making has long been relying on high-resolution low-level map information such as pointclouds, occupancy grids, etc. Therefore, this article makes an effort to use low-level perception information combined with cues from a high-level semantic map to carry out the decision-making. To the best of our knowledge, limited literature exists on this idea, which is a great candidate for further improvements and developments. In our current setup, the error correction between the semantic map origin and origin of the robot that is performing decision-making can be improved. This room for improvement is highlighted in Section 3.6 and Section 3.8. Moreover, since the focus of this research has been on semantic reasoning and decision-making instead of mapping itself, the position history-labeled semantic map could be replaced by other more sophisticated semantic mapping methods that exist in the current literature to further improve the search performance. The POMDP state transition and observation models also have a potential to be extended to various other environment types that do not have a topology necessarily consisting of corridors, rooms, and junctions. In addition, the mapping and reasoning techniques allow for the use of semantic labels that can be inferred from other multiple sensing modalities than just a laser scan. Since the observations are recorded probabilistically, a joint probability distribution of labels inferred using different sensing modalities at the same time can conveniently fit into the proposed framework. This in fact can greatly improve the observation uncertainty because, for instance, if labels inferred using a laser scan are different that those inferred using a vision sensor, a better distinction among semantic nodes can be achieved.