Abstract
In this paper, for the first time, experimental tests of complete offline walking gaits generated by the essential model are performed. This model does not make simplifications in the dynamics of the robot, and its main advantage is the definition of desired Zero Moment Point trajectories. The designed gaits are implemented in the NAO robot, where starting and stopping stages are also included. Simulations in MATLAB and Webots, and experiments with the real robot are shown. Also, important remarks about the implementation of walking trajectories in the NAO robot are included, such as dealing with the hip joint shared by both legs. A comparison between the linear inverted pendulum (LIP) model and the essential model is also addressed in the experiments. As expected, the robot fails following the offline gait generated by the LIP model, but it does not with the essential model. Moreover, in order to push the boundaries of the essential model, a complex gait is designed with a vertical motion of the center of mass and an abrupt movement of the arms. As shown in experiments, no external balance controller is required to perform this complex gait. Thus, the efficiency of the essential model to design stable open-loop complex gaits is verified.
1. Introduction
The most important task for a humanoid robot is to generate stable walking patterns that ensure the robot will not fall. To achieve this task, different models and control techniques have been developed. This objective is not easy because humanoid robots are very complex systems and it is very difficult to work with the complete model of the robot. Therefore, an alternative to deal with this is to make assumptions in the whole dynamics to create a simplified model, like the linear inverted pendulum (LIP) model [1], the Linear Inverted Pendulum Plus Flywheel (LIPPF) model [2], the Cart-Table model [3], the Spring-Loaded Inverted Pendulum (SLIP) model [4,5], etc.
The problem with these simplified models is that they do not consider the whole dynamics of the robot, the dynamics of the simplified model differs quite a bit from the complete model of the robot, and, also, there is no guarantee that the gait generated by the simplified model will work in the real robot. Besides this, many researchers have designed successful walking gaits by using these simplified models with closed-loop control techniques. The use of these models is still beneficial to improve walking motions, for instance, in [2], the LIP model and the LIPPF model are used to develop the concept of the capture point, which is a useful tool to deal with perturbations during walking; in [6], the LIP model is used with Model Predictive Control (MPC) to generate stable gait trajectories that have been implemented in the NAO robot and HRP-2, and later was extended to adapt the footstep placement online, improving its capacity to deal with strong perturbations [7,8]; in [9,10,11], the LIPPF model is used as a push recovery strategy to deal with external perturbations using MPC; and, in [12,13,14], the SLIP model is used to generate walking and running motions.
Another method to achieve stable walking gaits is Hybrid Zero Dynamics with Virtual Constraints, which consists in reducing the order of the complete model of the robot by imposing virtual constraints in the system [15]. This method has the great advantage that no simplifications are made to reduce the model, which means that solutions of the reduced model are solutions of the complete model. The problem with this method is that it does not provide insight into the essential dynamics of walking (the relation between the Zero Moment Point (ZMP) and the center of mass (CoM)). Also, although there exist works in which the HZD has been implemented in 3D cases [16,17], the HZD method does not scale well to high dimensions as it will be a robot with 22 DoF, as the NAO robot, and that is why in many works the HZD method is only implemented in the 2D planar dynamics of the robot and stabilized in 3D by an extra stabilizer [18,19,20,21].
Recently, another model that does simplify the dynamics is the so-called centroidal dynamics model, which has been gaining popularity in the biped community, and numerous works have been published with successful results. This model consists in projecting the complete dynamics of the robot into CoM space [22]. In [23], centroidal dynamics is used to generate offline trajectories using nonlinear optimization for the Atlas robot in highly agile motion, such as running and jumping. In [24], an improved algorithm to calculate the centroidal momentum matrix used in centroidal dynamics is presented and, together with Whole-Body-Control joint torques, is obtained in real time for highly dynamic motions such as kicking a ball. As with HZD, “centroidal dynamics” also does not give an explicit relation between the CoM acceleration and the ZMP [25].
A few years ago, in [26], a new model to generate walking gaits, called the essential model, was introduced. This model, like the Hybrid Zero Dynamics method, does not simplify the dynamics, it can be implemented for 2D or 3D walking without major changes, and it has as its principal advantage the definition of desired trajectories for the ZMP, a concept usually used in the literature as a stability criterion to ensure dynamic equilibrium in biped locomotion. However, just a few works related to the essential model without experimental results have been published. In [26], the essential model is presented and used to design walking gait trajectories validated in simulations for the robot ROMEO; in [27], a self-stabilised walking gait by adjusting the landing position of the swing foot is achieved and validated through simulations on robots ROMEO and TALOS; and, in [28], the essential model is used to design a straight walking gait for the NAO robot validated by simulations.
This work follows on from [28], in which periodic walking is implemented in the NAO robot with an instantaneous Double Support (DS) phase, without starting and stopping stages, validated by simulations in MATLAB and Webots. The present paper aims to conclude that work by adding starting and stopping stages, and a continuous DS phase in periodic walking, in addition to highlighting two main contributions:
- A straightforward way of including holonomic constraints of any robot with the essential model. This is shown by dealing with the constraint of the hip joint of NAO, where one motor is shared by both legs.
- Validating the walking gaits generated by the essential model for the first time in any robot throughout experiments.
These experiments include a comparison between walking using the LIP model and the essential model to show the advantage of modeling the complete dynamics given by our method. We choose the LIP model because: (1) it is the most used model in biped walking and (2) it is the simplest model in biped walking and we want to highlight as best as possible the unmodeled dynamics effect when a simplified model is used.
The experimental results presented in this paper are applied to the NAO robot but are not limited to it. This model can be applied to many different robots, from fully actuated robots with feet to underactuated robots with point leg contact.
Gait pattern generation in the NAO robot has been almost exclusive to simplified models. For example, in [29,30,31], the LIP model with MPC is used to generate a CoM motion given a ZMP reference, and the results are presented in experiments in the NAO robot, and, in [32], the LIPPF model with MPC optimized by an ant colony algorithm is used to produce a gait pattern validated in experiments in real time. There are works with experiments in the NAO robot using models without dynamic simplifications; for example, in [18], the sagittal dynamic model of the NAO robot is used with HZD and virtual constraints to produce a stable periodic orbit, which later is implemented in a 3D gait by using an extra lateral stabilizer, and, in [33], the NAO robot is modeled using the Euler–Lagrange formulation and stabilized using Whole-Body Control.
In order to highlight the effectiveness of the essential model for generating offline walking trajectories, a complex gait is designed where abrupt movements for the arms are performed during walking. These experiments show that, with the essential model, the robot can achieve the designed movements and walk in an open loop, unlike the more common methods that need a control law to correct the walking trajectories.
This paper is structured as follows. First, the essential and LIP models are briefly introduced in Section 2. In Section 3, the NAO robot is introduced, along with the controlled variables used in this work, and an easy way to deal with the constraint of the hip of the NAO robot. In Section 4, the walking design and the three optimization problems (one for each stage) to produce a complete gait are presented. Section 5 shows the results of the designed gaits in simulations, and a comparison between the LIP model and the essential model is realized in the Webots simulator. Finally, in Section 6, the experimental results are presented, showing a better performance of the essential model over the LIP model when an intense movement of the arms is performed.
2. Dynamics of a Humanoid Robot
The dynamics of a humanoid robot is usually split into two parts: the one related to the states that are directly driven by the actuators (the joints of the robot) and the dynamics of the inner states (the positions and orientation of the frame at the CoM).
Breaking the problem of walking into these two parts is very important because the CoM is the key issue during walking: it is the point where the gravity, angular momentum, and also the reaction force due to the foot act. Therefore, a model that gives us trajectories for the CoM that are suitable for a gait is required. Later on, we compare the generated offline trajectories with the LIP model and the essential model with the purpose of showing how the trajectories generated by the essential model can be performed in an open loop way.
2.1. The Linear Inverted Pendulum Model
The linear inverted pendulum model (and its extension to the three-dimensional case) was proposed in [1], and, because of its simplicity, it is one of the most successful models in walking gaits design. It assumes that the mass of the robot is concentrated in a point neglecting angular momentum and constraining the evolution of the height of the CoM into a plane. The relation between the CoM and the ZMP is explicitly expressed by the next equation:
where x and y are the positions of the CoM in the transversal plane, and the accelerations, z is the constant height of the CoM, g the constant of gravity, and is the position of the ZMP in the i direction. It is a linear model that can be evaluated a relatively high number of times in a few milliseconds. That is why its use has been very popular with many control schemes such as MPC. As a drawback, it does not consider any mass or inertia information of the links of the robot, which, in a humanoid robot that generally has heavy links, could end in a CoM trajectory not suitable to produce a stable gait.
2.2. The Essential Model
The essential model, presented in [26], describes the evolution of two uncontrolled internal states of the robot, (usually the horizontal position of the CoM), as a function of user-defined controlled trajectories, (usually coordinate operations of the robot, such as the position of the foot, the orientation of the hip, etc.), a desired trajectory for the ZMP(, ) and possible external information, . The essential model does not make any simplifications in the robot dynamics; therefore, the ZMP of the essential model is equal to the ZMP of the complete model. Furthermore, unlike the LIP model, in the essential model the height of the CoM is not constrained to a plane.
There are different ways to perform the essential model based on the selection of the free internal states and the external information. The case studied in this paper is when the essential model is based on the CoM and time (t), i.e., and . Thus, the essential model is expressed by:
The function can be found numerically using the Newton–Euler algorithm (see Appendix A in [26]).
3. The Humanoid Robot NAO
The NAO robot, manufactured by the SoftBank Robotics Group (Figure 1), is a humanoid robot with 25 DoF and different sensors to communicate with the world. In this work, the actuators located on the wrists and hands of each arm are not considered, and only the 21 DoF that appear in Figure 1 are used.
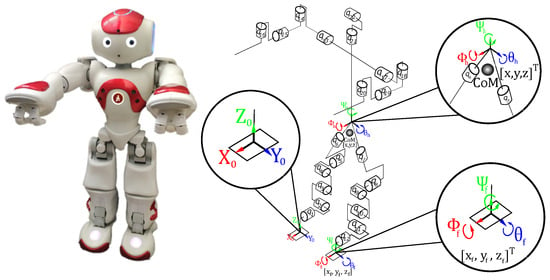
Figure 1.
NAO robot and joints used in this paper.
The NAO robot has a peculiarity in its architecture, where a joint in the hip is shared for both legs; moreover, the axis of these two joints is not aligned with “Yaw”, as it is in most humanoid robots. This joint is called “HipYawPitch” and corresponds to the joint variables y , as shown in Figure 1, which are actuated by the same motor [34]. This leads to a problem with the inverse geometric model since the constraint on and has to be considered.
It is possible to consider joints and as independent variables, as in [28]; however, only straight gaits can be achieved by this assumption. In this work, this constraint is considered to produce omnidirectional gaits. In order to achieve this, a simple constraint must be met at all times:
Since the essential model considers the motion of the whole body, a set of variables that allow parameterizing the motion of the body must be chosen. These variables are called controlled variables and they must be a vector of dimension, where n is the number of joints of the robot. Here, the selected controlled variables are , where z is the height of the CoM, , , and are the position of the free foot, , , and are the orientation of the free foot, and are the orientation of the hips, and to are directly the position of the joints of the upper body (arms and head). Note that the constraint (3) is considered as a controlled variable instead of the orientation of the hips in Yaw (). This is because only one actuator is used to produce a motion in Yaw, and therefore only one motion, or , can be controlled, In this case, we have chosen to control the Yaw motion of the foot. All these variables are measured with respect to the frame (−−).
The NAO robot has its own software called NAOqi, which provides functions that allow us to program the movements of the robot [34]. This software does not allow sending velocity or torque commands for the joints; only position commands are allowed. There are different ways to send these joint position commands; if a real-time application is required, the DCM (Device Communication Manager) is needed to send and read commands from the actuators to the CPU of the robot. On the other hand, if the desired motion is computed offline, as the case in this paper, the NAOqi framework provides the ALMotion module with functions such as angleInterpolation(), which, given a vector of times and a vector (or multiple vectors) of joint positions, position commands are sent to each joint, which are tracked by a PID control.
4. Walking Design
A complete gait in this paper consists of three stages: the starting stage, the periodic walking stage, and the stopping stage (Figure 2). Each stage deals with an optimization problem: (1) to reach a periodic motion from rest; (2) to obtain a periodic motion; and (3) to reach a resting posture from a periodic motion.
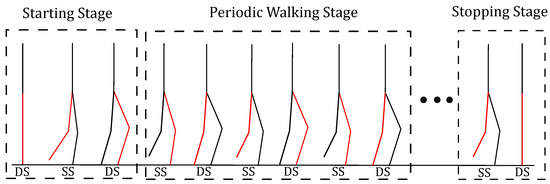
Figure 2.
Walking stages. The red lines indicate the right leg and the black lines the left leg.
In this work, every walking motion has the next considerations: the desired orientation of the free foot and the hips (except for Yaw) are always zero. The desired trajectory for the ZMP is described by a first-order equation with initial position and final position . The walking parameters for the legs are the step length, S; the step width, D; and the maximum height of the free foot, , usually arrived at , where T is the time step. For a straight gait, the trajectory of the free foot during a step goes in the -axis from to S, in the -axis it is kept constant with the value D, and the initial and final position in the -axis is zero.
Although there exist different criteria for the design of the upper body motion, for example by using motion capture [35], for the sake of simplicity in this paper the desired motion for the arms is arbitrarily chosen. The motion of each joint in the upper body is described by a third-order polynomial, where the initial and final positions are detailed in Section 5, and the initial and final velocities are zero for each joint to perform a smooth transition between steps. As it will be seen in the experiments section, there are two cases for the arms’ movement. In the first case, the initial and final values are proposed to resemble human motion during walking (a little swing in the shoulders and elbows). In the second case, for the purpose of clarifying the advantages of our model, a wider movement for the shoulders and elbows is carried out.
It is possible to also plan acceleration movements for the controlled variables trajectories and the ZMP trajectories to obtain smoother motions, but no benefits have been found by doing this. Also, the essential model is capable of handling impacts (such as the landing of the free foot) and, therefore, instantaneous changes in velocity if it is required.
4.1. Periodic Walking Stage
Although this stage is the second one, it needs to be computed first. The aim of this stage is to find some conditions of the CoM (positions and velocities of the CoM) such that, after a step with period T, and a desired trajectory for the ZMP defined by its initial and final position ( and in Figure 3), the same states occur again, i.e., a periodic motion appears. In order to take into account the possible change of velocities at the beginning of the step due to the landing of the free foot at the previous step, the problem is set to find
where the superscript indicates the instant just before the free foot lands to complete a step (end of the step). Obtaining Equation (4) means finding the CoM states at the end of the previous step that have the same value as the CoM states at the end of the current step. The states that satisfy this condition are called fixed points and are denoted by the superscript .
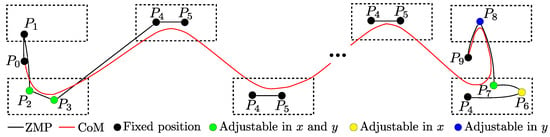
Figure 3.
ZMP and CoM motion during complete walking. indicates a desired ZMP position in the foot frame that must be achieved (some of them are fixed and others are adjusted by optimization).
Since the motion of the CoM is almost symmetric for a periodic motion (it is completely symmetric for the LIP model), only a few displacements on the position ( in the x-axis in the y-axis) with respect to that symmetry must be found. Therefore, the CoM positions at the beginning and end of a step can be written as
where the superscript indicates the instant just after the free foot lands to complete a step (beginning of a new step), S is the step length, and D the step width.
Hence, the optimization problem is to obtain the values of , , , and , such that Equation (4) is fulfilled, i.e.,
where
If the chosen gait parameters are suitable to produce a feasible gait, the states at the end of the stage that produce a periodic motion reducing to zero Equation (5) can be found:
where and .
4.2. Starting Stage
Once the fixed point that produces periodic walking is found, a starting stage has to be designed. The aim of this stage is to take the CoM from rest and reach the fixed point (10) in only one step. This step is divided into three phases: an initial DS phase, a Single Support (SS) phase, and a final DS phase. The initial position of the ZMP in the starting stage ( in Figure 3) is and its final position is the initial desired value for the ZMP during the periodic walking stage ( in Figure 3). An additional point during the initial DS phase ( in Figure 3) allows the transition from the initial DS phase to the SS phase with a suitable movement of the CoM.
The decision variables for the optimization are the initial and final positions of the ZMP, in both the x and y directions, during the SS phase ( and ), represented in Figure 3 as and . As in the periodic stage, the complete motion for the ZMP is linearly interpolated using these initial and final values, except for the initial DS phase, in which the desired ZMP path in the y-axis has a third desired value in the middle of the trajectory.
Then optimization problem for this stage is given by:
It is important to remark that inequality constraints during the optimization must be set in order to restrict the trajectory of the ZMP to be inside the support foot for the whole time and guarantee a stable step.
4.3. Stopping Stage
The aim of the stopping stage, after the periodic stage has ended, is to reduce the velocity of the CoM to zero and make the CoM’s position reach a stand rest position at (0, ). The stopping motion is divided into two phases: an SS phase and a DS phase.
Here, we cannot change the initial values of the ZMP in the SS phase because these values are the final values of the periodic motion, and also the final values of the ZMP in the DS phase cannot be changed ( in Figure 3) because these are , so that the CoM projection coincides with the ZMP position. Then, instead of a linear ZMP trajectory, as before, the trajectory for the ZMP in the x direction during the SS phase and the trajectory for the ZMP in the y direction during the DS phase are quadratic. The decision variables selected for this optimization are the final position of the ZMP during the SS phase, ( in Figure 3), the position of the ZMP in x in the middle of the SS phase, (the x coordinate of ), and the position in y of the ZMP in the middle of the DS phase, (the y coordinate of ).
The optimization problem for the stopping stage is
As the starting motion, the ZMP trajectory must be constrained to be in the support polygon during optimization.
5. Results
A comparison between the behavior of the ZMP by considering the whole dynamics with trajectories generated by the LIP model and the essential model is performed as Case I. These trajectories have the same gait parameters (desired ZMP, desired arm movement, etc.) and are realized in Webots Simulator. In order to test how the CoM’s trajectory can be affected by the whole dynamics, an abrupt movement for the arms was chosen for both models. This abrupt movement of the arms is a long and fast movement for some joints in the upper body. The intention is to apply a desired movement of the arms with a not negligible effect in the CoM linear and angular momentum, such that the benefit of considering the upper-body dynamics with the essential model versus the unmodeled dynamics of the LIP model shows up.
In Case II, a more challenging gait is designed with the essential model, a circular gait with a continuous DS phase, a variable height of the CoM, and even a more abrupt movement for the arms than in Case I. The gait parameters for both cases are shown in Table 1. All gaits include starting and stopping stages.

Table 1.
Gait parameters for each case.
The parameters for the upper body are presented in Table 2. The movement of these joints is defined by third-order polynomials with an initial and final position as indicated in Table 2. The desired initial and final velocities of these joints are zero.

Table 2.
Gait parameters for arm movements for each case.
The gait parameters for the starting and stopping stages for each gait are not shown but they were chosen such that no discontinuities are presented during the gait and also both feet have the same distance in the x-axis at the start and at the end of the gait.
5.1. Case I: Comparison between LIP Model vs. Essential Model with Instantaneous DS Phase
As mentioned before, the desired ZMP for the essential model is equal to the real ZMP, which is not the case for the LIP model and the simplified models where the real ZMP differs from the desired and sometimes even leaves the support polygon [26]. Figure 4 proves the above, with a gait designed to keep a desired ZMP fixed at point (0, 0) during walking. This trajectory is performed by both models. The ZMP computed by tracking the trajectory of the LIP model and considering the whole dynamics is not even close to the desired one; in fact, it leaves the support zone. Meanwhile, the essential model follows perfectly the desired ZMP because the whole dynamics is considered in this model.
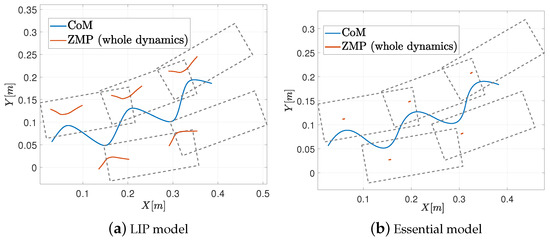
Figure 4.
Comparative ZMP whole dynamics LIP vs. essential.
To visualize this difference between both models, a simulation in Webots in the NAO robot is carried out using the gait parameters in Table 1 for Case I. The parameters for the upper body are shown in Table 2 Case I.
In order to make a fair comparison between these two models, a starting stage and a stopping stage were designed for the LIP model in the same way as the previous sections. Using these gait parameters and solving the optimization problems in Equations (5), (11) and (12), the optimized values that produce a complete periodic walking are found. These values are shown in Table 3.

Table 3.
Optimized values for each stage of walking in Case I.
The Newton–Euler algorithm was used to obtain the evolution of the real ZMP during the gait. Forces and torques are found at the support foot and the ZMP is computed. To perform the Newton–Euler algorithm, the joint’s position, velocities, and accelerations are needed. The NAO robot can only provide information on joint positions and velocities, and therefore the accelerations have to be computed numerically by derivating velocities with respect to time.
The results of the evolution of the ZMP are shown in Figure 5. As seen in this figure, the LIP model struggles to follow the desired ZMP and sometimes it is on the border of the foot. On the other hand, the essential model has a better performance, keeping the ZMP close to the reference and far from the borders of the foot. The root mean squared error and the standard deviation to quantify the tracking error of the desired ZMP for both models were computed. The error is computed as the Euclidean distance from the resulting ZMP to the reference at each time step. The mean squared error and the standard deviation from both models are shown in Table 4 and Figure 6. As it is expected, it can be seen the essential model has a better performance than the LIP model, with a lower error and a lower standard deviation.
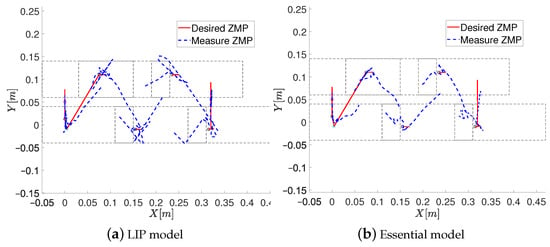
Figure 5.
Comparison of the evolution of the real ZMP for both models.

Table 4.
Mean squared error and standard deviation from the desired ZMP trajectory of the LIP model and the essential model.
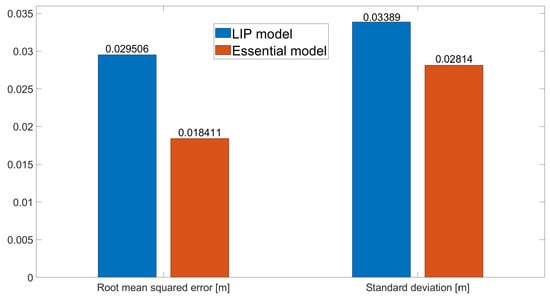
Figure 6.
Mean squared error and standard deviation.
Note that, in practice, the ZMP is not perfectly tracked (as expected with the essential model) due to several factors, such as: (a) the model used to compute the essential model is not perfect, namely, it does not consider friction, backlash, and other dynamics; and (b) in particular, for the NAO robot, the desired joint velocities cannot be given as desired inputs. The last point is a very important issue since the essential model assumes that a perfect tracking of the joints is achieved; nevertheless, this cannot be fulfilled by giving only the desired joint position trajectories. However, this issue highlights the power of the essential model, since, despite all, the generated walking gait can be achieved by the robot, as shown in this section and the next one.
As an additional comparison, we compute the mechanical cost of transport for both models. The mechanical cost of transport is computed as [36]:
where m is the total mass of the robot, g the constant of gravity, and d the distance traveled by the robot. is the mechanical power of each motor (22 in the case of the NAO robot). In our case, we compute as the absolute value of the product of the torques and velocities of each motor, this is:
The integral in Equation (13) was computed numerically and the distance traveled by the robot was chosen as the distance traveled by the free foot of the robot. As a result, two different comparisons are shown for a gait with six steps, one with an abrupt movement of the arms (Case I) and other with a regular movement of the arms (a little swing in the shoulders and elbows). The results are shown in Table 5.

Table 5.
Cost of transport of the LIP model and the essential model for two different arm movements.
Table 5 shows that the cost of mechanical transport using the essential model is lower than the LIP model, which means there is less mechanical energy consumption. The reason for this could be attributed to the fact that, in the essential model, the motion of the CoM is such that the desired ZMP is achieved and, therefore, the joint motions of the whole body are smoother. Several other factors can be involved in this phenomenon, but this is out of the scope of this paper. A deeper study that uses the essential model with a cost function that minimizes the mechanical energy consumption to produce a walking gait could be considered in the future.
5.2. Case II: Circular Gait with Continuous DS Phase Using the Essential Model
The previous case shows that even for a not-too-difficult gait the LIP model fails in the generation of suitable gait trajectories. In this section, a more challenging gait is designed to explode the power of the essential model: a gait with a circular path, a continuous DS phase, a variable height of the CoM, and even a more abrupt movement for the arms than Case I. The gait parameters are shown in Table 1 and Table 2 (Case II). To perform a circular gait, two different steps have to be realized, each one with an SS phase and a DS phase. The height of the CoM is described by a polynomial such that, at , the CoM reaches the maximum amplitude of oscillation, .
The results of the decision variables for the three optimization problems for each stage of walking are shown in Table 6.

Table 6.
Optimized values for each stage of walking in Case II.
With these decision variables, the essential model computes the CoM trajectory that generates a suitable gait. Figure 7 shows the trajectories for the CoM and the ZMP for a gait with 36 steps that starts and ends at the same place. The ZMP in Figure 7 is the ZMP of the whole dynamics, which is the same as the desired one.
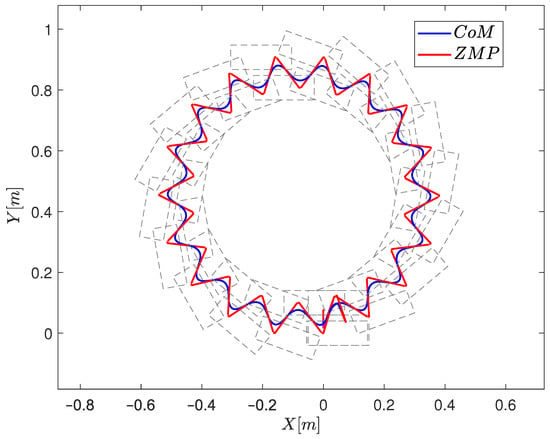
Figure 7.
Upper view of the CoM and ZMP trajectories for Case II.
6. Experiments
In order to validate the previous results, experiments were performed with the NAO robot for both cases. The experiments were realized in laboratory conditions on flat ground in the NAO V5 robot, which has its own software called NAOqi that provides functions that allow us to program the robot and interact with it [34], which was previously mentioned in Section 3. The optimization, computation of the essential model, solution of the inverse kinematics, and almost every math calculation are realized by a personal computer (PC) in MATLAB, and only the joint position commands are sent to the robot. The communication of the PC with the robot is via Wi-Fi, which does not involve a delay problem because all the computation is performed offline.
The experiments were run on a PC in Python by using the joint trajectories generated in MATLAB and sending the position commands to the actuators using the angleInterpolation() function. When realizing experiments, the autonomous life mode of the robot should be turned off to avoid unexpected movements, and the desired movements for the actuators not considered in this work (the wrists and the hands) are set to be constant.
The procedure to realize the experiments is the following. First, the essential model is optimized in each stage, as described in Section 4.1–Section 4.3, then, with these optimized values, the essential model is used to compute a complete gait to obtain the CoM motion of the complete walking with 1 millisecond of time step. The next step is to solve the inverse kinematics using the CoM motion along with the desired motion of the controlled variables (such as the arm motions) to obtain the joint motions, which are saved in a .txt file on the PC. A Python script with the NAOqi software sends the trajectories to the robot. The same process is applied to the experiments with the LIP model.
During the experimental tests, a common problem is observed in the Simple Support (SS) phase where, when all the weight of the robot is on one leg, the HipRoll joint of the supporting leg does not reach the desired position, which is due to the large torque required by the entire body weight. This causes the free foot to not perform the desired movement correctly, touching the ground before it should, thus destabilizing the robot. This problem has been solved in works such as [29,30] by adding an offset to the HipRoll joints for both legs. We avoid this solution because it could modify our previously modeled dynamics. Then multiple trajectories for the ZMP and step time (the time in which the robot takes a step) were tested to find gaits that do not present this problem. These tests resulted in the selection of a relatively fast step time (half of a second) and to select trajectories for the ZMP in the y direction away from the inside of the foot that were applied in the final experiments.
The results can be seen in Figure 8 and Figure 9, and on video at https://www.youtube.com/watch?v=2uo0IWQaYhw (Accessed 15 August 2024) and https://www.youtube.com/watch?v=DUljB0kHSEg (Accessed 15 August 2024). It was not possible to obtain reliable information on the sensors of the real robot during the gait that could lead to a graphical representation of the real ZMP. Only a few samples of the joints’ positions and velocities for all motors could be read during the gait. The velocity data were very noisy and the fact that acceleration must be computed numerically removes the possibility of computing the ZMP considering the whole dynamics. Nevertheless, the experiments highlight the benefits of the essential model for designing a complex gait for open loop walking.

Figure 8.
Experiment comparative between (a) LIP model and (b) essential model in a gait with arm movements.

Figure 9.
Experiment circular gait using the essential model.
6.1. Case I: Comparison between LIP Model and Essential Model in Experiments
In this experiment, a comparison between the LIP model and the essential model is realized by using the same gait parameters and upper body motion for both models (Case I). As in simulations, an abrupt movement of the arms is desired. The results of the experiments are shown in Figure 8; the first row of this figure corresponds to a gait produced by the LIP model, and the second row to a gait produced by the essential model. A video of the experiments can be found at https://www.youtube.com/watch?v=2uo0IWQaYhw (Accessed 15 August 2024).
As shown, there is a better performance of the robot with the gait of the essential model compared with the gait of the LIP model. The essential model provides a walking trajectory that produces a stable gait on the real robot, while the walking trajectory for the LIP model causes the robot to fall.
The fact that the LIP model does not consider the effect of the robot’s links in the trajectory of the CoM makes the robot susceptible to losing balance (namely, the ZMP leaves the support polygon). This is emphasized when a violent movement of the extremities is performed. On the other hand, the essential model considers the full dynamics of the system for generating a gait, including the upper body motion. Therefore, a stable gait even with violent motions of the extremities can be achieved with this model.
6.2. Case II: Circular Gait with Continuos DS Phase Using the Essential Model in Experiments
The second experiment is a circular trajectory with a continuous DS phase, a variable height of the CoM, and a more energetic movement for the arms than Case I. The gait parameters are shown in Table 1 and Table 2. As shown in Table 1, this case consists of two different steps.
The experimental results for Case II for 36 steps are shown in Figure 9 and a video of the experiment can be found at https://www.youtube.com/watch?v=DUljB0kHSEg (Accessed 15 August 2024). As shown in the parameters of Table 1, every two steps the free foot rotates 20 degrees, making a circular trajectory after several steps.
The results show a stable gait trajectory provided by the essential model for more demanding walking than Case I.
7. Conclusions
In this work, experiments for a complete walking gait generated by the essential model based on the CoM and time were performed for the first time. The benefits of the essential model to generate offline stable walking gaits that can be achieved in an open loop were shown. The simulations in MATLAB showed that the desired trajectory for the ZMP was perfectly followed. Meanwhile, the simulation in Webots showed these trajectories were not perfectly followed; however, they were always kept inside the support polygon for the whole time. The real ZMP trajectory in the experiments could not be computed due to several facts related to the sampling time of NAO and noisy signals. However, the experiments showed a good performance of the NAO robot in achieving walking gaits generated by the essential model.
It is important to remark that there is no closed-loop control of the CoM or the ZMP, and the computation of the joint’s trajectories is realized offline. Namely, without feedback, the essential model provides a stable gait even when abrupt movements of extremities are desired during walking.
A comparison between the LIP model and the essential model was realized in simulations and experiments. As anticipated, the robot encounters difficulty in following the offline gait generated by the LIP model and falls. By contrast, the essential model can produce stable gait patterns, so the robot can fulfill the gait. Furthermore, since the essential model considers the whole dynamics, it can produce more complex gaits in an open loop. This is demonstrated when the NAO robot performs experiments with a gait with a curved path, variable motion of the height of the CoM, DS phases, and an intense movement of the arms during walking. Any movement of the upper body and its effect on the center of mass dynamics is not modeled at all by the LIP model and is modeled completely by the essential model. These unmodeled dynamics when a simplified model is used have a potential effect on the center of mass dynamics, changing the linear and angular momentum when sudden movements of the upper body are performed. This results in a fall when an abrupt movement of the arms is presented in the LIP model and a successful walking when the abrupt movement of the arms is presented in the essential model.
In order to achieve a better performance of the walking of the robot with the essential model, not only joint desired position profiles but also joint desired velocities must be given to the robot. However, the NAO robot only accepts joint desired position trajectories, and the velocities are computed by the inner joint controller of the robot. Nevertheless, it was shown that, in practice, by only giving the joint desired position trajectories to the robot, a stable walking gait can be performed, highlighting the power of the essential model.
As future work, a feedback online controller will be used to improve the robustness of walking gaits generated by the essential model. Also, it is considered an optimization stage of the trajectories of the controlled variables to improve the efficiency of the essential model and perform a comparison with other models in the state of the art.
Due to the whole dynamics consideration, the essential model is not limited only to walking; several applications such as running, jumping, and manipulating can be developed using this model and are open problems at the date of the publication of this paper. Currently, the authors are working on using the essential model as a Whole-Body-Control formulation to achieve more complex tasks such as push recovery, and object manipulation while walking, among others.
Author Contributions
Conceptualization E.M.-A., V.D.-L.-G. and V.S.; methodology, E.M.-A. and V.D.-L.-G.; validation, E.M.-A.; formal analysis, C.C. and Y.A.; investigation, E.M.-A.; resources, C.C. and Y.A.; writing—original draft preparation, E.M.-A. and V.D.-L.-G.; writing—review and editing, E.M.-A., V.D.-L.-G. and V.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by TecNM projects.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
Emanuel Márquez-Acosta thanks the Mexican Council for Science and Technology (CONACyT) for its support with a PhD grant. This work was developed within the framework of RICCA “Red Internacional de Control y Computo Aplicados” of TecNM.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kajita, S.; Kanehiro, F.; KaneKo, K.; Yokoi, K.; Hirukawa, H. The 3D linear inverted pendulum mode: A simple modeling for a biped walking pattern generation. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. Expanding the Societal Role of Robotics in the the Next Millennium, Maui, HI, USA, 29 October–3 November 2001; pp. 239–246. [Google Scholar] [CrossRef]
- Pratt, J.; Carff, J.; Drakunov, S.; Goswami, A. Capture point: A step toward humanoid push recovery. In Proceedings of the 2006 6th IEEE-RAS International Conference on Humanoid Robots, Genova, Italy, 4–6 December 2006; pp. 200–207. [Google Scholar] [CrossRef]
- Kajita, S.; Kanehiro, F.; KaneKo, K.; Fujiwara, K.; Harada, K.; Yokoi, K.; Hirukawa, H. Biped walking pattern generation by using preview control of zero-moment point. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003; pp. 1620–1626. [Google Scholar] [CrossRef]
- Blickhan, R. The spring-mass model for running and hopping. J. Biomech. 1989, 22, 1217–1227. [Google Scholar] [CrossRef] [PubMed]
- Geyer, H.; Saranli, U. Gait based on the spring-loaded inverted pendulum. In Humanoid Robotics: A Reference; Goswami, A., Vadakkepat, P., Eds.; Springer: Dordrecht, The Netherlands, 2018; pp. 1–25. [Google Scholar] [CrossRef]
- Wieber, P. Trajectory free linear model predictive control for stable walking in the presence of strong perturbations. In Proceedings of the 2006 6th IEEE-RAS International Conference on Humanoid Robots, Genova, Italy, 4–6 December 2006; pp. 137–142. [Google Scholar] [CrossRef]
- Diedam, H.; Dimitrov, D.; Wieber, P.; Mombaur, K.; Diehl, M. Online walking gait generation with adaptive foot positioning through Linear Model Predictive Control. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 1121–1126. [Google Scholar] [CrossRef]
- Herdt, A.; Diedam, H.; Wieber, P.; Dimitrov, D.; Mombaur, K.; Diehl, M. Online Walking Motion Generation with Automatic Footstep Placement. Adv. Robot. 2010, 24, 719–737. [Google Scholar] [CrossRef]
- Dini, N.; Majd, V.J. An mpc-based two-dimensional push recovery of a quadruped robot in trotting gait using its reduced virtual model. Mech. Mach. Theory 2020, 146, 103737. [Google Scholar] [CrossRef]
- Luo, R.C.; Sheng, J.; Chen, C.-C.; Chang, P.H.; Lin, C.-I. Biped robot push and recovery using flywheel model based walking perturbation counteraction. In Proceedings of the 2013 13th IEEE-RAS International Conference on Humanoid Robots, Atlanta, GA, USA, 15–17 October 2013; pp. 50–55. [Google Scholar] [CrossRef]
- Jeong, H.; Lee, I.; Oh, J.; Lee, K.K.; Oh, J.H. A Robust Walking Controller Based on Online Optimization of Ankle, Hip, and Stepping Strategies. IEEE Trans. Robot. 2019, 35, 1367–1386. [Google Scholar] [CrossRef]
- Shahbazi, M.; Babuska, R.; Lopes, G.A.D. Unified modeling and control of walking and running on the spring-loaded inverted pendulum. IEEE Trans. Robot. 2016, 32, 1178–1195. [Google Scholar] [CrossRef]
- Tamaddoni, S.H.; Jafari, F.; Meghdari, A.; Sohrabpour, S. Biped hopping control bazsed on spring loaded inverted pendulum model. Int. J. Humanoid Robot. 2010, 7, 263–280. [Google Scholar] [CrossRef]
- Hereid, A.; Kolathaya, S.; Jones, M.S.; Why, J.V.; Hurst, J.W.; Ames, A.D. Dynamic multi-domain bipedal walking with atrias through slip based human-inspired control. In Proceedings of the 17th International Conference on Hybrid Systems: Computation and Control, HSCC ’14, Berlin, Germany, 15–17 April 2014; pp. 263–272. [Google Scholar] [CrossRef]
- Westervelt, E.R.; Grizzle, J.W.; Koditschek, D.E. Hybrid zero dynamics of planar biped walkers. IEEE Trans. Autom. Control 2003, 48, 42–56. [Google Scholar] [CrossRef]
- Hartley, R.; Grizzle, J.W. Stabilization of 3D underactuated biped robots: Using posture adjustment and gait libraries to reject velocity disturbances. In Proceedings of the IEEE Conference on Control Technology and Applications (CCTA), Maui, HI, USA, 27–30 August 2017; pp. 1262–1269. [Google Scholar] [CrossRef]
- Hereid, A.; Cousineau, E.A.; Hubicki, C.M.; Ames, A.D. 3D dynamic walking with underactuated humanoid robots: A direct collocation framework for optimizing hybrid zero dynamics. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1447–1454. [Google Scholar] [CrossRef]
- Ames, A.D.; Cousineau, E.A.; Powell, M.J. Dynamically stable bipedal robotic walking with NAO via human-inspired hybrid zero dynamics. In Proceedings of the 15th ACM International Conference on Hybrid Systems: Computation and Control, Beijing, China, 17–19 April 2012; pp. 135–144. [Google Scholar] [CrossRef]
- Da, X.; Harib, O.; Hartley, R.; Griffin, B.; Grizzle, J.W. From 2D Design of Underactuated Bipedal Gaits to 3D Implementation: Walking With Speed Tracking. IEEE Access 2016, 4, 3469–3478. [Google Scholar] [CrossRef]
- Da, X.; Grizzle, J.W. Supervised learning for stabilizing underactuated bipedal robot locomotion, with outdoor experiments on the wave field. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3476–3483. [Google Scholar] [CrossRef]
- Gong, Y.; Hartley, R.; Xingye, D.; Hereid, A.; Harib, O.; Huang, J.K.; Grizzle, J.W. Feedback Control of a Cassie Bipedal Robot: Walking, Standing, and Riding a Segway. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 9–11 July 2019; pp. 4559–4566. [Google Scholar] [CrossRef]
- Orin, D.E.; Goswami, A.; Lee, S.H. Centroidal dynamics of a humanoid robot. Auton. Robot. 2013, 35, 161–176. [Google Scholar] [CrossRef]
- Dai, H.; Valenzuela, A.; Tedrake, R. Whole-body motion planning with centroidal dynamics and full kinematics. In Proceedings of the 2014 IEEE-RAS International Conference on Humnaoide Robots, Madrid, Spain, 18–20 November 2014; pp. 295–302. [Google Scholar] [CrossRef]
- Wensing, P.M.; Orin, D.E. Improved Computation of the Humanoid Centroidal Dynamics and Application for Whole-Body Control. Int. J. Humanoid Robot. 2016, 13, 1550039. [Google Scholar] [CrossRef]
- Lee, S.H.; Hofmann, A.; Goswami, A. Angular Momentum Based Balance Control. In Humanoid Robotics: A Reference; Goswami, A., Vadakkepat, P., Eds.; Springer: Dordrecht, The Netherlands, 2017. [Google Scholar] [CrossRef]
- De-León-Gómez, V.; Luo, Q.; Kalouguine, A.; Pámanes, J.A.; Aoustin, Y.; Chevallereau, C. An essential model for generating walking motions for humanoid robots. Robot. Auton. Syst. 2019, 112, 229–243. [Google Scholar] [CrossRef]
- Luo, Q.; Chevallereau, C.; Ou, Y.; Pang, J.; De-León-Gómez, V.; Aoustin, Y. A self-stabilised walking gait for humanoid robots based on the essential model with internal states. IET Cyber-Syst. Robot 2022, 4, 283–297. [Google Scholar] [CrossRef]
- Marquez-Acosta, E.; De-Leon-Gomez, V.; Santibañez, V. A walking gait for robot nao using the essential model. In Advances in Automation and Robotics Research, Proceedings of the 3rd Latin American Congress on Automation and Robotics, Monterrey, Mexico, 17–19 November 2021; Springer International Publishing: Cham, Switzerland, 2021; pp. 62–67. [Google Scholar]
- Strom, J.; Slavov, G.; Chown, E. Omnidirectional Walking Using ZMP and Preview Control for the NAO Humanoid Robot. In RoboCup 2009: Robot Soccer World Cup XIII. RoboCup 2009; Baltes, J., Lagoudakis, M.G., Naruse, T., Ghidary, S.S., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 5949. [Google Scholar] [CrossRef]
- Gouaillier, D.; Collette, C.; Kilner, C. Omni-directional closed-loop walk for NAO. In Proceedings of the 2010 10th IEEE-RAS International Conference on Humanoid Robots, Nasville, TN, USA, 6–8 December 2010; pp. 448–454. [Google Scholar] [CrossRef][Green Version]
- Alcaraz-Jimenez, J.J.; Herrero-Perez, D.; Martinez-Barbera, H. Robust feedback control of ZMP-based gait for humanoid robot NAO. Int. J. Robot. Res. 2013, 32, 1074–1088. [Google Scholar] [CrossRef]
- Kashyap, A.K.; Parhi, D.R. Optimization of stability of humanoid robot NAO using ant colony optimization tuned MPC controller for uneven path. Soft Comput. 2021, 25, 5131–5150. [Google Scholar] [CrossRef]
- Kashyap, A.K.; Parhi, D.; Kumar, S. Dynamic Stabilization of NAO Humanoid Robot Based on Whole-Body-Control with Simulated Annealing. Int. J. Humanoid Robot. 2020, 17, 2050014. [Google Scholar] [CrossRef]
- Gouaillier, D.; Hugel, V.; Blazevic, P.; Kilner, C.; Monceaux, J.; Lafourcade, P.; Marnier, B.; Serre, J.; Maisonnier, B. The nao humanoid: A combination of performance and affordability. arXiv 2008, arXiv:0807.3223. [Google Scholar] [CrossRef]
- Kim, S.; Kim, C.; Park, J.H. Human-like Arm Motion Generation for Humanoid Robots Using Motion Capture Database. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–13 October 2006; pp. 3486–3491. [Google Scholar] [CrossRef]
- Hobbelen, D.G.E.; Wisse, M. Controlling the Walking Speed in Limit Cycle Walking. Int. J. Robot. Res. 2008, 27, 989–1005. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).