Task-Dependent Comfort Zone, a Base Placement Strategy for Mobile Manipulators Based on Manipulability Measures
Abstract
1. Introduction
2. Manipulability Measures
2.1. Jacobian Matrix
2.2. Velocity Manipulability Measure
2.3. Force Manipulability Measure
2.4. Stiffness Manipulability Measure
2.5. Dynamic Manipulability Measure
3. Task-Dependent Comfort Zone
3.1. Task Classification
3.2. Motivation
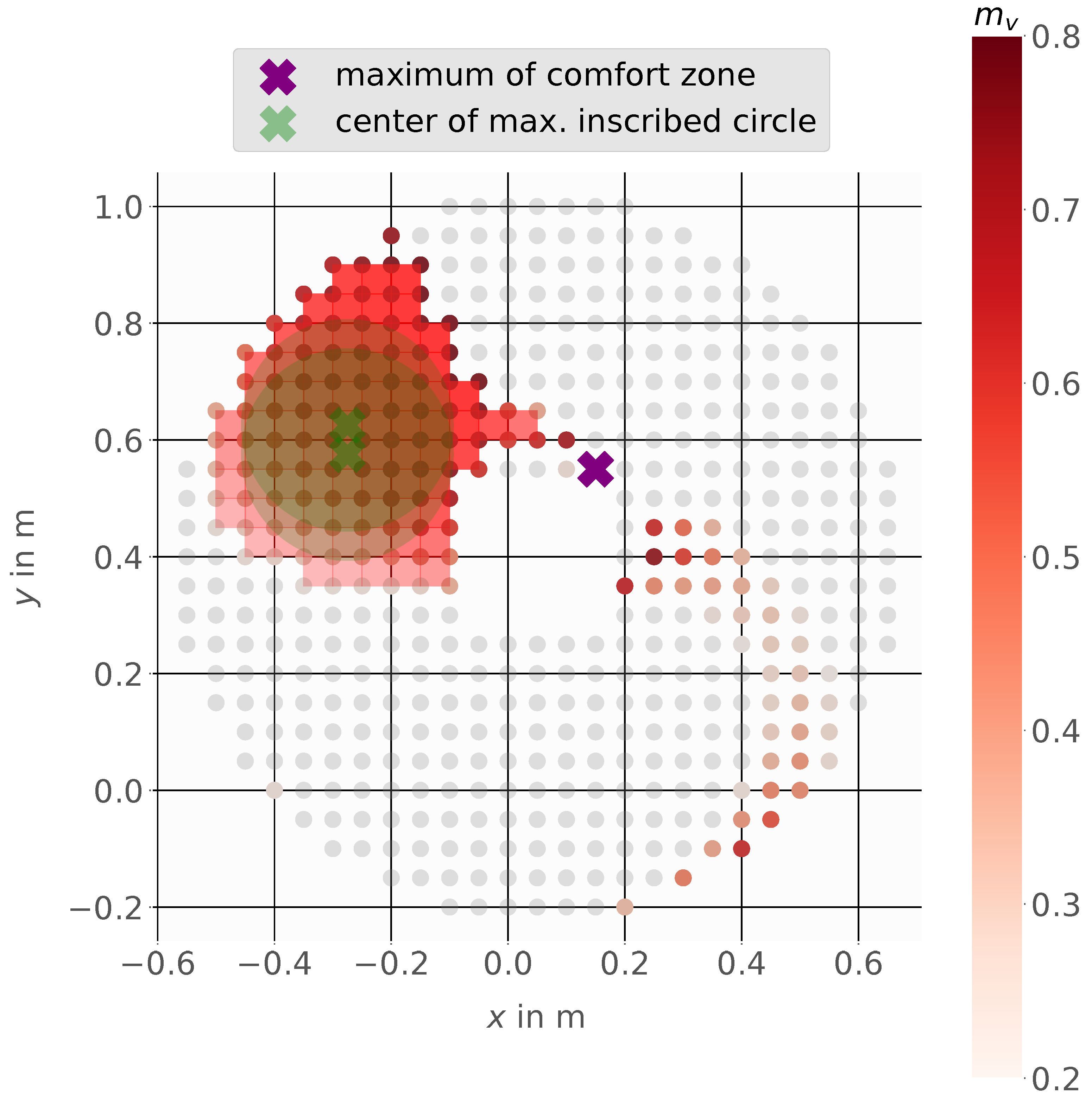
3.3. Recommended Workspace
3.4. Manipulability Measure Norm, Combination, and Constraints
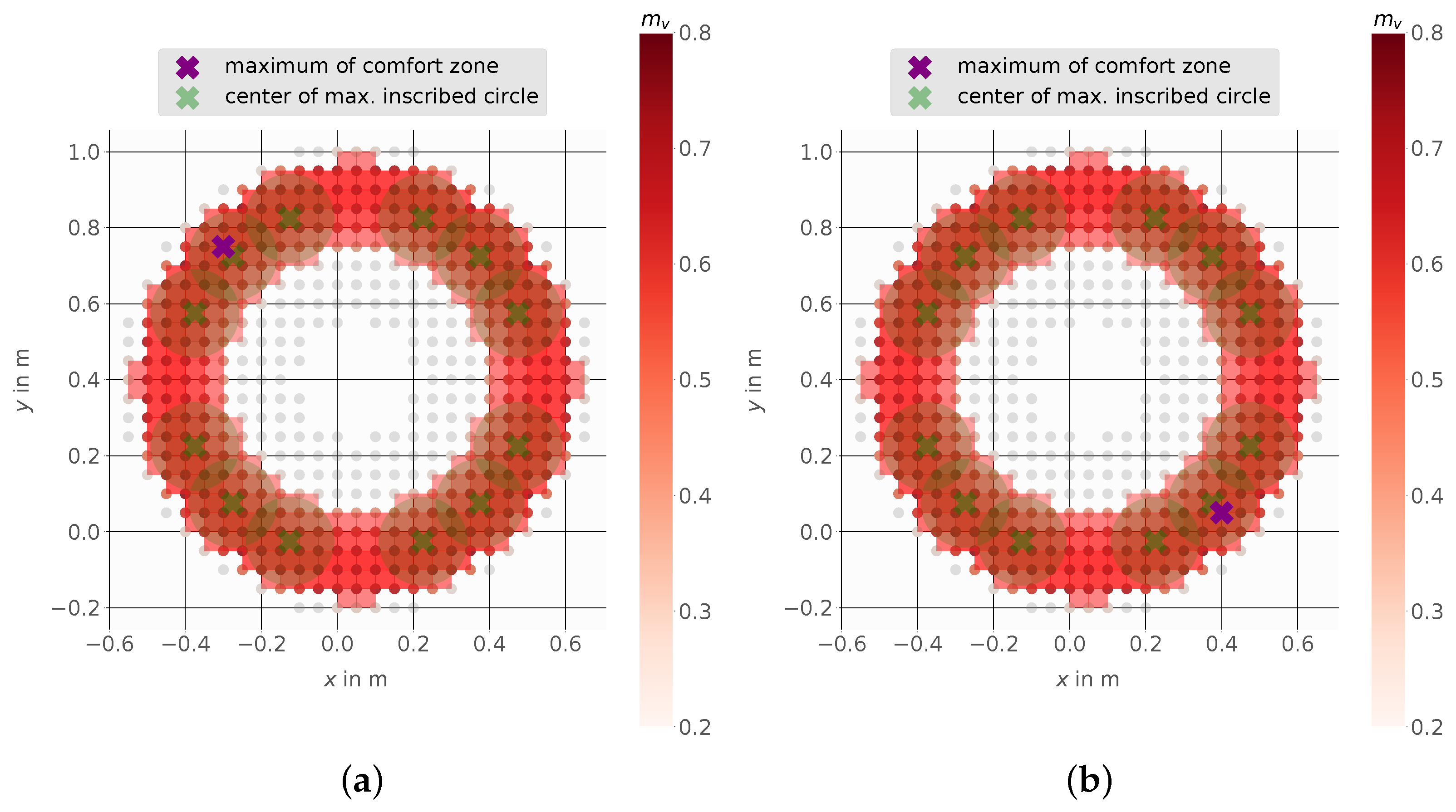
3.5. Comfort Zone Definition
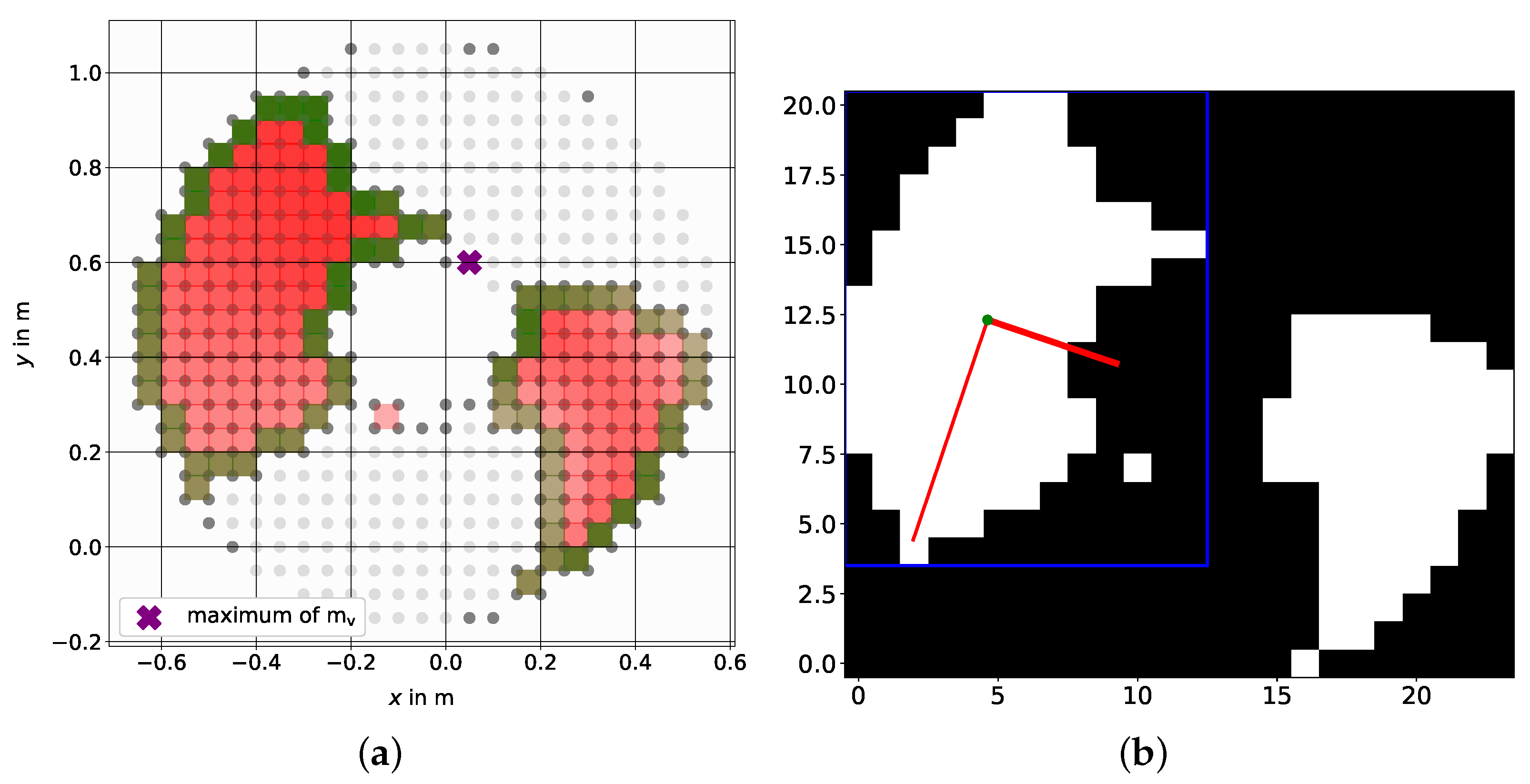
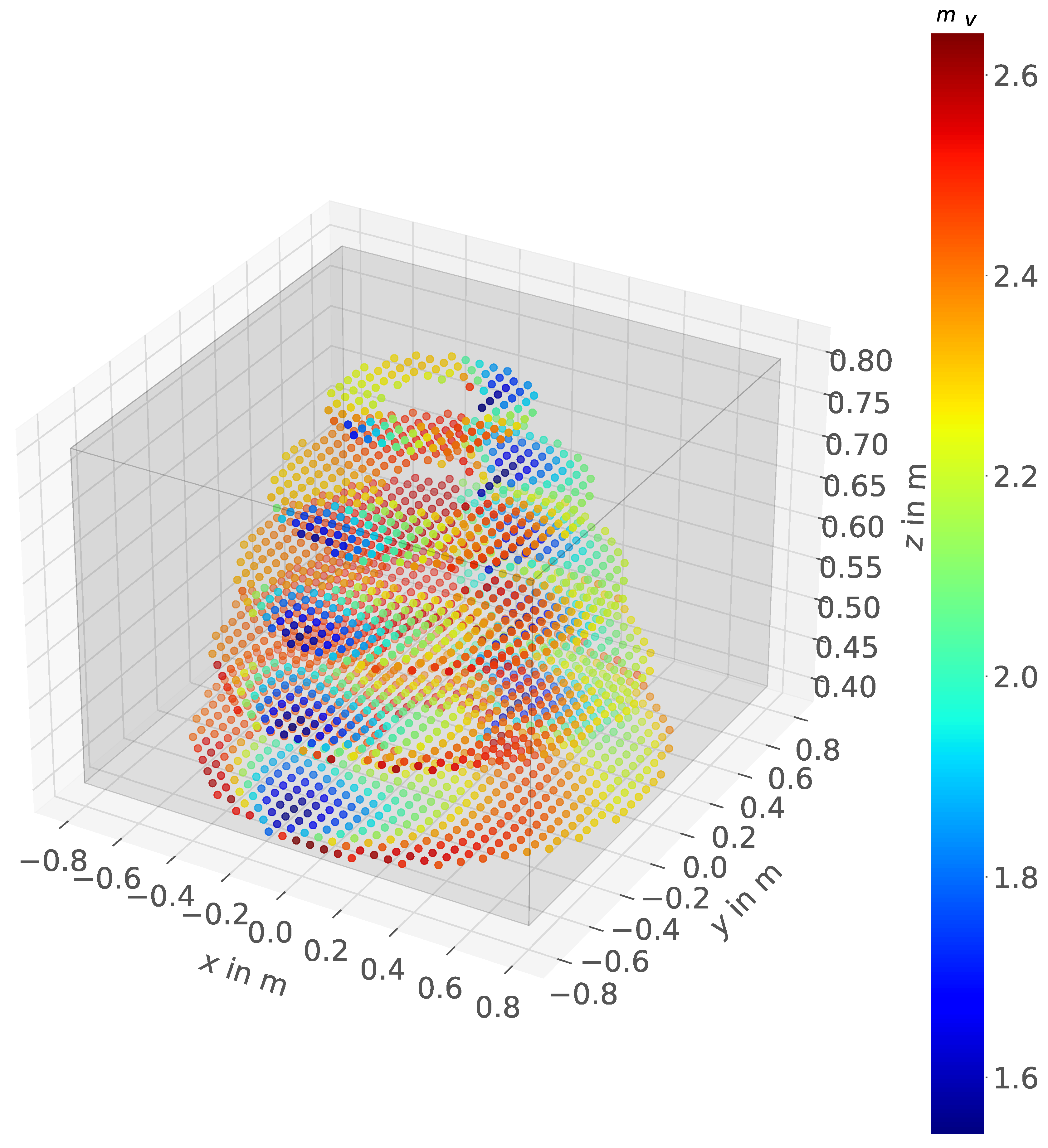
3.6. Comfort Zone Mesh Representation and Target Points
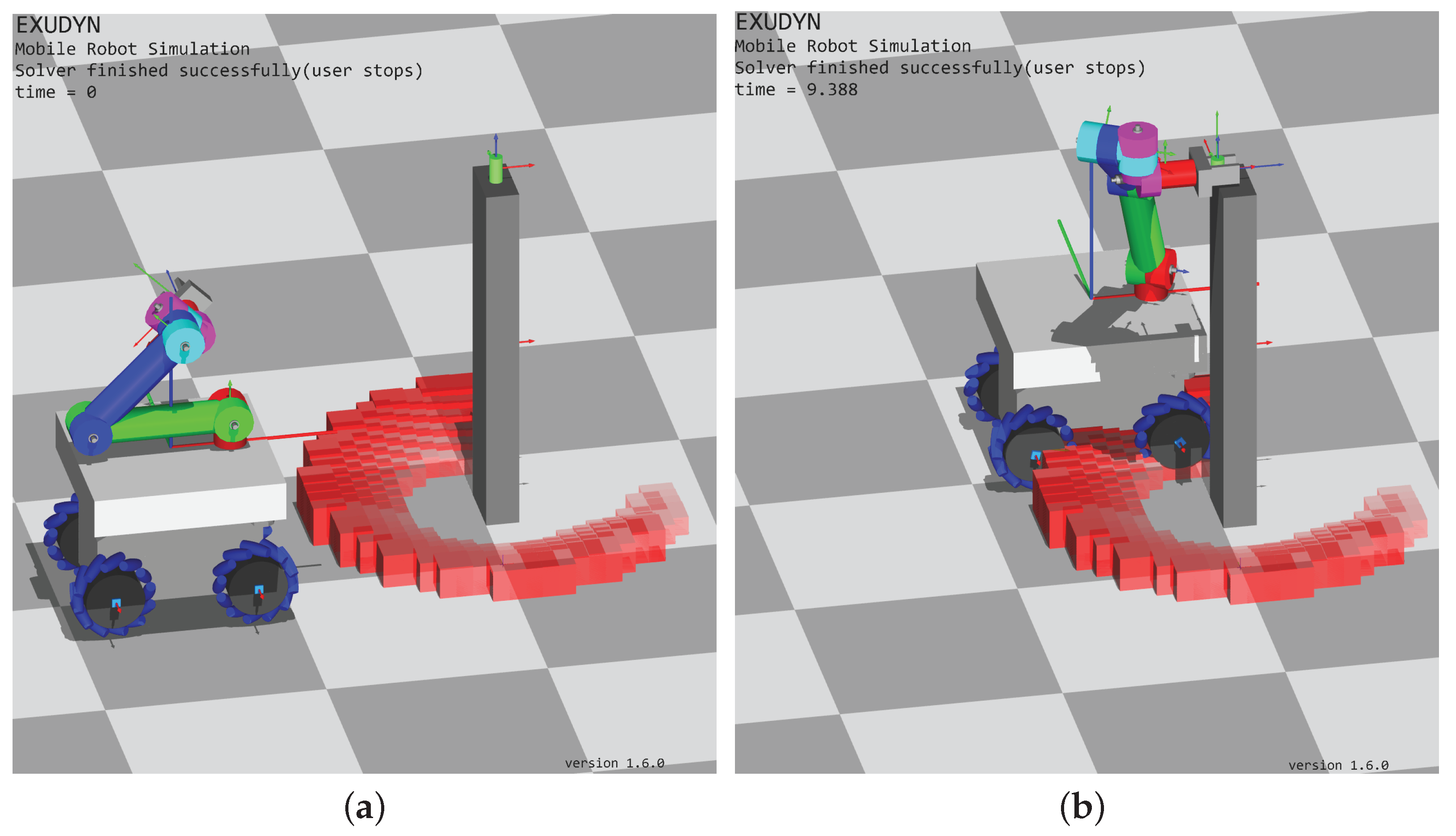
4. Comfort Zone Simulation Examples
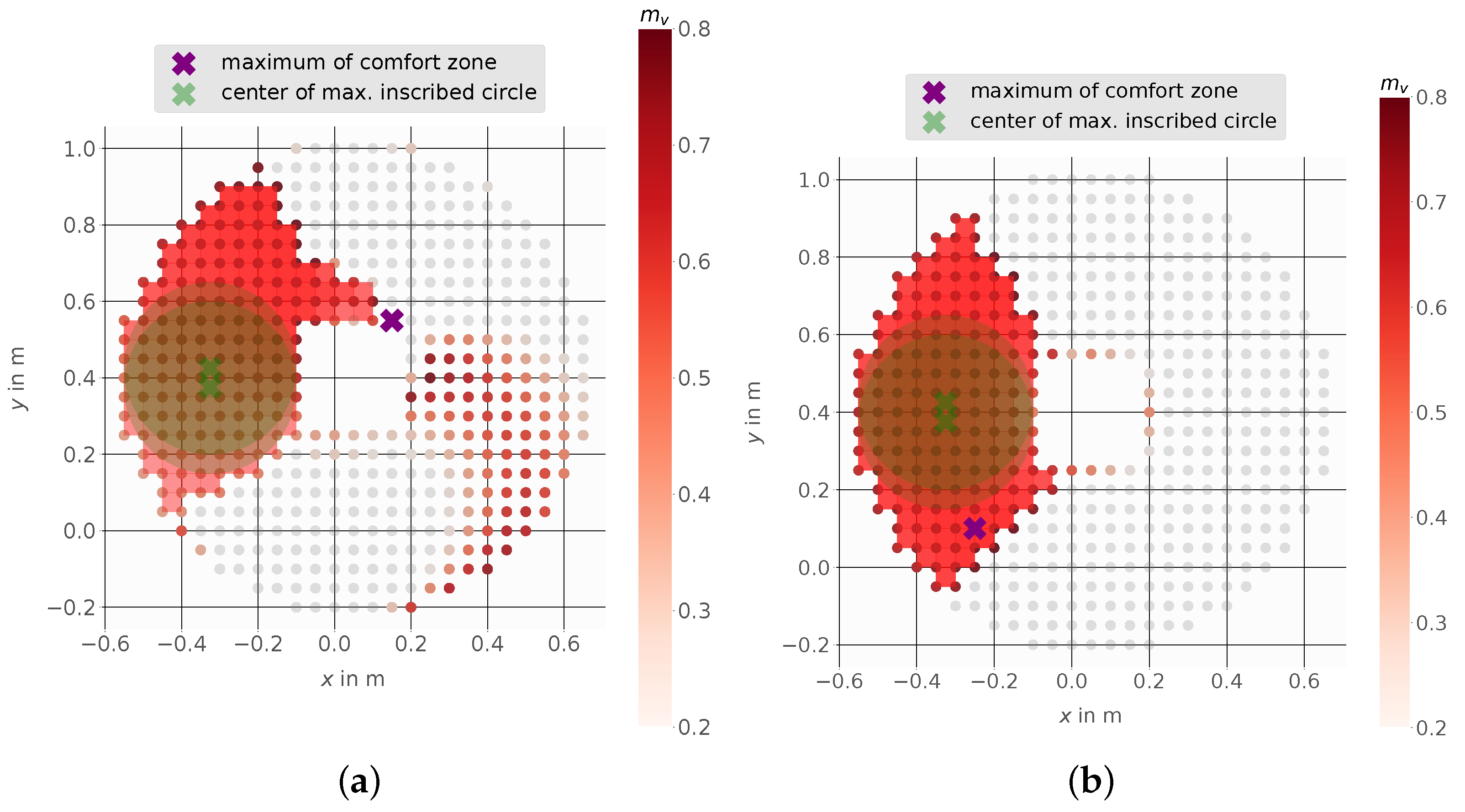
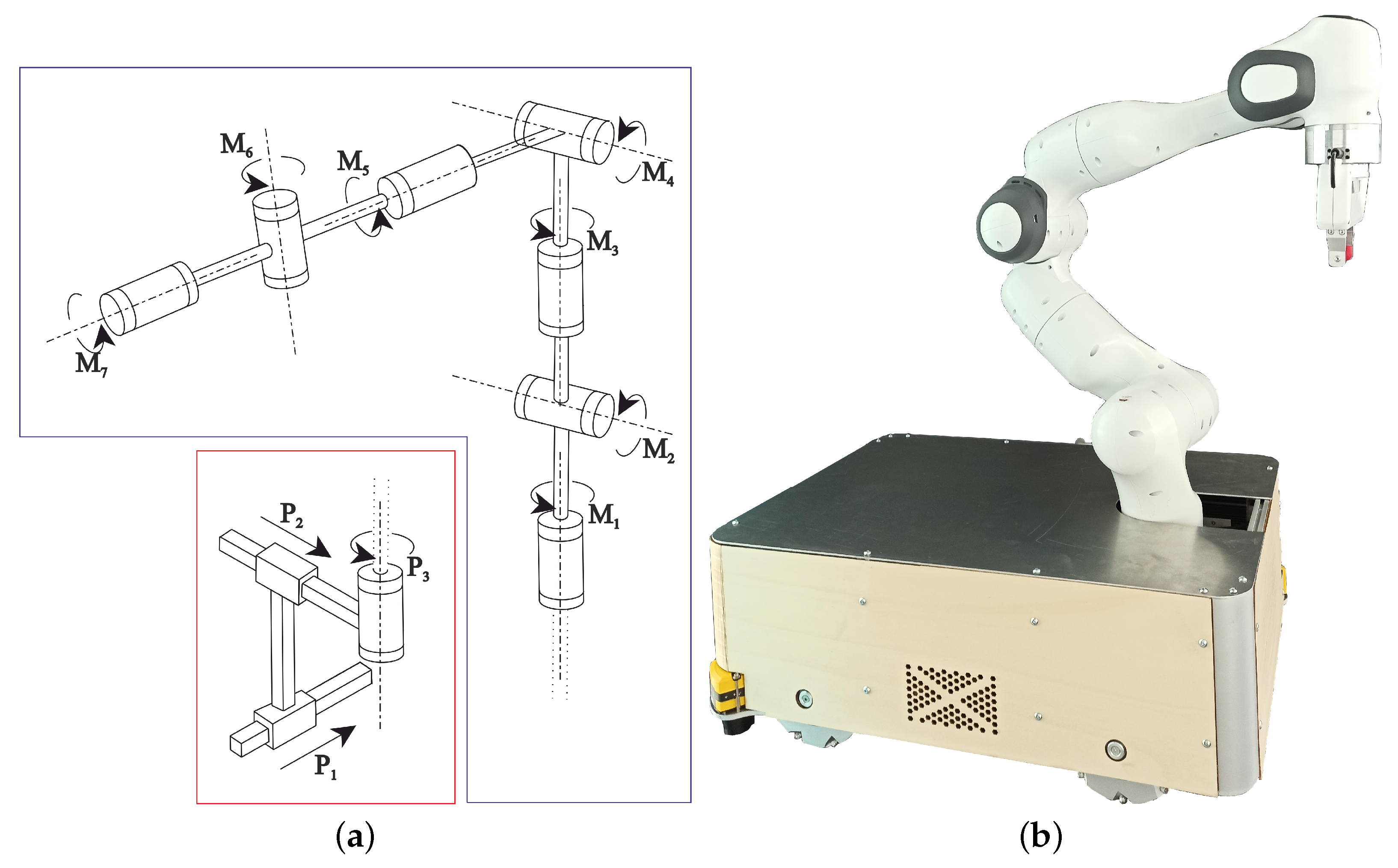
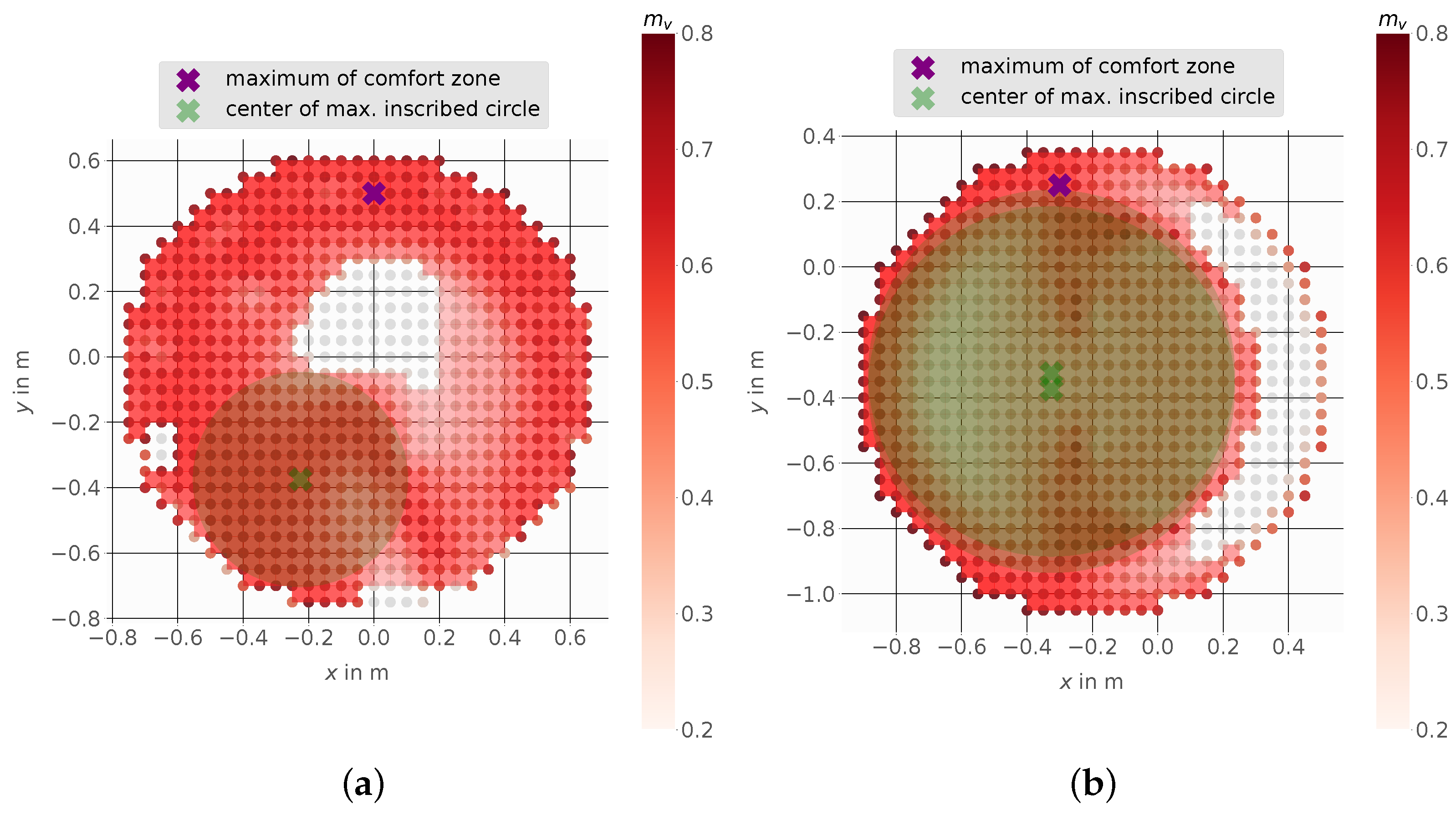
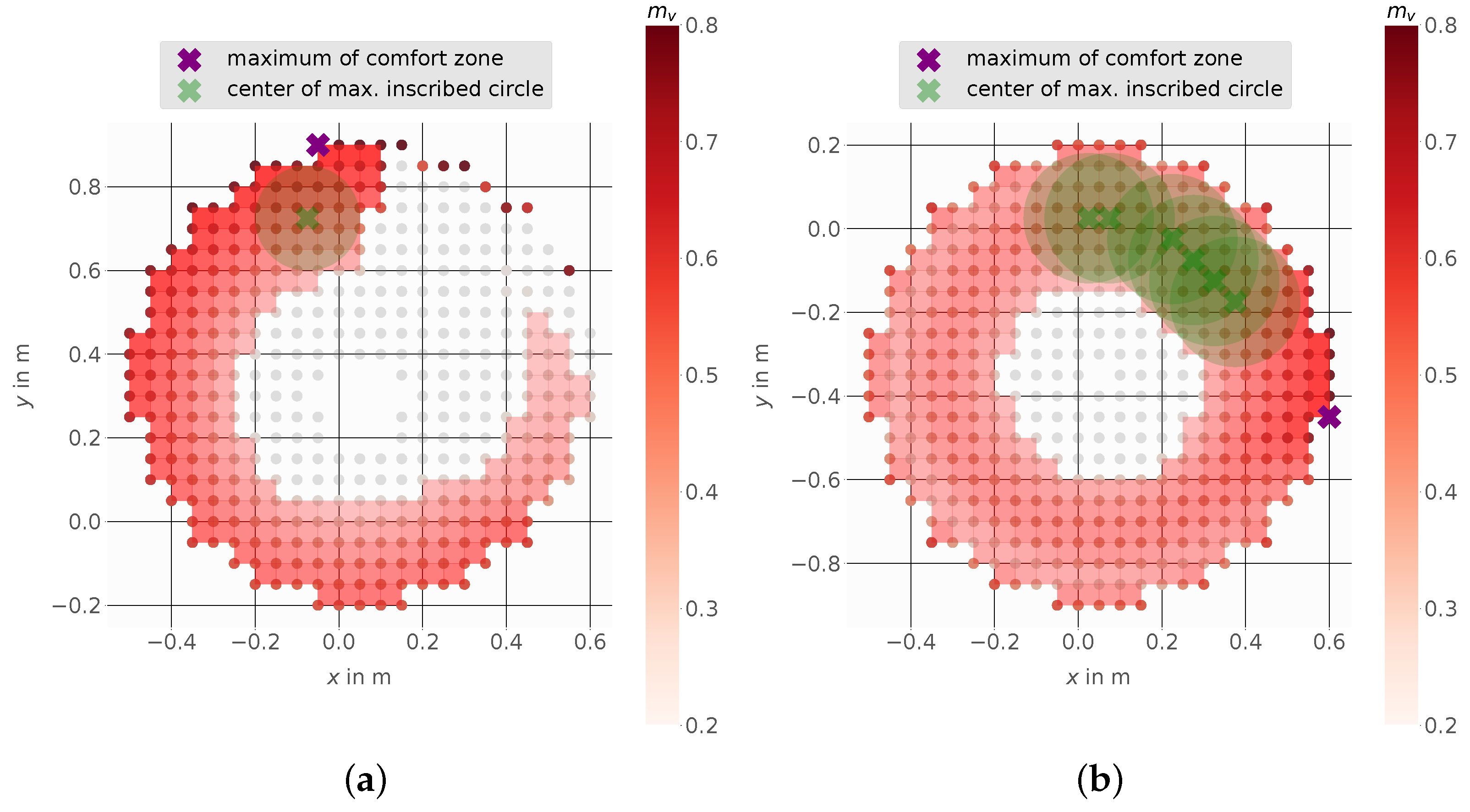
4.1. Stanford Robotics Platform
4.2. Mobile Manipulator LeoBot
4.3. Mobile Manipulator Kairos
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brandstötter, M.; Mirkovic, D.; Hofbaur, M. Mobile Manipulation—Eine altbekannte Technologie findet durch sensitive Robotertechnologie Einzug in die Industrie. In Proceedings of the C-AR2017—Conference on Automation and Robotics, Linz, Austria, 16–17 May 2017; pp. 1–6. [Google Scholar]
- Sereinig, M.; Werth, W.; Faller, L.M. A review of the challenges in mobile manipulation: Systems design and RoboCup challenges. Elektrotech. Informationstechnik 2020, 137, 297–308. [Google Scholar] [CrossRef]
- Haviland, J.; Sünderhauf, N.; Corke, P. A Holistic Approach to Reactive Mobile Manipulation. IEEE Robot. Autom. Lett. 2022, 7, 3122–3129. [Google Scholar] [CrossRef]
- Manzl, P.; Gerstmayr, J. An Improved Dynamic Model of the Mecanum Wheel for Multibody Simulations. In Proceedings of the Volume 9: 17th International Conference on Multibody Systems, Nonlinear Dynamics, and Control (MSNDC), International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Boston, MA, USA, 17–20 August 2021. [Google Scholar] [CrossRef]
- Luca, A.D.; Oriolo, G.; Giordano, P.R. Kinematic modeling and redundancy resolution for nonholonomic mobile manipulators. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, ICRA 2006, Orlando, FL, USA, 15–19 May 2006; pp. 1867–1873. [Google Scholar] [CrossRef]
- Chiaverini, S. Singularity-robust task-priority redundancy resolution for real-time kinematic control of robot manipulators. IEEE Trans. Robot. Autom. 1997, 13, 398–410. [Google Scholar] [CrossRef]
- Siciliano, B.; Khatib, O. Springer Handbook of Robotics; Springer Handbooks; Springer International Publishing: Berlin/Heideilberg, Germany, 2016. [Google Scholar]
- Zanchettin, A.M.; Rocco, P.; Bascetta, L.; Symeonidis, I.; Peldschus, S. Kinematic motion analysis of the human arm during a manipulation task. In Proceedings of the ISR 2010 (41st International Symposium on Robotics) and ROBOTIK 2010 (6th German Conference on Robotics), Munich, Germany, 7–9 June 2010; Volume 2, pp. 1–6. [Google Scholar]
- ISO15066; Robots and Robotic Devices—Collaborative Robots. International Organization for Standardization. Edition 1, 2016. Available online: https://www.iso.org/obp/ui/en/#iso:std:iso:ts:15066:ed-1:v1:en (accessed on 3 August 2024).
- ISO10218; Robots and Robotic Devices—Safety Requirements for Industrial Robots—Part 1: Robots. International Organization for Standardization. Edition 2, 2011. Available online: https://www.iso.org/obp/ui/en/#iso:std:iso:10218:-1:ed-2:v1:en (accessed on 3 August 2024).
- Rastegarpanah, A.; Gonzalez, H.C.; Stolkin, R. Semi-Autonomous Behaviour Tree-Based Framework for Sorting Electric Vehicle Batteries Components. Robotics 2021, 10, 82. [Google Scholar] [CrossRef]
- Saoji, S.; Rosell, J. Flexibly configuring task and motion planning problems for mobile manipulators. In Proceedings of the 2020 25th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Vienna, Austria, 8–11 September 2020; Volume 1, pp. 1285–1288. [Google Scholar] [CrossRef]
- Castaman, N.; Pagello, E.; Menegatti, E.; Pretto, A. Receding Horizon Task and Motion Planning in Changing Environments. Robot. Auton. Syst. 2021, 145, 103863. [Google Scholar] [CrossRef]
- Brock, O.; Kavraki, L. Decomposition-based motion planning: A framework for real-time motion planning in high-dimensional configuration spaces. In Proceedings of the 2001 ICRA IEEE International Conference on Robotics and Automation (Cat. No.01CH37164), Seoul, Republic of Korea, 21–26 May 2001; Volume 2, pp. 1469–1474. [Google Scholar] [CrossRef]
- Su, J.; Xie, W. Motion Planning and Coordination for Robot Systems Based on Representation Space. IEEE Trans. Syst. Man Cybern. Part B 2011, 41, 248–259. [Google Scholar] [CrossRef]
- LaValle, S.M.; Kuffner, J.J. Randomized Kinodynamic Planning. Int. J. Robot. Res. 2001, 41, 378–400. [Google Scholar] [CrossRef]
- Kavraki, L.; Svestka, P.; Latombe, J.C.; Overmars, M. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- Hsu, D.; Latombe, J.C.; Motwani, R. Path planning in expansive configuration spaces. In Proceedings of the International Conference on Robotics and Automation, Albuquerque, NM, USA, 20–25 April 1997; Volume 3, pp. 2719–2726. [Google Scholar] [CrossRef]
- Ratliff, N.; Zucker, M.; Bagnell, J.A.; Srinivasa, S. CHOMP: Gradient optimization techniques for efficient motion planning. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 489–494. [Google Scholar] [CrossRef]
- Kalakrishnan, M.; Chitta, S.; Theodorou, E.; Pastor, P.; Schaal, S. STOMP: Stochastic trajectory optimization for motion planning. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 4569–4574. [Google Scholar] [CrossRef]
- Coleman, D.; Sucan, I.; Chitta, S.; Correll, N. Reducing the Barrier to Entry of Complex Robotic Software: A MoveIt! Case Study. arXiv 2014. [Google Scholar] [CrossRef]
- Sandakalum, T.; Ang, M.H. Motion Planning for Mobile Manipulators: A Systematic Review. Machines 2022, 10, 97. [Google Scholar] [CrossRef]
- Makhal, A.; Goins, A.K. Reuleaux: Robot Base Placement by Reachability Analysis. In Proceedings of the 2018 Second IEEE International Conference on Robotic Computing (IRC), Laguna Hills, CA, USA, 13 January–1 February 2018; pp. 137–142. [Google Scholar]
- Zhang, H.; Sheng, Q.; Sun, Y.; Sheng, X.; Xiong, Z.; Zhu, X. A novel coordinated motion planner based on capability map for autonomous mobile manipulator. Robot. Auton. Syst. 2020, 129, 103554. [Google Scholar] [CrossRef]
- Zhang, H.; Sheng, Q.; Hu, J.; Sheng, X.; Xiong, Z.; Zhu, X. Cooperative Transportation with Mobile Manipulator: A Capability Map-Based Framework for Physical Human–Robot Collaboration. IEEE/ASME Trans. Mechatron. 2022, 27, 4396–4405. [Google Scholar] [CrossRef]
- Yoshikawa, T. Manipulability of Robotic Mechanisms. Int. J. Robot. Res. 1985, 4, 3–9. [Google Scholar] [CrossRef]
- Zacharias, F.; Borst, C.; Hirzinger, G. Capturing robot workspace structure: Representing robot capabilities. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 3229–3236. [Google Scholar] [CrossRef]
- Sereinig, M.; Manzl, P.; Gerstmayr, J. Komfortzone mobiler Manipulatoren. In Proceedings of the Sechste IFToMM D-A-CH Konferenz 2020, Campus Technik Lienz, Lienz, Austria, 27–28 February 2020; Volume 2020. [Google Scholar] [CrossRef]
- Spong, M.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Lynch, K.M.; Park, F.C. Modern Robotics: Mechanics, Planning, and Control, 1st ed.; Cambridge University Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Corke, P. Robotics, Vision and Control: Fundamental Algorithms in MATLAB, 1st ed.; Springer Publishing Company, Inc.: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Kim, J.-O.; Khosla, K. Dexterity measures for design and control of manipulators. In Proceedings of the IROS ’91: IEEE/RSJ International Workshop on Intelligent Robots and Systems, Osaka, Japan, 3–5 November 1991; Volume 2, pp. 758–763. [Google Scholar]
- Melchiorri, C. Force manipulability ellipsoids for general manipulation systems. IFAC Proc. Vol. 1994, 27, 235–240. [Google Scholar] [CrossRef]
- Ajoudani, A.; Tsagarakis, N.G.; Bicchi, A. Choosing Poses for Force and Stiffness Control. IEEE Trans. Robot. 2017, 33, 1483–1490. [Google Scholar] [CrossRef]
- Chen, C.; Peng, F.; Yan, R.; Li, Y.; Wei, D.; Fan, Z.; Tang, X.; Zhu, Z. Stiffness performance index based posture and feed orientation optimization in robotic milling process. Robot. Comput.-Integr. Manuf. 2019, 55, 29–40. [Google Scholar] [CrossRef]
- Kövecses, J.; Angeles, J. The stiffness matrix in elastically articulated rigid-body systems. Multibody Syst. Dyn. 2007, 18, 169–184. [Google Scholar] [CrossRef]
- Dumas, C.; Caro, S.; Cherif, M.; Garnier, S.; Furet, B. Joint stiffness identification of industrial serial robots. Robotica 2012, 30, 649–659. [Google Scholar] [CrossRef]
- Busson, D.; Bearee, R.; Olabi, A. Task-oriented rigidity optimization for 7 DOF redundant manipulators. IFAC-PapersOnLine 2017, 50, 14588–14593. [Google Scholar] [CrossRef]
- Salisbury, J.K. Active stiffness control of a manipulator in cartesian coordinates. In Proceedings of the 19th IEEE Conference on Decision and Control including the Symposium on Adaptive Processes, Albuquerqe, NM, USA, 10–12 December 1980; pp. 95–100. [Google Scholar]
- Guo, Y.; Dong, H.; Ke, Y. Stiffness-oriented posture optimization in robotic machining applications. Robot. Comput.-Integr. Manuf. 2015, 35, 69–76. [Google Scholar] [CrossRef]
- Yoshikawa, T. Dynamic Manipulability of Robot Manipulators. Trans. Soc. Instrum. Control. Eng. 1985, 21, 970–975. [Google Scholar] [CrossRef]
- Chiacchio, P.; Concilio, M. The dynamic manipulability ellipsoid for redundant manipulators. IEEE Int. Conf. Robot. Autom. 1998, 1, 95–100. [Google Scholar] [CrossRef]
- El Makrini, I.; Merckaert, K.; De Winter, J.; Lefeber, D.; Vanderborght, B. Task allocation for improved ergonomics in Human-Robot Collaborative Assembly. Interact. Stud. 2019, 20, 103–134. [Google Scholar] [CrossRef]
- Burdet, E.; Osu, R.; Franklin, D.W.; Milner, T.E.; Kawato, M. The central nervous system stabilizes unstable dynamics by learning optimal impedance. Nature 2001, 414, 446–449. [Google Scholar] [CrossRef]
- Khatib, O. A unified approach for motion and force control of robot manipulators: The operational space formulation. IEEE J. Robot. Autom. 1987, 3, 43–53. [Google Scholar] [CrossRef]
- Chen, H.; Lee, S.I.; Do, J.H.; Lee, J.M. Directional Manipulability to Improve Performance Index of Dual Arm Manipulator for Object Grasping. In Intelligent Autonomous Systems 12: Volume 1 Proceedings of the 12th International Conference IAS-12, Jeju Island, Republic of Korea, 26–29 June 2012; Lee, S., Cho, H., Yoon, K.J., Lee, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 595–602. [Google Scholar] [CrossRef]
- Kraetzschmar, G.K.; Hochgeschwender, N.; Nowak, W.; Hegger, F.; Schneider, S.; Dwiputra, R.; Berghofer, J.; Bischoff, R. RoboCup@Work: Competing for the Factory of the Future. In RoboCup 2014: Robot World Cup XVIII; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 171–182. [Google Scholar] [CrossRef]
- Abdel-Malek, K.; Yang, J. Workspace boundaries of serial manipulators using manifold stratification. Int. J. Adv. Manuf. Technol. 2006, 28, 1211–1229. [Google Scholar] [CrossRef]
- Cao, Y.; Lu, K.; Li, X.; Zang, Y. Accurate Numerical Methods for Computing 2D and 3D Robot Workspace. Int. J. Adv. Robot. Syst. 2011, 8, 76. [Google Scholar] [CrossRef]
- Patel, S.; Sobh, T. Task based synthesis of serial manipulators. J. Adv. Res. 2015, 6, 479–492. [Google Scholar] [CrossRef]
- Van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T.; The Scikit-Image Contributors. scikit-image: Image processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef]
- Fiorio, C.; Gustedt, J. Two linear time Union-Find strategies for image processing. Theor. Comput. Sci. 1996, 154, 165–181. [Google Scholar] [CrossRef]
- Jähne, B. Digital Image Processing, 6th ed.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar] [CrossRef]
- Felzenszwalb, P.; Huttenlocher, D. Distance Transforms of Sampled Functions. Theory Comput. 2004, 8, 415–428. [Google Scholar] [CrossRef]
- Doty, K.L.; Melchiorri, C.; Schwartz, E.M.; Bonivento, C. Robot manipulability. IEEE Trans. Robot. Autom. 1995, 11, 462–468. [Google Scholar] [CrossRef]
- Gerstmayr, J. Exudyn—A C++ based Python package for flexible multibody systems. Multibody Syst. Dyn. 2023, 60, 533–561. [Google Scholar] [CrossRef]
- Sugihara, T. Solvability-Unconcerned Inverse Kinematics by the Levenberg–Marquardt Method. IEEE Trans. Robot. 2011, 27, 984–991. [Google Scholar] [CrossRef]
- Corke, P.; Haviland, J. Not your grandmother’s toolbox—The Robotics Toolbox reinvented for Python. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 11357–11363. [Google Scholar]
- Holmberg, R.; Khatib, O. Development and Control of a Holonomic Mobile Robot for Mobile Manipulation Tasks. Int. J. Robot. Res. 2000, 19, 1066–1074. [Google Scholar] [CrossRef]
- Chang, K.S.; Holmberg, R.; Khatib, O. The augmented object model: Cooperative manipulation and parallel mechanism dynamics. In Proceedings of the ICRA, IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 24–28 April 2000; Volume 1, pp. 470–475. [Google Scholar] [CrossRef]
- Corke, P.I. Visual Control of Robots: High-Performance Visual Serving; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1997. [Google Scholar]
- Kim, H.; Streit, D. Configuration dependent stiffness of the PUMA 560 manipulator: Analytical and experimental results. Mech. Mach. Theory 1995, 30, 1269–1277. [Google Scholar] [CrossRef]
- Sereinig, M.; Manzl, P.; Hofmann, P.; Neurauter, R.; Pieber, M.; Gerstmayr, J. Omnidirectional Mobile Manipulator LeoBot for Industrial Environments, Developed for Research and Teaching. In Proceedings of the RoboCup 2022; Eguchi, A., Lau, N., Paetzel-Prüsmann, M., Wanichanon, T., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2023; pp. 127–139. [Google Scholar] [CrossRef]
- Gaz, C.; Cognetti, M.; Oliva, A.; Robuffo Giordano, P.; De Luca, A. Dynamic Identification of the Franka Emika Panda Robot with Retrieval of Feasible Parameters Using Penalty-Based Optimization. IEEE Robot. Autom. Lett. 2019, 4, 4147–4154. [Google Scholar] [CrossRef]
- Kebria, P.M.; Al-wais, S.; Abdi, H.; Nahavandi, S. Kinematic and dynamic modelling of UR5 manipulator. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 4229–4234. [Google Scholar]
- Kovincic, N.; Müller, A.; Gattringer, H.; Weyrer, M.; Schlotzhauer, A.; Brandstötter, M. Dynamic parameter identification of the Universal Robots UR5. In Proceedings of the ARW & OAGM Workshop 2019, Graz, Austria, 9–10 May 2019; pp. 44–53. [Google Scholar] [CrossRef]
- Lu, D.V.; Hershberger, D.; Smart, W.D. Layered costmaps for context-sensitive navigation. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 709–715. [Google Scholar] [CrossRef]
- Marder-Eppstein, E.; Berger, E.; Foote, T.; Gerkey, B.; Konolige, K. The Office Marathon: Robust navigation in an indoor office environment. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AL, USA, 3–8 May 2010; pp. 300–307. [Google Scholar] [CrossRef]







| Symbol | Formula | Description |
|---|---|---|
| Equation (13) | Proportional to the volume of the EE velocity ellipsoid, which represents the ability to move the EE with a certain velocity in all directions. | |
| Equation (17) | Proportional to the volume of the EE force ellipsoid, which represents the ability to act with a certain force in all directions. | |
| Equation (26) | Represents the minimum eigenvalue of the Cartesian stiffness matrix, which characterizes the smallest stiffness in a certain configuration. | |
| Equation (34) | Represents the minimum eigenvalue of the weighted dynamic manipulability matrix, which characterizes the smallest acceleration in a certain direction. |
| Task Type | Velocity | Force | Stiffness | Acceleration |
|---|---|---|---|---|
| Pick and Place | High | Moderate | Low | High |
| Assembly | Moderate | High | High | Moderate |
| Painting | Moderate | Low | Low | Low |
| Milling | Low | High | High | Low |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sereinig, M.; Manzl, P.; Gerstmayr, J. Task-Dependent Comfort Zone, a Base Placement Strategy for Mobile Manipulators Based on Manipulability Measures. Robotics 2024, 13, 122. https://doi.org/10.3390/robotics13080122
Sereinig M, Manzl P, Gerstmayr J. Task-Dependent Comfort Zone, a Base Placement Strategy for Mobile Manipulators Based on Manipulability Measures. Robotics. 2024; 13(8):122. https://doi.org/10.3390/robotics13080122
Chicago/Turabian StyleSereinig, Martin, Peter Manzl, and Johannes Gerstmayr. 2024. "Task-Dependent Comfort Zone, a Base Placement Strategy for Mobile Manipulators Based on Manipulability Measures" Robotics 13, no. 8: 122. https://doi.org/10.3390/robotics13080122
APA StyleSereinig, M., Manzl, P., & Gerstmayr, J. (2024). Task-Dependent Comfort Zone, a Base Placement Strategy for Mobile Manipulators Based on Manipulability Measures. Robotics, 13(8), 122. https://doi.org/10.3390/robotics13080122






