Design and Evaluation of a Novel Passive Shoulder Exoskeleton Based on a Variable Stiffness Mechanism Torque Generator for Industrial Applications †
Abstract
1. Introduction
2. Basic Design Concept of the VSM Torque Generator
3. Design Implementation of the Exoskeleton
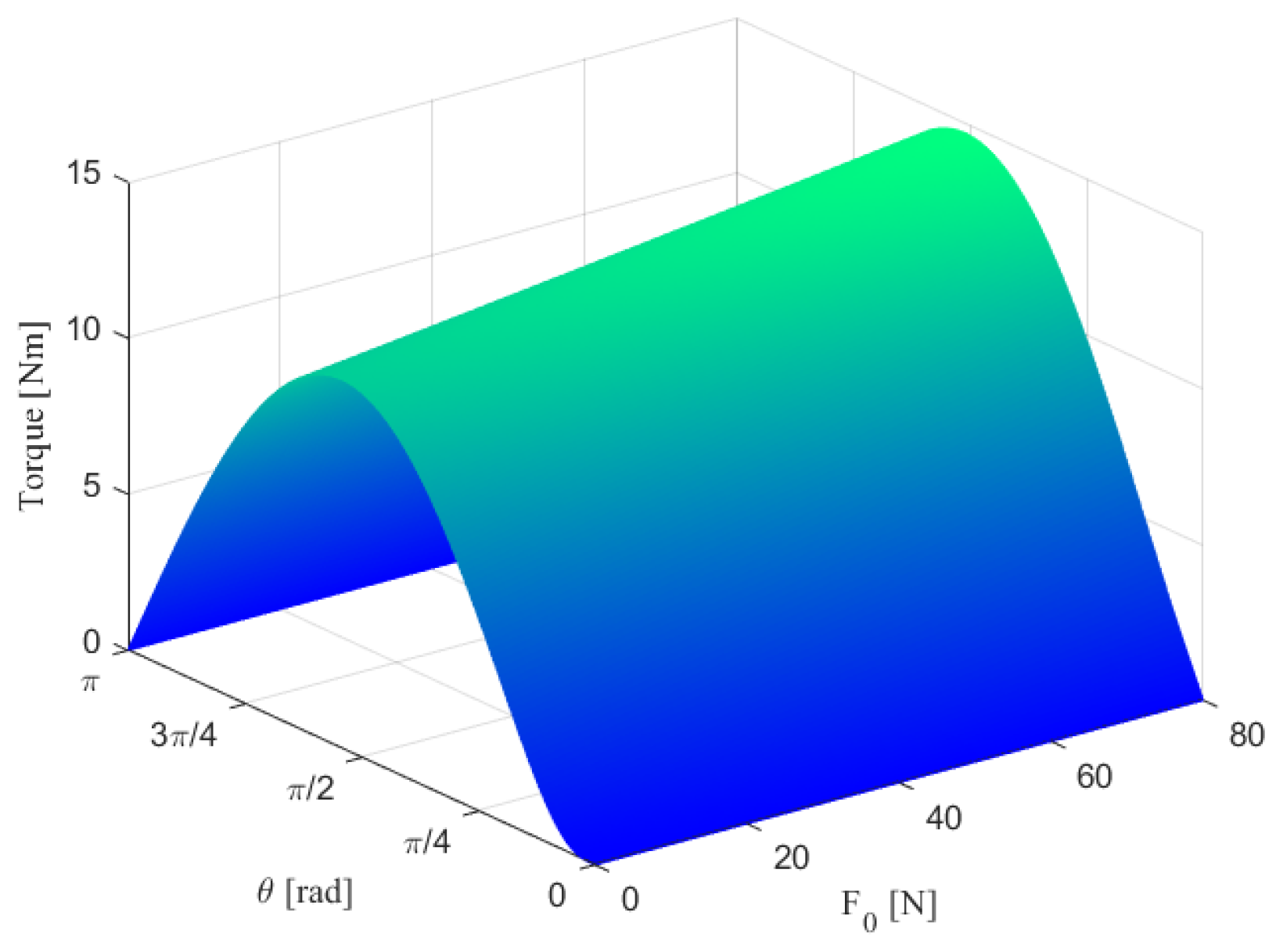
3.1. Parameter Optimization of the VSM
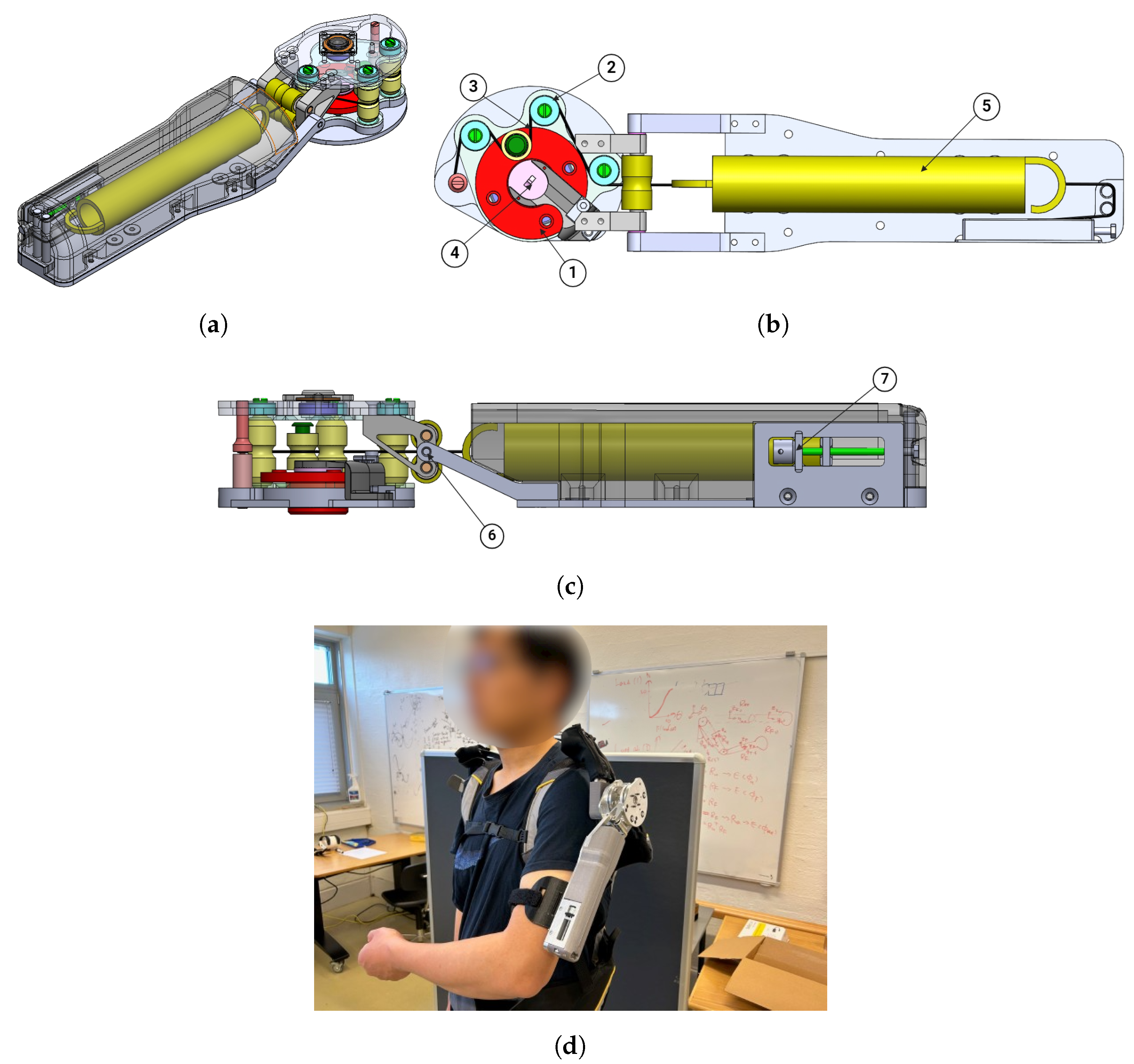
3.2. Prototype Development
4. Workspace Analysis of the Exoskeleton
5. Performance Evaluation of the Exoskeleton
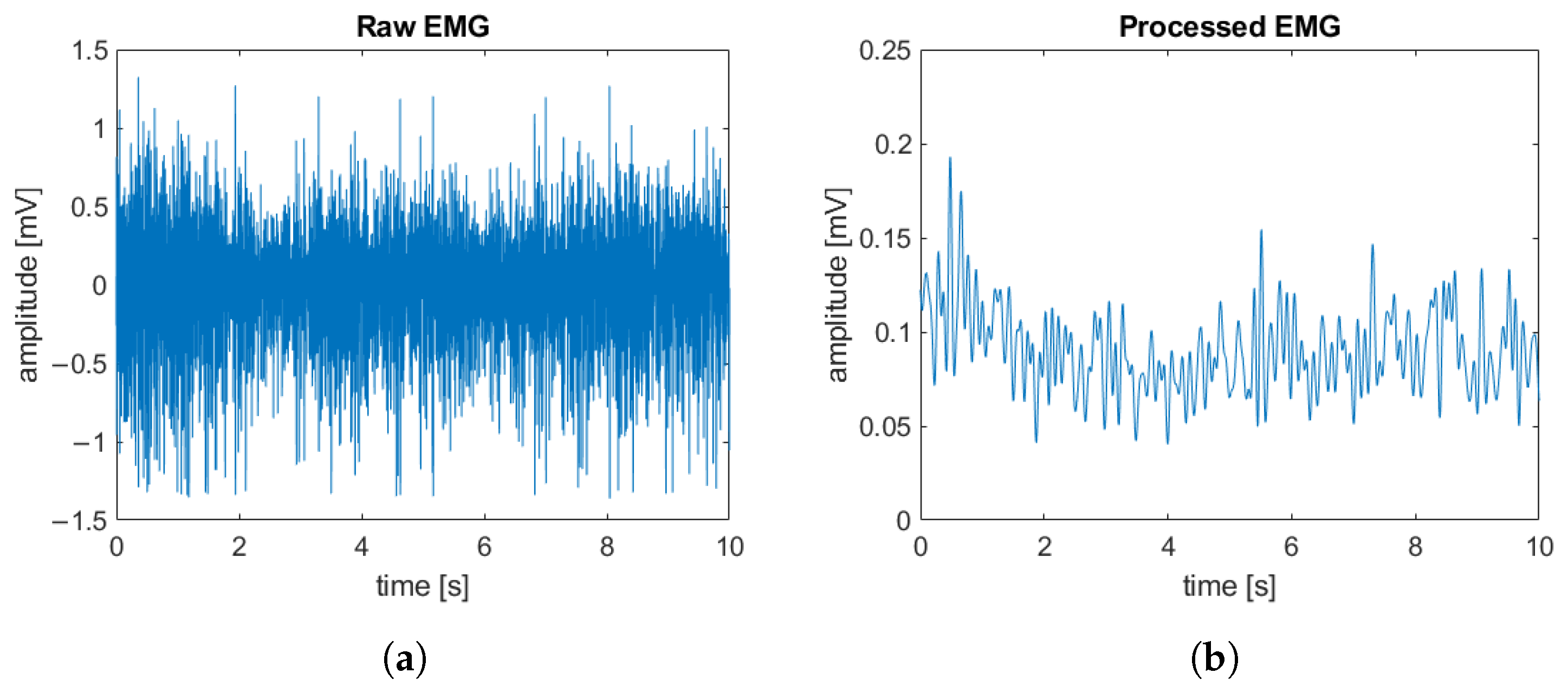
5.1. Experimental Protocol
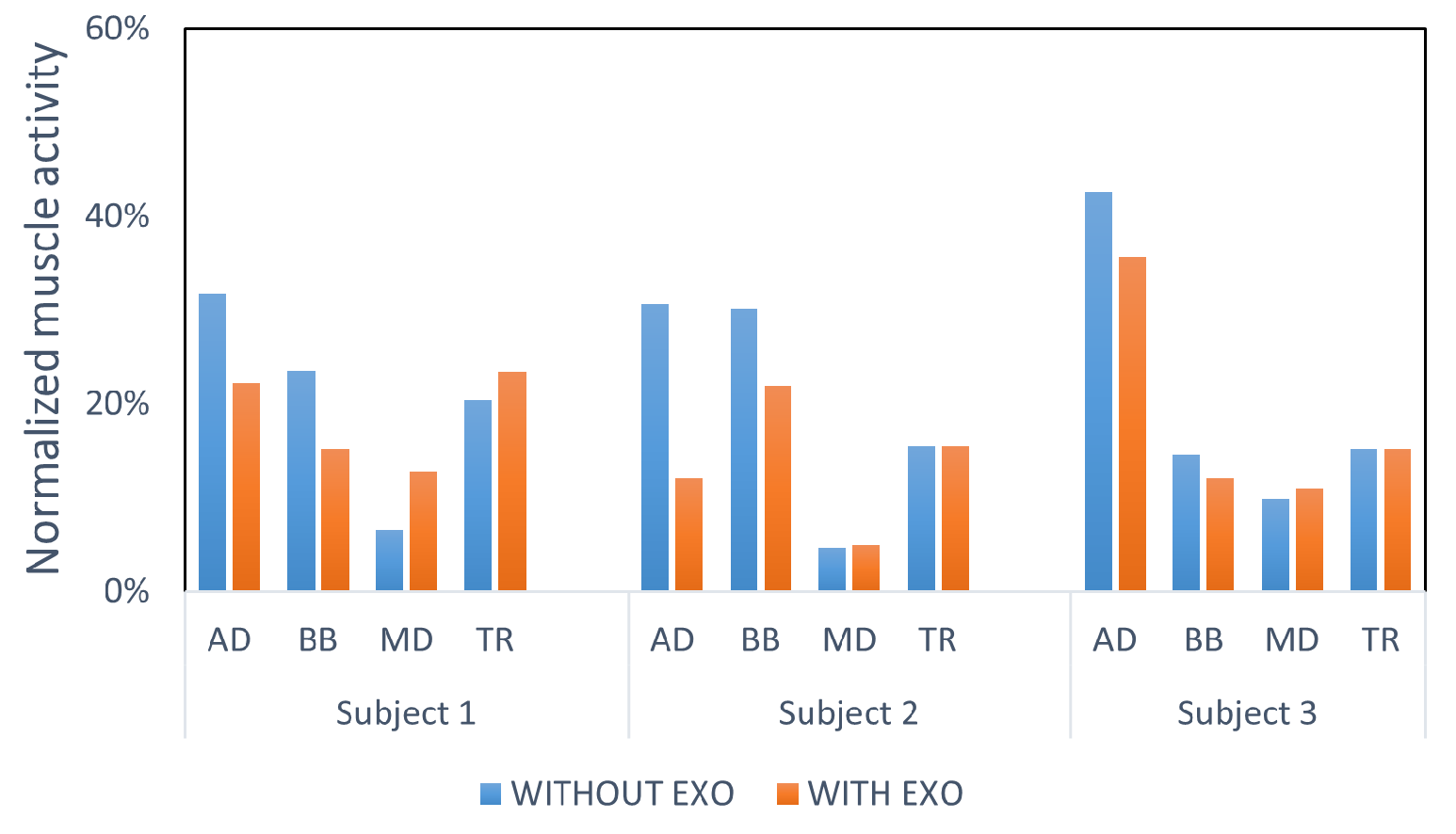
5.2. Results
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gull, M.A.; Bai, S.; Bak, T. A review on design of upper limb exoskeletons. Robotics 2020, 9, 16. [Google Scholar] [CrossRef]
- Qiu, S.; Pei, Z.; Wang, C.; Tang, Z. Systematic review on wearable lower extremity robotic exoskeletons for assisted locomotion. J. Bionic Eng. 2023, 20, 436–469. [Google Scholar] [CrossRef]
- Massardi, S.; Rodriguez-Cianca, D.; Pinto-Fernandez, D.; Moreno, J.C.; Lancini, M.; Torricelli, D. Characterization and evaluation of human–exoskeleton interaction dynamics: A review. Sensors 2022, 22, 3993. [Google Scholar] [CrossRef] [PubMed]
- Steinhilber, B.; Luger, T.; Schwenkreis, P.; Middeldorf, S.; Bork, H.; Mann, B.; von Glinski, A.; Schildhauer, T.A.; Weiler, S.; Schmauder, M.; et al. The use of exoskeletons in the occupational context for primary, secondary, and tertiary prevention of work-related musculoskeletal complaints. IISE Trans. Occup. Ergon. Hum. Factors 2020, 8, 132–144. [Google Scholar] [CrossRef] [PubMed]
- Govaerts, R.; Tassignon, B.; Ghillebert, J.; Serrien, B.; De Bock, S.; Ampe, T.; El Makrini, I.; Vanderborght, B.; Meeusen, R.; De Pauw, K. Prevalence and incidence of work-related musculoskeletal disorders in secondary industries of 21st century Europe: A systematic review and meta-analysis. BMC Musculoskelet. Disord. 2021, 22, 1–30. [Google Scholar] [CrossRef] [PubMed]
- Altundaş Hatman, E.; Öngel, F.S.; Yavuz, M.E.; Gülenç, N. Work-related diseases and risk factors associated with work-related musculoskeletal disorders among unionized metal industry workers: A cross-sectional study. Int. J. Occup. Saf. Ergon. 2024, 30, 194–204. [Google Scholar] [CrossRef] [PubMed]
- Ayub, Y.; Shah, Z. Assessment of work related musculoskeletal disorders in manufacturing industry. J. Ergon. 2018, 8, 1–5. [Google Scholar] [CrossRef]
- Nur, N.M.; Dawal, S.Z.; Dahari, M. The prevalence of work related musculoskeletal disorders among workers performing industrial repetitive tasks in the automotive manufacturing companies. In Proceedings of the 2014 International Conference on Industrial Engineering and Operations Management, Bali, Indonesia, 7–9 January 2014; pp. 1–8. [Google Scholar]
- Voilqué, A.; Masood, J.; Fauroux, J.; Sabourin, L.; Guezet, O. Industrial exoskeleton technology: Classification, structural analysis, and structural complexity indicator. In Proceedings of the 2019 Wearable Robotics Association Conference (WearRAcon), Scottsdale, AZ, USA, 25–27 March 2019; pp. 13–20. [Google Scholar]
- Luger, T.; Bär, M.; Seibt, R.; Rieger, M.A.; Steinhilber, B. Using a back exoskeleton during industrial and functional tasks—Effects on muscle activity, posture, performance, usability, and wearer discomfort in a laboratory trial. Hum. Factors 2023, 65, 5–21. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.F.; Yeh, C.M.; Huang, S.L.; Ho, C.C.; Li, R.H.; Wang, W.H.; Tang, F.C. Work ability and quality of life in patients with work-related musculoskeletal disorders. Int. J. Environ. Res. Public Health 2020, 17, 3310. [Google Scholar] [CrossRef] [PubMed]
- Jan de, K.; Paul, V.; Jacqueline, S.; Georgios, R.; Martin, C.; Kees, P.; Pim van, D.; Isusi, I. Work-Related Musculoskeletal Disorders: Prevalence, Costs and Demographics in the EU; Publications Office: Luxembourg, 2019; p. 20. [Google Scholar] [CrossRef]
- Ding, S.; Narayan, A.; Reyes, F.A.; Han, S.; Yu, H. Design and control of a novel active shoulder exoskeleton for overhead work assistance. IEEE/ASME Trans. Mechatron. 2024, 1–10. [Google Scholar] [CrossRef]
- Li, Y.; Guan, X.; Han, X.; Tang, Z.; Meng, K.; Shi, Z.; Penzlin, B.; Yang, Y.; Ren, J.; Yang, Z.; et al. Design and preliminary validation of a lower limb exoskeleton with compact and modular actuation. IEEE Access 2020, 8, 66338–66352. [Google Scholar] [CrossRef]
- Pirjade, Y.; Londhe, D.; Patwardhan, N.; Kotkar, A.; Shelke, T.; Ohol, S. Design and fabrication of a low-cost human body lower limb exoskeleton. In Proceedings of the 6th International Conference on Mechatronics and Robotics Engineering (ICMRE), IEEE, Barcelona, Spain, 12–15 February 2020; pp. 32–37. [Google Scholar]
- Inose, H.; Mohri, S.; Yamada, Y.; Nakamura, T.; Yokoyama, K.; Kikutani, I. Development of a lightweight power-assist suit using pneumatic artificial muscles and balloon-amplification mechanism. In Proceedings of the 2016 14th International Conference on Control, Automation, Robotics and Vision (ICARCV), Phuket, Thailand, 13–15 November 2016; pp. 1–6. [Google Scholar]
- Porter, A.P.; Marchesini, B.; Potryasilova, I.; Rossetto, E.; Newman, D.J. Soft exoskeleton knee prototype for advanced space suits and planetary exploration. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–13. [Google Scholar]
- Xu, M.; Wang, G.; Rong, C. Fiber-reinforced flexible joint actuator for soft arthropod robots. Sens. Actuators Phys. 2022, 340, 113522. [Google Scholar] [CrossRef]
- Otten, A.; Voort, C.; Stienen, A.; Aarts, R.; van Asseldonk, E.; van der Kooij, H. LIMPACT: A hydraulically powered self-aligning upper limb exoskeleton. IEEE/ASME Trans. Mechatron. 2015, 20, 2285–2298. [Google Scholar] [CrossRef]
- Kim, H.; Shin, Y.J.; Kim, J. Design and locomotion control of a hydraulic lower extremity exoskeleton for mobility augmentation. Mechatronics 2017, 46, 32–45. [Google Scholar] [CrossRef]
- Noda, T.; Morimoto, J. Development of upper-extremity exoskeleton driven by pneumatic cylinder toward robotic rehabilitation platform for shoulder elevation. In Proceedings of the 2015 IEEE International Conference on Rehabilitation Robotics (ICORR), Singapore, 11–14 August 2015; pp. 496–501. [Google Scholar]
- Holl, E. New optimized mechanism for linking a hydraulic actuator to the elbow joint of an upper arm exoskeleton. J. Test. Eval. 2022, 50, 2400–2409. [Google Scholar] [CrossRef]
- Toxiri, S.; Näf, M.B.; Lazzaroni, M.; Fernández, J.; Sposito, M.; Poliero, T.; Monica, L.; Anastasi, S.; Caldwell, D.G.; Ortiz, J. Back-support exoskeletons for occupational use: An overview of technological advances and trends. IISE Trans. Occup. Ergon. Hum. Factors 2019, 7, 237–249. [Google Scholar] [CrossRef]
- de Miguel-Fernández, J.; Lobo-Prat, J.; Prinsen, E.; Font-Llagunes, J.M.; Marchal-Crespo, L. Control strategies used in lower limb exoskeletons for gait rehabilitation after brain injury: A systematic review and analysis of clinical effectiveness. J. Neuroeng. Rehabil. 2023, 20, 23. [Google Scholar] [CrossRef]
- Pérez Vidal, A.F.; Rumbo Morales, J.Y.; Ortiz Torres, G.; Sorcia Vázquez, F.d.J.; Cruz Rojas, A.; Brizuela Mendoza, J.A.; Rodríguez Cerda, J.C. Soft Exoskeletons: Development, Requirements, and Challenges of the Last Decade. Actuators 2021, 10, 166. [Google Scholar] [CrossRef]
- Ding, S.; Francisco, A.R.; Li, T.; Yu, H. A novel passive shoulder exoskeleton for assisting overhead work. Wearable Technol. 2023, 4, e7. [Google Scholar] [CrossRef]
- Asgari, M.; Phillips, E.A.; Dalton, B.M.; Rudl, J.L.; Crouch, D.L. Design and preliminary evaluation of a wearable passive cam-based shoulder exoskeleton. J. Biomech. Eng. 2022, 144, 111002. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.; Jung, Y.; Lee, D.; Bae, J. A passive upper limb exoskeleton with tilted and offset shoulder joints for assisting overhead tasks. IEEE/ASME Trans. Mechatron. 2022, 27, 4963–4973. [Google Scholar] [CrossRef]
- Rossini, M.; De Bock, S.; van der Have, A.; Flynn, L.; Rodriguez-Cianca, D.; De Pauw, K.; Lefeber, D.; Geeroms, J.; Rodriguez-Guerrero, C. Design and evaluation of a passive cable-driven occupational shoulder exoskeleton. IEEE Trans. Med. Robot. Bionics 2021, 3, 1020–1031. [Google Scholar] [CrossRef]
- Karfidova, A.; Vasilyev, M.; Morozova, I. Modernization of an industrial passive exoskeleton prototype for lower extremities using rapid prototyping technologies. IOP Conf. Ser. Mater. Sci. Eng. 2020, 971, 052049. [Google Scholar] [CrossRef]
- Eguchi, Y.; Kadone, H.; Suzuki, K. Standing mobility device with passive lower limb exoskeleton for upright locomotion. IEEE/ASME Trans. Mechatron. 2018, 23, 1608–1618. [Google Scholar] [CrossRef]
- Hull, J.; Turner, R.; Asbeck, A.T. Design and preliminary evaluation of two tool support arm exoskeletons with gravity compensation. Mech. Mach. Theory 2022, 172, 104802. [Google Scholar] [CrossRef]
- Lee, H.H.; Yoon, K.T.; Lim, H.H.; Lee, W.K.; Jung, J.H.; Kim, S.B.; Choi, Y.M. A novel passive shoulder exoskeleton using link chains and magnetic spring joints. IEEE Trans. Neural Syst. Rehabil. Eng. 2024, 32, 708–717. [Google Scholar] [CrossRef]
- Rodríguez-León, J.F.; Chaparro-Rico, B.D.; Cafolla, D.; Lago, F.; Castillo-Castañeda, E.; Carbone, G. Design of a novel exoskeleton with passive magnetic spring self-locking and spine lateral balancing. J. Bionic Eng. 2024, 21, 236–255. [Google Scholar] [CrossRef]
- Vallée, A. Exoskeleton technology in nursing practice: Assessing effectiveness, usability, and impact on nurses’ quality of work life, a narrative review. BMC Nurs. 2024, 23, 156. [Google Scholar] [CrossRef]
- Coccia, A.; Capodaglio, E.M.; Amitrano, F.; Gabba, V.; Panigazzi, M.; Pagano, G.; D’Addio, G. Biomechanical effects of using a passive exoskeleton for the upper limb in industrial manufacturing activities: A pilot study. Sensors 2024, 24, 1445. [Google Scholar] [CrossRef]
- Skelex. Skelex Products. Available online: https://www.skelex.com/products (accessed on 24 July 2024).
- Hyundai Robotics. Wearable Robot VEX. Available online: https://robotics.hyundai.com/en/unveiled-robots/wearable/vex.do (accessed on 24 July 2024).
- Immo Denmark. Paexo Shoulder. Available online: https://immodenmark.dk/produkter/paexo-shoulder/ (accessed on 24 July 2024).
- Orthexo. Ekso Evo Upper Body Industrial Exoskeleton from Ekso Bionics. 2023. Available online: https://orthexo.de/en/exoskeletons/industrial-exoskeletons/ekso-evo/ (accessed on 24 July 2024).
- Van Engelhoven, L.; Poon, N.; Kazerooni, H.; Rempel, D.; Barr, A.; Harris-Adamson, C. Experimental evaluation of a shoulder-support exoskeleton for overhead work: Influences of peak torque amplitude, task, and tool mass. IISE Trans. Occup. Ergon. Hum. Factors 2019, 7, 250–263. [Google Scholar] [CrossRef]
- Balser, F.; Desai, R.; Ekizoglou, A.; Bai, S. A novel passive shoulder exoskeleton designed with variable stiffness mechanism. IEEE Robot. Autom. Lett. 2022, 7, 2748–2754. [Google Scholar] [CrossRef]
- Li, Z.; Bai, S. A novel revolute joint of variable stiffness with reconfigurability. Mech. Mach. Theory 2019, 133, 720–736. [Google Scholar] [CrossRef]
- Li, Z.; Bai, S.; Madsen, O.; Chen, W.; Zhang, J. Design, modeling and testing of a compact variable stiffness mechanism for exoskeletons. Mech. Mach. Theory 2020, 151, 103905. [Google Scholar] [CrossRef]
- Ye, Y. Interior Point Algorithms: Theory and Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Male-Female-Population-Denmark. Available online: https://www.statista.com/statistics/1008574/male-female-population-denmark-1769-2020 (accessed on 11 April 2023).
- Li, J.; Zhao, F.; Li, X.; Li, J. Analysis of robotic workspace based on Monte Carlo method and the posture matrix. In Proceedings of the 2016 IEEE International Conference on Control and Robotics Engineering (ICCRE), Singapore, 2–4 April 2016; pp. 1–5. [Google Scholar]
- Liao, Z.; Chen, B.; Qian, Z.; Chang, T.; Bai, D.; Liu, K.; Xu, J. Collaborative workspace design of supernumerary robotic limbs base on multi-objective optimization. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 354. [Google Scholar] [CrossRef]
- Criswell, E. Cram’s Introduction to Surface Electromyography; Jones & Bartlett Publishers: Burlington, MA, USA, 2010. [Google Scholar]
- Musso, M.; Oliveira, A.S.; Bai, S. Influence of an upper limb exoskeleton on muscle activity during various construction and manufacturing tasks. Appl. Ergon. 2024, 114, 104158. [Google Scholar] [CrossRef]
- Arora, A.; McIntyre, J.R. Quasi-passive lower and upper extremity robotic exoskeleton for strengthening human locomotion. Sustainable Innovation: Trends in Marketing and Management; Springer: Cham, Switzerland, 2020; pp. 1–14. [Google Scholar]
- Zhu, Y.; Bai, S. Human Compatible Stiffness Modulation of a Novel VSA for Physical Human-Robot Interaction. IEEE Robot. Autom. Lett. 2023, 8, 3023–3030. [Google Scholar] [CrossRef]
- Wang, X.; Guo, S.; Qu, B.; Bai, S. Design and experimental verification of a hip exoskeleton based on human–machine dynamics for walking assistance. IEEE Trans. Hum.-Mach. Syst. 2023, 53, 85–97. [Google Scholar] [CrossRef]








| k | |||
|---|---|---|---|
| 17.4 mm | 31.4 mm | 6.2 N/mm | 10 N |
| Description | Value |
|---|---|
| Length (without frame) | 58.6 mm |
| Width (without frame) | 293.8 mm |
| Weight (without frame) | 0.705 kg |
| Number of DOFs | 3 |
| Range of extension/flexion | |
| Range of abduction/adduction | |
| Range of internal/external rotations | |
| Designed payload | kg |
| Spring model | BUFSP22-2.5-91 |
| Link (i) | ||||
|---|---|---|---|---|
| 1 | 0 | 0 | ||
| 2 | 0 | 0 | ||
| 3 | 0 | |||
| 4 | 0 | 0 |
| Muscle Activation Reduction | ||||
|---|---|---|---|---|
| Tasks | AD | BB | MD | TR |
| Static load lifting (90°) | 8.72% | 4.55% | −3.16% | 0.34% |
| Static load lifting (135°) | 17.58% | 11.37% | −7.82% | −3.62% |
| Dynamic load lifting | 11.68% | 6.36% | −2.57% | −1.01% |
| Muscle Activation Reduction | ||||
|---|---|---|---|---|
| Task | AD | BB | MD | PD |
| Box moving | 7.65% | −1.60% | 1.73% | −2.02% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Balser, F.; Shen, M.; Bai, S. Design and Evaluation of a Novel Passive Shoulder Exoskeleton Based on a Variable Stiffness Mechanism Torque Generator for Industrial Applications. Robotics 2024, 13, 120. https://doi.org/10.3390/robotics13080120
Zhu Y, Balser F, Shen M, Bai S. Design and Evaluation of a Novel Passive Shoulder Exoskeleton Based on a Variable Stiffness Mechanism Torque Generator for Industrial Applications. Robotics. 2024; 13(8):120. https://doi.org/10.3390/robotics13080120
Chicago/Turabian StyleZhu, Yu, Felix Balser, Ming Shen, and Shaoping Bai. 2024. "Design and Evaluation of a Novel Passive Shoulder Exoskeleton Based on a Variable Stiffness Mechanism Torque Generator for Industrial Applications" Robotics 13, no. 8: 120. https://doi.org/10.3390/robotics13080120
APA StyleZhu, Y., Balser, F., Shen, M., & Bai, S. (2024). Design and Evaluation of a Novel Passive Shoulder Exoskeleton Based on a Variable Stiffness Mechanism Torque Generator for Industrial Applications. Robotics, 13(8), 120. https://doi.org/10.3390/robotics13080120








