Abstract
The most important research area in robotics is navigation algorithms. Robot path planning (RPP) is the process of choosing the best route for a mobile robot to take before it moves. Finding an ideal or nearly ideal path is referred to as “path planning optimization.” Finding the best solution values that satisfy a single or a number of objectives, such as the shortest, smoothest, and safest path, is the goal. The objective of this study is to present an overview of navigation strategies for mobile robots that utilize three classical approaches, namely: the roadmap approach (RM), cell decomposition (CD), and artificial potential fields (APF), in addition to eleven heuristic approaches, including the genetic algorithm (GA), ant colony optimization (ACO), artificial bee colony (ABC), gray wolf optimization (GWO), shuffled frog-leaping algorithm (SFLA), whale optimization algorithm (WOA), bacterial foraging optimization (BFO), firefly (FF) algorithm, cuckoo search (CS), and bat algorithm (BA), which may be used in various environmental situations. Multiple issues, including dynamic goals, static and dynamic environments, multiple robots, real-time simulation, kinematic analysis, and hybrid algorithms, are addressed in a different set of articles presented in this study. A discussion, as well as thorough tables and charts, will be presented at the end of this work to help readers understand what types of strategies for path planning are developed for use in a wide range of ecological contexts. Therefore, this work’s main contribution is that it provides a broad view of robot path planning, which will make it easier for scientists to study the topic in the near future.
1. Introduction
A robot is a machine that is able to react to its surroundings and collect information (from sensors) about its environment to perform different types of tasks safely. Autonomous robots can operate and move by themselves without a human directly controlling them. Unlike the robots used in manufacturing plants, where the environment is tightly controlled and completely known, autonomous robots cannot always be programmed to perform predefined actions because it is impossible to predict the various situations that the robot may encounter. Moreover, the environment could be unpredictable or change over time, which would mean that the robot’s movements would have to be changed quickly online [1]. Autonomous robot applications include couriers in hospitals, security guards, military surveillance, aerospace research, monitoring the environment, cleaners, and lawn mowers. Generally, one of the most important applications is the use of autonomous mobile robots in hazardous fields, such as minefields or the inside of nuclear plants. Due to the inherent autonomy of mobile robots, a number of challenges must be overcome, including uncertainty, sensing errors, planning, learning, reliability, and real-time responses [2]. Robots need to dynamically respond to changes and adapt to their environment.
The inception of the discipline of robotic path planning can be traced back to the mid-1960s. The problem of planning paths for robots, commonly known as robot path planning (RPP), is a crucial concern in the field of mobile robot navigation. The objective is to determine the optimal path that is free from any collisions within a specified environment, starting from a predefined location and ending at a target destination. In general, there are numerous ways for a robot to move to its destination, but the best route is actually chosen in accordance with a set of rules. The most widely used criteria are the shortest distance, the least amount of energy used, or the shortest time with the shortest distance. Since the goal of path planning is to find the shortest path while keeping in mind constraints such as the given environment and collision-free motion, it can be viewed as an optimization problem [3]. Maps, locations, and navigation for mobile robots can be aided by environmental models. However, the volume of data in these models needs to be manageable and able to meet the demands of real-time computing. A very difficult problem in the field of robotics is the planning of robot paths. The main goal is to find a route from where you start to where you end without hitting anything. Three key issues must be taken into consideration when solving the robot navigation problem: efficiency, safety, and accuracy. Efficiency requires that the algorithm avoid having the robot take extra steps or stop and turn repeatedly, which wastes time and energy, in order to determine the shortest distance in the shortest amount of time. Safety and accuracy depend on finding a path that will not hit anything while staying close to that path [4]. Robot navigation problems can be categorized into localization, path planning, motion control, and cognitive mapping, as illustrated in Figure 1. Path planning is possibly the most important aspect of robot navigation [5].
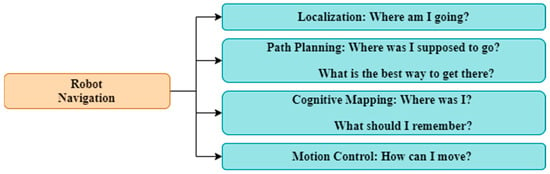
Figure 1.
Robot navigation problem.
Depending on where they are located [6], RPPs fall into one of two categories:
- (a)
- The RPP with fixed obstacles in a static environment.
- (b)
- The RPP, when faced with both still and moving obstacles in a dynamic environment.
Each of these two categories could be further subdivided into a subgroup. Global path planning, where robots in environments can plan their overall paths (offline) before they begin to move because they have complete information about the stationary obstacles, and the trajectory of the moving obstacles is known in advance. Because it is challenging to set up a new map, the cost of an environmental change in global navigation is very high, especially in dynamic environments. The inability to plan a local route with complete environmental knowledge is one limitation of local path planning. As it moves through the environment, a mobile robot uses sensors to gather information (online). The robot must repeatedly move to a new position, sense its surroundings, update the map, and plan its next course of action in order to create a map of its surroundings. Local path planning faces a number of challenges, including sensor reading errors, sensor constraints, variable environmental conditions, robot dynamics, location estimation, and robot motion restrictions [6]. In extremely complicated and vast environments, local path planning may not be able to locate the path to the target. This mostly occurs as a result of the sensors’ inability to supply enough data to send the robot to the desired location [7]. The base position of the robot, its rotation, and the rotation or translation of its entire links are called the robot’s configuration. A set of all possible configurations constitutes the configuration space or c-space, and it requires several elements:
- A description of the robot’s shape, such as whether it has legs, wheels, or no limbs at all (locomotion).
- An explanation of the robot’s environment, including its geometry (2- or 3-dimensional workspace).
- The environment must have a start and goal configuration, between which the robot’s path must be planned.
A number of parameters are used to describe the robot’s workspace configuration. For instance, two parameters, commonly referred to as x and y, can be used to describe the configuration of a robot, translating it into a two-dimensional workspace. Obstacles in the robot’s workspace prevent some configurations from being used. For instance, the robot configured at configuration C is prohibited if it collides with any of the workplace obstacles. The configuration space C is divided into a set of prohibited configurations Cforb and a set of permitted configurations Cfree as a result. In general, a path is defined as a continuous function parameterized by the length L of the path. The path-planning problem is to find a (collision)-free path between a given start configuration s ∈ C and goal configuration g ∈ C. Translating, in terms of the configuration space C, is by finding a path π so that and , and [8]. Mapping is the process of constructing a model of the environment. In order to make a map that is accurate enough to show what the robot will see along its path, the terrain must be shown accurately. Different types of maps exist to represent an environment. Some of them use a grid with cells that are either empty, where the robot can travel freely, or occupied to represent an obstacle, as shown in Figure 2. Others use two-dimensional (or three-dimensional) rectangular or square workspaces, with the obstacles being polygon, as shown in Figure 3.
Figure 2.
2D environmental map.
Figure 3.
Grid map.
Many researchers have presented a survey paper on mobile robot navigation [9,10,11]; however, these surveys are insufficient to provide an in-depth analysis of individual navigational techniques. This proposed survey paper on mobile robot navigation aims to discover the research gaps and scope of innovation in a particular area. It provides an in-depth analysis of an individual algorithm for a static environment, a dynamic environment in the presence of a moving obstacle and goal, simulation analysis, experimental analysis, multiple mobile robot navigation, hybridization with other intelligent techniques, and its application to a three-dimensional (3D) environment. The survey also highlights the differences between classical and reactive approaches based on their effectiveness and application for specific environments, such as aerial, land, underwater, industrial, and hazardous environments. In Ref. [9], the approach is limited to 3D path planning only, whereas Ref. [10] reviews multi-robot path-planning approaches and decision-making strategies for various robot types, including aerial, ground, and underwater robots. Ref. [11] focuses on multi-objective optimization algorithms for mobile robot path planning.
2. Robot Path Planning Techniques
The robot’s path should be optimized to meet certain criteria, making the path planning issue a type of optimization problem. The study of optimization algorithms has attracted much attention from researchers over the last few decades. The two types of optimization methods and algorithms are deterministic and stochastic [12]. Stochastic methods are more adept at discovering global optimal solutions for various objective functions, while deterministic methods rely on the mathematical properties of the problem. Conversely, stochastic methods are not contingent on the mathematical attributes of a specific function, as stated in reference [13]. Nevertheless, the initial approach exhibits certain limitations, including a reliance on gradients, susceptibility to local optima, inefficiencies in searching large-scale spaces, and an inability to address discrete functions. Stochastic process-based techniques are perceived to possess a higher degree of user-friendliness. Stochastic methods are necessary due to the complexity of many real-world optimization problems, particularly when it comes to optimizing non-differentiable, multimodal, and discrete complex functions—these algorithms have been found to outperform classical or gradient-based approaches. These nature-inspired paradigms are currently being widely applied in numerous engineering fields [14]. These techniques have been shown to be reliable and powerful search methods.
For many years, numerous scientists and researchers have offered a variety of methodologies for navigational approaches. The ways in which a mobile robot finds its way around can be roughly divided into two groups: classical and heuristic (Figure 4). Classical methods have a number of flaws that render them ineffective in real-world applications, including the issue of a high time complexity in high dimensions and the phenomenon of being trapped in local minima, which are significant concerns in the field. Heuristic approaches have outperformed conventional approaches and gained widespread popularity as a result of the NP-hardness of the PP problem. Heuristic techniques have also become increasingly popular due to their success in resolving issues involving multidimensionality, complex workspaces, and local minima [15]. In the following subsection of the research, we examine a group of scientific contributions that used classical and heuristic approaches to find the best single- or multi-objective path planning.
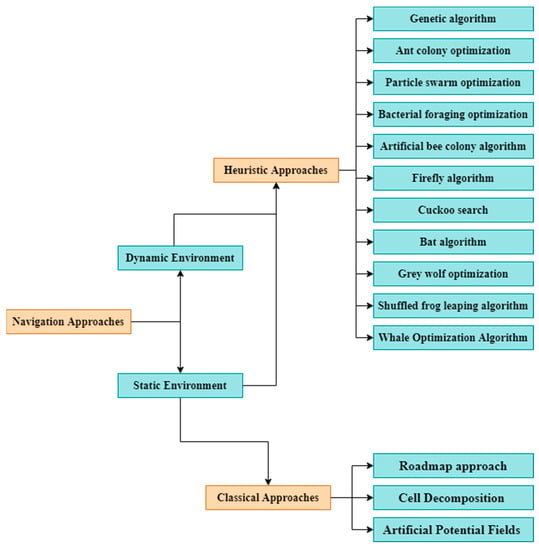
Figure 4.
Navigation approaches.
2.1. Classical Approaches
We discuss three classical approaches that were used to find the best single- or multi-objective paths in the following points:
- 1.
- Roadmap (visibility graph [16]; Voronoi diagram [17]): The roadmap approach (RM) involves the reformulation, reduction, or mapping of the free C-space onto a one-dimensional workspace, as illustrated in Figure 5. Salzman examines the application of the RM for the navigation of autonomous mobile robots [18]. During the planning phase, the configuration space of the robot is randomly generated, resulting in a specific number of nodes. A road map is then constructed by connecting pairs of nodes in a straight line while ensuring that the path does not intersect with any obstacles. Based on the results obtained during the planning stage, the query phase devises a path connecting the initial and target configurations. Enhancements were implemented to the efficient path planning of the Voronoi diagram in order to optimize its performance and mitigate issues, such as abrupt turns and extended loops, as cited in reference [19]. The optimal route is ascertained through the employment of a hybrid approach that amalgamates the visibility graph, Voronoi diagram, and potential field technique, as stated in reference [20]. Scholars have highlighted that the approach fails to identify the optimal pathway and presents challenges in its implementation.
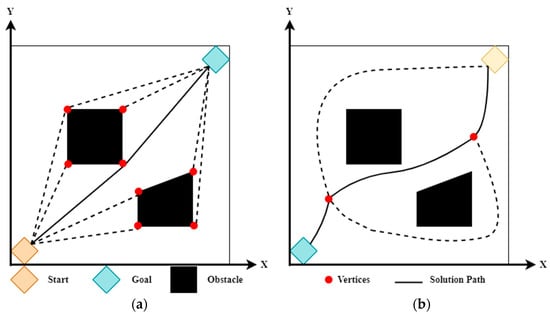 Figure 5. (a) Visibility graph; (b) Voronoi diagram.
Figure 5. (a) Visibility graph; (b) Voronoi diagram.
Yang et al. [21] employed skeleton maps and Voronoi diagrams, among other techniques, to effectively strategize their routes. Wein et al. [22] proposed a novel approach that integrates a visibility graph and a Voronoi diagram to determine the optimal route. In their work [23], Kavraki et al. demonstrated the use of probability in robotic motion (RM) for the purpose of comprehending and producing path-planning solutions. The method, however, is ineffective at obtaining the ideal path length. The probabilistic RM was slightly modified by Sanchez et al. [24] using a probabilistic roadmap method to improve the shortest-path determination (PRM), presenting the lazy collision-checking strategy as their solution to the practical path-planning problem. Yan et al. [25] have successfully tested an unmanned aerial vehicle’s ability to navigate in a 3D environment. This method uses both a probabilistic formula and a road map to determine the flight path. An innovative path-planning algorithm, which performs obstacle avoidance in dynamic environments, is called Temporal-PRM [26]. By adding the concept of time to the original probabilistic roadmap (PRM), it creates an enhanced structure that can be efficiently queried.
Huang et al. present in [27] the utilization of heuristics-informed robot online path planning (HIRO), which can significantly expedite the discovery of collision-free paths in comparison to conventional methods, regardless of whether or not the robot has prior knowledge of the environment. For quick path-finding, HIRO employs both an informed heuristic and a deterministic roadmap. The probabilistic roadmap (PRM) has been widely applied in mobile robot navigation for its simplicity. When there are narrow passages in the environment, the efficiency of the PRM is greatly reduced. Zhang et al. [28] proposed an improved potential field-based probabilistic roadmap algorithm. The path-planning problem can be successfully solved by a probabilistic roadmap (PRM) in a setting with numerous complex constraints and high dimensions. Its weaknesses include poor path-planning quality and efficiency in confined spaces and dynamic environments. Finally, You et al. [29] suggested that a dynamic PRM-blended potential field be used to plan paths for a mobile robot in an environment with more than one dimension.
- 2.
- Cell decomposition (CD) [30]: To determine a route connecting the initial and target configurations, the unobstructed configuration space is partitioned into a collection of compartments. As shown in Figure 6, the establishment of a connection between the commencement and termination cells and the subsequent establishment of a connection via a series of intermediary cells determines the cellular relationships. Samet [31] and Noborio [32] proposed a decomposition utilizing a quadtree. Large grid cells divide the environment; however, when a grid cell is only partially filled, it is broken into four smaller parts of the same size until it is empty. This system’s flaw is its inability to update the program when new information (such as the position of an obstacle) arrives, making it ineffective in dynamic environments. Lingelbach [33] has proven that the high-dimensional static configuration problem with path planning exists. He found a solution to the path-planning issue for robotic platforms that resembled chains and a maze. Using CAD-based data, Sleumer et al. [34] presented a path-planning strategy for mobile robots.
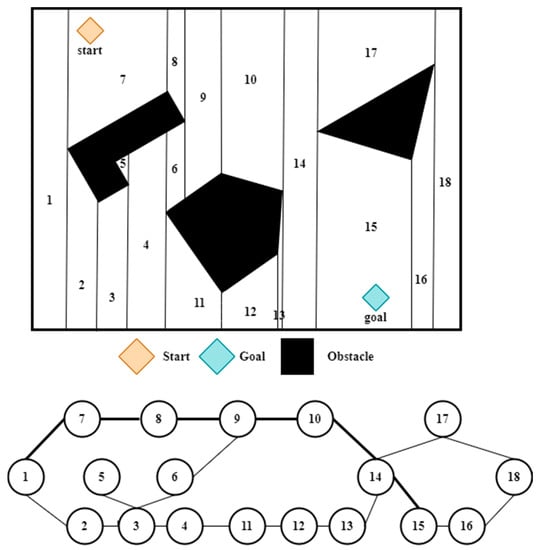 Figure 6. Exact cell decomposition example.
Figure 6. Exact cell decomposition example.
Cai et al. [35] have shown that rough CDs using sensors can be used to sort many fixed targets in a complicated environment into different groups. In a static environment, the developed method works best because it takes the shortest route and covers the whole environment. Dugarjav et al.’s [36] utilization of a sensor-based CD model remains applicable in addressing an unfamiliar rectilinear workspace for a mobile robot. The individuals utilized the CD strategy and a laser-scanning mechanism to circumvent unfamiliar locations and objects. Glavaski et al. [37] proposed a hybrid approach to address the disparity between theoretical advancements and practical considerations in path-planning problems. In order to reduce computational expenses, an exact CD path planner was developed based on the APF method. Tunggal et al. [38] introduce the utilization of CD and fuzzy logic as a means of achieving real-time operation in environments that are characterized by uncertainty.
Mark et al.’s [39] paper aimed to elucidate the mechanics of a greedy depth-first search algorithm and a CD technique that utilizes a genetic algorithm (GA) for the purpose of planning 3D paths for manipulator systems. Gonzalez et al. [40] presented quantitative analyses of the paths by changing the graph weights, the waypoint calculation method, and the CD. Wahyunggoro et al. [41] presented an application to a problem of aerial navigation using the CD approach for exploring the 3D environment. The CD method and fuzzy logic are used together in this method to guide and control the aerial vehicle. [42] In comparison to the vertical (VCD) algorithm, the radial CD (RCD) algorithm can produce shorter paths. Both cluttered and corridor environments can benefit from the RCD algorithm. The RCD’s effectiveness, in terms of the path length and processing time, is supported by the simulation results.
- 3.
- Artificial potential fields (APFs): The present approach involves a configuration space that comprises two distinct forces, namely a repulsive force that acts in a manner to expel the robot from the obstacles, as illustrated in Figure 7, and an attractive force that draws the robot towards the desired goal configuration. Khatib [43] was the pioneer in introducing the APF approach for mobile robot navigation in 1986. As per his statement, the objective and hindrances function as energized surfaces, and the automaton is subjected to a hypothetical force produced by the aggregate of their potential energies. This hypothetical force, shown in Figure 7, pushes the robot in the desired direction and keeps it from heading toward a barrier. Here, the robot travels along the negative gradient to bypass the obstruction and arrive at the desired location. Garibotto et al. [44] presented an application of this method for mobile robot navigation. Kim et al. [45] discussed a novel obstacle avoidance technique in an unexplored environment using APF. To bypass the issue of a local minimum, they used a harmonic function.
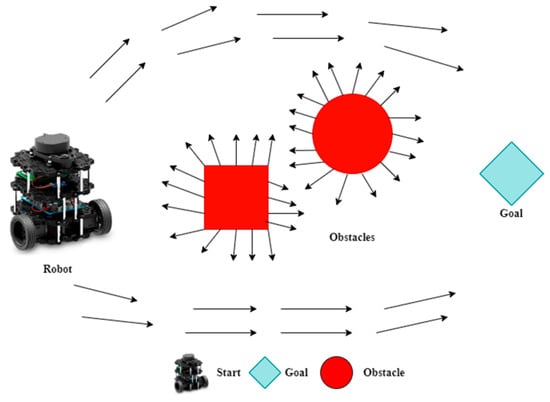 Figure 7. Attractive and repulsive functions.
Figure 7. Attractive and repulsive functions.
Another solution to the issue of the local minimum conditions has been provided by Borenstein et al. [46]. They have taken into account the dynamic navigational characteristics of robots in this study. In the references [47,48], it is done so as to study APFs in a dynamic context for obstacle avoidance. By utilizing the electrostatic laws, the APF method has been modified in some ways [49], where utilizing electrostatics enables the production of the potential function and the instantaneous determination of a collision-free path. Obstacle avoidance while moving is a difficult task in a real-time environment; thus, Huang [50] developed a way to control speed to figure out where the obstruction was and how it was moving. The terms “superior potential” and “superior repellent potential” refer to those two functions by Shi et al. [51] in order to prevent local minima and reach global maxima. Sfeir et al. [52] examined the problem of mobile robot navigation, which can be fixed by employing APF techniques such as oscillations and conflicts. They changed the APF to make it less likely to oscillate and cause problems when the target is close to an obstacle.
Pradhan et al. [53] tested the APF’s applicability using the ROBOPATH simulation tool. The artificial potential field method is thought to be one of the most popular path-planning techniques. In order to address the issue of unreachable targets, article [54] enhances the repulsion field function. When it becomes caught in a trap, it chooses a virtual target point to help free it. The application of the artificial potential field method to static obstacles with unknowable environmental data is the main topic of article [55]. The modified artificial possible field method can occasionally move around the local minima and reach its destination without any problems, as demonstrated by the MATLAB simulation. Shi et al. [56] dealt with multi-agent formation obstacle avoidance control, examined the impact of step sizes on path planning and suggested two ways to make the path more efficient. The informed rapidly exploring random tree star (RRT*) algorithm performs a quality check and re-optimizes the sampling path. A more effective local obstacle avoidance path-planning algorithm for APF was suggested by Liu et al. [57]. The stability of dynamic obstacle avoidance is improved, according to the simulation results, and the change in the heading angle obtained by the improved potential field method is reduced by 84%. The algorithm might be applied to real-time vehicle obstacle avoidance.
Several attempts were then introduced to enhance those classic methods, such as the probabilistic roadmaps (PRM) and rapidly exploring random trees (RRT*). Moreover, hybrid methods combining classic and heuristic approaches exist to exploit the advantages of both techniques (simulated annealing (SA) with artificial potential field (APF) [58]). Heuristic methodologies were devised to surmount the limitations of conventional methodologies, such as the issue of being trapped in local minima. Some of them are listed in the following subsections:
2.2. Heuristic Approaches
We discuss eleven heuristic approaches used to find the best single- or multi-objective paths in the following points:
- 1.
- Genetic algorithm (GA): This is a well-known search-based optimization tool that adheres to the 1958 Bremermann [59] discovery of genetics and natural selection. In 1975, Holland [60] was the first to present it in the context of computer science. Robot navigation is just one of the many areas of science and technology where it is currently widely used. Robot navigation is a prevalent application in the fields of science and technology. The subject matter pertains to the optimization of complex problems that require the maximization or minimization of the objective function while adhering to the pre-established constraints. This approach involves the allocation of a population, consisting of individuals with unique genetic traits, to a specified problem. Subsequently, each member of the population is assigned a fitness score, which is determined by the objective function. The selection of individuals is based on their fitness value, and they are permitted to undergo crossover with the succeeding generation to ensure the transmission of their genetic material. The mutation prevents premature convergence and maintains population diversity.
The algorithm is then finished if the population has converged. The GA is somewhat randomized; however, because it can also use historical data, it outperforms a random local search. The general flow chart for GA is shown in Figure 8. One of the difficulties in robotics is the planning of multi-robot paths. The multiple mobile robots’ path-planning strategy was discussed by Kala [61] with the help of GA. Through his research, researchers developed an efficient method of coordinating multiple robots to avoid colliding in a stationary environment. The strategy for multiple goals is illustrated in Ref. [62] for a static environment, similar to multiple robot path planning. Yang et al. [63] solved the problem of multi-mobile robot system navigation in a dynamic environment. They have demonstrated the outcomes in the presence of both static and moving barriers. Several research studies have indicated that the GA possesses certain limitations, such as a sluggish convergence rate, an absence of assurance in obtaining the optimal solution, a cumbersome approach for selecting the mutation rate, population size parameters, and so on.

Figure 8.
GA general flow chart.
The modified GA path planner, which incorporates a population-based co-evaluation mechanism for robot navigation, is presented by Hong et al. [64]. The authors have demonstrated enhanced simulation outcomes pertaining to obstacle avoidance and path optimality for multi-robot systems operating in an unfamiliar environment through the application of modified GAs. Jianjun et al. [65] presented a different modified form of GA for path optimization. To achieve the best results, their method modifies the chromosome’s length. The GA approach is used in the 2D path planning of a humanoid robot [66] as well as the 3D path planning problems for underwater [67] and aerial robots [68] because it effectively adapts to the environment (both known and unknown). Patle et al. [69], for both single-robot and multi-robot systems, a matrix-based GA utilizing binary code (MGA) was developed to address the moving target problem. In this method, the robot can quickly and easily follow a moving goal and an obstacle and arrive at its destination. A popular intelligent technique for defense equipment is the GA approach.
Creaser et al. [70] presented a missile control demonstration that combines fuzzy logic and the GA approach. In creating the guidance law for the missile, the GA is crucial. Lin et al. [71] introduced an innovative approach to military and ocean monitoring based on GA. With the help of GA, they were able to secure a crucial military asset and determine the optimal positioning strategy for a network of underwater sensors. The authors of [72] aimed to discover a solution to the robot path-planning problem that addresses the issues of slow convergence speed and easy local optimum fall-off and propose an adaptive selection technique based on an assessment of population diversity levels. Several simulations are run in a grid environment to demonstrate the algorithm’s viability and efficacy. The two-way RRT algorithm is used in [73] to replace a portion of the population in order to create an elite population after the population initialization method is improved. The results show that the elite population GA, proposed in this article, makes up for the flaws of traditional GAs.
- 2.
- Ant colony optimization (ACO): For his dissertation in 1992, Marco Dorigo developed this swarm intelligence algorithm [74]. In order to solve the combinatorial optimization problem, a population-based approach was used. The effectiveness with which ant colonies navigate from their nests to sources of food served as the inspiration for the ACO algorithm (Figure 9). The ACO algorithm has already been used in a number of scientific and engineering fields, including graph coloring, quadratic assignment problems, vehicle routing, traveling salesman problems, job-shop scheduling, and many others. ACO was applied to the real-time path planning of mobile robots by Guan-Zheng et al. [75]. When compared to other algorithms, such as GA, the ACO algorithm enhances dynamic convergence behavior, solution variation, convergence speed, and computational efficiency. Liu et al. [76] presented the use of ACO for multi-mobile robot navigation. They provided a collision avoidance method for different robot systems in a still setting. To enhance the selective strategy, they made use of a special function. When an ant encounters a dead corner, a penalty function is applied to the trail intensity to prevent the robot’s path from becoming immobile.
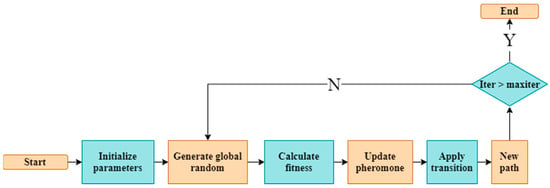 Figure 9. ACO general flow chart.
Figure 9. ACO general flow chart.
Castillo et al. [77] presented an ACO-fuzzy-based hybrid approach for mobile robot navigation in a static environment. Kumar et al. [78] presented an RA-ACO-based method for humanoid robot navigation in a cluttered environment. They used a Petri net to test the proposed method for the real-time navigation of multiple humanoid robots and found good agreement between the simulation and real-time results. Liu et al. [79] offer suggestions for how the current ACO method can be tweaked to work better in a static setting. They assert that convergence velocity is the single most important factor in determining performance. The search space for the pattern shrinks as the ants gravitate toward higher fitness subspaces, and the pheromone along the current path diffuses in the direction of the potential field force. They found the optimal route by combining pheromone diffusion and geometric local optimization. Rajput et al. [80] offered another modification for the dynamic environment. In order to prevent pointless looping and achieve faster convergence, they also presented a novel pheromone updating technique. The ACO algorithm has been applied for mobile robot navigation in an uncharted dynamic environment, according to Purian et al. [81]. For the selection and optimization of the fuzzy rules, they used ACO.
Brand et al. presented in [82] a comparison of simulated and real-world mobile robot operations in the same environment. Liu et al.’s [83] proposal for path planning in three dimensions for underwater vehicles uses an ACO-based search algorithm to find a collision-free path from one location to another. The ACO algorithm has been proposed by Chen et al. [84]. An issue with determining the best path for unmanned aerial vehicles on the battlefield can be resolved using reinforcement learning to address the original ant colony algorithm’s slow searching and stagnation behavior. The ant colony algorithm is also applied to military hardware. Gao et al. [85] presented improved performance when using ACO for missile route planning, including optimal route lengths and a faster rate of convergence. Zong et al. [86] suggested that an improved ant colony algorithm be used to plan paths for mobile robots. The algorithm’s pheromone update mechanism has the ability to accelerate convergence. The results of numerous simulation experiments demonstrate that the improved algorithm performs superior to other algorithms in challenging environments. In mobile robots, the traditional ant colony algorithm has redundant paths and is prone to local optimal solutions.
The ant colony algorithm’s convergence can be significantly improved by modifying the path to the target point [87]. The number of nodes is decreased, and it better meets the needs of robot movement. The working time and production efficiency of the automatic line are directly impacted by the welding path’s length [87]. A path-planning method based on the (ACO) algorithm is proposed to address the issue that traditional path-planning methods are unsuitable for multi-target points. Although the path is too long and there are too many turns [88], the basic ant colony algorithm (ACO) is simple to use to enter the local optimum. The walkable position points are set at random by an improved ACO in the area of the map where there are no obstacles. For mobile robots, an autonomous path-planning method based on evolutionary optimization is suggested.
- 3.
- Particle swarm optimization (PSO): This metaheuristic takes cues for group dynamics from animals in the wild, such as schools of fish and flocks of birds. It was developed in 1995 by Eberhart and Kennedy [89] and is an optimization tool with a rapidly growing user base for resolving various engineering and scientific issues. The PSO imitates social animal behavior, yet it does not require a group leader to complete the job. The flock of birds does not need a leader when searching for food; instead, they follow the member who is closest to the food (Figure 10). In this manner, the flock of birds successfully communicates with the other members of the population to arrive at the required solution. The PSO algorithm is made up of a collection of particles, each of which represents a potential resolution. PSO is now a widely used tool for mobile robot navigation. Using a multi-agent particle filter, Tang et al. [90] dealt with the issues of mapping and localization for a mobile robot navigating in an unknown environment. PSO is used because it has more stable convergence characteristics and helps to reduce calculation.
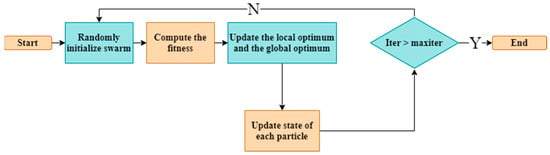 Figure 10. PSO general flow chart.
Figure 10. PSO general flow chart.
To obtain a precise trajectory and prevent becoming stuck in local optima, the PSO algorithm combined with the MADS (mesh adaptive direct search) algorithm was used by Xuan et al. [91]. When combined with the GA and EKF algorithms, the PSO–MADS algorithm produces an effective result (the extended Kalman filter). The Area Extended PSO (AEPSO) was created by Atyabi et al. [92]. Furthermore, problems with mobile robot navigation that are limited by time and change can be solved with a version of PSO that combines the basic PSO algorithm with other optimization techniques. The AEPSO strategy is successfully used in bomb defusing and the search and rescue of survivors. Tang et al.’s [93] cooperative motion path planning in a challenging environment addresses multi-mobile robot system navigation. The fault tolerance of the proposed method is then examined, with both the PSO and the multibody system dynamics (consisting of robot properties, such as acceleration, mass, force, and inertia) being taken into account. For the real-world navigation of numerous mobile robots, Couceiro et al. [94] made some modifications. They altered the PSO and Darwinian PSO (DPSO) systems to address communication and obstacle avoidance problems. They discovered that a system of 12 physical robots could increase both the best overall performance and the maximum communication distance by up to 90%.
Chen et al. [95] used a multi-category classifier to make a human expert control strategy for an uncertain environment that could learn. The particle swarm optimization (PSO) algorithm is employed in this context to efficiently attain enhanced precision in a timely manner. Compared to the conventional grid search method, it offers superior precision. The self-adaptive learning particle swarm optimization (SLPSO) technique, proposed by Li et al., was designed to tackle the challenge of path planning for robots in intricate environments while simultaneously satisfying diverse constraints. The authors initially converted the path-planning issue into a multi-objective optimization problem with the aim of satisfying the navigational objectives of minimizing the path length and collision risk and maximizing smoothness. Following the achievement of these objectives, a self-adaptive learning mechanism was incorporated to enhance the particle swarm optimization’s (PSO) capacity to explore a setting with numerous constraints. Das et al. [96] have provided a hybrid approach for creating effective path planning. They presented a hybrid methodology using the improved gravitational search algorithm (IGSA) and PSO to assess the best course of action for numerous mobile robots in a cluttered environment. The study by He et al. [97] investigated the utilization of particle swarm optimization (PSO) in addressing the challenge of navigating underwater environments in a multifaceted, three-dimensional setting. The study employed a combined PSO-UFastSLAM approach to enhance the estimation accuracy and restrict particle size, thereby yielding improved outcomes.
The particle swarm optimization (PSO) approach has been employed in the navigation of various types of robots, including underwater robots, aerial robots in 3D unknown environments [98], humanoid robots [99], and industrial robots [100]. Notably, these robots have demonstrated successful navigation outcomes. Algabri M et al. [101] conducted a comparative analysis of various navigational control techniques, such as GA, PSO, NN, and FL, to identify the optimal approach. The researchers arrived at the determination that the fusion of FL and PSO yielded the most optimal outcomes in relation to the distance traversed. Particle swarm optimization (PSO) has potential applications beyond the realm of mobile robot navigation, particularly in the defense sector. Banks et al. [102] conducted a study on the application of PSO in non-deterministic UAV navigation and its potential to facilitate inter-UAV collaboration for safeguarding a vast region against aerial threats. The environment in [103] is divided using the grid method to enable particle swarm optimization. The path’s distance is measured by the objective function, and avoiding obstacles on the way is penalized. Two path-planning issues involving emergency and regular vehicles are solved using particle swarm optimization. One of the current robotics field’s most active research areas is path planning. Chen et al. [104] make reference to the problem that the local search performance of particle swarms is subpar; thus, an ideal path can be planned more quickly, and the algorithm can enhance the quality of particle searches in both the early and late stages. Sarkar et al. [105] developed an adaptive fitness function that addresses three important issues, including the avoidance of obstacles and the choice of a shorter, smoother path. The fitness function is optimized by using the particle swarm optimization (PSO) algorithm.
- 4.
- Bacterial foraging optimization (BFO): A new nature-inspired optimization algorithm, derived from the behavior of E. coli and M. Xanthus bacteria, was introduced by Passino [106] in 2002. In order to find nutrients, these bacteria maximize their use of available energy per unit of time. Chemotaxis, a feature of the BFO algorithm, detects chemical gradients through which bacteria exchange specific signals with one another. Chemotaxis, swarming, reproduction and eradication, and dispersal are some of its four core tenets. Figure 11 depicts the general flowchart of bacteria behavior when searching for nutrients. On the map, bacteria are constantly moving in search of areas with more nutrients. Bacteria, when in an area with more nutrients, will spread out and die, whereas bacteria in an area with fewer nutrients will live longer and divide into two equal parts. Bacteria, when in an area with more food, are drawn to bacteria in the area with less food, and the bacteria in the area with less food send a signal to the bacteria in the area with more food that they are there. A region with abundant nutrients is mapped by bacteria.
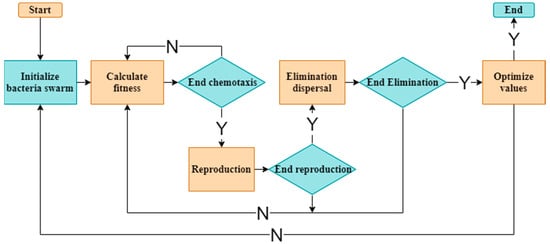 Figure 11. BFO general flow chart.
Figure 11. BFO general flow chart.
On the map, bacteria are spread out, once more in search of new nutrient sources. The study by Coelho and colleagues [107] demonstrated the use of a BFO algorithm with an adjustable velocity as a means for mobile robots to navigate within a stationary setting. The aforementioned distribution is derived from the uniform, Gauss, and Cauchy distributions. When encountering several obstacles in a stationary setting, refs. [108,109] employed a uniform approach to navigation. The authors of Gasparri et al. [110] demonstrated the implementation of a real-time navigation system for a mobile robot operating within various indoor settings, such as corridors, lobbies, and building floors. Abbas et al. [111] enhanced the efficacy of path planning for a robot with wheels through the development of an optimized BFO algorithm. The method devised utilizes an APF (artificial potential field) approach that incorporates two opposing forces, namely an attractive force towards the objective and a repulsive force away from the obstacles. The approach examines the adverse feedback of the algorithm in order to identify suitable direction vectors that guide the exploration process toward a more favorable region with improved local search capabilities. Jati et al. [112] proposed a BFO algorithm to address the challenging task of navigating in the presence of multiple robots. The authors integrated the binary firefly optimization (BFO) technique with the Harmony Search algorithm in their study. In addition to wheeled robots, the efficacy of the BFO algorithm has been demonstrated on industrial manipulators. Coelho et al. [113] have reported that the enhanced BFO algorithm yields superior outcomes compared to the conventional BFO algorithm. The UAV BFO navigation problem was presented by Oyekan et al. in their study [114]. The utilization of a proportional integral derivative (PID) controller for optimizing the search parameters of the BFO in three-dimensional space obviates the necessity for intricate modeling and enhances the performance of the UAV controller.
- 5.
- Artificial bee colony (ABC) algorithm: The ABC algorithm has been proposed as a swarm-based intelligent approach that employs the foraging behavior of honey bees as a metaphor, as depicted in Figure 12, Kharaboga [115]. The population-based artificial bee colony (ABC) algorithm comprises a set of inherent solutions that serve as the food source for the bees. The aforementioned technique pertains to swarm algorithms and is a stochastic search approach based on populations. It is characterized by its user-friendly nature. The processing time is relatively short. The food search cycle of ABC comprises three distinct rules: dispatching the employed Apis mellifera to a food source while evaluating the caliber of the nectar; observers make decisions regarding food sources based on the information provided by worker bees and their assessment of the nectar’s quality; the process involves the selection of scout bees and their guidance toward potential sources of sustenance. The authors in reference [116] demonstrated the utilization of the ABC algorithm for the purpose of mobile robot navigation in a stationary setting. The method that was developed employs an evolutionary algorithm to ascertain the optimal path and an (ABC) for conducting a local search. For the purpose of validating the results, real-time experiments in an indoor setting are presented.
 Figure 12. ABC general flow chart.
Figure 12. ABC general flow chart.
Saffari et al. [117] also presented a comparable method in a static environment; however, their results are only applicable to simulational settings. Ma et al. [118] demonstrated the ABC-based method for navigating in a dynamic, real-time environment. By using a time-rolling-window strategy in conjunction with the ABC algorithm, they presented a hybrid approach. It is difficult to navigate an environment with multiple mobile robots; however, Bhattacharjee et al. [119] and Liang et al. [120] implemented ABC successfully in a static environment and included testing of the ABC algorithm for use in aerial navigation [121], underwater navigation [122], routine issues with autonomous vehicles [123], and navigational methods for mobile robots with wheels. The goal of UCAV path planning is to find the best way to fly in a 3D environment, taking into account the dangers and limits of the battle field. This UCAV navigation issue was dealt with by Li et al. [124], who employed an enhanced ABC algorithm. The ABC algorithm was modified by a balance-evolution strategy (BES) that makes use of the convergence data obtained during iteration. This modification is aimed at enhancing exploration accuracy and achieving a balance between local exploitation and global exploration capabilities.
Ding et al.’s [125] application of the ABC algorithm in the defense industry has tested an unmanned helicopter for difficult tasks, such as data collection, precise measurement, and border patrol. They developed a novel identification algorithm using an ABC controller and a chaotic operator to find the two decoupled linear models’ unknown parameters based on the flight data gathered from the experiments. The ABC algorithm’s search and optimization steps are added to the improved particle swarm algorithm in [126]. An adaptive inertia weight method is suggested to increase the particle search’s effectiveness and precision. The end results demonstrate how quickly and effectively the algorithm in this article can locate the ideal path. For mobile robot path planning in variable space, a hybrid approach is suggested in [127]. It comprises online path-planning schemes and an offline global path optimization algorithm. The analysis was performed in a MATLAB/Simulink environment, and additional information, including visualization, is included.
- 6.
- Firefly (FF) algorithm: In 2008, Yang [128] introduced the FF, and although it is also known as the “meta-heuristics algorithm,” it is based on the flashing behavior of fireflies. Its basic idea is based on the stochastic survival of fireflies in nature and general identification as random states. The FF, a member of the Lampyridae family, is commonly known as a lightning bug due to its capacity to emit light. Light emission is produced via the prompt oxidation of luciferin in the presence of the enzyme, luciferase. Fireflies glow without wasting heat energy by using bioluminescence, a process that converts biological matter into light. Fireflies use this light to choose a mate, send messages, and occasionally frighten away predatory animals. The general flowchart for the FF algorithm is shown in Figure 13. The authors, Hidalgo-Paniagua et al. [129], have proposed a mobile robot navigational strategy utilizing the F algorithm when confronted with a stationary obstacle. The three fundamental goals of navigation, namely path length, path smoothness, and path safety, have been successfully accomplished. In a simulation-only environment, Brand et al. [130] presented the FF for a single mobile robot’s shortest collision-free path.
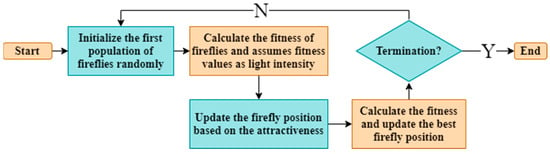 Figure 13. FF general flow chart.
Figure 13. FF general flow chart.
The FF was demonstrated by Sutantyon et al. [131] for underwater mobile robot navigation. They created the swarm robot scheduling method to prevent 3D marine conditioning interference and jamming. They applied the levy light-firefly approach to solving another real-world underwater navigation problem in the same partially known environment [132]. Christensen et al. [133] presented an FF-based cooperative strategy for dead robot detection in a multi-mobile robot system. Wang et al. [134] have developed and tested the use of FF to explore a 3D environment for aerial navigation. In their experiment, a UCAV’s path is planned using an improved version of FF to avoid hazardous areas, reduce fuel consumption, and avoid complex, crowded environments. The modified FF algorithm, based on concentric spheres presented in [135], prevented the fireflies from randomly moving while requiring less computational work. The results of the simulations and experiments demonstrate a strong commitment to achieving the objectives of navigation in a complex environment. The present study evaluates the analysis of a field function for a single-robot and a multi-robot system in the presence of various obstacles (concave, zigzag, and convex), as reported in reference [136]. Numerous researchers have conducted diverse experiments in the field of robot path planning. These experiments include an FF-vision-based system [137], an FF-Q learning approach [138], an FF–ABC hybrid approach [139], and several other approaches. Tighzert et al. [140] and Liu et al. [141] demonstrated the use of FF on a legged robot and an underwater robot, respectively. Patle et al. [142] discussed the difficulty of navigating in various circumstances. The fast Fourier transform (FFT) algorithm was employed to illustrate the approach for determining the optimal path in a dynamic setting, where the positions of both the target and obstacle were subject to continuous change. The present study proposes a method for path planning that utilizes a self-adaptive population-size-based FF algorithm. The proposed algorithm in [143] performs better than the fixed-population-size FF algorithm in terms of solution stability, convergence speed, and running time.
- 7.
- Cuckoo search (CS): Yang and Deb [144] introduced the CS algorithm, a metaheuristic algorithm, in 2009. The algorithm was developed on the basis of the slothful behavior of some cuckoos, which causes them to lay their eggs in the nests of other host birds. Yang claims that the algorithm adheres to the following three fundamental principles for an optimization problem: one egg is laid by each cuckoo at a time in a nest that is selected at random; the best nests with top-notch eggs will be passed down to the following generation; and the number of available host nests is fixed, and the host bird has a chance of finding the cuckoo egg with a probability of pa ∈ (0, 1). In this situation, the host bird has two options: either remove the egg or abandon the nest and create a new one. Figure 14 depicts the typical flow chart for a computer science algorithm. The novelty of the CS algorithm for mobile robot path planning has resulted in a limited number of scholarly articles utilizing it.
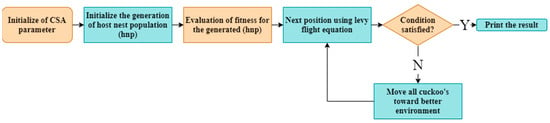 Figure 14. CS general flow chart.
Figure 14. CS general flow chart.
In their publication [145], Mohanty et al. provide the algorithm for navigating a wheeled robot in a static environment. The authors have conducted experiments involving both simulation and real-time scenarios on a wheeled robot navigating a complex environment, which includes areas that are partially unknown. The simulation and experiment exhibit a high degree of concurrence, as the discrepancy error is significantly reduced. The CS-based algorithm demonstrates effective functionality when employed in conjunction with other navigational strategies. Mohanty et al. [146] proposed a hybrid approach that combines CS and ANFIS to enhance navigational outcomes in an uncertain environment. Wang et al.’s [147] suggestion of combining the differential evolution algorithm with CS to speed up global convergence is another hybrid path-planning strategy for an unknowable 3D environment. The aerial robot can better explore the three-dimensional environment thanks to faster convergence. Xie et al. [148] provide an example of using the CS algorithm for 3D environment exploration, focusing on a battlefield. In their work, they have shown how to solve the 3D aerial path-planning problem using a hybrid approach that combines CS and the differential evolution algorithm. The improved CS model employs differential evolution to streamline the cuckoo selection process so that the birds can search for the best course of action as agents.
- 8.
- Shuffled frog-leaping algorithm (SFLA): Based on the behavior of frogs seeking food, Eusuff and Lansey’s [149] metaheuristic optimization approach was created. In the area of engineering optimization, the SFLA has gained popularity. It stands out from other metaheuristic algorithms due to its improved convergence speed, ease of implementation, fewer parameters, higher success rate, and improved search capacity in the presence of uncertainty. The general flow chart of SFLA is shown in Figure 15. Ni et al.’s [150] median strategy forms the basis of a path-planning method that can be used to escape from a problem with a local optimal solution. The position of the frog, which was optimized by changing the fitness function to obtain the best frog in the world, was used to guide the robot’s movement around obstacles that are both fixed and moving. Path safety, path length, and path smoothness are three primary navigational goals, and they have all been proven by Hidalgo-Paniagua et al. [151] with the help of an SFLA-based multi-objective strategy. In a static condition, the modified SFLA demonstrated notably smoother paths when compared to the GA.
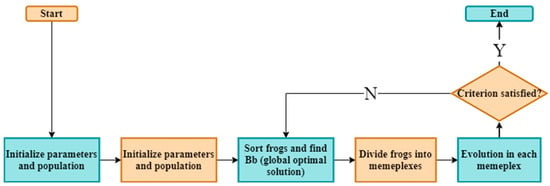 Figure 15. SFLA general flow chart.
Figure 15. SFLA general flow chart.
Kundu et al. [152] have conducted research and provided a navigational approach for 3D underwater environments. The target is traced through the implementation of an adaptive SFLA navigational strategy that is designed to accommodate dynamic conditions. The utilization of adaptation techniques results in the optimization of navigation paths and time by circumventing the occurrences of local minima. Validation is demonstrated by the achievement of a favorable concurrence between the simulation and experimental outcomes in a disorderly environment. A modified SFLA approach of a similar type is proposed for the purpose of UAV 3D path planning and vehicle routing, as stated in reference [153]. According to Liang et al. [154], a methodology for managing the flight of air-breathing hypersonic vehicles utilizing SFLA was devised with the intention of being utilized by the military. The modified SFLA technique can be employed to regulate flight during ascent, level flight, and descent by utilizing the proportional integral derivative approach in conjunction with the height loop, pitch angle loop, and velocity loop. A new algorithm combining the improved ant colony algorithm (IACO) with the (SFLA) algorithm is proposed in [155]. Numerical experiments show that the optimal path can be more effectively generated using the improved leapfrog algorithm and the simplified operator in the last step.
- 9.
- The bat algorithm (BA): Yang created a bio-inspired algorithm in 2010 [156]. It is based on microbats’ echolocation or biosonar abilities. Bats use echolocation, which involves sending out sound pulses and flying while listening for echoes that are reflected back from any obstacles. A bat can therefore determine the velocity, shape, and size of the prey and obstacles by using the interval between its ears, the loudness of the response, and the delay time. A bat can also alter the way its sonar functions. It can fly for a shorter amount of time while gathering comprehensive information about its surroundings when it sends sound pulses at a rapid rate. The slow convergence rate, poor convergence precision, and weak stability of the bat algorithm are drawbacks. The general flow chart of the BA is shown in Figure 16. Yuan et al. [157] created a logarithmic decreasing strategy-based bat algorithm with Cauchy disturbance in this study. When comparing hybrid path-planning techniques to the dynamic window approach, the path length can be significantly reduced. Wange et al. [158] noted that unmanned combat air vehicle (UCAV) path planning is a challenging, high-dimensional optimization problem. In order to resolve the UCAV path-planning issue, a new bat algorithm with mutation (BAM) is suggested. BAM can speed up global convergence while maintaining the strong robustness of the fundamental BA.
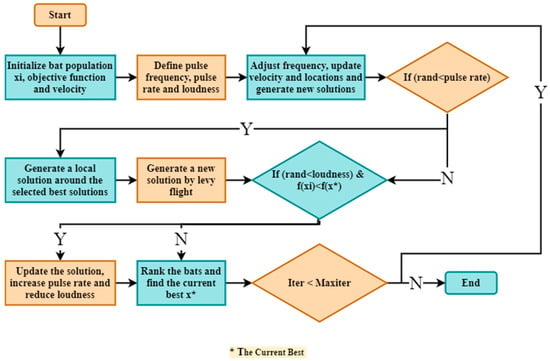 Figure 16. BA general flow chart.
Figure 16. BA general flow chart.
For planning the path of mobile robots, a reformative bat algorithm (RBA) by Xin et al. [159] is suggested. To improve the RBA, frequency updates are given the Doppler treatment. To select the loudness attenuation coefficient and pulse emission enhancement coefficient, Q-learning is incorporated into the RBA. To speed up the convergence of the bat’s position update, the improved artificial potential field (APF) method is used. The adaptive inertia weight of the bat algorithm is proposed by Lin et al. [160] to be improved using the optimal success rate strategy. The enhanced algorithm, CPFIBA, significantly raises the success rate of locating an appropriate planning path when compared to the traditional APF and chaos strategy in UAV path planning. Zhou et al.’s [161] unmanned aerial vehicle (UAV) flight path planning is based on the advanced swarm optimization algorithm of the bat algorithm. In order to improve the BA’s local search capabilities, IBA primarily employs ABC. The IBA can design a flight path for UAVs that are quicker, shorter, safer, and accident-free. Wang et al. [162] suggested an enhanced bat algorithm based on Levy flight and inertial weight. We used linear inertial weights to prevent the algorithm from converging too quickly. To improve the algorithm’s capability for local mining, a random exploration mechanism in a Cauchy distribution is used. The outcomes demonstrate the viability and efficiency of the suggested algorithm in dealing with path-planning issues.
Ajeil et al. [163] The present study outlines a methodology that utilizes a modified frequency bat algorithm to generate a robot path in an obstacle-free environment. The algorithm operates in two distinct steps. Upon detecting a nearby obstacle, the robot initiates its second mode with the purpose of evading it. The comparative analysis has revealed that the MFB algorithm exhibits superior performance in contrast to the conventional BAT algorithm. Ibraheem et al. [164] have made modifications to the bat algorithm (BA) in order to tackle the issue of mobile robot navigation. The primary objective of this study is to determine the most efficient and secure path between an initial location and a final destination while taking into account a dynamic setting with mobile obstructions.
- 10.
- Whale optimization algorithm (WOA): WOA is a swarm intelligence algorithm that is suggested for problems involving continuous optimization. It has been demonstrated that this algorithm performs as well as or better than some of the other algorithmic techniques currently in use [165]. WOA has drawn inspiration from the humpback whales’ hunting techniques. Each solution in WOA is regarded as a whale. In this answer, a whale attempts to fill in a new location in the search area that is referenced as the best member of the group. The whales use two different mechanisms to both attack and locate their prey. In the first, the prey is encircled, while in the second, bubble nets are made. In terms of optimization, whales search for prey by exploring their environment, and they exploit their environment during an attack. The general flow chart of WOA is shown in Figure 17. This algorithm is a new recent application on path planning in 2020, as seen in [166]. The authors, Chhillar et al., proposed that the modified WOA algorithm ensures an optimal collision-free path. The fitness of any whale will be calculated by taking into account the target location and the obstacles in the search space in the WOA algorithm.
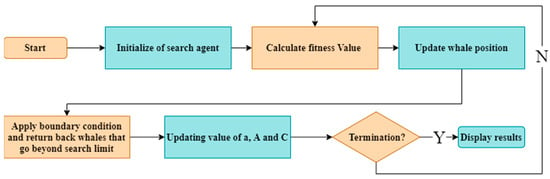 Figure 17. WOA general flow chart.
Figure 17. WOA general flow chart.
Dai et al. [167] put forth a new whale optimization algorithm (NWOA). In order to increase the convergence speed, NWOA uses adaptive technology. It also creates virtual barriers to help users avoid local optimal traps. Additionally, NWOA introduces an improved potential field factor to improve the ability to dynamically avoid obstacles. Dao et al. [168] noted the robot advances in order until it reaches the position of the whale, which is considered to be the best globally. The outcomes demonstrate that the suggested approach enables the robot to reach its target while colliding with no obstacles. In Yan et al. [169], the main determinants of autonomous underwater vehicles are perception, decision-making, and control systems. This article proposes a WOA that utilizes forward-looking sonar for the purpose of addressing path-planning concerns in the context of autonomous underwater vehicles. The aforementioned approach exhibits superior planning efficacy, an accelerated convergence rate, reduced execution duration, and heightened solution accuracy.
Liu et al.’s [170] study focused on the problem of autonomous path planning for mobile robots, which is tackled through the utilization of an enhanced whale optimization algorithm (IWOA). The IWOA algorithm is a fusion of Levy flight and inverse initial coding optimization techniques. The efficacy and feasibility of the improved weighted A* algorithm in the domain of path planning have been validated via simulation. Yan et al.’s [171] WOA algorithm is derived from the bubble-net hunting strategy employed by humpback whales. In order to effectively determine the worldwide optimal solution, the approach involves simulating the behavior of surrounding prey, utilizing a bubble-net strategy for attack, and engaging in the pursuit of prey. The optimization performance and robustness of the WOA algorithm surpass those of other algorithms, including the ABC, BA, CS, and flower pollination algorithms. On the basis of sensor technology and intelligent systems, intelligent path planning can be accomplished. Zan et al. [172] suggested using a novel path-planning algorithm along with computer perception technology. The new algorithm does a better job of figuring out the best path for mobile robots to take and can analyze and decide on that path quickly. The modified WOA algorithm, which guarantees the best collision-free path, is used in [166]. The target location and the obstacles in the search space will be taken into account when determining the fitness of any whale in the WOA. The simulation and findings demonstrate that the proposed modified WOA is workable for issues with mobile robot path selections.
- 11.
- Gray wolf optimizer (GWO): The GWO is based on gray wolves’ hunting tactics and social structure. Alpha, beta, delta, and omega wolves are the four groups that make up the gray wolf hierarchy. The alpha wolf is the dominant or leader of the pack and is usually followed by the other wolves. The best wolf for leading the pack is the alpha. Beta wolves are ranked second in the wolf group’s social hierarchy. The beta wolf assists the alpha in a variety of tasks. While it judges the omega wolves, the delta wolf must submit to the alpha and beta wolves. Scouts, guards, elders, hunters, and caregivers make up this group. The general flow chart of this algorithm is shown in Figure 18. The level-one gray wolf is known as the omega wolf [173]. The gray wolf optimizer (GWO) is a newly developed metaheuristic algorithm that emulates the hunting behavior and social structure of the gray delta, and omega, each with their own unique movement patterns [174]. Albina et al. [175] employed the GWO algorithm and coordinated multi-robot exploration (CME) to explore using multiple robots, surpassing the deterministic CME algorithm in terms of performance, with the aim of achieving optimal coordination and effectively optimizing the coverage area. Despite the fact that the mean coverage of the four distinct obstacle maps is 97.98%, complying with the obstacle avoidance constraint remains a challenging task.
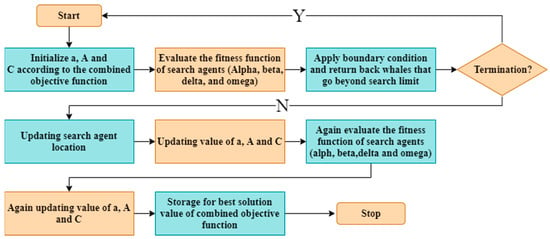 Figure 18. GWO general flow chart.
Figure 18. GWO general flow chart.
Kamalova et al. [176] conducted an experiment to showcase the robot’s coverage capability using a multi-objective GWO algorithm. However, the robots exhibited a tendency to revisit previously explored areas, resulting in an increase in the overall execution time. Furthermore, the utilization of step-size mechanisms in the GWO algorithm may lead to challenges in achieving optimal global solutions and surmounting dynamic barriers. Ge et al. [177] proposed a hybrid algorithm that combines the GWO and fruit fly optimization (FFO) algorithms to enhance the local optimal solution. Furthermore, Dewangan et al. [174] have exhibited that the enhanced gray wolf optimizer (GWO) algorithm possesses superior capabilities in avoiding local optima and exploring the search space. Kamalova et al. [178] generated frontier points within the unexplored areas of an environment by utilizing the global waypoints control technique for frontier-based exploration using an array of frontier points as input parameters. Notably, the sensor did not receive any transmitted signal during this process. The study found that the GWO algorithm exhibited superior performance compared to the PSO algorithm in relation to search actions. This was achieved through the utilization of a methodology that involved the estimation of the next global waypoint. Specifically, this estimation was based on the averaging of three distances, namely the mean alpha points, mean beta points, and mean delta points. These distances were measured from the current robot position to the positions of the frontier points. Despite the robot’s adeptness in navigating obstacles, it must traverse a considerable distance before the final analysis.
The gray wolf algorithm (GWO) is a widely recognized swarm intelligence algorithm. However, it exhibits a slow convergence rate and is susceptible to premature convergence on certain problems. The initial GWO algorithm incorporates the lion optimizer algorithm and dynamic weights in [179]. The gray wolf position update now includes dynamic weights to keep wolves from becoming homogeneous and settling into local optimums. To demonstrate that the improved algorithm is superior in terms of convergence accuracy and stability, a two-dimensional space model of mobile robot obstacle-avoidance path planning [180], the conversion of linear convergence factors in the GWO algorithm into nonlinear convergence factors, the addition of collaborative quantum optimization of the gray wolf population, and the use of four international test functions were all used.
Another miscellaneous algorithm is reinforcement learning (RL), which many researchers have used to perform the task of mobile robot navigation in various environments. Mobile robots are revolutionizing the automotive industry and on-demand services. Navigation is crucial for avoiding accidents. Work [181] proposes a neural network-based decision-making algorithm for navigation scenarios with an accuracy of nearly 90%. The model was tested on a virtual robot in a navigation simulator. Moreover, intelligent techniques, such as hunter–prey [182], invasive weed optimization (IWO) [183], the Harmony Search (HS) algorithm [184], memetic algorithms (MA) [185], variable neighborhood search (VNS) [186], and intelligent water drops (IWD) [187] are used to perform the task of mobile robot navigation.
For mobile robot localization, the significance of localization in wireless sensor networks (WSNs) and robotics cannot be overstated, as it provides a multitude of services, such as human–machine interactions, autonomous systems, and augmented reality. The present study introduces a revised Kalman filter (KF) framework for the purpose of localization, utilizing the UKF and PF localization approaches. The performance of these methods is compared and evaluated. The utilization of these algorithms can be extended to diverse applications, such as the localization of robots, resulting in an enhancement of their overall performances [188].
3. Discussion
The navigational strategies are separated into two categories following an extensive analysis of the research articles cited in the literature: heuristic approaches and classical approaches. Prior to a few decades ago, the vast majority of robotics research was conducted solely through traditional methods. The conventional methods exhibit several limitations, such as their high computational complexity, susceptibility to local minima entrapment, inability to manage maximum uncertainty, dependence on accurate environmental data, the necessity for a precise sensing mechanism for navigation in real-time, and various additional shortcomings. As a result, when using the traditional approach, it is never certain whether a solution will be found or if it is best to assume that one will not be found. These methods are unreliable and unpredictable, making them fragile when used in a real-time setting. Despite the efforts of several researchers to pinpoint deficiencies in conventional methodologies and devise innovative techniques, heuristic approaches continue to outperform these methods, including APF and certain hybrid algorithms, in real-world scenarios.
Conventional techniques are commonly employed for navigation in a familiar setting due to their lack of requirement for prior knowledge of the operational environment. However, heuristic approaches are used for navigation in places that have not been mapped out because they can deal with the high level of uncertainty in those places. Their use outperforms the efficacy of conventional techniques in addressing real-time navigation issues because they are simple to implement, intelligent, and more effective. The heuristic approaches still have a number of drawbacks, despite being more effective than the classical approaches, such as the need for a learning phase, a high memory requirement, and the inability to be used with inexpensive robots. Based on Figure 19, it has been demonstrated for many years that robots can navigate using both classical and heuristic methods. Between 1970 and 2022, the popularity of the heuristic approach rose from 0% to 95%, while that of the classical approaches fell from 95% to 5%. Heuristic systems exhibit greater sophistication compared to conventional approaches, albeit with certain limitations, such as protracted learning curves, intricate designs, and elevated memory requirements.
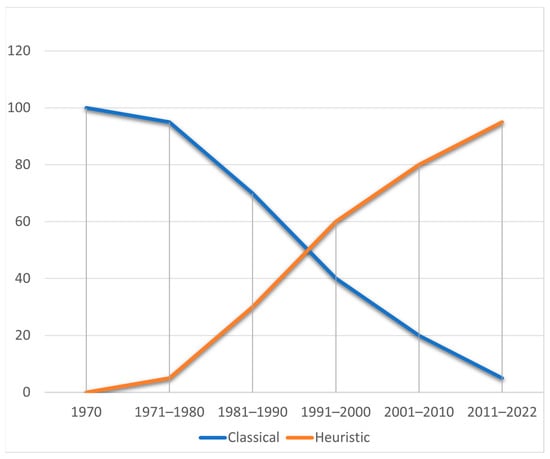
Figure 19.
Development of RPP approaches.
The utilization of artificial intelligence techniques is unsuitable for low-cost robots. Figure 20 depicts a comparison based on the number of articles published by each researcher using the heuristic methodology. Figure 21 displays the total number of research articles published using the classical methodology for each individual. Table 1 provides a thorough breakdown of the techniques used for robot navigation. Each algorithm is assessed according to a number of criteria. This inquiry pertains to the efficacy of the robot’s navigation capabilities in both static and dynamic environments, their applicability to various robot systems, their utilization in dynamic goal-oriented tasks, and their performance in both simulated and real-time scenarios, as well as whether to use a hybrid algorithm or not. The research discussed in Table 1 is from a research article published during the period from 1985 to 2022. Figure 22 depicts the distribution of these articles in terms of their number. A number of ideas have been covered over the past thirty-seven years, as shown in Table 1. A total of 82% of these studies discussed path planning in an environment containing fixed obstacles, while 18% of those studies concerned an environment containing moving obstacles (Figure 23).
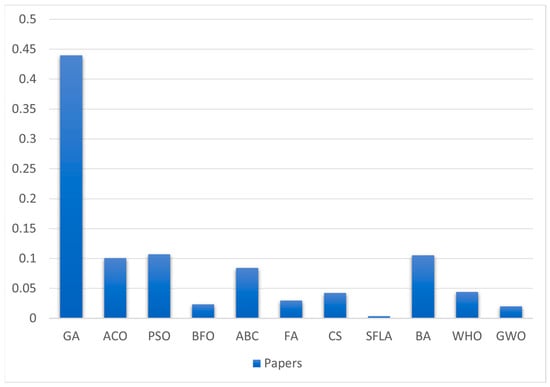
Figure 20.
A heuristic approach comparison based on work published.
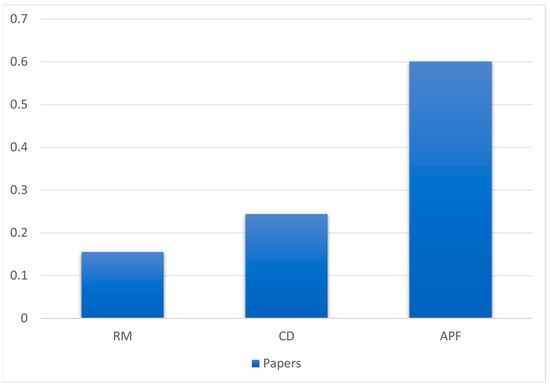
Figure 21.
A classical approach comparison based on a paper published.

Table 1.
Analyses of different RPP methods.
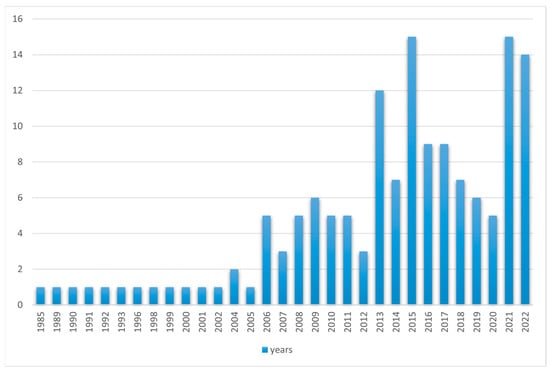
Figure 22.
Publication years studied.
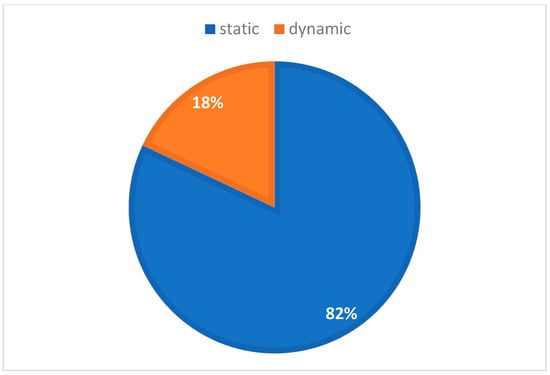
Figure 23.
Analysis of environmental navigation techniques.
In some research, the robot’s objective was to move from its starting point, and the APF algorithm outperformed classic methods, while the GA algorithm was most relevant for heuristic methods. Moreover, this type of problem was discussed in some research in which algorithms of this type were used (ACO, FA). Some research has discussed the topic of multi-robot systems, where each robot moves from its starting point to a specific target. Moreover, some researchers used traditional methods to solve this problem by using an algorithm (APF). Most of the research dealt with robot kinematics, especially in recent research, where applying geometry to the study of the movement of multi-degree-of-freedom kinematic chains that form the structure of robotic systems was considered, and some algorithms were combined with each other to obtain better results. This topic clearly appears in the classical methods using the CD algorithm. In the heuristic methods, the CS algorithm is considered the most receptive to merging with other algorithms for the purpose of improvement. There are also other algorithms, such as the GA, ACO, PSO, BFO, ABC, FA, SFL, BA, and GWO. These percentages and discussions are clearly shown in Figure 24.
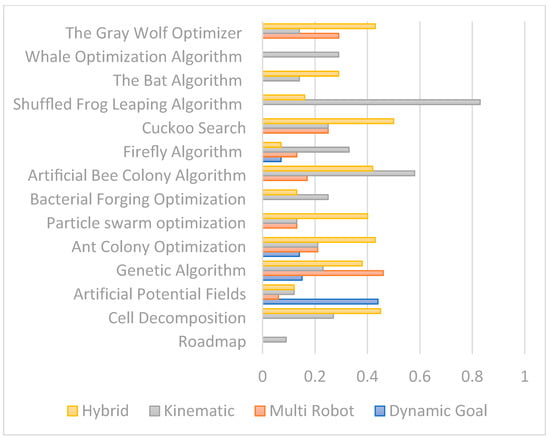
Figure 24.
Analysis of RPP techniques based on four factors.
4. Conclusions
This work presents a comprehensive survey of various robot path-planning techniques that are applicable to mobile robots. The aforementioned techniques were succinctly addressed. The text provides a thorough examination of the various techniques utilized in the expansive field of path planning for mobile robots. The aforementioned techniques are classified into two distinct categories, namely, classical and heuristic. Real-time applications are comparatively infrequent and are generally not the primary subject of contemporary publications. The quantity of literature pertaining to navigation by multiple mobile robot systems is notably limited in comparison to the quantity of literature on navigation by single mobile robot systems. Heuristic approaches exhibit superior performance compared to classical methods due to their ability to effectively manage environmental uncertainty. The prevalence of research articles pertaining to dynamic environments is comparatively lower than that pertaining to static environments. Heuristic methods are commonly employed to address real-time navigation challenges. The literature on robot navigation in dynamic environments with moving targets is relatively scarce compared to that on robot navigation in static environments. The literature on hybrid algorithms is considerably scarcer in comparison to that of standalone algorithms. The amalgamation of heuristic approaches with classical approaches has the potential to enhance performance. In scenarios where there are multiple objectives, it is common practice to integrate heuristic algorithms with classical algorithms as opposed to relying solely on the latter. Currently, there is a lack of academic research that incorporates multiple objectives that shift targets.
Author Contributions
Writing—original draft, J.A.A.; Conceptualization, J.A.A. and D.J.K.; Supervision, D.J.K.; Writing—review and editing, J.A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ehlert, P. The Use of Artificial Intelligence in Autonomous Mobile Robots; Report on Research Project; Delft University of Technology: Delft, The Netherlands, 1999. [Google Scholar]
- Abbas, N.; Abdulsaheb, J. An Adaptive Multi-Objective Particle Swarm Optimization Algorithm for Multi-Robot Path Planning. J. Eng. 2016, 22, 164–181. [Google Scholar]
- Ahmed Abdulsaheb, J.; Jasim Kadhim, D. Robot Path Planning in Unknown Environments with Multi-Objectives Using an Improved COOT Optimization Algorithm. Int. J. Intell. Eng. Syst. 2022, 15, 548–565. [Google Scholar] [CrossRef]
- Han, K.M. Collision Free Path Planning Algorithms for Robot Navigation Problem. Ph.D. Thesis, University of Missouri—Columbia, Columbia, MO, USA, 2007. [Google Scholar] [CrossRef]
- Buniyamin, N.; Ngah, W.A.J.W. Robot Global Path Planning Overview and a Variation of Ant Colony System Algorithm. Int. J. Math. Comput. Simul. 2011, 5, 9–16. Available online: https://www.researchgate.net/publication/265107519 (accessed on 15 May 2023).
- Miao, H. Robot Path Planning in Dynamic Environments using a Simulated Annealing Based Approach. Ph.D. Thesis, Queensland University of Technology, Brisbane, Australia, 2009. [Google Scholar]
- ChaborAlwawi, B.K.O.; Roth, H.; Kazem, B.I.; Abdullah, M.W. Mobile Robot Motion Planning and Multi Objective Optimization Using Improved Approach. Int. J. Mech. Eng. Robot. Res. 2015, 4, 325–330. [Google Scholar] [CrossRef]
- van den Berg, J. Path Planning in Dynamic Environments. Ph.D. Thesis, Utrecht University, Utrecht, The Netherlands, 2007. [Google Scholar]
- Yang, L.; Qi, J.; Song, D.; Xiao, J.; Han, J.; Xia, Y. Survey of Robot 3D Path Planning Algorithms. J. Control Sci. Eng. 2016, 2016, 7426913. [Google Scholar] [CrossRef]
- Lin, S.; Liu, A.; Wang, J.; Kong, X. A Review of Path-Planning Approaches for Multiple Mobile Robots. Machines 2022, 10, 773. [Google Scholar] [CrossRef]
- Abed, B.M.; Jasim, W.M. Multi Objective Optimization Algorithms for Mobile Robot Path Planning: A Survey. Int. J. Online Biomed. Eng. (IJOE) 2022, 18, 160–177. [Google Scholar] [CrossRef]
- Spall, J.C. Introduction to Stochastic Search and Optimization; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar] [CrossRef]
- Floudas, C.A. Deterministic Global Optimization; Springer: Boston, MA, USA, 2000; Volume 37. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, Y.; Hu, K. Adaptive Bacterial Foraging Optimization. Abstr. Appl. Anal. 2011, 2011, 108269. [Google Scholar] [CrossRef]
- Sedighizadeh, D.; Masehian, E.; Sedighizadeh, D. Classic and Heuristic Approaches in Robot Motion Planning—A Chronological Review. World Acad. Sci. Eng. Technol. 2007, 23, 101–106. Available online: https://www.researchgate.net/publication/249714449 (accessed on 15 May 2023).
- Asano, T.; Guibas, T.; Hershberger, J.; Imai, H. Visibility-polygon search and Euclidean shortest path. In Proceedings of the 26th Annual Symposium on Foundations of Computer Science, Portland, OR, USA, 21–23 October 1985; pp. 155–164. [Google Scholar]
- Canny, J. A Voronoi method for the piano-movers problem. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; pp. 530–535. [Google Scholar] [CrossRef]
- Salzman, O. Sampling-based robot motion planning. Commun. ACM 2019, 62, 54–63. [Google Scholar] [CrossRef]
- Bhattacharya, P.; Gavrilova, M. Roadmap-Based Path Planning—Using the Voronoi Diagram for a Clearance-Based Shortest Path. IEEE Robot. Autom. Mag. 2008, 15, 58–66. [Google Scholar] [CrossRef]
- Masehian, E.; Amin-Naseri, M.R. A voronoi diagram-visibility graph-potential field compound algorithm for robot path planning. J. Robot. Syst. 2004, 21, 275–300. [Google Scholar] [CrossRef]
- Yang, D.-H.; Hong, S.-K. A roadmap construction algorithm for mobile robot path planning using skeleton maps. Adv. Robot. 2007, 21, 51–63. [Google Scholar] [CrossRef]
- Wein, R.; van den Berg, J.P.; Halperin, D. The visibility–Voronoi complex and its applications. Comput. Geom. 2007, 36, 66–87. [Google Scholar] [CrossRef]
- Kavraki, L.E.; Svestka, P.; Latombe, J.-C.; Overmars, M.H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- Sánchez, G.; Latombe, J.-C. A Single-Query Bi-Directional Probabilistic Roadmap Planner with Lazy Collision Checking. In Robotics Research: The Tenth International Symposium; Springer: Berlin/Heidelberg, Germany, 2003; pp. 403–417. [Google Scholar] [CrossRef]
- Yan, F.; Liu, Y.-S.; Xiao, J.-Z. Path Planning in Complex 3D Environments Using a Probabilistic Roadmap Method. Int. J. Autom. Comput. 2013, 10, 525–533. [Google Scholar] [CrossRef]
- Huppi, M.; Bartolomei, L.; Mascaro, R.; Chli, M. T-PRM: Temporal Probabilistic Roadmap for Path Planning in Dynamic Environments. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 10320–10327. [Google Scholar] [CrossRef]
- Huang, X.; Soti, G.; Zhou, H.; Ledermann, C.; Hein, B.; Kroger, T. HIRO: Heuristics Informed Robot Online Path Planning Using Pre-computed Deterministic Roadmaps. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 8109–8116. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Lei, L.; Xu, F. An Improved Potential Field-Based Probabilistic Roadmap Algorithm for Path Planning. In Proceedings of the 2022 6th International Conference on Automation, Control and Robots (ICACR), Shanghai, China, 23–25 September 2022; pp. 195–199. [Google Scholar] [CrossRef]
- You, H.; Chen, G.; Jia, Q.; Huang, Z. Path Planning for Robot in Multi-dimensional Environment Based on Dynamic PRM Blended Potential Field. In Proceedings of the 2021 IEEE 5th Information Technology, Networking, Electronic and Automation Control Conference (IT-NEC), Xi’an, China, 15–17 October 2021; pp. 1157–1162. [Google Scholar] [CrossRef]
- Keil, J.M. Decomposing a Polygon into Simpler Components. SIAM J. Comput. 1985, 14, 799–817. [Google Scholar] [CrossRef]
- Samet, H. An overview of quadtrees, octrees, and related hierarchical data structures. In Theoretical Foundations of Computer Graphics and CAD; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Noborio, H.; Naniwa, T.; Arimoto, S. A quadtree-based path-planning algorithm for a mobile robot. J. Robot. Syst. 1990, 7, 555–574. [Google Scholar] [CrossRef]
- Lingelbach, F. Path planning using probabilistic cell decomposition. In Proceedings of the IEEE International Conference on Robotics and Automation, 2004. Proceedings. ICRA ’04, New Orleans, LA, USA, 26 April–1 May 2004; Volume 1, pp. 467–472. [Google Scholar] [CrossRef]
- Sleumer, N.; Tschichold-Gürmann, N. Exact Cell Decomposition of Arrangements Used for Path Planning in Robotics; ETH Zurich: Zurich, Switzerland, 1999. [Google Scholar] [CrossRef]
- Cai, C.; Ferrari, S. Information-Driven Sensor Path Planning by Approximate Cell Decomposition. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2009, 39, 672–689. [Google Scholar] [CrossRef]
- Dugarjav, B.; Lee, S.-G.; Kim, D.; Kim, J.H.; Chong, N.Y. Scan matching online cell decomposition for coverage path planning in an unknown environment. Int. J. Precis. Eng. Manuf. 2013, 14, 1551–1558. [Google Scholar] [CrossRef]
- Glavaški, D.; Volf, M.; Bonković, M. Robot motion planning using exact cell decomposition and potential field methods. In Proceedings of the 9th WSEAS International Conference on Simulation, Modelling and Optimization, Budapest, Hungary, 3–5 September 2009. [Google Scholar]
- Tunggal, T.P.; Supriyanto, A.; Rochman, N.M.Z.; Faishal, I.; Pambudi, I.; Iswanto, I. Pursuit Algorithm for Robot Trash Can Based on Fuzzy-Cell Decomposition. Int. J. Electr. Comput. Eng. (IJECE) 2016, 6, 2863. [Google Scholar] [CrossRef]
- Gill, M.A.C.; Zomaya, A.Y. A cell decomposition-based collision avoidance algorithm for robot manipulators. Cybern. Syst. 1998, 29, 113–135. [Google Scholar] [CrossRef]
- Gonzalez, R.; Kloetzer, M.; Mahulea, C. Comparative study of trajectories resulted from cell decomposition path planning approaches. In Proceedings of the 2017 21st International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 19–21 October 2017; pp. 49–54. [Google Scholar] [CrossRef]
- Iswanto, I.; Wahyunggoro, O.; Cahyadi, A. Quadrotor path planning based on modified fuzzy cell decomposition algorithm. TELKOMNIKA (Telecommun. Comput. Electron. Control) 2016, 14, 655–664. [Google Scholar] [CrossRef]
- Salama, O.A.A.; Eltaib, M.E.H.; Mohamed, H.A.; Salah, O. RCD: Radial Cell Decomposition Algorithm for Mobile Robot Path Planning. IEEE Access 2021, 9, 149982–149992. [Google Scholar] [CrossRef]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; pp. 500–505. [Google Scholar] [CrossRef]
- Garibotto, G.; Masciangelo, S. Path planning using the potential field approach for navigation. In Proceedings of the Fifth International Conference on Advanced Robotics’ Robots in Unstructured Environments, Pisa, Italy, 19–22 June 1991; Volume 2, pp. 1679–1682. [Google Scholar] [CrossRef]
- Kim, J.-O.; Khosla, P.K. Real-time obstacle avoidance using harmonic potential functions. IEEE Trans. Robot. Autom. 1992, 8, 338–349. [Google Scholar] [CrossRef]
- Borenstein, J.; Koren, Y. Real-time obstacle avoidance for fast mobile robots. IEEE Trans. Syst. Man Cybern. 1989, 19, 1179–1187. [Google Scholar] [CrossRef]
- Ge, S.S.; Cui, Y.J. Dynamic Motion Planning for Mobile Robots Using Potential Field Method. Auton. Robot. 2002, 13, 207–222. [Google Scholar] [CrossRef]
- Montiel, O.; Orozco-Rosas, U.; Sepúlveda, R. Path planning for mobile robots using Bacterial Potential Field for avoiding static and dynamic obstacles. Expert Syst. Appl. 2015, 42, 5177–5191. [Google Scholar] [CrossRef]
- Valavanis, K.P.; Hebert, T.; Kolluru, R.; Tsourveloudis, N. Mobile robot navigation in 2-D dynamic environments using an electrostatic potential field. IEEE Trans. Syst. Man Cybern.—Part A Syst. Hum. 2000, 30, 187–196. [Google Scholar] [CrossRef]
- Huang, L. Velocity planning for a mobile robot to track a moving target—A potential field approach. Robot. Auton. Syst. 2009, 57, 55–63. [Google Scholar] [CrossRef]
- Shi, P.; Zhao, Y. An efficient path planning algorithm for mobile robot using improved potential field. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guilin, China, 19–23 December 2009; pp. 1704–1708. [Google Scholar] [CrossRef]
- Sfeir, J.; Saad, M.; Saliah-Hassane, H. An improved Artificial Potential Field approach to real-time mobile robot path planning in an unknown environment. In Proceedings of the 2011 IEEE International Symposium on Robotic and Sensors Environments (ROSE), Montreal, QC, Canada, 17–18 September 2011; pp. 208–213. [Google Scholar] [CrossRef]
- Pradhan, S.K.; Parhi, D.R.; Panda, A.K.; Behera, R.K. Potential field method to navigate several mobile robots. Appl. Intell. 2006, 25, 321–333. [Google Scholar] [CrossRef]
- Zhang, H.; Li, M.; Wu, Z. Path Planning based on Improved Artificial Potential Field Method. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; pp. 4922–4925. [Google Scholar] [CrossRef]
- Li, Y.; Tian, B.; Yang, Y.; Li, C. Path planning of robot based on artificial potential field method. In Proceedings of the 2022 IEEE 6th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 4–6 March 2022; pp. 91–94. [Google Scholar] [CrossRef]
- Shi, M.; Nie, J. Improvement of Path Planning Algorithm based on Small Step Artificial Potential Field Method. In Proceedings of the 2022 9th International Conference on Dependable Systems and Their Applications (DSA), Wulumuqi, China, 4–5 August 2022; pp. 827–831. [Google Scholar] [CrossRef]
- Liu, C.; Zhai, L.; Zhang, X. Research on local real-time obstacle avoidance path planning of unmanned vehicle based on improved artificial potential field method. In Proceedings of the 2022 6th CAA International Conference on Vehicular Control and Intelligence (CVCI), Nanjing, China, 28–30 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Janabi-Sharifi, F.; Vinke, D. Integration of the artificial potential field approach with simulated annealing for robot path planning. In Proceedings of the 8th IEEE International Symposium on Intelligent Control, Chicago, IL, USA, 25–27 August 1993; pp. 536–541. [Google Scholar] [CrossRef]
- Bremermann, H.J. The Evolution of Intelligence. The Nervous System as a Model of Its Environment; University of Washington: Seattle, WA, USA, 1958. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Kala, R. Coordination in Navigation of Multiple Mobile Robots. Cybern. Syst. 2014, 45, 1–24. [Google Scholar] [CrossRef]
- Liu, F.; Liang, S.; Xian, X. Optimal Robot Path Planning for Multiple Goals Visiting Based on Tailored Genetic Algorithm. Int. J. Comput. Intell. Syst. 2014, 7, 1109. [Google Scholar] [CrossRef]
- Yang, S.; Hu, Y.; Meng, M. A Knowledge Based GA for Path Planning of Multiple Mobile Robots in Dynamic Environments. In Proceedings of the 2006 IEEE Conference on Robotics, Automation and Mechatronics, Bangkok, Thailand, 1–3 June 2006; pp. 1–6. [Google Scholar] [CrossRef]
- Qu, H.; Xing, K.; Alexander, T. An improved genetic algorithm with co-evolutionary strategy for global path planning of multiple mobile robots. Neurocomputing 2013, 120, 509–517. [Google Scholar] [CrossRef]
- Ni, J.; Wang, K.; Huang, H.; Wu, L.; Luo, C. Robot path planning based on an improved genetic algorithm with variable length chromosome. In Proceedings of the 2016 12th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), Changsha, China, 13–15 August 2016; pp. 145–149. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, P.B.; Parhi, D.R. Intelligent Navigation of Humanoids in Cluttered Environments Using Regression Analysis and Genetic Algorithm. Arab. J. Sci. Eng. 2018, 43, 7655–7678. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, H.; Zhang, L.; Sun, Y. Research on fuzzy control of path tracking for underwater vehicle based on genetic algorithm optimization. Ocean Eng. 2018, 156, 217–223. [Google Scholar] [CrossRef]
- Roberge, V.; Tarbouchi, M.; Labonte, G. Fast Genetic Algorithm Path Planner for Fixed-Wing Military UAV Using GPU. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2105–2117. [Google Scholar] [CrossRef]
- Patle, B.K.; Parhi, D.R.K.; Jagadeesh, A.; Kashyap, S.K. Matrix-Binary Codes based Genetic Algorithm for path planning of mobile robot. Comput. Electr. Eng. 2018, 67, 708–728. [Google Scholar] [CrossRef]
- Creaser, P.A. Evolutionary generation of fuzzy guidance laws. In Proceedings of the UKACC International Conference on Control (CONTROL ’98), Swansea, UK, 1–4 September 1998; pp. 883–888. [Google Scholar] [CrossRef]
- Lin, K.-P.; Hung, K.-C. An efficient fuzzy weighted average algorithm for the military UAV selecting under group decision-making. Knowl. Based Syst. 2011, 24, 877–889. [Google Scholar] [CrossRef]
- Zhang, Y. Research on Robot Path Planning Based on Improved Genetic Algorithm. In Proceedings of the 2022 14th International Conference on Advanced Computational Intelligence (ICACI), Wuhan, China, 15–17 July 2022; pp. 273–277. [Google Scholar] [CrossRef]
- Huang, F.; Fu, H.; Chen, J.; Wang, X. Mobile robot path planning based on improved genetic algorithm. In Proceedings of the 2021 4th World Conference on Mechanical Engineering and Intelligent Manufacturing (WCMEIM), Shanghai, China, 12–14 November 2021; pp. 378–383. [Google Scholar] [CrossRef]
- Dorigo, M.; Gambardella, L.M. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef]
- Tan, G.-Z. Ant Colony System Algorithm for Real-Time Globally Optimal Path Planning of Mobile Robots. Acta Autom. Sin. 2007, 33, 0279. [Google Scholar] [CrossRef]
- Liu, S.; Mao, L.; Yu, J. Path Planning Based on Ant Colony Algorithm and Distributed Local Navigation for Multi-Robot Systems. In Proceedings of the 2006 International Conference on Mechatronics and Automation, Luoyang, China, 25–28 June 2006; pp. 1733–1738. [Google Scholar] [CrossRef]
- Castillo, O.; Neyoy, H.; Soria, J.; Melin, P.; Valdez, F. A new approach for dynamic fuzzy logic parameter tuning in Ant Colony Optimization and its application in fuzzy control of a mobile robot. Appl. Soft Comput. 2015, 28, 150–159. [Google Scholar] [CrossRef]
- Kumar, P.B.; Sahu, C.; Parhi, D.R. A hybridized regression-adaptive ant colony optimization approach for navigation of humanoids in a cluttered environment. Appl. Soft Comput. 2018, 68, 565–585. [Google Scholar] [CrossRef]
- Liu, J.; Yang, J.; Liu, H.; Tian, X.; Gao, M. An improved ant colony algorithm for robot path planning. Soft Comput. 2017, 21, 5829–5839. [Google Scholar] [CrossRef]
- Rajput, U.; Kumari, M. Mobile robot path planning with modified ant colony optimization. Int. J. Bio-Inspired Comput. 2017, 9, 106. [Google Scholar] [CrossRef]
- Purian, F.K.; Sadeghian, E. Mobile robots path planning using ant colony optimization and Fuzzy Logic algorithms in unknown dynamic environments. In Proceedings of the 2013 International Conference on Control, Automation, Robotics and Embedded Systems (CARE), Jabalpur, India, 16–18 December 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Brand, M.; Masuda, M.; Wehner, N.; Yu, X.-H. Ant Colony Optimization algorithm for robot path planning. In Proceedings of the 2010 International Conference on Computer Design and Applications, Qinhuangdao, China, 25–27 June 2010; pp. V3-436–V3-440. [Google Scholar] [CrossRef]
- Liu, L.Q.; Yu, F.; Dai, Y.T. Path planning of underwater vehicle in 3D space based on ant colony algorithm. J. Syst. Simul. 2008, 20, 3712e6. [Google Scholar]
- Chen, Y.; Su, F.; Shen, L.C. Improved ant colony algorithm based on PRM for UAV route planning. J. Syst. Simul. 2009, 21, 1658e66. [Google Scholar]
- Gao, M.; Liu, Y.; Zhang, Q. Application of improved ant colony algorithm to route planning of anti-ship missile. J. Comput. Appl. 2013, 32, 2530–2533. [Google Scholar] [CrossRef]
- Zong, C.; Yao, X.; Fu, X. Path Planning of Mobile Robot based on Improved Ant Colony Algorithm. In Proceedings of the 2022 IEEE 10th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 17–19 June 2022; pp. 1106–1110. [Google Scholar] [CrossRef]
- Su, Q.; Yu, W.; Liu, J. Mobile Robot Path Planning Based on Improved Ant Colony Algorithm. In Proceedings of the 2021 Asia-Pacific Conference on Communications Technology and Computer Science (ACCTCS), Shenyang, China, 22–24 January 2021; pp. 220–224. [Google Scholar] [CrossRef]
- Chen, L.; Su, Y.; Zhang, D.; Leng, Z.; Qi, Y.; Jiang, K. Research on path planning for mobile robots based on improved ACO. In Proceedings of the 2021 36th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Nanchang, China, 28–30 May 2021; pp. 379–383. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’95—Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
- Tang, X.; Li, L.; Jiang, B. Mobile robot SLAM method based on multi-agent particle swarm optimized particle filter. J. China Univ. Posts Telecommun. 2014, 21, 78–86. [Google Scholar] [CrossRef]
- Ha, X.V.; Ha, C.; Lee, J. Novel hybrid optimization algorithm using PSO and MADS for the trajectory estimation of a four track wheel skid-steered mobile robot. Adv. Robot. 2013, 27, 1421–1437. [Google Scholar] [CrossRef]
- Atyabi, A.; Phon-Amnuaisuk, S.; Ho, C.K. Applying Area Extension PSO in Robotic Swarm. J. Intell. Robot. Syst. 2010, 58, 253–285. [Google Scholar] [CrossRef]
- Tang, Q.; Eberhard, P. Cooperative Motion of Swarm Mobile Robots Based on Particle Swarm Optimization and Multibody System Dynamics. Mech. Based Des. Struct. Mach. 2011, 39, 179–193. [Google Scholar] [CrossRef]
- Couceiro, M.S.; Rocha, R.P.; Ferreira, N.M.F. A PSO multi-robot exploration approach over unreliable MANETs. Adv. Robot. 2013, 27, 1221–1234. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Cheng, J.; Lin, C.; Wu, X.; Ou, Y.; Xu, Y. Classification-based learning by particle swarm optimization for wall-following robot navigation. Neurocomputing 2013, 113, 27–35. [Google Scholar] [CrossRef]
- Das, P.K.; Behera, H.S.; Panigrahi, B.K. A hybridization of an improved particle swarm optimization and gravitational search algorithm for multi-robot path planning. Swarm Evol. Comput. 2016, 28, 14–28. [Google Scholar] [CrossRef]
- He, B.; Ying, L.; Zhang, S.; Feng, X.; Yan, T.; Nian, R.; Shen, Y. Autonomous navigation based on unscented-FastSLAM using particle swarm optimization for autonomous underwater vehicles. Measurement 2015, 71, 89–101. [Google Scholar] [CrossRef]
- Rendón, M.A.; Martins, F.F. Path Following Control Tuning for an Autonomous Unmanned Quadrotor Using Particle Swarm Optimization. IFAC-PapersOnLine 2017, 50, 325–330. [Google Scholar] [CrossRef]
- Kumar, P.B.; Pandey, K.K.; Sahu, C.; Chhotray, A.; Parhi, D.R. A hybridized RA-APSO approach for humanoid navigation. In Proceedings of the 2017 Nirma University International Conference on Engineering (NUiCONE), Ahmedabad, India, 23–25 November 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Gao, Y.; Xie, W.; Li, Q.; Li, X.; Hu, M.; Zhao, L. Time-Jerk Optimal Trajectory Planning of Industrial Robot based on Hybrid Particle Swarm Optimization Algorithm. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; pp. 6327–6331. [Google Scholar] [CrossRef]
- Algabri, M.; Mathkour, H.; Ramdane, H.; Alsulaiman, M. Comparative study of soft computing techniques for mobile robot navigation in an unknown environment. Comput. Hum. Behav. 2015, 50, 42–56. [Google Scholar] [CrossRef]
- Banks, A.; Vincent, J.; Phalp, K. Particle Swarm Guidance System for Autonomous Unmanned Aerial Vehicles in an Air Defence Role. J. Navig. 2008, 61, 9–29. [Google Scholar] [CrossRef]
- Yuan, D. Research on path-planning of particle swarm optimization based on distance penalty. In Proceedings of the 2021 2nd International Conference on Computing and Data Science (CDS), Stanford, CA, USA, 28–29 January 2021; pp. 149–153. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Y.; Xue, Y.; Chen, Y. Robot Path Planning Based on Improved Particle Swarm Optimization. In Proceedings of the 2022 Power System and Green Energy Conference (PSGEC), Shanghai, China, 25–27 August 2022; pp. 507–511. [Google Scholar] [CrossRef]
- Sarkar, K.; Balabantaray, B.K.; Chakrabarty, A.; Biswal, B.B.; Mohanty, B. Path Planning of Mobile Robots Using Enhanced Particle Swarm Optimization. In Proceedings of the 2020 3rd International Conference on Energy, Power and Environment: Towards Clean Energy Technologies, Shillong, Meghalaya, India, 5–7 March 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Passino, K. Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Syst. 2002, 22, 52–67. [Google Scholar] [CrossRef]
- Dos, L.; Coelho, S.; Sierakowski, C.A. Bacteria colony approaches with variable velocity applied to path optimization of mobile robots. In ABCM Symposium Series in Mechatronics; ABCM: Hampton, IA, USA, 2006; Volume 2, pp. 297–304. [Google Scholar]
- Sierakowski, C.A.; Coelho, L.D.S. Path Planning Optimization for Mobile Robots Based on Bacteria Colony Approach. In Applied Soft Computing Technologies: The Challenge of Complexity; Springer: Berlin/Heidelberg, Germany, 2006; pp. 187–198. [Google Scholar] [CrossRef]
- Liang, X.; Li, L.; Wu, J.; Chen, H. Mobile robot path planning based on adaptive bacterial foraging algorithm. J. Cent. South Univ. 2013, 20, 3391–3400. [Google Scholar] [CrossRef]
- Gasparri, A.; Prosperi, M. A bacterial colony growth algorithm for mobile robot localization. Auton. Robot. 2008, 24, 349–364. [Google Scholar] [CrossRef]
- Abbas, N.H.; Ali, F.M. Path Planning of an Autonomous Mobile Robot using Enhanced Bacterial Foraging Optimization Algorithm. Al-Khwarizmi Eng. J. 2017, 12, 26–35. [Google Scholar] [CrossRef]
- Jati, A.; Singh, G.; Rakshit, P.; Konar, A.; Kim, E.; Nagar, A.K. A hybridisation of Improved Harmony Search and Bacterial Foraging for multi-robot motion planning. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, Brisbane, QLD, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar] [CrossRef]
- dos Santos Coelho, L.; da Costa Silveira, C. Improved bacterial foraging strategy for controller optimization applied to robotic manipulator system. In Proceedings of the 2006 IEEE Conference on Computer Aided Control System Design, 2006 IEEE International Conference on Control Applications, 2006 IEEE International Symposium on Intelligent Control, Munich, Germany, 4–6 October 2006; pp. 1276–1281. [Google Scholar] [CrossRef]
- Oyekan, J.; Hu, H. A novel bacterial foraging algorithm for automated tuning of PID controllers of UAVs. In Proceedings of the 2010 IEEE International Conference on Information and Automation, Harbin, China, 20–23 June 2010; pp. 693–698. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Erciyes University: Kayseri, Turkey, 2005. [Google Scholar]
- Contreras-Cruz, M.A.; Ayala-Ramirez, V.; Hernandez-Belmonte, U.H. Mobile robot path planning using artificial bee colony and evolutionary programming. Appl. Soft Comput. 2015, 30, 319–328. [Google Scholar] [CrossRef]
- Saffari, M.H.; Mahjoob, M.J. Bee colony algorithm for real-time optimal path planning of mobile robots. In Proceedings of the 2009 Fifth International Conference on Soft Computing, Computing with Words and Perceptions in System Analysis, Decision and Control, Famagusta, North Cyprus, 2–4 September 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Ma, Q.; Lei, X. Dynamic Path Planning of Mobile Robots Based on ABC Algorithm. In Artificial Intelligence and Computational Intelligence, Proceedings of the International Conference, AICI 2010, Sanya, China, 23–24 October 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 267–274. [Google Scholar] [CrossRef]
- Bhattacharjee, P.; Rakshit, P.; Goswami, I.; Konar, A.; Nagar, A.K. Multi-robot path-planning using artificial bee colony optimization algorithm. In Proceedings of the 2011 Third World Congress on Nature and Biologically Inspired Computing, Salamanca, Spain, 19–21 October 2011; pp. 219–224. [Google Scholar] [CrossRef]
- Liang, J.-H.; Lee, C.-H. Efficient collision-free path-planning of multiple mobile robots system using efficient artificial bee colony algorithm. Adv. Eng. Softw. 2015, 79, 47–56. [Google Scholar] [CrossRef]
- Xu, C.; Duan, H.; Liu, F. Chaotic artificial bee colony approach to Uninhabited Combat Air Vehicle (UCAV) path planning. Aerosp. Sci. Technol. 2010, 14, 535–541. [Google Scholar] [CrossRef]
- Li, B.; Chiong, R.; Gong, L. Search-evasion path planning for submarines using the Artificial Bee Colony algorithm. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 528–535. [Google Scholar] [CrossRef]
- Bhagade, A.S.; Puranik, P.V. Artificial Bee Colony Algorithm (ABC) for Vehicle Routing Optimization Problem. Int. J. Soft Comput. Eng. 2012, 2, 329–333. [Google Scholar]
- Li, B.; Gong, L.; Yang, W. An Improved Artificial Bee Colony Algorithm Based on Balance-Evolution Strategy for Unmanned Combat Aerial Vehicle Path Planning. Sci. World J. 2014, 2014, 232704. [Google Scholar] [CrossRef]
- Ding, L.; Wu, H.; Yao, Y. Chaotic Artificial Bee Colony Algorithm for System Identification of a Small-Scale Unmanned Helicopter. Int. J. Aerosp. Eng. 2015, 2015, 801874. [Google Scholar] [CrossRef]
- Li, Y.; Song, X.; Guan, W. Mobile robot path planning based on ABC-PSO algorithm. In Proceedings of the 2022 IEEE 6th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 4–6 March 2022; pp. 530–534. [Google Scholar] [CrossRef]
- Szczepanski, R.; Tarczewski, T. Global path planning for mobile robot based on Artificial Bee Colony and Dijkstra’s algorithms. In Proceedings of the 2021 IEEE 19th International Power Electronics and Motion Control Conference (PEMC), Gliwice, Poland, 25–29 April 2021; pp. 724–730. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-Inspired Metaheuristic Algorithms, 2nd ed.; Luniver Press: Bristol, UK, 2010. [Google Scholar]
- Hidalgo-Paniagua, A.; Vega-Rodríguez, M.A.; Ferruz, J.; Pavón, N. Solving the multi-objective path planning problem in mobile robotics with a FF-based approach. Soft Comput. 2017, 21, 949–964. [Google Scholar] [CrossRef]
- Brand, M.; Yu, X.-H. Autonomous robot path optimization using firefly algorithm. In Proceedings of the 2013 International Conference on Machine Learning and Cybernetics, Tianjin, China, 14–17 July 2013; pp. 1028–1032. [Google Scholar] [CrossRef]
- Sutantyo, D.; Levi, P. Decentralized underwater multi-robot communication using bio-inspired approaches. Artif. Life Robot. 2015, 20, 152–158. [Google Scholar] [CrossRef]
- Sutantyo, D.; Levi, P.; Moslinger, C.; Read, M. Collective-adaptive Levy flight for underwater multi-robot exploration. In Proceedings of the 2013 IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 4–7 August 2013; pp. 456–462. [Google Scholar] [CrossRef]
- Christensen, A.L.; O’Grady, R.; Dorigo, M. Synchronization and fault detection in autonomous robots. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 4139–4140. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Hong, D.; Duan, H.; Liu, L.; Wang, H. A modified firefly algorithm for UCAV path planning. Int. J. Hosp. Inf. Technol. 2012, 5, 123e44. [Google Scholar]
- Patle, B.K.; Parhi, D.R.; Jagadeesh, A.; Kashyap, S.K. On firefly algorithm: Optimization and application in mobile robot navigation. World J. Eng. 2017, 14, 65–76. [Google Scholar] [CrossRef]
- Kim, H.-C.; Kim, J.-S.; Ji, Y.-K.; Park, J.-H. Path Planning of Swarm Mobile Robots Using Firefly Algorithm. J. Inst. Control Robot. Syst. 2013, 19, 435–441. [Google Scholar] [CrossRef]
- Mitić, M.; Miljković, Z. Bio-inspired approach to learning robot motion trajectories and visual control commands. Expert Syst. Appl. 2015, 42, 2624–2637. [Google Scholar] [CrossRef]
- Sadhu, A.K.; Konar, A.; Bhattacharjee, T.; Das, S. Synergism of Firefly Algorithm and Q-Learning for Robot Arm Path Planning. Swarm Evol. Comput. 2018, 43, 50–68. [Google Scholar] [CrossRef]
- Abbas, N.H.; Saleh, B.J. Design of a Kinematic Neural Controller for Mobile Robots based on Enhanced Hybrid Firefly-Artificial Bee Colony Algorithm. AL-Khwarizmi Eng. J. 2016, 12, 45–60. [Google Scholar]
- Tighzert, L.; Fonlupt, C.; Mendil, B. A set of new compact firefly algorithms. Swarm Evol. Comput. 2018, 40, 92–115. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, Y.; Gao, F.; Liu, L. Three-Dimensional Path Planning Method for Autonomous Underwater Vehicle Based on Modified Firefly Algorithm. Math. Probl. Eng. 2015, 2015, 561394. [Google Scholar] [CrossRef]
- Patle, B.K.; Pandey, A.; Jagadeesh, A.; Parhi, D.R. Path planning in uncertain environment by using firefly algorithm. Def. Technol. 2018, 14, 691–701. [Google Scholar] [CrossRef]
- Li, F.; Fan, X.; Hou, Z. A Firefly Algorithm With Self-Adaptive Population Size for Global Path Planning of Mobile Robot. IEEE Access 2020, 8, 168951–168964. [Google Scholar] [CrossRef]
- Yang, X.; Wu, D. Atomic simulations for surface-initiated melting of Nb(111). Trans. Nonferrous Met. Soc. China 2009, 19, 210–214. [Google Scholar] [CrossRef]
- Mohanty, P.K.; Parhi, D.R. Optimal path planning for a mobile robot using cuckoo search algorithm. J. Exp. Theor. Artif. Intell. 2016, 28, 35–52. [Google Scholar] [CrossRef]
- Mohanty, P.K.; Parhi, D.R. A new hybrid optimization algorithm for multiple mobile robots navigation based on the CS-ANFIS approach. Memetic Comput. 2015, 7, 255–273. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Wang, H.; Liu, L.; Shao, M. A Hybrid Metaheuristic DE/CS Algorithm for UCAV Three-Dimension Path Planning. Sci. World J. 2012, 2012, 583973. [Google Scholar] [CrossRef]
- Xie, C.; Zheng, H. Application of Improved Cuckoo Search Algorithm to Path Planning Unmanned Aerial Vehicle. In Intelligent Computing Theories and Application, Proceedings of the 12th International Conference, ICIC 2016, Lanzhou, China, 2–5 August 2016; Springer International Publishing: Cham, Switzerland, 2016; pp. 722–729. [Google Scholar] [CrossRef]
- Eusuff, M.M.; Lansey, K.E. Optimization of Water Distribution Network Design Using the Shuffled Frog Leaping Algorithm. J. Water Resour. Plan. Manag. 2003, 129, 210–225. [Google Scholar] [CrossRef]
- Ni, J.; Yin, X.; Chen, J.; Li, X. An improved shuffled frog leaping algorithm for robot path planning. In Proceedings of the 2014 10th International Conference on Natural Computation (ICNC), Xiamen, China, 19–21 August 2014; pp. 545–549. [Google Scholar] [CrossRef]
- Hidalgo-Paniagua, A.; Vega-Rodríguez, M.A.; Ferruz, J.; Pavón, N. MOSFLA-MRPP: Multi-Objective Shuffled Frog-Leaping Algorithm applied to Mobile Robot Path Planning. Eng. Appl. Artif. Intell. 2015, 44, 123–136. [Google Scholar] [CrossRef]
- Shubhasri, K.; Parhi, D.R. Navigation Based on Adaptive Shuffled Frog-Leaping Algorithm for Underwater Mobile Robot. In Intelligent Computing, Communication and Devices; Springer: New Delhi, India, 2015; pp. 651–659. [Google Scholar] [CrossRef]
- Luo, J.; Chen, M.-R. Improved Shuffled Frog Leaping Algorithm and its multi-phase model for multi-depot vehicle routing problem. Expert Syst. Appl. 2014, 41, 2535–2545. [Google Scholar] [CrossRef]
- Liang, B.; Zhen, Z.; Jiang, J. Modified shuffled frog leaping algorithm optimized control for air-breathing hypersonic flight vehicle. Int. J. Adv. Robot. Syst. 2016, 13, 172988141667813. [Google Scholar] [CrossRef]
- Pu, X.; Xiong, C.; Zhao, L. Path Planning for Robot Based on IACO-SFLA Hybrid Algorithm. In Proceedings of the 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 4886–4893. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-Inspired Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Yuan, X.; Yuan, X.; Wang, X. Path Planning for Mobile Robot Based on Improved Bat Algorithm. Sensors 2021, 21, 4389. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Liu, L.; Wang, H. A Bat Algorithm with Mutation for UCAV Path Planning. Sci. World J. 2012, 2012, 418946. [Google Scholar] [CrossRef]
- Xin, G.; Shi, L.; Long, G.; Pan, W.; Li, Y.; Xu, J. Mobile robot path planning with reformative bat algorithm. PLoS ONE 2022, 17, e0276577. [Google Scholar] [CrossRef]
- Lin, N.; Tang, J.; Li, X.; Zhao, L. A Novel Improved Bat Algorithm in UAV Path Planning. Comput. Mater. Contin. 2019, 61, 323–344. [Google Scholar] [CrossRef]
- Zhou, X.; Gao, F.; Fang, X.; Lan, Z. Improved Bat Algorithm for UAV Path Planning in Three-Dimensional Space. IEEE Access 2021, 9, 20100–20116. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Z.; Si, L.; Tong, K.; Tan, C. A novel path planning method of mobile robots based on an improved bat algorithm. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2021, 235, 3071–3086. [Google Scholar] [CrossRef]
- Ajeil, F.H.; Ibraheem, I.K.; Humaidi, A.J.; Khan, Z.H. A novel path planning algorithm for mobile robot in dynamic environments using modified bat swarm optimization. J. Eng. 2021, 2021, 37–48. [Google Scholar] [CrossRef]
- Ibraheem, K.I.; Ajeil, F.H. Autonomous Mobile Robot Navigation and Obstacle Avoidance in Dynamic Environment using Modified Bat Swarm Optimization. In Proceedings of the 1st International Conference on Recent Trends of Engineering Sciences and Sustainability, Baghdad, Iraq, 17 May 2017; pp. 17–18. [Google Scholar]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Chhillar, A.; Choudhary, A. Mobile Robot Path Planning Based Upon Updated Whale Optimization Algorithm. In Proceedings of the 2020 10th International Conference on Cloud Computing, Data Science & Engineering (Confluence), Noida, India, 29–31 January 2020; pp. 684–691. [Google Scholar] [CrossRef]
- Dai, Y.; Yu, J.; Zhang, C.; Zhan, B.; Zheng, X. A novel whale optimization algorithm of path planning strategy for mobile robots. Appl. Intell. 2022, 53, 10843–10857. [Google Scholar] [CrossRef]
- Dao, T.-K.; Pan, T.-S.; Pan, J.-S. A multi-objective optimal mobile robot path planning based on whale optimization algorithm. In Proceedings of the IEEE 13th International Conference on Signal Processing (ICSP), Chengdu, China, 6–10 November 2016; pp. 337–342. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, J.; Zeng, J.; Tang, J. Three-dimensional path planning for autonomous underwater vehicles based on a whale optimization algorithm. Ocean Eng. 2022, 250, 111070. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Z.; Liu, Q.; Shen, R.; Hou, L.; Zhang, Y. Design of Mobile Robot Path Planning Algorithm Based on Improved Whale Optimization Algorithm. In Proceedings of the 2022 7th International Conference on Multimedia and Image Processing, Tianjin, China, 14–16 January 2022; pp. 231–235. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, J.; Yang, Z.; Tang, J. Two-dimensional optimal path planning for autonomous underwater vehicle using a whale optimization algorithm. Concurr. Comput. 2021, 33, e6140. [Google Scholar] [CrossRef]
- Zan, J.; Ku, P.; Jin, S. Research on robot path planning based on whale optimization algorithm. In Proceedings of the 2021 5th Asian Conference on Artificial Intelligence Technology (ACAIT), Haikou, China, 29–31 October 2021; pp. 500–504. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Dewangan, R.K.; Shukla, A.; Godfrey, W.W. Three dimensional path planning using Grey wolf optimizer for UAVs. Appl. Intell. 2019, 49, 2201–2217. [Google Scholar] [CrossRef]
- Albina, K.; Lee, S.G. Hybrid Stochastic Exploration Using Grey Wolf Optimizer and Coordinated Multi-Robot Exploration Algorithms. IEEE Access 2019, 7, 14246–14255. [Google Scholar] [CrossRef]
- Kamalova, A.; Navruzov, S.; Qian, D.; Lee, S.G. Multi-Robot Exploration Based on Multi-Objective Grey Wolf Optimizer. Appl. Sci. 2019, 9, 2931. [Google Scholar] [CrossRef]
- Ge, F.; Li, K.; Xu, W.; Wang, Y. Path Planning of UAV for Oilfield Inspection Based on Improved Grey Wolf Optimization Algorithm. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 3666–3671. [Google Scholar] [CrossRef]
- Kamalova, A.; Kim, K.D.; Lee, S.G. Waypoint Mobile Robot Exploration Based on Biologically Inspired Algorithms. IEEE Access 2020, 8, 190342–190355. [Google Scholar] [CrossRef]
- Liu, J.; Wei, X.; Huang, H. An Improved Grey Wolf Optimization Algorithm and its Application in Path Planning. IEEE Access 2021, 9, 121944–121956. [Google Scholar] [CrossRef]
- Yang, X.; Yuxi, H.; Qiuhong, L. Robot path planning based on the improved grey wolf optimization algorithm. In Proceedings of the 2022 Power System and Green Energy Conference (PSGEC), Shanghai, China, 25–27 August 2022; pp. 543–547. [Google Scholar] [CrossRef]
- Chen, Y.; Cheng, C.; Zhang, Y.; Li, X.; Sun, L. A Neural Network-Based Navigation Approach for Autonomous Mobile Robot Systems. Appl. Sci. 2022, 12, 7796. [Google Scholar] [CrossRef]
- Abdulsaheb, J.A.; Kadhim, D.J. Multi-Objective Robot Path Planning Using an Improved Hunter Prey Optimization Algorithm. Int. J. Intell. Eng. Syst. 2023, 16, 215–227. [Google Scholar] [CrossRef]
- Mohanty, P.K.; Parhi, D.R. A new efficient optimal path planner for mobile robot based on Invasive Weed Optimization algorithm. Front. Mech. Eng. 2014, 9, 317–330. [Google Scholar] [CrossRef]
- Kundu, S.; Parhi, D.R. Navigation of underwater robot based on dynamically adaptive harmony search algorithm. Memetic Comput. 2016, 8, 125–146. [Google Scholar] [CrossRef]
- Zhu, Z.; Xiao, J.; Li, J.-Q.; Wang, F.; Zhang, Q. Global path planning of wheeled robots using multi-objective memetic algorithms. Integr. Comput. Aided Eng. 2015, 22, 387–404. [Google Scholar] [CrossRef]
- Hidalgo-Paniagua, A.; Vega-Rodríguez, M.A.; Ferruz, J. Applying the MOVNS (multi-objective variable neighborhood search) algorithm to solve the path planning problem in mobile robotics. Expert Syst. Appl. 2016, 58, 20–35. [Google Scholar] [CrossRef]
- Salmanpour, S.; Monfared, H.; Omranpour, H. Solving robot path planning problem by using a new elitist multi-objective IWD algorithm based on coefficient of variation. Soft Comput. 2017, 21, 3063–3079. [Google Scholar] [CrossRef]
- Ullah, I.; Shen, Y.; Su, X.; Esposito, C.; Choi, C. A Localization Based on Unscented Kalman Filter and Particle Filter Localization Algorithms. IEEE Access 2020, 8, 2233–2246. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).