Variable Damping Actuator Using an Electromagnetic Brake for Impedance Modulation in Physical Human–Robot Interaction
Abstract
1. Introduction
2. The Variable Damping Actuator Concept
2.1. Operating Principle
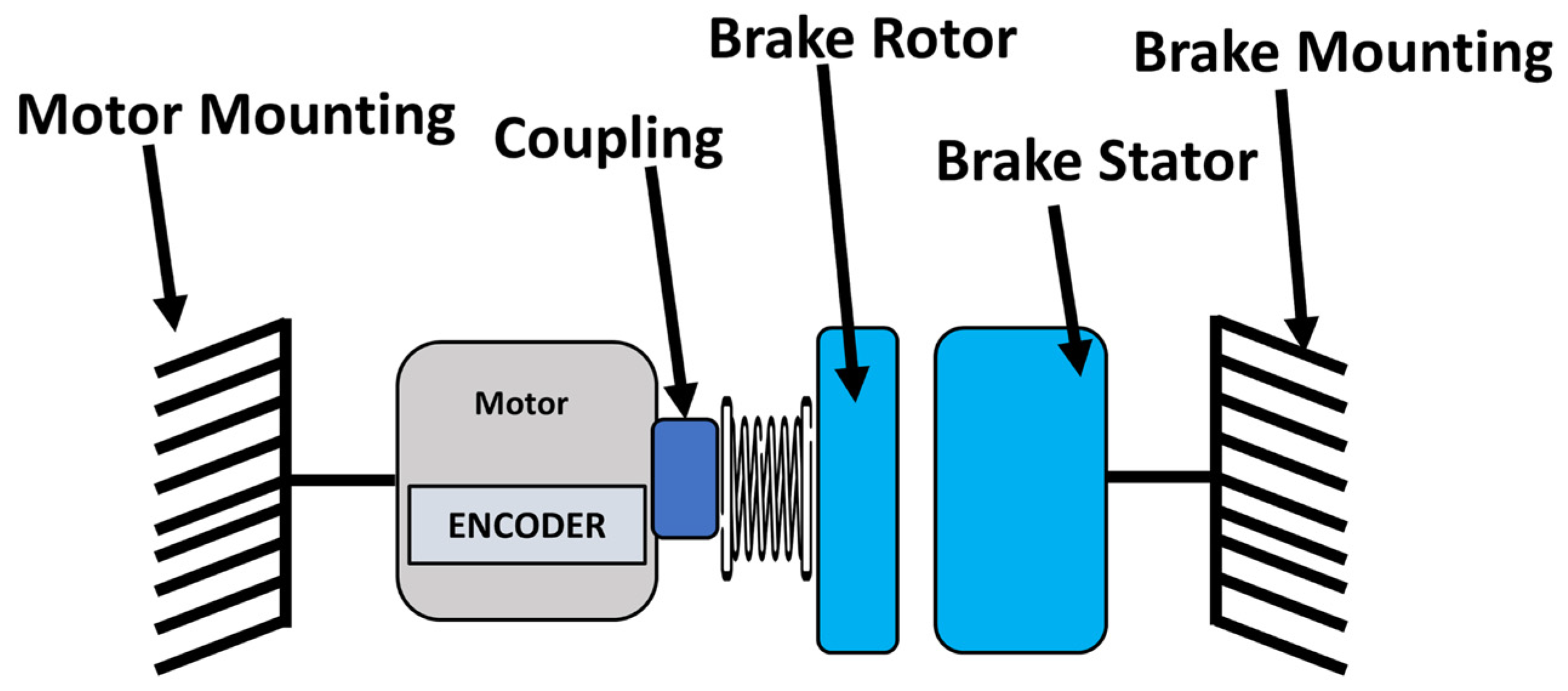
2.2. Conceptual Design
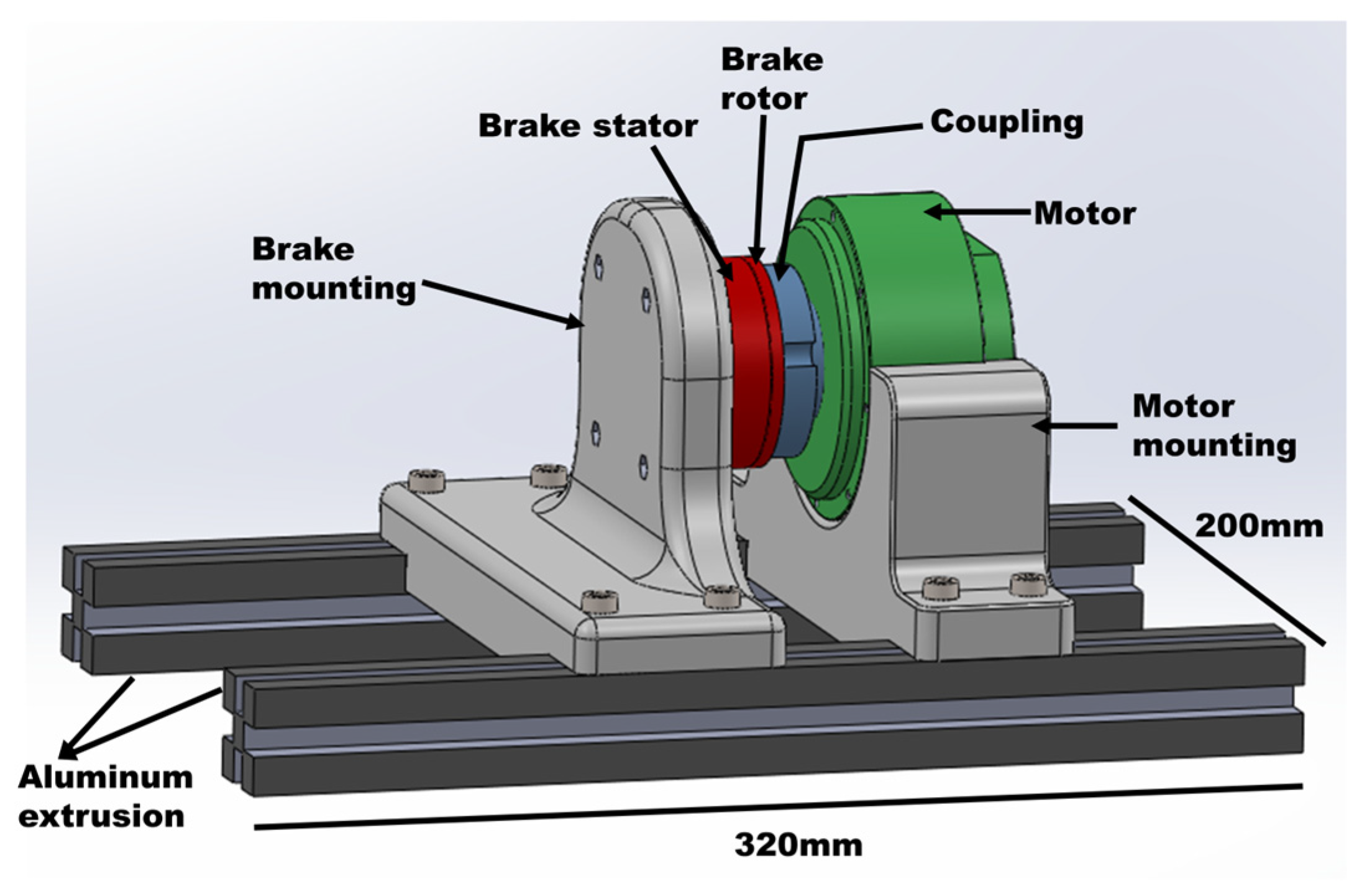
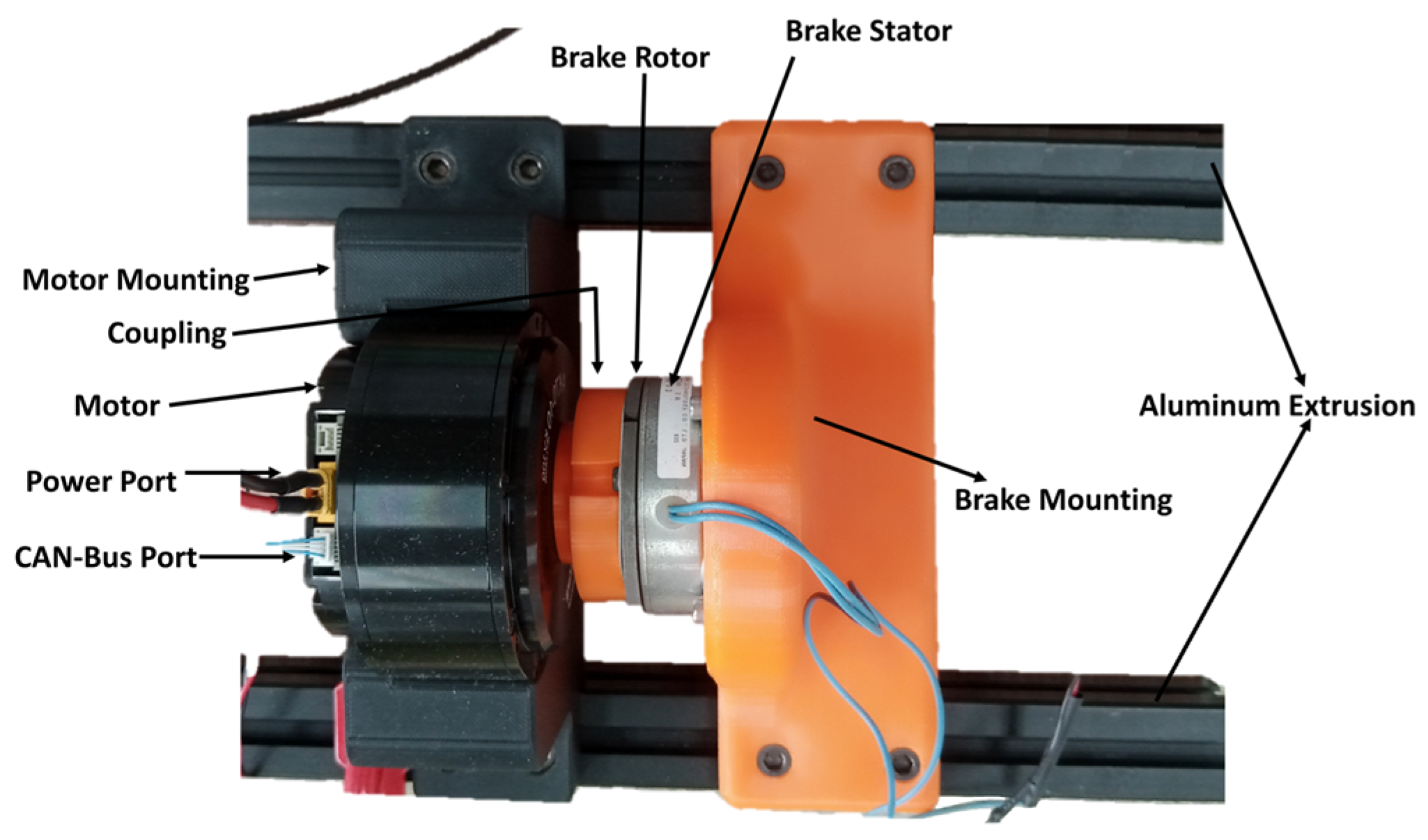
2.3. Mechanical Design
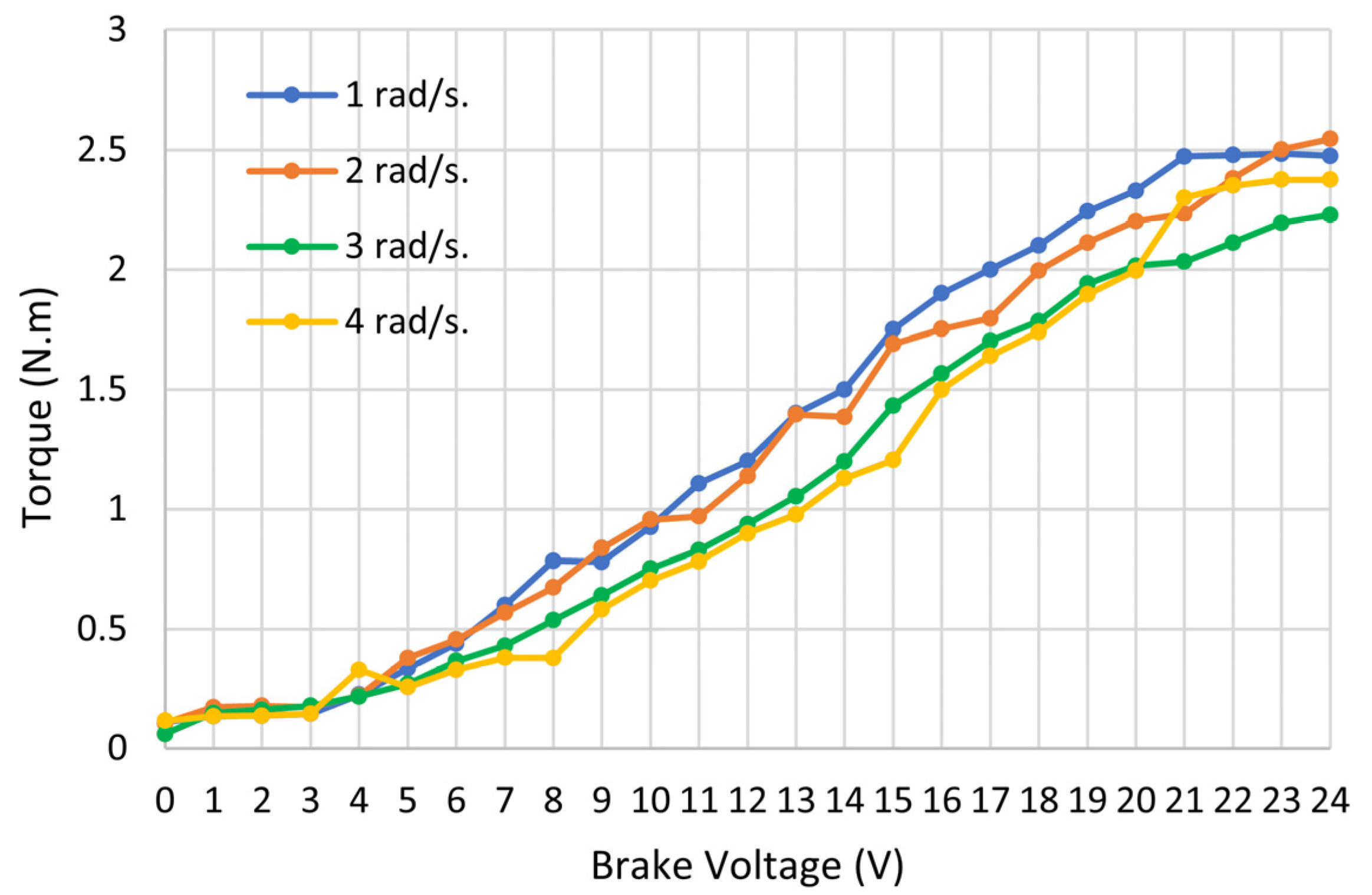
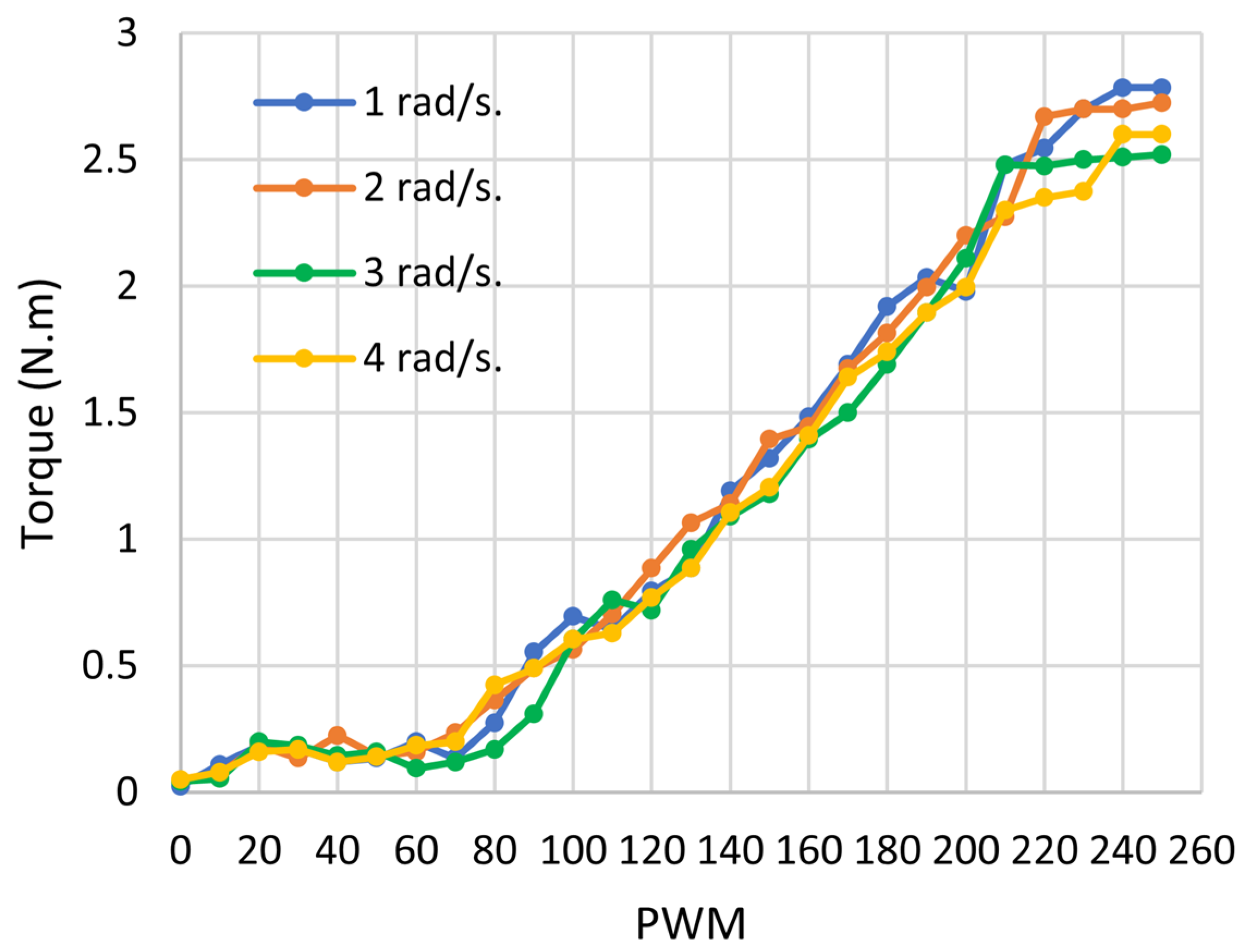
3. Electromagnetic Brake Characterization
4. Variable Damping Experiment Verification
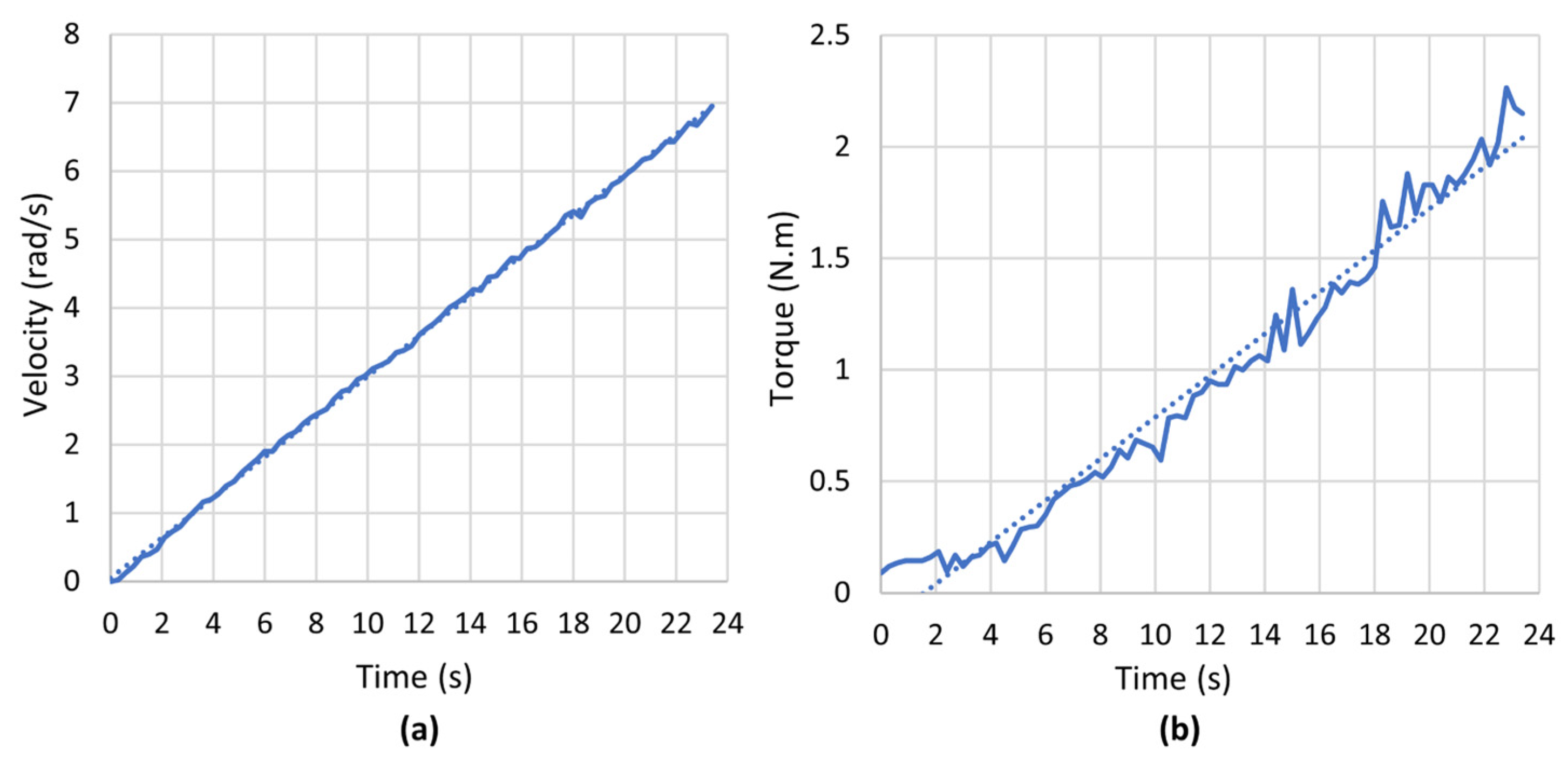
4.1. Experimental Setup and Procedure
4.2. Improved Model
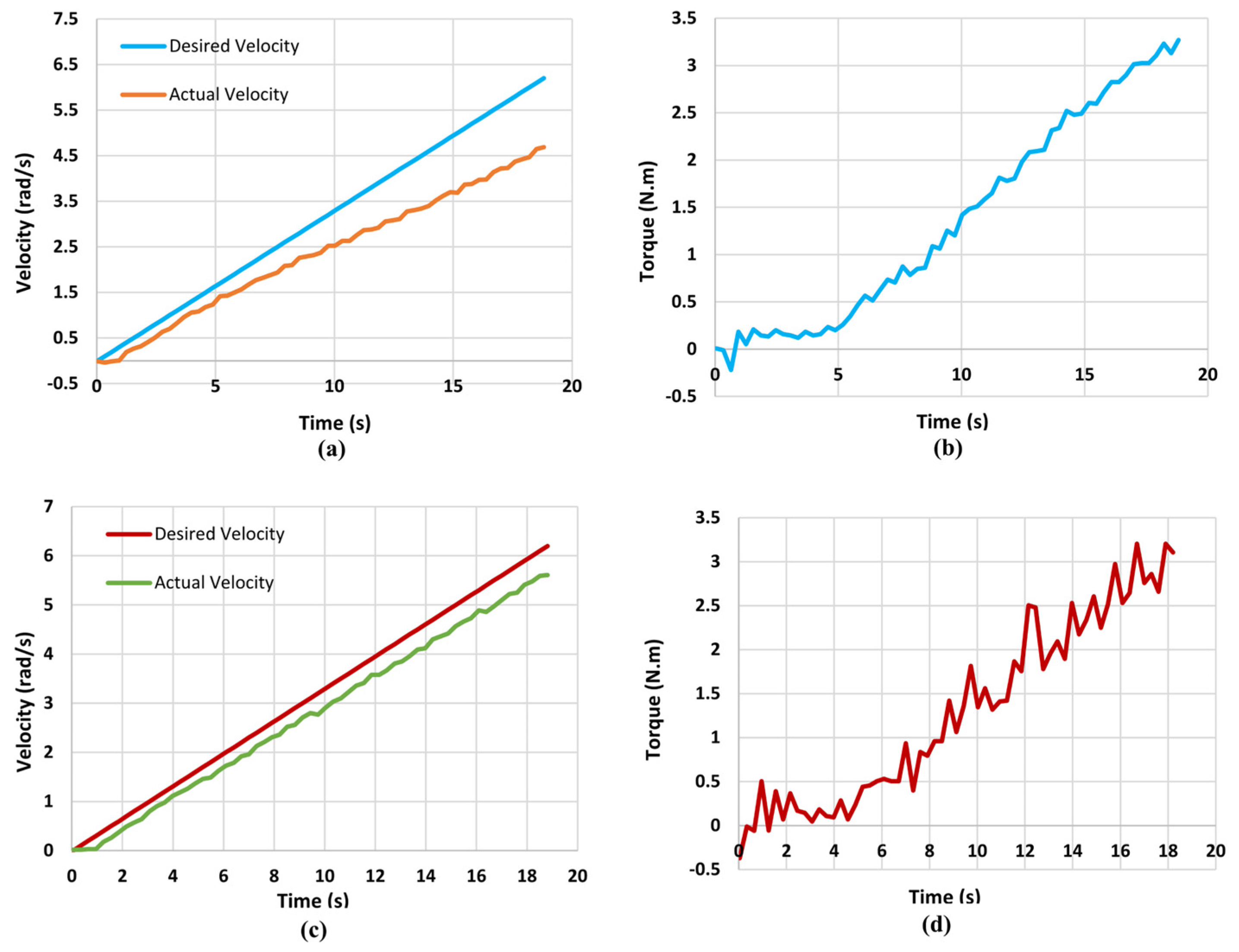
5. Damping Torque Validation
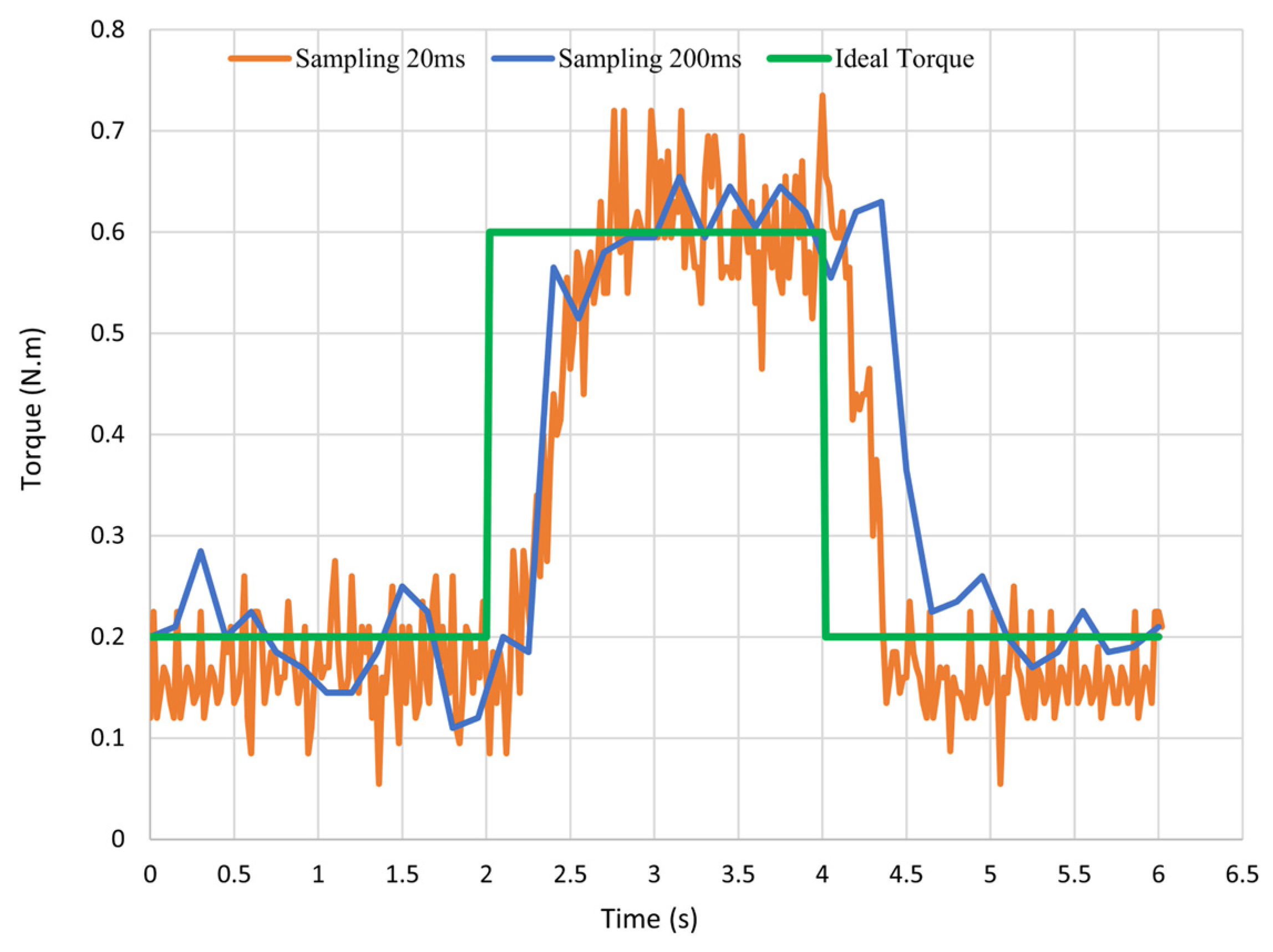
5.1. Step Reference
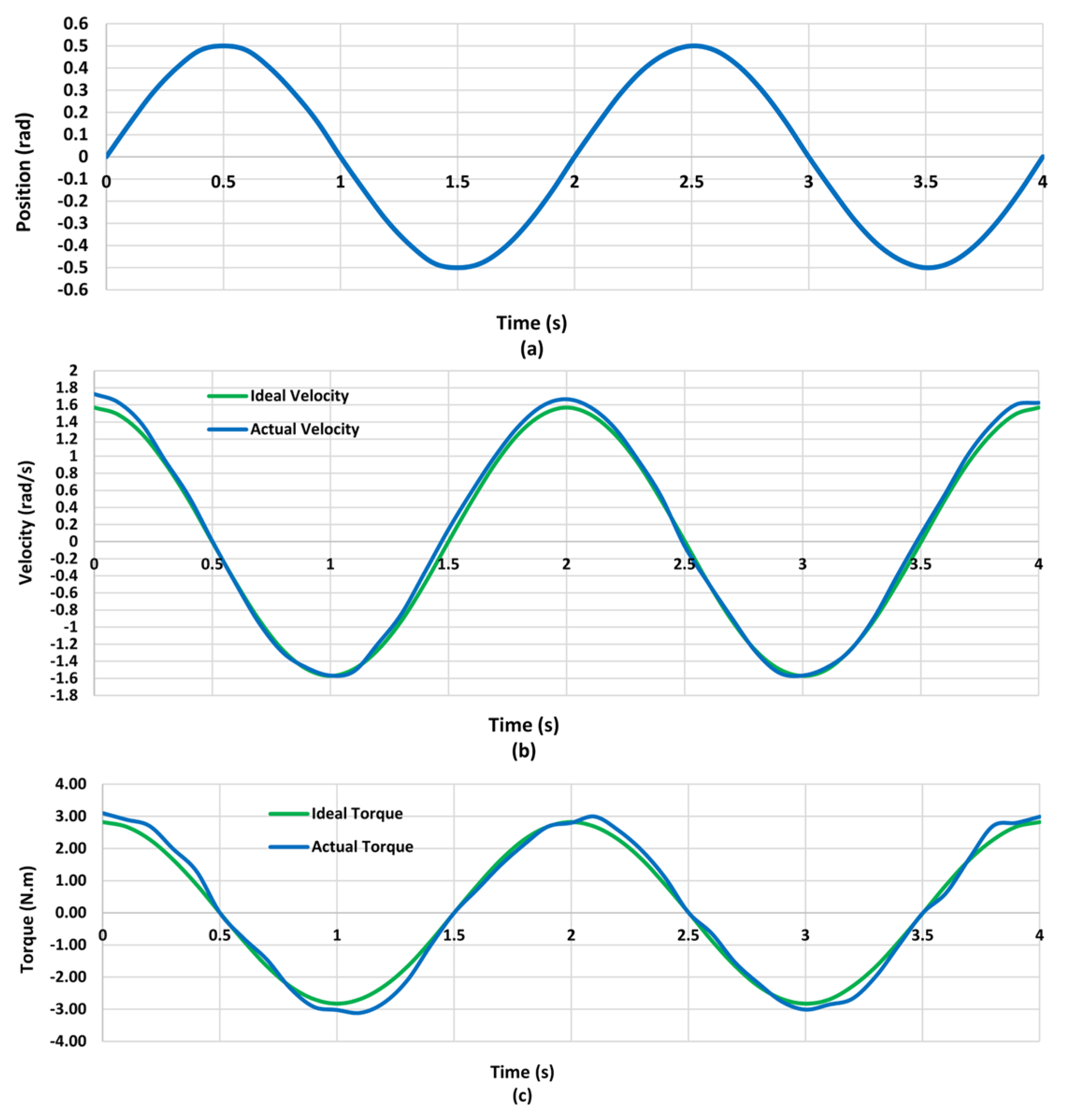
5.2. Sinusoidal Reference
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vanderborght, B.; Albu-Schaeffer, A.; Bicchi, A.; Burdet, E.; Caldwell, D.G.; Carloni, R.; Catalano, M.; Eiberger, O.; Friedl, W.; Ganesh, G.; et al. Variable impedance actuators: A review. Rob. Auton. Syst. 2013, 61, 1601–1614. [Google Scholar] [CrossRef]
- Sun, T.; Peng, L.; Cheng, L.; Hou, Z.G.; Pan, Y. Stability-guaranteed variable impedance control of robots based on approximate dynamic inversion. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 4193–4200. [Google Scholar] [CrossRef]
- Hogan, N. Impedance Control Part1-3. J. Dyn. Syst. Meas. Control. 1985, 107, 1–24. [Google Scholar] [CrossRef]
- Wannasuphoprasit, W.; Chanphat, S. T-Cobot: Transformable Collaborative Robot. In Proceedings of the 2005 ASME International Mechanical Engineering Congress and Exposition. Dynamic Systems and Control, Parts A and B, Orlando, FL, USA, 5–11 November 2005; pp. 1689–1696. [Google Scholar]
- Wannasuphoprasit, W.; Gillespie, R.B.; Colgate, J.E.; Peshkin, M.A. Cobot control. In Proceedings of the IEEE International Conference on Robotics and Automation, Albuquerque, NM, USA, 25 April 1997; Volume 4, pp. 3571–3576. [Google Scholar]
- Kashiri, N.; Medrano-Cerda, G.A.; Tsagarakis, N.G.; Laffranchi, M.; Caldwell, D. Damping control of variable damping compliant actuators. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 850–856. [Google Scholar]
- Lu, L.Y.; Chung, L.L.; Lin, G.L. A general method for semi-active feedback control of variable friction dampers. J. Intell. Mater. Syst. Struct. 2004, 15, 393–412. [Google Scholar] [CrossRef]
- Nakamura, T.; Saga, N. Viscous control of homogeneous ER fluid using a variable structure control. IEEE/ASME Trans. Mechatron. 2005, 10, 154–160. [Google Scholar] [CrossRef]
- Lakatos, D.; Petit, F.; Albu-Schäffer, A. Nonlinear oscillations for cyclic movements in human and robotic arms. IEEE Trans. Robot. 2014, 30, 865–879. [Google Scholar] [CrossRef]
- Chaichaowarat, R.; Kinugawa, J.; Kosuge, K. Cycling-enhanced Knee Exoskeleton Using Planar Spiral Spring. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 3206–3211. [Google Scholar]
- Chaichaowarat, R.; Kinugawa, J.; Seino, A.; Kosuge, K. A Spring—Embedded Planetary—Geared Parallel Elastic Actuator. In Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 6–9 July 2020. [Google Scholar]
- Hidaka, S.; Ahn, Y.K.; Morishita, S. Adaptive vibration control by a variable damping dynamic absorber using er fluid. J. Vib. Acoust. Trans. ASME 1999, 121, 373–378. [Google Scholar] [CrossRef]
- Tzou, H.S.; Wan, G.C. Distributed structural dynamics control of flexible manipulators -I. Structural dynamics and distributed viscoelastic actuator. Comput. Struct. 1990, 35, 669–677. [Google Scholar] [CrossRef]
- Lew, J.Y.; Moon, S.M. A simple active damping control for compliant base manipulators. IEEE/ASME Trans. Mechatron. 2001, 6, 305–310. [Google Scholar] [CrossRef]
- Siciliano, B.; Khatib, O. Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 9783319325521. [Google Scholar]
- Yadmellat, P.; Kermani, M.R. Adaptive modeling of a magnetorheological clutch. IEEE/ASME Trans. Mechatron. 2014, 19, 1716–1723. [Google Scholar] [CrossRef]
- Shafer, A.S.; Kermani, M.R. On the feasibility and suitability of mr fluid clutches in human-friendly manipulators. IEEE/ASME Trans. Mechatron. 2011, 16, 1073–1082. [Google Scholar] [CrossRef]
- Sun, J.Q.; Jolly, M.R.; Norris, M.A. Passive, adaptive and active tuned vibration absorbers—A survey. J. Mech. Des. Trans. ASME 1995, 117, 234–242. [Google Scholar] [CrossRef]
- Laffranchi, M.; Tsagarakis, N.G.; Caldwell, D.G. A variable physical damping actuator (VPDA) for compliant robotic joints. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 1668–1674. [Google Scholar]
- Tsagarakis, N.G.; Laffranchi, M.; Vanderborght, B.; Caldwell, D.G. A compact soft actuator unit for small scale human friendly robots. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 4356–4362. [Google Scholar]
- Pratt, G.A.; Williamson, M.M. Series elastic actuators. In Proceedings of the 1995 IEEE/RSJ International Conference on Intelligent Robots and Systems. Human Robot Interaction and Cooperative Robots, Pittsburgh, PA, USA, 5–9 August 1995; Volume 1, pp. 399–406. [Google Scholar]
- Okada, M.; Ban, S.; Nakamura, Y. Skill of Compliance with Controlled Charging/Discharging of Kinetic Energy. In Proceedings of the International Conference on Robotics & Automation (ICRA)Automation (ICRA), Washington, DC, USA, 11–15 May 2002; pp. 2455–2460. [Google Scholar]
- Niu, Z.; Awad, M.I.; Shah, U.H.; Boushaki, M.N.; Zweiri, Y.; Seneviratne, L.; Hussain, I. Towards Safe Physical Human-Robot Interaction by Exploring the Rapid Stiffness Switching Feature of Discrete Variable Stiffness Actuation. IEEE Robot. Autom. Lett. 2022, 7, 8084–8091. [Google Scholar] [CrossRef]
- Hussain, I.; Albalasie, A.; Awad, M.I.; Tamizi, K.; Niu, Z.; Seneviratne, L.; Gan, D. Design and Control of a Discrete Variable Stiffness Actuator with Instant Stiffness Switch for Safe Human-Robot Interaction. IEEE Access 2021, 9, 118215–118231. [Google Scholar] [CrossRef]
- Chaichaowarat, R.; Nishimura, S.; Krebs, H.I. Design and Modeling of a Variable-Stiffness Spring Mechanism for Impedance Modulation in Physical Human Robot Interaction. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 7052–7057. [Google Scholar]
- Javadi, A.; Chaichaowarat, R. Position and stiffness control of an antagonistic variable stiffness actuator with input delay using super-twisting sliding mode control. Nonlinear Dyn. 2022, 111, 5359–5381. [Google Scholar] [CrossRef]
- Catalano, M.; Grioli, G.; Garabini, M.; Belo, F.W.; Di Basco, A.; Tsagarakis, N.; Bicchi, A. A Variable Damping module for Variable Impedance Actuation. In Proceedings of the ICRA, St. Paul, MN, USA, 14–18 May 2012; pp. 2666–2672. [Google Scholar]
- Catalano, M.G.; Grioli, G.; Garabini, M.; Bonomo, F.; Mancini, M.; Tsagarakis, N.; Bicchi, A. VSA-CubeBot: A modular variable stiffness platform for multiple degrees of freedom robots. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 5090–5095. [Google Scholar]
- Yoon, S.S.; Kang, S.; Kim, S.J.; Kim, Y.H.; Kim, M.; Lee, C.W. Safe Arm with MR-based Passive Compliant Joints and Visco-elastic Covering for Service Robot Applications. In Proceedings of the International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 27–31 October 2003. [Google Scholar]
- Chew, C.M.; Hong, G.S.; Zhou, W. Series damper actuator system based on MR fluid damper. Robotica 2006, 24, 699–710. [Google Scholar] [CrossRef]
- Laffranchi, M.; Chen, L.; Kashiri, N.; Lee, J.; Tsagarakis, N.G.; Caldwell, D.G. Development and control of a series elastic actuator equipped with a semi active friction damper for human friendly robots. Rob. Auton. Syst. 2014, 62, 1827–1836. [Google Scholar] [CrossRef]
- Sukhnandan, R.; Dai, K.; Webster-Wood, V. A Magnetorheological Fluid-based Damper Towards Increased Biomimetism in Soft Robotic Actuators. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 11445–11451. [Google Scholar]
- Wang, Q.; Ahmadian, M.; Chen, Z. A novel double-piston magnetorheological damper for space truss structures vibration suppression. Shock Vib. 2014, 2014. [Google Scholar] [CrossRef]
- Oh, J.S.; Choi, S.B. Ride quality control of a full vehicle suspension system featuring magnetorheological dampers with multiple orifice holes. Front. Mater. 2019, 6, 8. [Google Scholar] [CrossRef]
- Zhu, X.; Jing, X.; Cheng, L. Magnetorheological fluid dampers: A review on structure design and analysis. J. Intell. Mater. Syst. Struct. 2012, 23, 839–873. [Google Scholar] [CrossRef]
- Gołdasz, J.; Sapiński, B. Insight into Magnetorheological Shock Absorbers; Springer International Publishing: Cham, Switzerland, 2015; ISBN 9783319132334. [Google Scholar]
- Radulescu, A.; Howard, M.; Braun, D.J.; Vijayakumar, S. Exploiting variable physical damping in rapid movement tasks. In Proceedings of the 2012 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Kaohsiung, Taiwan, 11–14 July 2012; pp. 141–148. [Google Scholar]
- Chaichaowarat, R.; Nishimura, S.; Krebs, H.I. Macro-Mini Linear Actuator Using Electrorheological-Fluid Brake for Impedance Modulation in Physical Human-Robot Interaction. IEEE Robot. Autom. Lett. 2022, 7, 2945–2952. [Google Scholar] [CrossRef]
- Li, J.; Jin, D.; Zhang, X. An Electrorheological Fluid Damper for Robots. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; pp. 2631–2636. [Google Scholar]
- Sarakoglou, I.; Tsagarakis, N.G.; Caldwell, D.G. Development of a hybrid actuator with controllable mechanical damping. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 1078–1083. [Google Scholar]
- Kemper, K.; Koepl, D.; Hurst, J. Optimal passive dynamics for torque/force control. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 2149–2154. [Google Scholar]
- Fumagalli, M.; Ivaldi, S.; Randazzo, M.; Natale, L.; Metta, G.; Sandini, G.; Nori, F. Force feedback exploiting tactile and proximal force/torque sensing: Theory and implementation on the humanoid robot iCub. Auton. Robot. 2012, 33, 381–398. [Google Scholar] [CrossRef]
- Abe, K.; Suga, T.; Fujimoto, Y. Control of a biped robot driven by elastomer-based series elastic actuator. Int. Work. Adv. Motion Control. AMC 2012. [Google Scholar]
- Zollo, L.; Siciliano, B.; Laschi, C.; Teti, G.; Dario, P. An experimental study on compliance control for a redundant personal robot arm. Rob. Auton. Syst. 2003, 44, 101–129. [Google Scholar] [CrossRef]
- Serio, A.; Grioli, G.; Sardellitti, I.; Tsagarakis, N.G.; Bicchi, A. A decoupled impedance observer for a variable stiffness robot. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 5548–5553. [Google Scholar]
- Flacco, F.; De Luca, A. Residual-based stiffness estimation in robots with flexible transmissions. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 5541–5547. [Google Scholar]
- Frémy, J.; Ferland, F.; Lauria, M.; Michaud, F. Force-guidance of a compliant omnidirectional non-holonomic platform. Rob. Auton. Syst. 2014, 62, 579–590. [Google Scholar] [CrossRef]
- Grioli, G.; Bicchi, A. A non-invasive, real-time method for measuring variable stiffness. Robot. Sci. Syst. 2011, 6, 89–96. [Google Scholar]
- Flacco, F.; De Luca, A.; Sardellitti, I.; Tsagarakis, N.G. On-line estimation of variable stiffness in flexible robot joints. Int. J. Rob. Res. 2012, 31, 1556–1577. [Google Scholar] [CrossRef]
- Hussain, I.; Albalasie, A.; Awad, M.I.; Gan, D. Modeling, identification, and control of a discrete variable stiffness actuator (DVSA). Actuators 2019, 8, 50. [Google Scholar] [CrossRef]
- Fumagalli, M.; Barrett, E.; Stramigioli, S.; Carloni, R. The mVSA-UT: A miniaturized differential mechanism for a continuous rotational variable stiffness actuator. In Proceedings of the 2012 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Rome, Italy, 24–27 June 2012; pp. 1943–1948. [Google Scholar]
- Enoch, A.; Sutas, A.; Nakaoka, S.; Vijayakumar, S. BLUE: A bipedal robot with variable stiffness and damping. In Proceedings of the 2012 12th IEEE-RAS International Conference on Humanoid Robots (Humanoids 2012), Osaka, Japan, 29 November–1 December 2012; pp. 487–494. [Google Scholar]
- Van Ham, R.; Vanderborght, B.; Van Damme, M.; Verrelst, B.; Lefeber, D. MACCEPA, the mechanically adjustable compliance and controllable equilibrium position actuator: Design and implementation in a biped robot. Rob. Auton. Syst. 2007, 55, 761–768. [Google Scholar] [CrossRef]
- Chanthasopeephan, T.; Jarakorn, A.; Polchankajorn, P.; Maneewarn, T. Impact reduction mobile robot and the design of the compliant legs. Rob. Auton. Syst. 2014, 62, 38–45. [Google Scholar] [CrossRef]
- Chaichaowarat, R.; MacHa, V.; Wannasuphoprasit, W. Passive knee exoskeleton using brake torque to assist Stair Ascent. In Proceedings of the 2020 IEEE Region 10 Conference (Tencon), Osaka, Japan, 16–19 November 2020; pp. 1165–1170. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, Z.; Chaichaowarat, R.; Wannasuphoprasit, W. Variable Damping Actuator Using an Electromagnetic Brake for Impedance Modulation in Physical Human–Robot Interaction. Robotics 2023, 12, 80. https://doi.org/10.3390/robotics12030080
Ullah Z, Chaichaowarat R, Wannasuphoprasit W. Variable Damping Actuator Using an Electromagnetic Brake for Impedance Modulation in Physical Human–Robot Interaction. Robotics. 2023; 12(3):80. https://doi.org/10.3390/robotics12030080
Chicago/Turabian StyleUllah, Zahid, Ronnapee Chaichaowarat, and Witaya Wannasuphoprasit. 2023. "Variable Damping Actuator Using an Electromagnetic Brake for Impedance Modulation in Physical Human–Robot Interaction" Robotics 12, no. 3: 80. https://doi.org/10.3390/robotics12030080
APA StyleUllah, Z., Chaichaowarat, R., & Wannasuphoprasit, W. (2023). Variable Damping Actuator Using an Electromagnetic Brake for Impedance Modulation in Physical Human–Robot Interaction. Robotics, 12(3), 80. https://doi.org/10.3390/robotics12030080






