Collision Avoidance for Redundant 7-DOF Robots Using a Critically Damped Dynamic Approach

Abstract

The presence of collaborative robots in industrial environments requires that their control strategies include collision avoidance in the generation of trajectories. In general, collision avoidance is performed via additional displacements of the kinematic chain that make the robot move far from the objects that are occasionally inserted into its safety workspace. The variability of the coordinates of the collision points inside the safety volume leads to abrupt movements for the robot. This paper presents a general method for smoothing abrupt movements in robots with one degree of redundancy for collision-avoidance trajectories, employing a second-order digital filter designed with adjustable critical damping. The method is illustrated by applying it to a redundant robot with a spherical–revolute–spherical type (SRS-type) kinematic chain, which is a benchmark used to test the algorithms ideated for solving this problem. This paper also presents an alternative algorithm for the inverse kinematics of the SRS-type robot and the computational experiments that show the collision avoidance proposal’s performance and its properties through graphical results.

1. Introduction

Complex tasks require interactions between robots and humans collaboratively. This collaboration comes from sharing tools, operations, and workspaces [1,2,3] and requires specific control techniques to overcome possible collisions between robots and humans or devices located inside the workspace [4]. Such collaboration implies a more significant number of restrictions on the volume available to the end-effector and the respective safety volume (i.e., the geometric spatial volume around the links and the end-effector, where the robot is considered free of collisions) available for the displacements of the robot’s kinematic chain [5]. In this sense, a new class of robots is arising, defined as collaborative robots [6,7], which are provided with strategies at the hardware and software levels to avoid collisions and improve the interactions between robots and humans. Collision-avoidance strategies require additional movements of the kinematic chains, which means that the robots need to have greater mobility than what is needed to perform their tasks; that is, they need to be redundant [6,8,9,10,11]

Elements inserted into a robot’s safety workspace [12] usually make the robot change its coordinates randomly, causing abrupt variation in the distances to the points belonging to the robot’s kinematic chain. If the values of these distances are used as references in collision-avoidance algorithms, the movements of the robot’s kinematic chain are abrupt and naturally undesirable. Indeed, abrupt changes in joint variables, besides being physically difficult to obtain, generate vibrations in a wide range of frequencies that cannot be tolerated during machine motion. This is why smoothing the additional motion that avoids a possible collision is an important requirement for any collision-avoidance strategy.

Collision-avoidance strategies consist of programming a set of internal movements of a robot’s kinematic chains based on sensor data to circumvent or deviate certain parts of the robot from an obstacle that has been inserted into its overall workspace, which can occur in online, offline, or autonomous tasks [3,4,12]. The internal movements are performed via changes in joint displacements, which often lead to abrupt variations in joint trajectories [13,14] and need to be treated to ensure smooth movement.

Improving the motion quality requires collision-avoidance strategies that generate smooth transients in terms of joint displacements and rates. Such strategies are, in general, based on optimization algorithms via energy minimization [15,16] or on differential geometric approaches [8,17,18], which, among other propositions, are based on the Moore–Penrose pseudoinverse approach [19,20] and are limited mainly by the problem of homogeneity and the lack of repeatability of the solutions [21,22]. A systematic proposition based on concepts of linear equations independent of numerical optimization methods [23] allows for better control over the performance and execution of the collision-avoidance strategy.

Some interesting trajectory generation proposals involve using digital filters in the definition of reference signal limits [24,25] or combined with curve formulations [26,27]. The complexity and limited adjustment possibilities make it difficult to replicate or use such strategies, limiting their application. The aim of this work is to overcome these applicative limitations.

This paper presents a new approach to collision avoidance based on the use of second-order digital filters [28], which solves the inverse kinematics through the resolved motion control technique (RMC) [14,29]. The proposal calculates the minimum distance straight line between the nearest collision point of a mobile obstacle and the robot’s links using a geometric formulation. The length of this straight-line segment changes as the collision point coordinates change inside the robot’s overall workspace. The collision-avoidance algorithm proposition calculates the internal movements (null space of the kinematic chain [30,31]), smoothing abrupt movements that eventually arise. The proposal uses a low-pass filter to minimize the possible peaks of the internal displacements, improving the transients of the trajectory in the kinematic chain while the robot executes a task. The proposal also considers an envelope defined by a geometric surface around the links as a safety region and obtains a smooth transition through a digital filter, which allows adjustments according to the desired performance and response-time criteria [21,22,28].

Several spherical–revolute–spherical-type (SRS-type) redundant robots have arisen as workbenches for the simulation and experimentation of such proposals [5,15,26,32,33,34], including the arms or legs of bipedal robots [33,35,36,37]; among these, the Kuka-LBR-iiwa models are the most adopted SRS-type redundant robots [8,9,11,38,39]. The experimentation on the proposed collision-avoidance strategy uses the Kuka-LBR-iiwa’s kinematic model with seven degrees-of-freedom (DOFs), which is commonly used to test collision-avoidance strategies in collaborative cells [4,7,8,27]. Such a choice will allow comparisons and a more accurate assessment of the proposition’s advantages.

Here, the proposed strategy is proven and discussed using a simulation experiment, where the collision-avoidance control acts to avoid the collisions between the links of the SRS-type redundant robot and two kinematic models of human arms that share the robot’s safety volume [12] while performing tasks in an industrial simulation environment.

This paper is organized as follows. Section 2 presents the proposed collision-avoidance strategy. Section 3 presents the SRS-type redundant robot benchmark and a proposal for solving its inverse kinematics. Section 4 presents the new approach for defining the safe region around the links and calculating the distance between a point and the robot. Section 5 presents the graphical results, and Section 6 discusses the results. Finally, Section 7 draws the conclusions.

2. Critically Damped Collision Avoidance

Let P_c be a point with an imminent possibility of collision with a redundant robot. Such a point may belong to a human operator or to another apparatus occasionally inserted into the robot’s safety volume [12,40,41]. The collision-avoidance strategy must avoid the collision by acting in the null space of a redundant robot so that the robot’s configuration changes using movements, chosen according to the degree of redundancy [11,30], that do not affect the task performed by the robot. In short, without redundancy, avoiding a possible collision can be achieved only by changing the motion task of the robot.

The collision-avoidance method proposed in this paper holds for robots with only one degree of redundancy. So, we can only exploit a movement with one DOF to avoid a collision. In the literature, for the case of the SRS-type redundant robot of Figure 1, which is a benchmark for this problem, angle α is usually chosen for controlling the distance between the elbow point P_e and the collision point P_c using criteria such as geometric approaches [1,38], differential maps [17,29], and energy [5,25,26,32]. The problem reduces itself to ideate an inverse-kinematics algorithm that makes angle α perform the internal movements (null-space) of the kinematic chain without changing the position and orientation of the end-effector.

From a geometric point of view, the problem consists of verifying the minimum distance, d_min, between the robot and the nearest point, P_c, of a mobile obstacle and then adjusting the value of angle α to guarantee a minimum desired distance, dr_min. Considering that point P_c may change its coordinates randomly or abruptly in the space at each measurement of its coordinates (e.g., obtained through sensors or video cameras [42]), the respective change of angle α may produce abrupt oscillations of the joint positions, calculated with inverse-kinematics algorithms, which is an undesirable and often, unpractical result.

To avoid abrupt oscillations in the values of the joint positions, it is interesting to smooth angle-α transients before using them as input data for the inverse-kinematics algorithms. Smoothing improves continuity in signal transitions and variations based on polynomial numerical interpolations [43]. Such an approach has limitations when the order of signals’ derivatives is greater than polynomials’ order; indeed, in this case, continuity is no longer guaranteed.

This work proposes that angle α be numerically filtered by using a time-continuous second-order transfer function, G(s), defined as follows, which is critically damped and has a static gain equal to 1 [28]:

$$\frac{{\alpha }_{\mathrm{f}}(s)}{{\alpha }_{\mathrm{c}}(s)}=G(s)=\frac{p^2}{{(s+p)}^2}$$

(1)

In Equation (1), α_c(s) corresponds to a time-continuous signal input for the α values on the complex s-domain calculated to avoid the collision; α_f(s) is the respective continuous output, signal-filtered; and p is an adjustable pole, which allows setting the speed of the transients [28]. The critically damped dynamics consist of second-order systems that have a time response with faster transients without overshoot, where the damping coefficient ξ = 1 [28].

Using the filtered signal, α_f, in a trajectory-generator algorithm needs the discretization of the transfer function, G(s), defined by Equation (1). The discretization of G(s) is given by its z-transform associated with a zero-order hold (ZOH) [28] as follows:

$$\frac{{\alpha }_{\mathrm{f}}(s)}{{\alpha }_{\mathrm{c}}(s)}=G(z)=\left(1-z^{-1}\right)Z\left\{\frac{G(s)}{s}\right\}=\frac{(1-e^{-m}(1+m))z^{-1}+e^{-m}(m-1+e^{-m})z^{-2}}{1-2e^{-m}{z}^{-1}+e^{-2m}{z}^{-2}}=\frac{h_1{z}^{-1}+h_2{z}^{-2}}{1-b_1{z}^{-1}-b_2{z}^{-2}}$$

(2)

where T is the desired sample time (in general defined as a function of the computer clock, or interfaces sample times); m is the product Tp; h₁ = (1 − e^−m(1 + m)); h₂ = e^−m (m – 1 + e^−m); b₁ = 2e^−m; and b₂ = −e^−2m.

Using the right-shift or delay theorem [28], the variable z behaves like a delay operator for the input and output variables of the discrete transfer function presented in Equation (2). In this way, it is possible to obtain a command line for the algorithm that filters the α angle as follows:

$${\alpha }_{\mathrm{f}}(n)=h_1{\alpha }_{\mathrm{c}}(n-1)+h_2{\alpha }_{\mathrm{c}}(n-2)+b_1{\alpha }_{\mathrm{f}}(n-1)+b_2{\alpha }_{\mathrm{f}}(n-2)$$

(3)

where “n” is the discrete parameter, that is, n = 0, 1, …, whereas ${\alpha }_{\mathrm{c}}$ and ${\alpha }_{\mathrm{f}}$ are the computed-input and the filtered-output angle α calculated at the instant “n”, respectively. It is worth noting that since the signal starts at n = 0, it is necessary to define the initial conditions of ${\alpha }_{\mathrm{f}}$ and ${\alpha }_{\mathrm{c}}$ for $n=-2,-1$.

3. SRS-Type Redundant Robot Benchmark

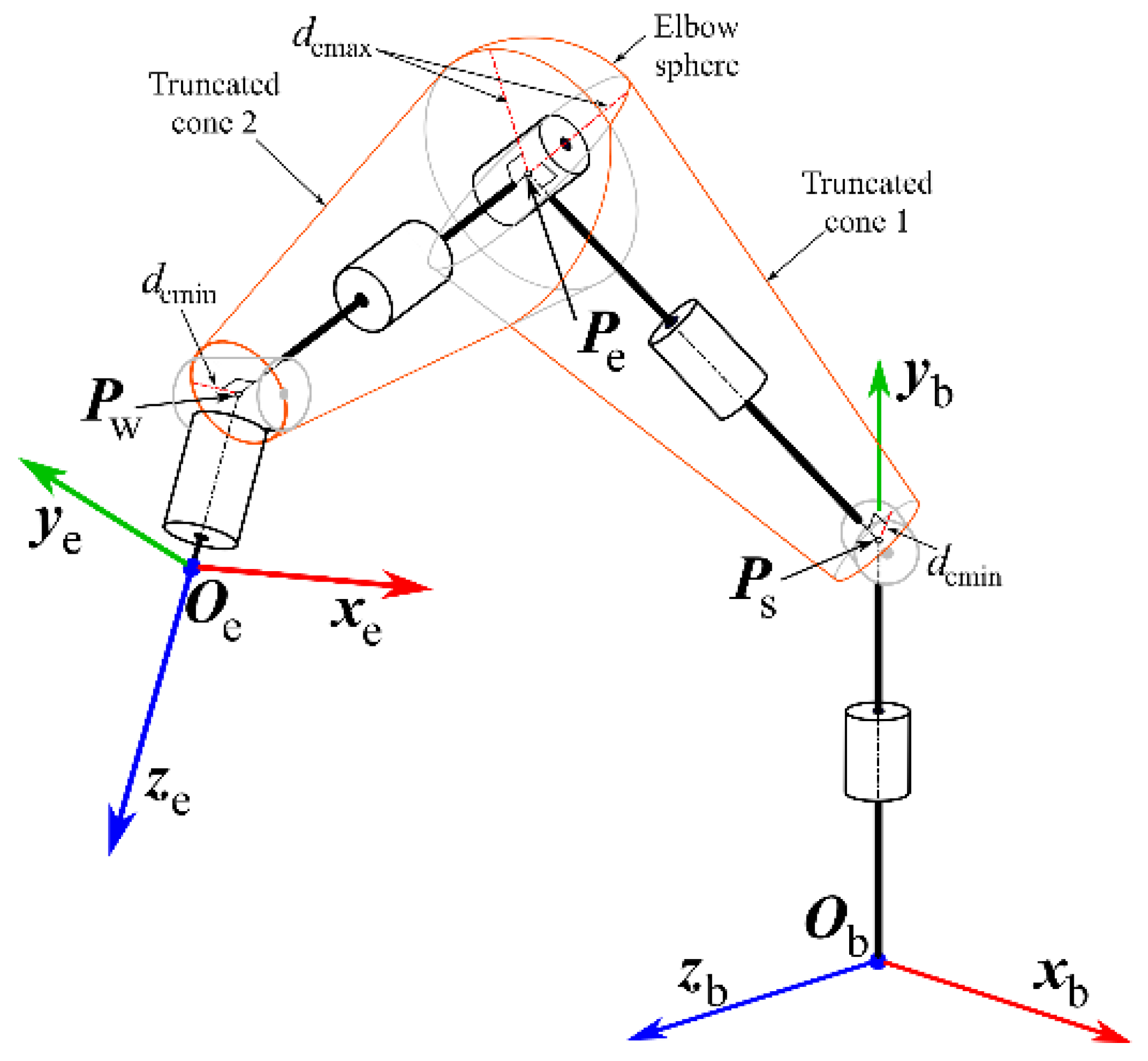
3.1. Geometric Description

The SRS-type robot is a redundant robot with seven revolute joints (7-DOF) with the possibility of elbow movement, adapted mainly for collaborative tasks between robots or robots and humans [9,44,45]. The scope of applications has encouraged several authors to develop research and proposals for the kinematic modeling of this robot [8,9,26,35,37,46]. A typical SRS-type redundant robot is the Kuka-LBR-iiwa [4,44], whose kinematic model is shown in Figure 1.

With reference to Figure 1, the links are numbered from 0 (the frame) to 7 (the end effector), and the revolute(R)-joint variables are $q={[\begin{array}{ccccccc}{\theta }_1& {\theta }_2& {\theta }_3& {\theta }_4& {\theta }_5& {\theta }_6& {\theta }_7\end{array}]}^T$ (see Figure 1a), whereas the constant lengths are $a={[\begin{array}{cccc}{a}_0& a_1& a_3& a_4\end{array}]}^T$ (see Figure 1b). Link 0 is the frame (base), and the Cartesian reference O_b-x_by_bz_b is fixed to the base, whereas link 7 is the end-effector and the Cartesian reference O_e-x_ey_ez_e is fixed to the end effector. Here, without losing generality, for the sake of simplicity, the assumption that the tool is displaced a₃ from the center of the spherical wrist is introduced. The seven R-joints are numbered from 1 to 7 following the order they are encountered by moving from the base to the end effector along the 7R kinematic chain of the robot.

The 7-DOF Kuka-LBR-iiwa robot is a serial chain of SRS-type. Indeed, the axes of the first three R-joints, with joint variables (θ₁, θ₂, θ₃), intersect at P_s, which is the center of the first S-pair, and the axes of the last three R-joints, with joint variables (θ₅, θ₆, θ₇), intersect themselves at P_w, which is the center of the second S-pair (i.e., the wrist of the robot). The axis of the first R-joint coincides with the y_b-axis, whereas the axis of the second R-joint is perpendicular to the y_b-axis and passes through P_s. The axis of the third R-joint is perpendicular to both the axes of the second and the fourth R-joints and intersects the axis of the fourth R-joint at P_e. Points O_b, P_s, and P_w lie on a plane, hereafter named plane-π₁, which contains the y_b-axis. Points P_s, P_e, and P_w lie on another plane, hereafter named plane-π₂, whose normal is parallel to the axis of the fourth R-joint. The axis of the fifth R-joint passes through P_e, is perpendicular to both the axes of the fourth and the sixth R-joints, and intersects the axis of the sixth R-joint at P_w: ${\theta }_5$ is the angle between the axes of the fourth and the sixth R-joints. Eventually, the axis of the seventh R-joint passes through P_w and is perpendicular to the axis of the sixth R-joint: θ₆ is the angle between the axes of the fifth and the seventh R-joints.

The constant lengths, shown in Figure 1b, are defined as follows: a₀ is the distance between points O_b and P_s; a₁ is the distance between points P_s and P_e; a₂ is the distance between points P_e and P_w; and a₃ is the distance between points P_w and O_e. In addition, three characteristic internal points are defined (see Figure 1b): P_s–shoulder point—in the center of the first S-pair; P_e–elbow point—in the crossing point of the joint axes 3, 4, and 5; and, lastly, P_w in the center of the second S-pair (the robot wrist). When ${\theta }_3=0$ rad, the points O_b, P_s, P_e, and P_w belong to the same plane (i.e., plane-π₁ and plane-π₂ coincide with one another), making the kinematic chain like a classical 6-DOF anthropomorphic robot. Differently, when ${\theta }_3\ne 0$ rad, point P_e goes out of plane-π₁, and the line passing through points P_s and P_w becomes the common intersection between plane-π₁ and plane-π₂, which P_e lies on. The angle α between these two planes (see Figure 1b) can be chosen as the seventh generalized coordinate that, together with the coordinates ^bp₇ = [x₇ y₇ z₇]^T of point P_w in O_b-x_by_bz_b and the end-effector’s orientation parameters ^bφ_e = [φ_e ϑ_e ψ_e ]^T with respect to O_b-x_by_bz_b, uniquely identifies the configuration of the 7-DOF robot in the operational space.

From a geometric point of view, angle α is a rotation angle around the line segment P_sP_w. In short, we have x = [^bp₇^T bφ_e^T α] ^T as operational-space coordinates and $q={[\begin{array}{ccccccc}{\theta }_1& {\theta }_2& {\theta }_3& {\theta }_4& {\theta }_5& {\theta }_6& {\theta }_7\end{array}]}^T$ as joint-space coordinates.

Mathematically the direct kinematics model: q→x, uses a common methodology such as Denavit–Hartenberg [10,11,30] or successive screws [14,31], among others. Such methodologies are well known and allow the systematic deduction of the kinematics equation. For the inverse kinematics: x→q, the angle α and the end-effector’s pose parameters, ^bp₇^T and ^bφ_e^T, are known and, in this case [9], the inverse kinematics has a finite number of solutions [14,30,31]. The next section presents a particular solution for the inverse kinematics, refining other propositions [8,11,46] for α Î [0, 2π].

3.2. An Analytical Approach to Solve the Inverse Kinematics of SRS-Type Redundant Robots

Let ^bT_e be a homogeneous transformation matrix built from the end-effector’s pose parameters, ^bp_e^T and ^bφ_e^T, which locates a Cartesian reference P_w-x₇y₇z₇ fixed to link 7 with respect to O_b-x_by_bz_b. Additionally, consider, without losing generality, that the tool action point of the end-effector is in the O_e-x_ey_ez_e frame, as shown in Figure 1a, and has its pose with respect to the Cartesian reference P_w-x₇y₇z₇ identified by a known and constant homogeneous matrix ⁷T_e. Thus, we have the two known homogeneous matrices (^jR_i and ^jp_i stand for the rotation matrix and the position vector, respectively, associated with the homogeneous transformation matrix ^jT_i):

$${}^b{T}_{\mathrm{e}}=\left[\begin{array}{cccc}& {}^b{R}_{\mathrm{e}}& & {}^b{p}_{\mathrm{e}}\\ 0& 0& 0& 1\end{array}\right] \mathrm{and} {}^7{T}_{\mathrm{e}}=\left[\begin{array}{cccc}& {}^7{R}_{\mathrm{e}}& & {}^7{p}_{\mathrm{e}}\\ 0& 0& 0& 1\end{array}\right]$$

(4)

The first step consists of setting θ₃ = 0 rad to make the SRS-type robot’s kinematic chain like a classical 6-DOF anthropomorphic robot. Considering the resultant 6-DOF sub-structure, the solution of the inverse kinematics calculates an intermediary joint position vector $\overline{q}={[\begin{array}{cccccc}{\theta }_1& {\theta }_2& {\theta }_4& {\theta }_5& {\theta }_6& {\theta }_7\end{array}]}^T$, with θ₃ = 0 rad through an analytical procedure [30,31,39].

With the values obtained for $\overline{q}$, it is possible to calculate the coordinates of P_s, P_eo, and P_w, where P_eo is the coordinates of P_e when α = 0 rad (or θ₃ = 0 rad). The next step consists of rotating P_eo around the axis P_sP_w by the known angle α for calculating the actual coordinates of P_e, as shown in Figure 1b.

Using Rodrigues’s rotation formula [14,31] to perform this rotation yields the following relationship:

$${\mathit{P}}_{\mathrm{e}}={\mathit{P}}_{\mathrm{s}}+{\mathit{R}}_{\mathrm{u}}\left({\mathit{P}}_{\mathrm{eo}}-{\mathit{P}}_{\mathrm{s}}\right)$$

(5)

with

$${\mathit{R}}_{\mathrm{u}}=\left[\begin{array}{ccc}{u}_x^2(1-c\alpha )+c\alpha & u_x{u}_y(1-c\alpha )-u_{z}s\alpha & u_x{u}_z(1-c\alpha )+u_{y}s\alpha \\ u_x{u}_y(1-c\alpha )+u_{z}s\alpha & u_y^2(1-c\alpha )+c\alpha & u_y{u}_z(1-c\alpha )-u_{x}s\alpha \\ u_x{u}_z(1-c\alpha )-u_{y}s\alpha & u_y{u}_z(1-c\alpha )+u_{x}s\alpha & u_z^2(1-c\alpha )+c\alpha \end{array}\right]$$

where $u={\left[\begin{array}{ccc}{u}_x& u_y& u_z\end{array}\right]}^T=\left({\mathit{P}}_{\mathrm{w}}-{\mathit{P}}_{\mathrm{s}}\right)/‖{\mathit{P}}_{\mathrm{w}}-{\mathit{P}}_{\mathrm{s}}‖$ is the unit vector that identifies the rotation axis with reference to which angle α is defined, whereas cα and sα stand for cosα and sinα, respectively.

The above-described two steps calculated the coordinates of the characteristic internal points P_s, P_e and P_w. Now, these computed data can be used in the third step for adjusting the joint-space vector according to the actual value of angle α of the final configuration of the robot. Note that after the rotation of angle α, only the angle θ₄ remains the same, and all the other joint variables require a correction that must be computed.

Joints θ₁, θ₂, and θ₃ compose the first spherical wrist with orientation defined by the consecutive elemental rotations of the YZX Tait–Bryan angles where the directions of the y, z, and x- axes coincide with the R-pair axes of the wrist (see Figure 1). This definition yields the following rotation matrix of link 3 with respect to the base:

$${}^b\mathit{R}{}_3=\left[\begin{array}{ccc}{c}_1{c}_2& -c_1{s}_2{c}_3+s_1{s}_3& c_1{s}_2{s}_3+s_1{c}_3\\ s_2& c_2{c}_3& -c_2{s}_3\\ -s_1{c}_2& s_1{s}_2{c}_3+c_1{s}_3& -s_1{s}_2{s}_3+c_1{c}_3\end{array}\right]$$

(6)

where c_i and s_i denote cosθ_i and sinθ_i, for i = 1, 2, 3, respectively.

Additionally, the same ^bR₃ rotation matrix can be obtained numerically using the coordinates of the characteristic internal points as follows:

$${}^b\mathit{R}{}_3=\left[\begin{array}{ccc}{}^b\mathit{x}{}_3& {}^b\mathit{y}{}_3& {}^b\mathit{z}{}_3\end{array}\right]=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]$$

(7)

where, considering that (see Figure 1b) ${\mathit{P}}_{\mathrm{eu}}={\mathit{P}}_{\mathrm{s}}+\left(\left({\mathit{P}}_{\mathrm{e}}-{\mathit{P}}_{\mathrm{s}}\right)\cdot u\right)u$ is the projection [31,43,47] of P_e onto the line defined by the segment P_sP_w and $v={\mathit{P}}_{\mathrm{e}}-{\mathit{P}}_{\mathrm{eu}}$:

$${}^{b}x{}_3=\left[\begin{array}{c}{r}_{11}\\ r_{21}\\ r_{31}\end{array}\right]=\frac{\left({\mathit{P}}_{\mathrm{e}}-{\mathit{P}}_{\mathrm{s}}\right)}{‖{\mathit{P}}_{\mathrm{e}}-{\mathit{P}}_{\mathrm{s}}‖}{}^{b}z{}_3=\left[\begin{array}{c}{r}_{13}\\ r_{23}\\ r_{33}\end{array}\right]=\frac{\left(u\times v\right)}{‖u\times v‖}{}^{b}y{}_3=\left[\begin{array}{c}{r}_{12}\\ r_{22}\\ r_{32}\end{array}\right]={}^{b}z{}_3\times {}^{b}x{}_3$$

(8)

The comparison of Equations (6) and (7) allows the deduction of the following explicit expressions for θ₁, θ₂, and θ₃:

$$\begin{array}{l}{\theta }_1=Atan2\left(-\mathrm{sign}\left({\theta }_2\right)r_{31},\mathrm{sign}\left({\theta }_2\right)r_{11}\right)\\ {\theta }_2=Atan2\left(r_{21},\mathrm{sign}\left({\theta }_2\right)\sqrt{r_{31}^2+r_{11}^2}\right)\\ {\theta }_3=Atan2\left(-\mathrm{sign}\left({\theta }_2\right)r_{23},\mathrm{sign}\left({\theta }_2\right)r_{22}\right)\end{array}$$

(9)

where sign(θ₂) is the chosen sign for θ₂ determining if ${\theta }_2\in \left(\frac{-\pi }{2},\frac{\pi }{2}\right)$ rad for sign(θ₂) > 0 or if ${\theta }_2\in \left(\frac{\pi }{2},\frac{3\pi }{2}\right)$ rad for sign(θ₂) < 0.

Note that for ${\theta }_2=k\pi \pm \frac{\pi }{2}$ rad, for k = 0, 1, …, it configures a singular posture in the first S-pair since, in this case, the axes of the R-joints 1 and 3 are aligned. Such a singularity is additional to the others, which are the alignment of links 3 and 4, when θ₄ = 0, and the axis alignment of joints 5 and 7 in the second S-pair (the robot wrist), both common to anthropomorphic robots with six DOFs.

Knowing the angles θ₁, θ₂, θ₃, and θ₄, the rotation matrix ^bR₄ describes the rotation of the frame of link 4 with respect to the base frame as follows:

$${}^b\mathit{R}{}_4={}^b\mathit{R}{}_3{}^3\mathit{R}{}_4$$

(10)

where ${}^3\mathit{R}{}_4$ is the rotation matrix that relates the orientation of link 4 with respect to link 3 described by an elementary rotation around the z-axis by the angle θ₄.

The known rotation matrices ${}^b\mathit{R}{}_{\mathrm{e}}$ and ${}^7\mathit{R}{}_{\mathrm{e}}$ that appear in Equation (4) and the rotation matrix ${}^b\mathit{R}{}_4$ computed through Equation (10) are related by the following relationship, which enables the computation of the remaining joint variables θ₅, θ₆, and θ₇:

$${}^b\mathit{R}{}_{\mathrm{e}}={}^b\mathit{R}{}_4{}^4\mathit{R}{}_7{}^7\mathit{R}{}_{\mathrm{e}}$$

(11)

Indeed, isolating ${}^4\mathit{R}{}_7$ in Equation (11) yields the following result:

$${}^4\mathit{R}{}_7={}^b\mathit{R}{}_4^T{}^b\mathit{R}{}_{\mathrm{e}}^{}{}^7\mathit{R}{}_{\mathrm{e}}^T=\left[\begin{array}{ccc}{n}_{11}& n_{12}& n_{13}\\ n_{21}& n_{22}& n_{23}\\ n_{31}& n_{32}& n_{33}\end{array}\right]$$

(12)

The second S-pair orientates link 7 with respect to link 4 through the angles θ₅, θ₆, and θ₇ defined as the consecutive elemental rotations of the XZX proper Euler angles, where the directions of the x, z, and x-axes coincide with the R-pair axes of the S-pair (see Figure 1). Therefore, the following expression of rotation matrix ${}^4\mathit{R}{}_7$ holds:

$${}^4\mathit{R}{}_7=\left[\begin{array}{ccc}{c}_6& -s_6{c}_7& s_6{s}_7\\ c_5{s}_6& c_5{c}_6{c}_7-s_5{s}_7& -c_5{c}_6{s}_7-s_5{c}_7\\ s_5{s}_6& s_5{c}_6{c}_7+c_5{s}_7& -s_5{c}_6{s}_7+c_5{c}_7\end{array}\right]$$

(13)

Comparing the rotation matrices presented in Equations (12) and (13) reaches the expressions for θ₅, θ₆, and θ₇ as follows:

$$\begin{array}{l}{\theta }_5=\mathrm{Atan}2\left(\mathrm{sign}\left({\theta }_6\right)n_{31},\mathrm{sign}\left({\theta }_6\right)n_{21}\right)\\ {\theta }_6=\mathrm{Atan}2\left(\mathrm{sign}\left({\theta }_6\right)\sqrt{n_{12}^2+n_{13}^2},n_{11}\right)\\ {\theta }_7=\mathrm{Atan}2\left(\mathrm{sign}\left({\theta }_6\right)n_{13},-\mathrm{sign}\left({\theta }_6\right)n_{12}\right)\end{array}$$

(14)

where sign(θ₆) is the chosen sign for θ₆ determining if ${\theta }_6\in \left(0,\pi \right)$ rad for sign(θ₆) >0 or if ${\theta }_6\in \left(-\pi ,0\right)$ rad for sign(θ₆) < 0.

The joint variables computed with Equations (9) and (14), together with the value of θ₄ obtained in the inverse kinematics of the intermediate 6-DOF sub-model, yield the sought-after joint-space vector q that solves the inverse kinematics.

4. Proposition of an Algorithm for Calculating the Distance between a Point and the Robot

4.1. Typical Strategy for Collision Avoidance

When an obstacle enters the robot’s safety volume, the collision-avoidance strategy must impose additional movements for the robot that prevent the possibility of a collision [14,30].

The typical collision-avoidance approach firstly measures the distance, d, between the nearest point of the obstacle (i.e., point P_c) and a relevant point of the robot, in general, the “elbow”, which, in Figure 1, is point P_e. Then, by moving point P_e, it tries to keep, in the worst case, point P_c on the spherical surface with the center at point P_e and radius equal to the minimum desired distance, dr_min; that is, it imposes d ≥ dr_min.

In an SRS-type robot, if the value of dr_min is less than the lengths of the segments P_sP_e and/or P_eP_w, point P_c can collide with one of the links belonging to the kinematic chain, thus making the strategy unfeasible.

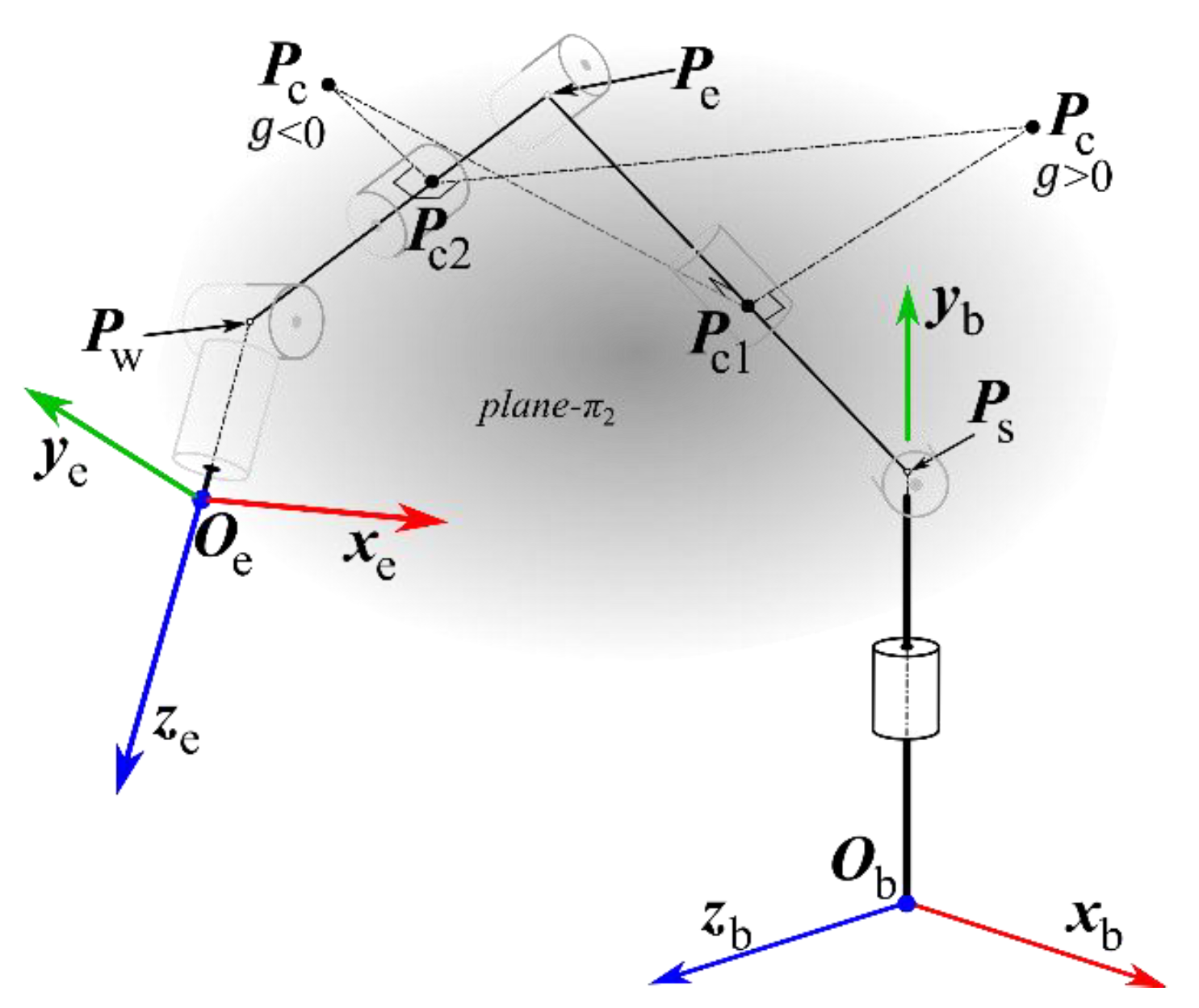
4.2. Proposition of a New Approach for Obstacle Measurement

Let the kinematic structure of a robot be defined through a set of relevant points, such as intersections of R-pair axes and centers of spherical wrists. Hereafter, the segments between any two relevant points will be called referential links. It is worth noting that the referential links are not constrained to keep their lengths constant during the robot’s motion.

This paper proposes the use of axis-symmetric solids, such as right circular cylinders and truncated right-cones (i.e., a right-cone whose top is cut by a plane parallel to the base), whose axes of symmetry are the referential links, to define the boundaries of safety regions around the links of the robot. In addition, for the relevant points, if necessary, the use of a sphere determines the boundaries of a safety region, as used in conventional approaches [4,9]. The objective of collision avoidance is to keep the points belonging to the obstacles out, or on the boundaries of the safety regions defined by all the above-defined solids. For the SRS-type model, therefore, we have P_s, P_e, and P_w as relevant points, and the segments P_sP_e and P_eP_w [11] as the respective referential links.

Considering the referential linksP_sP_e and P_eP_w, we propose the use of truncated right cones to define the boundary of a safety volume around the robot links. For the line segment P_sP_e, the truncated right cone has its smaller base circle with radius d_cmin centered at point P_s and the larger base circle with radius d_cmax centered at point P_e. Similarly, for the line segment P_eP_w, the truncated right cone has its larger base circle with radius d_cmax centered at point P_e and the smaller base circle with radius d_cmin centered at point P_w. Eventually, as the elbow is a relevant point that is exposed, a sphere, centered at point P_e with radius d_cmax, defines the boundary of its safety volume. Figure 2 shows the SRS-type robot together with its safety volume defined as explained above.

It is worth stressing that points P_s and P_w, when under the imminence of a collision, cannot be moved, since P_s is fixed with respect to the base coordinate system and a displacement of point P_w implies changes in the position or direction of the end-effector. In these cases, it is interesting to use d_cmin = 0, for real applications featuring a right cone, as a safety volume.

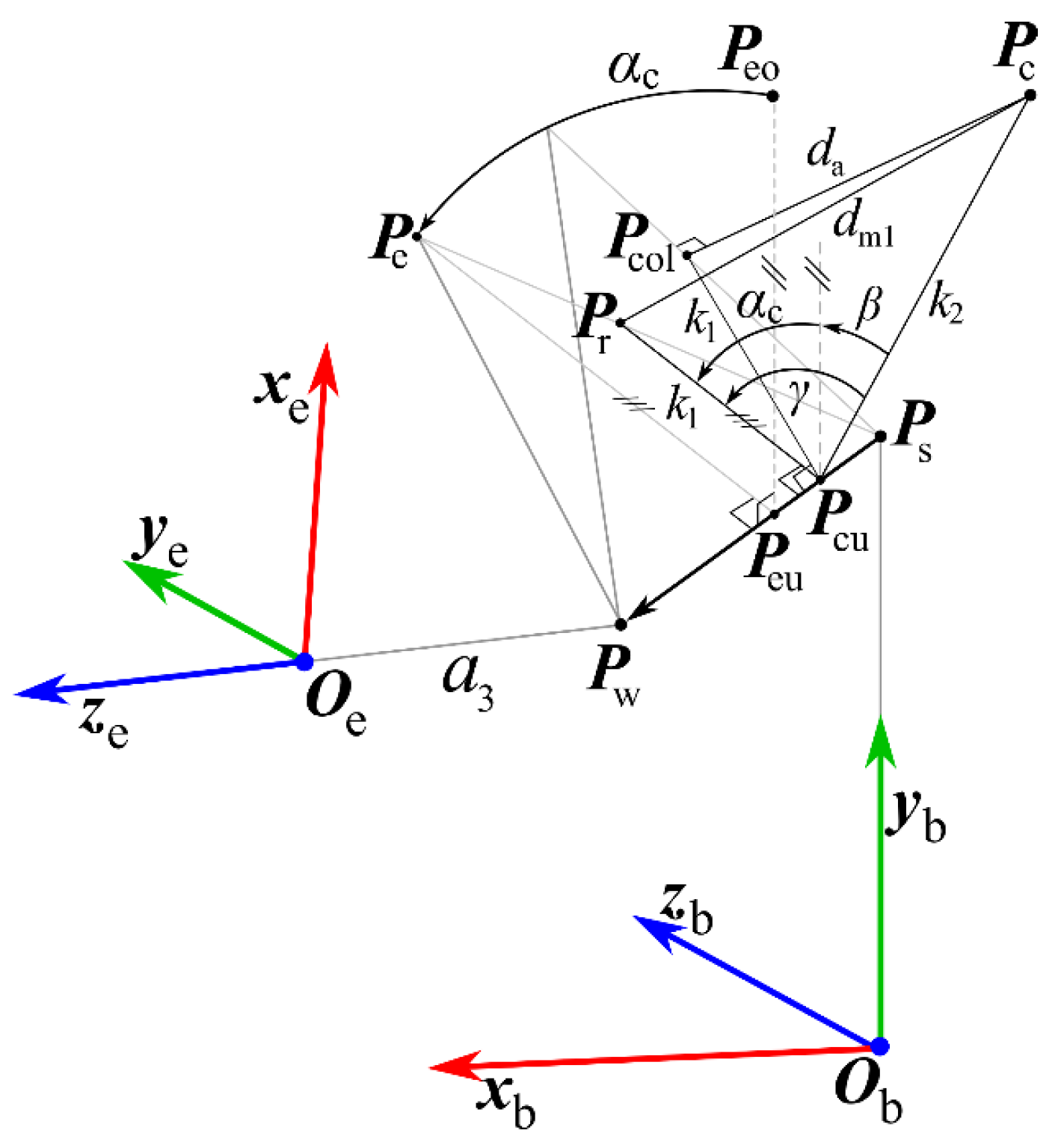
4.3. Computing the Minimum Distance and Respective Collision-Avoidance Angle α

Concerning Figure 3, let us consider a point, P_c, belonging to an obstacle located inside the space region where the robot moves and placed on one side of plane-π₂, which is identified by the sign $g$. Additionally, let us consider the P_c projection points P_c1 and P_c2 onto the lines defined by the referential links P_sP_e and P_eP_w, respectively [47]. The following relationships hold:

$$\begin{array}{l}{\mathit{P}}_{\mathrm{c}1}={\mathit{P}}_{\mathrm{s}}+\left({\mathit{P}}_{\mathrm{c}}-{\mathit{P}}_{\mathrm{s}}\right)\cdot \left({\mathit{P}}_{\mathrm{e}}-{\mathit{P}}_{\mathrm{s}}\right)\left(\frac{\left({\mathit{P}}_{\mathrm{e}}-{\mathit{P}}_{\mathrm{s}}\right)}{{‖{\mathit{P}}_{\mathrm{e}}-{\mathit{P}}_{\mathrm{s}}‖}^2}\right)\\ {\mathit{P}}_{\mathrm{c}2}={\mathit{P}}_{\mathrm{e}}+\left({\mathit{P}}_{\mathrm{c}}-{\mathit{P}}_{\mathrm{e}}\right)\cdot \left({\mathit{P}}_{\mathrm{w}}-{\mathit{P}}_{\mathrm{e}}\right)\left(\frac{\left({\mathit{P}}_{\mathrm{w}}-{\mathit{P}}_{\mathrm{e}}\right)}{{‖{\mathit{P}}_{\mathrm{w}}-{\mathit{P}}_{\mathrm{e}}‖}^2}\right)\end{array}$$

(15)

In the proposed algorithm, evaluating whether point P_c1 (P_c2) is inside the segment P_sP_e (segment P_eP_w) is the first step. Both, just one, or even none of the two points may belong to their respective segments. Such an evaluation will be true if it is true that for the two parameters u₁ and u₂, defined as follows:

$$u_1=\frac{\left({\mathit{P}}_{\mathrm{c}1}-{\mathit{P}}_{\mathrm{s}}\right)\cdot \left({\mathit{P}}_{\mathrm{e}}-{\mathit{P}}_{\mathrm{s}}\right)‖{\mathit{P}}_{\mathrm{c}1}-{\mathit{P}}_{\mathrm{s}}‖}{\left|\left({\mathit{P}}_{\mathrm{c}1}-{\mathit{P}}_{\mathrm{s}}\right)\cdot \left({\mathit{P}}_{\mathrm{e}}-{\mathit{P}}_{\mathrm{s}}\right)\right|‖{\mathit{P}}_{\mathrm{e}}-{\mathit{P}}_{\mathrm{s}}‖} u_2=\frac{\left({\mathit{P}}_{\mathrm{c}2}-{\mathit{P}}_{\mathrm{e}}\right)\cdot \left({\mathit{P}}_{\mathrm{w}}-{\mathit{P}}_{\mathrm{e}}\right)‖{\mathit{P}}_{\mathrm{c}2}-{\mathit{P}}_{\mathrm{e}}‖}{\left|\left({\mathit{P}}_{\mathrm{c}2}-{\mathit{P}}_{\mathrm{e}}\right)\cdot \left({\mathit{P}}_{\mathrm{w}}-{\mathit{P}}_{\mathrm{e}}\right)\right|‖{\mathit{P}}_{\mathrm{w}}-{\mathit{P}}_{\mathrm{e}}‖},$$

(16)

where the conditions $u_1\in \left[0,1\right]$ and $u_2\in \left[0,1\right]$ hold.

If P_c1 (P_c2) belongs to P_sP_e (to P_eP_w), the next step consists of the computation of the three distances: $d_{\mathrm{a}}=‖{\mathit{P}}_{\mathrm{c}}-{\mathit{P}}_{\mathrm{c}1}‖$ if $u_1\in \left[0,1\right]$, $d_{\mathrm{b}}=‖{\mathit{P}}_{\mathrm{c}}-{\mathit{P}}_{\mathrm{e}}‖$ and $d_{\mathrm{c}}=‖{\mathit{P}}_{\mathrm{c}}-{\mathit{P}}_{\mathrm{c}2}‖$ if $u_2\in \left[0,1\right]$, which are the distances of P_c, respectively, from the referential link P_sP_e, the relevant point P_e, and the referential link P_eP_w. Considering the minimum and maximum radii of the truncated cones (see Figure 2), the minimum allowed safety distance d_m1 and d_m2, for each cone of each link are calculated as follows:

$$\begin{array}{l}{d}_{\mathrm{m}1}=\left(1-u_1\right)d_{\mathrm{cmin}}+u_1{d}_{\mathrm{cmax}}\\ d_{\mathrm{m}2}=\left(1-u_2\right)d_{\mathrm{cmax}}+u_2{d}_{\mathrm{cmin}}\end{array}$$

(17)

The collision will be imminent if d_a < d_m1 or d_b < d_cmax or d_c < d_m2. The three inequalities can be false, which implies that there is no possibility of collision; that is, α_c(n) = 0 rad (see Equations (2) and (3)). Differently, if one or more inequalities are true, one or more points on the robot’s kinematic chain are under collision imminence. In this case, with only one degree of redundancy and, therefore, only one possible additional movement, the smallest among the minimum distances exceeded (d_a or d_b or d_c) will be identified and will serve as a reference for calculating angle α_c(n) (see Figure 4).

Let us consider the case (see Figure 4) where the minimum distance between the point P_c and the robot link P_sP_e is less than the allowed distance d_m1. Angle α_c(n) must make the distance between P_c and its projection, P_col, onto P_sP_e at least equal to d_m1, which implies moving P_col from its initial position to at least point P_r of Figure 4 by changing α (see Figure 1b).

Let P_cu be the projection point of P_c onto the line segment P_sP_w, calculated as follows:

$${\mathit{P}}_{\mathrm{cu}}={\mathit{P}}_{\mathrm{s}}+\left({\mathit{P}}_{\mathrm{c}}-{\mathit{P}}_{\mathrm{s}}\right)\cdot \left({\mathit{P}}_{\mathrm{w}}-{\mathit{P}}_{\mathrm{s}}\right)\left(\frac{\left({\mathit{P}}_{\mathrm{w}}-{\mathit{P}}_{\mathrm{s}}\right)}{{‖{\mathit{P}}_{\mathrm{w}}-{\mathit{P}}_{\mathrm{s}}‖}^2}\right)$$

(18)

Thus, inspecting Figure 4, one notes that the angle α_c(n) = $\gamma -\beta$, with

$$\begin{array}{l}\gamma =\mathrm{Atan}2\left(\mathrm{sign}(g)\sqrt{1-{\left(\frac{k_1^2+k_2^2-d_{\mathrm{m}1}^2}{2k_1{k}_2}\right)}^2},\frac{k_1^2+k_2^2-d_{\mathrm{m}1}^2}{2k_1{k}_2}\right)\\ \beta =\mathrm{Atan}2\left(\mathrm{sign}(g)\sqrt{1-{\left(v_1\cdot v_2\right)}^2},v_1\cdot v_2\right)\end{array}$$

(19)

where $k_1=‖{\mathit{P}}_{\mathrm{col}}-{\mathit{P}}_{\mathrm{cu}}‖$, and $k_2=‖{\mathit{P}}_{\mathrm{c}}-{\mathit{P}}_{\mathrm{cu}}‖$, $v_1=\frac{{\mathit{P}}_{\mathrm{eo}}-{\mathit{P}}_{\mathrm{eu}}}{‖{\mathit{P}}_{\mathrm{eo}}-{\mathit{P}}_{\mathrm{eu}}‖}$, $v_2=\frac{{\mathit{P}}_{\mathrm{c}}-{\mathit{P}}_{\mathrm{eu}}}{‖{\mathit{P}}_{\mathrm{c}}-{\mathit{P}}_{\mathrm{eu}}‖}$, and $g=\left(\left({\mathit{P}}_{\mathrm{c}}-{\mathit{P}}_{\mathrm{cu}}\right)\times \left({\mathit{P}}_{\mathrm{col}}-{\mathit{P}}_{\mathrm{cu}}\right)\right)\cdot \left({\mathit{P}}_{\mathrm{w}}-{\mathit{P}}_{\mathrm{s}}\right)$. The sign of g indicates which side of plane-π₂ point P_c belongs to (see Figure 3) and determines the rotation direction of the angles γ and β.

For the n^th iteration of the trajectory generation, the previous steps can be summarized in Algorithm 1.

Algorithm 1. Computation of angle ${\alpha }_{\mathrm{f}}$ at the nth iteration.
1	Input
2	Desired position and orientation of the end-effector at the iteration n;
3	Compute the inverse kinematics for αc = 0 rad;
4	Coordinates of the points belonging to the referential links and relevant points           % In this development Ps, Pe and Pw
5	$\mathrm{Retrieve} \mathrm{the} \mathrm{values} \mathrm{of} {\alpha }_c(n-1),\hspace{1em}{\alpha }_c(n-2),\hspace{1em}{\alpha }_f(n-1),\hspace{1em}{\alpha }_f(n-2)$
6	Pc % Coordinates of a possible collision point
7	find← false; % Boolean variable to indicate if a collision point exists inside safety volume.
8	dmc← 0; % Initializing the minimum of the minimal distances.
9	Pcol← []; % Point in the kinematic chain with the minor distance to Pc.
10	Compute u1 and u2;
11	if $u_1\in \left[0,1\right]$ then % Pc1 is between Ps and Pe
12	$d_{\mathrm{a}}=‖{\mathit{P}}_{\mathrm{c}}-{\mathit{P}}_{\mathrm{c}1}‖$;
13	$d_{\mathrm{m}1}=\left(1-u_1\right)d_{\mathrm{cmin}}+u_1{d}_{\mathrm{cmax}}$;
14	if da < dm1 then
15	dmc←dm1; % saving the minimal allowed distance
16	Pcol← Pc1; % saving the point on the kinematic chain
17	find← true;
	end
18	elseif$u_2\in \left[0,1\right]$ then % Pc2 is between Pe and Pw
19	$d_{\mathrm{c}}=‖{\mathit{P}}_{\mathrm{c}}-{\mathit{P}}_{\mathrm{c}2}‖$;
20	$d_{\mathrm{m}2}=\left(1-u_2\right)d_{\mathrm{cmin}}+u_2{d}_{\mathrm{cmax}}$;
21	if dc < dm2 then
22	if dc < da then
23	dmc←dm2; % saving the minimal distance
24	Pcol← Pc2; % saving the point on the kinematic chain
25	find← true;
	end if
	end if
	end if
26	$d_{\mathrm{b}}=‖{\mathit{P}}_{\mathrm{c}}-{\mathit{P}}_{\mathrm{e}}‖$; % evaluating the collision distance from Pcto the point Pe
27	ifdb<dcmaxthen   % considering a sphere as safety region around Pe–see Figure 2
28	if find=false then;
29	dmc←db;
30	Pcol← Pe;
31	find← true;
32	elseif db<dmc then
33	dmc←db;
34	Pcol← Pe;
	end if
	end if
35	if find=false % if there is no need to avoid collision
36	${\alpha }_c(n)=0$ rad;
37	dmc=0;
	else % computing the value of ${\alpha }_c$ to move the robot away from the collision point.
38	Compute γ and β;
39	${\alpha }_c(n)=\gamma -\beta$;
	end if
40	${\alpha }_{\mathrm{f}}(n)=h_1{\alpha }_{\mathrm{c}}(n-1)+h_2{\alpha }_{\mathrm{c}}(n-2)+b_1{\alpha }_{\mathrm{f}}(n-1)+b_2{\alpha }_{\mathrm{f}}(n-2)$; % Equation (3)
41	Solve inverse kinematics using ${\alpha }_{\mathrm{f}}(n)$;
42	Output Save joint positions;

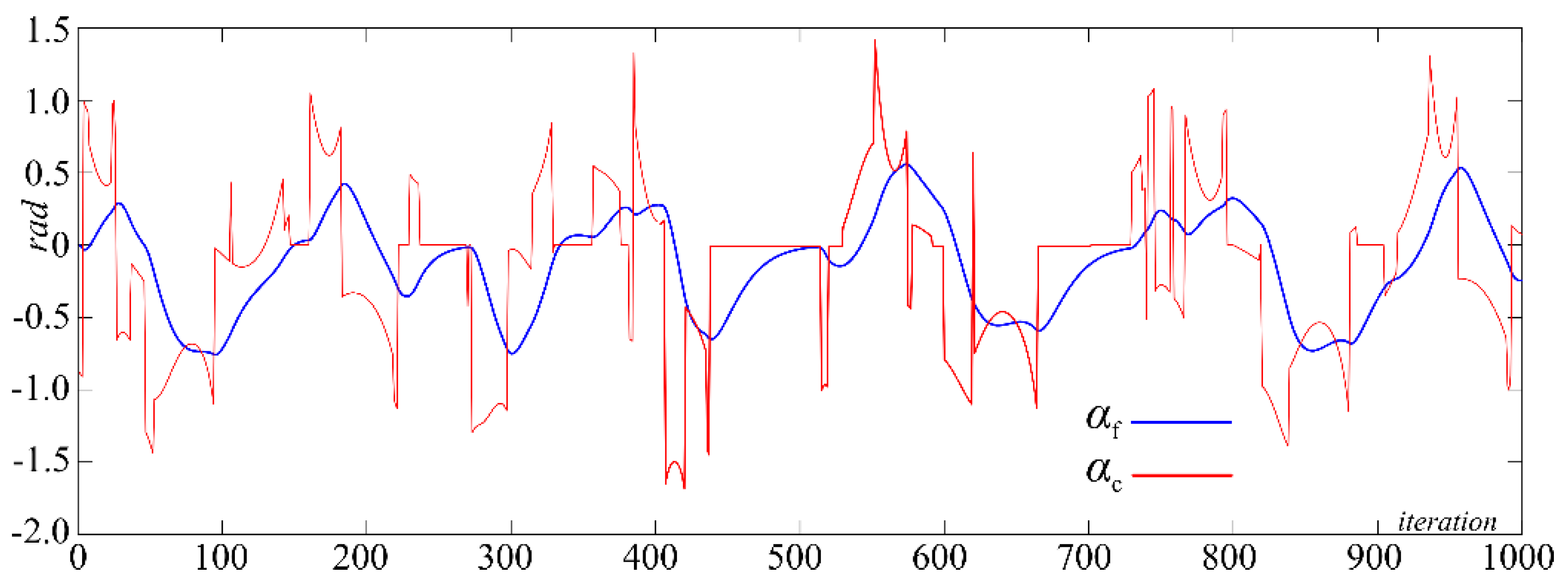
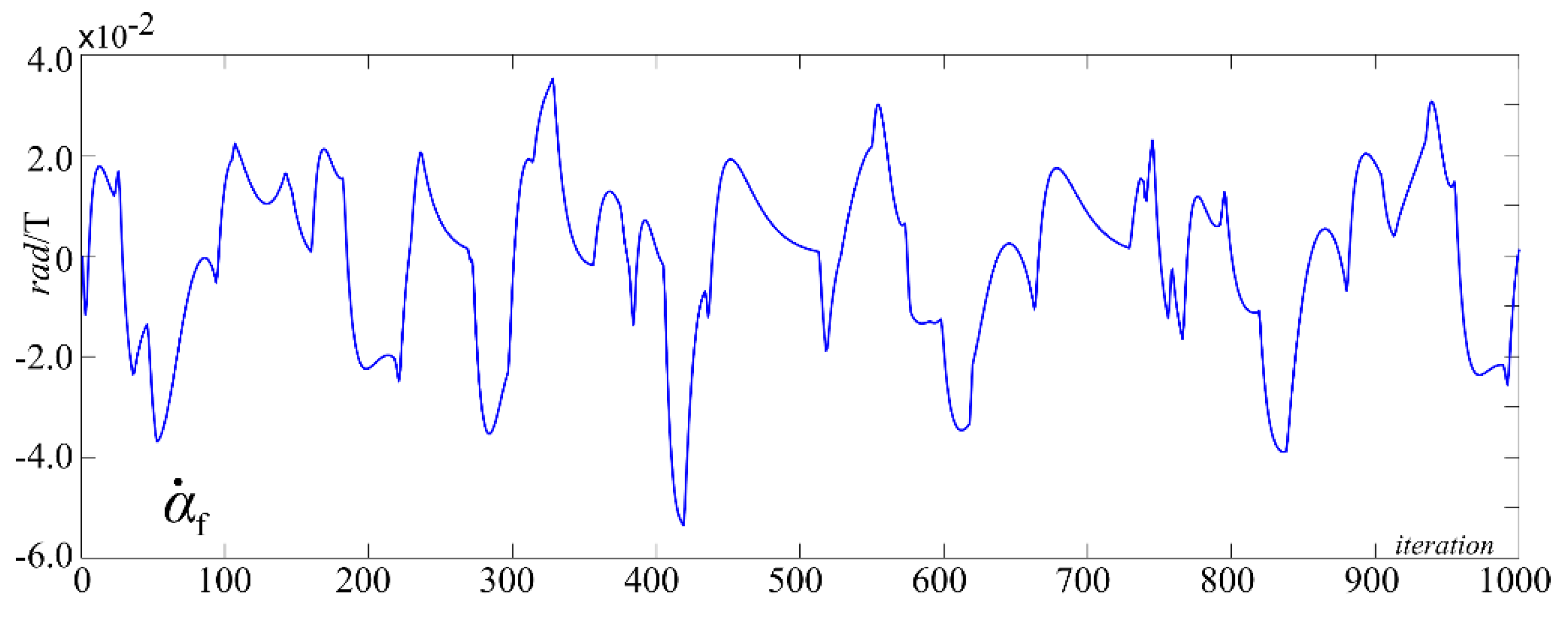
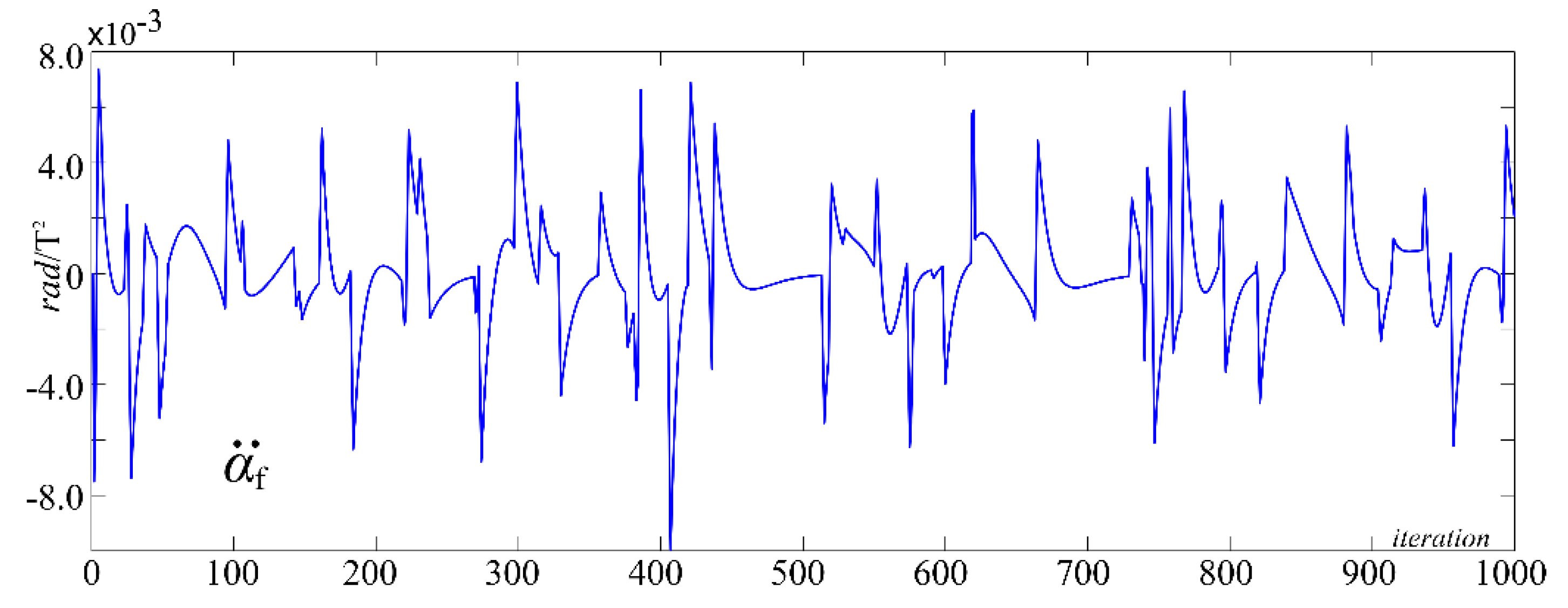
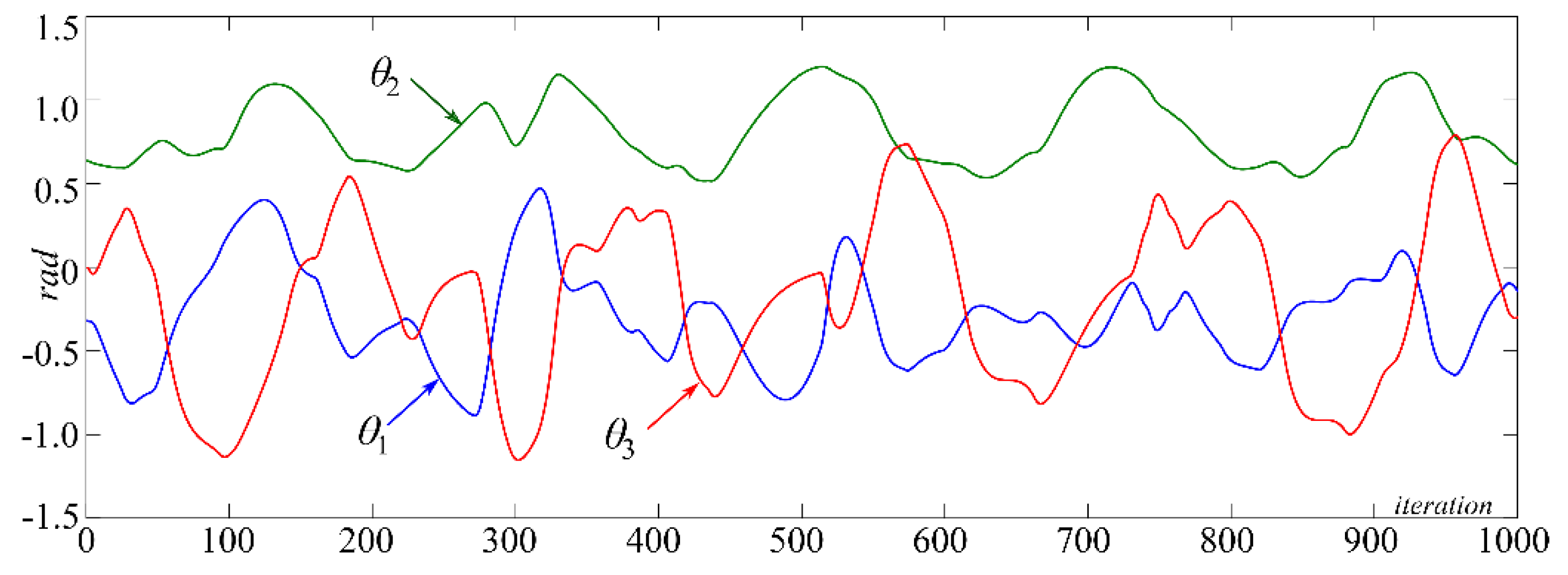
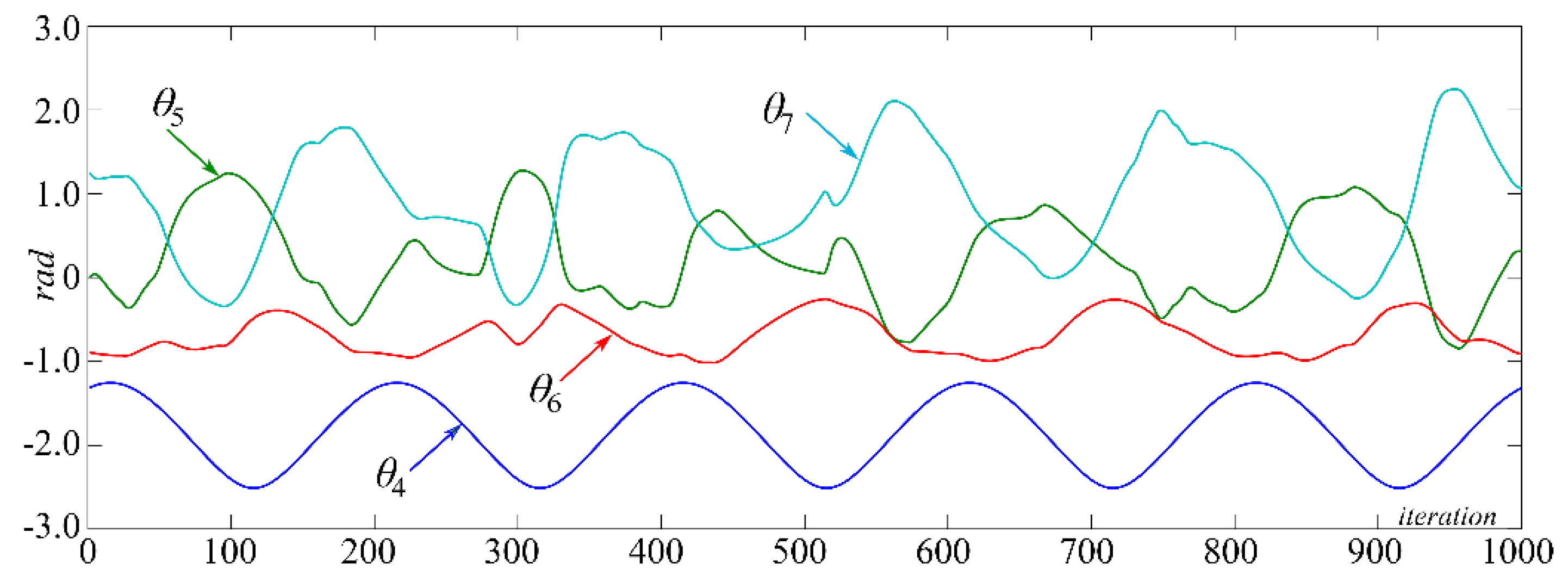
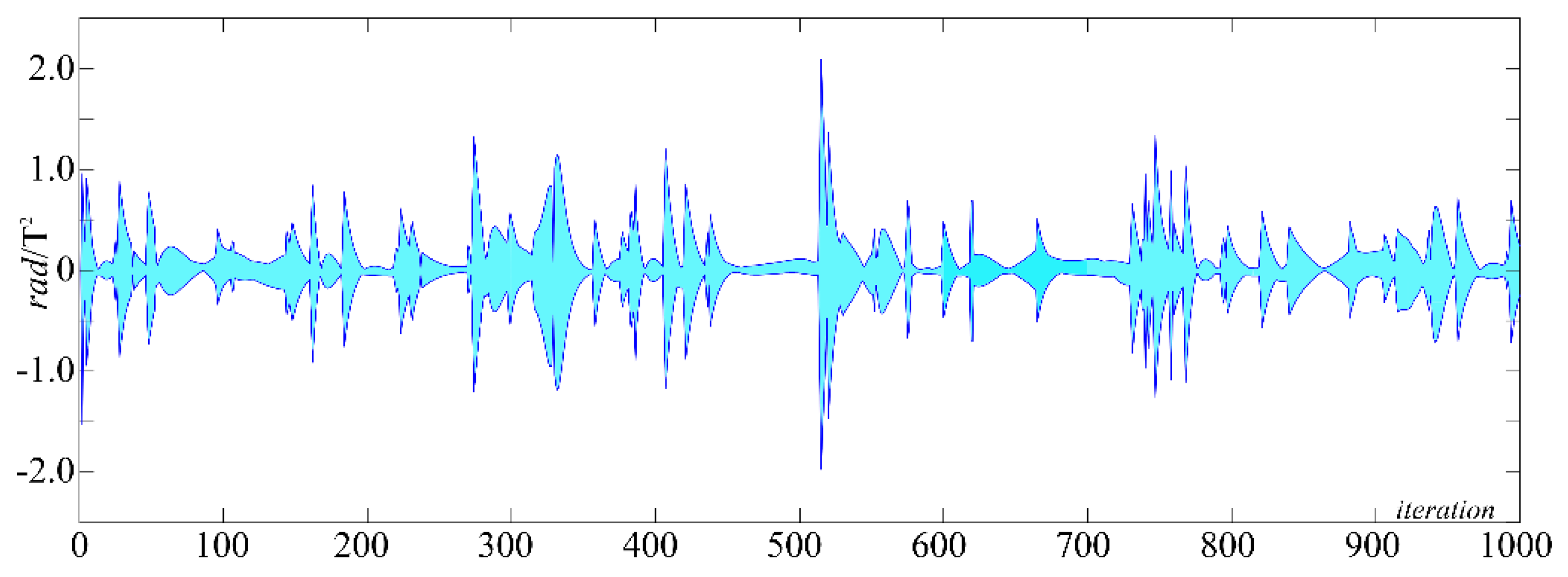
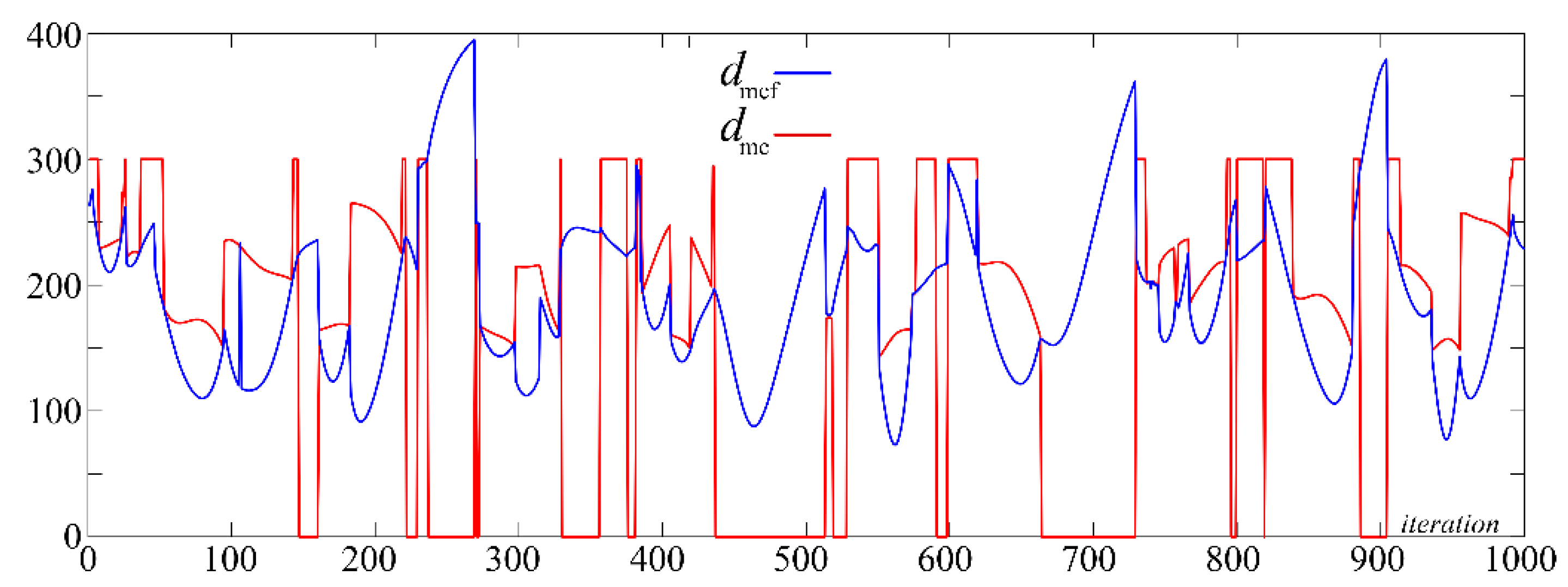
5. Graphical Results

Numerical simulations were conducted to validate the proposed collision-avoidance strategy. In these simulations, the Kuka-LBR-iiwa real lengths [45], that is, a₀ = 340 mm, a₁ = 400 mm, a₂ = 400 mm, and a₃ = 126 mm, were selected for the geometric model of the SRS-type robot. Additionally, the chosen motion task for the robot is an end-effector path (see Figure 2 and Figure 5) that keeps the z_e axis perpendicular to the x_bz_b coordinate-plane and makes point O_e perform five rides along the circular trajectory, with the center at point [400 200 200]^T mm and radius 200 mm, that lies on the plane y_b = 200 mm. The robot motion is sampled in 1000 equidistant time-instants, and at every sampling instant, Algorithm 1 is executed.

The simulation environment, over the robot, includes two human arms identified as Human-arm 1 and Human-arm 2, composed of two links and located in the space by three points named shoulder, elbow, and hand, thus improving the experiments presented in [48], where only one arm is used. The links shoulder–elbow and elbow–hand have lengths [49] of 319.6 mm and 246.5 mm with angle displacement defined with respect to the x_b-axis. The chosen motion for these two arms makes the three above-mentioned points perform oscillatory movements with the motion parameters reported in

Table 1. Human-arms simulation parameters.

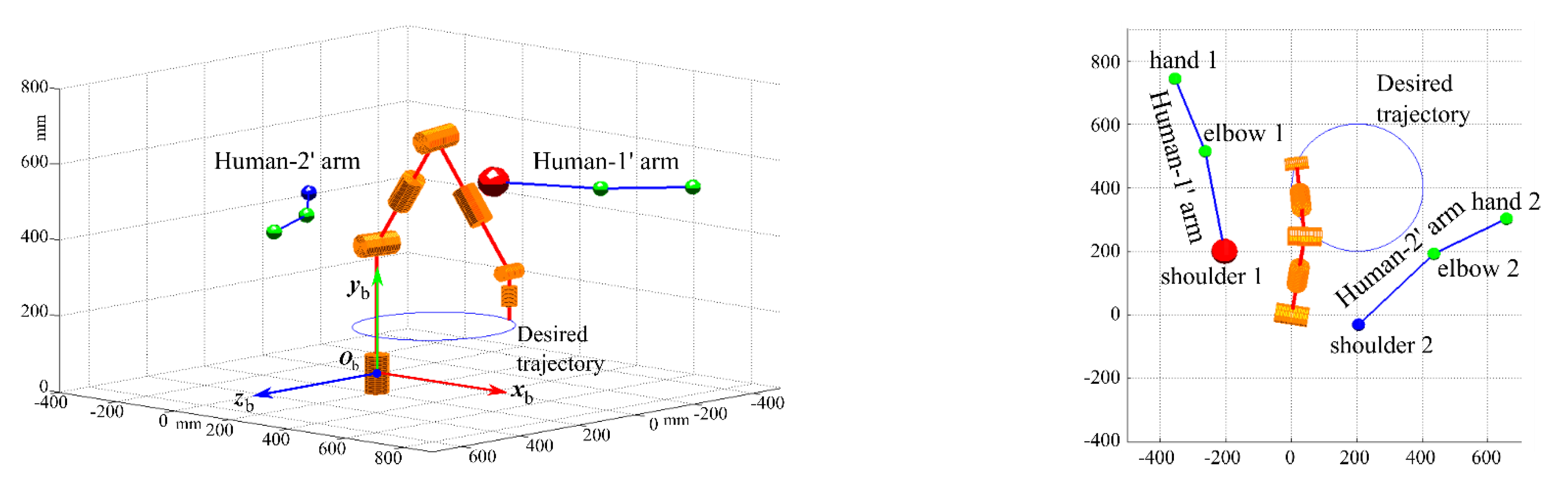
	Human-Arm 1	Human-Arm 2
Base (shoulder)	[−50 500 250]T mm	[150 500 −200]T mm
Base rotation radius (around y-axis)	50 mm	50 mm
Base number of turns	5	11
Shoulder angle range	0.4 rad	0.4 rad
Shoulder angle offset	0.4 rad	0.2 rad
Shoulder number of turns	9	13
Elbow angle range	0.4 rad	0.4 rad
Elbow angle offset	0.4 rad	0 rad
Elbow number of turns	7	9

. Human-arm motion takes place while the robot’s end-effector performs the above-defined five circular paths with the center at [400 200 200]^T mm and a radius of 200 mm.

The tests were developed on a laptop with an Intel Core i7 CPU (2.7 GHz, 8,00 Gb RAM), spending 3.68 s in execution. All the simulations were developed by using MATLAB R2021a. Eventually, the second-order transfer function, the reference for programming the filter, was adjusted with p = 0.2 s⁻¹, and the sampling time was adjusted to T = 0.06 s, which corresponds to m = pT = 0.012 and a simulation cycle of 60 s. It is worth stressing that, to avoid muscular injuries, a worker should not execute motion cycles with a period lower than 60 s; so, in these simulations, the human-arm motion is much faster than the admitted one (i.e., the chosen parameters make the simulation environment much faster than a realistic one).

The graphical simulation environment presented in Figure 5 enables us to observe the evolution of the proposed algorithm and the SRS-type’s end-effector performance following the desired trajectory while dealing with collision avoidance.

A video that presents the complete simulation experiment of the proposed algorithm is available at [50] and as “Supplementary Materials” accompanying this paper. Figure 6 presents three frames from the above-mentioned video showing the SRS-type robot while avoiding a collision. The video shows that, in this simulation environment, a sampling rate (=1/T) of 16.7 Hz is sufficient to avoid collision with the proposed strategy. It is worth stressing that since this sampling rate corresponds to a “reaction time” of 60 ms for the robot and the human reaction time is about 200 ms, the proposed strategy can enable the robot to react three times faster than a human being.

Figure 7 shows the computed angle α_c and its filtered counterpart α_f, used as a reference for the inverse kinematics, during the simulation cycle. The analysis of Figure 7 reveals that α_f is a regular curve.

Figure 8 and Figure 9 show the rates of angle and angular speed as a function of the sampling period T to evaluate the continuity and smoothness of the trajectory for the filtered angle α_f.

The inverse-kinematics solution of the SRS-type robot yields the position profile of joints 1, 2, and 3, which are θ₁, θ₂, and θ₃, respectively, presented in Figure 10; as well as joints 4, 5, 6, and 7, which are θ₄, θ₅, θ₆, and θ₇, respectively, presented in Figure 11.

For each iteration, and considering the known sampling time T, the rates of changes of joint variables and corresponding accelerations were calculated for each joint by first-order approximations. Thus, taking the maximum and minimum values obtained, Figure 12 and Figure 13 show the range achieved for the rate of change of position and acceleration, respectively, in each iteration of all robot joint variables. The rates of joint positions and acceleration behavior did not show abrupt variations, remaining in a limited range with similar magnitudes.

The angle α_f smooths the resultant distances between the robot and the collision point. Figure 14 shows the behavior of the distance between the SRS-type robot and the collision point (red) along the simulation, compared with the distances when under imminent collision (blue). It is worth mentioning that when the robot is out of collision avoidance, the distance d_mc used to calculate the angle α_f is adjusted to 0, as seen in line 37 of Algorithm 1.

6. Discussions

The results presented in the test showed that the proposed algorithm smoothed all the joints’ position and velocity profiles in a dynamic environment.

The test aims at replicating the relationship between a collision point crossing a circle and the consequent problem of variation in the resulting distances projected on the robot’s links. Although the collision curve is deterministic in the test, the procedure applies to random variations in the collision point coordinates or a more significant number of collision points, including the number of links and relevant robot points. The algorithm can deal with multiple collision points, attempting to move the robot away from that nearest collision point. For the collision avoidance on k simultaneous collision points, the robot should have a redundancy index r = k; for example, if it is necessary to have three collision points or control the three distances, such as d_a, d_b, and d_c discussed in Section 4.3, the robot should have degrees of redundancy r = 3. In this way, the algorithm should be executed three times for each collision point featuring its expandability.

The presented inverse kinematics, which solves the α angle for the four quadrants, is based on review propositions [8,39,48] and refines them, thus improving the formulation.

Additionally, in the presented simulation, the available degree of redundancy is 1, and it is strictly sufficient to solve the collision-avoidance problem without including the joint limits control, as was achieved in other papers [15,20,48,51,52,53] where the introduced redundancy was exploited by optimization procedures to find the best α that avoids reaching joint-position limits. The possible involvement of joint-position limits’ control, over collision avoidance, in programming trajectories and kinematic algorithms solely depends on the availability of redundancy degrees higher than one, which, if available, can be exploited by implementing one of the strategies proposed in the literature, even with the proposed algorithm.

Similar algorithms present safety volumes described by a limited number of points [44,54] or based on numerical approaches [4,20]. The here-discussed proposal uses a parametric surface around the links, instead of limited volumes as discussed in [4], to define the safety volume in the computation of the collision distance for any point of the link, which makes this new approach more realistic and reliable.

At the same time, the use of a second-order filter makes the strategy feasible, adjustable, and replicable, ensuring, together with the description of the safety volume, smooth transients in the trajectories as well as an analytical collision-avoidance algorithm without numerical procedures that increase the computational burden, as found in [23]. The smoothing of the collision-avoidance transients appears in the bounded rate of positions and acceleration profiles for the robot joints (see Figure 12 and Figure 13), continuously ensuring that discontinuities, such as those shown in [4,54,55], do not arise despite the dynamic environment.

Using a digital filter in the transition between paths to be followed by the joints additionally guarantees the smoothness of the programmed trajectories.

It is important to note that the collision-avoidance algorithm’s proposition has limitations when several collision points or several links lead to opposite displacements generating conflicts of movements characterizing singularities. Concerning the singularities, it is observed that collision avoidance does not occur when g = 0, or the collision point P_c belongs to the plane formed by the points P_s, P_w, and P_e, as can be seen in Figure 3 and Figure 4; that is,

$$D=\frac{\left|\left({\mathit{P}}_{\mathrm{c}}-{\mathit{P}}_{\mathrm{s}}\right)\cdot {\mathit{n}}_{\mathrm{p}}\right|}{‖{\mathit{n}}_{\mathrm{p}}‖}=0$$

(20)

where D corresponds to the distance between the point P_c and the plane formed by the points P_s, P_w, and P_e, and n_p is the result of a cross-product as follows:

$${\mathit{n}}_{\mathrm{p}}=\frac{\left({\mathit{P}}_{\mathrm{e}}-{\mathit{P}}_{\mathrm{s}}\right)}{‖\left({\mathit{P}}_{\mathrm{e}}-{\mathit{P}}_{\mathrm{s}}\right)‖}\times \frac{\left({\mathit{P}}_{\mathrm{w}}-{\mathit{P}}_{\mathrm{e}}\right)}{‖\left({\mathit{P}}_{\mathrm{w}}-{\mathit{P}}_{\mathrm{e}}\right)‖}$$

(21)

It is interesting to note that angle ${\alpha }_{\mathrm{f}}$ does not produce errors of position and orientation of the end effector, despite the need for a time of accommodation or convergence to the final values following trajectories, since its primary task is to control the distance from the collision.

However, the need for transitory times for collision avoidance means suitable adjustments to the filter time constant according to the desired performance and control specifications.

The proposed algorithm can deal with collision avoidance between multiple robots simultaneously. In this case, the distance between the robot’s links is controlled by calculating the geometric distance between the line segments to which the links belong. Thus, taking a robot as a reference, the P_c points belong to the other robots, and running the proposed algorithm in each robot’s trajectory generator allows several robots to share the same space without generating collisions.

7. Conclusions

Workspaces shared between robots and humans in collaborative tasks require strategies that include collision avoidance and the programming of smooth transitional displacements.

This paper presented an algorithm for the treatment of collision and posture adjustment of robots based on analytical spatial geometry and the use of digital second-order critically damped filters. The strategy includes a posture adjustment of the robot based on an additional movement, defined as α, available for the redundant 7-DOF SRS-type robot. The simulations showed the smoothing of the joints’ trajectory profiles and collision avoidance effectiveness without collisions in a dynamic environment.

The geometric approach allowed us to present a proposition for inverse kinematics considering the posture adjustment and the projection of the collision point on any point on the links of the robot’s kinematic chain.

Spatial surfaces were used as an example for the determination of the safety regions of the robot. For relevant points and links (under imminent collision), we used the formulation of spheres and truncated cones, which allows us to identify the possibility of collision and activate the collision-avoidance strategy. According to the geometry of links and components that form the environment where the robot is inserted, other formulations can be adapted and used as safety surfaces.

The proposed collision-avoidance solution is feasible and straightforward, providing a quick implementation solution for collaborative robots. The fact that the proposal is based only on analytical formulations reduces the computational effort, thus increasing the reliability of the solutions for trajectories and the efficiency of collision control and other processing in each sampling time.