A Reconfigurable Parallel Robot for On-Structure Machining of Large Structures
Abstract
1. Introduction
- Using reconfiguration by reassembly, we have a lighter robot when the basic build of the robot with three actuators is used. With other on-structure parallel robots having five or more actuators, the larger number of actuators results in larger weight. This is because such robots with five or more actuators have fixed topology, and hence, all their actuators should always be mounted on the robots although the robots are performing three-axis machining tasks.
- The modular design of the robot results in easier and less costly maintenance. When any additional module needs replacement, one can replace only that particular module, without a need to replace the whole robot. Replacement of such components is also easier due to the modular design.
- The modular robot can be sold as multiple packages using the same basic build. Each robot package is sold with its own topology and number of DOFs. The use of the same basic build for the various packages gives an advantage to the manufacturer in terms of the design, production, and sales. This is due to the modularity of the robot. On the user side, the purchase of the modular robot can be performed in multiple phases. One may start procuring the three-axis basic build with lower cost. This three-axis robot can already be used for three-axis machining tasks. At a later time, the additional modules can be procured when they are required.
- The joint motion planning in the three-axis motion, in both the reassembly and joint locking schemes, is simpler as the robot uses only three actuators. In contrast, other on-structure parallel robots with five or more actuators need to involve all of their actuators in the joint motion planning even when they are used for three-axis motion.
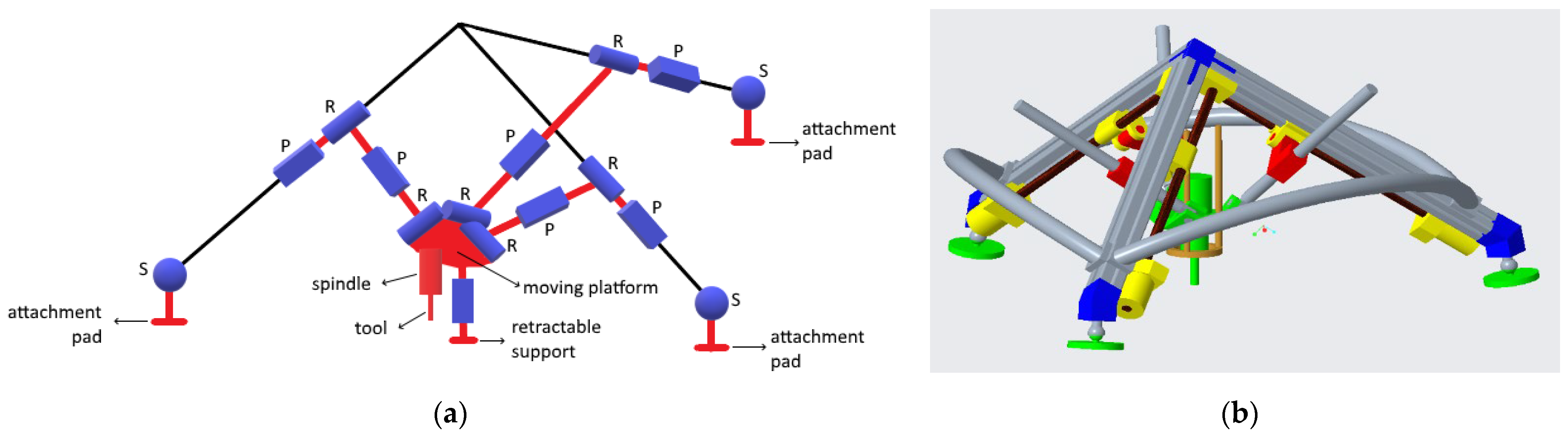
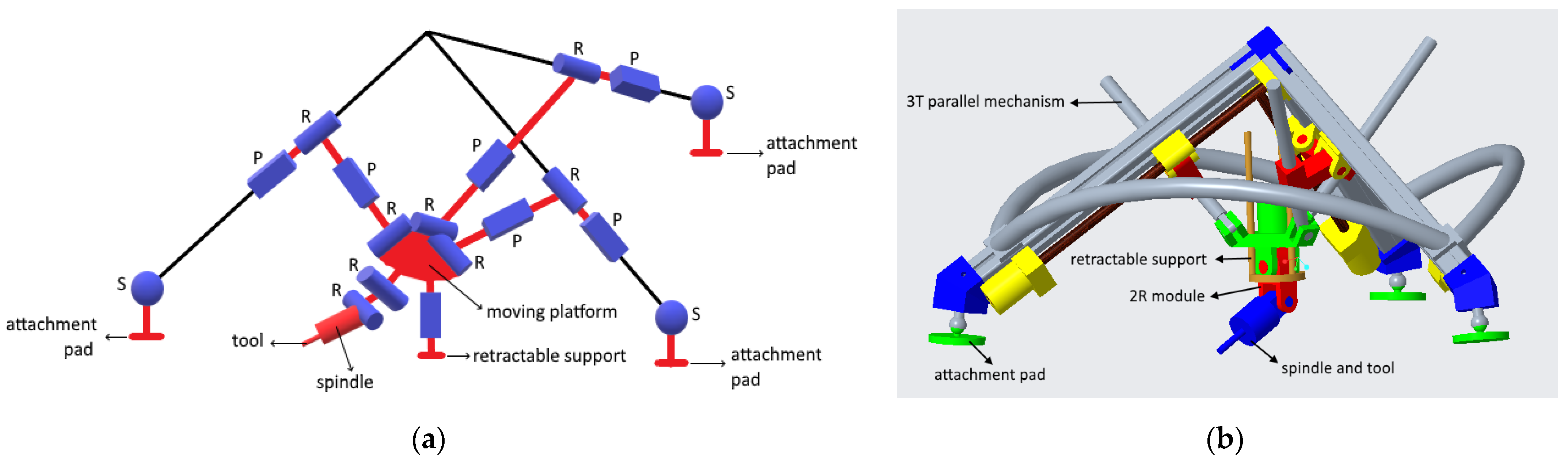
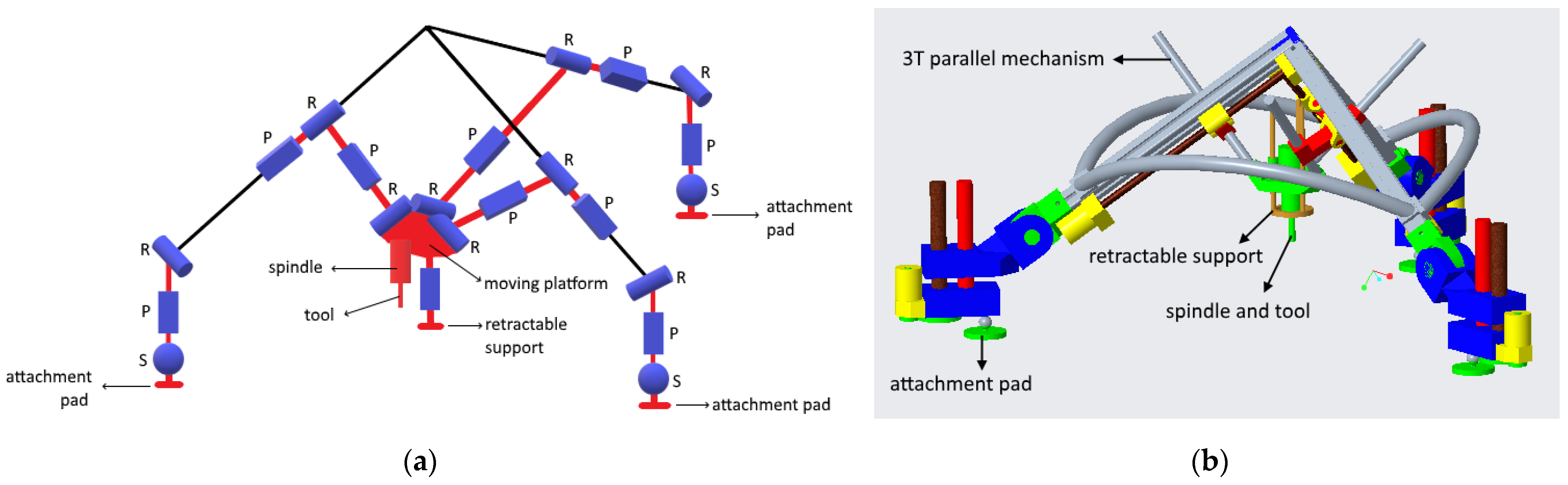
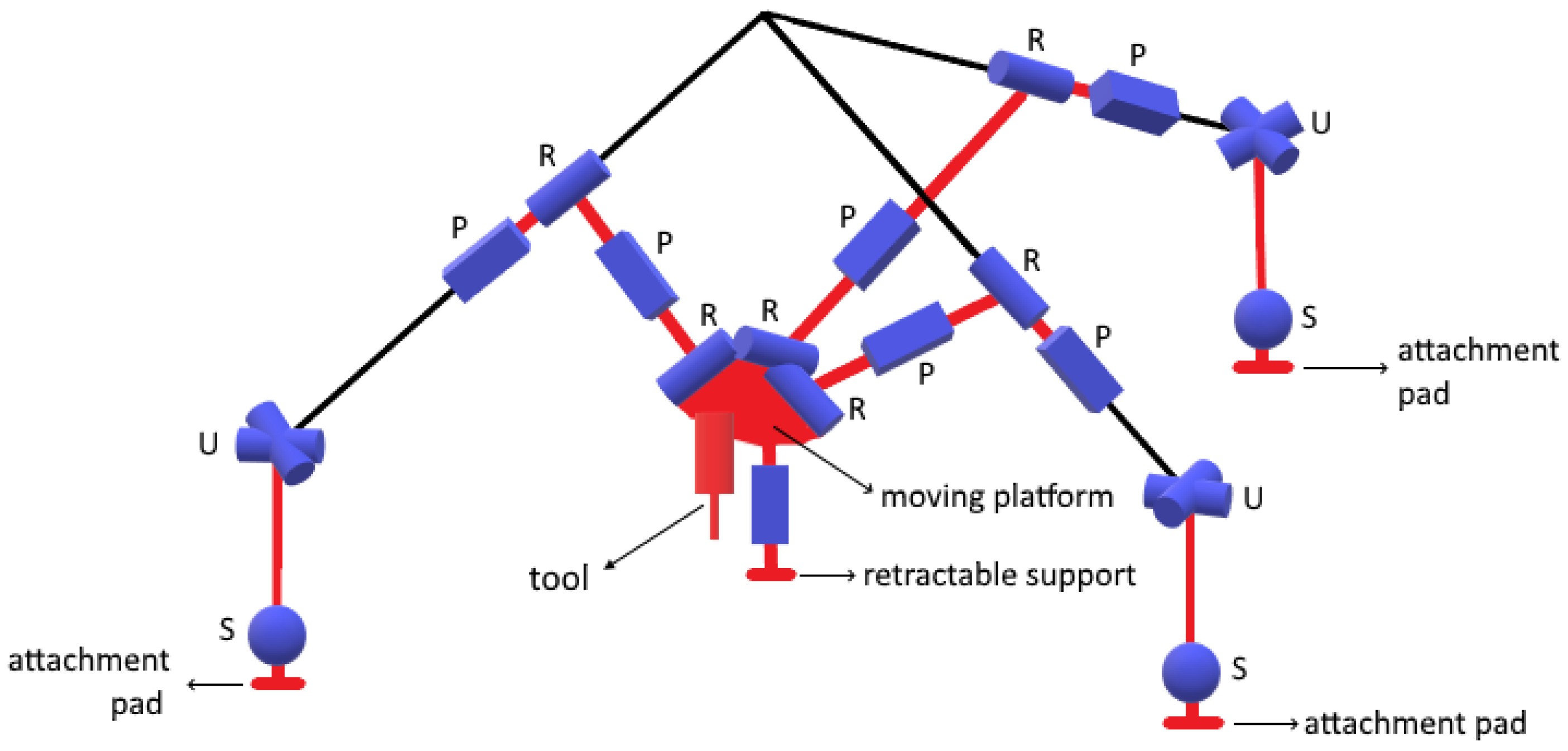
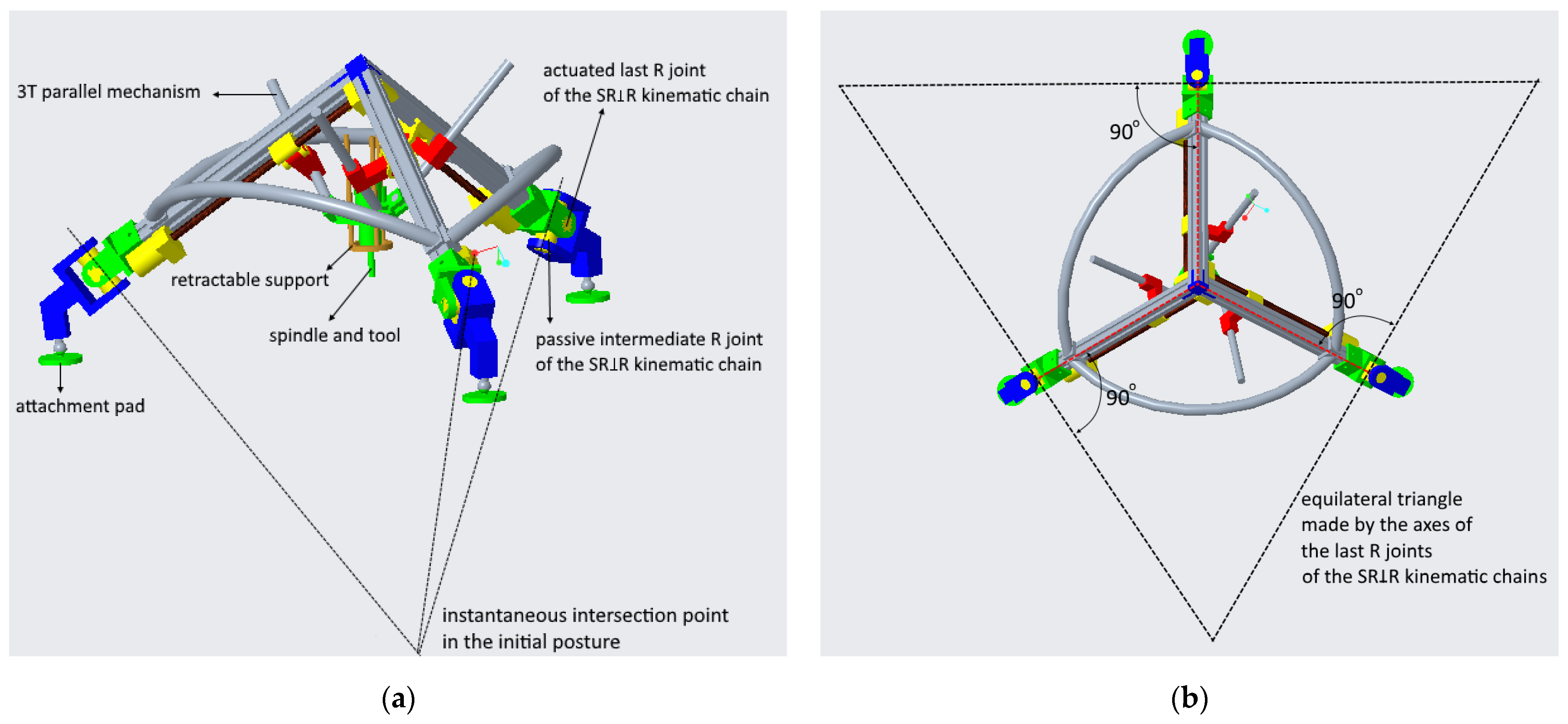
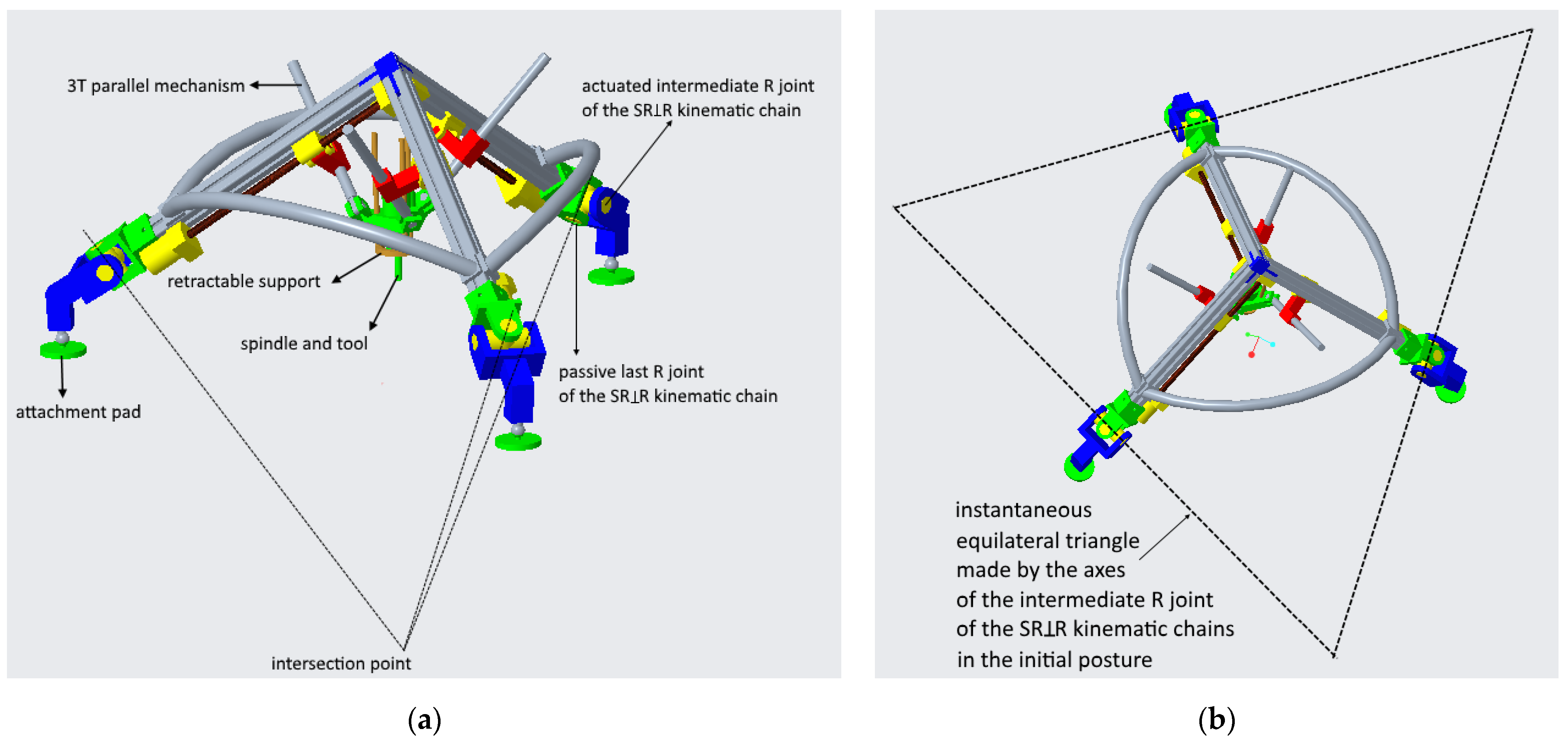
2. Topology
3. Mobility Analysis
3.1. Mobility of 3SPR Mechanism
3.2. Mobility of 3SU Mechanism
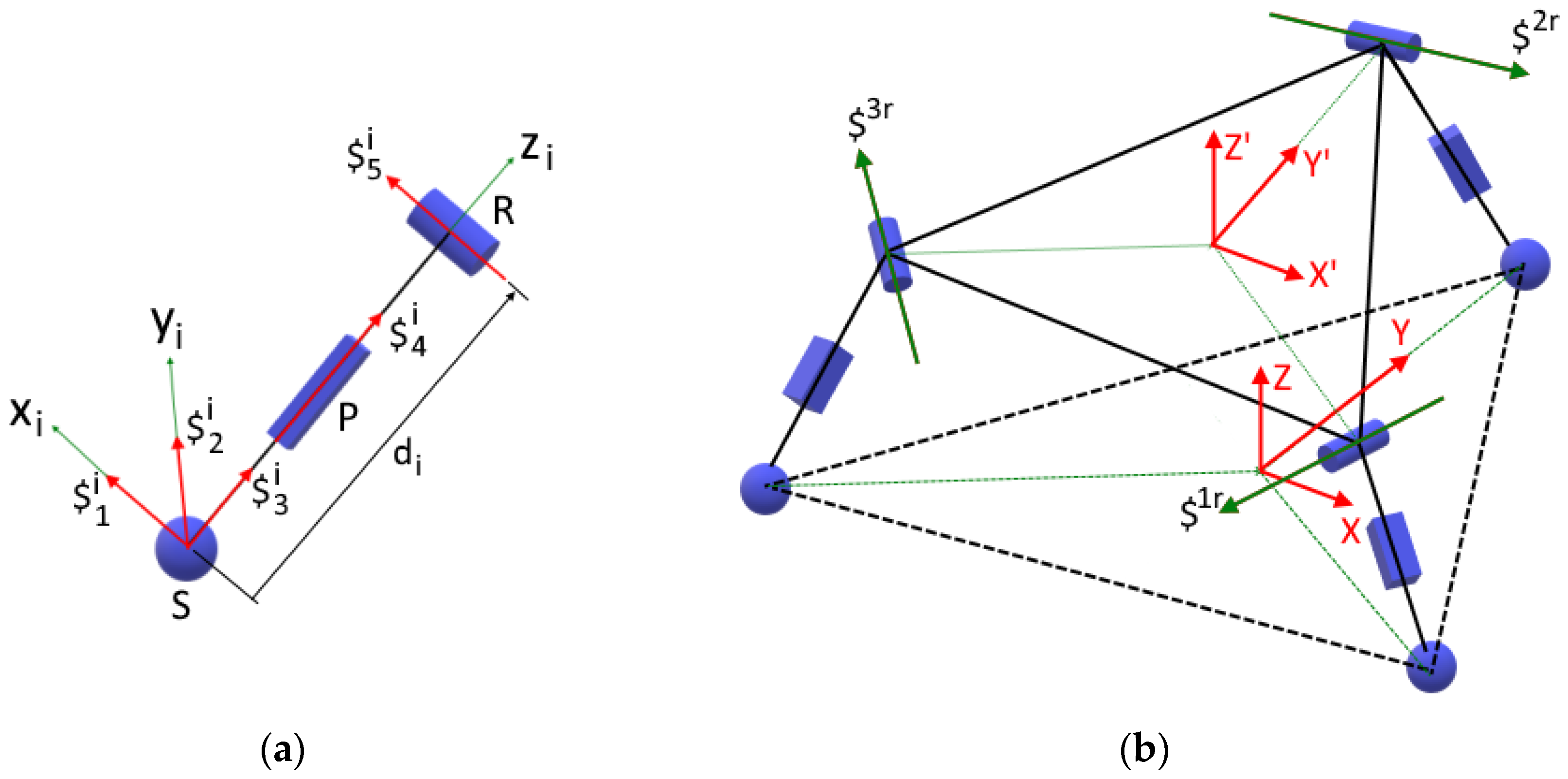
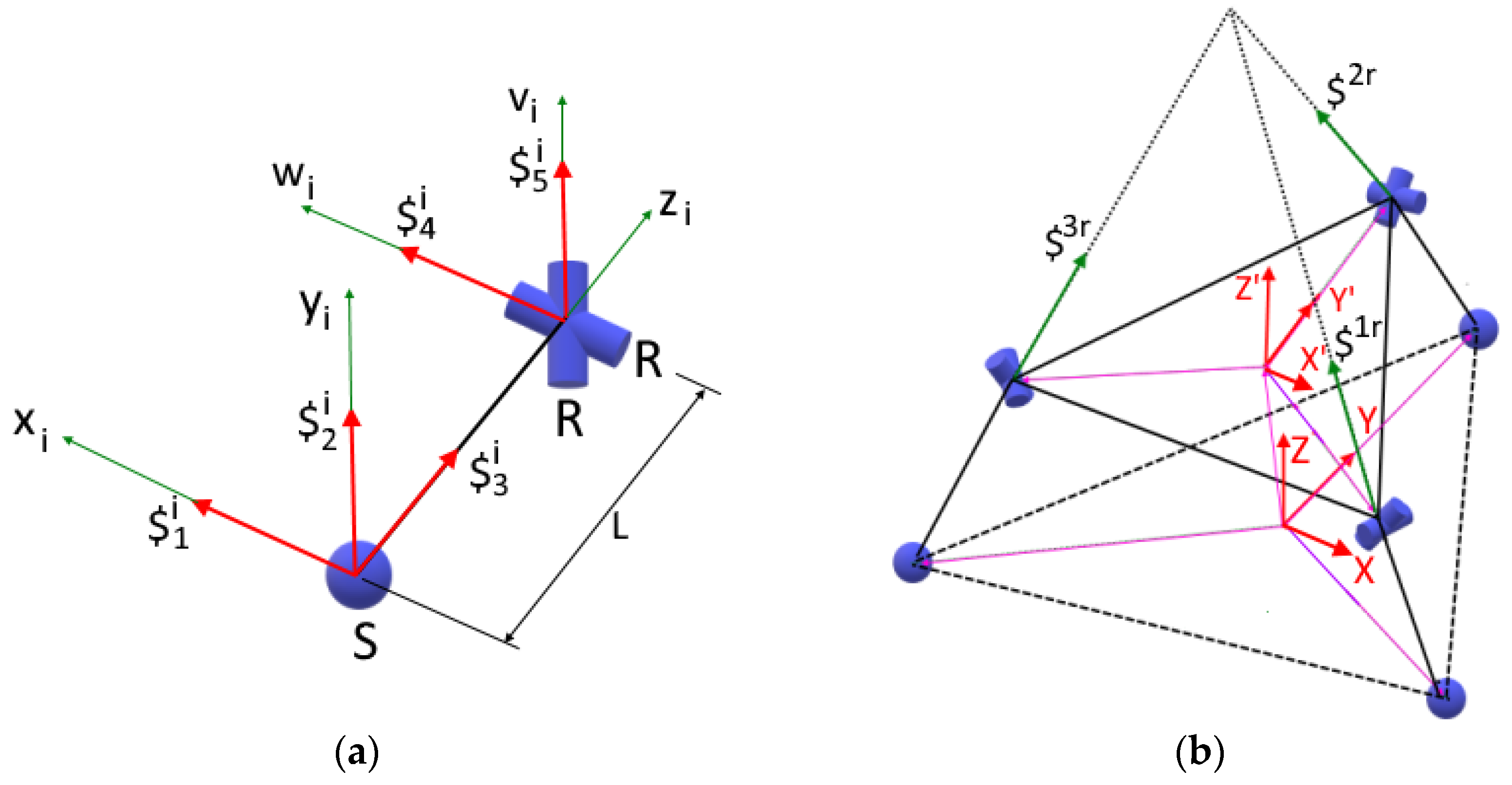
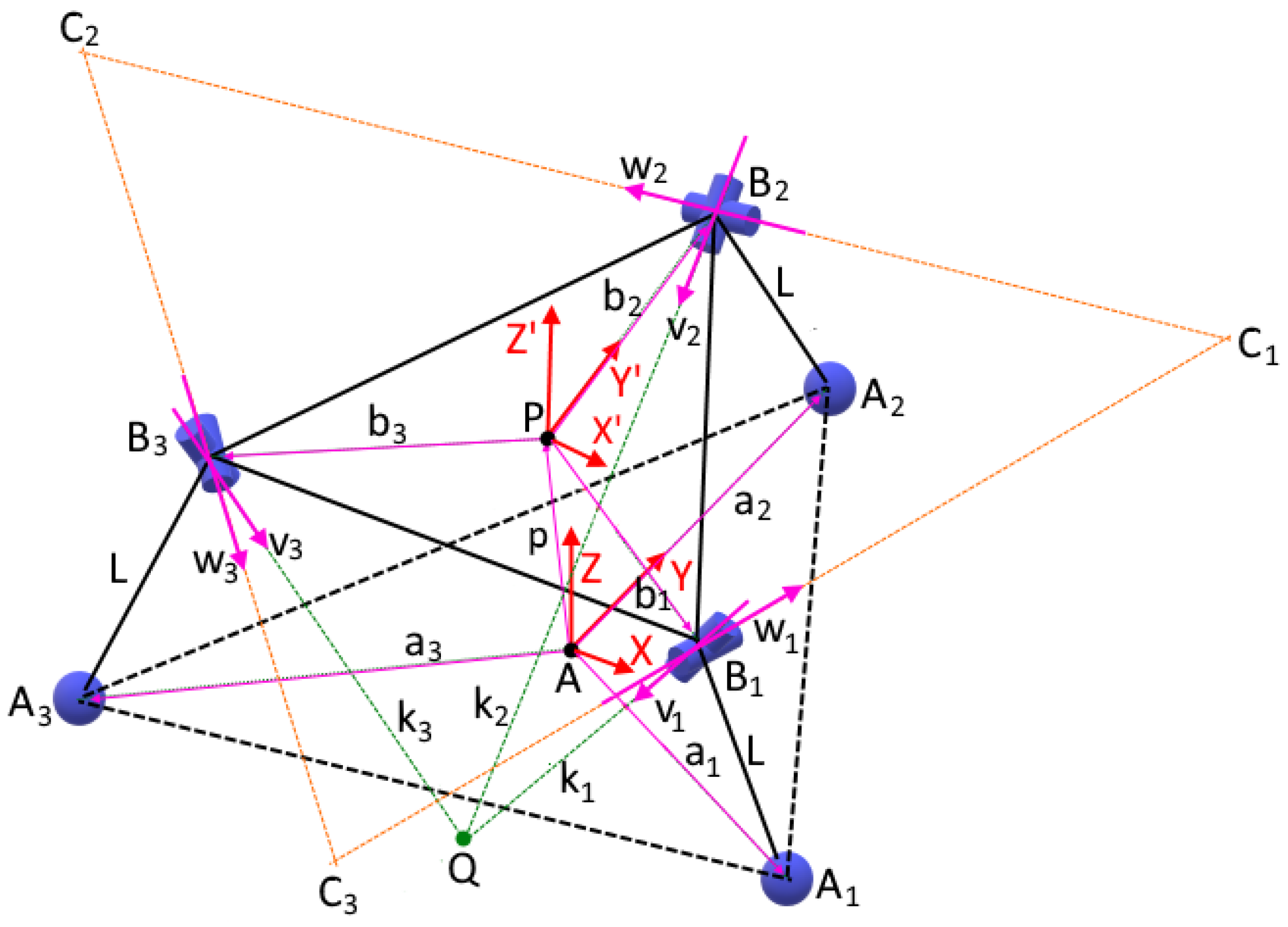
4. Pose Kinematics
4.1. Pose Kinematics of 3PRPR, 3PRRR, and Serial RR Mechanisms
4.2. Pose Kinematics of 3SPR Mechanism
4.3. Pose Kinematics of the 3SU Mechanism
4.4. Pose Kinematics of the Combined Mechanism
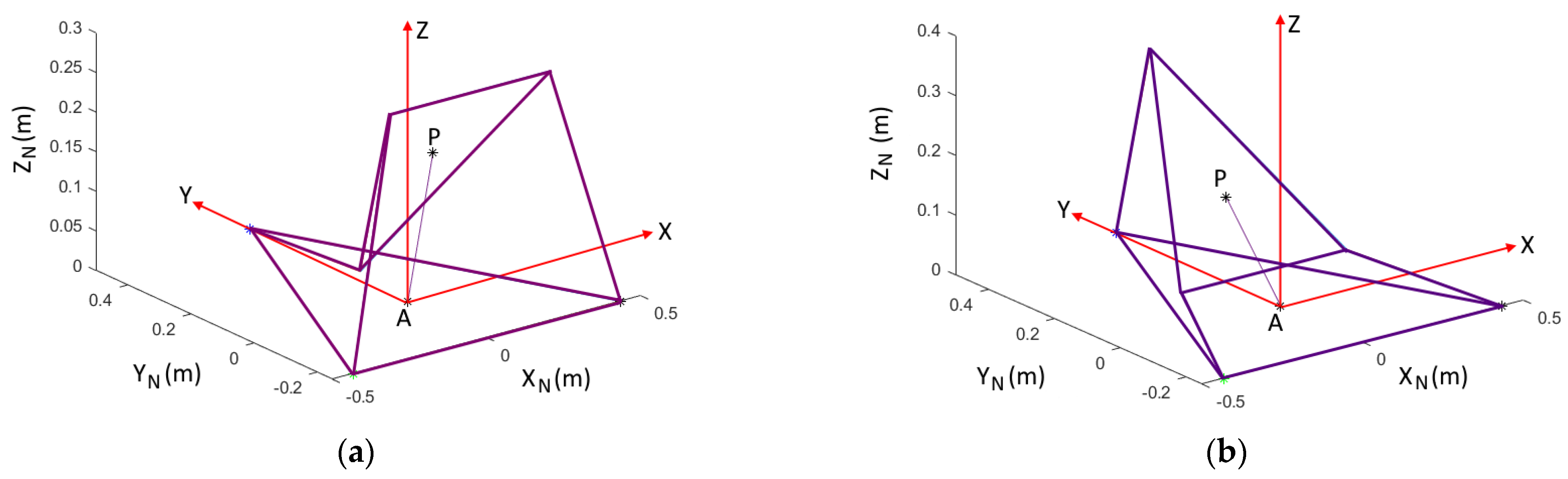
4.5. Numerical Example
5. Differential Kinematics and Singularity Analysis
5.1. Differential Kinematics and Singularity Analysis of 3PRPR and 3PRRR Mechanisms
5.2. Differential Kinematics and Singularity Analysis of 3SPR Mechanism
5.3. Differential Kinematics and Singularity Analysis of 3SU Mechanism
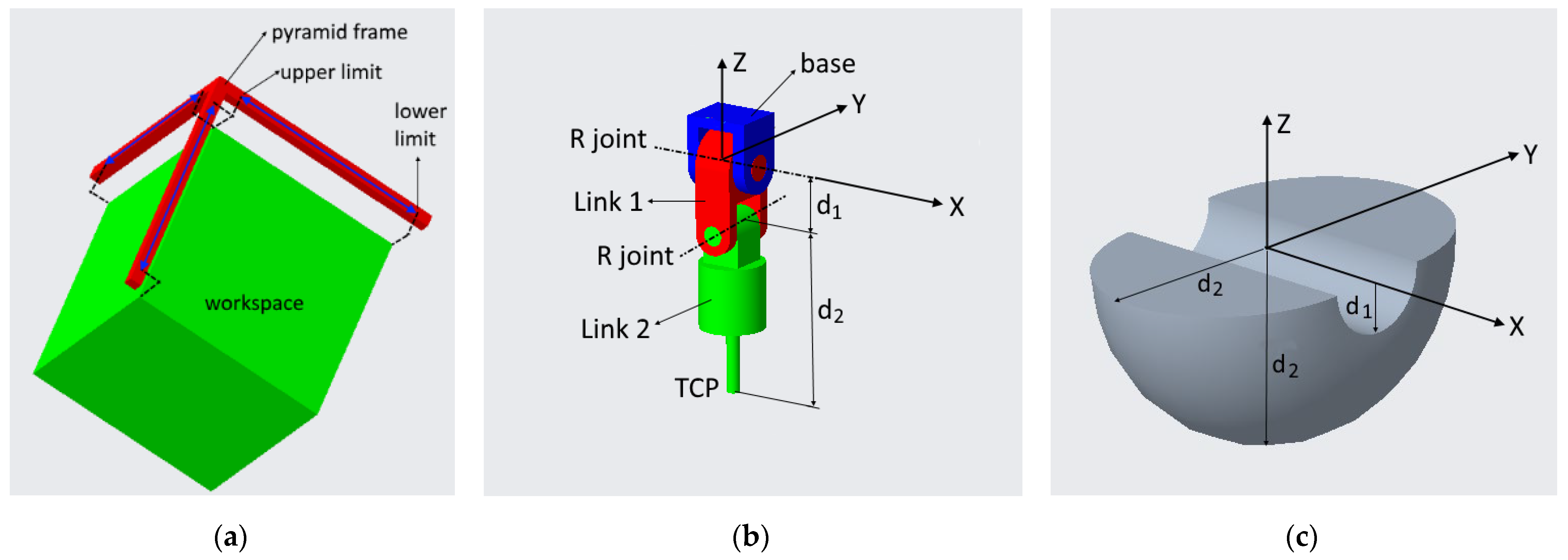
6. Workspace
6.1. Workspace of the 3T Mechanism
6.2. Workspace of the Serial RR Mechanism
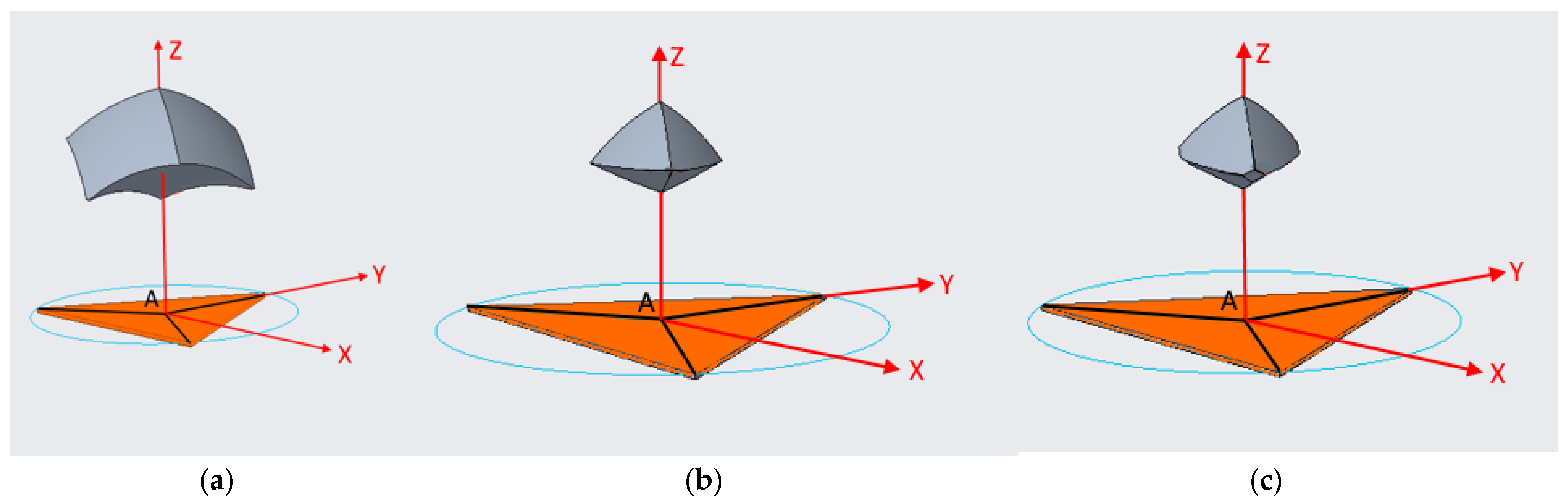
6.3. Workspace of the 3SPR and 3SU Mechanisms
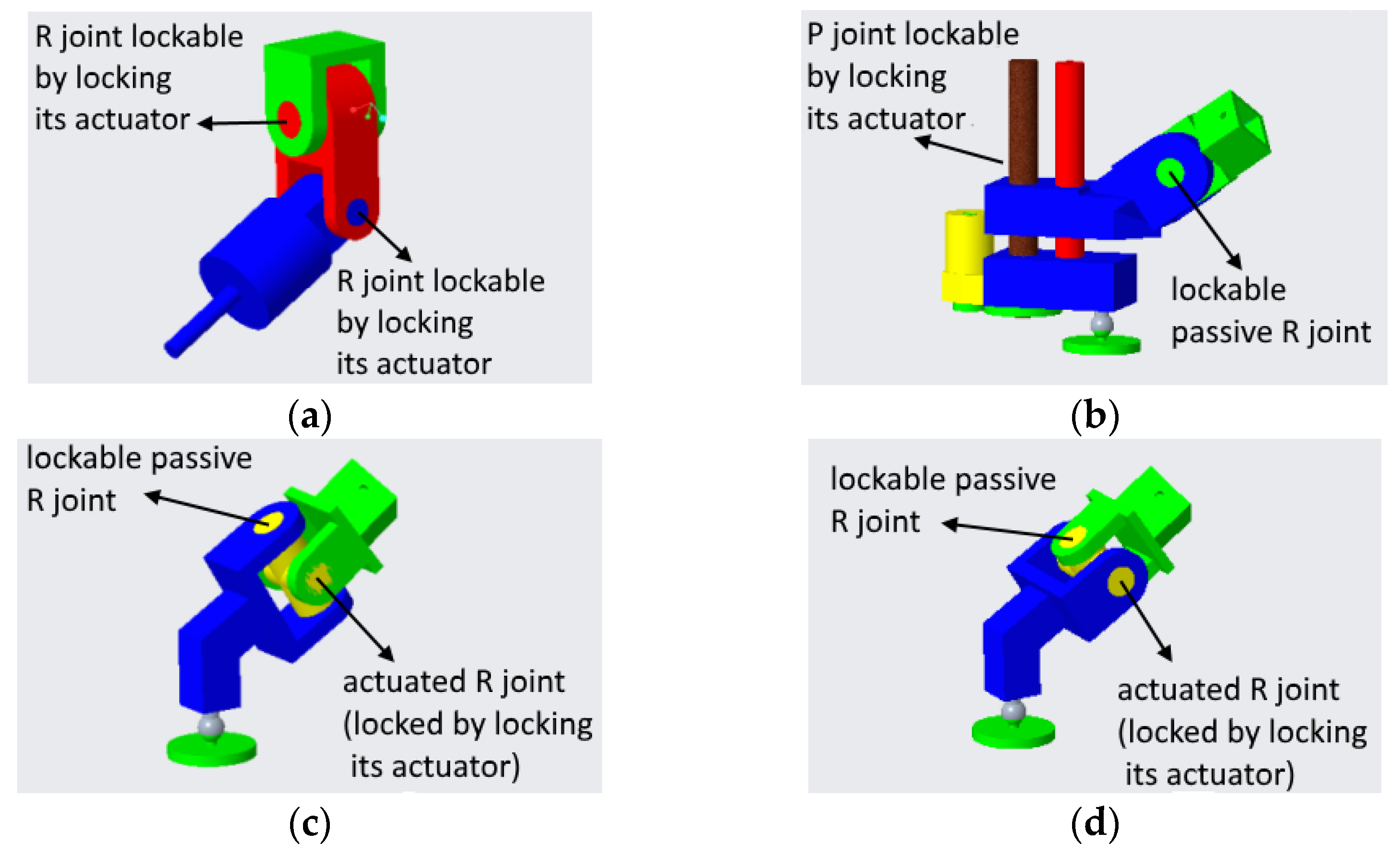
7. Reconfiguration Schemes
8. Dimensional Optimization
8.1. Optimization of the 3T Mechanism
8.2. Optimization of the Serial RR Mechanism
8.3. Optimization of the 3SPR and 3SU Mechanisms
8.3.1. Design Variables
8.3.2. Optimization Constraints
8.3.3. Objective Function
8.3.4. Optimization Formulation
- the lower and upper bounds of as written in Equation (36);
- the lower and upper bounds of as written in Equation (36);
- the inequality constraint written in Equation (38);
- the limits of the S joints, i.e., for i = 1,2,3 and j = 1,2,3;
- the limits of the R joints, i.e., for i = 1,2,3;
- the interference constraints written in Equations (39) and (40).
- the lower and upper bounds of as written in Equation (36);
- the lower and upper bounds of as written in Equation (36);
- the lower and upper bounds of as written in Equation (37);
- the inequality constraint written in Equation (38);
- the limits of the S joints, i.e., for i = 1,2,3 and j = 1,2,3;
- the limits of the U joints, i.e., and for i = 1,2,3;
- the interference constraints written in Equations (39) and (40).
8.3.5. Optimization Algorithm
- Step 1: Run the forward kinematics of the mechanism by inputting the active joints’ positions at a specific discretization interval within their ranges. The tilting angles of the moving platform and corresponding to the input active joints’ positions are obtained from the forward kinematics solution. It is worth mentioning that the lower and upper limits of the active P joints, and , determined a priori in the 3SPR mechanism, can be considered pre-determined constraints that are not part of the optimization. Similarly, the limits of the active joints in the 3SU mechanism that are determined a priori can also be considered pre-determined constraints that are not part of the optimization.
- Step 2: Extract the minimum and maximum values of the obtained tilting angles of the moving platform and . This gives us , , , and .
- Step 3: Compute the objective function written in Equations (41) or (42), depending on whether it is maximization or minimization.
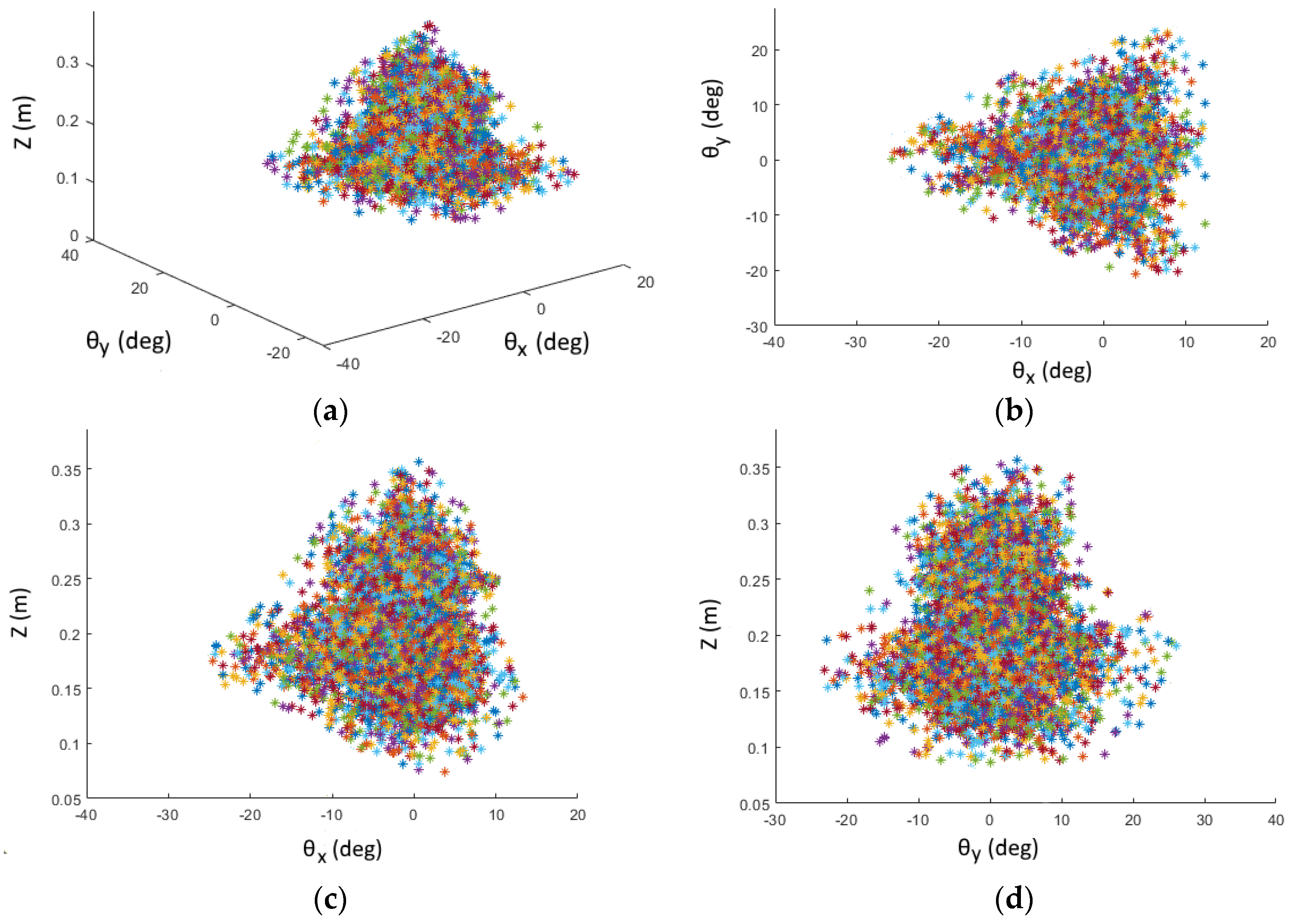
8.3.6. Numerical Example
9. Design Considerations
10. Conclusions
11. Patent
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Abbreviation | Meaning |
|---|---|
| DOF | Degree of freedom |
| P, R, U, S | Prismatic, revolute, universal, and spherical joints |
| A | Attachment |
| 3T | Three-translation |
| 2R | Two-rotation |
| 3R | Three-rotation |
| 3T2R | Three-translation and two-rotation |
| 1T2R | One-translation and two-rotation |
| TCP | Tool Center Point |
Appendix B
| Symbol | Meaning |
|---|---|
| Ʇ | Perpendicularity between two adjacent joint axes |
| Underline | Actuated joint |
| Joint screws in the i-th limb | |
| Screw of the j-th joint in the i-th limb | |
| Reciprocal screw in the i-th limb | |
| x1, x2, x3 | Positions of the three active P joints in the 3T mechanism |
| x,y,z | End-effector position |
| Coordinate frame of the i-th limb | |
| xyz | Coordinate frame attached to the apex of the pyramid of 3T mechanism |
| XYZ | Coordinate frame attached to the center of the base of the lower mechanism |
| X′Y′Z′ | Coordinate frame attached to the moving platform of the lower mechanism |
| X″Y″Z″ | Coordinate frame attached to a tip of the pyramid segments of the 3T mechanism |
| XNYNZN | Inertial (world) coordinate frame |
| Position vector of the moving platform with respect to the center of the base | |
| Rotation matrix of the moving platform with respect to the base | |
| Elementary rotation matrix about X and Y axes | |
| Tilting angles of the moving platform with respect to X, Y, and Z axes | |
| Minimum and maximum values of | |
| Minimum and maximum values of | |
| Angles of the active and passive R joints of the R or U joint in the i-th limb | |
| Minimum and maximum values of | |
| Minimum and maximum values of | |
| Angle of the i-th rotational DOF of the S joint in the j-th limb | |
| Minimum and maximum values of | |
| R | Circumradius of the base |
| Minimum and maximum values of R | |
| r | Circumradius of the moving platform |
| Minimum and maximum values of r | |
| Position vector r expressed with respect to point A | |
| Position vector of the i-th S joint with respect to the base center | |
| Position vector of the i-th distal joint with respect to the moving platform center | |
| Position vector of the active P joint in the 3SPR mechanism | |
| Lp | Length of each of the pyramid segments |
| Stroke length of the i-th actuator in the 3SPR mechanism | |
| Minimum and maximum values of | |
| L | Constant length of the link connecting the S and U joints in the SU mechanism |
| Unit directional vector of the i-th active P joint in the 3SPR mechanism | |
| Unit directional vector of the R joint in the i-th U joint perpendicular to | |
| Unit directional vector of the R joint in the i-th U joint perpendicular to | |
| Instantaneous twist of the moving platform | |
| Angular velocities of the moving platform with respect to X, Y, and Z axes | |
| Translational velocities of the moving platform in the X, Y, and Z directions | |
| Twist of the actuators | |
| Intensity of the j-th rotational and translational joints in the i-th limb | |
| j-th unit joint screw in the i-th limb | |
| s vector of the j-th unit joint screw in the i-th limb | |
| i-th actuation vector | |
| Forward Jacobian matrix | |
| Inverse Jacobian matrix | |
| Actuation Jacobian matrix | |
| Constraint Jacobian matrix | |
| Overall Jacobian matrix | |
| Maximization objective function | |
| Minimization objective function | |
| Weight of the i-th objective in the weighted sum |
References
- Axinte, D.A.; Allen, J.M.; Anderson, R.; Dane, I.; Uriarte, L.; Olara, A. Free-leg Hexapod: A novel approach of using parallel kinematic platforms for developing miniature machine tools for special purpose operations. CIRP Ann. 2011, 60, 395–398. [Google Scholar] [CrossRef]
- Rushworth, A.; Cobos-Guzman, S.; Axinte, D.A.; Raffles, M. Pre-gait analysis using optimal parameters for a walking machine tool based on a free-leg hexapod structure. Robot. Auton. Syst. 2015, 70, 36–51. [Google Scholar] [CrossRef]
- Olarra, A.; Axinte, D.; Uriarte, L.; Bueno, R. Machining with the WalkingHex: A walking parallel kinematic machine tool for in situ operations. CIRP Ann. 2017, 66, 361–364. [Google Scholar] [CrossRef]
- Chen, J.; Xie, F.; Liu, X.; Bi, W. Stiffness Evaluation of an Adsorption Robot for Large-Scale Structural Parts Processing. ASME J. Mech. Robot. 2021, 13, 040902. [Google Scholar] [CrossRef]
- Tedeschi, F.; Carbone, G. Design Issues for Hexapod Walking Robots. Robotics 2014, 3, 181–206. [Google Scholar] [CrossRef]
- Tedeschi, F.; Carbone, G. Design of a Novel Leg-Wheel Hexapod Walking Robot. Robotics 2017, 6, 40. [Google Scholar] [CrossRef]
- Wang, M.F.; Ceccarelli, M.; Carbone, G. A feasibility study on the design and walking operation of a biped locomotor via dynamic simulation. Front. Mech. Eng. 2016, 11, 144–158. [Google Scholar] [CrossRef]
- Russo, M.; Ceccarelli, M. Kinematic design of a tripod parallel mechanism for robotic legs. In International Workshop on Computational Kinematics; Springer International Publishing: Cham, Switzerland, 2018; pp. 121–130. [Google Scholar]
- Russo, M.; Herrero, S.; Altuzarra, O.; Ceccarelli, M. Kinematic analysis and multi-objective optimization of a 3-UPR parallel mechanism for a robotic leg. Mech. Mach. Theory 2018, 120, 192–202. [Google Scholar] [CrossRef]
- Giewont, S.; Sahin, F. Delta-Quad: An omnidirectional quadruped implementation using parallel jointed leg architecture. In Proceedings of the 12th System of Systems Engineering Conference (SOSE), Waikoloa, HI, USA, 18–21 June 2017; pp. 1–6. [Google Scholar]
- Li, L.; Fang, Y.; Guo, S.; Qu, H.; Wang, L. Type synthesis of a class of novel 3-DOF single-loop parallel leg mechanisms for walking robots. Mech. Mach. Theory 2020, 145, 103695. [Google Scholar] [CrossRef]
- Lin, R.; Guo, W.; Li, M. Novel Design of Legged Mobile Landers With Decoupled Landing and Walking Functions Containing a Rhombus Joint. ASME J. Mech. Robot. 2018, 10, 061017. [Google Scholar] [CrossRef]
- Lin, R.; Guo, W. Creative Design of Legged Mobile Landers With Multi-Loop Chains Based on Truss-Mechanism Transformation Method. ASME J. Mech. Robot. 2021, 13, 011013. [Google Scholar] [CrossRef]
- Yang, H.; Krut, S.; Pierrot, F.; Baradat, C. Locomotion Approach of REMORA: A Reonfigurable Mobile Robot for Manufacturing Applications. IROS: Intelligent Robots and Systems. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 5067–5072. [Google Scholar] [CrossRef][Green Version]
- Figliolini, G.; Rea, P.; Conte, M. Mechanical Design of a Novel Biped Climbing and Walking Robot. In ROMANSY 18 Robot Design, Dynamics and Control; Parenti Castelli, V., Schiehlen, W., Eds.; CISM International Centre for Mechanical Sciences; Springer: Vienna, Austria, 2010; Volume 524. [Google Scholar] [CrossRef]
- Dunlop, G.R. Foot Design for a Large Walking Delta Robot. In Experimental Robotics VIII; Springer Tracts in Advanced, Robotics; Siciliano, B., Dario, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 5. [Google Scholar] [CrossRef]
- Li, R.; Meng, H.; Bai, S.; Yao, Y.; Zhang, J. Stability and Gait Planning of 3-UPU Hexapod Walking Robot. Robotics 2018, 7, 48. [Google Scholar] [CrossRef]
- Brahmia, A.; Kelaiaia, R.; Chemori, A.; Company, O. On Robust Mechanical Design of a PAR2 Delta-Like Parallel Kinematic Manipulator. ASME J. Mech. Robot. 2022, 14, 011001. [Google Scholar] [CrossRef]
- Kelaiaia, R.; Zaatri, A.; Company, O. Multiobjective Optimization of 6-dof UPS Parallel Manipulators. Adv. Robot. 2012, 26, 1885–1913. [Google Scholar] [CrossRef]
- Kelaiaia, R.; Zaatri, A.; Company, O.; Chikh, L. Some investigations into the optimal dimensional synthesis of parallel robots. Int. J. Adv. Manuf. Technol. 2016, 83, 1525–1538. [Google Scholar] [CrossRef]
- Rosyid, A.; El-Khasawneh, B.; Alazzam, A. Genetic and hybrid algorithms for optimization of non-singular 3PRR planar parallel kinematics mechanism for machining application. Robotica 2018, 36, 839–864. [Google Scholar] [CrossRef]
- Rubbert, L.; Charpentier, I.; Henein, S.; Renaud, P. Higher-order continuation method for the rigid-body kinematic design of compliant mechanisms. Precis. Eng. 2017, 50, 455–466. [Google Scholar] [CrossRef][Green Version]




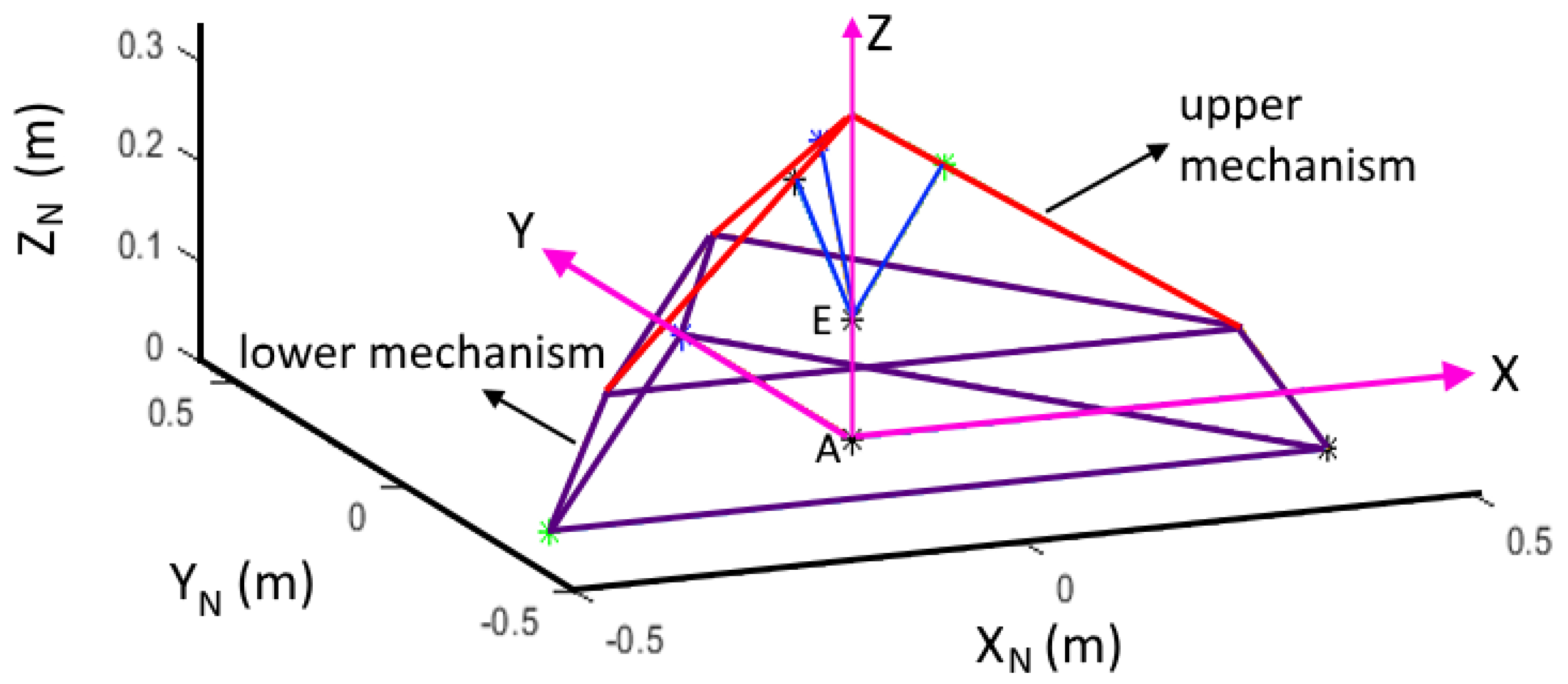
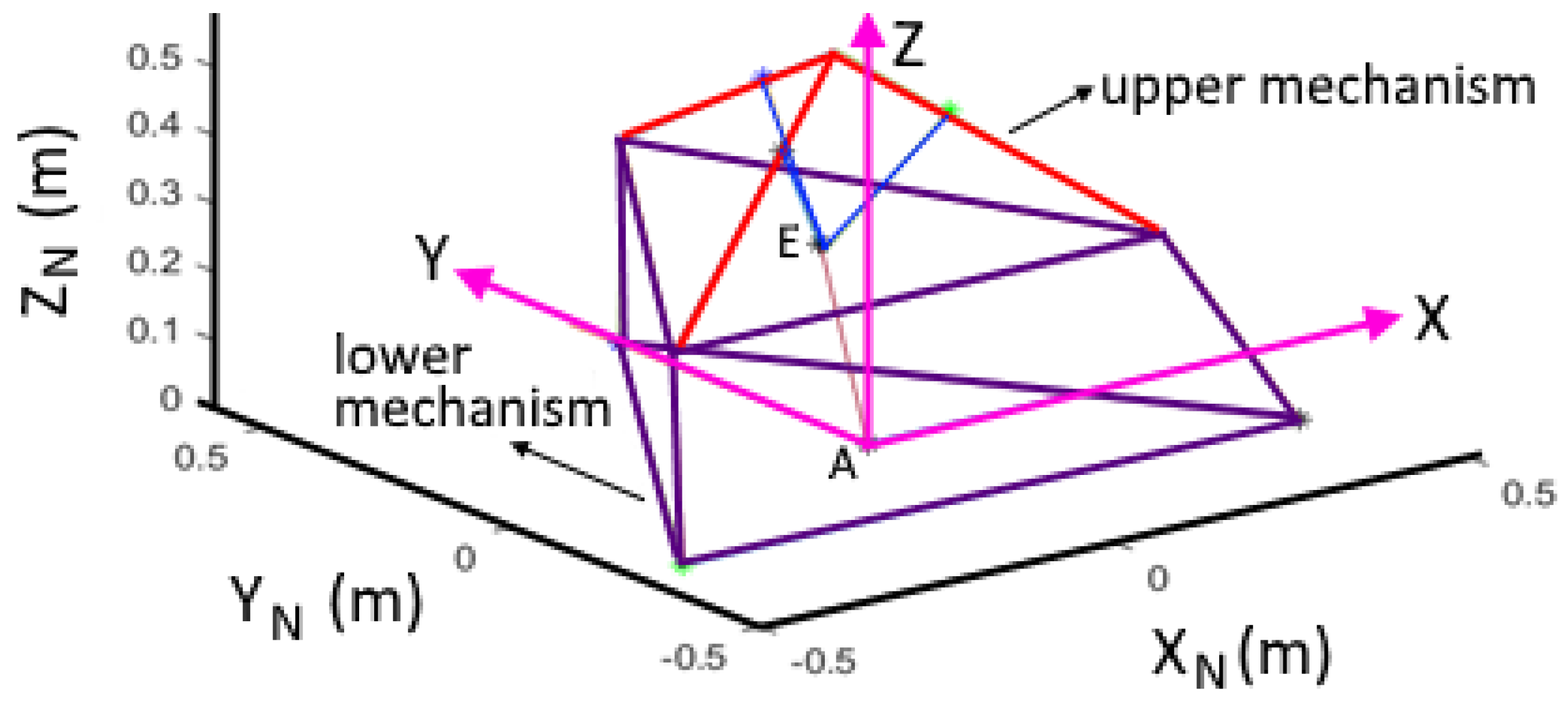





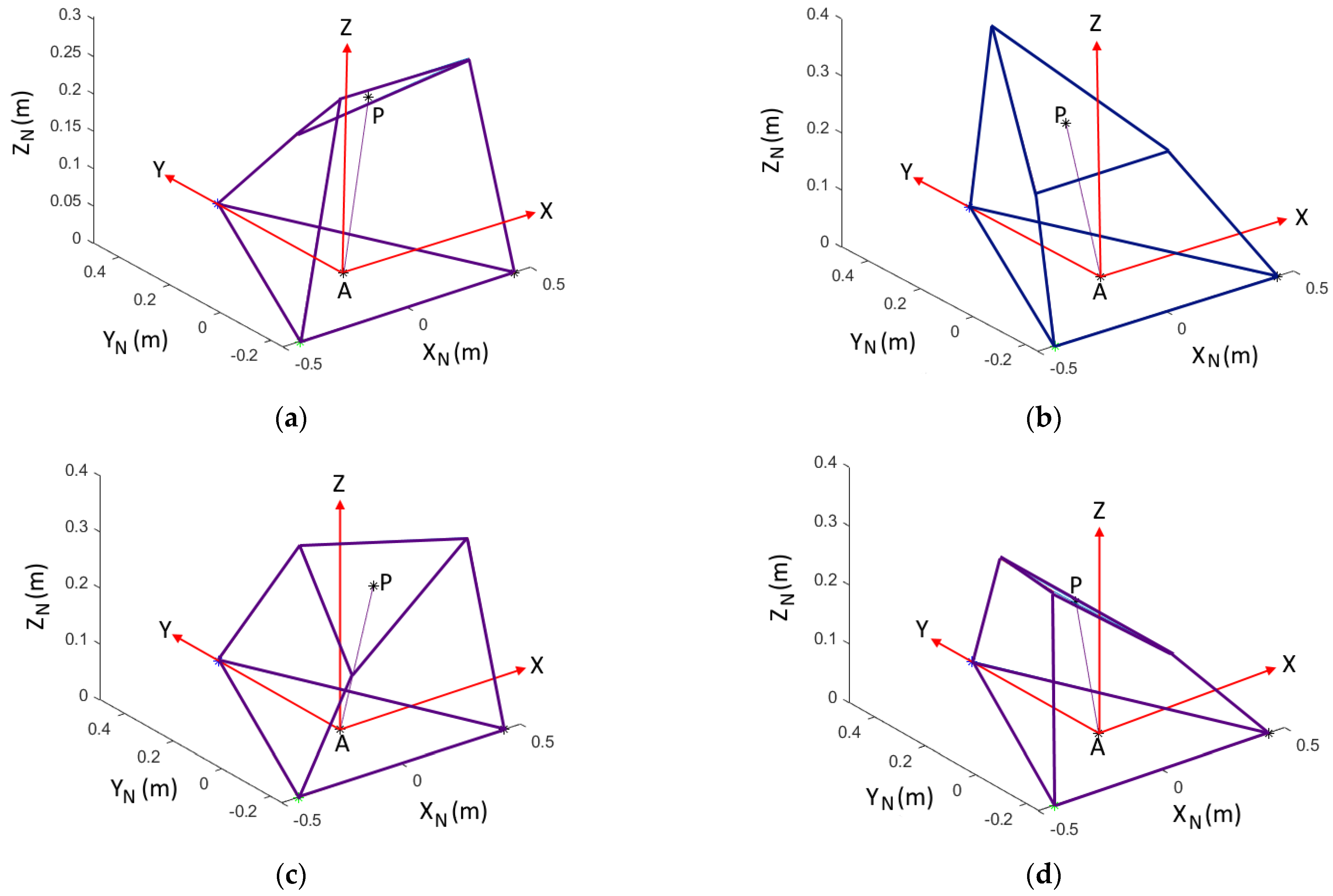
| Mechanism | Actuator Position | End-Effector Pose |
|---|---|---|
| 3SPR-3PRPR | = 0.1667 m L1 = L2 = L3 = 0.3262 m | x = 0, y = 0, z = 0.3000 m = 0 |
| 3SRꞱR-3PRPR | = 0.1667 m = 0, | x = 0, y = 0.0948 m, z = 0.2651 m = 0 |
| 3SRꞱR-3PRPR | = 0.1667 m = 0, | x = 0, y = 0.0948 m, z = 0.2651 m = 0 |
| Parameter | Value |
|---|---|
| Population size | 50 |
| Maximum generations | the number of design variables |
| Creation function | Random initial population satisfying bounds and linear constraints |
| Mutation function | Mutation Adapt Feasible |
| Selection function | Stochastic Uniform |
| Crossover function | CrossoverIntermediate (weighted average of the parents) |
| Crossover fraction | 0.8 |
| Elite count | 3 |
| Function tolerance | |
| Constraint tolerance | |
| Maximum stall generations | 50 |
| Maximum stall time | |
| Maximum time |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosyid, A.; Stefanini, C.; El-Khasawneh, B. A Reconfigurable Parallel Robot for On-Structure Machining of Large Structures. Robotics 2022, 11, 110. https://doi.org/10.3390/robotics11050110
Rosyid A, Stefanini C, El-Khasawneh B. A Reconfigurable Parallel Robot for On-Structure Machining of Large Structures. Robotics. 2022; 11(5):110. https://doi.org/10.3390/robotics11050110
Chicago/Turabian StyleRosyid, Abdur, Cesare Stefanini, and Bashar El-Khasawneh. 2022. "A Reconfigurable Parallel Robot for On-Structure Machining of Large Structures" Robotics 11, no. 5: 110. https://doi.org/10.3390/robotics11050110
APA StyleRosyid, A., Stefanini, C., & El-Khasawneh, B. (2022). A Reconfigurable Parallel Robot for On-Structure Machining of Large Structures. Robotics, 11(5), 110. https://doi.org/10.3390/robotics11050110









