Swarm Crawler Robots Using Lévy Flight for Targets Exploration in Large Environments
Abstract
1. Introduction
2. Related Work
3. Setup for Crawler Robots
4. Lévy Flight
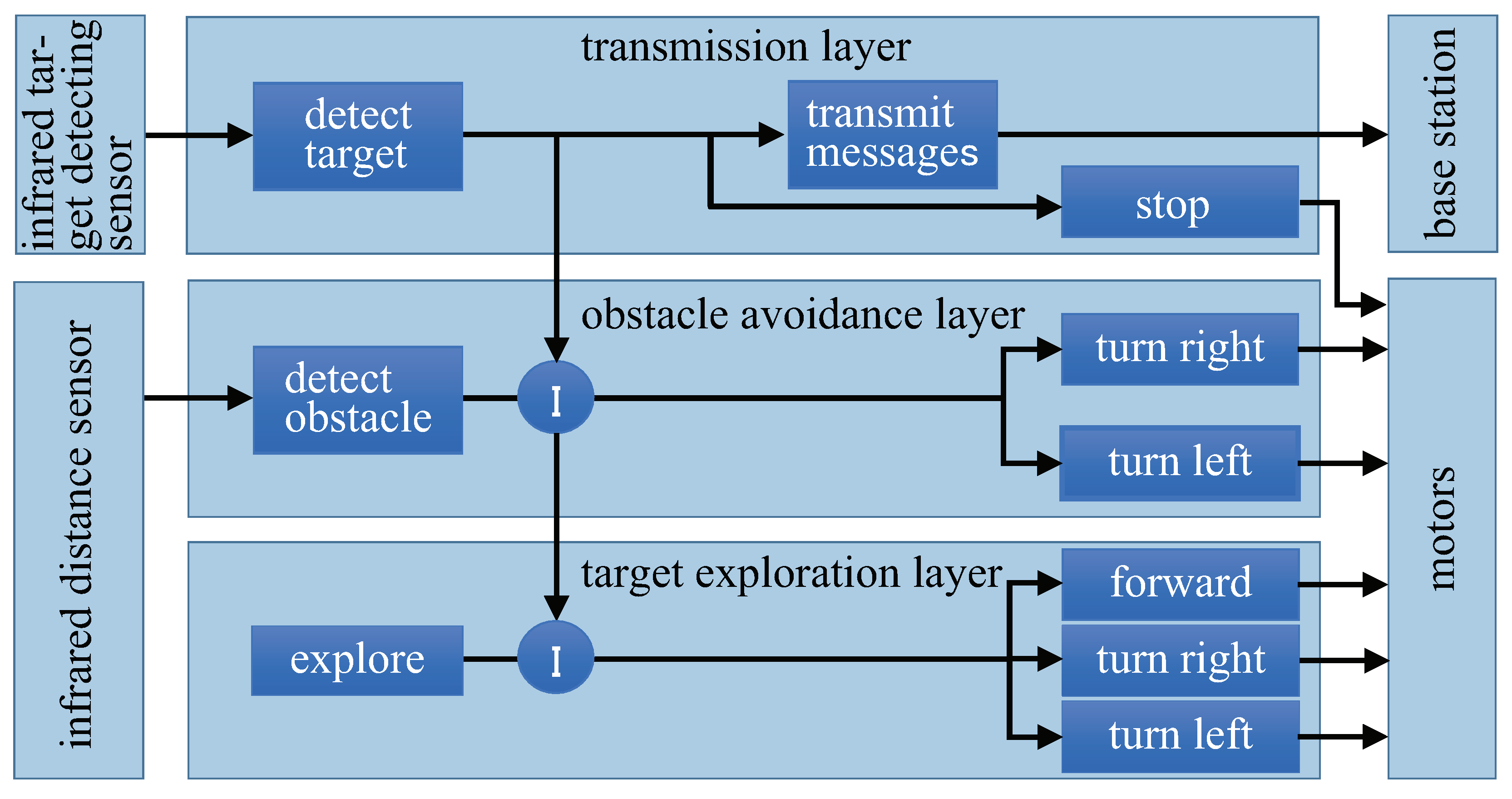
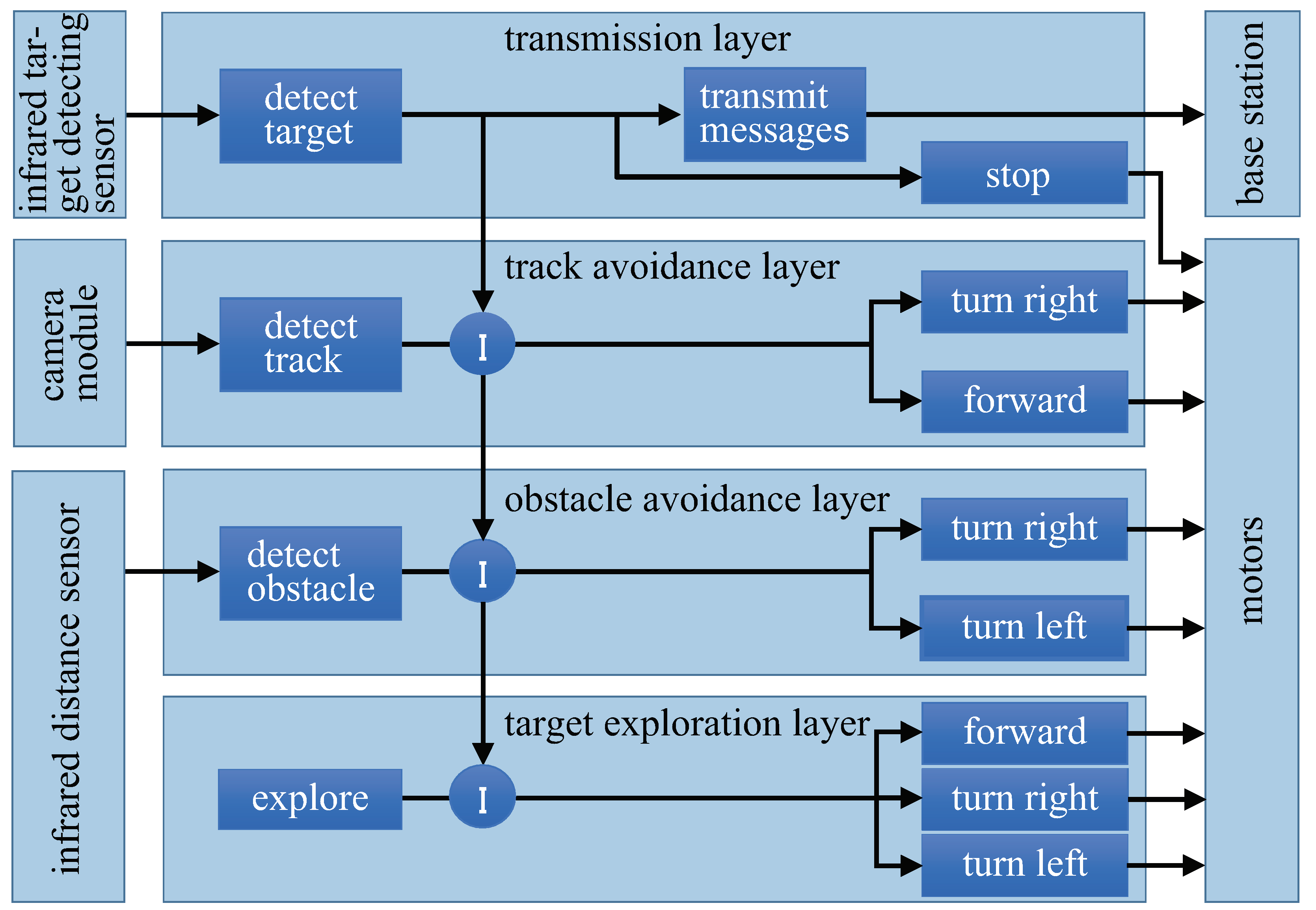
5. Controller
5.1. Subsumption Architecture
5.2. Implementation of a Random Walk in the SSA
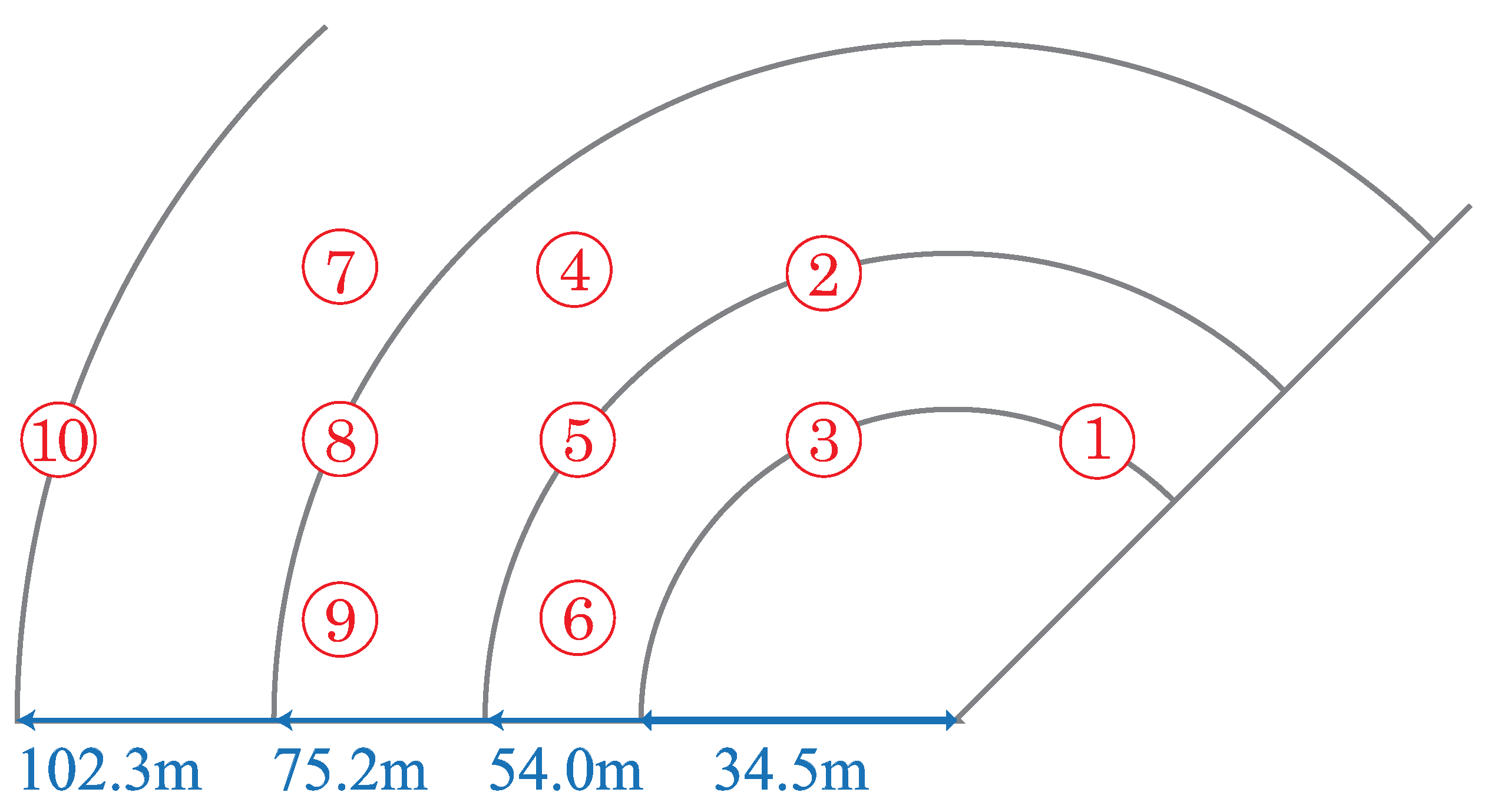
6. Experiment in Indoor Environment
6.1. Experimental Environment
6.2. Setting of the Experiment
6.3. Experimental Results
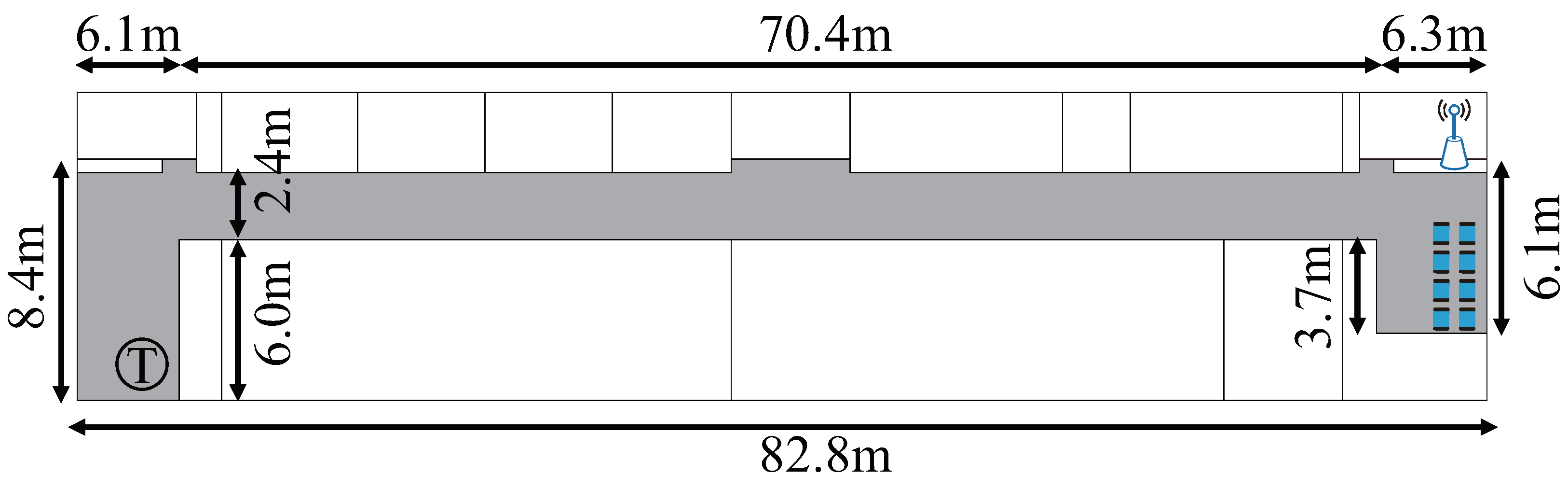
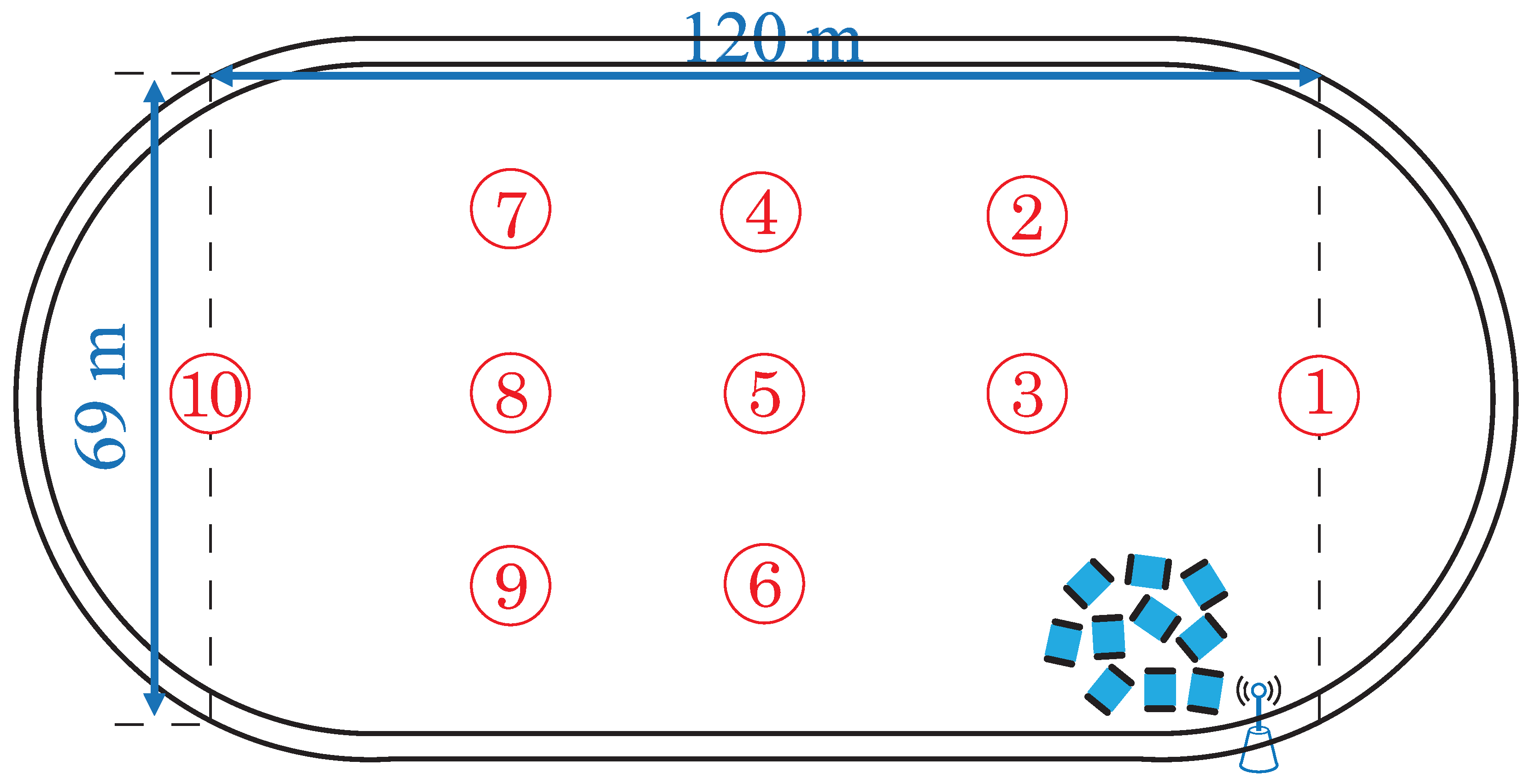
7. Experiment in Outdoor Environment
7.1. Experimental Environment
7.2. SSA for Outdoor Environment
7.3. Setting of the Real Experiment
7.4. Experimental Results
7.5. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SR | Swarm robotics |
| SSA | Subsumption architecture |
| LF | Lévy flight |
| BW | Brownian walk |
| CNN | Convolutional neural networks |
Appendix A. Convolutional Neural Networks
| Training Set | Test Set | ||
|---|---|---|---|
| Error | Classification [%] | Error | Classification [%] |
| 100 | |||
References
- Trianni, V. Evolutionary Swarm Robotics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Brambilla, M.; Ferrante, E.; Birattari, M.; Dorigo, M. Swarm robotics: A review from the swarm engineering perspective. Swarm Intell. 2013, 7, 1–41. [Google Scholar] [CrossRef]
- Hamann, H. Swarm Robotics: A Formal Approach; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Bayindir, L. A review of swarm robotics tasks. Neurocomputing 2016, 172, 292–321. [Google Scholar] [CrossRef]
- Garnier, S.; Jost, C.; Jeanson, R.; Gautrais, J.; Asadpour, M.; Caprari, G.; Theraulaz, G. Aggregation behaviour as a source of collective decision in a group of cockroach-like-robots. In Advances in Artificial Life. ECAL2005, Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3630, pp. 169–178. [Google Scholar]
- Soysal, O.; Bahçeci, E.; Şahin, E. Aggregation in swarm robotic systems: Evolution and probabilistic control. Turk. J. Electr. Eng. Comput. Sci. 2007, 15, 199–225. [Google Scholar]
- Gauci, M.; Chen, J.; Li, W.; Dodd, T.J.; Groß, R. Self-organised aggregation without computation. Int. J. Robot. Res. 2014, 33, 1145–1161. [Google Scholar] [CrossRef]
- Katada, Y. Evolutionary design method of probabilistic finite state machine for swarm robots aggregation. Artif. Life Robot. 2018, 23, 600–608. [Google Scholar] [CrossRef]
- Nouyan, S.; Campo, A.; Dorigo, M. Path formation in a robot swarm–Self-organized strategies to find your way home. Swarm Intell. 2008, 2, 1–23. [Google Scholar] [CrossRef]
- Nouyan, S.; Groß, R.; Bonani, M.; Mondada, F.; Dorigo, M. Teamwork in self-organized robot colonies. IEEE Trans. Evol. Comput. 2009, 13, 695–711. [Google Scholar] [CrossRef]
- Sperati, V.; Trianni, V.; Nolfi, S. Self-organised path formation in a swarm of robots. Swarm Intell. 2011, 5, 97–119. [Google Scholar] [CrossRef]
- Shucker, B.; Murphey, T.; Bennett, J.K. Convergence-preserving switching for topology-dependent decentralized systems. IEEE Trans. Robot. 2007, 24, 1405–1415. [Google Scholar] [CrossRef]
- Groß, R.; Tuci, E.; Dorigo, M.; Bonani, M.; Mondada, F. Object transport by modular robots that self-assemble. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, ICRA 2006, Orlando, FL, USA, 15–19 May 2006; pp. 2558–2564. [Google Scholar]
- Tuci, E.; Groß, R.; Trianni, V.; Mondada, F.; Bonani, M.; Dorigo, M. Cooperation through self-assembly in multi-robot systems. ACM Trans. Auton. Adapt. Syst. 2006, 1, 115–150. [Google Scholar] [CrossRef]
- Labella, T.H.; Dorigo, M.; Deneubourg, J.L. Division of Labor in a group of robots inspired by ants’ foraging behavior. ACM Trans. Auton. Adapt. Syst. 2006, 1, 4–25. [Google Scholar] [CrossRef]
- Ferrante, E.; Turgut, A.E.; Duéñez-Guzmán, E.; Dorigo, M.; Wenseleers, T. Evolution of self-organized task specialization in robot swarms. PLoS Comput. Biol. 2015, 11, e1004273. [Google Scholar] [CrossRef]
- Pini, P.; Brutschy, A.; Frison, M.; Roli, A.; Dorigo, M.; Birattari, M. Task partitioning in swarms of robots: An adaptive method for strategy selection. Swarm Intell. 2011, 5, 283–304. [Google Scholar] [CrossRef]
- Ikemoto, Y.; Miura, T.; Asama, H. Adaptive division-of-labor control algorithm for multi-robot systems. J. Robot. Mechatron. 2019, 22, 514–525. [Google Scholar] [CrossRef]
- Liu, W.; Winfield, A.; Sa, J. A macroscopic probabilistic model of adaptive foraging in swarm robotics systems. In Proceedings of the 6th Vienna International Conference on Mathematical Modelling, Vienna, Austria, 11–13 February 2009. [Google Scholar]
- Ducatelle, F.; Di Caro, G.A.; Pinciroli, C.; Mondada, F.; Gambardella, L.M. Communication assisted navigation in robotic swarms: Self-organization and cooperation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2011), San Francisco, CA, USA, 25–30 September 2011; pp. 4981–4988. [Google Scholar]
- Şahin, E. Swarm robotics: From sources of inspiration to domains of application. Lect. Notes Comput. Sci. 2005, 3342, 10–20. [Google Scholar]
- Li, J.; Andrew, L.L.; Foh, C.H.; Zukerman, M.; Chen, H.H. Connectivity, coverage and placement in wireless sensor networks. Sensors 2009, 9, 7664–7693. [Google Scholar] [CrossRef]
- Ghosha, A.; Das, S.K. Coverage and connectivity issues in wireless sensor networks: A survey. Pervasive Mob. Comput. 2008, 4, 303–334. [Google Scholar] [CrossRef]
- Katada, Y. Connectivity of swarm robot networks for communication range and the number of robots based on percolation theory. In Proceedings of the 2014 IEEE/SICE International Symposium on System Integration, Tokyo, Japan, 13–15 December 2014; pp. 93–98. [Google Scholar]
- Katada, Y.; Nishiguchi, A.; Moriwaki, K.; Watakabe, R. Swarm robotic network using Lévy flight in target detection problem. Artif. Life Robot. 2016, 21, 295–301. [Google Scholar] [CrossRef]
- Lévy, P. Theorie de L’addition des Veriables Aleatoires; Gauthier-Villars: Paris, France, 1937. [Google Scholar]
- Katada, Y.; Yamashita, K. Swarm robots using Lévy walk based on nonlinear dynamics for targets exploration. Artif. Life Robot. 2022, 27, 226–235. [Google Scholar] [CrossRef]
- Viswanathan, G.M.; Afanasyev, V.; Buldyrev, S.V.; Murphy, E.J.; Prince, P.A.; Stanley, H.E. Lévy flight search patterns of wandering albatrosses. Nature 1996, 381, 413–415. [Google Scholar] [CrossRef]
- Humphries, N.E.; Queiroz, N.; Dyer, J.R.M.; Pade, N.G.; Musyl, M.K.; Schaefer, K.M.; Fuller, D.W.; Brunnschweiler, J.M.; Doyle, T.K.; Houghton, J.D.R.; et al. Environmental Context Explains Lévy and Brownian Movement Patterns of Marine Predators. Nature 2010, 465, 1066–1069. [Google Scholar] [CrossRef]
- Nurzaman, S.G.; Matsumoto, Y.; Nakamura, Y.; Shirai, K.; Koizumi, S.; Ishiguro, H. From Lévy to Brownian: A Computational Model Based on Biological Fluctuation. PLoS ONE 2011, 6, e16168. [Google Scholar] [CrossRef]
- Humphries, N.E.; Weimerskirch, H.; Queiroz, N.; Southall, E.J.; Sims, D.W. Foraging success of biological Lévy flights recorded in situ. Proc. Natl. Acad. Sci. USA 2012, 9, 7169–7174. [Google Scholar] [CrossRef] [PubMed]
- López-López, P.; Benavent-Corai, J.; García-Ripollés, C.; Urios, V. Scavengers on the move: Behavioural changes in foraging search patterns during the annual cycle. PLoS ONE 2013, 8, e54352. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sakiyama, T.; Gunji, Y.P. Emergence of an optimal search strategy from a simple random walk. J. R. Soc. Interface 2013, 10. [Google Scholar] [CrossRef] [PubMed]
- Miramontes, O. Lévy flights and self-similar exploratory behaviour of termite workers: Beyond model fitting. PLoS ONE 2014, 9, e111183. [Google Scholar] [CrossRef] [PubMed]
- Murakami, H.; Niizato, T.; Tomaru, T.; Nishiyama, Y.; Gunji, Y.P. Inherent noise appears as a Lévy walk in fish schools. Sci. Rep. 2015, 5, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Khaluf, Y.; Havermaet, S.V.; Simoens, P. Collective Lévy walk for efficient exploration in unknown environments. In Artificial Intelligence: Methodology, Systems, and Applications, Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2018; Volume 11089. [Google Scholar]
- Nauta, J.; Havermaet, S.V.; Simoens, P.; Khaluf, Y. Enhanced foraging in robot swarms using collective Léevy walks. In Proceedings of the 24th European Conference on Artificial Intelligence-ECAI, Santiago de Compostela, Spain, 29 August–8 September 2020. [Google Scholar]
- Fricke, G.M.; Asperti-Boursin, F.; Hecker, J.; Cannon, J.; Moses, M. From Microbiology to Microcontrollers: Robot Search Patterns Inspired by T Cell Movement. In Proceedings of the ECAL 2013: The Twelfth European Conference on Artificial Life, Sicily, Italy, 2–6 September 2013; pp. 1009–1016. [Google Scholar]
- Koyama, H.; Namatame, A. Comparison of efficiency of random walk based search and Levy flight search. Inf. Process. Soc. Jpn. Tech. Rep. 2008, 20, 19–24. (In Japanese) [Google Scholar]
- Nurzaman, S.G.; Matsumoto, Y.; Nakamura, Y.; Shirai, K.; Koizumi, S.; Ishiguro, H. An adaptive switching behavior between Levy and Brownian random search in a mobile robot based on biological fluctuation. In Proceedings of the International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 1927–1934. [Google Scholar]
- Fujisawa., R.; Dobata, S. Lévy walk enhances efficiency of group foraging in pheromone-communicating swarm robots. In Proceedings of the 2013 IEEE/SICE International Symposium on System Integration, Kobe, Japan, 15–17 December 2013; pp. 808–813. [Google Scholar]
- Pang, B.; Song, Y.; Zhang, C.; Wang, H.; Yang, R. A swarm robotic exploration strategy based on an improved random walk method. J. Robot. 2019, 2019, 6914212. [Google Scholar] [CrossRef]
- Sardinha, H.; Dragone, M.; Vargas, P.A. Combining Lévy walks and flocking for cooperative surveillance using aerial swarms. In Multi-Agent Systems and Agreement Technologies, Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12520, pp. 226–242. [Google Scholar]
- Cao, M.-L.; Meng, Q.-H.; Luo, B.; Zeng, M. Experimental comparison of random search strategies for multi-robot based odour finding without wind information. Austrian Contrib. Vet. Epidemiol. 2015, 8, 43–50. [Google Scholar]
- Keeter, M.; Moore, D.; Muller, R.; Nieters, E.; Flenner, J.; Martonosi, S.E.; Bertozzi, A.L.; Percus, A.G.; Levy, R. Cooperative search with autonomous vehicles in a 3D aquatic testbed. In Proceedings of the American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 3154–3160. [Google Scholar]
- Sutantyo, D.; Levi, P.; Möslinger, C.; Read, M. Collective-adaptive Lévy flight for underwater multi-robot exploration. In Proceedings of the 2013 IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 4–7 August 2013; pp. 456–462. [Google Scholar]
- XBee, Digi International Inc. Available online: https://www.digi.com/products/models/xbp24bz7pit-004 (accessed on 10 June 2022).
- Robocupjunior Soccer Rules 2014. Available online: https://junior.robocup.org/wp-content/uploads/2014Rules/soccer_2014.pdf (accessed on 10 June 2022).
- Lee, C.Y.; Yao, X. Evolutionary programming using mutations based on the Lévy probability distribution. IEEE Trans. Evol. Comput. 2004, 8, 1–13. [Google Scholar] [CrossRef]
- Katada, Y. Swarm robotic network using Lévy flight for exploration–computer simulation for sweeping. Trans. Soc. Instrum. Control. Eng. 2018, 54, 22–30. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Brooks, R.A. A robust layered control system for a mobile robot. IEEE J. Robot. Autom. 1986, 2, 14–23. [Google Scholar] [CrossRef]
- Brooks, R.A. A Robot that Walks; Emergent Behaviors from a Carefully Evolved Network. Neural Comput. 1989, 1, 253–262. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet classification with deep convolutional neural networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 3–6 December 2012; Volume 1, pp. 1097–1105. [Google Scholar]








| Trial | Time [s] | Trial | Time [s] | Trial | Time [s] |
|---|---|---|---|---|---|
| No.1 | 953 | No.8 | 1530 | No.15 | 644 |
| No.2 | 833 | No.9 | 663 | No.16 | 808 |
| No.3 | 832 | No.10 | 648 | No.17 | 771 |
| No.4 | 557 | No.11 | 1209 | No.18 | 210 |
| No.5 | 956 | No.12 | 547 | No.19 | 729 |
| No.6 | 916 | No.13 | 868 | No.20 | 471 |
| No.7 | 915 | No.14 | 865 | average | 796 |
| Trial | Time [s] | Trial | Time [s] | Trial | Time [s] |
|---|---|---|---|---|---|
| No.1 | 1800 | No.8 | 1800 | No.15 | 1800 |
| No.2 | 1800 | No.9 | 1800 | No.16 | 1800 |
| No.3 | 1800 | No.10 | 1800 | No.17 | 1800 |
| No.4 | 1800 | No.11 | 1800 | No.18 | 1800 |
| No.5 | 1800 | No.12 | 1800 | No.19 | 1800 |
| No.6 | 1800 | No.13 | 1800 | No.20 | 1800 |
| No.7 | 1800 | No.14 | 1800 | average | 1800 |
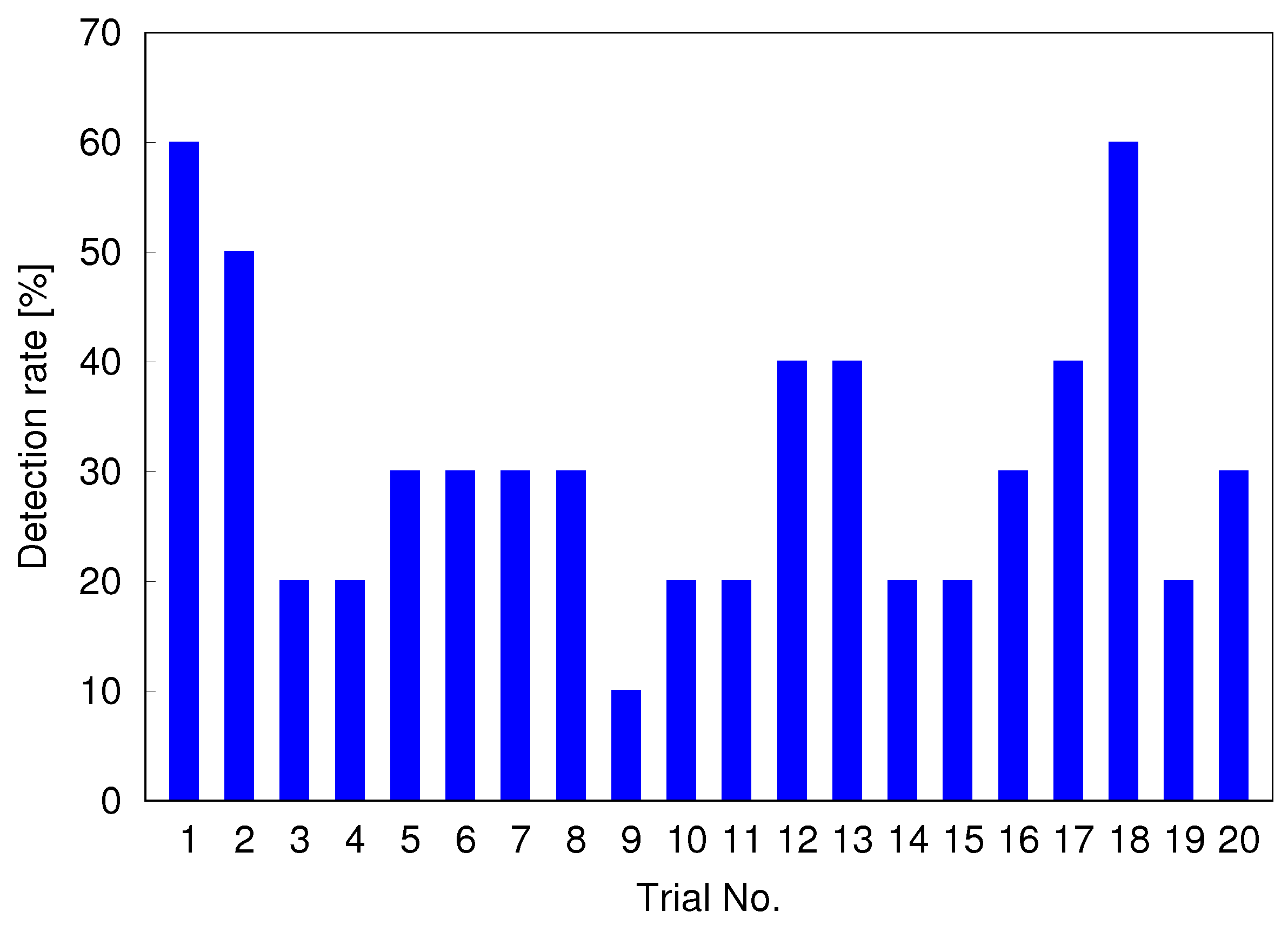
| Trial | Target No. | Detection Rate [%] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ➀ | ➁ | ➂ | ➃ | ➄ | ➅ | ➆ | ➇ | ➈ | ➉ | ||
| No.1 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | 60 | ||||
| No.2 | ∘ | ∘ | ∘ | ∘ | ∘ | 50 | |||||
| No.3 | ∘ | ∘ | 20 | ||||||||
| No.4 | ∘ | ∘ | 20 | ||||||||
| No.5 | ∘ | ∘ | ∘ | 30 | |||||||
| No.6 | ∘ | ∘ | ∘ | 30 | |||||||
| No.7 | ∘ | ∘ | ∘ | 30 | |||||||
| No.8 | ∘ | ∘ | ∘ | 30 | |||||||
| No.9 | ∘ | 10 | |||||||||
| No.10 | ∘ | ∘ | 20 | ||||||||
| No.11 | ∘ | ∘ | 20 | ||||||||
| No.12 | ∘ | ∘ | ∘ | ∘ | 40 | ||||||
| No.13 | ∘ | ∘ | ∘ | ∘ | 40 | ||||||
| No.14 | ∘ | ∘ | 20 | ||||||||
| No.15 | ∘ | ∘ | 20 | ||||||||
| No.16 | ∘ | ∘ | ∘ | 30 | |||||||
| No.17 | ∘ | ∘ | ∘ | ∘ | 40 | ||||||
| No.18 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | 60 | ||||
| No.19 | ∘ | ∘ | 20 | ||||||||
| No.20 | ∘ | ∘ | ∘ | 30 | |||||||
| detection rate [%] | 65 | 20 | 50 | 25 | 60 | 10 | 5 | 40 | 10 | 25 | 31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katada, Y.; Hasegawa, S.; Yamashita, K.; Okazaki, N.; Ohkura, K. Swarm Crawler Robots Using Lévy Flight for Targets Exploration in Large Environments. Robotics 2022, 11, 76. https://doi.org/10.3390/robotics11040076
Katada Y, Hasegawa S, Yamashita K, Okazaki N, Ohkura K. Swarm Crawler Robots Using Lévy Flight for Targets Exploration in Large Environments. Robotics. 2022; 11(4):76. https://doi.org/10.3390/robotics11040076
Chicago/Turabian StyleKatada, Yoshiaki, Sho Hasegawa, Kaito Yamashita, Naoki Okazaki, and Kazuhiro Ohkura. 2022. "Swarm Crawler Robots Using Lévy Flight for Targets Exploration in Large Environments" Robotics 11, no. 4: 76. https://doi.org/10.3390/robotics11040076
APA StyleKatada, Y., Hasegawa, S., Yamashita, K., Okazaki, N., & Ohkura, K. (2022). Swarm Crawler Robots Using Lévy Flight for Targets Exploration in Large Environments. Robotics, 11(4), 76. https://doi.org/10.3390/robotics11040076






